Accurate single-sequence prediction of solvent accessible surface area using local and global features

Abstract

We present a new approach for predicting the Accessible Surface Area (ASA) using a General Neural Network (GENN). The novelty of the new approach lies in not using residue mutation profiles generated by multiple sequence alignments as descriptive inputs. Instead we use solely sequential window information and global features such as single-residue and two-residue compositions of the chain. The resulting predictor is both highly more efficient than sequence alignment based predictors and of comparable accuracy to them. Introduction of the global inputs significantly helps achieve this comparable accuracy. The predictor, termed ASAquick, is tested on predicting the ASA of globular proteins and found to perform similarly well for so-called easy and hard cases indicating generalizability and possible usability for de-novo protein structure prediction. The source code and a Linux executables for GENN and ASAquick are available from Research and Information Systems at http://mamiris.com, from the SPARKS Lab at http://sparks-lab.org, and from the Battelle Center for Mathematical Medicine at http://mathmed.org.

1 Introduction

Proteins perform their functions mostly through interactions on their solvent exposed surface. A given residue along the protein chain can be surrounded by other residues in the chain or have a part of it accessible to the solvent housing the protein or to other interactions external to its own protein chain. The parameter associated with this quality of a residue is the accessible surface area (ASA) [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]. Specifically, the ASA is defined as the surface area of a protein that is accessible to a solvent and is given here in units of square Angstroms. First described by Lee and Richards [12] ASA is typically calculated using the ‘rolling ball’ algorithm [13, 14]. In this approach a computational ball is rolled on the surface of the protein coordinates and probes for which and how much of the residues are accessible, i.e., in contact with the ball. Recently Klenin et al. introduced a fast analytical method to calculate the ASA using power diagrams [15]. Other efforts in characterizing the surface of proteins were also carried out [16, 17, 18, 19, 20, 21, 22]. Since the ASA describes the amount of surface a given residue has that is accessible to the solvent or for other intermolecular interactions, it is easy to understand why the ASA is important for recognizing functional sites along the chain [23]. Accessibility is a prerequisite for a residue to be involved in external interactions. Hence knowledge of the solvent exposed residues along the residue chain of the protein can facilitate various approaches associated with function prediction and targeted mutations.

State of the art methods that were developed for the prediction of ASA have followed in the footsteps of approaches to similar problems such as prediction of secondary structure. Like there, they have relied on position specific sequence mutation profiles also known as a Position Specific Scoring Matrix (PSSM) generated from multiple sequence alignments. The benefit of using such an approach is that it allows a sequence based connection between members of protein super-families and to some extent protein folds which typically have similar structure but have varying degrees of sequence dissimilarity. Indeed, incorporation of PSSM to secondary structure prediction has raised its accuracy by over 10% [24, 25, 26, 27, 10].

The topic of ASA prediction has been well documented in many publications [1, 28, 29, 30, 31, 32, 33, 34, 35, 36, 2, 3, 6, 37]. As we mentioned the ASA captures how much of the surroundings of a residue are occupied by other parts of the chain and how much is accessible to the solvent or to other interactions external to the chain. For this reason the ASA has proved important in understanding and predicting those sites in the protein that are involved in interactions. A given site may change its ASA due to protein intrinsic flexibility. Unfortunately the science of protein structure dynamics and function are not so evolved and the ASA is usually obtained from rigid chain structures obtained from either X-ray or NMR studies. We shall continue this approach here.

Due to the importance of profiles in prediction, their use may lead to a washout of other, weaker, input signals, such as the single sequence pattern of the particular protein. In other words, the optimization of the model parameters may be biased to accommodate their strong signal. An example of this can be understood as follows. Profiles are calculated over similar sequences, creating the same or very similar signature to all those similar sequences. Since these in general also have similar structure, if the structure of one or several of them is known then we have established a relationship between sequence and structure that can be trained on. However, the most challenging and interesting cases are exactly those for which such information is missing. That is, we may be needlessly burdening our predictors if we use profile information in cases where it is not attached to a structure during its training. An additional reason for considering not using profiles is that profiles are obtained through alignments at the chain level, hence they are most useful connecting between structures on the chain level. Their abandonment allows for a machine learner to focus instead on sequence fragments. Since these fragments are typically considerably smaller than the chain length, issues associated with sequence similarity can be relatively better alleviated.

Furthermore, profiles are computationally very expensive since they require sequence alignments with an ever growing sequence database. A prediction method that can do without them is bound to be computationally faster. With the increasing number of fully sequenced genomes and with advances in personalized medicine based on the unique genetic code of individual patients, it is becoming necessary to produce accurate and fast proteome predictions for a given genome. This ability is an added benefit resulting from the approach we propose. We shall start off describing the neural network that was used to produce our ASA predictor. This same program was also used to produce Seder [38] and can be used to create various other predictors [39]. We shall then describe the ASA predictor and as we shall see, it reduces the time necessary for predictions by close to three orders of magnitude while maintaining reasonable accuracy. We term this predictor ASAquick (accessible surface area quick).

2 Materials and Methods

We use GENN (GEneral Neural Network) [39] for setting up the accessible surface area predictor. GENN was programmed in FORTRAN 90 and is constructed out of several subroutines that process the data, initialize the model, and train it. It is also capable of producing predictions from existing single models or producing ensemble predictions with expected deviations. Its execution is terminal based. It was built on Ubuntu Linux, under the BASH environment. We used the window-based part of GENN.

We predict consecutively the ASA for all residues. Due to the increasing amount of sequenced genetic data and to enable the possibility of fast structural/functional prediction we aim here to design a fast ASA predictor. To achieve this we remove the multiple sequence alignment profile which is the slowest part of the common predictor. Instead we use sequence information alone. We represent the sequence in several ways. For a given residue we include a set number of its neighbors (window) and represent the residue types with a constant length vector according to the BLOSUM62 substitution matrix representation of residues and with physicochemical parameters [3, 6]. The first representation allows for some information on the mutations between residues while the second captures some of the chemical properties of the molecules involved.

The first task is to prepare the knowledge from which to learn. Since we do not use multiple sequence alignment profiles there is less information sharing between sequentially similar chains. Hence, we have less of a problem of over-training. Potentially one may consider then that a more inclusive representation of the entire PDB [40] will facilitate learning from as many separate instances and will improve the overall prediction accuracy. This is indeed strongly suspected and is the topic of future work. For our case here, to maintain a reasonable comparison with previous methods we use a PISCES list [41, 42] of non-homologous protein chains with resolution better than 3 Angstrom and sequence identity lower than 40%. Structure files were downloaded for these chains from the PDB. This non-redundant set was 14361 proteins in size. A concern may arise here that we are using a higher sequence identity for clustering than is done in the training of most profile based predictors. One should realize that the common value of 25% sequence identity comes about in an attempt to eliminate redundancy in the training sets. Since proteins with sequence identity greater than 25% produce similar PSSMs. Hence, using more than one such sequence would mean a degenerate training example. However, ASAquick is trained at the sequence level. At this level, training examples are unique at 40% sequence identity.

For each residue in these chains we calculate the ASA using the DSSP program [43]. We then find the residue-type-dependent minimum and maximum values and use these to linearly normalize the ASA to get the Relative Solvent Accessible Area (RASA) between -1 (completely buried) and 1 (completely exposed). This scale choice was motivated by the inherent bipolarity of the neural network we use; a decision that is based on our previous work in this field [44, 6]. When searching for the maximum ASA we arbitrarily ignore the largest 1% of values. This is done to allow for exceptional behavior and various mishaps. These RASA values are the target output for GENN, and can be transformed back to their corresponding ASA values.

It is worth mentioning that we also attempted a z-score type normalization of the ASA. We shall refer to the normalization described in the previous paragraph as minimum-maximum normalization. We have found that comparisons between ASA and RASA accuracies can vary considerably. For RASA it was found that minimum-maximum normalization produced superior predictions. However, it was interesting and instructive to find that upon transformation to ASA values both normalization techniques yielded essentially the same MAE (mean absolute error) and correlation. Hence it would be beneficial for future studies to report their accuracies for ASA values. We take this approach here.

As mentioned previously, inputs for ASAquick were chosen with speed in mind. Hence, no alignment profiles were used. Instead, each residue type is represented by seven parameters characterizing their physicochemical properties, and by 20 parameters related to residue mutation probabilities taken from the BLOSUM62 matrix [45, 46, 47]. For a given residue we use a window of neighboring residues as inputs, capturing the local sequential environment of the residue. We also use the following global parameters: the length of the chain divided by 1000, the residue type composition of the whole chain (25 values), and the directional two-residue composition (625 values). We have 25 residue types because we allow for the various characters reported by DSSP, these include atypical residues, unknowns and chain gaps in the structure file. The output and each of the local inputs is stored in a separate file in a directory named for that chain. The global inputs are all stored in a single file in the same directory. Refer to the example provided with the distribution of GENN [39] for further information.

The parameters of the neural network were optimized using the following approach. First we tested various values for the hidden layer size and settled on a size of 31 nodes per hidden layer as a balance between speed, generalizability, and over-training avoidance. We then tested the dependence of the accuracy on the input window size. We also used this data to analyze the benefit of each of the input parameters.

3 results

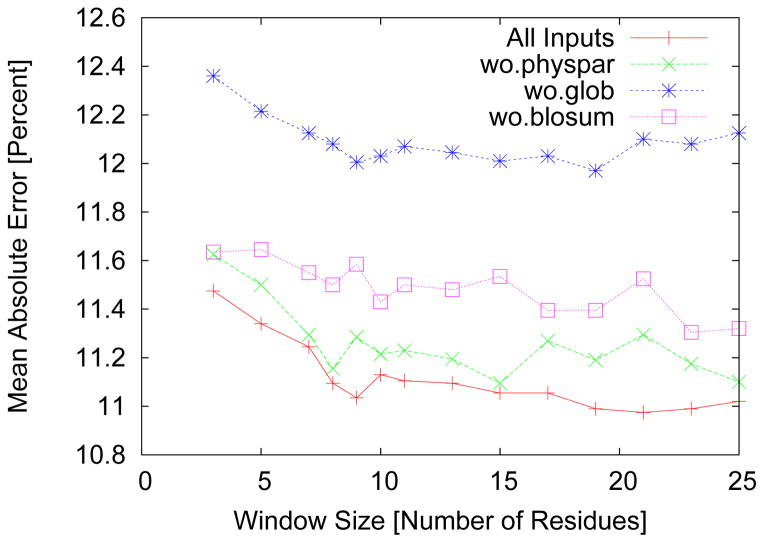
In Fig. 1 we give the accuracy as a function of window size for all inputs and with each of the parameters removed. We see that removing the global inputs reduces the accuracy the most. Following in order are the BLOSUM62 representation and physical parameters. All these results were found to be consistent across all window sizes. It should also be noted that the physical parameters seem to stabilize the fluctuations in accuracy for variations in window size. In fact, at the optimally chosen window size of 21 residues the physical parameters improve the accuracy by the most significant margin. We have also tried using an output window by predicting several residues together and taking an average over all the predictions for a given residue. This approach failed to improve the results but rather decreased the accuracy slightly (results not shown). Optimization was also carried out on the learning rate using a grid search. The optimal rate was found to be 0.001. Of major concern is the averaging over instances of prediction and an efficient use of this method. We have found, in agreement for previous studies, that five neural network instances produce good results.

Figure 1.

The mean absolute error in percent for predicting the normalized accessible surface area as a function of the input window size used to train the neural network. The best accuracy is achieved with all inputs at a window size of 21. In addition we remove each input and test the accuracy of the resulting server on the same independent test set. We see that removal of global features reduces the accuracy the most, indicating their significance.

We use two different datasets to test the accuracy of our prediction. In the first test we partition our non-redundant set with 14361 proteins in two parts. The first contains 5000 proteins and is used to train different neural network instances with different inputs as described below. We also use a subset of this first set for setting aside an over-protection set. The second partition contains 9361 and we use this set only to test the accuracy of prediction. We have found that inclusions of more proteins in the training set was beneficial.

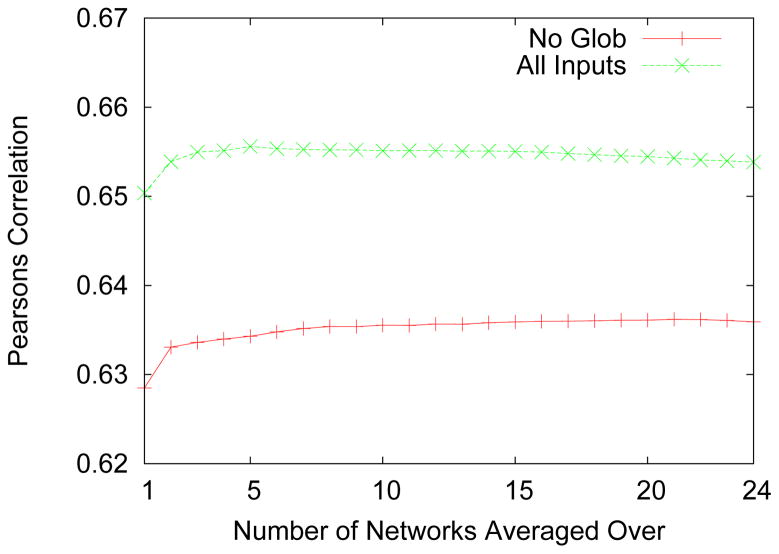
We started out with only the local inputs (physicochemical parameters and BLOSUM62 representation) with the above mentioned randomly chosen subset of 5000 proteins to train the network to predict the RASA and extracted the ASA from them. We use the Pearson’s correlation coefficient to measure the accuracy. It is important to note that these correlations are between the ASA and not RASA. A following round of training was performed using the same 5000 proteins but this time including the global inputs. We see that for pure sequence predictions (no profile) inclusion of global features improve the accuracy of prediction. This beneficial effect of inclusion of global features seemed lost when designing profile-based predictors [6, 48]. In general we found that the benefit of averaging plateaus at around five neural networks if global input features are used. We also ranked the weights according to their accuracy on the over fit protection set and progressively added the best neural networks to the ensemble. We found that in this case too an average of around five neural networks reaches a similar maximum accuracy. In Fig. 2 we summarize these results. It is interesting to note that using global features not only improves the prediction accuracy but also allows the accuracy to reach a peak after a relatively small number of networks (around five). In contrast, the predictor without global features seems to have not peaked even after 24 networks.

Figure 2.

The Pearson’s correlation coefficient for predicting the accessible surface area as a function of the number of neural network instances on which an average is taken. We test again the effect of removal of the global features and find similar results to before. Results were obtained on an independent test set as described in the text. Note that global features allow also for the accuracy to reach a peak after a relatively small number of networks (around 5). In contrast, without global features the networks do not peak even after 24 instances. Note that these correlations are for the ASA values and not normalized ASA.

4 Discussion

We conducted further testing on the CASP10 [49] set of structure prediction targets. The Critical Assessment of Protein Structure Prediction (CASP) is a biennial community-wide experiment involving protein structure prediction groups from around the world. Newly solved protein structures are collected from crystallographers and made available for blind predictions to assess accuracy of computational prediction methods before protein coordinates are publicly released. Usually around 200 protein structure prediction groups including both humans and automatic prediction servers participate in CASP. This approach enables to objectively test a variety of protein structure prediction methods, and assess the progress in development of prediction methodologies. It is interesting to note that a computational sibling of ASAquick, SEDER, which is also based on the GENN package, and was designed to discriminate between structures based on their similarity to the native conformation performed extremely well in recent CASP. According to the official statistics of group performance in CASP10 for top model prediction for all targets http://predictioncenter.org/casp10/groups_analysis.cgi and for the most difficult to model template-free (hard) targets http://predictioncenter.org/casp10/groups_analysis.cgi?type=all&fm=on&submit=FilterSEDER (Kloczkowski Lab) was the only method to rank at the top in both categories. More on this successful application of GENN will be discussed in a separate publication.

With regards to ASAquick, we developed the prediction server based on the optimizations described above. This server along with the GENN package is available from http://mamiris.com, http://sparks-lab.org/, and http://mathmed.org. We then used ASAquick server to predict the ASA for all of the CASP10 targets. For comparing ASAquick, which is a purely sequence based predictor (no profile) to profile based prediction, we also use SPINE-X [48, 10] to predict the ASA. SPINE-X has been repeatedly found to be among the top predictors of ASA available [8]. We find that ASAquick with only the local input features (physpar and blosnorm) achieves a correlation coefficient of 0.63. Inclusion of global features increases this correlation to 0.66. Hence, we see that with a pure sequence-based prediction one can reach a correlation approaching 0.7. Application of SPINE-X (that uses computationally costly multiple sequence alignments) to the same dataset found a correlation coefficient of 0.71. We see that while predictions are still slightly better with profile information that gap is closing and purely sequence-based prediction is about 5% worse than with profile. Further work is currently underway to improve this accuracy. As this work showed, inclusion of global input features improved the accuracy by a relative 5%.

Among the proteins in the CASP competition one subset of proteins are known as “hard targets”. By this it is meant that no sequence homologs with solved structure exist for these targets. In turn this means that for hard targets, the multiple alignments profile does not necessary lead to a better prediction as compared to pure sequence-based prediction. Unlike homology-based modeling which typically produces good results, currently there is no method to reasonably (with a good accuracy) predict the structural properties of hard targets. For the hard targets in CASP10 we find that the ASAquick correlation for ASA prediction is 0.66, slightly better than for prediction for all targets (accuracy improves in third digit). On the other hand, applying SPINE-X to this set of hard targets results in a considerable reduction in accuracy as compared to the general population. SPINE-X prediction for hard targets in CASP10 reach a correlation coefficient of only 0.68. The difference between sequence-based and profile-based predictions are almost completely erased when considering proteins with no experimentally solved structures of homologs.

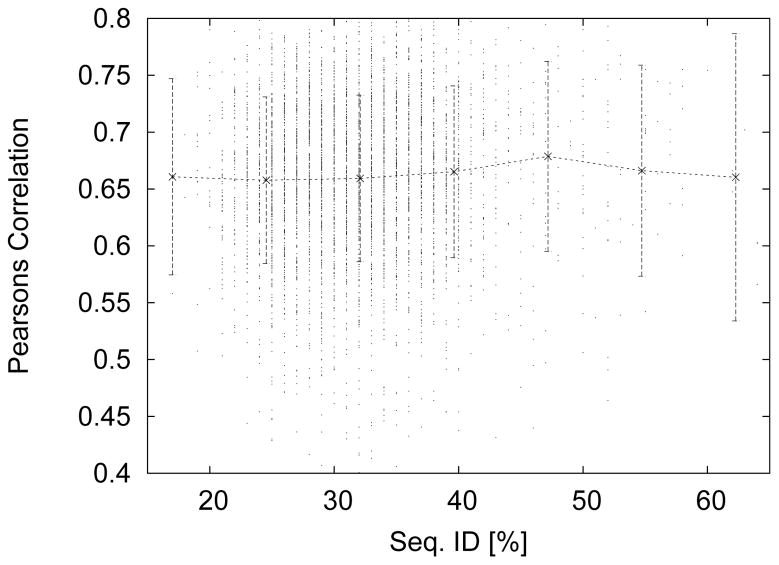
Since hard targets are characterized by low sequence similarity to previously solved structures we study the dependence of the accuracy on the sequence similarity between the test and training sets. For this we used the 9361 set to train a neural network as before. We also built a BLAST database [50] using the formatdb command. We then took the remaining 5000 proteins from the original 14361 set, predicted their ASA and found the correlation and MAE per protein for said prediction. In addition we calculated the maximum sequence similarity between the test proteins and the training proteins. In Fig. 3 we give the Pearson’s correlation coefficient for predicted ASA values versus the maximum sequence similarity between each of the 5000 test proteins to the 9361 training proteins. Indeed we find that there is no apparent relationship between prediction correlation and maximum sequence similarity. To quantify this relationship we also calculated the correlation between the prediction correlation and maximum sequence similarity and find a weak correlation of 0.086. However, the corresponding correlation between the prediction MAE and maximum sequence similarity is 0.105, i.e., the prediction error increases with sequence identity. This is an opposite trend from that of the prediction correlation. Hence, we surmise that our sequence only approach exhibits weak to no dependence on sequence similarity between protein chains in the training and test sets.

Figure 3.

Prediction correlation versus the maximum sequence similarity between 5000 test proteins and 9361 training/over-fit proteins. The correlation of this data is 0.086 showing that our sequence only approach exhibits applies equally to similar and dissimilar proteins. The solid line and error bars give the binned averages and standard deviations.

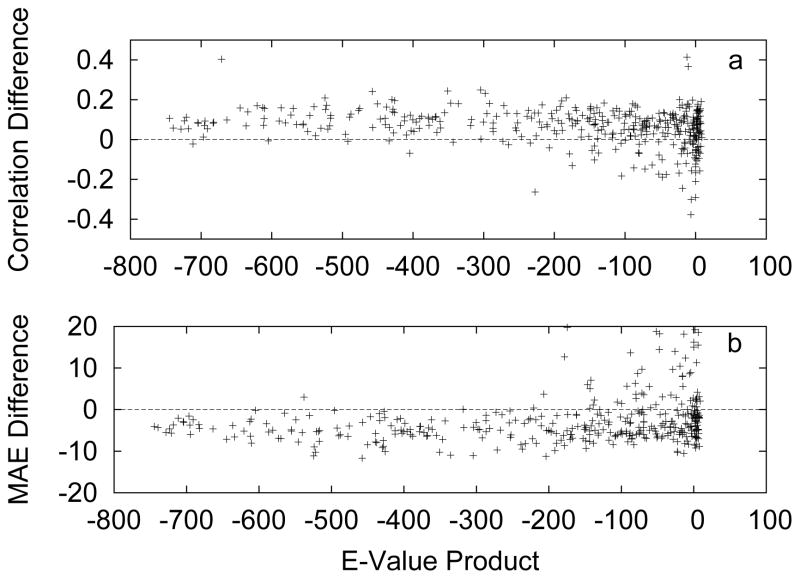
To further test the accuracy of ASAquick and its usefulness for harder targets we randomly selected 500 protein chains from PDB chains clustered at 25% sequence identity. This set of 500 proteins has approximately 112000 residues. For each one of these proteins we calculated a prediction using ASAquick and using SPINE-X [48, 10]. For each protein we also ran a BLAST search against the PDB and calculated the product of the top five e-values excluding the query protein. This measure, the e-value product, allows us to quantify the amount of similar sequences with a structure deposited in the PDB. Those query proteins with many similar sequences in the PDB will have a e-value product much smaller than one, while those with few homologs will have a value of order one. For assistance with visualization we take the logarithm of the e-value product. Note that by excluding sequences identical to the query protein we are ensuring that the e-value product is greater than zero.

In Fig. 4 we present the difference in accuracy between predicting with PSSM (using SPINE-X) or by pure sequence (using ASAquick). In Fig. 4a we have the difference in prediction correlation coefficients for each protein versus the e-value product, while in Fig. 4b we have the difference in MAE. In both cases, the solid line at zero represents no difference in prediction accuracy. The trend that emerges from this representation is clear and consistent with the results above. For proteins with similar sequence deposited in the PDB, a slight consistent advantage for using PSSM is evident. However, as we move right in the figures, towards harder and harder targets, we see many cases where using a pure sequence approach is advantageous. It is interesting to note that as before, pure sequence seems more useful for improving the MAE than the correlations.

Figure 4.

The difference in accuracy between predicting with PSSM (using SPINE-X) or by pure sequence (using ASAquick). a) Difference in prediction correlation coefficients and b) Difference in MAE. In both cases, the solid line at zero represents no difference in prediction accuracy.

As we described at the onset, one reason for designing ASAquick was to drastically increase the speed of predictions. Indeed, analysis on the time it takes to generate a prediction was carried out. It was found that ASAquick takes less than a second to produce a prediction on a single Intel Xeon E5410 at 2.33GHz processor. On the other hand it was found that SPINE-X takes considerable more time. Since the major bottleneck for producing prediction in SPINE-X is the generation of the profile, by default SPINE-X attempts to use four processors to carryout this job. It was found that for a protein for which ASAquick needs less than a second and a single processor, SPINE-X needs over two minutes and four processors to complete the job. Hence, ASAquick reduces the time necessary to get a prediction by almost three orders of magnitude.

5 Summary

We have presented ASAquick, a single sequence ASA predictor. By eliminating information from multiple sequence alignments this predictor was designed and trained to be less dependent on sequence similarity to known protein structures. Instead we focus on a local window around the residue to be predicted and global information: the residue length of the protein, its one-residue composition, and its directional two-residue composition. We demonstrate using several database and methodologies that ASAquick gives consistent predictions regardless of sequence similarity and perform only a few percent worse than a predictor that utilizes information from the PSSM. In addition, due to the removal of the PSSM from the input, ASAquick is orders of magnitude faster, enabling use of ASAquick for relatively quick whole genome studies and comparative genome studies. More exactly, we find ASAquick to be similar in accuracy to the SPINE-X profile based prediction method for CASP10 hard targets and approximately 5% worse than SPINE-X over all CASP10 targets which are mostly template-based modeled. For hard protein targets the difference between ASAquick and SPINE-X is reduced to about 2% in SPINE-X’s favor. In terms of resources ASAquick reduces the computation time by a factor of almost three order of magnitude, producing a prediction in less than a second.

ASAquick was implemented using GENN, a general neural network designed to train on ad-hoc data. GENN was designed with efficiency and modularity in mind as part of a more complex algorithm of an automated learner. It can take any numerical input/output problem and prepare a corresponding, non-memorizing, model structure to represent this data. Data can be organized in files containing individual instances or a collection of ordered instances where each line is an individual input/output target. GENN and ASAquick are available from Research and Information Systems at http://mamiris.com, from the SPARKS Lab at http://sparks-lab.org, and from the Battelle Center for Mathematical Medicine at http://mathmed.org.