A Variational Framework for Joint Detection and Segmentation of Ovarian Cancer Metastases

Abstract

Detection and segmentation of ovarian cancer metastases have great clinical impacts on women’s health. However, the random distribution and weak boundaries of metastases significantly complicate this task. This paper presents a variational framework that combines region competition based level set propagation and image matching flow computation to jointly detect and segment metastases. Image matching flow not only detects metastases, but also creates shape priors to reduce over-segmentation. Accordingly, accurate segmentation helps to improve the detection accuracy by separating flow computation in metastasis and non-metastasis regions. Since all components in the image processing pipeline benefit from each other, our joint framework can achieve accurate metastasis detection and segmentation. Validation on 50 patient datasets demonstrated that our joint approach was superior to a sequential method with sensitivity 89.2% vs. 81.4% (Fisher exact test p = 0.046) and false positive per patient 1.04 vs. 2.04. The Dice coefficient of metastasis segmentation was 92 ± 5.2% vs. 72 ± 8% (paired t-test p = 0.022), and the average surface distance was 1.9±1.5mm vs. 4.5±2.2mm (paired t-test p = 0.004).

1 Introduction

Detection and segmentation of ovarian cancer metastases contribute to the prognosis and treatment of women with ovarian cancer because 75% of them already have metastases spreading to the upper abdomen[6]. This task suffers many challenges. Metastases randomly touch liver or spleen in Fig. 1a; they have weak boundaries with surrounding fluids in Fig. 1b; they also present wide ranges of shapes, such as spherical structures in Fig. 1a and elongated shapes in Fig. 1c. Because of these challenges, there is very limited previous work on this important topic. Liu[4] developed a tumor sensitive matching flow to detect metastases by searching for metastasis-caused shape variance. However, this method yields metastasis over-segmentation caused by weak metastasis boundaries and unconstrained level set propagation.

Fig. 1.

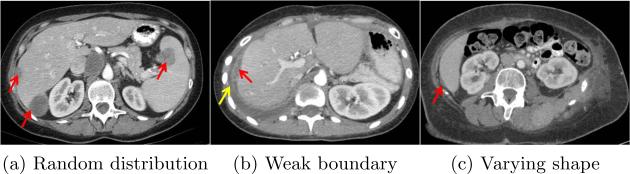
Challenges in detecting and segmenting ovarian cancer metastases, where red arrows indicate metastases and the yellow arrow points to fluids.

Joint detection and segmentation is a potential solution because metastasis detection gives tumor location indications while segmentation improves the accuracy of feature descriptors to identify tumors. Due to benefits from both sides, joint detection and segmentation of objects receive high interests in the computer vision field. Conditional random field (CRF)[3] was often exploited because CRF can predict a label for sequences of input samples, such as detected objects. Singaraju[8] introduced bag of features as the global feature descriptor and integrated them into CRF. Sliding window detectors were employed in Ladicky’s work[2] to perform global object recognition. Shotton[7] combined multiple visual cues to detect objects. In contrast to ovarian cancer metastasis, the objects detected in these methods have clear boundaries from backgrounds. Yezzi[10] developed a variational framework to evolve active contours to simultaneously carry out segmentation and registration on brain images. Joint segmentation and registration on MRI images was also studied in Wyatt’s work[9], except that Markov random field was chosen to establish the framework. Lu[5] equipped Wyatt’s framework with the capability of tumor detection by introducing tumor shape priors. However, varying metastasis shapes hinder this method to deal with our problems.

In this paper, we propose a novel joint detection and segmentation approach by integrating level set propagation and image matching flow computation within a variational framework. The main contribution is three-fold. First, the joint framework performs a tumor sensitive image matching process to steer the matching flow towards the metastasis regions, and metastases are detected by searching for large flow vectors. Second, the joint framework is also a level set segmentation process by using image regions with large matching flow vectors as shape priors to guide metastasis segmentation. Third, metastasis segmentation improves the accuracy of image matching flow by separating its computation in metastasis and non-metastasis regions. The validation on 50 patient datasets demonstrated that our joint framework outperforms the sequential approach[4] with more accurate metastasis detection and segmentation.

2 Variational Framework

This section describes a variational framework for joint detection and segmentation of ovarian cancer metastases. The framework not only integrates tumor sensitive matching flow computation[4] and region competition based level set segmentation[1], but also allow them to benefit from each other to yield accurate metastasis detection and segmentation.

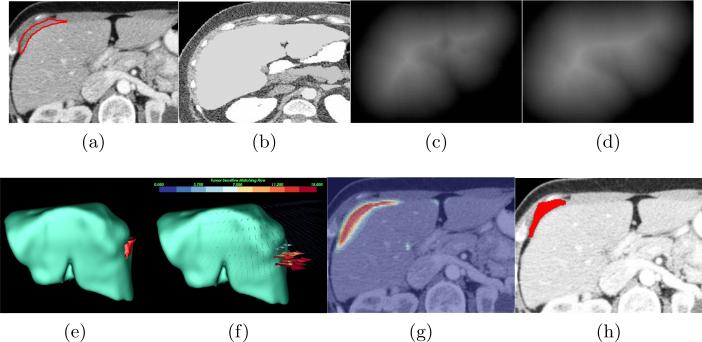
One rule of our joint framework is to embed a metastasis-likelihood function C(p) into the image matching process to identify metastasis-caused deformation in the abdomen, where p = (x, y, z). C(p) is defined in [4] based on the assumptions that the organ surface is locally presented as a cup shape and metastasis intensity values obey mixture Gaussian model trained from six patient datasets. Image matching flow u(p) = (u_x(p), u_y(p), u_z(p)) is computed by comparing the patient image I_p(p) (Fig. 2a) and the reference image I_r(p) (Fig. 2b) as well as distance maps D_p(p) (Fig. 2c) and D_r(p) (Fig. 2d) representing the shapes of the patient organ and the probabilistic atlas. Here, I_r(p) is created from a random CT image of a healthy subject. Additionally, we seek two sets of level set functions ψ_i(p), i = 1, 2, that partitions the patient image domain Ω into metastasis regions Ω₁ and non-metastasis regions Ω₂. To allow image matching to benefit from image segmentation, we estimate two flow fields u₁ and u₂ for metastasis and non-metastasis regions. Our joint framework is thus formulated by integrating image matching and segmentation into a variational functional.

$$E(\mathbf{u},\psi )=\sum _{i=1}^2{\int }_{\Omega }H\left({\psi }_i\right)\underset{\text{Intensity Constancy}}{\underbrace{(\Psi \left({\mid I_r(\mathbf{p}+{\mathbf{u}}_i)-I_p\left(\mathbf{p}\right)\mid }^2\right)}}+\alpha C\left(\mathbf{p}\right)\Psi \underset{\text{Gradient Constancy}}{\underbrace{\left({\mid \nabla I_r(\mathbf{p}+{\mathbf{u}}_i)-\nabla I_p\left(\mathbf{p}\right)\mid }^2\right)}}+\beta C\left(\mathbf{p}\right)\Psi \underset{\text{Distance Constancy}}{\underbrace{\left({\mid D_r(\mathbf{p}+{\mathbf{u}}_i)-D_p\left(\mathbf{p}\right)\mid }^2\right)}}d\mathbf{p}-\sum _{i=1}^2{\int }_{\Omega }H\left({\psi }_i\right)\left(\upsilon \underset{\text{Image Term}}{\underbrace{\log P_i\left(I_p\left(\mathbf{p}\right)\right)}}+\eta \underset{\text{Flow Term}}{\underbrace{\left(\log P_i\left(\Vert {\mathbf{u}}_i\Vert \right)\right)}}\right)d\mathbf{p}+\sum _{i=1}^2{\int }_{\Omega }\left(\gamma \Psi \underset{\text{Flow Smoothness}}{\underbrace{({\mid \nabla {\left(u_x\right)}_i\mid }^2+{\mid \nabla {\left(u_y\right)}_i\mid }^2+{\mid \nabla {\left(u_z\right)}_i\mid }^2)}}+\kappa \underset{\text{Contour Area}}{\underbrace{\mid \nabla H\left({\psi }_i\right)\mid }}\right)d\mathbf{p}$$ (1)

where H(ψ_i) is a Heaviside function[1] and $\Psi \left(s^2\right)=\sqrt{s^2+{0.001}^2}$ is a modified L1 norm that allows for handling outliers. α = 550; β = 1000; κ = 1:5, and γ = 5500, where are given by Brox[1]. η = 2000 and υ = 1 are experimentally determined. A statistical model is used to compose the image term and the flow term, which is given by $P_i\left(s\right)=\frac{1}{\sqrt{2\pi }{\sigma }_i}\exp (-\frac{{(s-{\mu }_i)}^2}{2{\sigma }_i^2})$ with the mean value μ_i and standard deviation σ_i in region i.

Fig. 2.

Our joint framework for metastasis detection and segmentation. (a) A patient image with metastases (inside the red contour) attaching to the liver, (b) the reference image, (c) the distance map of the segmented liver, (d) the distance map of the liver atlas, (e) the metastases in 3D, (f) the image matching flow results, (g) the shape prior constructed by the image regions in red with large flow vector magnitudes to assist the metastasis segmentation, (h) the final metastasis segmentation.

Image matching flow is computed by intensity, gradient and distance constancy models as well as the flow smoothness assumption in Eq. 1. Adjusting the weights of gradient and distance constancy terms by C(p) can force flow vectors only to be magnified in the metastases regions. Fig. 2e illustrates a metastasis touching the liver, and Fig. 2f shows that this metastasis can be detected by searching for image matching flow vectors with their lengths larger than 10mm as clinically relevant. Different from [4], our approach separates the matching flow computation in metastasis and non-metastasis regions by H(ψ_i). This partition strategy can leverage the accuracy of metastasis detection by C(p).

Eq. 1 can also be treated as a region competition based segmentation scheme[1] where the data term includes statistical models of intensity and flow magnitude in the second integral as well as the tumor sensitive matching flow computation in the first integral. We can note that the metastasis is roughly represented by image regions in red with large flow vectors in Fig. 2g. This is a desirable property to address the over-segmentation issue, as it dynamically provides shape priors adaptable to the current patient. The level set driven by the flow vector competition will be balanced approximately at metastasis boundaries. Competing intensity statistical model at metastasis and non-metastasis regions can refine the level set propagation constrained by the shape prior and ensure the level sets to stop at the metastasis boundaries. In addition, the area of the region contours is also penalized by κ in the third integral. Fig. 2h gives the final metastasis segmentation, which is similar to the metastasis groundtruth in Fig. 2a.

Therefore, minimizing Eq. 1 with respect to u and ψ can jointly detect (Fig. 2f) and segment (Fig. 2h) ovarian cancer metastases, and the final metastasis segmentation is inside the contour ψ₁.

3 Optimization

Eq. 1 is non-trivial to solve because it is a non-linear and non-convex energy functional, which might have several local optima. Multi-scale image representation[1, 4] is an efficient means to deal with this issue as multiple optima are rare in the coarse scale.

3.1 Initialization of the Joint Framework at the Coarsest Scale

The robust initialization of unknown variables u and ψ in Eq. 1 is critical to avoid local optimal as well as improve the accuracy of the metastasis detection by C(p). In this work, u is initialized by performing tumor sensitive matching flow computation[4] at coarse scale.

ψ can be initialized by segmenting the matching flow u. Since metastasis and non-metastasis regions are distinguished in terms of the vector magnitudes, we can employ the two-region segmentation strategy described in [1] to perform the flow segmentation.

$$E\left(\psi \right)={\int }_{\Omega }(-H\left(\psi \right)\log P_1\left(\Vert \mathbf{u}\Vert \right)-(1-H\left(\psi \right))\log P_2\left(\Vert \mathbf{u}\Vert \right)+\kappa \mid \nabla H\left(\psi \right)\mid )d\mathbf{p}$$ (2)

Here, P (∥u∥) follows the definition in Eq. ??. Finally, ψ in Eq. 1 can be assigned by the results of Eq. 2.

3.2 Minimization

Let’s first define some abbreviations to simplify the description.

$$\begin{array}{cc}\hfill {\left(I_x\right)}_i=& {\partial }_x{I}_r(\mathbf{p}+{\mathbf{u}}_i){\left(I_{xx}\right)}_i={\partial }_{xx}{I}_r(\mathbf{p}+{\mathbf{u}}_i){\left(\Delta I\right)}_i=I_r(\mathbf{p}+{\mathbf{u}}_i)-I_p\left(\mathbf{p}\right)\hfill \\ \hfill {\left(I_{xy}\right)}_i=& {\partial }_{xx}{I}_r(\mathbf{p}+{\mathbf{u}}_i){\left(I_{xz}\right)}_i={\partial }_{xx}{I}_r(\mathbf{p}+{\mathbf{u}}_i){\left({\Delta }_{x}I\right)}_i={\partial }_x{I}_r(\mathbf{p}+{\mathbf{u}}_i)-{\partial }_x{I}_p\left(\mathbf{p}\right)\hfill \end{array}$$ (3)

The abbreviations for y and z components and distance map D can be similarly derived according to the rules defined in Eq. 3. The Euler-Lagrange equation to minimize (u_x)_i in Eq. 1 is given by

$$H\left({\psi }_i\right)\left({\Psi }^{\prime }\left({\left(\Delta I\right)}_i^2\right){\left(Ix\right)}_i{\left(\Delta I\right)}_i+\alpha C\left(\mathbf{p}\right){\Psi }^{\prime }({\left({\Delta }_{x}I\right)}_i^2+{\left({\Delta }_{y}I\right)}^2+{\left({\Delta }_{x}I\right)}_i^2){\left({\Delta }_{x}I\right)}_i+{\left(I_{xy}\right)}_i{\left({\Delta }_{y}I\right)}_i+{\left(I_{xz}\right)}_i{\left({\Delta }_{z}I\right)}_i+\beta C\left(\mathbf{p}\right){\Psi }^{\prime }\left({\left(\Delta D\right)}_i^2\right){\left(D_x\right)}_i{\left(\Delta D\right)}_i\right)-\gamma \mathrm{div}({\Psi }^{\prime }({\mid \nabla {\left(u_x\right)}_i\mid }^2+{\mid \nabla {\left(u_y\right)}_i\mid }^2)\nabla {\left(u_x\right)}_i)=0$$ (4)

Similar equations can be derived for (u_y)_i and (u_z)_i components. The nested iteration approach[1] is applied to remove non-linearity and non-convexity in Eq. 4. Note that image matching flow u_i is computed only within the image regions confined by the Heaviside function H(ψ_i). This is a beneficial attribute because non-metastasis regions cannot affect image matching flow computation in the metastasis regions, which yields more accurate matching flow to detect metastases in comparison with [4].

The Euler-Lagrange equation regarding to _i is formulated as

$$H^{\prime }\left({\psi }_i\right)\left(-\Psi \left({\left(\Delta I\right)}_i^2\right)-\alpha C\left(\mathbf{p}\right)\Psi ({\left({\Delta }_{x}I\right)}_i^2+{\left({\Delta }_{y}I\right)}^2+{\left({\Delta }_{z}I\right)}_i^2)-\beta C\left(\mathbf{p}\right)\Psi \left({\left(\Delta D\right)}_i^2\right)+\upsilon \log P_i\left(I_p\left(\mathbf{p}\right)\right)=\eta \log P_i\left(\Vert {\mathbf{u}}_{\mathrm{i}}\Vert \right)+\kappa \mathrm{div}\left(\frac{\nabla {\psi }_i}{\mid \nabla {\psi }_i\mid }\right)\right)=0$$ (5)

We employ the region competition strategy developed in [1] to derive a gradient descent form of level set propagation.

$$\begin{array}{cc}\hfill & {\partial }_t{\psi }_i=H^{\prime }\left({\psi }_i\right)\left(e_i-\underset{\begin{array}{c}\hfill H^{\prime }\left({\psi }_j\right)>0.3\hfill \\ \hfill j\ne i\hfill \end{array}}{\max }(e_j,e_i-1)\right)\hfill \\ \hfill & e_i=-\left(\Psi \left({\left(\Delta I\right)}_i^2\right)+\alpha C\left(\mathbf{p}\right)\Psi ({\left({\Delta }_{x}I\right)}_i^2+{\left({\Delta }_{y}I\right)}^2+{\left({\Delta }_{z}I\right)}_i^2)+\beta C\left(\mathbf{p}\right)\Psi \left({\left(\Delta D\right)}_i^2\right)\right)∕\left(\frac{1}{\mid \Omega \mid }{\int }_{\Omega }\left(\Psi \left({\left(\Delta I\right)}_i^2\right)+\alpha C\left(\mathbf{p}\right)\Psi ({\left({\Delta }_{x}I\right)}_i^2+{\left({\Delta }_{y}I\right)}^2+{\left({\Delta }_{z}I\right)}_i^2)+\beta C\left(\mathbf{p}\right)\Psi \left({\left(\Delta D\right)}_i^2\right)\right)d\mathbf{p}\right)+\upsilon \log P_i\left(I_p\left(\mathbf{p}\right)\right)+\eta \log P_i\left(\Vert {\mathbf{u}}_i\Vert \right)+\kappa \mathrm{div}\left(\frac{\nabla {\psi }_i}{\mid \nabla {\psi }_i\mid }\right)\hfill \end{array}$$ (6)

Here, ψ_i is propagated by metastasis (e_i) and non-metastasis (e_j) region competition according to image matching flow computation, statistical models of intensity and flow magnitude, and the curvature term restricted to the narrow band given by H′(ψ_i) > 0.3. As discussed before, the image matching flow competition creates a dynamic shape prior because image regions with large flow vectors roughly represent the metastasis shapes. The competition between intensity models contributes to achieving accurate metastasis segmentation.

4 Experimental Data and Results

Our joint framework was validated on abdominal contrast-enhanced CT images from 50 patients (excluding six patients used for C(p) in Eq. 1). Slice thickness varies from 1.0mm to 2.0mm. Retrospective analysis of all images was approved by our IRB. 25 patients had at least one ovarian cancer metastasis. 102 metastases in these images were annotated by an experienced radiologist and used as the ground-truth. 92 metastases were attached to the liver, and the remaining 10 to the spleen. The size range of all metastases was 2.3-52.3mm (average: 21.1±12.8mm).

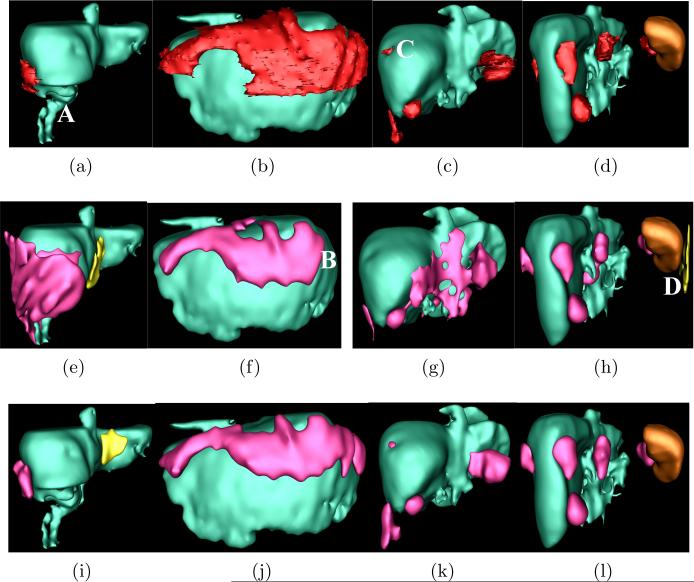
Eight metrics used in [4] were chosen to evaluate the accuracy of metastasis detection and segmentation. Sensitivity (Sen.) and false positive rate per patient (FP/Pat.) were used to evaluate detection results. FP was defined as independently segmented regions with which less than 50% of expert annotations overlap. The segmentation accuracy was appraised by volume overlap (VO), Dice coefficient (DC), relative absolute volume difference (RV), average symmetric absolute surface distance (AD), symmetric RMS surface distance (SD), and maximum symmetric absolute surface distance (MD). Table 1 indicates that the sensitivity of the joint framework increased substantially compared to the sequential method[4](Fisher exact test p = 0.046) with half the number of FP/Pat because metastasis segmentation separates image matching flow computation in metastasis and non-metastasis regions. The segmentation accuracy is also significantly improved due to the dynamical shape prior constructed by the joint framework (p = 0.004, paired t-test on DC). Fig. 3 compares metastasis detection and segmentation using sequential and joint approaches on four patients. Each column represents one patient. In Fig. 3a, part of liver is removed in the ‘A’ region and the abdomen also contains fluids. Without shape constraints, the metastasis was significantly over-segmented by the sequential method[4] in Fig. 3e. In contrast, our joint approach successfully addressed over-segmentation in Fig. 3i. The second column shows a patient with metastasis clusters warping around the liver. Although both sequential and joint methods can detect these metastases, metastases in area ‘B’ in Fig. 3f are missed by the sequential method while they are recovered by our joint approach. In the third patient, our joint approach can detect a small metastasis in area ‘C’ in Fig. 3k while it is missed by the sequential method. The fourth patient reveals that our joint method can also reduce false positives, such as one at ‘D’ in Fig. 3h. As illustrated, these four examples support our findings in Table. 1.

Table 1.

Accuracy evaluation of metastasis detection and segmentation.

Method	Sen.(%)	FP/Pat.	VO(%)	DC(%)	RV(%)	AD(mm)	SD (mm)	MD (mm)
Sequential	81.4	2.04	57±10	72 ± 8	33 ± 22	4.5 ± 2.2	7.8 ± 3.2	42 ± 9.4
Joint	89.2	1.04	82±7.1	92 ± 5.2	14 ± 10	1.9 ± 1.5	3.8 ± 2.4	18 ± 7.2

Fig. 3.

Comparison of metastasis detection and segmentation using sequential and joint approaches. Top row: ground-truth metastases are in red, liver in green and spleen in brown. Center row: results using sequential approach, where true detections in red and false positives in yellow. Bottom row: joint method.

5 Conclusion and Future Work

In this paper, we developed a variational framework to jointly detect and segment ovarian cancer metastases. Our framework unifies image matching flow computation and region competition based level set propagation, and allows them to benefit from each other. Image matching flow not only detect metastases, but also provides metastasis shape priors to avoid over-segmentation. Metastasis segmentation also improves the accuracy of image matching flow because flow computation is separated in metastasis and non-metastasis regions. The validation demonstrated that our joint framework generates more accurate metastasis detection and segmentation than sequential method[4] with sensitivity 89.2% vs. 81.4% (Fisher exact test p = 0.046) and the Dice coefficient 92±5.2% vs. 72±8% (paired t-test p = 0.004). In the future, we will investigate metastasis texture features to enhance the detection accuracy.