The visible ground surface as a reference frame for scaling binocular depth of a target in midair

Abstract

The natural ground surface carries texture information that extends continuously from one’s feet to the horizon, providing a rich depth resource for accurately locating an object resting on it. Here, we showed that the ground surface’s role as a reference frame also aids in locating a target suspended in midair based on relative binocular disparity. Using real world setup in our experiments, we first found that a suspended target is more accurately localized when the ground surface is visible and the observer views the scene binocularly. In addition, the increased accuracy occurs only when the scene is viewed for 5 sec rather than 0.15 sec, suggesting that the binocular depth process takes time. Second, we found that manipulation of the configurations of the texture-gradient and/or linear-perspective cues on the visible ground surface affects the perceived distance of the suspended target in midair. Third, we found that a suspended target is more accurately localized against a ground texture surface than a ceiling texture surface. This suggests that our visual system usesthe ground surface as the preferred reference frame to scale the distance of a suspended target according to its relative binocular disparity.

Introduction

The Ground Theory of Space Perception posits that the ground surface plays a critical role in space perception in the intermediate distance range (Gibson, 1950; 1979; Sedgwick, 1986). This is because the ground carries rich and reliable depth information, such as texture gradient cues, that often extend continuously from our feet to the far distance. The Ground Theory of Space Perception has received strong empirical support over the last decade (e.g., Aznar-Casanova et al, 2011; Bian & Andersen, 2011; Bian, Braunstein, & Andersen,2005, 2006; Feria, Braunstein, & Andersen,2003; He et al., 2004; Kavšek & Granrud, 2013; Meng & Sedgwick, 2001, 2002; Ooi & He, 2007; Ooi, Wu, & He, 2001, 2006; Ozkan & Braunstein, 2010; Philbeck & Loomis, 1997; Sinai, Ooi,& He, 1998; Wu, He, & Ooi, 2004, 2007a & b; Wu, He, & Ooi, 2005, 2008, 2013; Zhou, He, & Ooi, 2013). For example, observers can walk accurately to the location of previously viewed target in blindfold, i.e., without feedback, when the horizontal ground surface is continuous (e.g., Loomis, et al, 1992, 1996; Ooi et al, 2001; Philbeck, O’Leary, & Lew, 2004; Rieser et al, 1990; Sinai et al, 1998; Thomson, 1983). However, when the ground surface is interrupted by a gap, a partially occluding obstacle, or texture boundary, observers can no longer make accurate distance judgments (Feria et al, 2003; He et al, 2004; Ooi et al, 2001; Sinai et al, 1998; Wu et al, 2007a).

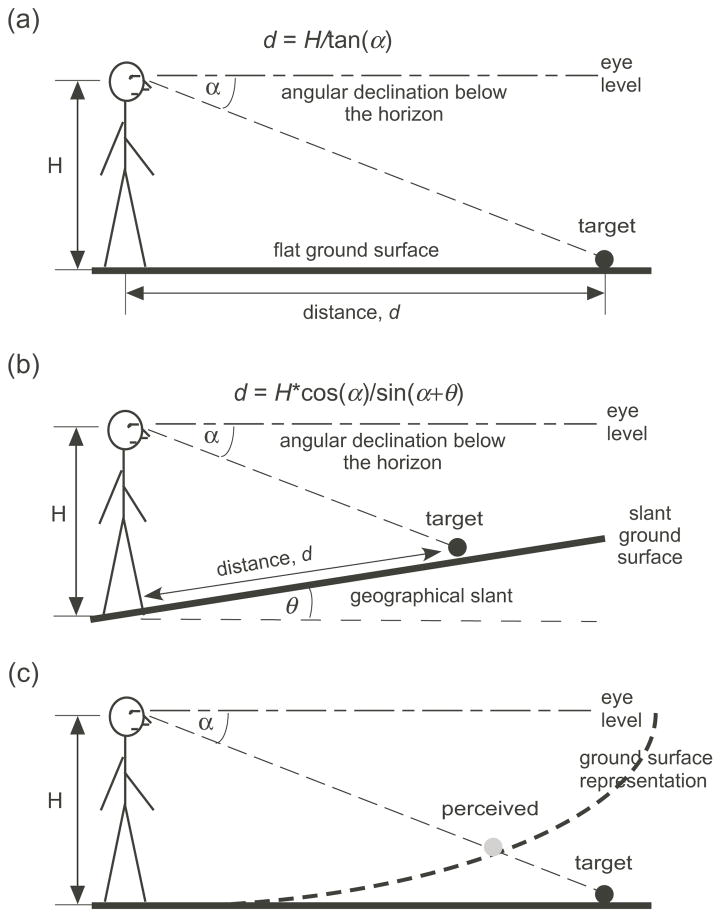
Mechanistically, the visual system can represent one less dimension and improve its coding efficiency when it codes 3-D object locations with reference to the common 2-D surface (He & Ooi, 2000). Using the ground surface representation as a reference frame, the visual system can trigonometrically derive the location of a target on the ground as shown in figures 1a and 1b. When the depth information on the ground is insufficient or inadequate in reduced cue environments, the ground surface representation is slanted, instead of being horizontal (Wu et al, 2007a; Wu et al, 2014). For example, when a sparse 2×3 m array of dimly lit elements are placed in a parallel pattern formation on the horizontal floor (parallel-texture, e.g., figure 3a) in the dark, the observer judges a dimly lit target on the floor as if located on an implicit slanted surface, reflecting the representation of the horizontal texture surface as slanted (figure 1c). Furthermore, changing the texture pattern from parallel to convergent (figures 3a & b) causes the observer to judge a dimly lit target on the horizontal floor as farther, indicating the significant influence of the ground surface representation on distance perception (Wu et al, 2014).

Figure 1.

Space perception based on the ground surface representation. (a) The visual system derives the location of a target on the horizontal ground surface based on the trigonometric relationship. (b) The visual system also derives the location of a target on the slanted ground surface based on the trigonometric relationship. (c) In the dark where the ground is not visible, the visual system determines the location of a dimly lit target at the intersection between the visual system’s intrinsic bias and the angular declination of the target. (d) In the reduced cue condition, the representation of the ground surface is slanted, though the slant is less than that of the intrinsic bias. A target on the ground is perceived as located at the intersection between its angular declination and the slanted surface representation.

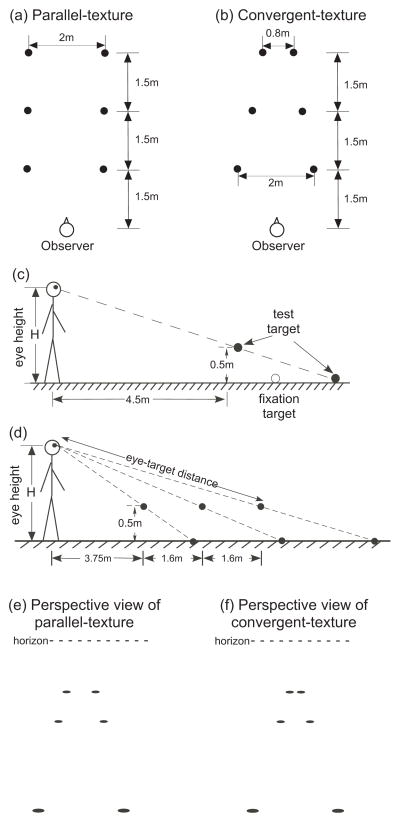
Figure 3.

(a) Top view of the parallel-texture condition. (b) Top view of the convergent-texture condition. (c) Side view of a suspended test target at near and a test target on the floor at far (filled circles) and their relationship to the fixation target (open circle) in Experiment 1. During the experiment, only one test target, near or far, was shown in a trial. (d) Side view of the three-paired targets used in Experiment 2. In each pair, which was shown together during a trial, the near target was suspended and far target was located on the floor. Each paired targets had the same angular declination. (e) and (f) Perspective views of the parallel-texture and convergent-texture conditions, respectively. The dashed horizontal lines depict the horizon.

Given the importance of the ground as a reference frame, one could argue that its influence should also be evident for space perception above the ground surface (Gibson, 1950, 1979). Everyday we execute actions on objects that have no direct surface contact with the ground, such as picking up an apple on the tabletop, catching a basketball in the air and shooting it into the hoop. Does the visual system also localize suspended targets above the ground by capitalizing on the ecological significance of the ground surface? Meng& Sedgwick (2001) found the answer in the affirmative. They revealed that for the case of an object with an indirect surface contact with the ground, such as the apple located on the tabletop, the visual system first determines the geometric relationship of the tabletop surface with respect to the ground, and then the relationship of the apple with respect to the tabletop. Through these nested contact relationships among surfaces, the visual system obtains the location of the object with respect to the observer (egocentric location).

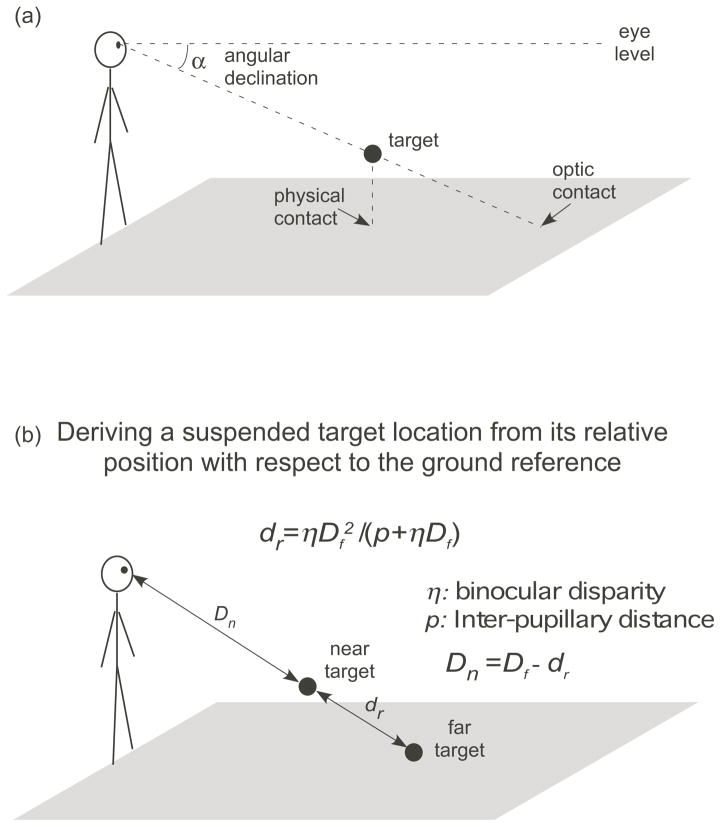
However, a different computational scheme must be used when the object is suspended in mid air above the ground surface, wherein the retinal image of the object overlaps with the retinal image of a distant location on the ground surface (optical contact, figure 2a) (Gibson, 1950; Sedgwick, 1986; 1989). This is because if the visual system fails to detect a spatial separation between the images of the object and the ground surface, it will wrongly assume the object is attached to the ground (Gibson, 1950). In theory, the visual system can directly obtain the egocentric distance of the object suspended in midair by relying on accommodation, absolute motion parallax or absolute binocular disparity (convergence angle of the two eyes) information. However, these absolute depth cues are only effective in the near distance range (<2–3m) (Beall et al, 1995; Cutting & Vishton, 1995; Fisher & Ciuffreda, 1988; Gogel & Tietz, 1973, 1979; Howard & Rogers, 1995; Viguier, Clement, & Trotter, 2001). Here, calling it the ground-reference-frame hypothesis, we propose that another way the visual system can reliably locate the target suspended in midair in the intermediate distance range (2–25m) is by using the ground surface representation as a reference frame. As shown in figure 2b, the visual system can determine the suspended target’s egocentric location by deriving the relative distance between the target and a reference point on the ground surface. Possible quantitative and effective local depth cues for doing so include relative motion parallax and relative binocular disparity (Allison, Gillam, & Vecellio, 2009; Gillam & Sedgwick, 1996; Gillam, Sedgwick, & Marlow, 2011; Madison et al, 2001; Ni & Braunstein, 2005; Ni et al, 2004; 2007; Ooi et al, 2006; Palmisano et al, 2010; Thompson, Dilda, & Creem-Regehr, 2007). Relative binocular disparity, in particular, is an effective cue for relative depth perception in the intermediate distance range (e.g., Loomis & Philbeck, 1999; Wu et al, 2008). [The role of relative binocular disparity has also been studied by Allison and his colleagues (2009). They observed that the estimated depth between two LED targets afforded by the relative binocular disparity information was larger (more veridical) when the room was lighted rather than darkened. Their experiments, however, did not address how the ground surface representation plays a role in the depth judgment.]

Figure 2.

Locating a target suspended in midair above the ground surface. (a) The image of the target overlaps with the optic contact on the ground surface. To determine the location of the suspended target, the visual system needs to determine the target’s relative position to the ground surface. For example, knowing its vertical height with respect to the ground, i.e., its distance to the physical contact, can help determine its distance. The horizontal distance of the physical contact on the ground is the same as the horizontal distance of the target. (b) The visual system can use the relative binocular disparity (η) between the suspended near target and a far target on the ground to derive the location of the suspended target. Specifically, if the distance of the far target on the ground surface (D_f) is known, the visual system can derive the relative distance, d_r, based on the relative binocular disparity (η) between the near and far targets and the observer’s inter-pupil distance (p). Knowing D_f and d_r,, the visual system can obtain the distance of the near target (D_n= D_f − d_r). The equation above the figure depicts the relationship between D_n and d_r.

Figure 2b illustrates how a target suspended in midair is located according to the ground-reference-frame hypothesis. The visual system first calculates the eye-to-target distance of a far reference target on the ground surface (D_f) by using: (i) the trigonometric relationship described in figure 1a, D_f=H/sinα, where H and α are the observer’s eye height and the target’s angular declination, respectively; and (ii) the relative binocular disparity (η) of the suspended target with respect to the far reference target on the ground. The visual system then scales the relative distance (d_r) between the suspended target and the reference target on the ground using the relationship, d_r=ηD_f²/(ρ+ηD_f), where ρ is the observer’s interocular distance and η is the relative binocular disparity in radians. Thus, by knowing, D_f and d_r, the visual system can derive the eye-to-target distance of the suspended target (i.e., D_n=D_f−d_r). Notably, this computational scheme predicts that for a constant magnitude of relative binocular disparity (η), a change in the representation of the ground surface can affect distance perception on the ground (D_f), which in turn affects both d_r and D_n.

Our first experiment tested the prediction that with binocular viewing, a visible ground surface facilitates the distance perception of a suspended target in midair. We conducted the experiment in a dark room to control the visibility of the floor. Figure 3c depicts the side view of a dimly lit target that is either suspended in midair or located on the ground. Figure 3a illustrates the top view of the parallel-texture ground condition where a 2×3 array of fluorescent elements is placed on the floor to delineate the ground surface. Since the perceived distance on the ground (D_f) is more veridical when the floor is delineated by parallel-texture elements than when it is not visible in the dark (Wu et a, 2013), we expected perceived distance above the ground to be more veridical in the parallel-texture condition with binocular viewing than with monocular viewing. Our second experiment tested the prediction that the texture patterns on the ground, which causes the ground surface to be differently represented, affect both judged relative distance (d_r) and eye-to-target distance (D_n)(figure 2b). Figures 3a and 3b, respectively, illustrate the top views of the parallel-texture and convergent-texture ground conditions. We previously found that whether with monocular or binocular viewing, observers perceive a target on the ground (D_f) as farther in the convergent- than the parallel-texture conditions (Wu et al, 2007b; Wu et al, 2014). Consequently, we predicted both the judged relative distance (d_r) and eye-to-target distance (D_n) to be longer in the convergent-texture condition.

Our third experiment tested the prediction that a ground surface affords a more reliable reference frame than a ceiling surface. There is accumulating evidence for the prevalent role of the common surface in influencing visual perception (such as stereopsis and motion perception) and in improving visual efficiency and attention deployment (e.g., He & Nakayama, 1994, 1995; He & Ooi, 1999; 2000; Marrara& Moore, 2000; McCarley & He, 2000, 2001; Morita & Kumada, 2003). These observations, together with our earlier findings in space perception (e.g., Sinai et al, 1998), led us to propose a quasi 2-D hypothesis, which states that the visual system can improve its efficiency of coding object locations in 3-D space by using the common surface as a reference frame (He & Ooi, 2000). Thus, the visual system uses the ground surface, which is the common background surface that often extends continuously from near to far, as a reference frame to code locations of objects on, or above, the ground in the intermediate distance range. The quasi 2-D hypothesis is not limited solely to the ground surface, and applies also to common background surfaces of various orientations. This is because in the real 3-D environment, while the ground surface is the principal common surface, we also encounter and interact with other common surfaces, such as the ceiling surface. The important difference between the ground and ceiling reference frames is that the perceptual process underlying the ground surface representation is more efficient and reliable than the process underlying the ceiling surface representation. Indeed, previous studies have found that the visual system has a preference for the ground surface over the ceiling surface (Bian et al, 2005; 2006, 2011; Imura & Tomonaga, 2013; Kavšek & Granrud, 2013; McCarley& He, 2000; McCarley& He, 2001; Morita & Kumada, 2003). For example, when searching for an odd target in a 3-D visual search display, the search reaction time was faster if the search elements were seen as belonging to a large implicit common plane than when the elements were seen as belonging to different planes (McCarley& He, 2000, 2001). This indicates that a common surface facilitates visual search. The facilitating effect of the common surface was found with both ground and ceiling surfaces, even though the search was more efficient upon the ground surface. Furthermore, it has been shown that the perceived relative depth between two targets can be affected by a vertical background surface (He & Ooi, 2000). These accumulating evidences for the significant role of the common surface suggest that space perception of a suspended target in the midair in the intermediate distance range would also utilize a large background surface of another orientation, other than the ground surface, as the reference frame. This claim not withstanding, we propose that the Ground Theory predicts that of all surfaces, the ground surface would be the most effective surface owing to its biological significance to its terrestrial inhabitants.

Experiment 1: Absolute target location in midair is more accurately judged with binocular vision when the ground surface is visible

We compared the observer’s judged target location in a dark condition (ground not visible) and a parallel-texture condition (ground visible) with monocular and binocular viewing. The parallel-texture condition was created by presenting a 2×3 array of dimly lit texture elements on the floor in an otherwise dark room to delineate the ground surface (figure 3a). If the visual system is able to use the relative binocular disparity between the suspended target and the parallel-texture surface to code its location, the perceived location of the suspended target will be more accurate with binocular viewing than with monocular viewing in the parallel-texture condition. On the other hand, in the dark condition, there is no visible texture on the ground to provide the relative binocular disparity information. Consequently, localization of the suspended target will not be facilitated with binocular viewing and will be similar to that with monocular viewing. During the experiment, we also measured judged target location on the floor. As will be elaborated in the Results and Discussion session, doing so allows us to estimate the compression of visual space.

Our experiment also investigated the visual system’s efficiency in utilizing the binocular depth cue to localize the suspended target. It has been shown that the visual system efficiently extracts the texture information on the ground to represent the ground and uses the angular declination information to determine the distance of a target on the ground (Gajewski et al, 2010; Philbeck, 2000; Wu et al, 2014). In a recent study, we presented an array of texture elements on the ground (same as in figure 3a) in an otherwise dark room, and asked the observer to judge the location of a target on the ground with monocular viewing (Wu et al, 2014). The stimulus presentation duration was either 0.15 sec or 5.0 sec. We found that judged locations were similar with both stimulus durations, suggesting that a duration as short as 0.15 sec is sufficient for the visual system to construct a global surface representation in the reduced cue condition and to register the location of the target on the ground. In the current experiment, we wanted to reveal whether the process responsible for locating a target above the ground is equally efficient. Specifically, is a stimulus duration of 0.15 sec sufficiently long for the visual system to construct the ground surface representation and to locate a suspended target?

Method

Observers

Eight observers with informed consent, ages 25 to 38 years old, participated in the experiment. The all had normal or corrected-to-normal visual acuity of at least 20/20 and stereoacuity of at least 40 arc sec. All observers were naïve to the purpose of the experiment. Their average eye height was 163 cm. Monocular viewing was achieved by patching the non-motor-dominant eye.

Design

We used a fully-crossed-factor design with four factors: (i) stimulus viewing duration (0.15 sec or 5 sec); (ii) ground condition (dark or parallel-texture); (iii) target location (near target suspended in midair or far target placed on the floor, figure 3c); (iv) viewing mode (monocular or binocular). The combination of all factors and levels yielded a total of 16 different test trial settings. The test order of the trial setting was randomized. Each trial setting was tested twice and their average was taken as the final result.

Stimulus configuration and environment

The experiment was conducted in an 11×3 m light-tight, rectangular test room with carpeted floor. All room lights were switched off during the experiment. Extra care was taken to ensure that no part of the visual environment was visible to the observer, except for the intended stimulus scene (target, textured background and fixation point). Matte black cloths covered potential light sources and highly reflective sidewall surfaces in the test room. A safety rope was tied across the room at about hip-height to guide the observer during the blindfolded walking task. Two fluorescent elements were taped to the floor at one end of the room to mark the observation spot (start location). The observer would step on the fluorescent elements, the front tip of each foot on one element, thereby readying him/herself to begin a trial.

The test target was an internally illuminated, red ping-pong ball that was housed in a small box with an adjustable aperture. The aperture was appropriately adjusted for viewing distance to maintain the target’s visual angle at 0.27° when measured at eye level. The target was placed at one of two possible locations (near or far) along the observer’s sagittal plane (figure 3c). The location of the target at near was fixed at a horizontal viewing distance (horizontal distance means distance in the depth dimension) of 4.5 m and suspended 0.5m above the floor (i.e., 4.5m, 0.5m). The location of the test target at far was on the floor and had a horizontal distance equaled to H/tanα, where the H was the observer’s eye height and α the angular declination of the near test target. In this way, the near and far targets had the same angular declination. We also employed two other pairs of targets [(6.25m, 0.5m); (3.75m, 0m)] for use as catch trials (not shown in figure 3c) to increase the number of possible target locations. The catch trials were randomly intermixed with the test trials and accounted for one-third of the total trials. Since the goal of adding the catch trials was to prevent the observers from becoming overly familiar with the test locations, we did not record the judged responses of the observers in the catch trials even though we went through the routine of measuring them.

Two ground conditions, dark (no-texture) and parallel-texture, were used (figure 3a). The texture element for the parallel-texture condition was made of internally illuminated white ping-pong ball (0.20 cd/m²) housed inside a small box with a fixed circular aperture of 6 cm in diameter. All texture elements were placed on the floor during the test trials, and 0.3 m above the floor during the catch trials. The catch trials accounted for one sixth of the total number of trials. The purpose of having the catch trials was to prevent the observers from assuming that the height of the texture background was constant. A dimly lit fixation target, with the same dimensions as the texture elements, was used to control the observer’s eye fixation position prior to the onset of the test display (figure 3c). It was always placed on the floor with its angular declination been halfway between the test target position with the largest angular declination and the test target position with the smallest angular declination among all six-target locations. The angular declination difference between these two extreme positions was about 14° for our observers.

Procedure

Before the proper experiment, the observer was led blindly into the totally darkened test room. He/she was given about 15 minutes to practice the test procedures in the dark. No information regarding the actual target location or texture background configuration was shared with the observer.

The observer stood at the starting point to begin a trial, which started with a 0.5 s beeping sound generated by the computer to alert the observer of the upcoming fixation target one sec later. The 1.5 sec fixation target was followed by another 1.5 sec of darkness for the observer to ready him/herself for the upcoming target presentation. Depending on the trial setting, the target was presented for either 0.15 sec or 5 sec. In the parallel-texture condition, the target was seen simultaneously against a parallel-texture background. In the dark condition, no background was visible. The observer was instructed not to make body and head movements while judging the target location.

After the stimulus presentation, the experimenter quickly and quietly removed the stimulus setup to clear a walking path for the observer. After which, the observer walked blindly to traverse the judged target distance and upon reaching the destination gestured the perceived height of the target with his/her right hand (Ooi et al, 2001). The walked distance and gestured height were recorded. Finally, the observer still wearing the blindfold returned to the starting point and stepped into the small, lighted waiting room adjacent to the starting point in the test room. The observer rested there until the next trial. No feedback regarding the performance was given. Music was played aloud during the experiment to prevent acoustic clues to distance.

Results and Discussion

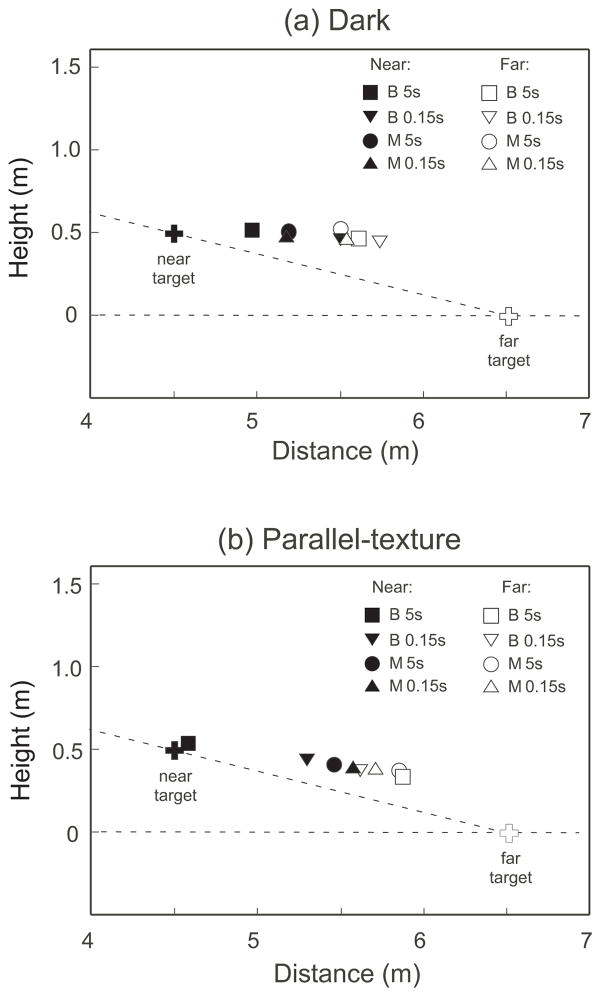
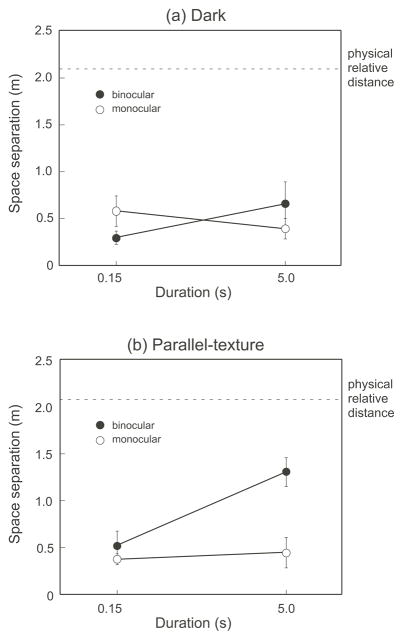
Figures 4a and 4b show the average judged target positions in the dark and parallel-texture conditions, respectively. The symbols, except for the crosses that symbolize the physical target locations, represent the judged locations of the near (filled) and far (open) targets. The most noticeable difference between figures 4a and 4b is the judged location of the suspended near target with the 5 sec stimulus duration and binocular viewing mode (filled squares). In the dark, the suspended target was perceived as farther than the actual/physical target location due to a strong influence of the intrinsic bias (figure 4a) (Ooi et al, 2001; 2006, Wu et al, 2005). However, the suspended target was perceived almost at its veridical location in the parallel-texture condition. We attribute the increased accuracy to the availability of the relative binocular disparity information between the suspended near target and the parallel-texture background with binocular viewing. This is because the parallel-texture background did not render the judged location of the suspended near target more accurate with monocular viewing. Yet, the advantage of binocular viewing and parallel-texture condition was not realized for the suspended near target when the stimulus duration was short (0.15 sec) (filled triangle symbols). This indicates that the underlying binocular depth mechanism that codes relative distance requires longer time to become effective. This conclusion is possible because we previously found the visual system exhibits the same accuracy in judging target location on the parallel-texture ground no matter whether the stimuli were presented for a short duration (0.15s) or for a long duration (5.0 sec), which indicates that the visual system is quite efficient in representing the ground surface in the reduced cue condition (Wu et al, 2014).

Figure 4.

The average judged locations of the near and far targets measured with the blind walking-gesturing task in Experiment 1. (a) Dark condition. (b) Parallel-texture condition. The filled and open crosses, respectively, represent the physical locations of the near and far targets.

Notably, even though our finding suggests that the visual system quite efficiently represents the ground surface, it does not indicate that the represented surface is accurate when the environmental condition is less than optimal (e.g., in the reduced cue condition such as in Wu et al, 2014). Similarly, Philbeck and his colleagues discovered that in the full cue environment, the observer could utilize angular declination to determine the distance of a target on the ground with stimulus duration as short as 9 msec (Gajewski et al, 2010; Philbeck, 2000). However, their observers did not judge the distance as accurately as one would expect to find when one performs the blind walking task without time constraint in full cue condition (e.g., Loomis, et al, 1992). This suggests the contribution of the intrinsic bias to space perception when the viewing duration is short. Future studies should explore the minimum duration for accurate ground surface representation in the full cue condition. More generally, there is a need for more comprehensive knowledge of the temporal properties of the space perception mechanisms that represent the ground surface for coding a target location on, and above, the ground.

A possible explanation for the reduced performance of the binocular depth mechanism at short viewing duration (0.15s vs 5s) is related to the ocular motor system’s resting states in the dark (dark vergence and dark focus). In our experiment, the fixation target was extinguished for 1.5 sec before the test target appeared. During this dark period, the observer’s ocular motor system could return to its resting state around a mean distance of 1.2 m (with a range from 0.62 to 5 m) from the eyes (Owens & Leibowitz, 1980). As such, the observer could not quickly shift his/her gaze to the test target when its presentation duration was only 0.15 sec. Consequently, the test target was too far from the resting state position and the binocular depth mechanism could not quantitatively extract the target’s depth. Also of significance, the resting position is similar for the accommodation system in the dark (~1.7 diopter) (e.g., Leibowitz & Owens, 1975). A similar explanation applies to one’s failure to readily shift focus to the test target within the short target duration.

The consideration above could also explain why our observers judged the near target as closer (~0.4–0.5 meters) than the far target at the short stimulus duration (0.15 sec) under both monocular and binocular viewing conditions (figure 5). As a consequence of the resting position, the retinal image of a near target would be less blurred than that of a far target since the observers could not quickly refocus within the short 0.15 sec stimulus duration. It is possible that this depth cue, i.e., more blurred target being interpreted as further away, was used by the visual system as a weighted contribution in judging target distance.

Figure 5.

The average judged relative distances between the near and far targets in Experiment 1. (a) Dark condition. (b) Parallel-texture condition. All the data points are below the dash horizontal line in each graph, which represents the physical relative distance between the near and far targets. This indicates underestimation of relative distances in both conditions and viewing modes. Nonetheless, the underestimation is least in (b) with binocular viewing and long stimulus duration (5s). This demonstrates the contribution of the relative binocular disparity information between the suspended target and the visible texture ground surface to distance perception.

To better characterize the impact of the parallel-texture background on the judged location of the suspended near target, we next analyzed the judged absolute (eye-to-target) distances of the near target and far target together. Specifically, the difference between the two absolute distances reflects how much the suspended near target was perceived as deviated from the represented ground surface upon which the far target was located. In our analysis, we took the difference (d_r) between the perceived absolute distance of the near and far targets (for each condition).

The average results for the dark and the parallel-texture conditions are shown in figures 5a and 5b, respectively. The dash horizontal line in each graph represents the physical distance between the near and far targets, i.e., the relative physical space between the two targets. Yet, all the data obtained are located below the horizontal dash line, indicating a compression of perceptual space. In the dark condition where there was no texture elements delineating the ground (figure 5a), we found that the difference between the two judged distances (i.e., the perceptual space separation) was not significantly affected by the viewing mode and stimulus duration [Main effect of viewing mode: F(1,7)=0.006, p=0.940; Main effect of duration: F(1,7)=1.026, p=0.344; Interaction effect: F(1,7)=5.025, p=0.060; 2-way ANOVA with repeated measure]. The finding that binocular viewing has no advantage over monocular viewing in the dark is consistent with a report by Philbeck and Loomis (1997).

In the parallel-texture condition (figure 5b), the difference between the two judged distances (perceptual space separation) became more veridical with binocular viewing and long stimulus duration (5 sec) [Main effect of viewing mode: F(1,7)=21.974, p<0.005; Main effect of duration: F(1,7)=20.583, p<0.005; Interaction effect: F(1,7)=15.067, p<0.01; 2-way ANOVA with repeated measure are significant]. Planned contrast analysis reveals that with the long duration (5 sec), the difference between the two judged distances was significantly longer with binocular viewing than with monocular viewing [t(7)=5.729, p<0.001, paired t-test]; whereas with the short duration, they were not significantly different [t(7)=1.907, p=0.309, paired t-test]. This indicates that when there exists texture on the ground and the stimulus duration is long, binocular depth information of the suspended target relative to the ground can cause perceptual space to be less compressed.

Finally, we calculated the angular declination (α) of the judged target using the relationship, Tan (α)=(H−h)/d, where d is the walked horizontal distance; H and h are the observer’s eye height and gestured target height, respectively. We then calculated the difference in angular declination for the same target in the dark and in the parallel-texture background conditions. The average differences are shown in the table below (unit in arc deg), where a positive value represents a larger angular declination in the dark condition.

	Binocular Viewing		Monocular Viewing
Duration	Near	Far	Near	Far
5.0s	−0.80 ± 0.58	−0.75 ± 0.54	−0.34± 0.53	−0.91± 0.81
0.15s	−0.86 ± 0.69	−1.03 ± 0.67	0.01± 0.76	−0.41± 0.82

None of average differences depart significantly from zero (p>0.05, t-test), indicating a similar judged angular declination in the dark and parallel-texture conditions. Since the judged angular declination depends on the perceived eye level, this finding suggests that the perceived eye level was the same in the two conditions. This finding is consistent with previous findings from our laboratory(e.g., Ooi et al, 2001; Wu B et al, 2007b; Wu J et al, 2005; 2014).

Experiment 2: Scaling binocular depth perception using the ground surface representation

The main finding in Experiment 1 (e.g., figure 5) that with binocular viewing, distance perception of a suspended target is more veridical in the parallel-texture than in the dark condition confirms the prediction of the ground-reference-frame hypothesis. However, there is an alternative hypothesis for the finding, which claims that a local-binocular-depth-integration mechanism independent of the ground surface representation process underlies the observed finding. The local-binocular-depth-integration mechanism is illustrated in figure 6, where the visual system first obtains the absolute distance (A) of the nearest texture element based on reliable absolute depth cues at its vicinity, such as absolute binocular disparity and/or absolute motion parallax. Then the mechanism sequentially computes relative distances, B, C, & D by relying on relative binocular disparities (the overall distance=A+B+C+D). Notably, the output of the local depth mechanism remains unchanged no matter whether the elements on the ground form a global surface representation or not. In the dark condition where the suspended target is the sole stimulus, the local-binocular-depth-integration mechanism does not operate. Therefore, as predicted by the local-binocular-depth-integration hypothesis as well as the ground-reference-frame hypothesis, distance perception is more veridical in the parallel-texture condition with binocular viewing.

Figure 6.

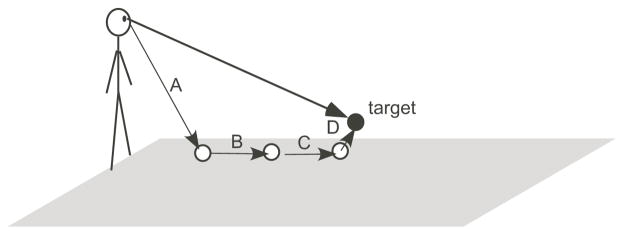
Illustration of the operation of the local-binocular-depth-integration mechanism. To derive the egocentric distance of a target, the visual system first obtains the absolute distance (A) of the nearest element based on reliable absolute depth cues at its vicinity, such as absolute binocular disparity and/or absolute motion parallax. Then the mechanism sequentially computes relative distances, B, C, & D by relying on relative binocular disparities (the overall distance=A+B+C+D).

However, the two hypotheses predict different space perception outcomes when parallel-texture versus convergent-texture pattern elements is used to delineate the ground surface (figure 3a and 3b). While the visual system represents both texture patterns as ground surfaces with similar slant errors, judged absolute distance on the ground surface is underestimated less with convergent-texture than with parallel-texture because the former carries false linear perspective information (Wu et al, 2007b; Wu et al, 2014). [This is due to a lowered judged eye level in the convergent-texture condition (Wu et al, 2007b); please refer to the next paragraph for an extended explanation.] And, according to the ground-reference-frame hypothesis, since the relative distance d_r is scaled according to the absolute distance of the reference point (D_f) on the ground, we can predict that the perceived distances of the suspended target (d_r and D_n) will be more veridical in the convergent-texture condition (figure 2b). In contrast, the local-depth-integration hypothesis, which does not consider the process of global surface representation, predicts that the two texture pattern conditions will lead to similar distance perception. This is because the local-depth-integration mechanism is only concerned with the absolute binocular disparity of the nearest texture element and the local binocular disparities between texture elements, which are similar in the two texture pattern conditions. Our current experiment pitted the two alternative hypotheses. We measured judged d_r and D_n under three conditions: dark, parallel-texture and convergent-texture conditions.

Note that the two texture patterns differ in their linear perspective information, which is considered a global, monocular depth cue on the ground (figures 3e & 3f). For example, Wu et al (2007) first observed that a target located on the ground, at a position similar to the far target on the floor in figure 3c or 3d, was judged as farther in the convergent-texture condition than in the parallel-texture condition. Wu et al (2007) then removed the left halves of the texture elements that delineated the linear perspective information, so that the parallel-texture condition became a parasagittal-line condition and the convergent-texture condition became an oblique-line condition. This led to the finding of similar judged distances in the parasagittal and the oblique conditions, indicating that the difference in perceived distance between the convergent-texture and parallel-texture condition is due to a difference in the global linear perspective structure (see figures 9a & 9b in Wu et al, 2007). Furthermore, Wu et al (2007) found that the impact of the linear perspective information on space perception extends beyond the perceived distance on the ground surface. They found the observer’s judged eye level was lowered in the convergent-texture condition compared to the parallel-texture condition (see figure 8 in Wu et al, 2007). However, the judged eye level in the oblique-line condition was no different from that in the parasagittal-line condition since they did not carry linear perspective information. Separately, our laboratory has shown that the perceived eye level acts as a reference for determining the angular declination of a target, which together with the ground surface representation determines the target’s absolute distance (Ooi et al, 2001). This led to the prediction that judged angular declination would be smaller in the convergent-texture condition than in the parallel-texture condition. This prediction was confirmed by Wu et al (2014) where it was shown that perceived angular declinations at all target locations were reduced in the convergent-texture condition relative to the parallel-texture condition.

Method

Observer

One author and seven naïve observers, ages 25 to 42 years old, participated in the experiment. Four of the naive observers also participated in Experiment 1. Similar to Experiment 1, all observers had at least 20/20 visual acuity and 40 arc sec of stereoacuity. Their average eye height was 158 cm, and they viewed the test display with both eyes.

At this juncture, one might raise the concern that we included the same four naïve-observers who were already tested in Experiment 1 in this experiment. It could be argued that the blind walking task could be subjected to a training or practice effect even when no feedback regarding the performance was given to the observer. This argument notwithstanding, our laboratory has employed the task for more than a decade and we have found that our observers’ performance remains largely stable once they become confident in performing the task. More importantly, if such a training effect were present, it would be found in all conditions and should not significantly affect the main conclusions of the current experiment since our experimental design was based on comparisons across conditions. Another possible concern is that one of the authors participated in the current experiment. But it should be noted that even though this author knew the purpose of the study, he was not aware of the location and duration of the target before each trial. [This author’s performance (data) was very close to the average performance of the remaining naïve observers.] We do not feel that this author’s participation as an observer unduly influenced the outcome of the experiment. This is because if the author had a bias or any intention to make his performance conform to the favored hypothesis, it would be counter productive as his data would then be outliers if other naïve observers did not produce the same trend in the data. Equally important, it does not serve any scientific purpose, or otherwise, to publish biased data and conclusions.

Stimuli and test environment

Three ground conditions were tested: dark, parallel-texture (figure 3a) and convergent-texture (figure 3b) conditions. In all conditions, the stimulus display was presented for 8 sec. No fixation target was presented since the stimulus display was long. The construction of the test targets and the parallel-texture condition were the same as those in Experiment 1. Figure 3b shows the top view of the convergent-texture condition. Figure 3d shows the side view with the three pairs of targets used in the experiment in all three conditions. Only one pair of targets was presented at a time during a trial. Each pair of targets was arranged with the farther one on the floor and the nearer one 0.5m above the floor, and subtending the same angular declination. The horizontal distances of the three 0.5m-above-the-floor target positions were fixed (3.75, 5.35, and 6.95m), while the horizontal distances of the three on-the-floor targets were determined according to H/tanα, where H was the individual observer’s eye height and α the angular declination of the paired 0.5m-above-the-floor target. Since each paired target had the same angular declination, they were laterally shifted by 5 cm in the opposite direction from the observer’s sagittal plane to prevent the near target from occluding the far target from view.

Design

Two measurements were obtained for each pair of near and far targets, which were always presented together. We measured the observer’s judged location of the suspended near target using the blind walking-gesturing task. We also measured the observer’s judged distance separation between the near and far targets using the verbal report task. The blind walking-gesturing measurement was a fully-crossed-factor design with two factors: (i) three eye-to-target distances for the 0.5m-above-the-floor targets; (ii) three ground conditions (dark, parallel-texture, and convergent-texture). The verbal report measurement was also a fully-crossed-factor design with two factors: (i) three depth separations (figure 3d); (ii) three ground conditions (dark, parallel-texture, and convergent-texture) (figures 3a &3b). Each test display condition was tested twice. The order of display condition and task type tested was randomized.

Procedure

A trial began with the observer stepping on two small fluorescent dots on the floor (start location), as in Experiment 1. After a 0.5 sec audio alert signal that was generated by the computer, the test display consisting of one of the three paired targets plus one of the three ground conditions was presented for 8 sec. Prior to each trial, the experimenter informed the observer whether he/she was to perform the blindfolded walking-gesturing task or the verbal report task. No feedback regarding the task performance was given to the observer. Music was played aloud during the trial to prevent possible acoustic clues to distance. Before the data collection, each observer was given about 15 minutes to practice the tasks for familiarity with the test procedure.

Results and discussion

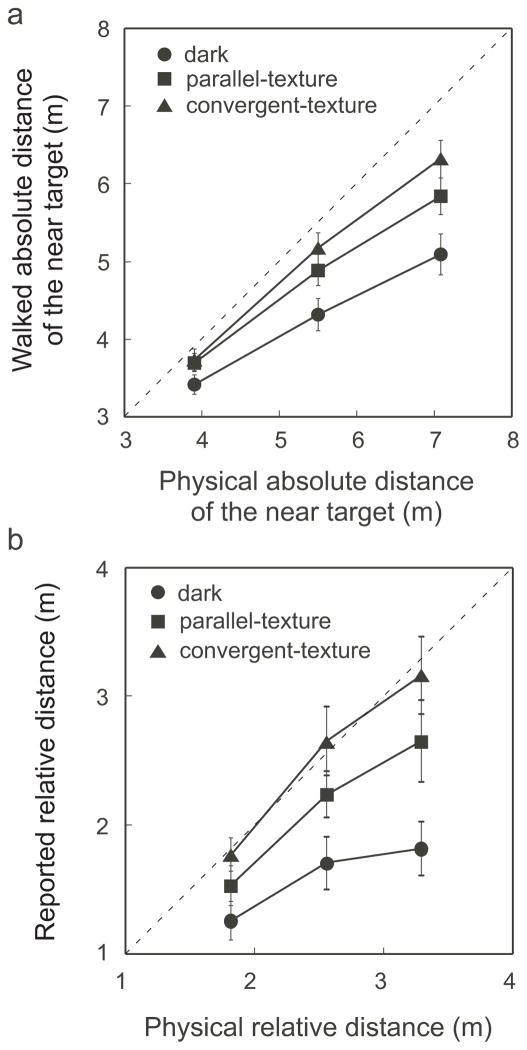
Figure 7a plots the average judged eye-to-target distances of the three near targets with the blind walking-gesturing task. As expected of space perception in reduced-cue environments, the observers underestimated the distances in all three ground conditions. Nevertheless, it is clear that the observers’ distance judgments were differently affected by the three ground conditions. This is confirmed by statistical analysis using two-way ANOVA with repeated measures [main effect of texture background condition: F(2,14)=45.879, p<0.001; main effect of eye-target distance: F(2,14)=136.569; p<0.001; interaction effect: F(4,28)=11.787; p<0.001]. Planned contrast analysis reveals a significant difference between the dark and parallel-texture conditions and the difference increases with the eye-to-target distance [main effect of ground condition: F(1,7)=30.259, p<0.001; main effect of eye-to-target distance: F(2,14)=117.7; p<0.001; interaction effect: F(2,14)=5.278; p<0.025]. There is also a significant difference between the parallel-texture and convergent-texture conditions and the difference increases with the eye-to-target distance [main effect of texture background condition: F(1,7)=14.116, p<0.01; main effect of eye-target distances, F(2,14)=135.957; p<0.001; interaction effect: F(2,14)=7.916; p<0.01]. The finding that the convergent-texture background, which adds false linear perspective, increases the perceived egocentric distance confirms the prediction of the ground-reference-frame hypothesis that the ground surface representation affects the perceived egocentric distance of a target suspended in midair (D_n).

Figure 7.

The average results of the three conditions in Experiment 2. (a) The judged locations of the near suspended target at three test distances measured with the blind walking-gesturing task. (b) The reported relative distance between the paired near and far targets measured with the verbal report task. In both (a) and (b), distance is most underestimated in the dark condition and least underestimated in the convergent-texture condition.

Figure 7b plots the average judged relative distance between each pair of near and far targets, for the three pairs of targets tested using the verbal report task. Judged relative distances were most underestimated in the dark followed by those in the parallel-texture condition. Judgments in the convergent-texture condition were least underestimated – they even appear to be accurate by falling along the diagonal line with a slope of unity on the graph. However, here, we must stress that our data should be considered in relative term rather than absolute. This is because although it is a useful task for comparing among conditions (relative difference), the verbally specified absolute value of distance is highly subjected to strong cognitive influence [Since the blind walking task is largely accurate in the full cue condition whereas the verbal report task is less so (e.g., Loomis et al, 1992), we can reasonably assume that the blind walking performance is closer to the observer’s perception than the verbal report performance in the reduced cue condition as well.] Thus, considered in relative term, it is clear that our observers’ performance is systematically affected by the ground surface conditions, in concordance with our prediction. Applying two-way ANOVA with repeated measures to the data, we found a significant effect of the ground condition [main effect of ground condition: F(2,14)=24.404, p<0.000; main effect of eye-to-target distance, F(2,14)=118.222; p<0.000; interaction effect: F(4,28)=1.974; p=0.126]. Planned contrast analysis reveals a significant difference between the dark and parallel-texture conditions [F(1,7)=26.374, p<0.005] and a significant difference between the parallel-texture and convergent-texture conditions [F(1,7)=12.709, p<0.01]. These findings thus confirm the prediction of the ground-reference-frame hypothesis that the ground surface representation affects the perceived relative distance between the target suspended in midair and a reference on the ground (d_r).

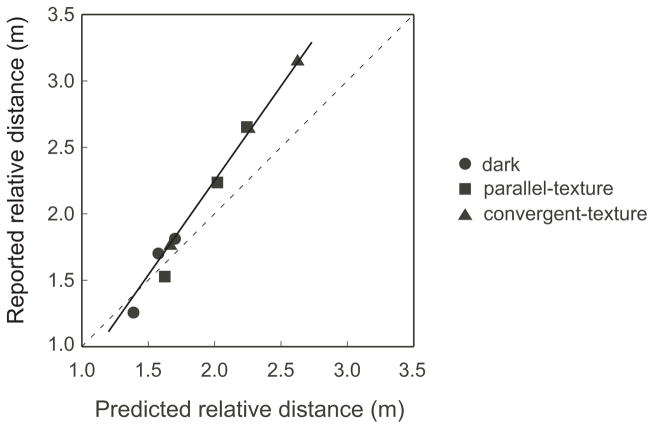
Overall, we showed that varying the monocular depth cue on the ground (parallel-texture vs. convergent-texture) affects the judged eye-to-target distance of the near target (D_n, figure 7a) and the relative distance between the near and far targets (d_r, figure 7b) in the same manner. According to the analysis in figure 2b, there exists a relationship between d_r, and D_n that is defined by the equation, d_r=D_n²η/(p−D_nη). To verify this, we correlated the perceived relative distance between the near and far targets with the predicted relative distance according to the equation. We derived the predicted relative distance (d_r) between each pair of near and far targets with the same angular declination from the measured D_n, according to the equation, d_r=D_n²η/(p−D_nη). [Note: For each pair, we used the physical relative binocular disparity (η) between the two targets and the judged eye-to-target distance of the near target (D_n)]. We then plotted the verbally reported relative distance as a function of the predicted relative distance for the results from the three ground conditions (dark, parallel-texture and convergent-texture) in figure 8. We found that the data points follow a linear trend (y=1.54x+0.67, R²=0.95) with a slope larger than unity. While a non-unity slope indicates that the measured D_n, and measured d_r do not exactly follow the equation, the linear relationship between the two indicates predictability. The larger than unity slope suggests the perceived D_n and d_r has a systematic deviation from the equation. The deviation from unity could be related to the fact that the judged D_n and d_r were obtained from different tasks, namely, blind walking-gesturing and verbal report. The two tasks differ in two aspects. First, the blind walking-gesturing task and the verbal report task may not be based on the same scaling mechanism. Wu et al (2007b) found that the verbal report task in the reduced cue condition exaggerates the scaling of space. Second, in our experiment, the blind walking-gesturing task measured egocentric distance representation (observer to target), whereas the verbal report task measured exocentric distance representation (relative distance between two targets). It is known that the perceptual processes underlying egocentric distance and exocentric distance operate differently, with exocentric distance judgment exhibiting a tendency for larger distance underestimation (e.g., Gilinsky, 1951; Loomis et al, 1992; Loomis, Philbeck, & Zahorik, 2002; Ooi & He, 2007; Wu et al, 2004; Wu et al, 2008). This factor should contribute to a reduction of the slope in figure 8 from unity. But since the slope in figure 8 is larger than unity, the first (scaling) factor above likely had a larger impact.

Figure 8.

A linear relationship is found between the judged relative distances measured with the verbal report task and the predicted relative distances using the data from all three conditions in Experiment 2. The predicted relative distance is obtained from the equation described in figure 2, d_r=D_n²Xtanη/(p−D_nXtanη). D_n is the judged eye-to-target distance of the suspended near target measured with the blind walking-gesturing task. η and p, respectively, are the relative binocular disparity between the suspended near target and far target on the ground, and the inter-pupillary distance.

Another factor might also contribute to the slope in figure 8. Our experiment used a reduced cue condition with a 2×3 array of (limited and dimly-lit) texture elements on the ground in total darkness, which rendered ground surface representation inaccurate. Moreover, the texture elements did not extend very far on the ground surface (He et al, 2004; Wu et al, 2004), which rendered the angular declination of a far target smaller than that of the farthest texture element (i.e., higher in the visual field). This factor not withstanding, the current study reveals that the texture pattern on the ground still affected the localization of (far) test targets higher in the visual field, indicating that the ground surface representation was used as a reference frame. It would be interesting to explore how using an extended texture array with higher density that leads to a more accurate ground surface representation and consequently more accurate egocentric distance and relative distance judgments, will affect the linear relationship in figure 8.

It should be noted that the linear relationship revealed in figure 8 was obtained from a stimulus display using two targets with the same angular declination. Having the same angular declination of the paired targets allows for simplicity of computation for deriving the predicted relative distance from the physical binocular disparity. While there is no reason to argue against the prediction that the linear relationship also holds for other paired targets with different angular declinations, future investigation to confirm it is warranted.

Lastly, it should be emphasized that the current experiment was conducted only with binocular viewing because our main goal was to reveal the interactive roles of the ground surface and binocular depth processes in determining the space perception of a midair target. Recall that the main goal of Experiment 1 was to reveal whether binocular depth plays a significant role in perceiving absolute distance of a midair target. Accordingly, it tested both the monocular and binocular viewing conditions, and showed that with sufficiently long stimulus duration (5 s), perceived absolute distance is more veridical with binocular than monocular viewing. Similarly, a number of previous studies have revealed that perceived relative depth in the intermediate distance range is more veridical with binocular viewing (e.g., Allison et al, 2009; Loomis & Philbeck, 1999; Wu et al, 2008). Taken together, we can surmise that the binocular depth processes due to binocular viewing render both absolute and relative depth perception more veridical. As such, it is reasonable to conclude that the results in figure 8 reflect the impact of the texture pattern delineating the ground surface on the binocular depth processes.

Experiment 3: Ground vs. ceiling surface as a reference frame

We predicted that the ground surface located below the eye level in the lower visual field affords more accurate localization of a suspended target in midair than the ceiling surface in the upper visual field. To test the prediction, we placed a parallel texture background that was similar to the one used in Experiment 2 above (figure 3a) to delineate the surface in a dark room (figure 9a), either above (upper field/ceiling) or below (lower-field/ground) the eye level, and measured the judged location of a dimly lit target with binocular viewing.

Figure 9.

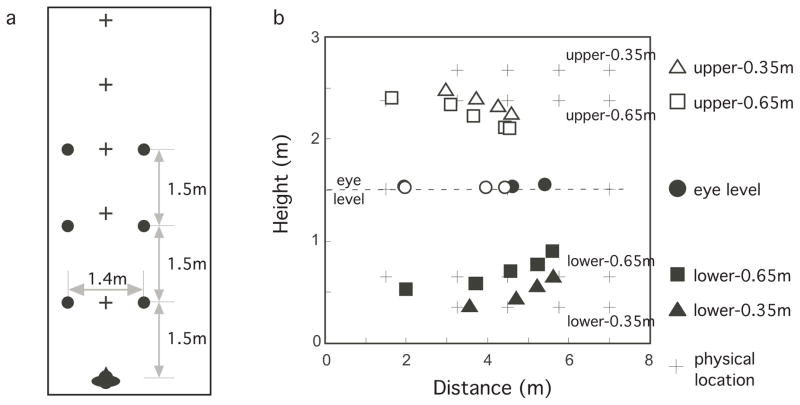
Experiment 3. (a) Top-view of the 2×3 parallel texture background layout (black dots) and the target’s horizontal distances (plus symbols). (b) Targets at the same height in either the upper (open symbols) or lower (filed symbols) visual fields are judged not at their physical locations (plus symbols) but along implicit curved surfaces.

Method

Observers

Nine new naïve observers with informed consent participated in the experiment. All had normal, or corrected-to-normal, visual acuity (at least 20/20), and a stereoscopic resolution of 20 sec arc or better. Their average eye height was 151 cm and they viewed the test display with both eyes.

Design

We measured the observer’s judged location of the target using the blind walking-gesturing task (Giudice et al, 2013; Ooi et al, 2001) and the observer’s judged eye-to-target distance using the verbal report task in different experimental sessions. The blind walking-gesturing measurement was a fully-crossed-factor design with two factors: (i) texture surface location conditions (lower and upper fields) and (ii) target locations. The verbal report measurement adopted a similar fully-crossed-factor design with two factors.

Stimulus configuration and test environment

All tests were run in a dark room (8×13m) whose layout and dimension were unknown to the observer. Its ceiling (3.1m height) and walls were painted black and the floor had black carpeting. A 15m long rope (0.8m above the floor) tied to both ends of the room was used to guide the observer while blind walking. Music was played a loud during the testing to mask possible acoustic cues from revealing the target location.

The test target was constructed from a ping-pong ball that was internally illuminated by a green LED (0.16 cd/m²) and controlled by a computer. An iris-diaphragm aperture in the front of the ping-pong ball kept its visual angle at 0.20deg when measured at the eye level. In the blind walking-gesturing task, the suspended test target was located at one of 21 locations with a combination of distances (1.5, 3.25, 4.5, 5.75, 7m) and heights [lower visual field: 0.35 and 0.65m above the floor (labeled as lower-0.35m and lower-0.65m); at the eye level; upper visual field: 2 × observer’s eye height - 0.35 cm and 2 × observer’s eye height - 0.65 cm (labeled as upper-0.35m and upper-0.65m)] (plus symbols in fig. 9b). The target heights were specially chosen to ensure that the heights in the upper and lower visual fields were symmetrical about the observer’s eye level. In the verbal report task, the test target was placed at one of nine locations with a combination of 2 distances (5.75m and 7m) and 4 heights (lower-0.35m, lower-0.65m, upper-0.35m, upper-0.65m), and at 7m at the eye level. During testing in each of the two tasks, we also inserted catch trials, which comprised 1/3 of the total trials, in a random order. The target locations of the catch trials were different from the test trials and their combination of distance and height were: (3.25m, upper-0.35m), (3.25m, lower-1m), (4.50m, upper-0.65m), (4.50m, lower-0.35m), (4.50m, eye level), (5.75m, on the floor).

The texture background that delineated the ground or ceiling surface was constructed from six ping-pong balls with internally illuminated red LEDs (0.08 cd/m²). Each ball was housed inside a small box with a 2.5 cm (diameter) circular opening. The balls were arranged in a 2×3 formation (fig. 9a). The texture background was placed either 1.25m above or 1.25m below each observer’s eye level to ensure symmetry between the lower and upper surfaces. During the test, if the target was not at the eye level, only the texture background in the same field was presented simultaneously (5 Hz flickering for 5 sec duration). If the target was at the eye level, the texture background in either the upper or lower field was displayed (with an overall 50% chance of each texture background been presented). The texture backgrounds and their presentation were the same in both the walking-gesturing and verbal report sessions.

Procedures

(1) Blind-walking-gesturing session

At the start of the experimental session, the observer was blindfolded and brought into a waiting area within the test room. He/she then removed the blindfold and sat on a chair that faced away from the test area to wait for further instructions from the experimenter. To begin a trial, the experimenter turned on a computer-generated tone to alert the observer to get ready for the trial. Thereupon, the observer turned off the room’s light, walked to the starting point (observation position marked by fluorescent elements on the floor) with the aid of the guidance rope, stood upright and called out “ready”. After a 5 sec delay, the test target and texture background flickering at 5 Hz was turned on for 5 sec for the observer to judge the target location. After judging the target location, he/she donned the blindfold and verbally indicated that he/she was ready to walk. The experimenter immediately removed the target and shook the guidance rope to indicate the course was clear for walking. The observer walked to the remembered target location while sliding his/her left hand through the guidance rope. Upon arriving at the remembered target location, he/she indicated the remembered target height with the 1m-rod and called out “done”. [The purpose of the 1m-rod was to allow the observer to “gesture” the perceived location of the target when it was beyond the reach of the observer’s hand (higher) (also see Giudice et al, 2013).] The experimenter marked the observer’s feet location, measured the height indicated by the tip of the rod, and informed the observer to turn and walk back to the waiting area. Upon reaching the waiting area, he/she switched on the lamp, removed the blindfold, and sat down to wait for the next trial. Meanwhile, the experimenter prepared for the next trial. A total of 104 trials were run over four days (sessions) (i.e., 21 test and 5 catch trials per session). The order of stimulus presentation was randomized, with the first and fourth sessions adopting the same randomization sequence and the second and third sessions having the reversed randomization sequence. Observers were given up to five practice trials before each session to familiarize themselves with the experimental protocol.

(2) Verbal-report session

As in the blind walking-gesturing sessions, the observer was walked into the test room blindfolded and sat at the waiting area while the experimenter prepared the test target. Once the target was in place, a computer-controlled tone alerted the observer to switch off the light and walk to the observation/starting point. Five sec after the observer indicated that he/she was ready, the 5 Hz target and texture background were presented for 5 sec. A tone indicated the end of target presentation and the observer verbally reported the eye-to-target distance of the target. He/she then turned around, walked back to the waiting area and switched on the light while the experimenter recorded the distance and prepared the next target. Each test location was repeated twice. A total of 26 trials (20 test and 6 catch trials) were run in one test session. The observers were given up to five practice trials before the test session for familiarization with the experimental protocol.

Results and discussion

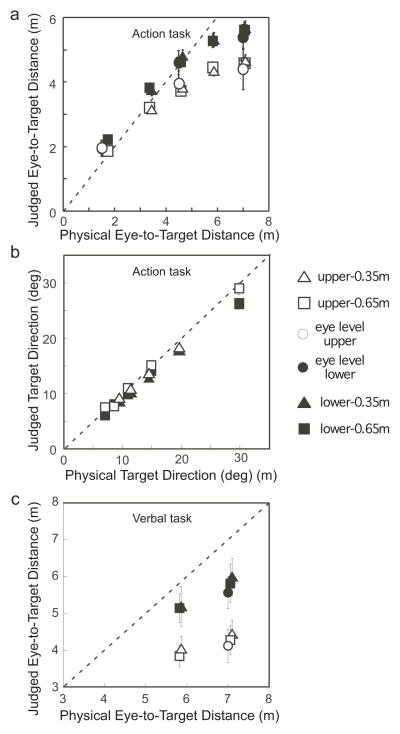
The plus symbols in figure 9b depict the physical locations of the test stimuli in the upper and lower visual fields, and at the eye level, while the square, circle and triangle symbols indicate the average judged target locations. The data points for targets at the same height, shown with the same symbols, form a slanted curve profile. Notably, there exists a significant difference between the perceived target locations in the two fields. The target was judged more accurately, i.e., closer to the physical target location, when the texture background was in the lower field than in the upper field. This suggests a ground surface superiority. These data are re-plotted in figure 10a, which compares the perceived eye-to-target distance to the physical eye-to-target distance. The dash line in the graph depicts the equidistance location. Clearly, judged target location in the lower visual field were more accurate for all distances tested than those in the upper field [Main effect of the field (upper/lower): F(1, 8)=66.94, p<0.001; Main effect of the eye-to-target distance: F(1.82, 14.59)=130.79, p<0.001; Interaction effect between the field and eye-to-target distances: F(8,64)=6.08, p<0.001; 2-way ANOVA with repeated measures and the Greenhouse–Geisser correction]. Equally revealing, is the judged locations of the targets at the eye level, wherein the judged eye-to-target distance was also significantly shorter (less accurate) when the texture background was placed in the upper field (open disks) than in the lower field (filled disks) [Main effect of the texture field (upper/lower): F(1, 8)=48.52, p<0.001; Main effect of eye-to-target distance: F(2, 16)=245.67, p<0.001; Interaction effect between the texture field and eye-to-target distance: F(2, 16)=30.32, p<0.001; 2-way ANOVA with repeated measures]. These results confirm that the surface of a ground is more reliably represented for object localization than the surface of a ceiling.

Figure 10.

Experiment 3. (a) The asymmetric surface representation of the texture surface causes judged eye-to-target distance to be more accurately located in the lower (filled symbols are closer to the dash equidistance line) than in the upper (open symbols) visual field. (b) Judged target direction (angular declination in the lower visual field or angular elevation in the upper visual field relative to the eye level) is similar in the two visual fields. (c) Verbally reported judged eye-to-target distance is also more accurate in the lower (filled symbols are closer to the dash equidistance line) than in the upper (open symbols) visual field.

The data in figure 9b allow us to derive the mean judged target direction, i.e. the angular declination (of the target in the lower field) or angular elevation (of the target in the upper field) with reference to the eye level. Figure 10b plots the average judged target directions (open symbols: angular elevation in the upper field; filled symbols: angular declination in the lower field). There is no significant vertical asymmetry between the two fields [Main effect of the field (upper/lower): F(1, 8)=2.43, p=0.158; Main effect of direction: F(2.08, 16.62)=340.92, p<0.001; Interaction effect between the field and direction: F(8, 64)=1.93, p=0.071; 2-way ANOVA with repeated measures and the Greenhouse–Geisser correction]. Together with the eye-to-target distance data in figure 10a, this indicates that the space perception difference between the upper and lower fields is largely due to errors in the judged eye-to-target distance rather than errors in the judged target direction.

Figure 10c plots the verbal report results. The reported eye-to-target distance was longer(more accurate) when the texture background was in the lower field than in the upper field, both for targets at the eye level [t(8)=7.61, p<0.001] and for targets not located at the eye level [Main effect of visual field (upper/lower): F(1, 8)=52.51, p<0.001; Main effect of the eye-to-target distance: F(3, 24)=8.55, p<0.001; Interaction effect between the texture field and distance: F(1.35, 10.78)=1.79, p=0.213, 2-way ANOVA with repeated measures and the Greenhouse–Geisser correction].

A finding of a more accurate performance in object localization with the ground surface reference frame is consistent with the notion that our visual system is shaped to interact effectively in the terrestrial environment. Thus, our finding of a more veridical space perception on the ground adds to those of previous studies that found the visual system has a preference to efficiently process ground over ceiling surfaces (Bian et al, 2005; 2006, 2011; Imura & Tomonaga, 2013; Kavšek & Granrud, 2013; McCarley& He, 2000; McCarley& He, 2001; Morita & Kumada, 2003).

General discussion

We tested the ground-reference-frame hypothesis that the visual system can locate a target suspended in midair in the intermediate distance range (2–25m) by using the ground surface representation as a reference frame. In particular, the ground surface allows the visual system to obtain the relative binocular disparity between it and the midair target to facilitate space perception. Supporting the hypothesis, our first experiment shows that the judged distance of a suspended target is more veridical with binocular viewing when the ground surface is delineated with texture-gradient and/or linear-perspective information. Judged distance is less accurate with monocular viewing or when the ground surface is not visible in the dark. Then our second experiment finds that manipulation of texture-gradient and/or linear perspective cues on the ground surface (parallel vs. convergent), which is known to affect the ground surface representation and perceived distance on the ground, significantly influences the judged distance of the suspended target. The effect of texture-gradient and/or linear perspective cues cannot be caused by the local-binocular-depth-integration mechanism that is independent of global surface representation. Finally, our quantitative analysis suggests that the visual system scales relative distance from binocular disparity using the ground surface representation as a reference.

Our study adds to the knowledge of space perception in the intermediate distance range in three ways. First, according to the Ground Theory of Space Perception, the visual system uses the ground surface as reference frame for localizing objects (Gibson, 1950, 1979; Ooi & He, 2007; Sedgwick, 1986; Sinai et al, 1998). Further supporting the theory, we now show that in the real world setting, the configuration of the ground surface can influence distance perception of an object suspended in midair. Therefore, the role of the ground surface as a reference frame is not limited to the ground itself and to those surfaces having nested contact relationships to the ground, but extends also to the empty space beyond the ground (Bian et al, 2006; Madison et al, 2001; Meng& Sedgwick, 2001, 2002; Ni et al, 2004, 2007).

Second, the current study provides an answer to the open question of how binocular depth perception is obtained for a single target suspended in midair in the intermediate distance range. To compute, or scale metric relative depth from relative binocular disparity between two targets, the absolute distance of one of the two targets is required. Our study demonstrates one way this is derived, namely, by relying on the ground surface. For a target on the ground in the intermediate distance range (figure 2a), the visual system can obtain its absolute distance, D_f, by relying on monocular depth cues as such texture gradient and linear perspective (Wu et al, 2014). Then, as shown in figure 2b, the visual system employs the absolute distance information, D_f, to derive relative depth, d_r, according to the relationship, d_r=ηD_f²/(ρ+ηD_f).

Third, by measuring the judged location (egocentric distance) of the suspended target and its distance relative to another target on the floor in the same setting, we are able to investigate the relationship between perceived relative distance and perceived egocentric distance (figures 6 & 7). Such a relationship has not been investigated by previous depth perception studies, which only measured one of the two perceived distances.

Overall, the current study reveals that the mechanisms underlying our perceptual space have a preference to utilize the ground surface as a reference frame for locating a target suspended in midair. More generally, our findings support the view that the common surface has a prevalent role in influencing our visual perception and affording efficient attention deployment. Furthermore, the ground surface is an effective common surface owing to its biological significance to its terrestrial inhabitants.