Exposure to Alcohol Outlets in Rural Towns

Abstract

Background

Lower income populations are exposed to excess risks related to the presence of greater concentrations of alcohol outlets in their communities. Theory from economic geography suggests this is due to dynamic processes that shape urban retail markets (as outlets are attracted to areas of higher population density due to the increased demand but are excluded from higher income areas due to land and structure rents). This mechanism may explain increased exposure to alcohol outlets for lower income populations in rural areas. This study tests the hypothesis that the distribution of outlets between rural towns will reflect these market dynamics, such that outlets are concentrated in towns with (i) greater resident and temporary populations, (ii) lower income, and (iii) are adjacent to towns with higher income.

Method

Bayesian conditional autoregressive Poisson models examined counts of bars, restaurants and off-premise outlets within 353 discrete towns of rural Victoria, Australia (mean population = 4,326.0, SD = 15,754.1). Independent variables were each town’s total resident population, net changes to population (due to commuter flow, visitors, and the flow of local residents to other towns (spatial interaction)), and income for the local and adjacent towns.

Results

Lower local income and increased income in adjacent towns were associated with more outlets of all types. Greater resident populations and greater net population due to commuters also predicted greater numbers of all outlets. Bars and restaurants were positively related to greater net population due to visitors, and negatively related to spatial interaction.

Conclusions

The economic geographic processes that lead to greater concentrations of alcohol outlets in lower income areas are common to all retail markets. Lower income populations are exposed to increased risk associated with the presence of additional outlets that service demand from non-residents. In rural areas these processes appear to operate between discrete towns.

INTRODUCTION

Alcohol has a marked impact on global health, accounting for 3.8% of deaths and 4.6% of disability adjusted life years worldwide (Rehm et al., 2009). Alcohol related problems (e.g. trauma, chronic disease, suicide) occur more frequently in areas with a greater density of alcohol outlets (Campbell et al., 2009), and outlets themselves tend to be concentrated in lower income areas. (Gorman and Speer, 1997, Hay et al., 2009, Pearce et al., 2008, Romley et al., 2007, Berke et al., 2010). Cumulatively, these observations suggest that lower income populations are exposed to excess risk related to the presence of additional outlets in their neighborhoods. Theory from economic geography explains this health disparity as the product of dynamic social and economic processes common to urban retail markets; specifically, because outlets are attracted to areas with greater demand for alcohol and are excluded from higher income areas. However, the different scale and topological structure (i.e. transport systems, land use) of urban compared to rural areas may mean these processes cannot be generalized from urban to rural settings (Rodrigue et al., 2006). This study examines the extent to which residents of rural towns in Victoria, Australia, are exposed to alcohol outlets in light of this hypothesized mechanism.

Gorman and Speer (1997) framed examination of alcohol outlet locations as a study of drug markets, defining a market as a geographic space in which buyers and sellers perform transactions. In that context, competition for market share will encourage operators to locate in and near to areas with high population due to the increased overall alcohol consumption (i.e. demand) in that area. However, purchases by the resident population are not the sole driver of demand in an area. Consumers who purchase alcohol outside their local area (e.g. while visiting entertainment districts, shopping, commuting) effectively increase demand at the destination. Conversely, where that purchase replaces one that would otherwise have occurred in the area of residence, demand at the origin reduces (Aoyama et al., 2011, Hanson, 2005, Harris, 1954). Income is also related to demand, because higher income populations tend to consume more alcohol (Pollack et al., 2005). The increased demand will therefore attract outlets to high income areas. However, land and structure rents in high income areas tend to exclude retail space, and higher income populations are better resourced to oppose undesirable land uses (DiPasquale and Wheaton, 1992). Excluded from the high income areas, more outlets will be located in low income areas adjacent to high income areas so as to reduce convenience costs. Assuming equilibrium between supply and demand (Gruenewald, 2007), these dynamic processes will be observable in the total supply which individual areas of a market can support.

This study uses counts of licensed venues (bars, restaurants and off-premise outlets) as a proxy for alcohol supply within areas, then examines population level predictors of outlet location. Previous studies have used this approach within census or administrative regions (Gorman and Speer, 1997, Hay et al., 2009, Pearce et al., 2008, Romley et al., 2007, Berke et al., 2010); however, convenient spatial units are arbitrary, non-random, and not representative of the micro-spatial patterns within communities (Openshaw and Rao, 1995). This criticism is particularly relevant to rural geographies which span high density population centers and uninhabited or very low density regional tracts. To address this problem, I aggregated small spatial units into a population-density based geography to represent rural towns in Victoria, then used Census demographic and trip to work data to estimate the characteristics of each town. To account for demand by local residents I calculated the total population and average income of each town; to account for demand by non-residents I estimated the net change in population (due to commuters, visitors, and the flow of a town’s residents to other towns). I then tested the specific hypotheses that residents of towns (i) with greater resident and temporary populations, (ii) with lower income, and (iii) that were adjacent to higher income areas would be exposed to greater numbers of alcohol outlets.

MATERIALS AND METHODS

Spatial Unit Definition

This study utilized publically accessible data from three sources: population data from the Australian 2011 Census, roadway network data from the Victorian Department of Sustainability and Environment (VicMap Transport (version 3.4)), and liquor license data from June 2011 from the Victorian Commission for Gambling and Liquor Regulation.

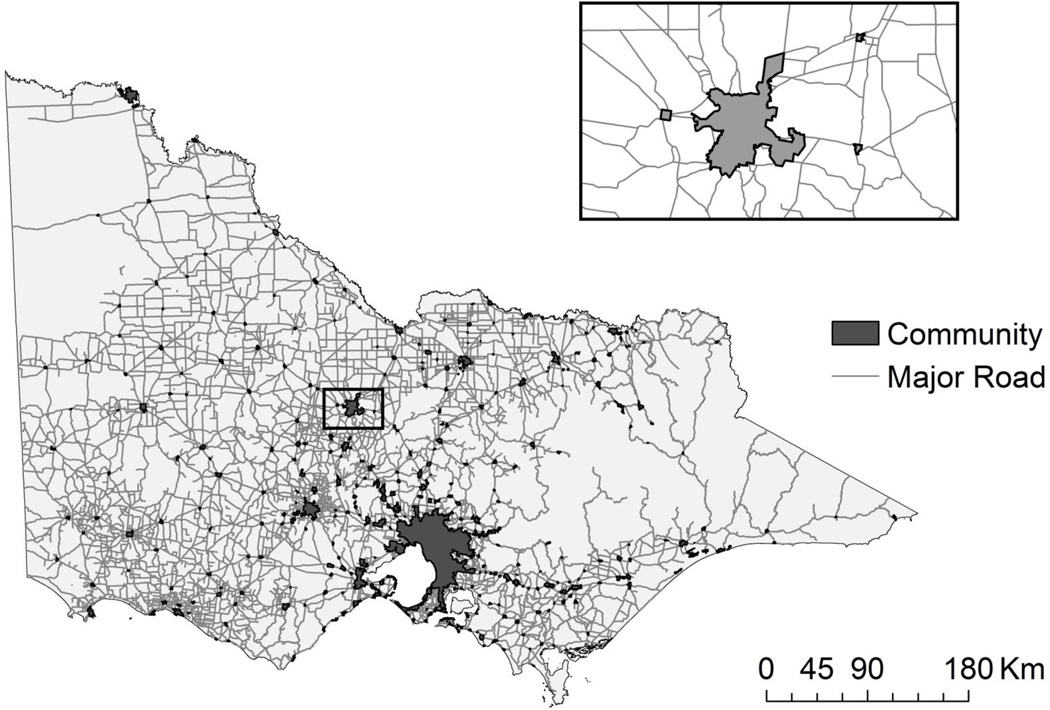
Statistical Area level 1 (SA1) regions (mean population = 400.1; SD = 194.5) are the smallest spatial unit at which the Australian Bureau of Statistics releases Census data (ABS, 2011). In order to construct spatial units which identified rural population centers areas wholly surrounded by sparsely populated areas, all SA1 regions with a population density greater than 50 people per km² or with a total land area less than 5 km² were selected. Dissolving contiguous selected SA1 regions and including any excluded SA1 region wholly surrounded by included regions transformed these units into convex hulls (i.e. polygons without donut holes)(Figure 1). This procedure produced 354 non-contiguous population density-defined units which contained 93.0% of the state’s resident population. After overlaying roadways with class code 0 (freeway), 1 (highway), 2 (arterial), 3 (sub-arterial) or 4 (collector road), these units were conceptualized as a network of towns connected by a system of major roads; every town in the network was connected to every other town. Based on local knowledge of the study area this approach provided a good approximation of the rural population centers of Victoria. To define an adjacency matrix, I constructed Thiessen polygons around the centroid of each town (such that every location within the polygon was closer to that town’s centroid than any other). Towns with adjacent polygons were considered neighbors; adjacencies for neighboring pairs not connected by road were manually removed from the matrix.

Figure 1.

Population density-defined towns (n = 354) and the major roadway network; Victoria, Australia. The inset shows the town of Bendigo (population = 83,901) and three surrounding towns (populations = 218 to 351).

Importantly, the major metropolitan area of Melbourne was represented in the network by a single town with a population of 3.5 million (220.1 standard deviations compared to the mean population of the other towns). Such an extreme outlier has the potential to substantially affect estimates, so this unit was excluded from the final analyses. However, Melbournians may travel to other towns, and residents of other towns may travel to Melbourne, affecting alcohol demand (and therefore, supply) in both locations. As such, Melbourne and its resident population were allowed to interact with the network when calculating the characteristics of other towns.

Variables

The dependent variable was exposure to alcohol outlets, measured using counts of bars (General and Late Night-General licenses), restaurants (Restaurant and Café license) and off-premise (Packaged or a Late Night-Packaged licenses) inside the boundary of each town; 99.7% were geocoded to a street address.

Independent variables representing income were the population weighted mean of the median household income (i.e. local income), and the population weighted mean income of towns with topologically-corrected adjacent Thiessen polygons (i.e. lagged income). Other variables were the town’s total resident population and other factors which were theoretically related to net changes in population: commuters, visitors, and spatial interaction (i.e. the flow of residents from a town to all other towns). Total resident population was calculated as the sum of the populations of the SA1 regions in the town. For commuters, a matrix of one day journeys to work is available at the Statistical Area Level 2 (SA2) geography (mean population = 14,452.2; SD = 6,736.5), enabling calculation of flow between regions. Taking the SA2 unit in which the centroid of each rural town fell, the proportion increase relative to SA2 population provided an estimate of additional population due to commuters in each town. For visitors, the ABS also reports the total number of people who were in each SA1 on Census night but reside in another SA2. To calculate the additional population due to visitors for each town, the total number of visitors was denominated by the town’s total resident population.

The procedure to estimate spatial interaction was more involved. The flow of residents from origin town i to destination town j is a function of the “attractiveness” of town j, the distance between them, and a parameter describing the rate of distance decay (β) (Rodrigue et al., 2006, Griffith, 1979, Wilson, 1970). The spatial interaction term (I) estimates the overall flow of residents of the origin town to all other towns in the state by summing their distance decayed attractiveness:

$$I_i=\sum _{m=i}{}_1{}^m(p_j\times {d_{ij}}^{{\beta }_j})$$ (1)

Given that the true attractiveness of each town is unknown, the population (p) of town j is commonly used as a proxy (Rodrigue et al., 2006). The road distance between towns was calculated using the major roadway network, such that a 354 by 354 distance matrix represented the road distance in kilometers between the centroids of a given pair of towns.

An origin-destination matrix of one-day commute journeys between SA2 census regions and the roadway distance between SA2 centroids combined to provide a destination-specific distance decay parameter (β_j). For each destination SA2 region (x), the logged proportion of commuters (c) who came from origin SA2 (y) was regressed on the logged road distance between the two SA2 regions (Fotheringham, 1981).

$$\text{ln}(c_{xy})={\beta }_0+{\beta }_1(\text{ln}(d_{xy}))+e$$ (2)

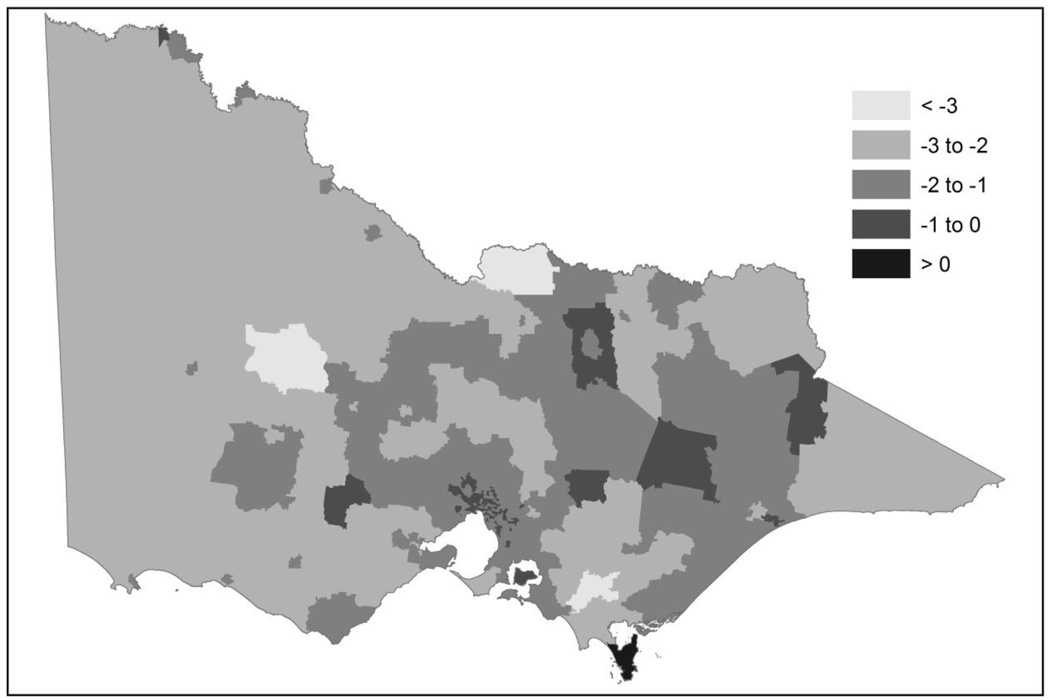
The slope of this ordinary least squares model estimated the destination-specific rate of distance decay (β₁). Parameter estimates for all SA2 regions in the state were between −3.37 and 0.18 (mean = −1.25; SD = 0.56) (Figure 2). Only one SA2 region (Wilson’s Promontory National Park) had an estimate > 0, indicating that as distance from that destination increased the proportion of commuters from other origin regions increased. This region was outside the boundary of all included towns. Distance decay tended to be greater for travel to very rural areas of northern and western Victoria compared to the urban areas around Port Phillip Bay, indicating that commuters were more sensitive to increased commute distance in these remote regions.

Figure 2.

Destination-specific distance decay coefficients for commute journeys between SA2 regions; Victoria, Australia

In order to calculate the spatial interaction terms (I), each town j was assigned the β₁ parameter for the SA2 region in which its centroid was located. By this method, a one unit increase in spatial interaction was equivalent to an increased population of 10,000 in a town 100km away with a distance decay coefficient of β = −2. As greater spatial interaction represented a greater flow of residents of a town to other towns in the state, it was expected to be negatively associated with the number of outlets due to the reduced demand at the origin.

Statistical Analysis

After excluding Melbourne, there were 353 rural towns in the network. Bayesian conditional autoregressive Poisson models predicted counts of outlets (y) within these towns (i) according to the association (b) with predictors (x):

$$y_i=b_0+b{x}_i+{\theta }_i+{\alpha }_i$$ (3)

A random effects term (θ_i) was included to account for the spatially unstructured heterogeneity within individual towns, as was a conditional autoregressive (CAR) random effect (α_i) that controls for spatially autocorrelated errors and addresses the small area problem by borrowing strength from surrounding regions (Waller and Gotway, 2004). This term also effectively controls for over-dispersion of the of the count data (Lord et al., 2005).

Three final models predicted counts of bars (Model 1), restaurants (Model 2), and off-premise outlets (Model 3) according to the independent variables representing population and income. Geo-processing was performed using ArcGIS v10.1 (ESRI, 2011) and non-spatial data management was performed using Stata v12.0 (StataCorp, 2011). Bayesian models were estimated using WinBUGS v4.3.1 (Lunn et al., 2000). Uninformed priors were specified for all random effects, and all models were allowed to converge over a 50,000 iteration burn-in before 50,000 iterations were sampled to provide model results.

RESULTS

The 353 towns had a mean land area of 7.9 km² (SD = 17.2) and a mean total resident population of 4,236.0 (SD = 15,754.1) (Table 1). Household income ranged between $25,237 and $125,091 per year. The average income for adjacent towns was between $28,939 and $95,411. Towns had between 0% and 91.6% additional residents on census night due to visitors (the highest values were for alpine resort areas), and net commuter flow was between −34.2% and 90.0% of the total resident population. There were 908 bars, 809 restaurants, and 676 off premise outlets in the 353 towns.

Table 1.

Characteristics of rural towns in Victoria, Australia (n = 353)

	Mean	SD	Min	Max
Area (km2)	7.86	17.17	0.19	160.76
Distance decay parameter	−1.64	0.51	−3.16	−0.46
Demand
Total resident population	4235.96	15754.10	22.00	197280.00
Commuters (%)	−7.79	14.29	−34.19	89.96
Visitors (%)	5.28	9.13	0.00	91.59
Spatial interaction (I)	17158.38	13614.91	3823.94	76068.56
Median Household Income
Local	51309.00	16547.63	25237.21	125091.10
Lagged	51105.73	12685.47	28939.37	95411.18
Alcohol Outlets
Bars	2.57	6.03	0.00	64.00
Restaurants	2.29	7.54	0.00	88.00
Off Premise	1.92	5.11	0.00	63.00

Table 2 presents the results of the Bayesian spatial models. Model 1 shows that a 10,000 person increase in the total resident population (i.e. a 23.7% increase from the mean) was associated with a 28.8% increase in the number of bars (IRR = 1.29; 95% CI: 1.21, 1.37). An additional 10% population due to visitors was associated with 17% more bars (IRR = 1.17; 95% CI: 1.05, 1.31) and an additional 10% population due to commuters was related to 19% more bars (IRR = 1.19; 95% CI: 1.10, 1.29), while greater spatial interaction was associated with fewer bars (IRR = 0.83; 95% CI: 0.73, 0.95). A $10,000 increase in local income was associated with 20.2% fewer bars (IRR = 0.80; 95% CI: 0.72, 0.89), whereas a $10,000 increase in the average income of adjacent towns was associated with 23.3% more bars (IRR = 1.23; 95% CI: 1.08, 1.41). For restaurants (Model 2) there was a similar pattern as for bars, however the effect sizes differed. The relationships for commuter flow, visitors and spatial interaction were stronger in the same respective directions. For off-premise outlets (Model 3), credible intervals for visitors and spatial interaction included the possibility of no association.

Table 2.

Bayesian conditional autoregressive Poisson models of counts of alcohol outlets within towns in rural Victoria (n = 353)^*

	Model 1 (Bars)			Model 2 (Restaurants)			Model 3 (Off Premise)
Variable	median	2.5%	97.5%	median	2.5%	97.5%	median	2.5%	97.5%
Demand
Resident population (×10,000)	1.288	1.213	1.372	1.538	1.349	1.757	1.339	1.263	1.424
Commuters (×10%)	1.191	1.103	1.289	1.261	1.074	1.487	1.151	1.063	1.247
Visitors (×10%)	1.172	1.047	1.314	1.468	1.181	1.835	1.032	0.883	1.187
Spatial interaction (×10,000 units)	0.833	0.727	0.950	0.752	0.589	0.953	0.929	0.823	1.048
Median Household Income
Local (× $10,000)	0.798	0.716	0.887	0.751	0.603	0.927	0.811	0.717	0.907
Lagged (× $10,000)	1.233	1.082	1.412	1.697	1.355	2.198	1.304	1.135	1.499
Proportion of SA1 variance explained by CAR random effect	0.025	0.001	0.345	0.001	0.000	0.068	0.003	0.000	0.043
SD of CAR random effect	0.109	0.017	0.428	0.037	0.014	0.408	0.035	0.014	0.141
SD of noise random effect	0.669	0.545	0.787	1.546	1.315	1.825	0.681	0.562	0.814
Global Moran’s I for CAR random effect	0.855			0.805			0.725

^*Intercept suppressed from table; bolded odds ratios denote a 95% credible interval that does not include 1.000, thereby indicating support for an association between the corresponding independent variable and counts of alcohol outlets.

Global Moran’s I for the CAR random effects for the three models was between 0.73 and 0.87, indicating that the spatially structured heterogeneity was highly autocorrelated. Were the analyses not adjusted appropriately, the likelihood of making a type I error would have been high. The spatial pattern of the CAR posteriors was not consistent between models, suggesting this autocorrelation was not due to a single unmeasured regional variable common to the three outlets types.

DISCUSSION

These findings support the hypothesis that alcohol outlets are distributed in rural towns in a manner consistent with the economic processes that shape retail markets. Indicators of greater demand predicted greater supply: total resident population was positively associated with the number outlets, and net increases in population were related to increased numbers of outlets. Higher income was related to fewer outlets in local areas and more outlets in adjacent areas. These factors have the overall effect that residents of lower income towns are exposed to excess risk associated with exposure to additional outlets that service demand from residents of other towns.

This study is the first to explicitly examine relationships between net changes in population and the exposure of local residents to additional outlets. This contribution is substantial. The simplified topological structure of this rural setting allowed commuters, visitors and spatial interaction to all be included in the models. Estimated effects were very strong (for example, the 47% increase in restaurants related to a 10% increase in population from visitors is an elasticity of +4.7), suggesting that analyses that do not account for this additional demand will greatly underestimate the exposure of resident populations to outlets. However, it may be difficult to characterize the movement of people and resources between places in geographically complex metropolitan settings, and to differentiate the effects of these dynamics on alcohol supply from background noise (Rodrigue et al., 2006). This presents a major obstacle for future analyses, particularly given that distance decay coefficients were greatest around metropolitan Melbourne, so these net changes in population appear to be most pronounced in dense urban areas.

There were key differences between the outlet types and these indicators of net population change. Specifically, counts of bars and restaurants were related to visitors and to spatial interaction, but off-premise outlets were not. The lack of an association between off-premise outlets and visitors suggests that these non-residents (e.g. tourists, business travelers) tend not to contribute to increased off-premise alcohol sales (though, notably, the proportion of visitors was very strongly related to restaurants). The lack of an association between off-premise outlets and spatial interaction is best understood through a conceptual framework from transport geography (Rodrigue et al., 2006). For spatial interaction to occur, three independent conditions must be met: (i) complementarity between demand at the origin and supply at the destination; (ii) the absence of an intervening opportunity (i.e. another outlet closer to the origin offering an equivalent or better product or experience); and (iii) transferability (i.e. the origin and destination must be linked by transport infrastructure). The social, physical and economic dimensions of bars and restaurants differ markedly compared to other bars and restaurants (Gruenewald, 2007), so another outlet near the home may not represent an equivalent unit to one further away. By contrast, the product ranges of off-premise outlets are generally similar, so the location of a nearby outlet creates an intervening opportunity, preventing spatial interaction. In sum, the differential effects of spatial interaction for on- and off-premise outlets and the positive effects of adjacent income for all three license types suggest that off-premise outlets service demand from only the local and adjacent towns, but bars and restaurants service demand from residents of adjacent towns and those further afield.

The negative relationships between local income and outlet density were similar to those reported in studies conducted in other rural areas (Berke et al., 2010, Hay et al., 2009, Pearce et al., 2008). Results mostly concurred with the findings of another study in rural Victoria (Livingston, 2012) which used 2006 Census Collection Districts (similar to the SA1 units in the 2011 Census) and found that there were more general (pubs, hotels, taverns) and packaged (off-premise) liquor licenses in low socio-economic areas. However, evidence of an association between socio-economic status and exposure to on-premise venues (cafes, bars, restaurants) was very weak in that analysis. The current study’s underlying geographic structure and adjustment for spatial autocorrelation made more efficient use of the available data.

This study was limited by the assumption of market equilibrium and the use of population and income as proxies for alcohol demand. The node and vector formation of the towns along a roadway network assumed that the areas between towns were absent of population and alcohol outlets. Residents in these areas who access outlets in the included towns will affect the alcohol market, as will town residents who use excluded outlets. Additionally, the approach for calculating spatial interaction assumes commute journeys are representative of all travel between towns (Fotheringham, 1983). Greater precision could conceivably be achieved using origin-destination specific estimates derived from data representing all-purpose travel from a random sample or census of residents from each town (Openshaw, 1998).

Importantly, the relationships identified in this analysis of rural towns are consistent with theory that explains the etiology of health disparities related to exposure to alcohol outlets. The underlying mechanism is not specific to any region or spatial structure, but the resolution at which it manifests will be related to the underlying topology of the market area. This study demonstrated that, in one rural region, the effects of these processes are observable between discrete towns. The findings are important for public health because the predictable dynamic relationship between supply and demand and other economic determinants in retail markets suggests that greater concentrations of outlets will inevitably appear in lower income areas. Interventions that actively prevent this occurring (e.g. density limits, planning and zoning) will reduce the extent to which residents of these lower income areas are disproportionately exposed to and experience problems.