Multiscale Dynamics of Macromolecules Using Normal Mode Langevin

Abstract

Proteins and other macromolecules have coupled dynamics over multiple time scales (from femtosecond to millisecond and beyond) that make resolving molecular dynamics challenging. We present an approach based on periodically decomposing the dynamics of a macromolecule into slow and fast modes based on a scalable coarse-grained normal mode analysis. A Langevin equation is used to propagate the slowest degrees of freedom while minimizing the nearly instantaneous degrees of freedom. We present numerical results showing that time steps of up to 1000 fs can be used, with real speedups of up to 200 times over plain molecular dynamics. We present results of successfully folding the Fip35 mutant of WW domain.

1. Introduction

Proteins are unique among polymers since they adopt 3D structures that allow them to perform functions with great specificity. Many proteins are molecular machines that serve numerous functions in the cell. For instance, protein kinases serve as signal transductors in the cell by catalyzing the addition of phosphate to specific residues in the same or different proteins. Different signals cause kinases to change from an inactive to an active state. To understand these biophysical processes, it is necessary to understand how proteins move (the mechanism), the kinetics (rates, etc.), and the stability of these conformations (thermodynamics).¹

Despite many years of research, simulating protein dynamics remains very challenging. The most straightforward approach, molecular dynamics simulations using standard atomistic models (e.g. force fields such as CHARMM² or AMBER³), quickly runs into a significant sampling challenge for all but the most elementary of systems. Detailed atomistic simulations are currently limited to the nanosecond to microsecond regime. The fundamental challenge to overcome is the presence of multiple time scales: typical bond vibrations are on the order of femtoseconds (10⁻¹⁵ sec) while proteins fold on a time-scale of microsecond to millisecond. The identification of the slowest variables in the system (e.g. associated with the slowest time scales and transition rates) is to a large extent an unresolved problem.

We introduce a novel scheme for propagating molecular dynamics (MD) in time, using all-atom force fields, which currently allows real speedups of 200-fold over plain MD. We have an automatic procedure for discovering the slow variables of MD even as a molecule changes conformations, based on recomputing coarse-grained normal modes (CNMA). CNMA is fast, with cost comparable to force computation rather than diagonalization. We propose a scheme to propagate dynamics along only these slowest degrees of freedom, while still handling the near instantaneous dynamics of fast degrees of freedom. We present successful results for folding a WW domain mutant, and simulating dynamics of calmodulin and a tyrosine kinase (details in http://www.normalmodes.info).

Our slow variables are approximate low-frequency modes. Normal modes are the eigenvectors of the Hessian matrix H of the potential energy U at an equilibrium or minimum point x₀ with proper mass normalization. More formally assume a system of N atoms with 3N Cartesian positions and diagonal mass matrix M. Then, $M^{-\frac{1}{2}}H{M}^{-\frac{1}{2}}\mathcal{Q}=\mathcal{Q}\mathrm{\Lambda }$, where Λ is the diagonal matrix of ordered eigenvalues and 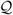the matrix of column eigenvectors q₁, … ,q₃N. The frequency of a mode is equal to √λ where λ is the eigenvalue. What we accomplish with normal mode analysis (NMA) is a partitioning in frequency. Low frequency modes correspond to slow motions of the protein while the fastest modes are associated with fast local bond vibrations. This allows for efficient propagation of the slow dynamics. The following algorithm is used for ‘partitioned propagation’ for a system of N atoms.

1.1. Initial setup

Starting at an initial conformation x₀ ∈ 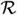^3N, we define X and Y as vectors ∈ 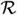^3N of displacements from x₀ in the slow and fast spaces, respectively. Then any configuration, x, can be written as x = X + Y + x₀, for projection matrices P(x) and its complement P^⊥(x) = (I−P)(x)

$$X=\mathit{P}(x)x,Y={\mathit{P}}^{\perp }(x)x.$$ (1)

The initial conformation x₀ is chosen as a local minimum so that we can expand the potential energy U(x) about x₀. The essence of the method is to select Q₀ ∈ 3N × m, as the first m column eigenvectors (q₁, … , q_m), ordered according to their eigenvalues, as the basis for the projection matrix s.t.

$${\mathit{P}}_0=M^{-\frac{1}{2}}{Q}_0{Q}_0^{\mathrm{T}}{M}^{\frac{1}{2}}.$$ (2)

In the linear case the time step is bounded by the asymptotic stability of the method⁴ at a frequency equal to √λ_i, rather than the highest frequency in the system. Our results show this is a good heuristic to choose the time step.

1.2. General step

At step i we propagate the system using the mapping Φ, which is based on a complete all-atom force-field, not a harmonic approximation:

$$\left[\begin{array}{c}{X}_i\\ Y_i\end{array}\right]={\mathrm{\Phi }}_{P_{i-1}}\left[\begin{array}{c}{X}_{i-1}\\ Y_{i-1}\end{array}\right],$$ (3)

such that the system is minimized w.r.t. the fast variables, i.e. ∇_YU(X_i +Y_i + x_o) = 0. At the initial step, ∇_XU(X + Y + x_o) =0 as well, which is required for the initial frequency partitioning. We then find the projection matrix, which is a function of x, from the eigenvectors of $M^{-\frac{1}{2}}{H}_i{M}^{-\frac{1}{2}}$, Q_i,

$${\mathit{P}}_i=M^{-\frac{1}{2}}{Q}_i{Q}_i^{\mathrm{T}}{M}^{\frac{1}{2}}.$$ (4)

This leads to a quadratic approximation for small Y and hence we can determine the frequencies for the fast variables by diagonalization to find the new projection matrix P_i = P(x_o + X_i−1). Note that without the initial frequency partitioning, it would not be possible to obtain a new projection matrix. We assume that the distribution of frequencies in the model remains constant. Figure 1 shows that this is a reasonable assumption for most folded proteins. In particular, this means that the eigenvalues associated with Y are nearly invariant with X.

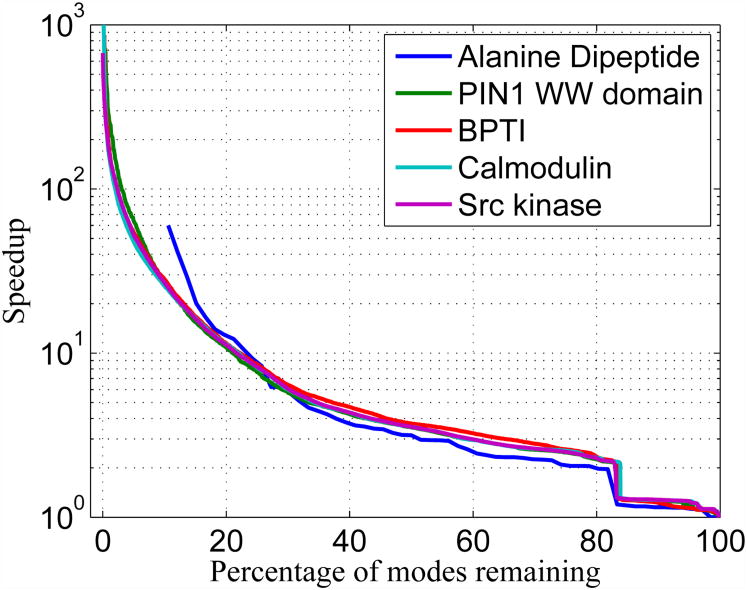
Fig. 1.

Maximum speedup possible for the dynamics in the slow subspace defined by keeping a certain percentage of modes for different molecules.

It is common to increase time steps in MD by constraining bonds to hydrogen, although indiscriminate constraining of bond angles significantly alters the dynamics. Similarly, some approaches to coarse-graining dynamics describe molecules as collections of rigid and flexible bodies. It is difficult to determine a priori the flexibility of different parts of a macromolecule, and there are numerical difficulties associated with the fastest timescales still present in the system which limit time steps to about a third of the fastest period.⁵ Equations of motion for low frequency modes allow substantially larger time step discretizations than fine-grained MD. This approach is more general than constraining parts of the molecule. The speedups possible are illustrated in Figure 1 for systems from 22 to 7200 atoms. These speedups are computed as the ratio of the largest time step possible by only keeping some percentage of modes over the time step needed when keeping all the modes. Notably, several different proteins show similar behavior, with potential speedups of three orders of magnitude when one resolves only a small numbers of modes. To make this discussion concrete, using 10 modes for calmodulin allows one a maximum time step of 1,000 fs, and for src kinase a time step of 2,000 fs.

1.3. Partition Function

We can now define the partition function for the method as

$$Z={\int }_{X+x_0}{\int }_Y\rho (\overline{Y}|\overline{X}+\overline{X}+x_0)\mathrm{d}\overline{Y}\mathrm{d}\overline{X}={\int }_x\rho (\overline{x})\mathrm{d}\overline{x},$$ (5)

as required.

1.4. Partition Function Approximations

Exact solutions of Eqn. (5) require sampling the entire fast variable Y phase-space for a given slow variable value X (computing potential of mean force). This would require additional computation to the algorithm described above. For the initial implementation we choose the approximation, for slow variable X,

$${\int }_Y\rho (\overline{Y}|X+X+x_0)\mathrm{d}\overline{Y}\approx \rho ((Y_{min}|X)+X+x_0),$$ (6)

which is readily available from the algorithm. For ρ(a) = exp(−βa) this is a reasonable approximation, but assumes we are at a global minimum w.r.t. X. In that case, it represents the most probable value of ρ(Y|X). Even though this approximation may seem crude, our numerical results show that this is a good approximation for thermodynamics and kinetics, except perhaps when very few modes are used to form P.

1.5. Numerical discretization

We discretize Eqn. (3) using a numerical integrator that generates dynamics that sample Eqn. (6). Equations for the rate of change of the slow variables X with associated momenta Π need to be formulated. We wish to find a way to calculate dΠ/dt in terms of X and Π only. The following exact equation can be derived (which can also be found in⁶):

$$\frac{\mathrm{d}X(t)}{\mathrm{d}t}=\prod ,\frac{\mathrm{d}\prod (t)}{\mathrm{d}(t)}=-\stackrel{\text{drift}}{\overbrace{{\nabla }_{X}A}}-\stackrel{\text{friction}}{\overbrace{{\int }_0^t{C}_r(s)\cdot \prod (t-s)\mathrm{d}s}}+\stackrel{\text{noise}}{\overbrace{r(t),}}$$ (7)

$$C_r(s)=\langle r(\tau +s)r{(\tau )}^T\rangle ,{\forall }_{\tau }(\text{fluctuation dissipation theorem})$$ (8)

These equations are in reduced units and we omitted the dependence of the memory kernel C_r on X and Π. The brackets 〈〉 define the thermodynamic average in the canonical ensemble. Eqn. (7) can be derived using the Mori-Zwanzig projection.⁶ The potential A(X) is the Potential of Mean Force (PMF, or Helmholtz free energy) for variable X. The integral in Eqn. (7) represents a friction. In this model the friction includes memory so this equation is often called the Generalized Langevin Equation (GLE). The last term r(t) is a fluctuating force with zero mean: 〈r(t) |X₀, Π₀〉 = 0. This is a conditional average over Cartesian coordinates x and momenta p_x keeping X = X₀ and Π = Π₀ fixed. This equation can be rigorously derived from statistical mechanics and is therefore an attractive starting point to build coarse grained models.

We model the protein using implicit solvent models (ISM), which have been shown to be sufficiently accurate for a number of applications, including protein folding studies. They are attractive because they greatly reduce the cost of simulating a protein. Using the approximation of Eqn. (6), Eqn. (7) can be simplified into a Langevin equation:

$$\mathrm{d}X=V\mathrm{d}t,M\mathrm{d}V=f\mathrm{d}t-\gamma MV\mathrm{d}t+{(2k_{\mathrm{B}}T\gamma )}^{1/2}{M}^{1/2}\mathrm{d}W(t),$$ (9)

where f = −P^f ∇U(Y_min|X + X + x₀) is the instantaneous projection of the force unto the slow subspace, P^f = MPM⁻¹, t is time, W(t) is a collection of Wiener processes, k_B is the Boltzmann constant, T is the system temperature, V are the velocities and γ is a scalar friction coefficient, for instance γ = 91ps⁻¹ for water-like viscosity. A Wiener process is a random function which is continuous but nowhere differen-tiable, and its derivative is white noise. A standard Wiener process has means and covariances 〈W(t)〉 = 0, 〈W(s)W(t)〉 = min{s, t}. Systematic determination of the friction and noise can be done using efficient numerical algorithms proposed by Darve and collaborators.⁷ The latter is important for kinetics but not for computing thermodynamic averages.

2. Methods

2.1. Normal Mode Langevin (NML)

We have previously published a numerical discretization of Eqn. (9) called Normal Mode Langevin (NML), which calculates the evolution of low frequency normal modes, while relaxing the remaining modes to their energy minimum or performing Brownian dynamics in the fast mode space (these two are equivalent).⁸ NML was originally formulated using only an initial frequency partitioning to determine the slow and fast variables. However, the approximation to the low frequency dynamics afforded by NMA is only valid around an equilibrium configuration. After propagation of the slow modes, parasitic fast frequencies are introduced into the slow dynamics space, which invalidate the original frequency partitioning (both eigenvalue and eigenvector sets). Nonetheless, there is evidence that the physically relevant motions of proteins can be captured by a low frequency space,^9–15 which motivates our approach of keeping track of the low frequency space as the molecule changes conformation.

While the partitioning of slow and fast variables in the partition function above is dependent on the configuration x, in practical implementations, we only need to update this partitioning by rediagonalization when the frequency partitioning is no longer valid. Currently, we determine the rediagonalization frequency empirically, although we are exploring use of bounds on frequency content of the spaces to trigger diagonalization.

This paper presents several novel improvements of NML: The first is use of the algorithm for partitioned propagation of normal mode dynamics presented above, which does not depend on validity of the initial partitioning throughout a trajectory. The second is a scalable direct method, CNMA, for computing low frequency modes from the Hessian, which allows scaling to large molecules and long timescales. The third is a new numerical integrator, Langevin Leapfrog, that can more accurately take larger time steps when discretizing the equations of motion of NML than existing algorithms. Finally, we show that this formulation of NML can simulate protein folding.

A method similar in spirit to NML is LIN, developed by Schlick and collaborators.¹⁶ LIN also performs a partitioning in frequency. However, LIN uses implicit integration for the low frequency modes and determines the evolution of the fast frequency modes using normal mode analysis. Langevin dynamics is used to dampen resonances. Clearly, the choices of numerical discretizations are very different: NML uses an explicit integrator for the low frequency modes, minimization or Brownian Dynamics to maintain the fast modes around their equilibrium values, and the scalable diagonalization to make rediagonalization affordable. A deeper difference is that in NML the Langevin equation is motivated by coarse-graining of the dynamics and the choice of implicit solvent model, rather than purely numerical reasons.

2.2. Langevin Leapfrog

In the original NML Eqn. (9) was discretized using the Langevin Impulse (LI) integrator.¹⁷ LI is exact for constant force, and has shown numerical advantages over other commonly used Langevin integrators.¹⁸ Schematically, a step of the NML propagator performs the following steps:

Update velocities

advance velocities using a long time step using the projection of forces unto slow subspace C.

Slow fluctuation

advance positions based on the projected velocities computed above.

Fast mode minimization

minimize positions on fast subspace C^⊥. The smaller the coupling between C and C^⊥, the fewer steps of minimization are needed. With very few modes in C coupling is very small.

In this paper we examine numerically the ability of Langevin integrators (including NML based on them) to correctly resolve dynamics for large time steps. We observe that even LI is not accurate and has a large discretization time step dependent over-damping. We derive a new integrator which we call Langevin Leapfrog, which can take large time steps with much greater accuracy. This is particularly true when used in the NML schemes.

Langevin Leapfrog is derived as a splitting method where velocities and positions are updated separately. Splitting methods arise when a vector field can be split into a sum of two or more parts that are each simpler to integrate than the original. Thus, we first integrate Eqn. (9) over time t for the velocities (from initial velocity V(0) at time 0), assuming X to be constant during the velocity update:

$$V(\mathrm{t})=e^{-\gamma \mathrm{t}}\left[{\int }_0^{\mathrm{t}}{e}^{\gamma \tau }\right(M^{-1}f(X)+\sqrt{2k_{\mathrm{B}}T\gamma }{M}^{-\frac{1}{2}}\mathrm{d}W(\tau ))\mathrm{d}\tau +C_1],$$ (10)

for constant C₁. Then,

$$V(\mathrm{t})=\left(\frac{1-e^{-\gamma \mathrm{t}}}{\gamma }\right)M^{-1}f(X)+\sqrt{2k_{\mathrm{B}}T\gamma }{M}^{-\frac{1}{2}}{e}^{-\gamma \mathrm{t}}{\int }_0^{\mathrm{t}}{e}^{\gamma \tau }\mathrm{d}W(\tau )\mathrm{d}\tau +C_1{e}^{-\gamma \mathrm{t}}.$$ (11)

The expression e^−γt ∫ e^γτ dW(τ) dτ is equivalent to multiplying a random variable Z with mean zero and unit variance by the factor

$$e^{-\gamma \mathrm{t}}\sqrt{{\int }_0^{\mathrm{t}}{(e^{\gamma \tau })}^2\mathrm{d}\tau }=\sqrt{\frac{1-e^{-2\gamma \mathrm{t}}}{2\gamma }}.$$ (12)

If we assume t = 0 at initial velocity Vⁿ, initial positions Xⁿ and t = Δt/2 at $V^{n+\frac{1}{2}}$ then

$$C_1=V^n,$$ (13)

and

$$V^{n+\frac{1}{2}}=e^{-\gamma \frac{\mathrm{\Delta }t}{2}}{V}^n+\left(\frac{1-e^{-\gamma \frac{\mathrm{\Delta }t}{2}}}{\gamma }\right)M^{-1}f(X^n)+\sqrt{2k_{\mathrm{B}}T\gamma }{M}^{-\frac{1}{2}}\sqrt{\frac{1-e^{-\gamma \mathrm{\Delta }t}}{2\gamma }}{Z}^n,$$ (14)

for random variable Zⁿ with zero mean and unit variance.

Positions can be found, assuming constant velocity during the position update, from:

$$X^{n+1}=X^n+\mathrm{\Delta }t{V}^{n+\frac{1}{2}},$$ (15)

and finally the remaining half step for the velocities

$$V^{n+1}=e^{-\gamma \frac{\mathrm{\Delta }t}{2}}{V}^{n+\frac{1}{2}}+\left(\frac{1-e^{-\gamma \frac{\mathrm{\Delta }t}{2}}}{\gamma }\right)M^{-1}f(X^{n+1})+\sqrt{2k_{\mathrm{B}}T\gamma }{M}^{-\frac{1}{2}}\sqrt{\frac{1-e^{-\gamma \mathrm{\Delta }t}}{2\gamma }}{Z}^{n+1},$$ (16)

for random variable Zⁿ⁺¹, again with zero mean and unit variance.

2.3. Coarse-grained Normal Mode Analysis

The need to re-diagonalize a mass-weighted Hessian in NML, while greatly improving the accuracy of the model and making it possible to track conformational change, is very expensive, with 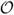(N³) computational time and 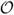(N²) memory. We have developed a coarse-grained normal mode analysis that is scalable. CNMA is a 2-level, direct method that uses a dimensionality reduction strategy that allows computation of low frequency modes in 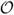(N^9/5) time and 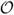(N) memory.

2.3.1. Dimensionality reduction strategy

The coarse-graining strategy to computing the frequency partitioning is based on 2 ideas. The first is to find a reduced set of normalized vectors E whose span contains the low frequency space of interest, C. The second is to find an orthogonal set of vectors V with the same span as E, which are ordered according to the diagonal elements of V^THV. The span of the first m columns of V, where m is the number of reduced collective motions, still spans C and constitute the approximate low frequency eigenvectors. To keep computational cost low, we form H, and matrix-vector products involving H, in linear cost, 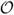(N). A brief description follows.

2.3.2. Choice of reduced matrix E

In order to form E, we use a model of a protein that is easier to diagonalize than the full-atom forcefield model, but that nonetheless contains the same low frequency motion space. Our model is that of independent blocks of residues with arbitrary rotation, translation, and low frequency dihedrals. Clearly, such a model allows more flexibility than the full-atom protein model. We show that it can indeed contain the low frequency motion space of interest. We start from a block Hessian in which each block H^∼_ij (composed of 1 or more residues) is zero if i ≠ j. The remaining blocks on the diagonal are assumed to be independent of all other blocks. This block Hessian is then diagonalized, which is equivalent to performing independent diagonalization for each block. The block Hessian eigenvectors and eigenvalues, 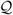_i and D_i, are calculated as follows:

$${\stackrel{\sim }{\mathit{H}}}_{ii}{\mathcal{Q}}_i={\mathcal{Q}}_i{D}_i.$$

Our hypothesis is that interactions among residues responsible for the low frequency space of interest will be included, either by projection or directly, in the first few eigenvectors of 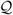_i, and need to be included in E. The source of these vectors is as follows:

1. External low frequency motions due to nonbonded interactions are projected onto the first 6 eigenvectors of 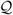_i, corresponding to conserved degrees of freedom (d.o.f.) per block. In other words, external forces manifest themselves in rotations or translations of each residue-block.

2. External low frequency motions due to bonded interactions are projected onto the dihedral space, and will consist of 2 vectors of 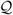_i, due to backbone dihedrals of up to 2 connecting blocks.

3. Internal low frequency motions, for instance due to side-chain dihedral motions, will also be in the dihedral space and thus will be in _i.

The number of vectors of _i included in E varies according to the residue composition. We refer to the average number of these vectors by block as the block d.o.f. (bdof). We expect that the eigenvectors identified above will correspond to the first k ordered eigenvalues. The number k varies between blocks and is determined by selecting a cutoff frequency from the block eigenvalues. Table 1 gives values of k for BPTI, where the bdof = 12, and where each block has only 1 residue. As expected, larger residues such as ARG require a greater number of vectors to describe their low frequency motions than smaller ones like GLY.

Table 1.

Number of vectors, k, selected per residue for BPTI, showing that larger residues require greater numbers of vectors.

Residue:	ARG	PRO	ASP	PHE	CYS	LEU	GLU	TYR	GLY
No. vectors:	15	9	11	13	10	12	13	13	8
Residue:	LYS	ALA	ILE	ASN	GLN	THR	VAL	SER	MET
No. vectors:	14	9	14	12	14	11	11	11	15

2.3.3. Finding orthogonal matrix V

Figure 2 illustrates the dimensionality reduction strategy. The dimensions of E are 3N × n, where n ≪ N. The quadratic product E^TH E produces a matrix S of reduced dimensions n × n. H is a Hessian that includes interactions among residue-blocks, i.e., the full Hessian or an approximation thereof. We use the Hessian coming from using cutoff in the nonbonded forces. From the diagonalization of S we can obtain Q. In particular, we (cheaply) diagonalize the symmetric matrix S to find orthonormal matrix Q^∼ s.t.

Fig. 2.

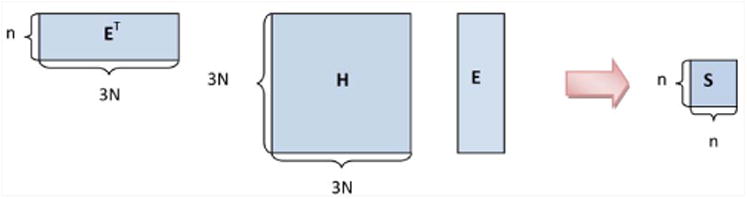
Dimensionality reduction strategy.

$$S\stackrel{\sim }{Q}=\stackrel{\sim }{Q}\Omega ,$$

for diagonal matrix Ω We can then write

$$Q^{\mathrm{T}}HQ=\Omega ,$$

for Q = EQ^∼. V is defined as the first m columns of Q, where m is typically in the range of 10 - 100. Our subspace of dynamical interest, C, is included in the span of.

We can evaluate how well the span of E represents C using the following result: Let the i^th ordered diagonal of Ω be σ_i = Ω_ii. It can be shown that the highest frequency mode in C, f_max, satisfies

$$f_{max}\le \sqrt{|{\sigma }_m|}.$$

The Rayleigh quotient ${\sigma }_m=E_m^{\mathrm{T}}H{E}_m$ can be used to establish the maximum time step that can be taken in subspace C for stability. It follows that if σ_m is close to the m^th ordered eigenvalue of H, then V is a good representation of the low frequency space of interest. Since this result does not take account of conserved d.o.f., with zero eigenvalues, we need to be careful to include these in our target E.

2.3.4. Efficient implementation

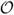The quadratic product E^THE, which naively implemented would still be an (N³) operation, is made (N) by exploiting the quasi-block structure of H and E and using cutoff for the electrostatics. This cost can still be maintained if full electrostatics are needed by using coarse-grained electrostatic representations. Figure 3 illustrates the block structure of H, which is similar to a protein contact map. Contiguous residues give a tri-diagonal block structure. Non-contiguous residues within a cutoff form off-diagonal blocks due to nonbonded forces. The block structure of E follows from its composition from eigenvectors of the block Hessians H^∼_ii.

Fig. 3.

Segment of a BPTI molecule and its associated Hessian entries. Here, for illustration, a block is defined by one residue. Each residue corresponds to a Hessian block containing all of the forces within the residue, denoted ‘Full’. Adjacent residues have a corresponding electrostatic block denoted ‘Elec.’, e.g. Elec. 13-14. Physically local residues within the cutoff distance have a corresponding electrostatic block, e.g. Elec. 13-38. Bonds connecting non-adjacent residues, such as the disulfide bonds shown, correspond to small 3×3 blocks in the Hessian.

3. Results

3.1. Normal Mode Langevin dynamics

We performed folding simulations of the Fip35 mutant of WW domain using NML, discretized with Langevin Leapfrog, with periodic rediagonalization using CNMA. The force field is CHARMM 27 with the screened Coulomb potential implicit solvent model (SCPISM).¹⁹ The temperature T = 300K and friction coefficient γ = 91 ps⁻¹. We compared to a set of 1000 simulations using plain Langevin dynamics with same T and γ, with combined sampling of 393 μs from Ensign and Pande,²⁰ where 2 simulations fold. From a set of 200 NML simulations with combined sampling of 198μs, we found 2 that folded. Folding is determined as in their work: the 3 β-sheets are fully formed and the RMSD of their residues to the native structure is less than 3 Å. These NML simulations used 10 modes, CNMA parameters of bdof = 14 and 2 residues per block, and time step of 100 fs. Figures 4(a) and 4(b) show the RMSD, and snapshots from an NML folding simulation, respectively. We estimated a folding rate of 〈k〉 = (66μs)⁻¹ with σ(k) = (114μs)⁻¹. The rate reported by Ensign and Pande is 〈k〉 = (131μs)⁻¹ with σ(k) = (226μs) ⁻¹. An experimental rate has been reported²¹ as (13.3μs) ⁻¹. Our results suggest agreement of the free energy of activation within a factor of 2, a reasonable expectation for these force fields. The folding rate was computed using a Bayesian modification of a maximum likelihood estimate.²² With n folding simulations out of N total simulations, with total necessary simulation time Θ, the estimators for the mean rate and its variance are:

Fig. 4.

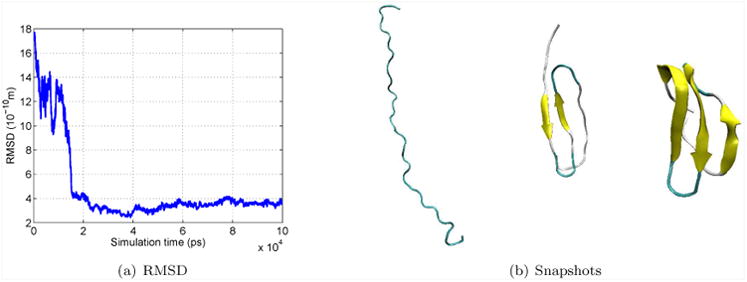
(a) RMSD of C_α of β-sheets (in Å) for Fip35 WW folding NML simulation. (b) Snapshots from the same simulation, (i) at the start, (ii) after 125 ns, and (iii) after 330 ns.

$$\langle k\rangle =\frac{n+1}{\mathrm{\Theta }},var(k)=\frac{n+1}{{\mathrm{\Theta }}^2}.$$

Θ is the sum of the first-passage times for simulations that folded, plus total simulation time for simulations that did not fold. In our NML simulations, one simulation folded after 33 ns and another one after 303 ns, and all the simulations ran for 1 μs.

These results were not significantly different when running folding simulations with 15 and 20 modes. The number of residues per block used in CNMA is chosen to optimize runtime, and is a function of N as explained below. We determine the bdof to use for CNMA by comparing the L2 norm for the difference of the low frequency eigenvalues against those of a full diagonalization, or when this is too costly, against a diagonalization with large bdof. We use the minimum bdof after which the norm reaches a plateau.

It would be desirable to have more folding events for computation of the rate in order to reduce the standard deviation. The significance of our result is that NML with periodic rediagonalization can track large conformational change with very few modes.

Timings of NMLL and MD on one core of Xeon E5420 2.5 GHz, computed by running 100 ps of equilibration and 1 ns of simulation are in Table 2. These results show that there is not a significant overhead in our NMLL approach, considering the performance gained from a significantly larger time step (in comparison with previous approaches, which could take large time steps as well, but with a large overhead that limited their applicability¹⁶).

Table 2.

Speedup of NMLL vs. MD. Rows with time step Δt of 1 fs correspond to MD. “Itrs” is the average number of minimization iterations. “Speedup” is the speedup of using NMLL vs. plain MD. All NMLL runs use 10 modes and rediagonalization every ps.

Molecule	Atoms	Δt (fs)	Itrs	ns/day	Speedup
Fip35 WW	544	1	-	6	-
Fip35 WW	544	100	1.0	240	40
Fip35 WW	544	200	1.2	360	60
Fip35 WW	544	500	4.0	455	76
Calmodulin	2262	1	-	0.4	-
Calmodulin	2262	100	1.0	13.7	34
Calmodulin	2262	500	1.9	60.4	151
Calmodulin	2262	1000	8.2	90.9	227
Tyr kinase	7214	1	-	0.07	-
Tyr kinase	7214	100	1.2	1.6	23
Tyr kinase	7214	500	1.3	7.4	106
Tyr kinase	7214	1000	1.8	14.4	206

3.2. Coarse grained normal mode analysis (CNMA)

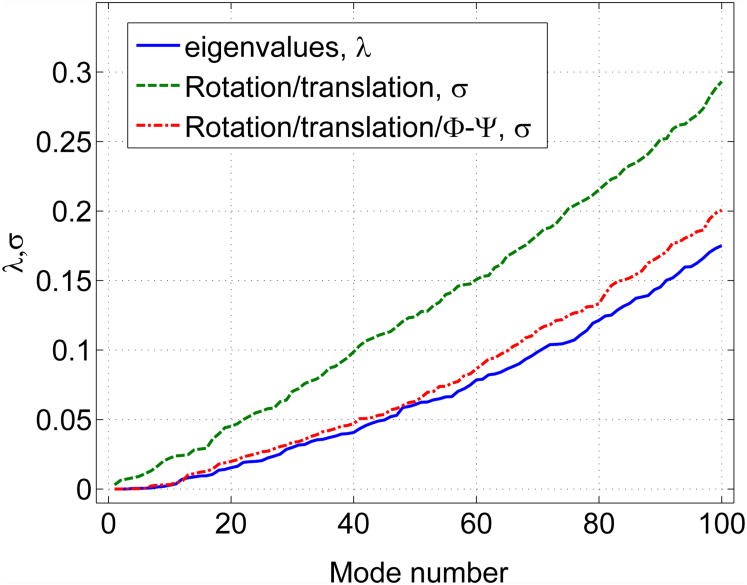
Figure 5 shows how well these choices of coarse-graining represent the low frequency space of a protein. Results were obtained by using different values of k in constructing E vs. the true eigenvalues for BPTI. The closer the line is to the true eigenvalues, the better the coarse-graining strategy. Rotation/translation means that E is made from the first 6 eigenvectors of each residue-block matrix. Rotation/translation/Φ – Ψ means that in addition vectors are included that correspond to low frequency dihedral motions. Note that only including the first 6 eigenvectors of the block Hessians in E diverges from the true eigenvalues, whereas also including the low frequency dihedral vectors gives very good results. We can thus evaluate the fitness of any proposed Hessian coarse-graining procedure.

Fig. 5.

Rayleigh quotients and true eigenvalues for different Hessian coarse graining schemes.

3.2.1. Scaling results

Five models were used for the comparison of the ‘brute force’ diagonalization and the CNMA method: Pin1 WW domain (PDB 1I6C), BPTI (PDB 4PTI), Calmodulin (PDB 1CLL), Tyrosine kinase (PDB 1QCF), and F1-ATPase (PDB 2HLD). The results can be seen in Table 3. The scaling with time for the ‘brute force’ Lapack diagonalization method is known to be (N³). For the coarse grained CNMA method using b blocks we have the cost of diagonalizing all b blocks as 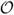((N/b)³) × b = 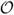(N³/b²) and for the small projected matrix as 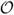(b³), which has a minimum cost when b∝N^3/5, giving an estimated cost of 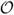(N^9/5). This is borne out by the numerical evidence. For the coarse grained method the RAM resource usage is reduced from the ‘brute force’ scaling of 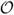(N²) to 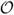(N).

Table 3.

Comparison of the ‘brute force’ Lapack diagonalization and the coarse grained method for different atomic models.

Molecule	Atoms	Lapack Time [s]	Lapack RAM [Gb]	CNMA Time [s]	CNMA RAM [Gb]
WW	551	14.4	0.04	0.37	0.01
BPTI	882	59.9	0.11	0.89	0.03
CaM	2262	980.6	0.74	3.89	0.12
Tyr Kinase	7214	31450.0	7.49	31.90	0.69
F1-ATPase	51181	11.2E6	377.0	1827.0	2.04

Other diagonalization techniques to obtain low frequency eigenvectors are reported in the literature, such as the ODMG energy functional, which was recently used by Dykeman and Sankey to analyze viral capsids.²³ Unlike these methods, which are iterative, and where convergence is highly system dependent, CNMA is a direct method, has been validated in a rigorous way, both through useful bounds on the eigenvalues, and through its application in NML. Our own numerical experiments with Tracemin and other iterative methods for solving our eigenvalue problem indicate that convergence of these iterative methods is very slow, since they require an approximation to the inverse of the Hessian from the start. Our dimensionality reduction strategy for CNMA is more effective.

3.3. Langevin Leapfrog

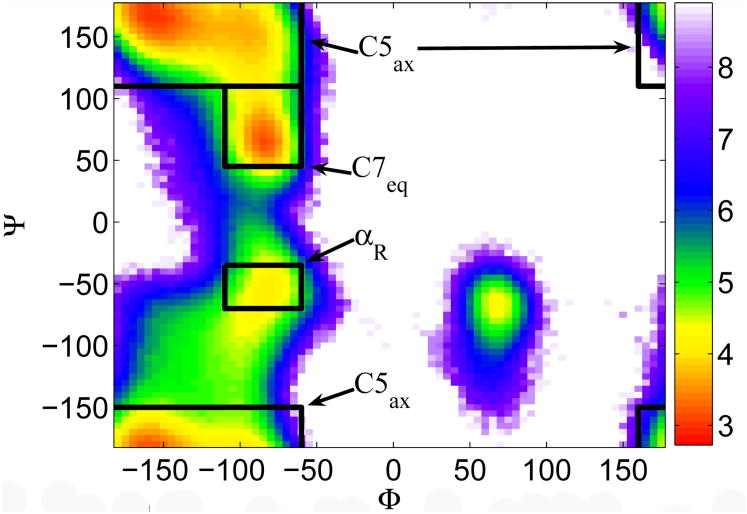
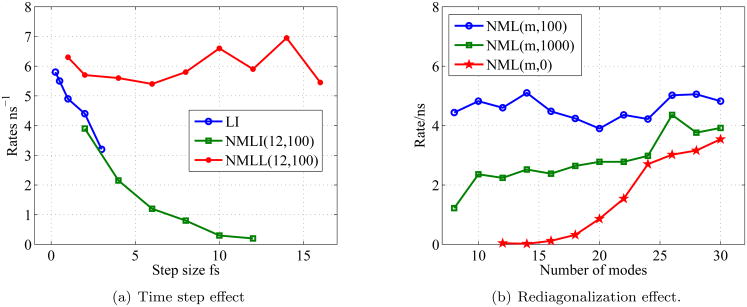
We applied NML to study the isomerization kinetics of blocked alanine dipeptide (ACE ALA NME) between the C7 equatorial and α_r conformations. Conformation A is C7 equatorial and C5 axial combined, and conformation B is α_R. Figure 6 shows the free energy as a Ramachadran plot for Alanine Dipeptide using a sigmoidal screened Coulomb potential.²⁴ We refer to NML with redi-agonalization to update the low frequency modes as NML(m,period) where m is the number of slow modes propagated, and period the rediagonalization period in femtoseconds. LL greatly eliminates the over-damping due to the discretization time step of LI. Figure 7(a) shows the isomerization rates for alanine dipeptide using LI, NML using LI (NMLI) and NML using LL (NMLL). Note that NMLL can compute the rate with time steps of 16fs using 12 modes (6 conserved plus 6 real modes) with rediagonalization every 100 steps, whereas LI and NMLI's rate significantly decreases with increasing time step.

Fig. 6. Free energy for alanine dipeptide.

Fig. 7.

Isomerization rate as (a) function of time step for different Langevin integrators, and (b) different rediagionalization periods. Error bars are smaller than the symbol sizes.

Figure 7(b) shows the isomerization rate for alanine dipeptide for varying rediagonalization periods: the rate is correctly computed for NMLL(m,100) for even 7 modes (6 conserved plus 1 real mode).

4. Conclusions

We have presented a novel scheme to propagate multiscale dynamics of proteins and other macromolecules, based on computing periodically coarse-grained normal mode dynamics. We have presented results of folding a WW domain, as well as speedups on different proteins. A major advance detailed herein is a scheme to calculate NML dynamics in a very efficient way, i.e. with scaling of the form 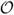(N^9/5), which allows for the rapid calculation of long timescale dynamics. This was further demonstrated with specific examples, including the microsecond dynamics of the folding of a WW-domain. Thus, in its current implementation described herein, NML can greatly accelerate molecular dynamics calculation for a wide variety of applications, while retaining quantitative fidelity to more traditional methods.

The main approximation in NML is the assumption of Eqn. (6) regarding fast frequency motion. Numerical evidence suggests this is a reasonable assumption, but this issue needs to be more thoroughly evaluated, and if necessary, computationally efficient approximations of the PMF need to be derived. Since NML prescribes frequent rediagonalization, the PMF needs only be valid in a neighborhood of phase space around a given value of the slow variable X. Thus, this is a less formidable problem than in the general coarse-graining case.

Current work includes extending the Langevin equation to include memory, which may be relevant when using very few low frequency modes if one wants to compute kinetics; implementing a multilevel formulation of CNMA with O(N log N) complexity, and combining NML with Markov State Models to reach millisecond time scale dynamics. All these methods are included in the open source software Protomol.²⁵ There is an implementation reference and a tutorial on running NML, along with a discussion of how to choose the bdof parameter of CNMA and the number of modes in NML (http://sourceforge.net/projects/protomol). NML will be included in future releases of the library OpenMM.