Dynamic Modulation of the Action Observation Network by Movement Familiarity

Abstract

When watching another person's actions, a network of sensorimotor brain regions, collectively termed the action observation network (AON), is engaged. Previous research suggests that the AON is more responsive when watching familiar compared with unfamiliar actions. However, most research into AON function is premised on comparisons of AON engagement during different types of task using univariate, magnitude-based approaches. To better understand the relationship between action familiarity and AON engagement, here we examine how observed movement familiarity modulates AON activity in humans using dynamic causal modeling, a type of effective connectivity analysis. Twenty-one subjects underwent fMRI scanning while viewing whole-body dance movements that varied in terms of their familiarity. Participants' task was to either predict the next posture the dancer's body would assume or to respond to a non–action-related attentional control question. To assess individuals' familiarity with each movement, participants rated each video on a measure of visual familiarity after being scanned. Parametric analyses showed more activity in left middle temporal gyrus, inferior parietal lobule, and inferior frontal gyrus as videos were rated as increasingly familiar. These clusters of activity formed the regions of interest for dynamic causal modeling analyses, which revealed attenuation of effective connectivity bidirectionally between parietal and temporal AON nodes when participants observed videos they rated as increasingly familiar. As such, the findings provide partial support for a predictive coding model of the AON, as well as illuminate how action familiarity manipulations can be used to explore simulation-based accounts of action understanding.

Introduction

Perceiving and interacting with others form the foundation of human social behavior. When watching others in action, we readily extract information about their goals and intentions (Hamilton and Grafton, 2006; Hamilton, 2013) and predict their subsequent behavior in a rapid, online fashion (Blakemore and Frith, 2005; Falck-Ytter et al., 2006). Neuroimaging studies identify frontal, parietal, and occipitotemporal regions collectively termed the Action Observation Network (AON) (Cross et al., 2009; Grafton, 2009; Keysers and Gazzola, 2009; Caspers et al., 2010) as critically involved in processing others' actions. Previous research demonstrates greater AON activity when watching visually or physically familiar actions (Buccino et al., 2004; Calvo-Merino et al., 2005; Cross et al., 2006; Vogt et al., 2007; Shimada, 2010; Press, 2011). These findings support a theory of action understanding that posits the AON is tuned to respond most to actions that are “like me” (Meltzoff, 2007) via experience-driven simulation mechanisms (Sinigaglia, 2013). However, most studies into how observers' prior action experience or familiarity impacts AON engagement have used magnitude-based approaches, investigating which brain regions show increased or decreased response amplitudes based on familiarity with an observed action. Some have suggested that such analyses might not be sufficient to construct a nuanced or complete picture of how sensorimotor brain regions support action understanding (Schippers and Keysers, 2011). One promising approach for further characterization of the relationship between familiarity and AON engagement is to examine functional connectivity between individual AON nodes during action observation, and ask how a particular task modulates these connections (Smith, 2012).

Prior theoretical work on the AON can inform predictions about how familiarity might modulate connectivity when observing others in action. Predictive coding models of AON function (Keysers and Perrett, 2004; Kilner et al., 2007a,b; Gazzola and Keysers, 2009; Schippers and Keysers, 2011) are predicated on the use of perceptuomotor maps to predict and interpret observed actions (Lamm et al., 2007; Schubotz, 2007; Urgesi et al., 2010). According to this account, forward models facilitate processing of familiar actions through use of stored action representations and propagate information in a top-down manner from premotor to parietal to occipitotemporal regions. Unfamiliar actions are processed via a bottom-up, data-driven approach, where information propagates anteriorly from occipitotemporal to parietal to premotor cortices. To test whether and how action familiarity modulates effective connectivity among the component regions of the AON, we used dynamic causal modeling to test hypotheses under a predictive coding model of action observation. Our task involved observing whole-body movements followed by a short occlusion, after which participants chose which posture should follow in the movement sequence (similar to Stadler et al., 2011). By using an offline rating task, we examined how this noncategorical measure of familiarity impacts AON engagement (compare Cross et al., 2013; Liew et al., 2013). According to a predictive coding model, dynamic causal modeling (DCM) should demonstrate that increasingly familiar movements are associated with decreased feedforward influence from sensory/posterior nodes, as prediction errors are minimized when viewing more familiar actions, whereas feedback influence from anterior to posterior nodes should increase.

Materials and Methods

Participants

Twenty-one adult volunteers (mean age 21.95 years, SD = 3.02 years) with normal or corrected to normal vision were recruited from the student population at Radboud University Nijmegen. Of this sample, 13 were female; 17 right-handed, 2 left-handed, and 2 ambidextrous based on the Edinburgh Handedness Questionnaire (Oldfield, 1971). All participants' data were used for the GLM analyses, and a subsample of 19 participants was used for the DCM analysis (see Definition of ROIs). All participants spoke English fluently and had no history of psychiatric or neurological disorders. All participants provided written informed consent, and the study procedures were approved by local ethics committees at both Bangor University and the Donders Centre for Cognitive Neuroimaging at Radboud University Nijmegen. Participants were reimbursed for their time with €15.

Experimental design and stimuli

The paradigm included two task manipulations that fell within a 2 × 2 factorial design. The two factors were familiarity (levels: familiar and unfamiliar) and task (levels: posture prediction or dot color tracking). Action stimuli were consistent across the two tasks (only the instructions changed).

Stimuli construction and selection

Stimuli were created by filming a professional dancer performing a range of improvised and choreographed movement in a contemporary dance style that ranged from extremely simple (and thus relatively predictable) to much more complex (and much less predictable). To ensure these stimuli encapsulated a broad range of more and less familiar actions for dance-naive observers, we first piloted 157 video clips (each with a duration of 6 s) with a separate sample of 23 participants. From this pilot study, we selected the 30 movement stimuli rated as most familiar, and the 30 movement stimuli rated most unfamiliar by pilot participants. This split allowed us make a stimuli set that should subjectively differ across the familiarity spectrum.

Prediction task

In the Prediction condition, participants were asked to monitor the movements of the agent in preparation for a two-way forced choice question asking them to choose which posture should follow on in the video clip after an occlusion of 0.6 s. The forced choice consisted of one coherent still frame (chosen from 0.6 s after when the video was occluded) and one that was plausible to the video but not chronological to the flow based on the occlusion duration (for an example, see Fig. 1).

Figure 1.

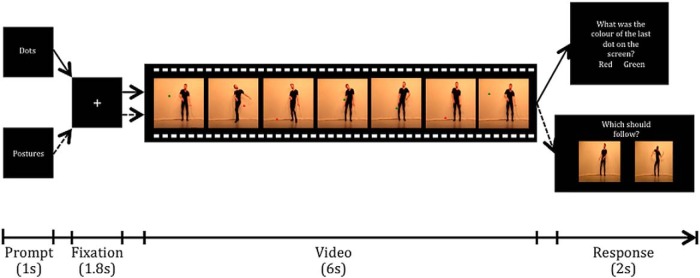
An illustration of the experimental trials. The prompt screen was shown at the beginning of each block (10 trials) to orient participants' attention to the dots or postures. A fixation cross was shown at the start of each trial, followed by a video. This was followed by a question about the dot color or which posture should follow, depending on the block type. The response screen was displayed for 2 s; and if participants responded before the end of the 2 s window, a blank screen would remain until the 2 s window ceased.

Attentional control task

A control task was built into paradigm so that, for half the trials, participants were asked to monitor the color of a dot that would randomly appear on the screen in different locations and in different colors (either red or green). The size of the dots was 5 mm and appeared at a rate of 1 per second (to clarify, colored dots appeared during all video stimuli in the experiment, but participants were asked to attend to them during only half the trials). When participants were performing the attentional control task, they were asked to monitor the color of the dot throughout the duration of the video clip. When the video clip ended, a question appeared asking participants to specify the color of the last dot they saw on the screen.

Postscanning ratings

After the fMRI experiment, participants rated the videos on a Likert scale of 1–9 as to how familiar they found the movements within each video (0 = very unfamiliar; 5 = neutral; 9 = very familiar). The dots were removed from these videos, and the response window was not fixed. Still, participants were encouraged to answer as quickly and accurately as they could. The concept of familiarity was explained by the experimenter as how easily participants would be able to say what move should come next in each video, and participants were made explicitly aware that familiarity did not mean which videos had been recognized or remembered from the scanning experiment. Each video was displayed only once and in a randomized order.

To ensure that familiarity ratings and number or speed of movements were not confounded, we calculated the mean “motion energy” of each video stimulus based on a previously developed algorithm (Cross et al., 2012). Once we obtained an objective numeric score for how much pixel displacement each video contained, we computed a Pearson product-moment correlation coefficient to assess the relationship between the motion energy of each video and the average familiarity rating given by participants. The results revealed no correlation between the two variables (r = −0.06, n = 60, p = 0.646). This suggests that the participants did not rate the stimuli based on how much movement each stimulus contained; instead, they were rating them on a more holistic, subjective view of familiarity.

fMRI design and procedure

Each participant completed one fMRI session that followed an event-related design. Participants completed two runs, lasting 13 min and containing 60 trials each. Trials were blocked into more familiar and less familiar stimuli (based on pilot data), and both kinds of stimuli were presented for both task conditions. At the beginning of the first run and the end of the second run, a 15 s rest period occurred. At the start of each block, a prompt (1 s) indicated which task participants were to perform for the upcoming block of trials (predicting postures or reporting on the dot color). The ensuing blocks, consisting of 10 trials, were all from the same condition. At the start of each trial, a white fixation cross appeared on the center of the screen for 1.8 s, followed by a video clip (6 s). Based on the prompt at the start of the block, participants had 2 s to respond to the task and identify which still frame they thought would follow or identify the color of the last dot on the screen. This response period lasted for 2 s. If a button was pressed before 2 s had elapsed, the screen changed to a blank black screen until the 2 s time limit was reached. The order of the blocks and the video shown in each trial were pseudo-randomized so that each video was shown once in each of the conditions.

Stimulus presentation and response collection were performed using Psychophysics Toolbox (version 3) via MATLAB R2010a (MathWorks). The stimuli were projected onto a mirror above the head coil from a projector outside of the scanner. Participants made their responses with the forefinger and middle finger of the right hand, and responses were recorded from a custom-made MR-compatible button box.

Data acquisition was conducted at the Donders Centre for Cognitive Neuroimaging at Radboud University Nijmegen. Functional images were acquired on a 3.0T Siemens MRI scanner using a 32-channel head coil. Functional images were acquired covering the whole brain using an echo-planar imaging (EPI) sequence (35 axial slices, ascending slice acquisition, repetition time = 2000 ms, echo time = 30 ms, 90° flip angle, matrix = 64 × 64, slice thickness: 3 × 3 × 3 mm, field of view (FOV): 224 mm). Before the functional run, 196 two-dimensional anatomical images (256 × 256 pixel matrix, T1-weighted) were obtained for normalization purposes.

fMRI data preprocessing and statistical analysis

A total of 338 volumes per participant per run were used in the analysis. Because of a technical error, two participants' data were not collected correctly at the start of the first functional run, resulting in a reduced number of volumes for these participants (615 volumes in total compared with 676 for all other participants). Data were analyzed using Statistical Parametric Mapping (SPM8: Wellcome Trust Centre for Neuroimaging, London) (Friston, 2007) implemented using MATLAB R2010a (MathWorks). The data were first realigned and then slice-time corrected and preliminarily preorientated within standard stereotaxic space as defined by the MNI (Friston, 2007). This preorientation allowed for a better spatial normalization to the MNI template. Participants' EPI images were then coregistered to their T1 anatomical scans, which were then spatially normalized to standard stereotaxic space. The spatially normalized EPI images were filtered using a Gaussian kernel of 8 mm full-width at half maximum in the x, y, and z axes. A design matrix was fitted for each subject with a single regressor for all trials from the prediction task and a single regressor for all trials from the colored dot-tracking task. A parametric regressor column was added to the design that included participants' individual ratings of each video from the posture prediction task (assigned outside the fMRI session). In modeling a single parametric effect of familiarity, we are effectively modeling the main effects of action observation and familiarity but not their interaction. The fixation, prompt, and response were fitted as noise regressors for each individual and combined into a single regressor of noninterest. Each trial was then modeled as a boxcar function for the duration of the video. For the GLM analyses, a cluster threshold of k = 10 and a p value of <0.005 (uncorrected) was set to best observe the sensitive effects of the parametric analysis.

Although participants were encouraged to use the entire scale when rating the videos, many participants used a reduced range of the 9 point scale (for example, 2–8). Because we were interested in using each individual's ratings as a parametric regressor in the group fMRI model, it was important to equalize the relative rating scales across participants. To achieve this, participants' ratings were standardized via a z transformation.

The GLM neuroimaging analyses were designed to achieve two main objectives

Neural processes engaged during action prediction.

The first analysis identified brain regions that responded to the task demands to predict movements by evaluating the task-based contrast of posture prediction > attentional control task. This contrast allowed us to explore the effects of online monitoring of an action while controlling for familiarity of the movements.

Parametric effects of increasing familiarity of an observed action.

The second analysis allowed us to explore the sensitive measure of subject-specific (standardized) ratings of observed movements on AON activity. This parametric contrast was used to test the hypothesis that AON regions should show greater activity as a function of increasing familiarity. Unlike contrasts that would use segmentation of the stimuli into familiarity categories, our measure allows us to capitalize upon individual differences in familiarity ratings to identify brain regions that become increasingly or decreasingly active the more familiar a movement is rated by an observer.

DCM

Evaluation.

DCM is a method of analyzing effective connectivity that uses a bilinear model of neural population dynamics, combined with a hemodynamic model, which aims to describe the neural activity in the measured BOLD response (Friston et al., 2003). By modeling feasible neuronal parameters, DCM aims to make a modeled BOLD response that is similar to the actual experimentally manipulated BOLD signal. The neural dynamics model created using DCM is then combined with a hemodynamic forward model that incorporates a balloon model (Buxton et al., 1998). The hemodynamic model provides a transformation of how the neural dynamics would propagate as a BOLD response, estimated via a standard Bayesian approach (variational Laplace). The fit of the combined neural model and hemodynamic forward model is estimated via a Bayesian approach, which uses conservative shrinkage priors for the coupling parameters.

A model is specified to have the fit to the data estimated by the previously mentioned routine. The input into the estimation procedure is three matrices (for bilinear DCMs, but see also Nonlinear DCMs) (Stephan et al., 2008). The first is the endogenous connection strengths (the A matrix), which represents the connectivity between the regions of the model, sometimes called the fixed connectivity. The B and C matrices represent the experimentally manipulated conditions. Matrix B represents the modulation of an external input on a fixed connection, which describes the change in the value of the effective connectivity for a connection under a particular condition. The C matrix represents the input into the system, which describes the activity that is perturbing, or creating activity, in the system. This equation models the state changes by known inputs. By user-created variations of combinations of fixed connectivity, modulatory influences, and inputs, multiple DCMs can be created for the same set of regions and then compared with which fits the data best (while controlling for complexity).

Hypothesis.

The experimental hypothesis tested in the current study is that differential connectivity will exist between the three core AON regions based on subjective familiarity ratings made by the participants. Moreover, we expected that more familiar actions would increase the influence of top-down connections (IFG-IPL-MTG) while decreasing the corresponding influence of bottom-up connections (MTG-IPL-IFG). Mechanistically, this corresponds to increasingly precise or confident top-down predictions afforded by familiar actions that, in our model, would be encoded by the modulatory effects of familiarity on the B parameters.

Preprocessing for DCM.

To evaluate the effective connectivity of this network using DCM, volumes from the two separate runs were concatenated to form one single time series per participant. We repeated the GLM analysis in SPM12b to exploit recent developments in dynamic causal modeling (see below). The GLM was effectively the same as described above. However, in this case, we adjusted the data for the main effect of action observation. We then used the effect of stimulus movement as a driving input to the action observation network, whereas familiarity was used to modulate extrinsic (between node) connectivity. Effectively, this models the effect of familiarity in terms of context-sensitive changes in coupling induced under action observation. Notice that we effectively removed responses to movement videos during the attend dots conditions, enabling us to focus on the effect of familiarity during action observation. These will be subsequently referred to as the movement effect. The remaining conditions were modeled as a nuisance variable to ease DCM model specification (Stephan et al., 2010). These preprocessing steps allowed us to examine the effects of familiarity of actions on the effective connectivity of the system.

We allowed for stochastic effects within the model to more accurately model noise (Li et al., 2011). We also centered the input into the node. This gives the input a mean of zero and means that modulating parameters can increase and decrease the fixed connectivity, as opposed to simply increasing it as when the input is always positive. To allow for biological plausibility, we opted for two-state models that allow for both excitatory and inhibitory connectivity (Marreiros et al., 2008). Because we used a two-state DCM, we were able to enforce positivity constraints on the connection strengths and lend our interpretation a greater biological plausibility or validity. This is because all connection strengths and two-state DCMs are excitatory, where intrinsic (within node) excitatory connections activate inhibitory neurons to ensure stability of the modeled network. Crucially, the coupling strengths are log scale parameters. In other words, they represent the log of the scaling of an effective connection, such that a log of zero corresponds to a 100% scaling. This means that a negative log scaling parameter corresponds to a weaker connection and a positive parameter corresponds to a stronger connection. We will report the parameter estimates in log space (and perform T tests on the log scaling parameters). This additional step allowed us to further examine the proposal by Keysers and Perrett (2004) that the MTG would exhibit inhibitory responses to familiar stimuli as well as help us understand how it relates to the predictive coding model proposed by Kilner et al. (2007b).

To identify the winning model (in this case, the model that best explains the system of interest), we used random-effects Bayesian model selection (BMS) to account for outliers (Stephan et al., 2009). This Bayesian approach used for DCM gives each model an exceedance probability, the probability that a model is more likely than any other model tested (subject to a trade-off between model fit and complexity). The family comparison technique pools model evidence by the user-defined groups, where all models within a given group share a common feature (Penny et al., 2010).

System of interest

Definition of ROIs.

The coordinates for the ROIs were identified from the parametric contrast of increasing familiarity (for coordinates, see Table 1). The time series for the ROIs were taken from the subject level F-contrast of movement > implicit baseline as this was the most revealing contrast. This contrast revealed all regions that were active (two-tailed) when viewing movement, including the defined coordinates for MTG, IPL, and IFG in the left hemisphere.

Table 1.

The coordinates used for the ROIs

x	y	z	Region	BA	Cluster size
−48	−31	34	Inferior parietal lobule	40	141
−51	−58	−2	Middle temporal gyrus	39	60
−45	8	25	Inferior frontal gyrus	44	12

All ROIs were extracted by locating the nearest local maximum voxel to the coordinates of the group contrast of increasing familiarity. Nineteen of the 21 participants showed significant activity within the search radius of 16 mm. The 2 remaining participants were excluded from the connectivity analysis. The ROI time series for each region, for each participant, was extracted by using the eigenvariate (threshold of p < 0.05), with sphere radius 8 mm and adjusted for effects of no interest.

Definition of network models.

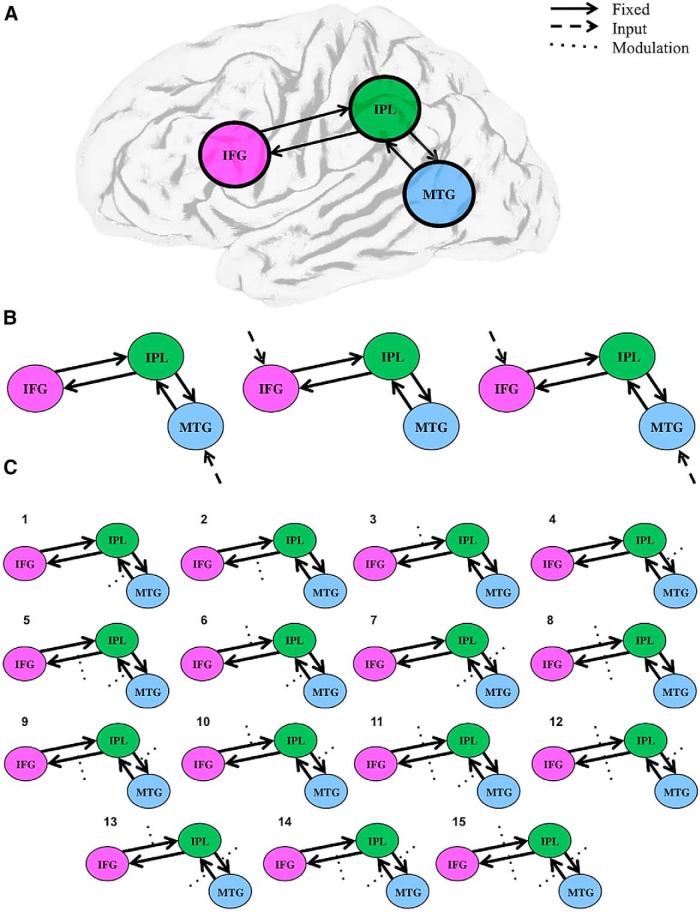
To test our hypothesis, all models were manipulated with regard to their modulation and direct inputs but not endogenous connectivity. To counter the problem of expanding model space, the endogenous connectivity of all models was anatomically informed by the theoretical models from which our hypothesis was based (Keysers and Perrett, 2004; Kilner et al., 2007b). The connections between the nodes were reciprocal between MTG and IPL and reciprocal between IPL and IFG (Fig. 2). This limiting of model space allowed us to examine the modulatory effects of increasing familiarity within a refined selection of models. These modulatory effects (B parameters) were tested on all extrinsic (between-node) excitatory connections and all combinations. For the direct inputs to the system, we modeled the movement effect. We tested the hypothesis of direct input into the system through MTG as well as direct input into IFG for all variants as well as direct input into both of these regions, resulting in 45 models per person, with a total of 855 models overall (Fig. 2).

Figure 2.

The model space. A, The endogenous (fixed) connectivity between the three regions. B, The three families of inputs (movement) tested: MTG, IFG and MTG, and IFG. For each of these three families, 15 models, shown in C, were tested to identify the modulation of increasing familiarity, resulting in 45 models for each participant. Solid lines indicate fixed connectivity. Dashed arrows indicate input into the system by movement. Dotted arrows indicate modulations on the given connection by increasing familiarity.

Results

Whole-brain GLM analyses

Neural processes engaged during action prediction

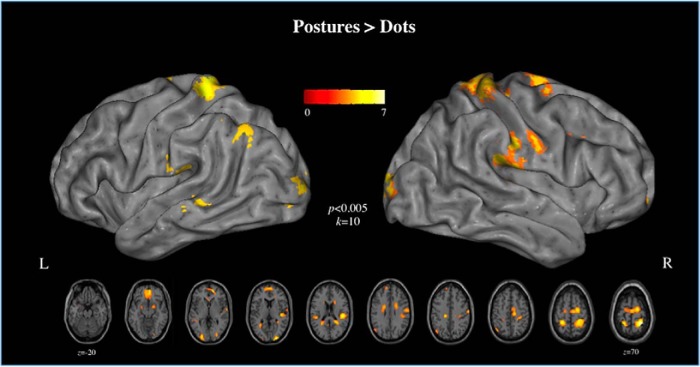
To address how action familiarity impacts AON activity using random-effects analyses, we report two contrasts. The first contrast identified brain regions more engaged when participants watched whole-body movements with the intention to predict which posture should follow after an occlusion, compared with watching the same videos but attending to the color of a dot that was superimposed on top of the dancer (Fig. 3).

Figure 3.

The GLM results of the main effect of performing the posture prediction task compared with the dot color identification task. All p values <0.005; k = 10 voxels.

This analysis revealed significant activity in M1 and the anterior regions of STG (for all peak coordinates from this contrast, see Table 2). This contrast shows the effects of the online updating of observed movements in anticipation of the decision-making period. The activity seen in the motor regions could perhaps represent the fact that, even though dance movements were observed in both conditions, the posture prediction task elicits more extensive engagement of motor cortical activity. Specifically, maintaining representations of actions so that they may be simulated during a period of occlusion may require more activity within primary motor regions (Kilner et al., 2009; Stadler et al., 2011; Cross et al., 2013; Hari et al., 2014; compare mu suppression in this region during action observation). Interestingly, activity within higher-level occipital cortices (V4v and V3v) also emerged from this contrast. This pattern of activity could reflect increased visual attention demands of biological motion tracking, as opposed to what was required for the dot-tracking task.

Table 2.

Localization of averaged BOLD response for the posture prediction versus dot tracking tasks

Anatomical region	BA	MNI coordinates			Putative functional name	t value	Cluster size	pcorrected value
		x	y	z
Postures versus dots
R postcentral gyrus	1	27	−43	70	M1	7.25	326	0.032
R postcentral gyrus	2	27	−37	55	M1	5.13	—	0.140
R superior occipital gyrus	17	21	−100	7	V3v	6.77	90	0.032
R lingual gyrus	18	24	−88	−11	V4v	3.25	—	0.744
R rolandic operculum	41	48	−25	22	S2	6.70	345	0.032
R Heschl's gyrus	41/42	45	−22	10	PAC/STG	5.30	—	0.135
R postcentral gyrus	1	63	−13	34	M1	4.34	—	0.284
R mid orbital gyrus	10	6	50	−14	MPFC	5.72	415	0.129
R mid orbital gyrus	32/10	15	50	−2	ACC	5.40	—	0.129
R superior medial gyrus	10	9	59	10	MPFCv	4.34	—	0.284
L postcentral gyrus	2	−27	−40	58	M1	5.50	158	0.129
L postcentral gyrus	2	−21	−43	70	M1	5.10	—	0.140
L superior parietal lobule	31	−15	−25	43	PCC	5.46	32	0.129
R superior frontal gyrus	6	18	−10	67	PMd	5.16	382	0.140
R middle cingulate cortex	6	15	−22	46	PMd	5.01	—	0.145
R supplemental motor area	6	3	−16	67	SMAd	4.71	—	0.214
R parahippocampal gyrus	19/30	24	−46	16	—	4.98	102	0.145
L middle occipital gyrus	18	−24	−88	1	MOG	4.66	76	0.219
L middle temporal gyrus	22	−51	−40	−2	MTG	4.48	42	0.268
L medial temporal gyrus	22/37	−42	−46	1	MTG/STS	3.00	—	0.285
L inferior parietal lobule	19	−30	−55	13	IPL	4.47	91	0.915
L superior temporal gyrus	42	−45	−31	19	pSTG	4.30	45	0.285
L superior temporal gyrus	42/43	−60	−28	16	STG	2.96	—	0.344
R caudate nucleus	23	24	2	28	—	4.24	96	0.720
L caudate nucleus	23	−18	−1	28	—	4.02	82	0.344
L caudate nucleus	23	−18	14	22	—	3.29	—	0.462
L inferior parietal cortex	40/7	−42	−67	49	IPC	4.02	51	0.462
L amygdala	25	−48	−73	34	AMYG	3.77	—	0.529
R amygdala	25	−21	−1	−14	AMYG	3.75	34	0.529
R amygdala	25	21	−1	−11	AMYG	3.61	28	0.627
L superior frontal gyrus	9	−12	53	31	SFG	3.49	25	0.285
L posterior cingulate cortex	31	−6	−52	25	PCC	3.46	43	0.915

MNI coordinates of peaks of relative activation within regions responding to the main effects of task: postures versus dots. Results were calculated at p_uncorrected <0.005; k = 10 voxels. Up to 3 local maxima are listed when a cluster has multiple peaks more than 8 mm apart. V4v, Ventral visual area 4; S2, sensorimotor area; PAC, primary auditory cortex; STG, superior temporal gyrus; M1, primary motor cortex; MPFC, medial prefrontal cortex; ACC, anterior cingulate cortex; MPFCv, ventral medial prefrontal cortex; PCC, posterior cingulate cortex; PMd, dorsal premotor cortex; SMAd, dorsal supplemental motor area; MOG, middle occipital gyrus; MTG, middle temporal gyrus; STS, superior temporal sulcus; pSTG, posterior superior temporal gyrus; AMYG, amygdala; IPL, inferior parietal lobule; SFG, superior frontal gyrus; IPC, inferior parietal cortex.

Evaluated regional activations sensitive to increasing familiarity

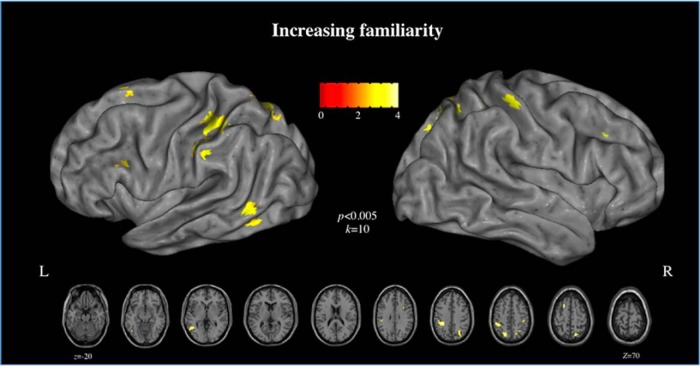
The second random-effects analysis evaluated brain regions sensitive to the increasing familiarity of a complex whole-body movement (for all peak coordinates from this contrast, see Table 3). This contrast allows us to locate the regions of interest for the DCM analysis as well as assess general effects of perceived action familiarity based on participants' individual subjective ratings of each action stimulus. As can be seen in Figure 4, the parametric contrast of increasing familiarity reveals activity within bilateral premotor, parietal cortices, and left temporal cortices. This contrast suggests that, as the movements are rated as increasingly familiar, the stronger the response becomes within core AON regions. These results add support to the view that the more familiar an observed action is, the stronger activity is within the AON (Buccino et al., 2004; Calvo-Merino et al., 2005; Cross et al., 2006). The three nodes in the left hemisphere form the ROIs for the DCM analysis, which evaluates their effective connectivity during action observation and how increasing familiarity modulates connections within this triad of brain regions.

Table 3.

Localization of averaged BOLD response for observation of actions rated as increasingly familiar

Anatomical region	BA	MNI coordinates			Putative functional name	t value	Cluster size	pcorrected value
		x	y	z
Increasing familiarity
Left supramarginal gyrus	40	−48	−31	34	SmG	4.02	141	0.837
Left inferior parietal lobule	7/40	−33	−37	40	IPL	3.99	—	0.837
Left inferior parietal lobule	7/40	−48	−37	52	IPL	3.80	—	0.837
Left middle temporal gyrus	39	−51	−58	−2	MTG	3.96	60	0.837
Left superior frontal gyrus	6	−18	11	61	SFG	3.74	10	0.837
Left superior parietal lobule	7	−21	−67	46	SPL	3.74	83	0.837
Left superior parietal lobule	7	−15	−67	52	SPL	3.63	—	0.837
Right superior parietal lobule	7	18	−67	61	SPL	3.68	96	0.837
Right angular gyrus	7/19	30	−70	37	AG	3.49	—	0.881
Right angular gyrus	7	27	−61	43	AG	3.27	—	0.897
Right inferior frontal gyrus (pars opercularis)	44	33	11	28	IFG	3.63	13	0.837
Right postcentral gyrus	2	48	−28	52	M1	3.41	25	0.881
Right inferior parietal lobule	40	36	−43	55	IPL	3.02	—	0.993
Left inferior frontal gyrus (pars opercularis)	44	−45	8	25	IFG	3.24	12	0.897

MNI coordinates of peaks of relative activation within regions responding to the parametric effects of increasing familiarity. Results were calculated at p_uncorrected <0.005; k = 10 voxels. Up to 3 local maxima are listed when a cluster has multiple peaks more than 8 mm apart. SmG, Supramarginal gyrus; IPL, inferior parietal lobule; MTG, middle temporal gyrus; SFG, superior frontal gyrus; SPL, superior parietal lobule; AG, angular gyrus; IFG, inferior frontal gyrus; M1, primary motor cortex.

Figure 4.

The GLM results of the parametric rating contrast for the posture prediction task. All p values <0.005; k = 10 voxels.

Effective connectivity analyses

The DCMs were created using the three ROIs listed in Table 1: MTG, IPL, and IFG (all in the left hemisphere). The input(s) into the system was movement, and the modulations were increasing familiarity. First, we identify where there is input into the system using a family comparison analysis. Next, we report the BMS analysis of the models within the winning family. Finally, we used Bayesian model averaging (BMA) to present the parameter estimates of the winning family of models.

Family level inference

As described in Materials and Methods, we classified our 45 models into three families based on input into the system. To recap, the families were MTG input, IFG input, and input into both MTG and IFG.

The results of the family comparison of inputs showed that there is unequivocally strong evidence for the family with input into both regions of the system. The exceedance probability of this family was (almost) 1, implying that there is a near certainty that this class of input explains the network. This identification of the inputs into the system allowed us to concentrate our model comparison on the 15 models with MTG and IFG input into the system.

BMS and BMA within optimal family

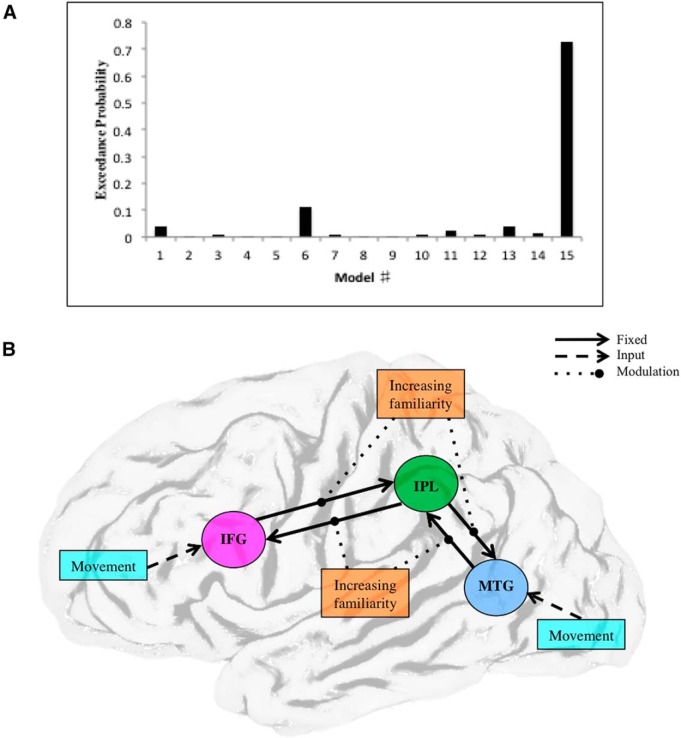
After assessing the existence of input parameters with family comparisons, we were then able to perform a BMS analysis on the 15 models within the MTG and IFG input family. As shown in Figure 5A, there is a clear optimal model, model 15.

Figure 5.

BMS on the 15 models in the MTG and IFG input family. A, Exceedance probability of all models. There is one clear winner, model 15, which had the posterior probability of 0.72. B, Model 15, the winning model, had modulation of increasing familiarity on all fixed connections.

The optimal model was the model that had modulation by increasing familiarity on all fixed connections (Fig. 5C). The probability of this model was 0.72 (Fig. 5B), which is a high probability. The next best model, model 6, had an exceedance probability of 0.11. In relation to our hypothesis that there would be greater top-down modulation for increasing familiarity, a winning model that had fully modulated connections would neither confirm nor refute this hypothesis. Although the posterior probability of the winning model was 0.72, this does not provide definitive evidence for this and only this model. Therefore, we used BMA to obtain estimates of effective connectivity (and their modulation) that accommodate uncertainty about models (Stephan et al., 2010). It is not always possible to find sufficient evidence for one model being the optimal model. Depending on which model is declared the best fitting, different inferences will be made regarding the behavior of a system. BMA helps to resolve this ambiguity by averaging over the models, accounting for the model evidence in the averaging; therefore, models with a low probability will not contribute very much to the BMA. This BMA also incorporates Bayesian parameter averaging over subjects to provide robust estimates of quantitative changes in coupling that are weighted by our relative confidence in the 15 models considered. The results of the BMA for the IFG and MTG input family are shown in Figure 6.

Figure 6.

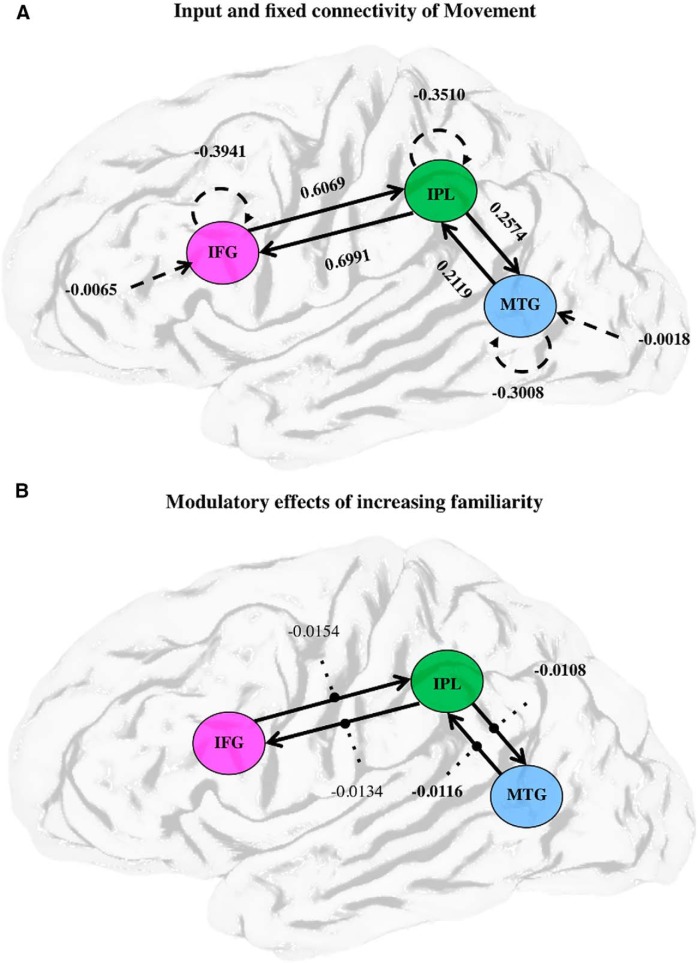
The resulting BMA of the winning model in Figure 5. A, The input and fixed connectivity of the model, subject to the input of movement. The dashed semicircled arrows indicate self-connections. Solid arrows indicate the endogenous connectivity. Straight dashed lines indicate the input into the system. B, The modulatory effects of increasing familiarity on the fixed connections. In all cases, the numerical value represents the connection strength/modulation in log scaling parameters.

Upon examination of the effects of movement on the network, the BMA results demonstrate that all the connections are significantly >0, supported by a one-sample t test, shown in Table 4 (the use of t tests provides a way of scoring the standardized effects sizes in relation to intersubject variability). Beginning with the inputs into the network, the coupling strengths are relatively weak and inhibitory. The reason for this may be that we allowed for stochastic effects, which means that the endogenous connectivity within the system is not reliant on a deterministic input into the network (Li et al., 2011). The inclusion of stochastic effects accounts for an unmodeled node modulating the input, meaning that the endogenous connectivity is not affected by weak inputs.

Table 4.

Results of a one sample t test for coupling parameters of endogenous activity of movement: endogenous connectivity

	From
	IFG	IPL	MTG
To
IFG	−0.3941 (0.0267)* (p < 0.0001)	0.6991 (0.0107)* (p < 0.0001)	—
IPL	0.6069 (0.0108)* (p < 0.0001)	−0.3510 (0.0285)* (p < 0.0001)	0.2119 (0.0141)* (p < 0.0001)
MTG	—	0.2574 (0.0100)* (p < 0.0001)	−0.3008 (0.0220)* (p < 0.0001)

Data are mean (SEM) for each connection. —, Not investigated. The threshold was set at p < 0.007 (corresponding to an FDR-corrected threshold of p < 0.05 for multiple comparisons).

*Significant connection.

The endogenous connections between the nodes show us that the anatomical basis of our models was correct; movement reveals connections. The reciprocal connections between IPL and IFG appear stronger than the connections between MTG and IPL. It should be noted that the movement input contained videos that were rated as both familiar and unfamiliar, so these coupling parameters can be considered the average of the two polarities. Therefore, to understand these coupling strengths, we next investigated the modulatory effects of increasing familiarity.

The impact on the network's modulatory connectivity from increasing familiarity can be seen in Figure 6B. These modulatory connections were then placed into a one-sample t test that revealed that not all significantly differed from zero (Table 5). Only the modulatory influences between MTG-IPL and between IPL-MTG were significantly different from zero across individuals.

Table 5.

Results of a one sample t test for coupling parameters of modulatory activity of increasing familiarity: modulatory

	From
	IFG	IPL	MTG
To
IFG	—	−0.013 (0.005) (p = 0.017)	—
IPL	−0.068 (0.0520) (p = 0.207)	—	−0.012 (0.003)* (p = 0.001)
MTG	—	−0.011 (0.004)* (p = 0.005)	—

Data are mean (SEM) for each connection. —, Not investigated. The threshold was set at p < 0.0125 (corresponding to an FDR-corrected threshold of p < 0.05, corrected for multiple comparisons).

*Significant connection.

The modulatory effect of increasing familiarity on the fixed connection reveals several noteworthy findings described here and reconciled in the Discussion. The first is that, when a video is rated as increasingly familiar, the connection from MTG to IPL is attenuated. The sign change indicates that the bottom-up connection is attenuated by more familiar movements, thus supporting our hypothesis and assumptions made by a predictive coding model. The second finding is an attenuation of the connection from IPL to MTG. This finding was not predicted and, as such, does not clearly support our hypothesis, as we would have predicted significantly augmented modulation in this top-down direction. However, as discussed below, this finding nonetheless informs our understanding of a predictive coding account of action perception.

Discussion

Our aim was to characterize how subjective familiarity of an observed action impacts AON engagement through complementary use of parametric GLM and effective connectivity analyses. We found that, as observed movements were rated as more familiar, BOLD signal in left MTG, IPL, and IFG increased. We then used DCM to explore effective connectivity between these regions to evaluate the hypothesis that, as movements are rated as increasingly familiar, the anterior influence (MTG → IPL → IFG), representing bottom-up, feedforward action coding, attenuates, whereas connectivity for posterior influence (IFG → IPL → MTG), representing top-down, feedback action coding, is upregulated. DCM provided partial support of this hypothesis by demonstrating attenuated influence from connections leading to and originating from MTG. In the following, we consider these findings in terms of a predictive coding model of AON function and how they advance our understanding of the impact of familiarity on action perception.

The impact of familiarity on the AON and the “like me” hypothesis

The main GLM findings show that primary motor and AON regions are recruited during perception and prediction of movements and that increasingly familiar movements are associated with concomitant increases in activity. The first result corroborates research demonstrating sensorimotor engagement during tasks that explicitly tap into prediction processes (Blakemore and Frith, 2005; Falck-Ytter et al., 2006; Stadler et al., 2011; Cross et al., 2013). The parametric analyses reveal that increasingly familiar movements preferentially engage core AON regions, supporting the general premise of a “like me” hypothesis of AON function (Buccino et al., 2004; Calvo-Merino et al., 2005; Cross et al., 2006; Meltzoff, 2007; Liew et al., 2011; Press, 2011). The parametric contrast allowed us to examine the relationship between AON activity and familiarity in a nonbinary fashion, thus advancing knowledge from previous studies. This approach subsequently enabled examination of causal connectivity between core AON regions to further characterize AON contributions to action understanding.

Effective connectivity

Our first effective connectivity aim was to create a feasible model space based on AON regions proposed previously (Keysers and Perrett, 2004). By tailoring this model space, we could address where movement inputted to the system and examine the models within this family (Penny et al., 2010). We showed inputs to both IFG and MTG in a reciprocally connected network. Next, we sought to identify the optimal model of modulation/modulatory activity (B matrix) based on these fixed connections. The BMS results revealed the optimal model as one where increasing familiarity modulates all fixed connections. By use of BMA, we found that increasing movement familiarity attenuates anterior influence between MTG and IPL while also attenuating posterior influence between IPL and MTG.

The parameter estimates (from the BMA) suggest that increasing familiarity causes diffuse and small reductions in effective connectivity among the three areas studied. The small effect sizes deserve some comment; in this analysis, we used stochastic DCM. In stochastic DCM, one estimates both the neuronal activity and effective connectivity that best explain observed responses. Generally, this provides smaller estimates of changes in coupling because condition-specific effects can also be modeled by differences in neuronal activity. Although small, our Bayesian model comparison suggests that familiarity-related changes in effective connectivity are evident in the data. The effect sizes are expressed in terms of log-scale parameters and can be interpreted (approximately) as proportional changes. In other words, familiarity induces a change of ∼1% of the underlying connectivity strengths. Furthermore, as predicted, ascending connections to IPL show a familiarity-related decrease greater in magnitude than the decrease in descending connections from IPL.

Predictive coding models revisited

Our findings support several assumptions made by models of action perception that rely on notions of predictive coding (Keysers and Perrett, 2004; Kilner et al., 2007a,b). These models suggest greater influence from visual to motor regions when an observed movement is unfamiliar. Such activity is hypothesized to be indicative of action representations being built in a perceptually driven, bottom-up manner. When an observed movement is familiar, top-down predictions should have a greater influence on perceptual processing at lower levels. These predictions are formally identical to corollary discharge (i.e., the expected consequences of an intended movement). This connects predictive coding accounts of action perception to machine learning accounts of motor control (Wolpert et al., 2003) that appeal to notions of corollary discharge. In the predictive coding account of action observation (Kilner et al., 2007a,b), the more familiar a movement, the more precise top-down predictions become. Effectively, increasing familiarity should increase influence of top-down predictions relative to bottom-up information (which, in this model, originates in MTG). We therefore anticipated that more familiar actions should be associated with increasing influence from connections spanning posteriorly from IFG → IPL and IPL → MTG, and decreasing influence from connections spanning anteriorly from MTG → IPL and IPL → IFG.

DCM analyses partially support these hypotheses. We show that, with increasing familiarity, MTG exerts an attenuated influence on IPL in an anterior direction, as hypothesized. A similar dampening of influence from IPL to IFG with increasing familiarity is also observed, although this finding did not survive corrections for multiple comparisons. Our hypotheses concerning the influence of familiarity on posterior-projecting connections were not supported. Increasing action familiarity did not significantly upregulate influence from IFG to IPL, as was expected. One possible explanation for this could be that the influence IFG exerts on IPL is impervious to variations in familiarity examined in the present study. Most crucially, and contrary to our original hypothesis, a significant attenuation of influence was observed in posterior connections from IPL to MTG.

At first glance, this finding might appear to contradict a predictive coding account of action observation. However, our initial hypotheses might have been overly simplistic, as they did not take into account the range of excitatory and inhibitory influences between nodes within a predictive coding framework (Keysers and Gazzola, 2014). In keeping with our original hypotheses, the reason why effective connectivity between MTG and IPL in both directions attenuates with increasing familiarity could be that increasingly accurate predictions decrease demand on incoming or ongoing perceptual processing. As such, the present findings illustrate a version of predictive coding in which outputs from, and inputs to, MTG attenuate with increasing familiarity, whereas reciprocal influence between parietal and premotor areas is less impacted by increasing action familiarity. To an extent, these findings support a predictive coding framework of the AON in a nuanced and subtle manner. The general idea that increased familiarity is associated with decreased prediction error, and a dampening of sensory inputs is supported by our data. However, the present findings do not yield clear support for more specific predictions concerning the concurrent upregulation of posterior-projecting connections (IFG → IPL and IPL → MTG) and downregularion of anterior-projecting connections (MTG → IPL and IPL → MTG).

An alternative framing of these DCM results is that, with increasing familiarity, localized representations become sufficient to perform the task at hand, resulting in decreased cross-node coordination within the AON (as this coordination becomes less necessary). Such an interpretation would be consistent with the univariate findings reported in the present study and others (Buccino et al., 2004; Calvo-Merino et al., 2005; Cross et al., 2006; Vogt et al., 2007; Shimada, 2010; Liew et al., 2011), which show increased activity within the individual AON nodes during familiar action observation. This interpretation remains speculative at this stage. To test this possible explanation, follow-up research could investigate observation of actions that cover a broader range of familiarity to determine whether the degree of familiarity drives the connection strengths between AON nodes, such that observation of highly unfamiliar actions is associated with stronger AON connections, whereas observation of actions rated as highly familiar is associated with attenuated connections. Were this alternative theoretical framing to be supported by follow-up work, it would call for an updating and reconsideration of a predictive coding account of action perception.

In conclusion, the present findings provide partial support for a predictive coding account of action observation, as well as offer novel insights into how familiarity modulates effective connectivity within the AON. By using participants' individual, subjective ratings of familiarity, we show greater AON activity when movements were perceived as increasingly familiar. Through the use of effective connectivity analyses, we demonstrate attenuation of reciprocal connections between IPL and MTG with increasing familiarity and presumed decreasing prediction error. Although this finding is broadly in line with a predictive coding account of action perception (Kilner et al., 2007b), the data do not provide clear or complete support for this theoretical model for how familiarity should impact influence between AON nodes. An alternative possibility is that increased familiarity of an observed action results in a shift away from coordinated activity between AON nodes and toward more individuated processing within individual nodes. A challenge for future work is to further explore how familiarity modulates influence between AON regions. Of particular importance for future investigation is how different levels of familiarity impact parietal and premotor regions, as our findings less clearly demonstrate marked changes in effective connectivity between these two regions with increasing familiarity. As a whole, the present study demonstrates the utility of effective connectivity analyses to explore simulationist accounts of social information processing.