Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Jan 28;5:8080. doi: 10.1038/srep08080

Direct evidence for kinetic effects associated with solar wind reconnection

Xiaojun Xu 1,2,3,a, Yi Wang 4, Fengsi Wei 4, Xueshang Feng 4, Xiaohua Deng 1, Yonghui Ma 3, Meng Zhou 1, Ye Pang 1, Hon-Cheng Wong 5,3,b
PMCID: PMC4308709  PMID: 25628139

Abstract

Kinetic effects resulting from the two-fluid physics play a crucial role in the fast collisionless reconnection, which is a process to explosively release massive energy stored in magnetic fields in space and astrophysical plasmas. In-situ observations in the Earth's magnetosphere provide solid consistence with theoretical models on the point that kinetic effects are required in the collisionless reconnection. However, all the observations associated with solar wind reconnection have been analyzed in the context of magnetohydrodynamics (MHD) although a lot of solar wind reconnection exhausts have been reported. Because of the absence of kinetic effects and substantial heating, whether the reconnections are still ongoing when they are detected in the solar wind remains unknown. Here, by dual-spacecraft observations, we report a solar wind reconnection with clear Hall magnetic fields. Its corresponding Alfvenic electron outflow jet, derived from the decouple between ions and electrons, is identified, showing direct evidence for kinetic effects that dominate the collisionless reconnection. The turbulence associated with the exhaust is a kind of background solar wind turbulence, implying that the reconnection generated turbulence has not much developed.

In collisionless magnetic reconnection, kinetic effects are required to break the frozen-in condition1,2. As a result, the ions (electrons) decouple from the magnetic fields in the ion (electron) diffusion region of the order of the ion (electron) inertial scale near the reconnection X-line, resulting in Hall effects as observable signatures3,4. Recent simulations have shown that the decoupled (from ions) electron outflow jet, which is embedded in the central current sheet, can greatly exceed the regular electron-diffusion scale along the exhaust in open-boundary conditions system5,6,7,8. Further simulations found that the prolonged electron jet can be deflected by the Lorentz force under the guide field (Bg)9,10, which has been proved by in-situ observations in the Earth's magnetosphere11,12.

The solar wind is a natural laboratory to study reconnection with open-boundary conditions by in-situ observations. Relatively recent observational studies on solar wind Petschek-like reconnection exhausts13 have shown that the reconnection configuration can be extremely extended both along the exhaust14 and the X-line15. It can persist quasi-steadily for several hours but with no substantial heating16. However, kinetic effects of two-fluid physics associated with solar wind reconnection have never been identified yet. These different features from the Earth's magnetospheric reconnection rise the question whether solar wind reconnections are still ongoing at the encounter site with spacecraft.

As shown in computer simulations, only a proper set of βe and Bg in small ranges allow the existence of the prolonged electron jet10, while most of these two parameters in solar wind reconnections are not proper. A large number of exhausts are associated with small magnetic shears17, corresponding to too strong guide fields to be proper. Besides, the crossing spacecraft are usually so far away from the reconnection X-line that the electron jet cannot reach in order to be detected. In addition, the current sheets in the solar wind are oblique in the original-data coordinates. We have to converse the measurements into the LMN coordinates18. When the crossing spacecraft detects a narrow current sheet, which may be close to the reconnection site, the very small number of measurement samples due to present low-resolution data makes the conversion of coordinates unreliable. Therefore, one still can hardly identify the kinetic effects in data. Here, we fortunately observed a solar wind reconnection exhaust with clear kinetic effects, suggesting that the solar wind reconnection can be active and hence ongoing at 1 AU.

Results

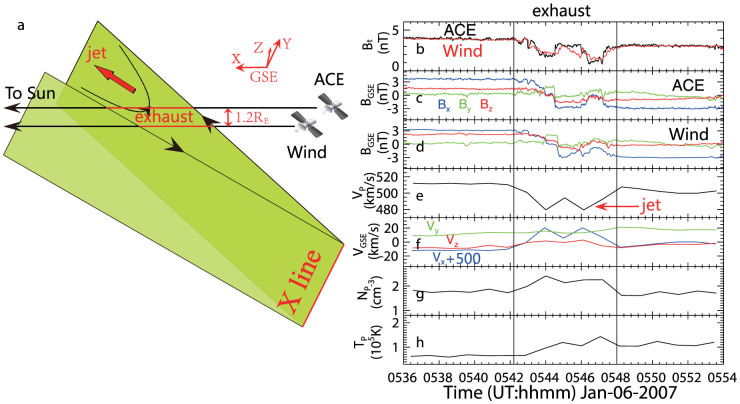
On January 6 2007, Wind spacecraft first crossed a complex current sheet at 05:34 UT and 8 minutes later (~05:42 UT), ACE spacecraft encountered the same current sheet in the solar wind. At the crossing time, ACE and Wind located at (218.64, −24.34, 22.46) and (254.32, −25.18, 21.60) RE (Earth radii) in Geocentric Solar Ecliptic (GSE) coordinates (hereafter, GSE is used unless noted), respectively. Although having a very large distance in the x direction, the trajectories of the two spacecraft are very close, namely about 1.2 RE from each other. Similar measurements of the two spacecraft (Figures 1b–h) around the encountering time show first anticorrelated and then correlated variations of B and V at the edges of the current sheet (marked by the two vertical lines in Figure 1). Such characteristics of back-to-back Alfvenic or slow-mode waves together with a decrease in magnetic magnitude, enhancements in plasma density and temperature within the current sheet and a corresponding jet jointly identify a solar wind reconnection exhaust19.

Figure 1. Schematics of spacecraft crossing a reconnection exhaust and selected measurements of magnetic field and plasma around the exhaust.

Figure 1

Open in a new tab

(a), sketch of the geometry of spacecraft encountering a solar wind reconnection exhaust. (b), magnetic magnitude. (c), the three components of magnetic field from ACE/MAG data. (d), the three components of magnetic field from Wind/MFI data. (e), the plasma bulk speed, showing a plasma jet. (f), the three components of plasma velocity by ACE. (g), proton density by ACE. (h), plasma temperature by ACE. The two vertical lines indicate the leading and trailing boundaries of the reconnection exhaust. The Wind/PM3DP data of 3-s resolution is not available during this interval. The main acceleration occurring in the +x direction indicates that a sunward directed exhaust was encountered. The X line is almost along the y-axis as illustrated below.

To analyze the exhaust we construct a LMN system, where L along the antiparallel magnetic field direction, N along the current sheet normal, M along the X line direction and L, M, N forming a right-handed system. The LMN directions calculated from Wind measurements are (0.91, −0.01, 0.41), (−0.08, 0.98, 0.20), (−0.41, −0.21, 0.89) and (0.93, 0.02, 0.38), (−0.04, 0.998, 0.04), (−0.38, −0.05, 0.96) from ACE data. The M direction is almost along the +y direction in the GSE coordinates. Therefore, the wedge angles are about 3°, 9° and 9° between L–L, M–M and N–N components, respectively. The small discrepancy between the two L directions implies that the reconnection current sheet is consistent with the roughly planar nature as reported previously by multiple spacecraft observations20,21,22,23.

Figures 2a–d show selected measurements around the exhaust in the LMN coordinates. The profiles of velocity and magnetic field coincide well with the features of reconnection outflow region: the field reversal almost occurs in BL and the plasma jet is nearly along VL. Apparent bipolar BM is presented by both ACE and Wind through the whole current sheet. However, the Hall magnetic fields here are much turbulent rather than laminar as it performs close to the X-line. The magnetic shear across the exhaust is about 168° corresponding to a weak guide field of ~0.35 nT. The bipolar structure is consistent with the prediction of reconnection Hall effect as illustrated in Figure 3. The velocity of the ion jet is 35 km/s in the rest frame of the solar wind. The inflow Alfven speed for asymmetric magnetic strengths24, 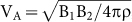Inline graphic, is about 56 km/s based on a density of 1.8 cm3 and BL of 4 nT and 3 nT in opposite sides, respectively. The normal speed of the current sheet, VN, is about 180 km/s. In this event, the shift in VN across the current sheet is very small (Figure 2d). It is beyond the accuracy of the plasma measurements and boundary normal determination from the minimum variance analysis so that we cannot use the half of this shift to estimate the inflow speed, Vin. Therefore the dimensionless reconnection rate can hardly be derived by using Vin/VA.

Figure 2. Observations around the exhaust by ACE and Wind (in green) in the LMN coordinates.

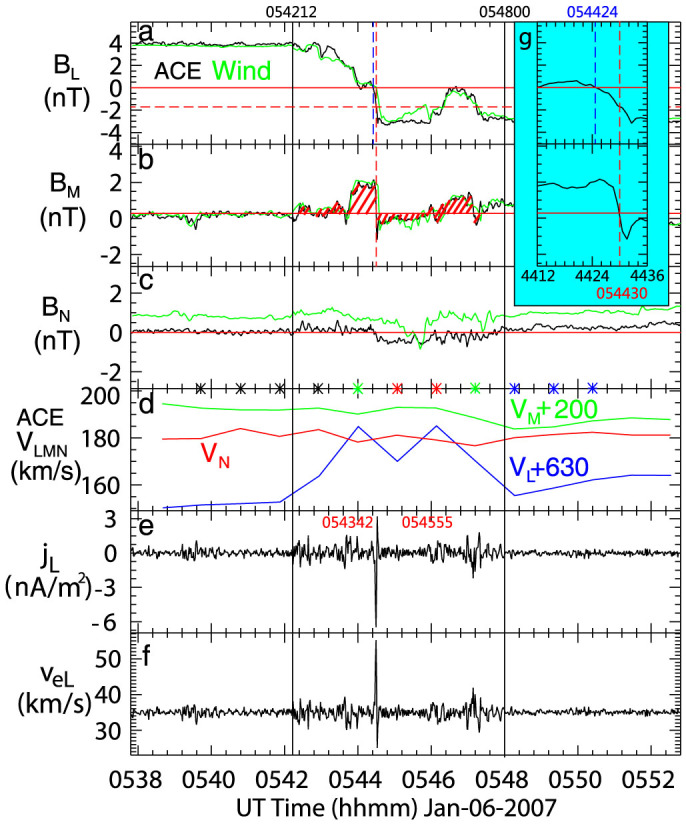
Figure 2

Open in a new tab

The magnetic field of Wind has been overplotted by a time shift of about +8 minutes. (a), BL component. The blue vertical dashed line indicates the time when BL changed its sign. (b), BM component: apparent bipolar BM with a weak guide field is shown. The red vertical dashed line indicates the time when BM − Bg changed its polarity. (c), BN component. The black, green, red and blue stars on the bottom mark the times of suprathermal electrons plotted in Figure 3. (d), the three components of velocity in LMN system (VL and VM have been shifted by 630 and 200 km/s, respectively). (e), the current density along the L direction calculated from the curl of magnetic field by ACE. (f), the electron velocity along the L direction. The black vertical lines indicate the edges of the current sheet. g, zoom-in measurements of the BL and BM from 05:44:12-05:44:36 UT.

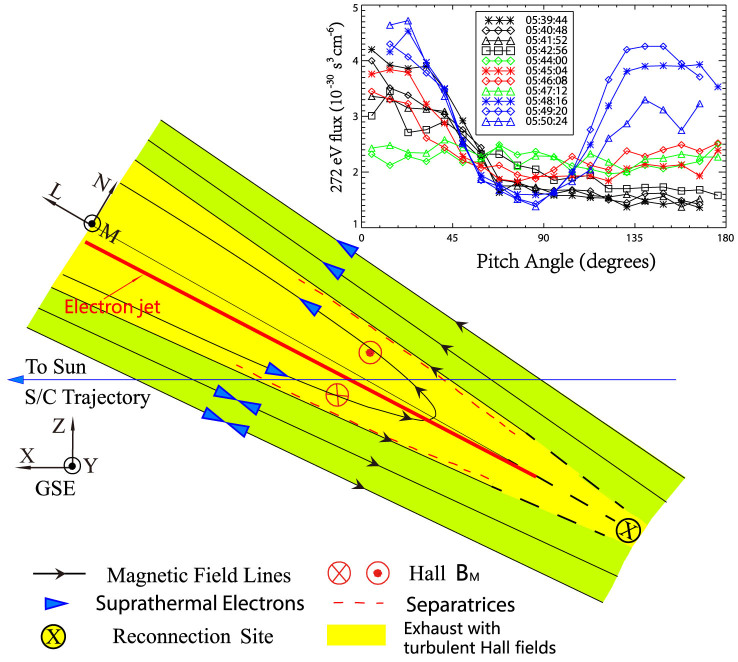
Figure 3. Diagram of the spatial scale of the encounter of ACE and Wind with the exhaust and pitch angle distributions of 272 eV electrons.

Figure 3

Open in a new tab

The M direction is almost along +y in GSE, so the reconnection plane is nearly in the X-Z plane. The spacecraft trajectories are along the +x. The top small panel shows the pitch angle distributions of 272 eV electrons continuously crossing the exhaust.

Besides the back-to-back Alfven waves, electron strahls, indicating the magnetic topology, can provide further evidence for the identification of reconnection25,26. Suprathermal electron pitch angle distribution of much longer time interval shows that this current sheet is the leading boundary of a region with counterstreaming electron strahls lasting to ~06:20 UT (not shown). The top panel of Figure 3 shows the continuous pitch angle distribution of 272 eV electrons at times marked in Figure 2c. The electron strahls before the current sheet center at 0° whereas they are bidirectional after the current sheet as revealed by black lines before 05:44:00 UT and blue lines after 05:47:12 UT, respectively. While at 05:44:00 and 05:47:12, the suprathermal electrons are isotropic (green lines) probably suggesting that they are near the separatrices of the reconnection. Because the inflow magnetic field lines cannot reach the separatrices, the strahl electrons thus cannot approach them. Between them, the suprathermal electrons are unidirectionally centering at 0° again (red lines). It should be noted that the neutral line (BL = 0) is no later than 05:44:24 (marked by the dashed blue line in Figure 2a and 2g), which is before the red stars in Figure 2c. That's to say, there are mainly two kinds of corona-connectivity of the field lines throughout the portion that behind the neutral line: the field lines near the neutral line are connected with the solar corona at one end (red stars in Figure 2) while the field lines farther away from the neutral line are connected with the solar corona at both ends (blue stars in Figure 2). If there was no reconnection in this current sheet, the corona-connectivity of the field lines behind the neutral lines (marked by the red, the second green and all blue stars) should be more likely uniform, which is not the situation seen in this event. But the reconnection can very reasonably explain the distributions of the suprathermal electrons. Since the reconnection can cut off the corona-connectivity from one side, the field lines after reconnection (those near the neutral line within the exhaust) are thus connected with the solar corona at only one end while those filed lines not reconnected are still two-end connected with the solar corona. The magnetic topology indicated by electron strahls is consistent with the pattern of the magnetic field lines across the reconnection exhaust as illustrated in Figure 3. The boundaries of the exhaust determined based on the profiles of magnetic field and plasma measurements are roughly at 05:42:12 and 05:48:00 in Figure 2.

The current system that supports the Hall field is made up of electrons flowing toward the X-line along the separatrices and the electron jet at the center of the exhaust. The Hall field is seen even in the largest simulations carried out to date27,28,29. The rapid change of the Hall magnetic fields in the central part of the exhaust suggests an intense current along the exhaust. The current density, jL, can be calculated by the curl of the magnetic field, jL = ΔBM/(μ0VNΔt). Figure 2d shows the result of jL, with a peak of 6.5 nA/m2 along the negative L direction corresponding to the change of the sign of (BM − Bg). An electron flow in positive L is required to provide this current. The velocity of the electron flow can be estimated as veL = viL − jL/nje. Figure 2f shows the velocity of the electron flow, which has a maximum of 55 km/s, nearly Alfvenic. Compared with that the reversal of (BM − Bg) is at 05:44:30, the nearest time of the BL changing from positive to negative is 05:44:24. It is thus suggested that the electron jet was deflected as shown by kinetic simulations. The Lorentz force due to the guide field is believed to be responsible for the deflection of electron jet. In the present study, the guide field is in the positive M direction and then the Lorentz force of the electron is in the negative N direction, resulting in a deflection of the electron jet into the negative BL region as illustrated in Figure 3. The corresponding BL at 05:44:30 is −1.73 nT, which is in agreement with the prediction of deflection due to Lorentz force. In this case, the inflow 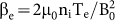Inline graphic, where Te is the electron temperature in the inflow region, is 0.23 and Bg/B0 = 0.10. The large electron βe could probably make the weak guide field in this event strong enough to approach the firehose condition to be in regime (3) in the simulations by Le et al10.

Discussion

In this study, we first identified a solar wind reconnection exhaust using the “direct evidence” provided by Gosling et al19, i.e. back-to-back Alfven waves, together with other reconnection signals including plasma jet associated with decrease of magnetic strength and enhancements of plasma density and temperature. We further using 272 eV suprathermal electron distributions to demonstrate the existence of reconnection instead of only a current sheet. On the basis of the identification of reconnection, we found clear Hall magnetic field associated with the reconnection. Meanwhile, the corresponding electron jet that supports the Hall field is consistent with the prediction of deflection in the guide field which has been proved by both simulations9,10 and in-situ observations11,12. And it is important to note that both ACE and Wind with a time delay of more than 8 minutes observed these evidences, which strongly suggests that the kinetic effects associated with the solar wind existed in a quasi-steady way rather than resulted from stochastic fluctuations.

Nevertheless, the low resolution plasma data by ACE could also result in an inaccurate identification of the boundaries of the very complex exhausts, especially the trailing boundary in this study. However, even only using the magnetic field data to identify the exhaust boundaries as the places where the field direction reaches the complete reversal of BL, we can still derive a bipolar structure of BM. As shown in Figure 2g, the place where BM − Bg = 0 occurs at 05:44:30 when BL has not yet reached its maximum negative value. That means the trailing boundary should be later than 05:44:30 and thus the Hall fields still exist. Therefore, it is convinced that the kinetic effects are identified to be associated with the solar wind reconnection. Our findings indicate that the solar wind reconnection can be active and dynamic at 1 AU.

It should be pointed out that the Hall field in this event was very turbulent rather than laminar. The width of the exhaust can be roughly estimated by W = VNΔt to be about 360 ion inertial lengths, which indicates that the encounter site is very far away from the X-line. Large-scale simulations both in two-dimension27 and three-dimension30 have clearly shown that Hall fields downstream can be much more complex than the simple laminar picture close to the X-line at the end of evolution. Using in-situ observations in the Earth's magnetosphere, Eastwood et al.31 has already demonstrated that turbulence can be generated by reconnection. However, the solar wind itself is also full of MHD turbulence. The reconnection generated turbulence and background solar wind turbulence have different properties. Solar wind turbulence usually present a −5/3 power-law spectrum above the ion gyroscale, while the spectral index varies from −4 to −2 at smaller scales32,33. Moreover, turbulence in the high-speed solar wind stream has a monoscaling property in the dissipation range34. On the other hand, the turbulence generated by collisionless reconnection has been found to be multifractal or intermittent by both simulation35 and observation31.

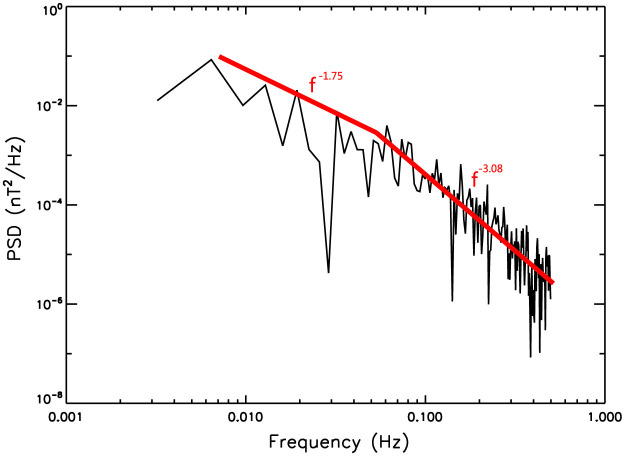
The turbulence in the solar wind reconnection could be very complicated, since the reconnection generated turbulence and the background solar wind turbulence would probably mix together. Figure 4 shows the power spectrum density of the BM component. The local ion cyclotron frequency is about 0.05 Hz. Below this frequency, the spectral index is −1.75 (~5/3), while above this frequency, the spectral index is -3.08. Therefore, the turbulence in our data is more likely a kind of background solar wind turbulence. The Hall field mainly supported by the central electron jet in our data is basically maintained though it is disturbed near the edge of the exhaust, while the Hall field shown in Eastwood et al.31 is very turbulent and no corresponding central jet can be identified. The reason for this may be that the turbulence generated by reconnection in this event is not much developed. As a result, the central part of the exhaust is minimally affected by the background solar wind turbulence while the near edge portion of plasma could be disturbed. However, as pointed by Browning and Lazarian36, the couple between microscale kinetic effects and macroscale turbulence generated by reconnection remains an open question.

Figure 4. Illustration of the power spectrum density of the BM component.

Figure 4

Open in a new tab

In the regime below ion cyclotron frequency (0.05 Hz marked by the vertical dashed line), the spectral slope is about −5/3. In the regime above ion cyclotron frequency, the spectral slope is −3.08. It is more likely that the turbulence is a kind of background solar wind turbulence.

Methods

We employ the minimum variances analysis of magnetic field (MVAB) (Ref. 18) to obtain the L, M and N directions of the current sheet. When the measurements of magnetic field (Bm, m is the number of all measurements considered) around the current sheet is given, the N (normal) direction, 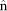Inline graphic = (nx, ny, nz), makes that 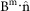Inline graphic has the minimun variance. Then we can calculate the variance of 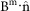Inline graphic and make the differential of this variance over nx, ny and nz equaling to zero, respectively, to obtain 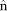Inline graphic. It becomes to derive the eigenvalues and eigenvectors of the matrix 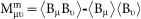Inline graphic, where〈〉indicates the average value37. Since 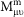Inline graphic is symmetric, the eigenvalues are all real and the corresponding eigenvectors are orthogonal. The eigenvectors corresponding to the maximum, intermediate and minimum eigenvalues are the L, M and N directions, respectively. It should be noted that when the ratio of the intermediate to minimum eigenvalue is close to unit, the M and N directions are not reliable, but the L direction is still available anyway. In this study, the ratio is about 4 and thus the M and N directions are useable.

Author Contributions

X.X. carried out the data analysis and wrote the manuscript. Y.W. contributed to the data processing. F.W. and X.F. led the project on solar wind reconnection. X.D. contributed to the identification of the Hall effect. H.C.W. helped revising and proofreading the manuscript. Y.H., M.Z. and Y.P. helped identifying the reconnection exhaust. All of the authors discussed the results and commented on the paper.

Acknowledgments

We thank N. Ness and D. J. McComas for using the ACE/MAG and ACE/SWE data, A. Szabo, and K. Ogilvie for the Wind/MFI and Wind/SWE data and NASA CDAWeb. This work was jointly supported by National Natural Science Foundation of China (41204123, 41231068, 41031066, 41374174), the Science and Technology Development Fund of Macao SAR (080/2012/A3) and the Specialized Research Fund for State Key Laboratories.

References

  1. Birn J. & Priest E. R. Reconnection of magnetic fields: magnetohydrodynamics and collisionless theory and observations (Cambridge University Press. NewYork, 2006). [Google Scholar]
  2. Vasyliunas V. M. Theoretical models of magnetic field line merging. I. Reviews of Geophysics and Space Physics 13, 303–336 (1975). [Google Scholar]
  3. Deng X. H. & Matsumoto H. Rapid magnetic reconnection in the Earth's magnetosphere mediated by whistler waves. Nature 410, 557–560 (2001). [DOI] [PubMed] [Google Scholar]
  4. Øieroset M., Phan T. D., Fujimoto M., Lin R. P. & Lepping R. P. In situ detection of collisionless reconnection in the Earth's magnetotail. Nature 412, 414–417 (2001). [DOI] [PubMed] [Google Scholar]
  5. Daughton W., Scudder J. & Karimabadi H. Fully kinetic simulations of undriven magnetic reconnection with open boundary conditions. Phys. Plasmas 13, 072101 (2006). [Google Scholar]
  6. Fujimoto K. Time evolution of the electron diffusion region and the reconnection rate in fully kinetic and large system. Phys. Plasmas 13, 072904 (2006). [Google Scholar]
  7. Shay M. A., Drake J. F. & Swisdak M. Two-scale structure of the electron dissipation region during collisionless magnetic reconnection. Phys. Rev. Lett. 99, 155002 (2007). [DOI] [PubMed] [Google Scholar]
  8. Karimabadi H., Daughton W. & Scudder J. Multi-scale structure of the electron diffusion region. Geophys. Res. Lett. 34, L13104 (2007). [Google Scholar]
  9. Goldman M. V., Lapenta G., Newman D. L., Markidis S. & Che H. Jet deflection by very weak guide fields during magnetic reconnection. Phys. Rev. Lett. 107, 135001 (2011). [DOI] [PubMed] [Google Scholar]
  10. Le A. et al. Regimes of the electron diffusion region in magnetic reconnection. Phys. Rev. Lett. 110, 135004 (2013). [DOI] [PubMed] [Google Scholar]
  11. Shay M. A., Drake J. F. & Swisdak M. Two-scale structure of the electron dissipation region during collisionless magnetic reconnection. Phys. Rev. Lett. 99, 155002 (2007). [DOI] [PubMed] [Google Scholar]
  12. Zhou M. et al. Evidence of deflected super-Alfvenic electron jet in a reconnection region with weak guide field. J. Geophys. Res. Space Physics 119, 1541–1548 (2014). [Google Scholar]
  13. Petscheck H. E. in AAS-NASA Symp. on the Physics of Solar Flares (28–30 October 1963, Goddard Space Flight Centre, Greenbelt, Maryland) (ed. Hess, W. N.) 425–437 (NASA Spec. Publ. SP-50, NASA Science and Technical Information Division, Washington DC, 1964). [Google Scholar]
  14. Phan T. D. et al. A magnetic reconnection X-line extending more than 390 Earth radii in the solar wind. Nature 439, 175 (2006). [DOI] [PubMed] [Google Scholar]
  15. Gosling J. T. et al. Five spacecraft observations of oppositely directed exhaust jets from a magnetic reconnection X-line extending >4.26 × 106 km in the solar wind at 1 AU. Geophys. Res. Lett. 34, L20108 (2007). [Google Scholar]
  16. Gosling J. T. Magnetic reconnection in the solar wind. Space Sci. Rev. 172, 187–200 (2012). [Google Scholar]
  17. Gosling J. T., Phan T. D., Lin R. P. & Szabo A. Prevalence of magnetic reconnection at small field shear angles in the solar wind. Geophys. Res. Lett. 34, L15110 (2007). [Google Scholar]
  18. Sonnerup B. U. Ö. & Cahill L. J. Jr. Magnetopause structure and attitude from Explorer 12 observations. J. Geophys. Res. 72, 171 (1967). [Google Scholar]
  19. Gosling J. T., Skoug R. M., McComas D. J. & Smith C. W. Direct evidence for magnetic reconnection in the solar wind near 1 AU. J. Geophys. Res. 110, A01107 (2005). [Google Scholar]
  20. Davis M. S., Phan T. D., Gosling J. T. & Skoug R. M. Detection of oppositely directed reconnection jets in a solar wind current sheet. Geophys. Res. Lett. 33, L19102 (2006). [Google Scholar]
  21. Phan T. D., Gosling J. T. & Davis M. S. Prevalence of extended reconnection X-lines in the solar wind at 1 AU. Geophys. Res. Lett. 36, L09108 (2009). [Google Scholar]
  22. Wang Y. et al. Energetic Electrons Associated with Magnetic Reconnection in the Magnetic Cloud Boundary Layer. Phys. Rev. Lett. 105, 195007 (2010). [DOI] [PubMed] [Google Scholar]
  23. Xu X., Wei F. & Feng X. Observations of reconnection exhausts associated with large- scale current sheets within a complex ICME at 1 AU. J. Geophys. Res. 116, A05105 (2011). [Google Scholar]
  24. Cassak P. A. & Shay M. A. Scaling of asymmetric magnetic reconnection: General theory and collisional simulations. Phys. Plasmas 14, 102114 (2007). [Google Scholar]
  25. Gosling J. T., Skoug R. M., McComas D. J. & Smith C. W. Magnetic disconnection from the Sun: Observations of a reconnection exhaust in the solar wind at the heliospheric current sheet. Geophys. Res. Lett. 32, L05105 (2005). [Google Scholar]
  26. Gosling J. T., McComas D. J., Skoug R. M. & Smith C. W. Magnetic reconnection at the heliospheric current sheet and the formation of closed magnetic field lines in the solar wind. Geophys. Res. Lett. 33, L17102 (2006). [Google Scholar]
  27. Higashimori K. & Hoshino M. The relation between ion temperature anisotropy and formation of slow shocks in collisionless magnetic reconnection. J. Geophys. Res. 117, A01220 (2012). [Google Scholar]
  28. Liu Y.-H., Drake J. F. & Swisdak M. The structure of the magnetic reconnection exhaust boundary. Phys. Plasmas 19, 022110 (2012). [Google Scholar]
  29. Le A. et al. Current sheets and pressure anisotropy in the reconnection exhaust. Phys. Plasmas 21, 012103 (2014). [Google Scholar]
  30. Daughton W. et al. Role of electron physics in the development of turbulent magnetic reconnection in collisionless plasmas. Nature Phys. 7, 539–542 (2011). [Google Scholar]
  31. Eastwood J. P., Phan T. D., Bale S. D. & Tjulin A. Observations of turbulence generated by magnetic reconnection. Phys. Rev. Lett. 102, 035110 (2009). [DOI] [PubMed] [Google Scholar]
  32. Sahraoui F., Goldstein M. L., Robert P. & Khotyaintsev Yu. V. Evidence of a cascade and dissipation of solar-wind turbulence at the electron gyroscale. Phys. Rev. Lett. 102, 231102 (2009). [DOI] [PubMed] [Google Scholar]
  33. Alexandrova O., Lacombe C., Mangeney A., Grappin R. & Maksimovic M. Solar wind turbulent spectrum at plasma kinetic scales. Astrophys. J. 760, 121 (2012). [Google Scholar]
  34. Kiyani K. H., Chapman S. C., Khotyaintsev Yu. V., Dunlop M. W. & Sahraoui F. Global scale-invariant dissipation in collisionless plasma turbulence. Phys. Rev. Lett. 103, 075006 (2009). [DOI] [PubMed] [Google Scholar]
  35. Leonardis E., Chapman S. C., Daughton W., Roytershteyn V. & Karimabadi H. Identification of intermittent multifractal turbulence in fully kinetic simulations of magnetic reconnection. Phys. Rev. Lett. 103, 205002 (2013). [DOI] [PubMed] [Google Scholar]
  36. Browning P. & Lazarian A. Notes on Magnetohydrodynamics of magnetic reconnection in turbulent media. Space Sci. Rev. 178, 325–355 (2013). [Google Scholar]
  37. Sonnerup B. U. Ö. & Scheible M. Minimum and maximum variance analysis in Analysis Methods for Multi-spacecraft Data (Eds. Paschmann, G. & Patric, W. D.) 185–220 (Eur. Space Agency, Noordwijk, Netherlands, 1998). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES