LineUp: Statistical Detection of Chromosomal Homology With Application to Plant Comparative Genomics

Abstract

The identification of homologous regions between chromosomes forms the basis for studies of genome organization, comparative genomics, and evolutionary genomics. Identification of these regions can be based on either synteny or colinearity, but there are few methods to test statistically for significant evidence of homology. In the present study, we improve a preexisting method that used colinearity as the basis for statistical tests. Improvements include computational efficiency and a relaxation of the colinearity assumption. Two algorithms perform the method: FullPermutation, which searches exhaustively for runs of markers, and FastRuns, which trades faster run times for exhaustive searches. The algorithms described here are available in the LineUp package (http://www.igb.uci.edu/∼baldig/lineup). We explore the performance of both algorithms on simulated data and also on genetic map data from maize (Zea mays ssp. mays). The method has reasonable power to detect a homologous region; for example, in >90% of simulations, both algorithms detect a homologous region of 10 markers buried in a random background, even when the homologous regions have diverged by numerous inversion events. The methods were applied to four maize molecular maps. All maps indicate that the maize genome contains extensive regions of genomic duplication and multiplication. Nonetheless, maps differ substantially in the location of homologous regions, probably reflecting the incomplete nature of genetic map data. The variation among maps has important implications for evolutionary inference from genetic map data.

Comparative genetic maps are constructed by identifying the location of homologous genes or other markers on two different chromosomes. From this location information, one important goal is to identify conserved (or homologous) chromosomal regions between chromosomes. Identification of chromosomal homology can be based on synteny, which refers to shared molecular markers between chromosomes, or colinearity, which includes shared markers and shared order. Once homologous regions have been identified between or within genomes, these regions form the basis for studying genome organization, evolution, and function.

Given homologous regions either within or between genomes, several statistical models have been devised to estimate the size and number of conserved regions (Nadeau and Taylor 1984; Nadeau and Sankoff 1998; Burt et al. 1999; Waddington et al. 2000; Kumar et al. 2001). In turn, these estimates are used to infer the number of genome rearrangements (Nadeau and Taylor 1984; Schoen 2000). The unfortunate drawback of all of these models is that they assume that homologous chromosomal segments are easily identifiable. However, homology may not be easy to determine in many instances, that is, when marker genes have been duplicated, deleted, or rearranged extensively. The misidentification of homology may be a substantial shortcoming of comparative mapping approaches, and correct identification of homologous segments remains an important problem.

In some cases, the problem of chromosomal homology has been addressed by the use of guidelines, or definitions. For example, the Human Genome Organization (HUGO) defines a conserved (or homologous) chromosomal segment as “the syntenic association of two or more homologous genes in two separate species” (Andersson et al. 1996). Although this definition is helpful, it is obvious that it is not a meaningful measure in some situations. For example, two species with thousands of mapped homologous markers will have a “syntenic association of two or more homologous genes,” even when the location of genes is randomized in one genome relative to the other. Thus, with a great deal of data, conserved segments (as per the HUGO definition) accrue as a function of the number of mapped markers and may not reflect chromosomal homology. Furthermore, the HUGO definition does not explicitly incorporate order or distance information among markers; this is crucial because closely clustered markers provide stronger evidence of homology than do widely dispersed markers.

At the very least, then, guidelines for identifying homologous regions should have some adjustment for the number of markers under consideration, their order, and the distances between them. More importantly, the guidelines should include some explicit statistical justification to determine if putative homologous regions provide a pattern beyond random expectation. Also note that the problem of homology identification does not apply exclusively to molecular genetic maps. With genomic DNA sequences, genome comparisons can be reduced to thousands of inter- and intra-specific BLAST hits that indicate gene homology. When the locations of homologous genes are known, this information can be used to infer chromosomal homologies (see Wolf et al. 2001; Wong et al. 2002).

Simple definitions of homology are very limited, but even these have not been applied to many study systems. For example, no consistent standard has been applied to plant comparative maps, and statistical criteria for establishing homology have been applied only occasionally (see Grant et al. 2000; Vision et al. 2000). Chromosomal homology is particularly difficult to identify in plants because many plants have histories of extensive gene, chromosome, and genome duplication (Wendel 2000).

Recently, Gaut (2001) introduced a method to test whether colinear runs of genetic markers are expected at random between two chromosomes (i.e., are consistent with statistical noise) or instead provide evidence of an underlying nonrandom pattern. In brief, the method identifies colinear markers between two chromosomes. Each set (or run) of colinear markers is measured by the number of markers in the run and by the distance covered by the run (the distance may be in centimorgans [cM] or base pairs, or in any other distance measure). The map data are then randomized, and colinear runs are identified in the randomized data. After many randomizations, it is possible to determine whether the original colinear run either has more markers than expected by chance or is more clustered than expected by chance. With this method, observed runs that are rare in randomized data are considered regions of potential homology. This statistical approach was applied to maize (Zea mays ssp. mays) genetic map data. The method detected roughly 2.5-fold more duplicated regions within maize than were previously noted and also indicated that up to one third of the maize genome is multicopy (Gaut 2001).

Although the method applies statistical criteria to the problem of homology identification, it suffers from several important limitations. For example, it relies on colinearity to identify chromosomal homology. The emphasis on colinearity ensures that the method is conservative, but it can also miss regions of chromosomal homology that have undergone substantial rearrangement of marker order. In addition, the method does not consider sub-runs of colinear markers within a larger run. In situations in which a run contains many markers but is later found not to be statistically significant, potentially significant sub-runs are ignored. Finally, the method is computationally intensive, limiting its application.

In the present study, we extend the method of Gaut (2001) by introducing two new algorithms that make the general approach more computationally feasible. These algorithms also relax the emphasis on colinearity and examine sub-runs nested within longer colinear runs. We investigate the performance of the algorithms by exploring their power to identify simulated regions of chromosomal conservation. We also apply the method to four different molecular genetic maps of maize. These maps are based on a different number of molecular markers and, in some cases, on different parental crosses. They thus provide a resource for determining whether information about chromosomal homology is consistent among maps. All maps indicate that maize has extensive regions of chromosomal duplication, but information among maps differs substantially, underscoring the weaknesses of genetic map data for inferring chromosomal structure and evolution.

RESULTS

Simulated Data

Detection of colinear runs can be very time- and memory-intensive when marker density is high, and there is a commensurately large number of colinear runs. We constructed simulated data to examine two aspects of the FastRuns and FullPermutation algorithms (described in Methods): (1) performance with increasing data complexity and (2) statistical power to identify conserved regions.

Performance With Increasing Data Complexity

We constructed simulated data by placing cross-hybridizing marker pairs randomly on two artificial chromosomes of 100 cM in length. We then identified colinear runs in the simulated data. For each of 100 data sets, run analysis was performed six times: FullPermutation with D = 0, 1, and 2 cM; and FastRuns with D = 0, 1, and 2 cM. The I and O parameters of the FullPermutation algorithm were set to zero. (Each parameter is explained in the Methods).

As expected, the number of identified runs increased with marker density (Table 1). The number of runs also increased with D. With FullPermutation and 400 marker pairs, the number of runs increased >60-fold between D = 0 and D = 1 and >40-fold between D = 1 and D = 2. For all data sets, FastRuns identified substantially fewer runs than did FullPermutation analysis, but analysis was more rapid. For example, with 400 marker pairs and D = 2, FastRuns completed run detection in 5 sec, whereas run detection was terminated after 4 h with FullPermutation. The important issue, which we address below, is whether the identification of fewer runs substantially hampers the ability of FastRuns to detect regions of significant colinearity.

Table 1.

Analysis of Random Data Constructed Under the Null Hypothesis of No Regional Homology

No. marker pairs	50		100		200		400
Method	no.a	prop (SD)b	no.a	prop (SD)b	no.a	prop (SD)b	no.a	prop (SD)b
Full D = 0	28	0.06 (0.07)	72	0.05 (0.04)	155	0.05 (0.02)	382	0.05 (0.02)
Full D = 1	81	0.06 (0.05)	350	0.05 (0.03)	2201	0.05 (0.02)	25,529	0.05 (0.01)
Full D = 2	165	0.05 (0.04)	1053	0.05 (0.02)	11,657	0.05 (0.02)	>106	NAc
FastRun D = 0	23	0.06 (0.08)	54	0.06 (0.04)	120	0.05 (0.03)	293	0.05 (0.02)
FastRuns D = 1	64	0.06 (0.05)	264	0.05 (0.03)	1480	0.05 (0.02)	11,596	0.05 (0.01)
FastRuns D = 2	126	0.05 (0.04)	707	0.05 (0.02)	5527	0.05 (0.02)	61,921	0.05 (0.01)

^aAverage number of identified runs, based on 100 data sets.

^bAverage proportion of significant runs, based on 100 data sets, under α = 0.05. For each of the 100 data sets, significance was based on 100 Monte Carlo simulations.

^cNA indicates not available; analysis was terminated owing to lack of memory.

To investigate type I error, we determined the average proportion of runs that were statistically significant for the 100 data sets (Table 1). When significance was based on 100 Monte Carlo simulations per data set, the average type I error was not significantly different from 0.05 for all conditions examined (Table 1). Furthermore, the standard deviation of this proportion decreased with the number of markers in the data set, indicating that the type I error converges on 5% with unlimited data. Altogether, statistics were well behaved under the null hypothesis of random data for both algorithms.

Statistical Power

It is unclear to what extent differences between the FastRuns and FullPermutation algorithms affect the statistical power to identify significant runs. To explore the statistical power of both algorithms, we generated data for two chromosomes. These two chromosomes were given a “random background” of markers that mimicked the maize UMC98 genetic map (Davis et al. 1999). In the UMC98 map, the average chromosome length is 170 cM, and each chromosome contains ∼60 markers that are assigned to that chromosome but also cross-hybridize to one other location in the maize genome. Thus, simulated data consisted of two chromosomes of 170 cM, each of which was assigned 60 markers. On average, 20% (reflecting that we are simulating two out of 10 chromosomes) of the 120 total markers were found in two copies.

On top of this random background, 5, 10, or 20 marker pairs were placed in colinear order on the two chromosomes. These were distributed uniformly over a distance of 20 cM in the middle of the chromosomes. The resulting data sets had “real” and “perfect” colinear runs buried in a random background. On one of the two chromosomes, we also inverted adjacent markers within the 20-cM region to simulate chromosomal divergence.

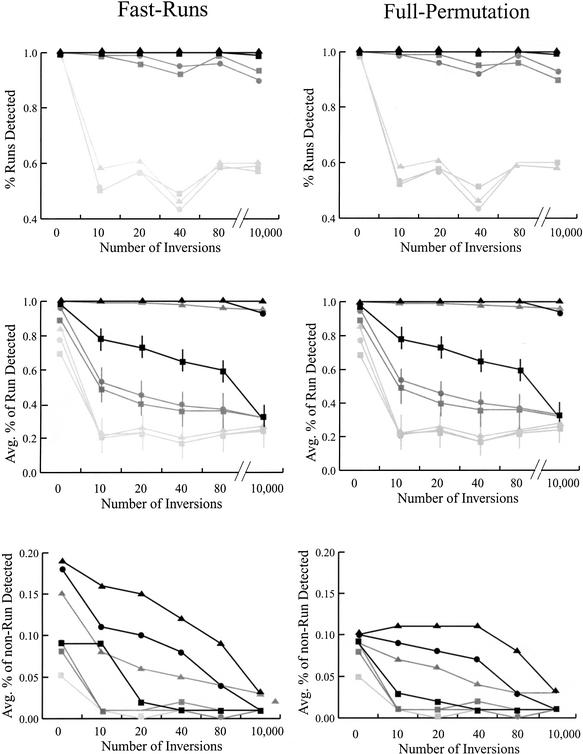
Each of the 100 simulated data sets were subjected to run analysis with the FastRuns and FullPermutation algorithms. We first counted the proportion of data sets in which some portion of the 20-cM conserved region was identified at the 0.01 significance level (Fig. 1). When either 10 or 20 markers comprised the colinear run, some of the region was detected in >90% of simulated data sets with both algorithms. The conserved 20-cM region was identified even after 10,000 inversions effectively randomized the order of markers, even with D = 0. Presumably part of the region was still identified as statistically significant with D = 0, because some small number of markers, representing a small proportion of the 20-cM region, remained colinear by chance after inversion and also remained closely spaced relative to the random background. With conserved regions of five colinear markers, a perfect run was detected in ∼100% of data sets, but after only 10 inversions, the conserved region was detected in <60% of data sets.

Figure 1.

The power to detect simulated regions of chromosomal homology with the FastRuns and FullPermutation algorithms. (Top) The proportion of data sets in which some portion of the homologous region was detected. (Middle) The average proportion of the homologous region detected. (Bottom) The average proportion of the nonhomologous region detected. For all graphs, black lines represents results based on simulations in which 20 markers define the homologous region; dark gray, 10 markers; and light gray, five markers. The symbols represent analyses with different values of D: D =  2 (triangles); D =  1 (circles); and D =  0 (squares). Horizontal lines represent approximate standard deviations when available. The apparent dip in ability to identify a portion of the conserved region after 40 inversions (but not 80 or 10,000) disappears as the size of the simulated data set increases (data not shown).

We also calculated the average percentage of the 20-cM region that was identified as conserved (Fig. 1). When the region contained 20 colinear markers and no inversions, the entire region was identified in all 100 data sets, regardless of the value of D. After up to 10,000 inversions, >90% of the region was detected with D = 1 or D = 2, but with D = 0, detection tailed off considerably to 35%. Similarly, when the region contained 10 colinear markers, >90% of the region was detected with D =  2 no matter the number of inversions, but detection tailed off as a function of the number of inversions with D =  0 and D = 1. These observations can be explained by the D parameter: When markers were located within the distance stipulated by D, the algorithms rearranged inverted markers and found most of the original colinear run. In effect, the D parameter serves to relax the colinearity assumption, not unlike the O parameter (see Methods). In the absence of a random background, FullPermutation will always find the complete original run when all markers are ±D cM apart. In contrast, on average only ∼20% of the 20-cM region was detected when the region contained five inverted markers. In this case, the markers were too physically distant (20 / 5 = 4 cM) to permit rearrangement with any D < 4.

The FastRuns and FullPermutation algorithms identified the conserved 20-cM region equally well (Fig. 1). The two methods differed, however, in one aspect: the misidentification of the 150-cM nonconserved region as part of a conserved chromosomal segment (Fig. 1). For example, FastRuns misidentified ∼20%, on average, of the nonconserved region when D = 2 and the conserved region contained 20 markers. In contrast, the FullPermutation method misidentified 11%, on average, of the nonconserved region, but 11% is still high. Investigation of data sets in which misidentification was common indicated that misidentified regions were almost always adjacent to the conserved region (data not shown). Basically, colinear runs were overextended from the real conserved region by including an additional one or two markers from the adjacent nonconserved region. This phenomenon occurred more often with high D, when the definition of colinearity was less strict.

There is a pragmatic solution to the over-extension problem, which is to examine sub-runs that contain only a small number of markers, such as four or five. Most of a large conserved region can be detected by numerous overlapping sub-runs of three, four, or five markers, and limiting the number of markers in a run reduces the statistical significance of runs extended beyond the boundary of a conserved region. As a concrete example of this pragmatic solution, we limited runs to a maximum of five markers in length and simulated a conserved region of 20 markers, with FastRuns, D = 0 and 80 inversions. Compared with analyses in which the length of runs was not limited (Fig. 1), the average proportion of the conserved region was detected at roughly the same frequency (72% versus 76% when there was no limitation on the number of markers in a run) but far less of the nonconserved region was misidentified as conserved (1% on average versus 16%). These favorable comparisons held over all of the simulation parameters in Figure 1 (data not shown).

Colinear Runs Within Maize Genetic Maps

Comparison of Methods

To assess the performance of the two algorithms on real data, we applied them to the maize UMC98 genetic map. The results can be browsed interactively at http://www.igb.uci.edu/∼baldig/lineup. The FullPermutation and the FastRuns methods were both applied with D = 0, D = 1, and D = 2, with I and O = 0. We used several metrics to compare the results of the six alternative applications. The least precise but simplest metric was recording the chromosome pairs between which runs were detected (Table 2). Twenty-six directed chromosomal pairs (i.e., from one chromosome to another) out of 100 possible pairs (10 × 10) were detected by at least one application. Nineteen of these were detected by all six applications, indicating a high level of general agreement. Of the seven chromosome pairs that were found by some, but not all, methods, six and seven were not detected by FullPermutation and FastRunss, respectively, when there was no allowance for map error (i.e., D = 0). This is not surprising considering D = 0 represents the strictest run definition and assumes, incorrectly, that there is no error in the map order of markers.

Table 2.

Chromosome Pairs Containing Colinear Runs Identified by Different Methods

	Reference chromosome
	1	2	3	4	5	6	7	8	9	10
1	a	a	a	a
2	a	a	a
3	a	a	a
4	a	a
5	a	a
6	f
7	a	g
8	a	b	c	b
9	a	d	e
10		a	a

^aDetected by all methods.

^bDetected by all methods except Full D = 0, Fast D = 0.

^cDetected by all methods except Full D = 0.

^dDetected by Full and Fast methods with D = 1.

^eDetected by Full with D = 2 and Fast methods with D = 1,2.

^fDetected by Full with D = 1.

^gDetected by Fast with D = 2.

This chromosome-by-chromosome comparison was fine-tuned to the level of map units. Precise portions of the map were scored according to whether they were detected as runs by both, neither, or one of the methods under comparison. In the first two cases, the methods are in agreement, and in the latter, they disagree. This comparison was expressed as the proportion of the genome in colinear runs in the reference data set that is also in colinear runs in the compared data set (Table 3). This measure is asymmetric by definition, because one data set can be a subset of a larger dataset, in which case the overlap is 1.00 in one direction and some fraction in the other.

Table 3.

Comparison of Methods at 1% Significance Implemented on the UMC98 Data Set

	Reference method
	Full D = 0	Full D = 1	Full D = 2	Fast D = 0	Fast D = 1	Fast D = 2
Full D = 0	0.79	0.78	1.00	0.77	0.80
Full D = 1	0.99	0.94	0.99	0.97	0.95
Full D = 2	0.91	0.87	0.91	0.84	0.95
Fast D = 0	0.99	0.78	0.77	0.76	0.79
Fast D = 1	0.99	0.99	0.93	0.99	0.95
Fast D = 2	0.95	0.90	0.98	0.95	0.88

Each column shows the proportion of overlap of the results from the reference method (column label) with the results from the compared method (row label). A value of 1.00 indicates that the reference method is a subset of the compared method.

This metric uncovers a surprisingly high level of agreement between the FullPermutation and the FastRuns methods despite the algorithmic compromises of the latter. For example, the two algorithms agree ≥95% of the time when applied with the same D value. Thus, with these data, the FastRuns algorithm is a reasonable compromise. More substantial differences between results arise when the map error allowance (D) is changed. Regardless of the algorithm (FullPermutation or FastRuns), the results with D = n are almost completely a subset of D ≥ n, with an overlap of 91% (Table 3).

Comparison of Maize Genetic Maps

With the statistical tools available in LineUp, it is now possible to compare inferences about intra-genomic homology based on different maize genetic maps. Different genetic maps of the same genome may vary in many respects, including marker density, marker selection, and perhaps the parents on which the mapping population was based. Genetic maps therefore differ by both investigator biases and stochastic (sampling) effects. Here we assess variation among the maps with respect to the extent and location of chromosomal duplication. The four maps are described in Methods.

We compared colinear runs from four maps, as detected by the FastRuns algorithm with D = 2. We used D = 2 because it approximates the uncertainty in mapping position for UMC98. Four features of these comparisons were noteworthy. The first feature was the total number of runs and the numbers that were significant (Table 4). For all four maps, at least 17% of runs were significant at α = 0.01, and thus, there are far more significant runs than expected under random marker order. For the purpose of presentation, it is easiest to combine significant sub-runs and report the number of significant “blocks” of homology. BNL96 and UMC98, two maps that contain a similar number of cross-hybridizing markers but were based on different mapping populations, had similar numbers (42 and 41, respectively) of blocks (Table 4). A composite map (Pio99), with four times the number of markers, had eightfold more blocks (323). The relatively data-poor IBM02 map had only five significant colinear blocks. Altogether, each map contained evidence of substantial intra-genomic homology, but the number of significant homologous blocks increased as a function of the number of cross-hybridizing markers.

Table 4.

Properties of Runs at 1% Significance Detected in Different Maize Genetic Maps by the FastRuns Method With D = 2

Map	Multicopy markers	No. runs	% significant	No. blocks	Genome coverage
BNL96	613	31,235	17.1	42	0.64
IBM2002	138	50	48.0	5	0.17
Pio99	2415	105,637	16.5	323	0.85
UMC98	616	3173	41.1	41	0.63

The second noteworthy feature of comparisons was the proportion of the maize genome inferred to be duplicated or multicopy. The location and centimorgan length of runs in UMC98 indicated that ∼63% of the genome is duplicated or multicopy (Table 4). This result was consistent with the BNL96 map, which indicated that 64% of the maize genome is duplicated or multicopy. In contrast, the Pio99 map data implied that ∼85% of the genome is at least duplicated. Only 17% of the genome was inferred to be duplicated from the IBM2002 data, probably reflecting the low number of cross-hybridizing markers in this map (Table 4).

The third feature was the chromosomal pairs inferred to contain homologous regions. Although the BNL96 and UMC98 maps contained similar numbers of significant blocks, the chromosomes that contained runs varied substantially between maps. For example, the BNL96 map contained 31 directed chromosome pairs and the UMC98 map contained 23 directed chromosomal pairs (Table 5), yet the maps concurred on only 12 of these directed pairs. When chromosomal pairs were counted in either direction, only five chromosomal pairs were inferred to contain duplicated regions with both maps, out of 27 total pairs inferred from both maps (Table 5). Thus, remarkably, the two maps are more different than similar regarding the location of inferred duplicated regions.

Table 5.

Chromosome Pairs With Colinear Runs Identified in Different Maps at 1% Significance

	Reference chromosome
	1	2	3	4	5	6	7	8	9	10
1	p	bp	bpu	pu	bpiu	p	p	bp	bpu	p
2	bp	p	bp	p	pu	p	bpu	bp	bpiu
3	bpu	p	bp	p	p	p	bpu	p	pu
4	pu	p	p	bp	bpiu	p	bp	p	bp	p
5	bpiu	p	p	bpu	p	bp	p
6	p	p	p	p	p	p	p
7	p	bpu	p	bp	b	p	p
8	bp	p	bpu	bp	p	pu	pu	pu	bp
9	pu	bp	p	bp	pu	p
10		piu	pu	bp		p		bp		p

The map names are abbreviated to the first letter: b, BNL96; p, Pio99; i, IBM2002; and u, UMC98.

In contrast, analysis of the Pio99 map detects 69 of 100 possible directed chromosomal pairs, including all of the chromosomal pairs detected in BNL96 and UMC98. This latter observation may not be surprising, however, considering that Pio99 is an amalgamation of UMC98, BNL96, and other maps. Only three chromosome pairs (chromosomes 1 and 5, 2 and 10, and 4 and 5) were detected in IBM02; all three were identified in the other maps.

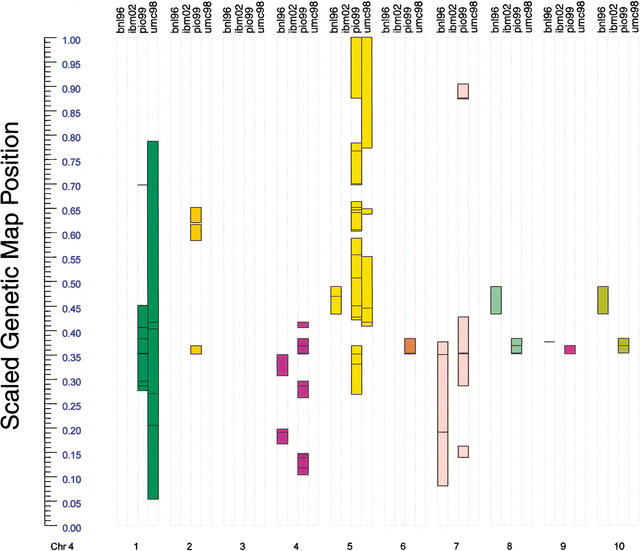
The final feature was the centimorgan location of the duplicated runs, which varied from map to map, even when the same directed chromosome pairs were identified. For example, three of the four maps detected a homologous segment between chromosome 4, as reference, and chromosome 5 (Fig. 2; complete results are found at http://www.igb.uci.edu/∼baldig/lineup/). In this case, the duplications based on BNL96 and UMC98 largely overlapped with Pio99 duplications but did not overlap with each other, again indicating that the BNL96 and UMC98 maps contain different information regarding the location, but not the extent, of duplication within the genome.

Figure 2.

Regions of maize chromosome 4 detected as colinear with other maize chromosomes in BNL96, IBM2002, Pio99, and UMC98 genetic maps. Chromosome 4 is shown on the left of the figure, with map units scaled between zero and one to allow comparisons between the genetic maps. A map position of one represents the end of the chromosome in each of the maps.

DISCUSSION

Detection of Homology With LineUp

One goal of this study is to improve a preexisting method to identify conserved chromosomal regions by using data from cross-hybridizing markers, their locations, and their colinearity. To this end, we have created a program, called LineUp, that incorporates two algorithms to detect conserved chromosomal regions. The first algorithm, FullPermutation, detects all possible runs between two chromosomes and incorporates three parameters: I, O, and D. All three parameters allow the assumption of colinearity to be relaxed. Although we did not examine the effects of I explicitly here, it has been included to permit the user to relax the colinearity assumption on the reference chromosome by allowing inserted non-colinear markers. The parameter O allows a run on the test chromosome to have O order violations. Both I and O are measured in terms of the number of markers that are allowed to interrupt colinearity and are probably best applied in the context of exploratory data analysis.

The exhaustive approach can be computationally intensive, and hence, an approximate method, FastRuns, has also been implemented. FastRuns incorporates only the D parameter, which simplifies the algorithm but still permits substantial flexibility (see below). Both algorithms can be applied to chromosomes from the same or different genomes. Other approaches for detecting homology between chromosomes from different genomes have been published (Sankoff et al. 1997; Wolf et al. 2001). For example, Sankoff et al. (1997) determined the number of conserved segments between two chromosomes by minimizing a single metric that incorporates all data between two chromosomes. By minimizing or maximizing a single function across the data, this and other optimality approaches do not perform an exhaustive search of individual runs. LineUp differs from optimality methods because it is exhaustive; that is, it considers all runs, scores all runs, and computes a probability score for all runs. This exhaustive approach is algorithmically feasible in part because runs are defined so that only a linear, as opposed to quadratic, number of possible runs needs to be considered (see Methods).

The D parameter was incorporated initially to represent uncertainty in mapping order (Gaut 2001). We have shown, however, that with efficient algorithms, D can also be used to relax the colinearity assumption. When D is large, the D parameter aids recovery of homologous regions that have diverged from colinearity by inversion. Increasing D increases the total number of runs identified (Table 1), but does not always increase the number of significant runs. One example may suffice to show why this is the case. A run of three markers between chromosomes 1 and 8 is significant (p ≤ 0.05) under the FastRuns method with D = 0 and the Pio99 data, but not for other D values. This three-marker run is identified with other D values, but it is not significant because the D parameter gives the algorithm sufficient flexibility to detect similarly sized runs frequently via Monte Carlo permutation. If the data contain many runs like this, increasing D need not necessarily result in more significant runs.

The boundary condition of D = ∞ is particularly noteworthy. In this case, LineUp rearranges all markers along a chromosome until the longest possible colinear run is constructed. As a consequence, the marker order from the original map is not retained, the assumption of colinearity is relaxed completely, and LineUp becomes a test for marker clustering. Clustering relies on only two pieces of information: the number of markers and the distance in which they are located. Although there are more efficient methods to examine clustering without consideration of colinearity (S. Hampson, unpubl.), the flexibility of D permits researchers to detect homology while varying the rigor of the colinearity assumption.

For a given D value, the FullPermutation and FastRuns algorithms behave almost identically. For example, their power to detect simulated regions of colinearity are equally high; with a colinear run of 10 markers in 20 cM, the algorithms can detect the homologous region ≥90% of the time (Fig. 1). Furthermore, results based on the UMC98 data set are virtually identical between methods (Tables 2, 3). They do differ, however, in run time; FullPermutation was terminated after 5 h with the most marker-dense simulated data. This density (400 marker pairs in 100 cM) was similar to the overall density observed in regions of the maize Pio99 genetic map, which averages 3.84 markers per centimorgan. However, some regions of the Pio99 map contain >20 markers per centimorgan, and hence, some regions exceed simulated densities. Thus, with D > 0, FullPermutation may not be computationally feasible on particularly dense genetic maps or on genomic sequence data.

In addition to run time, the biggest difference between the FastRuns and FullPermutation algorithms is the extent to which runs within a conserved segment are “over-extended” into the nonhomologous region (Fig. 1). The algorithms share this negative feature, but it is not clear why the two algorithms differ in this trait (Fig. 1). We have shown, however, that a pragmatic solution to this problem is to limit the maximal number of markers in a run, and this solution is valid over a wide range of D values. We should also note that this negative feature is overstated by our simulations. Our simulations placed markers at the boundary of conserved segments, so that all over-extension incorporated nonhomologous regions. In real data, markers are rarely located at the precise boundary of a homologous region (Nadeau and Taylor 1984). As a result, extension beyond markers in a homologous region will often incorporate regions of true homology.

Both algorithms use asymmetric run definitions (see Methods). When I = 0 and D = 0, markers must be in colinear order without an intervening gene on the reference chromosome, but can be interrupted on the test chromosome. This asymmetry arises through algorithmic compromises to reduce the order complexity of comparisons (see Methods), but it does have some use for biological interpretation. The first is that we have greater confidence in the homology of genomic arrangements when at least one of the chromosomal segments does not contain any intervening genes. This is analogous to inter-genomic studies of synteny conservation, in which genes that are adjacent in one genome are assessed for their proximity (not adjacency) in another genome (see McLysaght et al. 2000a).

The second biological interpretation that can be gleaned from the asymmetry of colinear runs is inference about the rearrangement history of genomic segments. When a pair of homologous chromosomal segments contain many of the same genes in the same order, but on one chromosome these genes are interrupted by other genes, then one or both of these segments must have been affected by local rearrangements and/or gene deletions and insertions. These rearrangements must have been primarily local, because they did not substantially change the contents of the genome segment. There is already considerable evidence from various eukaryote genomes that small local rearrangements may be common (Bennetzen 2000; McLysaght et al. 2000b; Seoighe et al. 2000).

Application to Maize

A second goal of this study was to determine the extent to which duplicated regions were consistently inferred among different maize maps. Typically, both comparative mapping and evolutionary studies rely on a single genetic map from any one species. Consideration is rarely, if ever, given to the fact that a genetic map is the single realization of an experimental process that includes stochastic effects and investigator biases. As a result, information must vary to some degree from map to map. In the present study, we have examined variation among four maize genetic maps, with the overall goal of gaining a more accurate picture of maize genome organization. A more accurate picture can help guide ongoing physical mapping efforts and the potential complete genome sequencing of this important crop.

We first consider results based on UMC98. A similar but less complete approach detected extensive genome duplication in maize based on these data (Gaut 2001). Here we have improved the algorithm but obtained similar results. The main differences arise in the significance of reported runs; some runs that are significant in one study were found to be just beyond the significance threshold in another. These differences may be attributable, in part, to some errors we discovered in the UMC98 data set used by Gaut (2001) and also to the identification of significant sub-runs within nonsignificant runs. The results reported here and on our Web page should be considered definitive. Nonetheless, both analyses of UMC98 infer that >60% of the maize genome is either duplicated or multicopy (Table 4). Many of these regions are multicopy. The multicopy proportion can be estimated from blocks that overlap on more than two chromosomes. In the present study, we estimate that 20% of the genome is multicopy from UMC98 data; Gaut (2001) estimated that from 12% to 35% of the genome was multicopy.

UMC98 and BNL96 yield similar information about the maize genome in many respects. Both UMC98 and BNL96 contain ∼40 significant blocks, both indicate that the genome consists of ∼60% duplicated chromosomal regions (Table 4), and both indicate that the multicopy region is ≥13% of the genome. Nonetheless, the maps disagree far more than they agree regarding the location of interchromosomal homologies (Table 5). The location information from the two maps is sufficiently different to consider factors that contribute to these differences.

Two biological factors could contribute to map differences between UMC98 and BNL96. First, the distribution of recombination along chromosomes can vary substantially, depending on the mapping population. This is especially true in maize, in which recombination is physically heterogeneous and some allelic combinations may not recombine (Freeling 1976; Fu et al. 2002). This observation is salient for our purposes because the standardized distance used to compare maps in Figure 2 may not accurately represent the physical position of duplicated regions, if recombination rates vary among regions and among mapping populations. However, this explanation does not fully explain why the two maps implicate different chromosomes (not just different locations along the same chromosomes) in duplications. Second, there may be real differences in genome organization, genic location, and gene arrangement, even among individuals within a single species. Recent comparison of an orthologous region between two maize inbred lines revealed that the region differed substantially in many features, including gene content and gene position (Fu and Dooner 2002). These local differences could extend throughout the genome, and thus, parents of different mapping populations could vary substantially in genomic content and organization. Unfortunately, it is unclear to what extent this explanation contributes to differences between the UMC98 and BNL96 maps.

Another important consideration is sampling. If neither map contains sufficient cross-hybridizing markers, than neither provides a complete picture of the organization of maize duplicated regions. If this is true, each map captures a “snapshot” of the genome but does not provide an accurate overall picture of genomic complexity. We favor this interpretation of the differences between UMC98 and BNL96, for three reasons. First, Arabidopsis thaliana genome data has shown that genetic map data may greatly underestimate genomic complexity. The A. thaliana genome sequence indicates that ∼70% of the genome is duplicated (Arabidopsis Genome Initiative 2001), but only 17% of markers on genetic maps cross-hybridized (McGrath et al. 2001). Second, analyses based on Pio99, which has four times the number of cross-hybridizing markers, identify chromosomal homologies on all chromosomal pairs identified by both UMC98 and BNL96. Thus, analyses of the larger Pio99 data set indicate that inferences based on BNL96 and UMC98 are accurate but incomplete. Finally, the estimated proportion of maize duplicated regions increases with marker number, indicating that increasing the number of markers increases information. With Pio99 data, we estimate that 83% of the genome is at least duplicated and up to 69% of the genome is multicopy.

Pio99 provides a more complex picture of the genome than does either UMC98 or BNL96, but we must inject a cautionary note. Pio99 has more markers than does UMC98 or BNL96, has more total runs, and therefore has commensurately more runs significant at the 1% level (approximately three times more than BNL96). More significant runs could conceivably result in higher estimates of multicopy and duplicated regions in the Pio99 map. However, we do not believe that marker number alone accounts for increased genomic complexity with Pio99 data, for two reasons. First, BNL96 has fourfold more significant runs than does UMC98, but the estimated proportion of duplicated and multicopy regions is similar. There is thus no obvious relationship between the number of runs and the estimated duplicated proportion. Second, additional markers could contribute to the over-extension problem, thus artificially increasing estimates of the proportion of duplicated and multicopy regions with Pio99 data. We performed simulations to determine whether the number of markers in the random background increases the overextension problem, and it does not (in fact, it decreases the problem; data not shown). In addition, when we applied FastRunss with D = 2 and limited runs to five markers, estimates of the duplicated proportion of the maize genome decreased only slightly, from 85% to 78%.

One last observation merits discussion. All four maps, including the relatively sparse IMB02 map, identify interchromosomal homologies on chromosomal pairs 1 and 5, 2 and 10, and 4 and 5. These three chromosome pairs were also consistently identified in a series of previous studies (Helentjaris et al. 1988; Ahn and Tanksley 1993; Moore et al. 1995; Wilson et al. 1999), indicating that the signal of chromosomal duplication is particularly strong for these regions. Why? One possibility is that these regions were duplicated more recently than were other genomic regions. More recent duplications have had less time for deletion and rearrangement to obscure evidence of homology. A second possibility is that these regions were duplicated at the same time as other regions but have undergone fewer transposition and deletion events since duplication. DNA sequence data from duplicated regions are needed to definitively differentiate between these possibilities, but the former possibility seems more likely, given that many plant genomes have experienced multiple polyploid events in their past (Wendel 2000). It is thus likely that the history of maize includes multiple polyploid events (Wilson et al. 1999; Gaut 2001), both because the genome contains extensive multicopy regions and because some regions may be more recently duplicated than others.

Concluding Remarks

Homology identification is an increasingly important problem, both because of the proliferation of molecular genetic maps (O'Brien et al. 1999) and because similar approaches can be applied to genomic sequence data. In the case of genomic sequence, the cross-hybridizing markers are genes that have been identified as homologous by BLAST searches. The locations of these genes are known, and thus determining chromosomal conservation from genomic sequence data can be reduced to a problem that is similar to that considered in this paper. To our knowledge, however, only a few algorithms have been described to test statistically for chromosomal homology on either map or sequence data (Grant et al. 2000; Vision et al. 2000), and none are capable of testing the significance of a single colinear run while simultaneously considering rearrangements and physical distances among markers. Thus, the method described here has some important advantages. However, genomic sequence data also includes information about gene orientation and strand, both of which could aid accurate homology detection. Order and strand information may be incorporated eventually into the algorithms introduced here, but current versions of LineUp are available at http://www.igb.uci.edu/∼baldig/lineup.

Our analyses of maize genetic maps indicate that both BNL96 and UMC98 underestimate the complexity of the genome. Given the marked inconsistencies between these and other maps, it may not be possible to make accurate estimates of the degree of genomic duplication in maize without more genomic sequence data. It is clear, however, that the degree of duplication in maize is similar to, or exceeds, that of A. thaliana, at ∼70% duplication. It is also clear that much of the maize genome is multicopy, indicating that the evolutionary history of maize includes multiple polyploid and/or aneuploid events. Elucidation of these events requires DNA sequence analysis, but even with sequence data, the history of polyploid events may not become entirely clear (Wolfe 2001).

It has long been known that genetic map data are not ideal for evolutionary inference (see Bennetzen 2000; Gaut 2002), but the variance among maize maps has important consequences for comparative mapping. With complex genomes like that of maize, it is likely that a genetic map contains incomplete information about genome organization. If each genetic map of each species provides only a partial picture of genome structure, it follows that comparison of maps compounds the shortcomings and can therefore yield only a fraction of true genome relationships. In the absence of complete genome sequences from important crop plants, genetic maps remain an invaluable tool for comparing genomes among species. It is important, however, to be mindful of their limitations.

METHODS

General Considerations and Algorithmic Complexity

When a segment of DNA is duplicated, any markers that hybridize with it also hybridize with the duplicate region. If the segment is large enough to match a reasonable number of markers, the duplication is easy to detect because identical order and spacing of markers is unlikely to occur by chance. However, with time, point mutations, insertions, deletions, translocations, and inversions will modify both halves of the pair, so that the originally identical number, order, and spacing of markers is progressively degraded. The goal is to identify parts of, or all of, the duplicated region despite the accumulation of changes. For simplicity, the segments will be assumed to be on different chromosomes, although in practice they need not be. We will also assume that information about the strand on which the marker is located and its orientation are not available. In particular, if two markers, AB, are found in the reverse order, BA, we will not distinguish whether this is the result of a translocation that preserves orientation or an inversion that reverses orientation. We will use the mathematical term transposition to denote both.

If there are N markers shared between a pair of chromosomes, then there are O(N²) candidate runs on each chromosome. Exhaustive analysis of two chromosomes in principle requires all pair-wise comparisons of candidate runs on each chromosome, which is O(N⁴). A candidate pair of runs is a string of consecutive markers on each chromosome of the form [X₁, X_n] = X₁X₂…X_n on the first chromosome C₁ and [Y₁, Y_m] = Y₁Y₂…Y_m on the second chromosome C₂. Additional complexity is obtained from how the comparison between two runs is made; the number of insertions, deletions, and permutations that can be tolerated; and the distances in base pairs or centimorgans between the various markers. In particular, from these parameters one must be able to define a similarity or distance score d([X₁, X_n], [Y₁, Y_m]) between each pair of runs. The distance ought to have the flavor of an edit distance but possibly take into account also the distances between the markers. Furthermore, in many realistic situations, the exact ordering of closely spaced markers cannot be resolved, so a number of—if not all—different permutations may be tried, further adding to the algorithmic complexity. Unless specific parameter ranges or approximations are considered, the problem rapidly becomes intractable.

Here, for the sake of argument, we first restrict ourselves to the typical regime in which a marker that hybridizes to two chromosomes is typically found only once on each of the two chromosomes. Because only runs that start and end with a match need to be considered, this immediately reduces the total number of comparisons from O(N⁴) to O(N²) between each pair of chromosomes being considered. Even with only O(N²) comparisons to be carried out, the complexity of comparing two runs can be substantial. By simple sequence alignment using dynamic programming, a global alignment of two runs of n and m markers on two different chromosomes requires O(nm) operations, which typically adds another O(N²) factor to the complexity. In addition, this straightforward alignment approach would require defining scores for insertion, deletions, substitutions, and matches that could in principle depend also on distance from the previous marker for the detection of statistically significant homology. Finally, it would not be able to handle permutations of closely spaced markers.

We developed a number of algorithmic heuristics to address these problems in a practical way that is both computationally efficient and robust over a wide range of regimes found in biological applications. Although, in principle, the detection of homologous regions and the assessment of their significance can proceed in parallel, here we decouple these two steps. In particular, we first develop algorithms to detect candidate pairs of runs (candidate homologous regions) based purely on marker composition and relative marker positions and distances. We do so for simple colinear runs and then introduce three parameters, I, O, and D, to relax colinearity assumptions in several directions and to control algorithmic complexity and tradeoffs between specificity and sensitivity. We then score the candidate runs against different random background models by using Monte Carlo simulations. Decoupling the two steps allows us to test different notions of candidate runs and different background models to assess robustness and sensitivity issues.

The LineUp Algorithm

Intuitively, two runs that are good candidates for significant homology between two chromosomes C₁ and C₂ consist of two sets of neighboring markers, one on each chromosome, that share many markers in common. A precise definition, however, relies on the definitions of neighborhood and similarity. In particular, there are several issues to consider that may give rise to different definitions:

1. The presence of markers on one chromosome that are not found anywhere on the other chromosome.

2. Even when only markers common to both chromosomes are considered, there are, in general, marker insertions and deletions on each chromosome that disrupt colinearity and need to be considered.

3. The importance assigned to the ordering of the markers and, for instance, the number of local rearrangements or permutations one is willing to tolerate. These permutations could be the results of inversions.

4. A related issue, in some cases, is the uncertainty associated with the position of markers. In particular, the ordering of markers that are extremely close may not be reliable, and it may be necessary to permute completely the order of closely spaced markers.

Basic Algorithm

With respect to the first issue, we simplify the problem by considering only those markers that are found on both chromosomes. In practice, this approximation works well, although in some cases the presence of a number of markers within a run that are nowhere to be found on the other chromosome could be significant. Such orphan markers may eventually be included in the definition of similarity.

We then consider each ordered pair of chromosomes (C₁, C₂), and for each marker X on the reference chromosome C₁, we look for all the matches on the test chromosome C₂ (typically only one but occasionally there are a few). Then starting from X on both chromosomes, we extend the runs to the right on both chromosomes, using C₁ as the reference chromosome. During the extension process, the basic version of the algorithm does not allow insertions of markers on the reference chromosome C₁. Both insertions and deletions are allowed in C₂. If during the extension of a run, there is more than one possible match in C₂, the best one (colinear and close) is chosen. If the best or only choice is not colinear, run extension is terminated. All runs of three or more markers are saved, including sub-runs of longer runs.

Looking at pairs of runs that are colinear (order perfectly preserved), with no insertions allowed on the reference chromosome, has the advantage of yielding a very fast algorithm that in theory requires at most O(N ²) computations to find all the runs and, for all practical purposes, only O(N) computations because the typical length of the runs is bounded. This algorithm does not treat the two chromosomes symmetrically; therefore, when comparing two chromosomes, it must be run twice: first using C₁ as the reference, and then C₂. To see the effect of asymmetries, consider for example, the runs:

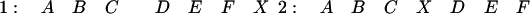Comparing one-to-two yields a run of length six (ABCDEF) while comparing two-to-one yields one run of length four (ABCX) and one of length three (DEF). This situation is unlikely to occur owing to point mutations or random deletions, but there are some biological events that could have a significant impact in this regard. For example, random insertions of a transposon or retrovirus could add multiple copies of X to both segments in the above example. This would progressively obscure the original run of six until it could no longer be detected.

Insertions in the Reference Run (I)

To address the second issue of possible insertions of markers in the reference run, we can modify the algorithm to allow up to I insertions on reference chromosome C₁. All possible combinations of up to I insertions can easily be incorporated by dynamic programming. The basic version above corresponds to the case in which I = 0. In the example above, setting I = 1 allows the insertion of up to one marker, allowing complete identification of the underlying run. With I = 1, any number of random insertions can be filtered out to recover the original run. In this limiting case, we end up looking for maximal subsequences of matching markers (P. Baldi, unpubl.).

Order Violations (O)

The third and fourth issues raised above are concerned with the ordering of the markers and any violation of perfect colinearity, owing to, for instance, inversions. Within this class of possibilities, we first consider order violations that do not result from markers that are too closely spaced so that their ordering cannot be resolved.

To address the issue of permuted markers, we introduce a new parameter O that represents the number of markers on the test chromosome that are allowed to be out of order as the runs are grown. When O = 0, the order must be preserved entirely. When O has an intermediate value, the growth of the run is aborted as soon as the number of out-of-order markers exceeds O. When O = ∞ any amount of rearrangement is acceptable, and the runs are best described in terms of local clusters of common markers.

For example, consider the following pair of runs with two transpositions, (AB) (EF), in the second chromosome:

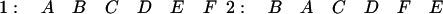If no out-of-order markers are allowed, the longest run when comparing one to two is (BCDE); if one is allowed (BCDEF) is recognized; and with two out of order markers, the entire run is recovered.

Distance Precision (D)

Finally, for the issue of precision on marker location, we consider here that the order of markers that are within a minimal distance D cannot be resolved. For example, a particular genetic map may have a mapping resolution of D = 2 cM, meaning that the order of markers ≤2 cM apart is uncertain. In this case, it is appropriate to permute the marker order within a 2-cM window in order to minimize false-negative rates. In practice, this is implemented by growing all the viable permutations on the reference chromosome C₁ based on the D = 2 limit and matching them to the runs on the test chromosome C₂, allowing for any possible permutation of closely spaced markers on C₂. More precisely, it permits marker X in C₁ to be temporarily swapped with any marker to the right occurring within a distance D. Likewise, the choice of the best matching marker in C₂ was modified to reflect resolution problems. In the unlikely case in which a marker occurs more than once in the run on C₁, but only once in the run on C₂, the marker on C₂ can be used only once. The procedure then recursively calls itself to continue developing the run. This allows all legal permutations of markers to be tried in C₁. By interleaving permutation and run extension, unproductive permutations can be cut off as soon as they cease to generate legal runs. This reordering is the most computationally intensive aspect of the program, so the choice of D can have significant impact on run time. In the rest of the paper, this algorithm that tries all viable permutations is called FullPermutation(I,O,D) or just FullPermutation.

For example:

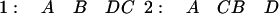The longest colinear run is length three (ABD) based on the given order, but if D and C in one and C and B in two are so close that their actual order is unknown, a run of four is also possible.

Fast Approximation

Because it tries all legal permutations of the markers on the C₁ chromosome, FullPermutation is computationally expensive and may generate an unmanageably large number of runs in regions of high marker density. To address both of these issues, a fast-run algorithm was developed that empirically finds the longest runs, but only some of the sub-runs. The basic idea is to avoid doing permutations in a permutable block on C₁ by simply taking them in the order they occur on C₂. This determines an appropriate permutation on C₁. More precisely, the FastRuns algorithm is a recursive algorithm that tries to grow a run to the right. Assuming that the current run has been grown up to marker X on C₁, the pseudo-code for the inner loop of FastRuns is given by

for i = X to last marker on C₁

{

if marker[i] cannot be swapped with marker[X], break

take markers X through i in the order that they occur on C₂ recurse with X = i+1

}

Because the D parameter adequately relaxes colinearity (see Results) by itself, the I and O parameters have not been incorporated into FastRuns.

Probabilistic Models: Computing Run Significance

Run detection, and all its variations, provides a minimal filter for what might be homologous regions. However, it is sufficiently broad that many runs will also occur purely by chance. Consequently, it is necessary to further evaluate these runs in the context of the given data set and select those that are least likely to occur by chance.

Two properties are used to evaluate a run: the number of matched markers and the length in centimorgans. Various measures of length (e.g., absolute value, squared length) were tried previously (Gaut 2001), and the summed squares (SS) measure was chosen, although all measures gave similar results. We continue to use it here. The SS value of a run is the sum of the squared lengths of its two halves.

To test for statistical significance, for each chromosome pair (C₁, C₂), the order of markers on C₂ is randomized and run detection repeated. This is done 1,000 times, and the results are binned by matched marker number. This provides an estimate of the background frequency and distribution of lengths for the runs in each bin. For each candidate run, the number of random runs with the same marker number but smaller SS value is tallied. This is divided by the number of runs in the bin or 1,000, whichever is bigger, to compute the significance of the run. A 5% cutoff is generally used, but results can be repeatedly displayed with different cutoffs.

Three methods of randomizing the markers on C₂ were tested: (1) assigning random values between the biggest and smallest observed in the real data on that chromosome, (2) leaving the locations the same but permuting the marker names, and (3) leaving the locations the same but permuting the marker names only for those markers that matched between the two chromosomes. The three methods provided qualitatively similar results (data not shown), and we report analyses based on the second method.

Maize Genetic Map Data

We applied the FullPermuation and FastRunss algorithms to simulated data and molecular genetic maps of maize. The algorithms were applied to maize for three reasons: (1) the initial method of Gaut (2001) was applied to maize, hence facilitating comparison; (2) the maize genome is complex, providing an indication of the feasibility of the methods with potentially difficult data; and (3) there are several genetic maps for maize, which allows comparison among them. Four maize maps were used: the Brookhaven National Lab 1996 (BNL96) map; the University of Missouri, Columbia 1998 (UMC98) map (Davis et al. 1999); the Intermated B73/Mo17 2002 map (IBM02); and the Pioneer 1999 (Pio99) composite map, which is amalgamated from several sources, including UMC98 and BNL96. Map data from BNL96, UMC98, and Pio99 were obtained from MaizeDB at http://www.agron.missouri.edu/. IBM02 data were obtained from the Maize Mapping Project at http://www.maizemap.org/.

WEB SITE REFERENCES

http://www.igb.uci.edu/∼baldig/lineup; URL where the LineUp package can be downloaded. This site also contains full results from analysis of maize data.

http://www.agron.missouri.edu/; the Maizedb database that contains data for UMC98 and BNL96.

http://www.maizemap.org/; the maize mapping project database that contains IBM02 data.