Abstract
Discriminative models are used to analyze the differences between two classes and to identify class-specific patterns. Most of the existing discriminative models depend on using the entire feature space to compute the discriminative patterns for each class. Co-clustering has been proposed to capture the patterns that are correlated in a subset of features, but it cannot handle discriminative patterns in labeled datasets. In certain biological applications such as gene expression analysis, it is critical to consider the discriminative patterns that are correlated only in a subset of the feature space. The objective of this paper is two-fold: first, it presents an algorithm to efficiently find arbitrarily positioned co-clusters from complex data. Second, it extends this co-clustering algorithm to discover discriminative co-clusters by incorporating the class information into the co-cluster search process. In addition, we also characterize the discriminative co-clusters and propose three novel measures that can be used to evaluate the performance of any discriminative subspace pattern mining algorithm. We evaluated the proposed algorithms on several synthetic and real gene expression datasets, and our experimental results showed that the proposed algorithms outperformed several existing algorithms available in the literature.
Keywords: Co-clustering, biclustering, discriminative pattern mining, gene expression data, negative correlation
1 Introduction
Discriminative models are used to extract patterns that are highly correlated in one class compared to another class. Mining such discriminative patterns can provide valuable knowledge toward understanding the differences between two classes and identifying class-specific patterns. For example, discriminative mining of gene expression data can lead to the identification of cancer-associated genes by comparing the expression patterns of the genes between healthy and cancerous tissues [13]. However, these genes can be correlated only in a subset of the cancerous samples due to the heterogeneity in the sample space [27]. Since the existing discriminative models are based on using all the features to find the discriminative patterns, it is crucial to develop a model that can identify discriminative patterns that are correlated in a subset of the feature space.
Co-clustering has been proposed to identify subsets of objects that are inter-related under subsets of features (co-clusters) [10], [16], [3], [27], [1]. However, co-clustering is an unsupervised procedure that does not consider the class labels to find the discriminative patterns in labeled datasets. In order to capture the subspace discriminative patterns (or discriminative co-clusters), discriminative co-clustering is being proposed in this paper by incorporating the class labels into the co-clustering process.
1.1 Co-clustering
Given a data matrix with two entities such as (genes, samples) in gene expression data [26], a subset of rows may be inter-related under a subset of columns forming blocks of substructures (or co-clusters) [14]. Applying traditional clustering techniques, such as k-means and hierarchical clustering, will not capture such co-clusters [10], [16], [22], [4], [32]. However, co-clustering (or biclustering)1 has been proposed to simultaneously cluster both dimensions of a data matrix by utilizing the relationship between the two entities [10], [16], [26], [34], [27]. Co-clusters have several characteristics that should be considered in the search process. Here, we describe the important characteristics of the co-clusters in the gene expression domain. However, many of these characteristics are applicable to several other domains. 1. Arbitrarily positioned co-clusters. Due to the heterogeneity of the samples, a subset of genes can be correlated in any subset of the samples. Hence, the co-clusters can be arbitrarily positioned in the matrix [27]. 2. Overlapping. A gene can be involved in several biological pathways. Hence, that gene can belong to more than one co-cluster [27], [15]. 3. Positive and negative correlations. In a positive (negative) correlation, genes show similar (opposite) patterns [39]. 4. Noisy data. The expression data contains a huge amount of noise [23]. Hence, the co-clustering algorithms should be robust against noise.
Recently, the (κ, ℓ) co-clustering model has been proposed to simultaneously find κℓ co-clusters [4], [15]. This model was shown to perform well in various applications [4], [15]. However, the main limitation of this model is that it assumes a grid structure comprised of κ×ℓ co-clusters as shown in Fig. 1(a). The assumption here is that the rows in each row cluster should be correlated under each of the ℓ column clusters. Such an assumption may not hold when a subset of rows is correlated in a limited subset of columns (or vice versa). To overcome this limitation, we propose a novel co-clustering algorithm that is able to identify arbitrarily positioned co-clusters as shown in Fig. 1(b). This algorithm is extended to efficiently find the discriminative co-clusters in the data.
Fig. 1.
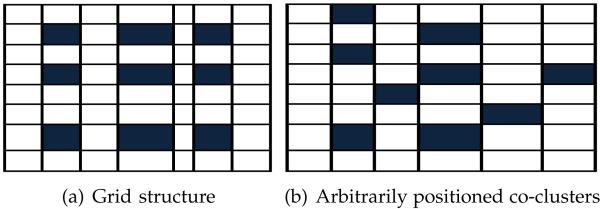
Types of co-cluster structures.
1.2 Discriminative Co-clustering
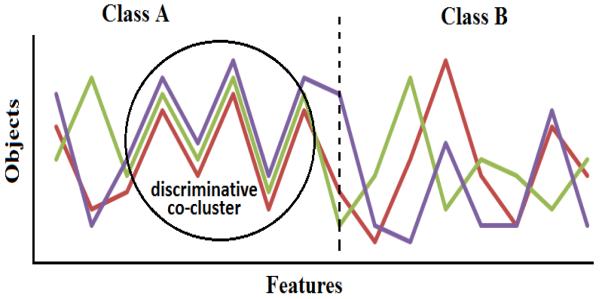
Discriminative models aim to extract patterns that are differentially correlated between two classes [19]. Figure 2 shows the correlations between three objects in two classes. These objects are highly correlated in a subset of the features in class A, but they are not correlated in class B. Such discriminative patterns cannot be discovered using standard discriminative models that use all the features. In order to capture these patterns, discriminative co-clustering is also being proposed in this paper.
Fig. 2.
A set of three objects that are highly correlated in a subset of the features in class A, but they are not correlated in class B. Hence, these objects are considered as a discriminative co-cluster.
In addition to the above mentioned characteristics of the co-clusters, the discriminative co-clusters must possess the following characteristics: 1. High discriminative coherence. Coherence (or correlation) is a measure of similarity between a set of objects [27]. The discriminative co-clustering algorithms should identify the set of co-clusters with the maximum difference in the coherence between the two classes. The co-clusters that have the same correlation in both of the classes should be ignored. 2. Low inter-class overlapping. The discriminative co-clusters discovered in one class should have a minimal number of rows that are common with the co-clusters discovered in the other class. 3. High discriminative power. Incorporating the class labels can improve the performance of classification algorithms [21]. Discriminative co-clusters must be able to make more accurate predictions.
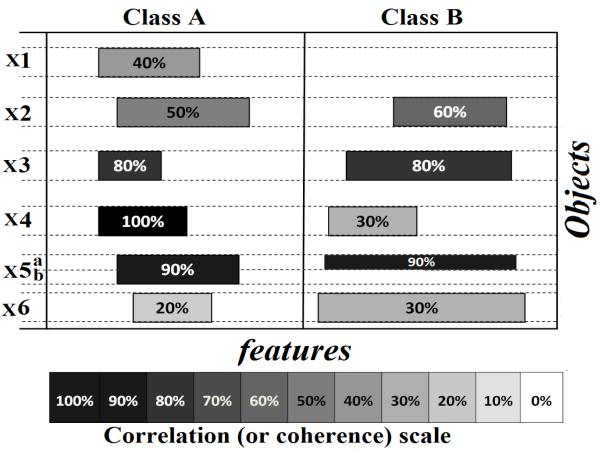
Example. Fig. 3 shows an example of discriminative and non-discriminative co-clusters. The width of each co-cluster (X) indicates the number of features in it, and its shade represents its correlation score, which is also displayed as a percentage inside each co-cluster. The correlation score can be measured by various functions such as the mean-squared residue (MSR) [10]. In this example, the higher the percentage (or the darker the shade), the stronger the correlation. The co-cluster properties (shade and width) are the main criteria used to distinguish between discriminative and non-discriminative co-clusters. A co-cluster is considered as a discriminative co-cluster if it is correlated only in one class (such as X1 and X5.b), if it is highly correlated in one class and less correlated in the other class (such as X4) or if it is correlated in relatively higher percentage of features (such as X3 and X6). The co-clusters X2 and X5.a are not considered as discriminative co-clusters because they are similarly correlated in both classes.
Fig. 3.
Example of discriminative co-clusters.
Can any co-clustering algorithm be used to identify the discriminative co-clusters?
A naive solution to this problem is to co-cluster each class separately and then identify the co-clusters that appear in only one class. However, there are many limitations in following such a procedure: (i) Standard co-clustering algorithms focus on identifying the most correlated co-clusters. Therefore, discriminative co-clusters that have low correlation score (such as X1 and X6) will not be discovered. (ii) Since the standard co-clustering algorithms do not detect all the co-clusters, it is possible that co-cluster X2 is discovered only in one class and considered as a discriminative co-cluster. (iii) Most co-clustering algorithms prefer large co-clusters. Therefore, the complete co-cluster X5 may be considered as a discriminative co-cluster because part a is not discovered in class B due to its size limitation. In this paper, we develop a novel algorithm that directly optimizes an objective function to efficiently identify the discriminative co-clusters, and we propose two metrics to score the discriminative co-clusters based on their correlation scores and the number of features in them.
1.3 Our Contributions
The primary contributions of this paper are as follows:
- A novel co-clustering algorithm, Ranking-based Arbitrarily Positioned Overlapping Co-Clustering (RAPOCC), to efficiently extract significant co-clusters.
- Propose a novel ranking-based objective function to find arbitrarily positioned co-clusters.
- Extract large and overlapping co-clusters containing both positively and negatively correlated rows.
- A novel discriminative co-clustering algorithm, Discriminative RAPOCC (Di-RAPOCC), to efficiently extract the discriminative co-clusters from labeled datasets.
- Find the discriminative co-clusters from labeled datasets efficiently by incorporating the class information into the co-clustering process.
- Propose three new evaluation metrics to quantify the results of the discriminative co-clustering algorithms on both synthetic and real gene expression datasets. Two metrics are used to measure the discriminative coherence property of the discriminative co-clusters, and the third one measures the inter-class overlap property.
In addition to summarizing some of the widely used co-clustering algorithms, we categorize the state-of-the-art approaches for discriminative co-clustering and characterize each category. We also empirically compare the performance of these categories with the proposed algorithm.
The rest of this paper is organized as follows: Section 2 presents an overview of the related work. Section 3 introduces the coherence measure and formulates the problems of co-clustering and discriminative co-clustering. Section 4 describes the RAPOCC algorithm. Section 5 presents the Di-RAPOCC algorithm. Section 6 presents the results of the proposed algorithms on synthetic and real datasets along with the comparisons with other algorithms available in the literature. Finally, we conclude our discussion in Section 7.
2 Related Work
In this section, we describe some of the widely-used co-clustering algorithms and categorize the state-of-the-art approaches for discriminative co-clustering.
2.1 Co-clustering Algorithms
Cheng and Church (CC) [10] proposed the first co-clustering algorithm that produces one co-cluster at a time. The obtained co-cluster is replaced with random numbers, which typically reduces the quality of the co-clusters. The Order-Preserving Submatrices (OPSM) algorithm [7] finds one co-cluster at a time in which the expression levels of all genes induce the same linear ordering of the experiments. This algorithm does not capture the negatively correlated genes. The Iterative Signature Algorithm (ISA) [22] defines a co-cluster as a co-regulated set of genes under a set of experimental conditions. It starts from a set of randomly selected rows that are iteratively refined until they are mutually consistent. The Robust Overlapping Co-clustering (ROCC) algorithm [15] finds κ × ℓ co-clusters using the Bregman co-clustering algorithm [6]. This algorithm does not handle the negative correlations. Our proposed co-clustering algorithm overcomes all of the above limitations by (i) capturing arbitrarily positioned co-clusters, (ii) handling overlapping and positive and negative correlations and (iii) being robust against noise.
2.2 Discriminative Co-clustering Algorithms
In general, the co-clustering algorithms work in an unsupervised manner. However, some algorithms incorporate a priori knowledge in the co-clustering process. For example, in constrained co-clustering, some information can be incorporated such as the must-link and cannot-link constraints [30], [36], [35]. In discriminative co-clustering, the class labels are incorporated to find class-specific co-clusters. As illustrated in Fig. 4, the existing discriminative co-clustering approaches can be categorized as two-step or one-step approaches.
Fig. 4.

Different approaches to obtain discriminative co-clusters.
2.2.1 Two-step approaches
There are two sub-categories of these approaches: (i) first co-clustering, and then discriminative analysis. In [29], differentially expressed gene modules are identified by applying co-clustering each class separately, then the identified co-clusters are ranked based on their discrimination between the two classes. (ii) first discriminative analysis, and then co-clustering. The DeBi algorithm [33] uses two steps to identify differentially expressed co-clusters. The first step is to find the up or the down regulated genes using fold change analysis. In the second step, the MAFIA algorithm [8] is used to find the co-clusters from the up-regulation and the down-regulation data. There are two limitations for the two-step approaches: (i) the co-clustering is done for each class separately, and (ii) the discriminative analysis step is independent of the co-clustering step. Therefore, the one-step approaches have been proposed to overcome these limitations.
2.2.2 One-step approaches
The subspace differential co-expression (SDC) algorithm [18] uses the Apriori search algorithm to identify the discriminative patterns. The Apriori approach depends on using thresholds to define the discriminative patterns [19]. For example, a given pattern is considered as a discriminative pattern if the difference between the correlations of this pattern in the two classes is above a fixed threshold. Otherwise, this pattern will be split into smaller patterns to be tested again using the same threshold. Therefore, the SDC method suffers from the following limitations: (i) It generates very small patterns [18]. (ii) The number of the discovered patterns dramatically grows with the size of the datasets, and it significantly varies with the threshold value [19]. (iii) It has computational efficiency problems and does not scale well to large-scale datasets. In addition, the SDC method does not identify the subset of columns in which a given pattern shows the maximum correlation. In our previous work [28], we proposed a discriminative co-clustering algorithm to analyze the differences in the biological activities of several genes between two classes. Although this algorithm generated large co-clusters compared to the SDC method, this algorithm does not scale to large datasets because it maintains, for each pair of rows (genes), the set of columns under which the two rows are differentially correlated. Recently, locally discriminative co-clustering was proposed in [40] to explore the inter-sample and inter-feature relationships, but it does not find discriminative co-clusters as defined in our paper. To overcome all of the above limitations of the existing approaches, we propose a novel discriminative co-clustering algorithm that directly optimizes an objective function to efficiently identify the discriminative co-clusters from a given labeled dataset. It should be noted that we primarily focus on co-clusters in our work rather than other concepts such as emerging patterns or contrast set patterns [17]. While we acknowledge the fact that these approaches are generic and probably can be modified for our problem, we emphasize that there is no existing work in the area of discriminative co-clustering and hence this is an exciting direction of future research.
3 Preliminaries
In this section, we introduce the coherence measure that can be used to measure the quality of the co-clusters, and we formulate the problems of co-clustering and discriminative co-clustering. The notations used in this paper are described in Table 1.
TABLE 1.
Notations used in this paper.
| Notation | Description |
|---|---|
|
| |
| D | input data matrix of M rows and N columns |
| κ | number of row clusters |
| ℓ | number of column clusters |
| ρ | mapping of row clusters |
| γ | mapping of column clusters |
| K | number of optimized co-clusters |
| X | Co-cluster of |I| rows and |J| columns |
| I | set of rows in co-cluster X |
| J | set of columns in co-cluster X |
| xj | the jth column in row x |
| |.| | the cardinality function |
|
| |
| Notations for discriminative co-clustering | |
| NA | No. of columns in class A |
| KA | number of optimized co-clusters in class A |
| jth column in class A, 1 ≤ j ≤ |NA| | |
| ith row of the kth co-cluster in class A | |
| jth column of the kth co-cluster in class B | |
3.1 Measuring the Coherence of Co-clusters
Coherence is a measure of how similar a set of gene expression profiles are. Cheng and Church proposed the mean-squared residue (MSR) score as a measure of coherence [10]. Since the the overall shapes of gene expression profiles are of greater interest than the individual magnitudes of each feature [23], we normalize the expression values of each gene to be between 0 and 1. As a result, the value of the objective function will also be bounded between 0 and 1.
Definition 1. (Coherence measure H)
The coherence of a co-cluster X of |I| rows and |J| columns is measured as
where Xij is the value in row i and column j in co-cluster X, is the row mean, is the column mean and is the overall mean of X.
Using Definition 1, a perfect co-cluster will have a score = 1. Given two rows (x and y) and J columns, the coherence measure can be re-written as follows:
| (1) |
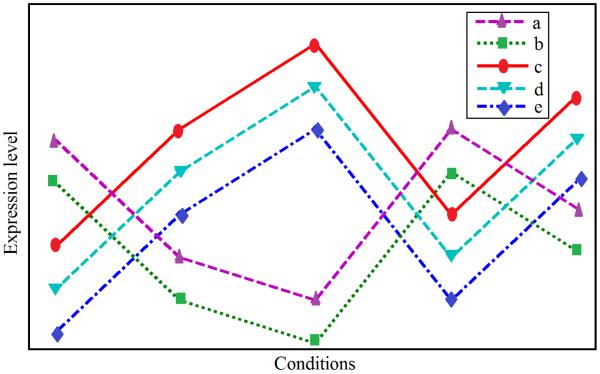
where x̄ and ȳ represent the mean of the values for the rows x and y, respectively. An optimal co-cluster has a value of H(X) = 1, which results from the case where (xj − x̄) = (yj − ȳ), ∀j ∈ J. This type of correlation is positive (h+(x, y, J)). In the negative correlation, the rows have opposite patterns (i.e. the two negatively correlated rows will get a perfect score when (xj − x̄) = −(yj − ȳ) ∀j ∈ J). Figure 5 shows an example these correlations. In a positive correlation, genes show similar patterns while in a negative correlation, genes show opposite patterns. The positive and negative correlations are defined in Definition 2.
Fig. 5.
Different types of relationships between genes in one co-cluster. The genes {a, b} are positively correlated with each other, and the genes {c, d, e} are positively correlated with each other. However, the genes {a, b} are negatively correlated with the genes {c, d, e}.
Definition 2. (Positive and negative correlations)
Given two rows (x and y) and J columns, the positive correlation between them is defined as
and the negative correlation is defined as
Definition 3. (Pairs-based Coherence HP)
Given a co-cluster X of |I| rows and |J| columns, the coherence of this co-cluster is measured based on all the pairs in X:
where o ∈ {−, +}.
The type of correlations between any two rows, referred to as o in Definition 3, is maintained for each pair of rows in each co-cluster in the proposed algorithms.
3.2 Problem Formulations
Here, we formally define the problems of co-clustering and discriminative co-clustering.
Definition 4. (Co-clustering)
Let D ∈ ℝM×N denote a data matrix; the goal of co-clustering is to find a row mapping (ρ) that maps the rows to the κ row clusters and a column mapping (γ) that maps the columns to the ℓ column clusters
such that the coherence of the top-K co-clusters is maximized.
The problem of finding the co-clusters is an NP-hard problem [10]. In this paper, we propose a novel co-clustering algorithm to efficiently find arbitrarily positioned co-clusters from a given data matrix.
Definition 5. (Discriminative Co-clustering)
If HPA(Xi) measures the coherence of the co-cluster Xi in class A, the goal is to find the set of co-clusters that has maximal discriminative coherence
where ψA(Xi) (ψB(Xi)) is the maximum coherence of any subset of the objects in Xi in class A (B). The challenge here is to find ψ(Xi), which is similar to the NP-hard problem of finding the maximum subspace in Xi [10]. In the proposed discriminative co-clustering algorithm, we propose two approximations for computing ψ(Xi) that can be used to efficiently discover discriminative co-clusters by incorporating the class labels into the co-clusters discovery process.
4 The Proposed RAPOCC Algorithm
In this Section, we describe the RAPOCC algorithm. This algorithm is proposed to efficiently extract the most coherent and large co-clusters that are arbitrarily positioned in the data matrix. These co-clusters can overlap and have positively and negatively correlated rows.
4.1 Ranking-based Objective Function
In the proposed iterative algorithm, the score of each of the κℓ co-clusters is computed at each iteration, and the overall value of the objective function is computed based on the coherence score of the top-K scores where K is the number of optimized co-clusters (1 ≤ K ≤ κ ≤ ℓ).
The set of the top-K co-clusters can be any subset of the κ * ℓ co-clusters. The objective function will be computed for each possible change in the row/column mapping to maintain non-decreasing values for the objective function. The advantage of using this objective function is that it allows the discovery of arbitrarily positioned co-clusters as shown in Fig. 1(b).
4.2 The RAPOCC Algorithm
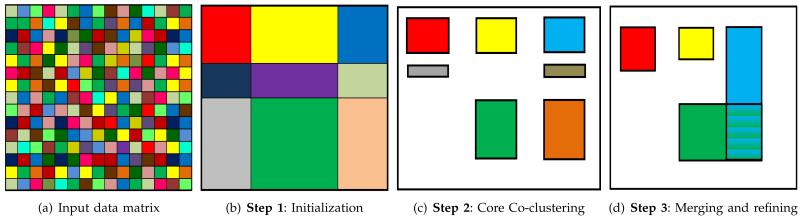
The main steps of the RAPOCC algorithm are shown in Fig. 6. The algorithm starts with a two-dimensional matrix (objects × features) as an input. In the first step, Fig 6(b), a divisive approach is used for initialization. Basically, it starts with all the rows and columns in one co-cluster; then the algorithm splits the co-cluster with the largest error. This iterative procedure continues until κ row clusters and ℓ column clusters are obtained. The core co-clustering step, Fig. 6(c), finds the optimal row and column clusterings (ρ, γ). In the third step, Fig. 6(d), similar co-clusters are merged using a hierarchical agglomerative approach. In this step, more rows and columns are added to each co-cluster individually. Finally, a pruning step is used to prune the co-clusters with low coherence scores. These steps are described in Algorithm 1. In this algorithm, H(u, v) and HP (u, v) indicate the coherence of the co-cluster formed by the row cluster u and column cluster v. The inputs to this algorithm include the data matrix D ∈ ℝM×N, the number of row clusters κ and the number of column clusters ℓ. These are common parameters in the co-clustering methods [15], and they can be set based on the size of the data matrix. K determines the number of the optimized co-clusters and can be set to any value between 1 and κ × ℓ. We set the parameters κ=5 and ℓ=3. The parameter K can be set to large value (we set it to 20 in our implementation) because the RAPOCC algorithm will only report the most coherent co-clusters, and the remaining ones will be pruned in the last step. In addition, we had a threshold that indicates that the minimum number of rows in a co-cluster to be 20 and the minimum number of columns in
Algorithm 1.
RAPOCC(D,κ, ℓ,K)
| 1: Input: Data matrix (D) |
| No. of row clusters (κ) |
| No. of column clusters (ℓ) |
| No. of optimized co-clusters (K) |
| 2: Output:: A set of K co-clusters ({X}) |
| 3: Procedure: |
| 4: Step 1 : initialization |
| 5: i ← 1, j ← 1 |
| 6: ρ(g) ← i, ∀ |
| 7: γ(c) ← j, ∀ |
| 8: while i < κ or j < ℓ do |
| 9: if i < κ then |
| 10: i ← i + 1 |
| 11: |
| 12: Partition α using bisecting clustering algorithm |
| 13: end if |
| 14: if j < ℓ then |
| 15: j ← j + 1 |
| 16: |
| 17: Partition β using bisecting clustering algorithm |
| 18: end if |
| 19: end while |
| 20: Step 2 : core co_clustering |
| 21: repeat |
| 22: / * Row clustering * / |
| 23: for a = 1 : M do |
| 24: ρ(a) = arg maxu∈{−κ,…,−1,0,1,…,κ} HP(ρ(a) = u, γ) |
| 25: end for |
| 26: / * Column clustering * / |
| 27: for b = 1 : N do |
| 28: γ(b) = arg maxb∈{0,1,…,ℓ} HP(ρ, γ(b) = v) |
| 29: end for |
| 30: until convergence |
| 31: Step 3 : Merging similar co_clusters and refinement |
| 32: Step 4 : Pruning |
a co-cluster to be 5. This is chosen because in biological problems, the number of conditions are usually far less compared to the number of genes.
Fig. 6.
The main steps of the proposed RAPOCC algorithm.
Step 1: Initialization
Inspired by the bisecting K-means clustering technique [37], we use a deterministic algorithm for the initialization. Each row is mapped to one of the κ clusters, and each column is mapped to one of the ℓ clusters, resulting in a checkerboard structure κ × ℓ as shown in Fig. 6(b). The initialization algorithm is a divisive algorithm that starts with the complete data assigned to one cluster as described in Algorithm 1 (lines 5-7).; then, the following steps are repeated until the desired number of row clusters is obtained. (1) Find the row cluster with the lowest coherence score (αmin). (2) Find the two rows in αmin with the lowest correlation (r1, r2). (3) Create two new row clusters α1 and α2. Add r1 to α1 and r2 to α2. (4) Add each of the remaining rows in αmin to α1 (α2) if it is more correlated to r1 (r2). The column clusters are initialized in the same manner. The algorithm alternates between clustering the rows and the columns as described in Algorithm 1 (lines 8-19).
Step 2: Core Co-clustering (ρ, γ)
This step finds the optimal row and column clusterings (ρ, γ) as shown in Fig. 6(c). To update ρ, each row (ri) is considered for one of the following three actions as described in Algorithm 1 (lines 20-30):
Exclude ri from any row cluster by setting ρ to 0.
Find the best row cluster to include ri as a positively correlated row {1, 2, .., κ}.
Find the best row cluster to include ri as a negatively correlated row {−κ, …, −2, −1}.
The objective function is computed for each possible action, and the action to be carried out is the one corresponding to the maximum value of the three objective function values. Within each co-cluster, there is a sign vector that determines the type of correlation (positive or negative) of each row. Therefore, a row can be positively correlated in some of the co-clusters and negatively correlated in other co-clusters. The column mapping (γ) is calculated in a similar manner, but there is no consideration for negatively correlated columns. Following this strategy, the value of the objective function is monotonically increasing, and the convergence is guaranteed as shown in Theorem 1. After convergence, the result will be a non-overlapping set of co-clusters.
Theorem 1. The Algorithm RAPOCC (Algorithm 4) converges to a solution that is a local optimum.
Proof: From Definition 3, the coherence measure HP is bounded between 0 and 1. Hence, the objective function given in Definition 4 is bounded. Algorithm 4 iteratively performs a set of update operations for the row clustering and the column clustering. In each iteration, it monotonically increases the objective function. Since this objective function is bounded for the top-K co-clusters, the algorithm is guaranteed to converge to a locally optimal solution.
Step 3: Merging the Co-clusters
The top-K co-clusters with the maximum coherence are retained from the previous step. In this step, similar co-clusters are merged as shown in Fig. 6(d) using an agglomerative clustering approach. Before merging, the co-clusters with the lowest scores are pruned. If there is no pre-determined threshold for pruning the co-clusters, the top η co-clusters will be retained, and the remaining co-clusters will be pruned. The similarity between any two co-clusters is defined using the coherence function of the union of the rows and columns of the co-clusters, and the merging is performed following an agglomerative clustering approach. The two most similar co-clusters are merged in each iteration. The goal of this step is two-fold: (i) it allows the discovery of large co-clusters, and (ii) it allows for overlapping co-clusters. In this step, the algorithm also adds more rows and columns to each co-cluster individually to obtain larger co-clusters and also allows for overlapping co-clusters. Hence, the same row/column can be added to several co-clusters.
Step 4: Pruning
In this step, we prune the co-clusters with the lowest coherence scores. To determine which co-clusters to prune, (i) sort the co-clusters based on their coherence (measured by HP), (ii) compute the difference between the consecutive scores and (iii) report the set of co-clusters just before the largest difference, and prune the remaining co-clusters. The time complexity of the RAPOCC algorithm is O (κ.ℓ(max(MN2, NM2))).
We now extend the RAPOCC algorithm to discover discriminative co-clusters from labeled datasets that has two classes. First, rather than looking at κ × ℓ co-clusters, we will search for KA × 1 and KB × 1 co-clusters. Second, the initialization step and the objective functions are changed to consider the two-classes problem. The core co-clustering, merging, refinement and pruning steps will be used with some modifications. The positive and negative correlations will be handled similarly.
5 The Proposed Di-RAPOCC Algorithm
Discriminative co-clustering aims to extract patterns that are highly correlated in a subset of the features in one class but not correlated in the other class. As illustrated in Fig. 3., the rows of a discriminative co-cluster in one class should not form a co-cluster in the other class. This implies that there are two tasks that should be performed simultaneously: (i) search for a co-cluster in one class, and (ii) find the coherence of the rows of the co-cluster in the other class (ψA(X) or ψB(X) in Definition 5). The challenge is to compute ψB(X) (ψA(X)) while searching for the co-cluster in class A (B).
Consider XA as a co-cluster in class A that has |I| rows and |JA| columns, and consider DB(I, .) as the sub-matrix composed of the I rows and all the columns in class B. XA will be considered as a discriminative co-cluster if there are no co-clusters in DB(I, .). An optimal solution for this would be to apply a co-clustering algorithm to find the maximal co-cluster in class DB(I, .). However, this is an NP-hard problem [10].
An alternative solution to this problem is to consider the correlations of each pair of rows in DB(I, .). Given two rows (x and y) in DB(I, .), the aim is to find the subset of columns where the coherence between the two rows is maximized. To find an exact solution, one should enumerate all possible subsets of the |NB| columns. However, this solution is computationally infeasible since it requires enumerating all the 2|NB| subsets, where NB is the number of columns in class B. To avoid such an exhaustive enumeration, we propose two efficient solutions: (i) a greedy-columns-selection solution and (ii) a clustering-based solution. Table 2 demonstrates a running example to illustrate how these solutions work.
TABLE 2.
An illustration using a running example.
| Row | c 1 | c 2 | c 3 | c 4 | c 5 | c 6 | c 7 | c 8 | c 9 | c 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | 9 | 8 | 6 | 5 | 3 | 2 | 1 | 6 | 8 | 5 |
| y | 10 | 4 | 10 | 6 | 9 | 3 | 2 | 9 | 9 | 10 |
| z | 2 | 5 | 8 | 4 | 5 | 9 | 8 | 9 | 1 | 8 |
5.1 Greedy-Columns-Selection
The intuition behind this measure is to iteratively compute the coherence between x and y based on the best Ji sets of columns for 1 ≤ Ji ≤ NB and then report a weighted average of these NB computations. In the first iteration, all the NB columns are used. In the second iteration, one of the columns (j) is removed, and the remaining NB − 1 columns are used to compute the coherence between the two rows. These are the set of NB − 1 columns that achieves the maximum coherence between the two rows. This will be repeated to compute the coherence of the two rows using the best NB − 2, NB − 3, …, 1 columns. The final value of this measure is a weighted average of {h(x, y, J1), …, h(x, y, JNB)}:
|Ji|/NB is the weight assigned to each set of columns such that larger sets of columns are assigned more weight than smaller sets of columns. This measure can be used to capture the negative correlations by applying h−(x, y, J) instead of h+(x, y, J). Since no prior knowledge about the correlations between the rows is used, hG will be computed twice, and the final value for this measure hG(x, y) is computed as the maximum of
Finally, is computed as:
As an example, Table 3 shows the results of applying hG on the x and y rows in Table 2. From this table, it should be noted that the two rows form a perfect co-cluster in the columns {c1, c4, c6, c7, c9}. Fig. 7(a) shows a plot for all the three rows in all the columns, and Fig. 7(b) shows a plot for all the three rows in the identified subset of the columns. Based on the greedy-columns-selection method, the first proposed discriminative coherence measure is defined as follows:
The range of and is (−1, 1).
TABLE 3.
Results of hG on the x and y rows in Table 2.
| (i) | Çolumns {Jm} | h+ (x, y, Ji) |
|---|---|---|
| 1 | J1 = {c1, c2, c3, c4 , c5, c6, c7, c8 , c9, c10} | 0.9723 |
| 2 | J2 = {c1, c3, c4, c5 , c6, c7, c8 , c9, c10} | 0.9860 |
| 3 | J3 = {c1, c3, c4, c6, c7, c8, c9, c10} | 0.9908 |
| 4 | J4 = {c1, c3, c4, c6, c7, c8, c9} | 0.9947 |
| 5 | J5 = {c1, c4, c6, c7, c8, c9} | 0.9978 |
| 6 | J6 = {c1, c4, c6, c7, c9} | 1.0 |
| 7 | J7 = {c4, c6, c7, c9} | 1.0 |
| 8 | J8 = {c6 , c7, c9} | 1.0 |
| 9 | J9 = {c6, c9} | 1.0 |
| 10 | J10 = {c9} | 1.0 |
| hG(x, y, J) (weighted average) | 0.994 | |
Fig. 7.
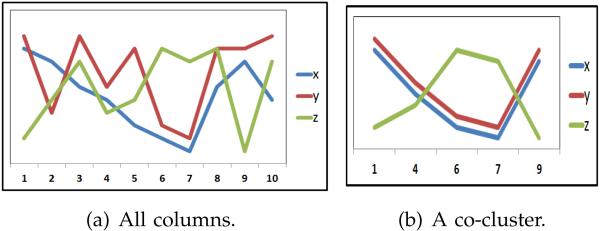
(a) a plot for the entire running datasets. (b) a plot for the co-cluster extracted from the running dataset.
5.2 Clustering-based Discretization
The goal of the discretization step is to create a new representation of the data using a standard one-dimensional clustering algorithm to cluster each row separately. We rank the clusters in each row, and each value in a row will be represented by the rank of the cluster it belongs to. After clustering, we estimate the coherence between any two rows using the new representation.
The intuition of using clustering is to guarantee that similar data points within each row will be represented by the same value. The basic idea is as follows: (i) Cluster the values of each row to c clusters. (ii) Rank the clusters based on the mean of the values of each cluster such that cluster 1 contains the lowest values in x, and cluster c contains the highest values in x. (iii) Map each value of x to the rank of the cluster the value belongs to.
As shown in Section 3, the positive correlation between two rows is defined as (xj − x̄) = (yj − ȳ) and the negative correlation between them is defined as (xj − x̄) = −(yj − ȳ). Using the new representation, the positive correlation can be represented as
where s+ is the positive shift parameter. Since ζ(xj) and ζ(yj) can take any value between 1 and c, the shift parameter (s+) can take any value from the following set: {−(c − 1), …, −1, 0, 1, …, c − 1}. Similarly, the negative correlation can be represented as
where s− is the negative shift parameter that can take any value from the following set: {2, 3, …, 2c}. Now, we can efficiently estimate the correlation between any two rows by finding the values of s+ and s− which will have a finite number of possible values. To estimate the positive correlation between x and y, we will subtract ζ(xj) from ζ(yj), and the most frequent value that appears in many columns will be considered as the value for s+. Similarly, to estimate the negative correlation between x and y, we will add ζ(xj) to ζ(yj), and the most frequent value that appears in many columns will be considered as the value for s−. To determine if the two rows are positively or negatively correlated, we compare the number of columns in which the two rows are considered positively correlated to the number of columns in which the two rows are considered negatively correlated.
If |JC+| ≥ |JC−|, x and y are considered positively correlated, and their coherence is computed as , else, x and y are considered negatively correlated, and their coherence is computed as . Finally, in class B can be computed as
To illustrate how this measure works, Table 4 shows the results of clustering each row in Table 2 (Here we used k-means, k=3. However, any other clustering algorithm can be used). The values in this table are the rankings of the clusters. For example, 1 indicates the cluster that has the lowest values in the corresponding row, and 3 indicates the cluster that has the maximum value. As an example, consider the first two rows. Subtracting ζ(x) from ζ(y) yields the following:
This means that the maximum positive correlation between x and y is in 5 columns {c1, c4, c6, c7, c9} with s+ = 0, while adding ζ(x) to ζ(y) yields
This means that the maximum negative correlation between x and y is in 3 columns: {2, 4, 5} with s− = 4 or {c3, c8, c10} with s− = 5). Hence, the coherence between x and y is computed as follows:
As another example, the last two rows (y and z) are negatively correlated in the same set of columns:
The results here are similar to those obtained using hG in terms of the set of columns in which the two rows have the maximum coherence, which is {c1, c4, c6, c7, c9}. Based on the clustering-based discretization method, the second proposed discriminative coherence measures is defined as follows:
TABLE 4.
Clustering of the running example dataset.
| Row | c 1 | c 2 | c 3 | c 4 | c 5 | c 6 | c 7 | c 8 | c 9 | c 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| ζ(x) | 3 | 3 | 2 | 2 | 1 | 1 | 1 | 2 | 3 | 2 |
| ζ(y) | 3 | 1 | 3 | 2 | 3 | 1 | 1 | 3 | 3 | 3 |
| ζ(z) | 1 | 2 | 3 | 2 | 2 | 3 | 3 | 3 | 1 | 3 |
Similar to and , the range of and is (−1, 1). Our preliminary results showed that ψC and ψG produced very similar results on some of the simulated datasets. Since the computation of ψC is much faster than the computation of ψG, ψC is implemented in the proposed discriminative co-clustering algorithm. However, both measures will be used for evaluation purposes to quantify the resulting discriminative co-clusters using the proposed and the existing algorithms.
The Di-RAPOCC algorithm, described in Algorithm 2, optimizes for the following objective function in order to extract the discriminative co-clusters.
Definition 6. (Discriminative Objective Function) To obtain the top-KA discriminative co-clusters from class A, the objective function can be written as: where . To obtain the top-KB discriminative co-clusters from class B, the objective function be can written as: where .
5.3 The Di-RAPOCC Algorithm
We will now explain the different steps of the proposed Di-RAPOCC algorithm.
Step 1: Initialize the KA and KB co-clusters
First, we compute and for all pairs of rows. This step is preceded by clustering the values of each class. The clustering is only used to identify the set of columns in which two rows have the maximum correlation, and the original values will be used in all the steps. Hence, there is no loss of information in this step. Then, we define as follows:
Similarly, we can also define . These will be used to identify KA groups of rows, SA, to be used as the seeds for the co-clusters (lines 7-12). For our experiments, we chose to have the values of both KA and KB equal to 5. If α is the minimum number of rows in any co-cluster (which is set to 3 in our experiments), the candidate set for each row Rx is computed as follows:
| (2) |
From all of the M candidate sets (since there are M rows in the data matrix, each row will be a candidate to be considered as a seed for a co-cluster), the top-KA sets are used as the initial co-clusters for each class.
| (3) |
Similarly, RB and SB will be computed for class B. Regarding the columns, all of them will be included in each co-cluster in the initialization.
Step 2: Updating the row/column clusterings
This is an iterative step in which we consider each row/column to be added/deleted from each co-cluster (lines 13-27). For each row, there are three possible assignments {−1, 0, 1}: 1 (−1) indicates adding the row to the co-cluster as positively (negatively) correlated, and 0 indicates removing the row from the corresponding co-cluster. The assignments of the columns do not consider a negative correlation since the definition of negative correlation only comes from the rows. The same row (or column) is allowed to be included in more than one co-cluster in this step. Similar to the RAPOCC algorithm, the convergence of the Di-RAPOCC algorithm is guaranteed since the maintained objective function is bounded and optimized to be monotonically increasing.
Algorithm 2.
Di-RAPOCC(D, K, α)
| 1: Input: Data matrix (D) |
| No. of co-clusters (KA and KB) |
| Minimum No. of rows in any co-cluster (α) |
| 2: Output:: Two sets of discriminative co-clusters ({XA}, {XB}) |
| 3: Procedure: |
| 4: Step 1: Compute δC for all the rows |
| 5: |
| 6: |
| 7: Initialize each of the K co-clusters for each class |
| 8: Compute SA and SB as defined in
Equation (3) / * Initialize rows and columns of each co-cluster * / |
| 9: for k = 1 : K do |
| 10: , |
| 11: , |
| 12: end for |
| 13: Step 2: Update the row and the column clusterings |
| 14: repeat |
| 15: for k = 1 : K do |
| 16: for i = 1 : M do |
| 17: |
| 18: |
| 19: end for |
| 20: for j = 1 : NA do |
| 21: |
| 22: end for |
| 23: for j = 1 : NB do |
| 24: |
| 25: end for |
| 26: end for |
| 27: until convergence |
| 28: Step 3: Merging similar co-clusters. |
| 29: Step 4: Pruning. |
Step 3: Merging the Co-clusters
Similar to the RAPOCC algorithm, the goal of this step is to merge similar co-clusters using an agglomerative clustering approach. The two most similar co-clusters, within the same class, are merged in each iteration. This step allows the discovery of large discriminative co-clusters, and it allows intra-class overlapping co-clusters.
Step 4: Pruning
In this step, we prune the co-clusters with the lowest discriminative scores. To determine which co-clusters to prune, (i) sort the co-clusters based on ΦA(X), in class A and ΦB(X), in class B, (ii) compute the difference between the consecutive scores and (iii) report the set of co-clusters just before the largest difference, and prune the remaining co-clusters.
6 The Experimental Results
To demonstrate the effectiveness of the proposed algorithms, several experiments were conducted using both synthetic and real-world gene expression datasets.
6.1 Experimental Setup
6.1.1 Datastes
For the synthetic datasets, a set of co-clusters were implanted in randomly generated datasets using the shifting and scaling patterns [39]. Given two rows, x and y, their relationship can be represented as:
where sshift and sscale are the shifting and scaling parameters. The sign of sshift determines the correlation type: if sshift > 0, then x and y are positively correlated, and if sshift < 0, then x and y are negatively correlated [39]. In addition, two types of synthetic datasets were used, one without noise and the other with Gaussian noise. For the real-world datasets, we used eight expression datasets in the co-clustering experiments as described in Table 5. In the discriminative co-clustering experiments, we only used the first four datasets in Table 5 since each of these datasets has two distinct classes of biological samples.
TABLE 5.
Description of the real-world gene expression datasets used in our experiments.
| Dataset | Genes | Total samples |
class A | class B | ||
|---|---|---|---|---|---|---|
| Description | samples | Description | samples | |||
| Leukemia [20] | 5000 | 38 | Acute lymphoblastic leukemia | 11 | Acute myeloid leukemia | 27 |
| Colon cancer [2] | 2000 | 62 | Normal | 22 | Tumor | 40 |
| Medulloblastoma [25] | 2059 | 23 | Metastatic | 10 | Non-metastatic | 13 |
| Scleroderma [38] | 2773 | 27 | Male | 12 | Female | 15 |
| Arabidopsis thaliana [31] | 734 | 69 | 69 Different biological samples and pathways | |||
| Gasch yeast [31] | 2993 | 173 | 173 Time series gene expression data | |||
| Cho yeast [12] | 6240 | 14 | 17 Time points (cell cycle) | |||
| Causton yeast [9] | 4960 | 11 | Response to environmental changes | |||
6.1.2 Comparisons with existing methods
In the co-clustering experiments, we compared the results of the RAPOCC algorithm against the CC [10], the OPSM [7], the ISA [22] and the ROCC [15] algorithms. We used BiCAT software (http://www.tik.ethz.ch/sop/bicat/) to run CC, ISA and OPSM algorithms using the default parameters. The code for the ROCC was obtained from the authors of [15]. In the discriminative co-clustering experiments, we compared the results of the Di-RAPOCC algorithm against the SDC algorithm [18] and the OPSM algorithm [7]. The OPSM algorithm is not a discriminative co-clustering algorithm. Therefore, we used the following procedure: (i) Apply OPSM on each class separately, (ii) compute the inter-class overlap, (iii) remove the co-clusters that have inter-class overlap ≥ 50%, and (iv) report the remaining co-clusters. We refer to this modified algorithm as Discriminative OPSM (Di-OPSM). The SDC algorithm takes as input three parameters (SDC, r, minpattsize) [18], which were set to the default values: (0.2, 0.2, 3) unless otherwise stated.
6.1.3 Evaluation Measures
Several measures were used such as the number of co-clusters, the average size and the average coherence of the co-clusters computed using Definition 3. We also used the recovery and relevance measures as defined in [31]. Recovery determines how well each of the implanted co-clusters is discovered, and relevance is the extent to which the generated co-clusters represent the implanted co-clusters. Given a set of implanted co-clusters denoted by Yimp and a set of co-clusters obtained by an algorithm denoted by Xres, the recovery and the relevance can defined as follows:
In addition, we used the following proposed metrics to evaluate the results of the discriminative co-clustering:
- Greedy-based discriminative coherence (ΔG)
- Clustering-based discriminative coherence (ΔC)
- Inter-class overlap. If XA (XB) is the set of discriminative co-clusters in class A (B), the inter-class overlap is defined as the average of:
where the union and intersection operations are computed using the rows in the co-clusters.
6.1.4 Biological Evaluation
The biological significance was estimated by calculating the p-values using the DAVID tool (http://david.abcc.ncifcrf.gov/) to test if a given co-cluster is enriched with genes from a particular category to a greater extent than would be expected by chance [24]. The range of the p-values is from 0 to 1. Lower p-values indicate biological significance [11].
6.2 Co-clustering Results
In this subsection, we present the results for the co-clustering experiments.
6.2.1 Results on Synthetic Data
Two types of datasets were used, one without noise and one with 10% noise. The size of each synthetic dataset is 200 × 150. Two co-clusters were implanted in each dataset, and the size of each co-cluster is 50 × 50. As shown in Fig. 8, the RAPOCC algorithm outperformed the other algorithms because it optimizes for high-quality co-clusters. As a result, fewer random data points are added to the co-clusters obtained by our algorithm.
Fig. 8.
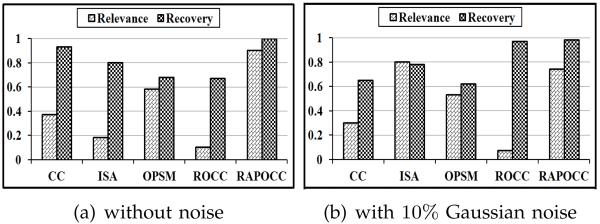
The co-clustering results on the synthetic datasets.
6.2.2 Results on Real Gene Expression Data
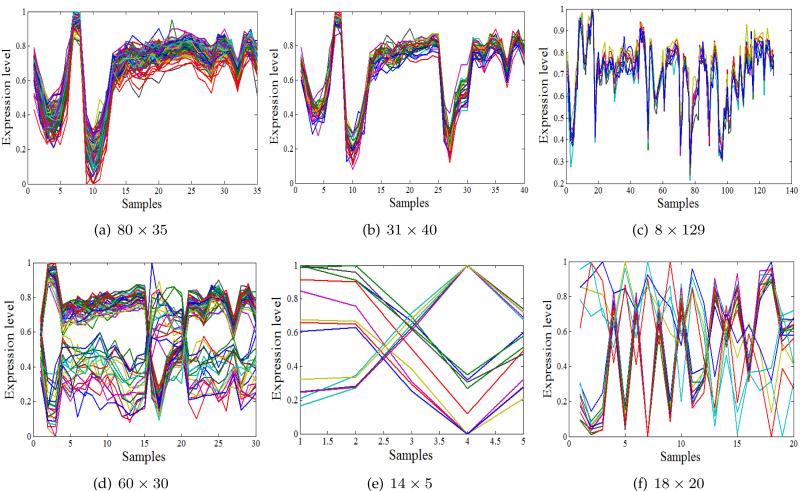
Fig. 9 shows two co-clusters obtained by the proposed algorithm. The first co-cluster contains positively correlated genes, while the second co-cluster contains both types of correlations. The results of the five co-clustering methods on the eight datasets are shown in Table 6 and summarized in the following observations:
Coherence of the co-clusters. The RAPOCC algorithm outperformed all the other algorithms on all the datasets. The OPSM and the ROCC algorithms performed better than the CC and the ISA algorithms. These results confirmed one of our initial claims that the proposed RAPOCC algorithm was designed to identify high-quality co-clusters.
Size of the co-clusters. Except for the Leukemia dataset, the RAPOCC produced either the largest or the second largest co-clusters in all the datasets. The OPSM and the RAPOCC algorithms produced the largest co-clusters in four datasets and three datasets, respectively.
Number of the co-clusters. The ROCC algorithm produced the largest number of co-clusters in all of the datasets. However, we observed that, in most of the cases, the co-clusters generated by this algorithm were either duplicates, subsets of each other or highly overlapping. On the other hand, the ISA algorithm did not produce any co-cluster for three datasets: Leukemia, Cho yeast and Causton yeast.
Biological significance of the co-clusters. Fig. 10 shows the average of the percentages of the biologically significant co-clusters using the DAVID tool from all the eight gene expression datasets. As shown in this figure, our proposed algorithm outperformed all other algorithms.
Fig. 9.
Examples of the co-clusters identified by the RAPOCC algorithm. The three co-clusters in the first row contain only the positively correlated genes which show similar patterns. These co-clusters were obtained from the Gasch yeast dataset. The three co-clusters in the second row contain positively and negatively correlated genes which show opposite patterns. These co-clusters were obtained from (d) Gasch yeast, (e) Scleroderma and (f) Causton yeast datasets.
TABLE 6.
Results of the five co-clustering methods on the eight gene expression datasets.
| Dataset | Average coherence of co-clusters (No. of co-clusters) |
Average volume of co-clusters (Avg No. of rows, Avg No. of columns) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CC | ISA | OPSM | ROCC | RAPOCC | CC | ISA | OPSM | ROCC | RAPOCC | |
| Leukemia | 0.9715 (20) |
– (0) |
0.9963 (37) |
0.9775 (44) |
0.9984 (25) |
7611.2 (310, 15) |
– |
8475 (708, 20) |
2544 (190, 10) |
3543.7 (219, 13) |
| Colon | 0.9884 (10) |
0.9902 (21) |
0.9810 (13) |
0.9946 (62) |
0.9986 (11) |
15.5 (5.9, 3.6) |
376 (148.3, 5.6) |
2435 (619.2, 8.1) |
881.2 (88, 10.6) |
1437 (230.3, 7.8) |
| Medulloblastoma | 0.9996 (10) |
0.9906 (1) |
0.9891 (10) |
0.9892 (93) |
0.9997 (15) |
16.6 (5.9, 6.5) |
10 (5, 2) |
639 (225, 6) |
258 (80.6, 3.2) |
409.3 (82, 5) |
| Scleroderma | 0.9838 (20) |
0.9813 (2) |
0.9862 (12) |
0.9895 (47) |
0.9950 (20) |
2273.8 (110, 16) |
15 (8, 2) |
1303.4 (403, 8) |
426 (63, 10) |
1949 (380, 7) |
| Arabidopsis | 0.9996 (20) |
0.9569 (27) |
0.9969 (12) |
0.9952 (36) |
0.9998 (20) |
146.2 (19, 8) |
40.6 (20, 2) |
330.7 (98,8) |
534.1 (41, 28) |
2282.1 (191, 12) |
| Gasch yeast | 0.9844 (20) |
0.9907 (63) |
0.9966 (14) |
0.9945 (87) |
0.9987 (25) |
2424 (304, 43) |
572.1 (67, 9) |
2019.6 (522, 9) |
2320.7 (115, 25) |
2582.5 (272, 29) |
| Cho yeast | 0.9322 (20) |
– (0) |
0.9923 (11) |
0.9854 (33) |
0.9960 (30) |
950.5 (80, 12) |
- |
2015 (682, 7) |
757.9 (152, 6) |
1958 (392, 5) |
| Causton yeast | 0.9220 (17) |
– (0) |
0.9907 (9) |
0.9831 (20) |
0.9965 (20) |
2202.9 (219, 10) |
- | 2656.3 (941, 6) |
800 (200, 4) |
3897.5 (780, 5) |
Fig. 10.
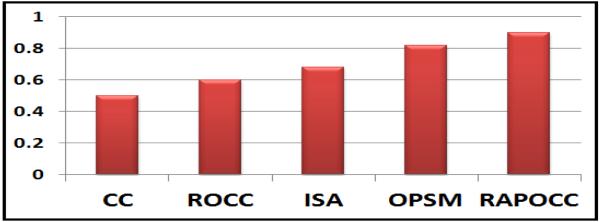
Proportion of co-clusters that are significantly enriched (average of the 8 datasets).
Overall, the proposed algorithm produced the higher quality, more biologically significant and relatively larger co-clusters compared to the other algorithm. Furthermore, the RAPOCC algorithm is more robust to noise.
6.3 Discriminative Co-clustering Results
In this subsection, we present the results for discriminative co-clustering experiments. Due to space limitations, in some of the tables we used OPM and RPC to refer to Di-OPSM and Di-RAPOCC algorithms, respectively.
6.3.1 Results on Synthetic Data
Using the shifting-and-scaling model [39], four co-clusters were generated of the size 10×10. Half of those co-clusters were designed to be discriminative, while the remaining co-clusters were common in both classes. The structure of the synthetic datasets is similar to the structure shown in Fig. 3. In the first experiment, we implanted the synthetic co-clusters in random matrices of different sizes given by s × 20, where s = (50, 100, 300, 500). Fig. 11 shows the relevance and recovery results of SDC, Di-OPSM and Di-RAPOCC co-clustering algorithms when applied to the synthetic datasets. The noise level, η, in this set of experiments is 0. The proposed algorithm outperformed other algorithms indicating that the proposed algorithm is capable of identifying the discriminative co-clusters. Since Di-OPSM was not directly designed to extract discriminative co-clusters, the identified co-clusters include both discriminative and non-discriminative co-clusters. The poor performance of the SDC algorithm can be explained by two main reasons. (i) SDC generates too many patterns as shown in Table 7. As the size of the dataset increases, the number of the generated patterns generated by the SDC algorithm increases dramatically. (ii) The SDC algorithm generates very small patterns (average of 3 rows per pattern). On the other hand, the Di-RAPOCC algorithm prunes any non-discriminative co-cluster.
Fig. 11.
Relevance and Recovery for SDC, Di-OPSM and Di-RAPOCC obtained from synthetic datasets.
TABLE 7.
Number of co-clusters from synthetic datasets.
| Synthetic dataset | SDC | Di-OPSM | Di-RAPOCC |
|---|---|---|---|
| s=50 | 256 | 15 | 2 |
| s=100 | 990 | 16 | 2 |
| s=300 | 4, 451 | 16 | 3 |
| s=500 | 10, 210 | 22 | 3 |
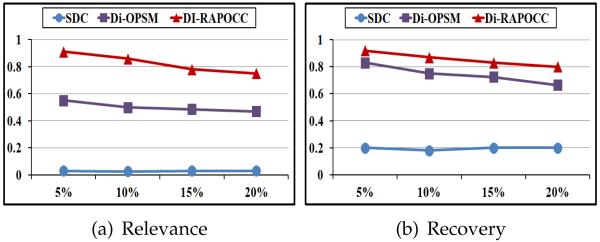
In the second experiment, different levels of noise were used, which are 0, 5%, 10%, 15% and 20%, respectively, to the synthetic dataset of size 100 × 20. Fig. 12 shows the recovery and the relevance of the three algorithms. As the noise level increases in the dataset, the relevance and the recovery values are degraded. However, our algorithm is still the algorithm most robust to noise due to the use of a clustering approach to estimate the coherence of any co-cluster. Table 8 shows the average results of the discriminative measurements ΔG and ΔC for all the different synthetic datasets. Unsurprisingly, our algorithm achieved the best results in all the datasets because it primarily focuses on identifying the most discriminative co-clusters in the search process. Fig. 13 shows the inter-class overlap on synthetic datasets. The Di-RAPOCC algorithm achieved the best results because it avoids common patterns in both of the classes.
Fig. 12.
Relevance and recovery obtained with noise levels of 5%, 10%, 15% and 20%, respectively.
TABLE 8.
Discriminative measures (synthetic datasets).
| Synthetic dataset |
Δ G | Δ C | ||||
|---|---|---|---|---|---|---|
| SDC | OPM | RPC | SDC | OPM | RPC | |
| s=50, η=0 | 0.51 | 0.54 | 0.69 | 0.51 | 0.55 | 0.72 |
| s=100, η=0 | 0.50 | 0.68 | 0.71 | 0.54 | 0.0.54 | 0.70 |
| s=200, η=0 | 0.49 | 0.63 | 0.70 | 0.54 | 0.66 | 0.71 |
| s=300, η=0 | 0.52 | 0.51 | 0.67 | 0.51 | 0.64 | 0.70 |
| s=500, η=0 | 0.51 | 0.64 | 0.71 | 0.52 | 0.63 | 0.72 |
| s=100, η=5% | 0.53 | 0.57 | 0.71 | 0.51 | 0.60 | 0.70 |
| s=100, η=10% | 0.52 | 0.65 | 0.67 | 0.53 | 0.61 | 0.65 |
| s=100, η=15% | 0.51 | 0.63 | 0.76 | 0.49 | 0.63 | 0.70 |
| s=100, η=20% | 0.52 | 0.64 | 0.72 | 0.50 | 0.61 | 0.65 |
Fig. 13.
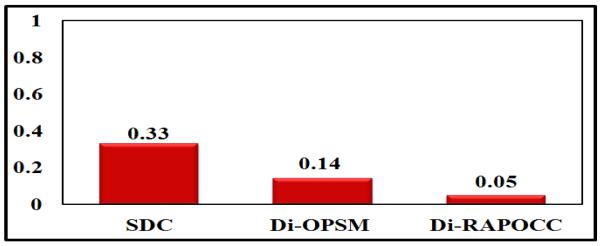
The inter-class overlapping on synthetic datasets.
6.3.2 Results on Real Gene Expression Data
The SDC algorithm was applied on the Medulloblastoma and the Scleroderma datasets with the parameters values set to (0.3, 0.3, 3) to avoid out of memory problems. For the Leukemia datasets, out of memory errors occurred for different combinations of the parameters; therefore, there are no results for this dataset. As shown in Table 9, the Di-RAPOCC algorithm achieved the best results in terms of the discriminative coherence measures (ΔG and ΔC). The results were also analyzed in terms of the number of co-clusters, the inter-class overlap and the average coherence as shown in Table 10. The coherence measure cannot be applied to the results of the SDC algorithm because it does not report the columns in which a set of rows is correlated. Here, we make some remarks regarding the performance of the three algorithms.
The SDC algorithm tends to produce a large number of small patterns. Since the SDC algorithm uses the Apriori approach, it has some computational efficiency problems, and the number of the discovered patterns grows dramatically with larger datasets.
The Di-OPSM algorithm tends to produce co-clusters that are too large. Therefore, it does not give good results in terms of the coherence, inter-class overlap and discriminative measures. Since it is not a discriminative co-clustering algorithm, we have to run it on each class independently.
The Di-RAPOCC algorithm keeps the top discriminative co-clusters and prunes the other co-clusters, and it works well on noisy and large datasets.
TABLE 9.
Discriminative measures (expression datasets)
| Dataset | Δ G | Δ C | ||||
|---|---|---|---|---|---|---|
| SDC | OPM | RPC | SDC | OPM | RPC | |
| Colon | 0.60 | 0.58 | 0.62 | 0.50 | 0.53 | 0.56 |
| Medulloblastoma | 0.49 | 0.54 | 0.59 | 0.51 | 0.53 | 0.55 |
| Leukemia | - | 0.57 | 0.59 | - | 0.56 | 0.58 |
| Scleroderma | 0.57 | 0.54 | 0.60 | 0.54 | 0.55 | 0.60 |
TABLE 10.
The average No. of co-clusters, the average overlap and the average coherence
| Dataset | No. of co-clusters in A | No. of co-clusters in B | Overlap | Average coherence (H) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SDC | OPM | RPC | SDC | OPM | RPC | SDC | OPM | RPC | OPM | RPC | |
| Colon | 155 | 10 | 15 | 1 | 3 | 13 | 0.0 | 0.01 | 0.04 | 0.992 | 0.997 |
| Medulloblastoma | 74,957 | 8 | 14 | 7,597 | 9 | 14 | 0.2 | 0.12 | 0.01 | 0.988 | 0.994 |
| Leukemia | - | 21 | 35 | - | 5 | 22 | - | 0.40 | 0.09 | 0.990 | 0.995 |
| Scleroderma | 48,623 | 12 | 10 | 469 | 10 | 9 | 0.04 | 0.17 | 0.0 | 0.986 | 0.998 |
Fig. 14 shows the biological evaluation of the results. The SDC algorithm was excluded from this analysis because it produced too many patterns. The Di-RAPOCC algorithm outperformed the Di-OPSM algorithm in three datasets, while OPSM was better in the Leukemia dataset. However, for this dataset, Di-RAPOCC outperformed Di-OPSM in terms of the inter-class overlap, the coherence and the discriminative coherence measures. In a different analysis, we found several significant biological pathways that were enriched in the co-clusters produced by the proposed algorithm. For example, the MAPK signaling pathway which has a p-value = 4.77E − 12 was reported as an up-regulated pathway in the metastatic tumors that is very relevant to the study of metastatic disease [25]. The summary of comparisons between the three algorithms is shown in Table 11.
Fig. 14.
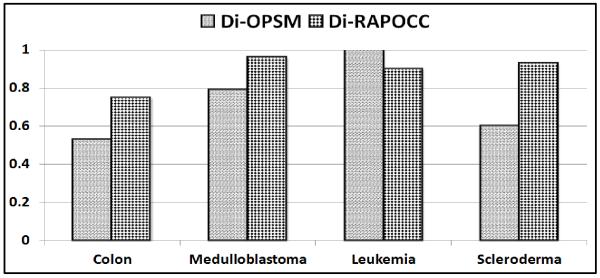
Proportion of the co-clusters that are significantly enriched in each dataset (significance level = 5%).
TABLE 11.
Comparisons between the three discriminative co-clustering algorithms.
| Measure | SDC | OPM | RPC |
|---|---|---|---|
| No. of the co-clusters | High | Low | Medium |
| Size of the co-clusters | Small | Large | Medium |
| Coherence | - | Low | High |
| Discriminative coherence | Low | Medium | High |
| Inter-class overlap | High | Medium | Low |
| Recovery | Low | Medium | High |
| Relevance | Low | Medium | High |
6.3.3 Discussion
We will now describe how the proposed model can overcome the limitations of the existing methods and can obtain the discriminative co-clusters that have all the desired characteristics mentioned earlier. (i) The proposed model incorporates the class label within each iteration step while optimizing the objective function. This will ensure to yield patterns with the maximum discriminative coherence and discriminative power. In addition, since ψ is computed for each feasible pair in both the classes, the model will generate patterns with minimum inter-class overlap. (ii) The proposed model will generate larger patterns compared to the SDC and other algorithms. This will be achieved by the update operations in which each row/column will be considered to be added to each pattern in each class. (iii) The pruning step will keep only the relevant patterns and remove the irrelevant ones. This will overcome the limitation of the SDC algorithm which generates too many unnecessary patterns. (iv) The efficient use of the clustering-based measure ψC for approximating the optimization criteria makes the proposed model an order of magnitude faster than the previous algorithms. (v) The proposed algorithm allows the patterns to share some columns (or conditions). This intra-class overlap is an important property of subspace patterns as described earlier.
7 Conclusion
In this paper, we presented a novel algorithm for discovering arbitrarily positioned co-clusters, and we extended this algorithm to discover discriminative co-clusters by integrating the class label in the co-clustering discovery process. Both of the proposed algorithms are robust against noise, allow overlapping and capture positive and negative correlations in the same co-cluster. Comprehensive experiments on synthetic and real-world datasets were carried out to illustrate the effectiveness of the proposed algorithms. The results showed that both of the proposed algorithms outperformed existing algorithms and can identify co-clusters that are biologically significant. As future work, we are interested in analyzing the discriminative power of the proposed approach and extending it to solve prediction problems. Also, we plan to extend the work to other forms of subspace clustering algorithms such as correlation clustering [5].
Acknowledgements
This work was supported in part by the National Cancer Institute of the National Institutes of Health under Award Number R21CA175974 and the U.S. National Science Foundation grants IIS-1231742 and IIS-1242304. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH and NSF.
Biographies

Omar Odibat received his Ph.D. from the Department of Computer Science at the Wayne State University. Earlier he received his M.S. from University of Jordan in 2005 and B.S. in Computer Science from Yarmouk University in 2003. His research interests are in the areas of data mining and bioinformatics. He is a student member of ACM and SIAM.

Chandan K. Reddy is an Associate Professor in the Department of Computer Science at Wayne State University. He received his Ph.D. from Cornell University and M.S. from Michigan State University. His primary research interests are in the areas of data mining and machine learning with applications to healthcare, bioinformatics, and social network analysis. His research is funded by the National Science Foundation, the National Institutes of Health, the Department of Transportation, and the Susan G. Komen for the Cure Foundation. He has published over 50 peer-reviewed articles in leading conferences and journals. He received the Best Application Paper Award at the ACM SIGKDD conference in 2010 and was a finalist of the INFORMS Franz Edelman Award Competition in 2011. He is a member of IEEE, ACM, and SIAM.
Footnotes
To be consistent, we will be using the term ‘co-clustering’ throughout the paper. The Bioinformatics research community preferably calls it as ‘biclustering’.
References
- [1].Aggarwal Charu C, Reddy Chandan K., editors. Data Clustering: Algorithms and Applications. Chapman and Hall/CRC; 2013. [Google Scholar]
- [2].Alon U, Barkai N, Notterman DA, Gish K, Ybarra S, Mack D, Levine AJ. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proceedings of the National Academy of Sciences of the United States of America. 1999;96(12):6745–6750. doi: 10.1073/pnas.96.12.6745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Alqadah Faris, Bader Joel S, Anand Rajul, Reddy Chandan K. Query-based biclustering using formal concept analysis; SIAM International Conference on Data Mining; 2012.pp. 648–659. [Google Scholar]
- [4].Anagnostopoulos Aris, Dasgupta Anirban, Kumar Ravi. Approximation algorithms for co-clustering; PODS ’08: Proceedings of the twenty-seventh ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems; NY, USA. 2008.pp. 201–210. [Google Scholar]
- [5].Aziz Mohammad S, Reddy Chandan K. Advances in Knowledge Discovery and Data Mining. Springer; 2010. A robust seedless algorithm for correlation clustering; pp. 28–37. [Google Scholar]
- [6].Banerjee Arindam, Dhillon Inderjit, Ghosh Joydeep, Merugu Srujana, Modha Dharmendra S. A generalized maximum entropy approach to bregman co-clustering and matrix approximation. J. Mach. Learn. Res. 2007;8:1919–1986. [Google Scholar]
- [7].Ben-Dor Amir, Chor Benny, Karp Richard, Yakhini Zohar. Discovering local structure in gene expression data: the order-preserving submatrix problem. Journal of computational biology. 2003;10(3-4):373–384. doi: 10.1089/10665270360688075. [DOI] [PubMed] [Google Scholar]
- [8].Burdick Doug, Calimlim Manuel, Gehrke Johannes. Mafia: A maximal frequent itemset algorithm for transactional databases. ICDE. 2001:443–452. [Google Scholar]
- [9].Causton HC, Ren B, Koh SS, Harbison CT, Kanin E, Jennings EG, Lee TI, True HL, Lander ES, Young RA. Remodeling of yeast genome expression in response to environmental changes. Mol Biol Cell. 2001;12(2):323–337. doi: 10.1091/mbc.12.2.323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Cheng Yizong, Church George M. Biclustering of expression data; Proceedings of the Eighth International Conference on Intelligent Systems for Molecular Biology; 2000; pp. 93–103. [PubMed] [Google Scholar]
- [11].Cho Hyuk, Dhillon Inderjit S. Coclustering of human cancer microarrays using minimum sum-squared residue coclustering. IEEE/ACM Trans. Comput. Biol. Bioinformatics. 2008;5(3):385–400. doi: 10.1109/TCBB.2007.70268. [DOI] [PubMed] [Google Scholar]
- [12].Cho RJ, Campbell MJ, Winzeler EA, Steinmetz L, Conway A, Wodicka L, Wolfsberg TG, Gabrielian AE, Landsman D, Lockhart DJ, Davis RW. A genome-wide transcriptional analysis of the mitotic cell cycle. Molecular cell. 1998;2(1):65–73. doi: 10.1016/s1097-2765(00)80114-8. [DOI] [PubMed] [Google Scholar]
- [13].de la Fuente Alberto. From ‘differential expression’ to ‘differential networking’ identification of dysfunctional regulatory networks in diseases. Trends in Genetics. 2010;26(7):326–333. doi: 10.1016/j.tig.2010.05.001. [DOI] [PubMed] [Google Scholar]
- [14].Deodhar Meghana, Ghosh Joydeep. SCOAL: A framework for simultaneous co-clustering and learning from complex data. ACM Trans. Knowl. Discov. Data. 2010;4:11:1–11:31. [Google Scholar]
- [15].Deodhar Meghana, Gupta Gunjan, Ghosh Joydeep, Cho Hyuk, Dhillon Inderjit. A scalable framework for discovering coherent co-clusters in noisy data; ICML ’09: Proceedings of the 26th Annual International Conference on Machine Learning; 2009.pp. 241–248. [Google Scholar]
- [16].Dhillon Inderjit S., Mallela Subramanyam, Modha Dharmendra S. Information-theoretic co-clustering; KDD ’03: Proceedings of the ninth ACM SIGKDD international conference on Knowledge discovery and data mining; New York, NY, USA. 2003.pp. 89–98. [Google Scholar]
- [17].Fan Hongjian, Ramamohanarao Kotagiri. Fast discovery and the generalization of strong jumping emerging patterns for building compact and accurate classifiers. Knowledge and Data Engineering, IEEE Transactions on. 2006;18(6):721–737. [Google Scholar]
- [18].Fang Gang, Kuang Rui, Pandey Gaurav, Steinbach Michael, Myers Chad L., Kumar Vipin. Subspace differential coexpression analysis: problem definition and a general approach; Pacific Symposium on Biocomputing; 2010; pp. 145–156. [PubMed] [Google Scholar]
- [19].Fang Gang, Pandey Gaurav, Wang Wen, Gupta Manish, Steinbach Michael, Kumar Vipin. Mining low-support discriminative patterns from dense and high-dimensional data. IEEE Transactions on Knowledge and Data Engineering. 2010;99 PrePrints. [Google Scholar]
- [20].Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, Bloomfield CD, Lander ES. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999 Oct;286(5439):531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
- [21].Hussain Syed Fawad, Bisson Gilles. Text categorization using word similarities based on higher order co-occurrences. SDM. 2010:1–12. [Google Scholar]
- [22].Ihmels Jan, Bergmann Sven, Barkai Naama. Defining transcription modules using large-scale gene expression data. Bioinformatics. 2004;20(13):1993–2003. doi: 10.1093/bioinformatics/bth166. [DOI] [PubMed] [Google Scholar]
- [23].Jiang Daxin, Tang Chun, Zhang Aidong. Cluster analysis for gene expression data: A survey. IEEE Trans. on Knowl. and Data Eng. 2004;16:1370–1386. [Google Scholar]
- [24].Liu Jinze, Yang Jiong, Wang Wei. Biclustering in gene expression data by tendency; Proceedings of the 2004 IEEE Computational Systems Bioinformatics Conference, CSB ’04; Washington, DC, USA. 2004; pp. 182–193. [DOI] [PubMed] [Google Scholar]
- [25].Macdonald Tobey J., Brown Kevin M., Lafleur Bonnie, Peterson Katia, Lawlor Christopher, Chen Yidong, Packer Roger J., Cogen Philip, Stephan Dietrich A. Expression profiling of medulloblastoma: PDGFRA and the RAS/MAPK pathway as therapeutic targets for metastatic disease. Nature Genetics. 2001 Oct;29(2):143–152. doi: 10.1038/ng731. [DOI] [PubMed] [Google Scholar]
- [26].Madeira Sara C., Oliveira Arlindo L. Biclustering algorithms for biological data analysis: a survey. IEEE/ACM transactions on computational biology and bioinformatics. 2004;1(1):24–45. doi: 10.1109/TCBB.2004.2. [DOI] [PubMed] [Google Scholar]
- [27].Odibat Omar, Reddy Chandan K. A generalized framework for mining arbitrarily positioned overlapping co-clusters; Proceedings of the SIAM International Conference on Data Mining (SDM).2011. pp. 343–354. [Google Scholar]
- [28].Odibat Omar, Reddy Chandan K., Giroux Craig N. Differential biclustering for gene expression analysis; Proceedings of the ACM Conference on Bioinformatics and Computational Biology (BCB); 2010.pp. 275–284. [Google Scholar]
- [29].Okada Yoshifumi, Inoue Terufumi. Identification of differentially expressed gene modules between two-class DNA microarray data. Bioinformation. 2009;4(4) doi: 10.6026/97320630004134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Pensa Ruggero G., Boulicaut Jean-François. Constrained co-clustering of gene expression data. SDM. 2008:25–36. [Google Scholar]
- [31].Prelic Amela, Bleuler Stefan, Zimmermann Philip, Wille Anja, Buhlmann Peter, Gruissem Wilhelm, Hennig Lars, Thiele Lothar, Zitzler Eckart. A systematic comparison and evaluation of biclustering methods for gene expression data. Bioinformatics. 2006;22(9):1122–1129. doi: 10.1093/bioinformatics/btl060. [DOI] [PubMed] [Google Scholar]
- [32].Reddy Chandan K, Chiang Hsiao-Dong, Rajaratnam Bala. Trust-tech-based expectation maximization for learning finite mixture models. Pattern Analysis and Machine Intelligence. IEEE Transactions on. 2008;30(7):1146–1157. doi: 10.1109/TPAMI.2007.70775. [DOI] [PubMed] [Google Scholar]
- [33].Serin Akdes, Vingron Martin. Debi: Discovering differentially expressed biclusters using a frequent itemset approach. Algorithms for Molecular Biology. 2011;6(1):18. doi: 10.1186/1748-7188-6-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Shan Hanhuai, Banerjee Arindam. Residual bayesian co-clustering for matrix approximation; Proc. SIAM International Conference on Data Mining; 2010.pp. 223–234. [Google Scholar]
- [35].Shi Xiaoxiao, Fan Wei, Yu Philip S. Efficient semi-supervised spectral co-clustering with constraints; IEEE International Conference on Data Mining; 2010.pp. 1043–1048. [Google Scholar]
- [36].Song Yangqiu, Pan Shimei, Liu Shixia, Wei Furu, Zhou Michelle X., Qian Weihong. Constrained coclustering for textual documents. AAAI. 2010 [Google Scholar]
- [37].Steinbach Michael, Karypis George, Kumar Vipin. In: Grobelnik Marko, Mladenic Dunja, Milic-Frayling Natasa., editors. A comparison of document clustering techniques; KDD-2000 Workshop on Text Mining, August 20; 2000.pp. 109–111. [Google Scholar]
- [38].Whitfield Michael L., Finlay Deborah R., Murray John Isaac, Troyanskaya Olga G., Chi Jen-Tsan, Pergamenschikov Alexander, McCalmont Timothy H., Brown Patrick O., Botstein David, Connolly M. Kari. Systemic and cell type-specific gene expression patterns in scleroderma skin. Proceedings of the National Academy of Sciences. 2003;100(21):12319–12324. doi: 10.1073/pnas.1635114100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Xin Xu, Ying Lu, Tung Anthony K. H., Wang Wei. Mining shifting-and-scaling co-regulation patterns on gene expression profiles; Proceedings of the 22nd International Conference on Data Engineering, ICDE ’06.2006. p. 89. [Google Scholar]
- [40].Zhang Lijun, Chen Chun, Bu Jiajun, Chen Zhengguang, Cai Deng, Han Jiawei. Locally discriminative coclustering. Knowledge and Data Engineering, IEEE Transactions on. 2012;24(6):1025–1035. [Google Scholar]