Abstract
The purpose of this study was to examine the influence of explanatory and confounding variables on health-related quality of life (HRQoL) after accounting for response shift, measurement bias, and response shift in measurement using structural equation modeling. Hypertensive patients with coronary artery disease randomized to anti-hypertensive treatment completed the SF-36 questionnaire at both baseline and one year (n=788). Three measurement biases were found and all three were considered as response shift in measurement. Older patients reported worse scores for both physical functioning (PF) and role physical at baseline and one year later compared to younger patients and males reported better PF than females, conditioning on latent trait of general physical health. Before controlling for response shift, patients’ PF scores were not statistically different over time, however, PF scores significantly improved (p<0.01) after controlling for recalibration response shift. Assessment of how patients perceive their change in HRQoL over time is warranted.
Keywords: SF-36, response shift, health-related quality of life, hypertensive coronary artery disease, measurement bias, verapamil-SR, atenolol-led
Introduction
Hypertensive medications from different pharmacologic classes sometimes have varying side effect profiles for patients with coronary artery disease (CAD). CAD is likely to have a direct impact on the patient’s functional status and health-related quality of life (HRQoL) such as reduced walking distances, shortness of breath, troubles in lifting and carrying objects and doing housework. Hypertensive medication may introduce the risk for depression [1,2] and evidence suggests that depression is highly prevalent (ranges from 17 to 44%) in hypertensive CAD patients [1,3–5]. However, some of HRQoL outcomes may be further compromised by depression-related anhedonia, typically walking and performing chores around the house that require certain levels of physical functioning, making it difficult to judge the effectiveness of CAD treatment [1].
Evidence regarding whether the use of antihypertensive medications (e.g. β-blocker (beta blocker) and calcium channel antagonist) is associated with depression is still mixed [6,7]. Some studies report that rates of depression are higher for patient taking β-blockers than for calcium antagonists [8]. These conclusions are based on findings that antidepressant prescriptions were more likely to be prescribed following β-blocker treatment [9,10]. In other instances, these findings have not been replicated [11,12]. However, other studies report an association of calcium channel antagonists with depression [13].
Comparative effectiveness research is complicated by a lack of methodology to separate the treatment effects on HRQoL improvements due to recovered cardiac function when depression is present from the possible changes in individual’s frame of reference, values or life priorities. Individuals whose health status is the same over time based on an objective measure may report a change in HRQoL. That change, in the face of objectively consistent health measures may reflect a difference in an individual’s frame of reference on important attributes of HRQoL [14]. This phenomenon is known as response shift. Response shift is defined as “a change in the meaning of one’s self-evaluation of a target construct as a result of (a) a change in the respondent’s internal standards of measurement (i.e., recalibration); (b) a change in the importance of component scales constituting the target construct (e.g., reprioritization); or (c) a redefinition of the target construct (i.e., reconceptualization)” [15,16]. The response shift theory suggests that the changes in health state and treatment interventions are the catalysts for the occurrence of response shift [17,18]. It is important to evaluate the potential response shift in patient-reported outcomes such as HRQoL when administering treatment evaluations since response shift may underestimate or overestimate the treatment effects as patients adapt to treatment modalities or disease progression over time.
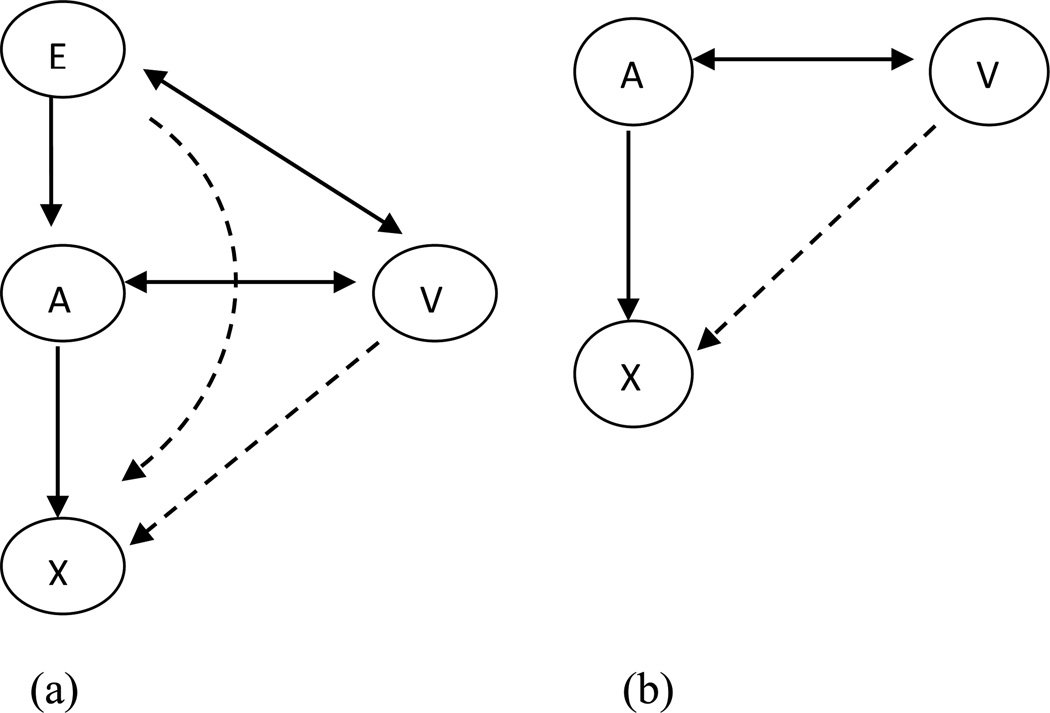
In an attempt to resolve the methodological concerns about response shift, Oort et al. [17] proposed a sophisticated framework to investigate the different measurement issues: measurement bias, response shift, and response shift in measurement [19]. This framework is presented in Figure 1(a) and 1(b), where X represents the observed variables (e.g., SF-36 scales) on the latent construct (denoted by A) such as HRQoL, explanatory variables (denoted by E) representing the causes or predictors (e.g., change in systolic blood pressure, change in depression scores) of HRQoL, and V representing the confounding variables (e.g., age and sex) that may influence HRQoL. Response shift is identified based on the relationship between X and A, and is estimated based on change in model parameters over time as described in Methods section. Measurement bias is estimated when the observed variables such as SF-36 scale scores are rated or interpreted differently by different levels of confounding variables (denoted by V) or explanatory variables E given the same level of latent construct of HRQoL, see Figure 1(a) and 1(b) [17,19]. The concept is also known as uniform differential item functioning that can be tested by the framework of Multiple Indicators, Multiple Causes (MIMIC) [20,21]. In the longitudinal study design, this concept corresponds to response shift in measurement: when the relationship between the observed variables X and confounding variables V or explanatory variables E through their relationship with the latent construct A is not consistent over time [17,19]. In other words, response shift in measurement represents the difference in measurement bias over time.
Figure 1.
Measurement bias and response shift in measurement model used in the present study.
E: explanatory variables (e.g., depression, treatment strategies); A: latent factors (e.g., General Physical and General Mental); V: confounding variables (e.g., age; sex); X: observed variables (e.g., physical functioning; social functioning; mental health scale scores).
The double-headed arrow represents correlations between all E and V variables and/or correlations between all V variables and A. Dashed arrows represent measurement bias/response shift in measurement. Single-headed arrow represents direct effects of E on A or A on X.
Adapted with permission from Oort FJ, Visser MRM, Sprangers MAG. Formal definitions of measurement bias and explanation bias clarify measurement and conceptual perspectives on response shift. J Clin Epidemiol 2009;62:1126–37.
To our knowledge, limited studies have investigated the presence of measurement bias and response shift in measurement [19] using the framework proposed by Oort et al. [17]. One previous study applied the framework presented in Figure 1(b) in the cancer population [19]. However, the authors accounted for the influence of explanatory and confounding variables in separate models as shown in Figure 1(a). The approach of accounting for explanatory variables and confounding variables in separate models does not address different measurement issues at the same time. Our prior work based on two different structural equation modeling (SEM) procedures has reported response shift phenomenon for hypertensive CAD patients which are used in the present study [22]. We found that HRQoL estimates in these patients may have been underestimated after accounting for response shift, leading to false negative results [22]. The present study is an extension of the previous study. In the present study, we hypothesized the phenomenon of response shift in HRQoL might have been caused by some clinical variables (such as antihypertensive treatment strategies, change in systolic and diastolic pressure) which are considered as catalysts in response shift theory [17,18]. Given limited evidence using framework proposed by Oort et al. (as shown in Figure 1(a)), the purpose of the present study was to extend our previous work [22]. To the best of our knowledge, this is the first study to investigate the influence of explanatory and confounding variables on HRQoL among hypertensive CAD patients by taking into account the issues of measurement bias and response shift in measurement.
Methods
Source of Data
The Study of Antihypertensive Drugs and Depressive Symptoms (SADD-Sx) was a substudy of the International Verapamil-SR Trandolapril Study (INVEST). INVEST was a randomized, open-label, blinded end-point study of 22,576 hypertensive patients with CAD aged >50 years conducted from September 1997 to February 2003 [23,24]. The present study is a secondary analysis using data from subjects enrolled in the SADD-Sx [2]. SADD-Sx patients residing in the United States were mailed surveys between April 1, 1999, and October 31, 1999 (N = 2,317). Patients randomized to antihypertensive treatment with either a verapamil SR- or atenolol-based strategy to achieve blood pressure control according to the sixth report of the Joint National Committee on Prevention, Detection, Evaluation, and Treatment of High Blood Pressure (JNC VI) [25] were included in this study. The SF-36 Questionnaire and demographic characteristics such as age, gender and race were included in the SADD-Sx survey. Patients were mailed the baseline survey the day after randomization and the follow-up survey after one year. Each time, patients were mailed a second survey if it was not returned within 10 working days. Patients were mailed a reminder letter approximately 2 weeks before the follow-up survey. 1,578 patients completed the baseline survey with the response rate of 68.11%. Only patients who completed both the baseline and one year follow-up surveys were included (n = 788 (34%)) in this study.
SADD-Sx was conducted according to the principles of the Declaration of Helsinki. The University of Florida Institutional Review Board approved the study protocol.
Variables
SF-36 Questionnaire
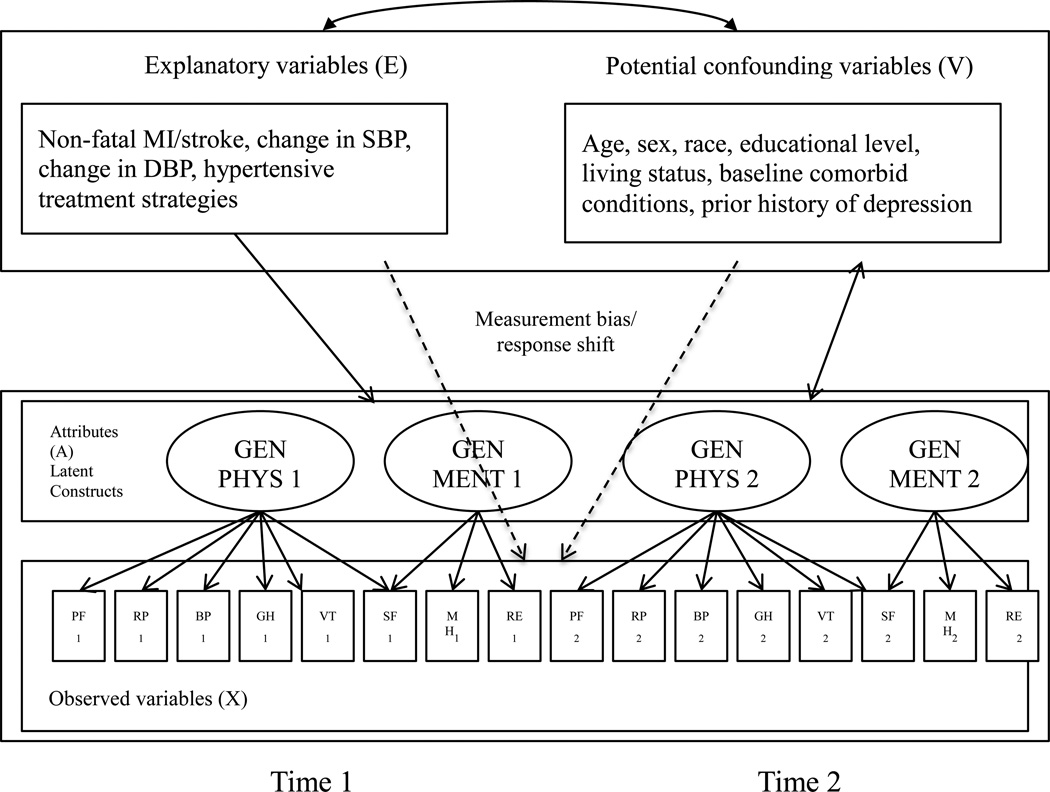
The SF-36 is a generic HRQoL measure that consists of eight scales: physical functioning (PF), role limitations due to physical health problems (role-physical, RP), bodily pain (BP), vitality (VT), general health perceptions (GH), social functioning (SF), role limitations due to emotional problems (role-emotional, RE), and mental health (MH). Raw scores of individual patients were transformed to a range of 0 to 100, with higher scores indicating better HRQoL [26,27]. General physical (Gen PHYS) and general mental (Gen MENT) represent the summary measures for two latent HRQoL factors derived from the literature [19,27] (see lower portion of Figure 2). The baseline (Time 1) and one-year follow-up data (Time 2) for the SF-36 Gen PHYS and Gen MENT latent constructs (denoted by A) and the eight SF-36 scale scores (denoted by X) were implemented in the same analytic model by introducing a correlation for Gen PHYS and another correlation for GEN MENT between the two time points, see Figure 2.
Figure 2.
Graphical representation of the model to identify measurement bias and response shift from a measurement perspective.
MI: myocardial infarction; SBP: systolic blood pressure; DBP: diastolic blood pressure; GenPHYS: general physical functioning latent factor; GenMENT: general mental health latent factor.
Note: Although not shown in the figure, all attributes A are correlated with each other, all explanatory variables E are correlated with each other, and all potential confounding variables V are correlated with each other. The double-headed arrow represents correlations between all E and V variables and correlations between all V variables and A. Dashed arrows represent measurement bias/response shift. Single-headed arrow represents direct effects of E on A. Time 1 and Time 2 indicates the two time points in this study, i.e., baseline and one year.
Explanatory variables (E)
INVEST patients were randomly assigned to either the atenolol-led or the verapamil-SR treatment strategy [24]. Change in systolic blood pressure (SBP) and diastolic blood pressure (DBP) over one year reported by patients assigned to atenolol-led treatment and verapamil-SR strategies were collected at baseline and one-year follow-up and were obtained from INVEST. Because myocardial infarction (MI) and stroke were observed in a small number of respondents, a composite variable was formed. Patients with a stroke or MI were categorized as one group and patients without a stroke and MI within one year of enrollment were categorized as another group.
Potential confounding variables (V)
Patient’s sex, age, race, living status, prior history of depression, and educational level were obtained by survey. Prior history of depression was self-reported based on the diagnosis from physicians or psychiatrists (yes/no). Gender was categorized as females or males. We treated age as a continuous variable instead of a categorical variable to increase the power of detecting any potential changes. Race was categorized as Caucasians or Non-Caucasians. Education was categorized as not completing a high school graduation or completing at least a high school graduation. Patients were also categorized as living alone or living with someone.
Comorbid conditions noted at the time of baseline medical examination was categorized as one group if the condition was present or another if absent. We specifically generated a CAD-specific index score for patients with CAD by removing CAD complications (i.e., myocardial infarction, congestive heart failure, angina, or arrhythmia) from the original Charlson comorbidity index [28,29] because CAD was common to all patients in our study. However, since some of the other disease conditions included in the CAD-specific index were different from the conditions present in our study sample, we assigned the comorbid conditions into the following five disease categories: (1) any neurological disorder including stroke, transient ischemic attack, Parkinson’s disease or Alzheimers disease; (2) cancer; (3) diabetes; (4) renal insufficiency; and (5) peripheral vascular disease. The presence of disease condition was assigned a score and summed to calculate the CAD-specific index score (range: 0 to 14) for each patient.
Statistical Analysis
A two-step procedure [17,19] was applied to investigate response shift, measurement bias and response shift in measurement in the HRQoL data gathered at baseline and after one year.
Step 1: Establishing an Appropriate Measurement Model
Step 1 was used to establish an appropriate measurement model for using the SF-36 in this study. If the measurement model does not fit the data adequately, it will lead to mistakenly identify response shift, measurement bias, and response shift in measurement. Results from confirmatory factor analyses and the literature [27] were used to identify an appropriate measurement model to the variance-covariance matrix of the eight SF-36 scales measured at baseline and at one year follow-up. In this step (Model 1), factor loadings and intercepts were not constrained to be equal over time.
Maximum likelihood estimation (MLE) was used given the slightly non-normal distribution of our data [30]. A variety of fit indices were adopted to assess the appropriateness of the SEM, including the goodness of- fit index χ2 (where a non-significant chi-square indicates good model fit); the standardized root mean square residual (SRMR) with a range between 0.0 and 1.0 where values less than 0.1 indicating an acceptable fit; root mean square error of approximation (RMSEA) with values below 0.08 indicating a good model fit and values below 0.05 indicating a close fit [30]; comparative fit index (CFI), normed fit index (NFI) and non-normed fit index (NNFI) with a range between 0.0 and 1.0 with values greater than 0.95 implying better model fit for all these three criteria [30].
Step 2a: Detecting different types of response shift
In Step 2a1, factor loadings and intercepts of the observed variables (i.e., SF-36 scale scores) related to the latent variables (i.e., Gen PHYS and Gen MENT) were constrained to be equal over one year (i.e., hypothesis of no response shift) (Model 2, Step 2a1). Explanatory variables (causes or predictors) with direct effects on the latent factors (Gen PHYS and Gen MENT) were included in the model. The seven variables, age, sex, race, living status, educational level, prior history of depression, and baseline comorbid conditions, were included in the model as confounding variables. All confounding variables were correlated with each other, explanatory variables and the latent factors, but they were assumed to not directly affect the observed scale scores (Figure 1 (a) andFigure 2). The presence of response shift was first tested through comparing models in Step 1 to Step 2a1. Chi-square difference tests were conducted to evaluate the statistical significance between the free (Step 1) and fully constrained models (Step 2a1). A statistically significant difference in χ2 tests suggests the presence of response shift. Subsequently, the change in parameter estimates between the model with a relaxation on some constrained parameters (Step 2a2) and the full constrained model (Step 2a1) was tested, and modification indices and significant difference in χ2 tests were used to suggest different types of response shift (reconceptualization, reprioritization, and recalibration). In other words, Step 2a2 was nested within Step 2a1 to identify different types of response shift.
The order of releasing parameter constraints on factor pattern, followed by factor loadings and intercepts, and then residuals (i.e., a backward approach) was implemented based on previous studies [22,31]. Parameter invariance was identified by releasing one parameter at a time and constraining all other parameters over time. The equality constraints were released on each factor loading while imposing equality constraints on the remaining factor loading parameters. After inspecting each parameter, a similar process was conducted by releasing equality constraints on intercepts while imposing equality constraints on the remaining intercepts and factor loadings when response shift was not identified.
Reconceptualization response shift is indicated if a change in the matrix pattern containing all factor loadings at Time 1 differs from the matrix pattern at Time 2. Reprioritization response shift has occurred if the factor loading of a specific scale is changed over time. Uniform recalibration response shift is indicated if the intercept of a specific scale is changed over time. Uniform recalibration response shift occurs when patients adjust their perception to all response options in the same direction and to the same extent [14,15]. Identification of different types of response shift was guided by the change in the modification index values and χ2 difference test (χ2 difference of ≥3.84 with df(1) (p<0.05) indicated response shift) [19].
Step 2b: Detecting measurement bias and response shift in measurement
Subsequent to the identification of different types of response shift related to the change in model parameters, measurement bias and response shift in measurement were investigated in Step 2b by taking into account the influence of explanatory (E) and confounding variables (V) on observed (X) scale scores. In the model process, a total of 208 modification indices were calculated. Due to a large number of tests, a Bonferroni-adjusted F-value [32,33] of 13.7 (associated with a probability of 0.05/208) was used to control for Type I error. Prior evidence [19] suggests that modification index values may underestimate χ2 difference test. Therefore, in this study, parameters (influence of explanatory and confounding variables on observed scale scores) associated with a modification index >13.7 were freed, and these parameters only remained freed if the overall model fit indicated by change in chi-square value was >3.84. This process was continued until the largest modification index value was <13.7. Response shift in measurement was identified when the influence of explanatory and confounding variables on observed scale scores were not found to be equal at baseline and at one year follow-up. Given the design of the MIMIC approach, response shift in measurement was essentially captured by the change of intercept parameters over time related to the specific observed variables which is related to recalibration.
LISREL 8.8 [34] was used to construct and test the SEM and SAS 9.1 software [35] was used for the remaining analyses. Based on the RMSEA values of 0.05 and 0.10, the present study had almost 100% statistical power to reject the hypothesis that the model does not fit our data.
Results
Description of the population
The initial SADD-Sx sample consisted of 2,317 INVEST patients assigned to either the verapamil SR-based (n = 1,184) or atenolol-based (n = 1,133) treatment strategy. 788 (34.0%) of the initial patient sample completed the baseline and one year follow-up surveys. Nearly 57% (n = 451) of the final patient sample were male and the majority was Caucasian (82.9%). The mean age of patients at baseline was 66.73 years old (range: 50–88 years old) (Table 1). In the final sample (n = 788), all characteristics of the patients being assigned to two treatment strategies were similar, suggesting that there was no differential dropout between the two intervention groups. A separate analysis comparing the responders (n = 788) and non-responders (n = 1,529) differed only in the variable of race.
Table 1.
Characteristics of SADD-Sx patients returning both baseline and one year SF-36 surveys (n = 788)
| Variable | n (%) |
|---|---|
| Mean age (SD) | 66.73 (9.028) |
| Gender | |
| Male | 451 (57.2%) |
| Female | 337 (42.8%) |
| Race | |
| Caucasian | 653 (82.9%) |
| Non-Caucasian | 135 (17.1%) |
| Education level | |
| High school graduation or higher | 556 (70.6%) |
| No high school graduation | 232 (29.4%) |
| Self-reported prior history of depression | |
| Yes | 140 (17.8%) |
| No | 648 (82.2%) |
| Living status | |
| Alone | 190 (24.1%) |
| With someone | 598 (75.9%) |
| Mean CAD-specific index score (SD) | 1.169 (1.977) |
| Antihypertensive treatment strategies | |
| Verapamil-SR treatment strategy | 411 (47.8%) |
| Atenolol-led treatment strategy | 377 (52.2%) |
| Non-fatal MI/stroke | |
| Yes | 14 (1.8%) |
| No | 774 (98.2%) |
| Mean change in systolic blood pressure (SD) | −12.694 (20.843) |
| Mean change in diastolic blood pressure (SD) | −6.377 (11.744) |
SADD-Sx: Study of Antihypertensive Drugs and Depressive Symptoms
SD: standard deviation
CAD: coronary artery disease
Table 2 gives means scores and standard deviations for all SF-36 scales at baseline and after one year. Conventional t-tests indicated statistically significant improvement in BP, GH, VT, MH and RE from baseline to one year follow-up (p<0.05).
Table 2.
Means, standard deviations, and Pre-Post Cohen’s “d” effect sizes for SF-36 scale scores
| Scale | Before treatment | After treatment | Cohen’s d# | ||
|---|---|---|---|---|---|
| Mean | Standard deviation |
Mean | Standard deviation |
||
| PF | 55.557 | 29.260 | 55.065 | 29.284 | −0.017 |
| RP | 49.228 | 40.780 | 51.840 | 41.250 | 0.064 |
| BP | 63.047 | 29.648 | 66.284 | 31.195 | 0.109** |
| GH | 52.834 | 22.041 | 55.051 | 22.143 | 0.101** |
| VT | 46.937 | 22.736 | 48.617 | 22.052 | 0.074* |
| SF | 70.963 | 24.063 | 72.303 | 23.071 | 0.056 |
| RE | 64.150 | 40.786 | 67.936 | 39.895 | 0.093** |
| MH | 72.475 | 18.744 | 74.132 | 18.920 | 0.088** |
N = 788; # Cohen’s effect size: <0.2, 0.2–0.49, 0.5–0.79, and >0.8 indicate “negligible’, ‘small’, ‘moderate’, and ‘large’ differences
p < 0.05
p < 0.01 in paired t-test.
PF: physical functioning; RP: role physical; BP: bodily pain; GH: general health; VT: vitality; SF: social functioning; RE: role-emotional; MH: mental health.
Identification of response shift, measurement bias and response shift in measurement
Step 1: Establishing an Appropriate Measurement Model
In Model 1, where all parameters were free to be estimated, the model fit indices for two latent factors over time indicated satisfactory results with RMSEA = 0.055, SRMR = 0.035, CFI = 0.991, NFI = 0.987, NNFI = 0.987 (Step 1, Table 3). In Model 1, factor loadings and intercepts were not constrained to be equal over time. The satisfactory model fit allows us to test for different types of response shift and influence of explanatory and confounding variables on the observed scale scores over time (i.e., response shift in measurement) [19].
Table 3.
Goodness of fit of models in measurement bias and response shift in measurement detection procedure (n = 788)
| Step | Model | df | χ2 | RMSEA (90% CI) |
SRMR | CFI | NFI | NNFI |
|---|---|---|---|---|---|---|---|---|
| Step 1: | Model 1: Measured Model |
84 | 287.554 | 0.055 (0.048 – 0.062) |
0.035 | 0.991 | 0.987 | 0.987 |
| Step 2a: Detect types of response shift | ||||||||
| Step 2a1 | Model 2: First model |
237 | 819.008 | 0.054 (0.050 – 0.058) |
0.035 | 0.976 | 0.967 | 0.965 |
| Step 2a2 | Uniform recalibration for PF |
236 | 802.802 | 0.053 (0.049 – 0.058) |
0.034 | 0.977 | 0.968 | 0.966 |
| Step 2b: Detect measurement bias and response shift in measurement | ||||||||
| Step 2b1 | Gender – TPF | 235 | 783.458 | 0.053 (0.049 – 0.057) |
0.034 | 0.978 | 0.969 | 0.967 |
| Step 2b2 | Gender – BPF | 234 | 765.301 | 0.052 (0.048 – 0.056) |
0.033 | 0.978 | 0.969 | 0.968 |
| Step 2b3 | Age – TPF | 233 | 741.998 | 0.051 (0.047 – 0.055) |
0.032 | 0.979 | 0.970 | 0.969 |
| Step 2b4 | Age – BPF | 232 | 713.315 | 0.050 (0.046 – 0.054) |
0.031 | 0.980 | 0.971 | 0.970 |
| Step 2b5 | Age – BRP | 231 | 695.721 | 0.049 (0.045 – 0.054) |
0.030 | 0.981 | 0.972 | 0.971 |
| Step 2b6 | Age – TRP (Final model) |
230 | 674.999 | 0.048 (0.044 – 0.053) |
0.028 | 0.982 | 0.973 | 0.972 |
PF: physical functioning; RP, role limitations because of physical health; BPF: baseline physical functioning; TPF: one year physical functioning; BRP, baseline role limitations because of physical health; TRP, one year role limitations because of physical health.
RMSEA, root mean square error of approximation; SRMR, standardized root mean square residual; CFI, comparative fit index; NFI, normed fit index; NNFI, non-normed fit index
RMSEA <= 0.05 close fit, 0.05 to 0.08 reasonable fit, >= 0.10 poor fit; values closer to 1.0 for NFI, NNFI, and CFI indicate better model fit; SRMR value of 0.0 indicates perfect model fit
Step 2a: Different Types of Response shift
Building upon Step 1, Step 2a includes four explanatory and seven confounding variables. The factor loadings and intercepts were constrained to be equal over time before the inclusion of the explanatory and confounding variables (Model 2, Step 2a1). The χ2 test of exact fit was significant (χ2 (237) = 819.008), RMSEA and other fit indices indicated reasonable fit (RMSEA = 0.054, SRMR = 0.035, CFI = 0.976, NFI = 0.967, NNFI = 0.965, Model 2, Step 2a1, Table 3). The difference in fit between Model 1 (Step 1) and Model 2 (Step 2a1) was found to be statistically significant through the χ2 difference test: χ2 (153) = 531.454, p < 0.001, suggesting that there was presence of response shift. One intercept for the PF scale was not equal across baseline and at follow-up, suggesting the presence of uniform recalibration response shift (see Step 2a2, Table 3 and Table 4). After accounting for uniform recalibration response shift, the fit of the model significantly improved ((χ2 difference test: χ2 (1) = 16.206, p < 0.0001), Step 2a2, Table 3). None of the remaining seven SF-36 scales showed evidence of response shift.
Table 4.
Parameter estimates in the final model (Step 2b6, Table 3) (n = 788)
| Before treatment | After treatment | ||||
|---|---|---|---|---|---|
| GEN PHYS1 | GEN MENT1 |
GEN PHYS2 | GEN MENT2 |
||
| Factor loadings (Ã) | |||||
| PF1 | 0.783 | PF2 | 0.783 | ||
| RP1 | 0.772 | RP2 | 0.772 | ||
| BP1 | 0.678 | BP2 | 0.678 | ||
| GH1 | 0.787 | GH2 | 0.787 | ||
| VT1 | 0.783 | VT2 | 0.783 | ||
| SF1 | 0.388 | 0.433 | SF2 | 0.388 | 0.433 |
| RE1 | 0.729 | RE2 | 0.729 | ||
| MH1 | 0.782 | MH2 | 0.782 | ||
| aIntercepts (ô) | |||||
| PF1 | 58.873 | PF2 | 55.946 | ||
| RP1 | 53.424 | RP2 | 53.424 | ||
| BP1 | 66.864 | BP2 | 66.864 | ||
| GH1 | 55.845 | GH2 | 55.845 | ||
| VT1 | 49.629 | VT2 | 49.629 | ||
| SF1 | 74.344 | SF2 | 74.344 | ||
| RE1 | 71.163 | RE2 | 71.163 | ||
| MH1 | 75.909 | MH2 | 75.909 | ||
| Common factor variances | |||||
| GEN PHYS1 | GEN MENT1 |
GEN PHYS2 | GEN MENT2 |
||
| 1.000 | 1.000 | 1.000 | 1.000 | ||
| Common factor correlations | |||||
| GEN PHYS1 | 1 | ||||
| GEN MENT1 | 0.799 | 1 | |||
| GEN PHYS2 | 0.831 | 0.668 | 1 | ||
| GEN MENT2 | 0.651 | 0.778 | 0.797 | 1 | |
GenPHYS: general physical health latent factor; GenMENT: general mental health latent factor; PF: physical functioning; RP: role limitations because of physical health; BP: bodily pain; SF: social functioning; MH: mental health; RE: role limitations because of emotional problems; VT: vitality; GH: general health.
Notes: (a) Bold values represent uniform recalibration response shift
1 and 2 indicates the two time points in this study, i.e., baseline and one year.
Step 2b: Measurement bias and response shift in measurement
Following discovering different types of response shift, the next step was to investigate the influence of explanatory and confounding variables on HRQoL after accounting for measurement bias and response shift in measurement. Modification index values >13.7 at baseline and/or at follow-up indicated that the fit of the model could be further improved by accounting for measurement bias and/or response shift in measurement. The highest value of modification index >13.7 was first allowed to freely vary followed by the second highest modification index >13.7. These steps were continued until all modification index values were <13.7.
The relationship between gender and PF at one year follow-up was identified with a modification value >13.7, suggesting measurement invariance at one year follow-up. After freely estimating the parameter, the overall model fit indicated by chi-square difference was >3.84, Step 2b1, Table 3. Next, the relationship between gender and PF at baseline was freely estimated based on similar search criteria, Step 2b2, Table 3. The relationship between gender and PF was not consistent at baseline and at one year follow-up (0.095 at baseline and 0.127 at follow-up, results not reported in study), indicating presence of response shift in measurement. The positive effect of gender on PF at both time points indicated that male patients reported better PF than female patients, conditioning on the latent trait of general physical health. We also found that PF was not only indicative of general physical latent factor but also of age, see Steps 2b3 and 2b4, Table 3. The effect of age on PF was negative at both time points (estimated at −0.177 at baseline and −0.197 at follow-up, results not reported in study), indicating that older patients (age range: 50–88 years old) reported worse PF than younger patients, conditioning on the latent trait of general physical health. Finally, we found that the relationship between age and RP was not fully determined by their relationship with the latent trait of general physical health, see Steps 2b5 and 2b6, Table 3. This indicated that RP was not only indicative of the latent trait of general physical health but also of age. These findings were also not consistent over time (estimated at −0.141 at baseline and −0.119 at follow-up, results not reported in study), indicating response shift in measurement. The negative effect of age on RP at both time points suggested that older patients reported worse RP than younger patients conditioning on the latent trait of general physical health. Neither measurement bias nor response shift in measurement was found to be associated with the remaining five confounding variables or four explanatory variables.
After testing for the influence of explanatory and confounding variables on HRQoL and accounting for all instances of response shift in measurement and measurement bias, the final model showed improvement and close fit (χ2 (230) = 674.999, RMSEA = 0.048, SRMR = 0.028, CFI = 0.982, NFI = 0.973, NNFI = 0.972, Step 2b6, Table 3).
Response Shift and True Change Contributions to Change in Observed Variables
The effect size of response shift was −0.100 for the uniform recalibration response shift (Table 5), suggesting response shift had a negligible impact on the estimation of true change in the PF mean scale scores. The effect of response shift and true change were in opposite directions.
Table 5.
Significance tests of response shifts and effect sizes for the observed and true change and in the final model
| Scale | Response shift | Significance test |
Cohen’s “d” effect-sizes# | |||
|---|---|---|---|---|---|---|
| χ2 (df =1) | p value# | Observed change |
Response shift contribution |
True change# contribution |
||
| PF | Uniform recalibration |
16.206 | p < 0.0001 |
−0.017a | −0.100b | 0.083 |
| RP | 0.064 | 0.064 | ||||
| BP | 0.109 | 0.109 | ||||
| GH | 0.101 | 0.101 | ||||
| VT | 0.074 | 0.074 | ||||
| SF | 0.056 | 0.056 | ||||
| RE | 0.093 | 0.093 | ||||
| MH | 0.088 | 0.088 | ||||
á significance level p < 0.05
effect size described as negligible (<0.2), small (0.2–0.49), medium (0.5–0.79), and large (>0.8).
PF: physical functioning; RP: role physical; BP: bodily pain; GH: general health; VT: vitality; SF: social functioning; RE: role-emotional; MH: mental health.
True change is the difference between observed change and response shift contribution.
Based on effect size calculations presented in Table 2
Effect size calculations based on values from Step 2b6, Table 2 and Table 4
Discussion
This study used Oort et al.’s conceptual framework [17] to investigate response shift, measurement bias, response shift in measurement and the influence of explanatory and confounding variables on the observed scale scores. We found that the relationships between age and the PF and RP scales were not consistent over time conditioning on the latent trait of general physical health. The negative effect of age (range: 50–88 years old) on PF and RP at both time points suggests that older patients reported worse PF and RP scores than younger patients given the same level of underlying general physical health. Consistent with our findings that older patients reported worse PF and RP scale scores than younger patients, few studies have reported an inverse relationship between age and SF-36 PF and RP scale scores [36,37]. It is plausible that elderly individuals with a chronic disease or when confronted with a long-term life changing event may transform their internal standards, values or priorities to judge their HRQoL [14,15,38,39]. The present study extends prior evidence by examining the influence of explanatory and confounding variables on observed scale scores after accounting for measurement bias and response shift in measurement. This emerging finding suggests that patients reporting worsened PF and RP scores can be explained by individuals undergoing the process of recalibration response shift over time.
We also found that patients recalibrated their perception of PF over a one year period, which was attributed to gender. This was evident by the fact that the relationship between PF and gender does exist and was not consistent over time event conditioning on the latent trait of general physical health. Male patients reported better PF than female patients, even if their health measured by the general physical latent factor was comparable at both baseline and one year follow-up. Our findings substantiate the association between gender and PF scale found in past research [36,37,40–42]. These findings support the notion of stereotypes that men are more physically oriented than females and may over-report their PF to maintain their perceptions of their masculinity and to protect their egos by reducing gender role conflict [41,42]. In this regard, assuming that other SF-36 scale scores remain similar, females’ lower PF ratings could lead to an over-evaluation of difference in utility between males and females. In turn, this could increase the cost-effectiveness of treatments and potentially direct health resources away from those who reported higher PF ratings but had poor health (i.e., male patients) [43].
HRQoL is considered as one of the important end points in randomized clinical trials for treatment regimens [44]. The effect size approach can better express how important a change is with respect to the typical variation found in the population under study. Patients’ PF revealed a non-significant decline one year after allocation to treatment strategies. Consistent with our previous findings [22], the present study found that estimated HRQoL decline may have been underestimated due to presence of recalibration response shift, leading to false negative findings. Assessment of self-reported instruments should account for an individual’s change in perception over time on important HRQoL concepts due to change in health and/or allocation to interventions, especially in clinical trials.
There is limited evidence available investigating the influence of specific explanatory and confounding variables on response shift of HRQoL ratings. Response shift research should be investigated other methodologies and fields of research, such as qualitative methodologies and cognitive interviewing [45], especially when examining the influence and mechanisms of several variables on HRQoL after controlling for response shift. In the situation where response shift is suspected and design methods are not feasible to assess response shift, appropriate statistical methods should continue to be useful. Future studies are encouraged to use other analytical approaches to detect response shift and confirm the findings derived from this present study. Identifying response shift has implications for interpreting the measurement of HRQoL change in clinical and research endeavors, and may provide considerable value to the evaluation of cost-effectiveness analysis, and potentially contribute to a more informed resource allocation strategy.
Limitations of this study should be noted when interpreting and applying these findings. In the absence of changes in health status [46], a one year period may not necessarily lead to a change in HRQoL and identify changes in internal standards, values, and conceptualization. Our approach to investigate response shift in measurement was based on the change in the parameter of intercept (i.e., related to recalibration). Future studies should investigate response shift in measurement based on change in other parameters related to reconceptualization and reprioritization. The study sample constitutes only one third (34%) of the total number of participants which limits the generalizability of the results. The patients randomly assigned to two treatment strategies at baseline demonstrated comparability across explanatory and confounding variables and no difference in dropouts. In other words, there was no systematic bias found with respect to selection or participants’ dropout in this study. As described in the Methods section, race is the only variable differentiated between responders and non-responders. However, race was not found to influence HRQoL after accounting for measurement bias and response shift in measurement in this study. Other factors not controlled for in this study may lead to systematic differences between responders and non-responders, thereby limiting the ability to extrapolate the findings from this study. Barclay-Goddard et al. suggest that not all individuals would experience response shift, even those who do may not experience it at the same time [31,45]. It is plausible that participants not included in this study may have experienced response shift to greater or lesser extent, in a different way or not at all. Future studies should investigate occurrence of response shift at different time points (e.g., at three months, six months) in a similar population to encourage application of specific interventions aimed to promote the process of response shift. On the other hand, it is plausible that a one-year time period probably is too short to detect clinically significant response shift.
Conclusion
Older patients reported worse scores for both PF and RP compared to younger patients and males reported better PF than females after conditioning on the latent trait of general physical health. It is important to investigate how different patient groups may undergo a shift in their HRQoL perception due to health status change or allocation to treatment strategies, especially in clinical trials. Assessment of response shift with further understanding of how patients perceive their HRQoL over time is warranted, especially in clinical trials.
Expert Commentary
Self-report measures of HRQoL are regarded as an important end point of interventions in randomized trials. Individuals experiencing improvement or deterioration in health status over time may result in changes in standard, value, and conceptualization of HRQoL (i.e., response shift). The use of structural equation modeling procedure to identify response shift has been proposed by several researchers. The identification of response shift in HRQoL measurements over time is important, especially in randomized clinical trials.
Five-Year View
Current evidence has shown the use of various statistical approaches to detect response shift in the context of HRQoL research [46]. The presence of a change in health status can trigger the lead to changes in standards, values, and conceptualization, known as response shift. Over the past decade, notable emphasis has relied on the use of secondary data sets and standard statistical or SEM methods to investigate the response shift issues. Limited evidence is available with the use of advanced SEM methods to assess the explanatory and confounding variables associated with response shift [19]. A recent study has highlighted challenges inherent to the use of secondary data sets for identification of response shift in HRQoL research [46]. Response shift research should be also conducted using other methodologies, such as qualitative methodologies and cognitive interviewing [45] to better understand how and why different variables contributing to response shift in HRQoL rating. The influence of response shift in the evaluation of cost-effectiveness analysis and health-care decision making process should also be investigated in future studies. The authors hope that future research will continue to follow appropriate guidelines and methodology to conduct response shift research in the context of HRQoL using primary and secondary data sets.
Key Issues.
-
-
Hypertensive medications from different pharmacologic classes sometimes have varying side effect profiles and impact patients’ HRQoL in different ways.
-
-
Response shift is defined as the change in the meaning of one’s perception of a target construct due to changes in standard, value, and conceptualization.
-
-
Older patients reported worse scores for both physical functioning and role limitations due to physical health problems at baseline and one year later than younger patients.
-
-
Males reported better physical functioning at baseline and one year later than females.
Our findings suggest that HRQoL estimates might have been underestimated if measurement issues are not taken into account.
Contributor Information
Pranav K. Gandhi, Assistant Professor, South College, 400 Goodys Lane, Knoxville, TN 37922, Phone: 8652885855, Fax: 8652885902, pgandhi@southcollegetn.edu.
L Douglas Ried, Senior Associate Dean for Academic Affairs, California Northstate University College of Pharmacy, 10811 International Drive, Rancho Cordova, CA 95670, Telephone: (916) 503-1902, Fax: (916) 631-8127, dried@cnsu.edu.
Carole L. Kimberlin, Professor, University of Florida College of Pharmacy, Department of Pharmaceutical Outcomes and Policy, P O Box 100496, HPNP Room 3324, Gainesville, FL 32610, Phone: 3522736263, kimber@cop.ufl.edu.
Teresa L. Kauf, Director, Health Economics and Outcomes Research, Cubist Pharmaceuticals, 65 Hayden Avenue, Lexington, MA 02421, Phone: 7818608660, teresa.kauf@cubist.com.
I-Chan Huang, Associate Professor, University of Florida, Department of Health Outcomes and Policy, 1329 SW 16th street, Room 5231, Gainesville, FL 32610, Phone: 3522652514, ichuang@ufl.edu.
References
- 1.Ried LD, Tueth MJ, Taylor MD, Sauer BC, Lopez LM, Pepine CJ. Depressive symptoms in coronary artery disease patients after hypertensive treatment. Ann Pharmacother. 2006;40:597–604. doi: 10.1345/aph.1G438. [DOI] [PubMed] [Google Scholar]
- 2.Chobanian AV, Bakris GL, Black HR, Cushman WC, Green LA, Izzo JL, Jr for the National Heart, Lung, and Blood Institute Joint National Committee on Prevention, Detection, Evaluation, and Treatment of High Blood Pressure; National High Blood Pressure Education Program Coordinating Committee. The seventh report of the Joint National Committee on Prevention, Detection, Evaluation, and Treatment of High Blood Pressure: the JNC 7 report. JAMA. 003;289:2560–2572. doi: 10.1001/jama.289.19.2560. [DOI] [PubMed] [Google Scholar]
- 3.Ried LD, Tueth MJ, Handberg E, Kupfer S, Pepine CJ and the INVEST study group. A Study of Antihypertensive Drugs and Depressive Symptoms (SADD-Sx) in Patients Treated With a Calcium Antagonist Versus an Atenolol Hypertension Treatment Strategy in the International Verapamil SR-Trandolapril Study (INVEST) Psychosom Med. 2005;67:398–406. doi: 10.1097/01.psy.0000160468.69451.7f. [DOI] [PubMed] [Google Scholar]
- 4.Khawaja IS, Westermeyer JJ, Gajwani P, Feinstein RE. Depression and coronary artery disease: The associations, mechanisms, and therapeutic implications. Psychiatry (Edgmont) 2009;6(1):38–51. [PMC free article] [PubMed] [Google Scholar]
- 5.Hance M, Carney RM, Freedland KE, et al. Depression in patients with coronary artery disease: a 12-month follow up. Gen Hosp Psychiatry. 1996;18:61–65. doi: 10.1016/0163-8343(95)00100-x. [DOI] [PubMed] [Google Scholar]
- 6.Ried LD, McFarland BH, Johnson RE, Brody KK. Betablockers and depression: the more the murkier? Ann Pharmacother. 1998;32:699–708. doi: 10.1345/aph.17185. [DOI] [PubMed] [Google Scholar]
- 7.Ko DT, Hebert PR, Coffey CS, Sedrakyan A, Curtis JP, Krumholz HM. Beta-blocker therapy and symptoms of depression, fatigue, and sexual dysfunction. JAMA. 2002;288:351–357. doi: 10.1001/jama.288.3.351. [DOI] [PubMed] [Google Scholar]
- 8.Lacy CF, Armstrong LL, Goldman MP, Lance LL. Drug Information Handbook. 8th ed. Hudson: OH: pp. 2000–2001. [Google Scholar]
- 9.Avorn J, Everitt DE, Weiss S. Increased antidepressant use in patients prescribed beta-blockers. JAMA. 1986;255:357–360. [PubMed] [Google Scholar]
- 10.Thiessen BQ, Wallace SM, Blackburn JL, Wilson TW, Bergman U. Increased prescribing of antidepressants subsequent to beta-blocker therapy. Arch Intern Med. 1990;150:2286–2290. [PubMed] [Google Scholar]
- 11.Bright RA, Everitt DE. Beta-blockers, depression Evidence against an association. JAMA. 1992;267:1783–1787. doi: 10.1001/jama.267.13.1783. [DOI] [PubMed] [Google Scholar]
- 12.Gerstman BB, Jolson HM, Bauer M, Cho P, Livingston JM, Platt R. The incidence of depression in new users of beta-blockers and selected antihypertensives. J Clin Epidemiol. 1996;49:809–815. doi: 10.1016/0895-4356(96)00017-0. [DOI] [PubMed] [Google Scholar]
- 13.Lindberg G, Bingefors K, Ranstam J, Rastam L, Melander A. Use of calcium channel blockers and risk of suicide: ecological findings confirmed in population based cohort study. Br Med J. 1998;316:741–745. doi: 10.1136/bmj.316.7133.741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ahmed S, Mayo N, Wood-Dauphinee S, Hanley J, Cohen S. The structural equation modeling technique did not show a response shift, contrary to the results of the then test and the Individualized approaches. J Clin Epidemiol. 2005;58:1125–1133. doi: 10.1016/j.jclinepi.2005.03.003. [DOI] [PubMed] [Google Scholar]
- 15. Sprangers MA, Schwartz CE. Integrating Response Shift into Health-Related Quality of Life Research: A Theoretical Model. Soc Sci Med. 1999;48:1507–1515. doi: 10.1016/s0277-9536(99)00045-3.This was one of the first studies to explain the concept of response shift in context of health-related quality of life research.
- 16.Schwartz CE, Sprangers MA. Methodological Approaches for Assessing Response Shift in Longitudinal Health-Related Quality of Life Research. Soc Sci Med. 1999;48:1531–1548. doi: 10.1016/s0277-9536(99)00047-7. [DOI] [PubMed] [Google Scholar]
- 17. Oort FJ, Visser MRM, Sprangers MAG. Formal definitions of measurement bias and explanation bias clarify measurement and conceptual perspectives on response shift. J Clin Epidemiol. 2009;62:1126–1137. doi: 10.1016/j.jclinepi.2009.03.013.This study explains and introduces the theoretical concepts of measurement bias, explanation bias and response shift in measurement in health-related quality of life research. The authors suggest that response shift can be associated at the measurement level, in that knowing someone’s underlying HRQoL still doesn’t help to predict their response on an item because their response not only is a function of HRQoL, but also a function of time (measurement bias). Explanation bias is more conceptual, in that you might think that age should only influence HRQoL because of its relationship with say health, if this is not true, than explanation bias has been found.
- 18.Rapkin BD, Schwartz CE. Toward a theoretical of quality-of-life appraisal: Implications of findings from studies of response shift. Health Qual Life Outcomes. 2004;2:14. doi: 10.1186/1477-7525-2-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. King-Kallimanis BL, Oort FJ, Visser MRM, Sprangers MAG. Structural equation modeling of health-related quality-of-life data illustrates the measurement and conceptual perspectives on response shift. J Clin Epidemiol. 2009;62:1157–1164. doi: 10.1016/j.jclinepi.2009.04.004.This is the only study to empirically test for different perspectives of response shift (i.e., measurement bias and explanation bias) in health-related quality of life research after controlling for specific variables of interest in cancer patients.
- 20.Muthén BO. Some uses of structural equation modeling in validity studies: extending IRT to external variables. In: Wainer H, Braun HI, editors. Test Validity. Hillsdale, NJ: Lawrence Erlbaum Associates; 1988. pp. 213–338. [Google Scholar]
- 21.Yu YF, Yu AP, Ahn J. Investigating differential item functioning by chronic diseases in the SF-36 health survey: a latent trait analysis using MIMIC models. Med Care. 2007;45(9):851–859. doi: 10.1097/MLR.0b013e318074ce4c. [DOI] [PubMed] [Google Scholar]
- 22. Gandhi PK, Ried LD, Huang IC, Kimberlin CL, Kauf TL. Assessment of response shift using two structural equation modeling techniques. Qual Life Res. 2012;22(3):461–471. doi: 10.1007/s11136-012-0171-1.This study is our previous work that identified response shift in the same sample as used in this study. We identified response shift using two different structural equation modeling (SEM) procedures where we found presence of recalibration response shift using both SEM procedures. However, our previous work did not account for the influence of explanatory and confounding variables on HRQoL after controlling for response shift.
- 23.Pepine CJ, Handberg-Thurmond E, Marks RG, Conlon M, Cooper-DeHoff R, et al. Rationale and design of the International Verapamil SR/Trandolapril Study (INVEST): an Internet-based randomized trial in coronary artery disease patients with hypertension. J Am Coll Cardiol. 1998;32:1228–1237. doi: 10.1016/s0735-1097(98)00423-9. [DOI] [PubMed] [Google Scholar]
- 24.Pepine CJ, Handberg EM, Cooper-DeHoff RM, Marks RG, Kowey P, Messerli FH, et al. A calcium antagonist vs a non-calcium antagonist hypertension treatment strategy for patients with coronary artery disease. The International Verapamil-Trandolapril Study (INVEST): a Randomized Controlled Trial. JAMA. 2003;290:2805–2816. doi: 10.1001/jama.290.21.2805. [DOI] [PubMed] [Google Scholar]
- 25.Joint National Committee on Prevention Detection Evaluation and Treatment of High Blood Pressure. The sixth report of the Joint National Committee on prevention, detection, evaluation, and treatment of high blood pressure. Arch Intern Med. 1997;157:2413–2446. doi: 10.1001/archinte.157.21.2413. [DOI] [PubMed] [Google Scholar]
- 26.Saris-Baglama RN, Dewey CJ, Chisholm GB, Kosinski M, Bjorner JB, Ware JE. SF-36 Health Outcomes Scoring Software. 2004:1–157. [Google Scholar]
- 27.Ware JE, Snow KK, Kosinski M, Gandek B. SF-36 Health Survey: Manual and Interpretation Guide. Boston, MA: The Health Institute, New England Medical Center; 1993. [Google Scholar]
- 28.Sachdev M, Sun JL, Tsiatis AA, Nelson CL, Mark DB, Jollis JG. The prognostic importance of comorbidity for mortality in patients with stable coronary artery disease. J Am Coll Cardiol. 2004;l43:576–582. doi: 10.1016/j.jacc.2003.10.031. [DOI] [PubMed] [Google Scholar]
- 29.Chirinos JA, Veerani A, Zambrano JP, Schob A, Perez G, Mendez AJ, et al. Evaluation of comorbidity scores to predict all-cause mortality in patients with established coronary artery disease. Int J Cardiol. 2007;117:97–102. doi: 10.1016/j.ijcard.2006.06.005. [DOI] [PubMed] [Google Scholar]
- 30.Brown TA. Confirmatory factor analysis for applied research. Guilford Press. New York: London: Guilford Press; 2006. [Google Scholar]
- 31.Barclay-Goddard R, Lix LM, Tate R, Weinberg L, Mayo NE. Response shift was identified over multiple occasions with a structural equation modeling framework. J Clin Epidemiol. 2009;62:1181–1188. doi: 10.1016/j.jclinepi.2009.03.014. [DOI] [PubMed] [Google Scholar]
- 32.MacCallum RC, Browne MW, Sugawara HM. Power analysis and determination of sample size for covariance structure modeling. Psychol Methods. 1996;1(2):130–149. [Google Scholar]
- 33.Hochberg Y, Benjamini Y. More Powerful Procedures for Multiple Significance Testing. Stat Med. 1990;9:811–818. doi: 10.1002/sim.4780090710. [DOI] [PubMed] [Google Scholar]
- 34.Jöreskog K, Sörbom D. LISREL 8. Lincolnwood, Il: Scientific Software Internatonal Inc; 1993. [Google Scholar]
- 35.SAS Institute. SAS users guide, version 9.1. Cary, NC: SAS institute, Inc; 2004. [Google Scholar]
- 36.de Graff JC, Ubbink DTh, Kools EJC, Chamuleau SAJ, Jacobs MJHM. The impact of peripheral and coronary artery disease on health-related quality of life. Ann Vasc Surg. 2002;16:495–500. doi: 10.1007/s10016-001-0121-9. [DOI] [PubMed] [Google Scholar]
- 37.Sevinc S, Akyol AD. Cardiac risk factors and quality of life in patients with coronary artery disease. J Clin Nurs. 2010;19:1315–1325. doi: 10.1111/j.1365-2702.2010.03220.x. [DOI] [PubMed] [Google Scholar]
- 38.Goodwin JS, Black SA, Satish S. Aging versus disease: The opinions of older black, Hispanic, and non-Hispanic white Americans about the causes and treatment of common medical conditions. J Am Geriatr Soc. 1999;47:973–979. doi: 10.1111/j.1532-5415.1999.tb01293.x. [DOI] [PubMed] [Google Scholar]
- 39.Levy BR, Slade MD, Kunkel SR, Kasl SV. Longevity increased by positive self perceptions of aging. J Pers Soc Psychol. 2002;83:261–270. doi: 10.1037//0022-3514.83.2.261. [DOI] [PubMed] [Google Scholar]
- 40.Norris CM, Ghali WA, Galbraith PD, Graham MM, Jensen LA, Knudtson ML for the APPROACH investigators. Women with coronary artery disease report worse health-related quality of life outcomes compared to men. Health Qual Life Outcomes. 2004;2:21. doi: 10.1186/1477-7525-2-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Macintyre S, Ford G, Hunt K. Do women “over-report” morbidity? Men’s and women’s responses to structured prompting on a standard question on long standing illness. Soc Sci Med. 1999;48:89–98. doi: 10.1016/s0277-9536(98)00292-5. [DOI] [PubMed] [Google Scholar]
- 42.McCreary DR, Newcomb MD, Sadava SW. Dimensions of the male gender role: A confirmatory analysis in men and women. Sex Roles. 1998;39:81–95. [Google Scholar]
- 43.Lenert LA, Treadwell JR, Schwartz CE. Associations between health status and utilities implications for policy. Med Care. 1999;37:479–489. doi: 10.1097/00005650-199905000-00007. [DOI] [PubMed] [Google Scholar]
- 44.Goodwin PJ, Black JT, Bordeleau LJ, Ganz PA. Health-related quality of life measurement in randomized clinical trials in breast cancer - taking stock. J Natl Cancer Inst. 2003;95(4):263–281. doi: 10.1093/jnci/95.4.263. [DOI] [PubMed] [Google Scholar]
- 45.Barclay-Goddard R, Epstein JD, Mayo NE. Response shift: a brief overview and proposed research priorities. Qual Life Res. 2009;18:335–346. doi: 10.1007/s11136-009-9450-x. [DOI] [PubMed] [Google Scholar]
- 46.Schwartz CE, Ahmed A, Sawatzky R, Sajobi T, Mayo N, Finkelstein J, et al. Guidelines for secondary analysis in search of response shift. Qual Life Res. 2013 doi: 10.1007/s11136-013-0402-0. [Epub ahead of print] [DOI] [PubMed] [Google Scholar]