Assessment of a University of California, Los Angeles 4‐Variable Risk Score for Advanced Heart Failure

Abstract

Background

The 4‐variable risk score from University of California, Los Angeles (UCLA) demonstrated superior discrimination in advanced heart failure, compared to established risk scores. However, the model has not been externally validated, and its suitability as a selection tool for heart transplantation (HT) and left ventricular assist device (LVAD) is unknown.

Methods and Results

We calculated the UCLA risk score (based on B‐type natriuretic peptide, peak VO₂, New York Heart Association class, and use of angiotensin‐converting enzyme inhibitor or angiotensin receptor blocker) in 180 patients referred for HT. The outcome was survival free from urgent transplantation or LVAD. The model‐predicted survival was compared to Kaplan‐Meier's estimated survival at 1, 2, and 3 years. Model discrimination and calibration were assessed. During a mean follow‐up of 2.1 years, 37 (21%) events occurred. One‐, 2‐ and 3‐year observed event‐free survival was 88%, 81%, and 75%, and the observed/predicted ratio was 0.97, 0.96, and 0.97, respectively. Time‐dependent receiver operating characteristic curve analyses demonstrated good discrimination overall (1‐year area under curve, 0.801; 2‐year, 0.774; 3‐year, 0.837), but discrimination between the 2 highest risk groups was poor. The difference between observed and predicted survival ranged from −14 to +17 percentage points, suggesting poor model calibration. Fairly similar results were found when the analyses were repeated in 715 patients after multivariate imputation of missing data.

Conclusions

The UCLA 4‐variable risk model calibration was inconsistent and high‐risk discrimination was poor in an external validation cohort. Further model assessment is warranted before widespread use.

Introduction

Objective risk assessment is critical in allocating scarce or expensive resources, such as heart transplantation (HT) or left ventricular assist devices (LVADs). Standard selection tools include the peak VO₂, the Heart Failure Survival Score (HFSS), and the Seattle Heart Failure Model (SHFM). Recently, a 4‐variable risk prediction model for patients with advanced heart failure (HF) was reported from University of California, Los Angeles (UCLA).¹ Model discrimination (distinction between risk strata) was better than for the HFSS and the SHFM. The investigators performed internal validation by splitting their data set into 2 subsets (a derivation cohort and a validation cohort) and further by reporting the bootstrap‐adjusted performance. However, the performance of a risk prediction model cannot be assessed by internal validation alone. It is essential to evaluate the performance in a different and independent patient population, known as external validation.² Furthermore, for clinical utility, a model must also have good calibration (similar observed vs. predicted risk) for all risk strata. Therefore, we performed external validation of discrimination and assessed calibration of the UCLA model in patients with severe HF referred for HT.

Methods

The local human investigations committee approved chart review. Individual patient consent was not required. From a population of 715 consecutive HF patients referred to the Columbia University Medical Center for HT evaluation, 180 patients with complete information regarding all 4‐variable UCLA risk score variables were included. The risk score was derived in each patient from the 4 variables: B‐type natriuretic peptide (BNP), peak oxygen consumption (pVO₂), New York Heart Association (NYHA) class, and use of angiotensin‐converting enzyme inhibitor (ACEI)/angiotensin receptor blocker (ARB). We also categorized the patients into the same 4 risk groups based on the risk score as described in the UCLA publication.¹ In a supplementary analysis, we calculated the 4‐variable risk score in the total population of 715 patients, enabled by a multivariable missing data imputation strategy. Outcome events were defined as death, urgent transplantation (United Network of Organ Sharing [UNOS] Status 1), or LVAD implantation. Patients who were transplanted as nonurgent (UNOS Status 2) were censored alive on the date of transplant. Vital status of patients lost to clinical follow‐up was assessed using the Social Security Death Index.

Statistical Methods

Kaplan‐Meier's method was used to calculate observed survival and 95% confidence intervals (95% CIs). For overall discrimination, we used Cox's model, with the calculated risk score as the only independent variable, and calculated the C index. Discrimination was also assessed by plotting the cumulative survival over 3 years for patients classified in 4 risk groups as in the original model derivation.¹ Time‐dependent receiver operating characteristic (ROC) curves were computed by using the risk score and the 1‐, 2‐, and 3‐year Kaplan‐Meier estimated survival, and the area under the curve (AUC) was calculated. For overall calibration, we calculated the ratio of observed/risk model‐predicted survival at 1, 2, and 3 years, according to the equation from the UCLA publication.¹

In the supplementary analysis, including 715 patients, data were missing regarding BNP (74%), pVO₂ (0.1%), NYHA (0.2%), and ACEI/ARB (2%). We used multiple imputation by chained equations to impute missing values.³ Multiple imputation by chained equations is a flexible, efficient technique for handling missing data, even in large data sets. The imputation procedure consists of a series of regression models (chained equations) where each variable with missing data is modeled conditional upon the other variables in the data. This means that each variable can be modeled according to its own distribution. Twenty‐four clinical variables, the event indicator, and the Nelson‐Aalen estimator of the cumulative baseline hazard were included in the imputation model. We generated and combined estimates from 50 multiply imputed data sets.

Data management and statistical analyses were performed using Stata 13.1 (StataCorp LP, College Station, TX) and R 3.0.2 (R Foundation for Statistical Computing, Vienna, Austria).

Results

Clinical characteristics of the study population are shown in the 1. Overall, baseline characteristics in our study population were similar to the original UCLA cohort. During a mean follow‐up of 2.1 years, 37 (21%) events occurred. Overall, event‐free survival (EFS) was 88% at 1 year, 81% at 2 years, and 75% at 3 years. In Kaplan‐Meier's EFS analysis, there was lack of discrimination between the 2 highest risk groups (P=0.692) (Figure 1). Cox's model, with the risk score as a continuous independent variable, had better discrimination (C‐index, 0.781), compared to the risk group Cox model (C‐index, 0.757). The time‐dependent ROC curve analyses demonstrated good overall discrimination; AUCs at 1, 2, and 3 years, by continuous risk score: 0.801 (95% CI, 0.722 to 0.891), 0.774 (95% CI, 0.691 to 0.857), and 0.837 (95% CI, 0.751 to 0.922), respectively; by risk groups: 0.776 (95% CI, 0.676 to 0.876), 0.748 (95% CI, 0.658 to 0.837), and 0.798 (95% CI, 0.709 to 0.887), respectively. The overall observed/predicted ratios were 0.97, 0.96, and 0.97, respectively. The observed and predicted EFS in the 4 risk groups are shown in Figure 2. The difference between observed and predicted survival ranged from −14 to +17 percentage points.

Table 1.

Baseline Characteristics in 180 Patients With Advanced Heart Failure Referred for Heart Transplantation

Characteristic	All Patients (n=180)	Patients Without Events (n=143)	Patients With Events (n=37)
Clinical
Age, y	52.7 (13.3)	52.2 (13.1)	54.4 (14.3)
Females, n	47 (26%)	35 (24%)	12 (32%)
NYHA class	2.7 (0.8)	2.6 (0.8)	3.3 (0.7)
Weight, kg	88 (21)	90 (20)	80 (21)
Resting sBP, mm Hg	112 (19)	114 (18)	101 (17)
Peak VO2, mL/min per kg	13.1 (4.81)	13.7 (4.89)	10.9 (3.76)
LVEF, %	21 (7.7)	22 (7.7)	18 (6.6)
Ischemic etiology	59 (33%)	45 (31%)	14 (38%)
Medications
ACEI	136 (76%)	109 (76%)	27 (73%)
Beta‐blockers	157 (87%)	122 (85%)	35 (95%)
Aldosterone blockers	72 (40%)	48 (34%)	24 (65%)
Statins	75 (42%)	62 (43%)	13 (35%)
Allopurinol	9 (5%)	9 (6%)	0
ARB	10 (6%)	10 (7%)	0
Loop diuretic equivalent, mg/kg	0.84 (0.95)	0.75 (0.81)	1.2 (1.3)
Laboratory data
Hemoglobin, g/dL	13.7 (1.7)	14.0 (1.6)	12.7 (1.7)
Lymphocytes percentages	26 (9.5)	27 (9.3)	22 (9.6)
Total cholesterol, mg/dL	183 (53)	188 (52)	162 (52)
Uric acid, mg/dL	7.7 (2.5)	7.6 (2.3)	8.1 (2.9)
Sodium, mEq/L	137 (3.2)	138 (2.8)	135 (3.6)
Device
CRT	7 (4%)	5 (4%)	2 (5%)
ICD	66 (37%)	47 (33%)	19 (51%)
CRT‐D	52 (29%)	40 (28%)	12 (32%)

Data are presented as mean (standard deviation) for continuous variables or n (%) for categorical variables. ACEI indicates angiotensin‐converting enzyme inhibitors; ARB, angiotensin receptor blockers; LVEF, left ventricular ejection fraction; NYHA, New York Heart Association; sBP, systolic blood pressure; VO₂, oxygen uptake; CRT, cardiac resynchronization therapy; ICD, implantable cardioverter defibrillator; CRT‐D, CRT+ICD.

Figure 1.

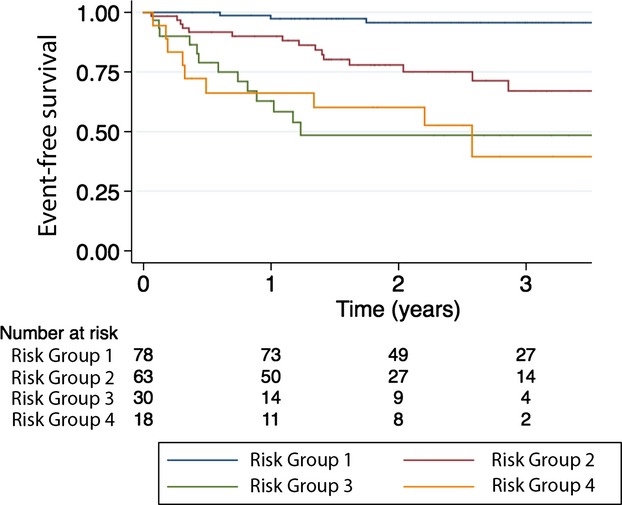
Kaplan‐Meier's estimated event‐free survival in 180 patients with advanced heart failure referred for heart transplantation assigned into 4 risk groups based on the UCLA risk model.

Figure 2.

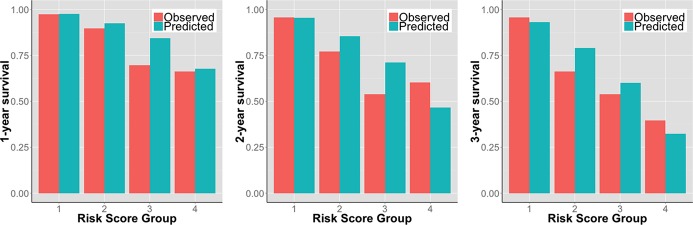
Observed versus the UCLA risk model‐predicted event‐free survival at 1, 2, and 3 years in 180 patients with advanced heart failure referred for heart transplantation assigned into 4 risk groups based on the UCLA risk score.

Supplementary Analyses in 715 Patients After Multivariate Imputation of Missing Data

Clinical characteristics of the total study population (n=715) have been reported in previous assessments of the HFSS and SHFM.⁴ During a mean follow‐up of 2.6 years, 354 (49.5%) events occurred. One‐, 2‐, and 3‐year observed EFS was 79%, 66%, and 55%, respectively. There was lack of discrimination between the 2 highest risk groups (P=0.695) (Figure 3). Cox's model, with the risk score as a continuous independent variable, had better discrimination (C‐index, 0.740), compared to the risk group Cox model (C‐index, 0.719). Overall discrimination was good; AUCs at 1, 2, and 3 years, by continuous risk score: 0.784 (95% CI, 0.746 to 0.821), 0.782 (95% CI, 0.745 to 0.819), and 0.808 (95% CI, 0.770 to 0.846), respectively; by risk groups: 0.753 (95% CI, 0.713 to 0.792), 0.758 (95% CI, 0.721 to 0.795), and 0.772 (95% CI, 0.733 to 0.810), respectively. The overall observed/predicted ratio was 0.87, 0.79, and 0.73, at 1, 2, and 3 years, respectively (Figure 4). Except for the lowest risk group, there were large differences between observed and predicted survival. The difference ranged from 1 to 34 absolute percentage points, depending on risk strata and time of follow‐up, and there was a consistent overestimation of EFS and thus underestimation of risk.

Figure 3.

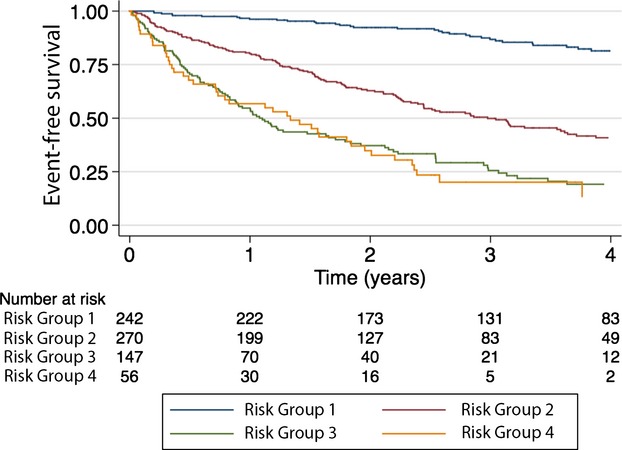
Kaplan‐Meier's estimated event‐free survival in 715 patients with advanced heart failure referred for heart transplantation assigned into 4 risk groups based on the UCLA risk model. UCLA indicates University of California, Los Angeles.

Figure 4.

Observed versus UCLA risk model‐predicted event‐free survival at 1, 2, and 3 years in 715 patients with advanced heart failure referred for heart transplantation assigned into 4 risk groups based on the UCLA risk score.

Discussion

Accurate risk assessment in severe HF is critical for proper selection for HT or LVAD. The peak VO₂ is a strong single variable,⁵ but is outperformed by the HFSS⁵ and SHFM.⁴ These have been extensively validated for risk assessment and HT selection in different populations.⁴ However, the HFSS and SHFM are cumbersome and inadequately used in practice. The new simple 4‐variable risk model from UCLA is promising in its simplicity and greater likelihood of widespread use. We assessed its performance by external validation in patients referred for HT. We found that the UCLA model had good discrimination overall, but was seriously limited by the inability to separate (discriminate between) patients in the highest risk groups into different risk strata. Furthermore, calibration (ie, the similarity between observed and predicted risk) was unsatisfactory, with a difference between predicted and observed EFS of up to 17 absolute percentage points. Additionally, calibration deteriorated and we found a consistent underestimation of risk in the supplementary analyses, which included 715 patients. This underestimation of risk, particularly in the highest risk groups, has been observed also for the SHFM,⁶ suggesting that the most ill patients have risk in addition to what is captured by the known and standard risk markers included in these models.

The performance of the HFSS and SHFM has previously been evaluated by our group^4–5 in the same study cohort that was used in the current external validation of the UCLA 4‐variable risk model. The ROC curve analyses for 1‐year EFS were 0.72 and 0.73 for HFSS and SHFM, respectively, compared to 0.78 for the UCLA 4‐variable risk model. Similarly, the ROC curve analyses for 2‐year EFS were 0.70 and 0.74 for HFSS and SHFM, respectively, compared to 0.78 for the UCLA 4‐variable risk model. These results suggest potentially a better overall discrimination for the UCLA 4‐variable risk model in this study population. However, with regard to calibration, the SHFM has been suggested to perform poorly, with overestimation of EFS in transplant referred patients.^6–8 Likewise, in the current work, the UCLA 4‐variable risk model also underestimated risk. We did not proceed with further comparisons of the performance between the UCLA risk model and, for example, the SHFM or HFSS. Such comparisons could be performed by using reclassification measures (Net Reclassification Improvement/Index and Integrated Discrimination Improvement).^9–10 However, these methods may not be appropriate if there is suspicion of poor model calibration^11–12; they are not suitable for time‐to‐event data; and for HF risk prediction, there is no widely adopted single baseline model with which to compare.

The widespread use of the HFSS is somewhat limited by the need for peak VO₂, but the SHFM is well suited for prognostication in general HF because of its overall accuracy, and the use is facilitated by the web application at www.SeattleHeartFailureModel.org. Admittedly, the SHFM depends on lymphocyte count, uric acid, and total cholesterol, which sometimes are not readily available. In contrast, the recently derived¹³ and externally validated¹⁴ MAGGIC project HF risk score includes 13 universally available variables. An easy‐to‐use online calculator is accessible at www.heartfailurerisk.org. The UCLA 4‐variable risk model is indeed simple, but shares the shortcomings of both the HFSS and the SHFM, including the need for peak VO₂ for the HFSS as well as the underestimation of risk among high‐risk patients for the SHFM. Technically, the UCLA risk model score can be calculated in patients with missing data on peak VO₂. However, the point of the 4‐variable UCLA risk score is to include specifically the 4 variables, and what distinguishes it from simple informal clinical judgment based on symptoms (NYHA class), natriuretic peptide levels, and drug treatment is the presence of the extensively validated, highly objective, and strongly prognostic peak VO₂.

The implications of our findings are that: (1) The performance of a new risk model needs to be evaluated in another patient cohort apart from the one it was developed in (ie, the training set); (2) the UCLA model should not replace any existing risk model without further validation; and (3) the UCLA model has good potential for clinical utility because of its simplicity, but may benefit from recalibration. Furthermore, the tendency for underestimation of risk among high‐risk patients, which seems to affect both the UCLA model as well as the SHFM, should be taken into account by clinicians when they assess overall risk or counsel patients regarding advanced treatment options, such as LVAD placement or HT. In general, these risk scores (UCLA, HFSS, and SHFM) apply to ambulatory or noninotrope, non‐LVAD‐dependent patients, which constitute a shrinking proportion of overall transplants,¹⁵ at least in the United States.

Limitations

Our study was limited by a small sample size, but our results were replicated in a larger population after accounting for missing data by multiple imputation. Both analytic strategies generated fairly similar findings, which add strength to our conclusions. Another limitation was the single‐center design.