Abstract
Human growth research requires knowledge of longitudinal statistical methods that can be analytically challenging. Even the assessment of growth between two ages is not as simple as subtracting the first measurement from the second, for example. This article provides an overview of the key analytical strategies available to human biologists in increasing order of complexity, starting with a review on how to express cross-sectional measurements of size, before covering growth (conditional regression models, regression with conditional growth measures), growth curves (individual growth curves, mixed effects growth curves, latent growth curves), and patterns of growth (growth mixture modeling). The article is not a statistical treatise and has been written by a human biologist for human biologists; as such, it should be accessible to anyone with training in at least basic statistics. A summary table linking each analytical strategy to its applications is provided to help investigators match their hypotheses and measurement schedules to an analysis plan. In addition, worked examples using data on non-Hispanic white participants in the Fels Longitudinal Study are used to illustrate how the analytical strategies might be applied to gain novel insight into human growth and its determinants and consequences. All too often, serial measurements are treated as cross-sectional in analyses that do not harness the power of longitudinal data. The broad goal of this article is to encourage the rigorous application of longitudinal statistical methods to human growth research. Am. J. Hum. Biol. 27:69–83, 2015. © 2014 Wiley Periodicals, Inc.
The assessment of human growth requires serial observation (Cameron, 2012), thereby resulting in longitudinal data that present an analytical challenge (Hauspie et al., 2004). This article describes the key analytical strategies available to human biologists. Each strategy has one or more applications; one of the applications of regression with conditional growth measures (Keijzer-Veen et al., 2005), for example, is to identify sensitive developmental periods for some outcome (Adair et al., 2009). By explaining each strategy, and summarizing this information and each strategies applications in Table1, researchers are provided with a guide to the best methods to test their hypotheses. This resource is not only for human biologists wanting to analyze existing data, but also for those wanting to design studies that correctly match their hypotheses and measurement schedule to an analysis plan.
Table 1.
Analytical strategies in growth research and their applications
| Strategy | Applications | |
|---|---|---|
| Size | Internal Z-scores | Standardize a measure for systematic differences between sexes (or systematic differences between any other sub-groups, such as ethnicities) |
| Standardize a measure for between-child differences in exact age at assessment (using the LMS method) | ||
| Transform a skewed measure so that it is normally distributed (using the LMS method) | ||
| External Z-scores | Compare the mean and distribution of a measure against that in some other sample (typically the reference sample of a growth chart) | |
| Standardize, to some extent, a measure for systematic differences between sexes (when a small sample size prohibits the use of internal Z-scores) | ||
| Standardize, to some extent, a measure for between-child differences in exact age at assessment (when a small sample size prohibits the use of internal Z-scores) | ||
| Transform a skewed measure so that it approximates a normal distribution (if the growth reference was constructed using LMS or some other technique that adjusts for skewness) | ||
| Indices | Standardize a measure for between-child differences in total body size (typically taken to be height) | |
| Conditional size measures | Standardize a measure for between-child differences in total body size (typically taken to be height) | |
| Growth | Conditional regression models | Quantify the association of size at one age with an outcome at a second age, conditional on size at the second age (combined with a life course plot to quantify the association of growth between the two ages with the outcome) |
| Quantify the association of growth between two ages with an outcome at the second age, conditional on size at the first age | ||
| Regression with conditional growth measures | Quantify the associations of growth during different consecutive age periods with some outcome, conditional on size at the first age | |
| Growth curves | Individual growth curves | Characterize a child's growth (by fitting a growth curve that summarizes his or her longitudinal data in a few biologically meaningful parameters and/ or derived traits) |
| Characterize average growth in a sample, after fitting multiple individual growth curves (by producing a mean-constant growth curve) | ||
| Characterize between-child and population variation in growth, after fitting multiple individual growth curves (by inspecting the pooled biologically meaningful parameters and/ or derived traits) | ||
| Relate growth to some distal outcome, other growth process, or survival process (using a two-step strategy) | ||
| Mixed effects growth curves | Simultaneously characterize the growth of every child in a sample and the average growth in that sample (by modeling and therefore quantifying within-child and between-child variation) | |
| Quantify systematic differences in growth due to independent variables, such as sex and ethnicity (by adding these variables into the model as fixed effects) | ||
| Relate growth to some distal outcome, other growth process, or survival process (using a one or two-step strategy) | ||
| Latent growth curves | *Same as for mixed effects growth curves* | |
| Patterns of growth | Growth mixture modeling | *Same as for mixed effects growth curves* |
| Identify distinct unobserved groups (i.e., latent classes) of individuals who share similar average growth curves | ||
| Characterize the determinants of latent class membership and investigate whether or not systematic differences in growth due to independent variables, such as sex and ethnicity, differ across the latent classes | ||
| Relate the latent classes to some distal outcome, other growth process, or survival process (using a one or two-step strategy) |
LMS, lambda-mu-sigma.
Clearly, the field of growth research is broad. This article does not cover all of the techniques available and is not a statistical treatise on growth analysis methods. Most growth research published by human biologists can be assigned to one of three themes. The first theme comprises questions about how children grow and normal variation and between-population variation in this process (Duran et al., 2013; Johnson et al., 2013b; Kurki, 2013; Staiano et al., 2013); the second about the evolutionary, intergenerational, bio-cultural, genetic, and other factors that affect the growth process (Alwasel et al., 2013; Azcorra et al., 2013; Bingham et al., 2013; Vazquez-Vazquez et al., 2013); and the third about the consequences of certain growth traits and patterns of growth (Moura-Dos-Santos et al., 2013; Redmond et al., 2013; Richards et al., 2013; Ruiz-Castell et al., 2013). After reading this article, the investigator should be well equipped to select the best analytical strategy to test any hypothesis that falls into one of these themes. The strategies are presented in increasing order of complexity, starting with a review on how to express cross-sectional measurements of size (internal Z-scores, external Z-scores, indices, conditional size measures), before covering growth (conditional regression models, regression with conditional growth measures), growth curves (individual growth curves, mixed effects growth curves, latent growth curves), and patterns of growth (growth mixture modeling). Each of the main sections ends with a worked example using data on non-Hispanic white participants in the Fels Longitudinal Study (Roche, 1992) to illustrate how the analytical strategies might be applied to gain novel insight into human growth and its determinants and consequences.
SIZE
The term size is used here to refer to any cross-sectional measurement of the body (e.g., lengths, breadths, circumferences, weight, etc.). This is a natural starting point and this section contains necessary knowledge for the following sections. Size varies according to age at assessment and studies in which all children are assessed at the same exact age are rare. In addition, most measures of size differ between sexes and vary according to total body size, which is normally taken to be height. One option is to adjust in an analysis for these variables. A more parsimonious approach, however, is to first compute a variable that is standardized for age, sex, and total body size, where necessary.
Internal Z-scores
The most common measure of size that is standardized for sex is obtained by converting values into internal Z-scores using sample statistics:
where is Z-score,
is Z-score, is size,
is size, is mean size, and
is mean size, and is the standard deviation (SD) of size.
is the standard deviation (SD) of size.
The Z-score is normally distributed if is normally distributed. Stratifying computation by sex standardizes for sex because boys and girls are placed on the same scale (i.e., mean 0 and SD 1). If the target assessment age was five years, a child measured at age 4.5 years is, however, likely to have a lower Z-score than a child measured at age 5.5 years, even if both children were average size for children of the same age. This means that
is normally distributed. Stratifying computation by sex standardizes for sex because boys and girls are placed on the same scale (i.e., mean 0 and SD 1). If the target assessment age was five years, a child measured at age 4.5 years is, however, likely to have a lower Z-score than a child measured at age 5.5 years, even if both children were average size for children of the same age. This means that and
and need to vary with age. To formalize the problem, and to adjust for possible skewness in the distribution, the lambda-mu-sigma (LMS) method of constructing a growth reference can be used to estimate age-specific statistics (Cole and Green, 1992). Briefly, LMS models variation in size across age as a function of three curves: (1) the lambda curve describes the Box-Cox power needed to remove skewness, (2) the mu curve describes the median, and (3) the sigma curve describes the coefficient of variation. After fitting the LMS model to estimate the three curves, Z-scores can be computed:
need to vary with age. To formalize the problem, and to adjust for possible skewness in the distribution, the lambda-mu-sigma (LMS) method of constructing a growth reference can be used to estimate age-specific statistics (Cole and Green, 1992). Briefly, LMS models variation in size across age as a function of three curves: (1) the lambda curve describes the Box-Cox power needed to remove skewness, (2) the mu curve describes the median, and (3) the sigma curve describes the coefficient of variation. After fitting the LMS model to estimate the three curves, Z-scores can be computed:
where is Z-score,
is Z-score, is size,
is size, is lambda,
is lambda, is mu, and
is mu, and is sigma.
is sigma.
In the same way that sex-specific statistics can be used to standardize for sex, age-specific statistics produced using LMS can be used to standardize for age. Both the child measured at age 4.5 years and the child measured at age 5.5 years would now have a Z-score close to zero. Data requirements for LMS can, however, be obstructive; 50 measurements per sex per binned age (e.g., week, month, year) will normally provide enough information to estimate M and S precisely, but up to 400 observations per sex per binned age may be needed to estimate L precisely (Cole, 2012). In the absence of definitive recommendations and no statistically justified way to estimate sample size for LMS through a power calculation, the latter number provides a “ball park” target.
External Z-scores
If a researcher has a small sample size, one option is to use statistics from some other sample. The most common type of external Z-score is computed using LMS values from a growth reference that is the basis of a growth chart, such as those produced by the Centers for Disease Control and Prevention in the United States of America (http://www.cdc.gov/growthcharts/) (Kuczmarski et al., 2000), the Royal College of Paediatrics and Child Health in the United Kingdom (http://www.rcpch.ac.uk/growthcharts) (Wright et al., 2010), and the World Health Organization (http://www.who.int/childgrowth/standards/) (WHO, 2006). These Z-scores describe how a sample compares against the growth reference source sample (De Onis et al., 2007; Johnson et al., 2012a,b). They are normally less standardized for age and sex than internal Z-scores computed using LMS because the sample differs from the growth reference source sample. They are, however, more convenient than internal Z-scores for making comparisons across datasets.
Indices
Indices can be used to standardize measures of size for total body size. Body mass index (BMI) is the obvious example; it works on the basis that weight increases proportionately to height squared, so dividing weight by height squared results in an index that is uncorrelated with height in a sample (Keys et al., 1972). In reality, however, the BMI is always at least party correlated with height, because the mathematical determination of the best index varies according to factors such as age, sex, ethnicity, etc (Cole, 1986; Franklin, 1999; Frontini et al., 2001; Hattori and Hirohara, 2002; Metcalf et al., 2011). Log-log regression can be used to find out how a measure of size scales with total body size (Benn, 1971; Cole, 1979). It is then possible to calculate an index that is uncorrelated with total body size in the sample used for computation:
where is index,
is index, is size,
is size,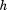 is height (or some other measure of total body size), and
is height (or some other measure of total body size), and is the coefficient obtained from regressing ln(
is the coefficient obtained from regressing ln( ) on ln(
) on ln(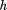 ).
).
Stratifying computation by sex will ensure that the index is standardized for total body size within each sex. It is then possible to convert to age and sex specific Z-scores to standardize for these variables, where necessary.
Conditional size measures
A different approach is to regress size on total body size and save the residuals (Keijzer-Veen et al., 2005). The formula (without the denominator) is actually the same as that obtained by applying a logarithmic transformation to the previous equation, with the exception that here the variables are not logged (Cole, 1991):
where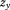 is conditional size Z-score,
is conditional size Z-score, is size,
is size,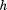 is height (or some other measure of total body size),
is height (or some other measure of total body size), is the coefficient obtained from regressing
is the coefficient obtained from regressing on
on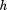 , and
, and is the residual SD from the regression.
is the residual SD from the regression.
The resulting measure is size conditional on total body size and as such the two variables should be uncorrelated. This formula needs to be modified if the relationship between size and total body size is non-linear; adding a total body size squared term to the regression works in many instances. The dependent variable is a Z-score with mean 0 and SD 1 because the residuals are standardized. Stratifying by sex will ensure that the conditional size measure is standardized both for total body size and sex. Alternatively, conditional size can be computed without the denominator, before converting to age and sex specific Z-scores to standardize for these variables, where necessary.
Worked example
Each of the strategies was applied to weight data on 402 boys and 383 girls born 1928 to 2000 and aged 12 years (range 11.8–12.2) and the properties of the resulting variables are shown in Table2. Girls weighed 2.3 kg more than boys and exhibited greater variation (P values <0.05), which was expected given that more girls than boys would have started puberty and their growth spurt at this age. The data were not correlated with age (ρ = 0.05, P value = 0.2), but were positively skewed (P-value < 0.001) and correlated with concurrent height (ρ = 0.7, P value <0.001), to the extent that 45% of the variance in weight was explained by height. Converting to Z-scores, either using the sex-specific mean and SD or sex and age-specific LMS values, placed boys and girls on the same scale, such that there no longer existed any differences between sexes in the mean and SD (P values >0.1). The LMS approach had the additional advantage of removing the skewness in the distribution and theoretically would have also removed any association with age.
Table 2.
The properties of different weight variables at age 12 years in 402 boys and 383 girls in the Fels Longitudinal Study
| Mean (SD) | Sex difference in the meana | Sex difference in the SDb | Skewness | Correlation with age | Correlation with height | Variance explained by heightc | |
|---|---|---|---|---|---|---|---|
| Estimate (P value) | % | ||||||
| Raw data | |||||||
| Weight (kg) | 42.976 (9.530) | 2.324 (<0.001) | 0.942 (0.045) | 1.120 (<0.001) | 0.045 (0.209) | 0.693 (<0.001) | 44.6 |
| Internal Z-scores | |||||||
| Computed using sample mean and SD | 0.000 (0.999) | 0.000 (>0.999) | 0.000 (>0.999) | 1.134 (<0.001) | 0.042 (0.241) | 0.680 (<0.001) | 43.4 |
| According to a FLS referenced | −0.012 (0.995) | −0.064 (0.368) | 0.035 (0.488) | 0.032 (0.711) | 0.043 (0.229) | 0.712 (<0.001) | 46.3 |
| External Z-scores | |||||||
| According to the CDC reference | 0.030 (0.996) | −0.097 (0.174) | 0.066 (0.190) | 0.043 (0.623) | 0.010 (0.771) | 0.711 (<0.001) | 46.2 |
| Indices | |||||||
| BMI (kg/m2) | 18.516 (3.066) | 0.505 (0.020) | 0.297 (0.056) | 1.115 (<0.001) | −0.004 (0.910) | 0.347 (<0.001) | 19.2 |
| Weight-for-heightp (kg/m∼3)e | 11.444 (1.818) | 0.878 (<0.001) | 0.310 (<0.001) | 1.054 (<0.001) | −0.037 (0.303) | 0.046 (0.202) | 2.3 |
| Conditional size measures | |||||||
| Unstandardized residuals from weight (kg) regressed on height (m)e | 0.000 (6.868) | 0.000 (>0.999) | 0.868 (0.012) | 1.007 (<0.001) | −0.046 (0.194) | 0.000 (>0.999) | 0.0 |
| Standardized residuals from weight (kg) regressed on height (m)e | 0.000 (1.001) | 0.000 (>0.999) | 0.000 (0.994) | 1.033 (<0.001) | −0.043 (0.224) | 0.000 (0.998) | 0.0 |
Computed as the mean for girls minus the mean for boys so that a positive value indicates a higher mean in girls compared with boys. P values are from t-tests.
Computed as the SD for girls minus the SD for boys so that a positive value indicates a higher SD in girls compared with boys. P values are from variance ratio tests.
Computed using the formula (1 − sqrt(1 − r2)) × 100, where r is the correlation with height.
The FLS reference was constructed by applying sex-stratified LMS models to all weight data collected between birth and age 18 years (1,509 participants, 31,121 observations).
Computation was sex stratified.
BMI body mass index, CDC Centers for Disease Control and Prevention, FLS Fels Longitudinal Study, LMS lambda-mu-sigma, SD standard deviation.
The only remaining adjustment was for height. The Z-scores could have been computed using BMI, but this would not have fully resolved the problem as BMI was correlated with height (ρ = 0.3, P value <0.001), with 19% of its variance explained by height. The power needed to create an index of weight independent of height was found by log-log regression to actually be closer to three than two in both sexes. On the original scale, this corresponded to sex-specific estimates of approximately a 90 kg increase in weight per 1 m increase in height that were used in the computation of conditional size measures. In addition to being uncorrelated with height, the conditional size measure that comprised standardized residuals had the advantage that it placed boys and girls on the same scale. All indices and conditional size measures were, however, skewed (P-values < 0.001) and could have theoretically been associated with age.
It is possible to convert variables that are standardized for total body size to LMS Z-scores that standardize for sex and age and adjust for skewness. However, that requires an appropriate growth reference that is unlikely to exist and may be difficult to create internally (e.g., if the power needed to create an index of weight independent of height changes over the studied age range). Alternatively, it is possible to compute an index or conditional size measure using Z-scores, but the resulting variable may be difficult to interpret and is not guaranteed to be standardized in the same way as the Z-scores used for computation. Clearly, expressing size is not straightforward. The scientist is tasked with striking a balance between using a variable that is interpretable and one that is perfectly standardized and normally distributed.
GROWTH
The term growth is used here to refer to change across age in any measurement of the body. The simplest assessment of growth is change in size between two ages, yet even this seemingly straightforward assessment has given rise to two different key analytical strategies.
Conditional regression models
Including size at one age and size at a subsequent age as independent variables in a regression model results in estimates of the association of each size measure with the dependent variable conditional on the other size measure (i.e., setting it at a value of 0):
where is the dependent variable,
is the dependent variable,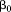 is the intercept,
is the intercept,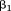 is the regression coefficient for size at the first age,
is the regression coefficient for size at the first age,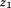 is size at the first age,
is size at the first age,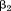 is the regression coefficient for size at the second age,
is the regression coefficient for size at the second age,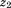 is size at the second age, and
is size at the second age, and is the residual error.
is the residual error.
Z-scores are often used to make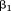 and
and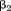 comparable. They can be plotted against age with a line connecting them together in a life course plot (Cole, 2004). This plot provides information about growth as well as size. If
comparable. They can be plotted against age with a line connecting them together in a life course plot (Cole, 2004). This plot provides information about growth as well as size. If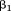 was −10% per Z-score and
was −10% per Z-score and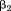 was +20% per Z-score, then a one Z-score increase between
was +20% per Z-score, then a one Z-score increase between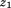 and
and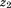 (i.e., growth) would indicate a 30% increase in
(i.e., growth) would indicate a 30% increase in . The life course plot is an easy way to visualize relationships of size and growth with a dependent variable. Alternatively, as discussed by others (Cole, 2004; De Stavola et al., 2006; Lucas et al., 1999), the equation can be re-parameterized to estimate the relationship of growth between
. The life course plot is an easy way to visualize relationships of size and growth with a dependent variable. Alternatively, as discussed by others (Cole, 2004; De Stavola et al., 2006; Lucas et al., 1999), the equation can be re-parameterized to estimate the relationship of growth between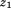 and
and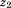 with
with :
:
or
Note that the estimates for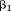 and
and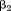 are unchanged. The fundamental difference between the three equations is that they address different questions. The first asks “how is size at the first age associated with the dependent variable (conditional on size at the second age)?”, the second asks “how is growth between the first and second age associated with the dependent variable (conditional on size at the first age)?”, and the third asks “how is growth between the first and second age associated with the dependent variable (conditional on size at the second age)?” The equations can easily be extended to include more than two measurements (De Stavola et al., 2006). The limitations of this strategy are that (1) conditioning on multiple future measurements can make interpretation difficult and (2) multicollinearity between the serial measurements can result in unstable estimates with wide confidence intervals. Only direct associations of size or growth with the outcome are estimated, but the same models can easily be specified in path analyses to also get estimates of indirect associations (i.e., those operating through subsequent body size or growth) (Gamborg et al., ,).
are unchanged. The fundamental difference between the three equations is that they address different questions. The first asks “how is size at the first age associated with the dependent variable (conditional on size at the second age)?”, the second asks “how is growth between the first and second age associated with the dependent variable (conditional on size at the first age)?”, and the third asks “how is growth between the first and second age associated with the dependent variable (conditional on size at the second age)?” The equations can easily be extended to include more than two measurements (De Stavola et al., 2006). The limitations of this strategy are that (1) conditioning on multiple future measurements can make interpretation difficult and (2) multicollinearity between the serial measurements can result in unstable estimates with wide confidence intervals. Only direct associations of size or growth with the outcome are estimated, but the same models can easily be specified in path analyses to also get estimates of indirect associations (i.e., those operating through subsequent body size or growth) (Gamborg et al., ,).
Regression with conditional growth measures
A conditional growth measure can be computed as the residuals from a regression of size at the second age on size at the first age, similarly to the computation of a conditional size measure (Keijzer-Veen et al., 2005). Because the conditional growth measure is the portion of size at the second age uncorrelated with size at the first age it can be interpreted as growth over the age period adjusted for regression to the mean (Cameron et al., 2005). For growth research, it may be important to use Z-scores so that catch-up or catch-down growth and regression to the mean are on the same scale and thus distinguishable (Cameron et al., 2005; Galton, 1886). Others have, however, argued that Z-scores should not be used for some measures, such as BMI, because within-child variance of serial measurements depends on the child's level of adiposity more when using Z-scores than when using original metrics (Berkey and Colditz, 2007; Cole et al., 2005). Nonetheless, if Z-scores are used, a simple equation is available for growth between two ages (Cole, ,):
where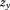 is conditional growth Z-score,
is conditional growth Z-score,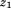 is size at the first age,
is size at the first age,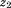 is size at the second age, and
is size at the second age, and is the correlation between
is the correlation between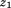 and
and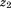 .
.
The denominator is not essential, but it ensures that the resulting conditional growth measure is a Z-score with mean zero and SD one. In a subsequent regression of a dependent variable on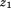 and
and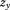 , the estimate for
, the estimate for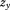 is interpreted as the association between growth and the dependent variable:
is interpreted as the association between growth and the dependent variable:
where is the dependent variable,
is the dependent variable,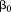 is the intercept,
is the intercept,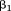 is the regression coefficient for size at the first age,
is the regression coefficient for size at the first age,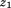 is size at the first age,
is size at the first age,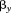 is the regression coefficient for growth between
is the regression coefficient for growth between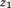 and size at the second age,
and size at the second age,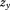 is growth between
is growth between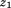 and size at the second age, and
and size at the second age, and is the residual error.
is the residual error.
This equation can easily incorporate multiple conditional growth measures (Tu et al., 2013), each computed to be independent of all previous size measures, and the estimate for each interpreted as the association of growth over the preceding age period with the dependent variable. It is also possible to make the conditional growth measures independent of concurrent growth in some other dimension (e.g., weight gain independent of linear growth) (Adair et al., 2013). Because conditional growth measures are uncorrelated, the problems of multi- collinearity and conditioning on the future seen in conditional regression models are alleviated somewhat. The last coefficient in a conditional regression model (i.e.,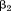 ) is the same as the last coefficient in a regression with conditional growth measures (i.e.,
) is the same as the last coefficient in a regression with conditional growth measures (i.e.,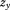 ), however, which has led to concerns about the advantage of regression with conditional growth measures over conditional regression models when just two serial observations are being analyzed (Tu and Gilthorpe, 2007). More importantly, both strategies require data to be collected at the same (or at least approximately the same) ages in all children. A single conditional growth measure can be used as a dependent variable, but otherwise both strategies also have limited utility if growth is the dependent variable.
), however, which has led to concerns about the advantage of regression with conditional growth measures over conditional regression models when just two serial observations are being analyzed (Tu and Gilthorpe, 2007). More importantly, both strategies require data to be collected at the same (or at least approximately the same) ages in all children. A single conditional growth measure can be used as a dependent variable, but otherwise both strategies also have limited utility if growth is the dependent variable.
Worked example
Each of the strategies was applied to data on 169 males and 165 females born 1929 to 1974 to investigate the associations of weight between ages 0 and 18 years with systolic blood pressure (SBP) at age 40 years (range 30.6–49.8) (Table3). Internal weight Z-scores at ages 0, 2, 10, and 18 years, computed using LMS values from a Fels Longitudinal Study reference, were used as they standardized the raw data for sex and age and adjusted for skewness. More frequent weight measurements are available in the Fels Longitudinal Study, but these ages were chosen for illustrative purposes as ages 0 to 2 years encompasses infancy, ages 2 to 10 years encompasses pre-puberty, and ages 10 to 18 years encompasses puberty in both sexes. The outcome was left on its original scale (i.e., mm Hg) and all models included an adjustment for sex, but not for birth year or age when the outcome was measured as these variables where not nominally significant at P value <0.05 when included (P values >0.8).
Table 3.
General linear regression models of systolic blood pressure (mm Hg) at age 40 years on weight Z-scoresa (model 1), changes in weight Z-scoresB (models 2 and 3), or conditional weight Z-score growth measuresc (model 4) between birth and age 18 years in 169 males and 165 girls in the Fels Longitudinal Study
| Conditional regression models | Regression with conditional growth measures | ||||||
|---|---|---|---|---|---|---|---|
| Model 1 | B (95% CI), P-value | Model 2 | B (95% CI), P-value | Model 3 | B (95% CI), P-value | Model 4 | B (95% CI), P-value |
| Intercept | 119.119 (117.458, 120.781), <0.001 | Intercept | 119.119 (117.458, 120.781), <0.001 | Intercept | 119.119 (117.458, 120.781), <0.001 | Intercept | 118.939 (117.267, 120.609), <0.001 |
| Sex | Sex | Sex | Sex | ||||
| Males | Referent | Males | Referent | Males | Referent | Males | Referent |
| Females | −11.368 (−13.765, −8.971), < 0.001 | Females | −11.368 (−13.765, −8.971), < 0.001 | Females | −11.368 (−13.765, −8.971), < 0.001 | Females | −11.368 (−13.765, −8.971), < 0.001 |
| Zwt0yr | −0.546 (−1.828, 0.735), 0.402 | Zwt0yr | 0.328 (−1.411, 2.067), 0.711 | Zwt2-0yr | 0.546 (−0.735, 1.828), 0.402 | Zwt0yr | −0.701 (−1.917, 0.515), 0.258 |
| Zwt2yr | −1.263 (−2.854, 0.329), 0.120 | Zwt2-0yr | 0.874 (−0.631, 2.379), 0.254 | Zwt10-2yr | 1.809 (0.056, 3.562), 0.043 | Conditional Zwt2yr | −0.251 (−1.482, 0.979), 0.688 |
| Zwt10yr | 0.515 (−1.584, 2.614), 0.629 | Zwt10-2yr | 2.136 (0.407, 3.866), 0.016 | Zwt18-10yr | 1.294 (−0.788, 3.375), 0.222 | Conditional Zwt10yr | 1.611 (−0.006, 3.573), 0.051 |
| Zwt18yr | 1.621 (−0.330, 3.573), 0.103 | Zwt18-10yr | 1.621 (−0.330, 3.573), 0.103 | Zwt18yr | 0.328 (−1.411, 2.067), 0.711 | Conditional Zwt18yr | 1.621 (−0.330, 3.573), 0.103 |
| R2 | 23.3% | R2 | 23.3% | R2 | 23.3% | R2 | 23.3% |
Computed according to a FLS reference, which was constructed by applying sex-stratified LMS models to all weight data collected between birth and age 18 years (1,509 participants, 31,121 observations).
Computed as Zwt at any given age minus Zwt at the previous age.
Computed as the unstandardized residuals from regression of Zwt at any given age on Zwt at all previous ages.
B beta, CI confidence interval, FLS Fels Longitudinal Study, LMS lambda-mu-sigma, Zwt weight Z-score.
Models 1 to 3 are conditional regression models. Each is an extension of one of the equations in the appropriate section of the text. Model 1 simply included Z-score at each age. Although none of the estimates were nominally significant at P value <0.05, the estimates at ages 0 and 2 years were negative while the estimates at ages 10 and 18 years were positive, thereby indicating that weight gain between ages 2 and 10 years may be associated with higher SBP. This was confirmed in model 2, which included variables of change in Z-score between consecutive ages and Z-score at age 0 years. A one unit increase in change in Z-score between ages 2 and 10 years incurred a 2.136 mm Hg (95% confidence interval 0.407–3.866) higher SBP. This estimate was attenuated to 1.809 (0.056–3.562) in model 3, which included the same variables as model 2 except for the replacement of Z-score at age 0 years for Z-score at age 18 years. The pre-pubertal weight gain-adulthood SBP association, therefore, appears to be more independent of weight at age 0 years than weight at age 18 years. Estimates of this association in models 2 and 3 are difficult to interpret, however, as they are also conditional on infant weight gain (i.e., ages 0–2 years) and pubertal weight gain (i.e., ages 10–18 years).
Model 4 is a regression with conditional growth measures. The formula in the appropriate section of the text was not used as some measures needed to be independent of more than one previous weight measurement. Instead, unstandardized residuals from regression of Z-score at any given age on Z-scores at all previous ages were used. Standardized residuals could have been used but that would have made model 4 less comparable to models 1 to 3. The same would have been true if residuals from sex-stratified regressions were used. Regardless of how the conditional growth measures are computed, their use helps with interpretability because each estimate represents the association of change in Z-score with the outcome, independent of Z-scores at all previous ages but not any future ages. The estimate for conditional Z-score at age 10 years (1.611; −0.006 to 3.573) also provided evidence for a pre-pubertal weight gain-adulthood SBP association.
Although all of the models appear to be telling the same story, it is important to remember that the estimates are making different contrasts because they are conditional on different variables (Wills et al., 2014). In addition, comparison of effect sizes across the models may be difficult because the change in Z-score and the conditional Z-score growth measures are not guaranteed to have mean 0 and SD 1. There was no evidence of non-linearity or effect modification by sex or birth year (data not shown), but the models could be further developed to consider interactions between the size/weight gain variables (e.g., is the pre-pubertal weight gain-adulthood SBP association stronger in those with lower birth weight?) and adjustment in some way for linear growth.
GROWTH CURVES
The most common data in growth research comprise a large number of serial measurements on a sample of children seen at varied ages. There are nearly always missing data due to missed assessments, drop out, and other factors. In these circumstances, data reduction techniques are necessary to summarize the available data for each child in a few biologically meaningful traits. This is done most effectively by fitting growth curves that describe how the measure changes over age.
Individual growth curves
The first growth curve was published in 1930 (Scammon, 1972). In that publication, Richard E. Scammon plotted, against age, the length/ height data of a child measured semiannually between birth and age 18 years and “fitted a curve” by connecting the dots together. By inspecting that growth distance curve and the first and second derivatives of that curve (i.e., growth velocity and acceleration curves) it was possible to identify certain traits that are now commonly used in growth research, such as the timing and magnitude of peak height velocity. Auxologists sought to improve this process by finding mathematical functions or models that best describe the growth process in individuals. These are called structural models because they postulate that the growth curve has a specific functional form. Hauspie and Molinari (2004) provide a good review of structural models. For the purpose of the present article, the Preece-Baines (1978) 1 (PB1) model for height growth between approximately eight to 18 years of age is used as an example:
where is height,
is height, is decimal age,
is decimal age,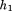 is adulthood height,
is adulthood height, is age at peak height velocity,
is age at peak height velocity,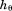 is height at peak height velocity,
is height at peak height velocity,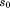 and
and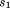 are growth rate constants related to prepubertal and postpubertal velocities, and
are growth rate constants related to prepubertal and postpubertal velocities, and is the residual error.
is the residual error.
Each parameter approximates a biologically meaningful trait, although analytical solutions using the model parameters were included in the original publication (Preece and Baines, 1978). Corrections to these solutions have recently been published, along with a Stata command called pbreg which allows the user to fit individual PB1 curves and derive the traits and their confidence intervals (Sayers et al., 2013).
The majority of structural models, of which PB1 is just one example, were developed for linear growth. Human biologists wanting to model change over age in some other measure, for which no structural model exists, typically employ some generic method of curve fitting that is not specific to human growth research. The reader may be familiar with some of these methods, in particular splines, kernel estimators, and local polynomials. These are called non-structural models because they do not postulate that the growth curve has a specific functional form. Gasser et al. (1993) provide a good review of the most important structural models. For the purpose of the present article, a cubic spline is used as an example:
where is size,
is size, is decimal age,
is decimal age,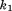 to
to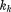 are a set of
are a set of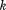 knots in the range of
knots in the range of ,
,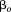 to
to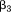 and
and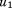 to
to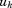 are estimates, and
are estimates, and is the residual error.
is the residual error.
The reader will notice that the first part of this model is a cubic polynomial. The latter part is a set of additional age cubed terms that “tweak” different sections of curve to better fit the data. The number and location of knots specify how the curve is split into different sections. More knots will result in more parameters and a greater degree of “smoothing.” Because there is no upper limit on the number of knots allowed, this model could be over-parameterized to produce a “wiggly line” that provides a perfect fit for the data. The scientist is tasked with compromising between a small degree of smoothing (which results in small bias and large variance) and a large degree of smoothing (which results in large bias and small variance). This subjectivity is common in non-structural model fitting. When the researcher is happy with their model, biologically meaningful traits can be derived using calculus (e.g., to estimate age at adiposity rebound after modeling childhood BMI data, find the age when the first derivative of the model is zero).
Nonstructural models are more flexible than structural models, but their parameters often have no biological interpretation. Both strategies share the assumptions that residuals (i.e., observed—fitted values) should be normally distributed, homoscedastic, and serially independent (Hauspie and Molinari, 2004). The residual SD (RSD) can be used to quantify the overall goodness of fit of the model in the original metric of measurement:
where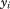 are the observed values at ages
are the observed values at ages ,
,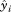 are the corresponding fitted values,
are the corresponding fitted values,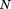 is the number of observations, and
is the number of observations, and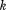 is the number of parameters in the model.
is the number of parameters in the model.
The benchmark that growth modelers aim for is to fit a curve with an RSD similar to the measurement error of the dimension under consideration (Hauspie and Molinari, 2004). Note that models for indices will inevitably have relatively large RSDs because the outcome includes two sources of measurement error (e.g., BMI includes measurement error in weight and height). Model fit should also be checked by visual inspection of (1) a plot of the fitted curve against the observed values and (2) a scatter plot of the residuals against age. After doing this for each child in a sample, it is possible to estimate a mean-constant curve using the mean values of the parameter estimates, thereby characterizing average growth in the sample. It also possible to quantify variation in the biologically meaningful parameters or derived growth traits and use them in secondary analyses to test their associations with other variables.
Fitting individual growth curves is a laborious process, but one that human biologists used to have to face. Fortunately, strategies are now available to fit growth curves for an entire sample in one model.
Mixed effects growth curves
Mixed effects models were largely developed in the 1980s and 1990s (Goldstein, 1986; Laird and Ware, 1982). The terminology “multilevel model” is used by others in recognition that longitudinal growth data have a hierarchical data structure, with serial measurements clustered within children; the first level is measurement occasion and the second level is child. Nonetheless, the terminology “mixed effects” is used here because these models handle longitudinal growth data on a sample of children by simultaneously estimating (1) sample average parameters called “fixed effects” that govern the sample average growth curve and (2) corresponding child specific parameters called “random effects” that are individual departures from the fixed effects. The fixed and random effects together (i.e., mixed effects) describe the growth of every child in a sample (Johnson et al., 2013a). A simple model is used to demonstrate how this is done:
where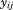 is the size at age
is the size at age of child
of child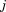 ,
,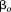 is a fixed effect indicating mean size in all children,
is a fixed effect indicating mean size in all children,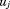 is a random effect indicating how each child's intercept differs from
is a random effect indicating how each child's intercept differs from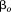 , and
, and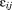 is the residual error. The
is the residual error. The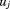 and
and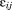 are assumed to be independent and normally distributed with zero means and variances
are assumed to be independent and normally distributed with zero means and variances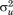 and
and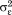 .
.
This is called a variance components model because it shows how, in a single model, variance in size is decomposed into between-child differences (i.e.,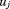 ) and within-child differences over age or residual error (i.e.,
) and within-child differences over age or residual error (i.e.,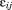 ). This is the fundamental difference from individual growth curve models that only capture the latter. The between-child differences are called “level two residuals” and the within-child differences over age are called “level one residuals” by some researchers. The proportion of total variance in the measure being modeled due to differences between children is given by the variance partition coefficient (VPC), which in this example is calculated as (
). This is the fundamental difference from individual growth curve models that only capture the latter. The between-child differences are called “level two residuals” and the within-child differences over age are called “level one residuals” by some researchers. The proportion of total variance in the measure being modeled due to differences between children is given by the variance partition coefficient (VPC), which in this example is calculated as (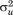 /(
/(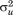 +
+ 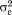 )) × 100 (Goldstein et al., 2002). The VPC of mixed effects growth curve models is typically very high because there is large variability between children in the growth process (Cameron, 2012), but nonetheless it is worth checking to provide reassurance that a mixed effect strategy is necessary.
)) × 100 (Goldstein et al., 2002). The VPC of mixed effects growth curve models is typically very high because there is large variability between children in the growth process (Cameron, 2012), but nonetheless it is worth checking to provide reassurance that a mixed effect strategy is necessary.
Any structural or nonstructural function can be expressed as a mixed effects growth curve model. For example, a quadratic polynomial could take the form:
where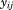 is the size at age
is the size at age of child
of child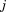 ,
,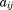 is the corresponding age,
is the corresponding age,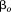 to
to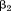 are fixed effects,
are fixed effects,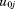 and
and are random effects, and
are random effects, and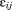 is the residual error. The
is the residual error. The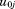 and
and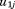 are assumed to follow a bivariate normal distribution with zero means, variances
are assumed to follow a bivariate normal distribution with zero means, variances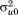 and
and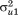 , and covariance
, and covariance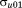 . The
. The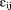 are assumed to be normally distributed with mean zero and variance
are assumed to be normally distributed with mean zero and variance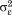 . The
. The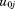 and
and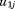 are assumed to be independent of
are assumed to be independent of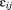 .
.
The reader will notice that there is no random effect for the quadratic age term. More complicated models are more computationally challenging, and researchers will often remove one or more random effects from their model to achieve convergence (Johnson et al., 2013a). This should be done with caution and only when confident that there is little between-child variation in the parameter in question. In the present example, there are two random effects that form a variance-covariance matrix. If we were modeling infant weight, a negative covariance between the intercept and the linear slope term would indicate that infants who were lighter at birth grew faster postnatally, for example. Centering the age scale (e.g., at birth) will help with interpretability of the variance-covariance matrix (and the other model estimates).
The same checks for model fit for individual growth curve models apply to mixed effects growth curve models, with the additional check that the level two residuals are normally distributed. Although there is a tendency to assess model fit using statistics summarizing the level one residuals in the whole sample, it is possible to use the level one residuals to compute the RSD of each child's estimated growth curve to identify those that did not provide a good fit for that child's observed data (Wen et al., 2012).
The real strength of mixed effects growth curve models is that children don't need to have been measured at the same ages or the same number of times. Selecting for analysis children who have a certain number of measurements spanning a certain age range may be prudent, but it is not a requirement. Statistical programs efficiently handle non-consistently collected data (assuming missing at random) using probability functions to describe the relative likelihood of each random effect occurring at a given point in the observation space (Rabe-Hesketh and Skrondal, 2008).
Independent variables can easily be included as fixed effects to investigate systematic differences in the sample average intercept or curve between sexes or ethnicities, for example (Johnson et al., 2013a). Further, the level two residuals or derived growth traits in the individual curves can be used in secondary analyses to test their associations with other variables. Linear spline models and the SuperImposition by Translation And Rotation (SITAR) model are becoming popular approaches to use for this purpose, namely because the level two residuals (or random effects in the case of SITAR) have some biological interpretation and thus their associations with other variables is meaningful (Cole et al., 2010; Howe et al., ). The caveats of this two-step strategy are that (1) level two residuals suffer from a statistical phenomenon of being shrunk toward the mean (Robinson, 1991) and (2) any secondary analysis does not properly consider uncertainty in the level two residuals or derived growth traits. As a result, some studies have weighted each child in secondary analyses by the number of serial observations used in the initial growth curve fitting process (Sovio et al., ,). More sophisticated one-step strategies are available to relate level two residuals to some distal outcome, other growth process, or survival process in a bivariate (i.e., two outcomes) model, but these go beyond the scope of the present article.
Latent growth curves
A child's growth is not directly observed from serial measurements, but is estimated by fitting a curve through those data. Latent growth curve models are a special type of structural equation model (SEM) (Schumacker and Lomax, 2010), where the parameters that govern the shape of the curve of each child in a sample are estimated as latent or unobserved variables using confirmatory factor analysis (Bollen and Curran, 2006). The reader will notice the similarity to mixed effects growth curve models, where fixed and random effects instead of latent variables are estimated. When a linear trajectory is specified, a mixed effects growth curve model and a latent curve model can in fact be analytically and empirically identical (Bauer, 2003; Curran, 2003). Non-linear models cannot always, however, be parameterized in the same way (Bauer, 2003; MacCallum et al., 1997).
Readers wanting to explore the algebra of latent growth curve models are directed to the book “Latent Curve Models: A Structural Equation Perspective” (Bollen and Curran, 2006). For the purpose of the present article, Figure 1 provides a pictorial representation of a latent curve growth model. In this example, there are three latent variables in circles that together describe a quadratic polynomial curve. The repeated measures of weight in rectangular boxes are related to the latent variables through factor loadings, which are generally specified a priori. All of the loadings for the intercept factor are set to one, so that it equally influences all of the serial measurements; the loadings for the linear factor reflect the passage of age, and are equally spaced because of the uniform age between consecutive assessments; and the loadings for the second factor reflect the passage of age squared (Bollen and Curran, 2006). The child specific F-scores for the intercept and linear factors are equivalent to the respective random effects estimates in the model in the previous section. The variance of the quadratic factor in the latent growth curve model could even be constrained to be zero, thereby making the two models identical.
Fig 1.
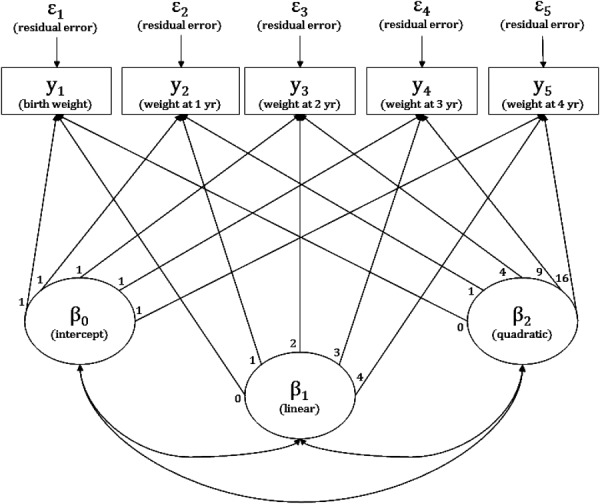
A latent quadratic polynomial growth curve model.
Given their similarity, why would a researcher be tempted to learn latent growth curve modeling instead of mixed effects growth curve modeling? In reality, nearly everything that can be done using one strategy can be done using the other, but with varying degrees of difficult. While mixed effects growth curve models might lend themselves specifically to the analysis of growth, latent growth curve models can easily be developed to take advantage of the SEM framework. Here, there are omnibus measures of model fit and it is easier to (1) incorporate other latent variables and time-varying confounders; (2) relate growth to some distal outcome, other growth process, or survival process; and (3) identify unobserved patterns of growth in the data (Curran, 2003).
Worked example
To illustrate the use of growth curve modeling, a mixed effects extension of the Berkey-Reed (1987) first order model was fitted to 7,518 measurements of infant weight (target assessment ages 0, 1, 3, 6, 9, 12, 18, and 24 months) on 391 boys and 362 girls born 1929–2011:
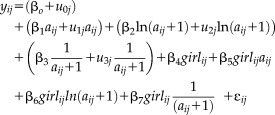 |
 |
where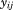 is the size at age
is the size at age of child
of child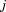 ,
,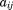 is the corresponding age,
is the corresponding age,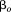 to
to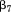 are fixed effects,
are fixed effects,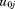 to
to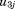 are random effects,
are random effects, is a dummy variable coded 0 for boys and 1 for girls, and
is a dummy variable coded 0 for boys and 1 for girls, and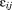 is the residual error. The
is the residual error. The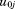 to
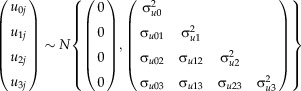
to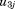 are assumed to follow a multivariate normal distribution with zero means, variances
are assumed to follow a multivariate normal distribution with zero means, variances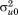 to
to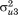 , and covariances
, and covariances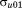 to
to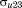 . The
. The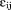 are assumed to be normally distributed with mean zero and variance
are assumed to be normally distributed with mean zero and variance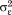 . The
. The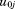 to
to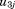 are assumed to be independent of
are assumed to be independent of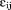 .
.
The base of the model comprises an intercept and three age terms. A transformation is required for the last two age terms as they are not defined at birth (e.g., it is impossible to log 0) and that proposed by Simondon et al (1992) was employed. Together, the four parameters postulate that the growth curve has a specific functional form, thus this is a structural model. Of particular importance, is that the third age term allows the distance curve to have one inflection point, where either (1) maximum velocity occurs and growth changes from acceleration to deceleration or (2) minimum velocity occurs and growth changes from deceleration to acceleration. In the present example, all of the functional parameters were allowed to have random effects, thereby ensuring that the individual growth curves were not constrained in any way to be the same. Not including a random effect for the third age term would have, for example, constrained all the individual curves to have the same inflection point. Including sex as an independent variable and interacting it with all of the age terms allowed the sample average growth curve to be different for boys and girls. The same model could have been specified as a latent growth curve model.
In order to capture inflection points in the individual curves, an a priori decision was taken to apply the model to data from infants with at least five serial measurements (median 8, interquartile range 7–9) spanning at least one year of the age range (median 2.00, interquartile range 1.99–2.04). Five measurements is the minimum number required to fit the Berkey-Reed model for each participant separately (i.e., number of parameters − 1), and 1 year ensures that each individual's curve is fitted to his or her data across a reasonable section of the age range. A less prudent approach would have been to apply to the model to all data and then restrict investigation of individual curve characteristics to infants with good longitudinal data. After fitting the model once, 44 observations with level one residuals greater than + 0.8 kg or less then −0.8 kg were removed from the dataset before fitting the model a second time. This “trimming of residuals” is becoming a popular approach used in growth curve modeling and works on the assumption that the deleted observations suffer from large measurement error and/ or mistakes made during data recording/ entry.
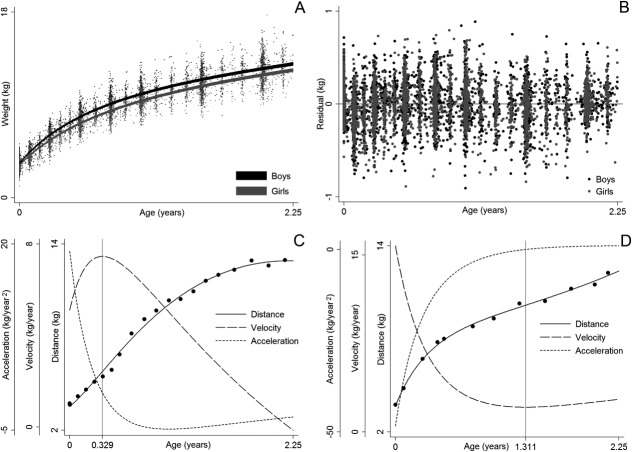
The final model provided a reasonable fit for the data with a RSD of 0.26 kg. The parameter estimates are not shown because they are not particularly easy to interpret. Instead, Figure 2 illustrates some key findings/ properties of the model. Panel A shows that the sample average growth curve was higher in boys than girls at birth, and that the magnitude of this difference increased to approximately age one year, after which it remained relatively stable. Panel B shows that the level one residuals were relatively homoscedastic over age and that there was little evidence of systematic fitting of curves that were too high or too low at any given age, perhaps with the exception of fitting too low at birth (causing positive level one residuals) and too high at age 1 month (causing negative level one residuals). This pattern has been reported before (Berkey and Reed, 1987; Johnson, 2010; Simondon et al., 1992) and could be expected given that the Berkey-Reed model cannot describe any period of neonatal weight loss. Nonetheless, it has consistently been found to be the best structural model for infant growth (Berkey and Reed, 1987; Chirwa et al., 2014; Johnson, 2010; Pizzi et al., 2014; Simondon et al., 1992). Panel C show the growth distance, velocity, and acceleration curves of one infant who had an early inflection point at age 0.3 years and Panel D shows the curves of one infant who had a late inflection point at age 1.311 years. The majority of infants (70%) actually had an inflection point that occurred outside the studied age range, with only 5% having an early inflection between ages 0.006 and 0.508 years and 25% having a late inflection between ages 0.807 and 1.992 years. Typical weight gain in the sample was therefore characterized by deceleration and declining velocity across the entire age period studied. Similar results were reported in the original publication of the Berkey-Reed (1987) model, but other studies with more frequent data early in life claim to have identified (using the Berkey-Reed model) early inflection points and thus a peak in velocity for all infants in their sample (Mook-Kanamori et al., 2011; Sovio et al., 2009; Tzoulaki et al., 2010). Clearly, the identification and location of traits in the distance, velocity, and acceleration curves are dependent on the number of inflection points the model allows and the amount and frequency of data to which the model fits. A relatively simple example has been used for demonstrative purposes; the model could be developed to account for secular trends, neonatal weight loss, more than one inflection point for some infants, possible complex level one variation (e.g., explicitly model the level one residuals as a function of age, sex, or some other variable), and possible autocorrelation of level one residuals.
Fig 2.
Example results from a mixed effects Berkey-Reed growth curve model applied to serial infant weight data on 391 boys and 369 girls in the Fels Longitudinal Study: 95% confidence interval of sample average curve plotted against the observed data by sex (A), residuals by sex (B), example girl with an early inflection point (C), and example boy with a late inflection point (D).
PATTERNS OF GROWTH
It should now be clear that three different strategies can be used to estimate individual growth curves in a sample, and subsequently (i.e., individual curve models) or simultaneously (i.e., mixed effects and latent growth curve models) estimate a mean-constant or sample average growth curve. The assumption here is that all individuals are drawn from a single population and that a single average growth curve adequately approximates the entire population. Given our knowledge of the growth process, this assumption is likely to be unrealistic in most instances. Take infant linear growth, for example; one group of infants will show catch-up growth, another will show catch-down growth, and another will adhere to a particular centile position (Cameron, 2012).
Growth mixture modeling
Growth mixture models relax the assumption of there being a single average growth curve by allowing parameter differences across unobserved subsamples; different average growth curves are thus estimated for different latent classes of people. In practice, growth mixture models combine a latent curve model (to estimate the average growth curves) with a multinomial logistic regression model (to estimate a categorical latent class variable) (Muthèn, ,). As with mixed effects growth curve models, there are child specific deviations from the average growth curve parameters within each latent class. Constraining this between-child variance within each latent class to be zero results in a special type of growth mixture model called a latent class growth model.
These models allow empirical quantification of different patterns of growth and epidemiological investigation of the determinants and consequences of latent class membership. Independent variables can also be included to investigate systematic differences in the sample average growth curves. A real strength of this strategy is that, when doing this, the estimates can be allowed to vary across the latent classes. The gradient of a curve may be steeper for girls compared with boys in one latent class but shallower in another latent class, for example. Conversely, in terms of limitations, the models are computationally challenging, which makes it difficult to fit anything other than linear or low order polynomial models; model selection is subjective, even if based on overall fit according to the Bayesian Information Criterion (BIC) (Schwarz, 1978), quality of classification judged by the entropy statistic (Muthèn, 2001), and interpretability of the latent classes; the models are likely to identify latent classes even if none exist; and interpretation of the latent classes is not always straightforward. As a result, this strategy should be approached with due caution.
Worked example
A series of growth mixture models with increasingly greater number of latent classes were applied to 4,929 serial measurements of BMI, collected semiannually between 10 and 18 years of age, on 417 girls born 1929 to 2000. The only requirement was that each girl had a minimum of three measurements. A quadratic polynomial function of age (such as that in Fig. 1) was used to account for any non-linearity in the BMI trajectories. The means of the growth factors were allowed to vary across the latent classes, but the variances and covariances of the growth factors were each constrained to be equal across the latent classes. In addition, residual errors were constrained to be constant over age and the same in all latent classes. Applying such constraints is common practice and can help model estimation.
The sample average growth curves of the different models are shown in Figure 3. The model with two latent classes in Panel A identified a “normal weight” class to which 94% of the girls were most likely to belong and an “obese” class to which 6% of the girls were most likely to belong. These classes were present in all subsequent models, with the addition of a “overweight/ pubertal obese” class in Panel B, the further addition of a “overweight/ pre-pubertal obese” class in Panel C, and the even further addition of an “overweight” class in Panel D. Growth mixture models compute probabilities for each participant of belonging to each class; entropy was high for each model (0.911–0.955), thereby indicating that the average probabilities of girls belonging to the class to which they were assigned (based on the one with the highest probability) were close to one. The BIC decreased across the models, from 14,844 in the model with two classes to 14,774 in the model with five classes, thereby indicating that there was marginal improvement in model fit as the number of classes increased.
Fig 3.
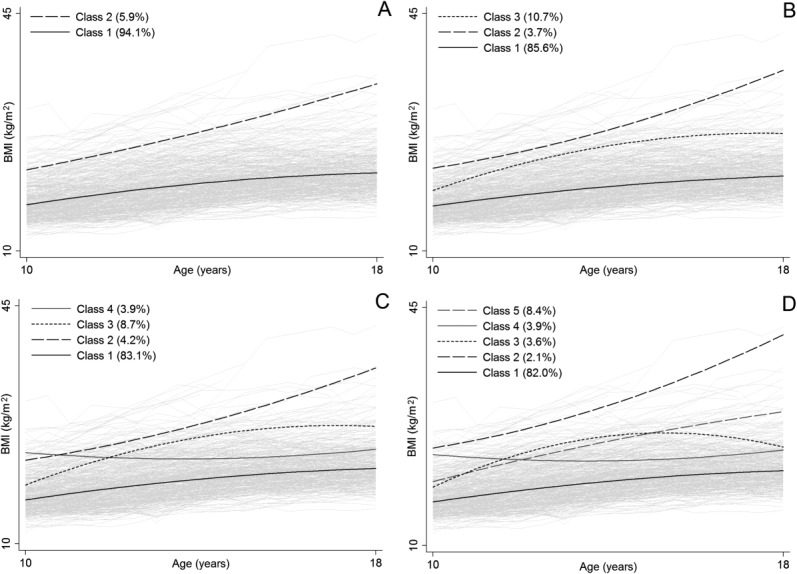
Example results from growth mixture models with two (A), three (B), four (C), or five (D) latent classes applied to serial body mass index (BMI) data on 417 girls aged 10 to 18 years in the Fels Longitudinal Study.
In this scenario, where all models seem to be biologically plausible and there is little distinction between them in terms of model fit, it is very difficult to pick a “best” model. It may not be sensible to select the three, four, or five class solutions because at least one of the classes comprises less than 5% of the sample (Muthèn, 2001; Nagin and Tremblay, 2001). The two class solution is easy to interpret, but could be viewed as being overly simplistic. Nonetheless, even this simple model provides the opportunity to explore how other variables are related to class membership and the sample average growth curves. It would have been possible, for example, to test whether or not more recent birth year (1) incurred increased odds of being in the obese class compared with the normal weight class, or (2) was more strongly related to a higher intercept and steeper slope of the sample average growth curve in the obese class compared with that in the normal weight class.
CONCLUSIONS
Human growth research requires grounding not only in human biology but also in statistics, and specifically in longitudinal data analysis techniques. This is true regardless of whether you are a human biologist, biological anthropologist, or epidemiologist, etc. The key analytical strategies for growth research in the present article are presented is in increasing order of complexity, such that a researcher using one strategy ought to already be competent in all the preceding strategies. “Jumping in at the deep end” will inevitably lead to reliance on overall model fit statistics, without really knowing what a model is doing or how to fine tune it to provide the most biologically plausible representation of the growth process.
Of course, none of the above negates the need to use the most appropriate strategy to address a research aim, given the available data. All too often, serial measurements are treated as cross-sectional in analyses that do not harness the power of longitudinal data. There is also a natural tendency to become accustomed to a strategy, without critiquing all of the options each time a new study is initiated. The table in the present article may be useful here, because it clearly shows when the key analytical strategies in growth research should be used. If the choice is not obvious, the logical thing to do is to analyze the data a number of different ways and compare the results. Such methodological investigation is, in itself, important because this will guide other researchers in their decision making.
Finally, it is necessary to reiterate that this article only provides as overview of growth analysis methods; it could in fact be given as a one or two hour lecture, complete with references for further reading. As the researcher delves deeper, they will quickly become aware that the statistical methods necessary to analyze human growth data can be as complex as the biology underlying the process.
Acknowledgments
The author thanks Professor Tim J Cole (UCL Institute of Child Health) for valuable feedback on an earlier version of this article and Doctor Graciela Muniz-Terrera (MRC Unit of Lifelong Health and Ageing at UCL) for statistical support.
Useful Resources
This is a core text book on human growth research methods and is recommended to all researchers considering any type of growth curve analysis:
Hauspie RC, Cameron N, Molinari L. 2004. Methods in Human Growth Research. Cambridge, UK: Cambridge University Press.
This book is recommended to researchers wanting to apply mixed effects growth curve models:
Goldstein H. 2010. Multilevel statistical models. London: Wiley-Blackwell.
This book is recommended to researchers wanting to apply latent growth curve models:
Bollen KA, Curran PJ. 2006. Latent curve models: A structural equation perspective. Hoboken, New Jersey, USA: John Wiley & Sons.
The website of the Centre for Multilevel Modelling is an excellent resource for researchers wanting to apply mixed effects growth curve models. There you can find online courses, videos and voice-over presentations, datasets with accompanying code, software, recommended books, and so on:
Although many universities and other organizations run short courses on statistical techniques relevant to human growth research, those provided by the Utrecht Summer School and the Interuniversity Consortium for Political and Social Research (ICPSR) are recommended to researchers wanting to apply latent growth curve models or growth mixture models:
http://www.utrechtsummerschool.nl/courses/social-sciences
http://www.icpsr.umich.edu/icpsrweb/landing.jsp
From the website of Harlow Healthcare, it is possible to download a free excel macro called LMSgrowth which, among other things, computes external Z-scores according to a number of growth references. Also available from this website is LMSchartmaker, a user-written program to construct your own growth reference: http://www.healthforallchildren.com/
The Centers for Disease Control and Prevention in the United States of America and the World Health Organization also have software that can be used to compute external Z-scores according to their growth references:
http://www.cdc.gov/growthcharts/computer_programs.htm
http://www.who.int/childgrowth/software/
Most statistical packages have the capability to fit the models described in this article, although Stata is recommended for everything up to and including mixed effects growth curve models and Mplus is recommended for latent growth curve models and growth mixture models:
The utility of Stata for mixed effects growth curve modeling is greatly improved with the use of the command runmlwin, which calls on MLwiN, a specialist software package for mixed effects modeling, to fit a model and returns the results to Stata:
http://www.bristol.ac.uk/cmm/software/runmlwin/
The statistical packages R and SAS are recommended for non-linear mixed effects growth curve models (i.e., where the dependent variable is not a linear function of the parameters), because Stata and MLwiN do not have this capability:
LITERATURE CITED
- Adair LS, Fall CH, Osmond C, Stein AD, Martorell R, Ramirez-Zea M, Sachdev HS, Dahly DL, Bas I, Norris SA, Micklesfield L, Hallal P, Victora CG. Associations of linear growth and relative weight gain during early life with adult health and human capital in countries of low and middle income: findings from five birth cohort studies. Lancet. 2013;382:525–534. doi: 10.1016/S0140-6736(13)60103-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adair LS, Martorell R, Stein AD, Hallal PC, Sachdev HS, Prabhakaran D, Wills AK, Norris SA, Dahly DL, Lee NR, Victora CG. Size at birth, weight gain in infancy and childhood, and adult blood pressure in 5 low- and middle-income-country cohorts: when does weight gain matter? Am J Clin Nutr. 2009;89:1383–1392. doi: 10.3945/ajcn.2008.27139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alwasel SH, Harrath A, Aljarallah JS, Abotalib Z, Osmond C, Al Omar SY, Khaled I, Barker DJ. Intergenerational effects of in utero exposure to Ramadan in Tunisia. Am J Hum Biol. 2013;25:341–343. doi: 10.1002/ajhb.22374. [DOI] [PubMed] [Google Scholar]
- Azcorra H, Varela-Silva MI, Rodriguez L, Bogin B, Dickinson F. Nutritional status of Maya children, their mothers, and their grandmothers residing in the City of Merida, Mexico: revisiting the leg-length hypothesis. Am J Hum Biol. 2013;25:659–665. doi: 10.1002/ajhb.22427. [DOI] [PubMed] [Google Scholar]
- Bauer DJ. Estimating multilevel linear models as structural equation models. J Educ Behav Stat. 2003;28:135–167. [Google Scholar]
- Benn RT. Some mathematical properties of weight-for-height indices used as measures of adiposity. Br J Prev Soc Med. 1971;25:42–50. doi: 10.1136/jech.25.1.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berkey CS, Colditz GA. Adiposity in adolescents: change in actual BMI works better than change in BMI z score for longitudinal studies. Ann Epidemiol. 2007;17:44–50. doi: 10.1016/j.annepidem.2006.07.014. [DOI] [PubMed] [Google Scholar]
- Berkey CS, Reed RB. A model for describing normal and abnormal growth in early childhood. Hum Biol. 1987;59:973–987. [PubMed] [Google Scholar]
- Bingham DD, Varela-Silva MI, Ferrao MM, Augusta G, Mourao MI, Nogueira H, Marques VR, Padez C. Socio-demographic and behavioral risk factors associated with the high prevalence of overweight and obesity in portuguese children. Am J Hum Biol. 2013;25:733–742. doi: 10.1002/ajhb.22440. [DOI] [PubMed] [Google Scholar]
- Bollen KA, Curran PJ. Latent curve models: A structural equation perspective. Hoboken, NY: John Wiley & Sons; 2006. [Google Scholar]
- Cameron N. The human growth curve, canalization, and catch-up growth. In: Cameron N, Bogin B, editors. Human growth and development. London, UK: Academic Press; 2012. pp. 1–22. [Google Scholar]
- Cameron N, Preece MA, Cole TJ. Catch-up growth or regression to the mean? Recovery from stunting revisited. Am J Hum Biol. 2005;17:412–417. doi: 10.1002/ajhb.20408. [DOI] [PubMed] [Google Scholar]
- Chirwa ED, Griffiths PL, Maleta K, Norris SA, Cameron N. Multi-level modeling of longitudinal child growth data from the Birth-to-Twenty Cohort: a comparison of growth models. Ann Hum Biol. 2014;41:166–177. doi: 10.3109/03014460.2013.839742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole TJ. A method for assessing age-standardized weight-for-height in children seen cross-sectionally. Ann Hum Biol. 1979;6:249–268. doi: 10.1080/03014467900007252. [DOI] [PubMed] [Google Scholar]
- Cole TJ. Weight/heightp compared to weight/height2 for assessing adiposity in childhood: influence of age and bone age on p during puberty. Ann Hum Biol. 1986;13:433–451. doi: 10.1080/03014468600008621. [DOI] [PubMed] [Google Scholar]
- Cole TJ. Weight-stature indices to measure underweight, overweight and obesity. In: Himes JH, editor. Anthropometric assessment of nutritional status. New York, NY: Wiley Periodicals; 1991. pp. 83–111. [Google Scholar]
- Cole TJ. The use and construction of anthropometric growth reference standards. Nutr Res Rev. 1993;6:19–50. doi: 10.1079/NRR19930005. [DOI] [PubMed] [Google Scholar]
- Cole TJ. Conditional reference charts to assess weight gain in British infants. Arch Dis Child. 1995;73:8–16. doi: 10.1136/adc.73.1.8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole TJ. Modeling postnatal exposures and their interactions with birth size. J Nutr. 2004;134:201–204. doi: 10.1093/jn/134.1.201. [DOI] [PubMed] [Google Scholar]
- Cole TJ. Growth references and standards. In: Cameron N, Bogin B, editors. Human growth and development. London, UK: Academic Press; 2012. pp. 537–566. [Google Scholar]
- Cole TJ, Donaldson MD, Ben-Shlomo Y. SITAR–a useful instrument for growth curve analysis. Int J Epidemiol. 2010;39:1558–1566. doi: 10.1093/ije/dyq115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole TJ, Faith MS, Pietrobelli A, Heo M. What is the best measure of adiposity change in growing children: BMI, BMI %, BMI Z-score or BMI centile? Eur J Clin Nutr. 2005;59:419–425. doi: 10.1038/sj.ejcn.1602090. [DOI] [PubMed] [Google Scholar]
- Cole TJ, Green PJ. Smoothing reference centile curves: the LMS method and penalized likelihood. Stat Med. 1992;11:1305–1319. doi: 10.1002/sim.4780111005. [DOI] [PubMed] [Google Scholar]
- Curran PJ. Have multilevel models been structural equation models all along? Multivariate Behav Res. 2003;38:529–568. doi: 10.1207/s15327906mbr3804_5. [DOI] [PubMed] [Google Scholar]
- De Onis M, Garza C, Onyango AW, Borghi E. Comparison of the WHO child growth standards and the CDC 2000 growth charts. J Nutr. 2007;137:144–148. doi: 10.1093/jn/137.1.144. [DOI] [PubMed] [Google Scholar]
- De Stavola BL, Nitsch D, dos Santos Silva I, McCormack V, Hardy R, Mann V, Cole TJ, Morton S, Leon DA. Statistical issues in life course epidemiology. Am J Epidemiol. 2006;163:84–96. doi: 10.1093/aje/kwj003. [DOI] [PubMed] [Google Scholar]
- Duran M, Gillespie J, Malina RM, Little BB. Growth and weight status of rural Texas school youth. Am J Hum Biol. 2013;25:71–77. doi: 10.1002/ajhb.22343. [DOI] [PubMed] [Google Scholar]
- Franklin MF. Comparison of weight and height relations in boys from 4 countries. Am J Clin Nutr. 1999;70:157S–162S. [PubMed] [Google Scholar]
- Frontini MG, Bao W, Elkasabany A, Srinivasan SR, Berenson G. Comparison of weight-for-height indices as a measure of adiposity and cardiovascular risk from childhood to young adulthood: the Bogalusa heart study. J Clin Epidemiol. 2001;54:817–822. doi: 10.1016/s0895-4356(01)00343-2. [DOI] [PubMed] [Google Scholar]
- Galton F. Regression towards mediocrity in hereditary stature. J Anthrop Inst. 1886;15:246–263. [Google Scholar]
- Gamborg M, Andersen PK, Baker JL, BudtZ-Jorgensen E, Jorgensen T, Jensen G, Sorensen TI. Life course path analysis of birth weight, childhood growth, and adult systolic blood pressure. Am J Epidemiol. 2009;169:1167–1178. doi: 10.1093/aje/kwp047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gamborg M, Jensen GB, Sorensen TI, Andersen PK. Dynamic path analysis in life-course epidemiology. Am J Epidemiol. 2011;173:1131–1139. doi: 10.1093/aje/kwq502. [DOI] [PubMed] [Google Scholar]
- Gasser T, Engel J, Seifert B. Nonparametric function estimation. In: Rao C, editor. Handbook of statistics. Amsterdam, The Netherlands: Elsevier Science; 1993. pp. 423–465. [Google Scholar]
- Goldstein H. Efficient statistical modeling of longitudinal data. Ann Hum Biol. 1986;13:129–141. doi: 10.1080/03014468600008271. [DOI] [PubMed] [Google Scholar]
- Goldstein H, Brown WL, Rabash J. Partitioning variation in multilevel models. Understanding Stat. 2002;1:223–231. [Google Scholar]
- Hattori K, Hirohara T. Age change of power in weight/height(p) indices used as indicators of adiposity in Japanese. Am J Hum Biol. 2002;14:275–279. doi: 10.1002/ajhb.10037. [DOI] [PubMed] [Google Scholar]
- Hauspie RC, Cameron N, Molinari L. Methods in human growth research. Cambridge, UK: Cambridge University Press; 2004. [Google Scholar]
- Hauspie RC, Molinari L. Parametric models for postnatal growth. In: Hauspie RC, Cameron N, Molinari L, editors. Methods in human growth research. Cambridge, UK: Cambridge University Press; 2004. pp. 205–233. [Google Scholar]
- Howe LD, Tilling K, Matijasevich A, Petherick ES, Santos AC, Fairley L, Wright J, Santos IS, Barros AJ, Martin RM, Kramer MS, Bogdanovich N, Matush L, Barros H, Lawlor DA. Linear spline multilevel models for summarising childhood growth trajectories: a guide to their application using examples from five birth cohorts. Stat Methods Med Res. doi: 10.1177/0962280213503925. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson W. PhD Thesis. The growth of Bradford infants. UK: Loughborough University; 2010. [Google Scholar]
- Johnson W, Balakrishna N, Griffiths PL. Modeling physical growth using mixed effects models. Am J Phys Anthropol. 2013a;150:58–67. doi: 10.1002/ajpa.22128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson W, Choh AC, Lee M, Towne B, Czerwinski SA, Demerath EW. Characterization of the infant BMI peak: sex differences, birth year cohort effects, association with concurrent adiposity, and heritability. Am J Hum Biol. 2013b;25:378–388. doi: 10.1002/ajhb.22385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson W, Vazir S, FernandeZ-Rao S, Kankipati VR, Balakrishna N, Griffiths PL. Using the WHO 2006 child growth standard to assess the growth and nutritional status of rural south Indian infants. Ann Hum Biol. 2012a;39:91–101. doi: 10.3109/03014460.2012.657680. [DOI] [PubMed] [Google Scholar]
- Johnson W, Wright J, Cameron N. The risk of obesity by assessing infant growth against the UK-WHO charts compared to the UK90 reference: findings from the Born in Bradford birth cohort study. BMC Pediatr. 2012b;12:104. doi: 10.1186/1471-2431-12-104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keijzer-Veen MG, Euser AM, van Montfoort N, Dekker FW, Vandenbroucke JP, Van Houwelingen HC. A regression model with unexplained residuals was preferred in the analysis of the fetal origins of adult diseases hypothesis. J Clin Epidemiol. 2005;58:1320–1324. doi: 10.1016/j.jclinepi.2005.04.004. [DOI] [PubMed] [Google Scholar]
- Keys A, Fidanza F, Karvonen MJ, Kimura N, Taylor HL. Indices of relative weight and obesity. J Chronic Dis. 1972;25:329–343. doi: 10.1016/0021-9681(72)90027-6. [DOI] [PubMed] [Google Scholar]
- Kuczmarski RJ, Ogden CL, Grummer-Strawn LM, Flegal KM, Guo SS, Wei R, Mei Z, Curtin LR, Roche AF, Johnson CL. CDC growth charts: United States. Adv Data. 2000;314:1–27. [PubMed] [Google Scholar]
- Kurki HK. Skeletal variability in the pelvis and limb skeleton of humans: does stabilizing selection limit female pelvic variation? Am J Hum Biol. 2013;25:795–802. doi: 10.1002/ajhb.22455. [DOI] [PubMed] [Google Scholar]
- Laird NM, Ware JH. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. [PubMed] [Google Scholar]
- Lucas A, Fewtrell MS, Cole TJ. Fetal origins of adult disease-the hypothesis revisited. BMJ. 1999;319:245–249. doi: 10.1136/bmj.319.7204.245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacCallum DM, Kim C, Malarkey WB, KiecoltGlaser JK. Studying multivariate change using multilevel models and latent curve models. Multivariate Behav Res. 1997;32:215–253. doi: 10.1207/s15327906mbr3203_1. [DOI] [PubMed] [Google Scholar]
- Metcalf BS, Hosking J, Fremeaux AE, Jeffery AN, Voss LD, Wilkin TJ. BMI was right all along: taller children really are fatter (implications of making childhood BMI independent of height) EarlyBird 48. Int J Obes. 2011;35:541–547. doi: 10.1038/ijo.2010.258. [DOI] [PubMed] [Google Scholar]
- Mook-Kanamori DO, Durmus B, Sovio U, Hofman A, Raat H, Steegers EA, Jarvelin MR, Jaddoe VW. Fetal and infant growth and the risk of obesity during early childhood: the Generation R Study. Eur J Endocrinol. 2011;165:623–630. doi: 10.1530/EJE-11-0067. [DOI] [PubMed] [Google Scholar]
- Moura-Dos-Santos M, Wellington-Barros J, Brito-Almeida M, Manhaes-de-Castro R, Maia J, Gois Leandro C. Permanent deficits in handgrip strength and running speed performance in low birth weight children. Am J Hum Biol. 2013;25:58–62. doi: 10.1002/ajhb.22341. [DOI] [PubMed] [Google Scholar]
- Muthèn B. Second-generation structural equation modeling with a combination of categorical and continuous latent variables: new opportunities for latent class/latent growth modeling. In: Collins LM, Sayers A, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 291–322. [Google Scholar]
- Muthèn B. Latent variable analysis: Growth mixture modeling and related techniques for longitudinal data. In: Kaplan D, editor. Handbook of quantitative methodology for the social sciences. Newbury Park, CA: Sage Publications; 2004. pp. 345–368. [Google Scholar]
- Nagin DS, Tremblay RE. Analyzing developmental trajectories of distinct but related behaviors: a group based method. Psychological methods. 2001;6:18–34. doi: 10.1037/1082-989x.6.1.18. [DOI] [PubMed] [Google Scholar]
- Pizzi C, Cole TJ, Corvalan C, Silva IDS, Richiardi L, De Stavola BL. On modeling early life weight trajectories. J Roy Stat Soc Ser A (Stat Soc) 2014;177:371–396. [Google Scholar]
- Preece MA, Baines MJ. A new family of mathematical models describing the human growth curve. Ann Hum Biol. 1978;5:1–24. doi: 10.1080/03014467800002601. [DOI] [PubMed] [Google Scholar]
- Rabe-Hesketh S, Skrondal A. Multilevel and longitudinal modeling using Stata. College Station, TX: Stata Press; 2008. [Google Scholar]
- Redmond JG, Gage TB, Kiyamu M, Brutsaert TD. The effect of intra-uterine growth restriction on blood lipids and response to exercise training. Am J Hum Biol. 2013;25:844–846. doi: 10.1002/ajhb.22442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richards AA, Fulford AJ, Prentice AM, Moore SE. Birth weight, season of birth and postnatal growth do not predict levels of systemic inflammation in Gambian adults. Am J Hum Biol. 2013;25:457–464. doi: 10.1002/ajhb.22413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson GK. That BLUP is a good thing: the estimation of random effects. Stat Sci. 1991;6:15–32. [Google Scholar]
- Roche AF. Growth, maturation and body composition: the Fels longitudinal study 1929–1991. Cambridge, UK: Cambridge University Press; 1992. [Google Scholar]
- Ruiz-Castell M, Carsin AE, Barbieri FL, Paco P, Gardon J, Sunyer J. Child patterns of growth delay and cognitive development in a Bolivian mining city. Am J Hum Biol. 2013;25:94–100. doi: 10.1002/ajhb.22346. [DOI] [PubMed] [Google Scholar]
- Sayers A, Baines M, Tilling K. A new family of mathematical models describing the human growth curve - Erratum: Direct calculation of peak height velocity, age at take-off and associated quantities. Ann Hum Biol. 2013;40:298–299. doi: 10.3109/03014460.2013.772655. [DOI] [PubMed] [Google Scholar]
- Scammon RE. The first seriatim study of human growth. Am J Phys Anthropol. 1972;10:329–326. doi: 10.1002/ajpa.1330540103. [DOI] [PubMed] [Google Scholar]
- Schumacker RE, Lomax RG. A beginner's guide to structural equation modeling. New York, NY: Routledge; 2010. [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. [Google Scholar]
- Simondon KB, Simondon F, Delpeuch F, Cornu A. Comparative study of five growth models applied to weight data from Congolese infants between birth and 13 months of age. Am J Hum Biol. 1992;4:327–335. doi: 10.1002/ajhb.1310040308. [DOI] [PubMed] [Google Scholar]
- Sovio U, Bennett AJ, Millwood IY, Molitor J, O'Reilly PF, Timpson NJ, Kaakinen M, Laitinen J, Haukka J, Pillas D, Tzoulaki I, Hoggart C, Coin LJ, Whittaker J, Pouta A, Hartikainen AL, Freimer NB, Widen E, Peltonen L, Elliott P, McCarthy MI, Jarvelin MR. Genetic determinants of height growth assessed longitudinally from infancy to adulthood in the northern Finland birth cohort 1966. PLoS Genet. 2009;5:e1000409. doi: 10.1371/journal.pgen.1000409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sovio U, Kaakinen M, Tzoulaki I, Das S, Ruokonen A, Pouta A, Hartikainen AL, Molitor J, Jarvelin MR. How do changes in body mass index in infancy and childhood associate with cardiometabolic profile in adulthood? Findings from the Northern Finland Birth Cohort 1966 Study. Int J Obes. 2014;38:53–59. doi: 10.1038/ijo.2013.165. [DOI] [PubMed] [Google Scholar]
- Sovio U, Mook-Kanamori DO, Warrington NM, Lawrence R, Briollais L, Palmer CN, Cecil J, Sandling JK, Syvanen AC, Kaakinen M, Beilin LJ, Millwood IY, Bennett AJ, Laitinen J, Pouta A, Molitor J, Davey Smith G, Ben-Shlomo Y, Jaddoe VW, Palmer LJ, Pennell CE, Cole TJ, McCarthy MI, Jarvelin MR, Timpson NJ. Association between common variation at the FTO locus and changes in body mass index from infancy to late childhood: the complex nature of genetic association through growth and development. PLoS Genet. 2011;7:e1001307. doi: 10.1371/journal.pgen.1001307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staiano AE, Broyles ST, Gupta AK, Malina RM, Katzmarzyk PT. Maturity-associated variation in total and depot-specific body fat in children and adolescents. Am J Hum Biol. 2013;25:473–479. doi: 10.1002/ajhb.22380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu YK, Gilthorpe MS. Unexplained residuals models are not solutions to statistical modeling of the fetal origins hypothesis. J Clin Epidemiol. 2007;60:318–319. doi: 10.1016/j.jclinepi.2006.07.004. ; author reply 319–320. [DOI] [PubMed] [Google Scholar]
- Tu YK, Tilling K, Sterne JA, Gilthorpe MS. A critical evaluation of statistical approaches to examining the role of growth trajectories in the developmental origins of health and disease. Int J Epidemiol. 2013;42:1327–1339. doi: 10.1093/ije/dyt157. [DOI] [PubMed] [Google Scholar]
- Tzoulaki I, Sovio U, Pillas D, Hartikainen AL, Pouta A, Laitinen J, Tammelin TH, Jarvelin MR, Elliott P. Relation of immediate postnatal growth with obesity and related metabolic risk factors in adulthood: the northern Finland birth cohort 1966 study. Am J Epidemiol. 2010;171:989–998. doi: 10.1093/aje/kwq027. [DOI] [PubMed] [Google Scholar]
- Vazquez-Vazquez A, Azcorra H, Falfan I, Argaez J, Kantun D, Dickinson F. Effects of Maya ancestry and environmental variables on knee height and body proportionality in growing individuals in Merida, Yucatan. Am J Hum Biol. 2013;25:586–593. doi: 10.1002/ajhb.22417. [DOI] [PubMed] [Google Scholar]
- Wen X, Kleinman K, Gillman MW, Rifas-Shiman SL, Taveras EM. Childhood body mass index trajectories: modeling, characterizing, pairwise correlations and socio-demographic predictors of trajectory characteristics. BMC Med Res Methodol. 2012;12:38. doi: 10.1186/1471-2288-12-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO Multicentre Growth Reference Study Group. WHO Child Growth Standards: methods and development: length/height-for-age, weight-for-age, weight-for-length, weight-for-height, and body mass index-for-age Geneva. Switzerland: World Health Organisation; 2006. [Google Scholar]
- Wills AK, Silverwood RJ, De Stavola BL. Comment on Tu et al. A critical evaluation of statistical approaches to examining the role of growth trajectories in the developmental origins of health and disease. Int J Epidemiol. 2014 doi: 10.1093/ije/dyu032. (in press) [DOI] [PubMed] [Google Scholar]
- Wright CM, Williams AF, Elliman D, Bedford H, Birks E, Butler G, Sachs M, Moy RJ, Cole TJ. Using the new UK-WHO growth charts. BMJ. 2010;340:c1140. doi: 10.1136/bmj.c1140. [DOI] [PubMed] [Google Scholar]