Testing concordance of instrumental variable effects in generalized linear models with application to Mendelian randomization

Abstract

Instrumental variable regression is one way to overcome unmeasured confounding and estimate causal effect in observational studies. Built on structural mean models, there has been considerale work recently developed for consistent estimation of causal relative risk and causal odds ratio. Such models can sometimes suffer from identification issues for weak instruments. This hampered the applicability of Mendelian randomization analysis in genetic epidemiology. When there are multiple genetic variants available as instrumental variables, and causal effect is defined in a generalized linear model in the presence of unmeasured confounders, we propose to test concordance between instrumental variable effects on the intermediate exposure and instrumental variable effects on the disease outcome, as a means to test the causal effect. We show that a class of generalized least squares estimators provide valid and consistent tests of causality. For causal effect of a continuous exposure on a dichotomous outcome in logistic models, the proposed estimators are shown to be asymptotically conservative. When the disease outcome is rare, such estimators are consistent due to the log-linear approximation of the logistic function. Optimality of such estimators relative to the well-known two-stage least squares estimator and the double-logistic structural mean model is further discussed.

1. Introduction

Causal effect in observational studies is often masked by unmeasured confounding variables. Instrumental variable regression is commonly used in econometrics to overcome the difficulty of inferring causality in the presence of unmeasured confounding [1], provided that instrumental variables are independent of unmeasured confounding, and affect the outcome only through the exposure. One emerging application of the instrumental variable research is the so-called “Mendelian randomization analysis”, where inherited genetic variants are used as instrumental variables to assess the causal effect of an intermediate exposure on a disease outcome [2, 3].

Mendelian randomization analysis exploits the concept that genetic predisposition was transmitted randomly at meiosis from parents to offspring, and therefore largely independent of non-genetic confounding variables. If the genetic variant is associated, preferably strongly, with the exposure, and there is no alternative pathway from the genetic variant to the disease outcome, the test of causality from the exposure to the disease is equivalent to the test of association between the genetic variant and the disease outcome [2, 4]. For continuous exposures and outcomes and with additional assumptions, classical instrumental variable approaches such as the two-stage least squares method yield consistent and asymptotically normally distributed estimator of the causal effect [5, 6].

The disease outcomes in epidemiological research, however, are predominantly dichotomous, upon which genetic effects are typically parameterized by odds ratios in logistic models. Estimation procedures developed in econometrics, for example the two-stage least squares method, are motivated by continuous outcomes, and therefore not exactly applicable to logistic models. With more restrictive, sometimes untestable, assumptions, estimation of causal effects on binary outcomes via instrumental variable regression has been studied. See, for example, recent reviews on this topic [7, 8]. In randomized clinical trials with noncompliance, instrumental variable regression has been formulated by potential outcomes and further developed to estimate the causal effect among those being treated [9, 10, 11]. Notably, a double-logistic structural mean model (SMM) has been proposed for binary trial outcomes [12], augmenting the structural mean model by an association logistic model to achieve identifiability. Non-saturated association models can be uncongenial to the logistic SMM, especially when there are covariates in addition to instrumental variables, leading to bias if misspecified [7]. Alternatively, a selection-bias function can be parameterized to avoid the uncongenial issue [11], though computationally demanding in the presence of covariates.

In the context of Mendelian randomization studies, various modeling frameworks, causal estimands and assumptions were carefully discussed [13, 7]. Use of the double-logistic SMM has been proposed [14], accounting for case-control sampling. In contrast to the use of randomized treatment assignment as instrumental variables, the use of genetic variants as instrumental variables received a fair share of criticisms [15, 16, 17], mainly on whether genetic variants can be independent of all confounding variables in the study population. Indeed, genetic association analyses typically have to adjust for covariates such as demographic factors, population stratification and possibly clinical predictors to avoid confounding. In genome-wide association studies top 5-10 principle components are routinely added into the regression as covariates to account for hidden population structures [18]. Adjusting for high dimensional covariates in double-logistic SMM, though theoretically capable, adds complexity to estimating equations on top of the uncongeniality issue of the association model [10, 7], therefore can be computationally challenging. Moreover, for weak instruments examplified by genetic variants, the moment condition used in the double-logistic regression often leads to poor or lack of identification of the causal parameter [19].

In this article, we focus on testing the causal effect in a generalized linear model via instrumental variables. Indeed, the original idea on Mendelian randomization put forth by Katan was based on the hypothesis test whether low serum cholesterol increase risk of cancer [2]. In his seminal paper, Katan reasoned that a simple comparison of APOE genotypes between cancer patients and controls should suffice to test the causal effect, that is, if the hypothesis of low serum cholesterol increasing cancer risk is true, than cancer patients would carry more cholesterol-lowing genotypes than controls. This testing framework was later developed more rigorously with proper IV assumptions [4]. In our view, assessing causal effect in epidemiological studies is exploratory and hypothesis-generating, an earlier step toward understanding the pathway of disease etiology. The estimation of causal odds ratio has been difficult, and often requires strenuous assumptions. Even for the double-logistic SMM that in theory shall deliver consistent estimates, there are computation issues as we showed in our simulations. It is therefore of interest to develop robust procedures to test the causal effect under a minimal set of assumptions, even if estimation of the causal effect can sometimes be difficult. Subsequent functional studies, or randomized clinical trials if feasible, will give a more definitive answer on causal effect.

The contributions of this work are summarized below:

• With standard instrumental variable assumptions and in generalized linear models, we developed a consistent and valid test of causal effect being zero using a test of concordance between two sets of instrumental variable effects. The concordance of instrumental variable effects strengthens the well-known dose-response criterion to assess causality in medical and epidemiological studies [20, 21, 22, 23].

• When the disease outcome is binary and the exposure is typically a continuous biomarker, we show a stronger result that the linear slope (concordance) parameter we obtain is indeed asymptotic conservative toward the true causal effect. This result echoes the previous result in randomization trials when important predictors are omitted [24].

• For rare diseases commonly occurred in epidemiologic studies, where logistic models can be approximated by log-linear models, we show the linear concordance parameter is indeed the causal parameter, and we compare the efficiency of the proposed estimators with the 2SLS estimator and the double-logistic SMM estimator.

This article is organized as follows. In Section 2.1, we consider causal effect defined in a structural generalized linear model with the presence of unmeasured confounding variables. The salient feature of our approach is that it examines whether the relationship between two sets of instrumental variable effects is concordant. The concordance of the instrumental variable effects means a bigger genetic effect on X leads to a bigger effect on Y, which shall be induced by the causal effect of interest. The multiple, distinct genotypes constitute over-identifying instrumental variables, since only one valid instrumental variable is needed for identifiability in this setting. We show in Section 2.3 that testing concordance of the two sets of genetic effects provides a valid and consistent test for the causal effect.

To operationalize testing, in Section 2.4 we propose a class of linear concordance estimators, which include an ordinary least squares estimator and a generalized least squares estimator. Both estimators are more powerful than the naive approach that tests the global genetic effect on the disease outcome. Notably, when the interest resides on causal effect of a continuous biomarker on a dichotomous disease trait, a stronger result is obtained in Section 2.5 that this class of estimators are asymptotically conservative for a non-zero causal effect.

Further results are derived in Section 2.6 when the disease outcome is rare, so that logistic models can be approximated by log-linear models. We show that the concordance of instrumental variable effects becomes exactly linear. The aforementioned estimators of linear concordance are indeed the minimal distance estimators in the econometric literature [25, 26], all of which are consistent and asymptotically normal estimator of the causal effect. The most efficient estimator is then identified. Interestingly, the two-stage least squares estimator belongs to this class of minimal distance estimators. Relative efficiency of various estimators and approximation of log-linear models is examined in Section 3 by simulation. An example of Mendelian randomization analysis was shown in Section 4, followed by a discussion of the proposed method in Section 5.

2. Methods

2.1. Causal effect

Consider an epidemiological study which measures a disease outcome Y and an observed exposure variable X for n independent subjects. The inferential goal is to assess the causal effect of the exposure X on the disease outcome Y, despite that there is likely unmeasured confounding, collectively denoted by U. To be general, let Y and X be any type of outcome whose distribution follows a generalized linear model [27]. Assuming there is a set of instrumental variables Z satisfying the three conditions Z ⊥ U, E(X∣Z) ≠E(X), and Y ⊥ Z∣(X, U). For ease of exposition, we defer the models adjusted for known covariates until Section 2.7.

We define the causal effect under the structural equation framework, which involves a “structural” model with a parameter that can be interpreted causally, conditional on all common causes U. For continuously distributed Y, consider a simple linear model in expectation

$$E(Y\mid X,U)={\theta }_0+{\theta }_{1}X+{\theta }_{2}U,$$ (1)

where U represent the contribution of all confounding covariates correlated with both X and Y. Y = E(Y∣X, U) + ∊ where ∊ is the residual error that is independent of X, that could include both measurement error and independent predictors of Y. This is a simple structural model assuming there is no interaction between X and U, and the causal effect θ₁ = E(Y∣X = x, U) – E(Y∣X = x – 1, U) is invariant of the level of X. Generalized to any outcome Y whose conditional distribution follows a generalized linear model, a causal effect can be defined as

$${\theta }_1=g\left\{E\right(Y\mid X=x,U\left)\right\}-g\left\{E\right(Y\mid X=x-1,U\left)\right\},$$ (2)

where g is a continuous and monotone increasing link function and θ₁ does not depend on the level of X and U. Popular g functions include the identical function for classical linear models, the logarithm function for multiplicative log-linear models, and the logit function for logistic models. This definition of causal effect is in the spirit of the standard practice in epidemiology that confounding variables, if known, are added into the regression model as covariates.

Causal effect can also be defined by the potential outcomes approach [28]. Let Y(x) denote the potential outcome of Y when X is experimentally altered to an arbitrary value x within the set of all attainable values. Two assumptions are commonly made: the “consistency assumption” that Y(x) = Y with probability 1 when X = x, and the “stable unit treatment value assumption” (SUTVA) that potential outcomes of any subject are not related to other subjects’ potential outcomes. The conditional causal effect in potential outcomes defined in SMM is

$${\tilde{\theta }}_1=g\left[E\right\{Y\left(x\right)\mid X=x,Z=z\left\}\right]-g\left[E\right\{Y(x-1)\mid X=x,Z=z\left\}\right],$$ (3)

which is interpreted as the change of g[E{Y(x)}] when we experimentally alter x by one unit, conditional on the observed X = x and Z = z [12, 11]. This is a simple version of the conditional causal estimand assuming the causal effect does not depend on the level of X and Z. Toward assessing the impact of policy making on the whole population, one may also be interested in the population-average causal effect g[E{Y(x)}] – g[E{Y(x – 1)}][7].

The comparison of the structural equation approach and the potential outcomes approach has been discussed [7, 8]. Structural models can be equivalently written using potential outcome notation [29, 8]. For classical linear causal models and for log-linear causal models, the causal effect defined in the two frameworks, e.g. θ₁ and ${\tilde{\theta }}_1$, are identical regardless of the distribution of U [4]. One criticism of the structural equation approach is that the effect measure is defined within the strata of U that are unobserved, thus harder to interpret, particularly for odds ratios due to the issue of non-collapsibility [30]. Let ⊥ denote stochastic independence between random variables. In the following lemma, we show that for the testing purpose, the two parameters are equivalent under the null hypothesis of no causal effect and have the same direction under the alternative.

Lemma 1

If g(·) is a strictly increasing function, then θ₁ = 0 if and only if ${\tilde{\theta }}_1=0$. Moreover, θ₁ > 0 if and only if ${\tilde{\theta }}_1>0$; θ₁ < 0 if and only if ${\tilde{\theta }}_1<0$.

The proof is straightforward. By IV conditions and the consistency assumption, X ⊥ Y(x)∣U, then E(Y∣X = x,U) = E{Y(x)∣U,Z}. If θ₁ = 0 and g(·) is a strictly increasing function, E{Y(x)∣U,Z} = E{Y(x – 1)∣U,Z} for all U, and so E{Y(x)∣Z} = E{Y(x – 1)∣Z}. This implies ${\tilde{\theta }}_1=0$, because if ${\tilde{\theta }}_1>0$ then E{Y(x)∣Z} > E{Y(x – 1)∣Z}; if ${\tilde{\theta }}_1<0$ then E{Y(x)∣Z} < E{Y(x – 1)∣Z}. The rest of proof follows immediately.

2.2. Instrumental variables and data-generating models

The fundamental problem in estimating θ₁ in observational studies is that U is not observed, yet it is potentially correlated with X. In classical linear causal models such as (1), this problem is neatly solved by exploiting the set of instrumental variables Z. Using the two-stage least squares (TSLS) method [5], θ₁ can be consistently estimated by plugging in a consistent estimate$\widehat{E}(X\mid Z)$ in the regression $E\{Y\mid \widehat{E}(X\mid Z\left)\right\}$. When there is only one instrumental variable, θ₁ reduces to the ratio of the instrumental variable effect on Y and the instrumental variable effect on X.

In Mendelian randomization study there are often several single nucleotide polymorphisms (SNPs). Let $\mathcal{G}=\{g_1,\dots ,g_{p+1}\}$ denote the set of p + 1 distinct genotypes in the population, collected as instrumental variables to overcome unmeasured confounding. $\mathcal{G}$ are formed by one or several SNPs, the simplest of which could be the three genotypes at a single SNP locus with 0, 1, or 2 mutations respectively. Let G denote the genotype of a subject. Without loss of generality, let g_p+1 be the reference group to which other genotype groups are compared for assessing genetic effects on Y and X. Denote the indicator variable Z_j = I_[G=gj], j = 1, …, p, and let Z = (Z₁, …, Z_p) so that it divides the population into p + 1 mutually exclusive groups with distinctive genotypes.

For dichotomous outcomes, multiplicative and logistic SMMs have been introduced to estimate causal risk ratios and causal odds ratios as defined in (3), respectively [12]. The estimating equations were based on the moment condition implied by the randomization property of IV, for example when Z is a simple dichotomous variable,

$$E\left\{Y\right(0)\mid Z=1\}=E\left\{Y\right(0)\mid Z=0\},$$

where Y(0) is the exposure-free potential outcome. For the multiplicative SMM, the implied moment condition is

$$E\left\{Y\exp \right(-{\tilde{\theta }}_{1}X)\mid Z=1\}=E\left\{Y\exp \right(-{\tilde{\theta }}_{1}X)\mid Z=0\}.$$

For the double logistic SMM, assuming a logistic association model

$$\text{logit}\left\{E\right(Y\mid X,Z\left)\right\}={\eta }_0+{\eta }_{1}X+{\eta }_{2}Z,$$ (4)

the implied moment condition is

$$E\left[\text{expit}\right\{{\eta }_0+({\eta }_1-{\tilde{\theta }}_1)X+{\eta }_{2}Z\}\mid Z=1]=E\left[\text{expit}\right\{{\eta }_0+({\eta }_1-{\tilde{\theta }}_1)X+{\eta }_{2}Z\left)\right\}\mid Z=0].$$

Although the causal risk ratio and the causal odds ratio are identifiable through SMMs, finding a unique root in the estimating functions can be problematic in typical Mendelian randomization studies where genes are usually weak instruments and sample size is limited [19]. As reported previously as well as we observed in our simulations, a substantial proportion of simulations could yield no solution or multiple solution. We used the GMM function in R to fit the double-logistic SMM, and we found that the solution of (4) can drift to large positive values or large negative values, as either can lead to numerical convergence of estimation, causing poor finite-sample performance. The standard error estimates and the confidence intervals in this situation can be unreliable.

In what follows, we propose a simple but robust procedure for testing θ₁ = 0 that will hopefully complement the SMMs when there are computation issues in finite samples. We start from structural equation models to define the causal effect. Suppose that conditional on (Z, U), the distributions of the exposure X and the outcome Y follow two structural generalized linear models, assuming that there is no interaction in either of the two models,

$$g_1\left\{E\right(X\mid Z,U\left)\right\}={\beta }_0+\sum _{j=1}^p{\beta }_{1j}{Z}_j+{\beta }_{2}U,$$ (5)

$$g\left\{E\right(Y\mid X,Z,U\left)\right\}={\theta }_0+{\theta }_{1}X+{\theta }_{2}U+\sum _{j=1}^p{\theta }_{3j}{Z}_j,$$ (6)

where g₁ and g are link functions for X and Y respectively, θ₁ is the causal effect of interest, θ_3j is the genetic effect that is not mediated through X, and θ₂ is the effect of the unknown confounding covariate U. The conditional distributions of X and Y follow the exponential family with a canonical parameter and a dispersion parameter, the latter of which is invariant to regression covariates. Model (6) is of primary interest, interpreted as structural in the sense that the causal parameter θ₁ is the effect of X on Y when holding both U and Z constant. The distribution of U is left unspecified for the moment except assuming E(U) = 0.

The effect of U is included in (5) and (6) as an additive term in the linear predictor, identical to that of observable (X, Z), as one would have done had U been observed. This same way of entry for observed variables and unobserved variables into nonlinear regression models is critical, as discussed previously [24, 26]. Built on this sequence of data-generating models, we next examine the relationship between the two sets of instrumental variable effects, namely the genetic effects on X and the genetic effects on Y, as a way to assess the causal effect θ₁.

2.3. Working models and concordance of instrumental variable effects

We consider two working models for E(X∣Z) and E(Y∣Z) which define the instrumental variable effects. Suppose the same link functions as in (5) and (6) are used. The instrumental variable effects of Z on X are defined as α_1j in a linear model

$$g_1\left\{E\right(X\mid Z\left)\right\}={\alpha }_0+\sum _{j=1}^p{\alpha }_{1j}{Z}_j.$$ (7)

Similarly, the instrumental variable effects of Z on Y are defined as γ_1j in a generalized linear model

$$g\left\{E\right(Y\mid Z\left)\right\}={\gamma }_0+\sum _{j=1}^p{\gamma }_{1j}{Z}_j.$$ (8)

We view (7) and (8) as working models since, if true models are (5) and (6), neither (7) nor (8) is necessarily correctly specified when covariates are neglected. Suppose estimators of α_1j and γ_1j are derived by maximizing the likelihood, the instrumental variable effects defined in (7) and (8) are essentially the limits of the solutions of the respective estimating equations [31].

Theorem 1

Suppose (Y,X) are generated based on model (5) - (6). If g(·) is a continuous and strictly increasing link function, and if the following conditions are met:

$$Z\perp U,$$ (A1)

$${\alpha }_{1j}\ne {\alpha }_{1j^{\prime }}\mathit{for}\mathit{all}j\ne j^{\prime }(j,j^{\prime }=1,\dots ,p),$$ (A2)

$${\theta }_{31}={\theta }_{32}=..={\theta }_{3p}=0,$$ (A3)

the following results will hold: the causal effect θ₁ ≠ 0 if and only if, for any two pairs j ≠ j’, (α_1j, γ_1j) and (α_1j’, γ_1j’) are concordant; moreover, θ₁ > 0 if and only if (γ_1j – γ_1j’)(α_1j – α_1j’) > 0 for any j ≠ j’; θ₁ < 0 if and only if (γ_1j – γ_1j’)(α_1j – α_1j’) < 0 for any j ≠ j’.

The proof is provided in the Appendix. Concordance of (α_1j, γ_1j) means that either α_1j strictly increases with γ_1j, or strictly decreases with γ_1j, depending on the sign of θ₁. Many widely used link functions, e.g., identical, logit and logarithm, are continuous and strictly increasing. The conditions (A1), (A2) and (A3) are the standard assumptions for IV regression, with the additional requirement that there are multiple, heterogeneous genetic effects on X.

Condition (A1-A3) roughly correspond to the usual IV conditions: independent of confounding, correlated with the intermediate and the exclusion restriction. The only difference between the three conditions we put forth in Theorem 1 and the classical IV conditions lies in (A2), that we will need multiple genetic variants with different strength of association with X. This is quite plausible in Mendelian randomization studies: there are typically multiple genetic susceptibility variants, either because one underlying causal allele manifests association through several adjacent loci due to linkage disequilibrium, or there are multiple causal genes or variants to the same phenotype. See examples of multiple genetic susceptibility genes in published Mendelian randomization studies [32, 33, 34].

Remark 1

Theorem 1 states that X has a causal effect on Y, if and only if there is concordance between the changes in X and the changes in Y, both of which are induced by the instrumental variable Z. Though conceptually connected, this concordance of instrumental variable effects is a stronger condition than the heuristically derived dose-response criterion to assess causality in medical and epidemiological studies [20, 21, 22], because instrumental variables are introduced to perturb X and Y “experimentally”. The dose-response criterion, though commonly discussed, may or may not reduce sensitivity to hidden bias in observational studies [23].

To illustrate we present a numerical example with 2 SNPs, a Gaussian-distributed exposure X and a binary disease outcome Y. The haplotypes formed by the two SNPs are (00, 01, 10) with frequencies (0.4,0.4,0.2). Six diploid genotypes were formed according to Hardy-Weinberg equilibrium, denoted by (00,01,02,10,11,20). There was an unobserved confounder U with a Gaussian distribution N(0, 1), that is independent of Z. The models generating X and Y are

$$\begin{array}{cc}\hfill \mathrm{E}(X\mid Z,U)& =1+\sum _{j=1}^5{\beta }_{1j}{Z}_j+{\theta }_{2}U,\hfill \\ \hfill \text{logit}\left\{\mathrm{E}\right(Y\mid X,U\left)\right\}& =-1+{\theta }_{1}X+{\theta }_{2}U,\hfill \end{array}$$

where β₁ = (β₁₁, …, β₁₅)=(0.1,0.3,0.2,0.5,0.4), and θ₂ captures the confounding effect of U.

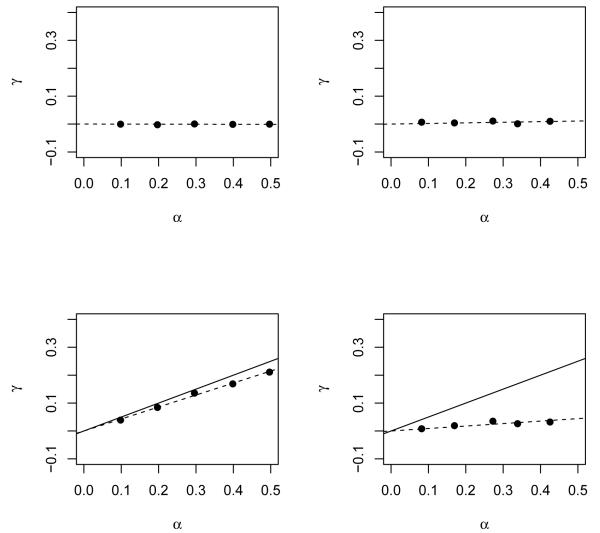
Figure 1 shows the scatter plot of (α, γ) for causal effect θ₁ = 0 or 0.5 (top or bottom panels), confounding level θ₂ = 0.5 or 1 (left or right panels). The ordinary least squares fit of (α, γ) across the origin were shown by the dotted line. When θ₁ = 0, the top two panels show that γ = 0 regardless the level of confounding. A valid test of causal effect is therefore testing γ = 0 as a whole [4]. When θ₁ = 1, the low two panels show that (α, γ) are concordant, almost falling in the least squares fitted line. Both fitted lines have a slope that is smaller than the causal effect (the slope of the solid line). The more confounding effect (the bottom right panel) seems to lead to the more attenuated slope. Numerical examples using other distributions of U and non-identical functions g₁(·) show a similar pattern to Figure 1, suggesting that a more powerful way to test causal effect is to assess the concordance somewhat linearly.

Figure 1.

A numerical example to show the concordance of (α, γ). The top and bottom panels show the scatter plot when there is no causal effect (θ₁ = 0) or there is a causal effect (θ₁ = 0.5). The left and right panels show the scatter plot when there is different level of confounding (θ₂ = 0.5 or θ₂ = 1).

2.4. Testing concordance of instrumental variable effects

We propose to test the linear concordance of instrumental variable effects by a class of generalized least squares estimators, regressing γ_1j on α_1j. Let α = (α₁₁, …, α_1p) and let γ = (γ₁₁, …, γ_1p), both of which are p × 1 vectors. Denote by D a p × p positive definite matrix, and define λ_D to be the minimizer of the quadratic function

$${(\gamma -\lambda \alpha )}^T\mathrm{D}(\gamma -\lambda \alpha ),$$ (9)

namely λ_D = (α^T Dα)⁻¹α^T Dγ. It is the slope of the weighted least squares regression for p pairs of (α_1j, γ_1j) through the origin, since under conditions (A1)-(A3) a zero α_1j would lead to a zero γ_1j. In classical instrumental variable analysis with Gaussian distributed Y and X, the concordance is exactly linear so that γ_1j = θ₁α_1j so that λ_D = θ₁. In generalized linear models, there is no close-form relationship between λ_D and θ₁, yet λ_D provides a valid and consistent test of θ₁ = 0, presented in the following corollary.

Corollary 1

Under the conditions (A1)-(A3) and for any positive definite matrix D, the null hypothesis of the causal effect θ₁ = 0 is true if and only if λ_D = 0. Moreover, θ₁ > 0 if and only if λ_D > 0; θ₁ < 0 if and only if λ_D < 0.

The proof is provided in the Appendix. Corollary 1 operationalizes testing causal effect by testing whether a weighted linear slope estimator equals to zero. A consistent estimator ${\widehat{\lambda }}_{\mathrm{D}}$ can be derived by plugging into (9) the consistent estimators $\widehat{\alpha }$ and $\widehat{\gamma }$, and solving (9) by

$${\widehat{\lambda }}_{\mathrm{D}}={\left({\widehat{\alpha }}^T\mathrm{D}\widehat{\alpha }\right)}^{-1}{\widehat{\alpha }}^T\mathrm{D}\widehat{\gamma }.$$ (10)

To establish the asymptotic distribution of ${\widehat{\lambda }}_{\mathrm{D}}$ and to optimize the choice of D , it is necessary to ascertain the joint distribution of $\widehat{\alpha }$ and $\widehat{\gamma }$. Let α* = (α₀, α₁₁, .., α_1p), γ* = (γ₀, γ₁₁, .., γ_1p) be the limits to which the estimators from the working models (7) and (8) converge. We often represent the estimators for α* and γ* by asymptotically linear estimators [35, 10]. An estimator ${\widehat{\alpha }}^{\ast }$ is asymptotically linear if $\sqrt{n}({\widehat{\alpha }}^{\ast }-{\alpha }^{\ast })=n^{-1∕2}{\sum }_{i=1}^n{B}_{1i}+o_p\left(1\right)$, E(B_1i) = 0, $\mathrm{E}\left(B_{1i}^T{B}_{1i}\right)<\infty$. The function B₁ is referred to as the influence function of ${\widehat{\alpha }}^{\ast }$ in the sense of [36]. The influence function B₂ of an ALE for γ* is defined similarly. ALE can be attained by solving a system of estimating equations that are sums of n independent score contributions. Let ${\sum }_{i=1}^n{S}_{1i}=0$ be the set of estimating equations solved for α*, and let ${\sum }_{i=1}^n{S}_{2i}=0$ be the set of estimating equations to be solved for γ*. Let A₁ = E(∂S_1i/∂α*), A₂ = E(∂S_2i/∂γ*). Thus the influence functions can be written as $B_{1i}=A_1^{-1}{S}_{1i}$, $B_{2i}=A_2^{-1}{S}_{2i}$. The random vector (S_1i, S_2i),i = 1, … , n, is independent and identically distributed with zero mean, but for the same i, S_1i and S_2i are possibly correlated. The joint distribution of ${\widehat{\alpha }}^{\ast }$ and ${\widehat{\gamma }}^{\ast }$ can be established using the Central Limit Theorem, Slutsky’s Theorem and the Cramer-Wold device. Specifically,

$$\sqrt{n}\left(\begin{array}{c}\hfill {\widehat{\alpha }}^{\ast }-{\alpha }^{\ast }\hfill \\ \hfill {\widehat{\gamma }}^{\ast }-{\gamma }^{\ast }\hfill \end{array}\right){\to }_d\mathcal{N}\left(\stackrel{‒}{0},\left[\begin{array}{cc}\hfill \mathrm{E}\left(B_{1i}^T{B}_{1i}\right)\hfill & \hfill \mathrm{E}\left(B_{2i}^T{B}_{1i}\right)\hfill \\ \hfill \mathrm{E}\left(B_{1i}^T{B}_{2i}\right)\hfill & \hfill \mathrm{E}\left(B_{2i}^T{B}_{2i}\right)\hfill \end{array}\right]\right)$$ (11)

where $\mathrm{E}\left(B_{\mathit{li}}^T{B}_{l^{\prime }i}\right)$, l, l^’ = 1, 2, are (p + 1) × (p + 1) submatrices of the full covariance matrix.

Following these developments, let $\mathrm{U}\left({\widehat{\lambda }}_{\mathrm{D}}\right)={\widehat{\alpha }}^T\mathrm{D}(\widehat{\gamma }-{\widehat{\lambda }}_{\mathrm{D}}\widehat{\alpha })=0$. Since U(λ_D) is linear in λ_D, $\sqrt{n}({\widehat{\lambda }}_{\mathrm{D}}-{\lambda }_{\mathrm{D}})={\left({\widehat{\alpha }}^T\mathrm{D}\widehat{\alpha }\right)}^{-1}\sqrt{n}\mathrm{U}\left({\lambda }_{\mathrm{D}}\right)$. Observe that ${\widehat{\alpha }}^T\mathrm{D}\widehat{\alpha }{\to }_p{\alpha }^T\mathrm{D}\alpha$ and ${\alpha }^T\mathrm{D}(\gamma -{\lambda }_{\mathrm{D}}\alpha )=0$, so

$$\sqrt{n}\mathrm{U}\left({\lambda }_{\mathrm{D}}\right)={\alpha }^T\mathrm{D}\sqrt{n}\left\{\right(\widehat{\gamma }-\gamma )-{\lambda }_{\mathrm{D}}(\widehat{\alpha }-\alpha \left)\right\}+\sqrt{n}({\widehat{\alpha }}^T-{\alpha }^T)\mathrm{D}(\gamma -{\lambda }_{\mathrm{D}}\alpha )+o_p\left(1\right).$$ (12)

It is useful to express $\sqrt{n}\mathrm{U}\left({\lambda }_{\mathrm{D}}\right)$ as the sum of two terms in (12): the second term is zero under the null hypothesis and under the alternative hypothesis for linear models and log-linear models, as we will discuss in Section 2.6.

Since $\sqrt{n}(\widehat{\alpha }-\alpha )$ and $\sqrt{n}(\widehat{\gamma }-\gamma )$ are both asymptotically normal, $\sqrt{n}\mathrm{U}\left({\lambda }_{\mathrm{D}}\right)$ is also asymptotically normal. Let Γ₁ denote the asymptotic variance of $\sqrt{n}\left\{\right(\widehat{\gamma }-\gamma )-{\lambda }_{\mathrm{D}}(\widehat{\alpha }-\alpha \left)\right\}$, that is derived by applying the delta method to (11). Let Γ₂ denote the asymptotic variance of $\sqrt{n}(\widehat{\alpha }-\alpha )$ and let Γ₁₂ denote the asymptotic covariance between $\sqrt{n}\left\{\right(\widehat{\gamma }-\gamma )-{\lambda }_{\mathrm{D}}(\widehat{\alpha }-\alpha \left)\right\}$ and $\sqrt{n}(\widehat{\alpha }-\alpha )$, the limiting distribution of ${\widehat{\lambda }}_{\mathrm{D}}$ is

$$\sqrt{n}({\widehat{\lambda }}_{\mathrm{D}}-{\lambda }_{\mathrm{D}}){\to }_d\mathcal{N}(0,{\left({\alpha }^T\mathrm{D}\alpha \right)}^{-1}\Omega {\left({\alpha }^T\mathrm{D}\alpha \right)}^{-1}),$$

where

$$\Omega ={\alpha }^T\mathrm{D}{\Gamma }_1\mathrm{D}\alpha +({\gamma }^T-{\lambda }_{\mathrm{D}}{\alpha }^T)\mathrm{D}{\Gamma }_2\mathrm{D}(\gamma -{\lambda }_{\mathrm{D}}\alpha )+2{\alpha }^T\mathrm{D}{\Gamma }_{12}\mathrm{D}(\gamma -{\lambda }_{\mathrm{D}}\alpha ).$$

The power for testing λ_D = 0 depends on the choice of D. An immediate choice is the identity matrix which leads to an ordinary least squares slope parameter

$${\lambda }_{\mathrm{ols}}={\left({\alpha }^T\alpha \right)}^{-1}{\alpha }^T\gamma .$$

Alternatively, let $\mathrm{D}={\Gamma }_1^{-1}$, that leads to a generalized least squares slope parameter

$${\lambda }_{\mathrm{gls}}={\left({\alpha }^T{\Gamma }_1^{-1}\alpha \right)}^{-1}{\alpha }^T{\Gamma }_1^{-1}\gamma .$$

The motivation of such estimator is that Ω is often dominated by, in some cases reduces to, α^TDΓ₁Dα. The asymptotic variance Γ₁ is derived from the variance of (${\widehat{\alpha }}_j$, ${\widehat{\gamma }}_j$), which can vary greatly depending on sample sizes in genotype groups. Weighting by the inverse of the covariance matrix typically yields more stable linear slope estimates. One can plug in a consistent estimator of Γ₁ to obtain a consistent estimator ${\widehat{\lambda }}_{\mathrm{gls}}$. In numerical studies we show in Section 3, the variance of ${\widehat{\lambda }}_{\mathrm{gls}}$ tends to be smaller than the variance of ${\widehat{\lambda }}_{\mathrm{ols}}$.

Both λ_ols and λ_gls parameterize the concordance between α_j and γ_j, which does not generally have an exact linear relationship except for a few special settings, as we discuss in Section 2.6. Under the null hypothesis θ₁ = 0, both λ_ols and λ_gls converge to zero when sample size gets large. Under the alternative hypothesis, however, λ_ols is generally not equal to λ_gls, so that testing λ_gls = 0 may not be always more powerful than testing λ_ols = 0.

2.5. Dichotomous disease outcome and continuous intermediate

When Y is a dichotomized outcome and X is a continuous biomarker, a stronger result pertaining to the bias of ${\widehat{\lambda }}_{\mathrm{D}}$ as an estimator θ₁ is given in the following corollary.

Corollary 2

Suppose g is the logit function and g₁ is the identity function, respectively. Under the conditions (A1)-(A3) and for any positive definite matrix D, λ_D is biased toward zero when θ₁ ≠ 0.

The proof extends that of Theorem 2 in [24], and is given in Appendix. The significance of this result is that, for the most common form of disease outcomes in epidemiology – diseased cases and healthy controls, and for the continuous intermediate exposures, the estimator of the linear concordance not only provides a valid and consistent test of the causal effect, but also is asymptotically conservative toward the true causal effect. One can interpret the causal effect estimate obtained herein as the least size of log odds ratio corresponding to 1 unit increase of X.

Remark 2

[24] assessed the bias of the treatment effect estimate in randomized clinical trials when covariates are omitted in nonlinear regression. Causal inference can be viewed as if confounding variables are omitted in regression, thereby connecting to [24]. In particular, when linear models are used for continuous intermediate biomarkers, as in Corollary 2, instrumental variable analysis essentially replaces X in (3) by E(X…Z), which is orthogonal to the omitted confounding variables. Therefore some of the results on the direction of the bias in [24] apply here. Because we don’t know the distribution of U, and we leverage multiple instrumental variables by generalized least squares, it is intractable to quantify the exact asymptotic bias of ${\widehat{\lambda }}_D$.

2.6. Log-linear models

Quite often in Mendelian randomization studies, the disease outcome Y is a rare dichotomous endpoint and the intermediate outcome is a continuous biomarker [32, 34]. The logistic model for a rare disease outcome can be approximated by log-linear models. The biomarker is often modeled by a Gaussian distribution. We show that, similar to the classical linear models, the concordance of instrumental variable effects in this setting becomes exactly linear. The weighted least squares estimator previously discussed becomes an efficient estimator of the causal effect.

To proceed, we define the causal effect and the instrumental variable effects in the following models:

$$\log E(Y\mid X,U)={\theta }_0+{\theta }_{1}X+{\theta }_{2}U,$$ (13)

$$E(X\mid Z)={\alpha }_0+\sum _{j=1}^p{\alpha }_{1j}{Z}_j,$$ (14)

$$\log E(Y\mid Z)={\gamma }_0+\sum _{j=1}^p{\gamma }_{1j}{Z}_j.$$ (15)

For simplicity, we assume X∣Z, U takes a Gaussian distribution with $E(X\mid Z,U)={\beta }_0+{\sum }_{j=1}^p{\beta }_{1j}{Z}_j+{\beta }_{2}U$ and var(X∣Z, U) = σ², but noting that a more flexible location-shift model should also suffice for the following lemma.

Lemma 2

For a rare disease outcome Y and a Gaussian-distributed exposure X, if the causal parameter and the instrumental variable effects are defined in (13) - (15), and the conditions in Theorem 1 are satisfied, it follows that γ_1j = θ₁α_1j and ${\gamma }_0={\theta }_1{\alpha }_0+{\theta }_0^{\ast }$, for j = 1, .., p, where ${\theta }_0^{\ast }={\theta }_0+\frac{1}{2}{\theta }_1^2{\sigma }^2+\log c$ and c = E{exp(θ₂U + θ₁β₂U)}.

The proof is given in the Appendix. The result in Lemma 2 states that the concordance of α_1j and γ_1j becomes exactly linear with the slope θ₁. We shall extend the generalized least squares method discussed in Section 2.2 to estimate (${\theta }_0^{\ast }$, θ₁) and pursue the optimal estimator.

Let = (${\theta }_0^{\ast }$, θ₁), a 2 × 1 vector. Define $\mathcal{A}$ to be the (p + 1) × 2 matrix with the first column (1, 0, … , 0) and the second column α*, then the equation

$${\mathcal{A}}_{\theta }={\gamma }^{\ast }$$

describes the linear relationship of instrumental variable effects in Lemma 1. Suppose ${\widehat{\alpha }}^{\ast }$ and ${\widehat{\gamma }}^{\ast }$ are the asymptotic linear estimators of α* and γ*. To estimate θ, we minimize the quadratic function

$${({\widehat{\gamma }}^{\ast }-\widehat{\mathcal{A}}\theta )}^T\mathrm{D}({\widehat{\gamma }}^{\ast }-\widehat{\mathcal{A}}\theta ),$$ (16)

where D is a (p + 1) × (p + 1) positive definite matrix. Let ${\widehat{\theta }}_{\mathrm{D}}$ denote the estimator of the causal effect corresponding to the choice of D.

The joint asymptotic distribution of ${\widehat{\alpha }}^{\ast }$ and ${\widehat{\gamma }}^{\ast }$ was shown in Section 2.2. Using the delta method, we derive that

$$\sqrt{n}({\widehat{\gamma }}^{\ast }-\widehat{\mathcal{A}}\theta ){\to }_d\mathcal{N}(0,\Gamma ),$$ (17)

where Γ is the (p + 1) × (p + 1) asymptotic covariance matrix. We define the generalized least square estimator for θ, when D = Γ⁻¹, to be

$${\widehat{\theta }}_{\mathrm{gls}}={\left({\widehat{\mathcal{A}}}^T{\Gamma }^{-1}\widehat{\mathcal{A}}\right)}^{-1}{\widehat{\mathcal{A}}}^T{\Gamma }^{-1}{\widehat{\gamma }}^{\ast }.$$

In contrast to generalized linear models in Section 2.2, where the estimators of the linear slope with different D could converge in probability to different values, such estimators in log-linear models all converge to the causal effect θ₁. The asymptotic efficiency of ${\widehat{\theta }}_{\mathrm{gls}}$ among the class of estimators ${\widehat{\theta }}_{\mathrm{D}}$ shall be discussed.

Theorem 2

For every positive definite matrix D, ${\widehat{\theta }}_D$ that minimizes (16) is consistent for θ and asymptotically normal, with the asymptotic expansion

$$\sqrt{n}({\widehat{\theta }}_D-\theta )={\left({\mathcal{A}}^{T}D\mathcal{A}\right)}^{-1}{\mathcal{A}}^{T}D\left\{\sqrt{n}\right({\widehat{\gamma }}^{\ast }-\widehat{\mathcal{A}}\theta \left)\right\}+o_p\left(1\right).$$

Among them, ${\widehat{\theta }}_{\mathit{gls}}$ has the smallest asymptotic variance.

The proof is given in the Appendix.

It has been noted that the two-stage least squares estimator of the causal effect is also applicable for log-linear models [26, 13]. Like the classical two-stage least squares estimator, the estimated E(X∣Z) is computed first, then plugged into the second-stage regression model log $E\{Y\mid \widehat{E}(X\mid Z\left)\right\}$ to obtain the causal effect estimate. For logistic models with a rare disease, the 2SLS estimator is thus approximately consistent to the true causal odds ratio. Denote the resulted estimator by ${\widehat{\theta }}_{2\mathrm{SLS}}$. One would be interested in comparing ${\widehat{\theta }}_{2\mathrm{SLS}}$ and ${\widehat{\theta }}_{\mathrm{gls}}$. Indeed, ${\widehat{\theta }}_{2\mathrm{SLS}}$ is one member of this class of minimal distance estimators, that has been shown in the econometrics literature on limited dependent variable models [25]. Following the notation in Section 2.2, let S₂ denote the estimating equation for γ* and let A₂ = E(∂S₂/∂γ). The following corollary gives the comparison between ${\widehat{\theta }}_{2\mathrm{SLS}}$ and ${\widehat{\theta }}_{\mathrm{gls}}$.

Corollary 3

The asymptotic expansion of the two-stage least squares estimator ${\widehat{\theta }}_{2\mathit{SLS}}$ is

$$\sqrt{n}({\widehat{\theta }}_{2\mathit{SLS}}-\theta )={\left({\mathcal{A}}^T{A}_2\mathcal{A}\right)}^{-1}{\mathcal{A}}^T{A}_2\left\{\sqrt{n}\right({\widehat{\gamma }}^{\ast }-\widehat{\mathcal{A}}\theta \left)\right\}+o_p\left(1\right),$$

and so it is one of ${\widehat{\theta }}_D$. According to Theorem 2, the asymptotic variance of ${\widehat{\theta }}_{2\mathit{SLS}}$ shall be greater than or equal to that of ${\widehat{\theta }}_{\mathit{gls}}$.

Remark 3

The efficiency of ${\widehat{\theta }}_{2\mathit{SLS}}$ relative to ${\widehat{\theta }}_{\mathit{gls}}$ depends on the matrix difference between A₂ and Γ. The scalar term in A₂ and Γ will be canceled out in the variance calculation. In linear models, one can verify that the two estimators are equivalent because the design matrices of the two models defining instrumental variable effects are same. For generalized linear models (14)-(15), under the null hypothesis θ₁ = 0, A₂ is nearly same as Γ, since the former is the model-based variance and the latter is the empirical sandwich variance. Under the alternative, we observe in simulations that the two estimators are also numerically close, likely due to the fact that the two models (14)-(15) share the same design matrix.

2.7. Known covariates

We have by far omitted known covariates. Regression adjustment for such covariates as demographic factors and population stratification is imperative in genetic association analyses. In the context of randomized clinical trials, controlling for posttreatment variables should be always avoided, for the reasons elaborated previously [37]. In observational genetic studies, however, situations are much more complicated. Generally the genetic background should be adjusted for, such as race, ethnicity and gender. More sophisticated adjustment includes the top eigen vectors from a principal component analysis - surrogates for underlying population substructures. If we view genetic variant as a “treatment” predisposed at conception, all phenotypes developed in the later stage of life are “post-treatment” variables. For complex traits such as cardiovascular diseases, many phenotypes are correlated such as blood pressure, BMI and diabetes. Such variables were almost always adjusted for, partly because the genetic effect of interest, if detected, is for the specific phenotype under interrogation, not due to mere genetic association with other related traits. Other reasons could also include that these adjusting variables could serve surrogates for environmental or behavioral exposure, for example BMI for diet and exercise, which is usually hard to measure directly. This rationale has been considered plausible in [37].

Denote W to be a collection of known covariates, so that the key assumption for instrumental variables becomes

$$Z\perp U\mid W.$$

Suppose W is added as covariates in the data-generating models:

$$g_1\left\{E\right(X\mid Z,W,U\left)\right\}={\beta }_0+\sum _{j=1}^p{\beta }_{1j}{Z}_j+{\beta }_{2}W+{\beta }_{3}U,$$ (18)

$$g\left\{E\right(Y\mid X,Z,W,U\left)\right\}={\theta }_0+{\theta }_{1}X+{\theta }_{2}W+{\theta }_{3}U+\sum _{j=1}^p{\theta }_{4j}{Z}_j.$$ (19)

Correspondingly, the working models now become

$$g_1\left\{E\right(X\mid Z,W\left)\right\}={\alpha }_0+\sum _{j=1}^p{\alpha }_{1j}{Z}_j+{\alpha }_{2}W,$$ (20)

$$g\left\{E\right(Y\mid Z,W\left)\right\}={\gamma }_0+\sum _{j=1}^p{\gamma }_{1j}{Z}_j+{\gamma }_{2}W.$$ (21)

For working model (20), the instrumental variable effects α_1j may not have the close form expression g₁E(X∣G = g_j, W)} – g₁{E(X∣G = g_p+1, W)} unless U ⊥ W. The latter restrictive condition is needed for extending the proof of Theorem 1 to GLM (18-21), where W was added as covariates. Alternatively, with one regular condition pertaining to the distribution of W conditional on Z, the concordance of instrumental variable effects holds for the common scenario where the exposure X is continuous and the disease outcome Y is dichotomized.

Lemma 3

Suppose g₁(.) is the identical link for a continuous X and g(·) is the logit function for a dichotomous Y. If for any j and j^’, W∣G = g_j and W∣G = g_j’ are in some stochastic order, that is, either pr(W > w∣G = g_j) ≥ pr(W > w∣G = g_j’) or pr(W > w∣G = g_j) ≤ pr(W > w∣G = g_j’) for all w, then the concordance of (α_j, γ_j) described in Theorem 1 holds under similar conditions.

The proof is left in Appendix. The condition that W∣G = g_j and W∣G = g_j’ are in some stochastic order is fairly mild. For example, if W belongs to the location-scale family of distributions, then genetic effects that shift the location would satisfy the condition.

3. Simulations

We simulated data based on the numerical example presented in Section 2.3. As explained before, we generated 2 SNPs forming 6 diploid genotypes in linkage disequilibrium as specified in Section 2.3, a Gaussian-distributed exposure X and a binary disease outcome Y. There was an unobserved confounder U with a Gaussian distribution N(0, 1), that is independent of Z. The models generating X and Y are

$$\begin{array}{cc}\hfill \mathrm{E}(X\mid Z,U)=& 1+\sum _{j=1}^5{\beta }_{1j}{Z}_j+{\theta }_{2}U,\hfill \\ \hfill \text{logit}\left\{\mathrm{E}\right(Y\mid X,U\left)\right\}=& -1+{\theta }_{1}X+{\theta }_{2}U,\hfill \end{array}$$

where β₁ = (β₁₁, …, β₁₅) is the instrumental variable effects on X, taking the values at (0.1,0.3,0.2,0.5,0.4). The causal effect parameter θ₁ is valued at 0, 0.5 and 1, representing a ladder of strength in causal odds ratio (1, 1.65, 2.72). A nonzero θ₂ indexes the confounding effect of U.

Table 1 shows the comparison of the two proposed tests to the standard Mendelian randomization test, which tests the global association between six diplotypes and the disease outcome, i.e. γ = 0 [2, 4], and the to the double-logistic SMM developed in [7]. The SMM was implemented using the GMM function in R, solving for estimating equations for both the association and causal parameters simultaneously. The optimization method chosen in the GMM function is “BFGS”, a gradient-based searching algorithm with the maximum iteration number 500. The initial value for parameters were obtained using a two-stage GMM method, in which association parameter were first estimated and the causal parameters were estimated subsequently. See, for example, using the GMM function to fit the double-logistic SMM in [38].

Table 1.

Comparison of the standard instrumental variable testing method (IVT), the proposed ordinary least squares estimator (OLS), the generalized least squares estimator of linear concordance (GLS), the double-logistic structural mean models (SMM) in type I error rate (θ₁ = 0)and power (θ₁ ≠ 0).

	θ2 = 0.5		θ2 = 1.0
θ1 = 0	n = 1000	n = 5000	n = 1000	n = 5000
IVT	0.044	0.055	0.045	0.045
OLS	0.016	0.048	0.024	0.039
GLS	0.028	0.045	0.032	0.039
SMM	0.084	0.066	0.143	0.060
θ1 = 0.5
IVT	0.113	0.455	0.084	0.296
OLS	0.191	0.618	0.201	0.535
GLS	0.230	0.738	0.245	0.660
SMM	0.374	0.749	0.392	0.696
θ1 = 1.0
IVT	0.241	0.930	0.156	0.714
OLS	0.495	0.980	0.443	0.893
GLS	0.583	0.994	0.537	0.952
SMM	0.591	0.993	0.479	0.943

The causal effect θ₁ and the confounding effect θ₂ are defined in the following data-generating models: $\mathrm{E}(X\mid Z,U)=1+{\sum }_{j=1}^5{\beta }_{1j}{Z}_j+{\theta }_{2}U$ and logit{E(Y∣X, U)} = −1 + θ₁X + θ₂U.

Across different parameter settings in Table 1, the marginal disease probabilities range from 0.28-0.54. When θ₁ = 0, the numbers shown in Table 1 are type I error; when θ₁ ≠ 0, the numbers shown in Table 1 are power. When θ₁ = 0, the standard IV test, the ordinary least squares test and the weighted least squares test maintain the nominal type I error probability at level 0.05 for either sample size of 1000 or 5000. The double-logistic SMM appears to have inflated type I error and the inflation is reduced for bigger sample size. As we show next in Table 2, this is because SMM has poor convergence and poor finite-sample performance. When θ₁ ≠ 0, both the ordinary least squares test and the weighted least squares test yield substantial power gain over the standard test. Across different parameter settings, the power of the weighted least square test is improved upon the power of the ordinary least square test consistently by 10-15%.

Table 2.

Comparison of the proposed ordinary least squares (OLS), the generalized least squares estimators (GLS) of linear concordance and the double-logistic structural mean models (SMM) in bias and variance.

	n=1000			n=5000
	λ OLS	λ GLS	λ SMM	λ OLS	λ GLS	λ SMM
θ2 =0.5 θ1 = 0
% zero or multiple roots	–	–	15.9%	–	–	3.3%
Bias: mean	−0.010	0.030	0.679	0.001	0.014	0.012
Bias: median	−0.022	0.039	0.127	0.011	0.017	0.009
Var	0.236	0.167	30.111	0.054	0.039	0.042
Robust Var	0.216	0.151	0.257	0.054	0.039	0.042
$\widehat{\mathrm{Var}}$: mean	0.286	0.222	1347.102	0.052	0.039	0.039
$\widehat{\mathrm{Var}}$: median	0.243	0.184	0.159	0.050	0.038	0.037
θ1 = 0.5
% zero or multiple roots	–	–	24.1%	–	–	2.2%
Bias: mean	−0.080	−0.056	1.131	−0.060	−0.057	0.007
Bias: median	−0.052	−0.047	0.073	−0.066	−0.053	0.007
Var	0.189	0.133	2054.416	0.039	0.028	0.040
Robust Var	0.174	0.128	0.238	0.041	0.027	0.036
$\widehat{\mathrm{Var}}$: mean	0.214	0.164	3254238	0.039	0.029	0.035
$\widehat{\mathrm{Var}}$: median	0.178	0.139	0.145	0.037	0.028	0.034
θ1 = 1.0
% zero or multiple roots	–	–	28.5%	–	–	3.1%
Bias: mean	−0.257	−0.255	−15.860	−0.270	−0.270	−0.098
Bias: median	−0.259	−0.260	−0.013	−0.275	−0.273	−0.024
Var	0.150	0.109	16882.62	0.030	0.022	3.905
Robust Var	0.131	0.091	0.389	0.030	0.023	0.044
$\widehat{\mathrm{Var}}$: mean	0.178	0.140	399169268	0.032	0.025	67.251
$\widehat{\mathrm{Var}}$: median	0.149	0.119	0.165	0.031	0.024	0.041
θ2 = 1 θ1 = 0
% zero or multiple roots	–	–	17.5%	–	–	2.5%
Bias: mean	0.010	0.081	0.672	0.012	0.028	0.033
Bias: median	0.025	0.099	0.197	0.008	0.029	0.031
Var	0.217	0.156	81.707	0.045	0.033	0.048
Robust Var	0.186	0.126	0.274	0.046	0.038	0.046
$\widehat{\mathrm{Var}}$: mean	0.299	0.224	9320.521	0.049	0.038	0.046
$\widehat{\mathrm{Var}}$: median	0.216	0.166	0.161	0.047	0.035	0.040
θ1 = 0.5
% zero or multiple roots	–	–	23.2%	–	–	2.3%
Bias: mean	−0.119	− 0.078	−0.951	−0.137	−0.125	0.017
Bias: median	−0.091	−0.068	−0.082	−0.127	−0.121	0.011
Var	0.160	0.116	172.469	0.033	0.024	0.062
Robust Var	0.119	0.091	0.333	0.030	0.022	0.040
$\widehat{\mathrm{Var}}$: mean	0.213	0.159	127871	0.035	0.027	0.045
$\widehat{\mathrm{Var}}$: median	0.150	0.116	0.157	0.033	0.025	0.041
θ1 = 1.0
% zero or multiple roots	–	–	30.6%	–	–	5.8%
Bias: mean	−0.398	−0.380	−13.591	−0.419	−0.414	−0.514
Bias: median	−0.386	−0.368	−0.117	−0.414	−0.407	−0.014
Var	0.140	0.096	12460.730	0.029	0.022	63.947
Robust Var	0.107	0.077	0.642	0.028	0.020	0.069
$\widehat{\mathrm{Var}}$: mean	0.176	0.132	128356550	0.029	0.022	3386.188
$\widehat{\mathrm{Var}}$: median	0.123	0.098	0.187	0.027	0.020	0.053

The causal effect θ₁ and the confounding effect θ₂ are defined in the following data-generating models: $\mathrm{E}(X\mid Z,U)=1+{\sum }_{j=1}^5{\beta }_{1j}{Z}_j+{\theta }_{2}U$ and logit{E(Y∣X,U)} = −1 + θ₁X + θ₂U.

Table 2 shows the performance of the proposed estimators and the double-logistic SMM estimator. The GLS estimator has much reduced variance than the OLS estimator, and as Corollary 2 predicts, both estimators are biased toward 0 under alternative hypothesis. Note that these results suggest that for small to moderate causal effect, the two proposed estimators give fairly good estimates. The small-sample performance for SMM is messy due to the convergence issue. First there are simulations which did not get to convergence in 500 iterations or converge to different roots if starting from different initial values. The second set of initial values we used were simply vector 0. Table 2 shows that 15%-30% simulations could have no or more than 1 roots using GMM when sample size is 1000. This is a serious problem to utility of the double-logistic SMM in moderate sample size studies. This problem is improved but not eliminated when sample size is 5000. Even among the simulations which did get converged using the two-stage GMM method, there are substantial outliers in the distributions of SMM estimators. We have to include robust measures such as median and MAD (median absolute deviation) based robust variance.When sample size is 1000 or θ₁ = 1, the mean bias of SMMis quite substantial, presumably due to outliers. The variance estimates can be quite large numerically, rendering resulted inference useless.

To examine the effect of varying spread and strength of instrumental variables, as requested by one reviewer, we let β₁ takes values at (0.05,0.15,0.1,0.25,0.2), representing a scenario where the strength of instrumental variable is much weaker and the heterogeneity of the instrumental variable effects is much reduced. As shown in Table 3, the type I error for the ordinary least squares method and the generalized least squares method is much more conservative, because the estimated variance is usually larger than the sample variance (Table 4), suggesting that the small-sample performance of the estimated variance is poor due to weak instrument. In Table Table 4, all three estimators show worse small-sample behavior compared to Table 2. The performance of SMM is particularly worrisome, in that the convergence rate, the estimated parameter and the estimated variance are very poor. These observations reinforce the importance of the necessity of strong instrumental variables to making meaningful inference.

Table 3.

Comparison of the standard instrumental variable testing method (IVT), the proposed ordinary least squares estimator (OLS), the generalized least squares estimator of linear concordance (GLS), the double-logistic structural mean models (SMM) in type I error rate (θ₁ = 0)and power (θ₁ ≠ 0).

	θ2 = 0.5		θ2 = 1.0
	n = 1000	n = 5000	n = 1000	n = 5000
θ1 = 0
IVT	0.026	0.032	0.054	0.045
OLS	0.004	0.017	0.033	0.032
GLS	0.008	0.023	0.020	0.034
SMM	0.066	0.074	0.161	0.133
θ1 = 0.5
IVT	0.042	0.133	0.051	0.113
OLS	0.070	0.251	0.094	0.235
GLS	0.095	0.290	0.145	0.309
SMM	0.300	0.422	0.334	0.471
θ1 = 1.0
IVT	0.064	0.315	0.062	0.223
OLS	0.196	0.557	0.223	0.519
GLS	0.229	0.654	0.289	0.614
SMM	0.329	0.684	0.320	0.595

The causal effect θ₁ and the confounding effect θ₂ are defined in the following data-generating models: $\mathrm{E}(X\mid Z,U)=1+{\sum }_{j=1}^5{\beta }_{1j}{Z}_j+{\theta }_{2}U$ and logit{E(Y∣X, U)} = −1 + θ₁X + θ₂U.

Table 4.

Comparison of the proposed ordinary least squares (OLS), the generalized least squares estimators (GLS) of linear concordance and the double-logistic structural mean models (SMM) in bias and variance.

	n=1000			n=5000
	λ OLS	λ GLS	λ SMM	λ OLS	λ GLS	λ SMM
θ2 = 0.5 θ1 = 0
% zero or multiple roots	–	–	37.1%	–	–	17.5%
Bias: mean	0.021	0.075	7.712	0.008	0.038	0.548
Bias: median	0.050	0.085	0.442	0.022	0.030	0.065
Var	0.738	0.539	14576.26	0.212	0.152	96.363
Robust Var	0.607	0.439	0.717	0.204	0.141	0.166
$\widehat{\mathrm{Var}}$: mean	2.428	1.627	5028211	0.223	0.177	2401.809
$\widehat{\mathrm{Var}}$: median	0.787	0.613	0.402	0.193	0.152	0.129
θ1 = 0.5
% zero or multiple roots	–	–	35.9%	–	–	12.7%
Bias: mean	−0.037	0.007	−0.727	−0.045	−0.030	0.258
Bias: median	0.015	0.036	0.099	−0.052	−0.032	0.050
Var	0.609	0.430	334.15	0.154	0.107	77.149
Robust Var	0.495	0.393	0.837	0.149	0.099	0.160
$\widehat{\mathrm{Var}}$: mean	1.704	1.057	119651.6	0.166	0.131	8940.424
$\widehat{\mathrm{Var}}$: median	0.584	0.463	0.373	0.145	0.114	0.117
θ1 = 1.0
% zero or multiple roots	–	–	47.8%	–	–	20.7%
Bias: mean	−0.197	−0.195	−21.687	−0.267	−0.261	−12.565
Bias: median	−0.217	−0.214	−0.374	−0.261	−0.268	0.005
Var	0.505	0.347	20805.530	0.120	0.091	25014.870
Robust Var	0.374	0.288	1.658	0.113	0.085	0.213
$\widehat{\mathrm{Var}}$: mean	1.201	0.927	80359120	0.137	0.109	146064571
$\widehat{\mathrm{Var}}$: median	0.478	0.380	0.466	0.120	0.094	0.130
θ2 = 1 θ1 =0
% zero or multiple roots	–	–	29.8%	–	–	15.1%
Bias: mean	0.150	0.236	0.318	0.047	0.087	0.213
Bias: median	0.163	0.258	0.462	0.041	0.105	0.172
Var	0.555	0.371	678.602	0.165	0.118	1.727
Robust Var	0.421	0.273	0.500	0.158	0.124	0.199
$\widehat{\mathrm{Var}}$: mean	1.735	1.000	256173.5	0.229	0.177	17.972
$\widehat{\mathrm{Var}}$: median	0.630	0.468	0.307	0.169	0.135	0.129
θ1 = 0.5
% zero or multiple roots	–	–	38.1%	–	–	18.9%
Bias: mean	0.000	0.047	−9.283	−0.103	−0.068	−0.412
Bias: median	0.030	0.050	0.100	−0.084	−0.045	0.128
Var	0.440	0.290	20578.09	0.127	0.090	41.464
Robust Var	0.302	0.219	0.836	0.105	0.078	0.215
$\widehat{\mathrm{Var}}$: mean	1.220	0.802	50799975	0.160	0.126	1084.917
$\widehat{\mathrm{Var}}$: median	0.425	0.333	0.318	0.121	0.096	0.123
θ1 = 1.0
% zero or multiple roots	–	–	43.1%	–	–	26.0%
Bias: mean	−0.295	−0.272	−36.371	−0.392	−0.373	−8.683
Bias: median	−0.288	−0.273	−0.562	−0.373	−0.367	−0.002
Var	0.351	0.248	82631.690	0.109	0.080	6509.888
Robust Var	0.234	0.176	1.888	0.096	0.069	0.358
$\widehat{\mathrm{Var}}$: mean	1.195	0.676	1218444016	0.128	0.102	5301082
$\widehat{\mathrm{Var}}$: median	0.351	0.272	0.403	0.101	0.080	0.154

The causal effect θ₁ and the confounding effect θ₂ are defined in the following data-generating models: $\mathrm{E}(X\mid Z,U)=1+{\sum }_{j=1}^5{\beta }_{1j}{Z}_j+{\theta }_{2}U$ and logit{E(Y∣X, U)} = −1 + θ₁X + θ₂U.

In the last set of simulations shown in Table 5, we compared the performance of generalized least squares estimators to two-stage least squares estimators and double-logistic SMM estimators in the rare disease setting. The distribution of (Y, X, G, U) is generated by the same aforementioned models, except the intercept of the logistic model was set to be either 4.5 or 3.5. Table 5 shows the bias, variance and 95% coverage probability of three estimators for different sample size, causal effect, and marginal disease probability. The performance of the two estimators is nearly identical in all parameter settings. For a moderate causal effect with the disease probability less than 4-5%, it seems that log-linear models approximate logistic models well, yielding unbiased estimators and proper confidence intervals, though this approximation deteriorates with more common disease prevalence. For these sample sizes, identifiability and convergence are not an issue for SMM but its variance is markedly bigger than the other two estimators, because it is built on moment conditions but not much more distributional assumptions.

Table 5.

Comparison of the proposed generalized least squares estimator and the two-stage least square estimator when the binary disease outcome is rare and the exposure is Gaussian.

	n=10000			n=50000			n = 10000			n = 50000
	GLS	2SLS	SMM	GLS	2SLS	SMM	GLS	2SLS	SMM	GLS	2SLS	SMM
θ1 = 0	pr(Y = 1) = 0.013						pr(Y =1) = 0.033
Bias	0.032	−0.006	0.234	−0.003	−0.012	0.076	0.024	0.010	0.083	0.001	−0.003	−0.003
Var	0.294	0.306	0.391	0.067	0.067	0.094	0.123	0.115	0.236	0.024	0.024	0.031
$\widehat{\mathrm{Var}}$	0.315	0.315	0.457	0.062	0.062	0.068	0.119	0.119	0.170	0.024	0.024	0.024
95% CP	0.962	0.957	0.970	0.951	0.953	0.954	0.952	0.951	0.949	0.955	0.953	0.948
θ1 = 0.25	pr(Y = 1) = 0.018						pr(Y = 1) = 0.048
Bias	0.033	0.010	0.151	−0.008	−0.012	0.028	0.016	0.007	0.072	−0.007	−0.009	0.001
Var	0.202	0.207	0.373	0.044	0.044	0.071	0.084	0.085	0.182	0.016	0.016	0.020
$\widehat{\mathrm{Var}}$	0.207	0.207	0.423	0.041	0.041	0.050	0.081	0.081	0.131	0.016	0.016	0.018
95% CP	0.955	0.951	0.947	0.989	0.945	0.934	0.949	0.949	0.962	0.955	0.957	0.941
θ1 = 0.5	pr(Y = 1) = 0.029						pr(Y = 1) = 0.071
Bias	0.016	0.003	0.110	−0.021	−0.023	0.011	−0.021	−0.025	0.045	−0.031	−0.032	0.004
Var	0.133	0.136	0.304	0.026	0.026	0.047	0.051	0.051	0.125	0.011	0.011	0.016
$\widehat{\mathrm{Var}}$	0.129	0.129	0.302	0.026	0.026	0.038	0.053	0.053	0.101	0.011	0.011	0.014
95% CP	0.949	0.948	0.930	0.952	0.951	0.939	0.958	0.956	0.957	0.937	0.933	0.943
θ1 = 0.75	pr(Y = 1) = 0.046						pr(Y = 1) = 0.105
Bias	−0.045	−0.052	0.066	−0.062	−0.063	0.001	−0.096	−0.099	0.020	−0.092	−0.093	0.009
Var	0.081	0.082	0.234	0.016	0.016	0.031	0.035	0.035	0.099	0.007	0.007	0.012
$\widehat{\mathrm{Var}}$	0.078	0.078	0.227	0.016	0.016	0.029	0.035	0.035	0.088	0.007	0.007	0.011
95% CP	0.939	0.939	0.889	0.912	0.913	0.936	0.924	0.921	0.941	0.806	0.805	0.935

The causal effect θ₁ and the confounding effect θ₂ are defined in the following data-generating models: $\mathrm{E}(X\mid Z,U)=1+{\sum }_{j=1}^5{\beta }_{1j}{Z}_j+{\theta }_{2}U$ and logit{E(Y∣X, U)} = −1 + θ₁X + θ₂U.

4. Data analysis

In the Cardiovascular Health Study, single nucleotide polymorphisms in the gene coding C-reactive protein were genotyped in 3941 white participants and 700 black participants, aged 65 years or older. Earlier analysis suggests that there is a genetic association between the gene and the circulating C-reactive protein levels, as well as cardiovascular events [39]. The role of C-reactive protein in the pathogenesis of cardiovascular disease remains in question. Using 3 genetic variants (1919 A/T, 2667 G/C, 3872 G/A) as instrumental variables, we assess the causal effect of the plasma C-reactive protein level on the risk of cardiovascular related mortality. We restricted our analysis to whites to avoid potential population stratification. The cumulative cardiovascular related mortality rate in whites is 12.4%. Diplotypes formed by these 3 single nucleotide polymorphisms were collapsed to 7 groups. The rare diplotypes with frequencies less than 0.05 were collapsed to one group. The most common diplotype was used as the reference group.

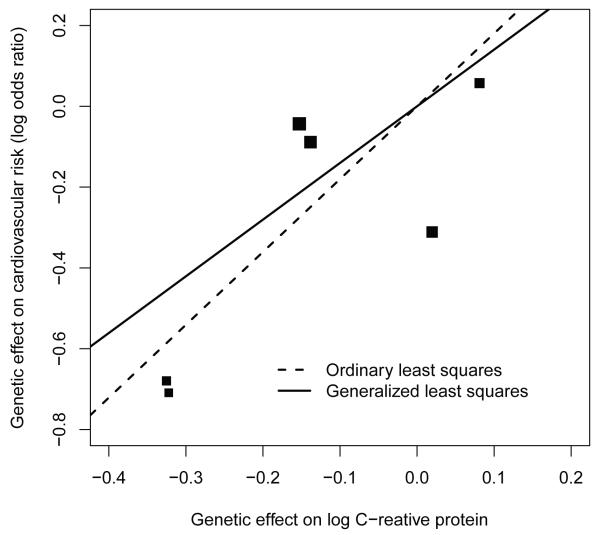
We focus on testing causal effect by linear concordance of instrumental variable effects. Two sets of genotype effects were computed: one is on the risk of cardiovascular related mortality in a logistic model, the other is on the logarithm of the plasma C-reactive protein level at baseline in an ordinary least squares model. Both effects are adjusted for baseline age, sex, clinic site, body mass index, systolic blood pressure, diabetes mellitus, hypertension and smoking status. The ordinary least squares fit yields the slope 1.803, with standard error 0.282. A Wald test of whether the slope is zero yields p-value 0.0007; The generalized least squares fit yields the slope 1.403, with standard error 0.222 and p-value 0.003. Because the sizes of diplotype group vary, the generalized least squares estimator is perhaps more robust than the ordinary least squares estimator. The instrumental variable effects and the fitted lines of two methods are shown Figure 2. The standard instrumental variable test, i.e., the global test for the association between diplotypes and the cardiovascular related mortality yields a p-value 0.0004, also suggesting a causal effect. In this example, although our proposed tests did not produce more significant p-values than the standard test, the linear concordance shown in Figure 2 provides additional evidence of causality.

Figure 2.

The two sets of genetic effects and the linear concordance estimates. Seven diplotypes were formed and all effects was compared to the most common diplotype. The sizes of square points are proportional to sample sizes in diplotype groups.

5. Discussion

In recent years, there has been a proliferation of Mendelian randomization analyses [32, 33, 34]. We have shown in this paper that, for generalized linear models under mild assumptions, if there is a causal effect of an observed exposure on the outcome, then instrumental variable effects on the exposure shall be concordant with instrumental variable effects on the outcome. We provide weighted least squares estimators for testing causality in general, for estimating causal effect in linear and log-linear models. These results broaden the scope of instrumental variable analysis for Mendelian randomization.

The niche of the proposed test resides in Mendelian randomization studies that have multiple genotypes serving as instrumental variables, each with distinct effects on the intermediate outcome. For complex traits such as cardiovascular diseases and cancers, it is common to have multiple susceptibility genes. If one use the diplotype as instrumental variables, as we did in the data example, it is quite plausible to have a dosage genetic effect depending on how many detrimental genetic variants were contained in the genotypes. Even in the situation where there is indeed limited heterogeneity in instrumental effects, the estimation should not be much different from other IV approaches, as we show in rare disease scenarios that the generalized least squares estimator resembles 2SLS estimators, both of which can be viewed as members of minimal distance estimators [25]. Again, as we showed in simulations, genetic epidemiologists should be aware of the importance of strong instrumental variables and preferably large sample size for making meaningful causal inference.

When the disease is rare, case-control sampling is commonly used to reduce the cost of genotyping while preserving estimation efficiency. Intermediate phenotypes may be ascertained in the case-control sample as secondary phenotypes. Ignoring this sampling scheme may bias genetic effect on the intermediate, if the latter is correlated with the disease status. Alternatively, intermediate phenotypes could be available in the entire cohort. Using the inverse probability weighted method, minimal distance estimators can readily account for the diverse sampling process that arise from complex epidemiological studies, since such estimators begin by estimating two separate sets of genetic effects. Future work is warranted to improve efficiency under diverse sampling schemes in Mendelian randomization analysis.

The proposed methods can also be used in randomized clinical trials to test the causal treatment effect when participants indeed complied [9, 11], if there are multiple, mutually exclusive instrumental variables available. For example, when there are several trials conducted for the same treatment modality, each treatment assignment in an individual trial serves as an instrumental variable. Under models (5-8) and Assumption (A1-A3), the concordance of the level of adherence and the intent-to-treat effect across different trials is strong evidence of causal treatment effect, as recently shown in pre-exposure prophylaxis trials for HIV prevention [40]. In a single trial, when there are subgroups with varying treatment effect and differential compliance rate, similar testing strategies developed in this article can also be applied, essentially using treatment assignment in each subgroup as multiple mutually exclusive instrumental variables.

Appendix.

Proof of Theorem 1

If the conditional distributions of Y and X are as described in (5) and (6), and if E(Y∣G = g_j) and E(X∣G = _gj) exist for every j, then α_1j = g₁{E(X∣G = _gj)} – g₁{E(X∣G = g_p+1)} and γ_1j = g{E(Y∣G = g_j)} – g{E(Y∣G = g_p+1)}, where g_p+1 is the reference genotype group. If θ₁ = 0, then for any j in (1, .., p)

$$E(Y\mid G=g_i)=E_U\left[E_{X\mid G=g_j,U}\right\{E(Y\mid X,G=g_j,U)\left\}\right]=E_U\left\{E\right(Y\mid G=g_i,U\left)\right\}=E\left(Y\right),$$

so that γ_1j = 0, and so γ_1j cannot be concordant with α_1j.

Conversely, suppose α_j > α_j’, E(X∣G = g_j) > E(X∣G = g_j’) because g₁(·) is a strictly increasing function. Let $f_1(\cdot )=g_1^{-1}(\cdot )$. By the mean value theorem,

$$E(X\mid G=g_j)-E(X\mid G=g_{j^{\prime }})=E_U\left\{f_1^{\prime }\right({\beta }_0+{\beta }_1^{\ast }+{\beta }_{2}U\left)\right({\beta }_{1j}-{\beta }_{1j^{\prime }}\left)\right\}$$

for some ${\beta }_1^{\ast }$ in (β_1j’, β_1j). Since f₁(·) is continuous and strictly increasing, $f_1^{\prime }(\cdot )>0$. Therefore if E(X∣G = g_j) > E(X∣G = g_j’) then β_1j > β_1j’. For a generalized linear model in the exponential family with a strictly increasing link function, this suggests that for all U, pr(X∣G = g_j,U)/pr(X∣G = g_j’,U) is monotone increasing with x, and so the distribution pr(X∣G = g_j,U) is stochastically greater than the distribution pr(X∣G = g_j’,U). If θ₁ > 0, E(Y∣X = x,G,U) is a strictly increasing function of x. Since E(Y∣G = g_j) = E_U[E_X∣G=gj,U{E(Y∣X,G = g_j,U)}], and since pr(X∣G = g_j,U) is stochastically greater than pr(X∣G = g_j’,U),then E(Y∣G = g_j) > E(Y∣G = g_j’) and hence γ_1j > γ_1j’. Similarly if θ₁ < 0, {−E(Y∣X = x,G,U)} is a strictly increasing function of x and {−E(Y∣G = g_j)} > {−E(Y∣G = g_j’)}. Hence γ_1j < γ_1j’.

Furthermore, we prove the statement that if (α_1j – α_1j’)(γ_1j – γ_1j’) > 0 then θ₁ > 0 by contradiction. If α_1j > α_1j’, following previous arguments, pr(X∣G = g_j,U) is stochastically greater than the distribution pr(X∣G = g_j’,U). Since E(Y∣G = g_j) = E_U[E_X∣G=gj,U{E(Y∣X,G = g_j,U)}], then if θ₁ ≤ 0, γ_1j cannot be greater than γ_1j’.

Proof of Corollary 1

If θ1 = 0, γ_1j = 0 for all j. The minimizer of (9) λ_D takes the form (α^TDα)⁻¹α^TDγ, and so will be zero. Conversely, if θ1 ≠ 0, γ_1j ≠ 0 for all j. From the proof of Theorem 1, let g_j’ to be the reference genotype group. It is clear that if θ1 > 0, then α_1jγ_1j > 0; if θ1 < 0, then α_1jγ_1j < 0. Let γ_1j = c_jα_1j and let C to be a diagonal matrix with diagonal element c_j. If θ₁ > 0, then c_j > 0 for all j, then C is also a positive definite matrix. Observe that α^TDγ = α^TDCα > 0, since the product of two positive definite matrix DC is also positive definite. Thus λ_D > 0. If θ₁ < 0, then c_j < 0 for all j, and so λ_D < 0. Following these arguments, the result for non-zero causal effect that λ_Dθ1 > 0 is proved by contradiction.

Proof of Corollary 2

Let $X={\beta }_0+{\sum }_{j=1}^p{\beta }_{1j}{Z}_j+{\beta }_{2}U+∊$, where ∊ is independent and identically distributed random error with zero mean. Since Z ⊥ U, α_1j = β_1j. For a subject with genotype G = g_j,

$$E(Y\mid G=g_j)=E_U{E}_{∊}\left[g^{-1}\right\{{\theta }_0+{\theta }_1({\beta }_0+{\alpha }_{1j}+{\beta }_{2}U+∊)+{\theta }_{3}U\left\}\right],$$

while for a subject with the reference genotype,

$$E(Y\mid G=g_{p+1})=E_U{E}_{∊}\left[g^{-1}\right\{{\theta }_0+{\theta }_1({\beta }_0+{\beta }_{2}U+∊)+{\theta }_{3}U\left\}\right].$$

Let S = θ₁β₂U + θ₁∊ + θ₃U. E(S) = 0 and denote by Ω the variance of S. Let h(·) = g⁻¹(·). Second order Taylor series expansion of E(Y∣G = g_j) and E(Y∣G = g_p+1) leads to good approximations

$$\begin{array}{cc}\hfill E(Y\mid G=g_j)=& h({\theta }_0+{\theta }_1{\beta }_0+{\theta }_1{\alpha }_j)+\frac{1}{2}\Omega h^{″}({\theta }_0+{\theta }_1{\beta }_0+{\theta }_1{\alpha }_{1j}),\hfill \\ \hfill E(Y\mid G=g_{p+1})=& h({\theta }_0+{\theta }_1{\beta }_0)+\frac{1}{2}\Omega h^{″}({\theta }_0+{\theta }_1{\beta }_0).\hfill \end{array}$$

Since γ_1j = g{E(Y∣G = g_j)} – g{E(Y∣G = g_p+1)}, first order Taylor series expansion of g{E(Y∣G = g_j)} at h₂(θ₀ + θ₁β₀ + θ₁α_1j) and g{E(Y∣G = g_p+1)} at h₂(θ₀ + θ₁β₀) results in

$${\gamma }_{1j}-{\theta }_1{\alpha }_{1j}\approx \frac{1}{2}\Omega \left\{\frac{h^{″}({\theta }_0+{\theta }_1{\beta }_0+{\theta }_1{\alpha }_{1j})}{h^{\prime }({\theta }_0+{\theta }_1{\beta }_0+{\theta }_1{\alpha }_{1j})}-\frac{h^{″}({\theta }_0+{\theta }_1{\beta }_0)}{h^{\prime }({\theta }_0+{\theta }_1{\beta }_0)}\right\}.$$

For a logistic model, $h(\cdot )=\frac{\exp (\cdot )}{1+\exp (\cdot )}$, and so $\frac{h^{″}(\cdot )}{h^{\prime }(\cdot )}$ is a decreasing function. Thus if θ₁α_1j > 0, γ_1j is negatively biased; if θ₁α_1j < 0, γ_1j is positively biased.

Let γ_1j = c_jα_1j. If θ₁ > 0, θ₁ > c_j > 0 for all j. Let E to be a diagonal matrix with diagonal element θ₁ – c_j. So θ₁ – λ_D = (α^TDα)⁻¹α^TDEα > 0. If θ₁ < 0, θ₁ < c_j < 0 and so θ₁ – λ_D < 0. Therefore λ_D is biased toward zero.

Proof of Lemma 1

Because Z ⊥ U, and X∣Z,U is normally distributed with mean ${\alpha }_0+{\sum }_{j=1}^p{\alpha }_{1j}{Z}_j+{\beta }_{2}U$ and variance σ², it follows that

$$\begin{array}{cc}\hfill E(Y\mid Z)=& E_{U\mid Z}{E}_{X\mid Z,U}E(Y\mid X,Z,U)\hfill \\ \hfill =& E_{U\mid Z}{E}_{X\mid Z,U}\exp ({\theta }_0+{\theta }_{1}X+{\theta }_{2}U)\hfill \\ \hfill =& E_{U\mid Z}\exp ({\theta }_0+{\theta }_{2}U+{\theta }_1{\alpha }_0+\sum _{j=1}^p{\theta }_1{\alpha }_{1j}{Z}_j+{\theta }_1^2{\sigma }^2+{\theta }_1{\beta }_{2}U)\hfill \\ \hfill =& \exp \left\{{\theta }_0+{\theta }_1{\alpha }_0+\frac{1}{2}{\theta }_1^2{\sigma }^2+\log c+\sum _{j=1}^p{\theta }_1{\alpha }_{1j}{Z}_j\right\},\hfill \end{array}$$

where c = E{exp(θ₂U + θ₁β₂U)}. Hence γ_1j = θ₁α_1j and ${\gamma }_0={\theta }_0+{\theta }_1{\alpha }_0+\frac{1}{2}{\theta }_1^2{\sigma }^2+\log c$.

Proof of Theorem 2

The asymptotic expansion of ${\widehat{\theta }}_{\mathrm{D}}$ closely follows the proof in Corollary 2. The asymptotic optimality of ${\widehat{\theta }}_{\mathrm{gls}}$ can be established by arguments similar to those used for the Gauss-Markov Theorem. Observe that

$$\begin{array}{cc}\hfill n^{1∕2}({\widehat{\theta }}_{\mathrm{D}}-\theta )=& n^{1∕2}({\widehat{\theta }}_{\mathrm{D}}-{\widehat{\theta }}_{\mathrm{gls}})+n^{1∕2}({\widehat{\theta }}_{\mathrm{gls}}-\theta )\hfill \\ \hfill =& n^{1∕2}\{{\left({{\widehat{\mathcal{A}}}^T}_{\mathrm{D}}\widehat{\mathcal{A}}\right)}^{-1}\widehat{\mathcal{A}}\mathrm{D}-{\left({\widehat{\mathcal{A}}}^T{\Gamma }^{-1}\widehat{\mathcal{A}}\right)}^{-1}\widehat{\mathcal{A}}{\Gamma }^{-1}\}({\widehat{\gamma }}^{\ast }-\widehat{\mathcal{A}}\theta )\hfill \\ \hfill & +n^{1∕2}{\left({\widehat{\mathcal{A}}}^T{\Gamma }^{-1}\widehat{\mathcal{A}}\right)}^{-1}\widehat{\mathcal{A}}{\Gamma }^{-1}({\widehat{\gamma }}^{\ast }-\widehat{\mathcal{A}}\theta )\hfill \\ \hfill =& n^{1∕2}\{{\left({\mathcal{A}}^T\mathrm{D}\mathcal{A}\right)}^{-1}\mathcal{A}\mathrm{D}-{\left({\mathcal{A}}^T{\Gamma }^{-1}\mathcal{A}\right)}^{-1}\mathcal{A}{\Gamma }^{-1}\}({\widehat{\gamma }}^{\ast }-\widehat{\mathcal{A}}\theta )\hfill \\ \hfill & +n^{1∕2}{\left({\mathcal{A}}^T{\Gamma }^{-1}\mathcal{A}\right)}^{-1}\mathcal{A}{\Gamma }^{-1}({\widehat{\gamma }}^{\ast }-\widehat{\mathcal{A}}\theta )+o_p\left(1\right).\hfill \end{array}$$ (22)

The last equation (22) uses Slutsky’s theorem. Some algebra can show that the first two terms in (22) are asymptotically uncorrelated. The asymptotic covariance matrix of $n^{1∕2}({\widehat{\theta }}_{\mathrm{D}}-\theta )$ can be decomposed as

$$\begin{array}{cc}\hfill \mathrm{cov}\left\{n^{1∕2}\right(\widehat{\theta }-\theta \left)\right\}=& {\left({\mathcal{A}}^T{\Gamma }^{-1}\mathcal{A}\right)}^{-1}+\{{\left({\mathcal{A}}^T\mathrm{D}\mathcal{A}\right)}^{-1}\mathcal{A}\mathrm{D}-{\left({\mathcal{A}}^T{\Gamma }^{-1}\mathcal{A}\right)}^{-1}\mathcal{A}{\Gamma }^{-1}\}\Gamma \hfill \\ \hfill & {\left({\left({\mathcal{A}}^T\mathrm{D}\mathcal{A}\right)}^{-1}\mathcal{A}\mathrm{D}-{\left({\mathcal{A}}^T{\Gamma }^{-1}\mathcal{A}\right)}^{-1}\mathcal{A}{\Gamma }^{-1}\right)}^T\hfill \\ \hfill \ge & {\left({\mathcal{A}}^T{\Gamma }^{-1}\mathcal{A}\right)}^{-1},\hfill \end{array}$$ (23)

since the second term in (23) is non-negative definite. The equality holds if D = Γ. This establishes the asymptotic optimality of ${\widehat{\theta }}_{\mathrm{gls}}$.

Proof of Corollary 3

To obtain ${\widehat{\theta }}_{2\mathrm{SLS}}$, one first compute the predicted value $\widehat{X}$ in (14), replace X in (13) by $\widehat{X}$, and solve the estimating equation for (13), denoted by S_n($\widehat{X}$; θ). Since ${\gamma }^{\ast }=\mathcal{A}\theta$, where $\mathcal{A}$ is a matrix composed of elements in α, the two-stage least squares estimating function can be equivalently presented as ${\sum }_{i=1}^n\widehat{\mathcal{A}}{S}_{2i}\left(\widehat{\mathcal{A}}\widehat{\theta }\right)∕n^{1∕2}$, where S_2i is the estimating function for (15). Taylor series expansion with respect to both α and θ yields

$${\mathcal{A}}^T{\mathrm{A}}_2\mathcal{A}{n}^{1∕2}(\widehat{\theta }-\theta )+{\mathcal{A}}^T{\mathrm{A}}_2{n}^{1∕2}(\widehat{\mathcal{A}}-\mathcal{A})\theta .$$

On the other hand, the estimating function for ${\widehat{\theta }}_{2\mathrm{SLS}}$ also equals to ${\mathcal{A}}^T{\mathrm{A}}_2{n}^{1∕2}({\widehat{\gamma }}^{\ast }-\gamma )+o_p\left(1\right)$, because $\widehat{\mathcal{A}}\widehat{\theta }$ is consistent for γ. It follows that

$$n^{1∕2}({\widehat{\theta }}_{2\mathrm{SLS}}-\theta )={\left({\widehat{A}}^T{\mathrm{A}}_2\mathcal{A}\right)}^{-1}{\widehat{\mathcal{A}}}^T{\mathrm{A}}_2\left\{n^{1∕2}\right({\widehat{\gamma }}^{\ast }-\widehat{\mathcal{A}}\theta \left)\right\}+o_p\left(1\right).$$

Proof of Lemma 2

If g₁(·) is the identity function, we obtain α_1j = β_1j by integrating U∣W in E(X∣Z,W,U). So if α_1j > α_1j’, E(X∣G = g_j,W) > E(X∣G = g_j’,W) for every W. Following the arguments in Theorem 1, we have E(Y∣G = g_j,W) > E(Y∣G = g_j’,W) for every W.

Some algebra leads to the result that the maximum likelihood estimates of γ_j and γ_j’ in the working model (21) have to satisfy the following equations

$$\begin{array}{cc}\hfill E_{W\mid G=g_j}E(Y\mid G=g_j,W)=& E_{W\mid G=g_j}\frac{\exp ({\gamma }_0+{\gamma }_{1j}+{\gamma }_{2}W)}{1+\exp ({\gamma }_0+{\gamma }_{1j}+{\gamma }_{2}W)}\hfill \\ \hfill E_{W\mid G=g_{j^{\prime }}}E(Y\mid G=g_{j^{\prime }},W)=& E_{W\mid G=g_{j^{\prime }}}\frac{\exp ({\gamma }_0+{\gamma }_{1j^{\prime }}+{\gamma }_{2}W)}{1+\exp ({\gamma }_0+{\gamma }_{1j^{\prime }}+{\gamma }_{2}W)}\hfill \end{array}$$

If W∣G = g_j and W∣G = g_j’ are in some stochastic order, whether stochastically greater or stochastically less, E(Y∣G = g_j,W) > E(Y∣G = g_j’,W) for every W, then γ_1j has to be greater than γ_1j’, otherwise the comparison of the upper two equations runs into contradiction. This suggests the concordance of α_1j and γ_1j.