Viscoelastic Characterization of Extraocular Z-Myotomy

Abstract

Purpose.

Z-myotomy is an extraocular muscle (EOM) weakening procedure in which two incisions are made from longitudinally-separated, opposite EOM margins for treatment of strabismus. We examined the in vitro biomechanics of Z-myotomy using tensile loading.

Methods.

Fresh bovine rectus EOMs were reduced to 20 × 10 × 2–mm dimensions, and clamped in a microtensile load cell under physiological conditions. Extraocular muscles were elongated until failure following scissors incisions made from opposite sides, spaced 8 mm apart and each encompassing 0%, 40%, 50%, 60%, or 80% EOM width. Initial strain to 30% elongation was imposed at 100 mm/s, after which elongation was maintained for greater than 100 seconds during force recording at maintained deformation. Stress relaxation tests with nonincised specimens having widths ranging from 1 to 9 mm were conducted for viscoelastic characterization of corresponding equivalence to 20% to 80% Z-myotomy. Data were modeled using the Wiechert viscoelastic formulation.

Results.

There was progressively reduced EOM failure force to an asymptotic minimum at 60% or greater Z-myotomy. Each Z-myotomy specimen could be matched for equivalent failure force to a non–Z-myotomy specimen with a different width. Both tensile and stress relaxation data could be modeled accurately using the Wiechert viscoelastic formulation.

Conclusions.

The parallel fiber structure results in low shear force transfer across EOM width, explaining the biomechanics of Z-myotomy. Z-myotomy progressively reduces force transmission to an asymptotic minimum for less than 60% surgical dose, with no further reduction for greater amounts of surgery. Equivalence to EOM specimens having regular cross-sections permits viscoelastic biomechanical characterization of Z-myotomy specimens with irregular cross-sections.

Z-myotomy comprises longitudinally spaced transverse incisions tolengthen and weaken extraocular muscle (EOM) for strabismus treatment. Because of generally parallel structure and scant transverse coupling among EOM fibers, 60percnt; or more Z-myotomy mechanically equates to completely dividing all fibers.

Introduction

Z-myotomy, also known as marginal myotomy, is a surgical technique for lengthening and weakening of extraocular muscle (EOM) for treatment of strabismus. This approach is similar to Z-tenotomy, a weakening and lengthening procedure for extraocular tendon (EOT), as it involved making transversely overlapping incisions, spaced some distance apart, from opposite sides of the EOM or EOT. Clinical effectivities of Z-myotomy^1–4 and Z-tenotomy^5–9 have been evaluated on the bases of surgical outcomes. Shin et al.¹⁰ reported the in vitro biomechanical effect of Z-tenotomy in proportions from 20% to 80% of EOT width¹⁰ by conducting tensile loading until failure, meaning rupture of the EOT specimen for each Z-tenotomy ratio. It was concluded that Z-tenotomy up to 50% progressively reduces force transmission, but greater Z-tenotomy is biomechanically equivalent to complete tenotomy. However, Z-myotomy has heretofore not been characterized biomechanically.

Biomechanical characterization has been described to define the behavior of tissues, including artery,¹¹ brain,^12–17 heart muscle,^18–20 kidney,^21–24 liver,^25,26 ligament and tendon,^27–31 and skin.^32–34 In ophthalmic research, a variety of mechanical techniques and modeling methods have been applied to EOM,^35–37 orbital connective tissue and fat,³⁸ cornea,³⁹ and sclera.⁴⁰ A recent biomechanical study by Shin et al.⁴¹ has provided mechanical evidence for differential compartmental function of the horizontal rectus EOMs, whose intramuscular innervation is segregated into superior and inferior compartments.^42,43 The plausibility of independent EOM compartmental action is suggested by showing low transverse mechanical coupling between compartments.⁴¹ The complex internal structure of EOM contrasts with the isotropic structure of a uniform elastic material such as latex rubber, which is uniform in all directions, and which shows high transverse mechanical coupling.

Viscoelastic materials, ranging from polymers to biological tissues, can be modeled for describing the stress or strain interactions of their temporal dependencies. Experimental studies of soft tissue have often been framed in the linear theory of viscoelasticity, relating stress and strain using Voigt, Maxwell, or Kelvin models. Buchthal et al.⁴⁴ formulated a general model having an infinite number of Voigt (parallel circuit of dampers and springs) and Maxwell (serial circuit of dampers and springs) elements. A nonlinear Kelvin model was proposed by Viidik as a sequence of springs of varying rest lengths.⁴⁵

For Z-myotomy exceeding 50% of ideally parallel fibers, no individual EOM fibers remain continuous across the two incisions, implying that any postoperative force transmission would be due to transverse coupling between fiber bundles. This has implications for independent mechanical behavior of EOM compartments,⁴¹ since transverse coupling has been proposed to be the main determinant of intercompartmental coupling. If fiber bundles are transversely independent, even 50% Z-myotomy would maximally reduce transmitted force, because all fibers would be divided. Therefore, it was hypothesized that Z-myotomy exceeding 50% from each margin would maximally weaken EOM biomechanics, and further myotomy would have no additional clinical effect. The current study aimed to confirm this supposition by investigating the biomechanical effect of various doses Z-myotomy of EOM of an in vitro bovine model. Since geometry after Z-myotomy becomes complicated by distortion and nonuniformity of cross sections along the longitudinal direction, simple stress–strain analysis would be difficult to interpret. However, conversion of the geometry from an irregular pattern to a simple prism shape could enable systematic biomechanical characterization of Z-myotomy, especially for viscoelastic behavior.

Methods

Custom Microtensile Testing

A custom, horizontally mounted microtensile load cell was constructed using heavy aluminum and steel hardware, a high speed linear motor, and strain gauge permitting specimen testing in a physiological environment as described elsewhere.¹⁰ Figure 1 is a photograph of experimental apparatus.

Figure 1.

Configuration of the load cell. A linear motor (1) was connected to a stain gauge (2) and transmitted its measured tensile force through a frictionless air bearing (3) and cylindrical shaft (4) to the moveable specimen clamp (5) to which one end of the specimen was affixed. The other specimen clamp at right was held immobile, anchoring the opposite end of the specimen. The environmental chamber at right surrounding the specimen was maintained at physiologic temperature and saturated humidity.

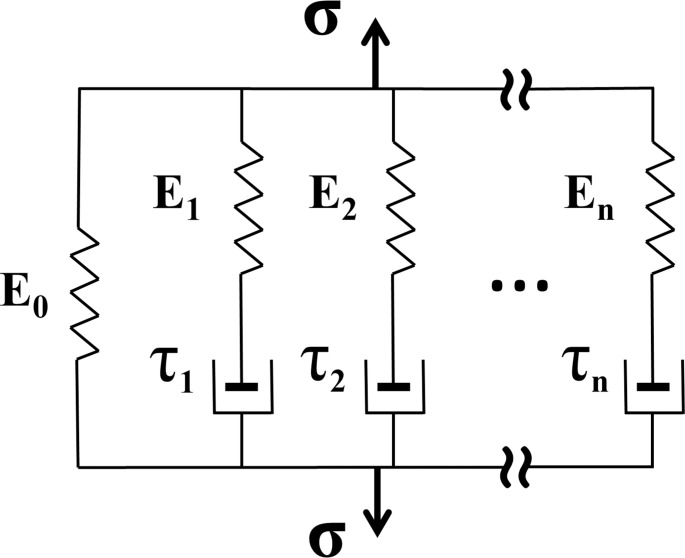
Wiechert Viscoelastic Model

There are two basic models for linear viscoelastic modeling: Maxwell and Voigt.⁴⁶ The Maxwell model uses a viscous damper and an elastic spring connected in series, so that it can predict relaxation describing how a material deformed by external perturbation returns to equilibrium. However, it cannot predict creep, which is the tendency of a material to deform permanently under constant force. Conversely, the Voigt model consists of a Newtonian damper and Hookean elastic spring connected in parallel that can describe creep accurately, but is poor for predicting relaxation. For the purpose of compensating these limitations, several models have been constructed as linear combinations of springs and dashpots. We elected to employ the Wiechert model, which provides for superposition of linear combinations arbitrarily many spring-dashpot elements (Fig. 2), and is convenient for finite element analysis. For stress relaxation, the total stress σ(t) transmitted by the Wiechert constitutive model is given by⁴⁷

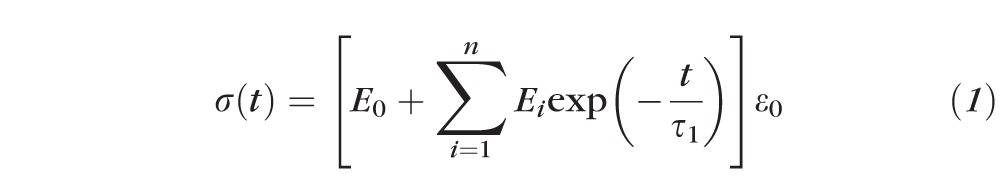where t is the time, E_i (i = 0, 1, …) the relaxation modulus of the i-th spring, τ_i (i = 1, 2, …) the relaxation time of the i-th dashpot, and ε₀ is the constant strain applied to the material during the stress relaxation testing. Both sides of Equation 1 can be divided by ε₀, giving

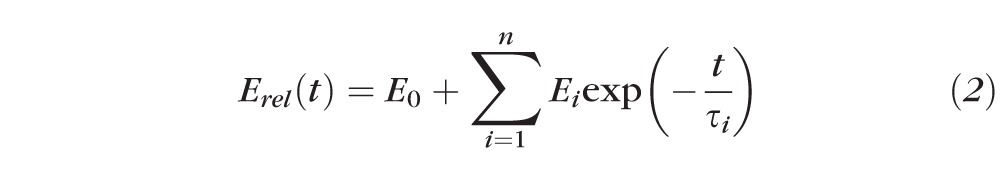where E_rel is called the time-dependent relaxation modulus.

Figure 2.

The Wiechert model consists of as many spring-dashpot elements as needed for the required precision.

Through experiments, a Wiechert model for a viscoelastic material can be defined by determination of constants E_i (i = 0, 1, …, n) and τ_i (i = 1, 2, …, n) in the Prony series of Equation 2. In this study, EOM specimens were characterized by Wiechert model of stress relaxation data.

Specimen Preparation

Fresh heads of cows aged 20 to 30 months were obtained immediately after slaughter from a nearby abattoir (Manning Beef LLC, Pico Rivera, CA, USA). Transport time from abattoir to laboratory was approximately 1 hour, and another hour was required for preparation of specimens in the laboratory. After extraction, specimens were maintained in lactated Ringer's solution at 37°C. Specimens prior to Z-myotomy were trimmed to 25 × 10 × 2 mm for tensile experiments with uniform dimensions. To minimize axial damage to EOM fibers, specimens were initially reduced to 25-mm length in the direction perpendicular to the fibers, by cutting the longer dimension. This left a 2.5-mm margin for clamping at each specimen end, so that the region subject to elongation was 20-mm long. Since EOM thickness is not negligible, specimen thickness was controlled to 2 mm by trimming fiber bundles in the longitudinal direction, with care not to create discontinuous fibers.

Z-incision of Control Material Isotropic Rubber

Isotropic latex rubber (abrasion-resistant natural latex rubber 1/16-inch thick; McMaster-Carr, Santa Fe Springs, CA, USA) was used as a control material. Specimens were prepared measuring 30-mm long and 20-mm wide. Unlike EOM specimens, only 20% elongation was applied to latex since this is well-characterized, linearly elastic material, so that maximum force transition for various Z-myotomy ratios should correspond to failure force transition of EOM. Each of three specimens was tested for five different Z-myotomy ratios from 0%, 20%, 40%, 60%, 80% specimen width at 1-mm/s loading rate.

Uniaxial Tensile Experiment With Z-Myotomy

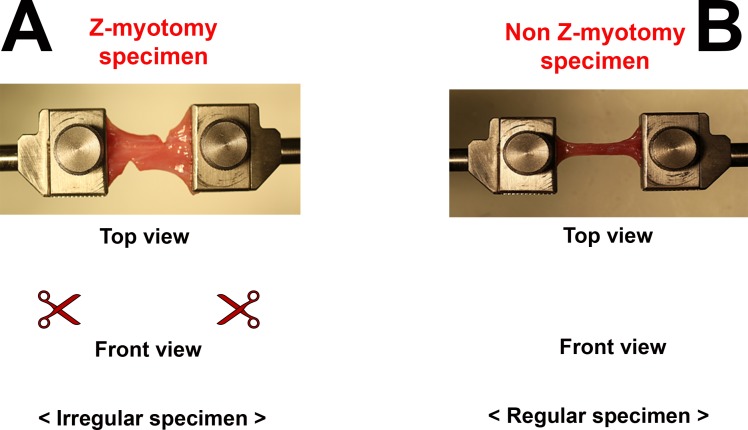
Preloading was applied to specimens to avoid slackness. Tensile testing was performed under the physiological conditions by loading EOM specimens to increasing tension until failure. Before loading, Z-myotomy was performed by making two transverse incisions, from opposite sides of the specimen, spaced 8 mm apart (Fig. 3A). In different specimens, Z-myotomy was performed from each margin at 0%, 20%, 40%, 50%, 60%, and 80% width. Figure 3B illustrates 40% Z-myotomy.

Figure 3.

Experimental approach to Z-myotomy. (A) Schematic. Extraocular muscles were clamped at both ends and preloaded to prevent slackness. The specimen was then incised from opposite margins 8 mm apart at predetermined ratios (20%, 40%, 50%, 60%, and 80%) of total width. Reprinted with permission from Shin A, Yoo L, Demer JL. Biomechanics of superior oblique Z-tenotomy. J AAPOS. 2013;17:612–617. © 2013 American Association for Pediatric Ophthalmology and Strabismus. (B) Forty percent Z-myotomy of LR muscle. After clamping the specimen (top), 40% of muscle width was incised from both margins (bottom).

Since all six EOMs exhibit similar time-dependent nature and elastic properties,³⁵ lateral rectus and superior rectus EOMs, which are most convenient to extract, were prepared for experiments. Before tensile loading, Z-myotomy was performed from each EOM margin at 0%, 20%, 40%, 50%, 60%, and 80% width. Failure force of the specimen was recorded as the peak force achieved during progressive tensile loading, before force decreased at the point of specimen rupture.

Z-Myotomy Equivalence Tensile Testing

Mathematical modeling of viscoelastic mechanical behavior faces the geometric problem of irregular cross-sectional areas produced by Z-myotomy. Although analytic solutions exist for fracture mechanics,⁴⁸ discontinuous cross section along the EOM specimen after Z-myotomy confounds mathematical models that customarily assume regular cross-sectional area. However, the authors propose that by matching failure force of irregular to regular cross-section specimens, viscoelastic modeling of the former can be inferred from the latter.

Uniaxial tensile tests were performed with EOM specimens ranging from 1- to 10-mm wide, in 1-mm increments, having same length × thickness (20 × 2 mm) as Z-myotomy specimens. Then, the behavior of each Z-myotomy specimen from 20% to 80% was matched to a specimen with a continuous cross section. Figure 4 illustrates the equivalence between Z-myotomy and non–Z-myotomy specimen.

Figure 4.

Schematic illustration of equivalence based upon failure force. Z-myotomy specimens (A) have irregular cross sections varying along the specimen length, precluding viscoelastic modeling. After matching the failure force of each Z-myotomy specimen to a non–Z-myotomy specimen (B), mathematical viscoelastic modeling can be executed for the equivalent specimen.

Stress Relaxation Testing of EOM and Viscoelastic Modeling

Stress relaxation experiments were performed using the microtensile load cell with equivalent Z-myotomy EOM specimens. Each sample was elongated to 30% in deformation with the highest speed of 100 mm/s. Length was then maintained for at least 100 seconds while recording the relaxation, the decline in tension over time. The Wiechert model was employed for viscoelastic characterization of each Z-myotomy equivalence specimen.

Results

Z-Myotomy With Control Material Isotropic Rubber

Isotropic latex rubber control specimens were elongated by 20% of initial length at 1 mm/s. Representative specimen photographs and force data for five different Z-myotomy ratios are illustrated in Figure 5. The latex between incisions became distorted to an oblique path by shear force. There was a linear trend of decreasing maximum force with increasing percentage Z-myotomy, as shown in Figure 5B. This reflects the combined effect of tensile and shear forces. Theoretically, with progressive Z-myotomy, tensile force would decrease to 0 at 50%, because of decreasing cross-section area for tensile loading. However, this effect is offset by shear force that increases to a maximum at 50% Z-myotomy, before decreasing progressively for greater myotomy. Consequently, the experimental data, reflecting the sum of tensile and shear forces, exhibited a linearly decreasing, isotropic coupling effect. The graph in Figure 5B extrapolates to nearly zero force at approximately 90% Z-myotomy.

Figure 5.

Z-myotomy of latex. Reprinted with permission from Shin A, Yoo L, Demer JL. Biomechanics of superior oblique Z-tenotomy. J AAPOS. 2013;17:612–617. © 2013 American Association for Pediatric Ophthalmology and Strabismus. (A) Eighty percent Z-myotomy tensile testing. The central portion of the specimen was distorted by shear force. (B) Maximum force transition from 0 to 80% Z-myotomy showing linear decline in maximum force. Error bars indicate SD.

Z-Myotomy Tensile Testing

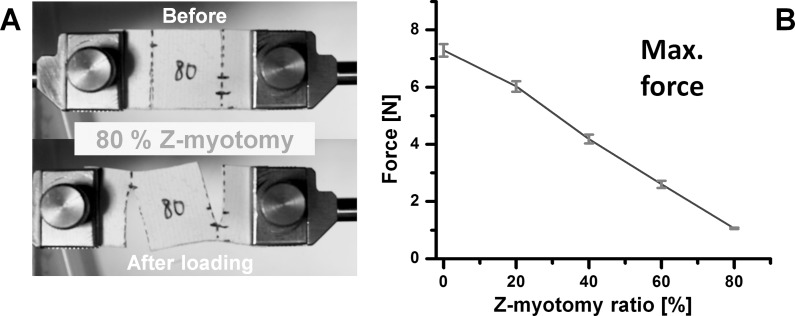
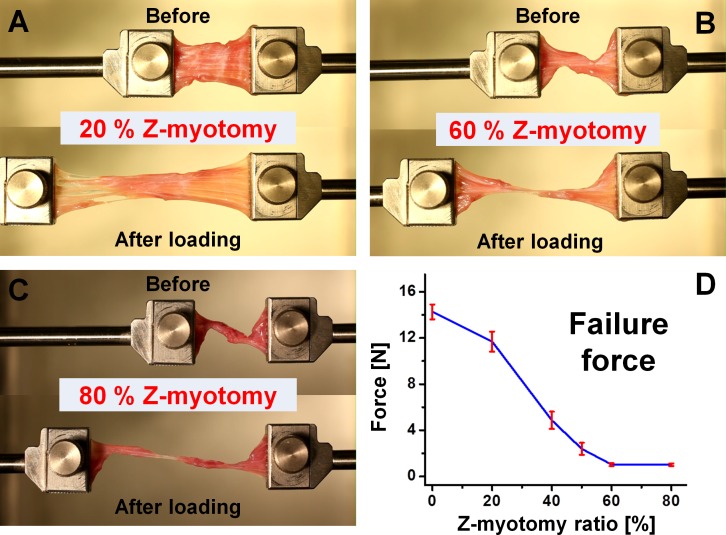
Tensile testing was performed on specimens after Z-myotomy. Five specimens were tested for each Z-myotomy ratio from 0% to 80%. Thus, a total 30 specimens was elongated until failure at 1-mm/s loading rate. Failure force exhibited a trend similar to Z-tenotomy,¹⁰ but with a slight difference. While minimum failure force was observed for 50% or greater Z-tenotomy, this occurred at 60% for Z-myotomy. Above 60%, there was no significant change in residual force with additional myotomy. For example, failure force was 1.04 N for 60% and 1.01 N for 80% Z-myotomy. Consequently, EOM tensile force showed a parabolic decline for increasing Z-myotomy until reaching an asymptotic minimum at 60%. Figure 6 illustrates the failure force trend.

Figure 6.

Tensile testing after Z-myotomy. (A) Twenty percent Z-myotomy before and after elongation. (B) Sixty percent Z-myotomy. (C) Eighty percent Z-myotomy. (D) Failure force transition from 0 to 80% Z-myotomy. Failure force was reduced to minimum by 60% or greater Z-myotomy. Error bars indicate SD.

Z-Myotomy Equivalence Tensile Testing

Z-myotomy equivalence tensile testing was examined with substitution of irregular by regular cross-section specimens equivalent in failure force. Three regular cross-section specimens were elongated until failure for each 1-mm increment in width from 1 to 10 mm for a total of 30 specimens having identical length and thickness. The failure force trend is illustrated in Figure 7A.

Figure 7.

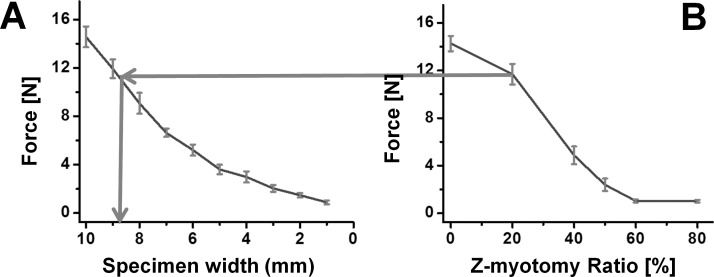
(A) Failure force of regular shaped bovine EOM specimens of varying widths for comparison with Z-myotomy. Error bars indicate SD. (B) Failure force result from Figure 6D was used to determine the equivalent width by force matching in each Z-myotomy ratio.

Linear interpolation of widths was used to estimate intermediate values matched to those observed for Z-myotomy specimens shown in Figure 7B, so that irregular Z-myotomy specimens could be considered equivalent to regular, non–Z-myotomy EOM specimens suitable for viscoelastic characterization. Table 1 shows the equivalent widths for five different Z-myotomy ratios from 20% to 80%.

Table 1.

Equivalent Uniform Specimen Width for Each Z-Myotomy Ratio Based Upon Failure Force Matching

Z-Myotomy Ratio	20%	40%	50%	60%	80%
Equivalent width	8.9 mm	5.8 mm	3.4 mm	1.3 mm	1.2 mm

Stress Relaxation Testing of EOM and Viscoelastic Modeling

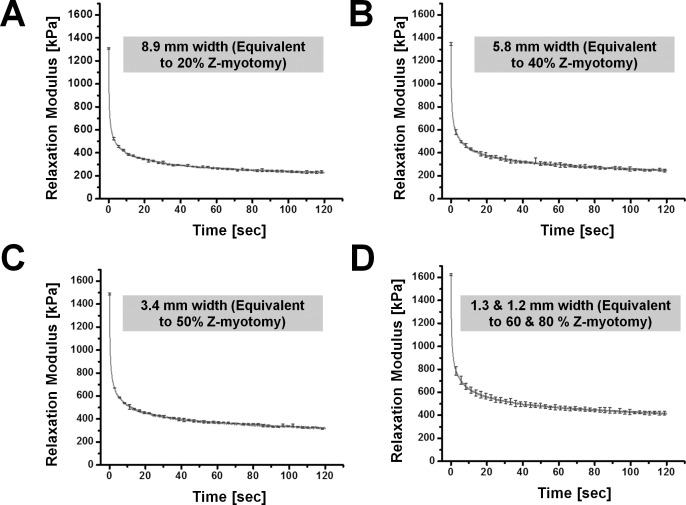
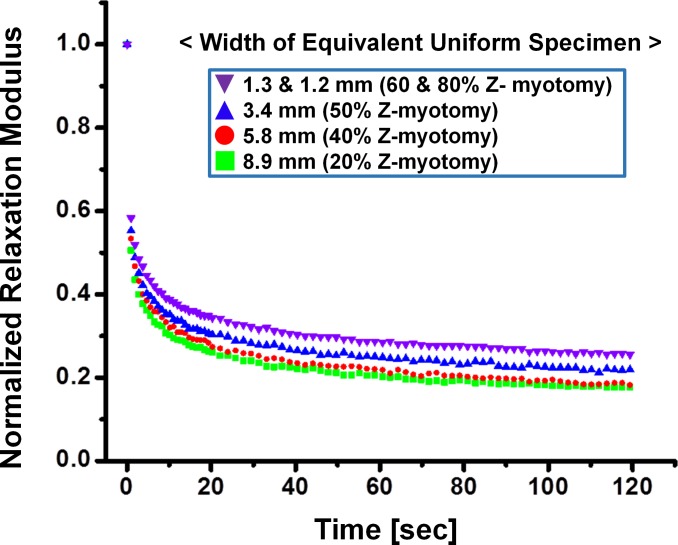
For stress relaxation testing, three specimens of each equivalent width from 8.9- to 1.2-mm width were tested; therefore, 15 specimens total were elongated to 30% of initial length. A similar relaxation trend was exhibited for both 1.3- and 1.2-mm widths, corresponding to the failure force data as 60% and 80% Z-myotomy. Thus, experimental behavior of the 1.3- and 1.2-mm specimens was regarded as identical. Figure 8 illustrates average relaxation data for each equivalent width. Relaxation moduli at 30% strain were 1308, 1347, 1489, and 1625 kPa, corresponding to 8.9-, 5.8-, 3.4-, 1.3-, and 1.2-mm widths, respectively. For comparison, relaxation data was normalized by the maximum relaxation modulus. Figure 9 shows normalized relaxation curves in each Z-myotomy equivalence case.

Figure 8.

Stress relaxation testing of each equivalent specimen. (A) A width of 8.9 mm corresponding to 20% Z-myotomy. (B) A 5.8-mm width (40% Z-myotomy). (C) A 3.4-mm width (50% Z-myotomy). (D) A 1.3- and 1.2-mm width (60% and 80% Z-myotomy, respectively). Error bars indicate SD.

Figure 9.

Normalized stress relaxation of Z-myotomy equivalent specimens normalized to their corresponding maxima. As Z-myotomy ratio increased, specimens relaxed less, as well as more slowly.

A Wiechert viscoelastic model with three spring-dashpot elements was chosen for approximation of the data. Equation 2 can be rewritten as

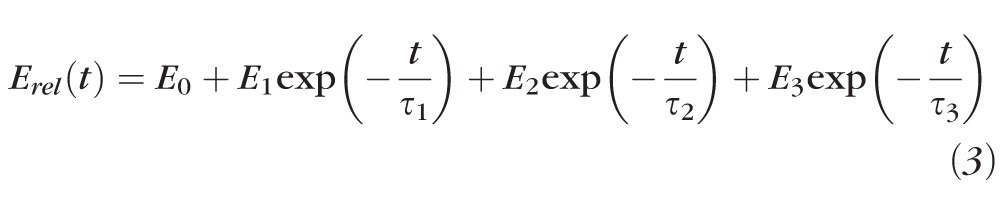Using the nonlinear data analysis software (OriginLab, Northampton, MA, USA), fits were made to average relaxation curves of four different type specimens. Parameters for Equation 3 were fit to the data as shown in Table 2.

Table 2.

Wiechert Viscoelastic Parameters, Extracted From Averaged Stress Relaxation Curves, for Uniform EOM Specimens Equivalent to Those After Z-Myotomy

Z-Myotomy Ratio, %	Equivalence Width, mm	E0	E1	E2	E3	τ1	τ2	τ3	R2
20	8.9	223	202	250	647	37.8	3.79	0.34	0.998
40	5.8	230	285	207	613	4.92	50.7	0.37	0.997
50	3.4	306	679	297	213	0.41	4.78	48.2	0.997
60 & 80	1.3 & 1.2	404	679	311	236	0.40	4.58	44.4	0.998

E₀, E₁, E₂, and E₃ are relaxation moduli of springs, and τ₁, τ₂, _and τ₃ are relaxation times of dashpots. Coefficients of determination R² are indicated for each fit.

Discussion

Both latex rubber and EOM exhibited declining force transmission as the percentage Z-myotomy increased, but with different trends. Rubber demonstrated linear decline of maximum force, while EOM exhibited nonlinear decline of failure force. These differences reflect structural differences between materials. Since latex rubber material has isotropic structure, the same in all directions, shear force is efficiently transferred through the remaining specimen bridging the two incisions. Thus, isotropic coupling resulted in roughly linear reduction of maximum force as a function of cutting ratio. In contrast, EOM has anisotropic structure, specifically orthotropic structure, the same along the length of the fibers, but different transversely. Unlike latex rubber, EOM is composed of roughly parallel fibers aligned in the longitudinal direction, with thinly woven transverse fibers and a small amount of viscous extrafibrillar matrix between fiber bundles. Extraocular muscle failure force declined at an accelerating rate with progressive myotomy until at or above 60%, there was hardly any force transmission at all. Z-myotomy of 60% or more divides all continuity between parallel fibers extending the full length of the EOM, so any remaining resistance to failure force would be attributable to transverse coupling between adjacent fibers. Understandably, this residual failure force must be very low since transverse coupling between fibers has been shown to be correspondingly low.⁴¹ Considering that the comparable threshold value was 50% for Z-tenotomy of flat, thin tendons,¹⁰ the difference probably comes from greater specimen thickness and likely internal twisting of fiber bundles to render them slightly nonparallel in 2-mm thick EOM specimens.

Relaxation modulus is a dynamic measure for viscoelastic characterization. The relaxation modulus, E_rel, at peak 30% strain increased (1308, 1347, 1489, and 1625 kPa) as specimen cross section decreased (8.9, 5.8, 3.4, and 1.3–1.2 mm), implying that smaller residual EOM width reflects greater tensile modulus. There have been similar reports that the tensile modulus of a portion of the tendon is greater than that of the whole.^49,50 Butler et al.⁵¹ suggested that the modulus of a small specimen of tendon may be more descriptive of the collagen in the tendon since the fascicle initial length and cross section can be more accurately determined, while fiber bundles tend to be more parallel than in whole tissue. Less connective tissues in a smaller tendon specimen might be another reason for increasing modulus.^52,53 Danylchuk et al.⁵² suggested that a precise definition of the tensile strength of the ligament ought to consider the relative contributions of collagen fasciculi and connective sheaths. This study showed that EOM follows the same trend as tendon and ligament.

Relaxation rate also changed with specimen width, as evident in Figure 9. As specimen size was reduced, for example equivalent to large Z-myotomy of 80%, the specimen relaxed more slowly, and asymptotic modulus increased. Atkinson et al.⁵⁴ reported a similar tendency in human patellar tendon.^3,53 More fluid inside a larger than smaller specimen may explain greater relaxation, presuming high fluid permeability. A larger specimen also exhibits a longer toe region representing straightening of the crimped fibrils at the beginning of the tensile phase. This longer toe suggests that tissue can be reoriented to align with the load, and thus relax faster after reaching peak force. Extraocular muscle can be analyzed in the same manner because of its similar parallel structure to EOT. Both tensile modulus and relaxation rate trends according to specimen size can be conceptualized in terms of Z-myotomy ratio; as Z-myotomy ratio increases, tensile modulus increases, and relaxation rate decreases.

Tensile elongation of any arbitrary proportion of any EOM fibers results in only approximately 5% coupling force transmission to the remainder of the fibers.⁴¹ Poor shear force transfer in EOM corresponds to substantial force decoupling between transverse layers, and represents the greatest biomechanical difference from an isotropic material such as latex. These findings are relevant for Z-myotomy exceeding 60%, which renders all fibers discontinuous that normally transmit longitudinal tensile force, leaving shear force coupling as the only means of force transmission. The current experiments were performed in vitro and deliberately isolated the EOMs from sheaths and other tissues that would be present in vivo, so that biomechanics could be studied without confounding by these other tissues. However, the in vivo biomechanical coupling of other tissues to EOM is probably relatively small at most, so findings in vitro should not be much different from in vivo. Moreover, in vitro experiments can give consistent data under the well-controlled conditions. The current data indicate that 60% or more Z-myotomy is mechanically equivalent to completely dividing all EOM fibers.

The present experiments were performed with EOM isolated from associated connective tissue in order to clarify EOM mechanics. Although the present study demonstrates that 60% or more Z-myotomy is mechanically equivalent to complete myotomy, this does not imply that Z-myotomy abolishes all oculorotary function of the operated EOM. Hakim et al.⁵⁵ reported that duction range remained normal after disinsertion of 76% of lateral rectus and 100% of oblique EOMs in young patients undergoing strabismus surgery under topical anesthesia. This maintenance of oculorotary effect after tendon disinsertion indicates a significant effect of noninsertional EOM force coupling due to orbital connective tissues. For example, detachment of the EOM tendon from the sclera severs only the direct insertion of the global layers on the eyeball, but has no direct effect on the other roughly one-half of total fibers in the orbital layer than insert on the muscle pulley.^56,57 Depending upon the distance of the Z-myotomy from the scleral insertion, the residual noninsertional coupling to the globe might vary modestly, but would likely remain significant since the surgery is performed anterior to the pulley. This is consistent with von Noorden's finding in 18 patients that there was no “functionally marked limitation of adduction” in 18 patients following 80% Z-myotomy of previously-recessed medial rectus muscles.⁴ Taken together with the current findings, Z-myotomy of 60% or greater may thus be considered equivalent to free disinsertion or complete transection of the EOM, both simpler procedures.