Modelling central metabolic fluxes by constraint-based optimization reveals metabolic reprogramming of developing Solanum lycopersicum (tomato) fruit

Abstract

Modelling of metabolic networks is a powerful tool to analyse the behaviour of developing plant organs, including fruits. Guided by our current understanding of heterotrophic metabolism of plant cells, a medium-scale stoichiometric model, including the balance of co–factors and energy, was constructed in order to describe metabolic shifts that occur through the nine sequential stages of Solanum lycopersicum (tomato) fruit development. The measured concentrations of the main biomass components and the accumulated metabolites in the pericarp, determined at each stage, were fitted in order to calculate, by derivation, the corresponding external fluxes. They were used as constraints to solve the model by minimizing the internal fluxes. The distribution of the calculated fluxes of central metabolism were then analysed and compared with known metabolic behaviours. For instance, the partition of the main metabolic pathways (glycolysis, pentose phosphate pathway, etc.) was relevant throughout fruit development. We also predicted a valid import of carbon and nitrogen by the fruit, as well as a consistent CO₂ release. Interestingly, the energetic balance indicates that excess ATP is dissipated just before the onset of ripening, supporting the concept of the climacteric crisis. Finally, the apparent contradiction between calculated fluxes with low values compared with measured enzyme capacities suggest a complex reprogramming of the metabolic machinery during fruit development. With a powerful set of experimental data and an accurate definition of the metabolic system, this work provides important insight into the metabolic and physiological requirements of the developing tomato fruits.

Introduction

As a consequence of its agronomical importance, Solanum lycopersicum (tomato) has been studied intensively with respect to genetics, physiology and biochemistry, eventually becoming an important model for fruit development. In order to identify metabolic properties underlying fruit quality that would be suitable targets for breeding or genetic manipulation, mathematical modelling of metabolism is particularly promising as it offers systems approaches, enabling the characterization of the structure, dynamics and behaviour of complex metabolic networks. In plant research, computational and mathematical modelling encapsulating the relationships between molecular components have been developed to study signalling and circadian rhythms, as well as growth and metabolism (Liu et al., ²⁰¹⁰). Metabolic pathways provide constituents for biomass and other outputs, and their description using flux models provides a dynamic depiction of the metabolic phenotype of the plant. Although modelling of metabolism in plant cells is not as advanced as in other organisms (Oberhardt et al., ²⁰⁰⁹), considerable progress has been made in recent years. For instance, steady-state metabolic flux analysis (MFA) has become a powerful tool for analysing metabolic fluxes in plants (Allen et al., ²⁰⁰⁹). This method relies on isotopic labelling experiments to analyse the distribution of labelled molecules; however, despite its proven capability to define metabolic phenotypes, steady-state MFA has a number of critical limitations, such as the small size of the networks studied, the requirement of a heterotrophic or mixotrophic tissue in culture for ease of labelling and the intensive labour required to generate flux maps. These limitations have driven the search for alternative and complementary approaches to characterize and explore plant metabolic networks. Initially developed in the field of microbial research (Borodina and Nielsen, 2005), flux balance analysis (FBA) has emerged as an alternative to MFA. FBA is a constraint-based modelling approach that allows the prediction of metabolic steady-state fluxes by applying mass balance constraints to a stoichiometric model. The fact that only the stoichiometry of the metabolic model needs to be known provides the advantage that specific kinetic parameters are not required. Mass-balance information, such as growth rate, biomass composition and substrate consumption rate, are used to fix boundaries on the flux solution space (Reed and Palsson, 2003). FBA has mainly been applied to microorganisms and unicellular organisms in order to predict optimal yields, maximal fluxes or the effects of gene deletion, and has only recently been applied to more complex plant systems. Flux-balance models have been published for Chlamydomonas (Cogne et al., ²⁰¹¹), Arabidopsis thaliana (Poolman et al., ²⁰⁰⁹; Dal'Molin et al., ^2010a; Radrich et al., ²⁰¹⁰), developing endosperm of seeds of Hordeum vulgare (barley; Grafahrend-Belau et al., ^{2013, 2009}), developing embryos of Brassica napus (Hay and Schwender, ^2011b; Pilalis et al., ²⁰¹¹), Zea mays (maize; Saha et al., ²⁰¹¹) and in the developing leaf cells of Oryza sativa (rice; Poolman et al., ²⁰¹³). It is noteworthy that FBA has been used to describe source–sink interactions during barley development with a multiscale model (Grafahrend-Belau et al., ²⁰¹³), but to date there is no model describing fruit development.

Importantly, FBA predictions are highly dependent on the objective function used in the analysis, and thus probably represent the most critical step in FBA modelling in order to accurately describe metabolism. Commonly used objective functions are growth-based, such as maximization of either biomass or the rate of product synthesis (Kauffman et al., ²⁰⁰³); however, such objective functions may not be appropriate to study complex metabolic networks of plant cells, such as those in mature fruits that participate in whole-plant metabolism without contributing to growth at all. Plant metabolism also comprises redundant pathways in multiple cellular compartments facilitating diversification of functions. Based on an assumption that evolution selects for cells able to fulfil vital functions (growth, DNA repair, etc.) by adjusting metabolic input, Holzhutter introduced the principle of flux minimization (Holzhutter, 2004). This principle stipulates that stationary metabolic fluxes attain minimum values based on the availability of external substrates and a given set of important ‘target’ fluxes required to accomplish a specific pattern of cellular functions. Applications of this approach have been shown to agree with the global behaviour of in vivo cellular systems, and yield biological flux values (Holzhutter, 2004; Cakir et al., ²⁰⁰⁷; Schuetz et al., ²⁰⁰⁷; Grafahrend-Belau et al., ^{2009, 2013}).

The aim of the present study is to describe the entire development of tomato fruits by modelling the fluxes of central metabolism. A network comprised of 71 metabolic conversions including energetic processes can explain the main biological activity required for the biosynthesis of the main biomass components. A comprehensive data set for fruit biomass components (Biais et al., ²⁰¹⁴) has been used to set up the constraints of the external fluxes at each stage of development. The results of the stoichiometric modelling are presented as metabolic states occurring at three main physiological transitions of fruit development, i.e. cell division, cell expansion and ripening, and we discuss the validity of the outcomes through comparison with other known metabolic behaviours.

Results

Stoichiometric model of tomato fruit cells

The flux-balance model was constructed by integrating biochemical and physiological knowledge about the stoichiometry of reactions and the boundary conditions, i.e. the definition of external compounds. The model describes a cell of tomato fruit pericarp and assumes that all cells are identical. Based on our previous work (Beurton-Aimar et al., ²⁰¹¹), the model describes the central metabolism that is dedicated to the breakdown and transformation of extracellular nutriments to produce energy and metabolic precursors of amino acids, proteins, cell wall, etc. This network of reactions (schematized in Figure 1; Appendices S1 and S5) includes glycolysis, the tricarboxylic acid cycle (TCA), the pentose phosphate pathway, starch metabolism and sucrose metabolism. Tomato fruit is mainly heterotrophic, so the carbon source was described through sucrose uptake (V_suc-up). In addition, the carboxylation of ribulose-1,5-bis-phosphate leading to two trioses phosphate, which is potentially active in green fruits (Carrara et al., ²⁰⁰¹; Schwender et al., ²⁰⁰⁴), was included (reaction named V_rbco). Two nitrogen sources were considered, one organic (glutamine, also a source of carbon V_gln-up) and one mineral (nitrate), involving enzymes of the nitrogen assimilation pathway [nitrite reductase (V_nr), glutamine synthetase (V_gs) and glutamate synthase (V_gogat)].

Figure 1.

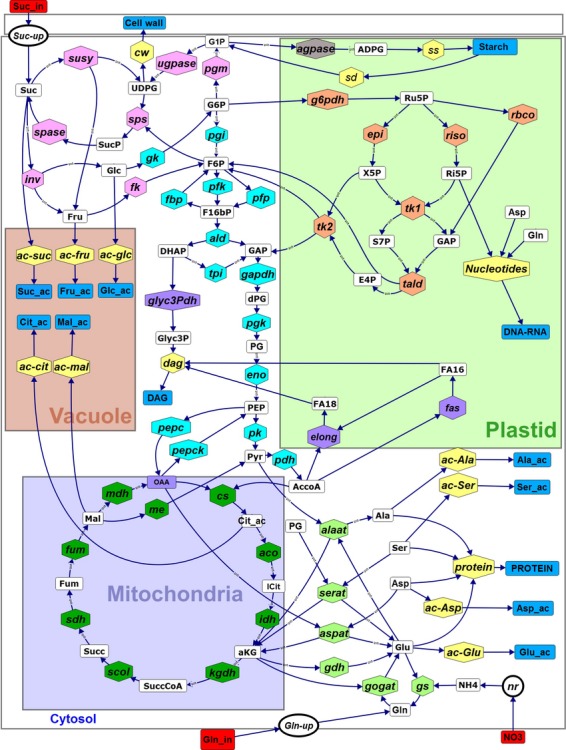
The metabolic network of tomato cells. The system is a cell with symbolic subcellular compartments. Each colour indicates a pathway: green for the TCA cycle; blue for glycolysis; orange for the pentose phosphate pathway; pink for sucrose and starch synthesis; and yellow for the fluxes towards external metabolites, which are in presented in blue boxes. Imported metabolites are in red boxes. The compartmentation indicated in the figure is reminiscent of the physiological situation, and for the sake of clarity co–factors were omitted. Irreversible reactions are indicated by unidirectional arrows. The illustration was designed with omix (Droste et al., ²⁰¹¹).

The main biosynthetic processes were described with overall reactions for: (i) the biosynthesis of cell wall polysaccharides from UDP-glucose (V_cw); (ii) protein synthesis (V_protein), with the molar proportion of four classes of amino acids (glutamate, aspartate, alanine and serine) according to the averaged amino acid composition of proteins in tomato (Friedman, 2002) (Table S2); (iii) fatty acids synthesis (diacyl glycerol; V_dag) from pyruvate and trioses phosphate; and (iv) nucleotide synthesis (DNA and RNA; V_nucleotides) from ribose-5-phosphate by using plant metabolic pathway databases (http://www.plantcyc.org). Synthesis and degradation of starch was described by two reactions, V_ss and V_sd, respectively, and all other accumulated compounds were described as a simple accumulation: (i) organic acids, i.e. malate (V_ac-mal) and citrate (V_ac-cit); (ii) soluble sugars, i.e. glucose (V_ac-glc), fructose (V_ac-fru) and sucrose (V_ac-suc); and (iii) four groups of free amino acids (glutamate V_ac-Glu, aspartate V_ac-Asp, alanine V_ac-Ala and serine V_ac-Ser), coming from the four metabolic precursors 2–oxoglutarate, oxaloacetate, pyruvate and 3–phospho-glutarate, respectively. These 15 fluxes – leading to accumulated metabolites and biomass components, and defined as external fluxes – have been determined experimentally (see below).

Biosynthesis of the main biomass components (cell wall, proteins, lipids, starch) require both ATP and NAD(P)H and, thus, energy costs were explicitly taken into account. The co–factors NADP/NADPH were linked to biomass production, and the co–factors NAD/NADH and FAD/FADH were linked to ATP synthesis via two essential reactions of oxidative phosphorylation (V_nrj1 and V_nrj2), which are associated with the mitochondrial respiration. Recycling of AMP by adenylate kinase is described by V_adk. The portion of synthesized ATP that is not used for growth has been balanced by the model as an ATP hydrolysing reaction (V_nga-ATPm) that, physiologically, represents cellular maintenance (Amthor, 2000). Finally, all the co–factors were defined as internal metabolites, which means that they can be balanced thus constraining the metabolic network not only through the carbon and nitrogen balance, but also through the redox and energy status. Among the metabolites of this network, 18 were external compounds, i.e. exogenous sucrose, glutamine, nitrate, CO₂ and the accumulated metabolites and biomass components, i.e. sugars (glucose, fructose and sucrose), organic acids (malate and citrate), free amino acids (glutamate, aspartate, serine and alanine), proteins, cell wall polysaccharides, starch, lipids and nucleotides.

Contrary to unicellular systems in culture where the specific growth rate (μ) can be adjusted by the dilution rate, here the specific growth rate was imposed by overall fruit growth. Thus, the whole fruit was considered as the modelled system and all the fluxes were expressed on the fruit basis (in mmol fruit⁻¹ day⁻¹) in order to take into account fruit expansion.

Biomass composition and external fluxes

Mass-balance information such as biomass composition is required for flux-balance modelling, thus the composition of the dry biomass, which is not constant during fruit development, was determined at nine stages of development (Figure 2; Tables S1–S6). The mass balance of accumulated metabolites and biomass components covered an average of 77% of the dry biomass when considering all of the developmental stages. The best balance (>82%) was achieved during cell division (at 8 and 15 days after anthesis, or DPA), when primary metabolites were mainly produced.

Figure 2.

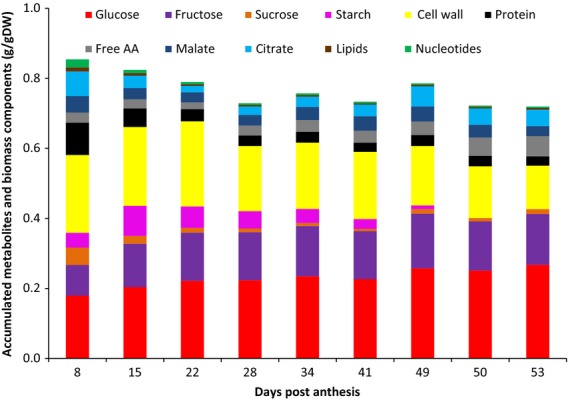
Mass balance of pericarp at nine stages of tomato fruit development. Accumulated metabolites (sugars, organic acids and free amino acids) and biomass components (starch, cell wall, protein, lipids and nucleic acids) measured in tomato pericarp. All data are expressed in mg g⁻¹ dry weight (DW).

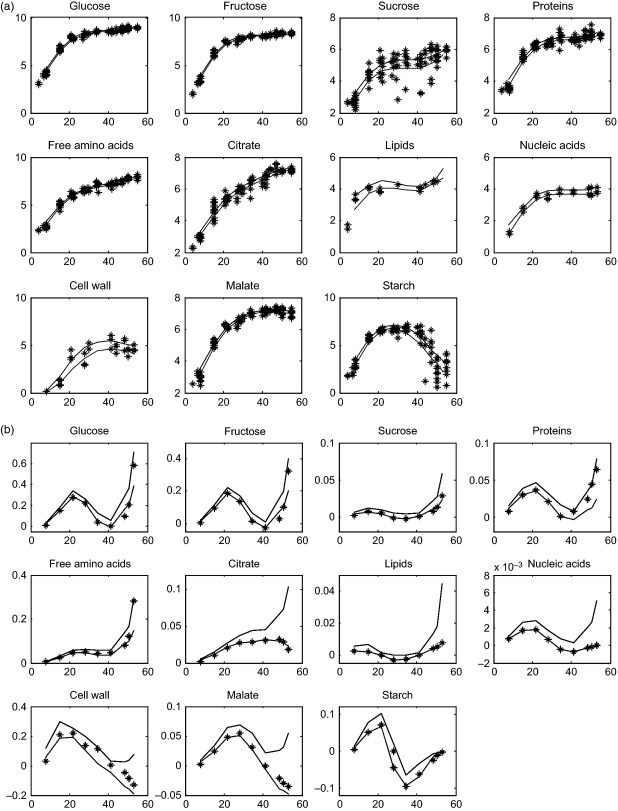
Concentrations of accumulated metabolites and biomass components were used to calculate both the lower and upper bounds for external fluxes, these bounds were used as constraints in flux-balance modelling. For this, data were log-transformed and fitted with polynomial functions (see Experimental procedures). The derivatives were calculated throughout development and we selected a 95% interval of prediction as boundaries to the corresponding fluxes (Figure 3). The flux profiles can be classified into three patterns. The first and largest comprises fluxes towards proteins, soluble sugars, citrate, free amino acids, lipids and nucleic acids. These fluxes undergo an increase during cell division, before decreasing during cell expansion and then, again, increasing during ripening. The decrease for amino acids observed during cell expansion was very limited and contrasted with the dramatic increase observed at the latest developmental stage. Also, the citrate flux displays a large interval at ripening, with a potentially decreasing flux. The second pattern comprising the fluxes towards cell wall and malate was characterized by a bell-shape curve, which peaked at early stages of fruit development (cell division and early expansion) and decreased during ripening. The last profile, observed for starch only, although quite similar to the first profile, was characterized by a dramatic decrease during the cell-expansion phase leading to negative values, indicating starch degradation. In the model each accumulated metabolite and biomass component corresponded to one external flux, except for starch (the flux of synthesis V_ss was distinct from that of degradation V_sd, and both had positive values). For free amino acids, the calculated flux was split into four fluxes towards the main groups (glutamate, alanine, aspartate and serine) according to their respective proportions (Table S3).

Figure 3.

Calculation of the external fluxes of the metabolic model.

(a) Time course of the concentrations of the accumulated metabolites and the biomass components (black stars) in log scale with a 95% interval of prediction from polynomial fits (black lines).

(b) The corresponding external fluxes (stars) calculated by derivative: minima values (dashed line) and maxima values (solid line) of the interval of prediction, and the calculated values by modelling (stars). Time after anthesis is expressed in day, concentrations are in mmol fruit⁻¹ and fluxes are in mmol fruit⁻¹ day⁻¹.

In summary, the model of the metabolic network (available in sbml in Appendix S1 and in an excel file in Appendix S5) describes the main growth components of the cell connected through a set of n = reactions involving m = metabolites divided into two groups, internal m_int and external m_ext metabolites (m_ext = 18; m_int = 46). To describe the metabolic network, the following notations are introduced (where a metabolite and its concentration are designated by the same letter):

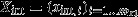, the vector of m_int internal metabolites;

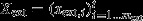, the vector of m_ext external metabolites;

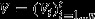, the flux vector composed by the rates of n reactions of the network;

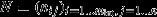, the stoichiometry matrix, where n_ij is the stoichiometric coefficient of metabolite x_int,i in reaction j.

Constraints limiting the flux space

Two types of constraints were applied to limit the flux space. The first was the assumption of steady state at each of the nine stages of tomato fruit development, because the metabolic composition of the tomato fruit varies very slowly on the scale of the tomato fruit development. Moreover, hexoses phosphate, which were described as internal metabolites, varied slightly between two stages (Biais et al., ²⁰¹⁴). Consequently, the tomato fruit development was described by a sequence of nine steady-state models concatenated along the time axis. At steady state, the mass balance equations are expressed by:

((1)

We split X_int = (X_I,int, X_E,int)^t and V = (V_int, V_ext)^t with X_I,int, the vector of m_I,int = 26 internal metabolites that interfered only with internal reactions, and X_E,int, the vector of m_E,int = m_int − m_I,int = 21 metabolites involved in both internal and external reactions, V_int, the flux vector composed by the rates of n_int = 56 internal reactions of the network (linking metabolites of X_I,int), and V_ext, the flux vector composed by the rates of n_ext = 15 external reactions of the network (linking metabolites of X_E,int with metabolites of X_ext).

The second type of constraint concerned the boundaries of the fluxes, where x stands for int or ext, and l = 1…9 for the stage number. We denote for a vector V_x by V^l_x,min ≤ V_x ≤ V^l_x,max, when we have the following inequalities for all components of V_x:

((2)

where (respectively v^l_x,max,j), the jth component of 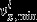(respectively ), is the lower (respectively upper) bound for flux v_x,j the jth component of V_x.

1. Constraints were applied to limit the flux space to flux directions inferred from the thermodynamic properties of reversibility or irreversibility. Thus, among the n_int = 56 internal reactions V_int of the metabolic network, n_int,irr = 48 are irreversible, as indicated by unidirectional arrows in Figure 1, which meant that their lower bounds were set to zero = 0 for j = 1…n_int,irr.

2. From our knowledge of tomato fruit physiology, if a given enzyme was not supposed to be active at one stage, the upper bound was set to zero: = 0. This is the case for the carboxylation (V_rbco) in red fruits, i.e. for the three last stages (Carrara et al., ²⁰⁰¹) and the phosphoenolpyruvate carboxykinase (V_pepck) before ripening, i.e. for the first six stages (Bahrami et al., ²⁰⁰¹).

3. At each developmental stage, the experimentally determined activities of 30 enzymes of central metabolism (Biais et al., ²⁰¹⁴), expressed in units of mmol fruit⁻¹ day⁻¹, were used to limit each flux in the metabolic network, considering that they correspond to maximal enzyme capacity. The same values, but negative, were used as lower bounds of reversible enzymes. When the capacity of a given enzyme was not known (less than 20 reactions), the bounds were set to infinity.

4. The essential constraints required to solve the system were the external fluxes V_ext. These n_ext = 15 fluxes were constrained with the corresponding interval of rates 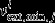and for j = 1…n_ext, calculated from the experimental data at each stage of development, as previously described (Figure 3b).

Objective function and resolution

In order to solve the system describing the development of tomato fruit, the same objective function, i.e. the minimization of the sum of all internal fluxes was used at each stage of development, in agreement with the principle of ‘minimal effort’, i.e. the minimal consumption of the available resources (Holzhutter, 2004).

The formulation of the problem is expressed (for l = 1…9) by:

(3)

subject to the constraints

In this case the objective function f is the Euclidean norm of V. From a computational point of view, as f is a strictly convex function, this objective function leads to a unique solution at each developmental stage (see the demonstration in Appendix S7).

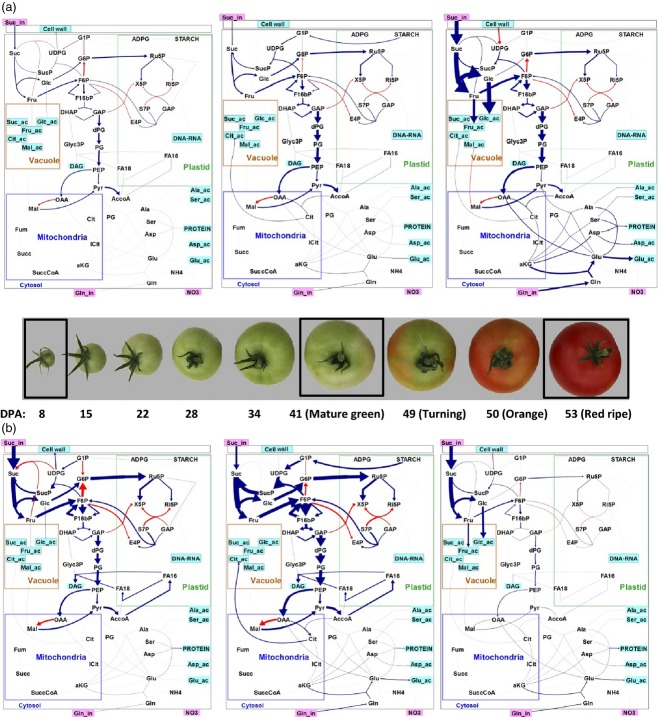
The system was solved for the nine stages of tomato fruit development (programs and files in Appendix S2 and S3) and the calculated fluxes (given in Table S7) were represented both as flux profiles (for the reaction subsets, see Figure S1a and Table S8) and as flux maps (for three selected stages at 8 DPA, 41 DPA, i.e. mature green stage, and 55 DPA, i.e. red ripe stage, see Figure 4; for all stages, see Figure S1b, c and d). When expressed on the fruit basis, an increasing metabolic activity, especially for sugar metabolism and glycolysis, was observed during fruit development, with a drastic import of sucrose and a high invertase flux at the end of maturation in order to supply the soluble sugars in the vacuole, especially glucose (Figure 4a). Conversely, when expressed on a dry-weight basis in grams (Figure S1c), the fluxes, which are very high at the first stage, as already noted by (Biais et al., ²⁰¹⁴), decreased rapidly during the division phase, and the similar flux maps for the six last stages did not reveal metabolic reprogramming. Interestingly, when fluxes were expressed in mmol C fruit⁻¹ day⁻¹ and normalized by the total carbon metabolized by fruit at the corresponding stage (Figure 4b), the flux maps revealed highly contrasting patterns for each stage. First, the fluxes were high during cell division: for instance, a high flux through the oxidative pentose phosphate pathway (OPPP) led to the protein and lipid synthesis required for biomass. Then a high contribution of starch degradation with an important metabolic activity around sugar cycles was revealed at the end of expansion. Finally, again, a high sucrose import and invertase flux was observed at the end of maturation.

Figure 4.

Flux maps at three stages of tomato fruit development. Metabolic fluxes during tomato fruit development with (a) fluxes expressed in mmol fruit⁻¹ day⁻¹, with a log-scale representation, and (b) normalized fluxes by the total carbon metabolized. Illustration designed with omix (Droste et al., ²⁰¹¹).

Consistent fluxes in pentose phosphate and anaplerotic pathways

From the calculated fluxes we examined flux partition into the main pathways. For instance, the ratio between glycolysis (V_gapdh) and the flux through the oxidative branch of OPPP (V_g6pdh) was calculated at each stage of fruit development (Table 1). Although decreasing during fruit development, this ratio ranged between 0.54 and 0.60, suggesting a consistent requirement of NADPH for biomass synthesis. Our results were in agreement with the known importance of the pentose phosphate pathway in heterotrophic tissues (Averill et al., ¹⁹⁹⁸), and with the observation that the oxidative reaction carries considerable fluxes in [¹³C]MFA-based flux maps, as found in B. napus embryos (Schwender et al., ²⁰⁰³), Glycine max (soybean) embryos (Sriram et al., ²⁰⁰⁴), Helianthus annuus (sunflower) embryos (Alonso et al., ²⁰⁰⁷) and an Arabidopsis cell culture (Masakapalli et al., ²⁰¹⁰). Recently the oxidative branch of the pentose phosphate pathway has been shown to carry no flux in FBA of heterotrophic plant metabolism (Williams et al., ²⁰¹⁰; Hay and Schwender, ^2011a), because the supply of NADPH was predicted to be performed by other plastidial NADP-dependent dehydrogenases (glyceraldehyde-3-phosphate dehydrogenase, NADP-malate dehydrogenase and malic enzyme). In our model, these NADP-dependent enzymes were not implemented, and thus the provision of NADPH required the reaction catalysed by glucose-6-phosphate dehydrogenase, which resulted in consistent values for the predicted flux of glucose–6P dehydrogenase (V_g6pdh). The NADPH demand was probably underestimated because the NADPH requirement specified in the model was restricted to the reactions of synthesis of biomass components (for protein and fatty acids), although there are several other known NADPH requirements in the cell (antioxidant enzyme activities, NADPH oxidase activity, etc.).

Table 1.

The carbon partition between the oxidative pentose phosphate pathway (V_g6pdh) and glycolysis (V_gapdh), and between phosphoenolpyruvate carboxylase (V_pepc) and pyruvate kinase (V_pk), at each stage of tomato fruit development

Day post-anthesis (DPA)	8	15	22	28	34	41	49	50	53
g6pdh/(g6pdh + gapdh)	0.62	0.59	0.56	0.54	0.54	0.55	0.55	0.55	0.54
pepc/(pepc + pk)	0.57	0.58	0.60	0.62	0.60	0.63	0.69	0.72	0.83

Fluxes (V_g6pdh and V_gapdh) were converted to mmol C fruit⁻¹ day⁻¹.

Another important metabolic crossroad is the split at the end of glycolysis between pyruvate kinase (V_pk) and phosphoenolpyruvate carboxylase (V_pepc). The importance of the anaplerotic pathway, from 57 to 83%, calculated at each stage of fruit development (Table 1), was in agreement with the requirement for the storage of organic acids and amino acids. An important contribution of the anaplerotic pathway (about 61%) has already been reported by a metabolic flux analysis of maize embryos (Alonso et al., ²⁰¹⁰), another organ dedicated to storage.

Carbon and nitrogen import by fruit

In order to investigate how the calculated fluxes actually reflect physiological behaviour, the fluxes of carbon and nitrogen demand were compared at each stage of development (Figure 3). The carbon demand, i.e. the total carbon metabolized, was expressed as the sum of import (here sucrose and glutamine, V_{suc_up} and V_{gln_up}, respectively), carboxylation via phosphoenolpyruvate carboxylase (V_pepc) and rubisco (V_rbco), and the degradation of starch and potentially cell wall polysaccharides was considered a source of endogenous carbon. The nitrogen demand was expressed as the sum of glutamine and nitrate imports (V_{gln_up} and V_nr, respectively). Whereas glutamine was predicted as the only nitrogen source in the system (Figure 5b), glutamine had a very small contribution as a carbon source (Figure 5a). As expected for a heterotrophic system such as a fruit, sucrose was the main source of carbon, independently of the stage of development, and low carboxylation was predicted. Nevertheless, the degradation of starch contributes about 30% of the metabolized carbon at the mature green stage (at 41 DPA, from the total carbon used, i.e. 1.16 mmol C fruit⁻¹ day⁻¹, 0.385 mmol C fruit⁻¹ day⁻¹ comes from starch), and the degradation of cell wall contributes about 10–15% of metabolized carbon during ripening. Interestingly, both of the overall profiles of carbon and nitrogen demand show an increase during the early stages of development, from 8 to 22 DPA, followed by a decrease during cell expansion, with a new increase during late ripening, after 49 DPA, especially for nitrogen. It was a remarkable issue to be able to estimate these uptake fluxes. In conventional flux-balance models of unicellular systems, tissues or embryos incubated in aqueous media, fluxes corresponding to substrate-consumption rates were measured experimentally and used as boundaries. But in the present study the uptake fluxes were unknown.

Figure 5.

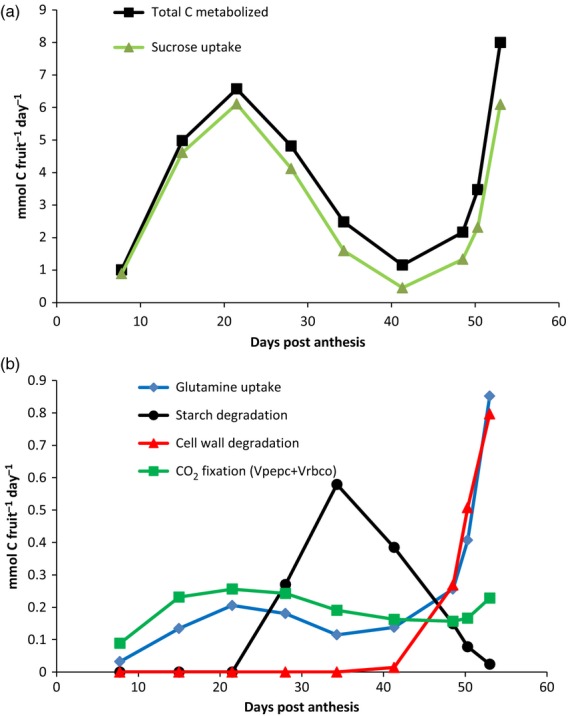
Carbon and nitrogen metabolized throughout tomato fruit development:

(a) total carbon metabolized and sucrose uptake.

(b) glutamine uptake, starch degradation, cell wall degradation and CO₂ fixation by phosphoenolpyruvate carboxylase (V_pepc) and rubisco (V_rbco). Fluxes are expressed in mmol C fruit⁻¹ day⁻¹.

From our results, assuming import by phloem sap, we estimated a carbon–nitrogen ratio in phloem sap calculated as the sum of carbon divided by the sum of nitrogen. This ratio decreased from 88 to 10 during fruit development. Our findings were in good agreement with the values recently reported by Lohaus and Schwerdtfeger (2014), indicating phloem sap ratios of 109 and 30 for Lophospermum erubescens and B. napus, respectively.

Respiration and energy balance

As CO₂ was not balanced in the model_, the relative contribution of fluxes in the overall release of CO₂ was examined by plotting both carboxylation and decarboxylation fluxes (Figure 6). Whereas the carboxylation by phosphoenolpyruvate carboxylase (V_pepc) displayed a significant contribution, the overall CO₂ released was positive, independent of the developmental stage. These data were in agreement with those previously obtained by metabolic flux analysis in plant tissues (Williams et al., ²⁰¹⁰; Sweetlove et al., ²⁰¹³). Interestingly, the CO₂ release stopped decreasing during ripening and even slightly increased at the end of ripening, suggesting a higher respiratory flux, as described for climacteric fruits.

Figure 6.

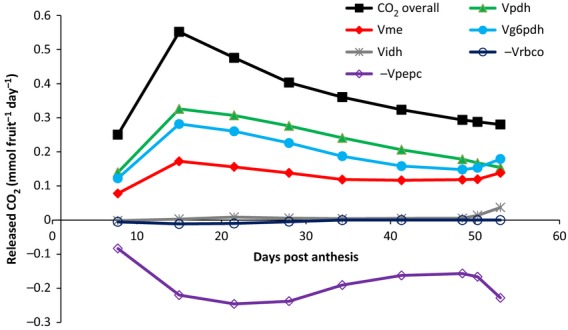
Contribution of the calculated fluxes to the overall CO₂ released throughout tomato fruit development. Carboxylation reactions [phosphoenolpyruvate carboxylase (V_pepc) and rubisco (V_rbco)] were conventionally negative, and decarboxylation reactions [isocitrate dehydrogenase (V_idh), malic enzyme (V_me), pyruvate dehydrogenase (V_pdh) and glucose-6-phosphate dehydrogenase (V_g6pdh)] were positive. Two fluxes carrying negligible fluxes (<10⁻⁵), 2–oxoglutarate dehydrogenase (V_kgdh) and phosphoenolpyruvate carboxykinase (V_pepck) were omitted.

One perceived outcome of the present approach was to yield insight into the energy balance throughout development, with fluxes expressed in mmol ATP fruit⁻¹ day⁻¹ (Figure 7). ATP was synthetized by kinase activities (i.e. pyruvate kinase, V_pk; succinyl coA ligase, V_scol; and phosphoglycerate kinase, V_pgk) and by oxidative phosphorylation (V_nj1 + V_nrj2). Conversely, all ATP synthetized was consumed for cell growth through both recycling by adenylate kinase (V_adk) and hydrolysis for cell maintenance (V_nga-ATPm). The overall ATP profile showed a sharp increase at the beginning of cell division, a decrease during cell expansion and an increase at ripening. Independently of the development stage, ATP was mainly produced by oxidative phosphorylation and the contribution of substrate level phosphorylation was about one-quarter of the ATP produced (Figure 7a). This result agrees with plant aerobic metabolism, characterized by a CO₂/O₂ ratio of nearly one (Rontein et al., ²⁰⁰²). The ATP was mainly used for growth, and about one-quarter (22–29%) was used for maintenance, regardless of the developmental stage (Figure 7b). Interestingly, the part of ATP used for maintenance increased by nearly 10% between 34 DPA and the end of ripening (Figure 7c), again in accordance with the occurrence of the climacteric crisis. Energy costs of maintenance can vary widely from one tissue and/or environmental growth condition to another. The accuracy of the predicted costs of ATP maintenance depend on how close the flux-balance solutions are to the metabolic flux state (Sweetlove and Ratcliffe, 2011). As there was no value of cell maintenance for tomato fruit, no constraint was applied on the maintenance flux of ATP hydrolysis; thus, this flux was balanced by its flux of synthesis and the requirement for biomass. Energy costs associated with ‘non-growing associated ATP-maintenance’ are required to keep the cell in equilibrium by adjusting its physiological processes, such as the turnover of proteins, the costs of maintaining the electrochemical potential differences across the plasmalemma and the tonoplast, via ATP, and PPi-dependent proton pumps. Alternatively, maintenance flux can also be viewed as a non-growth-associated respiration that is necessary to balance the reducing power generated by metabolism. In this case, setting a non-growth ATP reaction (i.e. V_nga-ATPm) in the model is conceptually the same as decreasing the ATP/O ratio of the oxidative phosphorylation reactions (in V_nrj1 and V_nrj2). The latter phenomenon can realistically occur when the growth rate dramatically decreases (Poolman et al., ²⁰⁰⁹), and when the respiratory chain alternative oxidase is induced during the climacteric crisis.

Figure 7.

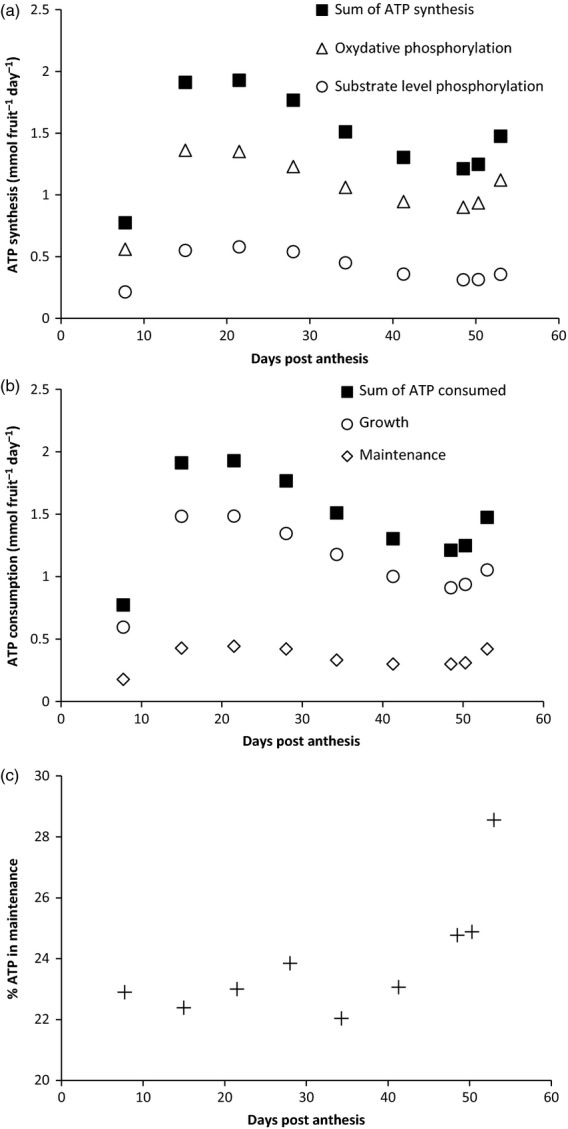
Energy balance throughout tomato fruit development.

(a) ATP synthesis from oxidative phosphorylation (V_nrj1 + V_nrj2) and from substrate level phosphorylation (V_pk + V_succ + V_pgk).

(b) ATP consumed for growth (V_ATPsynthesis + V_adk – V_nga-ATPm) and maintenance (V_nga-ATPm). All fluxes were expressed in mmol ATP fruit⁻¹ day⁻¹.

(c) Time course of the proportion of maintenance-associated ATP consumption.

Moreover, as flux-balance modelling is inherently good at examining energetic efficiencies of the metabolic networks, the quantity of ATP required to produce the biomass was estimated at each stage of fruit development, by dividing the ATP synthesis flux by the fruit growth rate (Figure S2). The energy input required remained constant at an average value of 11.2 ± 3 mmol ATP g⁻¹ dry weight, between 8 and 41 DPA, and then increased during the late stages. It is worth noting that this profile was in agreement with that of the maintenance described above (Figure 7c), and that the values were of the same order of magnitude as those reported by Poolman et al. (2009, and references therein).

Finally, a relevant comparison can be performed with the ecophysiological model TOMGRO (Jones et al., ¹⁹⁹¹), which predicts carbon import by fruit from carbon fixed into the biomass and from carbon respired. This latter flux is the sum of the growth and maintenance respiration (Figure S3). Whereas similar carbon fluxes into biomass were observed during division and expansion for both models (Baldazzi et al., ²⁰¹³), the respiration flux calculated with the flux-balance model was lower than that calculated by TOMGRO, especially during cell expansion and ripening. The discrepancy between models for maintenance and growth respiration profiles stems from the conceptual nature of each model, which is process-based for ecophysiological models and reaction-based for our model. With more details in the functioning of the metabolic network, the reaction-based model might be more accurate in energy predictions. The predicted flux increase of carbon import at ripening observed with our calculations was unexpected. It is possible to envisage an overestimation of this flux during ripening, because the fit by a polynomial regression of degree 3 could exaggerate the final increase; however, this final increase is observed from the fit of several independent components (amino acids, sugars, proteins, etc.), indicating that it is not an artefact of the model.

In conclusion, the model showed an increase in CO₂ release at the end of ripening and an increase in ATP hydrolysis required for growth starting at the end of cell expansion (Figure 7c). This behaviour coincides with the climacteric crisis, which starts just before ripening and involves energy dissipation by the alternative oxidase (Navet et al., ²⁰⁰³). The present observation is in line with the concept that this component of the climacteric crisis limits the redox stress that would result from the imbalance between energy supply and demand.

Fluxes lower than their corresponding enzyme capacities

When the V_max was available, i.e. for the 30 fluxes where an upper bound has been determined experimentally (Biais et al., ²⁰¹⁴), ratios between predicted fluxes and maximal capacities were calculated at each developmental stage (Appendix S6). The ratios of all 30 enzymes fell well below 1, of which 25 were below 0.1, suggesting that none of the enzyme capacities constrained the computation. Even if five enzymes had a ratio close to 0.5 at the first stage of development (phosphofructokinase, V_pfk; glucose-6-phosphate dehydrogenase, V_g6pdh; invertase, V_inv; enolase, V_eno; and fructose 1,6–biphosphatase, V_fbp), no enzyme capacities were essential to run the model. The results obtained for enzymes in sugar cycling (invertase, sucrose synthase) were cross-validated with a kinetic model (Beauvoit et al., ²⁰¹⁴), and similar results have also been reported for B. napus embryos (Junker et al., ²⁰⁰⁷) with enzyme activities present in a large surplus relative to their requirements for the observed in vivo fluxes. Given that most enzyme capacities varied quite dramatically throughout fruit development, we next investigated whether there were correlations between the measured V_max and the corresponding calculated fluxes (Appendix S6). Only three high correlations were found, for instance fluxes of invertase (V_inv), alanine aminotransferase (V_alaat) and citrate synthase (V_cs) were positively and significantly correlated with their corresponding maximal capacities (R > 0.70, P < 0.02). These enzymes are potential candidates for further investigation, especially for genetic transformation. It is striking that a close correlation has previously been found by principal component analysis between alanine aminotransferase and the accumulation of amino acids (Biais et al., ²⁰¹⁴); however, for most enzymes, abundance and flux were not directly related, which might be explained by post-translational and/or allosteric regulation, or by the impact of the thermodynamic poise of a reaction on the ability of an enzyme to support a net flux (Sweetlove and Ratcliffe, 2011).

Relevance of the objective function and the metabolic model

Flux computations are highly dependent on the objective function used for the analysis. Thus, selecting the ‘best’ objective function represents a critical step in flux-balance modelling, for two main reasons. Firstly, the objective function should appropriately describe metabolic ‘purposes’ (even if dedicated to several functions). Secondly, although boundaries are imposed on the flux solution space, often it will still be possible to accommodate multiple solutions that satisfy the chosen objective function. Here, the minimization of the sum of fluxes led to a unique solution and the relevance of this objective function is supported by similar results yielded by other plant systems (OPPP versus glycolysis, carbon and nitrogen import). The minimization of the sum of fluxes ensures maximal enzymatic efficiency, resulting in an efficient metabolic flux distribution. The objective function will result in a lower sum of fluxes and will minimize substrate cycles, i.e. the so-called futile cycles. This selection appears logical, as a low activity of these cycles has been reported (Nguyen-Quoc and Foyer, 2001). In order to describe fruit development, we could envisage various objective functions, such as the maximization of the substrate, the maximization of energy transformation efficiency or, more specifically, a relevant combination of objectives, depending on developmental stage. Combined with the search of alternative optimal solutions, in which flux variability analysis (FVA) provides information about the network and its potential in metabolic redundancy (Mahadevan and Schilling, 2003), a specific study of relevant objective functions might also be performed.

The main limit of modelling is the size of the metabolic model. The need to advance to large-scale metabolic models, including secondary metabolism, for example, is obvious. Plant metabolic networks are arguably the most complex of any organism, mainly because of the tremendous variation in their metabolite content. In this context, it will be interesting to implement a genome-scale metabolic model in tandem with flux-balance modelling using data of secondary metabolites. Moreover, the subcellular compartmentation is also clearly desirable for the model to reflect the biological reality (Lunn, 2007); however, at present, there is insufficient information to assess whether the inclusion of subcellular compartmentation improves the models. An important issue with introducing compartmentation into metabolic models is the lack of information about metabolite transport and the associated energetic cost; however, this issue raises the question of whether flux-balance models are sufficiently constrained to define compartmented fluxes. The addition of compartmentation and especially the addition of parallel pathways in more than one compartment increases the solution space, and it is likely that increased compartmentation in a model will simply increase the number of alternative solutions to the optimization problem (Sweetlove and Ratcliffe, 2011). Because of a lack of knowledge about the metabolite exchanges between subcellular compartments, the physical compartmentation of enzymes per se was not taken into account in our model; however, functional compartmentation of enzymes connected here by co–factors such as NADPH only dedicated to anaplerosis was – de facto – taken into consideration.

Finally, as a flux model is useful in explaining the metabolic phenotype in detail, it is necessary to provide information at a cell-type level instead of considering pericarp as a homogenous cell population. To date, only a few studies have attempted to account for the interaction of more than one cell type. For instance, Dal'Molin et al. (2010b) reported a flux-balance model describing the interaction between bundle sheath and mesophyll cells in C4 photosynthesis. But the reconstruction of metabolism at the whole-plant level is an interesting perspective, and recently Grafahrend-Belau et al. (2013) reported a multi-scale modelling approach to decipher the metabolic behaviour of source and sink organs during the generative phase of the barley plant with a dynamic flux-balance analysis on a whole-plant scale.

Changes in metabolic fluxes during the three main phases – cell division, expansion and ripening – of the tomato fruit development were modelled by means of nine concatenated steady states along the developmental time axis using constraint-based modelling. The combination of a medium-scale metabolic network of about 70 biochemical reactions, constrained by a robust set of experimental data, and the minimization of all internal fluxes allowed us to calculate about 40 internal fluxes within the network. This computational approach allowed us to circumvent the difficulty of performing direct experimental flux measurements in tomato fruits, while generating relevant flux maps describing tomato fruit development. The partitioning of carbon among the main pathways, the import of carbon and nitrogen by the fruit, the CO₂ release and the overall energy balance were in good agreement with reported results on other plant systems. Moreover, the increase of both respiration and energy dissipation during ripening pinpointed a climactic behaviour as an emergent property of the metabolic system. Finally, the comparison of 30 flux rates with their respective enzyme capacities (V_max) showed that no enzyme capacities are essential to run the model, and suggested a complex reprogramming of the metabolic machinery during fruit development. In the recent context of modelling plant cells, this work paves the way for explaining the metabolic and physiological requirements of the developing tomato cells. Whereas flux-balance modelling has its limitations, it enables generating novel insights into metabolic behaviour. This work demonstrates that systems modelling can be a valuable tool to yield insight into the physiology of plants when provided with an extensive set of experimental data and an accurate definition of the metabolic system.

Experimental procedures

Experiments were performed with the S. lycopersicum L. Moneymaker cultivar, and have been described in Biais et al. (2014). Briefly, tomato plants were grown in a glasshouse according to the usual production practices and flower anthesis was recorded. Nine developmental stages [at 8, 15, 21, 28, 34, 42 (mature green), 49 (turning), 50 (orange) and 53 (red ripe) DPA] were harvested on three different trusses (trusses 5, 6 and 7). For each sample, three biological replications were prepared with a minimum of four fruits per replication. Samples were prepared by cutting the fruits (after removing seeds, jelly and placenta) in small pieces of pericarp, and immediately frozen in liquid nitrogen. Samples were ground and stored at −80°C until analysis.

Metabolite contents and biomass composition

The three sugars (sucrose, glucose and fructose), the total and individual amino acids, the organic acids (malate and citrate), starch and protein content have been reported in Biais et al. (2014). Total cell wall polysaccharides were analysed on dry samples at the BIBS platform (http://www.bibs.inra.fr) on alcohol-insoluble material (AIM). The AIM was extracted using an accelerated solvent extraction unit ASE® 350 (DIONEX, http://www.dionex.com). Approximately 50–200 mg of frozen tomato flesh was lyophilized and ground into fine powder using the FastPrep-24 instrument (MP Biochemicals, http://www.mpbio.com) at a speed of 6.5 m s⁻¹ for 60 s. Samples were transferred in 22–mL cells of the ASE® 350, dried at 40°C overnight under vacuum over P₂O₅, weighed and AIM was extracted using 80% ethanol at a flow rate of 2 ml min⁻¹. The conditions for the ASE extraction were set at 100°C with a flow time of 8 min, followed by rinse volume 150% and a purge time (N₂) of 30 s. Cells of the ASE® 350 containing AIM were dried at 40°C overnight under vacuum over P₂O₅ before weighing in order to determine the yield of extraction. The AIM was gridded before chemical analyses. For cell wall sugar composition, the identification and quantification of cell wall neutral sugars was performed by gas–liquid chromatography (GC) after sulfuric acid degradation (Hoebler et al., ¹⁹⁸⁹). AIM (5 mg) was dispersed in 13 m sulfuric acid for 30 min at 30°C and then hydrolyzed in 1 m sulfuric acid (2 h, 100°C). Sugars were converted to alditol acetates according to the method described by Blakeney et al. (1983), and were chromatographed on a TG-225 GC column (30 × 0.32 mm inner diamater) using TRACE™ Ultra Gas Chromatograph (Thermo Scientific, http://www.thermoscientific.com; temperature 205°C, carrier gas H₂). Standard sugar solutions and inositol as an internal standard were used for calibration. Uronic acids in acid hydrolysates were quantified using the metahydroxydiphenyl colorimetric acid method (Blumenkrantz and Asboe-Hansen, 1973).

Lipids were analysed on dry samples: the transmethylation of fatty acids was performed overnight in 1 ml of methanol/H₂SO₄ solution (100:2.5, v:v) containing internal standards C17:0 (5 μg ml⁻¹). After cooling, 2 ml of NaCl 2.5% and 300 μl of hexane was added, and the hexane phase containing the resulting fatty acid methyl esters (FAMES) was recovered to be analysed in GC flame ionization detection. The FAMES (1 μl) samples were injected in an Agilent 7890 gas chromatograph equipped with a Carbowax column (15 m × 0.53 mm, 1.2 μm; Alltech Associates, Deerfield, IL, USA, https://grace.com/) and flame ionization detection. The temperature gradient was 160°C for 1 min, increased to 190°C at 20°C min⁻¹, increased to 210°C at 5°C min⁻¹ and then remained at 210°C for 5 min. FAMES were identified by comparing their retention times with commercial fatty acid standards (Sigma-Aldrich, http://www.sigmaaldrich.com) and quantified by using ChemStation (Agilent, http://www.agilent.com) to calculate the peak surfaces, and then comparing them with the C17:0 response.

The total DNA content has been measured using the deoxyribose-specific diphenylamine reaction (De Mey et al., ²⁰⁰⁶). Briefly, the acid-insoluble compounds were precipitated by adding 1 ml of ice-cold 5% (w/v) trichloracetic acid on 10 mg of dry material. After centrifugation (10 000 g at 4°C for 5 min) and removal of the supernatant, the procedure was repeated twice using, firstly, 1 ml of a 2/1 methanol/chloroform (v/v) solution, and secondly, 1 ml of 95% (v/v) ethanol. Finally, 0.5 ml of 5% (v/v) perchloric acid was added to the pellet and incubated for 30 min at 90°C. Then, 1 ml of a diphenylamine solution (containing 400 mg diphenylamine, 50 μl acetaldehyde, 150 μl H₂SO₄ qsp 10 ml acetic acid) was added and samples were incubated for one night at 40°C. The quantity of DNA was calculated by the difference between OD₆₀₀ and OD₇₀₀ by using a standard curve obtained with salmon sperm ranging from 0 to 20 μg. RNA was extracted from up to 100 mg of frozen material using the Ambion RNA TRIzol® Reagent (Invitrogen, now Life Technologies, http://www.lifetechnologies.com), following the manufacturer's instructions. The total RNA was resuspended in 40 μl of RNase-free water by incubating the tubes for 10 min at 55°C and was quantified by A260 measurement using a Nanodrop spectrophotometer.

Given the high reproducibility of the biochemical composition of fruit, irrespective of the truss (Biais et al., ²⁰¹⁴), the analyses performed on the three trusses were averaged at each developmental stage.

Fitting and modelling

Concentrations of external metabolites, i.e. the accumulated metabolites and biomass components, were fitted in order to calculate, by derivation, the corresponding fluxes used as boundaries in the present flux-balance modelling. For that, a regression method was used to evaluate the derivative as accurately as possible at each phase of development. A ‘smooth’ function that fits the experimental data was preferred. In order to take into account the variability (dispersion) of the experimental data, a bootstrap method was used to construct a number of resamples of the observed data set obtained by random sampling with replacement from the original data set. Then the best fit (in the least-squares sense, which minimizes the sum of squared residuals, i.e. the difference between an observed value and the fitted value provided by a model) was implemented to test several fitting methods (polynomial, spline or segmented polynomials, kernel as non-parametric regression). A third-order polynomial regression emerged as the best option (code provided in Appendix S4; polynomial fit results in Appendix S8). Moreover, as the data became more scattered in older fruits, data were log-transformed, otherwise the residuals terms show heteroscedasticity. Once the transformation and the fit were applied to all of the resamples, we obtained a large set of polynomials. From these curves, we derived a 95% interval of prediction for the derivatives, and these values were used as boundaries to the corresponding fluxes. Mathematical problems were implemented using matlab (Mathworks, http://www.mathworks.fr/) and the optimization toolbox, solver quadprod, with the interior-point-convex algorithm for the quadratic convex minimization (code provided in Appendix S2). Another optimization program with the fmincon solver and the sequential quadratic programming algorithm using a random start was implemented (code provided in Appendix S3).

SUPPORTING INFORMATION

Additional Supporting Information may be found in the online version of this article.

Figure S1. Flux results and comparison of the flux maps displayed at nine stages of tomato fruit development, with three different units.

Figure S2. Growth of tomato fruits and ATP required for biomass.

Figure S3. Comparison of the results of the model with TOMGRO.

Table S1. Accumulated metabolites and biomass components at nine stages of tomato fruit development.

Table S2. The amino acid composition of proteins.

Table S3. The proportion of the main amino acids in free amino acids.

Table S4. Cell wall analysis in tomato pericarp at nine stages of fruit development.

Table S5. Fatty acid analysis in tomato pericarp at nine stages of fruit development.

Table S6. Nucleic acid analysis in tomato pericarp at nine stages of fruit development.

Table S7. Calculated fluxes at nine stages of tomato fruit development.

Table S8. Subsets of the metabolic network.

Appendix S1. The metabolic model in sbml format.

Appendix S2. Archive with files in matlab format required to run the metabolic model with the solver quadprod.

Appendix S3. Archive with files in matlab format required to run the metabolic model with the solver fmincon.

Appendix S4. Archive with files in matlab format required to perform the fit for the concentrations of metabolites and biomass components.

Appendix S5. excel file with the lists of metabolites and reactions of the metabolic model.

Appendix S6. Comparison between fluxes and their respective maximal enzyme capacities (V_max).

Appendix S7. Mathematical demonstration of the unicity of the flux solution.

Appendix S8. Fitting parameters of the accumulated metabolites and biomass components.