Cell mechanics: principles, practices, and prospects

Abstract

Cells generate and sustain mechanical forces within their environment as part of their normal physiology. They are active materials that can detect mechanical stimulation by the activation of mechanosensitive signaling pathways, and respond to physical cues through cytoskeletal re-organization and force generation. Genetic mutations and pathogens that disrupt the cytoskeletal architecture can result in changes to cell mechanical properties such as elasticity, adhesiveness, and viscosity. On the other hand, perturbations to the mechanical environment can affect cell behavior. These transformations are often a hallmark and symptom of a variety of pathologies. Consequently, there are now a myriad of experimental techniques and theoretical models adapted from soft matter physics and mechanical engineering to characterize cell mechanical properties. Interdisciplinary research combining modern molecular biology with advanced cell mechanical characterization techniques now paves the way for furthering our fundamental understanding of cell mechanics and its role in development, physiology, and disease. We describe a generalized outline for measuring cell mechanical properties including loading protocols, tools, and data interpretation. We summarize recent advances in the field and explain how cell biomechanics research can be adopted by physicists, engineers, biologists, and clinicians alike.

CELL MECHANICS

21st century biomechanics research has entered an exciting era of investigation; where the mechanical behaviors of cells and tissues can be both a direct consequence, and a regulating factor of biological function and cellular architecture.^1,2 The underlying goal of current cell biomechanics research is to combine theoretical, experimental, and computational approaches to construct a realistic description of cell mechanical behaviors that can be used to provide new perspectives on the role of mechanics in disease.^3,4 In pursuit of this, biotechnological experimental methods are becoming increasingly diverse and the interpretation of results complex. Furthermore, achieving this goal requires a complement of both physical and biological research methods, which can prove daunting for non-experts in the field. Aiming to facilitate the understanding of the field to non-experts, we overview the principles, practices, and prospects of cell mechanics research. We summarize the choice of experimental tool, loading protocols, quantification, and examination of mechanical measurement results, and how these can be interpreted to perceive the underlying biological mechanisms of cellular force generation and physical behaviors. We summarize mechanical tools such as atomic force microscopy (AFM) and optical tweezers which are commercially available mechanical testing systems, and provide an overview of the most recent applications of these tools,^5,6,46,83 including rheological measurements.^7,8 We also place an emphasis on tools that do not require large amounts of specialized equipment such as particle tracking microrheology⁹ (PTM) and traction force microscopy (TFM),¹⁰ which can be easily adopted by laboratories that are new to the field. In the following sections we outline the interpretation of typical cell mechanical measurements using theories such as linear viscoelastic and power law models,^11–15 soft glassy rheology,^16,17 purified gel models^18,19 and poroelasticity.^20,21

Forces in Physiology

A basic requirement of every organism is that it can sustain, detect, and interact with physical forces within its environment. This requirement is so important to life and survival that it has become a cornerstone of biological design. The skeleton provides structural support to sustain the force of gravity. Skin provides a protective barrier that is maintained upon the application of external stretch and hinders the invasion of bacteria and microbes that would cause infection. Even the simplest of physiological functions, such as respiration and circulation, require the generation of forces to breathe in air and to pump blood around the body. These are but a few fundamental examples of how generating, sustaining, and detecting physical forces forms an integral part of everyday life. Biomechanics research in past decades has largely focussed on understanding and quantifying these behaviors at the organism and organ levels. Early research includes compression testing of bone, to quantify the levels of forces it can withstand before breaking and the amount of force a muscle can generate to lift a defined load.²² However, until the last decade the underlying mechanisms of force detection, load bearing, and force generation at the cellular level had remained largely elusive. With the development of new experimental methods in both cell culture and surface sciences, the role of physical interactions in development, physiology, and disease are beginning to be uncovered. In fact, sustaining, detecting, and generating physical forces at single cell level is a crucial intermediate between molecular mechanosensitivity, tissue and organ physiology.

Mechanical Properties

How a material responds to mechanical stimuli is defined by a group of characteristics referred to broadly as its ‘mechanical properties’ (Figure 1). In general, these terms describe how a material deforms in response to an applied stress, and how this deformation evolves over time. The scaling between stress and strain of a solid material is a constant called the Young#x0027;s modulus (often referred to as the material's elasticity with a unit of pascals), which is a fundamental property of solids as it determines their ability to sustain their shape under mechanical stress (Figure 1(a)). In contrast to elastic solids, fluids flow under the application of stress and are unable to store elastic energy. The rate at which a fluid flows under a defined load is quantified by its viscosity (given in the unit pascal-seconds) (Figure 1(b)). However, many materials exhibit both elastic and viscous properties and are referred to as viscoelastic. A viscoelastic material undergoing deformation simultaneously stores and dissipates mechanical energy and thus mechanical stress relaxes and deformation increases over time.

Figure 1.

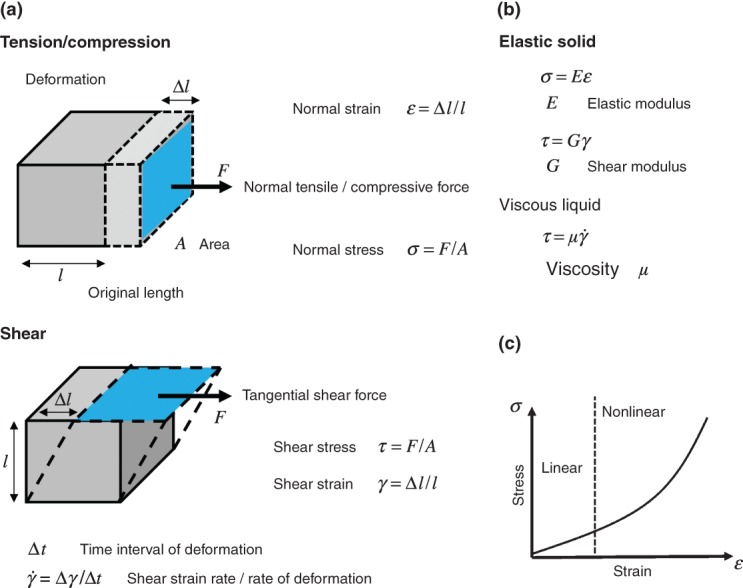
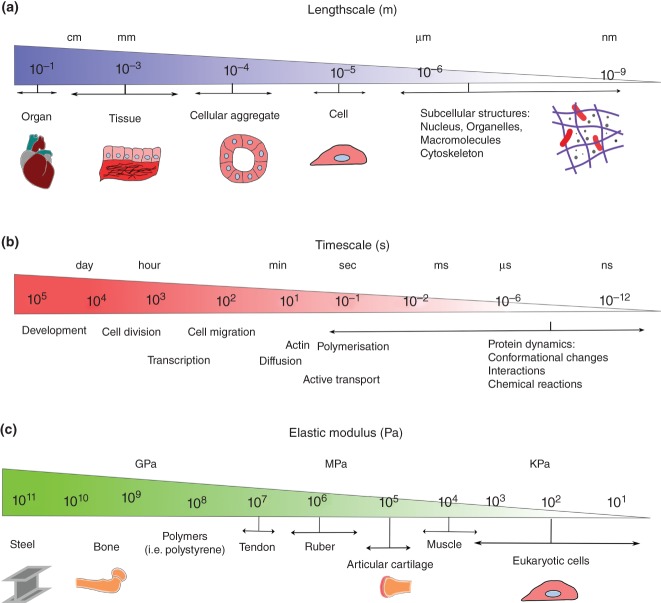
Fundamental quantities involved in mechanical characterization of a material. (a) Stress and strain defined as force per unit area and deformation per unit length respectively, are basic quantities that allow characterization of the mechanical response of materials. Materials deform differently under compressive, tensile, and shear forces. (b) The relationship between the stress and strain defines the material static mechanical properties. For simple elastic and purely viscous materials a simple linear relationship between the stress and strain/strain rate governs the mechanical properties. The elastic and shear moduli are measures of material rigidity and describe the tendency of a material to deform under normal and shear forces respectively. The viscosity is a measure of material resistance to flow under applied force and defined as the ratio of shear stress to shear strain rate. (c) For soft materials including cells, typically the stress is proportional to the strain under small deformations. However under larger deformations the stress–strain relationship is non-linear and the stress increases more rapidly under application of large strains.

Under physiologically relevant timescales cells are intrinsically viscoelastic, as they display a combination of both elastic and time-dependent responses to deformation. With an emphasis on the interplay between stress, strain, and the rate of flow, rheological measurements are used to investigate how cells flow rather than deform purely elastically in response to an applied force. At this point it is important to note that the simple mechanical terms elasticity and viscosity can be used as comparative quantities in cell mechanics. Many of the early cell mechanical measurements have shown links between local increases in cellular elasticity and subcellular structures such as stress fibres^23–25 and changes to cellular elastic and viscous properties under different treatments.^26–28 However, the applicability of these terms in a strict engineering sense is non-trivial and a range of complex rheological behaviors for cellular systems have been observed (see section, Universal Cell Behaviors and Beyond Simple Phenomenology). Typical values for the cell elastic modulus range from a few hundred pascals to tens of kilopascals (Figure 2(c)), and the cellular viscosity is in the order of a few hundred pascal-seconds.

Figure 2.

Main parameters involved in choosing the mechanical measurement tool. The choice of experimental tool requires consideration of (a) the lengthscale, (b) the timescale of the measurement and (c) the level of forces (or elasticity of the sample). A reasonable estimate of these three factors indicates which characterization tool is the most appropriate technique for mechanical study of a particular sample.

Even if thinking of a cell as an inert material, one of the main difficulties in cell mechanics is to understand the structural origins of the measured cellular mechanical properties. Indeed, cells are complex heterogeneous media containing a range of proteins, filaments, subcellular structures and organelles that can have different contributions to cell elasticity and viscosity. One particular example of this is the role of the nucleus in defining whole cell elasticity. The nucleus is known to be stiffer than the cytoplasmic portion of the cell.^29–31 During cell compression experiments, the cell membrane and cortex is deformed within the first 200 nm of compression.³⁰ As the compression increases there is a larger contribution from the underlying stiff nucleus, meaning that the stress–strain relationship cannot be characterized by a simple linear relationship (Figure 1(c)). Similar nonlinear features occur during cellular rheological measurements leading to the development of scale free models (see Beyond Simple Phenomenology). Nevertheless, a great deal of interesting information can be obtained via a simplistic mechanical models that enable comparative characterization of cell mechanics under genetic or pharmacological perturbations. In the following, we place cell mechanics in the context of physiological function, describe the classical cell mechanics measurements and then move to more complex descriptions of cell mechanics and their interpretation.

CELL MECHANICS IN CONTEXT

The interior of a single cell is a fluid, crowded with organelles, macromolecules, and structures that fulfill a variety of functions. Networks of subcellular filaments called the cytoskeleton form higher order meshes and bundles that endow individual cells with their ability to sustain external mechanical forces. Three cytoskeletal filaments are of specific interest to cell mechanical properties; actin microfilaments, microtubules, and intermediate filaments. Actin is one of the most abundant proteins in eukaryotes that forms polarized filaments that interact with an array of ancilliary proteins. From a mechanical perspective, actin filaments are semiflexible on the length-scale of the cell, having a persistence length on the order of the cellular length ∼20 µm (Box 1).³² Furthermore, actin filaments are highly dynamic and rapidly re-organize enabling cells to migrate and change shape. Despite their flexibility and high turnover rate, actin has long been known to be vital for the cell mechanically. The ability of the actin cytoskeleton to sustain mechanical stress is therefore not strongly influenced by single filament rigidity but a consequence of the higher level structures that they form and their interaction with crosslinkers and polymerizing factors. For example, the actin cytoskeleton forms a 200-nm-thick mesh below the apical plasma membrane that endows the cell with its mechanical integrity, basal fibers anchor the cell to the extracellular matrix (ECM), and linear bundles coordinate and sustain forces along intercellular junctions. Cells are active materials that carry an intrinsic pre-stress generated by myosin motors. As the myosin proteins crosslink and process along filaments they generate an internal stress between anti-parallel neighboring filaments. This pre-stress is particularly apparent in contractile actin structures such as stress fibers and intercellular junctions that rapidly relax following dissection with laser nano-scissors (Figure 5(b)).³⁴

Figure 5.

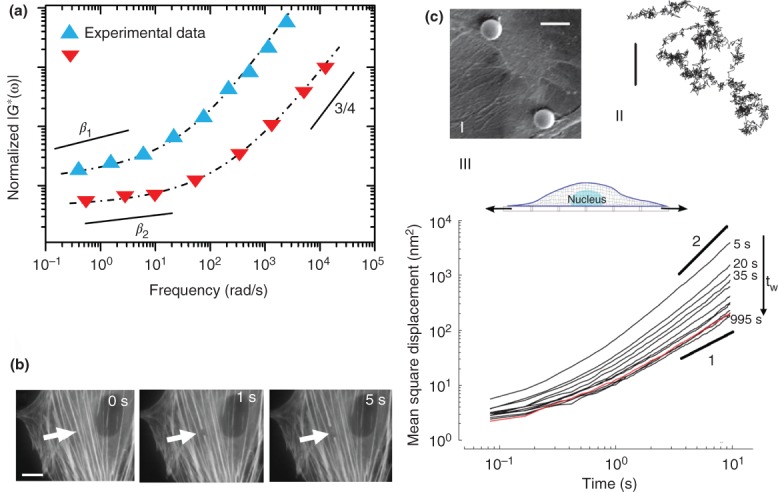
Cell universal behaviors. (a) The frequency response of cells measured with several mechanical measurement techniques (such as AFM, PTM, and magnetic twisting cytometry) collapses into two master curves after rescaling the experimental data from different rheological measurements (see Ref 33 for details). The frequency dependent dynamic modulus follow two distinct regimes in these master curves that can be fitted by a power law function: |G * (ω)| : ∼ω^β, where ω is frequency and β is power law exponent. At high frequencies both curves show β = 3/4 but at low frequencies they exhibit lower range of power-law exponents, β₁ ∼ 0.25 and β₂ ∼ 0.15 (see Ref 33 for further details). (b) Spontaneous retraction of a single actin stress fiber upon severing with a laser nanoscissor shows existence of prestress in the cytosketal bundles. Scale bar = 2 µm. (Reprinted with permission from Ref 34. Copyright 2006 Cell Press.) (c) Anomalous diffusion and response of the cell to stretch. (c-I, II) Spontaneous movements of beads attached firmly to the cell show intermittent dynamics. Scale bars = 10 µm. (Reprinted with permission from Ref 13. Copyright 2005 Nature Publishing Group.) (c-III) The mean square displacement (MSD) of a bead anchored to the cytoskeleton exhibits anomalous diffusion dynamics < r² > ∼ t^α (subdiffusive α < 1 at short time intervals and superdiffusive α > 1 at longer time intervals). Red curve indicates the MSD of the bead for a non-stretched cell and other curves show the MSD of the bead in response to a global stretch measured at different waiting times (t_ω) after stretch cessation. (Reprinted with permission from Ref 35. Copyright 2007 Nature Publishing Group.)

Chemical signaling between cells span a range of lengthscales; from hormones that travel between organs in the blood stream; to paracrine signaling between local groups of cells; small molecule signaling between contacting neighbors through gap junctions; and intracellular signaling cascades. A wealth of recent research has shown that cells are able to sense mechanical signals and forces in their environment.³⁶ The mechanical properties of the culture substrate determine cell differentiation and fate.^37,38 Cells tune their mechanical properties to match that of their substrate,^37,38 and migrate toward particular mechanical conditions (known as durotaxis). Complex sensory machineries located on different cellular sites, such focal adhesion complexes³⁹ and more recently focal adherens junctions,⁴⁰ have been shown to make up part of the molecular machinery involved in sensing mechanical stimulation.

PERSISTENCE AND ENTANGLEMENT LENGTHS

For a single filament, the persistence length or the length of thermal flexibility l_p is the lengthscale over which thermal bending fluctuations become appreciable and can change the direction of the filament, l_p = κ/k_BT where κ is the bending modulus of a single filament and k_BT the thermal energy. For network of filaments the entanglement length l is the confining lengthscale over which the motion of each filament is restricted via topological constraints from neighboring filaments.

The importance of sustaining, generating, and sensing mechanical forces at the cellular level is brought largely into context when examining diseases that target the cytoskeleton. Genetic disorders that disrupt the actin cytoskeleton or the binding of actin to the membrane of red blood cells, lead to abnormal cell shape and compromised function in diseases such as malaria⁴¹ and sickle cell anemia. One recent clinical example suggests that changes in cell rheology can have consequences for the health of patients. Some patients with a low neutrophil count exhibit a constitutively active mutation in the Wiskott Aldrich syndrome protein (CA-WASp) that results in increased actin polymerization through unregulated activation of the Arp2/3 complex. The overabundance of cytoplasmic F-actin increases cellular apparent viscosity resulting in kinetic defects in mitosis.³ Genetic mutations to the intermediate filament cytoskeleton are often linked to diseases such as Epidermolysis Bullosa Simplex which have symptoms that include increased tissue fragility.⁴² A hallmark of cancer is changes in the cell stiffness often resulting from perturbed cytoskeleton. The alterations in cancer cells stiffness could have significant effects in their ability to squeeze through the surrounding tissue, invade and metastasize.^43,44

One of the most exciting avenues of cell mechanics research is to make links between cellular level mechanosensitivity, force generation, mechanical properties and the underlying molecular mechanisms.⁴⁵ Several studies have now been able to monitor mechanical changes with the activity of molecular signaling pathways. Stretching the molecule talin using magnetic tweezers and AFM revealed binding domains for vinculin and its recruitment to focal adhesions.⁴⁶ AFM has been used to monitor the mechanical properties of cells and how they evolve following the activation of the angiotensin-1 receptor which induced an actin dependent contraction within the cell.⁴⁷ The influence of G-protein-coupled-receptors on cell morphology and contractility was studied using AFM to monitor variations in cell height.⁴⁸

MECHANICAL MEASUREMENTS IN PRACTICE

In comparison to typical materials such as metals, plastics and glass, cells are small soft objects. The ability to measure the mechanical properties of the cell on spatially accurate length scales has only arisen with the development of new technologies from the surface sciences including piezoelectric ceramics that can change shape in nanometer level increments, and microfabrication of micron-size cantilevers and mechanical parts. This has lead to the development of a vast number of cell mechanical measurement techniques, making choosing the appropriate tool puzzling. Taken broadly, mechanical measurement techniques can be put into two categories: those that can be used to apply controlled deformations and forces on part of, or on the entire cell (such as magnetic bead cytometry,^14,16,49 optical tweezers,^50–52 cell stretchers,^53–56 flow rheometry^54,57,58 and AFM⁵⁹), and those that monitor the ability of a cell to generate forces and deform its environment (such as TFM^60,61 and micropillar arrays⁶²). Local cell mechanical properties can also be extracted by tracking the motion of endogenous cellular structures, such as the movement of actin filaments, microtubules, mitochondria, or embedded particles of various sizes that are excited thermally or driven with an external force (PTM^63–65). In this section we outline the basic logic for choosing the appropriate experimental tool and what factors should influence this decision.

Choosing Forces, Lengthscales, Timescales, and Experimental Practicalities

The choice of experimental tool depends on three key considerations: the compliance and the lengthscale of the cellular material under investigation, the timescale at which mechanical properties are investigated, and the required environmental and experimental conditions (Figure 2).

First, eukaryotic cells are soft biological materials with an elastic modulus that varies from a few hundred pascals to tens of kilo-pascals and a size on the order of tens of microns (Figure 2(a,b)). Because of the cell size and low elastic modulus, the mechanical measurement technique needs to be capable of applying and monitoring deformations and forces in the range of micro to nano meters and nano to pico newtons respectively. Typical measurement techniques that are capable of applying these deformations and forces at a high spatial accuracy include atomic force microscopy.^59,66 To measure local cellular mechanical properties the size of the measurement probe must be much smaller than the cell length as in PTM. As the size of the cellular sample changes, for example to the multicellular aggregate and embryo level, then the experimental tool must be changed to apply larger forces over a greater area. For example mechanical shivering of multicellular aggregates has been observed using micropipette aspiration of entire aggregates rather than the more traditional single cell aspiration experiments.⁶⁷ As an alternative, AFM with a stiffer cantilever can be used to apply higher forces, and a larger bead can be attached to the end of the cantilever to increase the size of the probe.^68,69 Tools to study cellular force generation can be chosen with similar considerations to the lengthscales of the specimen and the degree of cellular force generation. Cells can typically generate forces on the order of nano-newtons meaning that the culture environment should have an appropriately tuned elasticity (e.g., kilo-pascal gels) for observable deformations (see case studies).

Second, the experimental tool can be chosen according to the frequency (timescale) of application and measurement of forces or deformations (Figure 2(c)). Simple conventional materials exhibit very simple frequency-dependent responses: for normal solids the response (dynamic modulus) is independent of excitation frequency and for liquids it is linearly correlated with excitation frequency through the viscosity of the liquid. However, materials, and in particular cells with more complex hierarchical structures and a high degree of heterogeneity, can exhibit a variety of complex time-dependent responses that depend on strength, frequency, and spatial application of deformations and forces (Figure 3). Tools such as AFM, magnetic and optical tweezers can be used with closed loop feedback systems to apply stress relaxation, creep, and oscillatory loading protocols^8,70–72 (Figure 3) and capture the time-dependent mechanical response of the cell over a wide range of timescales. On the other hand PTM techniques inherently capture the frequency dependent response. Here it worth emphasizing that further to cell structural complexity and passive processes, active biochemical processes (such as continuous turnover of cytoskeletal fibres, association/dissociation of crosslinkers and activity of molecular motors) also govern the cell rheology and therefore the timescale of active processes should also be considered when picking the mechanical tool and the loading protocol.

Figure 3.

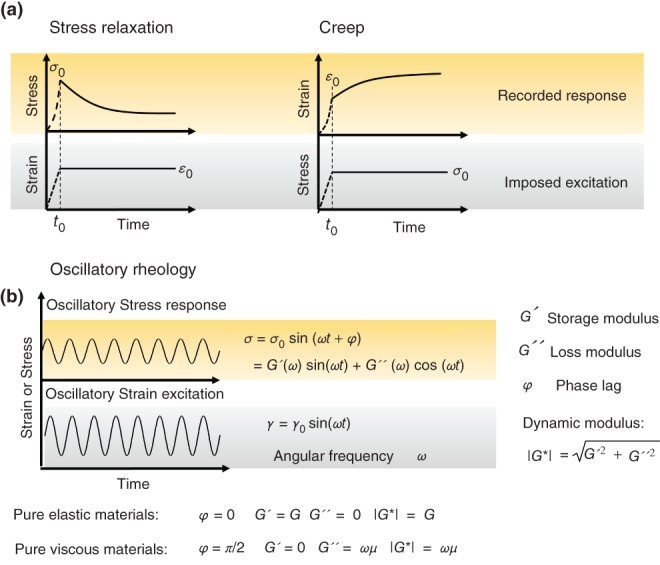
Common loading conditions for measuring time-dependent mechanical properties. (a) Typical rheological characterization incorporates measuring the temporal evolution of strain under application of a constant stress (creep) or the temporal evolution of stress under application of a constant strain (stress-relaxation). (b) Oscillatory techniques are another method of characterizing the viscoelastic properties of materials where normally a sinusoidal strain is applied and the cyclic stress response is monitored. In this approach the timescale of the test is defined by the frequency of oscillation ω. By observing material response at a range of frequencies the relative contribution of elastic (indicated by storage modulus G′) and viscous (indicated by loss modulus G″) responses can be characterized at different timescales. The dynamic modulus G* is the indicator of overall viscoelastic behavior. Oscillatory tests can reveal a set of material viscoelastic responses over specific span of frequencies (timescales).

Third, a variety of experimental and environmental conditions can determine the choice of experimental tool. To date many mechanical measurements are performed in ambient conditions, far from those of the true physiological environment. Some techniques that use optical traps can cause an increase in cell temperature.⁷³ Long time course experiments in particular should be combined with temperature control; one strategy includes incorporating an environmentally controlled chamber.^17,74 Another important concern is the bio-compatibility of materials used in mechanical measurements. For instance, one common material is PDMS, a bio-compatible elastomer used in microfabricated cell microfluidic devices, that is often used as a soft membrane for cell culture onto stretchable substrates and in the fabrication of micro-pillar arrays.^54,62 Designing alternative biologically and mechanically compatible synthetic hydrogels is indeed an important avenue of research in order to provide improved alternatives for polyacrylamide hydrogels in TFM experiments. Another goal of mechanical measurements is to observe changes in the localization of different proteins and protein activation during mechanical loading. Inverted fluorescence microscopes can be easily integrated with mechanical testing techniques^6,56 to image protein expression and localization.

In the next section, due to their wide range of applicability, commercial availability and ease of operation for novices, we discuss four mechanical measurement techniques in detail and summarize recent findings in our case studies. For in depth discussion of other techniques we refer readers to a recent review.⁷⁵

CASE STUDIES: MECHANICAL MEASUREMENT TECHNIQUES

Atomic Force Microscopy (AFM)

The atomic force microscope is a high resolution surface characterization technique, that has become rapidly adopted for imaging and mechanical characterization of a range of biological samples⁵⁹ (Figure 4(a)). AFM measurements utilize a micron-sized tip connected to a micro-fabricated cantilever beam to deform and interact with the sample. It is capable of probing surface topography and interaction forces with subnano-meter and pico-newton resolution. One of the most widespread uses of AFM in cell mechanics is AFM force spectroscopy to measure cellular elasticity and rheology. To extract the cell elasticity, the tip of AFM cantilever is pressed against the cell while the force and the imposed cellular deformation are monitored. Considering the tip geometry and using an appropriate contact model, the elasticity of the cell can be computed from the measured force versus indentation data.⁶ The success of cellular force spectroscopy measurements is in part due to the ease of the measurements, good measurement throughput and commercial systems that are readily available. Furthermore, because the levels of force and deformation can be very accurately measured over time, AFM has been applied for a variety of rheological measurements. Using a feedback loop (incorporated into most commercial systems) levels of strain and stress can be controlled over time, following indentation of the cell via AFM cantilever. Stress-relaxation and creep experiments^78,79 can be readily applied and oscillatory tests⁷¹ can also be conducted to measure time-dependent cellular mechanical properties.

Figure 4.

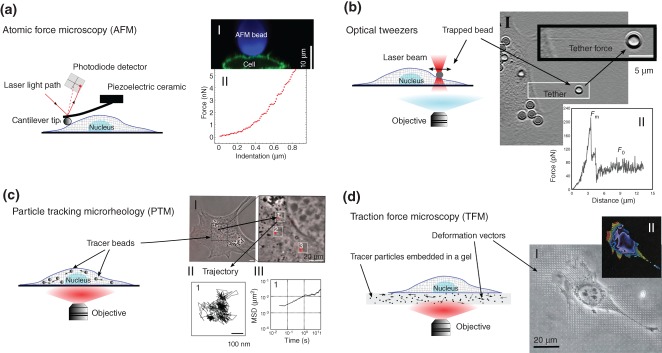
Four cell mechanical measurement techniques. (a) AFM: A laser beam is reflected off the back of the cantilever and collected by photodiodes. Interactions between the tip and the sample change the bending of the cantilever and consequently the reflection path of the laser beam which is precisely measured by the photodiodes. The bending of the cantilever is converted to force using its spring constant. A piezo-electric ceramic in a feedback loop is used to move the cantilever up and down to adjust bending of the cantilever and the applied force. (a-I) A confocal microscopy image shows the HeLa cell profile as the cell (green) is indented by a spherical bead (blue) attached to AFM cantilever. (a-II) A typical AFM force-indentation curve on cell. This curve can be fitted with an indentation model to estimate the cell elasticity. (Reprinted with permission from Ref 8. Copyright 2013 Nature Publishing Group.) (b) Optical tweezers: A small particle is stably trapped by a highly focused laser beam. The position of the optically trapped particle can be controlled by the movement of trap and small forces can be estimated from the changes in the displacement of the particle from the center of trap. (b-I, II) A tether extraction experiment involves pulling of an optically trapped bead attached to a cell membrane away from the cell. (b-II) The force-distance curve of tether extraction experiments on microglial cell. (Reprinted with permission from Ref 76. Copyright 2013 Public Library of Science.) (c) PTM: The micron or submicron beads disperse within the cytoplasm following injection into live cells. Using a high magnification objective the random spontaneous motions of the beads are captured with high spatial and temporal resolution. (c-I) 100 nm fluorescent beads injected into the cytoplasm of 3T3 fibroblasts. (c-II, III) The recorded time-dependent trajectories (c-II) of the beads are used to calculate their mean squared displacements (c-III) by which the nature of intracellular diffusion and microscopic viscoelastic properties of cellular environment can be studied. (Reprinted with permission from Ref 77. Copyright 2009 Public Library of Science.) (d) TFM: The cell is cultured onto (or within) a bead-embedded polymeric gel. Cellular contractions deform the gel and for a known gel elastic modulus the cellular traction forces can be calculated from the bead displacements. (d-I, II) Deformation vectors and traction stress field of fibroblast cultured on polyacrylamide gel were calculated by monitoring the displacement of fluorescent beads embedded in the gel. (Reprinted with permission from Ref 60. Copyright 2001 Cell Press.)

A recent close examination of AFM indentation and stress-relaxation tests on cells revealed that cells behave according to the theory of ‘poroelasticity’ (see section Beyond Simple Phenomenology) when mechanically stimulated in a way similar to that experienced in organs within the body.⁸ Of particular interest in cell biology and medicine is the capability of AFM to monitor changes in cell elasticity under different pharmacological and genetic perturbations.^3,80 For example, using the AFM indentation tests the elasticity of the vascular smooth muscle cells (VSMCs) isolated from thoracic aorta of old and young monkeys was measured.⁸¹ Increases in VSMCs elasticity with age suggested that cellular rheology has a significant contribution to aging-associated vascular stiffness and disease. Another recent use of AFM involves placing a tipless cantilever on a cell entering mitosis and monitoring the temporal changes of cell rounding forces during mitosis.⁸² Employing a perfusion system to apply drug and osmotic perturbations while measuring mitotic forces via AFM, it has been found that both actomyosin contractility and transmembrane ion gradient determine the levels of mitotic forces.⁸²

Optical Tweezers

The use of optical methods to image cells has been well established for decades. More recently, with the growing interest in cell mechanics there have been several methods developed that employ light trapping to manipulate part of a cell^83–85 or stretch the whole cell.^43,86 These techniques rely on the concept that as light enters a medium of a different refractive index the light path changes. Conservation of momentum means that there is a restoring force created by the light passing through the material that resists higher levels of refraction. Typically this means that a cell or a bead can be trapped/deformed optically and manipulated with a collimated light source. Because of the high sensitivity of these optical techniques (pico-newton resolution) and high spatio-temporal accuracy they are well suited to sub cellular measurements such as the pulling of membrane tethers.^76,83–85, In these experiments a small particle attached to the cell membrane is pulled away from the cell by optical tweezers and a tube-like structure, referred to as a membrane tether is created. Early measurements using this approach revealed the presence of a large amount of excess membrane at the cell surface that flows into the tether as it is pulled.⁸³ This technique has been also applied to study the adhesion strength of the plasma membrane to the actin cortex and the role of membrane proteins such as PIP2 in regulating this adhesion energy.^84,85 More recently elastic properties of the membrane of a variety of central nervous system cells have been reported using optical tweezers to perform tether extraction experiments.⁷⁶

Although optical tweezers provide a valuable tool for high precision measurements of small forces, there is an inherent limit on the amount of force that can be applied using these methods. In particular increasing the laser power to increase the optical forces induces local heating of the cell that might damage the cell structure and influence its mechanical properties. To increase the amount of optical forces, leaving minimal photodamage, another type of optical manipulation technique involves coupling a laser light to another optical fiber that enables trapping and stretching of the whole cell.⁸⁶ By combining this optical stretcher technique with a microfluidic platform, high throughput mechanical characterization of diseased and healthy cells in suspension has been reported.⁴³

Particle Tracking Microrheology (PTM)

One shortcoming of most cell rheological techniques, including AFM, is that they require external interventions and measure the combined response of subcellular structures (such as cell membrane, cytoplasm, and the nucleus) by application of external forces directly on the cell surface (Figure 4(a)). However, in PTM (Figure 4(c)), localized mechanical measurements inside the cytoplasm can be achieved by tracking thermally driven motion of embedded tracer particles, without a need for a direct contact of between the cell and an external probe.⁶⁵ Furthermore, using PTM it is possible to study mechanics of cells embedded in a 3D matrix⁶⁴ (a more physiologically relevant condition) while it is very difficult to probe cells in three dimensions by other mechanical techniques.

Microrheological analyzes of movement of particles in cell indicate existence of non-Brownian fluctuations. Indeed the movement of particles within the cell is perturbed by both elastic and viscous mechanical resistances.⁶³ Interaction of trapped particles inside the cell with elastic cellular network could be one main source of non-Brownian fluctuations (Box 2). Other possible contributions could include the influence of energy-consuming active processes and macromolecular crowding on tracer particles inside the cytoplasm. Generally PTM experiments on cells revealed a dominant elastic response at short timescales and a more viscous behavior over longer time periods. However, the magnitude and timescale of these viscoelastic responses may vary for various cell types, under different pharmacological treatments and physiological conditions.^77,87,88 For instance, in an in vivo study PTM was carried out by microinjection of nanoparticles into zygotes to extract viscoelastic properties of the Caenorhabditis elegans embryos.⁸⁹ Unlike differentiated cells, the cytoplasm of these embryos exhibits a highly viscous behavior over wide range of timescales. Another application of PTM discovered significant stiffening of intracellular environment of mesenchymal stem cells in response to the application of different growth factors such as TGF-β1.⁸⁸ Other recent studies employed PTM to investigate effects of mechanical perturbation (such as flow shear stress^87,90,91 and stretching³⁵) and also environmental changes (such as temperature and pH⁹²) on spatiotemporal cell viscoelastic properties.

BROWNIAN MOTION AND DIFFUSION

Microscopic mechanical properties of soft material including cells can be measured by tracking the movement of embedded tracer particles. In a purely viscous environment, particles move randomly due to thermal fluctuations and their mean squared displacement (MSD, < r² >) grows linearly in time t following 〈r²〉 = D_Tt, where D_T is the particle translational diffusion coefficient. This behavior is the characteristic of normal diffusion or Brownian motion. During normal diffusion the thermal motion of a particle with size a is slowed down by only a linear viscous drag from surrounding environment. Therefore by monitoring random motion of particles inside a purely viscous medium the MSD and subsequently particle diffusion constant D_T can be calculated to derive the viscosity of the medium using Stokes–Einstein relationship μ = k_BT/D_Ta where k_BT is the thermal energy. By contrast, in a purely elastic environment such as dense and cross-linked network of polymers, the embedded particles are stuck within the network and thermal agitations are not strong enough to induce significant random motion. In general the MSD of particles embedded in a complex viscoelastic environment such as cell follows a more complex time-dependence relationship than the described linear Brownian or weak fluctuating behaviors. In this case the MSD still grows continually with time due to thermal fluctuations but as the normal diffusion relationship is not applicable anymore the particle non-Brownian fluctuations can be characterized by a semi-empirical anomalous diffusion equation < r² > ∼ t^α where α can be any number except 1.

Traction Force Microscopy (TFM)

Force sensing techniques are another type of tool that have advanced our understanding of mechanotransduction³⁶ and improved quantitative modeling of cellular interactions with the ECM. These techniques measure traction forces generated by the cell on the surrounding environment using different detection mechanisms such as micropillar arrays⁶² or embedded beads in soft gels (Figure 4(d)). Traction forces drive cell spreading and migration during commonly occurring cell processes such as morphogenesis, wound healing, and tumor metastasis. Applications of high resolution time-lapse TFM in living neuronal growth cones enabled nanoscale probing of the complex dynamics of traction forces exerted by growth cone⁹³ and its filopodia.⁹⁴ These recent studies, had a major impact in unraveling the role of mechanical cues in neuronal development. These results showed that focal adhesions exhibit either stable or oscillating force transmission to the ECM via adhesion sites and ECM stiffness modulates the dynamics of focal adhesions. Using TFM other recent works also studied the oscillation of forces within focal adhesions and the impact of ECM compliance on force fluctuations and directed cell migration.^95,96 Most studies measure the traction forces of cells cultured on planar substrates but combining TFM with laser scanning confocal microscopy allows probing of the cellular traction forces in three dimensions.^61,97

UNIVERSAL CELL MECHANICAL BEHAVIORS

Having selected an experimental approach and a loading protocol it is important to know what type of behavior could be expected for cell rheology and what this means for the underlying microstructure and cellular function. Cell mechanical studies over the years have revealed a rich phenomenological landscape of rheological behaviors that are dependent upon the cell type, probe geometry, loading protocol, and loading frequency. Although assessing cellular elasticity and viscosity yield some useful information for comparative characterization between different treatments, the mechanical behavior of the cell is inherently much more complicated. Due to the heterogeneity and complexity of the cell and the cytoskeleton, submicrometer-scale measurements can lead to considerably different evaluations of mechanical properties compared to bulk (several micrometer-scale) measurements. However recent rheological measurements on eukaryotic cells agree on the presence of four cellular phenomenological behaviors that are universal.⁹⁸ (1) Cell rheology is scale free: plots of the frequency response of many cell types (obtained via different methods) on log–log scale display the same shape and follow a weak power law spanning several decades of frequency³³ (Figure 5(a)). (2) Cells are prestressed: mechanical stresses generated continuously by the internal activity of actomyosin or applied externally on the cell are counterbalanced by the tensional/compressional state of the cytoskeleton⁹⁹ (Figure 5(b)). (3) The Stokes–Einstein relation breaks down and diffusion is anomalous¹³: The spontaneous motions of endogenous particles or embedded/attached beads present in the cell do not follow the Stokes–Einstein relationship (see Box 2, Figure 5(c)). (4) Stiffness and viscous dissipation are altered by stretch³⁵: Application of stretch significantly perturbs the rheological properties of the cell, and depending on the experimental condition, the cell can exhibit different behaviors such as stress stiffening, fluidization and rejuvenation.

BEYOND SIMPLE PHENOMENOLOGY

One of the main ongoing challenges in the field of cell mechanics is to find a unified framework under which the measured phenomenological behaviors can be interpreted to obtain realistic information about the dynamics of the microstructure of the cell, or vice versa to estimate the bulk rheological properties from the observed microstructural interactions. Several top-down (linear viscoelastic, tensegrity, power law, and soft glassy rheology) and bottom-up (networks of polymers, poroelasticity) theoretical models (Figure 6) have been successfully applied to explain the observed phenomenological mechanical behaviors. However there is still no unifying mechanistic theory to explain the physical mechanisms that govern the universal cellular behaviors and encompasses such a rich phenomenological landscape. As will be described briefly in the following sections, linear viscoelastic, immobilized colloids/soft glasses, and the network of cytosketal filaments are the most widely used models that have been proposed to study cell mechanics and we provide a brief introduction to these concepts and frameworks.

Figure 6.

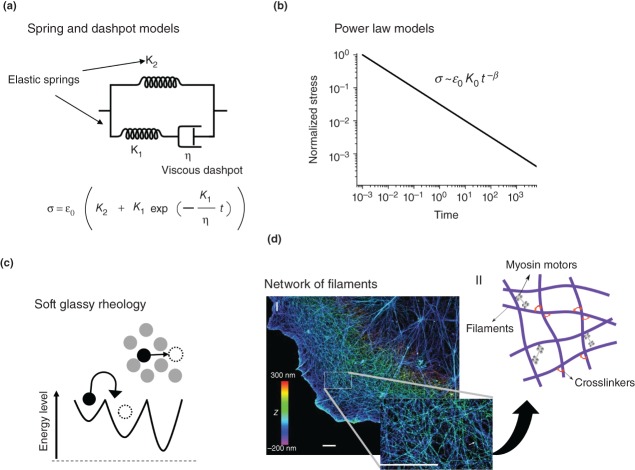
Models of cell rheology. (a) Spring and dashpot representation of Standard Linear Solid viscoelastic model and the functional form of its stress relaxation in response to sudden constant strain. (b) The power law type of relaxation in log–log scale is a line with the slope β which is the power law exponent. For purely elastic and viscos materials the power law exponents are β = 0 and β = 1 respectively. When 0 < β < 1 combination of elastic and viscous mechanisms contribute to relaxation response. (c) Schematic representation of soft glassy rheology: A rheological model that explains glassy and weak power-law behavior of soft disordered materials such as foams and colloids. (d) Dynamic network of cytoskeletal filaments such as actin network determine the cell rheology. (d-I) Image of actin filaments in a COS-7 cell taken by dual stochastic optical reconstruction microscopy (STORM) (Reprinted with permission from Ref 100. Copyright 2012 Nature Publishing Group). The height is color coded with respect to the scaling shown in the color scale bar. Scale bars = 2 µm. (d-II) In reconstituted gel models of cytoskeletal filaments, interaction of binding proteins with different properties (such as type, organization, and concentration) with filaments significantly influence the network rheology.

Linear Viscoelastic and Power Law Models

The majority of the work to date utilizes a viscoelastic description of cells that considers the cell as a single phase homogenous continuum material.^11,12 As we have described previously (see section Mechanical Properties), this assumption allows characterization of the cell time-dependent mechanical responses by introducing a finite number of elastic and viscous elements (springs and dashpots) coupled in series or parallel leading to exponential decay functions with a finite number of relaxation times. The combination of several springs and dashpots create a system that, for example, exponentially relaxes to a new size under the application of a constant stress (Figure 6(a)). In such models, the resultant exponential functions can have a single relaxation time if there is only one dashpot element or a distribution of relaxation times if there are several. Examples of such models are the Maxwell and the Standard Linear Solid (also known as the Zener) models that has been widely used to describe the time-dependent behaviors of biomaterials including living cells.^12,78 Beyond this, power law models also provide good fits to the experimental relaxation data⁵¹ but unlike spring-dashpot models, they do not have any characteristic relaxation time and cannot be easily described using mechanical analogs (Figure 6(b)). Power law structural damping models have been applied very commonly in recent microrheological experiments to describe the measured viscoelastic response of the cells over a broader range of timescales.^13,14

The main advantage of these empirical models is that they can be used as a diagnostic tool in cell biology. The mechanical properties of the cell in healthy and diseased states, under physiological changes and also with different genetic perturbations and drug treatments, can be characterized using these models. Despite their widespread use and offering good characteristic fits to the measured mechanical responses, the major limitation of these models is that they are not mechanistic, fail to relate the measured rheological properties to structural or biological parameters within the cell, and thus cannot predict changes in rheology due to microstructural changes.

Cell as a Soft Glassy Material

A large body of more recent research has found that some of the cellular rheological behaviors are empirically similar to the rheology of soft materials such as foams, emulsions, pastes, and slurries. Following some experimental observations,^{13,14,17,35,71} it was proposed that cells could be considered as soft glassy materials.¹⁰¹ As a conceptual model, soft glassy rheology (SGR) explains how macroscopic rheological responses are linked to localized structural rearrangements originating from structural disorder and metastability (Figure 6(c)). The SGR system consists of crowded particles that are trapped in energy landscapes arising from their interactions with surrounding neighbors. In such a system, thermal energy is not sufficient to drive structural rearrangement and, as a consequence out of equilibrium trapping occurs. Over time, remodeling/rearrangement (micro-reconfiguration) happens when particles escape the energy barriers of their neighbors and jump from one metastable state to another reaching a more stable state with relaxation rates slower than any exponential process.¹³ In such a system, injecting agitational energy, sourced from non-thermal origins (such as mechanical shear or ATP-dependent conformational changes of proteins³⁵), liberates particles from the energy cages in which they are trapped and facilitates structural rearrangements causing the material to flow.

Indeed, measuring the fluctuations of particles within the cytoplasm revealed that in many cases they exhibit a larger random amplitude of fluctuations than expected and a greater degree of directionality than could be developed solely from thermal fluctuations.¹⁰² These fluctuations deviate from the Stokes–Einstein relation and can be empirically characterized by anomalous diffusion processes (Box 2) that are similar to particle fluctuations in a soft glassy material. The deviation from the Stokes–Einstein relationship has been attributed to reaction forces from active cytosketal processes¹⁰³ and crowding of a large number of macromolecules inside the cytoplasm, such as mobile intracellular globular proteins and other fixed obstacles like cytoskeletal filaments and organelles, that reduce the available solvent volume and provide barriers to particle Brownian motion.^104–106 On the basis of these observations, it was proposed that the high concentration of different proteins in the cytoplasm can lead to liquid crystal and colloidal behaviors that can be interpreted in terms of the SGR model.¹⁰¹ Crowded colloidal suspensions or soft glasses exhibit anomalous diffusion and a weak power-law rheology corresponding to a continuous spectrum of relaxation times. Similar to this, the dynamic modulus of cells, except at high frequencies, scales with frequency as a weak power law valid over a wide spectrum of timescales.^14,71 Despite its ability to describe the cell rheology over a wide spectrum of timescale, the semi-empirical SGR model cannot yet explain many of cell mechanical features such as the cell rheological responses at high frequencies.

The Cell as a Dynamic Network of Polymers

At very short time scales (high frequencies), the cell dynamic modulus scales with frequency with a universal exponent of 0.75¹⁶ (Figure 5(a)). This behavior is analogous to the observed rheology of semiflexible polymer gels^{18,19,107,108} (Figure 6(d)). To understand the relation between polymer network rheology and cell mechanics, purified gels of entangled cytoskeletal filaments such as actin gels have been widely studied.^{18,19,107–109} For these reconstituted gels various linear and nonlinear viscoelastic responses have been observed that intrinsically depend on the filament concentrations and the properties of crosslinkers, such as their length, flexibility and concentration. The main advantage of in rheological study of these purified gels is that their measured rheological properties can be related to the gel structural parameters. On the basis of microscopic picture of the reconstituted network, several mechanical models have been developed that relate the measured viscoelastic properties to microstructural parameters such as the flexibility and degree of crosslinking of the filaments. For example the elasticity of dense crosslinked F-actin gels follow the scaling relationship¹⁹: 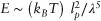where λ and l_p are the entanglement and persistent lengths respectively (Box 1). The principal shortcoming of these purified gel models is that because of the complex cytoplasmic environment and the rich involvement of active cellular processes, it is still not possible to directly apply such scaling relationships, derived for mechanics of purified gels, to give correct predictions about the relation between cell microstructure and measured cell mechanical properties.

Tensegrity

The experimentally determined elastic moduli of cells were found to be several orders of magnitude larger than those measured in in vitro studies of stress-free F-actin gels. This suggested that the main elastic properties of cells could not result solely from the interaction of reconstituted networks in a stress free state.¹¹⁰ It has been suggested that the prestressed state of filaments in the cytoskeleton (Figure 5(b)) could result in the high measured elasticities for cells¹¹¹ and a highly nonlinear tension, or deformation-dependent, viscoelastic behavior. Indeed the polymerization of cytoskeletal elements and contractility of actin-myosin network can generate tension and pre-stress that is transmitted through the cytoplasm by the cytoskeleton and balanced by adjacent cells and the ECM. These observations are consistent with a tensegrity model of the cell^99,112 that suggests that the prestress distribution inside the cytoplasm might be partly balanced by the compression of other cytoskeletal filaments such as microtubules.

Biphasic Models of Cells

Considering a cell to be a single phase material is counter-intuitive given that more than 60% of the cellular content is water. In mammalian cells, most studies view water solely as a solvent and an adaptive component of the cell that engages in a wide range of biomolecular interactions. However less attention has been given to the significance of water in the dynamics of the cytoskeleton, its role in cellular morphology, and motility. Recent experimental works showed the presence of transient pressure gradients inside cells and suggested that these could be explained by the biphasic nature of cytoplasm.^20,21,113 As a consequence, a fluid-filled sponge model of cells was proposed based on poroelasticity (or biphasic theory), in which the cytoplasm is biphasic consisting of a porous elastic solid meshwork (cytoskeleton, organelles, macromolecules) bathed in an interstitial fluid (cytosol).^20,21 In this framework, the viscoelastic properties of the cell are a manifestation of the time-scale needed for redistribution of intracellular fluids in response to applied mechanical stresses and the response of the cell to force application depends on a single experimental parameter: the poroelastic diffusion constant D_p, with larger poroelastic diffusion constants corresponding to more rapid stress relaxations. For this poroelastic picture of the cell, a minimal scaling law was proposed D_p ∼ Eξ²/μ that relates the diffusion constant to the drained elastic modulus of the solid matrix E, the pore size of the solid matrix ξ, and the viscosity of the cytosol μ.⁸ Therefore, contrary to viscoelastic models, the dynamics of cellular deformation in response to stress derived from poroelasticity can be described using measurable cellular parameters, allowing changes of rheology with E, ξ, and μ to be predicted which makes this framework particularly appealing conceptually.⁸

CONCLUSION

Cell mechanics research has great potential to provide new perspectives on pathologies and classic biological research questions. To facilitate wider use of mechanical experimental tools and cell rheological characterization we have outlined a simple set of considerations for non-experts in the field looking to attempt mechanical measurements. The choice of experimental tool depends on the lengthscale of the sample and the level of force that is needed to deform the sample. Many techniques are now spatially accurate to the subcellular level and sensitive enough to measure pico to nano newton levels of force and can be scaled appropriately by altering the size and stiffness of the measurement probe. There are also a variety of environmental and experimental conditions that need to be considered, such as temperature control and the interface with other measurement techniques, such as optical microscopy. Upon choosing the mechanical measurement tool that will be spatially accurate, can apply the correct forces and comply with physiological condition, there are also a variety of mechanical loading protocols that can be employed. Considering the cell active features, the loading condition and the timescale of mechanical measurement could have a direct relevance in probing the underlying active cellular processes. Typical loading protocols involve step changes in stress or strain while monitoring the ensuing relaxation response. Other loading protocols include application of oscillatory mechanical excitations that provide significant insight about time dependent mechanical properties.

While their ability to describe the complex cell rheological behavior is extremely limited, linear viscoelastic characterization of cellular mechanical responses in terms of spring-dashpot models lead to estimation of stiffnesses and viscosities that are useful for evaluating cell mechanics under different biological and chemical perturbations. Beyond simple linear mechanical descriptions are scale free models that better explain some of the commonly observed universal cell mechanical behaviors. These can be applied with great effect to capture some of the mechanical responses of the cell under different loading conditions and at a wide range of timescales. Other reconstituted gel and biphasic models provide a mechanistic insight about cell rheological measurements. However, a unifying theory that describes all of the complexities of cell mechanical behavior remains an exciting and active area of research.

Conflict of interest:

The authors have declared no conflicts of interest for this article.

FURTHER READING/RESOURCES

Kollmannsberger P, Fabry B. Linear and nonlinear rheology of living cells. Ann Rev Mater Res 2011, 41:75–97.

Lim C, Zhou E, Quek S. Mechanical models for living cells—a review. J Biomech 2006, 39:195–216.