Covariation in Frequencies of Substitution, Deletion, Transposition, and Recombination During Eutherian Evolution

Abstract

Six measures of evolutionary change in the human genome were studied, three derived from the aligned human and mouse genomes in conjunction with the Mouse Genome Sequencing Consortium, consisting of (1) nucleotide substitution per fourfold degenerate site in coding regions, (2) nucleotide substitution per site in relics of transposable elements active only before the human–mouse speciation, and (3) the nonaligning fraction of human DNA that is nonrepetitive or in ancestral repeats; and three derived from human genome data alone, consisting of (4) SNP density, (5) frequency of insertion of transposable elements, and (6) rate of recombination. Features 1 and 2 are measures of nucleotide substitutions at two classes of “neutral” sites, whereas 4 is a measure of recent mutations. Feature 3 is a measure dominated by deletions in mouse, whereas 5 represents insertions in human. It was found that all six vary significantly in megabase-sized regions genome-wide, and many vary together. This indicates that some regions of a genome change slowly by all processes that alter DNA, and others change faster. Regional variation in all processes is correlated with, but not completely accounted for, by GC content in human and the difference between GC content in human and mouse. [Supplemental material is available online at www.genome.org and http://www.soe.ucsc.edu/research/compbio/covariation/.]

In principle, the alignment of the human and mouse genome sequences provides the opportunity to find most functional sequences whose role is conserved in the two species. Nearly all such sequences are subject to purifying selection, and thus will change less than nonfunctional sequences, which will evolve at a faster, neutral rate. Thus, one way to find conserved functional elements of the human genome is to identify those DNA sequences that are changing significantly more slowly than the neutral rate.

This approach is complicated by variation in both the level of selection on various functional sequences, which affects the extent to which they change relative to the neutral rate, and regional variation in the neutral rate within the genome. Variation in the level of selection is well-known. Most protein-coding sequences change little in comparisons between orthologous human and mouse genomic sequences. The mean similarity is ∼85% identity, but the range varies between 36% and 100% identity (Makalowski et al. 1996; Makalowski and Boguski 1998b). Studies of a large number of protein families show that the nonsynonymous substitution rate varies about 300-fold (Nei 1987), presumably reflecting differences in the portion of the protein under functional constraint and the severity of that constraint. Other functional regions, such as those transcribed into RNAs that do not encode proteins and DNA sequences regulating gene expression, have been studied less, but it is reasonable to expect substantial variation in the level of selection for these as well.

Many investigators have found that the neutral substitution rate, primarily estimated from substitutions at synonymous sites, also varies regionally within a genome (Matassi et al. 1999; Williams and Hurst 2000; Chen et al. 2001; Castresana 2002b; Ebersberger et al. 2002; Lercher and Hurst 2002; Smith et al. 2002), but it is uncertain how consistent this variation is across different mammalian lineages (Williams and Hurst 2002), and there are dissenting opinions on the existence of rate variations (Kumar and Subramanian 2002). Early results showed that the synonymous substitution rate varied for different genes (Wolfe et al. 1989) and that it correlates with the nonsynonymous rate (Graur 1985). Additional studies have consistently seen wide variation in the rate of substitution per synonymous site for human and other mammalian species (primarily rodents; Makalowski et al. 1996; Casane et al. 1997; Makalowski and Boguski 1998a). Regional effects are evident from studies of correlations in the synonymous rates of neighboring genes and genes within fixed-size regions (Matassi et al. 1999; Williams and Hurst 2000; Chen et al. 2001; Castresana 2002a; Lercher and Hurst 2002; Smith et al. 2002).

The inferred regional variation in evolutionary rates has been examined directly by comparisons of long genomic DNA sequences between humans and other mammals (usually mouse). Alignments of these sequences showed that some loci have extensive matches outside the coding region (Koop and Hood 1994; Epp et al. 1995; Oeltjen et al. 1997; Ellsworth et al. 2000), whereas in others the matches are largely limited to the coding regions (Lamerdin et al. 1996; Endrizzi et al. 1999), and still others have an intermediate level of noncoding sequence matches (Margot et al. 1989; Shehee et al. 1989; Lamerdin et al. 1995; Ansari-Lari et al. 1998). Quantitative analysis showed that the fraction of noncoding, nonrepetitive genomic sequence that aligns in comparisons between mammalian orders varies over a 10-fold range at different loci (Endrizzi et al. 1999; DeSilva et al. 2002). Thus, analysis both of substitutions at apparently neutral sites in coding regions and the extent of aligning DNA in noncoding regions reveals substantial regional differences in the amount of divergence between mammalian genomic DNA sequences.

The search for functional genomic DNA sequences based on comparative analyses requires a much better understanding of this regional variation in the rate of evolution. The goal is to determine which sequences have changed significantly less than expected, given a particular underlying rate of change for the region encompassing those sequences, knowing that the underlying rates can vary. Several things are needed to accomplish this goal. Reliable, well-understood measures of divergence must be developed (Nei and Kumar 2000), and they need to be applied genome-wide to ascertain their variation along each chromosome. The extent of correlation among the measures of divergence needs to be examined; for example, one study on a small scale (relative to a whole genome) has shown that the fraction of human DNA sequences aligning with mouse is negatively correlated with the frequency of insertion and retention of interspersed repeats (Chiaromonte et al. 2001). Any covariation should be explained to the extent possible. However, the literature has conflicting reports on the ability of parameters such as GC content to explain variation in divergence (Wolfe et al. 1989; Wolfe and Sharp 1993; Bernardi 1995; Matassi et al. 1999). Once these steps have been accomplished, approaches for finding sites that are candidates for being under selection (given variation in underlying rates) can be applied (Elnitski et al. 2003; Li and Miller 2002; Roskin et al. 2002; Waterston et al. 2002).

This paper reports our initial results analyzing divergence between human and mouse genome-wide, done in conjunction with the Mouse Genome Sequencing Consortium (Waterston et al. 2002). Three measures of evolutionary change were derived from the aligned human and mouse genomes; these are nucleotide substitution per fourfold degenerate site in coding regions, nucleotide substitution per site in ancestral repeats, and the nonaligning fraction of human DNA that is nonrepetitive or in ancestral repeats. The first two are measures of nucleotide substitutions, one at a class of sites commonly used to model neutral evolution, and the other at a newly studied class of sites that may provide a superior model of neutral evolution. The third is a measure dominated by deletions in mouse (Waterston et al. 2002). Three additional measures of divergence were derived from the human genome alone: the frequency of insertion of transposable elements, the density of single nucleotide polymorphisms in human, and the meiotic recombination rate.

We show that all six of these measures of chromosomal DNA change vary regionally in their rates, and most of the rates covary. Some of these observations extend previous results obtained on smaller data sets, as discussed below. Thus large (megabase-sized) segments of mammalian genomes vary substantially in their rate of change by substitution, deletion, insertion, and recombination, and regions with more changes acquired recently (high SNP density) also have accumulated more substitutions since the human–mouse divergence. We show that variation in GC content accounts for some but not all of this variation, and has a quadratic relationship with the level of divergence. Similar results are obtained for the change in GC content between human and mouse: It can account for part of the variation, but cannot account for all the variation in divergence. The involvement of double-strand breaks during recombination and DNA repair processes is a potential mechanism to explain the variation (Lercher and Hurst 2002), although many possibilities will need to be examined in future studies.

RESULTS

Measurement of Rates of Neutral Substitution

We used a whole-genome alignment between the June 2002 human genome assembly and the mouse genome assembly as reported in Waterston et al. (2002) built by the BLASTZ alignment program (Schwartz et al. 2003). This alignment covers ∼40% of the human genome sequence, with 69.8% of the aligned bases matching. To attempt to separately study substitutions representing neutral evolutionary drift (Kimura 1983) from those influenced by selection, it is common to look separately at substitutions in fourfold degenerate sites in codons, that is, sites marked “x” in the codons GCx (ALA), CCx (PRO), TCx (SER), ACx (THR), CGx (ARG), GGx (GLY), CTx (LEU), and GTx (VAL), which we call 4D sites (see Methods). We have found about two million such sites in our human–mouse genome alignment using codons defined by human gene annotations from BLAT (Kent 2002) alignments of 9562 RefSeq cDNAs that passed certain quality checks.

The overall observed percent identity in the 4D sites is 67.2%, but it varies depending on the human GC content of the surrounding 100-kb region, from 69.1% in low (<36.2%) GC regions, to 68.4% in medium (between 36.2% and 41.2%) GC regions, and 66.4% in high (>41.2%) GC regions. (These GC ranges divide the data roughly into equal thirds.) Because hypermutable CpG dinucleotides can sometimes skew estimates of the levels of conservation (Fryxell and Zuckerkand 2000), we also recalculated the percent identities after removing all sites that are in a CpG either in human or in mouse. This increased them to 74.4% in low-GC regions, 74.1% in medium-GC regions, and 73.6%, in high-GC regions. The frequencies of the 16 observed changes in 4D sites for medium-GC-content regions, not excluding CpGs, are given in Table 1A; similar tables for the other cases are given as Supplementary Material (available online at www.genome.org and http://www.soe.ucsc.edu/research/compbio/covariation/).

Table 1.

Observed Changes in Aligned Sites

A. Observed Changes in 4D Sites
	Mouse
	A	C	G	T
Human A	0.1779	0.0246	0.0499	0.0192
Human C	0.0135	0.1597	0.0169	0.0348
Human G	0.0358	0.0169	0.1641	0.0134
Human T	0.0187	0.0495	0.0257	0.1793
B. Observed Changes in AR Sites
Mouse
A	C	G	T
Human A	0.2163	0.0198	0.0508	0.0207
Human C	0.0160	0.1184	0.0116	0.0463
Human G	0.0463	0.0116	0.1183	0.0159
Human T	0.0207	0.0509	0.0199	0.2166

Frequency of observed changes in (A) 4D sites and (B) ancestral repeat sites in 100-kb windows with medium human GC content (between 36.2% and 41.2% G or C). GC content was calculated using all aligned bases in the window. Frequencies are expressed as the fraction of the total observed changes.

Using the general time-reversible Markov model of base substitution, REV (Tavaré 1986; Yang 1994; Whelan et al. 2001), we used the frequencies of observed changes in Table 1A to estimate the average number of substitutions per 4D site on the combined primate and rodent lineages since their divergence from a common ancestor. For medium-GC-content regions, not excluding CpGs, we obtained 0.42 substitutions per site, which can be broken down into the 12 types of substitution shown in Table 2A. Recomputing this number for other GC contents, we obtained related estimates for the number of substitutions per site, varying between 0.41 and 0.47; excluding CpGs, we obtained much smaller estimates of 0.32–0.34 substitutions per site, as shown in the Supplementary Material. Other Markov models (Lio and Goldman 1998) that distinguish between transitions and transversions, such as K2P, HKY, and TN93, gave similar estimates, whereas simpler models, such as JC and FEL, gave slightly lower estimates, as expected (Yang 1994; data not shown). There is insufficient information in two-species data sets to effectively use more complex models that include rate variation among sites, and separate parameters for each branch.

Table 2.

Estimated Number of Substitutions per Site in the Evolution of the Human and Mouse Genomes From Their Common Ancestor

A. Substitutions per Site in 4D Sites
	Base arising
	A	C	G	T
Base replaced	A	0.0232	0.0623	0.0218
C	0.0232	0.0197	0.0613
G	0.0623	0.0197	0.0238
T	0.0218	0.0613	0.0238
B. Substitutions per Site in AR Sites
Base arising
A	C	G	T
Base replaced	A	0.0223	0.0748	0.0213
C	0.0223	0.0136	0.0748
G	0.0748	0.0136	0.0224
	T	0.0213	0.0748	0.0224

For each type of substitution, the expected number of substitutions of that type per site is estimated from the REV model using data in Table 1. Estimates are for the combined number of substitutions of the given type in both the primate and rodent lineages since they diverged from their common ancestor.

With two million data points, and approximately one-third of these for each of the GC levels, the asymmetries between human and mouse in the frequencies of observed changes (especially in the transition rates at extreme GC contents) are statistically significant, and indicate either lack of time-reversibility or lack of stationarity to a certain degree, which very likely creates some inaccuracies in the REV estimates that will need to be reexamined when large data sets from other mammals become available. Unfortunately, pooling of the data into such large data sets also introduces inaccuracies because of the regional variability in the substitution process. Indeed, if the REV model is applied separately to the 4D sites in every 1-Mb region of the human genome that has at least 1000 4D sites (including CpGs), and an average of the resulting regional estimates of the number of substitutions per site is taken, weighted by the number of 4D sites in each window, then the resulting genome-wide average is 0.467 substitutions per site (Waterston et al. 2002), very similar to what we observe in the highest third of the GC range when we combine all that data and do one estimate. Therefore, one must also be careful in how one breaks down the data when making genome-wide estimates of substitution rates.

Bases at 4D sites are not a perfect data source for models of neutral evolution. They can sometimes be under selection for their role in mRNA splicing and other nuclear functions. In some species, 4D sites show biased base frequencies relating to differences in tRNA abundances, also indicating possible selection effects. Bernardi and coworkers have suggested human 4D sites are under selection (Bernardi 1995, 2001), but others argue that it has not been convincingly shown that tRNA-abundance-based codon bias or other kinds of selection affect 4D-site substitution rates in mammals (Graur and Li 2000; Iida and Akashi 2000). Also, the flanking bases can have a significant impact on substitution rates, as with the hypermutable CpG sites, but flanking bases are not equally represented in 4D sites. For instance, no bases 5′ to a 4D site are ever an A. For these reasons, we suggest another data source for modeling neutral evolution that we call an ancestral repeat, or AR, site (Waterston et al. 2002).

AR sites are aligned nucleotides within copies of transposable elements that were fixed in the common ancestor of human and mouse. A set of such elements was selected based on an average divergence level in human indicative of an age predating the mammalian radiation, and the whole-genome alignments confirmed that individual copies are at orthologous sites in human and mouse (Waterston et al. 2002). Thus, copies of these elements were already present as interspersed repeats in the common ancestor of human and mouse. We chose to focus on these sequences as they are highly likely to have been under no functional constraint. In contrast, single-copy DNA not annotated as exons can contain unidentified coding regions, RNA-coding genes, and other functional sequences, and thus does not provide a good model for neutral evolution. The ancestral repeats are abundant: Half of the interspersed repeats identifiable in the human genome with RepeatMasker (Smit and Green 1999) predate the human–mouse split (22% of all human DNA). The distribution of all ancestral repeats is uniform across the human genome, with little bias toward A + T-rich or G + C-rich DNA (Lander et al. 2001). Orthologous ancestral repeats can be reliably found and aligned by extending alignments of nearby unique genomic DNA (Schwartz et al. 2003).

We identified ∼165 million aligned AR sites in our human–mouse alignment. The overall observed percent identity in these AR sites is 66.7%, and varies between 66.1% and 67.0% in the three different GC levels. These numbers increase only slightly to 66.6%–67.9% if we exclude CpGs, in contrast with the big increases observed in 4D sites. Observed substitutions in medium-GC regions, not excluding CpGs, are shown in Table 1B, and for other cases in the Supplementary Material. Estimates from the REV model are ∼0.46 substitutions per site for medium-GC content, not excluding CpGs (Table 2B), and vary from 0.44–0.48 in the other cases, including cases in which CpGs are excluded and cases in which they are not (Supplementary Material). Overall, the substitution levels in AR are roughly similar to the 4D sites when CpGs are included, but show a generally higher number of transitions, are much less affected by the removal of CpGs, and show less asymmetry between human and mouse as well. Hence AR sites provide a different, and possibly better model of neutral evolution.

If we use a range of 65–105 Mya (million years ago) as an estimate for the origins of the eutherian orders, and the above estimates of 0.44–0.48 substitutions per site from the AR sites data, then we obtain estimates of the rate of neutral substitution in the range of 2.1–3.7 × 10⁻⁹ substitutions per year, averaged over both lineages, which includes most published estimates (Li et al. 1985; Kondrashov and Crow 1993; Kumar and Subramanian 2002).

Inference of Rate of Deletion

Analysis of the genome-wide alignments between human and mouse indicates that the majority of the nonaligning regions that are not identifiable as insertions of lineage-specific transposons represent deletions in the other species since divergence from their common ancestor (Waterston et al. 2002; see also Ogata et al. 1996). Thus, to measure regional variation in mouse-lineage deletion rate, we assume the human DNA not occupied by primate lineage-specific repeats represents the DNA that shares a common ancestor with mouse, and we use the nonaligning fraction of this DNA (NA_anc) as a rough estimate of the amount of DNA deleted from mouse. In the following sections, we discuss how this measure and the two measures of neutral substitution rate covary in the human genome.

Large-Scale Regional Variation and Covariation in Rates of Substitution

As noted above, significant variation in the level of sequence conservation between human and mouse from locus to locus has been reported in several studies of long DNA sequences of single loci (Hardison et al. 1991, 1997; Koop 1995; DeBry and Seldin 1996; Göttgens et al. 2001; Shiraishi et al. 2001; Wilson et al. 2001) and in comparative studies of gene sequences in these and other mammals (Wolfe et al. 1989; Bernardi 1993, 1995; Casane et al. 1997; Matassi et al. 1999; Williams and Hurst 2000; Lercher et al. 2001; Castresana 2002a,b), albeit with some dissenting analysis (Williams and Hurst 2000; Kumar and Subramanian 2002). With ∼700 4D sites/Mb and 50,000 AR sites/Mb genome-wide, we were able to do a much larger scale study of regional variation in rates of substitution, and found correlated fluctuations in regional substitution rates for both types of sites.

A series of 3038 5-Mb windows of human DNA was taken from the June 2002 assembly of the human genome with consecutive windows overlapped by 4 Mb. From the 4D sites in each window we estimated the quantity t_4D, the expected number of substitutions per 4D site in the evolution of human and mouse from their common ancestor, and from the AR sites the analogous quantity, t_AR. These estimates were made using the REV model of nucleotide evolution, using only data within the window. Windows with <800 4D sites were discarded. (Simulation experiments on 5000 replicates showed that this ensures that the standard deviations of the estimates of t_AR and t_4D will be <0.0338 and 0.0319, respectively.) This left 2504 windows for analysis, all of which had at least 800 4D sites and at least 4666 AR sites. The standard deviation of t_4D in this data set was 0.0702, compared with a sampling standard deviation of 0.0209, and the standard deviation of t_AR was 0.0187, compared with a sampling standard deviation of 0.0030, indicating that the observed regional variation cannot be explained from sample size effects. (The sampling deviations were computed using random replicates as above, chosen to have the same numbers of sites and base compositions as the actual data.) Even accounting for the smaller sampling deviation, the variation in t_AR is substantially less than that in t_4D.

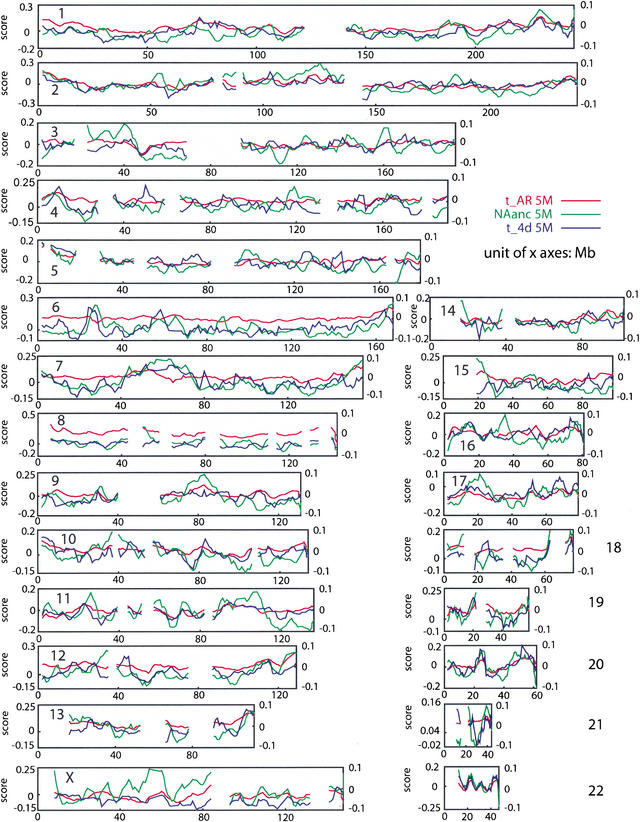
The above analysis was repeated with a set of 510 nonoverlapping 5-Mb windows, each with at least 800 4D sites, and with a set of 1430 nonoverlapping 1-Mb windows, each with at least 400 4D sites. The results also showed variance larger than can be explained from sample size effects. Genome-wide, using the nonoverlapping windows we found t_4D and t_AR to be very significantly correlated (r² = 0.26 for 5-Mb windows and 0.27 for 1-Mb windows), often showing quite similar behavior along a human chromosome, as well as correlation with deletion rate N_anc (see below), as shown in Figure 1 for all human chromosomes. This suggests that some regional chromosome property is leading to a variable rate of substitution in different parts of the chromosome.

Figure 1.

Variation in neutral substitution rates (t_AR and t_4D) and fraction not aligning (NA_anc, determined largely by deletions) for 22 autosomes and the X-chromosome. Values for these functions in windows of 5 Mb are plotted and shifted by 1 Mb between windows. After removing the quadratic effect of fraction GC for each variable, the residuals of t_AR are plotted as the red line (values on right vertical axis), of t_4D as the blue line, and of NA_anc as the green line (values for residuals of t_4D and NA_anc on left vertical axis). Only windows with at least 800 4D sites were used in the graphs for t_AR and t_4D, respectively, leading to the discontinuities in the lines, in addition to sequence gaps.

One possibility is that regional variation in GC content accounts for the covariation between t_4D and t_AR, so that this is entirely a function of isochore structure (Bernardi 1986, 2000; Hurst and Williams 2000; Eyre-Walker and Hurst 2001). This is explored in detail below, in a combined analysis that also includes the other measures of divergence that we examine. We factor out the effects of GC content by computing residuals of a quadratic regression of t_4D and t_AR on GC content, and then compute the correlation between the residuals. The resulting residuals are plotted for 5-Mb overlapping windows along all the human chromosomes in Figure 1. By factoring out GC content in this way, the genome-wide correlation between t_4D and t_AR is actually enhanced (r² jumps from ∼0.22 to 0.33 for overlapping 5-Mb windows, and similarly for nonoverlapping 5-Mb windows; see Figure 4B below), indicating that GC content does not fully explain this correlation, and other factors must also be at work (Waterston et al. 2002).

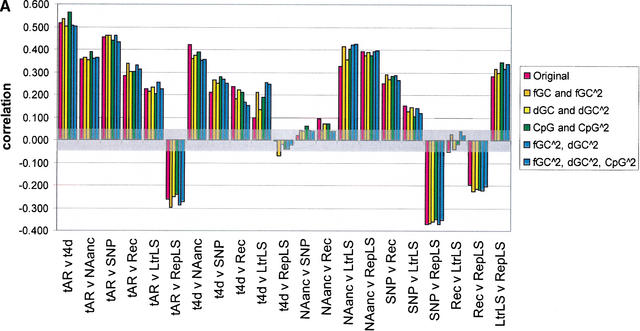
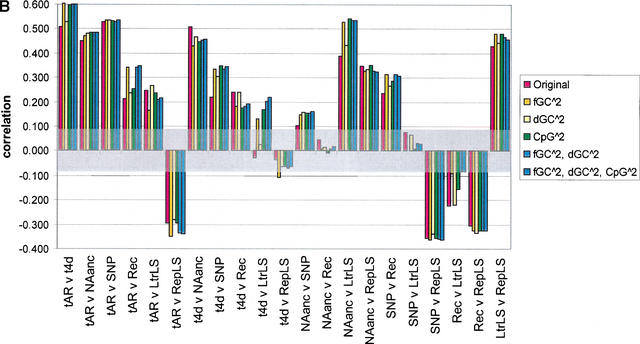
Figure 4.

Pairwise correlations for various divergence measures, before and after correcting for the effect of GC content, difference in GC content between human and mouse, and CpG density in human. The seven divergence measures are neutral substitution rates in ancestral repeats (t_AR, noted as tAR in the graph) and 4D sites (t_4D, noted as t4d in the graph), deletion proxied by NA_anc, SNP density, recombination rate (Rec), and insertion proxied by density of lineage specific LTR repeats (LtrLS) and density of lineage-specific repeats in general (RepLS). Correlations are plotted as bars for (1) original divergence measures (in red); (2) residuals from quadratic regressions on GC content (the regression terms are a constant intercept, fGC and fGC squared) (in gold, noted in the key as fGC^∧2); (3) residuals from quadratic regressions on change in GC content between human and mouse (the regression terms are a constant intercept, dGC and dGC squared) (in yellow, noted in the key as dGC^∧2); (4) residuals from quadratic regressions on CpG density (the regression terms are a constant intercept, CpG density and CpG density squared) (in green, noted in the key as CpG^∧2); (5) residuals from quadratic regressions on GC content and difference in GC content between human and mouse (the regression terms are a constant intercept, fGC, fGC squared, dGC, and dGC squared) (in lighter blue, noted in the key as fGC^∧2, dGC^∧2); and (6) residuals from quadratic regressions on GC content, difference in GC content between human and mouse, and CpG density in humans (in darker blue, noted in the key as fGC^∧2, dGC^∧2, CpG^∧2) (A) The results for 1-Mb nonoverlapping windows; (B) the results for 5-Mb nonoverlapping windows. A transparent gray rectangle encompasses correlations for which the p-values fall above 0.050 (i.e., a correlation that is not significant at the 5% Type-I error level).

It has been noted that rates of nonsynonymous and synonymous changes in genes are correlated (Graur 1985; Li et al. 1985; Ticher and Graur 1989; Lercher et al. 2001). Correlations between rates in coding regions and rates in introns have also been observed in some studies (Castresana 2002b) but not in others (Hughes and Yeager 1998) (see critique in Smith and Hurst 1998). Correlations between rates in coding regions and UTR regions have also been observed (Makalowski and Boguski 1998b). We find that regional variation in substitution rates in AR sites is also significantly correlated with variation in sites in and around genes.

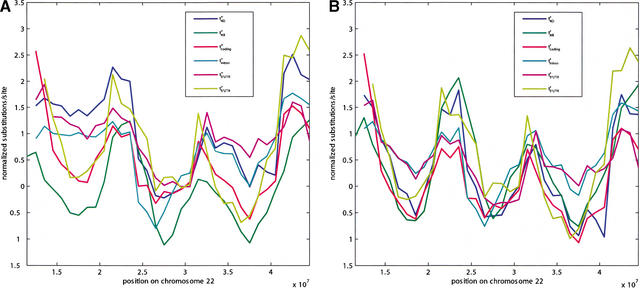
Specifically, using the REV model as above, let t_intron, t_coding, t_5′UTR and t_3′UTR be the estimated number of substitutions per site in aligned positions from a given window from sites in intron, coding exons, 5′-UTR and 3′-UTR regions, respectively. (AR sites are excluded from introns in this calculation.) Let dN, dS, and dN/dS be the rates of nonsynonymous substitutions per nonsynonymous site, synonymous substitutions per synonymous site, and their ratio, computed by the method of Goldman and Yang (1994), also described as the ML method of Yang and Nielsen (2000), using the PAML software package of Yang (1997). These quantities are computed from the same set of human RefSeq genes used to collect 4D sites. We computed the correlation between t_AR and each of these gene-feature substitution rates, measured in a set of 510 nonoverlapping 5-Mb windows, and found significant (p < 0.001) but not always large correlation with all of them except dN and dN/dS (r² = 0.44 for t_intron, 0.06 for t_coding, 0.06 for t_5′UTR, 0.05 for t_3′UTR, 0.003 for dN, 0.15 for dS, and 0.03 for dN/dS). Correlations with t_4D were higher (r² = 0.46 for t_intron, 0.43 for t_coding, 0.18 for t_5′UTR, 0.34 for t_3′UTR, 0.07 for dN, 0.86 for dS, and 0.03 for dN/dS), and significant with P < 0.001 for all but dN/dS. Similar results were obtained for 1-Mb windows. Figure 2A shows how t_intron, t_coding, t_5′UTR and t_3′UTR vary with t_AR and t_4D along human Chromosome 22 for overlapping 5-Mb windows. As above, the correlations are also present after factoring of GC content (Fig. 2B). The experiments were repeated removing CpG sites from the calculation of all quantities except dN and dS, and the results were very similar (data not shown). These data indicate that substitutions in all sites in and around genes, with the possible exception of nonsynomous substitutions in nonsynonymous sites, are affected by the same conditions that cause regional covariation in t_4D and t_AR substitution rates.

Figure 2.

Variation in t_4D, t_AR, t_intron, t_coding, t_3′UTR, and t_5′UTR along human Chromosome 22 (A) and residuals of t_4D, t_AR, t_intron, t_coding, t_3′UTR, and t_5′UTR after quadratic regressions on human CG content along human Chromosome 22 (B). All values were calculated from 5-Mb overlapping by 4-Mb windows of the human–mouse alignment and were normalized using the genome-wide mean and standard deviation (denoted by superscript + in A and * in B). The normalization was done to ensure that all values have the same dynamic range.

Covariation of Rates of Substitution With Rates of Deletion and Density of Lineage-Specific Transposable Elements

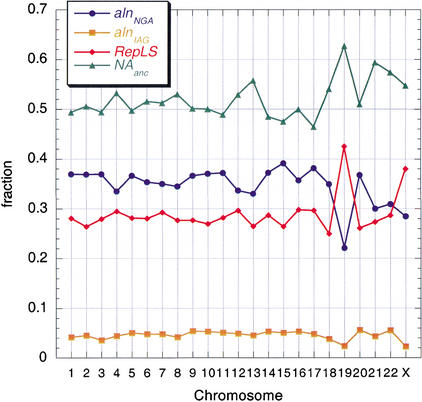
The fraction of human DNA aligning with mouse varies among chromosomes (Fig. 3). The portion of human DNA that is nonrepetitive or in ancestral repeats (i.e., non-lineage-specific repeats) is the DNA that is likely derived from the common ancestor to human and mouse, and hence it is the portion that could align with mouse. As discussed above, the fraction of the human genome derived from the common ancestor that does not align with mouse (NA_anc) is an estimate of the amount of DNA deleted from the mouse lineage. This function also varies among chromosomes (Fig. 3). One extreme is illustrated by Chromosome 19, which has the smallest fraction aligning, the largest fraction of lineage-specific repeats, and a substantial amount inferred as deleted. In contrast, Chromosome 20 is about the same size but has a substantial fraction aligning, a roughly average fraction of repeats, and one of the smaller amounts of inferred deletion.

Figure 3.

Variation in the fraction aligning with mouse, lineage-specific repeats and inferred deletions in mouse for the human chromosomes. For each human autosome and the X-chromosome, the amount of sequence aligned with mouse was computed. The aligning DNA was separated into two categories; the fraction of sequenced bases in alignments not including gaps (i.e., matches and mismatches) is plotted in blue (aln_NGA), and the fraction of bases in gaps within alignments is plotted in orange (aln_IAG). The fraction of sequenced bases on each chromosome in lineage-specific repeats (RepLS) is plotted in red. The sequenced bases not in lineage-specific repeats (i.e., nonrepetitive DNA plus ancestral repeats) are considered the DNA derived from the last common ancestor to mouse and human; these are the bases potentially able to align with mouse. The fraction of the nonrepetitive DNA plus ancestral repeats in each chromosome that does not align with mouse is plotted in green (NA_anc). This measure is likely dominated by deletions in mouse.

When measured in the same 5-Mb overlapping windows as above, the estimate of amount of DNA deleted in mouse, NA_anc, varies widely across the genome, and it tends to covary with both measures of substitutions per neutral site (Fig. 1). This graph shows the variation in NA_anc, t_4D, and t_AR after factoring out the effect of GC content, as discussed below. The pairwise correlations among the three divergence measures are positive and highly significant (p < 0.001), whether measured in nonoverlapping windows of 1 Mb (Fig. 4A) or 5 Mb (Fig. 4B). Thus the rate of nucleotide substitution at two different types of neutral sites and NA_anc covary in large regions of DNA. Some part of this effect could be explained by an ascertainment bias, because ancestral DNA in the faster-evolving regions will be harder to align. However, as discussed above, it is likely that a substantial portion of the nonaligning DNA reflects deletions. To the extent that NA_anc reflects deletions, these data demonstrate a correlation between neutral substitutions and deletions.

The relationship of these divergence measures with the frequency of insertion of transposable elements was then examined, using the proportion of DNA in a window composed of lineage-specific repeats (RepLS) as an estimate of the frequency of insertion and retention of transposons. This function has a strong positive correlation with NA_anc, but a negative correlation with t_AR and no correlation with t_4D (for the original data) at all window sizes and configurations tested (Fig. 4). Thus the frequency of insertions of several families of retrotransposons covaries with the inferred deletion rate, but the relationships with substitution rates are complex. The type of correlation observed with any measure of divergence depends to some extent on the particular families and ages of repeats included in the comparison. For example, in contrast to the correlations seen for RepLS, if the analysis is confined to the density of lineage-specific LTRs (LtrLS), a significant positive correlation is observed with all three measures of divergence in most window configurations (Fig. 4). A full examination of the correlations with different families of repeats will be the subject of other studies.

The positive correlation between NA_anc and RepLS was confirmed by a randomization study using methods described in Chiaromonte et al. (2001). The positions of interspersed repeats were randomized independently 100 times, while keeping the alignment constant. None of the randomized data sets showed a correlation as strong as the overall data, giving an empirical P-value < 0.01. Local correlations were also computed at the 10-kb scale, both for the original data and for the 100 randomized data sets. The distribution of local correlations is plotted in Figure 5, along with envelopes derived from the randomizations. In comparison with the “null” scenario represented by these envelopes, the histogram of the actual data shows a significant concentration on large positive values, demonstrating that covariation between deletion and insertion can be detected also at much smaller scales on individual chromosomes. Similar results (data not shown) were obtained for all chromosomes and various window sizes.

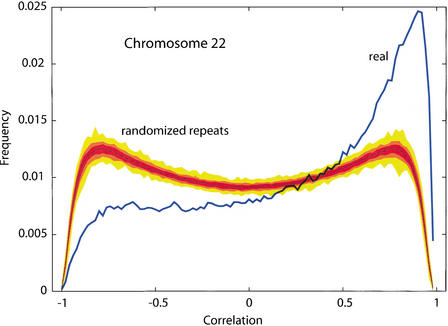
Figure 5.

Segments of DNA that accumulate many repetitive elements also have less nonrepetitive, noncoding DNA that aligns with mouse. The correlation between NA_anc and density of lineage-specific interspersed repeats (RepLS) was measured for human Chromosome 22, using 10-kb overlapping windows with 1-base increments. The overall correlation is r = 0.3353. An empirical P-value was evaluated by performing 100 independent randomizations of the positions of the repeats, while keeping the alignments constant. Local correlations were also computed in the 10-kb sliding windows, for the original data and the 100 randomizations. The blue line represents the histogram of local correlations on the original data, whereas the frequencies of local correlations from the 100 randomizations are summarized by their median curve (dotted line) and envelopes of different shades of brown (50% darkest, 80% lighter, and 100% lightest).

Covariation With the Frequency of Polymorphisms in Human

We also examined the density of single-nucleotide polymorphisms, as compiled by The SNP Consortium (Sachidanandam et al. 2001), for association with these divergence measures, and again obtained strong positive correlations (Fig. 4). An exception is NA_anc, which shows no correlation with SNP density at 1-Mb windows, but does at 5-Mb windows, perhaps reflecting the greater amount of data in each window. Thus the frequency of nucleotide substitutions accumulating recently in human populations correlates with several measures of divergence between human and mouse. This can be explained by regional variation in substitution rates, both recently (SNPs) and long-term (human–mouse divergence).

Covariation With Recombination Rate in Human

Correlations of human meiotic recombination rates (Kong et al. 2002) are positive with divergence at neutral sites and density of human polymorphisms (Fig. 4), and are significant. The correlation between recombination rate and NA_anc is significant with 1-Mb windows but not with 5-Mb windows (Fig. 4). We also note that the high-density genetic map of Chromosome 22 (Dawson et al. 2002) shows regions of high linkage disequilibrium (low recombination) that correspond to the regions of low divergence and lower inferred deletions. In contrast, a negative correlation is seen for recombination rate and frequency of insertions of lineage-specific repeats, both for all families and also for the lineage-specific LTRs (Fig. 4).

GC Content Correlates With Variation in Conservation, But in Opposite Ways for Low-GC and Moderate- to High-GC DNA, and Does Not Fully Explain the Variation

The physical and biological properties of genomic DNA may be strong contributors to the variation in conservation, but some previous studies have led to differing conclusions. For instance, some of the studies cited above have found regional variation in substitution rates to be significantly correlated with fluctuations in the G + C content of the aligned human bases, or with the difference between G + C content in the aligned human and mouse bases (Castresana 2002a), whereas others have not found significant correlations (see discussion in Hurst and Williams 2000). The whole-genome alignments provide an opportunity to carry out a more comprehensive analysis.

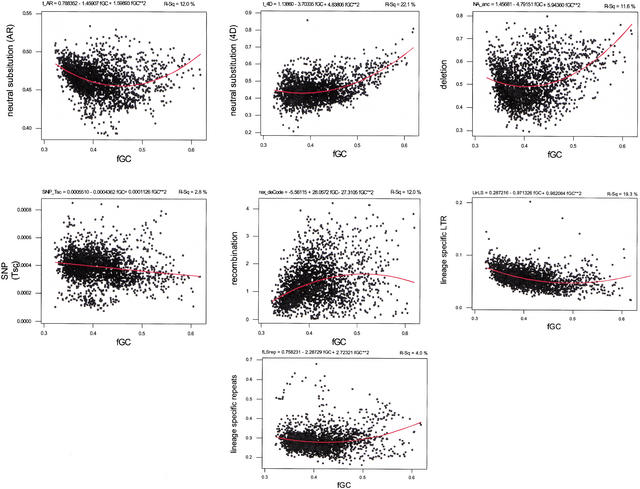
The relationship of t_AR and t_4D with GC content (fraction GC, or fGC) is not linear, but is better fit by a quadratic relationship (Hurst and Williams 2000; Waterston et al. 2002; see also Bernardi 2001). Indeed, substitutions, NA_anc, RepLS, and LtrLS all show a quadratic relationship when plotted against GC content (Fig. 6). The divergence tends to decrease with fGC for the portion of the genome with a lower GC content, whereas the divergence tends to increase with fGC for the portion of the genome that is higher in GC content. These data can be fit to a quadratic expression, with a negative coefficient for fGC but a positive coefficient for the square of fGC. The quadratic fits for t_4D, t_AR, NA_anc, and LtrLS on fGC have r² of 24.0%, 11.0%, 10.2%, and 18.7%, respectively, for 5-Mb nonoverlapping windows. This implies that fluctuations in GC content predict an appreciable amount of the regional variation we see in neutral substitution rates and deletions, but still leaves the majority of this variation to be explained, because there is little sampling variance in the rates estimated in these large windows. The dependence of recombination rate on fGC is also fit by a quadratic function, but the curvature is opposite to that seen for substitutions and NA_anc (Fig. 6).

Figure 6.

Quadratic fits on GC content for two measures of neutral substitution (t_AR and t_4D), a proxy for deletion (NA_anc), polymorphisms (SNP_tsc), recombination rate, and two measures of insertion of lineage-specific repeats in human (LtrLS and RepLS).

Next, we considered change in GC content between human and mouse (dGC, expressed as the difference between human GC and mouse GC in aligning segments in the windows) as an additional predictor as well as CpG density. Fitting expressions comprising fGC, dGC, and their squares, we obtain significant gains in explained variability for some but not all functions. Combining second-order effects of fGC and dGC, we can predict 29.9% of the variation in t_4D, whereas the explained variation in t_AR and NA_anc increase only slightly, to 12.8% and 10.4%, respectively. Another potential predictor is the density of CpG dinucleotides. However, adding second-order effects of the CpG density to those of fGC and dGC increased the explained variation very little, to 30.8%, 13.0%, and 11.6% for t_4D, t_AR, and NA_anc, respectively. Summary statistics for all three predictors, and for all measures of divergence are given in Table 3.

Table 3.

Descriptive Statistics for Measures of Divergence, Interspersed Repeat Densities, SNP Densities, Recombination Rates, GC Content, and Change in GC Content

Variable	Minimum	Maximum	Mean	Median	SD
tAR	0.39111	0.53377	0.46317	0.46389	0.01929
t4D	0.20867	0.85917	0.44608	0.43759	0.06628
NAanc	0.29468	0.80029	0.50696	0.49322	0.08460
SNP	0.00008	0.00085	0.00039	0.00039	0.00010
Rec	0.0280	4.2156	1.2773	1.1376	0.6954
LtrLS	0.01581	0.20228	0.05671	0.05544	0.01577
RepLS	0.16229	0.68071	0.28538	0.27807	0.05284
fGC	0.32202	0.61873	0.40956	0.39808	0.05121
dGC	−0.06588	0.08245	−0.01127	−0.01346	0.01985
CpG density	0.00019	0.08102	0.00787	0.00544	0.00798

Data are the 2489 windows of 5 Mb (overlapping by 4 Mb). Windows were filtered so that they contained at least 800 4D and AR sites and well-defined values for the other attributes.

As discussed in the analysis of the mouse genome (Waterston et al. 2002), because all divergence measures are predicted to some extent by GC content, the latter constitutes a confounding variable in evaluating their covariation. The predictors dGC and CpG density may have a similar effect. To account for this, pairwise correlations were computed not just among divergence variables, but also among residuals from their quadratic regressions on fGC, dGC, and the density of CpG dinucleotides. In most cases, passing to residuals enhanced the observed correlations (Fig. 4). This effect was dramatic in some cases, such as the correlation t_4D with LtrLS. The fact that correlations are significant and often enhanced after removing the effect of fGC, dGC, and CpG density confirms that additional factors beyond GC and CpG content are needed to explain the covariation among divergence variables.

DISCUSSION

These results show that six measures of change in chromosomal DNA vary regionally in their rates, and those rates covary. Thus substitutions, deletions, insertions, and recombinations are all correlated, and changes occurring over ∼65–90 million years (Li et al. 1985; Kondrashov and Crow 1993; Archibald et al. 2001; Huchon et al. 2002) correlate with polymorphisms arising much more recently in the human populations. These results indicate that some regions of the human genome are changing slowly by all processes that alter DNA, whereas others change faster. Because of this, it is challenging to develop a single criterion for likely selection that will be effective when applied to all regions of the genome; a simple similarity cutoff will not work well globally (Hardison 2000; Pennachio and Rubin 2001).

The regional variation in rates of divergence is partially predicted by human GC content. The relationship with GC content is complex and best fit by a quadratic function. The divergence decreases with GC content for low-GC DNA and increases with GC content for higher-GC DNA, consistent with important differences in the patterns of evolution in these two classes of genomic DNA (Bernardi 1995, 2001; Fullerton et al. 2001; Castresana 2002a).

GC content is an explanatory variable in the sense that it allows one to predict a certain portion of the variability of each divergence measure. This raised the possibility that the divergence measures vary together simply because they all vary with GC content. We show that this is not the case, because removing the components explained by GC content enhances, instead of suppressing, the covariation. Thus in some ways GC content is a confounding variable in this type of analysis.

It has been suggested that disruption of isochores in the mouse lineage has been associated with rapid divergence in some regions of the genome (Castresana 2002a). However, introducing change in GC content as an additional predictor after GC content still does not explain most of the variation in the measures of divergence examined. A similar effect is seen for CpG density. Removing the components explained by GC content, difference in GC content between human and mouse, and CpG density preserves or enhances covariation.

It has been proposed that slowly changing genomic regions are under stronger selection (Shabalina et al. 2001), but purifying selection is unlikely to explain fully the variation in divergence described here. The regions examined are very large (5 Mb), so a substantial fraction of those regions would have to be functional for direct selection to act on them. Substitutions have been measured not only at 4D sites in coding regions but also in ancestral repeats. The latter are good models for neutral DNA, and it is particularly difficult to imagine how selection could be working on defunct transposable elements. Lower levels of polymorphism in regions of higher recombination have been explained by background selection against deleterious mutations also removing linked polymorphisms (Begun and Aquadro 1992; Charlesworth 1994; Hudson and Kaplan 1995), but it is not clear that this effect, or genetic hitchhiking (Maynard Smith and Haigh 1974) can be extended to divergence between mouse and human. Rather, it appears that some property of genomic DNA, or its location, makes it a more or less active template for several aspects of DNA metabolism. Regional variation in rates of mutation would be expected to lead to variation in rates of substitutions in AR, 4D, intron, UTR, and other types of sites, and to significant correlations between those substitutions rates, as we observe.

The correlation of neutral substitution with recombination frequency, insertion rate, and deletion rate points to a class of potential explanations for the variation in divergence involving regional variations in frequency of double-stranded breaks, which may be prone to faulty repair (Lercher and Hurst 2002). Other effects associated with differences in DNA repair could also be responsible for regional variation in divergence, as briefly reviewed by Matassi et al. (1999). Through these or other repair or mutation mechanisms, the proximity of a DNA sequence to segments involved in some aspects of nuclear metabolism could also affect their underlying rate of divergence. We have no evidence that proximity to particular types of transcription units can explain the fluctuations we see and, as discussed by Eyre-Walker and Hurst (2001), the relationship between GC content, neutral substitution rate, and differences in the timing of replication in S-phase (Wolfe 1991; Gu and Li 1994) are potentially quite complex and cannot be resolved with this type of data. However, future examination of intranuclear localization, including proximity to matrix attachment sites, pericentromeric heterochromatin, the nuclear membrane, and sites of chiasmata during meiosis may show significant correlations with divergence.

Bioinformatics Resources

The source code for BLASTZ is available at http://bio.cse.psu.edu. Precomputed percent identity plots (pip) of all alignments are available at the PipDispenser (http://bio.cse.psu.edu). Entering either a location in the human genome or a RefSeq gene name will return a pip of the 1-Mb interval including the query. Aligning regions, measures of level of conservation, and nucleotide-level alignment are available from the UCSC Human Genome Browser (http://genome.ucsc.edu; Kent et al. 2002), using the Mouse Cons track.

METHODS

Generating Whole-Genome Alignments Using BLASTZ

The program BLASTZ was used to align the human and mouse genome assemblies on a 1024-node Pentium III cluster, as described by Schwartz et al. (2003) and the MGSC (Waterston et al. 2003). The alignments were processed to get single coverage of human sequences with mouse sequences using the program axtBest (Schwartz et al. 2003). The human assembly from June 2002 was aligned to the February 2002 assembly of mouse.

Measurements of Divergence, Recombination, and Polymorphisms

The function t_AR was calculated as the number of substitutions per site in ancestral repeats, determined by the REV model on the observed base changes in ancestral repeats. The function t_4D was calculated as the number of substitutions per site in fourfold degenerate sites that were preceded by matches in the other two positions of the codon, determined by the REV model on the observed base changes at these sites. (An alternate definition that did not require the 4D site to be preceded by two matches produced similar data with slightly higher divergence; see Supplementary Material). When searching for 4D sites, the RefSeq (Pruitt and Maglott 2001) alignments to the human genome were used and checked to ensure that the human CDS begins with a start codon, ends with a stop codon, and has no in-frame stop codons; human introns are GT/AG, GC/AG, or AT/AC; aligned mouse sequence has no in-frame stop codons except in the last 20 codons of the human gene.

The portion of the human genome derived from the common ancestor to mouse and human (the “ancestral part of the genome”) is approximately the portion of the genome not in lineage-specific repeats. This part of the human genome was identified by analyzing the output of the program RepeatMasker (Smit and Green 1999). Lineage-specific repeats are those that are not ancestral. The fraction of this ancestral part of the genome that aligns (aln_anc) was calculated as the number of aligned bases (disregarding intra-alignment gaps) in DNA that is not lineage-specific repeats divided by the amount of non-lineage-specific repetitive DNA in each window. The nonaligning portion (NA_anc) is 1 − aln_anc, and is our estimate of the fraction of the human genome likely deleted from mouse.

The frequency of insertions was monitored as the density of all lineage-specific repeats again analyzing output from RepeatMasker (Smit and Green 1999). The frequency of particular families of repeats was also determined, and broken down into ancestral and lineage-specific subfamilies.

Recombination data were from Kong et al. (2002). The markers were mapped onto the June 2002 assembly of the human genome, and recombination frequencies were determined from the genetic distances reported and the measured physical distances from the assemblies. Each base is assigned the recombination rate calculated by assuming a linear genetic distance across the immediately flanking genetic markers. The recombination rate assigned to each 1-Mb window is the average recombination rate of the bases contained within the window. These regional estimates substantially agree with those obtained by the spline method of Kong et al. (2002).

SNP density was computed using the tables of SNPs from the SNP Consortium (Sachidanandam et al. 2001) for SNPs derived from random reads.

Analysis of Covariation and Predictive Variables

We considered data relative to the 5-Mb windows (overlapping by 4 Mb), again filtered so as to contain at least 800 4D sites, and required to have a defined recombination measurement. Data were also computed for nonoverlapping 1-Mb and 5-Mb windows. Covariation among different measures of divergence was assessed through pairwise correlation coefficients. As discussed above, these were computed on the original variables, as well as on residuals from various regressions, in order to remove GC-related effects. In particular, for each divergence measure, we considered residuals from five second-order regressions, namely, (1) quadratic regression on GC content (comprising intercept, fGC, and fGC squared); (2) quadratic regression on difference in GC content between human and mouse (comprising intercept, dGC, and dGC squared); (3) quadratic regression on CpG density in human (comprising intercept, CpG density and CpG density squared, dGC and dGC squared); (4) quadratic regression on GC content and difference in GC content between human and mouse, without interaction (comprising intercept, fGC, fGC squared, dGC, and dGC squared); and (5) quadratic regression on GC content, difference in GC content between human and mouse, and human CpG density, without interaction (comprising intercept, fGC, fGC squared, dGC, dGC squared, CpG density, and CpG density squared). Inclusion of interaction terms between the variables did not improve the correlations (data not shown). Correlation computations and regression fits were implemented using the MINITAB software package (Ryan and Joiner 2000).

Methods for Calculating Genomic Parameters

The tables at the UCSC Genome Browser (Kent et al. 2002) were used to compute most genomic parameters. Data for repeats (all classes) came from RepeatMasker (Smit and Green 1999). GC content was computed from the human sequence using aligned bases only. The change in GC content is the fraction GC for human in alignments in a window minus the fraction GC for mouse in alignments in a window.

WEB SITE REFERENCES

http://bio.cse.psu.edu; PipDispenser and source code for BLASTZ.

http://genome.ucsc.edu; UCSC Human Genome Browser.

http://www.soe.ucsc.edu/research/compbio/covariation/; frequency tables.