False Discovery Control in Large-Scale Spatial Multiple Testing

Summary

This article develops a unified theoretical and computational framework for false discovery control in multiple testing of spatial signals. We consider both point-wise and cluster-wise spatial analyses, and derive oracle procedures which optimally control the false discovery rate, false discovery exceedance and false cluster rate, respectively. A data-driven finite approximation strategy is developed to mimic the oracle procedures on a continuous spatial domain. Our multiple testing procedures are asymptotically valid and can be effectively implemented using Bayesian computational algorithms for analysis of large spatial data sets. Numerical results show that the proposed procedures lead to more accurate error control and better power performance than conventional methods. We demonstrate our methods for analyzing the time trends in tropospheric ozone in eastern US.

1. Introduction

Let X = {X(s) : s ∈ S} be a random field on a spatial domain S:

$$X(s)=\mu (s)+\epsilon (s),$$ (1.1)

where μ(s) is the unobserved random process and ε(s) is the noise process. Assume that there is an underlying state θ(s) associated with each location s with one state being dominant (“background”). In applications, an important goal is to identify locations that exhibit significant deviations from background. This involves conducting a large number of spatially correlated tests simultaneously. It is desirable to maintain good power for detecting true signals while guarding against too many false positive findings. The false discovery rate (FDR, Benjamini and Hochberg, 1995) approach is particularly useful as an exploratory tool to achieve these two goals and has received much attention in the literature. In a spatial setting, the multiple comparison issue has been raised in a wide range of problems such as brain imaging (Genovese et al., 2002; Heller et al., 2006; Schwartzman et al., 2008), disease mapping (Green and Richardson, 2002), public health surveillance (Caldas de Castro and Singer, 2006), network analysis of genome-wide association studies (Wei and Li, 2007; Chen et al., 2011), and astronomical surveys (Miller et al., 2007; Meinshausen et al., 2009).

Consider the following example for analyzing time trends in tropospheric ozone in the Eastern US. Ozone is one of the six criteria pollutants regulated by the US EPA under the Clean Air Act and has been linked with several adverse health effects. The EPA has established a network of monitors for regulation of ozone, as shown in Figure 1a. We are interested in identifying locations with abrupt changing ozone levels using the ozone concentration data collected at monitoring stations. In particular, we wish to study the ozone process for predefined sub-regions, such as counties or states, to identify interesting sub-regions. Similar problems may arise from disease mapping problems in epidemiology, where the goal is to identify geographical area with elevated disease incidence rates. It is also desirable to take into account region specific variables, such as the population in or the area of a county, to reflect the relative importance of each sub-region.

Fig. 1.

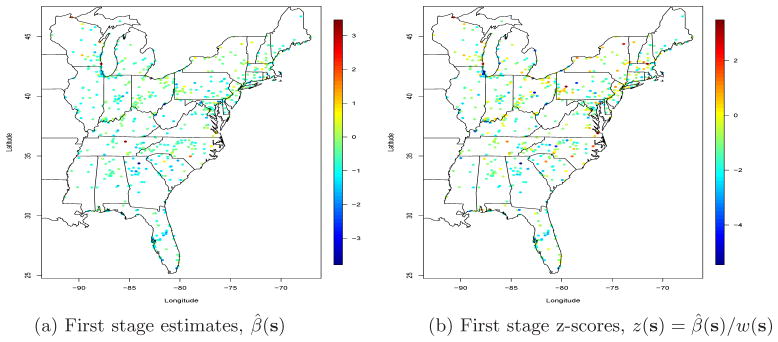
OLS analysis of ozone data, conducted separately at each site.

Spatial multiple testing poses new challenges which are not present in conventional multiple testing problems. Firstly, one only observes data points at a discrete subset of the locations but often needs to make inference everywhere in the spatial domain. It is thus necessary to develop a testing procedure which effectively exploits the spatial correlation and pools information from nearby locations. Secondly, a finite approximation strategy is needed for inference in a continuous spatial domain – otherwise an uncountable number of tests needs to be conducted, which is impossible in practice. Thirdly, it is challenging to address the strong dependency in a two or higher dimensional random field. Finally, in many important applications, it is desirable to aggregate information from nearby locations to make cluster-wise inference, and to incorporate important spatial variables in the decision-making process. The goal of the present paper is to develop a unified theoretical and computational framework to address these challenges.

The impact of dependence has been extensively studied in the multiple testing literature. Efron (2007) and Schwartzman and Lin (2011) show that correlation usually degrades statistical accuracy, affecting both estimation and testing. High correlation also results in high variability of testing results and hence the irreproducibility of scientific findings; see Owen (2005), Finner et al. (2007) and Heller (2010) for related discussions. Meanwhile, it has been shown that the classical Benjamini-Hochberg (BH) procedure is valid for controlling the false discovery rate (FDR, Benjamini and Hochberg, 1995) under different dependency assumptions, indicating that it is safe to apply conventional methods as if the tests were independent (see Benjamini and Yekutieli, 2001; Sarkar, 2002; Wu, 2008; Clarke and Hall, 2009; among others). Another important research direction in multiple testing is the optimality issue under dependency. Sun and Cai (2009) introduced an asymptotically optimal FDR procedure for testing hypotheses arising from a hidden Markov model (HMM) and showed that the HMM dependency can be exploited to improve the existing p-value based procedures. This demonstrates that informative dependence structure promises to increase the precision of inference. For example, in genome-wide association studies, signals from individual markers are weak, hence a number of approaches have been developed to increase statistical power by aggregating multiple markers and exploiting the high correlation among adjacent loci (e.g., see Peng et al., 2009; Wei et al., 2009; Chen et al., 2011). When the intensities of signals have a spatial pattern, it is expected that incorporating the underlying dependency structure can significantly improve the power and accuracy of conventional methods. This intuition is supported both theoretically and numerically in our work.

In this article, we develop a compound decision theoretic framework for spatial multiple testing and propose a class of asymptotically optimal data-driven procedures that control the FDR, false discovery exceedance (FDX) and false cluster rate (FCR), respectively. The widely used Bayesian modeling framework and computational algorithms are adopted to effectively extract information from large spatial datasets. We discuss how to summarize the fitted spatial models using posterior sampling to address related multiple testing problems. The control of the FDX and FCR is quite challenging from the classical perspective. We show that the FDR, FDX and FCR controlling problems can be solved in a unified theoretical and computational framework. A finite approximation strategy for inference on a continuous spatial domain is developed and it is shown that a continuous decision process can be described, within a small margin of error, by a finite number of decisions on a grid of pixels. This overcomes the limitation of conventional methods which can only test hypotheses on a discrete set of locations where observations are available. Simulation studies are carried out to investigate the numerical properties of the proposed methods. The results show that by exploiting the spatial dependency, the data-driven procedures lead to better rankings of hypotheses, more accurate error control and enhanced power.

The proposed methods are developed in a frequentist framework and aims to control the frequentist FDR. The Bayesian computational framework, which involves hierarchical modeling and MCMC computing, provides a powerful tool to implement the data-driven procedures. When the goal is to control the FDR and tests are independent, our procedure coincides with the Bayesian FDR approach originally proposed by Newton et al. (2004). Müller et al. (2004) and Müller et al. (2007) showed that controlling the Bayesian FDR implies FDR control. However, those type of results do not immediately extend to correlated tests (see Remark 4 in Pacifico et al. (2004) and Guindani et al. (2009)). In addition, existing literature on Bayesian FDR analysis (Müller et al., 2004, 2007 and Bogdan et al., 2008) has focused on the point-wise FDR control only, and the issues related to FDX and FCR have not been discussed. In contrast, we develop a unified theoretical framework and propose testing procedures for controlling different error rates. The methods are attractive by providing effective control of the widely used frequentist FDR.

The article is organized as follows. Section 2 introduces appropriate false discovery measures in a spatial setting. Section 3 presents a decision theoretic framework to characterize the optimal decision rule. In Section 4, we propose data-driven procedures and discuss the computational algorithms for implementation. Sections 5 and 6 investigate the numerical properties of the proposed procedures using both simulated and real data. The proofs and technical details in computation are given in the Appendix.

2. False Discovery Measures for Spatial Multiple Testing

In this section we introduce some notation and important false discovery measures in a random field, following the works of Pacifico et al. (2004) and Benjamini and Heller (2007). Both point-wise analysis and cluster-wise analysis will be considered.

2.1. Point-wise inference

Suppose for each location s, we are interested in testing the hypothesis

$$H_0(s):\mu (s)\in A\text{versus}{H}_1(s):\mu (s)\in A^c,$$ (2.1)

where A is the indifference region, e.g. A = {μ : μ ≤ μ₀} for a one-sided test and A = {μ : |μ| ≤ μ₀} for a two-sided test. Let θ(s) ∈ {0, 1} be an indicator such that θ (s) = 1 if μ(s) ∈ A^c and θ(s) = 0 otherwise. Define S₀ = {s ∈ S : θ(s) = 0} and S₁ = {s ∈ S : θ(s) = 1} as the null and non-null areas, respectively. In a point-wise analysis, a decision δ(s) is made for each location s. Let δ(s) = 1 if H₀(s) is rejected and δ(s) = 0 otherwise. The decision rule for the whole spatial domain S is denoted by δ = {δ(s) : s ∈ S}. Then R = {s ∈ S : δ(s) = 1} is the rejection area, and S_FP = {s ∈ S : θ(s) = 0, δ(s) = 1} and S_FN = {s ∈ S : δ(s) = 1, δ(s) = 0} are the false positive and false negative areas, respectively. Let ν(·) denote a measure on S, where ν(·) is the Lebesgue measure if S is continuous and a counting measure if S is discrete. When the interest is to test hypotheses at individual locations, it is natural to control the false discovery rate (FDR, Benjamini and Hochberg, 1995), a powerful and widely used error measure in large-scale testing problems. Let c₀ be a small positive value. In practice if the rejection area is too small, then we can proceed as if no rejection is made. Define the false discovery proportion as

$$\text{FDP}=\frac{\nu (S_{\text{FP}})}{\nu (R)}I\{\nu (R)>c_0\}.$$ (2.2)

The FDR is the expected value of the FDP: FDR = E(FDP). Alternative measures to the FDR include the marginal FDR, mFDR = E{ν(S_FP)}/E{ν(R)}(Genovese and Wasserman, 2002) and positive FDR (pFDR, Storey, 2002).

The FDP is highly variable under strong dependence (Finner and Roters, 2002; Finner et al., 2007; Heller, 2010). The false discovery exceedance (FDX), discussed in Pacifico et al. (2004), Lehmann and Romano (2005), and Genovese and Wasserman (2006), is a useful alternative to the FDR. FDX control takes into account the variability of the FDP, and is desirable in a spatial setting where the tests are highly correlated. Let 0 ≤ t ≤ 1 be a pre-specified tolerance level, the FDX at level τ is FDX_τ = P(FDP > t), the tail probability that the FDP exceeds a given bound.

To evaluate the power of a multiple testing procedure, we use the missed discovery rate MDR = E{ν(S_FN)}. Other power measures include the false non-discovery rate and average power; our result can be extended to these measures without essential difficulty. A multiple testing procedure is said to be valid if the FDR can be controlled at the nominal level and optimal if it has the smallest MDR among all valid testing procedures.

2.2. Cluster-wise inference

When the interest is on the behavior of a process over sub-regions, the testing units become spatial clusters instead of individual locations. Combining hypotheses over a set of locations naturally reduces multiplicity and correlation. In addition, set-wise analysis improves statistical power as data in a set may show an increased signal to noise ratio (Benjamini and Heller, 2007). The idea of set-wise/cluster-wise inference has been successfully applied in many scientific fields including large epidemiological surveys (Zaykin et al., 2002), meta-analysis of microarray experiments (Pyne et al., 2006), gene set enrichment analysis (Subramanian et al., 2005) and brain imaging studies (Heller et al., 2006).

The definition of a cluster is often application specific. Two existing methods for obtaining spatial clusters include: (i) to aggregate locations into regions according to available prior information (Heller et al., 2006; Benjamini and Heller, 2007); (ii) to conduct a preliminary point-wise analysis and define the clusters after inspection of the results (Pacifico et al., 2004). Let = {C₁, ···, C_K} denote the set of (known) clusters of interest. We can form for each cluster C_k a partial conjunction null hypothesis (Benjamini and Heller, 2008), H₀(C_k) : π_k ≤ γ versus H₁(C_k) : π_k > γ, where π_k = ν({s ∈ C_k : θ(s) = 1})/ν(C_k) is the proportion of non-null locations in C_k and 0 ≤ γ ≤ 1 is a pre-specified tolerance level. The null hypothesis could also be defined in terms of the average activation amplitude μ̄(C_k) = ν(C_k)⁻¹ ∫_Ckμ(s)ds, that is, H₀(C_k) : μ̄(C_k) ≤ μ̄₀ versus H₁(C_k) : μ̄(C_k) > μ̄₀, for some pre-specified μ̄₀. Each cluster C_k is associated with an unknown state ϑ_k ∈ {0, 1}, indicating whether the cluster shows a signal or not. Let S₀ = ∪_k:ϑk=0C_k and S₁ = ∪_k:ϑk=1C_k denote the corresponding null and non-null areas, respectively. In cluster-wise analysis, a universal decision rule is taken for all locations in the cluster, i.e. δ(s) = Δ_k, for all s ∈ C_k. The decision rule is Δ = (Δ₁, ···, Δ_K). Then, the rejection area is R = ∪_k:Δk=1C_k.

In many applications it is desirable to incorporate the cluster size or other spatial variables in the error measure. We consider the weighted multiple testing framework, first proposed by Benjamini and Hochberg (1997) and further developed by Benjamini and Heller (2007) in a spatial setting, to reflect the relative importance of various clusters in the decision process. The general strategy involves the modifications of either the error rate to be controlled, or the power function to be maximized, or both. Define the false cluster rate

$$\text{FCR}=E\left\{\frac{{\sum }_k{w}_k(1-{\vartheta }_k){\mathrm{\Delta }}_k}{({\sum }_k{w}_k{\mathrm{\Delta }}_k)\vee 1}\right\},$$ (2.3)

where w_k are cluster specific weights which are often pre-specified in practice. For example, one can take w_k = ν(C_k), the size of a cluster, to indicate that a false positive cluster with larger size would account for a larger error. Similarly, we define the marginal FCR as mFCR = E{Σ_k w_k(1 − ϑ_k) Δk}/E(Σ_k w_kΔ_k).

We can see that in the definition of the FCR, a large false positive cluster is penalized by a larger weight. At the same time, correctly identifying a large cluster that contains signal may correspond to a greater gain; hence the power function should be weighted as well. For example, in epidemic disease surveillance, it is critical to identify aberrations in areas with larger populations where interventions should be first put into place. To reflect that some areas are more crucial, we give higher penalty in the loss function if an important cluster is missed. The same weights w_k are used as a reflective of proportional error and gain. Define the missed cluster rate MCR = E{Σ_k w_kϑ_k (1 − Δk)}. In cluster-wise analysis the goal is to control the FCR while minimizing the MCR.

3. Compound Decision Theory for Spatial Multiple Testing

In this section we formulate a compound decision theoretic framework for spatial multiple testing problems and derive a class of oracle procedures for controlling the FDR, FDX and FCR, respectively. Section 4 develops data-driven procedures to mimic the oracle procedures and discusses their implementations in a Bayesian computational framework.

3.1. Oracle procedures for point-wise analysis

Let X₁, ···, X_n be observations at locations $S^{\ast }=\{s_1^{\ast },\cdots ,s_n^{\ast }\}$. In point-wise analysis, S* is often a subset of S, and we need to make decisions at locations where no observation is available; therefore the problem is different from conventional multiple testing problems where each hypothesis has its own observed data. It is therefore necessary to exploit the spatial dependency and pool information from nearby observations. In this section, we discuss optimal results on point-wise FDR analysis from a theoretical perspective.

The optimal testing rule is derived in two steps: first the hypotheses are ranked optimally and then a cutoff is chosen along the rankings to control the FDR precisely. The optimal result on ranking is obtained by connecting the multiple testing problem to a weighted classification problem. Consider a general decision rule δ = {δ(s) : s ∈ S} of the form:

$$\delta (s)=I(T(s)<t),$$ (3.1)

where T(s) = T_s(Xⁿ) is a test statistic, T_s(·) is a function which maps Xⁿ to a real value, and t is a universal threshold for all T(s), s ∈ S. To separate a signal (θ(s) = 1) from noise (θ(s) = 0), consider the loss function

$$L(\mathit{\theta },\mathit{\delta })=\lambda \nu (S_{\text{FP}})+\nu (S_{\text{FN}}),$$ (3.2)

where λ is the penalty for false positives, and S_FP and S_FN are false positive and false negative areas defined in Section 2. The goal of a weighted classification problem is to find a decision rule δ to minimize the classification risk R = E{L(θ, δ)}. It turns out that the optimal solution to the weighted classification problem is also optimal for mFDR control when a monotone ratio condition (MRC) is fulfilled. Specifically, define G_j(t) = ∫_S P(T(s) < t, θ(s) = j)dν(s), j = 0, 1. G₀(t) can be viewed as the overall “Type I error” function at all locations in S where the null is true, and G₁(t) can be viewed as the overall “power” function at all locations in S where the alternative is true. In Section XXX of the supplementary material, we show that it is reasonable to assume that G₀ and G₁ are differentiable when X(s) are continuous random variables on S. Denote by g₀(t) and g₁(t) their derivatives. The MRC can be stated as

$$g_1(t)/g_0(t)\text{is}\text{monotonically}\text{decreasing}\text{in}t.$$ (3.3)

The MRC is a reasonable and mild regularity condition in multiple testing which ensures that the mFDR increases in t and the MDR decreases in t. Therefore in order to minimize the MDR, we choose the largest threshold subject to mFDR ≤ a. The MRC reduces to the monotone likelihood ratio condition (MLRC, Sun and Cai, 2007) when the tests are independent. The MLRC is satisfied by the p-value when the p-value distribution is concave (Genovese and Wasserman, 2002). In a hidden Markov model, the MRC is satisfied by the local index of significance (Sun and Cai, 2009).

Let Xⁿ = {X₁, ···, X_n}. Consider a class of decision rules of the form δ = {I{T(s) < t} : s ∈ S}, where T = {T(s) : s ∈ S} satisfies the MRC (3.3). The next theorem derives the optimal classification statistic and gives the optimal multiple testing rule for mFDR control.

Theorem 1

Let Ψ be the collection of all parameters in random field (1.1) and we assume that Ψ is known. Define the oracle statistic

$$T_{OR}(s)=P_{\mathrm{\Psi }}\{\theta (s)=0\mid {\mathit{X}}^n\}$$ (3.4)

and assume that G_j(t) are differentiable, j = 0, 1. Then

1. The classification risk is minimized by δ = {δ(s) : s ∈ S}, where

   $$\delta (s)=I\left\{T_{OR}(s)<{(1+\lambda )}^{-1}\right\}\mathit{and}.$$ (3.5)

2. Let T_OR = {T_OR(s) : s ∈ S}. Then T_OR satisfies the MRC (3.3).

3. There exists an oracle threshold

   $$t_{OR}(\alpha )=sup\{t:\mathit{mFDR}(t)\le \alpha \}$$ (3.6)
   such that the oracle testing procedure

   $${\mathit{\delta }}_{OR}=\{I[T_{OR}(s)<t_{OR}(\alpha )]:s\in S\}$$ (3.7)

   has the smallest MDR among all α-level mFDR procedures in .

Remark 1

Theorem 1 implies that, under the MRC (3.3), the optimal solution to a multiple testing problem (for mFDR control at level α) is the solution to an equivalent weighted classification problem with the loss function (3.2) and penalty λ(α) = {1 − t_OR(α)}/t_OR(α). The procedure is called an “oracle” procedure because it relies on the knowledge of the true distributional information and the optimal threshold t_OR(a), which are typically unknown in practice.

Remark 2

The result in Theorem 1(c) can be used to develop an FDX-controlling procedure. First the hypotheses are ranked according to the values of T_OR(s). Since the MDR decreases in t, we choose the largest t subject to the constraint on the FDX. The oracle FDX procedure is then given by

$${\mathit{\delta }}_{OR,\mathit{FDX}}=\{I(T_{OR}(s)<t_{OR,\mathit{FDX}}):s\in S\},$$ (3.8)

where t_OR,FDX = arg max_t{FDX_t (t) ≤ α} is the oracle FDX threshold.

3.2. Oracle procedure for cluster-wise analysis

Let 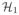, ···, 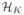be the hypotheses on the K clusters 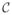= {C₁, ···, C_K}. The true states of nature (e.g. defined by partial conjunction nulls) can be represented by a binary vector ϑ = {ϑ_k : k = 1, ···, K} ∈ {0, 1}^K. The decisions based on Xⁿ = {X₁, ···, X_n} are denoted by Δ = (Δ₁, ···, Δ_K) ∈ {0, 1}^K. The goal is to find Δ to minimize the MCR subject to FCR ≤ a. It is natural to consider the loss function

$$L_w(\mathit{\vartheta },\mathbf{\Delta })=\sum _{k=1}^K\{\lambda w_k(1-{\vartheta }_k){\mathrm{\Delta }}_k+{\omega }_k{\vartheta }_k(1-{\mathrm{\Delta }}_k)\},$$ (3.9)

where λ is the penalty for false positives. As one would expect from Remark 1, the FCR control problem can be solved by connecting it to a weighted classification problem with a suitably chosen λ. In practice λ is an unknown function of the FCR level α and needs to be estimated. In contrast, the weights w_k are pre-specified. Let T_k be a cluster-wise test statistic. Define p_k = P (ϑ_k = 1), G_jk(t) = P(T_k < t|ϑ_k = j) and g_jk(t) = (d/dt)G_jk(t), j = 0, 1. Consider the generalized monotone ratio condition (GMRC):

$$\frac{{\sum }_{k=1}^K{w}_k{p}_k{g}_{1k}(t)}{{\sum }_{k=1}^K{w}_k(1-p_k)g_{0k}(t)}\text{is}\text{decreasing}\text{in}t.$$ (3.10)

The GMRC guarantees that the MCR is decreasing in the FCR. Let 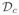be the class of decision rules of the form Δ = {I(T_k < t) : k = 1, ···, K}, where T = (T₁, ···, T_k) satisfies the GMRC (3.10). We have the following results.

Theorem 2

Let Ψ be the collection of all parameters in random field (1.1). Assume that Ψ is known. Define the oracle test statistic

$$T_{OR}(C_k)=P_{\mathrm{\Psi }}({\vartheta }_k=0\mid {\mathit{X}}^n)$$ (3.11)

and assume that G_jk(t) are differentiable, k = 1, ···, K, j = 0, 1. Then

1. the classification risk with loss (3.9) is minimized by Δ = {Δ_k : k = 1, ···, K}, where

   $${\mathrm{\Delta }}_k=I\{T_{OR}(C_k)<{(1+\lambda )}^{-1}\}.$$ (3.12)

2. T_OR = {T_OR(C_k) : k = 1, ···, K} satisfies the GMRC (3.10).

3. Define the oracle mFCR procedure

   $${\mathit{\Delta }}_{OR}=\{{\mathrm{\Delta }}_{OR}^k:k=1,\cdots ,K\}=\{I(T_{OR}(C_k)<t_{OR}^c(\alpha )):k=1,\cdots ,K\},$$ (3.13)

   where $t_{OR}^c(\alpha )=sup\{t:\mathit{mFCR}(t)\le \alpha \}$ is the oracle threshold. Then the oracle mFCR procedure (3.13) has the smallest MCR among all α-level mFCR procedures in .

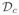In Section 4 we develop data-driven procedures to mimic the above oracle procedures.

4. False Discovery Controlling Procedures and Computational Algorithms

The oracle procedures are difficult to implement because (i) it is impossible to make an uncountable number of decisions when S is continuous, and (ii) the optimal threshold t_OR and the oracle test statistics are essentially unknown in practice. This section develops data-driven procedures for FDR, FDX and FCR analyses to overcome these difficulties. We first describe how a continuous decision process can be approximated, within a small margin of error, by a finite number of decisions on a grid of pixels, then discuss how to calculate the test statistics.

4.1. FDR and FDX procedures for point-wise inference

To avoid making inference at every point, our strategy is to divide a continuous S into m “pixels,” pick one point in each pixel, and use the decision at that point to represent all decisions in the pixel. We show that as the partition becomes finer, the representation leads to an asymptotically equivalent version of the oracle procedure.

Let ${\cup }_{i=1}^m{S}_i$ be a partition of S. A good partition in practice entails dividing S into roughly homogeneous pixels, within which μ(s) varies at most a small constant. This condition is stated precisely as Condition 2 when we study the asymptotic validity of the proposed method. Next take a point s_i from each S_i. In practice it is natural to use the center point of S_i but we shall see that the choice of s_i is nonessential as long as Condition 2 is fulfilled. Let $T_{OR}^{(1)}\le T_{OR}^{(2)}\le \cdots \le T_{OR}^{(m)}$ denote the ordered oracle statistics defined by (3.4) and S_(i) the region corresponding to $T_{OR}^{(i)}$. The following testing procedure is proposed for FDR control.

Procedure 1

(FDR control). Define $R_j={\cup }_{i=1}^j{S}_{(i)}$ and

$$r=max\left\{j:\nu {(R_j)}^{-1}\sum _{i=1}^j{T}_{OR}^{(i)}\nu S_{(i)}\le \alpha \right\}.$$ (4.1)

The rejection area is given by $R={\cup }_{i=1}^r{S}_{(i)}$.

Next we propose an FDX procedure at level (γ, α) based on the same ranking and partition schemes. Let $R_j^m=\{s_1,\cdots ,s_m\}\cap R_j$ be the set of rejected representation points. The main idea of the following procedure is to first obtain a discrete version of the FDX_τ based on a finite approximation, then estimate the actual FDX level for different cutoffs, and finally choose the largest cutoff which controls the FDX.

Procedure 2

(FDX control). Pick a small ε₀ > 0. Define $R_j={\cup }_{i=1}^j{S}_{(i)}$ and

$${\text{FDX}}_{\tau ,j}^m=P_{\mathrm{\Psi }}\left(\nu {(R_j)}^{-1}\sum _{s_i\in R_j^m}\{1-\theta (s_i)\}\nu (S_i)>\tau -{\epsilon }_0\mid {\mathit{X}}^n\right),$$ (4.2)

where θ(s_i) is a binary variable indicating the true state at location s_i. Let $r=max\{j:{\text{FDX}}_{\tau ,j}^m\le \alpha \}$, then the rejection region is given by $R={\cup }_{i=1}^r{S}_{(i)}$.

Now we study the theoretical properties of Procedures 1 and 2. The first requirement is that μ(s) is a smooth process that does not degenerate at the boundaries of the indifference region A = [A_l, A_u]. To see why such a requirement is needed, define

$${\mu }^m(s)=\sum _{i=1}^m\mu (s_i)I(s\in S_i),\theta (s)=I\{\mu (s)\in A^c\}\text{and}{\theta }^m(s)=I\{{\mu }^m(s)\in A^c\}.$$

For a particular realization of μ(s), μ^m(s) is a simple function which takes a finite number of values according to the partition S = ∪_iS_i, and converges to μ(s) point-wise as the partition becomes finer. Note that at locations close to the boundaries, a small difference between μ^m(s) and μ(s) can lead to different θ(s) and θ^m(s). The following condition, which states that μ(s) does not degenerate at the boundaries, guarantees that θ(s) ≠ θ^m(s) only occurs with a small chance when |μ^m(s) − μ(s)| is small. The condition holds when μ(s) is a continuous random variable.

Condition 1

Let A = [A_l, A_u] be the indifference region and ε a small positive constant. Then ∫_S P(A_* − ε < μ(s) < A_* + ε)dν(s) → 0 as ε → 0, for A_* = Al or Au.

To achieve asymptotic validity, the partition S = ∪_iS_i should yield roughly homogeneous pixels so that the decision at point s_i is a good representation of the decision process on pixel S_i. Consider the event that the variation of μ(s) on a pixel exceeds a small constant. The next condition guarantees that the event only occurs with a vanishingly small chance. The condition holds for the Gaussian and Matérn models that are used in our simulation study and real data analysis.

Condition 2

There exists a sequence of partitions { $S={\cup }_{i=1}^m{S}_i:m=1,2,\cdots$} such that for any given ε > 0, lim_m→∞ ∫_S P{|μ(s) − μ^m(s)| ≥ ε}dν(s) = 0.

Conditions 1 and 2 together guarantee that θ(s) = θ^m(s) would occur with overwhelming probability when the partition becomes finer. See Lemma 2 in Section 7.

The next theorem shows that Procedures 1 and 2 are asymptotically valid for FDR and FDX control, respectively. We first state the main result for a continuous S.

Theorem 3

Consider T_OR(s) and ${\mathit{FDX}}_{\tau ,j}^m$ defined in (3.4) and (4.2), respectively. Let { ${\cup }_{i=1}^m{S}_i:m=1,2,\cdots$} be a sequence of partitions of S satisfying Conditions 1–2. Then

1. the FDR level of Procedure 1 satisfies FDR ≤ α + o(1) when m → ∞;

2. the FDX level of Procedure 2 satisfies FDX_τ ≤ α + o(1) when m → ∞.

When S is discrete, the FDR/FDX control is exact; this (stronger) result follows directly from the proof of Theorem 3.

Corollary 1

When S is discrete, a natural partition is $S={\cup }_{i=1}^m\{s_i\}$. Then

1. the FDR level of Procedure 1 satisfies FDR ≤ α;

2. the FDX level of Procedure 2 satisfies FDX_τ ≤ α.

4.2. FCR procedure for cluster-wise inference

Now we turn to the cluster-wise analysis. Let C₁, · · ·, C_K be the clusters and 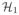, ···, 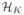the corresponding hypotheses. We have shown that T_OR(C_k) = P_Ψ(ϑ_k = 0|Xⁿ) is the optimal statistic for cluster-wise inference.

Procedure 3

(FCR control). Let $T_{(1)}^c\le \cdots \le T_{(K)}^c$ be the ordered T_OR(C_k) values, and 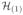, ···, 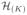and w₍₁₎, · · ·, w_(K) the corresponding hypotheses and weights, respectively. Let

$$r=max\left\{j:\frac{{\sum }_{k=1}^j{w}_k{T}_{(k)}^c}{{\sum }_{k=1}^j{w}_{(k)}}\le \alpha \right\}.$$

Then reject , · · ·, .

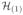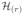The next theorem shows that Procedure 3 is valid for FCR control.

Theorem 4

Consider T_OR(C_k) defined in (3.11). Then the FCR of Procedure 3 is controlled at the level α.

It is not straightforward to implement Procedures 1–3 because T_OR(s_i), ${\text{FDX}}_{\tau ,j}^m$ and T_OR(C_k) are unknown in practice. Next section develops computational algorithms to estimate these quantities based on Bayesian spatial models.

4.3. Data-driven procedures and computational Algorithms

An important special case of (1.1) is the Gaussian random field (GRF), where the signals and errors are generated as Gaussian processes with means μ̄ and 0, and covariance matrices Σ₁ and Σ₂, respectively. Let Ψ be the collection of all hyperparameters in random field (1.1).

Consider a general random field model (1.1) defined on S. Let Ψ̂ be the estimate of Ψ. Denote by Xⁿ = (X₁, · · ·, X_n) the collection of random variables associated with locations $s_1^{\ast },\cdots ,s_n^{\ast }$. Further let f(μ|Xⁿ, Ψ̂) ∝ π(μ)f(Xⁿ|μ, Ψ̂) be the posterior density function of μ given Xⁿ and Ψ̂. The numerical methods for model fitting and parameter estimation in spatial models have been extensively studied (see Gelfand et al. (2010) and the references therein). We provide in the web appendix the technical details in a Gaussian random field model (GRFM), which is used in both the simulation study and real data example. The focus of discussion is on how the MCMC samples, generated from the posterior distribution, can be used to carry out the proposed multiple testing procedures.

We start with a point-wise testing problem with H₀(s) : μ(s) ∈ A versus H₁(s) : μ(s) ∉ A, s ∈ S. Let S^m = (s₁, · · ·, s_m) denote the collection of the representative points based on partition $S={\cup }_{i=1}^m{S}_i$. We only discuss the result for a continuous S (the result extends to a discrete S by simply taking S^m = S). Suppose the MCMC samples are { ${\widehat{\mathit{\mu }}}_b^m:b=1,\cdots ,B$}, where ${\widehat{\mathit{\mu }}}_b^m=({\widehat{\mu }}_b^{m,1},\cdots ,{\widehat{\mu }}_b^{m,m})$ is a m-dimensional posterior sample indicating the magnitudes of the signals at locations s₁, · · ·, s_m in replication b. Let ${\widehat{\theta }}_b^{m,i}=I({\widehat{\mu }}_b^{m,i}\notin A)$ denote the estimated state of location s_i in replication b. To implement Procedure 1 for FDR analysis, we need to compute

$$T_{OR}(s_i)=P_{\mathrm{\Psi }}\{\theta (s_i)=0\mid {\mathit{X}}^n\}=\int I\{\mu (s_i)\in A\}{f}_{\mathit{\mu }\mid {\mathit{X}}^n}(\mathit{\mu }\mid {\mathit{X}}^n,\mathrm{\Psi })d\mathit{\mu }.$$

It is easy to see that T_OR(s_i) can be estimated by

$${\widehat{T}}_{OR}(s_i)=\frac{1}{B}\sum _{b=1}^{B}I({\widehat{\mu }}_b^{m,i}\in A)=\frac{1}{B}\sum _{b=1}^B(1-{\widehat{\theta }}_b^{m,i}).$$ (4.3)

To implement Procedure 2, note that the FDX defined in (4.2) can be written as

$${\text{FDX}}_{\tau ,j}^m=\int I\left[\nu {(R_j)}^{-1}\sum _{s_i\in R_j^m}\{1-\theta (s_i)\}\nu (S_i)>\tau -{\epsilon }_0\right]f_{\mathit{\mu }\mid {\mathit{X}}^n}(\mathit{\mu }\mid {\mathit{X}}^n,\mathrm{\Psi })d\mathit{\mu },$$

where j is the number of points in s^m which are rejected, $R_j={\cup }_{i=1}^j{S}_{(i)}$ is the rejection region and $R_j^m=S^m\cap R_j$ is subset of points in S^m which are rejected. Given the MCMC samples { ${\widehat{\mathit{\mu }}}_b^m:b=1,\cdots ,B$}, the ${\text{FDX}}_{\tau ,j}^m$ can be estimated as

$${\widehat{\text{FDX}}}_{\tau ,j}^m=\frac{1}{B}\sum _{i=1}^{B}I\left\{\nu {(R_j)}^{-1}\sum _{s_i\in R_j^m}(1-{\widehat{\theta }}_b^{m,i})\nu (S_i)>\tau -{\epsilon }_0\right\}.$$ (4.4)

Therefore Procedures 1 and 2 can be implemented by replacing T_OR(s_i) and ${\text{FDX}}_{\tau ,j}^m$ by their estimates given in (4.3) and (4.4).

Next we turn to cluster-wise testing problems. Let ${\cup }_{i=1}^{m_k}{S}_i^k$ be a partition of C_k. Take a point $s_i^k$ from each $S_i^k$. Let s^m_k = (s^m_k,1, · · ·, s^m_km_k) be the collection of sampled points in cluster C_k, $m={\sum }_{k=1}^K{m}_k$ be the count of points sampled in S and s^m = (s^m₁, · · ·, s^m_K). If we are interested in testing partial conjunction of nulls H₀(C_k) : π_k ≤ γ versus H₁(C_k) : π_k > γ, where π_k = ν({s ∈ C_k : θ(s) = 1})/ν(C_k), then we can define ${\vartheta }_k^m=I\{{\sum }_{i=1}^{m_k}\theta (s_i^k)\nu (S_i^k)>\gamma \nu (C_k)\}$ as an approximation to ϑ_k = I(π_k > γ). If the goal is to test average activation amplitude, i.e., H₀(C_k) : μ̄(C_k) ≤ μ̄₀ versus H₁(C_k) : μ̄(C_k) > μ̄₀, then we can define ${\vartheta }_k^m=I\{{\sum }_{i=1}^{m_k}\mu (s_i^k)\nu (S_i^k)>{\overline{\mu }}_0\nu (C_k)\}$. Let $T_{OR}^m(C_k)=P({\vartheta }_k^m=0\mid {\mathit{X}}^n)$.

To implement Procedure 3, we need to compute $T_{OR}^m(C_k)$. Suppose we are interested in testing partial conjunction of nulls, then

$$T_{OR}^m(C_k)=\int I\left\{\sum _{i=1}^{m_k}\theta (s_i^k)\nu (S_i^k)<\gamma \nu (C_k)\right\}{f}_{\mathit{\mu }\mid {\mathit{X}}^n}(\mathit{\mu }\mid {\mathit{X}}^n)d\mathit{\mu }$$

Denote by ${\widehat{\mathit{\mu }}}_b^{m_k}=({\widehat{\mu }}_b^{m_k,1},\cdots ,{\widehat{\mu }}_b^{m_k,m_k})$ be the MCMC samples for cluster C_k at points s^m_k in replication b, b = 1, · · ·, B. Further let ${\widehat{\theta }}_b^{m_k,i}=I({\widehat{\mu }}_b^{m_k,i}\notin A)$. Then ∫_Ck θ(s)ds in a particular replication b can be approximated by ${m_k}^{-1}{\sum }_{i=1}^{m_k}{\widehat{\theta }}_b^{m_k,i}\nu (S_i^k)$ and the oracle statistic $T_{OR}^m(C_k)$ can be estimated by ${\widehat{T}}_{OR}(C_k)=\frac{1}{B}{\sum }_{b=1}^{B}I\left\{\frac{1}{m_k}{\sum }_{i=1}^{m_k}{\widehat{\theta }}_b^{m_k,i}\nu (S_i^k)<\gamma \nu (C_k)\right\}$. If the goal is to test average activation amplitude, $T_{OR}^m(C_k)$ can be estimated as ${\widehat{T}}_{OR}(C_k)=\frac{1}{B}{\sum }_{b=1}^{B}I\left\{\nu {(C_k)}^{-1}{\sum }_{i=1}^{m_k}{\widehat{\mu }}_b^{m_k,i}\nu (S_i^k)<{\overline{\mu }}_0\right\}$.

5. Simulation

We conduct simulation studies to investigate the numerical properties of the proposed methods. A significant advantage of our method over conventional methods is that the procedure is capable of carrying out analysis on a continuous spatial domain. However, to permit comparisons with other methods, we first limit the analysis to a Gaussian model for testing hypotheses at the n locations where the data points are observed. Therefore we have m = n. Then we conduct simulations to investigate, without comparison, the performance of our methods for a Matérn model to test hypotheses on a continuous domain based on a discrete set of data points. The R code for implementing our procedures is available at: http://www-bcf.usc.edu/~wenguans/Spatial-FDR-Software.

5.1. Gaussian model with observed data at all testing units

We generate data according to model (1.1) with both the signals and errors being Gaussian processes. Let ||·|| denote the Euclidean distance. The signal process μ has mean μ̄ and powered exponential covariance $\text{Cov}[\mu (s),\mu (s^{\prime })]={\sigma }_{\mu }^{2}exp[-{(\Vert s-s^{\prime }\Vert /{\rho }_{\mu })}^k]$, while the error process ε has mean zero and covariance Cov[ε(s), ε(s′)] = (1−r)I(s = s′)+r exp[− (||s−s′||/ρ_ε)^k] so that r ∈ [0, 1] controls the proportion of the error variance with spatial correlation. For each simulated data set, the process is observed at n data locations generated as $s_1,\dots ,s_n\stackrel{i.i.d.}{\sim }\text{Uniform}({[0,1]}^2)$. For all simulations, we choose n = 1000, r = 0.9, μ̄ = −1, and σ_μ = 2; under this setting the expected proportion of positive observations is 33%. We generate data with k = 1 (exponential correlation) and k = 2 (Gaussian correlation), and for several values of the spatial ranges ρ_μ and ρ_ε. We only present the results for k = 1. The conclusions from simulations for k = 2 are similar in the sense that our methods control the FDR more precisely and are more powerful than competitive methods. For each combination of spatial covariance parameters, we generate 200 datasets. For simulations studying the effects of varying ρ_μ we fix ρ_ε = 0.05, and for simulations studying the effects of varying ρ_ε we fix ρ_μ = 0.05.

5.1.1. Point-wise analysis

For each of the n locations, we test the hypotheses H₀(s) : μ(s) ≤ 0 versus H₁(s) : μ(s) > 0. We implement Procedure 1 (assuming the parameters are known, denoted by Oracle FDR) and the proposed method (4.3) using MCMC samples (denoted by MC FDR), and compare our methods with three popular approaches: the step-up p-value procedure (Benjamini and Hochberg, 1995), the adaptive p-value procedure (Benjamini and Hochberg, 2000; Genovese and Wasserman, 2002), and the FDR procedure proposed by Pacifico et al. (2004), which are denoted by BH, AP and PGVW FDR, respectively. We then implement Procedure 2 (assuming the parameters are known, denoted by Oracle FDX) and its MCMC version (MC FDX) based on (4.4), and compare the methods with the procedure proposed by Pacifico et al. (2004) (denoted by PGVW FDX).

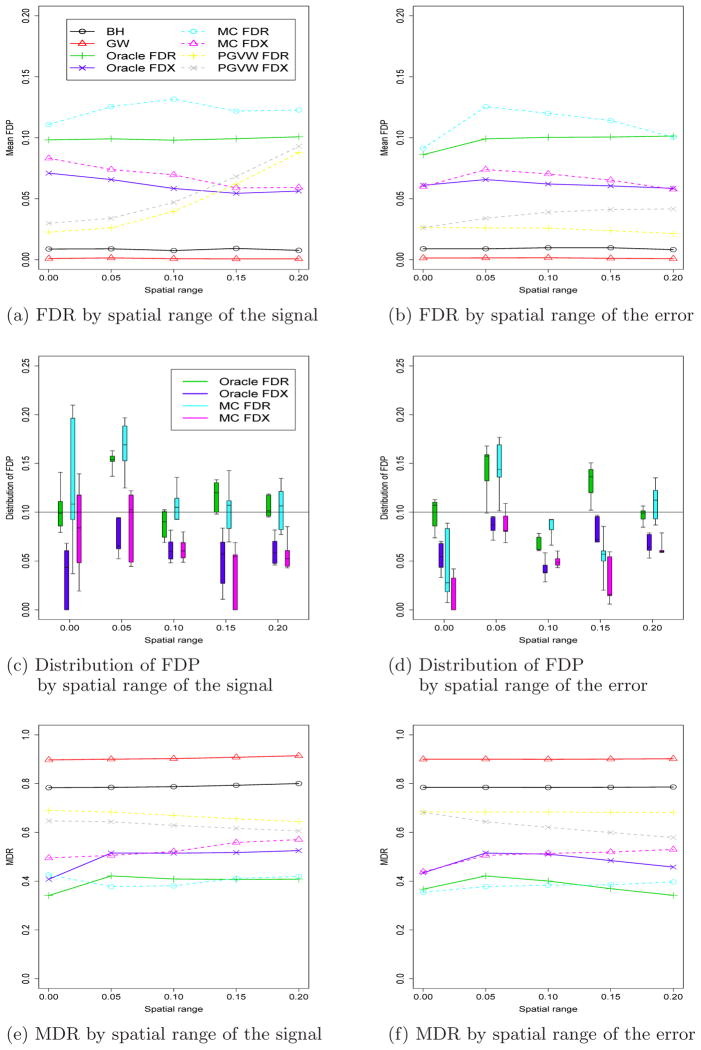
We generate the MCMC samples using a Bayes model, where we assume that k is known, and select uninformative priors: μ̄ ~ N(0, 100²), ${\sigma }_{\mu }^{-2}~\text{Gamma}(0.1,0.1)$, and r, ρ_μ, ρ_ε ~ Uniform(0, 1). The Oracle FDR/FDX procedure fixes these five hyperparameters at their true values to determine the effect of their uncertainty on the results. For each method and each data set we take α = τ = 0.1. Figures 2 plots the averages of the FDPs and MDPs over the 200 datasets.

Fig. 2.

Summary of the site-wise simulation study with exponential correlation. The horizontal lines in the boxplots in Panels (c) and (d) are the 0.1, 0.25, 0.50, 0.75, and 0.9 quantiles of FDP.

We can see that the Oracle FDR procedure controls the FDR nearly perfectly. The MC FDR procedure, with uninformative priors on the unknown spatial correlation parameters, also has good FDR control, between 10–12%. As expected, the Oracle and MC FDX methods tuned to control FDX are more conservative than the FDR methods, with observed FDR between 5–8%. The FDX methods become increasingly conservative as the spatial correlation of the signal increases to appropriately adjust for higher correlation between tests. In contrast, the BH, GW and PGVW procedures are very conservative, with much higher MDR levels. The distribution of FDP is shown in Figures 2c and 2d. In some cases, the upper tail of the FDP distribution approaches 0.2 for the MC FDR procedure. In contrast, the Oracle FDX method has FDP under 0.1 with very high probability for all correlation models. The MC FDX procedure also effectively controls FDX in most cases. The 95^th percentile of FDP is 0.15 for the smallest spatial range in Figure 2c, and less than 0.12 in all other cases.

5.1.2. Cluster-wise analysis

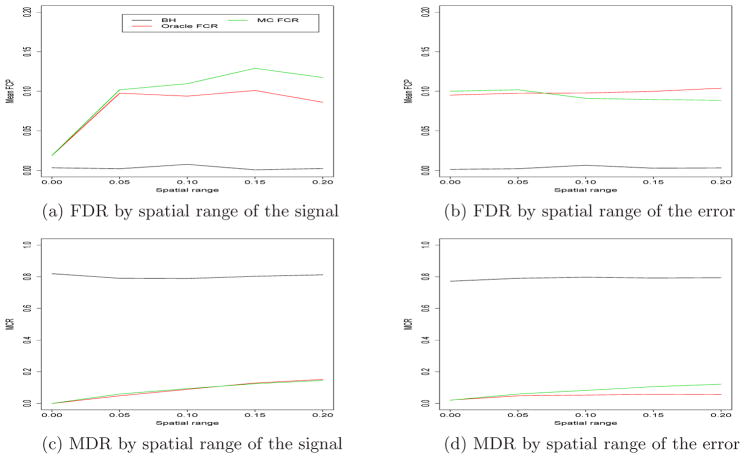
We use the same data-generating schemes and MCMC sampling methods as in the site-wise simulation in the previous section. The whole spatial domain is partitioned into a regular 7 ×7 grid, giving 49 clusters. We consider partial conjunction tests, where a cluster is rejected if more than 20% of the locations in the cluster contain true positive signal (μ(s) > 0). We implement Procedure 3 (assuming parameters are known, denoted by Oracle FCR) and the corresponding MCMC method with non-informative priors (denoted by MC FCR). We compare our methods with the combined p-value approach proposed by Benjamini and Heller (2007). To make the methods comparable, we restrict the analysis to the n = 1000 data locations. We assume α = 0.1 and an exponential correlation with k = 1. The simulation results are summarized in Figure 3. We can see that the Oracle FCR procedure control the FCR nearly perfectly. The MC FCR procedure has FCR slightly above the nominal level (less than 0.13 in all settings). In contrast the combined p-value method is very conservative, with FCR less than 0.02. Both Oracle FCR and MC FCR procedures have much lower missed cluster rate (MCR, the proportion of missed clusters which contain true signal in more than 20% of the locations).

Fig. 3.

Summary of the cluster simulation study.

5.2. Matérn model with missing data on the testing units

We use the model z(s) = μ(s) + ε(s), but generate the signals μ(s) and errors ε(s) as Gaussian processes with Matérn covariance functions. The signal process {μ(s) : s ∈ S} has mean μ̄ and covariance $\text{Cov}[\mu (s),\mu (t)]={\sigma }_{\mu }^{2}M(\Vert s-t\Vert ;{\rho }_{\mu },{\kappa }_{\mu })$, where the Matérn correlation function, M, is determined by the spatial range parameter ρ_μ > 0 and smoothness parameter κ_μ. The error process {ε(s) : s ∈ S} has mean zero and covariance Cov[ε(s), ε(t)] = (1 − r)I(s = t)+rM(||s−t||; ρ_ε, κ_ε) so that r ∈ [0, 1] controls the proportion of the error variance with spatial correlation.

For each simulated data set, data are generated at n spatial locations $s_i\stackrel{i.i.d.}{\sim }\text{Uniform}(\mathcal{D})$, where 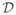is the unit square 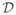= [0, 1]². Predictions are made and tests of 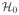: μ(s) ≤ μ₀ versus 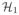: μ(s) > μ₀ are conducted at the m² locations forming the m × m square grid covering 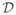. For all simulations, we choose n = 200, m = 25, r = 0.9, μ̄ = 0, μ₀ = 6.41, and σ_μ = 5; under this setting the expected proportion of locations with μ(s) > μ₀ is 0.1. We generate data with two correlation functions: the first is exponential correlation with κ_μ = κ_ε = 0.5 and ρ_μ = ρ_ε = 0.2; the second has κ_μ = κ_ε = 2.5 and ρ_μ = ρ_ε = 0.1 which gives a smoother spatial process than the exponential but with roughly the same effective range (the distance at which correlation is 0.05). For both correlation functions we generate 200 datasets, and fit the model with Matérn correlation function and priors μ̄ ~ N(0, 1000²), ${\sigma }_{\mu }^{-2}~\text{Gamma}(0.01,0.01)$, r ~ Unif(0, 1), and κ_μ, κ_ε, ρ_μ, ${\rho }_{\epsilon }\stackrel{i.i.d.}{\sim }N(-1,1)$. For comparison we also fit the oracle model with hyperparameters μ̄, σ_μ, r, κ_μ, κ_ε, ρ_μ, and ρ_ε fixed at their true values.

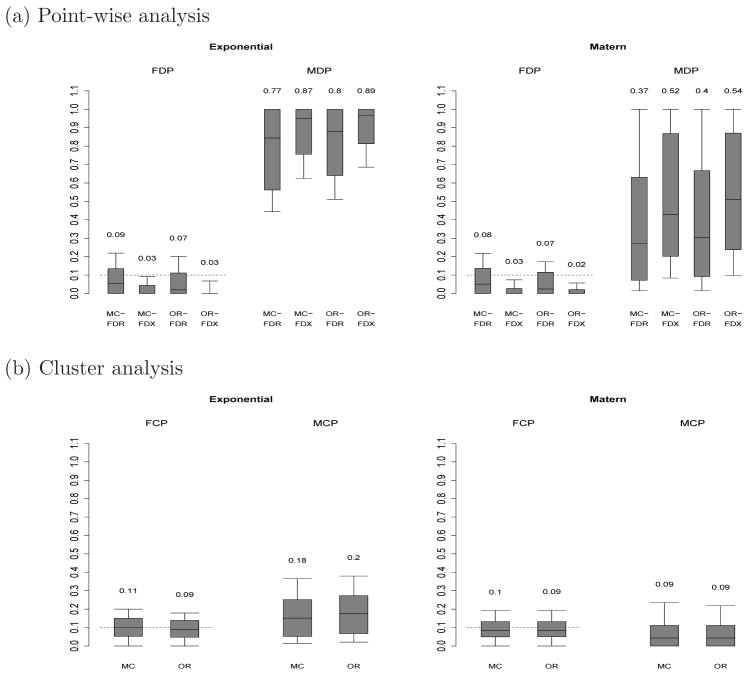
The results are summarized in Figure 4. For data simulated with exponential correlation, both the data-driven procedure and oracle procedure with FDR-thresholding maintain proper FDR (0.09 for the data-driven procedure and 0.07 for the oracle procedure). The 0.9 quantile of FDP for the data-driven procedure with FDR control is over 0.20. In contrast, the 0.9 quantile for the data-driven procedure with FDX threshold is slightly below 0.1, indicating proper FDX control. The results for the Matérn data are similar, except that all models have lower missed discovery rate because with a smoother spatial surface the predictions are more precise.

Fig. 4.

Simulation results with n = 200 with data generated with exponential and Matérn spatial correlation. Plotted are the FDP and MDP for the 200 simulated datasets. The boxplots’ horizontal lines are the 0.10, 0.25, 0.50, 0.75, and 0.90 quantiles of FDP and MDP, and the numbers of above the boxplots are the means of FDP (FDR) and MDP (MDR).

We also evaluate the cluster FDR and FDX performance using this simulation design. Data were generated and the models were fit as for the point-wise simulation. We define the spatial cluster regions by first creating a 10×10 regular partition of , and then combing the final two columns and final two rows to give unequal cluster sizes. This gives 81 clusters and between 4 and 25 prediction locations per spatial cluster. We define a cluster as non-null if μ(s) > μ₀ for at least 20% of its locations. The FDR and FDX are controlled in all cases, and the power is much higher for the smoother Matérn data. The FDR and FDX of the data-driven procedures are comparable to the oracle procedure with these parameters fixed at their true values, suggesting the proposed testing procedure is efficient even in this difficult setting.

6. Ozone data analysis

To illustrate the proposed method, we analyze daily surface-level 8-hour average ozone for the eastern US. The data are obtained from the US EPA’s Air Explorer Data Base (http://www.epa.gov/airexplorer/index.htm). Ozone regulation is based on the fourth highest daily value of the year. Therefore, for each of the 631 stations and each year from 1997–2005, we compute the fourth highest daily value of 8-hour average ozone. Our objective is to identify locations with a decreasing time trend in this yearly value.

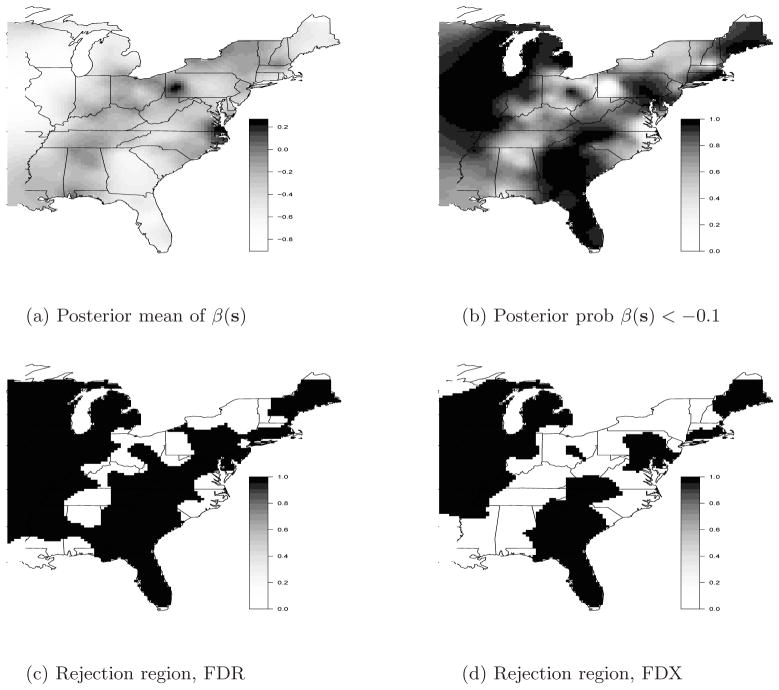
The precision of our testing procedure shows some sensitivity to model misspecification; hence we must be careful to conduct exploratory analysis to ensure that the spatial model fits the data reasonably well. See the web appendix for a more detailed discussion. After some exploratory analysis, we fit the model β̂(s) = β(s)+w(s)ε(s), where β̂(s) and w(s) are the estimated slope and its standard error, respectively, from the first stage simple linear regression analysis with predictor year, conducted separately at each site. After projecting the spatial coordinates to the unit square using a Mercator projection, the model for β and ε and the priors for all hyperparameters are the same to those in the simulation study in Section 5. The estimated slopes and corresponding z-values are plotted in Figure 1. We can see that the estimated slope is generally negative, implying that ozone concentrations are declining through the vast majority of the spatial domain. Thus we choose to test whether the decline in ozone is more than 1 ppb per decade, that is, H₀:β(s) ≥ −0.1 versus H₁:β(s) < −0.1.

We choose k = 1 (exponential correlation) and generate MCMC samples based on the posterior distribution of β on a rectangular 100 × 100 grid of points covering the spatial domain (including areas outside the US), and test the hypotheses at each grid cell in the US. Comparing Figures 5a and 1a, we see considerable smoothing of the estimated slopes. The posterior mean is negative throughout most of the domain, but there are areas with a positive slope, including western Pennsylvania and Chesapeake Bay. The estimated decrease is the largest in Wisconsin, Illinois, Georgia, and Florida. The estimates of 1 − T̂_OR(s_i) are plotted in Figure 5b. The estimated FDR (α = 0.1) and FDX (α = τ = 0.1) thresholds for T̂_OR are 0.30 and 0.16, respectively. Figures 5c and 5d show that the null hypothesis is rejected using both thresholding rules for the western part of the domain, Georgia and Florida, and much of New England. As expected, the FDX threshold is more conservative; the null is rejected for much of North Carolina and Virginia using FDR, but not FDX.

Fig. 5.

Summary of the ozone data analysis. Panels (a) and (b) give the posterior mean of β(S) and the posterior probability that β(S) < −0.1. Panels (c) and (d) plot the rejection region using FDR and FDX (rejection plotted as a one, and vice versa).

We also conduct a cluster-wise analysis using states as clusters. Although these clusters are fairly large, spatial correlation persists after clustering. For example, denote β̄_j as the average of β(s) at the grid locations described above for state j. The posterior correlation between β̄_j for Florida and other states is 0.51 for Georgia, 0.36 for Alabama, and 0.33 for North Carolina. Table 6 summarizes the cluster-wise analysis. We define the state to have a significant change in ozone if at least 80% of the state has slope less than −0.1ppb. Using this criteria gives T̂_OR(C_k) a threshold of 0.27 for an FCR analysis at level α = .1, and 10 of the 26 states have a statistically significant trend in ozone. An alternative way to perform cluster-wise analysis is to define a cluster as active if its mean β̄_j < −0.1. Table 6 gives the posterior probabilities that β̄_j < −0.1 for each state. All 26 states have a statistically significant trend in ozone using an FCR analysis at level 0.1.

7. Proofs

Here we prove Theorems 1 and 3. The proofs of Theorems 2 and 4 and the lemmas are provided in the web appendix.

7.1. Proof of Theorem 1

We first state a lemma, which is proved in the web appendix.

Lemma 1

Consider a decision rule δ = [I{T (s) < t}:s ∈ S]. If T = {T (s):s ∈ S} satisfies the MRC (3.3), then the mFDR level of δ monotonically increases in t.

1. Let θ = {θ(s):s ∈ S} and δ = (δ(s):s ∈ S) denote the unknown states and decisions, respectively. The loss function (3.2) can be written as

   $$L(\mathit{\theta },\mathit{\delta })=\lambda \nu (S_{FP})+\nu (S_{FN})={\int }_S\lambda \{1-\theta (s)\}\delta (s)d\nu (s)+{\int }_S\theta (s)\{1-\delta (s)\}d\nu (s).$$
   The posterior classification risk is

   $$\begin{array}{l}{E}_{\mathit{\theta }\mid {\mathit{X}}^n}\{L(\mathit{\theta },\mathit{\delta })\}={\int }_S[\delta (s)\lambda P\{\theta (s)=0\mid {\mathit{X}}^n\}+\{1-\delta (s)\}P\{\theta (s)=1\mid {\mathit{X}}^n\}]d\nu (s)\\ ={\int }_S\delta (s)[\lambda P\{\theta (s)=0\mid {\mathit{X}}^n\}-P\{\theta (s)=1\mid {\mathit{X}}^n\}]d\nu (s)+{\int }_{S}P(\theta (s)=1\mid {\mathit{X}}^n)d\nu (s)\end{array}$$
   Therefore, the optimal decision rule which minimizes the posterior classification risk (also the classification risk) is given by δ_OR = {δ_OR(s):s ∈ S}, where

   $${\delta }_{OR}(s)=I[\lambda P\{\theta (s)=0\mid {\mathit{X}}^n\}-P\{\theta (s)=1\mid {\mathit{X}}^n\}<0]=I[T_{OR}(s)<{(1+\lambda )}^{-1}].$$
2. We have assumed that G₀(t) = ∫_s P{θ(s) = 0, T_OR(s) < t}dν(s) and G₁(t) = ∫_SP{θ(s) = 1, T_OR(s) < t}dν(s) are differentiable. Let g₁(t) and g₀(t) be the derivatives. The goal is to show that g₁(t)/g₀(t) decreases in t for t ∈ (0, 1). Consider a weighted classification problem with loss function

   $$L(\mathit{\theta },\mathit{\delta })=\frac{1-t}{t}\nu (S_{FP})+\nu (S_{FN}).$$
   Suppose T_OR = {T_OR(s):s ∈ S} is used in the weighted classification problem and the threshold is c. By Fubini’s Theorem the classification risk is

   $$\begin{array}{l}E\left\{\frac{1-t}{t}\nu (S_{FP})+\nu (S_{FN})\right\}=\frac{1-t}{t}{\int }_{S}P\{\theta (s)=0,T_{OR}(s)<c\}d\nu (s)+{\int }_{S}P\{\theta (s)=1,T_{OR}(s)>c\}d\nu (s)\\ =\frac{1-t}{t}{G}_0(c)+{\int }_{S}P\{\theta (s)=1\}d\nu (s)-G_1(c)\end{array}$$
   The threshold c = t^* which minimizes the classification risk satisfies: t⁻¹(1 − t)g₀(t^*) = g₁(t^*). By part (a), the optimal threshold t^* = 1 + t⁻¹(1 − t)⁻¹ = t. Therefore we have

   $$\frac{g_1(t)}{g_0(t)}=\frac{1-t}{t},\text{for}\text{all}0<t<1,$$

   and the result follows.

3. Let T be a test statistic that satisfies the MRC (3.3). Lemma 1 indicates that for a given α ∈ (0, α^*) (α^* is the largest mFDR level when the threshold t = 1), there exists a threshold t(α) such that the mFDR level of δ = [I{T (s) < t(α)}:s ∈ S] is α, which completes the first part of the proof.

Let ERA(T, t(α)), ETPA(T, t(α)) and EFPA(T, t(α)) be the expected rejection area, expected true positive area and expected false positive area of the decision rule δ = [I{T (s) < t(α)}:s ∈ S], respectively. Then we have

$$\text{ERA}(\mathit{T},t(\alpha ))=E\left[{\int }_{S}I\{T(s)<t(\alpha )\}d\nu (s)\right]={\int }_{S}P\{T(s)<t(\alpha )\}d\nu (s).$$

By definition, ERA(T, t(α)) = ETPA(T, t(α)) + EFPA(T, t(α)). Also note that the mFDR level is exactly α. We conclude that ETPA(T, t(α)) = α∫_S P{T(s) < t(α)}dν(s), and EFPA(T, t(α)) = (1 − α)∫_SP{T (s) < t(α)}dν(s).

Now consider the oracle test statistic T_OR defined in (3.5). Part (b) of Theorem 1 shows that T_OR satisfies the MRC (3.3). Hence, from the first part of the proof of (c), there exists t_OR(α) such that δ_OR = [I{T_OR(s) < t_OR(α)}:s ∈ S] controls the mFDR at level α exactly. Consider a weighted classification problem with the following loss function

$$L(\mathit{\theta },\mathit{\delta })=\frac{1-t_{OR}(\alpha )}{t_{OR}(\alpha )}\nu (S_{FP})+\nu (S_{FN}).$$ (7.1)

Part (a) shows that the optimal solution to the weighted classification problem is δ_OR = [I{T_OR(s) < t_OR(α)}:s ∈ S]. The classification risk of δ_OR is

$$\begin{array}{l}E\{L(\mathit{\theta },{\mathit{\delta }}_{OR})\}=\frac{1-t_{OR}(\alpha )}{t_{OR}(\alpha )}E\left[{\int }_S\{1-\theta (s)\}{\delta }_{OR}(s)d\nu (s)\right]+E\left[{\int }_S\theta (s)\{1-{\delta }_{OR}(s)\}d\nu (s)\right]\\ =\frac{1-t_{OR}(\alpha )}{t_{OR}(\alpha )}\text{EFPA}({\mathit{T}}_{OR},t_{OR}(\alpha ))+{\int }_{S}P\{\theta (s)=1\}d\nu (s)-\text{ETPA}({\mathit{T}}_{OR},t_{OR}(\alpha ))\\ =\left\{\frac{\alpha -t_{OR}(\alpha )}{t_{OR}(\alpha )}\right\}\text{ERA}({\mathit{T}}_{OR},t_{OR}(\alpha ))+{\int }_{S}P\{\theta (s)=1\}d\nu (s)\end{array}$$

The last equation is due to the facts that ETPA(T, t(α)) = α∫_S P{T(s) < t(α)}dν(s), EFPA(T, t(α)) = (1 − α)∫_SP{T(s) < t(α)}dν(s) and ETPA(T, t(α)) = αERA(T, t(α)).

According to a Markov type inequality, double expectation theorem, and the fact that ETPA(T, t(α)) = αERA(T, t(α)), we conclude that

$$\begin{array}{l}{t}_{OR}(\alpha ){\int }_{S}E[I\{T_{OR}(s)<t_{OR}(\alpha )\}]d\nu (s)>{\int }_{S}E[I\{T_{OR}(s)<t_{OR}(\alpha )\}{T}_{OR}(s)]d\nu (s)\\ ={\int }_{S}E[T_{OR}(s)<t_{OR},\theta (s)=0]d\nu (s)\\ =\alpha {\int }_{S}E[I\{T_{OR}(s)<t_{OR}(\alpha )\}]d\nu (s)\end{array}$$

Hence we always have t_OR(α) − α > 0.

Next we claim that for any decision rules δ = [I{T (s) < t(α)}:s ∈ S] in , the following result holds: ERA(T, t(α)) ≤ ERA(T_OR, t_OR(α)). We argue by contradiction. If there exists δ^* = [I{T ^*(s) < t^*(α)}:s ∈ S] such that

$$\text{ERA}({\mathit{T}}^{\ast },t^{\ast }(\alpha ))>\text{ERA}({\mathit{T}}_{OR},t_{OR}(\alpha )).$$ (7.2)

Then when δ^* is used in the weighted classification problem with loss function (7.1), the classification risk of δ^* is

$$\begin{array}{l}E\{L(\mathit{\theta },{\mathit{\delta }}^{\ast })\}=\left\{\frac{\alpha -t_{OR}(\theta )}{t_{OR}(\alpha )}\right\}\text{ER}A({\mathit{T}}^{\ast },t^{\ast }(\alpha ))+{\int }_{S}P\{\theta (s)=1\}d\nu (s)\\ <\left\{\frac{\alpha -t_{OR}(\alpha )}{t_{OR}(\alpha )}\right\}\text{ERA}({\mathit{T}}_{OR},t_{OR}(\alpha ))+{\int }_{S}P\{\theta (s)=1\}d\nu (s)\\ =E\{L(\mathit{\theta },{\mathit{\delta }}_{OR})\},\end{array}$$

The first equation holds because δ(T^*, t^*(α)) is also an α level mFDR procedure. This contradicts the result in Theorem 1, which claims that δ_OR minimizes the classification risk with loss function (7.1).

Therefore we claim that δ_OR has the largest ERA, hence the largest ETPA (note we always have ETPA=αERA) and the smallest missed discovery region MDR among all mFDR procedures at level α in .

7.2. Proof of Theorem 3

We first state and prove a lemma. Define θ(s) = I{μ(s) ∈ A^c} and θ^m(s) = I{μ^m(s) ∈ A^c}, where A = [A_l, A_u] is the indifference region.

Lemma 2

Consider the discrete approximation based on a sequence of partitions of the spatial domain { $S={\cup }_{i=1}^m{S}_i:m=1,2,\cdots$}. Then under the conditions of the theorem, we have ∫_SP{θ(s) ≠ θ^m(s)}dν(s) → 0 as m → ∞.

Proof of Theorem 3

(a). Suppose T_OR(s) = P_Ψ{θ(s) = 0|Xⁿ} is used for testing. Then Procedure 1 corresponds to the decision rule δ^m = {δ^m(s):s ∈ S}, where ${\delta }^m(s)={\sum }_{i=1}^{m}I\{T_{OR}(s_i)<t\}I(s\in S_i)$. We assume that r pixels are rejected and let R_r be the rejected area. The FDR level of δ^m is

$$\begin{array}{l}\text{FDR}\le E\{\frac{{\int }_S\{1-\theta (s)\}{\delta }^m(s)d\nu (s)}{\nu (R_r)\vee c_0}\}\\ =E\left(\frac{1}{\nu (R_r)\vee c_0}\left[\sum _{i=1}^m\delta (s_i){\int }_{S_i}E\{1-\theta (s)\mid {\mathit{X}}^n\}d\nu (s)\right]\right)\\ =E\left(\frac{1}{\nu (R_r)\vee c_0}\left[\sum _{i=1}^m\delta (s_i)T_{OR}(s_i)\nu (S_i)+\sum _{i=1}^m\delta (s_i){\int }_{S_i}E\{\theta (s_i)-\theta (s)\mid {\mathit{X}}^n\}d\nu (s)\right]\right)\\ \le E\left\{\frac{1}{\nu (R_r)\vee c_0}\sum _{i=1}^r{T}_{OR}^{(i)}\nu S_{(i)}\right\}+Z_m,\end{array}$$

where Z_m = E {ν(R_r) ∨ c₀}⁻¹∫_SE{θ(s) − θ^m(s)|Xⁿ}δ^m(s)dν(s). The second equality follows from double expectation theorem. The third equality can be verified by first adding and subtracting θ(s_i), expanding the sum, and then simplifying.

Next note that an upper bound for the random quantity {ν(R_r) ∨ c₀}⁻¹ is given by $c_0^{-1}$. Applying Lemma 2,

$$\begin{array}{l}{Z}_m\le \frac{1}{c_0}{\int }_{S}E[{\delta }^{(m)}(s)E\{\theta (s)-{\theta }^m(s)\mid {\mathit{X}}^n\}]d\nu (s)\\ \le \frac{1}{c_0}{\int }_{S}P\{\theta (s)\ne {\theta }^m(s)\}d\nu (s)\to 0.\end{array}$$

Since the operation of procedure δ^m guarantees that

$$\frac{1}{\nu (R_r)\vee c_0}\sum _{i=1}^r{T}_{OR}^{(i)}\nu (S_{(i)})\le \alpha$$

for all realizations of Xⁿ, the FDR is controlled at level α asymptotically.

(b). Suppose that r pixels are rejected by Procedure 2. Consider δ^m(s) defined in part (a). Then the FDX at tolerance level τ is

$$\begin{array}{l}{\text{FDX}}_{\tau }\le P\left[{\{\nu (R_r)\vee c_0\}}^{-1}{\int }_S{\delta }^m(s)\{1-\theta (s)\}d\nu (s)>\tau \right]\\ =P\left[{\{\nu (R_r)\vee c_0\}}^{-1}\sum _{i=1}^m\delta (s_i){\int }_{S_i}\{1-\theta (s)\}d\nu (s)>\tau \right]\\ =P\left[{\{\nu (R_r)\vee c_0\}}^{-1}\sum _{i=1}^m\delta (s_i)\{1-\theta (s_i)\}\nu (S_i)+{\{\nu (R_r)\vee c_0\}}^{-1}{\int }_S{\delta }^m(s)\{{\theta }^m(s)-\theta (s)\}d\nu (s)>\tau \right]\\ \equiv P(A+B>\tau ).\end{array}$$

where A and B are the corresponding terms on the left side of the inequality. Let ε₀ ∈ (0, τ) be the small positive number defined in Procedure 2. Then A+B > τ implies that A > τ−ε₀ or B > ε₀. It follows that

$$P\{A+B>\tau \}\le P\{A>\tau -{\epsilon }_0\text{or}B>{\epsilon }_0\}\le P(A>\tau -{\epsilon }_0)+P(B>{\epsilon }_0).$$

Let I denote an indicator function. Apply the double expectation theorem to the first term P(A > τ − ε₀), we have

$$P(A>\tau -{\epsilon }_0)=E[I\{A>\tau -{\epsilon }_0\}]=E\{P(A>\tau -{\epsilon }_0\mid X^n)\}.$$

Replacing A and B by their original expressions, we have

$${\text{FDX}}_{\tau }\le E\left(P\left[{\{\nu (R_r)\vee c_0\}}^{-1}\sum _{i=1}^m\delta (s_i)\{1-\theta (s_i)\}\nu (S_i)>\tau -{\epsilon }_0|{\mathit{X}}^n\right]\right)+P\left[{\{\nu (R_r)\vee c_0\}}^{-1}{\int }_S{\delta }^m(s)\{{\theta }^m(s)-\theta (s)\}d\nu (s)\ge {\epsilon }_0\right]$$

It is easy to see that

$${\text{FDX}}_{\tau ,r}^m\ge P\left[{\{\nu (R_r)\vee c_0\}}^{-1}\sum _{i=1}^m\delta (s_i)\{1-\theta (s_i)\}\nu (S_i)>\tau -{\epsilon }_0|{\mathit{X}}^n\right].$$

The operation property of Procedure 2 guarantees that ${\text{FDX}}_{\tau ,r}^m\le \alpha$ for all realizations of Xⁿ. Therefore the first term of in the expression of FDX_τ is less than α. The second term in the upper bound of FDX_τ satisfies

$$\begin{array}{l}P\left[{\{\nu (R_r)\vee c_0\}}^{-1}{\int }_S{\delta }^m(s)\{{\theta }^m(s)-\theta (s)\}d\nu (s)\ge {\epsilon }_0\right]\le {({\epsilon }_0{c}_0)}^{-1}E\left[{\int }_S{\delta }^m(s)\mid {\theta }^m(s)-\theta (s)\mid d\nu (s)\right]\\ \le {({\epsilon }_0{c}_0)}^{-1}{\int }_{S}P\{\theta (s)\ne {\theta }^m(s)\}d\nu (s)\to 0\end{array}$$

and the desired result follows.

Table 1.

Cluster analysis for the ozone data. “State ave trend” is the posterior mean of the average of the β(S) at the grid cells in the state.

State	Number of Monitors	Number of grid points	State ave trend	Prob state ave < −0.1	Proportion non-null	Post prob active
Alabama	25	234	−0.19	0.78	0.65	0.25
Connecticut	9	28	−0.38	0.97	0.92	0.86*
Delaware	6	8	−0.36	0.95	0.91	0.81*
Florida	43	235	−0.53	1.00	0.93	0.93*
Georgia	23	271	−0.54	1.00	0.96	0.97*
Illinois	35	277	−0.66	1.00	0.98	0.99*
Indiana	41	185	−0.32	0.98	0.84	0.68
Kentucky	32	195	−0.25	0.91	0.75	0.45
Maine	8	159	−0.51	0.99	0.94	0.90*
Maryland	19	55	−0.30	0.96	0.83	0.64
Massachusetts	14	36	−0.26	0.91	0.76	0.51
Michigan	26	296	−0.50	1.00	0.92	0.92*
Mississippi	8	220	−0.27	0.87	0.76	0.52
New Hampshire	13	46	−0.23	0.85	0.73	0.46
New Jersey	13	39	−0.27	0.92	0.81	0.59
New York	33	262	−0.15	0.65	0.59	0.18
North Carolina	41	227	−0.23	0.88	0.71	0.33
Ohio	48	202	−0.16	0.77	0.62	0.15
Pennsylvania	46	219	−0.23	0.90	0.70	0.20
Rhode Island	3	8	−0.47	0.99	0.98	0.96*
South Carolina	20	144	−0.42	0.98	0.89	0.81*
Tennessee	25	185	−0.25	0.89	0.73	0.41
Vermont	2	55	−0.18	0.69	0.63	0.34
Virginia	23	188	−0.25	0.88	0.73	0.40
West Virginia	9	115	−0.24	0.83	0.72	0.45
Wisconsin	31	292	−0.64	0.98	0.92	0.86*

States which is significant at α = 0.1 are denoted “*”.