Structural pursuit over multiple undirected graphs

Summary

Gaussian graphical models are useful to analyze and visualize conditional dependence relationships between interacting units. Motivated from network analysis under di erent experimental conditions, such as gene networks for disparate cancer subtypes, we model structural changes over multiple networks with possible heterogeneities. In particular, we estimate multiple precision matrices describing dependencies among interacting units through maximum penalized likelihood. Of particular interest are homogeneous groups of similar entries across and zero-entries of these matrices, referred to as clustering and sparseness structures, respectively. A non-convex method is proposed to seek a sparse representation for each matrix and identify clusters of the entries across the matrices. Computationally, we develop an e cient method on the basis of di erence convex programming, the augmented Lagrangian method and the block-wise coordinate descent method, which is scalable to hundreds of graphs of thousands nodes through a simple necessary and sufficient partition rule, which divides nodes into smaller disjoint subproblems excluding zero-coe cients nodes for arbitrary graphs with convex relaxation. Theoretically, a finite-sample error bound is derived for the proposed method to reconstruct the clustering and sparseness structures. This leads to consistent reconstruction of these two structures simultaneously, permitting the number of unknown parameters to be exponential in the sample size, and yielding the optimal performance of the oracle estimator as if the true structures were given a priori. Simulation studies suggest that the method enjoys the benefit of pursuing these two disparate kinds of structures, and compares favorably against its convex counterpart in the accuracy of structure pursuit and parameter estimation.

1 Introduction

Graphical models are widely used to describe relationships among interacting units. Major components of the models are nodes that represent random variables, and edges encoding conditional dependencies between the nodes. Of great current interest is the identification of certain lower-dimensional structures for undirected graphs. The central topic of this paper is maximum penalized likelihood estimation of multiple Gaussian graphical models for simultaneously pursuing two disparate kinds of structures–sparseness and clustering.

In the literature on Gaussian graphical models, the current research e ort has concentrated on reconstruction of a single sparse graph. Methods to exploit matrix sparsity include [1, 5, 11, 13, 14, 15, 24], among others. For multiple Gaussian graphical models, existing approaches mainly focus on either exploring temporal smoothing structure [7, 25] or encour aging common sparsity across the networks [6, 10]. In this paper, we focus on pursuing both clustering and sparseness structures over multiple graphs, including temporal clustering as a special case while allowing for abrupt changes of structures over graphs. For multiple graphs without a temporal ordering, our method enables to identify possible element-wise heterogeneity among undirected graphs. This is motivated by heterogeneous gene regulatory networks corresponding to disparate cancer subtypes [18, 21]. In such a situation, the overall associations among genes remain similar for each network, whereas specific pathways and certain critical nodes (genes) may be di erentiated under disparate conditions.

For multiple Gaussian graphical models, estimation is challenging due to enormous can didate graphs of order 2^Lp2, where p is the total number of nodes and L is total number of graphs. To battle the curse of dimensionality, we explore two dissimilar types of structures simultaneously: (1) sparseness within each graph and (2) element-wise clustering across graphs. The benefit of this exploration is three-fold. First, it goes beyond sparseness pursuit alone for each graph, which is usually inadequate given a large number of unknown parameters relative to the sample size, as demonstrated in four numerical examples in Section 5. Second, borrowing information across graphs enables us to detect the changes of sparseness and clustering structures over the multiple graphs. Third, pursuit of these two structures at the same time is suited for our problem, which seeks both similarities and di erences among the multiple graphs.

To this end, we propose a regularized/constrained maximum likelihood method for simultaneous pursuit of sparseness and clustering structures. Computationally, we develop a strategy to convert the optimization involving matrices to a sequence of much simpler quadratic problems. Most critically, we derive a necessary and sufficient partition rule to partition the nodes into disjoint subproblems excluding zero-coe cient nodes for multiple arbitrary graphs with convex relaxation, where the rule is applied before computation is performed. Such a rule has been used in [12] for convex estimation of a single matrix, but has not been available for multiple arbitrary graphs, to our knowledge. This makes e cient computation possible for multiple large graphical models, which otherwise is rather di cult if not impossible. Theoretically, we develop a novel theory for the proposed method, and show that it enables to reconstruct the oracle estimator as if the true sparseness and element-wise clustering structures were given a priori, which leads to reconstruction of the two types of structures consistently. This occurs roughly when the size of L matrices p²L is of order exp(An), where p is the dimension of the matrices and A is related to the Hessian matrices of the negative log-determinant of the true precision matrices and the resolution level for simultaneous pursuit of sparseness and element-wise clustering, c.f., Corollary 2. Moreover, we quantify the improvement due to structural pursuit beyond that of sparsity.

The rest of this article is organized as follows. Section 2 introduces the proposed method. Section 3 is devoted to estimation of partial correlations across multiple graphical models, and develops computational tools for e cient computation. Section 4 presents a theory concerning the accuracy of structural pursuit and parameter estimation, followed by some numerical examples in Section 5 and an application to signaling network inference in Section 6. Section 7 discusses various issues in modeling. Finally, the appendix contains proofs.

2 Proposed method

Consider the L−sample problem with the l−th sample ${\mathit{X}}_1^{\left(l\right)},\cdots ,{\mathit{X}}_{n_l}^{\left(l\right)}$ from $\mathcal{N}({\mu }_l,{\Sigma }_l)$; l = 1,...,L, we estimate Ω = (Ω₁,..., Ω_L), where ${\Omega }_l={\Sigma }_l^{-1}$ is the p × p inverse covariance matrix and positive definite, denoted by ${\Omega }_l\succ 0$, μ_l and Σ_l are the corresponding mean vector and covariance matrix, and the sample size $n={\sum }_{l=1}^L{n}_l$

For maximum likelihood estimation, the profile likelihood for Ω, after μ₁,..., μ_L are maximized out, is proportional to

$$\sum _{l=1}^L{n}_l(\log \det \left({\Omega }_l\right)-tr\left({\mathit{S}}_l{\Omega }_l\right)),$$ (1)

where ${\stackrel{‒}{\mathit{X}}}_l=n_l^{-1}{\sum }_{i=1}^{n_l}{\mathit{X}}_i^{\left(l\right)}$ and ${\mathit{S}}_l=n_l^{-1}{\sum }_{i=1}^{n_l}({\mathit{X}}_i^{\left(l\right)}-{\stackrel{‒}{\mathit{X}}}_l){({\mathit{X}}_i^{\left(l\right)}-{\stackrel{‒}{\mathit{X}}}_l)}^T$ are the corresponding sample mean and covariance matrix, det and tr denote the determinant and trace. In (1), the number of unknown parameters in Ω can greatly exceed the sample size n.

2.1 General penalized multiple precision matrices estimation

TO avoid non-identifiability in (1) and encourage low dimensional structures, we propose a regularized maximum likelihood approach through penalty functions J_jk(·):

$${\mathrm{maximize}}_{\Omega \succ 0}S\left(\Omega \right)=\sum _{l=1}^L{n}_l(\log \det \left({\Omega }_l\right)-tr\left({\mathit{S}}_l{\Omega }_l\right))-\sum _{j\ne k}{J}_{jk}({\omega }_{jk1},\cdots ,{\omega }_{jkL}),$$ (2)

where Ω = (Ω₁,... ,Ω_L) and only the off-diagonals {ω_jkl} of Ω_l are regularized. Note that J_jk(·) could be any function that penalizes jk-th entries across Ω_l's. This encompasses many existing penalty-based approaches for multiple Gaussian graphical models [6, 22] as special cases.

In general, the maximization problem (2) involving L matrices is computationally difficult. To meet the computational challenges, we develop a general block-wise coordinate descent strategy to reduce (2) to an iterative procedure involving much easier subproblems. Before proceeding, we introduce some notations. Let the jth row (or column) of Ω_l be ω_jl, let ω_−jl = (ω_j1l, . . . ,ω_j(j−1)l,... ,ω_j(j+1)l, . . . ,ω_jpl) be a (p — 1)-dimensional vector, excluding the jth component of ω_jl, and Ω_−jl be the sub-matrix without the jth row and column of Ω_l, and ${\Omega }_{-jl}^{-1}$ be the inverse of Ω_−jl.

Our proposed method maximizes (2) by sweeping each row (or column) of Ω across l = 1,... ,L. Using the property that $\det \left({\Omega }_l\right)=\det \left({\Omega }_{-jl}({\omega }_{jjl}-{\omega }_{-jl}^T{\Omega }_{-jl}^{-1}{\omega }_{-jl})\right)$ with ^T indicating the transpose, we rewrite (2), after ignoring constant terms, as a function

$$\sum _{l=1}^L{n}_l\left(\log ({\omega }_{jjl}-{\omega }_{-jl}^T{\Omega }_{-jl}^{-1}{\omega }_{-jl})\right)-s_{jjl}{\omega }_{jjl}-2s_{-jl}^T{\omega }_{-jl})-\sum _{k\ne j}{J}_{jk}({\omega }_{jk1},\cdots ,{\omega }_{jkL}).$$ (3)

First, for each fixed row (or column) of Ω across l = 1,... ,L, we maximize (3) over the diagonals (ω_jj1,... ,ω_jjl) given the corresponding o -diagonals (ω_−j1,..., ω_−jl). Setting the partial derivatives of (3) in the diagonals to be zero yields the profile maximizer of (2)

$${\widehat{\omega }}_{jjl}=1∕s_{jjl}+{\omega }_{-jl}^T{\Omega }_{-jl}^{-1}{\omega }_{-jl},l=1,\cdots ,L.$$ (4)

Second, substituting (4) into (3) yields the negative profile likelihood of (2) for (ω_−jl,... ,ω_−jl)

$$\sum _{l=1}^L{n}_l(s_{jjl}{\omega }_{-jl}^T{\Omega }_{-jl}^{-1}{\omega }_{-jl}+2{\mathit{s}}_{-jl}^T{\omega }_{-jl})+\sum _{k\ne j}{J}_{jk}({\omega }_{jk1},\cdots ,{\omega }_{jkL}).$$ (5)

Third, the aforementioned process is repeated for each rows (or columns) of Ω until a certain stopping criterion is satisfied. By Theorem 1, profiling is equivalent to the original problem for separable convex penalty functions summarized as follows.

Theorem 1 Iteratively minimizing (5) over the off-diagonals (ω_−j1,... ,ω_−jL) and updating diagonals ω_jjl by (4); j = 1,... ,p, l = 1,... ,L converges to a local maximizer of (2). Moreover, if J_jk(·) are convex, it converges to a global maximizer.

Theorem 1 reduces (2) to iteratively solving (5) which is quadratic in its argument. On this ground we design e cient methods for solving (2) with a specific choice of J_jk(·) next.

2.2 Pursuit of sparseness and clustering structures

A zero element in Ω_l corresponds to conditional independence between two components of Y^(l) given its other components [9]. Thus, within each precision matrix Ω_l, estimating its elements reconstructs its graph structure, where a zero-element of Ω_l corresponds to no edges between the two nodes, encoding conditional independence. In addition, the nodes connecting many other nodes are identified, called network hubs. On the other hand, over multiple precision matrices, estimating element-wise clustering structure can reveal the change of sparseness and clustering structures.

To detect clustering structures, consider element-wise clustering of entries of Ω₁,... ,Ω_L based on possible prior knowledge. The prior knowledge is specified loosely in an undirected graph $\mathcal{U}$ with each node corresponding to a triplet (j, k, l); 1 ≤ j < k ≤ p, 1 ≤ l ≤ L. That is, an edge between node (j, k, l) and (j, k, l′) means that the (j, k)th entry of Ω_l and the (j, k)th entry of Ω_l′ tend to be similar a priori and thus can be pushed to share the same value. Specifically, let ${\mathcal{E}}_{jk}$ denote a set of edges between two distinct nodes (j, k, l) ≠ = (j, k, l′) of $\mathcal{U}$, where (l, l′) $\in {\mathcal{E}}_{jk}$ indicates a connection between the two nodes (j, k, l),(j, k, l′). To identify homogeneous subgroups of off-diagonals {ω_jkl} of Ω_l across l = 1,... ,L over $\mathcal{U}$, including the group of zero-elements, we propose a non-convex penalty of the form

$$J_{jk}({\omega }_{jk1},\dots ,{\omega }_{jkL})={\lambda }_1\sum _{l=1}^L{J}_{\tau }\left(\mid {\omega }_{jkl}\mid \right)+{\lambda }_2\sum _{(l,l^{\prime })\in {\mathcal{E}}_{jk}}{J}_{\tau }\left(\mid {\omega }_{jkl}-{\omega }_{jk{l}^{\prime }}\mid \right),$$ (6)

to regularize (2), where λ₁ and λ₂ are nonnegative tuning parameters controlling the degrees of sparseness and clustering, $J_{\tau }\left(z\right)=\min (\mid z\mid ,\tau )$ is the truncated L₁-penalty of [17], called TLP in what follows, which, after rescaled by $\frac{1}{\tau }$, approximates the L₀-function when tuning parameter $\tau >0$ tends to 0⁺.

Note that our approach is applicable to a variety of applications by specifying the graph $\mathcal{U}$. For time varying graphs, our method can be used to detect the change of clustering structure, where ${\mathcal{E}}_{jk}$ is a serial graph as in the fused Lasso [19], and a serial temporal relation is defined only for elements in adjacent matrices. One key di erence between our method and the smoothing method [25, 7] is that it enables to accommodate abrupt changes of structures over networks. For multiple graphs without a serial ordering, the proposed method enables to identify possible element-wise heterogeneity among undirected graphs, such as gene regulatory networks corresponding to disparate cancer subtypes [18, 21]. Heterogeneity of this type can be dealt with by specifying a complete graph for each ${\mathcal{E}}_{jk}$.

3 Computation

This section proposes a relaxation method to treat non-convex penalties in (6). For large-scale problems, a partition rule may be useful, which breaks large matrices into many small ones to process separately. A novel necessary and sufficient partition rule is derived for our non-convex penalization method as well as its convex counterpart, generalizing the results for single precision matrix estimation [12, 22].

3.1 Non-convex optimization

For the non-convex minimization (2) with (6), we develop a relaxation method by solving a sequence of convex problems. This method integrates di erence convex (DC) programming with block-wise coordinate descent method based on the foregoing strategy.

For DC programming, we first decompose S(Ω) into a di erence of two convex functions: S(Ω) = S₁(Ω) – S₂(Ω), with

$$\begin{array}{cc}\hfill & S\left(\Omega \right)=S_1\left(\Omega \right)-S_2\left(\Omega \right),\text{with}\hfill \\ \hfill & S_1\left(\Omega \right)=\sum _{l=1}^L{n}_l(\log \det \left({\Omega }_l\right)-tr\left({\mathit{S}}_l{\Omega }_l\right))+{\lambda }_1\sum _{(j,k,l):j\ne k}\mid {\omega }_{jkl}\mid +{\lambda }_2\sum _{1\le j\ne k\le p}\sum _{(l,l^{\prime })\in {\mathcal{E}}_{jk}}\mid {\omega }_{jkl}-{\omega }_{j^{\prime }{k}^{\prime }{l}^{\prime }}\mid ,\hfill \\ \hfill & S_2\left(\Omega \right)=\sum _{j\ne k}{\lambda }_1\sum _{l=1}^L\max (\mid {\omega }_{jkl}\mid -\tau ,0)+{\lambda }_2\sum _{1\le j\ne k\le p}\sum _{(l,l^{\prime })\in {\mathcal{E}}_{jk}}\max (\mid {\omega }_{jkl}-{\omega }_{j^{\prime }{k}^{\prime }{l}^{\prime }}\mid -\tau ,0),\hfill \end{array}$$ (7)

where a DC decomposition of $J_{\tau }\left(\mid z\mid \right)=\mid z\mid -\max (\mid z\mid -\tau ,0)$ is used. Then the trailing convex function S₂(Ω) is iteratively approximated by its minorization, say at iteration m, ${\lambda }_1{\sum }_{l=1}^L{\sum }_{j\ne k}(\mathbb{I}(\mid {\widehat{\omega }}_{jkl}^{\left(m\right)}\mid \le \tau )\mid {\omega }_{jkl}\mid +{\lambda }_2{\sum }_{1\le j\ne k\le p}{\sum }_{(l,l^{\prime })\in \mathcal{E}}\mathbb{I}(\mid {\widehat{\omega }}_{jkl}^{\left(m\right)}-{\widehat{\omega }}_{jk{l}^{\prime }}^{\left(m\right)}\mid \le \tau )\mid {\omega }_{jkl}-{\omega }_{jk{l}^{\prime }}\mid$. This obtained through minorization $\mid z^{\left(m\right)}\mid +\zeta \left(\mid z^{\left(m\right)}\mid \right)(\mid z\mid -\mid z^{\left(m\right)}\mid$ of $\max (\mid z\mid -\tau ,0)$ at $\mid {\widehat{\omega }}_{jkl}^{\left(m\right)}\mid$, which is the solution at iteration m − 1, where $\zeta \left(\mid z^{\left(m\right)}\mid \right)$ is the gradient of $\max (\mid z\mid -\tau ,0)$ at $\mid z^{\left(m\right)}\mid$; see [17] for more discussions about minorization of this type. At iteration m, the cost function to minimize is

$$-\sum _{l=1}^L{n}_l(\log \det \left({\Omega }_l\right)-tr\left({\mathit{S}}_l{\Omega }_l\right))+{\lambda }_1\sum _{(j,k,l)\in E^{\left(m\right)}}\mid {\omega }_{jkl}\mid +{\lambda }_2\sum _{\{(j,k,l),(j,k,l^{\prime })\}\in F^{\left(m\right)}}\mid {\omega }_{jkl}-{\omega }_{jk{l}^{\prime }}\mid$$ (8)

subject to ${\Omega }_l\succ 0$; l = 1, ···, L, where $E^{\left(m\right)}=\{(j,k,l):\mid {\widehat{\omega }}_{jkl}^{\left(m\right)}\mid \le \tau ,j\ne k\}$; $F^{\left(m\right)}=\{\{(j,k,l),(j,k,l^{\prime })\}:(l,l^{\prime })\in {\mathcal{E}}_{jk},\mid {\widehat{\omega }}_{jkl}^{\left(m\right)}-{\widehat{\omega }}_{jk{l}^{\prime }}^{\left(m\right)}\mid \le \tau \}$.

To solve (8), we apply Theorem 1 to iteratively minimize:

$$\sum _{l=1}^L{n}_l(s_{jjl}{\omega }_{-jl}^T{\Omega }_{-jl}^{-1}{\omega }_{-jl}+2{\mathit{s}}_{-jl}^T{\omega }_{-jl})+{\lambda }_1\sum _{(j,k,l)\in E^{\left(m\right)}}\mid {\omega }_{jkl}\mid +{\lambda }_2\sum _{\{(j,k,l),(j,k,l^{\prime })\}\in F^{\left(m\right)}}\mid {\omega }_{jkl}-{\omega }_{jk{l}^{\prime }}\mid ,$$ (9)

and update diagonal elements using (4). This quadratic problem can then be e ciently solved using augmented Lagrangian methods as in [26].

Unlike the coordinate descent method updating one component at a time, we update one component of ζ and two components (ω_jkl, ω_jjl) for Ω_l at the same time.

In (9), computation of ${\Omega }_{-jl}^{-1}$ by directly inverting Ω_−jl has a complexity of O(p³) operations for each (j, l). For e cient computation, we utilize the special property of our sweeping operator in that the (p − 1)² elements of Ω_l are unchanged except one row and one column are swept, in addition to the rank one property for updating the formula. In (9), we derive an analytic formula through block-wise inversion and the Neumann formula of a square matrix, to compute (Ω_−jl)⁻¹ from $({\omega }_{jjl},{\omega }_{-jl},{\Omega }_l^{-1})$ and ${\Omega }_l^{-1}$ from $({\omega }_{jjl},{\omega }_{-jl},{\left({\Omega }_{-l}^{-1}\right)}_{-j})$ for each (j, l). That is,

$${\left({\Omega }_{-jl}\right)}^{-1}={\left({\Omega }_l^{-1}\right)}_{-j}-\frac{{\left({\Omega }_l^{-1}\right)}_j{\left({\Omega }_l^{-1}\right)}_j^T}{{\left({\Omega }_l^{-1}\right)}_{jj}},$$ (10)

$${\Omega }_l^{-1}=\left(\begin{array}{cc}\hfill {\left({\Omega }_l^{-1}\right)}_{-j}+b\mathit{a}{\mathit{a}}^T\hfill & \hfill -b\mathit{a}\hfill \\ \hfill -b{\mathit{a}}^T\hfill & \hfill b\hfill \end{array}\right),\mathit{a}={\left({\Omega }_l^{-1}\right)}_{-j}{\omega }_{-jl},b={({\omega }_{jjl}-{\mathit{a}}^T{\omega }_{-jl})}^{-1}.$$ (11)

This amounts to O(p²) operations.

The foregoing discussion leads to our DC block-wise coordinate descent algorithm through sweeping operations over p(p−1) off-diagonals of (Ω₁,... ,Ω_L), with each operation involving the L corresponding off-diagonals.

Algorithm 1:

Step 1. (Initialization) Set ${\widehat{\Omega }}_l^{\left(0\right)}=I$; l = 1, ···, L, E⁽⁰⁾ = {(j,k,l) : 1 ≤ j ≠ k ≤ p, 1 ≤ l ≤ L}, $F^{\left(0\right)}=\mathcal{E}$, m = 0 and precision tolerance ε = 10⁻⁵ for Step 2.

Step 2. (Iteration) At current iteration m, $\text{initialize}\Omega ={\widehat{\Omega }}^{\left(m\right)}$. Then solve (8) applying the block-wise coordinate descent algorithm to update Ω to yield ${\widehat{\Omega }}^{(m+1)}$. And set $E^{(m+1)}=\{(j,k,l):\mid {\widehat{\omega }}_{jkl}^{(m+1)}\mid \le \tau ,j\ne k\}$; $F^{(m+1)}=\{\{(j,k,l),(j^{\prime },k^{\prime },l^{\prime })\}:(l,l^{\prime })\in {\mathcal{E}}_{jk},\mid {\widehat{\omega }}_{jkl}^{(m+1)}-{\widehat{\omega }}_{j^{\prime }{k}^{\prime }{l}^{\prime }}^{(m+1)}\mid \le \tau \}$. Specifically,

1. For each row (column) index j = 1,... ,p, compute ${\Omega }_{-jl}^{-1}$ using (10); l = 1,... ,L. Solve (9) to obtain ${\widehat{\omega }}_{-jl}^{\left(m\right)}$ and then compute ${\widehat{\omega }}_{jjl}^{\left(m\right)}$ through (4); l = 1,... ,L. Update ${\Omega }_l^{\left(m\right)}$ with its jth row replaced by $({\widehat{\omega }}_{jjl}^{\left(m\right)},{\widehat{\omega }}_{-jl}^{\left(m\right)})$ and its jth column by symmetry. Finally update ${\left({\Omega }_l^{\left(m\right)}\right)}^{-1}$ using (11). Go to next iteration j + 1 until all rows of ${\Omega }_l^{\left(m\right)}$ have been swept.

2. Repeat a) until the decrement of the objective function is less than ε. After convergence, update Ω to yield ${\widehat{\Omega }}^{(m+1)}=\Omega$ based on a).

Step 3. (Stopping criterion) Terminate when E^(m+1) = E^(m) and F^(m+1) = F^(m), otherwise, repeat Step 2 with m = m + 1.

The overall complexity of Algorithm 1 is of order O(p³L²). And real computational time of our algorithm depends highly on values of λ₁, λ₂ and the number of iterations. In Example 1, it takes about 30 seconds for one simulation run with (p, L) = (200,4) over 100 grids on a 8-core computer with Intel(R) Core(TM) i7-3770 processors and 16GB of RAM.

3.2 Partition rule for large-scale problems

This section establishes a necessary and sufficient partition rule for our non-convex penal ization method and its convex counterpart using the sample covariances, permitting fast computation for large-scale problems by partitioning nodes into disjoint subsets excluding the zero-coeffcient subset then applying the proposed method to each nonzero subset. Such a result exists only for a single matrix or a special case of multiple matrices, c.f., [12, 22].

In what follows, we only consider the case where ${\mathcal{E}}_{jk}=\mathcal{E}$ are identical. Given this graph $\mathcal{G}=(V,\mathcal{E})$, with $(V=\{1,\cdots ,L\},\mathcal{E}={\mathcal{E}}_{jk},1\le j<k\le p)$ denoting the node and edge sets, we write l ~ l′ if $(l,l^{\prime })\in \mathcal{E}$, or two nodes are connected. First consider the convex grouping penalty over $\mathcal{G}$, followed by a general case, where the penalized log-likelihood is

$$\sum _{l=1}^L\left(n_l(-\log \det \left({\Omega }_l\right)=tr\left({\Omega }_l{\mathit{S}}_l\right))+{\lambda }_1{\Vert {\Omega }_{l,\mathrm{off}}\Vert }_1\right)+{\lambda }_2\sum _{l\sim l^{\prime }}{\Vert {\Omega }_{l,\mathrm{off}}-{\Omega }_{l^{\prime },\mathrm{off}}\Vert }_1,$$ (12)

where Ω_l,off denotes the off-diagonal elements of Ω_l and S_l = (s_jkl)_1≤j,k≤p are the sample covariance matrices, l = 1,... ,L.

The next theorem derives a necessary and sufficient condition for the jkth element of ${\widehat{\Omega }}_l$ ${\widehat{\Omega }}_{jkl}=0$ across l = 1,... ,L, for $j\in \mathcal{J},k\in {\mathcal{J}}^c$, where $({\widehat{\Omega }}_1,\cdots ,{\widehat{\Omega }}_L)$ is the minimizer of (12), and $\mathcal{J}\subset \{1,\cdots ,p\}$ is any subset. This partitions the node set into disjoint subsets of connected nodes, with no connections between these subsets.

Theorem 2 (Partition rule for (12)) ${\widehat{\Omega }}_{jkl}=0$ for all $j\in \mathcal{J};k\in {\mathcal{J}}^c$ and l = 1,... ,L, if and only if (s_jk1,... ,s_jkL) $\in \mathcal{S}$, for all $j\in \mathcal{J},k\in {\mathcal{J}}^c$, where $\mathcal{S}=\{\mathit{s}=(s_1,\cdots ,s_L):\mid {\sum }_{l\in \mathcal{I}}{n}_l{s}_l\mid \le {\lambda }_1\mid \mathcal{I}\mid +{\lambda }_{2}d(\mathcal{I},{\mathcal{I}}^c),\forall \mathcal{I}\subseteq V\}$ with $d(\mathcal{I},{\mathcal{I}}^c)={\sum }_{l\in \mathcal{I},l^{\prime }\in {\mathcal{I}}^c}\mathbb{I}(l\sim l^{\prime })$ denoting the number of edges between the nodes in $\mathcal{I}$ and the remaining nodes in ${\mathcal{I}}^c$.

Similar results hold for the proposed non-convex regularized estimators.

Theorem 3 (Partition rule for non-convex regularization) Denote by ${\widehat{\Omega }}^{dc}$ the solution obtained from Algorithm 1 for (2). Similarly, given any $\mathcal{J}$, ${\widehat{\Omega }}_{jkl}^{dc}=0$ for all $j\in \mathcal{J}$; $k\in {\mathcal{J}}^c$; l = 1,... ,L, if and only if $(s_{jk1},\cdots ,s_{jkL})\in \mathcal{S}$, where $\mathcal{S}=\{\mathit{s}=(s_1,\cdots ,s_L):\mid {\sum }_{l\in \mathcal{I}}{n}_l{s}_l\mid \le {\lambda }_1\mid \mathcal{I}\mid +{\lambda }_{2}d(\mathcal{I},{\mathcal{I}}^c),\forall \mathcal{I}\subseteq V\}$.

Corollary 1 simplifies the expression of $\mathcal{S}$ for specific graphs.

Corollary 1 In the cases of the fused graph and the complete graph, we have

$$\begin{array}{cc}\hfill \mathcal{S}=& \left\{\mathit{s}:\mid \sum _{i=1}^l{n}_i{s}_i\mid \le l{\lambda }_1+{\lambda }_2,\mid \sum _{i=L-l+1}^L{n}_1{s}_i\mid \le l{\lambda }_1+{\lambda }_2,l=1,\cdots ,L-1,\mid \sum _{i=l_1+1}^{l_2}{n}_i{s}_i\mid \le (l_2-l_1){\lambda }_1+2{\lambda }_2,1\le l_1<l_2<L;\mid \sum _{i=1}^L{n}_i{s}_i\mid \le L{\lambda }_1\right\},\hfill \\ \hfill \mathcal{S}=& \left\{\mathit{s}:\mid \sum _{i=1}^l{n}_{k_i}{s}_{k_i}\mid \le l{\lambda }_1+l(L-l){\lambda }_2,\mid \sum _{i=L-l+1}^L{n}_{k_i}{s}_{k_i}\mid \le l{\lambda }_1+l(L-l){\lambda }_2,l=1,\cdots ,L,s_{k_1}\ge \cdots \ge s_{k_L}\right\}.\hfill \end{array}$$

The partition rule is useful for e cient computation, as it may reduce computation cost substantially. It can be used in several ways. First, the rule partitions nodes into disjoint connected subsets through the sample covariances s_jkl's. This breaks the original large problem into smaller subproblems, owing to this necessary and sufficient rule. Second, Algorithm 1

can be applied to each subproblem independently, permitting parallel computation.

Algorithm 2 integrates the partition rule in Theorem 3 with Algorithm 1 to make the proposed method applicable to large-scale problems.

Algorithm 2 (A partition version of Algorithm 1):

Step 1. (Screening) Compute the sample-covariance matrix S_l; l = 1,... ,L. Construct a p × p symmetric matrix T = (t_jk)_1≤j,k≤p, with t_jk = 0 if $(s_{jk1},\cdots ,s_{jkL})\in \mathcal{S}$ and t_jk = 1 otherwise. Treating T as an adjacency matrix of an undirected graph, we compute its maximum connected components to form a partition of nodes $\{{\mathcal{J}}_1,\cdots ,{\mathcal{J}}_q\}$ using breadth-first search or depth-first search algorithm, c.f., [3]

Step 2. (Subproblems) For i = 1,... ,q, solve (2) for each subproblem consisting of nodes in ${\mathcal{J}}_i$, by applying Algorithm 1 to obtain the solution ${\widehat{\Omega }}^{\left(i\right)}=({\widehat{\Omega }}_1^{\left(i\right)},\cdots ,{\widehat{\Omega }}_L^{\left(i\right)});i=1,\cdots ,q$.

Step 3. (Combining results) The final solution ${\widehat{\Omega }}_l=\mathrm{Diag}({\widehat{\Omega }}_l^{\left(1\right)},\cdots ,{\widehat{\Omega }}_l^{\left(q\right)});l=1,\cdots ,L$.

4 Theory

This section investigates theoretical aspects of the proposed method. First we develop a general theory on maximum penalized likelihood estimation involving two types of L₀-constraints for pursuit of sparseness and clustering. Then we specialize the theory for estimation of multiple precision matrices in Section 4.3. Now consider a constrained L₀-version of (2):

$$\underset{\theta =(\beta ,\eta )}{\max }L\left(\theta \right),\text{subject to}\sum _{j=l}^d\mathbb{I}(\mid {\beta }_j\mid \ne 0)\le C_1,\sum _{\left(j{j}^{\prime }\right)\in \mathcal{E}}\mathbb{I}(\mid {\beta }_j-{\beta }_{j^{\prime }}\mid \ne 0)\le C_2.$$ (13)

as well as its computational surrogate

$$\underset{\theta =(\beta ,\eta )}{\max }L\left(\theta \right),\text{subject to}\sum _{j=1}^d{J}_{\tau }\left(\mid {\beta }_j\mid \right)\le C_1,\sum _{\left(j{j}^{\prime }\right)\in \mathcal{E}}{J}_{\tau }\left(\mid {\beta }_j-{\beta }_{j^{\prime }}\mid \right)\le C_2,$$ (14)

where θ = ( β,η) with $\beta \in {\mathbb{R}}^d$ and η representing the off-diagonals and diagonals of Ω, and three non-negative tuning parameters ($C_1,C_2,\tau$). Note that Algorithm 1 yields a local minimizer of (14), relaxing it by solving a sequence of convex problems.

In what follows, we will prove that global minimizers of (13) and (14) reconstruct the ideal oracle estimator as if the true sparseness and clustering structures of the precision matrices were known in advance. As a result of the reconstruction, key properties of the oracle estimator are simultaneously achieved by the proposed method.

4.1 The oracle estimator and consistent graph

To define the oracle estimator, let $\mathcal{G}\left(\beta \right)$ denote a partition of $\mathcal{I}\equiv \{1,\cdots ,d\}$ by the parameter β, i.e. $\mathcal{G}\left(\beta \right)=({\mathcal{I}}_0\left(\beta \right),\cdots ,{\mathcal{I}}_{K\left(\beta \right)}\left(\beta \right))$, with ${\mathcal{I}}_0\left(\beta \right)=\mathcal{I}\backslash A\left(\beta \right)$ and ${\mathcal{I}}_k\left(\beta \right)$ satisfying ${\beta }_j={\beta }_{j^{\prime }};j,j^{\prime }\in {\mathcal{I}}_k\left(\beta \right);k=1,\cdots ,K\left(\beta \right)$, where K(β) is the number of nonzero clusters and A(β) is the support of β. Let ${\mathcal{G}}^0=\mathcal{G}\left({\beta }^0\right)$ be the true partition induced by β⁰, with θ⁰ = (β⁰,η⁰) the true parameter value and ${\beta }^0\in {\mathbb{R}}^d$.

Definition 1 (Oracle estimator) Given ${\mathcal{G}}^0$, the oracle estimator is defined as: ${\widehat{\theta }}^o=({\widehat{\beta }}^o,{\widehat{\eta }}^o)={\mathrm{argmax}}_{\beta :\mathcal{G}\left(\beta \right)={\mathcal{G}}^0}L\left(\theta \right)$, the corresponding maximum likelihood estimator.

In (13) and (14), the edge set $\mathcal{E}$ of $\mathcal{U}$ is important for clustering. In order for simultaneous pursuit of sparseness and clustering structures to be possible, we may need $\mathcal{U}$ to be consistent with the clustering structure of the true precision matrices. In other words, a consistent graph is a minimal requirement for reconstruction of the oracle estimator, where there must exist a path connecting any nodes within the same true cluster.

Definition 2 (Consistent graph $\mathcal{U}$) An undirected graph $\mathcal{U}=(\mathcal{I},\mathcal{E})$ is consistent with the true cluster ${\mathcal{G}}^0=\{{\mathcal{I}}_0^0,\cdots ,{\mathcal{I}}_{K_0}^0\}$, if the subgraph restricting nodes on ${\mathcal{I}}_j^0$ is connected; j = 1,... ,K₀

4.2 Non-asymptotic probability error bounds

This section derives a non-asymptotic probability error bound for simultaneous sparseness and clustering pursuit, based on which we prove that (13) and (14) reconstruct the oracle estimator. This implies consistent identification of the sparseness and clustering structures of multiple graphical models, under one simple assumption, called the degree-of-separation condition.

Before proceeding, we introduce some notations. Given a graph $\mathcal{U}=(\mathcal{I},\mathcal{E})$, let $\mathcal{S}=\{\theta =(\beta ,\eta ):\mid A\left(\beta \right)\mid \le d_0,C(\beta ,\mathcal{E})\le c_0,\mathcal{G}\left(\beta \right)\ne \mathcal{G}(\times {\beta }^0)\}$ be a constrained set with $C(\beta ,\mathcal{E})={\sum }_{\left(j{j}^{\prime }\right)\in \mathcal{E}}\mathbb{I}(\mid {\beta }_j-{\beta }_{j^{\prime }}\mid \ne 0)$, where $d_0=\mid A^0\mid$ with $A^0=A\left({\beta }^0\right)$ as defined above. Given a partition $\mathcal{G}$, let ${\mathcal{S}}_{\mathcal{G}}=\{\theta \in \mathcal{S}:\mathcal{G}\left(\beta \right)=\mathcal{G}\}$. Given an index set $A\subseteq \mathcal{I}$, let ${\mathcal{S}}_A=\{\theta \in \mathcal{S}:\mathit{A}\left(\beta \right)=A\}$. Let ${\mathcal{S}}_i={\cup }_{A:\mid A^0\backslash A\mid =i}{\mathcal{S}}_A,S_i^{\star }={\max }_{A:\mid A^0\backslash A\mid =i}\mid \{\mathcal{G}\left(\beta \right):\theta =(\beta ,\eta )\in {\mathcal{S}}_A\}\mid ;i=0,\cdots ,d_0$, and $S^{\ast }=\exp \left({\max }_{0\le i\le d_0}\frac{\log S_i^{\ast }}{\max (i,1)}\right)$. Roughly, S^* quantifies complexity of the space of candidate precision matrices scaled by the number of nonzero entries.

The degree-of-separation condition will be used to ensure consistent reconstruction of the oracle estimator: For some constant c₁ > 0,

$$C_{\min }\left({\theta }^0\right)\ge c_1\frac{\log d+\log S^{\ast }}{n},$$ (15)

where $C_{\min }\left({\theta }^0\right)\equiv {\inf }_{\{\theta =(\beta ,\eta )\in \mathcal{S}\}}\frac{-\log (1-h^2(\theta ,{\theta }^0))}{\max (\mid A^0\backslash A\left(\beta \right)\mid ,1)}$ with | · | and denoting the size of a set and that of set difference, respectively, $h(\theta ,{\theta }^0)={(\frac{1}{2}\int {(g^{1∕2}(\theta ,y)-g^{1∕2}({\theta }^0,y))}^{2}d\mu \left(y\right))}^{1∕2}$ is the Hellinger-distance for densities with respect to a dominating measure μ.

We now define the bracketing Hellinger metric entropy of space $\mathcal{F}$, denoted by the function H(·, $\mathcal{F}$), which is the logarithm of the cardinality of the u-bracketing (of $\mathcal{F}$) of the smallest size. That is, for a bracket covering $S(\epsilon ,m)=\{f_1^l,f_1^u,\cdots ,f_m^l,f_m^u\}\subset {\mathcal{L}}_2$ satisfying ${\max }_{1\le j\le m}{\Vert f_j^u-f_j^l\Vert }_2\le \epsilon$ and for any $f\in \mathcal{F}$, there exists a j such that $f_j^l\le f\le f_j^u$, a.e. P , then H(u, $\mathcal{F}$) is log(min{m: S(u, m)}), where ${\Vert f\Vert }_2=\int f^2\left(z\right)d\mu$. For more discussions about metric entropy of this type, see [8].

Assumption A: (Complexity of the parameter space) For some constant c₀ > 0 and any 0 < t < ε ≤ 1, $H(t,{\mathcal{B}}_{\mathcal{G}})\le c_0{\left(\log p\right)}^2,1)\mid A\mid \log (2\epsilon ∕t)$, where ${\mathcal{B}}_{\mathcal{G}}={\mathcal{F}}_{\mathcal{G}}\cap \{h(\theta ,{\theta }^0)\le 2\epsilon \}$ is a local parameter space, and ${\mathcal{F}}_{\mathcal{G}}=\{g^{1∕2}(\theta ,y):\theta =(\beta ,\eta ):\mathcal{G}\left(\beta \right)=\mathcal{G}\}$ be a collection of square-root densities indexed by any subset $\mathcal{G}\in \{\mathcal{G}\left(\beta \right):\theta =(\beta ,\eta )\in \mathcal{S}\}$.

Next we present our non-asymptotic probability error bounds for reconstruction of the oracle estimator ${\widehat{\theta }}^0$ by global minimizers of (13) and (14) in terms of C_min( θ⁰), n, d and d₀, where d₀ and d can depend on n. Consistency is established for reconstruction of ${\widehat{\theta }}^0$ as well as structure recovery. Note that ${\widehat{\theta }}^0$ is asymptotically optimal, hence the optimality translates into the global minimizers of (13) and (14).

Theorem 4 (Global minimizer of (13)) Under Assumption A, if $\mathcal{U}$ is consistent with ${\mathcal{G}}^0$, then for a global minimizer of (13) ${\widehat{\theta }}^{l_0}$ with estimated grouping ${\widehat{\mathcal{G}}}^{l_0}=\mathcal{G}\left({\widehat{\beta }}^{l_0}\right)$ at (C₁, C₂) = (d₀, c₀) with c₀ = C(β⁰, ε),

$$\mathbb{P}({\widehat{\mathcal{G}}}^{l_0}\le {\mathcal{G}}^0)=\mathbb{P}({\widehat{\theta }}^{l_0}\ne {\widehat{\theta }}^o)\le \exp (-c_{2}n{C}_{\min }\left({\theta }^0\right)+2\log d+\log S^{\ast }).$$ (16)

Under (15), $\mathbb{P}({\widehat{\mathcal{G}}}^{l_0}={\mathcal{G}}^0)=\mathbb{P}({\widehat{\theta }}^{l_0}={\widehat{\theta }}^0)\to 1$ as n, d → ∞.

For the constrained truncated L₁-likelihood, one additional condition–Assumption B is necessary. We requires the Hellinger-distance to be smooth so that the approximation of the truncated L₁-function to the L₀-function becomes adequate by tuning τ.

Assumption B: For some constants d₁-d₃ > 0,

$$-\log (1-h^2(\theta ,{\theta }^0))\ge -d_1\log (1-h^2({\theta }^{\tau },{\theta }^0))-d_3{\tau }^{d_2}d,$$ (17)

where θ^τ = ( β^τ, η) with ${\beta }^{\tau }=({\beta }_1^{\tau },\cdots ,{\beta }_p^{\tau })$, and ${\beta }_j^{\tau }=\frac{{\sum }_{j^{\prime }\in {\mathcal{I}}_k}{\beta }_j^{\prime }}{\mid {\mathcal{I}}_k\mid }$ for $j\in {\mathcal{I}}_k\left(\beta \right)$; k = 0, 1, · · · , K(β).

Theorem 5 (Global minimizer of (14)) Assume that Assumption A with ${\mathcal{F}}_{\mathcal{G}}$ replaced by ${\mathcal{F}}_{\mathcal{G}}^{\tau }=\{g^{1∕2}(\theta ,y):\theta =(\beta ,\eta ):{\mathcal{G}}^{\tau }\left(\beta \right)=\mathcal{G}\}$ and Assumption B are met. If $\mathcal{U}$ is consistent with ${\mathcal{G}}^0$, then for a global minimizer of (14) with estimated grouping ${\widehat{\theta }}^g$ with estimated grouping ${\widehat{\mathcal{G}}}^g=\mathcal{G}\left({\widehat{\beta }}^g\right)$ at (C₁,C₂) = (d₀, c₀) with c₀ = C(β⁰, ε) and $\tau \le {\left(\frac{(d_1-c_3)C_{\min }\left({\theta }^0\right)}{d_{3}d}\right)}^{1∕d_2}$,

$$\mathbb{P}({\widehat{\mathcal{G}}}^g\ne {\mathcal{G}}^0)=\mathbb{P}({\widehat{\theta }}^g\ne {\widehat{\theta }}^o)\le \exp (-c_{3}n{C}_{\min }\left({\theta }^0\right)+2\log d+\log S^{\ast }).$$ (18)

Under (15), $\mathbb{P}({\widehat{\mathcal{G}}}^g={\mathcal{G}}^0)=\mathbb{P}({\widehat{\theta }}^g={\widehat{\theta }}^o)\to 1$ as n, d → ∞.

4.3 An illustrative example

We now apply the general theory in Theorems 2 and 3 to the estimation of multiple precision matrices, in which the true precision matrices in each cluster are the same, with $g_0\equiv {\sum }_{l=1}^{L-1}{\sum }_{j>k}\mathbb{I}({\omega }_{jkl}^0\ne {\omega }_{jkl(l+1)}^0)$ the number of break points among these clusters. In this case, a serial graph $\mathcal{U}$ is considered for clustering.

Denote by p and L₀ the dimension of the precision matrix and the number of distinctive clusters, respectively. Let $H_l=\left(\frac{{\partial }^2(-\log \det \left({\Omega }_l\right))}{{\partial }^2\Omega }\right){\mid }_{{\Omega }_l={\Omega }_l^0}$ be the p² × p² Hessian matrix of – log det(Ω_l, whose (jk, j′k′) element is tr(Σ_lΔ_jkΣ_lΔ_j′k′), c.f., [2]. Define

$${\eta }_{min}=\min \left(\underset{(j,k,l):{\omega }_{jkl}^0\ne 0}{\min }\mid w_{jkl}^0\mid ,\frac{1}{\sqrt{2}}\underset{(j,k,l):{\omega }_{jkl}^0\ne {\omega }_{jk(l+1)}^0}{\min }\mid {\omega }_{jkl}^0-{\omega }_{jk(l+1)}^0\mid \right)$$

to be the resolution level for simultaneous sparseness and clustering pursuit.

An application of Theorems 2 and 3 with β and η being off-diagonals and diagonals of Ω leads to the following result.

Corollary 2 (Multiple precision matrices with a serial graph) When U is a serial graph, all the results in Theorems 2 and 3 for simultaneous pursuit of sparseness and clustering hold under two simple conditions:

$$C_{min}\left({\theta }^0\right)\ge c_4\underset{1\le l\le L}{\min }{c}_{min}\left(H_l\right){\eta }_{min}^2,and\log S^{\ast }\le 2g_0\max (\log (d_0∕g_0),1),$$ (19)

for some constant c₄ > 0. Sufficiently, if

$$\underset{1\le l\le L}{\min }{c}_{min}\left(H_l\right){\eta }_{min}^2\ge c_0\frac{\log (Lp(p-1)∕2)-g_0\max (\log (d_0∕g_0),1)}{n},$$ (20)

holds for some constant c₀ > 0, then $\mathbb{P}({\widehat{\Omega }}^{{\ell }_0}\ne {\widehat{\Omega }}^o)$ and $\mathbb{P}({\widehat{\Omega }}^g\ne {\widehat{\Omega }}^o)\to 0$ as n, d → +∞.

Corollary 2 suggests that the amount of reconstruction improvement would be of the order of 1/L if the L precision matrices are identical. In general, the amount of improvement of joint estimation over separate estimation is L/ log(L) when g₀ is small, i.e. g₀ max (log (d₀/g₀), 1) ≲ log (L_p(p – 1)/2), by contrasting the sufficient condition in (20) with that for a separate estimation approach in [17], where ≲ denotes inequality ignoring constant terms. Here g₀ describes similarity among L precision matrices with a small value corresponding to a high-degree of similarity shared among precision matrices.

5 Numerical examples

This section studies operational characteristics of the proposed method via simulation in sparse and nonsparse situations with di erent types of graphs in both low- and high-dimensional settings. In each simulated example, we compare our method against its convex counterpart for seeking the sparseness structure for each graphical model and identifying the grouping structure among multiple graphical models, and contrast the method against its counter part seeking the sparseness structure alone. In addition, we also compare against a kernel smoothing method for time-varying networks [7, 25] in Examples 1-3, whenever appropriate. The smoothing method defines a weighted average over sample covariance matrices at time points as ${\tilde{\mathit{S}}}_l\left(h\right)=\frac{{\sum }_{l^{\prime }=1}^L{w}_{l{l}^{\prime }}\left(h\right){\mathit{S}}_l^{\prime }}{{\sum }_{l^{\prime }=1}^L{w}_{l{l}^{\prime }}\left(h\right)}$ with w_ll′(h) = K(h⁻¹|l – l′|); l = 1, · · · , L, where K(x) = (1 – |x|)∏(|x| < 1)is a triangular kernel, h is a bandwidth, and l = 1, · · · , L denotes clusters. Then within each cluster l, the precision matrix estimate ${\widehat{\Omega }}_l(h,\lambda )$ is obtained by solving

$${\widehat{\Omega }}_l(h,\lambda )=\underset{{\Omega }_l\succ 0}{\mathrm{argmin}}\left(-\log \det \left({\Omega }_l\right)+tr\left(\Omega {\tilde{\mathit{S}}}_l\left(h\right)\right)+\lambda \sum _{j<j^{\prime }}\mid {\omega }_{j{j}^{\prime }l}\mid \right),l=1,\cdots ,L$$ (21)

using the glasso algorithm [5], and the final estimate is obtained through tuning over (h,, λ)-grids. Two performance metrics are used to measure the accuracy of parameter estimation as well as that of correct identification of the sparseness and grouping structures.

In Examples 1-3, temporal clustering pursuit is performed over Ω₁, · · · , Ω_L through a serial graph ε = {{(j, k, l), (j′, k′, l′) : j = j′, k = k′, |l| − l′| = 1}. That is, only adjacent matrices may be possibly clustered. In Example 4, general clustering pursuit is conducted through a complete graph ε = {{(j, k, l), (j′, k′, l′) : j = j′, k = k′, l < l′}.

For the accuracy of parameter estimation, the average entropy loss (EL) and average quadratic loss (QL) are considered, defined as

$$EL=\frac{1}{L}\sum _{l=1}^L\left(tr\left({\Omega }_l^{-1}{\widehat{\Omega }}_l\right)-\log \det \left({\Omega }_l^{-1}{\widehat{\Omega }}_l\right)\right),QL=\frac{1}{L}\sum _{l=1}^{L}tr\left({({\Omega }_l^{-1}{\widehat{\Omega }}_l-\mathit{I})}^2\right).$$

For the accuracy of identification, average false positive (FPV) and false negative (FNV) rates for sparseness pursuit, as well as those (FPG) and (FNG) for grouping are used:

$$\begin{array}{c}\hfill FPV=\frac{1}{L}\sum _{l=1}^L\frac{{\sum }_{1\le j<j^{\prime }\le p}\mathbb{I}({\omega }_{j{j}^{\prime }l}=0,{\widehat{\omega }}_{j{j}^{\prime }l}\ne 0)}{{\sum }_{1\le j<j^{\prime }\le p}\mathbb{I}({\omega }_{j{j}^{\prime }l}=0)}\left(1-\mathbb{I}({\Omega }_{l,\mathrm{off}}\ne 0)\right)\hfill \\ \hfill FNV=\frac{1}{L}\sum _{l=1}^L\frac{{\sum }_{1\le j<j^{\prime }\le p}\mathbb{I}({\omega }_{j{j}^{\prime }l}=0,{\widehat{\omega }}_{j{j}^{\prime }l}=0)}{{\sum }_{1\le j<j^{\prime }\le p}\mathbb{I}({\omega }_{j{j}^{\prime }l}\ne 0)}\mathbb{I}({\Omega }_{l,\mathrm{off}}\ne 0),\hfill \\ \hfill FPG=\frac{1}{\mid \mathcal{E}\mid }\sum _{l\sim l^{\prime }}\frac{{\sum }_{1\le j<j^{\prime }\le p}\mathbb{I}({\omega }_{j{j}^{\prime }l}={\omega }_{j{j}^{\prime }{l}^{\prime }},{\widehat{\omega }}_{j{j}^{\prime }l}\ne {\widehat{\omega }}_{j{j}^{\prime }{l}^{\prime }})}{{\sum }_{1\le j<j^{\prime }\le p}\mathbb{I}({\omega }_{j{j}^{\prime }l}={\omega }_{j{j}^{\prime }{l}^{\prime }})}\left(1-\mathbb{I}({\Omega }_{l,\mathrm{off}}\ne {\Omega }_{l^{\prime },\mathrm{off}})\right).\hfill \\ \hfill FNG=\frac{1}{\mid \mathcal{E}\mid }\sum _{l\sim l^{\prime }}\frac{{\sum }_{1\le j<j^{\prime }\le p}\mathbb{I}({\omega }_{j{j}^{\prime }l}\ne {\omega }_{j{j}^{\prime }{l}^{\prime }},{\widehat{\omega }}_{j{j}^{\prime }l}={\widehat{\omega }}_{j{j}^{\prime }{l}^{\prime }})}{{\sum }_{1\le j<j^{\prime }\le p}\mathbb{I}({\omega }_{j{j}^{\prime }l}\ne {\omega }_{j{j}^{\prime }{l}^{\prime }})}\mathbb{I}({\Omega }_{l,\mathrm{off}}\ne {\Omega }_{l^{\prime },\mathrm{off}}),\hfill \end{array}$$

where Ω_l,off denotes the off-diagonal elements of Ω_l. Note that FPV and FNG as well as FNV and FNG are not comparable due to normalization with and without the zero-group, respectively.

For tuning, we minimize a prediction criterion with respect to the tuning parameter(s) on an independent test set with the same sample size as the training set. The prediction criterion is $CV\left(\lambda \right)=\frac{1}{L}{\sum }_{l=1}^L(-\log \det \left({\widehat{\Omega }}_l\left(\lambda \right)\right)+tr\left(S_l^{\mathrm{tune}}{\widehat{\Omega }}_l\left(\lambda \right)\right))$, where ${\mathit{S}}_l^{\mathrm{tune}}$ is the sample covariance matrix for the tuning data; l = 1, · · · , L. Then estimated tuning parameter is obtained: λ^* = argmin_λCV(λ ), which is used in the estimated precision matrices. Here minimization of CV(λ) is performed through a simple grid search over the domain of the tuning parameter(s).

All simulations are performed based on 100 simulation replications. Three di erent types of networks are considered. Specifically, Example 1 concerns a chain network with small p and L but large n, where each Ω_l is relatively sparse and a temporal change occurs at two different l values. Example 2 deals with a nearest neighbor networks for each Ω_l and the same temporal structure as in Example 2. Examples 3 and 4 study exponentially decaying networks in nonsparse precision matrices in high and low-dimensional situations with large and small L, respectively. In Examples 1-3 and Example 4, Algorithms 1 and 2 are respectively applied.

Example 1: Chain networks: This example estimates tridiagonal precision matrices as in [4]. Specifically, ${\Omega }_l^{-1}={\Sigma }_l$ is AR(1)-structured with its ij-element being σ_ijl = exp(−|s_il− s_jl|/2), and s_1l < s_2l < · · · s_pl are randomly chosen: s_il−s(_i−1)l ~ Unif(0.5, 1); i = 2, · · · , p, l = 1,..., L. The following situations are considered: (I) (n, p, L) = (120, 30, 4), (n, p, L) = (120, 200, 4), with Ω₁ = Ω₂, Ω₃ = Ω₄; (II) (n, p, L) = (120, 20, 30), (n, p, L) = (120, 10, 90), with Ω₁ = · · · = Ω_L/₃, Ω^(1+L/³) = · · · = Ω_2L/₃, Ω₁₊2_L/₃ = · · · = Ω_L. Then, we study the proposed method's performance as a function of the number of graphs and the number of nodes.

Example 2: Nearest neighbor networks. This example concerns networks described in [11]. In particular, we generate p points randomly on a unit square, and compute the k nearest neighbors of each point based on the Euclidean distance. In the case of k = 3, three points are connected to each point. For each ”edge” in the graph, the corresponding off-diagonal in a precision matrix is sampled independently according to the uniform distribution over [−1, −0.5] υ [0.5, 1], and the ith diagonal is set to be the sum of the absolute values of the ith row off-diagonals. Given the previous cluster, the matrices in the current cluster are obtained by randomly adding or deleting a small fraction of nonzero elements in the matrices from previous cluster. Finally, each row of a precision matrix is divided by the square root of the product of corresponding diagonals (${\omega }_{ij}\leftarrow \frac{{\omega }_{ij}}{\sqrt{{\omega }_{ii}{\omega }_{jj}}}$) so that diagonals of the final precision matrices are one. The following scenarios are considered: (I) (n, p, L) = (300, 30, 4) and (n, p, L) = (300, 200, 4), where Ω₁ = Ω_L/₃, Ω_1+L3/₃ = · · · = Ω_2L/₃, Ω₁+_2L/₃ = · · · = Ω_l. In (I), the first cluster of matrices (Ω₁,Ω₂) are generated using the above mechanism, with the second cluster of matrices (Ω₃, Ω₄) obtained by deleting one edge for each node in the network. In (II), the generating mechanism remains except that the third cluster of matrices (Ω_1+2L/₃, · · · , Ω_L) are generated by adding an edge for each node in its previous adjacent network.

Example 3: Exponentially decaying networks. This example examines a nonsparse situation in which elements of precision matrices are nonzero, and decay exponentially with respect to their Euclidean distances to the corresponding diagonals. In particular, the (i, j)th entry of the lth precision matrix ω_ijl is exp (a_l|i − j|) with a_l sampled uniformly over [1, 2]. In this case, it is sensible to report the results for parameter estimation as opposed to identifying nonzeros As in Examples 1 and 2, several scenarios are considered: (I) (p, L) = (30, 4), (p, L) = (200, 4), and the sample size n = 120 or 300 with Ω₁ = Ω₂ = Ω₃ = Ω₄, and (II) (p, L) = (20, 30), (p, L) = (10, 90), and the sample size n = 120 or 300 with Ω₁ = · · · = Ω_L/3, Ω_1+L/3 = · · · = Ω_2L/3, Ω_1+2L/3 = · ·· = Ω_L.

Example 4: Large precision matrices. This example utilizes the partition rule to treat large-scale simulations. First, we examine two cases (n, p, L) = (120, 1000, 4) and (n, p, L) = (500, 2000, 4) with Ω₁ = Ω₂ and Ω₃ = Ω₄, where four precision matrices are considered with size 1000 × 1000 and 2000 × 2000 for pairwise clustering, where $\mathcal{U}$ is the complete graph. Here each precision matrix is set to be a block-diagonal matrix: Ω_l = Diag( _l1, · · · , Ω_lq); l = 1,· · · L, where Ω_1j = Ω_2j, Ω_3j = Ω_4j are 20 × 20 matrices generated in the same fashion as that in Examples 1. Finally, the complete graph is used as opposed to the fused graph. Overall, the complexity is much higher than the previous examples.

As suggested by Tables 1-4, the proposed method performs well against its competitors in parameter estimation and correct identification of the sparseness and grouping structures across all the situations. With regard to accuracy of identification of the sparseness and clustering structures, the proposed method has the smallest false positives in terms of FPV and FPG, yielding sharper parameter estimation than the competitors. This says that shrinkage towards common elements is advantageous for parameter estimation in a low-or high-dimensional situation. Note that the largest improvement occurs for the most difficult situation in Example 4.

Table 1.

Average entropy loss, denoted by EL, (SD in parentheses) and average quadratic loss, denoted by QL, (SD in parentheses), average false positive for sparseness pursuit, denote by FPV, (SD in parentheses), average false negative for sparseness pursuit, denoted as FNV, (SD in parentheses), average false positive for grouping, denoted by FPG, (SD in parentheses), and average false negative for grouping, denoted by FNG, (SD in parentheses), based on 100 simulations, for estimating precision matrices in Example 1 with n = 120. Here “Smooth”, “Lasso”, “TLP”, “Our-con” and “Ours” denote estimation of individual matrices with kernel smoothing method proposed in [25], the L₁ sparseness penalty, that with non-convex TLP penalty, the convex counterpart of our method with the L₁-penalty for sparseness and clustering, and our non-convex estimates by solving (2) with penalty (6). The best performer is bold-faced.

(p, L)	Method	EL	QL	FPV	FNV	FPG	FNG
(30, 4)	Smooth	0.570(.005)	2.617(.266)	.312(.016)	.000(.000)	.392(.020)	.000(.000)
	Lasso	1.547(.074)	5.416(.393)	.200(.009)	.000(.000)	.377(.015)	.000(.000)
	TLP	0.746(.084)	4.688(.617)	.043(.006)	.001(.002)	.108(.008)	.000(.000)
	Our-con	1.288(.064)	3.700(.270)	.129(.016)	.000(.000)	.045(.020)	.251(.032)
	Ours	0.525(.055)	3.494(.418)	.040(.009)	.000(.000)	.009(.007)	.267(.043)
(200, 4)	Smooth	7.118(.173)	22.45(2.61)	.087(.017)	.000(.000)	.106(.018)	.000(.000)
	Lasso	36.48(.426)	69.21(1.97)	.013(.001)	.000(.000)	.027(.001)	.000(.000)
	TLP	5.305(.351)	33.67(2.22)	.004(.000)	.005(.003)	.014(.000)	.000(.000)
	Our-con	36.28(.422)	66.53(1.87)	.010(.001)	.000(.000)	.012(.001)	.122(.021)
	Ours	3.500(.164)	23.71(1.33)	.003(.000)	.000(.000)	.001(.000)	.280(.007)
(20, 30)	Smooth	1.122(.023)	1.983(.056)	.131(.006)	.000(.000)	.223(.006)	.000(.000)
	Lasso	1.685(.028)	3.770(.113)	.152(.005)	.000(.000)	.314(.008)	.000(.000)
	TLP	0.507(.023)	3.081(.180)	.077(.004)	.000(.000)	.198(.005)	.000(.000)
	Ours-con	1.593(.028)	3.256(.097)	.136(.007)	.000(.000)	.055(.003)	.024(.004)
	Ours	0.236(.015)	1.812(.130)	.068(.016)	.000(.000)	.020(.002)	.032(.004)
(10, 90)	Smooth	0.339(.007)	0.603(.017)	.271(.014)	.000(.000)	.420(.012)	.000(.000)
	Lasso	0.575(.010)	1.439(.038)	.273(.007)	.000(.000)	.541(.009)	.000(.000)
	TLP	0.250(.009)	1.404(.061)	.196(.006)	.000(.000)	.434(.008)	.000(.000)
	Our-con	0.519(.009)	1.190(.032)	.284(.018)	.000(.000)	.071(.005)	.008(.002)
	Ours	0.100(.005)	0.748(.043)	.017(.020)	.000(.000)	.028(.004)	.012(.002)

Table 4.

Average entropy loss, denoted by EL, (SD in parentheses) and average quadratic loss, denoted by QL, (SD in parentheses), average false positive for sparseness pursuit, denote by FPV, (SD in parentheses), average false negative for sparseness pursuit, denoted as FNV, (SD in parentheses), average false positive for grouping, denoted by FPG, (SD in parentheses), and average false negative for grouping, denoted by FNG, (SD in parentheses), based on 100 simulations, for estimating precision matrices in Example 4. Here “Lasso”, “TLP”, “Our-con” and “Ours” denote estimation of individual matrices with the L₁ sparseness penalty, that with non-convex TLP penalty, the convex counterpart of our method with the L₁-penalty for sparseness and clustering, and our non-convex estimates by solving (2) with penalty (6). The best performer is bold-faced.

(p, L)	Method	EL	QL	FPV	FNV	FPG	FNG
(1000, 4)	Lasso	378.5(2.09)	829.4(13.3)	.0005(.0000)	.0270(.0030)	.0020(.0000)	.0002(.0003)
	TLP	36.05(.1.78)	201.9(8.81)	.0004(.0000)	.0270(.0030)	.0020(.0000)	.0002(.0003)
	Our-con	377.3(2.07)	805.2(12.9)	.0004(.0000)	.0110(.0020)	.0017(.0000)	.0497(.0040)
	Ours	26.8(1.35)	160.9(7.266)	.0003(.0000)	.0130(.0020)	.0017(.0000)	.0267(.0027)
(2000, 4)	Lasso	225.6(.413)	358.1(1.13)	.0009(.0000)	.0000(.0000)	.0018(.0000)	.0000(.0000)
	TLP	9.160(.083)	54.17(.654)	.0007(.0000)	.0000(.0000)	.0015(.0000)	.0000(.0000)
	Our-con	225.6(.413)	358.1(1.12)	.0009(.0000)	.0000(.0000)	.0018(.0000)	.0000(.0000)
	Ours	8.617(.081)	51.79(.657)	.0006(.0000)	.0000(.0000)	.0005(.0000)	.1750(.0020)

Compared with pursuit of sparseness alone–TLP, the amount of of improvement of our method is from 143% to 244% and 118% % to 236% in terms of the EL and QL when n = 120, and from 80.5% to 228% and 96.5% to 240% in terms of the EL and QL when n = 300, as indicated in Table 3. This comparison suggests that exploring the sparseness structure alone is inadequate for multiple graphical models. Pursuit of two types of structures appears advantageous in terms of performance, especially for large matrices.

Table 3.

Average entropy loss, denoted by EL, (SD in parentheses) and average quadratic loss, denoted by QL, (SD in parentheses), based on 100 simulations, for estimating multiple precision matrices in Example 3. Here “Smooth”, “Lasso”, “TLP”, “Our-con” and “Ours” denote estimation of individual matrices with kernel smoothing method proposed in [25], the L₁ sparseness penalty, that with non-convex TLP penalty, the convex counterpart of our method with the Li-penalty for sparseness and clustering, and our non-convex estimates by solving (2) with penalty (6). The best performer is bold-faced.

Set-up	Method	n = 120		n = 300
(p,L)		EL	QL	EL	QL
(30, 4)	Smooth	0.468(.042)	0.941(.097)	0.231(.056)	0.476(.034)
	Lasso	1.158(.062)	2.534(.175)	0.736(.036)	1.434(.086)
	TLP	1.546(.100)	3.625(.262)	0.575(.045)	1.301(.121)
	Our-con	0.897(.066)	1.823(.166)	0.699(.038)	1.317(.085)
	Ours	0.501(.063)	1.143(.160)	0.247(.017)	0.524(.042)
(200, 4)	Smooth	6.882(.220)	13.26(.535)	2.578(.066)	4.843(.130)
	Lasso	10.37(.173)	21.92(.498)	5.449(.094)	10.84(.211)
	TLP	12.34(.202)	25.87(.560)	5.523(.153)	12.08(.365)
	Our-con	6.091(.199)	12.34(.484)	4.625(.098)	8.625(.209)
	Ours	5.079(.265)	11.84(.658)	1.682(.038)	3.551(.096)
(20, 30)	Smooth	0.490(.021)	0.878(.042)	0.278(.008)	0.492(.015)
	Lasso	0.786(.020)	1.670(.052)	0.564(.012)	1.066(.027)
	TLP	0.987(.036)	2.454(.107)	0.355(.014)	0.819(.035)
	Our-con	0.653(.023)	1.281(.055)	0.528(.012)	0.959(.027)
	Ours	0.317(.013)	0.730(.036)	0.183(.005)	0.391(.014)
(10, 90)	Smooth	0.230(.008)	0.409(.017)	0.115(.003)	0.203(.005)
	Lasso	0.318(.008)	0.694(.022)	0.205(.004)	0.398(.008)
	TLP	0.402(.012)	1.010(.043)	0.148(.004)	0.346(.011)
	Our-con	0.240(.008)	0.487(.019)	0.180(.004)	0.335(.007)
	Ours	0.158(.005)	0.369(.014)	0.082(.002)	0.176(.005)

Compared with its convex counterpart “our-con”, our method leads to between a 19.9% and a 106% improvement, and between a 4.2% improvement and a 75.5% improvement in terms of the EL and QL when n = 120, and between a 18.3% improvement and a 120% improvement, and a 90.3% improvement and a 151% improvement in terms of the EL and QL when n = 300; see Table 3. This is expected because more accurate identification of structures tends to yield better parameter estimation.

In contrast to the smoothing method [7, 25] for time-varying network analysis, across all cases except one low-dimensional case of L = 4 and p = 30 in Table 3, our method yields a 54.5% improvement and a 20.3% improvement in terms of the EL and QL when n = 120, and a 51.9% improvement and a 25.8% improvement in terms of the EL and QL when n = 300 when L is not too small, c.f. Tables 1-4.

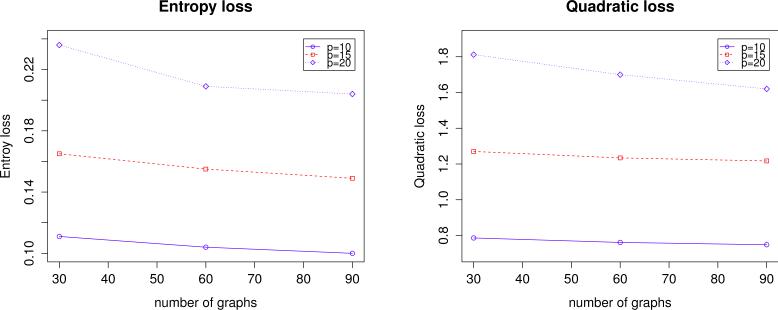
To understand how the proposed method performs relative to (n, p, L), we examine Table 3 and Figure 1 in further detail. Overall, the proposed method performs better as n, L increases and worse as p increases. Interestingly, as suggested by Figure 1, the method performs better as L increases, which confirms with our theoretical analysis.

Figure 1.

Average entropy and quadratic losses of the proposed method over di erent p and L values over 100 simulation replications in Example 1.

In summary, the proposed method achieves the desired objective of pursuing simultaneous both sparseness and clustering structures to battle the curse of dimensionality in a high-dimensional situation.

6 Signaling network inference

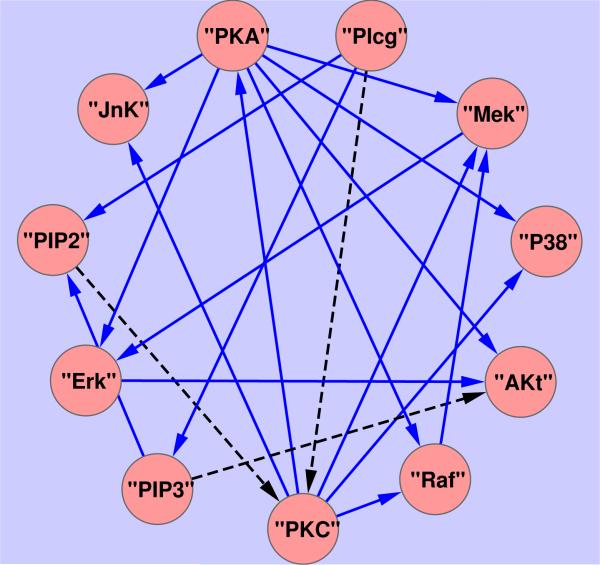
This section applies the proposed method to the multivariate single cell flow cytometry data in [16] to infer a signaling network or pathway; a consensus version of the network with eleven proteins is described in Figure 3. In this study, a multiparameter flow cytometry recorded the quantitative amounts of the eleven proteins in a single cell as an observation. To infer the network, experimental perturbations on various aspects of the network were imposed before the amounts of the eleven proteins were measured under each condition. The idea was that, if a chemical was applied to stimulate or inhibit the activity of a protein, then both the abundance of the protein and those of its downstream proteins in the network would be expected to increase or decrease, while those of non-related proteins would barely change. There were ten types of experimental perturbations on di erent targets: 1) activating a target (CD3) in the upstream of the network so that the whole network was expected to be perturbed; 2) activating a target (CD28) in the upsteam of the network; 3) activating a target (ICAM2) in the upsteam of the network; 4) activating PKC; 5) activating PKA; 6) inhibiting PKC; 7) inhibiting Akt; 8) inhibiting PIP2; 9) inhibiting Mek; 10) inhibiting a target (PI3K) in the upstream of the network. In [16], data were collected under nine experimental conditions and then used to infer a directed network; each of the nine experimental conditions was either a single type of perturbation or a combination of two or three types of perturbations. Interestingly, data were also collected under another five conditions, each of which was a combination of two of the previous nine conditions. Hence, the data o ered an opportunity to infer the two networks under the two sets of the conditions: since the two sets of conditions largely overlapped, we would expect the two networks to be largely similar to each other; on the other hand, due to the di erence between the two sets of the conditions, some deviations between the two networks were also anticipate. There were n₁ = 7466 and n₂ = 4206 observations under the two sets of the conditions respectively.

Figure 3.

Signaling network reproduced from Figure 3(A) of [16], where the black dashed line represents links that have been missed by methods in [16].

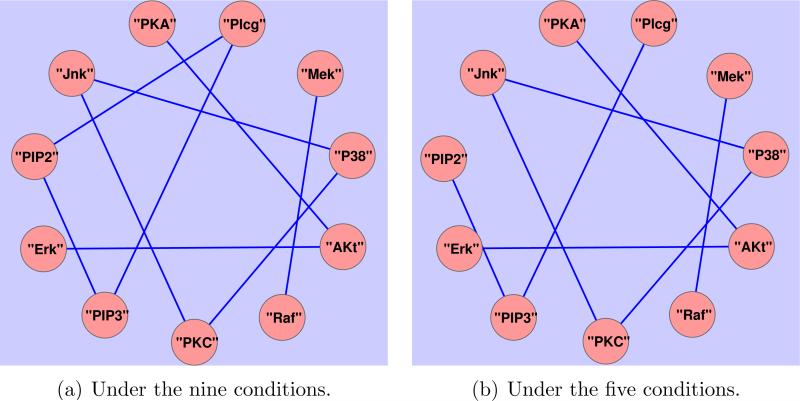
We apply the proposed method to the normalized data under the two sets of the conditions respectively. Due to the expected similarities between the two networks, we consider grouping to encourage common structure defined by connecting edges between the two networks. The tuning parameters are estimated by a three-fold cross-validation. The reconstructed two undirected networks are now displayed in Figure 2, with 9 and 8 estimated (undirected) links for the two groups of conditions, being a subset of the 20 (directed) links in the gold standard signaling network as displayed in Figure 3, which is a consensus network that has been verified biologically, c.f. [16]. The reconstructed undirected graphs miss some edges as compared to the gold standard network, for instance, the links from protein “PKC” to “Raf” and “Mek”. The three edges missed by [16], “PIP3” to “Akt”, “Plcg” to “PKC”, and “PIP2” to “PKC”, are also missed by our method, possibly reflecting lack of information in the data due to no direct interventions imposed on “PIP3” and ”Plcg”.

Figure 2.

Reconstructed networks for simultaneous pursuit of clustering and sparsity.

Overall, the proposed method appears to work well in that the network inferred from the first set of conditions recovers one more dependence relationships than that from the second set of conditions, which is expected given that the second set of interventional conditions is less specific than the first one.

Here we analyze the data by contrasting the network constructed under the nine conditions with n₁ = 7466 against that under the five conditions with n₂ = 4206. Of particular interest is the detection of network structural changes between the two sets of conditions.

7 Discussion

This article proposes a novel method to pursue two disparate types of structures—sparseness and clustering for multiple Gaussian graphical models. The proposed method is equipped with an e cient algorithm for large graphs, which is integrated with a partition rule to break down a large problem into many separate small problems to solve. For data analysis, we have considered signaling network inference in a low-dimensional situation. Worthy of note is that the proposed method can be equally applied to high-dimensional data, such as reconstructing and comparing gene regulatory networks across four subtypes of glioblastoma multiforme based on gene expression data [21].

To make the proposed method useful in practice, inferential tools need to be further developed. A Monte Carlo method may be considered given the level of complexity of the underlying problems. Moreover, the general approach developed here can be expanded to other types of graphical models, for instance, dynamic network models or time-varying graphical models [7]. This enables us to build time dependency into a model through, for example, a Markov property. Further investigation is necessary.

Table 2.

Average entropy loss, denoted by EL, (SD in parentheses) and average quadratic loss, denoted by QL, (SD in parentheses), average false positive for sparseness pursuit, denote by FPV, (SD in parentheses), average false negative for sparseness pursuit, denoted as FNV, (SD in parentheses), average false positive for grouping, denoted by FPG, (SD in parentheses), and average false negative for grouping, denoted by FNG, (SD in parentheses), based on 100 simulations, for estimating precision matrices in Example 2 with n = 300. Here “Smooth”, “Lasso”, “TLP”, “Our-con” and “Ours” denote estimation of individual matrices with kernel smoothing method proposed in [25], the L₁ sparseness penalty, that with non-convex TLP penalty, the convex counterpart of our method with the L₁-penalty for sparseness and clustering, and our non-convex estimates by solving (2) with penalty (6). The best performer is bold-faced.

(p, L)	Method	EL	QL	FPV	FNV	FPG	FNG
(30, 4)	Smooth	0.418(.025)	1.081(.072)	.387(.054)	.009(.008)	.543(.060)	.002(.002)
	Lasso	0.732(.041)	1.840(.122)	.229(.011)	.061(.013)	.466(.016)	.006(.005)
	TLP	0.772(.055)	2.290(.192)	.038(.005)	.184(.020)	.162(.010)	.037(.014)
	Our-con	0.591(.039)	1.373(.104)	.081(.019)	.033(.013)	.056(.035)	.146(.021)
	Ours	0.359(.036)	1.012(.111)	.044(.009)	.031(.015)	.004(.002)	.233(.012)
(200, 4)	Smooth	3.198(.069)	7.823(.187)	.129(.010)	.030(.006)	.161(.010)	.013(.002)
	Lasso	6.902(.140)	17.91(.435)	.049(.001)	.234(.010)	.110(.002)	.039(.004)
	TLP	8.350(.215)	23.71(.710)	.003(.001)	.493(.015)	.017(.001)	.116(.010)
	Our-con	6.151(.148)	15.58(.439)	.014(.005)	.198(.013)	.030(.010)	.142(.046)
	Ours	2.977(.135)	8.108(.399)	.001(.000)	.191(.010)	.001(.000)	.284(.012)
(20,30)	Smooth	0.409(.011)	0.839(.006)	.063(.007)	.024(.004)	.290(.007)	.005(.001)
	Lasso	0.470(.011)	1.157(.034)	.290(.006)	.034(.004)	.611(.008)	.001(.001)
	TLP	0.491(.017)	1.421(.057)	.081(.004)	.118(.007)	.341(.006)	.004(.001)
	Our-con	0.303(.010)	0.682(.025)	.071(.013)	.008(.002)	.044(.014)	.023(.002)
	Ours	0.111(.006)	0.317(.019)	.012(.005)	.006(.003)	.011(.002)	.032(.003)
(10, 90)	Smooth	0.123(.003)	0.248(.007)	.132(.013)	.008(.002)	.518(.008)	.001(.000)
	Lasso	0.170(.003)	0.419(.010)	.405(.010)	.007(.002)	.798(.008)	.000(.000)
	TLP	0.155(.005)	0.439(.014)	.175(.007)	.020(.003)	.609(.007)	.000(.000)
	Our-con	0.099(.008)	0.230(.007)	.135(.024)	.000(.000)	.043(.015)	.001(.001)
	Ours	0.040(.002)	0.117(.005)	.015(.014)	.000(.000)	.009(.001)	.001(.001)

8 Appendix

Proof of Theorem 1: The equivalence follows directly from Theorem 4.1 in [20].

Next we present two lemmas to be used in the proof of Theorem 2.

Lemma 1 For any ${\mathit{x}}_0,{\mathit{x}}_1,\cdots ,{\mathit{x}}_m\in {\mathbb{R}}^L$, (22) and (23) are equivalent:

$$\exists \mid b_1\mid ,\cdots ,\mid b_m\mid \le 1s.t.{\mathit{x}}_0+b_1{\mathit{x}}_1+\cdots +b_m{\mathit{x}}_m=0,$$ (22)

$$for\forall \mathit{c}\in {\mathbb{R}}^L,\mid {\mathit{c}}^T{\mathit{x}}_0\mid \le \mid {\mathit{c}}^T{\mathit{x}}_1\mid +\cdots +\mid {\mathit{c}}^T{\mathit{x}}_m\mid .$$ (23)

Proof: If (22) holds, then for any $\mathit{c}\in {\mathbb{R}}^L$, |c^Tx₀| = |b₁c^Tx₁ + · · · + b_mc^Tx_m| ≤ |b₁||c^Tx₁| + · · · + |b_m||c^Tx_m, which is no greater than |c^Tx₁| + · · · + |c^Tx_m|, implying (23). For the converse, assume that for any $\mathit{c}\in {\mathbb{R}}^L$, |c^Tx₀| ≤ |c^Tx₁| + · · · + |c^Tx_m|. Consider the following convex minimization:

$${\min }_{\{b_1,\cdots ,b_m\}}\sum _{i=1}^{m}B\left(b_i\right)\text{subject to}{\mathit{x}}_0+b_1{\mathit{x}}_1+\cdots +b_m{\mathit{x}}_m=0,$$ (24)

where B(x) is an indicator function with B(x) = 0 when |x| ≤ 1 and B(x) = +∞ otherwise. First, we need to show that the constraint set in (24) is nonempty. Suppose that it is empty. Let c₀ = (I − P(_x1, · · · , _xm))x₀, where P_{(x1, · · · , xm)} is the projection matrix onto the linear space spanned by x₁, · · · , x_m. Since x₀, x₁, · · · , x_m are linearly independent, we have that ||c₀||₂ > 0. Therefore $\mid {\mathit{c}}_0^T{\mathit{x}}_0\mid ={\Vert {\mathit{c}}_0\Vert }_2^2>0=\mid {\mathit{c}}_0^T{\mathit{x}}_1\mid +\cdots +\mid {\mathit{c}}_0^T{\mathit{x}}_m\mid$, contracting to that |c^Tx₀| ≤ |c^Tx₁| + · · · + |c^Tx_m|. Hence the constraint set of (24) is nonempty and we denote its optimal value by p^* . Next we convert (24) to its dual by introducing dual variable $\nu \in {\mathbb{R}}^L$ for the equality constraints in (24) through Lagrange multipliers:

$${\max }_{\{\nu \in {\mathbb{R}}^L\}}{\nu }^T{\mathit{x}}_0-\mid {\nu }^T{\mathit{x}}_1\mid -\cdots -\mid {\nu }^T{\mathit{x}}_m\mid .$$ (25)

By the assumption that |c^Tx₀| ≤ |c^Tx₁| + · · · + |c^Tx_m| for any c, the maximal of (25) d^* must satisfy d^* ≤ 0. Hence d^* = 0 because it is attained by ν = 0. Moreover, Slater's condition holds because constraint set of (24) is nonempty. By the strong duality principle, the duality gap is zero, and hence that p^* = d^* = 0. Consequently, a minimizer of (24) (b₁, · · · , b_m) exists with |b₁| ≤ 1, · · · , |b_m| ≤ 1, satisfying the constraints x₀ + b₁x₁ + · · · + b_mx_m = 0. This implies (23). This completes the proof.

Lemma 2 For s = (s₁,..., s_L) and a connected graph $\mathcal{G}=(V,\mathcal{E})$, there exist |gl| ≤ 1, |gu′| ≤ 1, gu′ = –gl′l; 1 ≤ l, l′ ≤ L such that

$$\{\begin{array}{cc}{n}_1{s}_1+{\lambda }_1{g}_1+{\lambda }_2\sum _{l^{\prime }\sim 1}{g}_{1l^{\prime }}\hfill & =0\hfill \\ ⋮\hfill & ⋮\hfill \\ n_L{s}_L+{\lambda }_1{g}_L+{\lambda }_2\sum _{l^{\prime }\sim L}{g}_{L{l}^{\prime }}\hfill & =0,\hfill \end{array}\phantom{\}}$$ (26)

is equivalent to $\mid {\sum }_{l\in \mathcal{I}}{n}_l{s}_l\mid \le {\lambda }_1\mid \mathcal{I}\mid +{\lambda }_{2}d(\mathcal{I},{\mathcal{I}}^c)$ for any $\mathcal{I}\subseteq V$ with $d(\mathcal{I},{\mathcal{I}}^c)={\sum }_{l\in \mathcal{I},l^{\prime }\in {\mathcal{I}}^c}\mathbb{I}(l\sim l^{\prime })$.

Proof: First, for some |gl| ≤ 1, |gu′| ≤ 1, gu′ = –gl′l; 1 ≤ l, l′ ≤ L, if (26) holds then,

$$\mid \sum _{l\in \mathcal{I}}{n}_l{s}_l\mid ={\lambda }_1\mid \sum _{l=1}{g}_l\mid +{\lambda }_2\mid \sum _{l\in \mathcal{I}}\sum _{l^{\prime }\sim l}{g}_{l{l}^{\prime }}\mid ={\lambda }_1\mid \sum _{l=1}{g}_l\mid +{\lambda }_2\mid \sum _{l\in \mathcal{I}}\sum _{l^{\prime }\in {\mathcal{I}}^c}\mathbb{I}(l\sim l^{\prime })g_{l{l}^{\prime }}\mid ,$$

which is no greater than ${\lambda }_1\mid \mathcal{I}\mid +{\lambda }_{2}d(\mathcal{I},{\mathcal{I}}^c)$ for any $\mathcal{I}\subseteq V$. Conversely, by Lemma 1, it suffices to show that for any $\mathit{c}\in {\mathbb{R}}^L$,

$$\mid \sum _{l=1}^L{c}_l{n}_l{s}_l\mid \le {\lambda }_1\sum _{l=1}^L\mid c_l\mid +{\lambda }_2\sum _{l\sim l^{\prime }}\mid c_l-c_{l^{\prime }}\mid$$ (27)

provided that $\mid {\sum }_{l\in \mathcal{I}}{n}_l{s}_l\mid \le {\lambda }_1\mid \mathcal{I}\mid +{\lambda }_{2}d(\mathcal{I},{\mathcal{I}}^c)$ for any $\mathcal{I}\subseteq V$. To this end, for any permutation (k₁, · · · , k_L) ∈ σ(1, · · · , L) and l = 1, · · · , L, define convex region ${\mathcal{C}}_{l{k}_1\cdots k_L}=\{\mathit{c}=(c_1,\cdots ,c_L):c_{k_1}\ge \cdots \ge c_{k_l}\ge 0\ge \cdots \ge c_{k_L}\}$, where σ(1, · · · , L) denotes the set of all possible permutation (1, · · · , L). It's easy to see that ${\cup }_{l=1}^L{\cup }_{(k_{1,}\cdots ,k_L)\in \sigma (1,\cdots ,L)}{\mathcal{C}}_{l{k}_1}\cdots k_L={\mathbb{R}}^L$ Then, consider the function $g\left(\mathit{c}\right)=\mid {\sum }_{l=1}^L{c}_l{n}_l{s}_l\mid -{\lambda }_1{\sum }_{l=1}^L\mid c_l\mid -{\lambda }_2{\sum }_{l\sim l^{\prime }}\mid c_l-c_{l^{\prime }}\mid$. Note that g(c) over each region ${\mathcal{C}}_{l{k}_1\cdots k_L}$ is a convex function. BY the maximal principle, its maximum (over each region) can be attained at the extreme points ${\mathcal{C}}_{l{k}_1\cdots k_L}$. It is easy to show that the extreme points must be of the form $\mathit{c}=(t{1}_{\mathcal{I}},0_{{\mathcal{I}}^c})$ for some $\mathcal{I}\subseteq V$ and t ≠ 0, that is the non-zero components must be equal to each other. Hence, g(c) evaluated at the extreme points of ${\mathcal{C}}_{l{k}_1\cdots k_L}$ reduces to $\mid {\sum }_{l\in \mathcal{I}}{n}_l{s}_l\mid -{\lambda }_1\mid \mathcal{I}\mid -{\lambda }_{2}d(\mathcal{I},{\mathcal{I}}^c)$ for some $\mathcal{I}\subseteq V$, which, by assumption, is always nonpositive. This completes the proof.

Proof of Theorem 2: We shall use the KKT condition of (12), or local optimality, which is in the form of

$$n_l{\widehat{\Omega }}_l^{-1}+n_l{\mathit{S}}_l+{\lambda }_1\partial {\Vert \widehat{\Omega }\Vert }_{1,\mathrm{off}}+{\lambda }_2\sum _{l^{\prime }:l\sim l^{\prime }}\partial {\Vert {\widehat{\Omega }}_l-{\widehat{\Omega }}_{l^{\prime }}\Vert }_{1,\mathrm{off}}=0,l=1,\cdots ,L,$$ (28)

where ${\widehat{\Omega }}_l^{-1}$ is the inversion of matrices ${\widehat{\Omega }}_l$ and ∂||.||₁ denotes the subgradient of the l₁ function. If ${\omega }_{jkl}=0$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L, then ${\left({\widehat{\Omega }}_l^{-1}\right)}_{jk}=0$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L. By Lemma2, we must have $(s_{jk1},\cdots ,s_{jkL})\in \mathcal{S}$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$. Conversely, if $(s_{jk1},\cdots ,s_{jkL})\in \mathcal{S}$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, again by Lemma 2, the KKT condition in (28) holds at ${\widehat{\omega }}_{jkl}=0$, l = 1, · · · , L for jkth components for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L. Hence, ${\widehat{\omega }}_{jkl}=0$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L. This completes the Proof.

Proof Theorem 3: Let $({\widehat{\Omega }}_1^{\left(m\right)},\cdots ,{\widehat{\Omega }}_L^{\left(m\right)})$ be the DC solution at iteration m. If the diagonal matrix is initialized as in Algorithm 1, then an application of Theorem 2 on $({\widehat{\Omega }}_1^{\left(1\right)},\cdots ,{\widehat{\Omega }}_L^{\left(1\right)})$ yields that $(s_{jk1},\cdots ,s_{jkL})\in \mathcal{S}$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, implying that ${\widehat{\omega }}_{jkl}^{\left(1\right)}=0$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L. Next, we prove by induction that if $(s_{jk1},\cdots ,s_{jkL})\in \mathcal{S}$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, then ${\widehat{\omega }}_{jkl}^{\left(m\right)}=0$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L holds for any m ≥ 1. Suppose that ${\widehat{\omega }}_{jkl}^{(m-1)}=0$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L holds for some m ≥ 2, then at DC iteration m, $\mid {\widehat{\omega }}_{jkl}^{(m-1)}\mid =0\le \tau ,\mid {\widehat{\omega }}_{jkl}^{(m-1)}-{\widehat{\omega }}_{jk{l}^{\prime }}^{(m-1)}\mid =0\le \tau$. This, together with

Theorem 2, again implies that ${\widehat{\omega }}_{jkl}^{\left(m\right)}=0$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L. Using the finite convergence of the DC algorithm, c.f., Theorem 1, we have $(s_{jk1},\cdots ,s_{jkL})\in \mathcal{S}$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, implying that ${\widehat{\omega }}_{jkl}^{dc}=0$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L. Conversely, if for some $\mathcal{J}{\widehat{\omega }}_{jkl}^{dc}=0$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L consider the next DC iteration, we have ${\widehat{\omega }}_{jkl}^{m\ast +1}=0$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$, 1 ≤ l ≤ L. Using the same argument as above with the converse part of Theorem 2, we obtain that $(s_{jk1},\cdots ,s_{jkL})\in \mathcal{S}$ for any $j\in \mathcal{J}$, $k\in {\mathcal{J}}^c$. This completes the proof.

Proof of Corollary 1: For the fused graph, let $\mathcal{I}=\{1,\cdots ,l\},\{L-l+1,\cdots ,L\},\{l_1+1,\cdots ,l_2\}$ and {1, · · · , L}, then if $\mid {\sum }_{l\in \mathcal{I}}{n}_l{s}_l\mid \le {\lambda }_1\mid \mathcal{I}\mid +{\lambda }_{2}d(\mathcal{I},{\mathcal{I}}^c)$ then $\mid {\sum }_{i=1}^l{n}_i{s}_i\mid \le l{\lambda }_1+{\lambda }_2,\mid {\sum }_{i=L-l+1}^L{n}_i{s}_i\mid \le l{\lambda }_1+{\lambda }_2,\mid {\sum }_{i=l_1+1}^{l_2}{n}_i{s}_i\mid \le (l_2-l_1){\lambda }_1+2{\lambda }_2,\mid {\sum }_{i=1}^L{n}_i{s}_i\mid \le L{\lambda }_1$. Conversely, if $\mathcal{I}=\{1,\cdots ,L\}$, then $\mid {\sum }_{i\in \mathcal{I}}{n}_i{s}_i\mid \le {\lambda }_1\mid \mathcal{I}\mid +{\lambda }_{2}d(\mathcal{I},{\mathcal{I}}^c)=L{\lambda }_1$. Next, assume that $\mathcal{I}\ne \{1,\cdots ,L\}$, and write $\mathcal{I}={\cup }_{k=1}^q\{i_k,i_k+1,\cdots ,i_k+l_k\}$ with i₁ ≤ i₁ + l₁ < i₂ < i₂ + l₂ > · · · > i_q < i_q + l_q. Then

$$\mid \sum _{i\in \mathcal{I}}{n}_i{s}_i\mid \le \sum _{k=1}^q\mid \sum _{i=i_k}^{i_k+l_k}{n}_i{s}_i\mid \le {\lambda }_1\sum _{k=1}^q{l}_k+2(q-2){\lambda }_2+(\mathbb{I}(i_1\ne 1)+\mathbb{I}(i_q+l_q\ne L)+2){\lambda }_2=\mid \mathcal{I}\mid {\lambda }_1+2(q-1)){\lambda }_2+(\mathbb{I}(i_1\ne 1)+\mathbb{I}(i_q+l_q\ne L)){\lambda }_2=\mid \mathcal{I}\mid {\lambda }_1+d(\mathcal{I},{\mathcal{I}}^c){\lambda }_2.$$

In the case of the complete graph, set $\mathcal{I}=\{k_1,\cdots ,k_1\},\{k_{L-l+1},\cdots ,k_L\}$, given S_k1 ≥ · · · ≥ S_KL, then we have $\mid {\sum }_{i=1}^l{n}_{k_i}{s}_{k_i}\mid \le l{\lambda }_1+l(L-1){\lambda }_2,\mid {\sum }_{i=L-l+1}^L{n}_{k_i}{s}_{k_i}\mid \le l{\lambda }_1+l(L-l){\lambda }_2$. Conversely, for any $\mathcal{I}$, $\mid {\sum }_{i\in \mathcal{I}}{n}_i{s}_i\mid \le \max (\mid {\sum }_{i=1}^{\mid \mathcal{I}\mid }{n}_{k_i}{s}_{k_i}\mid ,\mid {\sum }_{i=L-\mid \mathcal{I}\mid +1}^L{n}_{k_i}{s}_{k_i}\mid )\le l{\lambda }_1+l(L-l){\lambda }_2$. This completes the proof.

Proof of Theorem 4: The proof uses a large deviation probability inequality of [23] to treat one-sided log-likelihood ratios with constraints. This enables us to obtain sharp results without a moment condition on both tails of the log-likelihood ratios.

Recall that $\mathcal{S}=\{\theta =(\beta ,\eta ):\mid A\left(\beta \right)\mid \le d_0,C(\beta ,\mathcal{E})\le c_0,\mathcal{G}\left(\beta \right)\ne \mathcal{G}\left({\beta }^0\right)\}$ and ${\mathcal{S}}_A=\{\theta \in \mathcal{S}:A\left(\beta \right)=A\}$. Let a class of candidate subsets be $\mathcal{A}\equiv \{A\ne A^0:\mid A\le d_0\}$ for sparseness pursuit. Note that any A ⊂ {1, · · · , d} can be partitioned into $(A\backslash A^0)\cup (A\cap A^0)$. Then we partition $\mathcal{S}$ accordingly with $\mathcal{S}={\cup }_{i=0}^{d_0}{\cup }_{A\in {\mathcal{B}}_i}{\mathcal{S}}_A$, where ${\mathcal{B}}_i=\mathcal{A}\cap \{A:\mid A^0\backslash A\mid =i\}$, with $\mid {\mathcal{B}}_i\mid =\left(\begin{array}{c}\hfill d_0\hfill \\ \hfill d_0-1\hfill \end{array}\right){\sum }_{j=0}^i\left(\begin{array}{c}\hfill d-d_0\hfill \\ \hfill j\hfill \end{array}\right),i=0,\cdots d_0$. Moreover, ${\mathcal{S}}_A={\cup }_{\mathcal{G}\in \{\mathcal{G}\left(\beta \right):\theta =(\beta ,\eta )\in {\mathcal{S}}_A\}}{\mathcal{S}}_{\mathcal{G}}$, where ${\mathcal{S}}_{\mathcal{G}}=\{\theta =(\beta ,\eta )\in \mathcal{S}:\mathcal{G}\left(\beta \right)=\mathcal{G}\}$. So $\mathcal{S}={\cup }_{i=0}^{d_0}{\cup }_{A\in {\mathcal{B}}_i}{\cup }_{\mathcal{G}\in \{\mathcal{G}\left(\beta \right):\theta =(\beta ,\eta )\in {\mathcal{S}}_A\}}{\mathcal{S}}_{\mathcal{G}}$.

To bound the error probability, note that if ${\widehat{\mathcal{G}}}^{l_0}={\mathcal{G}}^0$ then ${\widehat{\theta }}^{{\ell }_0}={\widehat{\theta }}^o$ then ${\widehat{\theta }}^{{\ell }_0}={\widehat{\theta }}^o$, by Definition 1. Conversely, if ${\widehat{\theta }}^{{\ell }_0}={\widehat{\theta }}^o$ or ${\widehat{\beta }}^{{\ell }_0}={\widehat{\beta }}^o$, then ${\widehat{\mathcal{G}}}^{l_0}={\mathcal{G}}^0$. Thus ${\widehat{\mathcal{G}}}^{l_0}={\mathcal{G}}^0$ $\{{\widehat{\theta }}^{{\ell }_0}={\widehat{\theta }}^o\}$. So $\{{\widehat{\theta }}^{{\ell }_0}\ne {\widehat{\theta }}^o\}\subseteq \{L\left({\widehat{\theta }}^{{\ell }_0}\right)-L\left({\widehat{\theta }}^o\right)\ge 0\}\subseteq \{l\left({\widehat{\theta }}^{{\ell }_0}\right)-l\left({\theta }^0\right)\ge 0\}$. This together with $\{{\widehat{\theta }}^{{\ell }_0}\ne {\widehat{\theta }}^o\}\subseteq \{{\widehat{\theta }}^{{\ell }_0}\in \mathcal{S}\}$ implies that $\{{\widehat{\theta }}^{{\ell }_0}\ne {\widehat{\theta }}^o\}\subseteq \{l\left({\widehat{\theta }}^{{\ell }_0}\right)-l\left({\theta }^0\right)\ge 0\}\cap \{{\widehat{\theta }}^{{\ell }_0}\in \mathcal{S}\}$. Consequently $I\equiv \mathbb{P}({\widehat{\theta }}^{{\ell }_0}\ne {\widehat{\theta }}^o)\le \mathbb{P}(L\left({\widehat{\theta }}^{{\ell }_0}\right)-L\left({\theta }^0\right)\ge 0;{\widehat{\theta }}^{{\ell }_0}\in \mathcal{S})$ is upper bounded by

$$\sum _{i=0}^{d_0}\sum _{A\in {\mathcal{B}}_i}\sum _{\mathcal{G}\in \{\mathcal{G}\left(\beta \right):\theta \in {\mathcal{S}}_A\}}{\mathbb{P}}^{\ast }\left(\underset{\theta \in {\mathcal{S}}_{\mathcal{G}}}{\sup }(L\left(\theta \right)-L\left({\theta }^0\right))\ge 0\right)\le \sum _{i=0}^{d_0}\sum _{A\in {\mathcal{B}}_i}\sum _{\mathcal{G}\in \{\mathcal{G}\left(\beta \right):\theta \in {\mathcal{S}}_A\}}{\mathbb{P}}^{\ast }\left(\underset{\{-\log (1-h^2(\theta ,{\theta }^0))\ge \max (i,1)C_{\min }\left({\theta }^0\right),\theta \in {\mathcal{S}}_{\mathcal{G}}\}}{\sup }(\lambda \left(\theta \right)-L\left({\theta }^0\right))\ge 0\right).$$

where ${\mathbb{P}}^{\ast }$ is the outer measure and the last two inequalities use the fact that $\mathcal{S}={\cup }_{i=0}^{d_0}{\cup }_{A\in {\mathcal{B}}_i}{\cup }_{\mathcal{G}\in \{\mathcal{G}\left(\beta \right):\theta =(\beta ,\eta )\in {\mathcal{S}}_A\}}{\mathcal{S}}_{\mathcal{G}}$ and ${\mathcal{S}}_{\mathcal{G}}\subseteq \{\theta :\max (\mid A^0\backslash A\mid ,1)C_{\min }\left({\theta }^0\right)\le -\log (1-h^2(\theta ,{\theta }^0))\}$ for $\mathcal{G}\in \{\mathcal{G}\left(\beta \right):\theta =(\beta ,\eta )\in {\mathcal{S}}_A\}$.

For I, we apply Theorem 1 of [23] to bound each term. Towards this end, we verify their entropy condition (3.1) for the local entropy over ${\mathcal{S}}_{\mathcal{G}}$ for $\mathcal{G}\in \{\mathcal{G}\left(\beta \right):\theta =(\beta ,\eta )\in {\mathcal{S}}_A\}$, $A\in {\mathcal{B}}_i$ and i = 0, · · · , d₀. Under Assumption A $\epsilon ={\epsilon }_{n,p_0,p}={\left(2c_0\right)}^{1∕2}{c}_4^{-1}\log (2^{1∕2}∕c_3)\log p{\left(\frac{p_0}{n}\right)}^{1∕2}$ satisfies there with respect to ε > 0, that is,

$$\underset{\{0\le \mid A\mid \le p_0\}}{\sup }{\int }_{1^{-8}{\epsilon }^2}^{2^{1∕2}\epsilon }{H}^{1∕2}(t∕c_3,{\mathcal{B}}_A)dt\le p_0^{1∕2}{2}^{1∕2}\epsilon \log (2∕2^{1∕2}{c}_3)\le c_4{n}^{1∕2}{\epsilon }^2.$$ (29)

for some constant c₃ > 0 and c₄, say c₃ = 10 and $c_4=\frac{{(2∕3)}^{5∕2}}{512}$. By Assumption A, $C_{\min }\left({\theta }^0\right)\ge {\epsilon }_{n,p_0,p}^2$ implies (29), provided that $d_0\ge {\left(2c_0\right)}^{1∕2}{c}_4^{-1}\log (2^{1∕2}∕c_3)$.

Now, let $S_i^{\star }={\max }_{A\in {\mathcal{B}}_i}\#\{\mathcal{G}:{\mathcal{I}}_0^c=A\}$ and $\log \left(S^{\star }\right)={\max }_{1\le i\le p_0}\log \left(S_i^{\star }\right)∕i$. Using inequalities for binomial coefficients: ${\sum }_{j=0}^i\left(\begin{array}{c}\hfill d-d_0\hfill \\ \hfill j\hfill \end{array}\right)\le {(d-d_0)}^i$ and $\left(\begin{array}{c}\hfill d_0\hfill \\ \hfill i\hfill \end{array}\right)\le d_0^i$, $\mid {\mathcal{B}}_i\mid =\left(\begin{array}{c}\hfill d_0\hfill \\ \hfill d_0-i\hfill \end{array}\right){\sum }_{j=0}^i\left(\begin{array}{c}\hfill d-d_0\hfill \\ \hfill j\hfill \end{array}\right)\le {\left(d(d-d_0)\right)}^i\le {(d^2∕4)}^i$, we have, by Theorem 1 of [23], that for a constant c₂ > 0, say $c_2=\frac{4}{27}\frac{1}{1926}$,

$$I\le \sum _{i=0}^{d_0}\mid \mathcal{B}\mid S_i^{\star }\exp (-c_{2}ni{C}_{\min }\left({\theta }^0\right))\le \sum _{i=0}^{d_0}{\left(\frac{d^2}{4}\right)}^i{S}_i^{\star }\exp (-c_{2}ni{C}_{\min }\left({\theta }^0\right))\le \exp (-c_{2}n{C}_{\min }\left({\theta }^0\right)+2\log d+\log \left(S^{\ast }\right)).$$

This completes the proof.

Proof of Theorem 5: The proof is similar to that of Theorem 4 with some minor modifications. Given τ and $\beta \in {\mathbb{R}}^d$, a partition ${\mathcal{G}}^{\tau }\left(\beta \right)=({\mathcal{I}}_0\left(\beta \right),\cdots ,{\mathcal{I}}_{K\left(\beta \right)}\left(\beta \right))$ associated with is defined to satisfy the following (i) ${\max }_{j\in {\mathcal{I}}_0\left(\beta \right)}\mid {\beta }_j\mid \le \tau$; (ii) |β_j1 − β_j2| ≤ τ for any j different groups. Let $A^{\tau }\left(\beta \right)=\mathcal{I}\backslash {\mathcal{I}}_0\left(\beta \right)$.

The rest of the proof is basically the same as that in Theorem 2 with a modification that $\mathcal{G}\left(\beta \right)$ and $A\left(\beta \right)$ are replaced by ${\mathcal{G}}^{\tau }\left(\beta \right)$ and $A^{\tau }\left(\beta \right)$ respectively. Here, $\mathcal{S}=\{\theta =(\beta ,\eta ):{\sum }_{j=1}^p{J}_{\tau }\left(\mid {\beta }_j\mid \right)\le d_0,{\sum }_{\left(j{j}^{\prime }\right)\in \mathcal{E}}{J}_{\tau }\left(\mid {\beta }_j-{\beta }_{j^{\prime }}\mid \right)\le c_0,{\mathcal{G}}^{\tau }\left(\beta \right)\ne \mathcal{G}\left({\beta }^0\right)\}$, $C^{\tau }(\beta ,\mathcal{E})={\sum }_{\left(j{j}^{\prime }\right)\in \mathcal{E}}I(\mid {\beta }_j-{\beta }_{j^{\prime }}\mid \ne 0)$, ${\mathcal{S}}_A=\{\theta \in \mathcal{S}:A^{\tau }\left(\beta \right)=A\}$ and ${\mathcal{S}}_{\mathcal{G}}=\{\theta =(\beta ,\eta )\in \mathcal{S}:{\mathcal{G}}^{\tau }\left(\beta \right)=\mathcal{G}\}$.

Next, we show ${\widehat{\theta }}^g={\widehat{\theta }}^o$ if and only if ${\widehat{\mathcal{G}}}^g={\mathcal{G}}^0$, where ${\widehat{\mathcal{G}}}^g\equiv {\mathcal{G}}^{\tau }\left({\widehat{\beta }}^g\right)$. Now $d_1\equiv \mid \mathcal{I}\backslash {\widehat{\mathcal{I}}}_0^0\mid =d_0$. By (14), $\frac{1}{\tau }{\sum }_{j\in {\widehat{\mathcal{I}}}_0}\mid {\widehat{\beta }}_j^g\mid +d_1\le d_0$, with d₀ = d₁, yields that ${\widehat{\beta }}_j^g=0$; $j\in {\mathcal{I}}_0^1$. In addition, the second constraint of (14) implies ${\sum }_{i=1}^K{\sum }_{j{j}^{\prime }\in {\mathcal{I}}_i,\left(j{j}^{\prime }\right)\in \mathcal{E}}\frac{\mid {\widehat{\beta }}_j^g-{\widehat{\beta }}_{j^{\prime }}^g\mid }{\tau }\le 0$, yielding that ${\widehat{\beta }}_{j_1}^g={\widehat{\beta }}_{j_1}^g$ for any j₁, j₂ $\in {\widehat{\mathcal{I}}}_i$, $(j_1,j_2)\in \mathcal{E}$, i = 1, · · · , K. By graph consistency of $\mathcal{U}$, $\mathcal{U}$ is connected over ${\widehat{I}}_i$, implying that ${\widehat{\beta }}_{j_1}^g={\widehat{\beta }}_{j_1}^g$ for any j₁, $j_2\in {\widehat{\mathcal{I}}}_i$, i = 1, · · · , K. This further implies that ${\widehat{\beta }}^g={\widehat{\beta }}^o$ and ${\widehat{\theta }}^g={\widehat{\theta }}^o$, meaning that that $\{{\widehat{\mathcal{G}}}^g={\mathcal{G}}^0\}\subseteq \{{\widehat{\theta }}^g={\widehat{\theta }}^o\}$. On the other hand, it is obvious that if ${\widehat{\theta }}^g={\widehat{\theta }}^o$ then $\{{\widehat{\mathcal{G}}}^g={\mathcal{G}}^0\}$. Hence, $\{{\widehat{\mathcal{G}}}^g={\mathcal{G}}^0\}=\{{\widehat{\theta }}^g={\widehat{\theta }}^o\}$ from which we conclude that $\{{\widehat{\theta }}^g\ne {\widehat{\theta }}^o\}\subseteq \{{\widehat{\theta }}^g\in \mathcal{S}\}$. This together with $\{{\widehat{\theta }}^g\ne {\widehat{\theta }}^o\}\subseteq \{L\left({\widehat{\theta }}^g\right)-L\left({\theta }^o\right)\ge 0\}\subseteq \{L\left({\theta }^0\right)\ge 0\}$ implies that $\mathbb{P}({\widehat{\theta }}^g\ne {\widehat{\theta }}^o)\le \mathbb{P}(L\left({\widehat{\theta }}^g\right)-L\left({\theta }^o\right)\ge 0;{\widehat{\theta }}^g\in \mathcal{S})$ is bounded by

$$\sum _{i=0}^{d_0}\sum _{A\in {\mathcal{B}}_i}\sum _{\mathcal{G}\in \{{\mathcal{G}}^{\tau }\left(\beta \right):\theta =(\beta ,\eta )\in {\mathcal{S}}_A\}}{\mathbb{P}}^{\ast }\left(\underset{\theta \in {\mathcal{S}}_{\mathcal{G}}}{\sup }(L\left(\theta \right)-L\left({\theta }^{\ast }\right))\ge 0\right)\le \sum _{i=0}^{d_0}\sum _{A\in {\mathcal{B}}_i}\sum _{\mathcal{G}\in \{{\mathcal{G}}^{\tau }\left(\beta \right):\theta \in {\mathcal{S}}_A\}}{\mathbb{P}}^{\ast }\left(\underset{\{-\log (1-h^2(\theta ,{\theta }^0))\ge d_1\max (i,1)C_{\min }\left({\theta }^0\right)-d_3{\tau }^{d_2}d,\theta \in {\mathcal{S}}_{\mathcal{G}}\}}{\sup }(L\left(\theta \right)-L\left({\theta }^0\right))\ge 0\right),$$

where the last step uses the fact that $\{\theta \in {\mathcal{S}}_{\mathcal{G}}\}\subseteq \{-\log (1-h^2({\theta }^{\tau },{\theta }^0))\ge \max (i,1)C_{\min }\left({\theta }^0\right)\}\subseteq \{-\log (1-h^2(\theta ,{\theta }^0))\ge d_1\max (i,1)C_{\min }\left({\theta }^0\right)-d_3{\tau }^{d_2}d\}$, under Assumption B. Then, for some constant c₃, $\mathbb{P}({\widehat{\theta }}^g\ne {\widehat{\theta }}^o)$ is upper bounded by

$$\sum _{i=0}^{d_0}\mid {\mathcal{B}}_i\mid S_i^{\star }\exp (-c_{3}ni{C}_{\min }\left({\theta }^0\right))\le \sum _{i=0}^{d_0}{\left(\frac{d^2}{4}\right)}^i{S}_i^{\star }\exp (-c_{3}ni{C}_{\min }\left({\theta }^0\right))\le \exp (-c_{3}n{C}_{\min }\left({\theta }^0\right)+2\log d+\log \left(S^{\star }\right)),$$

provided that $\tau \le {\left(\frac{(d_1-c_3)C_{\min }\left({\theta }^0\right)}{d_{3}d}\right)}^{1∕d_2}$. This completes the proof.

Proof of Corollary 2: First we derive an upper bound of S^*. Let $p_l^0$ the number of nonzero elements of the precision matrix in the sth cluster for l = 1, · · · , L. Let $p_0=d_0∕L=\frac{p_1^0+\cdots +p_L^0}{L}$ be the average number of nonzero elements. For any $\theta \in {\mathcal{S}}_A$ with $\mid A^0\backslash A\mid =i$, let $\mathcal{Q}=\{(j,k):j>k,\exists l,x_{jul}\ne 0\}$ and $\mid \mathcal{Q}\mid =q_0$. Let a_jk = #{l : x_jkl ≠ 0} for $(j,k)\in \mathcal{Q}$. Note that q₀ ≤ p⁰ and ${\sum }_{(j,k)\in \mathcal{Q}}{a}_{jk}\le d_0$ since |A| ≤ d₀. By the definition of $S_i^{\ast }$, we have

$$S_i^{\ast }\le \sum _{{\Sigma }_{(j,k)\in \mathcal{Q}}{r}_{jk}\le g_0}\prod _{(j,k)\in \mathcal{Q}}\left(\begin{array}{c}\hfill a_{jk}-1\hfill \\ \hfill r_{jk}\hfill \end{array}\right)=\sum _{g=0}^{g_0}\left(\begin{array}{c}\hfill {\Sigma }_{(j,k)\in \mathcal{Q}}{a}_{jk}-q_0\hfill \\ \hfill g\hfill \end{array}\right)\le \sum _{g=0}^{g_0}\left(\begin{array}{c}\hfill d_0-p_0\hfill \\ \hfill g\hfill \end{array}\right)\le (g_0+1){\left(e\frac{d_0-p_0}{g_0}\right)}^{g_0}.$$ (30)

This together with log(1 + g0) ≤ g0 implies log S^* ≤ 2_g0 max(log(d₀/g0),1). To lower bound C_min(θ⁰), we proceed similarly with the proof of Proposition 2 in [17]. Specifically, note that $h^2(\theta ,{\theta }^0)=1-{\prod }_{l=1}^L(1-h^2({\Omega }_l,{\Omega }_l^0))$. Thus,

$$-\log (1-h^2(\theta ,{\theta }^0))=\sum _{l=1}^L\left(-\log (1-h^2({\Omega }_l,{\Omega }_l^0))\right).$$ (31)

An application of Proposition 2 of [17] yields that each term in (31) is lower bounded by $c^{\star }{\Vert {\Omega }_l-{\Omega }_l^0\Vert }_2^2$. Therefore, $-\log (1-h^2(\theta ,{\theta }^0))\ge c^{\star }{\min }_{1\le l\le L}{c}_{min}\left(H_l\right){\sum }_{l=1}^L{\Vert {\Omega }_l-{\Omega }_l^0\Vert }_2^2$. Now if $A_0\backslash A\ne \varnothing$, we have ${\sum }_{l=1}^L{\Vert {\Omega }_l-{\Omega }_l^0\Vert }_2^2\ge \mid A_0\backslash A\mid {\min }_{(j,k,l):{\omega }_{jkl}\ne 0}{\omega }_{jkl}^2$. If $A_0\backslash A=\varnothing$, then by definition of $\mathcal{S}$, there must exist (j, k, l) such that ω_jkl = ω_jk(l+1) and ${\omega }_{jkl}^0\ne {\omega }_{jk(l+1)}^0$. Here

$$\begin{array}{cc}\hfill \sum _{l=1}^L{\Vert {\Omega }_l-{\Omega }_l^0\Vert }_2^2& \ge {({\omega }_{jkl}-{\omega }_{jkl}^0)}^2+{({\omega }_{jk(l+1)}-{\omega }_{jk(l+1)}^0)}^2\ge \frac{1}{2}{({\omega }_{jkl}^0-{\omega }_{jk(l+1)}^0)}^2\hfill \\ \hfill & \ge \frac{1}{2}\underset{\{(j,k,l):{\omega }_{jkl}^0\ne {\omega }_{jk(l+1)}^0\}}{\min }{({\omega }_{jkl}^0-{\omega }_{jk(l+1)}^0)}^2.\hfill \end{array}$$

A combination of both the cases yield that

$$-\log (1-h^2(\theta ,{\theta }^0))∕\max (\mid A_0\backslash A\mid ,1)\ge c^{\star }\underset{1\le l\le L}{\min }{c}_{min}\left(H_l\right){\eta }_{min}^2.$$

which, after taking infimum over $\mathcal{S}$, leads to $C_{min}\left({\theta }^0\right)\ge c^{\star }{c}_{min}\left(H_l\right){\eta }_{min}^2$. This, together with, the upper bound on log S^* in Theorems 4 and 5, gives a sufficient condition for simultaneous pursuit of sparseness and clustering: ${\min }_{1\le l\le L}{c}_{min}\left(H_l\right){\eta }_{min}^2\ge c_0\frac{\log \left(p^{2}L\right)-g_0\max (\log (d_0∕g_0),1)}{n}$, for some c₀ > 0. Moreover, under this condition, $\mathbb{P}({\widehat{\Omega }}^{{\ell }_o}\ne {\widehat{\Omega }}^o)$ and $\mathbb{P}({\widehat{\Omega }}^g\ne {\widehat{\Omega }}^o)\to 0$ as n, d → +∞. This completes the proof.