The parametric G-formula for time-to-event data: towards intuition with a worked example

Abstract

Background

The parametric g-formula can be used to estimate the effect of a policy, intervention, or treatment. Unlike standard regression approaches, the parametric g-formula can be used to adjust for time-varying confounders that are affected by prior exposures. To date, there are few published examples in which the method has been applied.

Methods

We provide a simple introduction to the parametric g-formula and illustrate its application in analysis of a small cohort study of bone marrow transplant patients in which the effect of treatment on mortality is subject to time-varying confounding.

Results

Standard regression adjustment yields a biased estimate of the effect of treatment on mortality relative to the estimate obtained by the g-formula.

Conclusions

The g-formula allows estimation of a relevant parameter for public health officials: the change in the hazard of mortality under a hypothetical intervention, such as reduction of exposure to a harmful agent or introduction of a beneficial new treatment. We present a simple approach to implement the parametric g-formula that is sufficiently general to allow easy adaptation to many settings of public health relevance.

Imagine an oncologist knocks on your door with the following problem: she wants to know how much she could reduce mortality among her bone marrow transplant patients by prescribing a new drug that prevents graft-versus-host disease, a side effect of allogeneic marrow transplantation.¹ While graft-versus-host disease is associated in observational studies with an increased risk of mortality, it also reduces the risk of leukemia relapse – thus, any drug that prevents graft-versus-host disease may have the very undesirable side effect of increasing the rate of relapse.² She wants to compare the mortality in her cohort with what mortality would be in that same cohort if they had taken this new drug. We cannot answer this question with a regression model because leukemia relapse is a risk factor for mortality and subsequent graft-versus-host disease and it will also decrease the incidence of subsequent relapse (i.e. relapse is a confounder affected by exposure).^{3, 4} However, we can answer this question using the g-formula.

The g-formula is an analytic tool for estimating standardized outcome distributions using covariate (exposure and confounders) specific estimates of the outcome distribution.⁵The g-formula can be used to estimate familiar measures of association, such as the hazard ratio. In the current paper, we address the oncologist’s question: we compare observed mortality in our cohort with the expected mortality in that cohort under the new treatment.

Epidemiologists often use regression models (for example, the Cox proportional hazards model) to adjust for confounding; this is equivalent to estimating stratum-specific hazard ratios and then averaging the information-weighted hazard ratios. When some of those confounders are also causal intermediates, this amounts to adjusting away some of the effect of exposure.^{6, 7} The g-formula works differently: first, one finds weighted averages of the stratum-specific hazards, and then those averaged (standardized) hazards are combined in a summary hazard ratio. Thus, bias resulting from time-varying covariates that can be both confounders and causal intermediates is a shortcoming of using regression models to control for confounding, rather than a general principle of observational data analysis.^{8, 9} The g-formula is a tool that overcomes this shortcoming, but its use in the literature has been sparse – we could find only 9 examples using observational data.^{8, 10-17} We hypothesize that the dearth of software packages and lack of useful, yet simple, examples of the g-formula have been the main barriers to broader use.

We show how the g-formula can be used with standard software tools that many epidemiologists already employ, and we illustrate it using publicly-available data from a small cohort study with accompanying SAS code in an eAppendix. We illustrate how we can estimate the net (total) effect of a hypothetical treatment to prevent graft-versus-host disease on mortality and compare the g-formula approach with a regression approach. The g-formula (as with any statistical method) relies on making assumptions in order to make sense of the complex processes underlying the data. We discuss possible ways to assess how well we meet the assumptions as well as the robustness of the g-formula to violations of these assumptions.

METHODS

The g-formula

Using regression methods to control confounding requires making the assumption that the effect measure is constant across levels of confounders included in the model. Alternatively, standardization allows us to obtain an unconfounded summary effect measure without requiring this assumption. The g-formula is a generalization of standardization and can be expressed similarly. For example, the 10-year risk of death for a group of individuals, standardized across some dichotomous (1,0) risk factor Z could be expressed as

$$\mathrm{Pr}(\mathit{death}=1)=\sum _z\mathrm{Pr}(\mathit{death}=1\mid Z=z)\mathrm{Pr}(Z=z)$$

where Σ_z indicates that we are summing over each possible value of Z, and Pr (Z = z) is the probability that Z takes on the value z in the reference population. If the 10-year risk of death among the group with Z=1 was 0.1 and the risk among the group with Z=0 was 0.05, and we were studying a population with a 60 individuals with Z=1 and 40 individuals with Z=0, the Z-standardized 10-year risk of death would be 0.1*(60/100)+0.05*(40/100) = 0.08.

The g-formula relies on this same set of calculations. Suppose now that we have a cohort of 50-year-old men and we wish to estimate the change in 10-year risk of death from some exposure, X, that has no effect on mortality among 50-55 year olds but increases mortality after age 55. The overall 10-year risk of death, Pr(death₁₀=1), could be calculated using the probabilities expressed by the g-formula:

$$\begin{array}{lll}\mathrm{Pr}({\mathit{death}}_{10}=1)& =& \sum _x\mathrm{Pr}({\mathit{death}}_{10}=1\mid X=x,\mathit{age}>55,{\mathit{death}}_5=0)\mathrm{Pr}(X=x\mid \mathit{age}>55,{\mathit{death}}_5=0)\\ & \times & (1-\mathrm{Pr}({\mathit{death}}_5=1\mid X=x,\mathit{age}\le 55)\mathrm{Pr}(X=x\mid \mathit{age}\le 55))\\ & +& \mathrm{Pr}({\mathit{death}}_5=1\mid X=x,\mathit{age}\le 55)\mathrm{Pr}(X=x\mid \mathit{age}\le 55)\end{array}$$

Assume 50% are exposed at the start. As shown in the calculations from Table 1, if the probability of death in our cohort after 5 years (at age 55 - death₅) is 0.025 for everyone and the conditional probability of death between 5 and 10 years of follow-up (i.e. between age 55 and 60) is 0.06 for exposed and 0.051 for unexposed individuals, the overall standardized 10-year risk of death (Pr(death₁₀=1)) would be 0.08. We consider the probability of death in the second period to be conditional because we condition (restrict) our data to the individuals still alive at the beginning of year 6. The overall standardized risk is often referred to as the “natural course”, because we are estimating the risk under no interventions. In this setting (in which we can observe all covariate specific probabilities), the observed 10-year risk will equal the 10-year risk calculated using the “natural course.”

Table 1.

Estimating risk under interventions using the g-formula with the hypothetical example given in methods section of the main text.

G-formula component	Value
Conditional probabilities
First 5 years	PR(exposed): 0.5
	Risk among exposed: 0.025
	Risk among unexposed: 0.025
Last 5 years	Pr(exposed): 0.5
	Risk among exposed: 0.060
	Risk among unexposed: 0.051
Risk under interventions
Observed/Natural course	0.051*(1/2)*(1-0.025*(1/2)) + 0.025*(1/2) +
	0.060*(1/2)*(1-0.025*(1/2)) + 0.025*(1/2) = 0.080
Always exposed	0.051*(0)*(1-0.025*(0)) + 0.025*(0) +
	0.060*(1)*(1-0.025*(1)) + 0.025*(1) = 0.084
Never exposed	0.051*(1)*(1-0.025*(1)) + 0.025*(1) +
	0.060*(0)*(1-0.025*(0)) + 0.025*(0) = 0.075
Expose if survive to year 5	0.051*(0)*(1-0.025*(0)) + 0.025*(1/2) +
	0.060*(1)*(1-0.025*(1)) + 0.025*(1/2) = 0.084

Use of the g-formula for effect estimation proceeds using the standardization formula above and substituting new values for probabilities of exposure defined by a hypothetical intervention. For example, if we wished to estimate the effect of exposure on the 10-year risk of death, we would use the g-formula to calculate the risk of death if we intervened to make all individuals “always exposed “ (i.e. set Pr(X = 1∣age) = 1.0 (and Pr(X =0∣age) = 0.0) regardless of age) versus the risk if we intervened to make all individuals “never exposed” (e.g. set Pr(X =0∣age) = 1.0) (and Pr(X = 1∣age) = 0.0)). As shown in Table 1, we substitute 1.0s (and 0.0s) into the standardization formula for these conditional exposure probabilities and arrive at a 10-year risk for the intervention “always exposed” of 0.084 and for the intervention “always unexposed” of 0.075 (g-formula standardized risk difference = 0.009). For an intervention in which we expose all participants in the last 5 years only (the treatment plan “expose if still alive at 5 years”), we would “intervene” by setting conditional probabilities Pr(X∣ age > 50) to 1.0 and Pr(X∣ age ≤ 55 to the conditional proportions observed in the original data (risk=0.084).

The parametric g-formula

While standardization using the g-formula is simple enough to do by hand in our hypothetical example, epidemiologic studies often have richer covariate sets and longer periods of follow-up. In such studies, stratification by many covariates can quickly lead to strata in which there are not enough data to calculate the conditional probabilities, and use of continuous covariates does not allow this stratification approach. Instead of directly calculating every conditional probability, we can use parametric regression modeling to calculate the conditional probabilities used to carry out computations shown above. Further, we can simulate data from the conditional probability distributions to approximate standardization. Robins referred to this approach of using modeled conditional probabilities to estimate standardized effect measures as the parametric g-formula.^{14, 18} The data from our illustrative example and SAS code to carry out our algorithm are provided in eAppendices 1 through 4.

Illustrative example

We use the parametric g-formula to estimate the hazard ratio comparing mortality in a cohort of bone marrow transplant recipients (described in detail by Copelan etal¹⁹ and by Klein and Moeschberger) ²⁰ under different treatments by a hypothetical drug that prevents graft-versus-host disease. Use of the g-formula for our example was motivated by hypothesized time-varying confounding shown in the causal diagram in Figure 1, and by the desire to estimate the reduction in mortality from an intervention that could prevent graft-versus-host disease.

Figure 1.

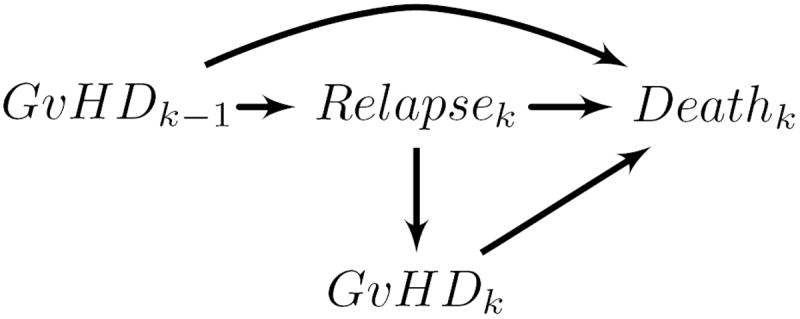
Directed acyclic graph showing hypothesized causal relationships among study variables for days k − 1 and k. This graph demonstrates bias in regression stratification methods in estimating the effect of exposure over time (GνHD_k−1, GνHD_k) on subsequent death when time-varying factors on confounding pathways (Relapse_k) may be affected by prior exposure.

Study population

The study population arose from a multicenter trial of leukemia patients and comprises 137 individuals prepared for bone marrow transplants under a radiation-free regimen at four medical centers. Allogeneic bone marrow transplants were performed between 1 March 1984 and 30 June 1989, and patients were followed until death or administrative censoring at 5 years following transplant. Baseline covariates at time of transplant included age, sex, leukemia type (acute lymphocytic or acute myeloid leukemia), wait time from leukemia diagnosis to transplantation, and cytomegalovirus immune status (yes or no). Patients were followed to assess when, if at all, platelets returned to the normal range (as a measure of immune function) and the patient experienced leukemia relapse.

We illustrate how to apply the parametric g-formula to the cohort of bone marrow transplant recipients to estimate the effect of a hypothetical intervention that prevents graft-versus-host disease from occurring. While the cohort is small, our example can be easily adapted to larger observational studies with long-term follow-up.

The parametric g-formula algorithm for the bone marrow transplant data

We use a 3-step algorithm for the parametric g-formula to estimate hazard ratios comparing: a new drug that prevents graft-versus-host disease from occurring during follow up (“prevented”) versus no intervention (“natural course”). We compare “natural course” to “prevented” as a measure of how effective a drug that prevents graft-versus-host disease would have been at preventing mortality in our cohort (or similar populations). We present the algorithm in compact form in Figure 2, and interested readers may find it of use to follow our algorithm with the SAS code and data given in eAppendices 1-4 and the more formal (and technical) presentation of the g-formula of our data in eAppendix 5.

Figure 2.

Parametric g-formula algorithm for bone marrow transplant data.

Step 1) Probability modeling

We start with a person-period data set in which each record corresponds to one person-day and time-varying covariates are represented as (0,1) dichotomous variables for each person day. Within this person-period data, we fit a pooled logistic model (i.e. a logistic model fit to all person periods) to estimate the log-odds of each of the time-varying covariates (graft-versus-host disease, platelet level, relapse, death), for each person period (i.e. the conditional log-odds of the covariate taking on the value “1”).²¹ We included time (i.e. days since transplant) in the model using a set of polynomial terms. Because we modeled the onset of graft-versus-host disease (and other time-varying covariates), the models for each covariate on day k were fit using only person-days for which the patient had not yet experienced each time-varying covariate on day k − 1. We transformed the log-odds of each covariate into probabilities using the transformation Pr(·) = exp (·)/(1+exp (·)).

Step 2) Monte Carlo sampling

From our original data of N=137 patients, we re-sampled with replacement M=137,000 “pseudo-patients,” retaining only baseline covariates. The sample should be as large as practical to minimize simulation error. This simulation is carried out as follows.

We simulated time-varying covariate and outcome data for each of the pseudo-patients using conditional probabilities generated in Step 1 and baseline covariates (with time-varying covariates set to 0 at baseline). Each pseudo-patient received values for these covariates on each day based on a draw from a Bernoulli distribution with the conditional mean given by the probability modeled in Step 1, above. Essentially, on each day k, we flipped biased coins to choose whether or not the pseudo-patient became exposed, experienced relapse, returned to normal platelet levels, was censored, or died, and the probability of a coin coming up “heads” depended on values of those covariates on prior days and the baseline covariates.

The dataset from this step is known as the “natural course” because there is no intervention. To ensure that covariate distributions from the “natural course” closely follow distributions in the observed data, we examined the Kaplan-Meier survival curve for death (Figure 4) as well as the complement of the Kaplan-Meier curves for time to onset of graft-versus-host disease, relapse, and normal platelet count (Figure 3). We fit multiple parametric forms for each model in Step 2 and based our final choice of model on how closely these graphs and covariate means from the “natural course” matched those in the observed data. For example, we compared the fit of models using linear, quadratic, cubic polynomial, quadratic spline, unrestricted cubic spline, and restricted cubic splines. Model components and coefficient values are given in eAppendix 6.

Figure 4.

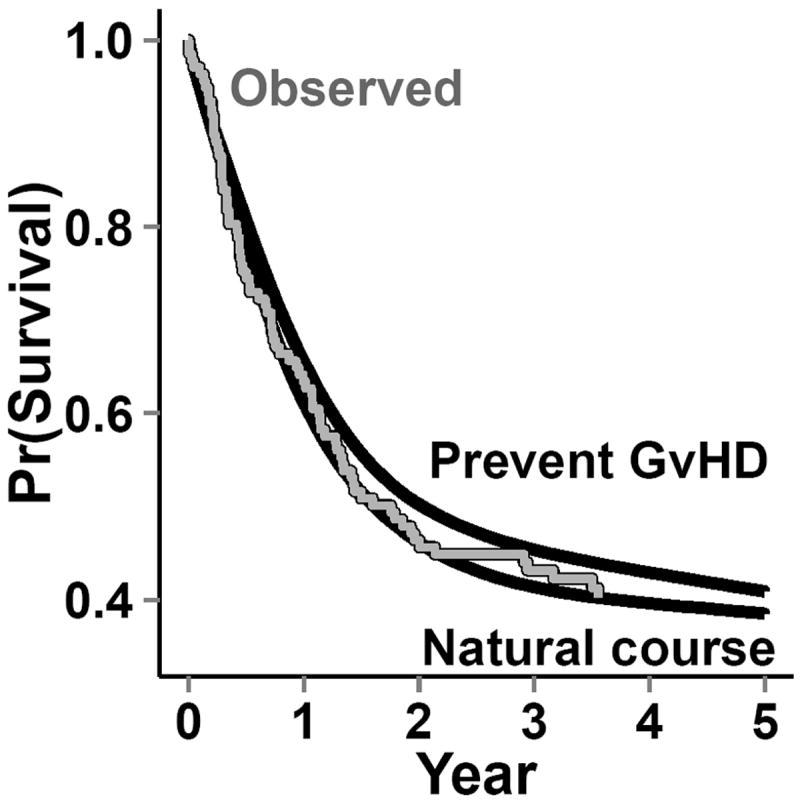
Survival functions: observed from the bone marrow transplant data; from the natural-course intervention in the g-formula; and from the hypothetical intervention “prevented” graft-versus-host disease (top line) after bone marrow transplants using the g-formula. The gray line indicates the observed survival curve, while the solid black lines indicate the survival curves from the Monte Carlo data for the g-formula interventions.

Figure 3.

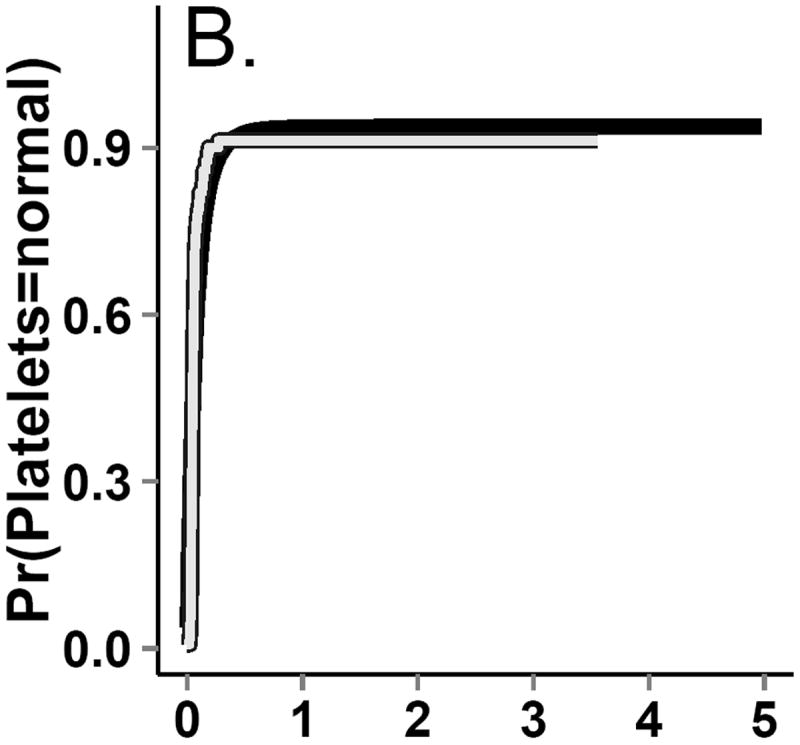
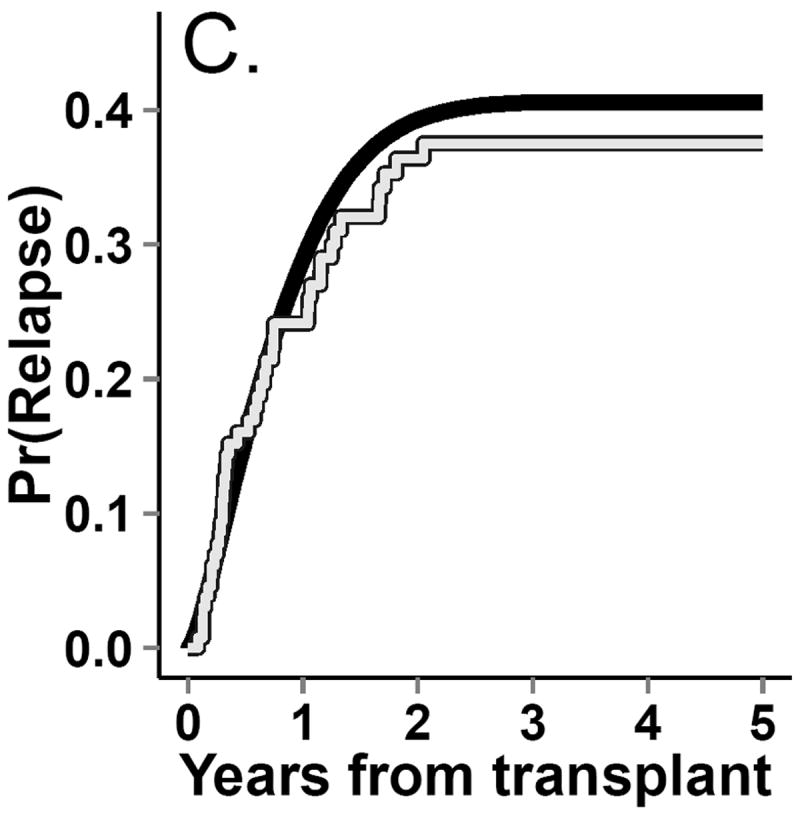
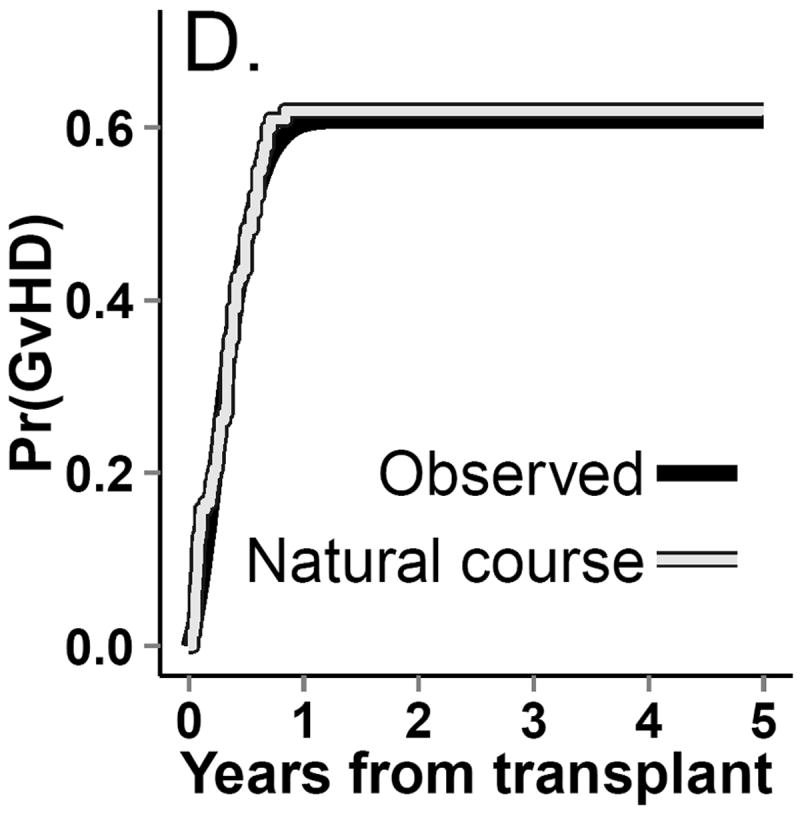
Incidence curves for (A.) death. (B.) return to normal platelet levels, (C.) relapse and (D.) graft-versus-host-disease (GvHD) from both observed (gray line) and g-formula natural course Monte Carlo (black line) data.

We repeated Step 2 using an intervention “prevented,” set graft-versus-host disease to 0 and generate all other covariates, forcing graft-versus-host disease to remain 0. By setting the values of graft-versus-host disease in the dataset, the proportion of deaths in the simulated dataset in which we set graft-versus-host disease=0 approximates the solution to the explicit formulas shown in our hypothetical example (in which the conditional probabilities of graft-versus-host disease onset are all set to 0).

Step 3) Effect estimation

We concatenated the datasets from Step 2, estimating the hazard ratio by comparing the hazards in the “natural course” dataset with those in the “prevented” dataset. This was done by using an indicator variable for the dataset (1=“natural course,” 0=“prevented”) and using that indicator as the exposure variable in a Cox model.

To estimate confidence intervals for the hazard ratio, we repeated Steps 1-3 on 4000 samples of size 137 taken at random with replacement from the original data. The standard deviation (SD) of the 4000 log-hazard ratios approximates the standard error of the log-hazard ratio, and was used to calculate 95% confidence intervals (CIs) using the normal approximation: log-hazard ratio ±1.96*SD(log-hazard ratio).

Statistical methods for comparison

To compare the g-formula with standard methods, we estimated crude and covariate conditional hazard ratios (and 95% confidence intervals) for the effect of graft-versus-host disease on mortality using a Cox proportional hazards model for time-varying data (with observed data).²² We controlled for possible confounding by baseline and time-varying covariates by including indicator terms in the Cox model. A test of proportional hazards in crude and regression-adjusted models indicated that a summary hazard ratio over the five-year course of the study was adequate.

RESULTS

Patients had a median age of 28 years (interquartile range=21-35), and 60% were male (Table 2). Half of the patients tested positive for cytomegalovirus at baseline (n=68; 50%). In the first 5 years of the study, 72 patients developed graft-versus-host disease and 43 patients relapsed. Platelet levels returned to normal for 88% of patients (n=120). Five years after receiving a transplant, 58% of the patients had died (n=80).

Table 2.

Characteristics^a of 137 patients receiving bone marrow transplants during treatment for leukemia at 4 study sites between 1985 and 1989.

Sex	Male	80	(58)
	Female	57	(42)
GvHD onset within 5 years	No	65	(47)
	Yes	72	(53)
Relapse within 5 years	No	94	(69)
	Yes	43	(31)
Return to normal platelet count within 5 years	No	17	(12)
	Yes	120	(88)
Leukemia type	ALL	38	(28)
	Low-risk AML	54	(39)
	High-risk AML	45	(33)
CMV status at baseline	Negative	69	(50)
	Positive	68	(50)
Vital status 5 years after transplant	Alive or censored	57	(42)
	Dead	80	(58)
Age (years); median (IQR)		28	(21-35)
Days to transplant; median (IQR)		6	(4-8)
Follow up; median (IQR)		547	(183-1377)
Days to relapse; median (IQR)		467	(122-1363)
Days to normal platelets; median (IQR)		18	(14-27)

^aNo. (%), unless otherwise specified

ALL indicates acute lymphocyte leukemia; AML, acute myeloid leukemia; IQR, interquartile range

Regression adjustment

The crude hazard ratio comparing the hazard of all-cause mortality among patients with and without graft-versus-host disease was 1.2 (95% CI=0.77-2.0; Table 3). The hazard ratio was unchanged after regression adjustment for baseline covariates, but was notably larger after regression adjustment for baseline and time-varying covariates (hazard ratio=2.3 [95% CI=1.4-3.9]).

Table 3.

Hazard ratios comparing the hazard of all-cause mortality between patients with and without graft-versus-host disease (regression) or comparing cohorts with and without hypothetical intervention to prevent graft-versus-host disease (g-formula)

Method		HR	(95% CI)
Regression
	Crude	1.2	(0.77-2.0)
	Baseline adjusted a	1.2	(0.71-1.9)
	Fully adjusted b	2.3	(1.4-3.9)
G-formula
	Natural course vs. Prevent c	1.1	(0.91-1.3)

^aBaseline covariates include age at date of bone marrow transplant, wait time until transplant, sex, and cytomegalovirus status at baseline.

^bAdjusted for baseline covariates above and time-varying covariates, including days during which platelets had not returned to normal, cumulative days the patient had not experienced relapse, and indicators for relapse and platelets returning to normal on a given day.

^cComparing the hazard of all-cause mortality between the entire cohort simulated under no intervention and the entire cohort of simulated to be unexposed (referent) at all time points.

G-formula

In the simulated data under the natural course, the cumulative distribution functions for platelet count, relapse, death, and graft-versus-host disease closely followed those in the observed data (Figures 3 and 4). The 5-year cumulative risk of death using the g-formula under the natural course was 61%. The hazard ratio comparing the “natural course” to “prevented” (referent) was 1.1 (95% CI=0.91, 1.3).

DISCUSSION

In our analysis of survival data using a simple and yet easily adaptable application of the g-formula, we estimated the effects on mortality of an intervention to prevent graft-versus-host disease immediately after bone marrow transplant. Almost 60% of the bone marrow transplant patients in this cohort experienced graft-versus-host disease under the natural course; however, compared with a hypothetical intervention to prevent graft-versus-host disease, under the natural course we observed an increase in the relative mortality hazard of only 10%. Preventing graft-versus-host disease does not appear to markedly reduce mortality risk because other factors that influence the risk of subsequent mortality, such as leukemia relapse, are not decreased by the hypothetical intervention to prevent graft-versus-host disease. Rather, preventing graft-versus-host disease may increase the rate of relapse: 42% of “pseudo-individuals” experienced relapse under the “prevented” intervention, whereas 33% experienced relapse under the “natural course.” These observations agree with the typically coincident occurrences of graft-versus-host disease and graft-versus-leukemia, in which donor cells attack residual leukemia cells in the transplant recipient and may help to prevent relapse. Graft-versus-host disease has been observed to correlate with a lower rate of leukemia relapse and is hypothesized to reduce the probability of relapse through immune mediation processes, of which normal platelet count is an indicator.¹

Cox regression analysis with adjustment for time-varying covariates suggested a substantially higher mortality hazard for persons who have graft-versus-host disease when compared with those who do not have this disease. Because the Cox model cannot appropriately control time-varying confounding when the confounders are causal intermediates, we hypothesize that the Cox model overestimates the total effect of graft-versus host disease on mortality. Therefore, the difference between the g-formula estimate and the regression adjustment method may be due, in part, to over-adjustment, which introduces bias into our estimate of the total effect of graft-versus-host disease.²³ In addition, another reason for the difference between the g-formula estimate and the adjusted Cox regression model estimate is that these analyses estimate different quantities. The g-formula yielded an estimate of the hazard ratio comparing the observed mortality in our cohort (the natural course) with the expected mortality in that cohort under the new treatment. The Cox model yielded an estimate of the mortality hazard for those with graft-versus-host disease compared with those without graft-versus-host disease.²⁴

The g-formula can be used to estimate risk ratios or differences, which are easier to interpret and less subject to some biases than are hazard ratios.²⁵ Like Westreich et al, ¹⁴ we have estimated hazard ratios as effect measures to ease the comparison with results from conventional methods. However, when a confounder is a strong predictor of the outcome, marginal hazard ratios from the g-formula and conditional hazard ratios from regression approaches may differ even if there is no time-varying confounding, a condition known as “non-collapsibility.”²⁶ Because the set of time-varying covariates includes relapse, a strong predictor of mortality, this is not a trivial concern for our example, but adjustment via regression modeling simply replaces confounding bias with bias due to conditioning on an effect of the exposure. However, the g-formula estimates a hazard ratio we could observe in a population intervention (marginal, or standardized to the population), and is arguably more useful than a conditional hazard ratio when estimating the public health impact of interventions.

There is little knowledge about how potential time-varying confounding by relapse and platelet levels affects estimates of excess mortality due to graft-versus-host disease. G-methods (the body of methods that derive from the g-formula, including structural nested models and marginal structural models) may provide an avenue toward a clearer understanding. G-methods have previously been shown to yield results congruent with clinical trial data (where time-varying confounding may be minimized) in situations where conventional analyses of observational data yield incongruous estimates.^{14, 27, 28} There are few examples in the literature in which the parametric g-formula has been used to estimate the effects of policies or interventions. Robins^{8, 10} estimated the effect of interventions capping arsenic exposure on the risk of lung cancer in a cohort 8,047 copper smelter workers in Montana. Ahern et al. ¹¹ used the parametric g-formula to estimate the effect of interventions to change neighborhood smoking norms on the prevalence of smoking using data collected from 4000 New York City residents. Using data from the Nurses’ Health Study, Taubman et al. ¹² estimated the 20-year risk (cumulative incidence) of coronary heart disease under interventions on dietary factors, exercise, smoking, alcohol consumption, and body mass index; using data from the same study, Danaie et al. ¹⁶ estimated the effects of similar interventions on the 24-year risk of type-2 diabetes and Garcia-Aymerich et al. ¹⁷ estimated the effect of joint interventions on physical activity and weight loss on adult onset asthma incidence. In a cohort of 8392 HIV-infected participants in the HIV-CAUSAL collaboration, Young et al. ¹³ applied the parametric g-formula to estimate 5-year mortality risks under seven dynamic treatment regimes to determine the optimal CD4 count at which to begin antiretroviral therapy. Westreich et al. ¹⁴ used the parametric g-formula to estimate hazard ratios comparing the hazard of AIDS or death among 1498 HIV-infected patients enrolled in the Multicenter AIDS Cohort Study and the Women’s Interagency HIV Study had all study participants received antiretroviral therapy with the hazard had none of the study participants received therapy. Finally, using data from a cohort of 3,002 textile workers, Cole et al. ¹⁵ estimated effect on lung cancer mortality if recent occupational limits on annual exposures to chrysotile asbestos fibers had been in place during the workers’ tenure.

In all of these studes except the one by Ahern et al., the potential for time-varying confounding precluded the use of conventional regression approaches. In all cases, the g-formula naturally lent itself to estimating the effects of potential interventions. Rather than estimating the more familiar contrast in measures of disease occurrence for a unit change in the exposure, the g-formula provides an estimate of outcome occurrence under a specific treatment regime under study. While regression adjustment and the g-formula allow for estimation of “etiologic” hazard ratios, only the g-formula easily allows estimation of the effect of preventing graft-versus-host disease in the population, which may be more useful for informing population-level interventions.

We must make several assumptions when using of the g-formula to estimate the effects of exposure on an outcome in observational data.⁸ We provide a brief discussion of these assumptions for our analysis, which are reviewed in depth elsewhere.^{29, 30} These assumptions are not unique to the g-formula, but estimating effect measures in the g-formula requires explicitly confronting these assumptions, which may be valuable in informing the interpretation of observational studies.

Conditional exchangeability

As epidemiologists, we may strive to measure and control for strong confounders of the exposure-outcome relationship to avoid making inference based on spurious relationships, and we often assume we have been successful – this is the assumption of conditional exchangeability. In our g-formula example, we impute the potential outcomes for each person based on an evolving covariate history generated by predictive models for the exposure, covariates and the outcome. If there were a strong, unmeasured, baseline confounder, we would have omitted an important variable from both the exposure model and the outcome model. However, as Robins et al¹⁸ note, the exposure model does not need to be correct in order to make inference from the g-formula. To see this, recall our original hypothetical example in which, to make interventions, the probability of exposure is set to 0 in the “prevent” intervention. Thus, because we “set” exposure, the hazard under some intervention will be subject to bias only through the model for the outcome. The practical consequence of this is that unmeasured confounder bias should be (approximately) the same under the g-formula and a standard regression model, when we are comparing two interventions. However, unmeasured confounding bias may be greater in the g-formula when comparing an intervention versus the “natural course,” since this analysis requires a model for the exposure.

In more complex settings, such as if the omitted confounder were also a cause of another time-varying covariate, the g-formula may be subject to more bias than conventional models due to unmeasured confounding. Intuitively, this is because we could be accumulating bias over multiple models, rather than a single outcome model (as in the standard Cox model). However, we should note that, in complex time-varying settings, conventional models require stratification over time-varying confounders, which may be problematic for reasons discussed above, and conventional models may not be able to estimate useful effect measures, such as the impact of an intervention on a population. The g-formula is not subject to either of these shortcomings. Ultimately, the impact of unmeasured confounding in the g-formula (versus conventional models) is an open question; future work will provide guidance to epidemiologists working in settings where unmeasured confounding is expected to be problematic.

While sensitivity analyses exist for examining robustness to the assumption of no unmeasured confounding,³¹ they are most informative when one can hypothesize both a source of confounding and the plausible levels of the strength of the confounder associations in the study.³² We know of no factors that could strongly influence the estimated effect of graft-versus-host disease on mortality, and so in the case of our g-formula example, the sensitivity of the hazard ratio to unmeasured confounding would either be purely speculative or be focused on finding the level of confounding that could explain the observed association.

Treatment version irrelevance

We assume the effect of exposure is the same whether we set it, as in the case of Step 5 of our algorithm or a clinical trial, or if it occurs naturally.^{33, 34} When we “intervene” to set graft-versus-host disease to 0 for all pseudo-patients in our Monte Carlo sample, treatment version irrelevance means we assume that this emulates a process in which a researcher could prevent graft-versus-host disease. We hypothesize this assumption may be violated in our example, because acute and chronic forms of graft-versus-host disease may not affect mortality with the same magnitude.² In this case, we could improve on how well we meet this assumption by including models for both chronic and acute graft-versus-host disease, as well as estimating effects for both on mortality. However, because we are estimating the population-averaged effect of graft-versus-host disease on mortality, such an analysis would not likely give substantially different results. Our analysis applies to graft-versus-host disease, as it occurs in populations similar to our cohort in which graft-versus-host disease can be either acute or chronic. Consistency requires that we specify interventions which are unambiguous.³⁵ Thus, the sensitivity of the g-formula results to violations of treatment version irrelevance depends, in some respect, on how well one can emulate one’s analysis with a clinical trial.

As an anonymous referee pointed out, our analysis can be used to guide future clinical trials by informing on the effects of a drug that completely prevents graft-versus-host disease – our estimate of a 10% reduction in 5-year mortality could used to plan such a study. If one were to study the effect of, say, a population intervention that dictated an instantaneous shift in body-mass-index (BMI) category, then g-formula results would not estimate the effect we could observe in any clinical trial.³⁵

Correct model specification

The parametric g-formula is especially vulnerable to the assumption of correct model specification, due to the use of multiple models. As an example from our study, if the true effect of wait time to transplant had a quadratic association with exposure and a cubic association with mortality, then we would have misspecified two models and would likely have introduced bias into the hazard ratio. Our g-formula algorithm allows informal checking of this assumption by comparing the observed data to the data simulated under the natural course (e.g. Figures 3 and 4). Nonetheless, similarity to the natural course cannot completely rule out model misspecification.¹⁸ The g-formula may not be ideal for hypothesisgenerating studies, in which causal relationships are more uncertain and model misspecification is potentially severe.

Summary, recommendations and conclusions

The g-formula does not require more information than standard methods to estimate effects of exposures or interventions, and its is not subject to bias due to stratifying on variables affected by exposure. The g-formula does not assume that the hazard ratio is homogenous over the levels of the confounders – that is, we are not restricted to estimating a summary hazard ratio that conditions on the covariates. Unlike methods that use stratification of the data by covariates, and then obtain a summary hazard ratio under the assumption of a constant hazard ratio over levels of the confounder, the g-formula permits us to obtain a summary hazard ratio without stratifying the effect measure over covariates. This relaxed assumption comes at the cost of wider confidence intervals, so there is a bias-variance trade-off to consider when deciding if the g-formula is an appropriate statistical tool for an epidemiologic analysis. If one knows that time-varying confounding is not present, or that exposure could not affect subsequent confounders, then standard regression methods may be more appropriate, due mainly to concerns about model misspecification in the g-formula. However, if time-varying confounding is possible, use of the g-formula provides some assurance that one is not introducing bias by inappropriately stratifying on effects of exposure, and it is useful to check results from standard regression models against those from the g-formula, as we have shown.

We could have estimated the hazard ratio for the marginal effect of graft-versus-host disease on mortality using inverse-probability weighted marginal structural models or adaptations of structural nested models.^36-38 In principle, these models would yield similar effect estimates as our method, although our small data set would likely result in practical violations of additional assumptions necessary for inverse-probability-weighting methods,³⁹ and, without knowledge about the baseline hazard of potential outcomes, structural nested models may yield larger confidence intervals.⁴⁰ These methods may be more desirable when model misspecification is a primary concern, because they require fewer models than the g-formula.¹⁸

Though the g-formula was first described in 1986 by Robins,⁸ the availability of rich data from large cohort studies and the acceleration of computing speeds have only recently made the method feasible for widespread use. While the g-formula may be more sensitive to model misspecification than standard regression models, we show how inappropriate control of time-varying confounding could lead to incorrect conclusions about the strength of the effect of graft-versus-host disease on mortality. Moreover, we illustrate how the g-formula allows estimation of the effects of realistic interventions and give concrete examples of situations in which the g-formula should be used by epidemiologists. We have provided both publicly available data and the SAS code as appendices to this paper. The current analysis represents the first published use of the g-formula for a time-varying exposure that can be easily replicated by other investigators using a real-world example. Future implementations of the g-formula can extend our example easily to an array of epidemiologic problems and further explore the impacts on inference from unmeasured confounding and model misspecification.