Inferences on relative failure rates in stratified mark-specific proportional hazards models with missing marks, with application to HIV vaccine efficacy trials

Abstract

This article develops hypothesis testing procedures for the stratified mark-specific proportional hazards model in the presence of missing marks. The motivating application is preventive HIV vaccine efficacy trials, where the mark is the genetic distance of an infecting HIV sequence to an HIV sequence represented inside the vaccine. The test statistics are constructed based on two-stage efficient estimators, which utilize auxiliary predictors of the missing marks. The asymptotic properties and finite-sample performances of the testing procedures are investigated, demonstrating double-robustness and effectiveness of the predictive auxiliaries to recover efficiency. The methods are applied to the RV144 vaccine trial.

1 Introduction

The primary objective of a preventive HIV vaccine efficacy trial is to assess vaccine efficacy (VE) to prevent HIV infection, where typically VE is defined as one minus the hazard ratio (vaccine/placebo) of HIV infection diagnosis. However, the great genetic variability of HIV poses a central challenge to developing a highly efficacious vaccine (Fauci et al., 2008). The trial population is exposed to many HIV genotypes but the vaccine only contains a few, and the vaccine is less likely to protect against HIVs with greater genetic distance from the sequences inside the vaccine (Gilbert et al., 1999). The trial has objectives to assess whether and how the vaccine impacts the infection rate with any HIV genotype and whether and how the vaccine effect varies by HIV genotype; assessment of these objectives has been named ‘sieve analysis’ (Gilbert et al., 1998).Gilbert et al. (2008),Sun et al. (2009), and Sun and Gilbert (2012) developed sieve analysis methods using the competing risks failure time framework (Prentice et al., 1978), which attach a continuous ‘mark’ variable to HIV infected subjects that measures the genetic distance of an infecting HIV sequence to a sequence inside the vaccine. The goal of the sieve analysis methods is evaluation of mark-specific vaccine efficacy, here defined as one minus the mark-specific hazard ratio (vaccine/placebo) of infection. Beyond HIV, the methods apply generally to any preventative vaccine efficacy trial for which the pathogen targeted by the vaccine is genetically diverse, which include influenza, malaria, tuberculosis, dengue, streptococcus pneumoniae, human papilloma virus, and hepatitis C virus.

Gilbert et al. (2008) and Sun et al. (2009) assumed no missing mark data in infected subjects, whereas Sun and Gilbert (2012) allowed missing at random (MAR) marks. In practice there are missing marks, for example in the Vax004 trial 32 of 368 infected subjects had no HIV sequence data (Gilbert et al., 2008), due to drop-out or to inability of the HIV sequencing technology to measure the infecting HIV sequence, and in the ‘Step’ trial 22 of 88 infected subjects had no HIV sequence data (Rolland et al., 2011). While it is of scientific interest to evaluate amark defined based on the earliest available HIV sequence, a mark of particular scientific interest is defined based on an HIV sequence measured near the time of acquisition, which is missing in a much larger fraction of infected subjects due to the periodic (typically 6-monthly) diagnostic tests for HIV infection. Specifically, HIV sequences are measured from the earliest available post-infection blood sample, and a ‘near acquisition’ or ‘early’ sample may be defined as one documented to be sufficiently near acquisition. In the Step trial, only 23 of the 66 infected subjects with sequence data had an early mark measured, defined as sampling within 3 weeks. Sun and Gilbert (2012) provide details on the HIV testing algorithm that is used to define an early mark.

Sun and Gilbert (2012) is currently the only paper on sieve analysis that accommodates missing continuous marks. It develops two valid estimation approaches based on the stratified mark-specific proportional hazards model. The first uses inverse probability weighting (IPW) of the complete-case estimator, which leverages auxiliary predictors of whether the mark is observed, whereas the second, adapting Robins et al. (1994), augments the IPW complete-case estimator with auxiliary predictors of the missing marks. Sun and Gilbert (2012) restricted attention to estimation methods, and this article is a sequel that develops corresponding inferential/hypothesis testing methods based on the augmented IPW estimator. An important new component of this work compared to the previous work is to center it around the sieve analysis of the RV144 Thai trial, which recently delivered the landmark result that a prime-boost HIV vaccine appeared to provide partial protection against HIV infection (estimated VE = 31%, 95% CI 1% to 51%, Rerks-Ngarm et al., 2009). This result has stimulated intense interest in the sieve analysis, for two reasons. First, there is controversy about whether the vaccine is really partially working versus a false positive result (Gilbert et al., 2011), and the sieve analysis of HIV sequences can help resolve this question. In particular, if evidence is found that the vaccine efficacy declines with genetic distance, and the distance is defined based on known parts of HIV that contain putatively protective antibody epitopes, then an interpretation of real vaccine efficacy is supported. Secondly, the HIV vaccine field is grappling with how to modify the tested vaccine to increase its potential vaccine efficacy for the next efficacy trial, and understanding the relationship between vaccine efficacy and the genetic distance provides direct guidance on which HIV sequences to put inside of the next generation vaccines.

This article is organized as follows. Notations, assumptions, and the stratified mark-specific proportional hazards model are introduced in Section 2. Background on the estimation procedures needed for the testing procedures are described in Section 3. The testing procedures are developed, and asymptotic properties described, in Section 4. The finite-sample performances of the tests are evaluated via simulations in Section 5. The application to the Thai trial is given in Section 6, and the asymptotic results and their proofs are placed in the Appendix.

2 Model and missing mark data

2.1 Stratified mark-specific proportional hazards (PH) model

Let T be the failure time, V a continuous mark variable with bounded support [0, 1], and Z(t) a possibly time-dependent p-dimensional covariate. The mark V is only observable when T is observed. Suppose that the conditional mark-specific hazard function at time t given the covariate history Z(s), for s ≤ t, only depends on the current value Z(t). We consider the stratified mark-specific proportional hazards (PH) model

$${\lambda }_k(t,v|\mathbf{z}(t))={\lambda }_{0k}(t,v)\text{exp}\{\mathit{\beta }{(v)}^T\mathbf{z}(t)\},k=1,\dots ,K,$$ (1)

where λ_k(t, v|z(t)) is the conditional mark-specific hazard function given covariate z(t) for an individual in the kth stratum, λ_0k (·, v) = λ_k(t, v|z(t) = 0) is the unspecified baseline hazard function for the kth stratum, β(v) is the p-dimensional unknown regression coefficient function of v, and K is the number of strata. Model (1) allows different baseline functions for different strata and flexibly allows for arbitrary mark-specific infection hazards over time in the placebo group. In practice, different key subgroups (e.g., men and women in the Thai trial) are assigned different baseline mark-specific hazards of HIV infection.

Arranging $\mathit{\beta }(v)={({\beta }_1(v),{\mathit{\beta }}_2^T(v))}^T$, so that β₁ (v) is the coefficient for vaccination status and β₂ (v) for other covariates, the covariate and stratum adjusted mark-specific vaccine efficacy VE(v) equals 1 − exp(β₁ (v)).Sun et al. (2009) developed some statistical procedures for model (1) with K = 1 based on observations of the random variables (X,Z(·), V) for δ = 1 and (X,Z(·)) for δ = 0, where X = min{T,C}, λ = I(T ≤ C), and C is a censoring random variable. Sun and Gilbert (2012) developed estimation procedures for model (1) with general K allowing V to be missing for some subjects with δ = 1; these methods incorporate auxiliary covariates and/or auxiliary mark variables that inform about the probability V is observed and about the distribution of V. This article develops parallel hypothesis testing procedures for assessing VE(v). As summarized in the Introduction, the two objectives are to assess if the vaccine efficacy ever deviates from 0 [i.e., test VE(v) = 0] and to assess if the vaccine efficacy changes with the mark [i.e., test VE(v) = VE].

2.2 Missing data assumptions

Let R be the indicator of whether all possible data are observed for a subject; R = 1 if either δ = 0 (right-censored) or if δ = 1 and V is observed; and R = 0 otherwise. Auxiliary variables A may be helpful for predicting missing marks. Since the mark can only be missing for failures, supplemental information is potentially useful only for failures, for predicting missingness and for informing about the distribution of missing marks. For example, if V is defined based on the early virus, then V*, the auxiliary mark information, may include sequences of later sampled viruses, and can be considered a subset of A. In general, A could include multiple viral sequences per infected subject at multiple time-points, giving information on intra-subject HIV evolution. The relationship between A and V can be modelled to help predict V (see Section 5 for a simulated example).

We assume C is conditionally independent of (T, V ) given Z(·) and the stratum. We also assume V is MAR (Rubin, 1976); that is, given δ = 1 and W = (T,Z(T), A), the probability V is missing depends only on the observed W, not on the value of V; this assumption is expressed as

$$r_k(W)\equiv P(R=1|\delta =1,\mathbf{W})=P(R=1|V,\delta =1,\mathbf{W}).$$ (2)

Let π_k(Q) = P(R = 1|Q) where Q = (δ, W). Then π_k(Q) = δr_k(W) + (1 − δ). The MAR assumption (2) also implies that V is independent of R given Q:

$${\rho }_k(v,\mathbf{W})\equiv P(V\le v|\delta =1,\mathbf{W})=P(V\le v|R=1,\delta =1,\mathbf{W}).$$ (3)

Define r_k (w) = P(R = 1|δ = 1, W = w) and ρ_k(v, w) = P(V ≤ v|λ = 1, W = w). The stratum-specific definitions of r_k (w) and ρ_k(v, w) allow the models of the probability of complete-case and of the mark distribution to differ across strata.

Let τ be the end of the follow-up period, and n_k be the number of subjects in the kth stratum; the total sample size is $n={\sum }_{k=1}^K{n}_k$. Let {X_ki, Z_ki (·), δ_ki, R_ki, V_ki, A_ki ; i = 1,…, n_k } be iid replicates of {X,Z(·), δ, R, V, A} from the kth stratum. The observed data are {O_ki ; i = 1,…, n_k, k = 1,…, K}, where O_ki = {X_ki, Z_ki (·), R_ki, R_ki V_ki, A_ki } for δ_ki = 1 and O_ki = {X_ki, Z_ki (·), R_ki = 1} for δ_ki = 0. We assume the O_ki are independent for all subjects.

2.3 Hypotheses to test

We develop procedures for testing the following two sets of hypotheses. Let [a, b] ⊂ (0, 1). The first set of hypotheses is

• H₁₀ : VE(v) = 0 for v ∈ [a, b]

• versus H_1a : VE(v) ≠ 0 for some v (general alternative)

• or H_1m : VE(v) ≥ 0 with strict inequality for some v (monotone alternative).

The second set of hypotheses is

• H₂₀ : VE(v) does not depend on v ∈ [a, b]

• versus H_2a : VE(v) depends on v (general alternative)

• or H_2m : VE(v) decreases as v increases (monotone alternative).

The null hypothesis H₁₀ implies the vaccine affords no protection (nor increased risk) against any HIV genotype. The ordered alternative H_1m indicates that the vaccine provides protection for at least some of the HIV genotypes, while H_1a indicates that the vaccine provides protection and/or increased risk for some HIV genotypes. The null hypothesis H₂₀ implies there is no difference in vaccine protection against different HIV genotypes. The ordered alternative H_2m indicates that vaccine efficacy decreases with v and H_2a indicates that the vaccine efficacy changes with v. With β₁ (v) the first component of β(v), the first set of hypotheses is equivalent to H₁₀ : β₁ (v) = 0 for v ∈ [a, b] versus H_1a : β₁ (v) ≠ 0 for some v or H_1m : β₁ (v) ≤ 0 with strict inequality for some v. The second set of hypotheses is equivalent to H₂₀ : β₁ (v) does not depend on v ∈ [a, b] versus H_2a : β₁ (v) depends on v or H_2m : β₁ (v) increases as v increases. We develop testing procedures for detecting departures from H₁₀ in the direction of H_1a and H_1m and for detecting departures from H₂₀ in the direction of H_2a and H_2m. The procedures are developed based on the augmented IPW complete-case estimator developed by Sun and Gilbert (2012).

3 Estimation procedure with missing marks

The augmented IPW estimator for model (1) is obtained in two stages. First the IPW complete-case estimator is derived and second the augmented IPW estimator is obtained, which improves efficiency by accounting for information in the conditional distribution of V given the auxiliaries.

Let r_k (W_ki, ψ_k) be the parametric model for the probability of complete-case, r_k (W_ki) defined in (2), where W_ki = (T_ki, Z_ki (T_ki), A_ki) and ψ_k is a q-dimensional parameter. For example, one can assume the logistic model with $\text{logit}(r_k({\mathbf{W}}_{ki},{\psi }_k))={\psi }_k^T{\mathbf{W}}_{ki}==$ for those with λ_ki = 1, where W_ki = (T_ki, Z_ki (T_ki), A_ki). By (2), the maximum likelihood estimator ψ̂ = (ψ̂₁,…, ψ̂_K)^T of ψ = (ψ₁,…, ψ_K)^T is obtained by maximizing the observed data likelihood,

$$\prod _{k,i}{\{r_k(W_{ki},{\psi }_k)\}}^{R_{ki}{\delta }_{ki}}{\{1-r_k(W_{ki},{\psi }_k)\}}^{(1-R_{ki}){\delta }_{ki}}.$$ (4)

Let K(x) be a kernel function with support [−1, 1] and let h = h_n be a bandwidth. Let N_ki (t, v) = I(X_ki ≤ t, δ_ki = 1, V_ki ≤ v) and Y_ki (t) = I(X_ki ≥ t). Let Q_ki = (δ_ki, W_ki) and π_k (Q_ki, ψ_k) = δ_ki r_k (W_ki, ψ_k) + (1 − δ_ki). The first-stage estimator is the IPW estimator β̂^ipw (v), which solves the following estimating equation for β: U_ipw (v, β, ψ̂) = 0, where

$$U_{\mathit{\text{ipw}}}(v,\mathit{\beta },\widehat{\psi })=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^1{\int }_0^{\tau }{K}_h(u-v)({\mathbf{Z}}_{ki}(t)-{\tilde{\mathbf{Z}}}_k(t,\mathit{\beta },{\widehat{\psi }}_k))\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki},{\widehat{\psi }}_k)}{N}_{ki}(dt,du),$$ (5)

where $K_h(x)=K(x/h)/h,{\tilde{\mathbf{Z}}}_k(t,\mathit{\beta },{\psi }_k)={\tilde{\mathbf{S}}}_k^{(1)}(t,\mathit{\beta },{\psi }_k)/{\tilde{\mathbf{S}}}_k^{(0)}(t,\mathit{\beta },{\psi }_k)\text{and}{\tilde{\mathbf{S}}}_k^{(j)}(t,\mathit{\beta },{\psi }_k)=n_k^{-1}{\sum }_{i=1}^{n_k}{R}_{ki}{({\pi }_k({\mathbf{Q}}_{ki},{\psi }_k))}^{-1}{Y}_{ki}(t)\text{exp}\{{\beta }^T{\mathbf{Z}}_{ki}(t)\}{\mathbf{Z}}_{ki}{(t)}^{\otimes j}$ for j = 0, 1, where z^⊗0 = 1 and z^⊗1 = z for any z ∈ ℝ^p. The score function (5) can be viewed as an extension of the score function used for the cause-specific Cox model (Prentice et al., 1978) for a particular failure cause J = j, for which the counting process only counts events of type j. It borrows strength from observations having marks in the neighborhood of v. The kernel function is designed to give greater weight to observations with marks near v than those further away.

The baseline function λ_0k (t, v) can be estimated by ${\widehat{\lambda }}_{0k}^{\mathit{\text{ipw}}}(t,v)$, obtained by smoothing the increments of the following estimator of the doubly cumulative baseline function ${\Lambda }_{0k}(t,v)={\int }_0^t{\int }_0^v{\lambda }_{0k}(s,u)dsdu$:

$${\widehat{\Lambda }}_{0k}^{\mathit{\text{ipw}}}(t,v)=\sum _{i=1}^{n_k}{\int }_0^t{\int }_0^v\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki},{\widehat{\psi }}_k)}\frac{N_{ki}(ds,du)}{n_k{\tilde{S}}_k^{(0)}(s,{\widehat{\mathit{\beta }}}^{\mathit{\text{ipw}}}(u),{\widehat{\psi }}_k)}.$$ (6)

For example, one can use the following kernel smoothing

$${\widehat{\lambda }}_{0k}^{ipw}(t,v)={\int }_0^{\tau }{\int }_0^1{K}_{h1}^{(1)}(t-s)K_{h2}^{(2)}(v-u){\widehat{\Lambda }}_{0k}^{\mathit{\text{ipw}}}(ds,du),$$ (7)

where $K_{h_1}^{(1)}(x)=K^{(1)}(x/h_1)/h_1\text{and}{K}_{h_2}^{(2)}(x)=K^{(2)}(x/h_2)/h_2$, with K⁽¹⁾ (·) and K⁽²⁾ (·) the kernel functions and h₁ and h₂ the bandwidths.

Following Robins et al. (1994), Sun and Gilbert (2012) proposed a more efficient procedure for estimating (1) by incorporating the knowledge of ρ_k (w, v) into the estimation procedure. Let w = (t, z, a) and g_k (a|t, v, z) = P(A_ki = a|T_ki = t, V_ki = v, Z_ki = z, δ_ki = 1). Then

$${\rho }_k(\mathbf{w},v)={\int }_0^v{\lambda }_k(t,u|\mathbf{z})g_k(\mathbf{a}|t,u,\mathbf{z})du/{\int }_0^1{\lambda }_k(t,u|\mathbf{z})g_k(\mathbf{a}|t,u,\mathbf{z})du.$$ (8)

If no auxiliary variables are available or if A_ki is conditionally independent of V_ki given (T_ki, Z_ki, δ_ki), then ${\rho }_k(\mathbf{w},v)={\int }_0^v{\lambda }_k(t,u|\mathbf{z})du/{\int }_0^1{\lambda }_k(t,u|\mathbf{z})du$. In this case, ρ_k(w, v) can be estimated by ${\widehat{\rho }}_k^{\mathit{\text{ipw}}}(w,v)={\int }_0^v{\widehat{\lambda }}_k^{\mathit{\text{ipw}}}(t,u|\mathbf{z})du/{\int }_0^1{\widehat{\lambda }}_k^{\mathit{\text{ipw}}}(t,u|\mathbf{z})du,\text{where}{\widehat{\lambda }}_k^{\mathit{\text{ipw}}}(t,u|\mathbf{z})={\widehat{\lambda }}_k^{\mathit{\text{ipw}}}(t,u)\text{exp}\{{({\widehat{\beta }}^{\mathit{\text{ipw}}}(u))}^T\mathbf{z}\}$. When the auxiliary marks A_ki are correlated with V_ki conditional on T_ki, Z_ki and δ_ki = 1, the conditional distribution ρ_k(w, v) involves the function g_k (a|t, u, z), for which a parametric or semiparametric model may be developed to describe the dependence between A_ki and V_ki. Let ĝ_k (a|t, u, z) be an estimator of g_k (a|t, u, z) with a convergence rate of at least (nh)^−1/2. Then ρ_k(w, v) can be estimated by

$${\widehat{\rho }}_k^{\mathit{\text{ipw}}}(\mathbf{w},v)={\int }_0^v{\widehat{\lambda }}_k^{\mathit{\text{ipw}}}(t,u|\mathbf{z}){\widehat{g}}_k(\mathbf{a}|t,u,\mathbf{z}){\widehat{g}}_k(\mathbf{a}|t,u,\mathbf{z})du/{\int }_0^1{\widehat{\lambda }}_k^{\mathit{\text{ipw}}}(t,u|\mathbf{z}){\widehat{g}}_k(a|t,u,\mathbf{z})du.$$ (9)

Let $N_{ki}^x(t)=I(X_{ki}\le t,{\delta }_{ki}=1)\text{and}{N}_{ki}^v(v)=I(V_{ki}\le v)$. The augmented IPW (AIPW) estimating equation for β is U_aug (v, β, ψ̂, ρ̂ (·)) = 0, where

$$U_{\mathit{\text{aug}}}(v,\mathit{\beta },\widehat{\psi },\widehat{\rho }(·))=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^1{\int }_0^{\tau }{K}_h(u-v)({\mathbf{Z}}_{ki}(t)-{\overline{\mathbf{Z}}}_k(t,\mathit{\beta }))\{\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki},{\widehat{\psi }}_k)}{N}_{ki}(dt,du)+(1-\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki},{\widehat{\psi }}_k)})N_{ki}^x(dt)d({\widehat{\rho }}_k^{\mathit{\text{ipw}}}({\mathbf{W}}_{ki},u))\},$$ (10)

and ${\overline{\mathbf{Z}}}_k(t,\mathit{\beta })={\mathbf{S}}_k^{(1)}(t,\mathit{\beta })/{\mathbf{S}}_k^{(0)}(t,\mathit{\beta }),{\mathbf{S}}_k^{(j)}(t,\mathit{\beta })=n_k^{-1}{\sum }_{i=1}^{n_k}{Y}_{ki}(t)\text{exp}\{{\mathit{\beta }}^T{\mathbf{Z}}_{ki}(t)\}{\mathbf{Z}}_{ki}{(t)}^{\otimes j}$ for j = 0, 1. The AIPW estimator of β(v) solves the above equation and is denoted by β̂^aug (v). The estimator of the cumulative function $\mathbf{B}(v)={\int }_0^v\mathit{\beta }(u)du\text{is given by}{\widehat{\mathbf{B}}}^{\mathit{\text{aug}}}(v)={\int }_0^v{\widehat{\mathit{\beta }}}^{\mathit{\text{aug}}}(u)du$. Note that there is no ψ̂_k in Z̄_k (t, β); this is a difference between the IPW and AIPW estimators.

To implement the estimation procedures in practice, one can use arbitrary auxiliaries for estimating ψ̂_k ; these auxiliaries may include covariates and marks at multiple time-points pre-infection and post-infection, respectively. In contrast, while in principle arbitrary auxiliaries may also be used for the terms ĝ_k (a|t, u, z) in (9), due to the curse of dimensionality the method is expected to perform best in practice with a univariate auxiliary, where semiparametric or fully parametric models for g_k (a|t, u, z) would be required to include multivariate auxiliaries.

Sun and Gilbert (2012) proved that the estimators β̂_ipw (t, v) and β̂^aug (t, v) are consistent and that β̂^aug (v) is more efficient than β̂^ipw (v). In the next section, we develop some hypothesis testing procedures for assessing mark-specific vaccine efficacy based on B̂^aug (v).

4 Testing of mark-specific vaccine efficacy

The covariate-adjusted vaccine efficacy VE(v) is defined through the first component of β(v). Let B₁ (v) be the first component of the cumulative coefficient function B(v). The hypothesis tests concerning VE(v) are constructed based on the first component ${\widehat{B}}_1^{\mathit{\text{aug}}}(v)$ of the AIPW estimator B̂^aug (v). The cumulative estimator B̂^aug (v) has more stable large-sample behavior and a faster convergence rate than β^aug (v).

Let W_B (v) = n^1/2 {B̂^aug (v) − B̂^aug (a)} − n^1/2 {B(v) − B(a)} for v ∈ [a, b]. In the Appendix we show that W_B (v), v ∈ [a, b], converges weakly to a p-dimensional mean-zero Gaussian process with continuous sample paths on v ∈ [a, b]. Further, the distribution of W_B (v), for v ∈ [a, b], can be approximated using the Gaussian multipliers resampling method [of Lin et al. (1993)] based on ${\mathbf{W}}_B^{*}(v)=n^{-1/2}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\xi }_{ki}{\widehat{\mathbf{H}}}_{k}i(v)$ v ∈ [a, b], where {ξ_ki, i = 1,…, n_k, k = 1,…,K} are iid standard normal random variables and Ĥ_k i(v) is defined in (22) in the Appendix. Let W_B1 (v) and $W_{B1}^{*}(v)$ be the first component of W_B(v) and ${\mathbf{W}}_B^{*}(v)$, respectively. With the Gaussian multipliers method, the variance $\text{Var}\{{\widehat{B}}_1^{\mathit{\text{aug}}}(v)-{\widehat{B}}_1^{\mathit{\text{aug}}}(a)\}$ can be consistently estimated by $\widehat{\text{Var}}\{{\widehat{B}}_1^{\mathit{\text{aug}}}{(v)-\widehat{B}}_1^{\mathit{\text{aug}}}{(a)\}=n}^{-1}\text{Var}*(W_{B_1}^{*}(v)),\text{where Var}*(W_{B_1}^{*}(v))$ is the first component on the diagonal of the covariance given in (23) in the Appendix.

4.1 Testing the null hypothesis H₁₀

Consider the test process $Q^{(1)}(v)=n^{1/2}\{{\widehat{B}}_1^{\mathit{\text{aug}}}(v)-{\widehat{B}}_1^{\mathit{\text{aug}}}(a)\},v\in [a,b]$. Then Q⁽¹⁾ (v) = W_B1(v) + n^1/2 {B₁ (v) − B₁ (a)}, v ∈ [a, b]. Under H₁₀, B₁ (v) − B₁ (a) = 0 for v ∈ [a, b], which motivates the following test statistics for testing H₁₀:

$$T_{a1}^{(1)}=\underset{v\in [a,b]}{\text{sup}}|Q^{(1)}(v)|,T_{a2}^{(1)}={\int }_a^b{\{Q^{(1)}(v)\}}^{2}d\text{Var}*\{W_{B1}^{*}(v)\},T_{m1}^{(1)}=\underset{v\in [a,b]}{\text{inf}}|Q^{(1)}(v)|,T_{m2}^{(1)}={\int }_a^b{Q}^{(2)}(v)d\text{Var}*\{W_{B1}^{*}(v)\},$$

The test statistics $T_{a1}^{(1)}\text{and}{T}_{a2}^{(1)}$ capture general departures H_1a, while the test statistics $T_{m1}^{(1)}\text{and}{T}_{m2}^{(1)}$ are sensitive to the monotone departures H_1m. It is easy to derive that all the test statistics $T_{a1}^{(1)},T_{a2}^{(1)},T_{m1}^{(1)}\text{and}{T}_{m2}^{(1)}$ are consistent against their respective alternative hypotheses, and the Appendix derives their limiting distributions under H₁₀.

Under H₁₀, the distribution of Q⁽¹⁾ (v), v ∈ [a, b], can be approximated by the conditional distribution of $W_{B_1}^{*}(·)$, v ∈ [a, b], given the observed data sequence. Hence, the distributions of $T_{a1}^{(2)},T_{a2}^{(2)},T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ under H₁₀ can be approximated by the conditional distributions of $T_{a1}^{*(1)}={\text{sup}}_{v\in [a,b]}|W_{B_1}^{*}(v)|,T_{a2}^{*(1)}={\int }_a^b{\{W_{B_1}^{*}(v)\}}^{2}d\text{Var}*\{W_{B_1}^{*}(v)\},T_{m1}^{*(1)}={\text{inf}}_{v\in [a,b]}{W}_{B_1}^{*}(v)\text{and}{T}_{m2}^{*(1)}={\int }_a^b{W}_{B_1}^{*}(v)d\text{Var}*\{W_{B_1}^{*}(v)\}$, given the observed data sequence, respectively. The critical values, $c_{a1}^{(1)}\text{and}{c}_{a2}^{(1)}$, of the test statistics $T_{a1}^{(1)}\text{and}{T}_{a2}^{(1)}$ can be approximated by the (1 − α)-quantile of $T_{a1}^{*(1)}\text{and}{T}_{a2}^{*(1)}$, which can be obtained by repeatedly generating a large number, say 500, of independent sets of normal samples {λ_ki, i = 1,…, n_k, k = 1,…, K} while holding the observed data sequence fixed. Similarly, the critical values, $c_{m1}^{(1)}\text{and}{c}_{m2}^{(1)}$, of the test statistics $T_{m1}^{(1)}\text{and}{T}_{m2}^{(1)}$ can be approximated by the α-quantile of $T_{m1}^{*(1)}\text{and}{T}_{m2}^{*(1)}$, which again can be obtained by repeatedly generating independent sets of normal samples {ξ_ki, i = 1,…, n_k, k = 1,…, K}. At significance level α, the tests based on $T_{a1}^{(1)}\text{and}{T}_{a2}^{(1)}$ reject H₁₀ in favor of H_1a if $T_{a1}^{(1)}>c_{a1}^{(1)}\text{and}{T}_{a2}^{(1)}>c_{a2}^{(1)}$, respectively, and the tests based on $T_{m1}^{(1)}\text{and}{T}_{m2}^{(1)}$ reject H₁₀ in favor of H_1m if $T_{m1}^{(2)}<c_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}<c_{m2}^{(2)}$, respectively.

4.2 Testing the null hypothesis H₂₀

Let $Q^{(2)}(v)={(v-a)}^{-1}{n}^{1/2}\{{\widehat{B}}_1^{\mathit{\text{aug}}}(v)-{\widehat{B}}_1^{\mathit{\text{aug}}}(a)\}-{(b-a)}^{-1}{n}^{1/2}\{{\widehat{B}}_1^{\mathit{\text{aug}}}(b)-{\widehat{B}}_1^{\mathit{\text{aug}}}(a)\}$.Then

$$Q^{(2)}(v)=\Gamma (v,W_{B_1})+n^{1/2}\Gamma (v,B_1)\text{for}a<v\le b,$$ (11)

where Γ(v, F₁) = (v − a)⁻¹ {F₁ (v) − F₁ (a)} − (b − a)⁻¹ {F₁ (b) − F₁ (a)} is a transformation of F₁ (·). We note that Γ(·, B₁) = 0 under H₂₀ and Γ(·, B₁) ≠ 0 under the alternatives, motivating Q⁽²⁾ (v) as the test process and the following test statistics for testing H₂₀:

$$T_{a1}^{(2)}=\underset{v\in [a\prime ,b]}{\text{sup}}|Q^{(2)}(v)|,T_{a2}^{(2)}={\int }_{a\prime }^b{\{Q^{(2)}(v)\}}^{2}d\text{Var}*\{W_{B1}^{*}(v)\},T_{m1}^{(2)}=\underset{v\in [a\prime ,b]}{\text{inf}}|Q^{(2)}(v)|,T_{m2}^{(2)}={\int }_{a\prime }^b{Q}^{(2)}(v)d\text{Var}*\{W_{B1}^{*}(v)\},$$

where a < a′ < b. We choose a′ > a to avoid zero in the denominator of Q⁽²⁾ (v). In practice, one can choose a′ close to a to make use of available data and to ensure the tests are consistent.

By the asymptotic results shown in the Appendix and the continuous mapping theorem, under H₂₀ the distribution of Q⁽²⁾ (v), v ∈ [a, b], can be approximated by the conditional distribution of $\Gamma (v,W_{B_1}^{*})$, v ∈ [a, b], given the observed data sequence. Hence, the distributions of $T_{a1}^{(2)},T_{a2}^{(2)},T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ under H₂₀ can be approximated by the conditional distributions of $T_{a1}^{*(2)}={\text{sup}}_{v\in [a\prime ,b]}\Gamma (v,W_{B_1}^{*})|,T_{a2}^{*(2)}={\int }_{a\prime }^b{\{\Gamma (v,W_{B_1}^{*})\}}^{2}d\text{Var}*\{W_{B_1}^{*}(v)\},T_{m1}^{*(2)}={\text{inf}}_{v\in [a\prime ,b]}\Gamma (v,W_{B_1}^{*}),T_{m2}^{*(2)}={\int }_{a\prime }^b\Gamma (v,W_{B_1}^{*})\text{and}{T}_{m2}^{*(2)}={\int }_{a\prime }^b\Gamma (v,W_{B_1}^{*})d\text{Var}*\{W_{B_1}^{*}(v)\}$, given the observed data sequence, respectively. Similar to Section 4.1, the respective critical values $c_{a1}^{(2)}\text{and}{c}_{a2}^{(2)}$ of the test statistics $T_{a1}^{(2)}\text{and}{T}_{a2}^{(2)}$ can be approximated by the (1 − α)-quantiles of the conditional distributions of $T_{a1}^{*(2)}\text{and}{T}_{a2}^{*(2)}$ obtained through repeatedly generating independent sets of normal samples {ξ_ki, i = 1,…, n_k, k = 1,…, K} while holding the observed data sequence fixed. The critical values $c_{m1}^{(2)}\text{and}{c}_{m2}^{(2)}\text{for}{T}_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ can be approximated similarly. At the significance level α, the tests based on $T_{a1}^{(2)}\text{and}{T}_{a2}^{(2)}$ reject H₂₀ in favor of H_2a if $T_{a1}^{(2)}>c_{a1}^{(2)}\text{and}{T}_{a2}^{(2)}>c_{a2}^{(2)}$, respectively, and the tests based on $T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ reject H₂₀ in favor of H_2m if $T_{m1}^{(2)}<c_{m1}^{(2)}\text{and},T_{m2}^{(2)}<c_{m2}^{(2)}$, respectively.

The tests $T_{a1}^{(2)}\text{and}{T}_{a2}^{(2)}$ capture general departures H_2a while the tests $T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ are sensitive to the monotone departure H_2m. Note that the derivative dΓ(v, B₁)/dv = (v − a)⁻¹ [β₁ (v) − (v − a)⁻¹ B₁ (v)] ≥ 0 under H_2m with strict inequality for at least some v ∈ [a, b]. This plus the fact that Γ(v,B₁) is non-decreasing with Γ(b,B₁) = 0 lead to the results that the tests based on $T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ are consistent against H_2m and the tests based on $T_{a1}^{(2)}\text{and}{T}_{a2}^{(2)}$ are consistent against H_2a. The proofs are given in the second paragraph following Theorem 1 in the Appendix.

In Sections 4.1 and 4.2, we considered two types of test statistics, namely the integration-based test statistics and the supremum-based test statistics, for each pair of hypotheses. The former are generalizations of the Cramér-von Mises test statistic, and involve integration of deviations over the whole range of the mark, whereas the latter are extensions of the classic Kolmogorov-Smirnov test statistic for testing goodness-of-fit of a distribution function, and take the supremum of such deviations. As demonstrated in a comprehensive analysis of the relative powers of the classic Kolmogorov-Smirnov test and the Cramér-von Mises test by Stephens (1974), we expect that the two types of test statistics have different powers for different true alternative distributions. The integration-based test statistics are best-suited for situations where the true alternative distribution deviates a little over the whole support of the mark and the supremum-based test statistics may have more power against situations where the true alternative has large deviations over a small section of the support. For example, for testing differential VE(v), H₂₀, the supremum-based tests will tend to be relatively more powerful if $\widehat{VE}(v)$ is very high for a small range of marks near a and declines sharply to zero and is constant at zero for all other marks.

5 Simulation study

5.1 Numerical assessment of the tests under correctly specified models

We conduct a simulation study to evaluate the finite-sample performance of the proposed testing procedures. The empirical sizes and powers of the test statistics are assessed for various models, sample sizes (500 and 800) and choices of bandwidths. The powers of the tests are evaluated in both situations where a correlated auxiliary variable is used and where it is absent.

We consider K = 1 stratum. Let Z_ki be the treatment indicator with P(Z_ki = 1) = 0.5. The (T_ki, V_ki) are generated from the following mark-specific proportional hazards model:

$$\lambda (t,v|z)=\text{exp}\{\gamma v+(\alpha +\beta v)z\},t\ge 0,0\le v\le 1,$$ (12)

where α, β and γ are constants. Under model (12), λ₀ (t, v) = exp(v) and VE(v) = 1 − exp (α + βv). For α = 0 and β = 0, VE(v) = 0, indicating no vaccine efficacy, and for β = 0, VE(v) = VE, indicating mark-invariant vaccine efficacy; whereas β > 0 indicates VE(v) decreasing in v. We examine the hypothesis testing procedures for the following specific models:

• (M1) (α, β, γ) = (0, 0, 0.3), implying VE(v) = 0;

• (M2) (α, β, γ) = (−0.69, 0, 0.3), implying VE(v) does not depend on v;

• (M3) (α, β, γ) = (−0.6, 0.6, 0.3), implying VE(v) decreases;

• (M4) (α, β, γ) = (−1.2, 1.2, 0.3), implying VE(v) decreases;

• (M5) (α, β, γ) = (−1.5, 1.5, 0.3), implying VE(v) decreases.

We generate the censoring times from an exponential distribution, independent of (T, V), with censoring rates ranging from 20% to 30%. We take τ = 2.0. The complete-case indicator R_ki is generated with conditional probability r_k(W_ki) = P(R_ki = 1|δ_ki = 1, W_ki), where

$$\text{logit}(r_k(W_{ki}))={\psi }_{k}0+{\psi }_{k1}{Z}_{ki},i=1,\dots ,n_k,k=1,\dots ,K.$$ (13)

With ψ_k0 = 0.2 and ψ_k1 = −0.2 about 50% of observed failures are missing marks.

Conditional on (T_ki, Z_ki, V_ki), we assume that the auxiliary marks follow the model

$$A_{ki}={(0+1)}^{-1}(V_{ki}+\theta U_{ki}),\theta >0,$$ (14)

for i = 1,…, n_k, k = 1,…, K, where V_ki are the possibly missing marks, U_ki is uniformly distributed on [0, 1] independent of V_ki, and θ > 0 is an association parameter between A_ki and V_ki. The correlation coefficient ρ between A_ki and V_ki is 1 for θ = 0. Since A_ki is observed for all observed failure times, the AIPW estimator in this case is the full data estimator. The A_ki and V_ki are independent for θ = ∞, yielding ρ = 0. In addition, the θ values of 0.8, 0.4 and 0.2 correspond to ρ = 0.78, 0.92 and 0.98.

Under model (14), the conditional density of A_ki given (T_ki, Z_ki, V_ki) is

$$g_k(a|t,v,z;\theta )=\frac{1+\theta }{\theta }I\{\frac{v}{1+\theta }\le a\le \frac{v+\theta }{1+\theta }\},0\le a\le 1,0\le v\le 1.$$ (15)

The likelihood function for θ is

$$L(\theta )=\prod _{{\delta }_{ki}=1,R_{ki}=1}\left(\frac{1+\theta }{\theta }I\right\{\frac{V_{ki}}{1+\theta }\le A_{ki}\le \frac{V_{ki}+\theta }{1+\theta }\left\}\right)\text{for}\theta >0.$$

It is easy to show that the maximum likelihood estimator equals

$$\widehat{\theta }\underset{{\delta }_{ki}=1,R_{ki}=1}{\text{max}}\{V_{ki}/A_{ki},(1-V_{ki})/(1-A_{ki})\}-1.$$

The density estimator g_k (a|t, v, z; θ̂) is plugged into (9) to obtain ${\widehat{\rho }}_k^{ipw}(w,v)$, which is used to construct the AIPW estimator of β in (10).

The performances of the proposed test procedures are evaluated through simulations for the models described in (12), (13) and (14) under the settings (M1)–(M5), where (M1) is a setting under the null hypothesis H₁₀ and (M2) is a setting under the null hypothesis H₂₀. We consider the situations where no auxiliary information is provided and where the correlation between the auxiliary mark and the mark of interest is ρ = 0.92 [under model (14) with θ = 0.4]. Table 1 presents the empirical sizes and powers of the tests $T_{a1}^{(1)},T_{a2}^{(1)},T_{m1}^{(1)}\text{and}{T}_{m2}^{(1)}$ for testing H₁₀ at the nominal level 0.05. Table 2 presents the empirical sizes and powers of the tests $T_{a1}^{(2)},T_{a2}^{(2)},T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ for testing H₂₀ at the nominal level 0.05. The results are presented for n = 500 with h₁ = 0.1 and h = h₂ = 0.15 and 0.2, and for n = 800 with h₁ = 0.1 and h = h₂ = 0.1 and 0.15. We take a = 0, b = 1 and a′ = 0.5 for the tests. The Epanechnikov kernel K(x) = .75(1 − x²)I{|x| ≤ 1} is used throughout the numerical analysis.

Table 1.

Empirical sizes and powers of the tests $T_{a1}^{(1)},T_{a2}^{(1)},T_{m1}^{(1)}\text{and}{T}_{m2}^{(1)}$ for testing H₁₀ at the nominal level 0.05 for ρ = 0 and 0.92 when 50% of the marks are missing. The bandwidths are h₁ = 0.1 and h₂ = h. Each entry is based on 500 Gaussian multipliers samples and 500 repetitions.

				Size/Power
				ρ = 0				ρ = 0.92
Model	(α, β, γ)	n	h	$T_{a1}^{(1)}$	$T_{a2}^{(1)}$	$T_{m1}^{(1)}$	$T_{m2}^{(1)}$	$T_{a1}^{(1)}$	$T_{a2}^{(1)}$	$T_{m1}^{(1)}$	$T_{m2}^{(1)}$
M1	(0, 0, 0.3)	500	0.15	5.4	4.0	4.0	5.0	4.6	4.2	3.8	4.2
			0.20	5.0	4.4	4.6	5.2	4.8	4.0	4.2	3.6
		800	0.10	3.8	3.6	4.2	4.2	3.8	3.8	5.4	4.8
			0.15	4.0	3.8	4.6	4.6	5.0	4.4	5.4	5.6
M3	(−0.6, 0.6, 0.3)	500	0.15	68.2	67.0	79.4	76.0	73.2	74.6	83.2	85.4
			0.20	63.2	65.0	75.8	74.2	69.2	71.4	79.8	82.6
		800	0.10	88.2	86.2	94.6	90.4	92.0	93.0	95.0	97.2
			0.15	87.4	86.6	92.8	90.8	89.2	90.6	93.4	95.2
M4	(−1.2, 1.2, 0.3)	500	0.15	99.6	99.4	99.8	99.8	99.8	100	99.8	100
			0.20	99.4	99.0	99.6	99.8	99.6	99.8	99.8	100
		800	0.10	100	100	100	100	100	100	100	100
			0.15	100	100	100	100	100	100	100	100
M2	(−0.69, 0, 0.3)	500	0.15	100	100	100	99.8	100	100	100	100
			0.20	100	100	100	100	100	100	100	100
		800	0.10	100	99.8	100	100	99.8	99.8	99.8	99.8
			0.15	100	100	100	100	100	100	100	100

Table 2.

Empirical sizes and powers of the tests $T_{a1}^{(2)},T_{a2}^{(2)},T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ for testing H₂₀ at the nominal level 0.05 for ρ = 0 and 0.92 when 50% of the marks are missing. The bandwidths are h₁ = 0.1 and h₂ = h. Each entry is based on 500 Gaussian multipliers samples and 500 repetitions.

				Size/Power
				ρ = 0				ρ = 0.92
Model	(α, β, γ)	n	h	$T_{a1}^{(2)}$	$T_{a2}^{(2)}$	$T_{m1}^{(2)}$	$T_{m2}^{(2)}$	$T_{a1}^{(2)}$	$T_{a2}^{(2)}$	$T_{m1}^{(2)}$	$T_{m2}^{(2)}$
M2	(−0.69, 0, 0.3)	500	0.15	5.6	4.8	5.8	5.8	7.6	7.2	7.4	7.0
			0.20	5.8	4.8	5.4	5.2	6.6	6.6	6.6	7.4
		800	0.10	6.4	5.0	5.6	5.8	6.2	5.8	7.2	7.0
			0.15	6.6	5.2	5.8	5.6	6.0	5.6	6.0	6.6
M3	(−0.6, 0.6, 0.3)	500	0.15	16.8	17.0	22.4	25.2	20.6	25.8	32.6	37.4
			0.20	14.2	15.8	22.2	24.8	19.4	24.2	31.8	34.6
		800	0.10	26.0	25.8	35.2	36.4	36.0	38.0	46.0	49.2
			0.15	25.4	25.8	34.8	35.6	34.0	36.0	45.4	47.4
M4	(−1.2, 1.2, 0.3)	500	0.15	44.4	46.2	59.0	63.2	63.6	68.4	76.4	80.2
			0.20	42.2	44.0	57.2	59.6	61.4	65.8	73.2	75.8
		800	0.10	66.2	67.6	75.2	78.0	82.8	86.6	90.6	91.8
			0.15	64.6	66.2	74.0	77.0	80.6	84.4	88.4	91.2
M5	(−1.5, 1.5, 0.3)	500	0.15	64.5	66.5	75.0	76.5	81.0	85.6	88.8	90.4
			0.20	61.0	62.6	72.2	72.2	77.8	82.4	86.8	89.4
		800	0.10	80.8	85.6	87.6	91.4	94.6	96.2	97.6	98.4
			0.15	78.6	84.8	87.8	91.4	94.4	95.6	95.8	97.8

Tables 1 and 2 show that all of the tests have satisfactory empirical sizes close to the nominal level 0.05. The powers of the tests increase with sample size and they are not overly sensitive to the selected bandwidths. The powers of the tests for testing H₁₀ increase as the model moves in the direction M1 → M3 → M4 → M2, representing increased departure from the null hypothesis H₁₀. The powers of the tests for testing H₂₀ increase as the model moves in the direction M2 → M3 → M4 → M5, representing increased departure from the null hypothesis H₂₀. The tests utilizing the auxiliary marks have higher power than those without using the auxiliary marks.

As with any nonparametric smoothing procedure, one needs to carefully select bandwidths. In practice, the appropriate bandwidth selection can be based on a 𝒦-fold cross-validation method [e.g., Efron and Tibshirani (1993), Hoover et al. (1998), Cai et al. (2000) and Tian et al. (2005)].

The proposed testing procedures properly handles missing marks under MAR with asymptotically correct significance levels. However, if only the observations with complete information are used, i.e., the complete-case analysis, then the testing procedures are expected to often not provide correct type I error control. We conduct a simulation study to evaluate the observed sizes of the proposed tests using the complete cases under two different models for missing the indicator R_ki – model (13) and the following model:

$$\text{logit}(r_k(W_{ki}))=0.8-Z_{ki}-0.3T_{ki},i=1,\dots ,n_k,k=1,\dots ,K.$$ (16)

For K = 1 both models (13) and (16) yield about 50% missing marks among the observed failures. The sizes of $T_{a1}^{(1)},T_{a2}^{(1)},T_{m1}^{(1)}\text{and}{T}_{m2}^{(1)}$ for testing H₁₀ are evaluated under model (M1) and the sizes of $T_{a1}^{(2)},T_{a2}^{(2)},T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ for testing H₂₀ are evaluated under model (M2) (Table 3). Under model (13), the observed sizes for testing H₁₀ are elevated (around 7–15%), whereas those for testing H₂₀ remain around 5%. Under model (16), the observed sizes for testing H₁₀ exceed 37% for all tests, whereas those for testing H₂₀ reach 12% and 14% for the tests $T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ when n = 800.

Table 3.

Empirical sizes of the tests for H₁₀ and H₂₀ at the nominal level 0.05 using the complete cases under MCAR when 50% of the marks are missing. The bandwidths are h₁ = 0.1 and h₂ = h. Each entry is based on 100 Gaussian multipliers samples and 100 repetitions.

Model	Missing Model	n	h	Size
				testing H10
				$T_{a1}^{(1)}$	$T_{a2}^{(1)}$	$T_{m1}^{(1)}$	$T_{m2}^{(1)}$
M1	(13)	500	0.20	0.14	0.10	0.12	0.15
		800	0.15	0.10	0.07	0.11	0.11
	(16)	500	0.20	0.39	0.37	0.50	0.42
		800	0.15	0.50	0.46	0.63	0.55
				testing H20
				$T_{a1}^{(2)}$	$T_{a2}^{(2)}$	$T_{m1}^{(2)}$	$T_{m2}^{(2)}$
M2	(13)	500	0.20	0.08	0.04	0.08	0.05
		800	0.15	0.06	0.09	0.06	0.10
	(16)	500	0.20	0.08	0.07	0.08	0.05
		800	0.15	0.07	0.06	0.12	0.14

These simulation results verify that the testing procedures applied to complete cases generally do not have nominal size, although for some of the scenarios the sizes are nominal. To explain this, it can be shown that, under MAR, λ_k (t, v|z,R_ki = 1) = λ_k (t, v|z)h_k (t, z), where h_k (t, z) = P(R_ki = 1|T_ki = t,Z_ki = z)/P(R_ki = 1|T_ki ≥ t, Z_ki = z). If h_k (t, z) does not depend on z and MAR holds, then the observations for individuals with the observed marks only can be viewed as a random sample from a mark-specific proportional hazards model with a different baseline hazard function but the same regression function β(v). In this case, the tests for both H₁₀ and H₂₀ based on the complete cases are valid. If h_k (t, z) depends on z but not on t and MAR holds, then h_k (t, z) can be expressed as $h_k(t,z)=\text{exp}({\vartheta }_k^{\prime }z)$ [the scenario under model (13)], and the tests of H₁₀ based on the complete cases will be biased. However, the tests of H₂₀ remain unbiased since the biases in the estimation of β(v) that do not depend on v, such that the test process Q⁽²⁾ (v) is still asymptotically a mean zero process. In general, if h_k (t, z) depends on both z and t and MAR holds, which is the scenario under the missing model (16), then the test process Q⁽²⁾ (v) is not an asymptotically mean zero process. The magnitude of departure of the asymptotic sizes of the test statistics of H₂₀ from the nominal level depends on h_k (t, z) in a complicated manner.

5.2 Numerical assessment of the tests under mis-specified models

This subsection evaluates robustness of the proposed test procedures to mis-specifications of r_k (w) and/or g_k (a|t, v, z), and to violation of the MAR assumption. The Z_ki, (T_ki, V_ki), and C_ki are generated using the same models as above, again with approximately 30% censoring.

Robustness of the tests to mis-specification of r_k (w) is examined by assuming model (13) while the actual complete-case indicator R_ki is generated with the conditional probability r_k (W_ki) = P(R_ki = 1|δ_ki = 1, W_ki), where

$$\text{logit}(r_k({\mathbf{W}}_{ki}))=1.1+Z_{ki}-2T_{ki},i=1,\dots ,n_k.$$ (17)

This model yields approximately 50% missing marks among observed failures under (M1)–(M5).

Robustness of the tests is also examined when g_k (a|t, v, z) is mis-specified. This is carried out by assuming model (14) for the auxiliary mark, or, equivalently, model (15) for g_k (a|t, v, z), while the actual mark for λ_ki = 1 is generated from

$$A_{ki}={(1.4+2\tau )}^{-1}(V_{ki}+0.4U_{ki}+2X_{ki}),$$ (18)

for i = 1,…, n_k. Here U_ki is uniformly distributed on [0, 1] and is independent of V_ki.

Robustness of the tests to violation of the MAR assumption (2) is examined by assuming model (13), while the actual R_ki depends on V_ki through the model

$$\text{logit}(r_k(W_{ki}))=0.6+Z_{ki}-2V_{ki},i=1,\dots ,n_k.$$ (19)

The proportion of missing marks among the observed failures is kept around 50% in all scenarios.

The models (17), (18) and (19) are similar to those used in Sun and Gilbert (2012) for examining robustness of the AIPW estimator. However, instead of examining biases and standard errors of the estimators, here we check whether the empirical sizes of the tests are close to their nominal level 0.05 and how the powers of the tests are affected by these mis-specifications. For sample size n = 500 and bandwidths h₁ = 0.1 and h = h₂ = 0.20, Table 4 shows the empirical sizes and powers of the tests of H₁₀ and Table 5 shows the empirical sizes and powers of the tests of H₂₀. In both tables, the first block shows the results when r_k (w) is mis-specified following (17) and g_k (a|t, v, z) is correctly specified by (15) with λ = 0.4; the second block shows the results when g_k (a|t, v, z) is mis-specified following (18) and r_k (w) is correctly specified by (13) with ψ_k1 = 0.2 and ψ_k1 = −0.2; the third block shows the results when r_k (w) is mis-specified following (17) and g_k (a|t, v, z) is mis-specified following (18); and the fourth block shows the results when r_k (w) depends on V_ki following (19) and g_k (a|t, v, z) is correctly specified by (15) with λ = 0.4.

Table 4.

Robustness of the tests for H₁₀. Empirical sizes and powers of the tests $T_{a1}^{(1)},T_{a2}^{(1)},T_{m1}^{(1)}\text{and}{T}_{m2}^{(1)}$ for testing H₁₀ at the nominal level 0.05 for n = 500 and h = 0.2 when 50% of the marks are missing. The bandwidths are h₁ = 0.1 and h₂ = h. Each entry is based on 500 Gaussian multipliers samples and 500 repetitions.

		Size/Power
Model	(α, β, γ)	$T_{a1}^{(1)}$	$T_{a2}^{(1)}$	$T_{m1}^{(1)}$	$T_{m2}^{(1)}$
		rk(w) is misspecified
M1	(0, 0, 0.3)	4.2	5.2	3.6	4.2
M3	(−0.6, 0.6, 0.3)	62.0	74.4	74.0	81.8
M4	(−1.2, 1.2, 0.3)	99.6	99.8	99.8	99.8
M2	(−0.69, 0, 0.3)	100	100	100	100
		gk(a|t, v, z) is misspecified
M1	(0, 0, 0.3)	3.4	4.2	5.8	4.6
M3	(−0.6, 0.6, 0.3)	59.6	64.4	72.8	74.4
M4	(−1.2, 1.2, 0.3)	99.2	99.4	99.6	99.6
M2	(−0.69, 0, 0.3)	100	99.8	100	99.8
		rk(w) and gk(a|t, v, z) are misspecified
M1	(0, 0, 0.3)	4.0	4.0	3.8	3.4
M3	(−0.6, 0.6, 0.3)	61.8	61.8	71.8	73.8
M4	(−1.2, 1.2, 0.3)	99.6	98.6	99.8	99.8
M2	(−0.69, 0, 0.3)	100	100	100	100
		missing-at-random assumption is violated
M1	(0, 0, 0.3)	3.4	3.8	3.6	5.0
M3	(−0.6, 0.6, 0.3)	60.6	67.0	73.0	77.8
M4	(−1.2, 1.2, 0.3)	99.2	99.6	99.8	99.6
M2	(−0.69, 0, 0.3)	100	100	100	100

Table 5.

Robustness of the tests for H₂₀. Empirical sizes and powers of the tests $T_{a1}^{(2)},T_{a2}^{(2)},T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ for testing H₂₀ at the nominal level 0.05 for n = 500 and h = 0.2 when 50% of the marks are missing. The bandwidths are h₁ = 0.1 and h₂ = h. Each entry is based on 500 Gaussian multipliers samples and 500 repetitions.

		Size/Power
Model	(α, β, γ)	$T_{a1}^{(2)}$	$T_{a2}^{(2)}$	$T_{m1}^{(2)}$	$T_{m2}^{(2)}$
		rk(w) is misspecified
M2	(−0.69, 0, 0.3)	5.0	3.8	5.4	6.2
M3	(−0.6, 0.6, 0.3)	24.0	25.2	34.2	36.0
M4	(−1.2, 1.2, 0.3)	60.8	66.6	72.8	78.4
M5	(−1.5, 1.5, 0.3)	76.6	82.0	85.8	88.8
		gk (a|t, v, z) is misspecified
M2	(−0.69, 0, 0.3)	4.8	6.6	6.0	5.8
M3	(−0.6, 0.6, 0.3)	17.2	18.0	28.4	28.2
M4	(−1.2, 1.2, 0.3)	44.8	47.2	56.4	61.0
M5	(−1.5, 1.5, 0.3)	58.0	60.4	68.6	73.2
		rk (w) and gk (a|t, v, z) are misspecified
M2	(−0.69, 0, 0.3)	4.0	4.8	4.4	4.4
M3	(−0.6, 0.6, 0.3)	16.6	19.6	26.8	26.6
M4	(−1.2, 1.2, 0.3)	43.2	46.6	55.6	60.6
M5	(−1.5, 1.5, 0.3)	53.8	58.8	67.4	71.4
		missing-at-random assumption is violated
M2	(−0.69, 0, 0.3)	6.8	6.0	7.6	7.8
M3	(−0.6, 0.6, 0.3)	28.6	33.6	39.6	42.0
M4	(−1.2, 1.2, 0.3)	61.8	67.0	74.0	78.4
M5	(−1.5, 1.5, 0.3)	77.4	81.6	85.4	89.2

Tables 4 and 5 show that the empirical sizes of the tests are very close to the nominal level 0.05 when one of r_k (w) and g_k (a|t, v, z) is mis-specified, reflecting the double robustness property of the AIPW estimator. The empirical sizes are also close to 0.05 when both r_k (w) and g_k (a|t, v, z) are mis-specified and when the MAR assumption is violated, which is intriguing. When only r_k (w) is mis-specified and MAR holds, the empirical powers in Tables 4 and 5 closely track the corresponding powers in Tables 1 and 2 under correct model specifications. The empirical powers are lower than those observed in Table 1 and 2 when g_k (a|t, v, z) is mis-specified or when both r_k (w) and g_k (a|t, v, z) are mis-specified, whereas the empirical powers in Tables 4 and 5 are very close to those in Tables 1 and 2 when MAR is violated. Apparently for our particular data simulation, the bias due to the MAR violation counter-balances the bias due to mis-specification of both r_k (w) and g_k (a|t, v, z); however, in general these violations could distort sizes and powers.

5.3 Simulation study for the Thai trial

We conduct a simulation of the Thai trial, to gain insight about the power available for this real trial. Specifically, we simulated data to yield about the numbers of infections observed (74 in the placebo group and 51 in the vaccine group), the overall vaccine efficacy from the proportional hazards model is about 31%, and the true VE(v) curve decreases with v to be around 65–70% for v close to zero and around 0% for v close to 1. The actual infection rate was only 0.3% over 3.5 years; to speed the simulations we use a 20% placebo infection rate and retain 74 infections on average.

Again with K = 1 stratum, the (T_ki, V_ki) are generated from the following model:

$$\lambda (t,v|z)=\gamma \text{exp}\{(\alpha +\mathit{\beta }v)z\},t\ge 0,0\le v\le 1,$$ (20)

where α, β and γ are constants. Under model (20), VE(v) = 1 − exp(λ+ βv), the marginal hazards are λ₀ (t) = σ for z = 0, and λ₁ (t) = γ exp(α)(exp(β)−1)/β for z = 1, and the Cox proportional hazards vaccine efficacy equals VE_C = 1 − λ₁ (t)/λ₀ (t) = 1 − exp(α)(exp(β) − 1)/β. We choose (α, β, γ) = (−1.1, 1.3, 0.068), yielding VE_C = 0.32, VE(0) = 0.67, and VE(0.85) = 0. We study 400 subjects each in the vaccine and placebo groups. Matching the actual trial, the censoring rate before τ is kept very low, just under 5%. The missing mark indicator is generated from model (13), with (ψ_k0, ψ_k1) set to yield about 0%, 25% (−1.2, −0.2), 50% (0.2, −0.2), and 75% (−1.0, −0.2) missing marks among observed failures. We assume the auxiliary variable A_ki follows the model (14) given in Section 5.1, where the θ values of ∞, 0.8, 0.4 and 0.2 correspond to λ = 0, 0.78, 0.92 and 0.98 for the correlation coefficient between A_ki and V_ki.

Because of lost information on the mark, we choose larger bandwidths for higher percentages of missing marks. We use h = 0.4 for the case with 75% missing marks; h = 0.3 for the case with 50% missing marks; h = 0.2 for the case with 25% missing marks; and h = 0.15 for the case with 0% missing marks. The bandwidths h₁ and h₂ in (7) in the estimation of ${\widehat{\lambda }}_{0k}^{ipw}(t,v)$ are taken to be 0.50 and h₂ = h in each case. Power of the proposed tests $T_{a1}^{(1)},T_{a2}^{(1)},T_{m1}^{(1)},T_{m2}^{(1)},T_{a1}^{(2)},T_{a1}^{(2)},T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ for the simulations based on the Thai trial at the nominal level 0.05 are reported in Table 6. The tests show similar performance as was found in the simulation study of Section 5.1. As only 10% of infected subjects had missing marks in RV144 and the auxiliary was very weakly predictive, we focus on the entries with 0% or 25% missing marks and ρ = 0. There is 67%–95% power to reject H₁₀, and 33%–60% power to reject H₂₀. These results show that a fairly strong sieve effect with V E(v) declining from 67% to 0% could readily be missed in the Thai trial due to limited power. The only slightly improved power with an excellent auxiliary ρ = 0.98 shows that greater numbers of events would be needed to achieve high power for testing H₂₀.

Table 6.

Power of the tests $T_{a1}^{(1)},T_{a2}^{(1)},T_{m1}^{(1)},T_{m2}^{(1)},T_{a1}^{(2)},T_{a1}^{(2)},T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ for the Thai trial at the nominal level 0.05. Each entry is based on 100 Gaussian multipliers samples and 100 repetitions.

			Power
			testing H10				testing H20
ρ	% missing marks	h	$T_{a1}^{(1)}$	$T_{a2}^{(1)}$	$T_{m1}^{(1)}$	$T_{m2}^{(1)}$	$T_{a1}^{(2)}$	$T_{a2}^{(2)}$	$T_{m1}^{(2)}$	$T_{m2}^{(2)}$
	0	0.15	77	85	86	95	48	48	59	60
0	25	0.2	67	76	79	85	36	33	50	47
	50	0.3	63	71	71	82	29	27	37	42
	75	0.4	41	51	59	58	21	18	35	31
0.78	25	0.2	67	79	82	89	36	39	46	50
	50	0.3	60	71	74	84	28	28	41	39
	75	0.4	49	53	63	65	25	25	34	34
0.92	25	0.2	70	80	84	91	37	41	50	56
	50	0.3	61	71	73	87	35	39	50	51
	75	0.4	54	58	62	71	30	33	40	44
0.98	25	0.2	71	81	82	91	39	47	53	55
	50	0.3	66	76	75	86	44	42	50	52
	75	0.4	56	66	68	76	41	43	51	49

6 Analysis of the RV144 Thai trial

In the RV144 Thai trial, 125 subjects (51 of 8197 in the vaccine group and 74 of 8198 in the placebo group) were diagnosed with HIV infection over a 42 month follow-up period, from whom full-length HIV genomes were measured from 121; 3 missed data because their HIV viral load was too low for the Sanger sequencing technology to work, and 1 dropped out [Rerks-Ngarm et al. (2009), Rolland et al. (2012)]. We focus on the gp120 region of the HIV Env protein, because this region stimulates anti-HIV antibody responses which are the putative cause of the observed partial vaccine efficacy. Three gp120 sequences were included in the vaccine: 92TH023 in the ALVAC canarypox vector prime component; and CM244, MN in the AIDSVAX gp120 protein boost component. 92TH023 and CM244 are subtype E HIVs where as MN is subtype B, and 110 of the 121 subjects were infected with subtype E sequences. The subtype E vaccine-insert sequences are much closer genetically to the infecting (and regional circulating) sequences than MN, and thus are more likely to stimulate protective immune responses. Accordingly, the analysis focuses on the 92TH023 and CM244 reference sequences, and right-censors the 15 subjects HIV infected with subtype B or with unknown subtype. One subject who acquired HIV infection during the trial was documented to have acquired HIV from another trial participant who had previously become HIV infected; the analysis excludes this subject because his/her inclusion would violate the independent observations assumption. In the context of our model set-up, T is the time to HIV infection diagnosis with subtype E HIV. The time to HIV infection diagnosis with subtype B or with unknown HIV subtype is treated as censoring.

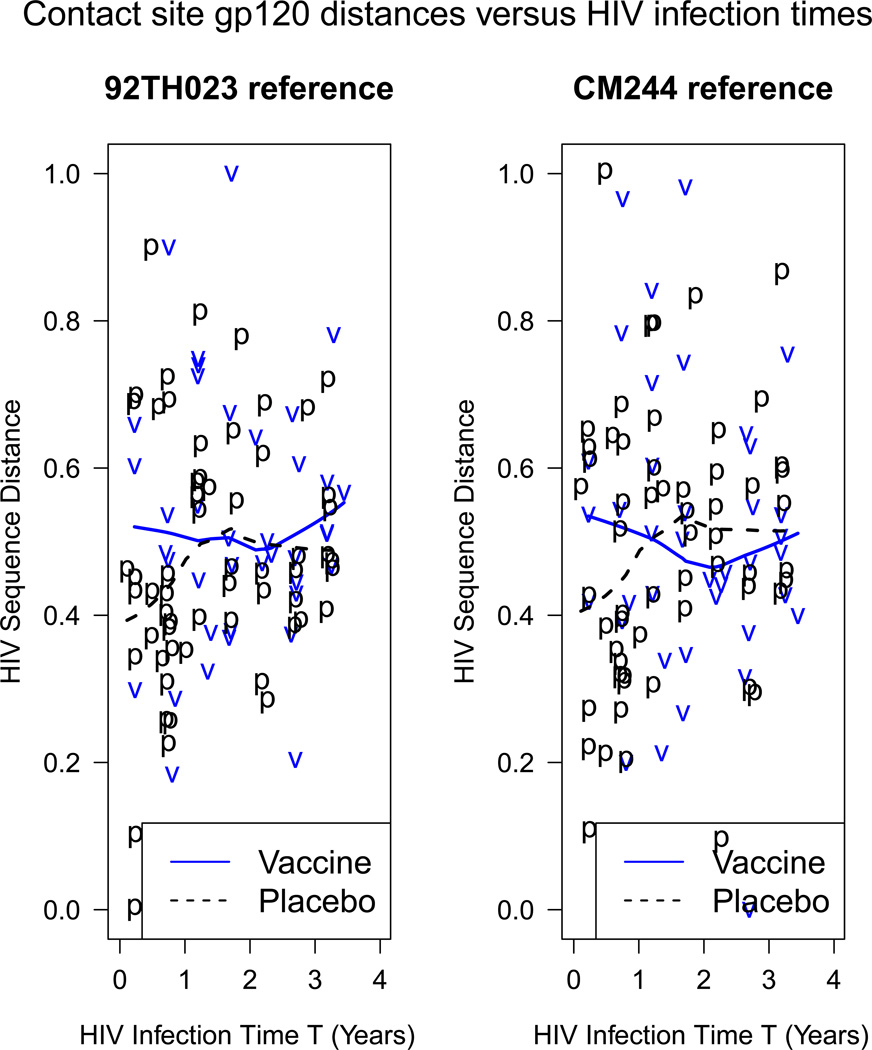
We define V based on HIV sequence data measured from a blood sample drawn at or before the HIV diagnosis date. (The trial documented acute-phase/pre-seroconversion infection in only a few subjects, prohibiting defining the mark based on acute-phase sequences.) Eleven of the 109 (11%) subtype E infected subjects have sequences measured from a post-diagnosis sample and hence are missing V. To maximize biological relevance and statistical power, we restrict the gp120 distances to the published set of gp120 sites in contact with known broadly neutralizing monoclonal antibodies (Moore et al., 2009; Wei et al., 2003). For each HIV sequence from a subject and each of the two reference vaccine sequences, V is computed as a weighted Hamming distance using the PAM-between scoring matrix (Nickle et al., 2007). Between 2 and 13 sequences (total 1030) sequences) were measured per infected subject, and V is defined as the subject’s sequence closest to his or her consensus sequence (the consensus sequence is comprised of the majority amino acids at each site, one site at a time). Finally, the distances are re-scaled to values between 0 and 1. In total, 109 infected subjects (43 vaccine, 66 placebo) are included in the analysis, of which 98 (39 vaccine, 59 placebo) have an observed mark V ; Figure 1 displays the observed V’s.

Figure 1.

Scatterplots of the marks V versus the HIV infection time T for the 98 HIV infected subjects in the Thai trial with an observed mark. The mark V is the HIV-specific PAM-matrix (Nickle et al., 2007) weighted Hamming distances between a subject’s HIV Envelope gp120 amino acid sequence (nearest to his/her consensus sequence) and the 92TH023 or CM244 vaccine reference sequence; the distances restrict to the 172 amino acid sites in gp120 documented to contact broadly neutralizing monoclonal antibodies. The lines are lowess smooth fits (Cleveland, 1979).

To predict the probability of observing V among the 109 infected subjects, we use all-subsets logistic regression model selection considering demographics, host genetics, and biomarker data post-infection. The best model by BIC includes only the years from entry until HIV infection diagnosis (X₁), with model fit logit(P̂ (R = 1|δ = 1, X₁)) = 1.17 + 0.70X₁ for the CM244 reference sequence. The model was very similar for the 92TH023 reference sequence (not shown). In addition, we consider linear and logistic regression models for relating the mean of various potential auxiliary variables (A) to V, X₁, and treatment indicator Z. Model selection did not reveal any significantly predictive auxiliary variables; we expect that HIV sequence information measured after V is defined would be a good predictor, but these data were not collected. Nevertheless, to implement the AIPW method we select the best available auxiliary variable, gender (A = X₂, 1=male; 0=female), and use the logistic regression model that results; for CM244 the fitted model ĝ(A = a|V, X₁, Z) is logit(P̂(X₂ = 1|δ = 1, V, X₁, Z) = 0.24 − 0.33V + 0.16X₁ + 0.38Z, and the model was very similar for 92TH023 (not shown).

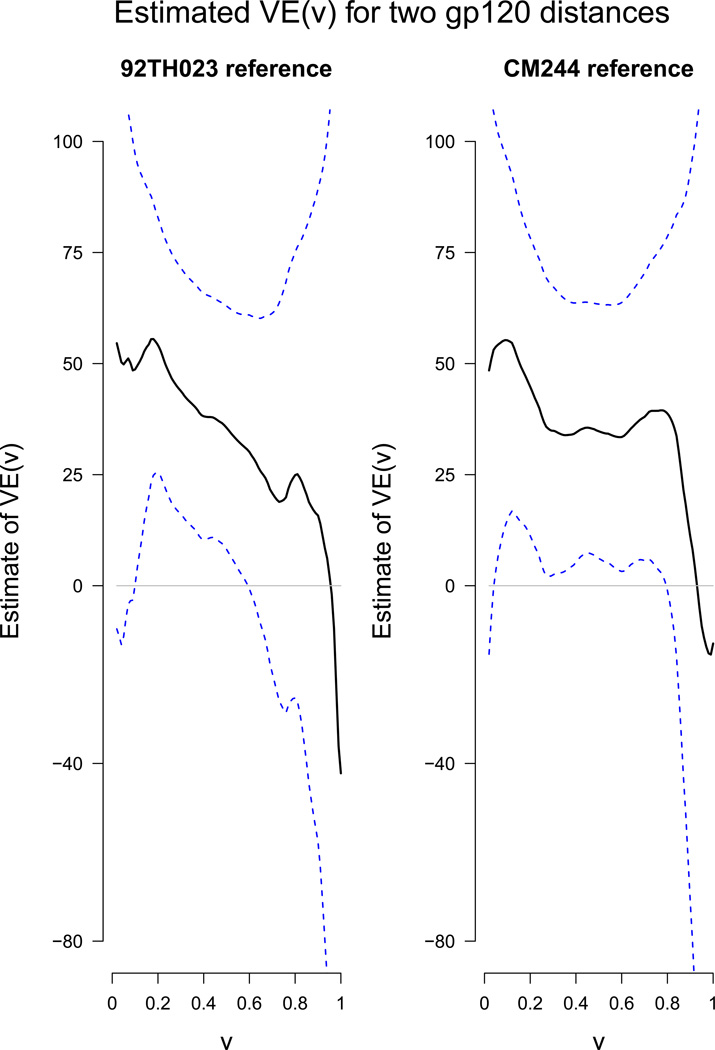
The AIPW estimation and testing procedures are applied to the Thai trial data set with bandwidths h₁ = 0.5 and h₂ = h = 0.3, a = 0.05, b = 1 and a′ = a + 0.01 (a and a′ are near the minimum observed marks). As in the simulation study, 500 simulated Gaussian multipliers are used. Because the results are nearly identical with and without the auxiliary variable, only the latter results are presented. Figure 2 shows the estimated VE(v) along with 95% pointwise confidence bands, indicating that vaccine efficacy appears to be high against HIVs near to the 92TH023 reference sequence [estimated VE(0.01) = 56%], and declines to zero against HIVs farthest from the 92TH023 reference sequence [estimated VE(1.0) = 2.4%]. The decline is similar for the CM244 reference sequence, with estimated VE(0.01) = 45% and estimated VE(0.95) = −9.1%.

Figure 2.

AIPW estimation of VE(v) and 95% pointwise confidence bands without using auxiliary variables for the Thai trial with bandwidths h₁ = 0.5, h₂ = h = 0.3, for the monoclonal antibody contact site distances to the 92TH023 and CM244 reference sequences.

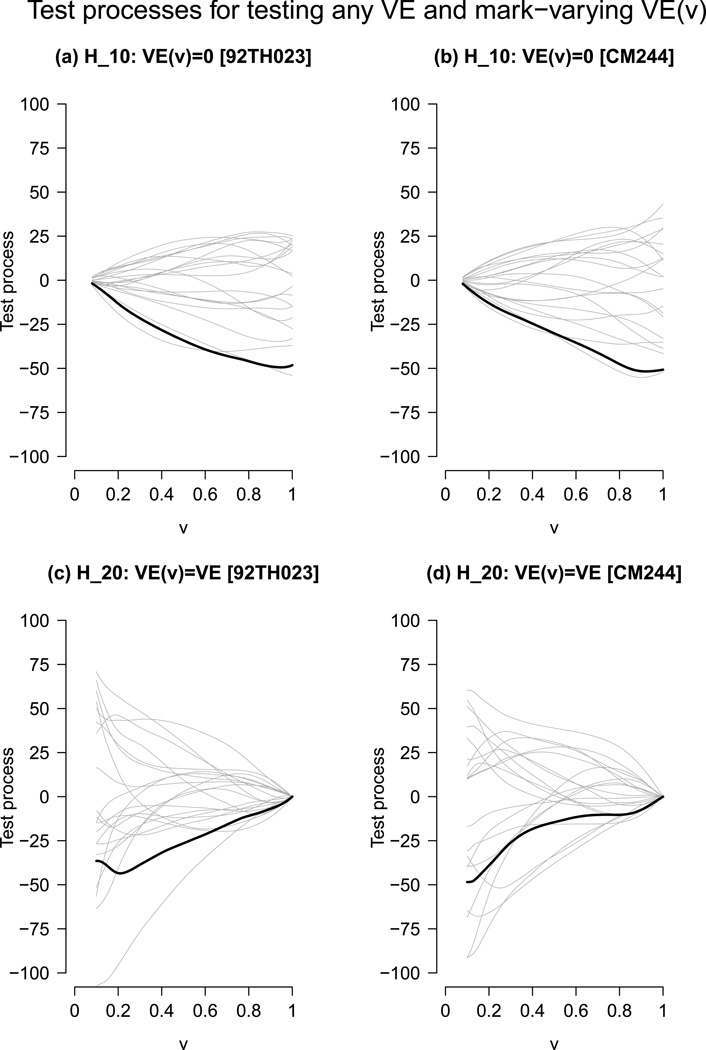
Figure 3 (a) and (b) shows the test processes Q⁽¹⁾ (v) versus 20 realizations from the Gaussian multiplier process $W_{B_1}^{*}(v)$ given the observed data, and Figure 3 (c) and (d) shows the parallel results for the test process Q⁽²⁾ (v), each suggesting departures from the null hypothesis H₁₀ and from the null hypothesis H₂₀ for each reference sequence. The p-values of the tests based on the test statistics $T_{m1}^{(1)}\text{and}{T}_{m2}^{(1)}$ for testing H₁₀ against the monotone alternative over v ∈ [0, 1] are 0.032 and 0.008 for 92TH023, and 0.014 and 0.010 for CM244. The p-values of the test statistics $T_{a1}^{(1)}\text{and}{T}_{a2}^{(1)}$ for testing H₁₀ against the general alternative are 0.054 and 0.018 for 92TH023 and 0.030 and 0.010 for CM244. For testing H₂₀ over v ∈ [0, 1], the p-values of the supremum-type tests based on the test statistics $T_{a1}^{(2)}\text{and}{T}_{m1}^{(2)}$ are 0.53 and 0.27 for 92TH023 and 0.37 and 0.18 for CM244. The p-values of the integrated square type tests based on the test statistics $T_{a2}^{(2)}\text{and}{T}_{m2}^{(2)}$ are 0.35 and 0.14 for 92TH023 and 0.44 and 0.19 for CM244.

Figure 3.

Diagnostic plots of the test processes for the Thai trial data set with bandwidths h₁ = 0.5, h₂ = h = 0.3 and a = 0.05, b = 1 and a′ = a + 0.01 without using auxiliary variables. (a) and (b) Plots of Q⁽¹⁾(v) (solid dark line) versus 20 realizations (grey lines) from the Gaussian multiplier process $W_{B_1}^{*}(v)$ (92THf023, CM244 reference). (c) and (d) Plots of Q⁽²⁾(v) (solid dark line) versus 20 realizations (grey lines) from the Gaussian multiplier process $\Gamma (v,W_{B_1}^{*})$ (92TH023, CM244 reference).

These analyses provide more evidence that the vaccine had some protective efficacy than the original primary analysis that did not account for the mark information (Rerks-Ngarm et al., 2009): the primary analysis test for any vaccine efficacy yielded p=0.04 whereas the tests for any vaccine efficacy against any mark reported here yielded median p-value of 0.016 across the four test statistics and two reference sequences. The analyses also showed a nonsignificant trend (p-values around 0.14–0.19) that the vaccine protected better against HIVs closely matched to the vaccine strain HIVs in the monoclonal antibody contact sites, but had less or absent protection against HIVs with many mismatches in these sites. While the significance levels are not compelling, the simulation study presented in Section 5.3 of the power available for detecting a vaccine sieve effect in the Thai trial showed that the study is well-powered only to detect large sieve effects [with greater decline of V E(v) in v than what was observed in the estimated V E(v) curves]; thus a moderate-to-large sieve effect is consistent with the observed results. These results may guide future vaccine research by suggesting modifications of future vaccine candidates to include HIV sequences more closely matched to circulating HIVs in the monoclonal antibody contact sites. They may also motivate the design of future experiments to understand functional effects of amino acid mutations at the monoclonal antibody contact sites.

Appendix: Asymptotic results

The following regularity conditions from Sun and Gilbert (2012) are assumed.

Condition A

• (A.1)β(v) has component wise continuous second derivatives on [0, 1]. For each k = 1,…, K,the second partial derivative of λ_0k (t, v) with respect to v exists and is continuous on [0, τ]×[0, 1]. The covariate process Z_k (t) has paths that are left continuous and of bounded variation, and satisfies the moment condition E[‖Z_k (t)‖⁴ exp(2M‖Z_k (t)‖)] < ∞, where M is a constant such that (v, β(v)) ∈ [0, 1] × (−M, M)^p for all v and ‖A‖ = max_k,l |a_kl| for a matrix A = (a_kl).
• (A.2)Each component of ${\mathbf{s}}_k^{(j)}(t,\theta )$ is continuous on [0, τ] × [−M, M]^p, ${\tilde{\mathbf{s}}}_k^{(j)}(t,\theta ,\psi )$ is continuous on [0, τ] × [−M, M]^p × [−L, L]^q for some M, L > 0 and j = 0, 1, 2. ${\text{sup}}_{t\in [0,\tau ],\theta \in {[-M,M]}^p}\Vert {\mathbf{S}}_k^{(j)}(t,\theta )\Vert =O_p(n^{-1/2})\text{and}{\text{sup}}_{t\in [0,\tau ],\theta \in {[-M,M]}^p,{\psi }_k\in }\Vert {\tilde{\mathbf{S}}}_k^{(j)}(t,\theta ,{\psi }_k)-{\tilde{\mathbf{s}}}_k^{(j)}(t,\theta ,\psi )\Vert =O_p(n^{-1/2})$
• (A.3)The limit p_k = lim_n→∞ n_k/n exists and 0 < p_k < ∞. ${\mathbf{s}}_k^{(0)}(t,\theta )>0$ on [0, τ] × [−M, M]^p and the matrix $\Sigma (v)={\sum }_{k=1}^K{p}_k{\Sigma }_k(v)$ is positive definite, where ${\Sigma }_k(v)={\sum }_{k=1}^K{\int }_0^{\tau }{I}_k(t,\beta (v)){\lambda }_{0k}(t,v){\mathbf{s}}_k^{(0)}(t,\mathit{\beta }(v))dt\text{and}{I}_k(t,\mathit{\beta })={\mathbf{s}}_k^{(2)}(t,\mathit{\beta })/{\mathbf{s}}_k^{(0)}(t,\mathit{\beta })-{({\overline{\mathbf{z}}}_k(t,\beta ))}^{\otimes 2}$.
• (A.4)The kernel function K(·) is symmetric with support [−1, 1] and of bounded variation. The bandwidth h satisfies nh² → ∞ and nh⁴ → 0 as n → ∞.
• (A.5)There is a σ > 0 such that r_k (W_ki) ≥ σ for all k, i with δ_ki = 1.

Let ℱ_t = σ{I(X_ki ≤ s, δ_ki = 1), I(X_ki ≤ s, δ_ki = 0), V_ki I(X_ki ≤ s, δ_ki = 1), Z_ki (s); 0 ≤ s ≤ t, i = 1,…, n_k, k = 1,…, K} be the (right-continuous) filtration generated by the full data processes {N_ki (s, v), Y_ki (s), Z_ki (s); 0 ≤ s ≤ t, 0 ≤ v ≤ 1, i = 1,…, n_k, k = 1,…, K}. Assume E(N_ki (dt, dv)|ℱ_t−) = E(N_ki (dt, dv)|Y_ki (t), Z_ki (t)), that is, the mark-specific instantaneous failure rate at time t given the observed information up to time t only depends on the failure status and the current covariate value. By the definition of the conditional mark-specific hazard function, E(N_ki (dt, dv)|ℱ_t−) = Y_ki (t)λ_k(t, v|Z_ki (t)) dtdv. Hence, the mark-specific intensity of N_ki (t, v) with respect to ℱ_t equals Y_ki (t)λ_ki (t, v|Z_ki (t)). Let $M_{ki}(t,u)={\int }_0^t{\int }_0^u[N_{ki}(ds,dx)-Y_{ki}(s){\lambda }_k(s,x|{\mathbf{Z}}_{ki}(s))dsdx]$. By Aalen and Johansen (1978), M_ki (·, v₁) and M_ki (·, v₂) − M_ki (·, v₁) are orthogonal square integrable martingales with respect to ℱ_t for any 0 ≤ v₁ ≤ v₂ ≤ 1.

The weak convergence of W_B (v) = n^1/2 {B̂^aug (v) − B(v)} − n^1/2 {B̂^aug (a) − B(a)} for v ∈ [a, b] is given in Theorem 1 below.

Theorem 1. Under conditions (A.1)–(A.5), ${\mathbf{W}}_B(v)=n^{-1/2}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\mathbf{H}}_{k}i(v)+o_p(1)$, uniformly in v ∈ [a, b], where

$${\mathbf{H}}_{k}i(v)={\int }_a^v{\int }_0^{\tau }{\{\Sigma (u)\}}^{-1}[{\mathbf{Z}}_{ki}(t)-{\overline{\mathbf{z}}}_k\{t,\mathit{\beta }(u)\}][\frac{R_{ki}}{{\pi }_k(Q_{ki})}{M}_{ki}(dt,du)+\{1-\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki})}\left\}E\right\{M_{ki}\}(dt,du)|{\mathbf{Q}}_{ki}\left\}\right].$$ (21)

The processes W_B (v) converges weakly to a p-dimensional mean-zero Gaussian process with continuous sample paths on v ∈ [a, b], where ${\overline{\mathbf{z}}}_k(t,\mathit{\beta })={\mathbf{s}}_k^{(1)}(t,\mathit{\beta })/{\mathbf{s}}_k^{(0)}(t,\mathit{\beta })\text{and}{\mathbf{s}}_k^{(j)}(t,\mathit{\beta })=E{\mathbf{S}}_k^{(j)}(t,\mathit{\beta })$.

Theorem 1 provides the basis for obtaining asymptotically correct critical values for the testing procedures for H₁₀ and for H₂₀. In particular, let G(v) be the limiting Gaussian process ofW_B1 (v), v ∈ [a, b], as n → ∞. Then under H₁₀, $Q^{(1)}(v)\stackrel{𝒟}{\to }G(v)$, v ∈ [a, b], as n → ∞. By Theorem 1 and the continuous mapping theorem, $T_{a1}^{(1)}\stackrel{𝒟}{\to }{\text{sup}}_{v\in p[a,b]}|G(v)|,T_{a2}^{(1)}\stackrel{𝒟}{\to }{\int }_a^b{\{G(v)\}}^{2}dVar\{G(v)\},T_{m1}^{(1)}\stackrel{𝒟}{\to }{\text{inf}}_{v\in [a,b]}G(v)\text{and}{T}_{m2}^{(1)}\stackrel{𝒟}{\to }{\int }_a^{b}G(v)d\text{Var}\{G(v)\}$ under H₁₀ as n → ∞. Under H₂₀, $Q^{(2)}(v)=\Gamma (v,W_{B_1})\stackrel{𝒟}{\to }\Gamma (v,G)$, v ∈ [a, b], as n → ∞. Applying the continuous mapping theorem, under H₂₀, $T_{a1}^{(2)}\stackrel{𝒟}{\to }{\text{sup}}_{v\in [a\prime ,b]}|\Gamma (v,G)|,T_{a2}^{(2)}\stackrel{𝒟}{\to }{\int }_{a\prime }^b{\{\Gamma (v,G)\}}^{2}d\text{Var}\{G(v)\},T_{m1}^{(2)}\stackrel{𝒟}{\to }{\text{inf}}_{v\in [a\prime ,b]}\Gamma (v,G)\text{and}{T}_{m2}^{(2)}\stackrel{𝒟}{\to }{\int }_{a\prime }^b\Gamma (v,G)dVar\{G(v)\}$, as n → ∞.

The proof of the consistency of the tests for testing H₁₀ are straightforward. To show the consistency of the tests for testing H₂₀, we note that the derivative dΓ(v, B₁)/dv = (v − a)⁻¹ [β₁ (v) − (v − a)⁻¹ B₁ (v)] ≥ 0 under H_2m with strict inequality for at least some v ∈ [a, b]. The function Γ(v, B₁) is non-decreasing with Γ(b, B₁) = 0. We have, under H_2m, Γ(v, B₁) ≤ 0 with strict inequality for at least some v ∈ [a, b]. Let v₀ ∈ [a, b] be such that Γ(v₀, B₁) < 0. Then Γ(v, B₁) < 0 for v ≤ v₀. Now defining $v_m^{*}=\text{sup}\{v:\Gamma (v,B_1)<0,a\le v\le b\}$, we have Γ(v, B₁) < 0 for $v<v_m^{*}$ and Γ(v, B₁) = 0 for v^* ≤ v < b. It follows from (11) and Theorem 1 that $T_{m1}^{(2)}\stackrel{P}{\to }-\infty \text{and}{T}_{m2}^{(2)}\stackrel{P}{\to }-\infty$ under H_2m as n → ∞ for $a\prime <v_m^{*}$. Thus the tests based on $T_{m1}^{(2)}\text{and}{T}_{m2}^{(2)}$ are consistent against H_2m. Similarly, let $v_a^{*}=\text{sup}\{v:{\text{sup}}_{u\in [v,b]}|\Gamma (u,B_1)|>0,a\le v\le b\}$. Then under H_2a, |Γ(v, B₁)| > 0 for $v<v_a^{*}$, and |Γ(v, B₁)| = 0 for $v_a^{*}\le v\le b$. Hence $T_{a1}^{(2)}\stackrel{P}{\to }\infty \text{and}{T}_{a2}^{(2)}\stackrel{P}{\to }\infty$ under H_2a as n → ∞ for $a\prime <v_a^{*}$, resulting in the consistent tests against H_2a.

We use the Gaussian multiplier resampling method [Lin et al. (1993)] to approximate the distribution of W_B (v), v ∈ [a, b]. Let {ξ_ki, i = 1,…, n_k, k = 1,…, K} be iid standard normal random variables. Replacing each term of (26), which is asymptotically equivalent to (21), by its empirical counterpart and multiplying by ξ_ki, we obtain ${\mathbf{W}}_B^{*}(v)=n^{-1/2}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\xi }_{ki}{\widehat{\mathbf{H}}}_{k}i(v)$, where

$${\widehat{\mathbf{H}}}_{k}i(v)={\int }_0^1{\int }_0^{\tau }H(v,u)\{{\mathbf{Z}}_{ki}(t)-{\overline{\mathbf{Z}}}_k(t,{\widehat{\mathit{\beta }}}^{\mathit{\text{aug}}}(u))\}\{\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki},{\widehat{\psi }}_k)}{N}_{ki}(dt,du)+(1-\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki},{\widehat{\psi }}_k)})N_{ki}^x(dt)d({\widehat{\rho }}_k^{\mathit{\text{aug}}}({\mathbf{W}}_{ki},u))-Y_{ki}(t)\text{exp}(({\widehat{\mathit{\beta }}}^{\mathit{\text{aug}}}{(u)}^T{\mathbf{Z}}_{ki}(t)){\widehat{\Lambda }}_{0k}^{\mathit{\text{aug}}}(dt,du)\},$$ (22)

where $H(v,u)={\int }_a^v{({\widehat{\Sigma }}_{\mathit{\text{aug}}}(x))}^{-1}{K}_h(u-x)dx.$.

Following an application of Lemma 1 of Sun and Wu (2005), the distribution of W_B (v), v ∈ [a, b], can be approximated by the conditional distribution of ${\mathbf{W}}_B^{*}(v)$, v ∈ [a, b], given the observed data sequence, which can be obtained through repeatedly generating independent sets of 23 {ξ_ki, i = 1,…, n_k, k = 1,…, K}. Hence, the distribution of Q⁽¹⁾ (v), v ∈ [a, b], under H₁₀, can be approximated by the conditional distribution of $W_{B_1}^{*}$, v ∈ [a, b], given the observed data sequence. By the continuous mapping theorem, the distribution of Q⁽²⁾ (v), v ∈ [a, b], under H₂₀, can be approximated by the conditional distribution of Γ (v, $W_{B_1}^{*}$), v ∈ [a, b], given the observed data sequence.

With the Gaussian multiplier method, the variance $\text{Var}\{{\widehat{B}}_1^{\mathit{\text{aug}}}(v)-{\widehat{B}}_1^{\mathit{\text{aug}}}(a)\}$ can be consistently estimated by $\widehat{\text{Var}}\{{\widehat{B}}_1^{\mathit{\text{aug}}}(v)-{\widehat{B}}_1^{\mathit{\text{aug}}}(a)\}=n^{-1}\text{Var}*(W_{B_1}^{*}(v))\text{where Var}*(W_{B_1}^{*}(v))$ is the first component on the diagonal of

$$\text{Cov}*({\mathbf{W}}_B^{*}(v))=\text{Cov}({\mathbf{W}}_B^{*}(v)|\text{observed data})=n^{-1}\sum _{k=1}^K\sum _{i=1}^{n_k}[{\int }_0^1{\int }_0^{\tau }H(v,u)\{{\overline{Z}}_{ki}(t)-{\overline{\mathbf{Z}}}_k(t,{\widehat{\mathit{\beta }}}^{\mathit{\text{aug}}}(u))\}\{\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki},{\widehat{\psi }}_k)}{N}_{ki}(dt,du)+\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki},{\widehat{\psi }}_k)}{N}_{ki}^x(dt)d({\widehat{\rho }}_k({\mathbf{W}}_{ki},u))-Y_{ki}(t)\text{exp}({({\widehat{\mathit{\beta }}}^{\mathit{\text{aug}}}(u))}^T{\mathbf{Z}}_{ki}(t)){\widehat{\Lambda }}_{0k}^{\mathit{\text{aug}}}{(dt,du)\left\}\right]}^{\otimes 2}.$$ (23)

Proof of Theorem 1

Let

$${𝒜}_{ki}(v)={\int }_0^1{\int }_0^{\tau }{K}_h(u-v)({\mathbf{Z}}_{ki}(t))-{\overline{\mathbf{z}}}_k(t,\mathit{\beta }(u)))\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki})}{M}_{ki}(dt,du),{ℬ}_{ki}(v)={\int }_0^1{\int }_0^{\tau }{K}_h(u-v)({\mathbf{Z}}_{ki}(t)-{\overline{\mathbf{z}}}_k(t,\mathit{\beta }(u)))(1-\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki})}\left)E\right\{M_{ki}(dt,du)\left|{\mathbf{Q}}_{ki}\right\}.$$ (24)

Following the proof of Theorem 4 of Sun and Gilbert (2012, the web Appendix (W.19)) and under nh₄ → 0,

$$n^{1/2}\{{\widehat{\mathit{\beta }}}^{\mathit{\text{aug}}}(v)-\mathit{\beta }(v)\}=-{(\Sigma (v))}^{-1}{n}^{-1/2}\sum _{k=1}^K\sum _{i=1}^{n_k}({𝒜}_{ki}(v)+{ℬ}_{ki}(v))+o_p(1).$$ (25)

Hence

$$n^{1/2}({\widehat{\mathbf{B}}}^{\mathit{\text{aug}}}(v)-\mathbf{B}(v))=-n^{-1/2}\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^v{(\Sigma (u))}^{-1}({𝒜}_{ki}(u)+{ℬ}_{ki}(u))du+o_p(1),$$

which, by exchanging the order of integrations, equals to

$$n^{-1/2}\sum _{k=1}^K\sum _{i=1}^{n_k}({\int }_0^1{\int }_0^{\tau }[{\int }_0^v{K}_h(u-x){\{\Sigma (x)\}}^{-1}dx][{\mathbf{Z}}_{ki}(t)-{\overline{\mathbf{z}}}_k\{t,\mathit{\beta }(u)\}][\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki})}{M}_{ki}(dt,du)+\{1-\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki})}\}E\{M_{ki}(dt,du)|{\mathbf{Q}}_{ki}\left\}\right]).$$ (26)

Let

$${\tilde{\mathbf{J}}}_n(v)=n^{-1/2}\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^v{\int }_0^{\tau }[{\mathbf{Z}}_{ki}(t)-{\overline{\mathbf{z}}}_k(t,\mathit{\beta }(u))][\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki})}{M}_{ki}(dt,du)+\left\{1-\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki})}\right\}E\{M_{ki}(dt,du)\left|{\mathbf{Q}}_{ki}\right\}].$$

It follows that

$$n^{1/2}({\widehat{\mathbf{B}}}^{\mathit{\text{aug}}}(v)-\mathbf{B}(v))=-{\int }_0^v{(\Sigma (u))}^{-1}{\int }_0^1{K}_h(x-u){\tilde{\mathbf{J}}}_n(dx)du+o_p(1)=-{\int }_0^1[{\int }_0^1{(\Sigma (u))}^{-1}{K}_h(x-u)du]{\tilde{\mathbf{J}}}_n(dx)+o_p(1).$$ (27)

Since the kernel function K(·) has compact support on [−1, 1], (27) equals to

$$-{\int }_h^{v-h}[{\int }_0^v{(\Sigma (u))}^{-1}{K}_h(x-u)du]{\tilde{\mathbf{J}}}_n(dx)-{\int }_{-h}^h[{\int }_0^v{(\Sigma (u))}^{-1}{K}_h(x-u)du]{\tilde{\mathbf{J}}}_n(dx)-{\int }_{v-h}^{v+h}[{\int }_0^v{(\Sigma (u))}^{-1}{K}_h(x-u)du]{\tilde{\mathbf{J}}}_n(dx)+o_p(1).$$ (28)

It can be shown that J̃_n (x) converges weakly to a mean-zero Gaussian process with continuous paths. Under the assumption (A.4), ${\int }_0^v{(\Sigma (u))}^{-1}{K}_h(x-u)du$ has bounded variation and converges uniformly to Σ(x)⁻¹ for x ∈ (h, v − h). By Lemma 2 of Gilbert et al. (2008), the first term in (28) is equal to $-{\int }_0^v{(\Sigma (u))}^{-1}{\tilde{\mathbf{J}}}_n(dx)+o_p(1)$. Similar arguments lead to the second and the third terms in (28) to be o_p (1). Hence,

$$n^{1/2}({\widehat{\mathbf{B}}}^{\mathit{\text{a}}}(v)-\mathbf{B}(v))=n^{-1/2}\sum _{k=1}^K\sum _{i=1}^{nk}({\int }_0^v{\int }_0^{\tau }{\{\Sigma (u)\}}^{-1}[{\mathbf{Z}}_{ki}(t)-{\overline{\mathbf{z}}}_k\{t,\mathit{\beta }(u)\}][\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki})}{M}_{ki}(dt,du)\left|\right\{1-\frac{R_{ki}}{{\pi }_k({\mathbf{Q}}_{ki})}\left\}E\right\{M_{ki}(dt,du)\left|{\mathbf{Q}}_{ki}\right\}\left]\right)+o_p(1),$$

which converges weakly to a p-dimensional mean-zero Gaussian process on v ∈ [a, b] with continuous sample paths by Lemma 1 of Sun and Wu (2005). Theorem 1 follows since W_B (v) = n^1/2 {B̂^aug (v) − B(v)} − n^1/2 {B̂^aug (a) − B(a)} is a linear transformation of n^1/2 (B̂^aug (·) − B(·)).