Inferring Active and Prognostic Ligand-Receptor Pairs with Interactions in Survival Regression Models

Abstract

Modeling signal transduction in cancer cells has implications for targeting new therapies and inferring the mechanisms that improve or threaten a patient’s treatment response. For transcriptome-wide studies, it has been proposed that simple correlation between a ligand and receptor pair implies a relationship to the disease process. Statistically, a differential correlation (DC) analysis across groups stratified by prognosis can link the pair to clinical outcomes. While the prognostic effect and the apparent change in correlation are both biological consequences of activation of the signaling mechanism, a correlation-driven analysis does not clearly capture this assumption and makes inefficient use of continuous survival phenotypes. To augment the correlation hypothesis, we propose that a regression framework assuming a patient-specific, latent level of signaling activation exists and generates both prognosis and correlation. Data from these systems can be inferred via interaction terms in survival regression models allowing signal transduction models beyond one pair at a time and adjusting for other factors. We illustrate the use of this model on ovarian cancer data from the Cancer Genome Atlas (TCGA) and discuss how the finding may be used to develop markers to guide targeted molecular therapies.

Background

Biochemically, the binding of a ligand-receptor pair (LRP) is a signal transduction event passing information from the outside of the plasma membrane to the interior of the cell. This event sets off a complex network of protein signaling cascades and interacting complexes that cause phenotypic changes on the level of the cell and in the context of cancer.¹

Ligand-receptor systems are a major focus for targeted anti-cancer therapies. For example, Yarden² reviewed the epidermal growth factor receptor (EGFR) pathway and the known molecular mechanisms that the cell processes to lead to proliferation or survival or migration, noting that these signals can be attacked by anti-EGFR monoclonal antibodies and tyrosine kinase inhibitors. These options face a long translational process³ as aberrant signaling is first identified in pre-clinical models and candidate therapies progress to early clinical trials. As Gschwind and colleagues observe, there are a number of these therapies in the development pipeline,⁴ so for a given cancer, we might imagine that the first task is to begin to compile evidence that a targetable receptor may be active and important. To rapidly identify promising candidate LRPs, Graeber and Eisenberg⁵ hypothesized that the correlation between mRNA levels of a known LRP is a way to infer pairs with active autocrine signaling for a given disease. They used the hypothesis to rapidly screen about 200 cancer samples for candidate informative pairs using high-throughput gene expression data. With the increasing volume of genomic studies, this technique has been repeated by Castellano and colleagues⁶ with increasing emphasis on finding an association with survival times for advanced ovarian cancer.

Statistically, the standard approach to merging survival responses with two genes at a time is a differential correlation (DC) or differential co-expression analysis. These methods tie signaling to prognosis by stratifying patients into empirically defined survival groups and then testing whether correlation between the ligand and the receptor differs between the two. This is an inelegant solution from the perspective of continuous survival regression models because dichotomization ignores patients with intermediate survival times and because regression models can adjust for other factors. Instead, we might regress the ligand on the receptor (or receptor on ligand; it is unclear which is preferable) using a dummy variable or transformation of survival time to account for prognosis. This is difficult because survival times are frequently censored. Further, the result can only confirm the effect of survival on correlation and not estimate the more valuable effect of correlation on prognosis.

In our previous work,⁷ we noted that survival time regression model’s interactions were sensitive to DC-type interactions, but we did not investigate why this association exists. In this article, we attempt to address these inconsistencies by conjecturing that there exists an underlying data-generating process that links survival and correlation through an unobserved activation level. We are able to show that this assumption is consistent with the properties of data observed to date, and we consider the implications of this model for data analysis.

Methods

Activation signal hypothesis

We hypothesize that signal transduction can be described as a continuous level that generates the correlation between ligand and receptor. This activation level may not be directly observed, but its influence on survival (or another phenotype) may be seen. Let Z ∈ ℜ denote the level of signaling activation, and the influence of activation on a survival time Y be

$$\log Y={\beta }_0+{\beta }_{1}Z+\sigma \epsilon$$ (1)

where the standard normal error ε captures the influence of other factors on survival; β₁ controls the importance of activation, and (β₀, σ) are chosen to set the marginal distribution of Y. Supposing that both Z and ε are symmetric about zero, then exp(β₀) is the median survival time and σ can be set by assuming a clinically derived side condition like P(Y > t₀) = p₀ for some known time t₀ and survival percent p₀. Note that we will assume ε is normal for our simulations, but we will evaluate general semiparametric methods (namely, Cox proportional hazards (PH) regression) to establish the validity of the use of popular survival analysis methods for this model. Let X_L and X_R denote the expression levels of the ligand and receptor genes, respectively, which are bivariate normal with correlation dependent on the activation level:

$$\left(\begin{array}{c}{X}_L\\ X_R\end{array}\right)\left|\right\{Z=z\}~N\left\{\left(\begin{array}{c}0\\ 0\end{array}\right),{\sigma }^2\left(\begin{array}{cc}1& p(z)\\ p(z)& 1\end{array}\right)\right\}$$ (2)

The activation-dependent correlation is p(Z) = αΨ(Z) with Ψ(·) as the cumulative distribution function and the effect size |α| ≤1. The name and concept for the activation function come from the neural network literature where Ψ is interpreted as the firing rate of a neuron given input current Z. This is an appealing analogy for the ligand–receptor system.

Now, the inference problem is to detect the fact that these ligand and receptor are correlated and that this is somehow related to survival. We will demonstrate the result that the interaction between the ligand and receptor expression levels can be detected in a regression model. This is surprising for three reasons: the degree of correlation is patient specific (σψ(Z)), we have not specified that log(Y) is some function of (X_L, X_R), and there is no correlation between Z and X_L or X_R.

Illustrations

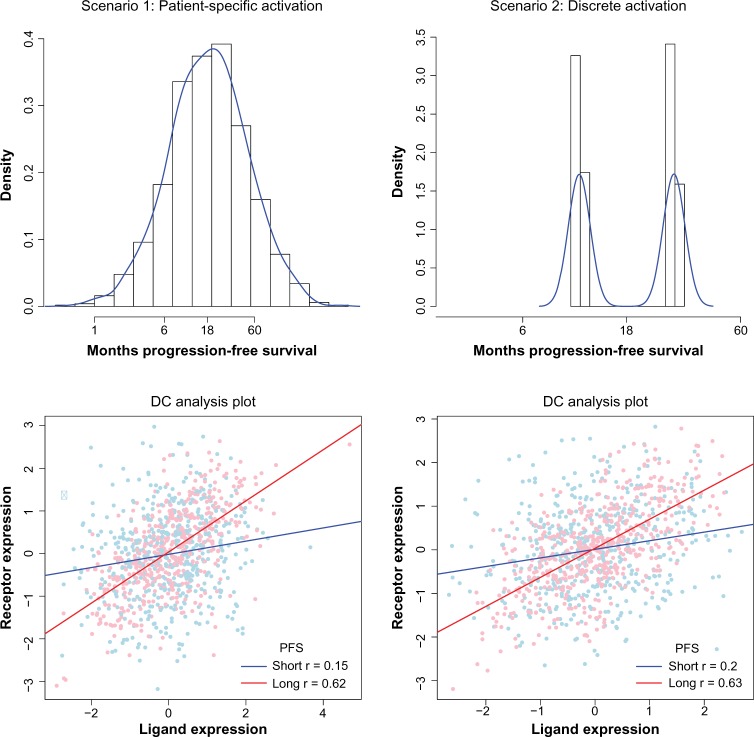
Figure 1 comprises two simulated examples, motivated by the clinical prognosis for advanced ovarian cancer, showing the relationship between the activation hypothesis and the analysis of the LRP. In each scenario, described below, we set β₁ = 1, α = 0.8, β₀ = log18, and σ = 0.025, corresponding to a median progression-free survival (PFS) of 18 months and 12% survival at 60 months when Z is standard normal. We generate n = 1000 patients in each scenario. In both scenarios, the function Ψ₁(Z) = (tanh(z) + 1) / 2 translates activation to correlation of the LRP.

Figure 1.

Simulated data illustrate survival times (top row) and correlation (bottom row), showing that the activation hypothesis generates DC in both a patient-specific (left) and a discrete (right) scenario.

Scenario 1. Patient-specific activation levels

We generated standard normal patient-specific activation level Z, meaning that each patient has their own level of activation and that the values are spread on a continuum (they are simply active or not). Expression values (X_L, X_R) are generated as mean zero, bivariate normal random variates with the individual correlation indicated by Ψ₁(Z) (Fig. 1, left).

We note that the marginal correlation between the ligand and the receptor is r = 0.39, so we would infer that this is an active signaling pair. In a typical DC analysis, we might stratify patients based on survival past the median of the observed survival times and compute the correlation in the short survival set (r = 0.15) and in the long survival set (r = 0.62). The differences are all strongly significant (P < 0.001), so we conclude that the activation of this LRP is associated with survival and that a DC analysis is a valid approach.

We performed a standard Cox PH regression that found no marginal association between PFS, and $X_L(\widehat{\beta }=0.03,P=0.46)$ and $X_R(\widehat{\beta }=-0.04,P=0.30)$ jointly and univariately. Thus, it is likely that standard analyses will have overlooked this effect. Surprisingly, when we consider the statistical interaction between the ligand and the receptor, we find that it is a strong prognostic factor $(\widehat{\beta }=-0.19,P=7.4\mathrm{e}-09)$. This result leads us to conjecture that the statistical interaction in a survival regression model can identify signaling LRPs.

Scenario 2. Extreme DC model

DC analysis implicitly assumes that patients can be classified into an active or inactive LRP state. We consider an extreme scenario that strongly favors a DC-type analysis. Let inactive patients have level Z = −1/2 and active patients have level Z = 1/2; then, Ψ₁(Z) takes two values, Ψ₁(−1/2) = 0.215 and Ψ₁ (1/2) = 0.585. This selection generates a clearly bimodal survival distribution (Fig. 1, right) where inactive patients have a mean survival of 11 months (exp[E(Y|Z = −1/2)] = 18exp(−1/2)) and the active patients have a mean survival of 30 months. This assumption tends to be unrealistic for cancer applications; the marginal distribution of ovarian cancer survival times is continuous and patient survival times is unimodal, and the decision to split patients is likely to fit poorly with patients near the threshold.

By design, this scenario generates significant DC (r = 0.20 and r = 0.63) similar to scenario 1, so DC analysis is a valid approach for identifying this pair. Again, by Cox PH regression, we find that the ligand $(\widehat{\beta }=-0.05,P=0.25)$ and receptor $(\widehat{\beta }=-0.03,P=0.37)$ expressions are not associated with prognosis, but the interaction is $(\widehat{\beta }=-0.14,P=5.5\mathrm{e}-05)$.

Therefore, we conclude that the latent activation model is a viable data-generating model for the LRPs and their effect on survival. It possesses properties consistent with analysis by DC and regression. A viable measure of association can be derived by studying the interaction term between the ligand and the receptor through a survival time regression.

Simulation Studies

Power to detect signaling

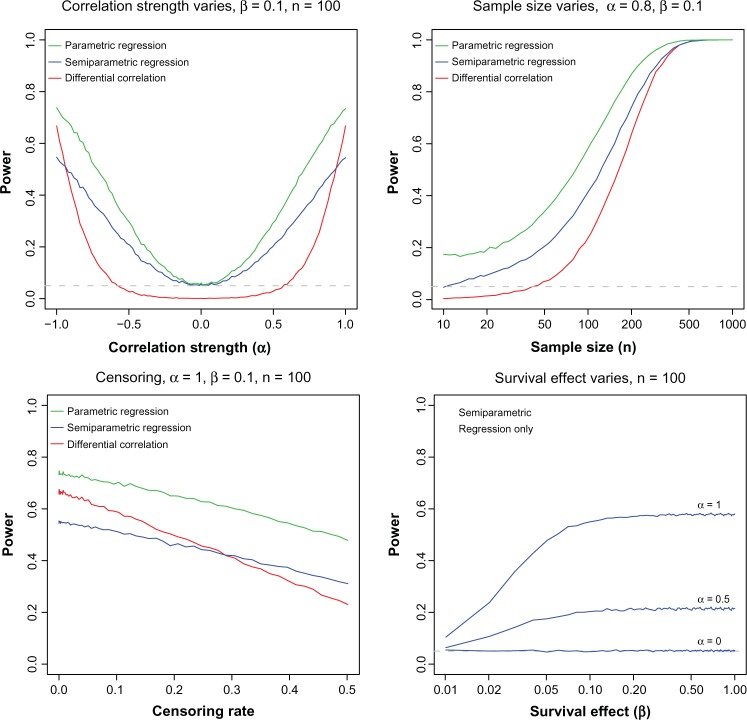
We consider the power of an activation regression-type model and a standard DC analysis to identify the presence of an active LRP. The DC algorithm is a single test statistic based on Fisher’s transformation and standard normal theory (see the Appendix for details). We test both Cox PH regression and Weibull parametric regression (PR), expecting the latter to be competitive with the parametric DC model. There are three parameters to vary: α the strength of correlation induced by activation, β the effect of activation on survival, and n the sample size. A total of 10,000 simulations were performed for each scenario. A sufficient number of simulations were done to avoid needing standard errors. The results are shown in Figure 2.

Figure 2.

Power and sample size simulations demonstrate the sensitivity to α and n for DC, semiparametric activation regression, and parametric activation regression, and the sensitivity to β of the semiparametric activation regression under a patient-specific activation scenario. Power at different censoring rates is given for each model.

As the sample size increases, the ordering and shape are as we would expect. Specifically, the PR performs better than semiparametric regression and both are more powerful than the DC method. As the sample size gets very large (n = 1000), the models perform about the same with powers near 1. In practice, such large sample sizes are not always available. Hence, a model should be chosen that performs the best for smaller sample sizes. We selected n = 100 as a realistic sample size for further studies.

For α = 1, α = 0.5, and α = 0, the survival effect was varied for the semiparametric model. We omitted the other models for clarity. As β grows from 0, it seems to reach an equilibrium power between 0.05 and 0.1 for each value of α. |β| = 0.1 is very small for a one standard deviation change in x, so it seems that the value of β does not matter as much as α or n. Hence, the power of our models depends more on sample size and α than on β. The outperformance of the semiparametric and PR models over the DC model for the majority of α values and sample sizes supports the superiority of the activation regression model over other models.

Correlation has a strong impact on the power. The power of the DC model is not significant for small α values (−0.5 < α < 0.5). α = 0 represents the null hypothesis. The tails of α matter for DC; it is only the superior model near −1 and 1. Loss of power for the semiparametric model is expected; however, it is important to note that it outperforms DC model at most levels. The PR model maintains the highest power for all values of α between −1 and 1. This demonstrates that DC is a flawed model.

Effect of censoring on power

We consider the power of each model as a function of increasing censoring rate. We analyze the effect of censoring on the three models at parameter values of α = 1.0, β = 0.8, and n = 100. These parameter values reflect values where α and β reach maximum power and a realistic effect size. In all, 10,000 simulations are performed for each set of parameter values. Note that censored data are handled naturally by the survival analysis methods. DC analysis has no equivalent, so it must analyze complete observations, ie, patients for whom an event is observed. Therefore, we expect DC analysis to be highly sensitive to censoring.

Figure 2 (lower right) shows the power of each model as the censoring rate increases. PR consistently outperforms the DC and semiparametric regression models across the varying censoring rates. For censoring rates of about 0.3 and above, the semiparametric regression model outperforms the DC model. All three models decrease as the censoring rate increases; however, the DC model decreases at a greater rate than the semiparametric regression model and the PR model. The uncensored data have a power of 0.67, 0.55, and 0.73 for the DC, semiparametric regression, and PR models respectively. The DC, semiparametric regression, and PR models have powers of 0.23, 0.31, and 0.48, respectively, at a censoring rate of 0.5.

It is clear that DC is most affected by censoring. Results from before are neutral or favor the activation model in uncensored data. Therefore, we expect censoring will magnify the superiority of activation regression models over DC models.

Correlation of activation of multiple pairs

Suppose that the activation level Z corresponds to the activation of several LRPs simultaneously. This corresponds to a multivariate signaling phenotype where several pairs act together. In particular, consider independently drawn pairs k = 1, 2, …, K, where cor(X_Lk, X_Rk) = αΨ(Z) with a survival time generated by log Y = β₀ + β₁Z + σε. If we fit a linear model, $\log Y={\gamma }_0+{\displaystyle {\sum }_{k=1}^K{X}_{LK}{X}_{RK}+\delta }$, using the interactions as predictors, we conjecture that the linear estimate, ${\widehat{\eta }}_K={{\displaystyle {\sum }_{k=1}^K\widehat{\gamma }}}_k{X}_{LK}{X}_{RK}$, is correlated with the unobserved activation level Z. If so, ${\widehat{\eta }}_K$ can serve as a surrogate measure of activation.

We evaluated the degree to which a multivariate model using these pairs is able to recover the unobserved activation level by simulation. Again, β₀ = log(18), β₁ = 1, and we draw n = 100 for 1000 simulations under the patient-specific scenario. Figure 3 (left) plots the correlation between Z and ${\widehat{\eta }}_K$ for α = 0.4, selected to produce about 80% power (at n = 1000) to detect a single interaction. Because we expect any linear model to improve as we add predictors (as K increases), we compare this curve to one where α = 0.01 represents noise. There is a significant difference between the two curves, so we conclude that the activation level can be estimated given a sufficient number of active pairs.

Figure 3.

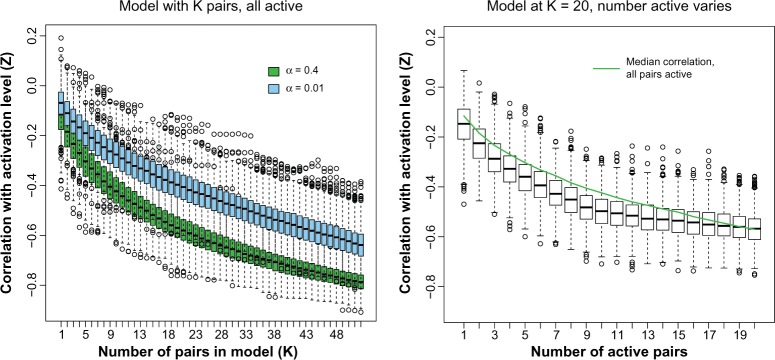
Estimation of latent activation by multiple LRPs as a function of the number of active pairs (left) and as a function of noise variables added to the model (right).

It is unrealistic to assume that we know a priori which pairs are active (ie, which pairs follow the bivariate normal correlation model). Consider the K = 20, α = 0.4 case where the overall correlation between Z and ${\widehat{\eta }}_K$ is close to r = −0.62. Holding the number of pairs in the model at 20, we varied the number of pairs that are truly active substituting noise vectors for the inactive pairs. Figure 3 (right) demonstrates that correlation remains relatively unaffected for this model versus the models fit for the true number of active pairs.

Taken together, the result implies that a two-step process may be possible: first, we may quickly screen an unselected set of pairs to estimate the per-patient activation level and, second, verify the association of individual pairs with the estimated activation level to identify the active set.

Data Analysis

Ovarian cancer is the leading source of death because of gynecologic cancer.⁸ This is due in part to the fact that patients rapidly develop resistance to primary chemotherapies and remain in a phase of palliative care where alternative, targeted therapies may have an effect.⁹ In particular, bevacizumab, an anti-angiogenic therapy targeting vascular endothelial growth factor A (VEGFA), is developing as an option to augment primary therapy.^10,11 Thus, we might consider what other LRPs may be associated with prognosis in ovarian cancer to find candidate targets for therapy.

In this analysis, we consider gene expression data from the Cancer Genome Atlas (TCGA) ovary project, which as been measured on Affymetrix U133A arrays (note that the TCGA study uses three different platforms, and we have selected the Affymetrix version for analysis as it is most complete and straightforward to analyze by reproducible bioinformatic workflows). These data have been processed by the robust multi-array analysis (RMA)¹², aggregated at the gene name level by choosing the brightest spot, and scaled and centered across 503 TCGA patients. In addition, we have a validation data set from an Australian observational study of ovarian cancer¹³ (GEO: GSE9899) using an equivalent Affymetrix array with which we can conduct an independent evaluation of our findings. Throughout, we consider PFS (the time from surgery to the progression or recurrence of disease or death, whichever occurs first) as the clinical outcome and employ the less-powerful, but more common semiparametric Cox PH regression model. A hybrid approach might be used (given below): selection of interesting pairs by the powerful DC model and follow-up by activation modeling.

We examined a known set of LRPs taken from the Database of Ligand-Receptor Partners,⁵ where 162 ligands and 131 receptors accounting for 419 interacting pairs were present on the array. We added the KEGG pathways,¹⁴ hsa04060 (cytokines/chemokines), hsa04512 (cell adhesion molecules), and hsa04514 (ECM interactions), to this set to update the database for recent discoveries. In total, there are 475 pairs (200 ligands, 166 receptors) for consideration after verifying the ligand/receptor functions (Supplementary Table 1).

A key difference between the regression and DC approaches is that we can incorporate multiple LRPs into a multivariate model. We performed screening of all 475 pairs and found 27 LRPs that are significantly associated with PFS (unadjusted screening P < 0.05) from this set. We considered model building. We built stepwise models using Akaike information criterion (AIC) and the Bayesian information criterion (BIC). The former selects 21 pairs in a multivariate Cox PH regression model and the latter 8 pairs. We also considered the unpenalized model with all 27 pairs, and the lasso-penalized solution selected 26 of 27 pairs following five-fold cross-validation to select the tuning parameter. We omit discussion of the lasso solution as it is not appreciably different from the full model.

Of these three models (full fit, AIC, BIC), the BIC model with eight predictors fit to the TCGA data was able to produce predicted risk scores associated with prognosis in the independent cohort (HR = 1.3, 95%CI: 1.03–1.64, P = 0.028). These eight LRPs are PVRL3∼PVRL1, VEGFA∼NRP1, FGF1∼FGFR4, TGFB1∼TGFBR3, BMP5∼BMPR1B, IL7∼IL7R, CCL4∼CCR8, and TNFSF14∼TNFRSF14 (Table 1). Each of these is significant in the fitted model (score test P < 0.02) with strong effects. Descriptions are taken from NCBI’s gene resource (http://www.ncbi.nlm.nih.gov/gene/). The reported P-value is the score test from the fitted multivariate BIC model. The overall significance is given below.

Table 1.

Multivariate model, BIC selection.

	HR (95%CI)	P-VALUE	#FOLDS VALIDATED	RELEVANCE
PVRL3~PVRL1	1.20 (1.10–1.30)	0.00084	4	Nectin family adhesion molecules
VEGFA~NRP1	1.20 (1.10–1.40)	0.00110	4	Pro-angiogenic signaling target of bevacizumab
FGF1~FGFR4	0.86 (0.77–0.96)	0.00940	2	Fibroblast growth factor family targeted therapy candidate17
TGFB1~TGFBR3	0.85 (0.77–0.94)	0.00190	2	TGFβ signaling
BMP5~BMPR1B	0.84 (0.73–0.97)	0.01700	3	TGFβ signaling
IL7~IL7R	0.83 (0.74–0.93)	0.00140	4*	T cell development
CCL4~CCR8	0.78 (0.65–0.94)	0.00760	2*	T cell migration
TNFSF14~TNFRSF14	0.75 (0.63–0.89)	0.00110	5	TNF-receptor signaling

Notes: Discovery data set: likelihood ratio test P = 4.06e–12, n = 503, and number of events = 361. Independent data set: likelihood ratio test P = 0.0255, n = 238, and number of events = 184.

^*Selected as a predictor if trained on independent data.

As we noted above, bevacizumab, which targets VEGFA, has recently shown promise in primary ovarian cancer therapy.¹⁰ In addition, both VEGFA and TGFB1 were shown to induce immunosuppressive responses; targeting these factors may aid in preventing tumor progression.¹⁵ Zaid and colleagues demonstrated that overexpression of FGF1∼FGFR4 indicated poor prognostic results and inferred that targeting this LRP may lead to better survival outcomes.¹⁶

We considered a sensitivity analysis by conducting five-fold cross-validation, repeating model selection in each fold and predicting on the withheld one-fifth of the data (approximately 100 patients). The result is shown in Table 1 for BIC and the remainder in Supplementary Table 2. There we have tabulated the number of times the AIC, BIC or full-fit model selects each of the 27 pairs and the corresponding hazard ratio and significance of the predictions in the withheld subset. The number of folds validated refers to the number of times an LRP was selected out of the five-fold cross-validation processes. In this sense, TNFSF14∼TNFRSF14 was a strong result, selected in every fold in each model. Similarly, IL7∼IL7R, VEGFA∼NRP1, and PVRL3∼PVRL1 were selected in all but one fold in every case. Note that all of these were present in the BIC model.

In the independent data set, only CCL4∼CCR8 and IL7∼IL7R are significant in this set of eight pairs. However, fitting this two pair model into the TCGA cohort and testing in the independent cohort yields a significant association (HR = 3.14, 95%CI: 1.56–6.32, P = 0.0014) as well as vice versa (HR = 2.38, 95%CI: 1.57–4.69, P = 0.00038). In this sense, these two pairs are the strongest associations; they both reflect immune-related processes likely related to general chemotherapy response.¹⁸

We now consider the estimated activation level fit using the TCGA data. In the independent data set, the predicted activation shows that the 27-pair model is correlated with the 2-pair model (r = 0.43, 95%CI: 0.33–0.54) as is the 8-pair BIC model (r = 0.55, 95%CI: 0.46–0.63). So as in the simulations, little is lost by including extra predictors. The activation level is fairly prognostic when stratifying on the median level for the 27-pair (16 vs. 14 months PFS, P = 0.083) and strongly for the 8-pair model (19 vs. 13 months, P = 0.0043) and 2-pair model (19 vs. 13 months, P = 0.0075).

Discussion

In this article, we have developed a model that links correlation between a signaling ligand and receptor pair to prognosis. Because this association can be seen through statistical interactions, the analysis is amenable to multivariate regression and is therefore useful for practical genomic data analysis. The novelty of this activation model approach lies in the connection between correlation and survival. This connection may be patient specific – different patients can have different correlation levels – and it does not rely on dichotomizing the population wasting statistical power on estimating the correlation instead of modeling the association with survival. Further, we find the power of the semiparametric Cox PH regression competitive with DC analysis, especially in the context of right-censored data.

Because standard regression model building usually searches for main effects before interactions, it is likely that prior studies have overlooked useful LRP associations. We have shown that main effects can be insignificant versus the statistical interaction. Throughout the article, we have referred to the interaction term in the survival regression model. While the proposed model building and testing does not include the main effect terms, classically, these are included to account for rescaling the expression variables. In this situation, we note that the main effects are expected to be uncorrelated with survival by construction.

We have demonstrated the ability of multiple LRPs to estimate an underlying activation level, under the assumption that they are driven by a singular process of activation. In our data analysis, we have shown that this level is a useful tool for prognostic stratification and meaningful biological and translational hypothesis generation.

The activation model makes little assumption on the survival time distribution. While we employed log-normal survival times throughout this analysis, we have little reason to believe that the form of the hazard will dramatically affect the results for the semiparametric model. The PR may be viewed as an exercise in model misspecification.

We see this activation model as a tool that may be deployed along with other correlation-based bioinformatic techniques. Our data illustration highlights how multiple LRPs can be considered together. By focusing on LRPs that are highly likely to be targetable or to have an approved or pre-clinical compound, this type of analysis has a strong potential for clinical benefit.

Supplementary Material

Supplementary Table 1. This table lists the 475 LRPs considered for screening after verifying the ligand/receptor functions.

Supplementary Table 2. This table shows the results of five-fold cross-validation for the AIC, BIC and full-fit models.

Appendix

Let ${\{(L_k,R_k)\}}_{i=1}^{n_k},k=1,2$, be a random sample of ligand and receptor expression from a bivariate normal distribution with mean μ, and variance Var (L_k) = Var (R_k) = σ² and covariance Cov (L_k, R_k) = σ²pk. Denote the usual Pearson correlation as r_k, k = 1, 2, where Fisher’s transform is F(x) = 2⁻¹ In ((1+ x)/(1− x)). Then we have that

$$F(r_k)~N\left(\frac{1}{2}\log \left(\frac{1+p_k}{1-p_k}\right),\frac{1}{n_k-3}\right)$$ (3)

Under H₀: ρ₁ = ρ₂, it holds that

$$F(r_1)~F(r_2)~N\left(0,\frac{1}{n_1-3}+\frac{1}{n_2-3}\right)$$ (4)

so that

$$T=\sqrt{\frac{(n_1-3)(n_2-3)}{n_1+n_2-6}}[F(r_1)-F(r_2)]~N(0,1)$$ (5)

can be controlled by Pr(|T| ≥ z_α/2) = α, where z_α/2 is the appropriate normal quantile.