Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Dec 30;31(3):1086–1094. doi: 10.1021/la504082x

Phase Separation Behavior of Mixed Lipid Systems at Neutral and Low pH: Coarse-Grained Simulations with DMD/LIME

Emily M Curtis †, Xingqing Xiao †, Stavroula Sofou ‡, Carol K Hall †,*
PMCID: PMC4310635  PMID: 25549801

Abstract

graphic file with name la-2014-04082x_0003.jpg

We extend LIME, an intermediate resolution, implicit solvent model for phospholipids previously used in discontinuous molecular dynamics simulations of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) bilayer formation at 325 K, to the description of the geometry and energetics of 1,2-distearoyl-sn-glycero-3-phospho-l-serine (DSPS) and 1,2-dihenarachidoyl-sn-glycero-3-phosphocholine (21PC) and mixtures thereof at both neutral and low pH at 310 K. A multiscale modeling approach is used to calculate the LIME parameters from atomistic simulation data on a mixed DPPC/DSPS system at different pH values. In the model, 17 coarse-grained sites represent DSPS and 18 coarse-grained sites represent 21PC. Each of these coarse-grained sites is classified as 1 of 9 types. LIME/DMD simulations of equimolar bilayers show the following: (1) 21PC/DSPS bilayers with and without surface area restrictions separate faster at low pH than at neutral pH, (2) 21PC/DSPS systems separate at approximately the same rate regardless of whether they are subjected to surface area restrictions, and (3) bilayers with a molar ratio of 9:1 (21PC:DSPS) phase separate to form heterogeneous domains faster at low pH than at neutral pH. Our results are consistent with experimental findings of Sofou and co-workers (Bandekar et al. Mol. Pharmaceutics, 2013, 10, 152–160; Karve et al. Biomaterials, 2010, 31, 4409–4416) that more doxorubicin is released from 21PC/DSPS liposomes at low pH than at neutral pH, presumably because greater phase separation is achieved at low pH than at neutral pH. These are the first molecular-level simulations of the phase separation in mixed lipid bilayers induced by a change in pH.

Introduction

Phospholipids are amphiphilic molecules that spontaneously form bilayers in aqueous solution to minimize the interaction between their hydrophobic tails and to maximize the interaction between their hydrophilic heads. In recent years, scientists have been working to exploit the tunable properties of mixed lipid systems for a range of applications including imaging,1 biosensors,2,3 and membrane trafficking.4,5 In particular, mixed lipid systems are being used as novel liposomal delivery carriers for drugs,6,7 vaccines,8 genes,9,10 and antimicrobial agents.11,12 While scientists have successfully demonstrated that liposomal formulations improve drug efficacy,13,14 research efforts are still dedicated to optimizing their structure and function. For example, Karve and co-workers showed that liposomes composed of mixed lipid membranes could become permeable to encapsulated drug molecules in response to a decrease in pH.15 Mixed lipid systems are also being used to create temperature-sensitive liposomes that can rapidly and efficiently release drug molecules in response to heat.16−19 In order to fully realize the potential of these new technologies, a better understanding of the structure and interactions between lipids on a molecular level under various physiological conditions is needed. This would enable researchers to design and develop liposomes with optimal properties to release drug molecules in response to specific stimuli. An approach commonly used to gain insight into the behavior of such systems on a molecular level is computer simulation.

In a previous paper, we demonstrated how computer simulations of lipid systems can complement experimental work by providing detailed molecular-level information regarding their dynamics and self-assembly.20 In that work, we introduced LIME (lipid intermediate resolution model), a new implicit solvent lipid force field for use with discontinuous molecular dynamics (DMD), that enabled the rapid simulation of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) lipids in water. The structural properties of the DPPC bilayer formed during our LIME/DMD simulations, including the area per lipid, bilayer thickness, bond order, and mass density profiles, were in agreement with experimental observations or atomistic simulation results.

In this article, we take a multiscale modeling approach to expand LIME to include parameters for (1) 1,2-dihenarachidoyl-sn-glycero-3-phosphocholine (21PC) and (2) 1,2-distearoyl-sn-glycero-3-phospho-l-serine (DSPS) at 310 K. We demonstrate how discontinuous molecular dynamics (DMD) simulations with this expanded LIME force field can be used to model the behavior of lipid systems containing mixtures of different molar ratios of DSPS and 21PC over long time scales at neutral pH and at a pH of 5.5. Throughout this article, we define a neutral pH as 7.0–7.4 and low pH as <5.5. We show that LIME/DMD simulations can be used to study the phase separation of mixed lipid systems into heterogeneous domains on a molecular level. Our results are the first reported simulations of the pH-dependent phase separation of mixed lipid bilayers.

A number of different approaches to modeling mixed lipid systems with simulations have been described in the literature. Various levels of detail are used in these models, which can be divided roughly into two categories: high- and low-resolution models. High-resolution, or atomistic, models are based on a realistic representation of membrane geometry and energetics and typically account for the motion of every atom, including every solvent atom. Jiang and co-workers performed GROMACS21 atomistic simulations on bilayer ribbons containing dimyristoylphosphatidylcholine (DMPC), dihexanoylphosphatidylcholine (DHPC), and didecanoyl PC (DDPC) to investigate how each species partitions between the flat and curved microenvironments of the bilayer and the role DHPC plays in stabilizing the bilayer edge.22 In another study, Hall and co-workers performed atomistic molecular dynamics simulations to investigate the role of glycolipids in lipid rafts; systems of galactosylceramide (GalCer), cholesterol (CHOL), palmitoyloleoylphosphatidylcholine (POPC), and palmitoyl-sphingomyelin (PSM) were simulated using GROMACS.23 Addition of GalCer increased the thickness of the raft membranes and induced changes in the lateral diffusion of raft lipids, but it did not influence the average area per lipid or the lipid conformation order.23 In another atomistic simulation, Pandit and co-workers studied mixed bilayers containing a 5:1 ratio of DPPC and DSPS in NaCl electrolyte solutions to learn how DPPC and DSPS interact to form complexes.24 GROMACS was used to perform all simulations based on force field parameters from the work of Berger.24 These simulations showed that NH···O and CH···O hydrogen bonding between lipids serves as the basis of interlipid complexation and that DPPC alone is less likely to form interlipid complexes than in the presence of bound ions or DSPS.24

Low-resolution models, which are based on a simplified representation of molecular geometry and energetics, have also been used to study the behavior of mixed lipid systems. For example, Illya and co-workers developed a low-resolution model designed for use with dissipative particle dynamics simulations to study the domain formation and the material properties of a two-component amphiphilic bilayer membrane.25 In this solvent-explicit model, the amphiphile geometry was chosen to represent the general shape of a typical phospholipid. The amphiphile H3(T6)2 was represented by 3 head spheres and 2 tails, each composed of 6 spheres, and the amphiphile H3(T8)2 was represented by 3 head spheres and 2 tails, each composed of 8 spheres.25 The interaction parameters for the amphiphiles were chosen to mimic the properties of lipid membranes, not calculated from atomistic simulations of amphiphiles.25 The authors calculated the area stretch modulus and bending rigidity of the mixed amphiphilic bilayers and vesicles but could not compare their results directly to any experimental observations on a specific lipid mixture since the amphiphiles did not represent any specific lipids.

Another way to model mixed lipid systems in simulations is to use intermediate-resolution (coarse-grained) models, which represent the geometry and energetics of lipids at a level of detail that is in between that of high- and low-resolution models. This allows for the simulation of specific lipids while requiring shorter simulation times than that for atomistic models. In coarse-grained models, a single interaction site represents several atoms. This reduces the total number of sites whose trajectories must be calculated and helps to increase the speed of the simulation. One example of an intermediate-resolution explicit-solvent model is that of Faller and Marrink.26 In this model, distearoylphosphatidylcholine (DSPC) and dilauroylphosphatidylcholine (DLPC) are represented by 14 and 10 coarse-grained sites, respectively. The coarse-grained sites interact via a Lennard–Jones potential, and a Colulomb interaction is used to model electrostatics.26 Lipid mixtures composed of DLPC and DSPC were simulated to study the phase separation that occurs between these two lipids at phase transition temperatures such that the longer lipid enters the gel phase and the shorter lipid remains in the fluid phase.26 Simulations were performed using GROMACS with the interaction parameters previously described by Marrink and coworkers.27 All simulations were started from a bilayer composed of randomly assigned DSPC and DLPC lipid. Results showed that the higher the ratio of the number of longer lipids (DSPC) to the number of shorter lipids (DLPC), the higher the gel–fluid transition temperature. In another intermediate-resolution explicit-solvent model, Risselada and Marrink performed simulations of the spontaneous separation of a randomized mixture composed of dipalmitoyl-phosphatidylcholine (diC16-PC), dilinoleyl-phosphatidylcholine (diC18:2-PC), and cholesterol into liquid-ordered and -disordered phases.28 Simulations of a planar membrane composed of approximately 2000 lipid molecules and a liposome composed of approximately 3000 lipid molecules were performed. In this model, on average, 4 heavy atoms were represented by a single coarse-grained site, and approximately 3 heavy atoms were used to represent the rings in cholesterol.28 The simulations were performed with the GROMACS simulation package and the MARTINI CG force field, version 2.0.29

Intermediate-resolution implicit-solvent models of mixed lipid systems have also been described in the literature. For example, Lu and Voth used a multiscale coarse-graining approach to develop a solvent-free coarse-grained model for a mixed bilayer composed of dioleoylphosphatidylcholine (DOPC) and dioleoylphosphatidyethanolamine (DOPE).30 In this model, DOPC and DOPE are each represented by 15 coarse-grained sites. The results of the multiscale coarse-grained model, including radial distribution functions, bilayer thickness, and order parameters, show good agreement with atomistic results.30

Our motivation for studying 21PC/DSPS lipid systems is experimental work by Sofou and co-workers aimed at developing liposome-based drug delivery devices for the treatment of cancer.31,32 They examined the phase separation behavior of pH-triggered liposomes composed of cholesterol and two different types of phospholipids: 21PC phospholipids, which have a neutral headgroup at both neutral (pH 7.4–7.0) and endosomal pH (pH 5.5–5.0), and DSPS phospholipids, which have a negatively charged headgroup at neutral pH and a neutral headgroup at endosomal pH.31,32 They showed that at neutral pH the vesicles were much less permeable to encapsulated drug molecules than at endosomal pH. At endosomal pH, the cholesterol and 21PC and DSPS lipids allowed much more of the encapsulated drug molecules to leak out of the liposome than at neutral pH. This observation forms the basis of Sofou and co-workers proposed liposomal-based drug delivery scheme in which liposomes composed of cholesterol, 21PC, and DSPS are used to transport cancer drugs throughout the body at neutral pH. When the liposomes reach the endosome in cancer cells, the decrease in pH triggers the formation of heterogeneous domains and the encapsulated drug molecules leak out of them.31,32 Sofou’s pH-tunable liposomes have additional features including antibodies to target cancer cells.

In this work, we present the results of simulations of 21PC/DSPS bilayers at neutral and low pH. Our goal was to show that the expanded version of our LIME/DMD force field could accurately model the phase separation behavior of these bilayers at both neutral and low pH. We are currently running simulations of liposomes composed of 21PC/DSPS, that encapsulate drug molecules at neutral and low pH. We hope to soon report the results of these simulations, which will be the ultimate test of the accuracy of our LIME/DMD model for our mixed lipid system.

In this article, we describe the expansion of LIME, the implicit-solvent coarse-grained model previously used to simulate the spontaneous formation of DPPC bilayers at 325 K, to 21PC and DSPS lipids at 310 K.20 We analyze the extent of phase separation that occurs during simulations at both neutral and low pH in 21PC/DSPS bilayers containing 150 lipids and molar ratios of 1:1 or 9:1. The LIME geometrical and energetic parameters for 21PC and DSPS at low pH and 310 K are calculated using a multiscale modeling approach based on evaluating radial distribution functions obtained from an atomistic simulation of a fully hydrated bilayer composed of 64 DPPC lipids and 64 protonated DSPS lipids performed with the GROMACS simulation package and the GROMOS96 53a6 force field.21,33,34 The same method is used to extract parameters at neutral pH; the only difference is that the DSPS lipids are unprotonated.

Highlights of our results include the following: LIME/DMD simulations of equimolar bilayers composed of 21PC/DSPS phase separate into heterogeneous domains faster at a low pH value than at a neutral pH value regardless of whether surface area restrictions are imposed. In addition, without any surface area restrictions, bilayers composed of a 9:1 molar ratio of 21PC/DPPS also phase separate faster at low pH than at neutral pH. This observation is supported by experimental data from the Sofou lab. According to Sofou and co-workers, drug molecules encapsulated within liposomes composed of 21PC and DSPS escape from liposomes faster at low pH than at neutral pH.31,32 This is thought to be a consequence of having faster heterogeneous domain formation at low pH than at neutral pH.

Methods and Model

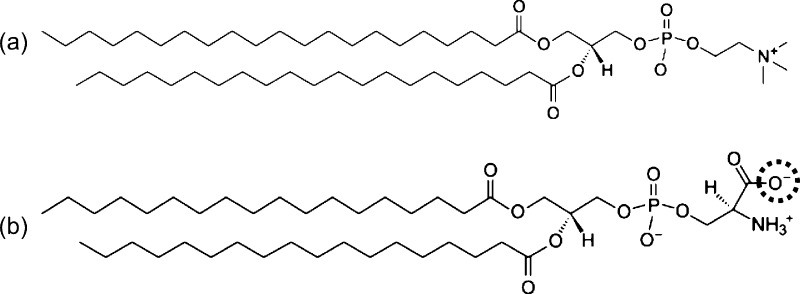
In LIME, 9 different coarse-grained types (I–IX) are used to represent the groups of atoms that make up the 21PC and DSPS molecules. 21PC is composed of a polar headgroup that includes a choline, phosphate, and two ester linkages and two nonpolar hydrophobic acyl tails. DSPS is composed of a headgroup that includes carboxyl, amine, and phosphate groups and two ester linkages and two nonpolar hydrophobic acyl tails. At neutral pH, the net charge carried by the DSPS headgroup is negative. This negative charge causes electrostatic repulsion between the DSPS lipids, which helps to prevent their phase separation.31 At a pH of approximately 5.5, the carboxyl group on DSPS becomes protonated and loses its negative charge.35 When the DSPS molecules lose their negative charge, the electrostatic repulsion between these lipids stops, allowing hydrogen bonds to form between their protonated amino groups and deprotonated phosphate groups on the head groups.31,36 Therefore, at low pH, DSPS lipids have a very strong attraction for each other. Figure 1 shows the structure of a (a) 21PC lipid and (b) DSPS lipid at neutral pH. At low pH, the oxygen atom that is circled becomes protonated.

Figure 1.

Figure 1

Open in a new tab

Structure of (a) 21PC and (b) DSPS at neutral pH. At low pH, the oxygen atom in the dotted circle becomes protonated.

Figure 2 illustrates the coarse-graining of (a) a DSPS molecule from 57 united atoms to 17 coarse-grained sites and (b) a 21PC molecule from 60 united atoms to 18 coarse-grained sites. In LIME, each coarse-grained site is assigned a different coarse-grained type, which is represented by a unique color. This figure and all other figures depicting lipid molecules throughout the article were generated with Visual Molecular Dynamics (VMD).37 Type Ia and Ib (black) are used to represent the unprotonated and protonated, respectively, carboxyl headgroup (site 1) on DSPS. Type II (magenta) is used to represent the amine group on DSPS. The phosphate groups on DSPS and 21PC are represented by type III (yellow) and type IX (yellow); we represent these phosphate groups with different types because the energy parameters calculated for these coarse-grained sites were significantly different from each other and we therefore felt it was important to treat them as unique coarse-grained types. Ester coarse-grained sites are assigned types IV (red) and V (orange), respectively. Two coarse-grained types for the ester are needed because coarse-grained III has one more carbon and hydrogen atom than coarse-grained type IV. Coarse-grained type VI (cyan) is used to represent the tail sites (each contains 3 carbons and 6 hydrogens) of DSPS and 21PC. Coarse-grained type VII (gray) is assigned to the terminal tail groups of 21PC and DSPS, representing 2 carbon and 5 hydrogen atoms. Finally, coarse-grained type VIII (purple) represents the choline entity on 21PC. Table 1 lists the atoms included in each coarse-grained site, the type assigned to each coarse-grained site, and the mass of each coarse-grained site.

Figure 2.

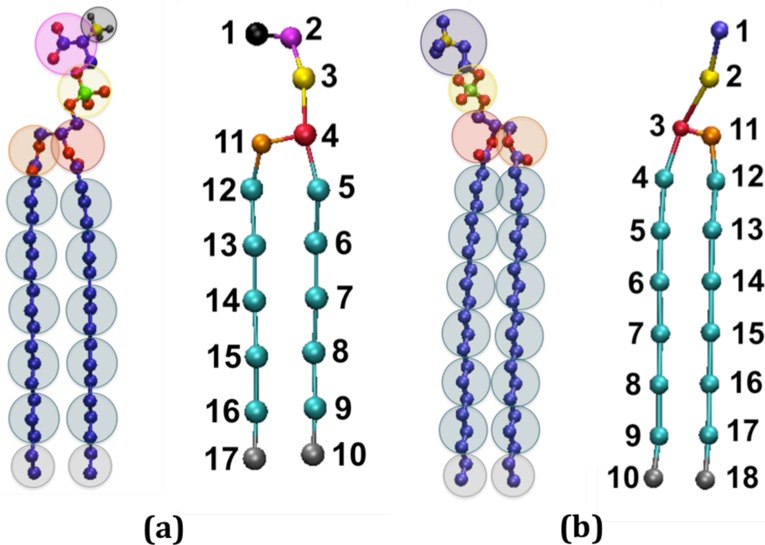
Figure 2

Open in a new tab

United atom and coarse-grained representations of (a) DSPS and (b) 21PC. The color scheme is black (negatively charged carboxyl group, type Ia; protonated carboxyl group, type Ib for DSPS site 1); magenta (amine group, type II for DSPS site 2); yellow (phosphate group, type III for DSPS site 3); red (ester group, type IV for DSPS site 4 and 21PC site 3); orange (ester group, type V for DSPS site 11 and 21PC site 11); cyan (alkyl tail groups, type VI for DSPS sites 5–9 and 12–16 and for 21PC sites 4–9 and 12–17); gray (terminal tail groups, type VII for DSPS sites 10 and 17 and for 21PC sites 10 and 18); purple (choline entity, type VIII for 21PC site 1); and yellow (phosphate group, type IX for 21PC site 2).

Table 1. Type, Number of Atoms, and Mass for All of the Coarse-Grained Sites in the LIME Representation.

CG type CG type color CG site atoms per CG type mass of CG type (amu)
Ia black DSPS 1 COO– 44.0
Ib black DSPS 1 COOH 45.0
II magenta DSPS 2 C2H3NH3 44.1
III yellow DSPS 3 PO4 95.0
IV red DSPS 4, 21PC 3 C3HO2 71.1
V orange DSPS 11, 21PC 11 C2H2O2 58.0
VI cyan DSPS 5–9 and 12–16 C3H6 42.1
    21PC 4–9 and 12–17    
VII gray DSPS 10 and 17 C2H5 29.1
    21PC 10 and 18    
VIII purple 21PC 1 C5H13N 87.2
IX yellow 21PC 2 PO4 95.0
Open in a new tab

The simulation method used in this article is the discontinuous molecular dynamics (DMD) algorithm, which is a very fast alternative to traditional molecular dynamics simulation that is applicable to systems of molecules interacting via discontinuous potentials, e.g., hard-sphere and square-well potentials.38,39 For this reason, all of the inter- and intramolecular interactions in our lipid model are represented by a combination of hard-sphere and square-well potentials, as opposed to the Lennard–Jones, Coulombic, and harmonic potentials found in traditional molecular dynamics simulations. A hard sphere is an impenetrable solid sphere; a square-well is a hard sphere surrounded by an attractive well. Expressions for the hard-sphere (HS) and square-well (SW) potentials between spheres i and j are, respectively

graphic file with name la-2014-04082x_m001.jpg 1
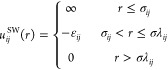graphic file with name la-2014-04082x_m002.jpg 2

where r is the distance between spheres, σij is the hard sphere diameters, σλij is the well diameter, and εij is the well depth. These parameters define the strength of the interaction between the coarse-grained spheres. Unlike continuous potentials, such as the Lennard–Jones potential, discontinuous potentials exert forces only when particles collide. This makes the simulation an efficient event-scheduling algorithm, which allows sampling of longer time scales and larger systems than that with traditional molecular dynamics.

A DMD simulation proceeds in the following way. Molecules are placed in an initial configuration consistent with excluded volume and angular constraints. Initial velocities are assigned based on a Maxwell–Boltzmann distribution about the desired simulation temperature. Particle trajectories are followed by calculating the time between each collision and advancing the simulation to the next event. Types of events include a collision between two hard spheres, a bond event when the distance between two bonded spheres reaches a minimum or maximum limit, and square-well events when two spheres enter (capture), unsuccessfully attempt to escape (bounce), or successfully leave (dissociation) a square well.38−41

In all LIME/DMD simulations, the simulation temperature is expressed in terms of the reduced temperature T*

graphic file with name la-2014-04082x_m003.jpg 3

where kB is Boltzmann’s constant, T is the temperature, and ε* is the reference interaction strength.42 For this work, a T* of 0.20 was used. This reduced temperature was chosen because it gave the most reasonable results for the bilayer assembly; at lower temperatures, the particles get kinetically trapped, and at higher temperatures they have too much kinetic energy.

The coarse-grained parameters in LIME were obtained using a multiscale modeling technique. Multiscale modeling is a method in which several atoms are grouped into a single coarse-grained site and the parameters used to represent the behavior of this coarse-grained site are extracted from atomistic simulations. Data used to calculate the LIME parameters was obtained by running united-atom explicit-solvent simulations at T = 310 K using the GROMACS simulation package,21,33 version 4.5.4, along with the GROMOS96 53a634 force field. Since the Sofou Lab conducted experiments at 310 K to study how liposomes behave in the body, we parametrized our model from GROMACS simulations at 310 K. Our GROMACS simulations consisted of bilayers composed of DPPC and DSPS, whereas our LIME/DMD simulations were of 21PC/DSPS bilayers. LIME parameters for the 21PC head groups were set equal to those of the DPPC head groups since 21PC and DPPC have identical head groups. Similarly, the 21PC tail group sites were parametrized from the alkyl tail groups of DPPC and DSPS.

To obtain the partial charges for DPPC and DSPS (at neutral and low pH) for our GROMACS simulations, we performed quantum mechanical (QM) calculations using the GAUSSIAN09 software package.43 To facilitate the QM calculations, each lipid molecule (DPPC, DSPS neutral pH, and DSPS low pH) was split into two parts. A methyl group was used to cap each of the three head groups, and a NH3PO4 group was used to cap the common tail group. In addition, we calculated partial charges only for the first 3 alkyl groups in each of the tails. The two-stage restrained electrostatic potential (RESP) charge-fitting protocol was performed to calculate the partial atomic charges.44−46 The geometry of each molecule was optimized at the HF/6-31G* level, and the electrostatic potential for each optimized molecule was calculated using the HF/6-31G* basis set.

The LIME low-pH intermolecular σij, σλij, and εij between coarse-grained types I–VI, VIIb, and VIII-X were obtained by analyzing results from a low-pH GROMACS simulation of a mixed bilayer composed of 64 DPPC lipids and 64 DSPS lipids in explicit solvent. The neutral-pH intermolecular values for σij, λij, and εij between coarse-grained types I–VI, VIIa, and VIII-X were calculated from a neutral-pH GROMACS simulation composed of 64 DPPC lipids and 64 nonprotonated DSPS lipids. Each GROMACS simulation was started from an initially homogeneous bilayer in a box with dimensions of 64 × 64 × 90 Å3 and was run at a temperature of 310 K and a pressure of 1.0 bar for 10 ns. Throughout both the neutral- and low-pH simulations, the bilayers remained intact. The net charge of all GROMACS simulation systems was neutralized with the addition of NaCl. The Berendsen thermostat47 was used to keep the temperature constant with a time constant of 0.1 ps. Throughout each GROMACS simulation, the coordinates of each atom were written to an output trajectory file every 1 ps. These output files were used to calculate the centers of mass for each of the coarse-grained sites.

The hard-sphere diameter (σHS) for each pair of interaction sites was determined by locating the smallest non-zero separation between the two sites. The σHS value for a pair of coarse-grained types was calculated by averaging all of the σHS values for pairs of interaction sites with the desired coarse-grained types. The depth of the square-well intermolecular interactions in LIME was calculated from the radial distribution functions collected during the atomistic GROMACS simulations using a one-step Boltzmann inversion approach. (The LIME intramolecular εij values were set to 0, making all intramolecular interactions hard-sphere collisions.) The one-step Boltzmann inversion procedure involves the following steps: (1) the average radial distribution function, g(r), between two nonbonded coarse-grained sites separated by distance r is determined, (2) the potential of mean force is calculated using

graphic file with name la-2014-04082x_m004.jpg 5

and (3) the minimum value of the potential of mean force between the coarse-grained sites, ε, is chosen to be the depth of the square-well potential. Mathematically, ε, is expressed as

graphic file with name la-2014-04082x_m005.jpg 6

where g(r)max is the maximum value of g(r) in the radial distribution function and T is the temperature of the system. If the ε value between two coarse-grained sites is greater than −0.01 eV, then the sites are assumed to have a hard-sphere interaction (ε = 0.0 eV). The ε values for pairs of coarse-grained types were determined by averaging all of the ε values for pairs of interaction sites with the same coarse-grained type.

We chose to use a different procedure for calculating the square-well diameter (σλ) for each pair of interaction sites than the approach described in our previous work. In this new procedure, the second virial coefficient associated with the potential of mean force between coarse-grained sites (which is calculated from atomistic simulations) is set equal to the second virial coefficient for the site–site square-well potential. The second virial coefficient, B2(T), for a system of molecules interacting via a potential u(r) is defined to be

graphic file with name la-2014-04082x_m006.jpg 7

where k is the Boltzmann constant and T is the temperature. If we take u(r) to be the potential of mean force calculated using eq 5, then this becomes

graphic file with name la-2014-04082x_m007.jpg 8

If, instead, we take u(r) to be a square-well potential as given in eq 2, then we obtain the second virial coefficient for a square-well interaction

graphic file with name la-2014-04082x_m008.jpg 9

where bo = 2πσ3/3 and β = −1/(kT).48 We determined the value of σλ for each pair of coarse-grained sites by the following steps. First, we numerically integrated the right-hand side of eq 8 from 0 to 10 Å. We chose to integrate only from 0 to 10 Å because the cutoff radius for our Lennard–Jones interactions in our GROMACS simulations was 10 Å. The g(r) in this step was the same as the g(r) used in determining the σHS and ε values for that pair of coarse-grained types. The square-well B2(T) (eq 9) was set equal to the value calculated from eq 8. The σHS and ε values previously calculated for that pair of coarse-grained sites were used to solve for σλ. Once λ was calculated, it was multiplied by σHS to determine the σλ for a pair of coarse-grained sites. The σλ value for a pair of coarse-grained types was calculated by averaging all of the σλ values for coarse-grained sites with the given coarse-grained types.

The minimum and maximum bond lengths between two bonded coarse-grained sites in LIME were also determined from the GROMACS simulation data using the same method as was used in our previous paper. In LIME, the stiffness of each lipid molecule is maintained by imposing pseudobonds, which limit the fluctuation of coarse-grained sites to the angles and torsional angles observed during the GROMACS simulations. Bond angles are maintained by imposing pseudobonds between all next-nearest neighboring sites. Torsional angles are maintained with pseudobonds between all next–next-nearest neighboring sites. The minimum and maximum pseudobond lengths were determined from the radial distribution functions for the coarse-grained sites in the same manner as that in our previous paper. The bond and pseudobond values calculated from the neutral-pH GROMACS simulations were very similar to those calculated from the low-pH GROMACS simulations. Therefore, for DSPS and 21PC lipids, we choose to approximate the σmin and σmax values for interactions between coarse-grained types at low pH with those calculated at neutral pH.

EMBLEM, a C++ program developed in the Hall research lab, was used to run all LIME/DMD simulations. EMBLEM uses the discontinuous molecular dynamics (DMD) algorithm to simulate the behavior of any type of molecule or mixture of molecules. Any DMD force field parameters can be used with EMBLEM. An Intel compiler was used to compile this code. EMBLEM is run with several efficiency techniques. Work is in progress to parallelize portions of EMBLEM; however, all of the simulations run for this work were done in serial.

Results

LIME/DMD simulations were run to study the behavior of bilayers composed of 21PC/DSPS lipids. Simulations were run on six systems, referred to here as Systems 1–6, which differed in the ratio of 21PC to DSPS lipids, the pH, and simulation box length. The six systems are summarized in Table 2. For each system, four replicate simulations, each composed of a total of 150 lipids, were run at T* = 0.20. Each simulation was started from a preformed bilayer in which the lipids of each species were randomly placed into an area of 60 × 60 Å2. To build each bilayer, the following steps were performed: (1) the phosphate group of a lipid molecule was placed at a random location within the x–y plane at a fixed distance from the bilayer normal (for the top leaflet of the bilayer), (2) a check was run to ensure that the lipid was not overlapping with any other lipid, (3) steps 1 and 2 were repeated until no overlap was detected, and (4) steps 1–3 were repeated for the bottom leaflet of the bilayer. In simulations on Systems 1–4, the bilayers, which spanned an area of 60 × 60 Å2, were placed in the center of a box with dimensions of 120 × 120 × 120 Å3. This was done to prevent the bilayers from interacting with their periodic images. We refer to the bilayers in these systems (1–4) as free surface bilayers because the surface area of these bilayers is free to expand or shrink by any amount. Although interacting with its periodic image would not force a bilayer to occupy a certain area, it might promote the bilayer to span the simulation cell so that the lipids could maximize the number of interactions that they have with each other. In simulations 5 and 6, the length of the simulation cell in the plane of the bilayer was 60 × 60 Å2, which allowed the bilayers to interact with their periodic images, thereby restricting the possible surface area. We chose to include surface area restrictions to ensure that our simulation environment was a reasonably faithful mimic of the experimental conditions in the Sofou lab. In experiments, the osmotic pressure inside liposomes composed of 21PC/DSPS in a solution composed of salt ions prevents the liposomes from shrinking to a large extent. These lipids would behave similarly to those in our simulations with surface area restrictions, i.e., with periodic boundary conditions.

Table 2. Type of Lipids, Molar Ratio of Lipids, pH, Bilayer Plane Box Lengths, and Free Surface versus Periodic Boundary Conditions for Systems 1–6.

system no. lipids molar ratio pH bilayer plane box lengths (Å2)
1 21PC:DSPS 1:1 neutral 120 × 120 (free surface)
2 21PC:DSPS 1:1 low 120 × 120 (free surface)
3 21PC:DSPS 9:1 neutral 120 × 120 (free surface)
4 21PC:DSPS 9:1 low 120 × 120 (free surface)
5 21PC:DSPS 1:1 neutral 60 × 60 (PBC)
6 21PC:DSPS 1:1 low 60 × 60 (PBC)
Open in a new tab

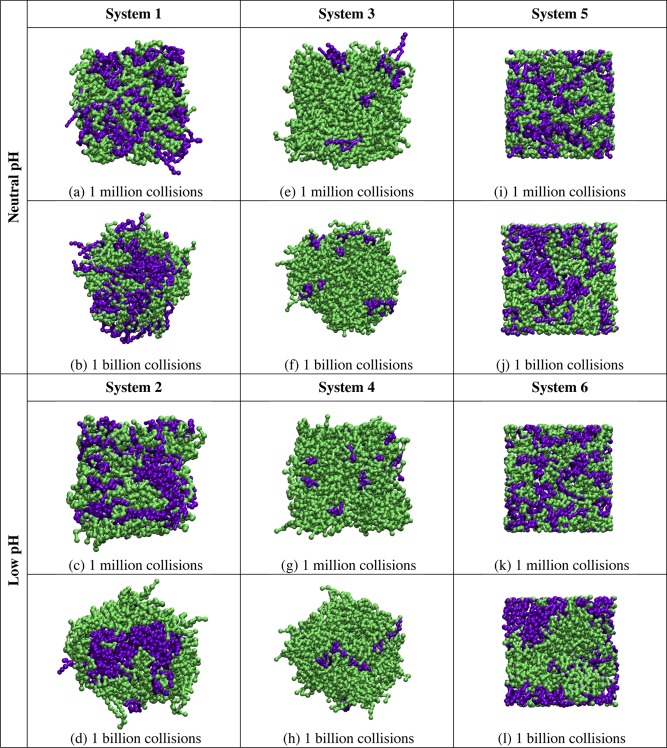
Simulations on Systems 1 and 2 were run to investigate the behavior of bilayers composed of equimolar ratios of 21PC:DSPS, with free surfaces, at both neutral and low pH. Figure 3 provides snapshots (aerial images) of the bilayer configurations at 1 million and 1 billion collisions for a single replicate in simulations on Systems 1–6. Figure 3a,c shows that after 1 million collisions little to no phase separation can be detected between 21PC and DSPS lipids in Systems 1 and 2. Figure 3b,d shows that after 1 billion collisions the 21PC and DSPS lipids in System 2 have separated to a greater extent than that in System 1. Simulations on Systems 3 and 4 (also with free surfaces) were run to investigate the heterogeneous domain formation of bilayers composed of a 9:1 molar ratio of 21PC:DSPS. Figure 3e,g shows that no detectable phase separation is achieved in Systems 3 and 4 after 1 million collisions. However, after 1 billion collisions, the snapshots provided in Figure 3f,h show that System 4 has separated to a greater extent than System 3.

Figure 3.

Figure 3

Open in a new tab

Snapshots (aerial images) of the bilayer formed at 1 million collisions in simulations of Systems 1 (a), 2 (c), 3 (e), 4 (g), 5 (i), and 6 (k) and at 1 billion collisions in simulations of Systems 1 (b), 2 (d), 3 (f), 4 (h), 5 (j), and 6 (l). The color scheme is lime (21PC lipids) and purple (DSPS lipids at neutral pH and low pH).

Figure 4 displays the normalized, time-averaged percentage of DSPS lipid molecules within a 5 Å radius of each DSPS headgroup (coarse-grained site 1 on each DSPS lipid molecule). The higher the fraction of DSPS lipid molecules within a 5 Å radius of each DSPS headgroup, the greater the phase separation of the bilayer. Figure 4 shows that the number of DSPS lipids with a DSPS nearest neighbor is higher for Systems 2 and 4 than it is for Systems 1 and 3. This indicates that Systems 2 and 4 separate to a greater extent by 1 billion collisions than do Systems 1 and 3. This is supported by the snapshots provided in Figure 3b,d,f,h.

Figure 4.

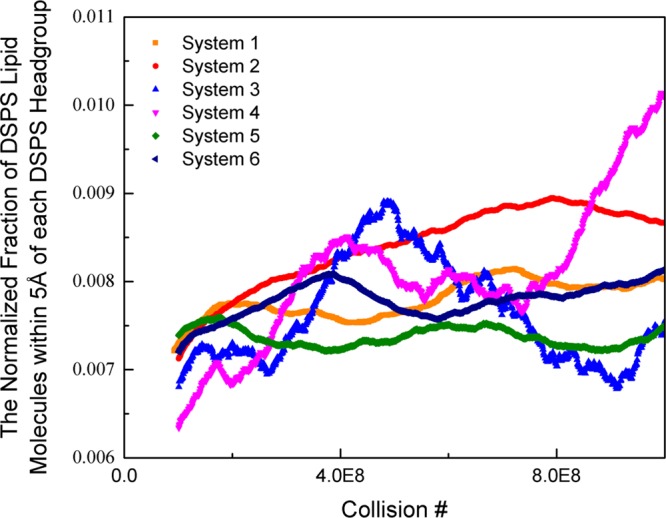
Figure 4

Open in a new tab

Normalized, time-averaged percentage of DSPS lipid molecules within a 5 Å radius of each DSPS headgroup (coarse-grained site 1 on each DSPS lipid molecule).

The rate of phase separation was estimated by measuring the change in the average maximum height of the radial distribution function over time between DSPS head groups of coarse-grained types I (a or b) and III. The larger the value of the maximum g(r) for a given pair of coarse-grained types, the closer, on average, those coarse-grained types would be to each other. The radial distribution function for coarse-grained types I (a or b) and III was chosen as our measure because this pair has the largest interaction at low pH. The maximum heights of each radial distribution function were averaged over all replicates from each system. Table 3 provides the average maximum g(r) at 3 different time points for Systems 1 and 2. At each time point, the g(r) was averaged over 1 million collisions.

Table 3. Average Maximum g(r) Value at Different Time Points for Systems 1 and 2.

  average maximum g(r)
system no. 0 to 1 million collisions 100 to 101 million collisions 1000 to 1001 million collisions
1 18.491 22.063 24.159
2 26.962 47.762 59.314
Open in a new tab

According to Table 3, System 2 has a higher average maximum g(r) value than that of System 1 at each time point. This indicates that at each time point System 2 had phase separated to a greater extent than that of System 1. In addition, the change in the maximum g(r) value between each time point was higher for System 2 than that for System 1. This shows that System 2 separated into heterogeneous domains at a faster rate than System 1. Similar to System 2, Systems 4 and 6, which were also run at low pH, showed an increase in the average maximum g(r) with time. However, Systems 3 and 5, which were run at neutral pH, did not show a monotonic increase in g(r) with time. This shows that Systems 4 and 6 are phase separating to a greater extent and at a faster rate than are Systems 3 and 5.

In order to learn how bilayer surface area constraints associated with periodic boundary conditions impacts the phase separation in 21PC:DSPS systems, we compare the results of simulations of Systems 1 and 2 with those on Systems 5 and 6. The goal was to determine if allowing the bilayer to interact with its periodic image had an effect on the rate at which the 21PC and DSPS lipids separated into different domains. Simulations on Systems 1, 2, 5, and 6 contained bilayers with equimolar ratios of 21PC/DSPS lipids, respectively. Each of these simulations was started from an initial bilayer with an area of 60 × 60 Å2. The box lengths for simulations on Systems 1 and 2 were 120 × 120 Å2, whereas the box lengths for simulations on Systems 5 and 6 were 60 × 60 Å2. Therefore, in simulations of Systems 1 and 2, the bilayers cannot interact with their periodic images, whereas in simulations of Systems 5 and 6, they can. Figure 3 provides snapshots (aerial images) after 1 million and 1 billion collisions from one of the replicates of the simulations that were run on Systems 1, 2, 5, and 6. At 1 billion collisions, the area per lipid for Systems 1, 2, 5, and 6 was 46.2, 46.2, 48.0, and 48.0 Å2, respectively. Therefore, when the bilayers do not interact with their periodic image, their surface area slightly decreases. In comparison to the bilayer in System 1 (no periodic boundary conditions, neutral pH), the bilayer in System 5 (periodic boundary conditions, neutral pH) appears to separate at approximately the same rate. Similarly, the bilayer in System 2 (no periodic boundary conditions, low pH) and the bilayer in System 6 (periodic boundary conditions, low pH) appears to achieve about the same amount of phase separation. According to Figure 4, Systems 2 and 6 (low pH) have the highest fraction of DSPS lipid molecules within a 20 Å radius of each DSPS headgroup. This indicates that Systems 2 and 6 phase separate to a greater extent than do Systems 1 and 5, which is supported by the snapshots of each of these systems at 1 billion collisions provided in Figure 3. Thus, we see that the 21PC/DSPS bilayers at low pH separate faster than 21PC/DSPS bilayers at neutral pH regardless of whether the bilayers had a free surface or periodic boundary conditions.

Conclusions

We described the extension of LIME, which was originally designed for a single type of lipid (DPPC), at a temperature of 325 K, to be applicable to DSPS and 21PC lipids at a temperature of 310 K. LIME is an intermediate-resolution, implicit-solvent coarse-grained model for phospholipid molecules, which is designed for use with DMD. One of the main advantages of combining LIME with DMD is that it makes it possible to sample much wider regions of conformation space and longer time scales than that in traditional molecular dynamics. By treating solvent implicitly, coarse-graining, and using a discontinuous potential, we can simulate the behavior of mixed lipid systems at a much faster rate than that in traditional molecular dynamics simulations. To our knowledge, our LIME/DMD simulations are the first molecular-level simulations that demonstrate pH-dependent phase separation in mixed lipid bilayers. The simulations that we describe in this work run at a rate of approximately 0.017 CPU hours per 1 million collisions (Intel Xeon E5520 2.27 GHz).

The expanded version of LIME was used to simulate the behavior of bilayers with and without surface area restrictions composed of different molar ratios of 21PC and DSPS at both neutral and low pH. According to our simulations, 21PC/DSPS systems separate faster at low pH than at neutral pH. These results are consistent with those of Sofou and co-workers, who found that the phase separation and the formation of DSPS-rich domains in lipid vesicles composed of 21PC, DSPS, 5 mol % cholesterol, and 1 mol % DSPE-PEG increases with a decrease in pH.31 The molecular mechanism driving this phase separation is thought to be the following: (1) at neutral pH (7.4–7.0), the net negative charge on the DSPS molecules causes electrostatic repulsion between them, which hinders their ability to phase separate, and (2) when the pH is lowered, the DSPS head groups become protonated and loose their negative charge, which allows these molecules to hydrogen bond to each other and phase separate into heterogeneous domains.31 The fact that our results are consistent with those of Sofou and co-workers is not proof that LIME/DMD can be used to model the behavior of Sofou’s liposomes. The ultimate test will be to simulate the escape of drug molecules from 21PC/DSPS liposomes at neutral and low pH using LIME/DMD. We are currently running such simulations and hope to report these results soon.

We found that bilayers interacting with their periodic images and free surface bilayers phase separated to approximately the same extent after 1 billion collisions. Bilayers interacting with their periodic images are expected to behave more similarly to liposomes in experiments because these bilayers will be promoted (but not forced) to maintain a certain surface area and not to shrink or expand to a large extent. In experiments, liposomes composed of 21PC/DSPS lipids in a solution containing salt ions cannot simply adjust to any desired size for the following reason: as 21PC/DSPS lipids begin to separate into heterogeneous domains, the lipids try to pack closer together. As they do this, the overall liposome size shrinks. During this process, water molecules can escape from the inner core of the liposome, whereas salt molecules cannot. This results in an osmotic pressure that prevents the liposome from shrinking to a large extent. This scenario is best mimicked by our simulations with bilayers interacting with their periodic images.

To make better contact with the experiments on 21PC, DSPS, and cholesterol, we are now calculating LIME parameters for cholesterol so that we can add it to our simulations to learn what role cholesterol plays in the heterogeneous domain formation of mixed lipid systems. While our simulations were inspired by experiments done in the Sofou lab, we have not, as yet, included the specific molecular embellishments associated with the Sofou liposomes, including the targeting ligand, fusion peptides, and cholesterol.15,31,32 The multiscale modeling procedure that we used to calculate LIME parameters for DPPC, 21PC, and DSPS could, however, be used to calculate parameters for these additional molecules. In the future, we plan to expand our model to include these molecules.

It is useful to discuss some of the limitations associated with DMD. One drawback of using DMD is that it is difficult to correlate collision times with real time. This is a result of the fact that DMD simulations are event-driven rather than time-driven and that solvent is modeled implicitly. If information is available regarding the experimental time required for a certain process or event to occur, then this can be correlated to the simulation time required for the same process or event to occur, allowing us to estimate a correlation between simulation and real time. Additionally, treating solvent implicitly prevents us from studying the diffusion and hydrodynamics associated with the phase separation of the lipid membranes. Our model cannot be used to predict how solvent molecules will interact at the interface of the bilayer with the 21PC and DSPS head groups and affect the rate of heterogeneous domain formation of these lipids. Another limitation of our model is that we do not have a systematic way of correlating temperature changes to real temperatures. We know that by setting T* = 0.2 in our simulation the results seem to mimic the behavior of 21PC/DSPS systems at 310 K. Multiscale modeling could be used to determine the temperature dependence of the interaction energies in our model, but this would require data from atomistic simulations at various temperatures, which is beyond the scope of this work. Finally, although our LIME/DMD simulations are currently run using the NVT ensemble, we could perform NPT simulations in the future. To do this, we would need to perform hybrid Monte Carlo–DMD simulations in which the volume change moves are made with Monte Carlo and particle displacement moves are made with DMD. This type of simulation has been performed by previous members of the Hall group in the past.49,50 Despite these limitations, we feel that our LIME/DMD model does a good job of modeling the behavior of liposomes observed experimentally and that it could be a useful tool to researchers trying to study the behavior of lipid systems on a molecular level.

Acknowledgments

This work was supported by the National Institutes of Health under grant nos. GM56766 and EB006006 and by the National Science Foundation under grant no. DMR-1206943. This work was also supported by the NSF’s Research Triangle MRSEC, DMR-1121107. E.M.C. received a GAANN (North Carolina State University Graduate Assistance in Areas of National Need) Computational fellowship and a NIH/North Carolina State University Molecular Biotechnology Training Program fellowship. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant no. ACI-1053573. E.M.C. received a startup research allocation from XSEDE, which helped to complete the work described in this article. We thank the National Institute for Computational Science (NICS), Texas Advanced Computing Center (TACC), and San Diego Supercomputer Center (SDSC) for providing us with computing time.

Supporting Information Available

Partial charges calculated for each molecule. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

la504082x_si_001.pdf (486.6KB, pdf)

References

  1. Strijkers G.; Kluza E.; Tilborg G.; Schaft D.; Griffioen A.; Mulder W.; Nicolay K. Paramagnetic and Fluorescent Liposomes for Target-Specific Imaging and Therapy of Tumor Angiogenesis. Angiogenesis 2010, 13, 161–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Nikolelis D.; Hianik T.; Krull U. Biosensors Based on Thin Lipid Films and Liposomes. Electroanalysis 1999, 11, 7–15. [Google Scholar]
  3. Bally M.; Bailey K.; Sugihara K.; Grieshaber D.; Voros J.; Stadler B. Liposome and Lipid Bilayer Arrays towards Biosensing Applications. Small 2010, 6, 2481–2497. [DOI] [PubMed] [Google Scholar]
  4. Lingwood D.; Simons K. Lipid Rafts as a Membrane-Organizing Principle. Science 2010, 327, 46–50. [DOI] [PubMed] [Google Scholar]
  5. Mukherjee S.; Maxfield F. Role of Membrane Organization and Membrane Domains in Endocytic Lipid Trafficking. Traffic 2000, 1, 203–211. [DOI] [PubMed] [Google Scholar]
  6. Liu Y.; Li K.; Pan J.; Liu B.; Feng S. Folic Acid Conjugated Nanoparticles of Mixed Lipid Monolayer Shell and Biodegradable Polymer Core for Targeted Delivery of Docetaxel. Biomaterials 2010, 31, 330–338. [DOI] [PubMed] [Google Scholar]
  7. Smet M.; Langereis S.; Bosch S.; Grull H. Temperature-Sensitive Liposomes for Doxorubicin Delivery under MRI Guidance. J. Controlled Release 2010, 143, 120–127. [DOI] [PubMed] [Google Scholar]
  8. Schwendener R.; Ludewig B.; Cerny A.; Engler O. Liposome-Based Vaccines. Methods Mol. Biol. 2010, 605, 163–175. [DOI] [PubMed] [Google Scholar]
  9. Shi G.; Guo W.; Stephenson S.; Lee R. Efficient Intracellular Drug and Gene Delivery Using Folate Receptor-Targeted pH-Sensitive Liposomes Composed of Cationic/Anionic Lipid Combinations. J. Controlled Release 2002, 80, 309–319. [DOI] [PubMed] [Google Scholar]
  10. Templeton N.; Lasic D.; Frederick P.; Strey H.; Roberts D.; Pavlakis G. Improved DNA: Liposome Complexes for Increased Systemic Delivery and Gene Expression. Nat. Biotechnol. 1997, 15, 647–652. [DOI] [PubMed] [Google Scholar]
  11. Drulis-Kawa Z.; Dorotkiewics-Jach A. Liposomes as Delviery Systems for Antibiotics. Int. J. Pharm. 2010, 387, 187–198. [DOI] [PubMed] [Google Scholar]
  12. Zhang L.; Pornpattananangkyl D.; Hu C.; Huang C. Development of Nanoparticles for Antimicrobial Drug Delivery. Curr. Med. Chem. 2010, 17, 585–594. [DOI] [PubMed] [Google Scholar]
  13. Needham D.; Anyarambhatia G.; Kong G. A New Temperature-Sensitive Liposome for Use with Mild Hyperthermia: Characterization and Testing in a Human Tumor Xenograft Model. Cancer Res. 2000, 60, 1197–1201. [PubMed] [Google Scholar]
  14. Park J.; Fong P.; Lu J.; Russell K.; Booth C.; Saltzmann W.; Fahmy T. PEGylated PLGA Nanoparticles for the Improved Delivery of Doxorubicin. Nanomedicine 2009, 5, 410–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Karve S.; Kempegowda G.; Sofou S. Heterogeneous Domains and Membrane Permeability in Phosphatidylcholine–Phosphatidic Acid Rigid Vesicles as a Function of pH and Lipid Chain Mismatch. Langmuir 2008, 24, 5679–5688. [DOI] [PubMed] [Google Scholar]
  16. Ferrara K.; Borden M.; Zhang H. Lipid-Shelled Vehicles: Engineering for Ultrasound Molecular Imaging and Drug Delivery. Acc. Chem. Res. 2009, 42, 881–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Yatvin M.; Weinstein J.; Dennis W.; Blumenthal R. Design of Liposomes for Enhanced Local Release of Drugs by Hyperthermia. Science 1978, 202, 1290–1293. [DOI] [PubMed] [Google Scholar]
  18. Chem Q.; Krol A.; Wright A.; Needham D.; Dewhirst M.; Yuan F. Tumor Microvascular Permeability Is a Key Determinant for Antivascular Effects of Doxorubicin Encapsulated in a Temperature Sensitive Liposome. Int. J. Hyperthermia 2008, 24, 475–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Smet M.; Heijman E.; Langereis S.; Hijnen N.; Grull H. Magnetic Resonance Imaging of High Intensiy Focused Ultrasound Mediated Delivery from Temperature-Sensitive Liposomes: An in Vivo Proof-of-Concept. J. Controlled Release 2011, 150, 102–110. [DOI] [PubMed] [Google Scholar]
  20. Curtis E.; Hall C. Molecular Dynamics Simulations of DPPC Bilayers Using “LIME”, a New Coarse-Grained Model. J. Phys. Chem. B 2013, 117, 5019–5030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Van der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A.; Berendsen H. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1719. [DOI] [PubMed] [Google Scholar]
  22. Jiang Y.; Wang H.; Kindt J. Atomistic Simulations of Bicelle Mixtures. Biophys. J. 2010, 98, 2895–2903. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hall A.; Rog T.; Karttunen M.; Vattulainen I. Role of Glycolipids in Lipid Rafts: A View through Atomistic Molecular Dynamics Simulations with Galactosylceramide. J. Phys. Chem. B 2010, 114, 7797–7807. [DOI] [PubMed] [Google Scholar]
  24. Pandit S.; Bostick D.; Berkowitz M. Mixed Bilayer Containing Dipalmitoylphosphatidylcholine and Dipalmitoylphosphatidylserine: Lipid Complexation, Ion Binding, and Electrostatics. Biophys. J. 2003, 85, 3120–3131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Illya G.; Lipowsky R.; Shillcock J. Two-Component Membrane Material Properties and Domain Formation from Dissipative Particle Dynamics. J. Chem. Phys. 2006, 125, 114710-1–9. [DOI] [PubMed] [Google Scholar]
  26. Faller R.; Marrink S. Simulation of Domain Formation in DLPC-DSPC Mixed Bilayers. Langmuir 2004, 20, 7686–7693. [DOI] [PubMed] [Google Scholar]
  27. Marrink S.; de Vries A.; Mark A. Coarse Grained Model for Semiquantitative Lipid Simulations. J. Phys. Chem. B 2004, 108, 750–760. [Google Scholar]
  28. Risselada H.; Marrink S. The Molecular Face of Lipid Rafts in Model Membranes. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 17367–17372. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; de Vries A. H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [DOI] [PubMed] [Google Scholar]
  30. Lu L.; Voth G. Systematic Coarse-Graining of a Multicomponent Lipid Bilayer. J. Phys. Chem. B 2009, 113, 1501–1510. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Bandekar A.; Zhu C.; Gomez A.; Menzenski M.; Sempkowski M.; Sofou S. Masking and Triggered Unmasking of Targeting Ligands on Liposomal Chemotherapy Selectively Suppress Tumor Growth in Vivo. Mol. Pharmaceutics 2013, 10, 152–160. [DOI] [PubMed] [Google Scholar]
  32. Karve S.; Bandekar A.; Ali M.; Sofou S. The pH-Dependent Association with Cancer Cells of Tunable Functionalized Lipid Vesicles with Encapsulated Doxorubicin for High Cell-Kill Selectivity. Biomaterials 2010, 31, 4409–4416. [DOI] [PubMed] [Google Scholar]
  33. Hess B.; Kutzner C.; Van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [DOI] [PubMed] [Google Scholar]
  34. Oostenbring C.; Villa A.; Mark A.; Van Gunsteren W. A Biomolecular Force Field Based on the Free Enthalpy of Hydration and Solvation: The GROMOS Force-Field Parameter Sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1675. [DOI] [PubMed] [Google Scholar]
  35. Bandekar A.; Sofou S. Floret-Shaped Solid Domains on Giant Fluid Lipid Vesicles Induced by pH. Langmuir 2012, 28, 4113–4122. [DOI] [PubMed] [Google Scholar]
  36. Kempegowda G.; Karve S.; Bandekar A.; Adhikari A.; Khaimchayev T.; Sofou S. pH-Dependent Formation of Lipid Heterogeneities Controls Surface Topography and Binding Reactivity in Functionalized Bilayers. Langmuir 2009, 25, 8144–8151. [DOI] [PubMed] [Google Scholar]
  37. Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
  38. Smith S. W.; Hall C. K.; Freeman B. D. Molecular Dynamics for Polymeric Fluids Using Discontinuous Potentials. J. Comput. Phys. 1997, 134, 16–30. [Google Scholar]
  39. Alder B.; Wainwright T. Studies in Molecular Dynamics. I. General Method. J. Chem. Phys. 1959, 31, 459–466. [Google Scholar]
  40. Rapaport DC. Molecular Dynamics Simulation of Polymer Chains with Excluded Volume. J. Phys. A: Math. Gen. 1978, 11, L213–L217. [Google Scholar]
  41. Rapaport DC. Molecular Dynamics Study of a Polymer Chain in Solution. J. Chem. Phys. 1979, 71, 3299–3303. [Google Scholar]
  42. Nguyen H. D.; Hall C. K. Molecular Dynamics Simulations of Spontaneous Fibril Formation by Random-Coil Peptides. Proc. Natl. Acad. Sci. U.S.A. 2004, 101, 16180–16185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam N. J.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas O.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09; Gaussian, Inc.: Wallingford, CT, 2009.
  44. Cornell W. D.; Cieplak P.; Bayly C. I.; Kollman P. A. Application of RESP Charges To Calculate Conformaltional Enerigies, Hydrogen Bond Energies, and Free Energies of Solvation. J. Am. Chem. Soc. 1993, 115, 9620–9631. [Google Scholar]
  45. Cornell W. D.; Cieplak P.; Bayly C. I.; Gould I. R.; Merz K. M.; Ferguson D. M.; Spellmeyer D. C.; Fox T.; Caldwell J. W.; Kollman P. A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar]
  46. Cieplak P.; Cornell W.D.; Bayly C.; Kollman P.A. Application of the Multimolecule and Multiconformational RESP Methodology to Biopolymers: Charge Derivation for DNA, RNA and Proteins. J. Comput. Chem. 1995, 16, 1357–1377. [Google Scholar]
  47. Berendsen H.; Postma J.; Van Gunsteren W.; DiNola A.; Haak J. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar]
  48. McQuarrie D. A.Statistical Mechanics; Harper & Row: New York, 1973; pp 224–237. [Google Scholar]
  49. Kenkare N.; Hall C.; Khan S. Theory and Simulation of the Swelling of Polymer Gels. J. Chem. Phys. 2000, 113, 404–418. [Google Scholar]
  50. Shultz A.; Hall C.; Genzer J. Box Length Search Algorithm for Molecular Simulation of Systems Containing Periodic Structures. J. Chem. Phys. 2004, 120, 2049–2055. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la504082x_si_001.pdf (486.6KB, pdf)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES