Implicit solvent methods for free energy estimation

Abstract

Solvation is a fundamental contribution in many biological processes and especially in molecular binding. Its estimation can be performed by means of several computational approaches. The aim of this review is to give an overview of existing theories and methods to estimate solvent effects giving a specific focus on the category of implicit solvent models and their use in Molecular Dynamics. In many of these models, the solvent is considered as a continuum homogenous medium, while the solute can be represented at the atomic detail and at different levels of theory. Despite their degree of approximation, implicit methods are still widely employed due to their trade-off between accuracy and efficiency. Their derivation is rooted in the statistical mechanics and integral equations disciplines, some of the related details being provided here. Finally, methods that combine implicit solvent models and molecular dynamics simulation, are briefly described.

Introduction

It is well accepted that the role of solvent in biochemical processes is crucial. The estimation of hydration energy, binding energy, pKa of ligands or titratable protein residues heavily depends on a good description of the solvent behavior. The delicate balance between entropic desolvation penalty and enthalpic gain, that often characterize protein-protein and protein-ligand binding, is an example of a phenomenon extremely challenging to be quantitatively described [1]. In Molecular Dynamics, the calculation of the evolution and the equilibration of the solvent degrees of freedom often constitute the main sources of computational cost of the simulation. When performing a Monte Carlo move in a system composed by biomolecules surrounded by explicit solvent, the probability of randomly drawing a configuration where the solute and solvent displacements are compatible is practically negligible. Interestingly, one is not usually interested in knowing the solvent behavior per se, but rather its effects on the solute. In this context, implicit solvent methods find their application, aiming at reproducing the overall, thermally averaged, solvent effect at a lower computational cost.

This approach can be justified by a mean field approximation of the solvent in statistical mechanical terms [2]. Intuitively, one of the underlying assumptions that justify considering water molecules as a continuum medium is their relatively short relaxation time. The time typically needed by water molecules to react to a perturbation is much shorter than that corresponding to macromolecular conformational changes. In a pictorial view, and within the time frame of a typical water molecule displacement, the aqueous solvent ‘sees’ the protein in a fixed conformation, and, conversely, the protein cannot ‘distinguish’ among contributions of individual bulk water molecules. Of course, this kind of reasoning cannot be applied to water molecules that are undergoing a specific interaction and its validity can be also questioned in the case of water molecules located in deep pockets where the diffusion can be very different from that in the bulk solvent. However, implicit solvent models neglect the individual molecular behavior of the solvent with respect to explicit solvent simulations. As a consequence, some important phenomena that involve, for instance, hydrogen bonds, hydrophobic effects and, in general, a non-bulk solvent behavior can be missed [2]. Despite the mentioned approximations, implicit methods are still of wide interest because of their algorithmic efficiency, the much reduced number of degrees of freedom requiring simulation and equilibration, and the relatively good compromise between model accuracy and efficiency [3].

Implicit solvent methods can be used for several aims: fixed point calculations, polarizable solvent simulations and scoring docking poses [4–6]. They can be run in conjunction with either a classical atomistic treatment of the solute [7,8], or with quanto-mechanical calculations [9]. The physical phenomenon that is mostly, but not exclusively, represented in implicit solvent approaches is the linear response to the electric field generated by the solute. Usually, this response is originated by molecular polarization but also the salt effects can be, to some extent, accounted for.

Here, a general derivation of several implicit solvent models from statistical mechanical foundations is provided and then some specific approaches are described, grouped in: Semi-Heuristic, Poisson-Boltzmann (PB) based, Generalized Born (GB), Integral Equation based and combined methods, i.e. those that join PB or GB methods with atomistic simulations. Finally, other approaches are mentioned with their own peculiarities.

1. Implicit solvent description in the statistical mechanics framework

Let us distinguish the Cartesian coordinates of a system in those, X, describing the solute, and those, Y, describing the solvent, which can also possibly contain a dissociated salt. For a system at the thermodynamic equilibrium characterized by the temperature T, the joint probability of given configuration, that is of the (X,Y) pair, is given by [2]:

$$P(\mathbf{X},\mathbf{Y})=\frac{exp(-U(\mathbf{X},\mathbf{Y})/(k_{B}T))}{\int exp(-U(\mathbf{X},\mathbf{Y})/(k_{B}T))d\mathit{X}d\mathit{Y}}$$ (1)

where U(X,Y) is the total potential energy of the system, the denominator is a normalization coefficient called partition function and k_B is the Boltzmann constant. We assume that the potential energy can be written as the sum of intra-solute (SS), intra-solvent (WW), and solvent-solute (WS) interactions. This assumption, which is always verified in traditional pair-wise additive force fields, reads:

$$U(\mathbf{X},\mathbf{Y})=U{(\mathbf{X})}_{ss}+U{(\mathbf{Y})}_{ww}+U{(\mathbf{X},\mathbf{Y})}_{ws}$$ (2)

Due to the fact that P(X,Y) is the probability density of the system, any macroscopic quantity can be obtained by computing the corresponding statistical average, or expectation value. Henceforth, the expectation of the microscopic function Q(X,Y) corresponding to the observable Q will be indicated as E_X,Y {Q(X,Y)}, where the subscript specifies on which variables the expectation operator acts, or, alternatively, by < Q(X,Y) >.

Let us now consider an observable Q corresponding to the average of a microscopic function of only the solute coordinates {X}:

$$Q=E_{\mathbf{X},\mathbf{Y}}\{Q(\mathbf{X})\}=\int Q(\mathbf{X})P(\mathbf{X},\mathbf{Y})d\mathit{X}d\mathit{Y}$$ (3)

From this equation it is clear that in order to get the needed average, the knowledge of the possible solvent configurations, together with their statistical weights, is needed. The global probability distribution governing the thermodynamic equilibrium in the canonical ensemble is the Boltzmann distribution. An important question that may arise is whether we can still get an average value of a solute observable without having a specific knowledge of the configurations of the solvent.

To this aim, instead of considering the joint probability, one can consider the restriction of the probability to the solute, by integrating over the solvent space. Therefore one can write:

$$P(\mathbf{X})=E_{\mathbf{Y}}\{1(\mathbf{X},\mathbf{Y})\}=\int 1(\mathbf{X},\mathbf{Y})P(\mathbf{X},\mathbf{Y})d\mathit{Y}=\int P(\mathbf{X},\mathbf{Y})d\mathit{Y}$$ (4)

This can be formally considered as the average value over Y, (expectation operator is over Y) of an observable always equal to 1 for each value of the pair X, Y. Then, in a system at temperature T, the reduced probability is:

$$P(\mathbf{X})=\frac{\int \mathbf{exp}(-[U{(\mathbf{X})}_{ss}+U{(\mathbf{Y})}_{ww}+U{(\mathbf{X},\mathbf{Y})}_{ws}]/(k_{B}T))d\mathit{Y}}{\int \mathbf{exp}(-[U{(\mathbf{X})}_{ss}+U{(\mathbf{Y})}_{ww}+U{(\mathbf{X},\mathbf{Y})}_{ws}]/(k_{B}T))d\mathit{X}d\mathit{Y}}$$ (5)

that we can more compactly rewrite as:

$$P(\mathbf{X})=\frac{\mathbf{exp}(-W(\mathbf{X})/(k_{B}T))}{\int \mathbf{exp}(-W(\mathbf{X})/(k_{B}T))d\mathit{X}}$$ (6)

This last formula has a nice analogy with the general form of the joint distribution. This time, however, the joint probability is replaced by its solvent-averaged version P(X) and for this reason the potential W(X) is called Potential of Mean Force (PMF). It can be shown that in cartesian coordinates if the chosen observable is the force then it holds:

$$E_{\mathbf{Y}}\{{\mathit{F}}_{\mathit{i}}(\mathbf{X},\mathbf{Y})\}=-\frac{\partial \mathrm{W}(\mathbf{X})}{\partial {\mathbf{x}}_{\mathbf{i}}}$$ (7)

From this fact derives the name potential of “mean force”, where “mean” means, in this case, average with respect to the solvent degrees of freedom. As other potentials, its absolute value is up to a constant offset. It is usual to set the PMF reference as the value where there are no interactions between solvent and solute, that is U(X, Y)_ws = 0, in particular we can set this relation:

$$W(\mathbf{X})=U{(\mathbf{X})}_{ss}+\mathrm{\Delta }{G}_s(\mathbf{X})$$ (8)

This relation is particularly interesting because it mixes the free energy ΔG_s(X) (solvent-solute related) to the intra-solute potential energy U(X)_ss; hence W(X) is a free energy.

In this setting, we can observe that the following relation holds:

$$\mathbf{exp}\left(-\frac{W(\mathbf{X})}{k_{B}T}\right)=\frac{\int \mathbf{exp}(-[U{(\mathbf{X})}_{ss}+U{(\mathbf{Y})}_{ww}+U{(\mathbf{X},\mathbf{Y})}_{ws}]/(k_{B}T))d\mathit{Y}}{\int \mathbf{exp}(-U{(\mathbf{Y})}_{ww}/(k_{B}T))d\mathit{Y}}$$ (9)

In particular when U(X, Y)_ws = 0, then we must have ΔG_s(X) = 0. Consistently, the term ΔG_s is named solvation free energy and it is the energy needed to transfer the solute from vacuum to the solvent.

We can introduce now the concept of thermodynamic integration. We write the potential energy as:

$$U(\mathbf{X},\mathbf{Y})=U{(\mathbf{X})}_{ss}+U{(\mathbf{Y})}_{ww}+U{(\mathbf{X},\mathbf{Y};\mathrm{\lambda })}_{ws}$$ (10)

where λ is a coupling parameter between the uncoupled (λ = 0) and the coupled system λ = 1). We can estimate the solvation free energy by again integrating over the solvent degrees of freedom and then over the coupling parameter λ. In other terms, we estimate the reversible work for moving from state λ = 0 to λ = 1:

$$\mathrm{\Delta }{G}_s(\mathbf{X})={\int }_0^1{E}_{\mathbf{Y}}\left\{\frac{\partial U{(\mathbf{X},\mathbf{Y};\mathrm{\lambda })}_{ws}}{\partial \mathrm{\lambda }}\right\}d\mathrm{\lambda }$$ (11)

The solvation free energy can be decomposed in both a polar (electrostatics) ΔG_es term and a non polar (van der Waals, Pauli exclusion principle), ΔG_np energy term [2]:

$$\mathrm{\Delta }{G}_s=\mathrm{\Delta }{G}_{es}+\mathrm{\Delta }{G}_{np}$$ (12)

Implicit methods are a way to estimate ΔG_s; other methods try to capture the full free energy of the system thus also estimating the expectation over X of U(X)_ss [10,11]. Following [12] and further detailing the term ΔG_np, one has:

$$\mathrm{\Delta }{G}_s=\mathrm{\Delta }{G}_{es}+\mathrm{\Delta }{G}_{\mathit{vdW}}+\mathrm{\Delta }{G}_{\mathit{cav}}$$ (13)

where ΔG_vdW accounts for solute-solvent the van der Waals interactions and ΔG_cav is the energy needed to create a cavity into the solvent to accommodate the solute. Figure 1 shows the thermodynamic cycle underlying this model.

Figure 1. Representation of the thermodynamic cycle for computing the solvation energy.

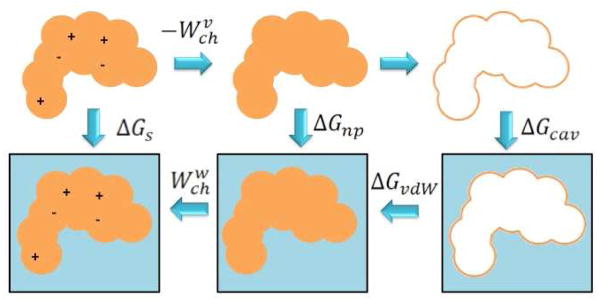
In the cycle the electrostatic energy component is split in the discharging in vacuum ${\mathbf{W}}_{\mathbf{ch}}^{\mathbf{v}}$, and charging in solvent ${\mathbf{W}}_{\mathbf{ch}}^{\mathbf{w}}$. “np” subscript stands for “non polar”, “cav” for “cavitation”, “s” for “solvation” and “vdW” for “Van der Waals”.

A key quantity very often estimated is the binding energy between a ligand and a target protein, it can be computed by:

$$\mathrm{\Delta }{G}_{\mathit{bind}}=\mathrm{\Delta }{G}_s^{pl}-\mathrm{\Delta }{G}_s^l-\mathrm{\Delta }{G}_s^p$$ (14)

Where $\mathrm{\Delta }{G}_s^{pl}$ is the solvation free energy of the complex, and $\mathrm{\Delta }{G}_s^l,\mathrm{\Delta }{G}_s^p$ are the solvation free energy of the ligand and the target, respectively.

2. Implicit solvent

With the aim of estimating ΔG_s within an implicit solvent framework, one can approximate the set of water molecules as a continuum, isotropic, linearly reactive medium. This mean-field approximation of the underlying system opposes to the more accurate explicit solvent modeling where each single particle is modeled in a “classical” way, in a deterministic or stochastic dynamics [13]. In statistical mechanical terms, as already discussed, one is approximating the total energy of the system with the Potential of Mean Force, that is, the solvent-averaged version of the energy.

A crucial role in implicit modeling is played by the electrostatic contribution (or its approximations) to the energy of the system, the polar part. Electrostatics is of particular relevance because of its long range nature; in biological molecular system we can say that at long distances electrostatic is the only interaction that takes place between molecules. From another perspective, at short distances, electrostatic interactions give specificity, for instance, to the binding between an enzyme and its substrate. Intensity and peculiarity of the electrostatic field in DNA minor/major grooves provides high specificity and permits its key role in biological processes [14].

Several specific implicit models have been proposed in the past. Some of them estimate the electrostatic potential and then deduce the energy of the system, while others skip the ‘potential computation’ and directly estimate the energy. We can try to split the methods in the following categories: some ad-hoc semi-heuristic methods (among other examples are ASP [15], EEF1 [16]), those based on Poisson-Boltzmann theory (PB) [17], those based on Generalized-Born (GB) approximation [18], ‘combined methods’, which use as internal ‘routines’ the previous models such as in the case of MMPB [19], LIE [20], LIECE [21], and other peculiar methods [22–27]. In the following, the above mentioned models will be discussed with particular emphasis on PB and GB that are among the most frequently used approaches.

2.1. Semi-Heuristic methods

This class of methods comprises a common geometry-driven approach. Among the others we consider here ASP and EEF1. These kinds of ‘geometric’ methods need the notion of Solvent Accessible Surface (SAS). The SAS or, Lee and Richards surface [28], is the union of a set of balls (atoms) whose van der Waals radii are increased by a probe radius. The probe radius represents the spherical approximation of a water molecule and is usually set to 1.4 Å.

The ASP [15] method, implemented in CHARMM [8] (a well known molecular dynamics software) is based on the concept of Solvent Accessible Surface Area: the Solvent Accessible Surface Area (SASA) of an atom is the area of the Lee and Richards solvent-accessible portion of an atom. All the approaches based on the SASA assume that the free solvation energy ΔG_s is a linear combination of the contribution of each single atom in the molecule, namely:

$$\mathrm{\Delta }{G}_S=\sum _{i=1}^{\mathit{Natoms}}\mathrm{\Delta }{\sigma }_i{A}_i$$ (15)

where A_i is the SASA of the i-th atom and Δσ_i is its atomic solvation parameter. The atomic solvation parameter Δσ_i, in units of [cal mol⁻¹ Å^.2], is an estimate of the free solvation energy required to transfer the atom from vacuum to water divided by the exposed surface area and depends on the atom type. In [15] the atom types are the following: C, uncharged O or N, S, O−, and N+.

From the previous equation we observe that the energy is not a function of a particular unknown (let’s say the potential) of a model equation, but it is a direct consequence of the geometry of the molecule. The formula is linear in the SASA elements thus leading to the simplest energy model and, practically, its accuracy depends on how ‘well’ the coefficients Δσ_i are estimated; the usual approach is the least squares fitting. The key advantage of the SASA approach is that its easy formula allows computing forces analytically for a molecular dynamics simulation [15]. This advantage is counterbalanced by the high degree of the approximation of the model.

Another proposed model, less heuristic and fitted on experimental data, is EEF1 from Karplus and Lazaridis [16]. This model combines an excluded volume approach with a modified version of the polar hydrogen energy function [8]. Again, as in the SASA/ASP method, the free solvation energy is a superposition of local energy components. This aspect is corroborated by theoretical studies on solvation thermodynamics [16]. In particular, the atoms are grouped so as that the contribution of each group to the total energy is equal to the energy of the group in a reference compound minus the energy due to the presence of the other atom groups. Consequently, the solvation free energy can be decomposed into a sum of pairwise interactions. EEF1 assumes that the decay with distance of the solvation free energy density is Gaussian-shaped. A distance dependent dielectric function is employed and the neutralization of ionic side chains is required. EEF1 has been successfully applied in molecular dynamics simulations.

2.2. Poisson-Boltzmann theory

Poisson-Boltzmann equation (PB) was historically first proposed by Gouy in 1910 and by Chapman in 1913. The version of the equation that nowadays we use is due to Debye and Huckel whose theory was successfully applied to ionic solutions. A key result is the study of Kirkwood who introduced the concept of Potential of Mean Force (PMF) and observed that the Poisson-Boltzmann assumption consists in the substitution of the PMF with the mean electrostatic potential. Despite this approximation and the non complete consistency with statistical mechanics of the non linear version of the equation [29], the Poisson-Boltzmann machinery was, and still is, able to explain interesting phenomena involving biomolecules in solution.

PB equation, as anticipated, is a non linear partial differential equation and the first numerical attempts to solve it were carried first via simple geometric models such as spheres (protein) and cylinders (DNA) [30][31] and, subsequently, by employing more realistic representations of the molecular surface [32]. The choice and definition of the molecular surface was [28] and still is [33] a matter that deserves a deep attention from several viewpoints.

In order to build the PB equation we can start from considering the electrostatic potential equation in a non-uniform dielectric medium in a region devoid of free charge. Its space varying value is described by ε(r) where r is a vector in R³. Differential Gauss’s law for the electric displacement sets a relationship for the electrostatic potential ϕ(r):

$$\nabla ·[\epsilon (\mathit{r})\nabla \phi (\mathit{r})]=0$$ (16)

When a charge density ρ(r) is present, the equation has to be complemented by a source term:

$$\nabla ·[\epsilon (\mathit{r})\nabla \phi (\mathit{r})]=-\rho (\mathit{r})$$ (17)

The assumption needed to obtain the PB equation consists in saying that the ionic potential of mean force is equal to the average electrostatic potential multiplied by the charge borne by the ion. In the light of this fact, the PB equation reads (in m.k.s units):

$$\nabla ·[\epsilon (\mathit{r})\nabla \phi (\mathit{r})]=-{\rho }^{\mathit{fixed}}(\mathit{r})-{\rho }^{\mathit{solv}}(\mathit{r},\phi (\mathit{r}))$$ (18)

where ρ^fixed(r) includes only fixed molecular (solute) charges and:

$${\rho }^{\mathit{solv}}(\mathit{r},\phi (\mathit{r}))=q\sum _{\mathrm{i}}{\mathrm{z}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{i}}^{\infty }exp\frac{-{\mathrm{z}}_{\mathrm{i}}\mathrm{q}\phi (\mathit{r})}{k_B\mathrm{T}}\chi (\mathit{r})$$ (19)

where ${\mathrm{c}}_{\mathrm{i}}^{\infty }$ is the bulk concentration of the i-th ionic species, Z_i is its valency, q is the proton charge, k_B is the Boltzmann constant, T is the temperature and χ(r) is 1 if the position r is accessible to the ionic cloud and zero otherwise. PB equation is often linearized by assuming that the potential has a small value, therefore inducing a linear relation between the solvent charge and the potential:

$$\nabla ·[\epsilon (\mathit{r})\nabla \phi (\mathit{r})]=-{\rho }^{\mathit{fixed}}(\mathit{r})+\frac{{\sum }_{\mathrm{i}}{\mathrm{c}}_{\mathrm{i}}^{\infty }{\mathrm{z}}_{\mathrm{i}}^2{\mathrm{q}}^2\phi (\mathit{r})}{k_B\mathrm{T}}\chi (\mathit{r})$$ (20)

In this context, a key parameter is the Debye constant k_D, which accounts for the screening effect of the salt and thus characterizes the rate of the exponential decay of the potential in the solvent:

$$k_D^2=\frac{{\sum }_{\mathrm{i}}{\mathrm{c}}_{\mathrm{i}}^{\infty }{\mathrm{z}}_{\mathrm{i}}^2{\mathrm{q}}^2}{{\epsilon }_w{k}_{B}T}=\frac{1}{{\mathrm{\lambda }}_D^2}$$ (21)

Where λ_D is the Debye length and ε_w is the dielectric constant of bulk water. Based on these premises, a possibly important discrepancy in the computed potential between the linearized equation and the full non linear version of the equation can be obtained for highly charged systems such as DNA/RNA. The linear version of the equation could lead to a wrong estimation of the electric field and to a lower screening effect. For most of the proteins, however, the linearized version of the equation gives sufficiently accurate electrostatic energy estimations.

Once the potential field is computed (i.e. the PB equation is solved) it can be shown by a variational argument [17] that the total electrostatic energy $\mathrm{\Delta }{G}_{es}^t$ can be decomposed in the sum of three terms:

$$\mathrm{\Delta }{G}_{es}^t=\mathrm{\Delta }{G}_{es}^{\mathit{fixed}}+\mathrm{\Delta }{G}_{es}^{\mathit{ions}}+\mathrm{\Delta }{G}_{es}^{\mathit{sol}}$$ (22)

The first is the usual energy due to fixed charges (solute) $\mathrm{\Delta }{G}_{es}^{\mathit{fixed}}$, the second term arises from ions $\mathrm{\Delta }{G}_{es}^{\mathit{ions}}$, and lastly we have a term due to the solvent $\mathrm{\Delta }{G}_{es}^{\mathit{sol}}$. The term $\mathrm{\Delta }{G}_{es}^{\mathit{fixed}}$ is

$$\mathrm{\Delta }{G}_{es}^{\mathit{fixed}}=\frac{1}{2}{\int }_V{\rho }^{\mathit{fixed}}(\mathit{r})\phi (\mathit{r})dv$$ (23)

Then the so-called osmotic term is:

$$\mathrm{\Delta }{G}_{es}^{\mathit{ions}}=k_B\mathrm{T}{\int }_V\sum _i[{\mathrm{c}}_{\mathrm{i}}^{\infty }-{\mathrm{c}}_{\mathrm{i}}(\mathit{r})]dv$$ (24)

This term is non zero when the ions concentration is space-varying and we indicate by c_i(r) the local ionic concentration:

$${\mathrm{c}}_{\mathrm{i}}(\mathit{r})={\mathrm{c}}_{\mathrm{i}}^{\infty }exp\frac{-{\mathrm{z}}_{\mathrm{i}}\mathrm{q}\phi (\mathit{r})}{k_B\mathrm{T}}$$ (25)

And finally the last solvent term:

$$\mathrm{\Delta }{G}_{es}^{\mathit{sol}}=-\frac{1}{2}{\int }_V{\rho }^{\mathit{sol}}(\mathit{r})\phi (\mathit{r})dv$$ (26)

When the linearized PB equation is considered it can be shown that all the energy terms boil down to $\mathrm{\Delta }{G}_{es}^{\mathit{fixed}}$.

Following [3], the electrostatic energy term $\mathrm{\Delta }{G}_{es}^{\mathit{fixed}}$ can be split in three further terms. In a first term, $\mathrm{\Delta }{G}_{es}^{\mathit{coulomb}}$, the Coulombic energy involving direct interaction between fixed charges, assuming each of them lie in uniform dielectric medium, is accounted for. The second term is the so-called reaction field energy, $\mathrm{\Delta }{G}_{es}^{rf}$, which is the energy due to the interaction between fixed charges and polarization charges, which are located where there is a change in dielectric constant. Finally, the third term accounts for the interaction with the potential generated by mobile ions in solution; it is called $\mathrm{\Delta }{G}_{es}^{\mathit{excess}}$ since it originates from excess charge in solution. Therefore, the total electrostatic energy can be written as:

$$\mathrm{\Delta }{G}_{es}^t=\mathrm{\Delta }{G}_{es}^{\mathit{coulomb}}+(\mathrm{\Delta }{G}_{es}^{rf}+\mathrm{\Delta }{G}_{es}^{\mathit{excess}}+\mathrm{\Delta }{G}_{es}^{\mathit{ions}}+\mathrm{\Delta }{G}_{es}^{\mathit{sol}})=\mathrm{\Delta }{G}_{es}^{\mathit{coulomb}}+\mathrm{\Delta }{G}_{es}$$ (27)

With this writing we can distinguish the solvent independent energy contribution $\mathrm{\Delta }{G}_{es}^{\mathit{coulomb}}$ from ΔG_es, which arises from the solvent.

In the linearized PB equation framework the energy reduces to:

$$\mathrm{\Delta }{G}_{es}^t=\mathrm{\Delta }{G}_{es}^{\mathit{coulomb}}+(\mathrm{\Delta }{G}_{es}^{rf}+\mathrm{\Delta }{G}_{es}^{\mathit{excess}})$$ (28)

Further, if no salt is present (i.e. no ions), the energy reduces to the Poisson equation (i.e. Laplace plus a discontinuous dielectric):

$$\mathrm{\Delta }{G}_{es}^t=\mathrm{\Delta }{G}_{es}^{\mathit{coulomb}}+\mathrm{\Delta }{G}_{es}^{rf}$$ (29)

In other terms, the only way the solute ‘feels’ the solvent is by the reaction field energy that is the energy due to the polarization charge localized at the solute-solvent interface. It is worth adding that this polarization charge arises from both the solute and the solvent media, the largest part being however contributed by the latter due to its large polarizability.

The numerical solution of the Poisson-Boltzmann equation poses interesting questions not only about efficiency but also from the geometrical model point of view. Indeed, a preliminary step that one must perform in order to solve the equation is defining the dielectric constant, ε(r), in space and the ion cloud characteristic function χ(r). This aspect is particularly interesting since the definition of the surface literally shapes the discontinuity of the system. Early implementations of PB solvers used the van der Waals surface as dielectric function and a Finite Difference Solver scheme [34][3]. More recently, the Solvent Excluded Surface, or Connolly surface has been widely used as a reference surface together with Boundary Element and Finite Element methods [34–41]. Despite the physical soundness and the widespread utilization of the Connolly surface, the latter however present some limitations [33] and alternative approaches have been investigated [33][41,42]. Finite difference PB solvers map fixed charges on point of a grid and use molecular surface information to assign a dielectric value to each grid midpoint (middle point between two grid points) and, indirectly, to map also the ionic accessibility function. In the simplest approaches, the latter is simply the geometric complement to the solvent excluded volume. In more advanced ones, however, a further region surrounding the molecular surface, named Stern layer, is considered, where the dielectric behavior is assumed to be the same as that of bulk water but where no ions are allowed to be present. Its width is usually quite short, around 2Å, and avoids unphysically high ionic concentrations in response to high charges located near the molecular surface. The resulting linear system can be solved via Gauss-Seidel or other iterative methods [34][3].

In order to compute the full PMF also non-polar energy term must be included. This energy component is often roughly estimated based on the Solvent Accessible surface area. Here, in contrast to what is done in the ASP approach, the SASA is only used to estimate the non polar component, that is:

$$\mathrm{\Delta }{G}_{np}=\gamma A_{\mathit{sasa}}$$ (30)

where γ has the physical dimension of a surface tension, its value is typically in the range of 20 to 30 [cal mol⁻¹ Å^.2] and A_sasa is the total solvent accessible surface area. The method by which one estimates the solvent free energy using both PB equation and the SASA is usually referred as PBSA [19]. SASA approach is quite a crude one, and still work has to be done to get a full modeling of hydrophobic effects.

2.3. Generalized Born

Poisson-Boltzmann equation is an elegant theory that captures some of the most relevant aspects of the underlying physics. However, the solution of either the linear or non-linear PB equation is a non trivial task from both the numerical and computational time point of view. For this reason, the so-called Generalized Born models [18] gained more attention. This is due to their relatively simple conceptual basis, their highly advanced parametrization, and their efficient practical implementation, largely originating from the fact that forces can be calculated analytically.

In the case of a simple ion of radius a and charge q immersed in a dielectric ε_w both the potential and the electrostatic component of the solvation free energy can be found analytically. This result is known as the Born formula:

$$\mathrm{\Delta }{G}_{es}=-\frac{1}{2}\left(1-\frac{1}{{\epsilon }_w}\right)\frac{q^2}{a}$$ (31)

If we try to model a molecule as set of N atoms (spheres) of radii a₁, a₂, … , a_N and charges q₁, q₂, … , q_N and if we denote by r_ij the pairwise distances of the atom centers, then the electrostatic solvation energy can be written.

$$\mathrm{\Delta }{G}_{es}=-\frac{1}{2}\left(1-\frac{1}{{\epsilon }_w}\right)\sum _i^N\frac{q_i^2}{a_i}-\frac{1}{2}\left(1-\frac{1}{{\epsilon }_w}\right)\sum _i^N\sum _{j\ne i}^N\frac{q_j{q}_i}{r_{ij}}$$ (32)

This formula contains both Born terms and pairwise Coulomb terms. This formula holds if we are assuming that r_ij ≫ a_i, ∀i. The purpose of GB theory consists in finding a form for the energy that somehow recalls equation (32) but that removes the hypothesis r_ij ≫ a_i, ∀i.. In order to overcome the limitations of (32), GB tries to give a unified model to a_i and to r_ij. GB theory prescribes to estimate the electrostatic solvation energy as:

$$\mathrm{\Delta }{G}_{es}=-\frac{1}{2}\left(1-\frac{1}{{\epsilon }_w}\right)\sum _{i,j}^N\frac{q_j{q}_i}{f_{GB}}$$ (33)

Where f_GB is a function that should be equal to the product of the “effective Born radii” R_i and R_j when r_ij is small and equal to r_ij at larger distances. Note that in this equation the reference to the interior dielectric constant is not present, and the geometry is assumed to be intrinsically spherical. Thus it is intuitive that the method will be as accurate as f_GB captures the geometry of the problem and the correct parameterization of this term is crucial. A typical [18] form for f_GB is the following:

$$f_{GB}=\sqrt{r_{ij}^2+R_i{R}_{j}exp\left(-\frac{r_{ij}^2}{4}{R}_i{R}_j\right)}$$ (34)

where R_i are the effective Born radii of atoms which, not only are different from van der Waals radii, but usually depend also on the position of other atoms. Depending on how these radii are approximated, different GB approaches can be obtained: however in all GB methods the key approximation to compute the radii stands in assuming that the electric displacement field behaves as a Coulomb term. Under this approximation, the Born radii are computed as:

$$\frac{1}{R_i}=\frac{1}{4\pi }{\int }_{\mathit{solvent}}\frac{1}{{(\mathbf{r}-{\mathbf{r}}_i)}^4}{d}^3\mathbf{r}$$ (35)

Several improvements can be added to the baseline model. It can be shown that if the internal dielectric constant ε_in is taken into account then GB equation becomes:

$$\mathrm{\Delta }{G}_{es}=\frac{1}{2}\sum _{i\ne j}^N\frac{q_i{q}_j}{{\epsilon }_{in}{r}_{ij}}-\frac{1}{2}\left(\frac{1}{{\epsilon }_{in}}-\frac{1}{{\epsilon }_w}\right)\sum _{i,j}^N\frac{q_j{q}_i}{f_{GB}}$$ (36)

The GB equations can also be modified in order to incorporate salt effects: in particular it has been shown that, at low salt concentrations, PB and GB methods give similar results [18]. Among other variations we cite: the Surface GB (SGB) [43] in which the pairwise nature of GB is mitigated by an integral of the entire surface, GBSA in which non polar energy terms are estimated by using the SASA [44], the Generalized Born using Molecular Volume or Generalized Born with simple Switching [45], multiple dielectric GB [46] and Generalized Born like models [47].

In general, a common trait of most of the GB literature consists in slightly different parameterizations and empirical correction terms used to better fit experimental or PB data with the consequent risk of over-fitting and a decrease of predictivity. Another caveat, as we already mentioned, is the key assumption of GB for which the displacement field behaves as a Coulombic term. Despite these drawbacks, GB models are interesting because not only they are able to capture a significant part of the electrostatic behavior of molecules, but, additionally, their closed form allows an easy manipulation, for instance in the computation of forces, thus leading to a relatively simple embedding of GB routines in molecular dynamics codes. In the following, we detail the state of the art AGBNP1/2 method proposed by Gallicchio and Coworkers [12][48].

2.3.1. Analytical Generalized Born Plus Non Polar

A particularly elaborate method is due to Gallicchio and coworkers [12][48]. In this model the solvation free energy is split in three components:

$$\mathrm{\Delta }{G}_s=\mathrm{\Delta }{G}_{es}+\mathrm{\Delta }{G}_{np}=\mathrm{\Delta }{G}_{es}+(\mathrm{\Delta }{G}_{\mathit{cav}}+\mathrm{\Delta }{G}_{\mathit{vdW}})$$ (37)

where the non polar term is further partitioned into a cavity solvation free energy ΔG_cav and a solute-solvent van der Waals dispersion interaction component ΔG_vdW. The solute volume is modeled using Gaussian overlap, as discussed in [49], where the solute volume is computed using the Poincaré formula (inclusion-exclusion principle); in order to speed-up calculations switching functions are used for trimming Gaussian tails.

From the electrostatics point of view, this method is based on the pairwise descreening GB scheme where the Born radius of each atom is obtained by summing a suitably defined descreening function over its neighbors [12]. In contrast to other GB implementations, in AGBNP the volume scaling factors, which account for atomic overlap, are computed from the geometry of the molecule rather than being fitted either experimentally or with respect to Poisson-Boltzmann calculations. In this way AGBNP method has much less degrees of freedom with respect to other methods thus improving its prediction ability (transferability) across possibly new functional groups. Additionally, the inverse Born radii are clipped by a filter function that sets as lower and upper bounds respectively the values of 0 and 50 Å.

Concerning the non polar component of the energy, the cavity term is accounted using a SASA approach that employs augmented heavy atoms radii. These radii are defined as the van der Waals radii augmented by 0.5 Å. The solute-solvent van der Waals free energy is modeled by the expression:

$$\mathrm{\Delta }{G}_{\mathit{vdW}}=\sum _i{\alpha }_i\frac{A_i}{(R_i+R_W)}$$ (38)

where α_i is a dimensionless parameter whose value is usually in the order of the unity and:

$$A_i=-\frac{16}{3}\pi {\rho }_w{\epsilon }_{iw}{\sigma }_{iw}^6$$ (39)

where ρ_w = 0.03328 Å⁻³ is the density of water at standard conditions, σ_iw, ε_iw are respectively the OPLS force field Lennard-Jones interaction parameters for the interaction of solute atom i with the oxygen atom of the TIP4P water model [50] and R_w = 1.4 Å is the radius of water molecule modeled as a sphere. AGBNP1 has been successfully applied to several applications involving molecular dynamics simulations [12].

In contrast to AGBNP1, in AGBNP2 the solvation free energy model takes into account explicitly hydrogen bonding with a dedicated energy term. The total energy reads as:

$$\mathrm{\Delta }{G}_s=\mathrm{\Delta }{G}_{es}+\mathrm{\Delta }{G}_{np}+\mathrm{\Delta }{G}_{hb}$$ (40)

where ΔG_hb represents a first solvation shell correction accounting for the solvation free energy that the continuum model for the solvent is not able to capture. Additionally, the pairwise descreening model is based on the Solvent Excluded Volume, rather than the van der Waals volume as per AGBNP1.

The model for ΔG_hb is based on the geometry of the molecule, and tries to guess how much a solute atom can interact with a hydration site at the solute surface. The basic idea is to find the points in space where a sphere of radius R_w, representing a water molecule, can be located in order to form a hydrogen bond. The position r_w of this water probe is a function of the positions of two or more neighboring atoms and can be written as:

$${\mathbf{r}}_w={\mathbf{r}}_D+\frac{{\mathbf{r}}_H-{\mathbf{r}}_D}{\mid {\mathbf{r}}_H-{\mathbf{r}}_D\mid }{d}_{HB}$$ (41)

where r_D is the position of the heavy solute atom, r_H is the position of the polar hydrogen and d_HB is the distance between the heavy atom donor and the center of the water sphere. Similar relations hold for linear, triangular and tetrahedral displacements. Given the displacements, one has to estimate the magnitude of the hydrogen bonding correction. The latter is a function of the estimated water occupancy in the previously identified positions [48]. Let w_w be the mentioned occupancy, the formula for hydrogen bonding reads:

$$\mathrm{\Delta }{G}_{hb}=\sum _w{h}_{w}S(w_w;w_a,w_b)$$ (42)

where h_w is a correction energy term that depends on the type of solute-water hydrogen bond, S(w_w; w_a, w_b) is a polynomial switching function in which the two switching limits are w_a = 0.15 and w_b = 0.5.

AGBNP2 was successfully applied in molecular dynamics simulations: among other results it was shown, rather impressively, that this model was able to recover both the solvation barrier at 5 Å and the “second minimum” of the PMF simulation of propyl guanidinium and ethyl acetate in a bidentate coplanar formation where classical continuum models fail [51][33].

3. Implicit solvent in the calculation of binding free energies

The methods discussed on the previous sections represent the basic different frameworks used in implicit solvent modeling. In the context of biophysical simulations, PB and GB are typically coupled with higher level of theories, or further external parameterizations, in order to improve their accuracy in the description, for instance, of the solute. In particular, implicit solvent modeling has received great interest for estimating the binding affinity via MD or MC sampling, and it has been applied quite successfully in several cases.

The underlying idea of most free energy methods based on implicit solvent modeling, is to take advantage of the fact that the free energy is a state function and, as such, it can be decomposed in several contributions that are separately calculated. In other words, rather than explicitly simulating the binding between the two interacting partners (typically a protein and a small molecule ligand), a Born-Haber-like thermodynamic cycle is envisioned, where one is only concerned in estimating free energy differences. This procedure can be computationally convenient in terms of convergence. Any physical or unphysical transformation can therefore be exploited, provided that the cycle is properly closed. The estimation of relative binding free energies (ΔΔG) with this approach is straightforward. However absolute binding free energies (ΔG^∘) could also be calculated with due precautions [52]. In the context of implicit solvent modeling, the solvation free energy comes as a natural contribution to the free energy of binding, and for this reason this quantity is usually (but not necessarily) used to build thermodynamic cycles.

It must be highlighted that whenever the transformation between states is performed by gradually mutating one state into another through intermediate steps, the free energy difference can be rigorously calculated by means of free energy perturbation [53] or thermodynamic integration [54] theories. These approaches, usually referred to as “pathway methods” regardless of the physical or unphysical nature of the transformation, are still relatively time consuming. For this reason, in the field of computer-assisted drug design, faster, albeit approximate, methods are often more advisable. The so called “end-points methods” necessitate the calculation of ensemble averages only for the initial and final states of the transformation, thus saving up valuable computational time. In general, the price to be paid for this is a loss in accuracy, and hence the need to introduce here and there corrections or ad hoc empirical parameters depending on the validity of the underlying approximations. Among these methods, in the following, we will focus our attention on two approaches which turned out to be particularly effective in calculating the binding free energy in the framework of implicit solvation models: the Linear Interaction Energy (LIE) method, and the Molecular Mechanics-Poisson Boltzmann/Generalized Born Surface Area (MM-PB/GB SA) methods.

3.1. Linear Interaction Energy (LIE) methods

The LIE method has been originally introduced by Åqvist and coworkers to calculate the absolute binding free energy of a series of 5 peptidomimetic inhibitors against endothiapepsin in the context of explicit solvent MD simulations [20]. Later, Sham and coworkers [55] have shown that LIE can be thought of as a special case of a more general and rigorous approach: it derives from a unified thermodynamic cycle based on the use of the Linear Response Approximation (LRA) to evaluate the electrostatic contribution to the binding free energy, and the Protein Dipoles Langevin Dipoles method (PDLD, or its semi-microscopic variant PDLD/S) [56] to estimate the non-electrostatic part. In particular, it can be shown that most of the weakest approximations underlying LIE are rooted in the latter contribution. Properly accounting for this term would require a formal derivation from statistical mechanics arguments similar to that employed in more advanced approaches such as the double-decoupling method [52]. The interested reader is referred to the paper by Sham and coworkers as well as to specific reviews [57] for further details. Here, our attention is rather directed on the theoretical basis of the linear response theory and on some technicalities required to employ LIE in the framework of implicit solvent models.

3.1.1. Linear response theory

The basic idea behind LIE and related methods is the possibility to calculate the electrostatic contribution of the solvation free energy by using the LRA. As it will be clear later, within the LIE terminology the word “solvation” is used in a fairly broad sense, meaning that the contribution one aims to calculate is related to the embedding of the solute in a certain medium having peculiar features, being it either the solvent itself or even the protein.

The linear response theory has been developed to describe electron transfer processes within a semi-macroscopic formalism, including quantum mechanical effects as well as solvent reorganization phenomena. It is based on the assumption, valid only under certain conditions, that the response of the system to the perturbation is linear with respect to the magnitude of the perturbation [58]. Here, the perturbation is represented by an electron transfer process (or, more in general, by a charge transfer process), and the response basically consists of the polarization of the solvent. It is worth noting that the linear regime is indeed the underlying assumption of most of implicit solvent approaches.

The change in free energy associated to the charge transfer between the initial and final states of the solute, can be described in terms of a coupling parameter λ varying from 0 to 1. Within a classical description, the 0 state represents an “uncharged” state of the solute, i.e. a solute with all partial charges set to zero. The 1 state rather indicates a “charged” solute where all partial charges are turned “on”, regardless of the overall net charge. In other words, the 0 and 1 states represent a solute that is electrostatically decoupled and coupled to the solvent, respectively. More formally, the electrostatic interaction energy between solute and solvent U in the state λ can be expressed as:

$$U_{\mathrm{\lambda }}=\mathrm{\lambda }{\sum }_i{q}_i{\phi }_i$$ (43)

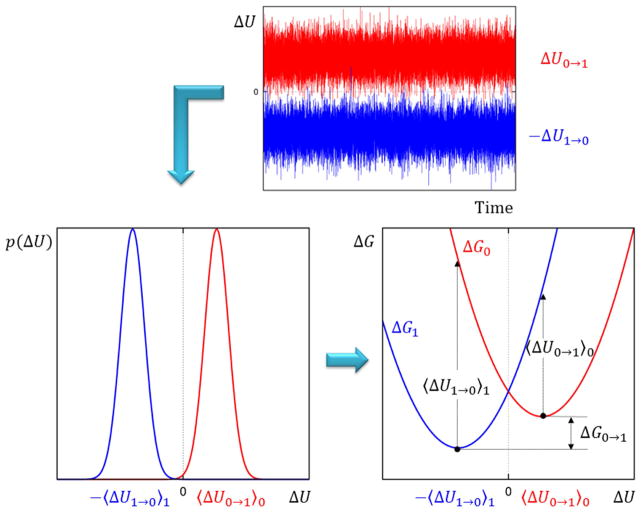
where q_i represents the partial charge at the solute’s atom i, ϕ_i is the electrostatic potential on the same atom due to instantaneous position and orientation of the solvent molecules, and the sum runs over all the atoms of the solute [59]. As the system evolves, the value of the electrostatic potential fluctuates around the average value for the given state (0 or 1), and so does the interaction energy U_λ, leading to a Gaussian probability distribution function. Now, suppose to instantaneously change the charge state of the system by operating on λ, and to measure the corresponding interaction energy while keeping on propagating the Newton’s equation of motions for the system in the reference state. If enough statistics is collected, the probability distribution function of the energy difference p(ΔU) will be Gaussian shaped too. By applying such procedure on two independent simulations, one sampling from the “uncharged” state and the other from the “charged” one, the average values <ΔU_0→1>₀ and <ΔU_1→0>₁ can be calculated, where the <…>_λ notation means that the ensemble average is evaluated over the configurations of the system sampled in the λ state. The probability distribution functions p(ΔU) can also be expressed as a configurational average, which for state 0 and state 1 takes the form [60]:

$$p{(\zeta )}_0=\frac{\int \delta (\zeta -\mathrm{\Delta }U)exp(-U_0/k_{B}T)\mathrm{d}\mathbf{X}}{\int exp(-U_0/k_{B}T)\mathrm{d}\mathbf{X}}$$ (44)

$$p{(\zeta )}_1=\frac{\int \delta (\zeta -\mathrm{\Delta }U)exp(-U_1/k_{B}T)\mathrm{d}\mathbf{X}}{\int exp(-U_1/k_{B}T)\mathrm{d}\mathbf{X}}$$ (45)

where dX indicates integration over the whole configurational space. The Dirac delta function δ is needed in order to consider only those configurations satisfying the condition: ζ = ΔU. These probabilities lead to free energy functions up to an additive constant:

$$\mathrm{\Delta }G{(\zeta )}_0=-k_{B}Tln\mathit{p}{(\zeta )}_0$$ (46)

$$\mathrm{\Delta }G{(\zeta )}_1=-k_{B}Tln\mathit{p}{(\zeta )}_1+\mathrm{\Delta }{G}_{0\to 1}$$ (47)

where ΔG_0→1 is the free energy difference between state 1 and state 0. Under the assumption that the probability distribution functions of eq. (44) and (45) are Gaussians, the corresponding free energy functions would be harmonic. It is useful to represent the free energy curves for the two states in a single plot. By borrowing the terminology from electron transfer theory, the “diabatic” free energy curves for two hypothetical states are reported in Figure 3. We stress that the reaction coordinate between the two states is the electrostatic energy difference between solute and solvent or, in other words, the solvent polarization energy. The free energy minima for state 0 and 1 are exactly located at <ΔU_0→1>₀ and <ΔU_1→0>₁, respectively, and it is possible to show that if the two curves are perfect parabolas with same curvature (meaning that the linear response approximation holds), they intersect exactly at ΔU = 0. This construction allows us to consider the charge transfer process as a jumping between surfaces driven by thermal fluctuations of the solvent [60]. By taking advantage of the cumulant expansion of the free energy characteristic of the perturbation theory,[53] the energetic components of this process can be made explicit. Accordingly, by truncating the expansion at the second order, the free energy difference from state 0 to 1 is:

$$\mathrm{\Delta }{G}_{0\to 1}={\langle \mathrm{\Delta }{U}_{0\to 1}\rangle }_0-\frac{1}{2k_{B}T}({\langle \mathrm{\Delta }{U}_{0\to 1}^2\rangle }_0-{\langle \mathrm{\Delta }{U}_{0\to 1}\rangle }_0^2)$$ (48)

where the first term on the left (average fluctuations in energy) represents the static energy gap between surfaces, that is the energy required to perturb the system while keeping it constrained in the reference state configuration, whereas the second term (mean squared fluctuations in energy) represents the relaxation (or reorganization) energy due to solvent polarization in response to the perturbation (see Figure 3). As pointed out by Levy and coworkers, [59] eq. (48) corresponds to a “one-step” thermodynamic perturbation calculation with a Gaussian fluctuation distribution. In a similar way, by taking state 1 as a reference, we have:

$$\mathrm{\Delta }{G}_{1\to 0}={\langle \mathrm{\Delta }{U}_{1\to 0}\rangle }_1-\frac{1}{2k_{B}T}({\langle \mathrm{\Delta }{U}_{1\to 0}^2\rangle }_1-{\langle \mathrm{\Delta }{U}_{1\to 0}\rangle }_1^2)$$ (49)

Figure 3. Pictorial representation of the linear-response approximation for a charging process of a solute in a polar solvent.

First, the interaction energy between solute and solvent <ΔU 0→1 >0 and <ΔU 1→0 >1 is calculated over time from two independent simulations sampling from the “uncharged” and “charged” state of the solute, respectively. Then, the probability distribution functions p(ΔU) and hence the free energy functions for both states are recovered. Under the assumption that fluctuations in interaction energies are Gaussian shaped, the free energy functions are harmonic, and they intersect exactly at zero. The charging process is finally described as a vertical jump from the red to the blue curve, followed by a dynamical relaxation on the latter free energy function. The free energy difference between the two states ΔG 0→1 is obtained by construction.

It is convenient to rearrange eq. 49 in order to express the free energy ΔG_0→1 as a function of the configurations sampled in state 1:

$$\mathrm{\Delta }{G}_{0\to 1}=-{\langle \mathrm{\Delta }{U}_{1\to 0}\rangle }_1+\frac{1}{2k_{B}T}({\langle \mathrm{\Delta }{U}_{1\to 0}^2\rangle }_1-{\langle \mathrm{\Delta }{U}_{1\to 0}\rangle }_1^2)={\langle \mathrm{\Delta }{U}_{0\to 1}\rangle }_1+\frac{1}{2k_{B}T}({\langle \mathrm{\Delta }{U}_{1\to 0}^2\rangle }_1-{\langle \mathrm{\Delta }{U}_{1\to 0}\rangle }_1^2)$$ (50)

Then, summing eq. 48 with eq. 50, and recalling that, under the assumption of a linear response, the mean squared fluctuations in state 0 and 1 are equal and then will cancel out, we finally obtain the LRA master equation [20]:

$$\mathrm{\Delta }{G}_{0\to 1}=\frac{1}{2}({\langle \mathrm{\Delta }{U}_{0\to 1}\rangle }_0+{\langle \mathrm{\Delta }{U}_{0\to 1}\rangle }_1)$$ (51)

Obviously, a similar expression would have been obtained for the reverse transition.

3.1.2. LIE variants and significance of the empirical parameters

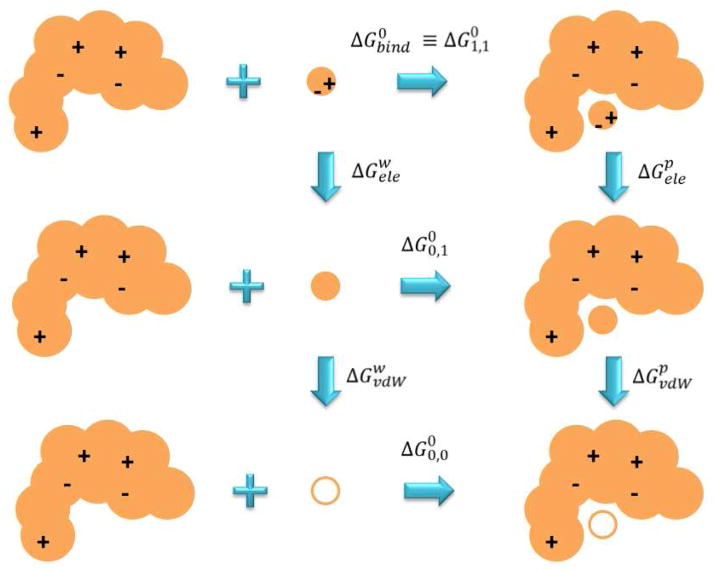
As previously mentioned, the LIE method can be derived in the context of the thermodynamic cycle reported by Sham and coworkers,[55] and illustrated in Figure 4. According to that cycle, the binding process is decomposed in several contributions that have to be estimated in order to recover the standard free energy of binding. Here, we will denote this quantity as ΔG^∘_1,1, where the subscript means that the binding free energy is evaluated for a ligand molecule having both electrostatic and van der Waals interactions “on”. This measure has to be distinguished from ΔG^∘_0,1, which represents the binding free energy of an “uncharged” ligand, and with ΔG^∘_0,0, that accounts for the free energy of binding of a ligand having both electrostatic and van der Waals interactions decoupled from the surroundings. Thus, the uppermost cycle of Figure 4 involves the estimation of the free energy required to “charge” a ligand in the solvent and in the protein environment (vertical legs on the right and on the left, respectively), and the estimation of the standard free energy of binding for the “uncharged” ligand. The binding free energy can be therefore calculated as:

$$\mathrm{\Delta }{G}_{1,1}^0=\mathrm{\Delta }{G}_{\mathit{ele}}^p+\mathrm{\Delta }{G}_{0,1}^0-\mathrm{\Delta }{G}_{\mathit{ele}}^w$$ (52)

Figure 4. Example of the thermodynamic cycle that can be used to calculate the free energy of binding by exploiting the LRA approximation.

Within the LIE class of methods, only the uppermost cycle is explicitly employed. “Ele” subscript stands for “electrostatics” and “vdW” for “Van der Waals”. Superscript “p” means protein, and “w” means solvent.

The exact value for ΔG^∘_0,1 can be estimated by further considering the cycle at the bottom of Figure 4, that can be expressed as:

$$\mathrm{\Delta }{G}_{0,1}^0=\mathrm{\Delta }{G}_{\mathit{vdw}}^p+\mathrm{\Delta }{G}_{0,0}^0-\mathrm{\Delta }{G}_{\mathit{vdw}}^w$$ (53)

where ΔG^p_vdw and ΔG^w_vdw are the free energy contributions required to create the ligand’s van der Waals cavity in the protein and in the solvent, whereas ΔG^∘_0,0 is a term related to the entropy loss for restraining a non-interacting ligand in the protein binding site with respect to the molar volume available at the standard concentration in water. We will not further describe these terms, we will rather focus on eq. 52 which, after some approximations, will lead us directly to the LIE master equation.

As already anticipated, the leading approximation behind LIE is to calculate the electrostatic contributions ΔG^p_ele and ΔG^w_ele relying on the linear response theory. Thus, according to eq. 51, these terms can be estimated as [20,61]:

$$\mathrm{\Delta }{G}_{\mathit{ele}}^{p/w}=\frac{1}{2}\left({\langle \mathrm{\Delta }{U}_{0\to 1}^{p/w}\rangle }_0+{\langle \mathrm{\Delta }{U}_{1\to 0}^{p/w}\rangle }_1\right)\equiv \frac{1}{2}\left({\langle U_{\mathit{ele}}^{p/w}\rangle }_0+{\langle U_{\mathit{ele}}^{p/w}\rangle }_1\right)$$ (54)

where U^p/w_ele is the solute-environment electrostatic interaction energy, and the second equality in eq. 54 is only introduced in order to simplify the notation and to get closer to the typical LIE formalism. We note that, while the linear response is a reasonable approximation to estimate such contribution in a solvent environment (see below), the same approximation cannot be equally justified for the same process in the protein, since in general protein binding sites do not behave as linear media. A second approximation virtually employed in all LIE implementations is to neglect <U^p/w_ele>₀, reducing ΔG^p/w_ele to:

$$\mathrm{\Delta }{G}_{\mathit{ele}}^{p/w}\approx \frac{1}{2}{\langle U_{\mathit{ele}}^{p/w}\rangle }_1$$ (55)

In an isotropic environment such as bulk water, this is justified by the assumption that solvent molecules will be randomly oriented around an “uncharged” solute (state 0). Again, since protein binding sites are intrinsically anisotropic, this approximation for the protein environment is not as appropriate as in water, and its use should only be regarded as a convenient way to simplify the calculations. Indeed, within this approximation, the electrostatic contribution to the free energy can be estimated by only sampling from the configurational space of the “charged” state, thus halving the computational cost of the whole procedure. Interestingly, in a thorough study aimed at investigating the validity of the linear response in polar solvents, Åqvist and Hannson have shown that LRA generally holds for monovalent ionic solutes, and deviations from predictions are mostly due to the neglect of <U^w_ele>₀, rather than to a real breakdown of the linear response approximation [61]. This means that solvent structure is not completely random even around an “uncharged” solute. On the contrary, for dipolar solutes, the major source of nonlinearity was actually found in the assumption of parabolic free energy functions with same curvature for the “charged” and “uncharged” states, with the larger deviations observed for solutes forming H-bond network with solvent [61].

By introducing eq. 55 in eq. 52, we obtain the following expression:

$$\mathrm{\Delta }{G}_{1,1}^0=\frac{1}{2}{\langle U_{\mathit{ele}}^p\rangle }_1+\mathrm{\Delta }{G}_{0,1}^0-\frac{1}{2}{\langle U_{\mathit{ele}}^w\rangle }_1$$ (56)

that can be further arranged in order to finally achieve the general form of the LIE master equation for explicit solvent calculations:

$$\mathrm{\Delta }{G}_{\mathit{bind}}^{\mathit{LIE}-\mathit{explicit}}=\alpha \left(\langle U_{\mathit{vdw}}^p\rangle -\langle U_{\mathit{vdw}}^w\rangle \right)+\beta \left(\langle U_{\mathit{ele}}^p\rangle -\langle U_{\mathit{ele}}^w\rangle \right)+\gamma$$ (57)

where the “1” subscript in the ensemble averages has been dropped for simplicity, since only the “charged” state sampling is considered from now on. In eq. 57, it is possible to recognize β as the LRA coefficient for the electrostatic term, which is equal to ½ in case of an ideally linear response, whereas α and γ are empirical parameters of less rigorous physical interpretation. Nonetheless, we note that the first term in eq. 57 can be considered as a measure of the non-polar contribution to the binding free energy, that is assumed to have a linear relationship with the van der Waals interaction energy difference in analogy with the observation that solvation energies of non-polar compounds scale approximately linearly with molecular size, [62] whereas γ is a correction term exploited to calibrate the offset of the absolute free energy. From this standpoint, it is also possible to relate the first and third terms of eq. 57 with the free energy contributions required to create the ligand’s van der Waals cavity in the protein and in the solvent, and the binding free energy of a non-interacting ligand, respectively, as shown in eq. 53.

In the original LIE formulation by Åqvist and coworkers, γ was set to zero and a van der Waals scaling factor of α = 0.163 was found to provide the best fit with experimental data [20]. It was only in later implementations that the use of γ as a further adjustable parameter started to be investigated. In the so-called “improved LIE”, Marelius and coworkers addressed the possibility to use α and γ as free parameters together with specific values of β assigned to different classes of compounds. Thus, chemical composition-dependent deviations from linear response were tabulated for their use in different practical applications (0.5 for compounds with ionic groups; 0.43, dipolar without hydroxyl groups; 0.37, dipolar with one hydroxyl group; 0.33, dipolar with more than one hydroxyl group)[63]. In the same study, the development of a more general version of eq. 57 was also attempted by using environment specific α and β parameters that, however, converged to similar values in the specific case investigated by the authors. Differently, in an alternate version of the method proposed by Jones-Hertzog and Jorgensen, the dependence of the non-polar contributions of the free energy of binding on the difference of the solvent accessible surface area (SASA) of the ligand in the two environments was considered [64,65]:

$$\mathrm{\Delta }{G}_{\mathit{bind}}^{\mathit{LIE}-\mathit{explict}}=\alpha \left(\langle U_{\mathit{vdw}}^p\rangle -\langle U_{\mathit{vdw}}^w\rangle \right)+\beta \left(\langle U_{\mathit{ele}}^p\rangle -\langle U_{\mathit{ele}}^w\rangle \right)+\gamma \left(\langle A_{\mathit{sasa}}^p\rangle -\langle A_{\mathit{sasa}}^w\rangle \right)$$ (58)

It is worth noting that all the coefficients in eq. 58 (as well as those in eq. 57) can be conveniently tuned in order to fit the computed free energies to available experimental data as in a linear-regression equation. By doing so, the method is clearly more resembling to a QSAR-like approach rather than a statistical mechanics derived method.

The combination of the LIE framework with continuum representations of the solvent is particularly attractive because, compared to explicit solvent formulations, a higher efficiency of sampling and a higher accuracy in the treatment of long-ranged electrostatics can be simultaneously achieved. Moreover, since continuum solvent models do rely on the LRA, the computation of the ligand-water interaction energy is straightforward, and equals to twice the electrostatic contribution to the solvation free energy:

$$\langle {\mathrm{U}}_{\mathit{ele}}^w\rangle =2\mathrm{\Delta }{G}_{\mathit{ele}}^{PB/GB}$$ (59)

In spite of this, the use of implicit solvent models also introduces some complications in the LIE formalism related to the fact that, in general, they are not pairwise decomposable, and care must be taken when evaluating the ligand-water interaction energies in the protein-bound state.

The first attempt to combine the LIE approach with a continuum representation of the solvent was made by Zhou and coworkers [66]. Relying on a surface-generalized Born (SGB) continuum solvation model, [67] the SGB-LIE directly follows from the Jones-Hertzog and Jorgensen version of the method, where the solvent accessible surface area term is naturally replaced by a cavity term which is more appropriate in an implicit solvent representation:

$$\mathrm{\Delta }{G}_{\mathit{bind}}^{\mathit{LIE}-\mathit{implicit}}=\alpha \left(\langle U_{\mathit{vdw}}^p\rangle -\langle U_{\mathit{vdw}}^w\rangle \right)+\beta \left(\langle U_{\mathit{ele}}^p\rangle -\langle U_{\mathit{ele}}^w\rangle \right)+\gamma \left(\langle U_{\mathit{cav}}^p\rangle -\langle U_{\mathit{cav}}^w\rangle \right)$$ (60)

However, in the SGB solvation model, the van der Waals energy is no longer explicit as it is included in the cavity term. Moreover, the implicit solvent contribution to the electrostatic energy is calculated for the whole protein-ligand complex, whereas the ligand interaction energy is rather required in eq. 60. To address this aspect, the authors evaluated the implicit ligand-water interactions in the bound state by counting the pairwise screened Coulomb energies as a whole if atoms are from the ligand, as half if one of the atoms is of the protein, and zero if both atoms are of the protein (see eq. 3). Then, <U^p_ele> is obtained by adding twice of this contribution (by virtue of the LRA) to the protein-ligand Coulomb energies [66]. The validity of such approach has been later questioned by Carlsson and coworkers who observed that the SGB-LIE model basically lacked the protein desolvation electrostatic contribution [68]. In their implementation, the LIE master equation takes the form:

$$\mathrm{\Delta }{G}_{\mathit{bind}}^{\mathit{LIE}-\mathit{implicit}}=\alpha \left(\langle U_{\mathit{vdw}}^p\rangle -\langle U_{\mathit{vdw}}^w\rangle \right)+\beta \left(\langle U_{\mathit{ele},l-p}^p\rangle +\langle U_{\mathit{ele},l-w}^p\rangle -\langle U_{\mathit{ele},l-w}^w\rangle \right)+\gamma$$ (61)

In eq. 61, the interaction energy for the protein-bound ligand is split in two terms, one evaluating the protein-ligand Coulomb interactions (<U^p_ele,l-p>), and the other accounting for the implicit ligand-water interactions (<U^p_ele,l-w>). This latter term is in turn evaluated by taking twice the difference between the electrostatic contribution to the solvation energy of a protein-ligand complex with the ligand in the “charged” state, and a protein-ligand complex with the ligand in the “uncharged” state. During these two calculations, only the terms involving ligand atoms are counted in the evaluation of the pairwise screened Coulomb energies. Both the use of GB and PB implicit solvent models were investigated, and, interestingly, the sampling was performed using an explicit solvent model that was later replaced by a continuum representation in a post-processing phase. In this respect, the methodology resembles some MM-PB/GB SA implementations that will be covered in the next section. A similar version of the LIE approach was developed by Su and coworkers in the context of the AGBNP implicit solvent model [69]. In that case, the electrostatic contribution included all the previous terms introduced by Carlsson and coworkers, plus a proper accounting for the desolvation of the protein (change in protein self-energies and pairwise screened Coulomb energies) due to the introduction of the ligand. Furthermore, differently from the two previous models, the AGBNP-LIE takes also into account changes in the protein-water and ligand-water van der Waals interactions. This is achieved through the following expression:

$$\mathrm{\Delta }{G}_{\mathit{bind}}^{\mathit{LIE}-\mathit{implicit}}=\alpha \left[\langle U_{\mathit{vdw}}^p+\left(G_{\mathit{vdw}}^{pl}-G_{\mathit{vdw}}^p\right)\rangle -\langle G_{\mathit{vdw}}^w\rangle \right]+\beta [\langle U_{\mathit{ele}}^p+2(G_{\mathit{ele}}^{pl}-G_{\mathit{ele}}^p)\rangle -\langle G_{\mathit{ele}}^w\rangle ]+\gamma \left[\langle G_{\mathit{cav}}^{pl}-G_{\mathit{cav}}^p\rangle -\langle G_{\mathit{cav}}^w\rangle \right]$$ (62)

In eq. 62, the terms (G^pl_x − G^p_x) stand for the difference in the x^th implicit solvent energy contribution evaluated for the protein-ligand complex with the ligand in the “on” and “off” state for the given interaction. Another fundamental difference between the AGBNP-LIE models compared to the above discussed methods, is the derivation of the linear-regression coefficients shown in eq. 62. The authors elegantly demonstrated that, under the linear response regime, the proportionality coefficient β might adopt different values depending on the magnitude of the mean squared fluctuations in energy, measured as <(δV)²>₀/k_BT, compared to the average electrostatic energy evaluated for the “uncharged” ligand state. In particular, they showed that when the fluctuations are much smaller than the average energy, β is equal to ½, whereas in the opposite limit, β = 1. Indeed, the former case is consistent with explicit solvent interactions energies, while when the solute is treated implicitly, a β value closer to 1 should be expected. A similar reasoning also applies to the van der Waals and the cavity term. We refer the interested reader to the original paper for the technicalities required to obtain eq. 62. Here, we limit ourselves to highlight the fact that an alternative version of the AGBNP-LIE model was also proposed, where the terms describing the ligand formation in protein and in water are decoupled and grouped together, thus leading to a fourth proportionality coefficient ω:

$$\mathrm{\Delta }{G}_{\mathit{bind}}^{\mathit{LIE}-\mathit{implicit}}=\alpha \left[\langle U_{\mathit{vdw}}^p+\left(G_{\mathit{vdw}}^{pl}-G_{\mathit{vdw}}^p\right)\rangle \right]+\beta \left[\langle U_{\mathit{ele}}^p+2\left(G_{\mathit{ele}}^{pl}-G_{\mathit{ele}}^p\right)\rangle \right]+\gamma \langle G_{\mathit{cav}}^{pl}-G_{\mathit{cav}}^p\rangle -\omega \langle G_{\mathit{vdw}}^w+G_{\mathit{ele}}^w+G_{\mathit{cav}}^w\rangle$$ (63)

In general, the LIE method allows an efficient estimation of the binding free energy for a set of chemically diverse compounds even when large and flexible ligands are considered. From the literature it emerges that estimates are generally in fair agreement with experimental data as long as substantially polar binding sites are considered. On the other hand, caution must be paid when hydrophobic binding sites are studied, where hydrophobic effects rather than electrostatics might play a dominant role in the binding free energy.

3.2. Molecular Mechanics-Poisson Boltzmann/Generalized Born Surface Area (MM-PB/GB SA) methods

The MM-PB SA (Molecular Mechanics Poisson-Boltzmann Surface Area) and its variant MM-GBSA (Molecular Mechanics Generalized-Born Surface Area) are approximate methods, originally introduced by Kollman and coworkers, aimed at calculating the binding free energy [70,11]. Unlike LIE, these methods do not contain any empirically adjustable parameter, thus a clear connection with fundamental statistical mechanics may be established [71]. Within the MM-PB/GB-SA framework the binding free energy is estimated exploiting a thermodynamic cycle were for each solute p, l, and pl, the solvation free energy is considered (see Figure 5). Accordingly, the binding free energy is expressed as follows [72]:

$$\mathrm{\Delta }{G}_{\mathit{bind}}^{MM-PB/BGSA}=\mathrm{\Delta }{G}_{\mathit{solv}}^{pl}-\mathrm{\Delta }{G}_{\mathit{solv}}^p-\mathrm{\Delta }{G}_{\mathit{solv}}^l+\left(\mathrm{\Delta }{U}_{\mathit{bind},\mathit{gas}}-T\mathrm{\Delta }{S}_{\mathit{bind},\mathit{gas}}^0\right)$$ (64)

Figure 5. Thermodynamic cycle employed in the MM-PB/GB SA method.

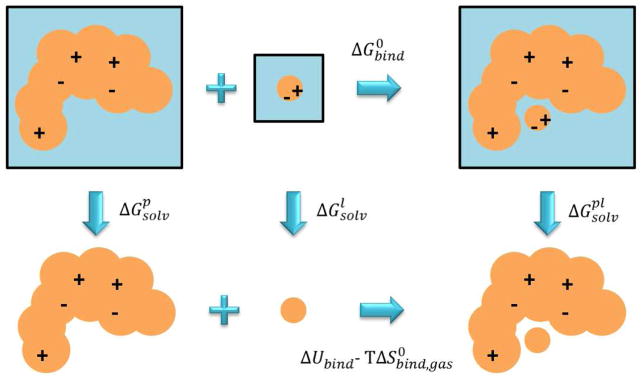
“Solv” subscript stands for “solvation”.

Within the approximation of implicit solvation models, the solvation free energy is expressed in terms of electrostatic and non-polar components. In particular, the electrostatic contribution is usually calculated by making use of PB solvers or GB solvation models, whereas the non-polar contribution is considered as proportional to the solvent-accessible surface area plus an additional surface tension term. The most difficult component to compute of the whole framework is the rightmost term of eq. 64, that is the one involving the internal energy and entropy differences for solutes in gas phase. The internal energy difference ΔU_bind,gas is calculated exploiting the following approximation:

$$\mathrm{\Delta }{U}_{\mathit{bind},\mathit{gas}}\cong \mathrm{\Delta }{E}_{\mathit{bind},\mathit{gas}}=E^{pl}-(E^p+E^l)$$ (65)

In order to estimate such a difference, ensemble average estimates from MD simulation are employed. To this end, two different approaches may be used: the two-states and the one-state model [73]. In the two-states model, the energies of each reactant and product are collected separately, meaning that a total of three simulations need to be performed:

$$\mathrm{\Delta }{E}_{\mathit{bind},\mathit{gas}}^{2-\mathit{state}}={\langle E^{pl}\rangle }_{pl}=\left({\langle E^p\rangle }_p+{\langle E^l\rangle }_l\right)$$ (66)

Conversely, in the one-state model only the bound complex is actually simulated, and the difference is recovered by calculating the average energies of the artificially isolated reactants from the ensemble of the sampled configurations belonging to the complex:

$$\mathrm{\Delta }{E}_{\mathit{bind},\mathit{gas}}^{1-\mathit{state}}={\langle E^{pl}\rangle }_{pl}=\left({\langle E^p\rangle }_{pl}+{\langle E^l\rangle }_{pl}\right)$$ (67)

Clearly, the two-state model is more attractive because, in principle, it should naturally take into consideration the ligand and protein reorganization upon binding, which is, in general, not negligible. However, due to the difficulty to achieve an exhaustive sampling with the currently available computational resources, different metastable states for reactants and products may be preferentially sampled and not properly relaxed, yielding the energy difference of eq. 66 very difficult to converge. For these reasons, in order to reduce the statistical uncertainty, the more naïve one-state model is often preferred [71,73]. From a practical standpoint, it should be stressed that, although the flexibility of the framework allows different solutions, MD simulations are usually performed in explicit solvent in order to better capture the physics of the system. Thus, the gas-phase energies and solvation free energies are calculated after water removal from configurations collected along the trajectory. The same sampled solute configurations are then used for the calculation of the entropic contribution. Regarding this point, harmonic or quasi harmonic approximations are generally employed, although the intrinsic plasticity of some proteins may invalidate the underlying assumption. The idea is to calculate vibrational frequencies for each of the species involved in the reaction, and to substitute them into the statistical mechanics vibrational entropy formula to obtain the respective absolute entropies (S^p_vib, S^l_vib, and S^pl_vib)[73]. If the normal mode approximation is employed, frequencies are calculated from the eigenvalues obtained upon diagonalization of the mass weighted matrix of the potential energy second derivatives with respect to coordinates. In contrast, when relying upon quasi-harmonic approximation, the mass weighted covariance matrix of atomic fluctuations is used instead. Besides, the entropy difference between products and reactants is estimated as:

$$\mathrm{\Delta }{S}_{\mathit{bind},\mathit{gas}}^0=S_{\mathit{vib}}^{pl}-\left(S_{\mathit{vib}}^p+S_{\mathit{vib}}^l\right)+\mathrm{\Delta }{S}_{\mathit{trans}}^0+\mathrm{\Delta }{S}_{\mathit{rot}}$$ (68)

where ΔS⁰_trans and ΔS_rot are the differences of the translational and rotational entropy of the solutes upon binding, which can be analytically calculated. As usual, the dependence on standard state must be properly taken into account [73]. Alternatively, the entropy difference may be calculated by separating the rigid body translational and rotational degrees of freedom of the ligand with respect to the protein frame. Thus, still relying upon a quasi-harmonic approximation, the entropy difference takes the following form [71,73]:

$$\mathrm{\Delta }{S}_{\mathit{bind},\mathit{gas}}^0=\left({\left(S_{\mathit{vib}}^p\right)}_{pl}+{\left(S_{\mathit{vib}}^l\right)}_{pl}\right)-\left({\left(S_{\mathit{vib}}^p\right)}_p+{\left(S_{\mathit{vib}}^l\right)}_l\right)+\mathrm{\Delta }{S}_{\mathit{trans}}^{l,0}+\mathrm{\Delta }{S}_{\mathit{rot}}^l$$ (69)

Due to the contribution separations, in eq. 69 the vibrational entropies of the protein and ligand in the complex must be calculated separately for consistency. The advantage of this approach is that the terms ΔS^l,0_trans and ΔS^l_rot may be directly estimated from the simulations by evaluating the translational and orientational volumes sampled by the ligand in the bound state (their correction to account for the standard state must be considered as well)[71,73]. As a matter of fact, the entropy estimate represents the weakest part of the whole framework since both inadequate sampling and assuming harmonic behaviors may severely hamper the accuracy of the entire calculations. To this extent, different corrections have been suggested [74,75]. From a practical perspective, because of the intrinsic challenging issue related to the entropy calculation, if a congeneric set of ligands is considered, the ΔS⁰_bind,gas term is sometimes neglected and assumed to be almost constant over the series of compounds. Despite those limitations, the MM-PB/GB-SA methods have been used by the biophysical community proving their helpfulness in rationalizing structure-activity relationships in different contexts.

4. Other methods

In this section we give a brief account of other implicit models that somehow are not easily classifiable in a given category and that possess some intrinsic peculiarities; in particular we concentrate on RISM, COSMO and ‘hybrid’ methods.

4.1. Molecular Integral Equations

The modern molecular integral equations, which basically provide a way to calculate pair correlations between molecules, are rooted in molecular Ornstein-Zernike equation coupled with a closure ansatz [76]. Such set of equations is six-dimensional in the case of homogeneous systems making them practically unsolvable (one must specify the distance between two molecules and their mutual orientations by five Euler angles). In early seventies Chandler and Andersen [23] proposed to average out the orientational degrees of freedom, thus giving rise to the well-known Reference Interaction Site Model (RISM) formalism. The first success in prediction of the structure of liquids comprising small non-polar molecules was followed by the problems with aqueous solutions, which were fully overcome only 20 years later, when the problem of trivial dielectric constant was solved within the dielectrically consistent RISM, which uses a special closure [77].

The advent of modern computers partially shifted the focus of the scientific community towards the simulations at the expense of new developments of the theory of integral equations, however, the newly available computational power made possible the solution of the three dimensional integral equations derived by Beglov and Roux [78]. In that work they proposed to average out the orientational degrees of freedom of solvent only, preserving thus the proper 3D geometry of the solute. These equations are now referred to as 3D-RISM theory. Interestingly, the nonlinear Poisson-Boltzmann equation can be considered as a special case of 3D-RISM where the short-range correlations are neglected.

Here we briefly consider the results achieved by the use of both RISM and 3D-RISM formalisms keeping in mind the model limitations of the former and computational demands of the latter. The application of RISM to bio molecules was aimed mainly to conformational equilibria of short polypeptide chains and the influence of solvent and co-solvents on these equilibria in Met-enkephalin [79] and C-peptide [80]. The simulated annealing combined with RISM treatment of water environment has given good agreement with the NMR [80] data and, moreover, appeared to be quite effective, since the convergence of simulated annealing algorithm was much faster in solution environment than in vacuum. The converged conformation was found to expose polar groups to solvent, which can be expected from the chemical intuition. Under the addition of alcohols, such as methanol and ethanol, the transition of the C-peptide from extended conformation to helix occurred, consistently with experimental findings.

Applications of 3D-RISM as an implicit solvent started only recently, when the solvers and the software have come to maturity and were implemented as a part of the AMBER package [7]. Due to its computational cost, the 3D-RISM solver must still be invoked a limited number of times during molecular dynamics evolution to get a significant performance improvement over conventional simulated evolution. Thus, most of the work in the recent years focused on increasing the time step to be used in implicit solvent MD simulations. The results show that a speedup of up to 100–500 [81] can be achieved over explicit-solvent MD simulations, making long time scaled studies of conformational changes in large biomolecules feasible. Although the 3D-RISM algorithms have a modest memory footprint and are difficult to be mapped into a GPU-computing hardware, latest solvers take advantage of the Tesla architecture and achieve speedups by a factor of 4–8 when compared to standard CPU implementations [82].

4.2. Conductor-Like Screening Model

COSMO method stands for Conductor-Like Screening Model [22]. The basic assumption of the method is that screening effects in media, such as water that exhibit high dielectric constants, can be well approximated by using an infinite dielectric constant i.e. a conductor. It is shown, from electrostatics, how, in this setting key quantities can be easily manipulated. Starting from the sphere case the Authors generalize the methodology to the case in which an arbitrary geometry (set of spheres) is possible. This approach allows to analytically compute the gradient of the energy with respect to atom positions. Also, this method assumes a rigid spherical geometry for each atom and employs a fast calculation method of the SAS. In CHARMM [8] a smooth version of COSMO has been developed to allow molecular dynamics simulations. A possible limit of COSMO is that it cannot easily deal with salts or space varying dielectrics.

4.3. Hybrid methods

Another class is that of ‘hybrid’ methods [24][25], which envision a mixed implicit/explicit solvent environment. The solute molecule is embedded in a sphere such that in the nearby of the molecule one has a reduced (with respect to the purely explicit solvent simulation) number of explicit water molecules. Beyond this sphere one retains the classical continuum representation (see Fig 6). The key advantage and purpose of this method is to maintain in the nearby of the molecule an accurate description, while at the same time avoiding the computational burden of explicit water, which beyond the sphere is replaced by a continuum medium. This method is particularly well suited when an accurate description of a binding site, or in general, of a part of a protein is required.

Figure 6.

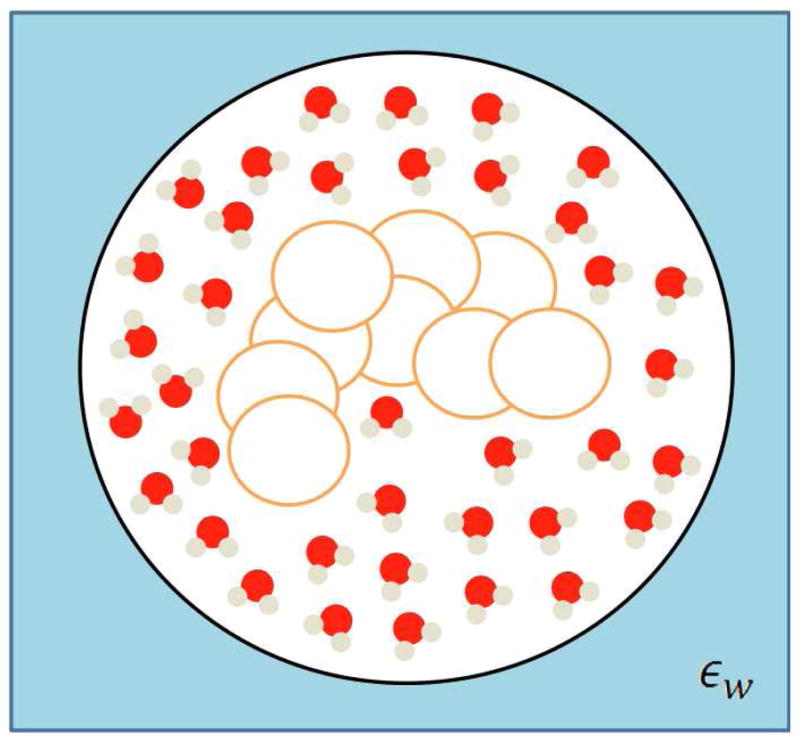
Pictorial representation of hybrid implicit/explicit methods.

Finally, other methods try to combine different approaches, such as Gran Canonical Monte Carlo, implicit and explicit solvent, in separate steps to characterize the water behavior in binding sites. In the so-called Watermap approach [83], one performs a molecular dynamics run to get a statistical thermodynamics analysis of the water molecules: this analysis is used to get both entropic and enthalpic properties of water within each hydration site. Differently, in SZMAP [26][27] a semi-continuum model is proposed where a single water molecule is explicitly used to probe the space and collect useful thermodynamics quantities.

5. Conclusions

In this review we discuss some of the most significant implicit solvent approaches in computational biophysics, and devote some attention to their use in molecular dynamics simulations and free energy estimation. What emerges is that there is no “one size fits all” method good for all intents and purposes. The user has to find the best compromise between the limitations of the underlying model, the desired accuracy and the available computational time, keeping in mind the numerical stability of the method, its applicability to the specific case and, importantly, the availability of a reliable and consistent parameterization. Implicit solvent modeling, as shown, has an approximate character but can be derived from statistical mechanics arguments, and relies on a strong theoretical background. These approximations, such as the hypothesis of linear response, go together with the need of suitable parameters and concepts such as the definition of the molecular surface and the computation of Born radii, just to name a few, the realization of which may heavily affect the effectiveness of the approaches. Finally, the most recent implementations try to move from full implicit models to hybrid ones where the solvent behavior is reconstructed from a combination of short explicit waters simulation (hybrid, single probe etc..) and suitable post processing analysis.

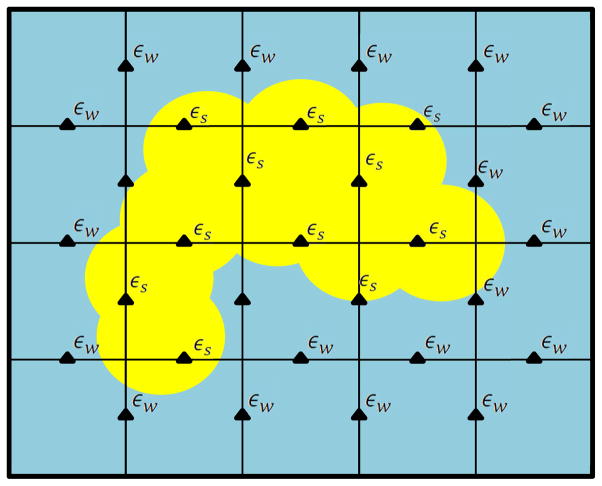
Figure 2. Discretization of the dielectric function in a finite difference solver of PB equation in a 2D domain.

The dielectric constant needs to be mapped on all the midpoints of the grid. For a cubic grid of side n, a data structure of size 3n³ must be allocated.

Highlights.

• We review several implicit solvent methods.

• Basic statistical mechanical foundations and derivations are provided.

• Implicit methods can be combined with molecular dynamics to estimate free energy.

• No “one size fits all” approach, the best method depends on the problem at hand.