Abstract
The presence of short-latency (SL), less compressive-growing components in bandpass-filtered transient-evoked otoacoustic emission (TEOAE) waveforms may implicate contributions from cochlear regions basal to the tonotopic place. Recent empirical work suggests a region of SL generation between ∼1/5 and 1/10-octave basal to the TEOAE frequency’s tonotopic place. However, this estimate may be biased to regions closer to the tonotopic place as the TEOAE extraction technique precluded measurement of components with latencies shorter than ∼5 ms. Using a variant of the non-linear, double-evoked extraction paradigm that permitted extraction of components with latencies as early as 1 ms, the current study empirically estimated the spatial-extent of the cochlear region contributing to 2 kHz SL TEOAE components. TEOAEs were evoked during simultaneous presentation of a suppressor stimulus, in order to suppress contributions to the TEOAE from different places along the cochlear partition. Three or four different-latency components of similar frequency content (∼2 kHz) were identified for most subjects. Component latencies ranged from 1.4 to 9.6 ms; latency was predictive of the component’s growth rate and the suppressor frequency to which the component’s magnitude was most sensitive to change. As component latency decreased, growth became less compressive and suppressor-frequency sensitivity shifted to higher frequencies. The shortest-latency components were most sensitive to suppressors approximately 3/5-octave higher than their nominal frequency of 2 kHz. These results are consistent with a distributed region of generation extending to approximately 3/5-octave basal to the TEOAE frequency’s tonotopic place. The empirical estimates of TEOAE generation are similar to model-based estimates where generation of the different-latency components occurs through linear reflection from impedance discontinuities distributed across the cochlear partition.
Keywords: two-tone suppression, basal reflection, different-latency components, TEOAE
INTRODUCTION
When analyzed across a narrow frequency band, transient-evoked otoacoustic emissions (TEOAEs) exhibit a long-latency (LL) and at least one short-latency (SL) amplitude peak, or component. SL components grow less compressively than their LL counterparts, with the effect that the largest contribution to the total TEOAE (i.e., the TEOAE analyzed across a time window spanning all components) shifts from the LL component at low stimulus levels to SL components at high stimulus levels (Withnell and McKinley 2005; Goodman et al. 2009; 2011). The latencies of the different components are approximately level invariant and separated in time by a factor of 1.6 (Carvalho et al. 2003; Goodman et al. 2011; Moleti et al. 2012). The difference in component latencies and level-dependent contributions to the total TEOAE underlies the decrease in the total TEOAE’s latency with increasing stimulus level (Moleti et al. 2012; Rasetshwane et al. 2013; Lewis and Goodman 2014). Contributions to the stimulus-frequency (SF) OAE from different-latency components analogous to those in the TEOAE (Sisto et al. 2013) may similarly underlie the level-dependency of SFOAE latency and account for non-monotonicity in SFOAE input/output (I/O) functions (e.g., Schairer et al. 2003; Choi et al. 2008; Lewis and Goodman 2014).
The contrasting latencies and growth rates of the different-latency TEOAE components suggest generation through different mechanisms and/or at different places in the cochlea. Generation of the LL component likely occurs at the tonotopic place, presumably through linear coherent reflection (LCR; Zweig and Shera 1995; Shera and Guinan 1999; Kalluri and Shera 2007a). (In this paper, the term “tonotopic place” refers to the place of maximum basilar membrane, BM, vibration for low-level stimuli.) The generation mechanism and place of the SL components are less certain, with both intermodulation distortion and basal coherent reflection being hypothesized (Withnell and McKinley 2005; Withnell et al. 2008; Goodman et al. 2009, 2011; Moleti et al. 2012; Moleti et al. 2013). The latencies of the SL components imply generation basal to the tonotopic place; however, the basal-extent of such contributions is unclear.
Modeling work by Moleti et al. (2013) has implicated a region of SL generation displaced basally from the tonotopic frequency place by approximately 1/3-octave. Empirical evidence concerning the generation place of SL components is limited. A single study by Moleti et al. (2014) estimated the region of SL TEOAE generation to be within ∼1/5- to 1/10-octave basal to the tonotopic place. However, this estimate was restricted to SL components with latency shorter than that of the LL component by a factor of approximately 1.6. Components with even shorter latencies have been reported (Goodman et al. 2009; 2011; Lewis and Goodman 2014), but the measurement of these by Moleti et al. was likely precluded as a result of their extraction technique. Specifically, to remove stimulus artifact, the initial 2.5 ms of the TEOAE were discarded and an onset ramp was applied to the subsequent 2.5 ms. As such, any components occurring within the initial 5 ms of the TEOAE were either eliminated or attenuated. Had shorter-latency components been measured, a more basally distributed region of generation may have been found.
The goal of the current study was to empirically estimate the cochlear regions contributing to the different-latency TEOAE components. A nonlinear extraction technique was used that preserved the earliest portion of the OAE while also minimizing stimulus artifact (Keefe 1998). In light of recent work demonstrating that SL components depend on the active elements for cochlear amplification (Mertes and Goodman 2013; Moleti et al. 2014), a two-tone suppression paradigm was used to examine how suppression of the active elements at different-frequency cochlear locations affects the magnitudes of the different-latency components in the 2 kHz TEOAE. The different-latency components were hypothesized to be differentially sensitive to suppressor frequency, with shorter-latency components being more sensitive to higher-frequency suppressors than longer-latency components. The first half of the study describes the latencies and growth rates of the components. The second half of the study describes the relationship between a component’s latency and sensitivity to suppressor frequency.
METHODS
Subjects
Ten subjects (4 male, 6 female) between the ages of 18–29 years old participated in the study. All subjects had normal hearing thresholds (≤20 dB HL) at the octave frequencies between 0.25–8 kHz and normal middle-ear function (assessed through 226 Hz tympanometry) in the test ear (5 right ears, 5 left ears). Data collection was completed over the course of 2 visits (∼2 h each) spaced within 1 month of one another. The research protocol was approved by the Institutional Review Board at the University of Iowa.
Signal Generation & Data Acquisition
Stimuli were generated using custom written software (MATLAB, The Mathworks, Inc). Stimuli were routed from the computer to an external 24-bit soundcard (UltraLite-mk3 Hybrid, Mark of the Unicorn). The two-channel electrical signal was directed through a pair of earphones (Sennheiser IE8). Silicone tubing was used to attach each earphone to a receiver port of an ER10B+ probe assembly (Etymotic Research, Inc.). The ear canal pressure responses to the stimuli were measured by the ER10B+ probe assembly, routed to the external soundcard, and digitized at a sampling rate of 44.1 kHz. The digital signal was sent to the computer and stored on the hard drive for offline analysis. Stimulus delivery and recording were controlled using MATLAB and custom written software.
Measurement and Analysis of TEOAEs
Stimuli
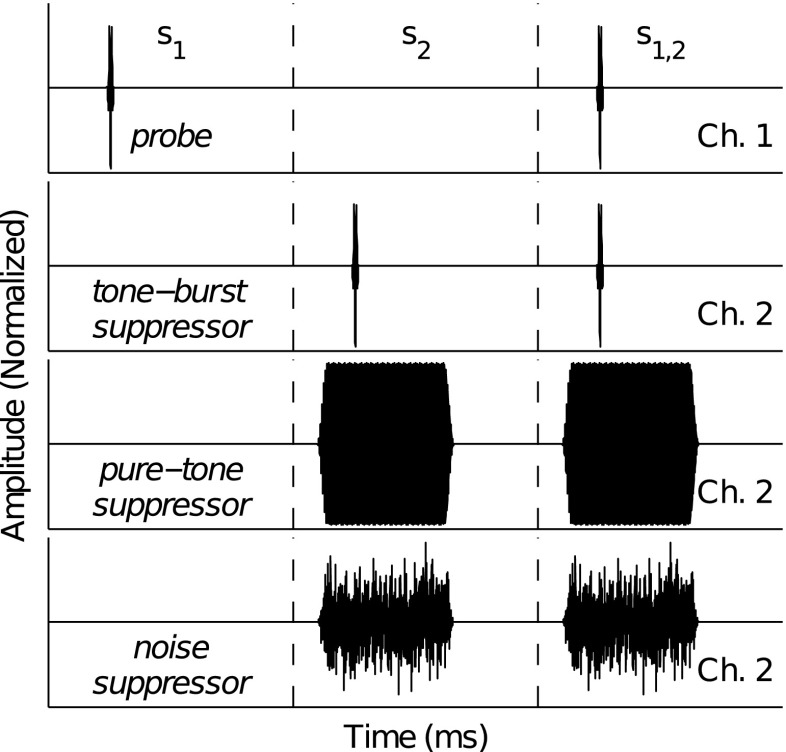
TEOAEs were evoked using three-cycle, 2 kHz tone bursts (hann-windowed) in the presence of different suppressor stimuli including: (a) 3-cycle, 2 kHz tone bursts, (b) pure tones ranging from 0.5–6 kHz, and (c) band-limited noise with a passband from 8–16 kHz. The tone-burst suppressor condition was used to (1) identify different-latency components in the TEOAE and (2) to quantify the level-dependence of the different-latency TEOAE components’ magnitude and latency. The purpose of the pure-tone and noise suppressor conditions was to examine contributions to the TEOAE from different cochlear places. For each suppressor condition, stimuli were presented to the ear using a double-evoked, double-source paradigm (Keefe 1998; Keefe and Ling 1998). A stimulus buffer was composed of three consecutive stimulus intervals (, , and ). Intervals were 40 ms long for the tone-burst suppressor condition (total buffer duration of 120 ms) and 50 ms long for the pure-tone and noise suppressor conditions (total buffer duration of 150 ms). Stimulus interval contained the TEOAE probe stimulus (a 3-cycle, 2 kHz tone burst) routed through channel 1 of the transducer. Stimulus interval contained the suppressor stimulus routed through channel 2 of the transducer. Both stimuli were presented simultaneously during stimulus interval . Figure 1 illustrates the double-evoked paradigm and the various suppressor stimuli. The top panel shows the probe (3-cycle, 2 kHz tone burst) and lower panels show the suppressor conditions.
FIG. 1.
Probe- and suppressor-stimulus paradigms used to evoke the TEOAE. Each panel includes three stimulus intervals (, , and ). During , only the probe is presented through channel 1 of the transducer. During , only the suppressor is presented through channel 2 of the transducer. During , the probe and suppressor are simultaneously presented through channels 1 and 2, respectively.
For the tone-burst suppressor condition, the probe and suppressor tone bursts were presented at equal levels across the and intervals (i.e., equal-level variant of the double-evoked paradigm, Schairer et al. 2003; two top-most panels in Fig. 1). Tone bursts were presented to the ear at levels from 44 dB peak SPL (pSPL) to 86 dB pSPL (6-dB steps). The number of stimulus buffers presented depended on the level of the tone bursts, with more presentations for lower level tone bursts to improve the signal-to-noise ratio (SNR) of the evoked emission: 2,000 buffers were presented for levels from 44–56 dB pSPL, 1,600 were presented for levels from 62 to 74 dB pSPL, and 1,200 were presented at 80 and 86 dB pSPL. These data were part of a larger data set analyzed in Lewis and Goodman (2014) to examine the effect of tone-burst duration on the level-dependent growth and latency of the total TEOAE.
The probe for the pure-tone suppressor conditions was a 74-dB pSPL 3-cycle, 2 kHz tone burst. Pure-tone suppressors were 28 ms with the initial and final 5 ms ramped-on and -off, respectively, by a 1/2-cycle hann window (3rd panel from the top in Fig. 1). Suppressor frequencies included 0.5, 0.71, 1-3.86 (1/7-octave steps), 5, and 6 kHz. Suppressor tones were presented at 50, 62, and 74 dB pSPL (-24 dB, -12 dB, and 0 dB re: probe level). Not all suppressor frequencies were presented at each suppressor level, as pilot data suggested minimal effects of certain suppressor frequencies when presented at 50 and 62 dB pSPL: All frequencies were presented for the 74 dB pSPL suppressor level, frequencies between 1 and 6 kHz were presented for the 62 dB pSPL suppressor level, and frequencies between 1 and 3.86 kHz were presented for the 50 dB pSPL suppressor level. The phase of the suppressor tone (for a given frequency) alternated between cosine and negative-cosine across adjacent stimulus buffers. The alternating of phase between adjacent stimulus buffers constituted a buffer pair and was necessary to cancel the SFOAE evoked by the pure-tone suppressor upon averaging. Eighteen hundred stimulus buffers (900 buffer pairs) were presented for each pure-tone suppressor frequency and level.
The probe for the noise suppressor condition was the same 2 kHz tone burst used for the pure-tone suppressor conditions. The noise suppressor was a 28-ms noise burst, band-limited from 8 to 16 kHz (bottom panel in Fig. 1). The noise was calibrated to have a flat spectrum from 8 to 16 kHz and a root-mean-square (RMS) pressure of 80 dB SPL (discussed below). Thirty different frozen-noise samples were randomly generated for each subject. The phase of each frozen-noise sample alternated between in-phase and out-of-phase across adjacent stimulus buffers to form buffer pairs, similar to the pure-tone suppressors. Each frozen-noise pair was consecutively presented 15 times before a different frozen-noise pair was presented. Altogether, 1,800 stimulus buffers (900 buffer pairs) were presented.
Calibration
Probe and suppressor stimulus levels were calibrated according to the pressure generated in a long, plastic tube (2 m length, 7 mm inner diameter) terminated at the distal end by a steel bearing. The inner diameter of the tube was selected to approximate that of the average adult ear canal (Stinson and Lawton 1989). The long-tube calibration was used as the pressure measured by the probe microphone at the entrance to the tube in insensitive to standing-wave effects which can otherwise introduce errors during in-situ SPL ear-canal calibrations (Sachs and Burkhard 1972; Stinson et al. 1982; Gilman and Dirks 1986). The long-tube calibration is also advantageous as it results in the same voltage being delivered to the transducers across all subjects, thereby ensuring that any transducer distortion is identical across subjects. The long-tube calibration does not account for differences in canal geometry across subjects; however, large variations in in-situ ear-canal pressure were not expected given the homogeneity of the subject population (all subjects were young adults). In the current study, tone-burst levels measured in the ear canals of the different subjects ranged from -3.1 dB to +4.6 dB relative to the stimulus level generated in the calibration tube.
To calibrate the levels of the 2 kHz tone bursts and pure-tone suppressors, 64 repetitions of a 10 ms tone burst of the target frequency were delivered to the calibration tube at a rate of 1/s, recorded, and averaged. The resulting waveform was highpass filtered using a finite-impulse-response (FIR) digital filter (250 Hz cutoff, 256 order). The peak incident pressure (i.e., pressure within the initial 10 ms of the recording and prior to the first reflection from the distal end of the tube) was measured and a calibration factor relating the transducer voltage drive to the measured tube pressure was calculated. The target stimulus (e.g., 6 kHz pure-tone suppressor) was then created in MATLAB, scaled to the target peak voltage (e.g., 74 dB pSPL), and multiplied by the calibration factor to yield the desired acoustic pressure in the long tube.
Calibration of the noise stimulus was similar to that of the tone bursts and pure-tone suppressors; however, the noise level was calibrated in terms of dB RMS instead of dB pSPL. Sixty-four repetitions of a 10-ms frozen, white-noise burst were delivered to the calibration tube at a rate of 1/s and recorded. Time-domain recordings were high-pass filtered (250 Hz cutoff, 256 order) and synchronously averaged. The voltage drive to the transducer for the noise, ( denotes time in terms of sample number and is implicit to all subsequent lower-case, with the exceptions of and in Eqs. 5 and 7, respectively), and the average pressure recorded in the long tube, , were transformed to the frequency domain ( and , respectively, denotes frequency bin number and is implicit to all subsequent upper-case variables) using the discrete Fast Fourier transform (FFT). The magnitude of the frequency-domain inverse transfer function of the calibration tube was then calculated,
| 1 |
To constrain the bandwidth of the noise between 8 and 16 kHz, the magnitudes for the frequency bins corresponding to 0–8 and 16–22.05 kHz were set to 0. Phase was set to 0 at all frequencies. was transformed to the time domain () via the inverse discrete FFT. was truncated to 128 samples and hann-windowed to generate an impulse response.
The original voltage drive () was convolved with the impulse response to yield a calibrated voltage drive, . was bandpass filtered by an FIR digital filter (8 kHz low-cut, 16 kHz high-cut, 1024 order) to further attenuate residual energy outside of the 8–16 kHz frequency band. Sixty-four repetitions of vcal were delivered to the calibration tube at a rate of 1/s, recorded, synchronously averaged and highpass filtered (250 Hz cutoff, 256 order) to describe the pressure generated in the tube (). A calibration factor was calculated as the ratio of the RMS voltage of to the RMS pressure of . For each subject, thirty 28 ms, frozen, white-noise bursts were generated and convolved with . Each frozen-noise burst was then scaled to have an RMS voltage of 80 dB SPL. The scaled frozen-noise bursts were subsequently multiplied by the calibration factor to yield an RMS pressure of 80 dB SPL in the calibration tube.
Analysis
TEOAEs were extracted from the ear canal pressure recordings by dividing the recording for each stimulus buffer into three time segments (). Each time segment corresponded to one of the three stimulus intervals (). The nonlinear differential response () was calculated as,
| 2 |
contains the nonlinear portion of the TEOAE. In the absence of nonlinearity, contains only noise. The advantage of this extraction technique is that the stimulus is effectively removed from the recording, assuming linear transducers, thereby permitting (1) retention of very early time portions of the OAE and (2) extraction of the OAE from the stimulus when the two overlap in time. This technique has been used to measure TEOAEs at frequencies up to 15 kHz (Goodman et al. 2009; Keefe et al. 2011), SFOAE I/O functions and latencies (Schairer et al. 2003; 2006), SFOAE suppression-tuning curves (Keefe et al. 2008), and I/O functions and latencies of SL TEOAE components (Goodman et al. 2011; Sisto et al. 2013).
While the nonlinear differential method allows examination of early-occurring emissions, such as SL TEOAE components, in some cases it may underestimate the emission’s true magnitude (Kalluri and Shera 2007b; Moleti et al. 2012). This may be especially problematic at low stimulus levels where OAEs typically exhibit linear growth. At these levels, the magnitude of the OAE extracted by the nonlinear differential method may exhibit a poor SNR (Schairer et al. 2003), thereby placing a lower-limit on the stimulus level at which an OAE may be measured. Magnitude differences may also occur in regions of compressive growth, depending on the level of the suppressor and where it falls along the I/O function underlying the growth of the OAE. As a result, I/O functions derived using a double-evoked technique may not always completely describe the I/O function for the total OAE (Goodman et al. 2011). This limitation will be further addressed in the “Discussion” section as it applies to interpretation of the I/O functions of the TEOAE components.
A second consequence of using the double-evoked extraction technique is that the direction of change in OAE magnitude associated with the simultaneous presentation of the probe and suppressor is lost (at least when using the variant described here). In other words, it is unclear as to whether the suppressor caused suppression or enhancement of the OAE evoked by the probe. Therefore, the effect of the pure-tone and noise suppressors on the TEOAE will simply be discussed in terms of magnitude change. The ambiguity of the direction of magnitude change caused by the suppressor as it may apply to interpretation of the data will be addressed in the “Discussion” section.
The nonlinear differential responses for each suppressor condition were highpass filtered using an FIR digital filter (250 Hz cut, 128 order). The highpass-filtered responses were then filtered using a 1/3-octave bandpass FIR digital filter (2 kHz center frequency, 512 order). The RMS levels (Pa) of the filtered responses were calculated and subjected to an artifact rejection algorithm (Goodman et al. 2009; see Hoaglin et al. 1983) in order to identify recordings contaminated by high-levels of intermittent noise. Recordings with an RMS exceeding the third quartile by more than 1.5 times the interquartile range were excluded from further analysis. Whenever a response was discarded, so was its pair (adjacent response where the suppressor was of opposite phase—pure-tone and noise suppressor conditions).
Retained responses were divided into two collection buffers. Odd numbered response pairs were stored in one buffer and even numbered pairs were stored in a second buffer. For each collection buffer, the recordings were synchronously averaged in the time domain. An estimate of the nonlinear-residual, 2 kHz TEOAE signal was calculated as the mean of the averaged recordings in the two collection buffers (). (Note that “nonlinear residual”, while not always explicitly stated, is implicit in all subsequent mentions of the TEOAE signal and/or TEOAE components). The analytic expression of the TEOAE signal was calculated using the discrete Hilbert transform,
| 3 |
From the analytic signal, the TEOAE instantaneous magnitude , or envelope, and phase were calculated. The instantaneous frequency of the TEOAE () was derived as
| 4 |
where was the sampling rate (44.1 kHz) and was the 1st-derivative of time. Instantaneous frequency describes the dominant frequency of the TEOAE at a given moment in time. An estimate of the time-domain noise () was calculated by subtracting the averaged responses of the two collection buffers and dividing by 2 (Kemp et al. 1990). The instantaneous magnitude of the noise was subsequently calculated from the analytic signal.
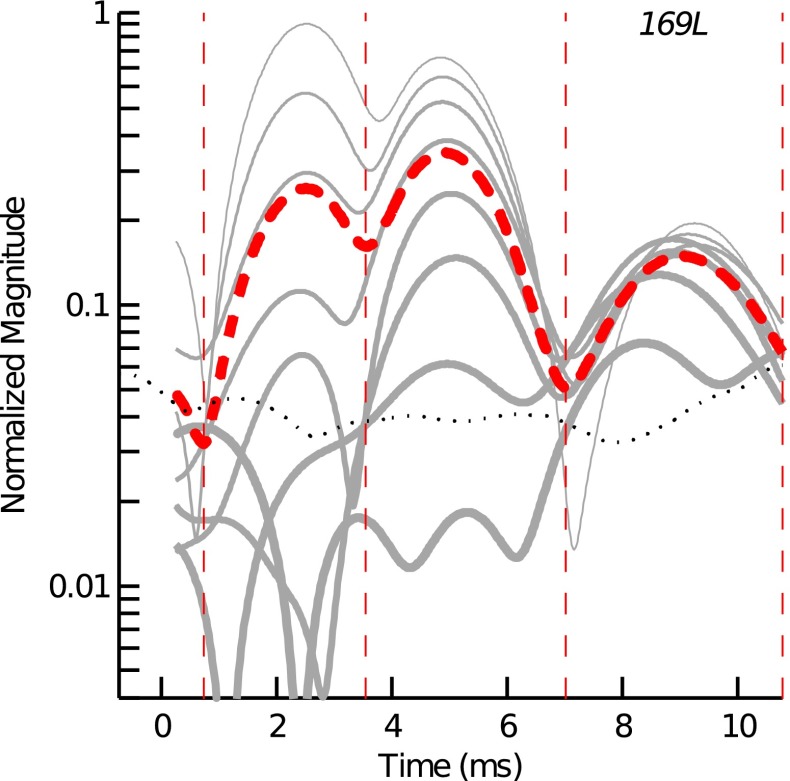
To measure the effects of the different suppressors on the TEOAE, the TEOAE signal and noise estimates were analyzed across several different time windows. The initial window extended from stimulus onset to 10 ms post-stimulus offset. The duration of this window was determined based on the longest expected latency of a low-level 2 kHz TEOAE (e.g., Neely et al. 1988; Tognola et al. 1997; Sisto and Moleti 2007). This analysis window included all the different-latency TEOAE components. A time vector was mapped to the analysis window with time zero corresponding to the peak of the tone-burst stimulus. The initial 1 ms of the envelope, associated with time from −0.75 to 0.25 ms, was set to zero in order to remove any non-cancelling stimulus artifact from the recording. In order to compare TEOAE components occurring earlier and later in time, the initial time window was partitioned into multiple, shorter-duration, windows. The following method, performed on a subject-by-subject basis, was used to determine the bounds of these windows: TEOAE envelopes (Pa) measured for the tone-burst suppressor condition were averaged across the different stimulus levels to yield the mean envelope. Magnitude nulls in the mean envelope were identified, and the time between consecutive nulls was used to define the time window for a specific TEOAE component. Figure 2 shows the time windows defined according to this method for a representative subject. Three components were identified for this particular subject; the associated time windows were bounded between 0.72–3.54, 3.54–7.06, and 7.06–10.77 ms.
FIG. 2.
Definition of TEOAE-component time windows for subject 169L. Gray lines indicate the TEOAE envelopes for the tone-burst suppressor condition (thicker lines indicate lower stimulus levels). The thick, red dashed line is the mean envelope across all stimulus levels. Vertical dashed lines delineate the time windows for the different-latency components. The dotted black line is the mean noise floor.
TEOAE magnitude and latency were calculated within each time window. Magnitude was calculated as the RMS of the TEOAE envelope within the analysis window. Calculating magnitude from the envelope results in a 3 dB increase in the RMS level compared to magnitude calculated from the waveform. This increase is due to the inclusion of both the real and imaginary parts of the analytic signal, which effectively doubles the intensity. Latency () was calculated as the energy-weighted mean of the time vector () for the respective analysis window,
| 5 |
To determine whether a TEOAE was present in the analysis window, the SNR was calculated by dividing the RMS level of the TEOAE envelope by the RMS level of the noise envelope (linear units). The SNR was calculated for each time window. An SNR criterion value of 9 dB was adopted. Whenever the SNR of the time-windowed portion of the TEOAE equaled or exceeded 9 dB, a TEOAE component was defined as being present.
Screening for Synchronous-Spontaneous OAEs
Data for the tone-burst suppressor conditions were examined to determine whether the early time windows of the TEOAE included synchronous-spontaneous (SS) OAEs. SSOAEs may present as SL TEOAE components if the time interval between adjacent tone-burst presentations is shorter than the time required for the SSOAE to decay into the noise floor (Keefe 2012). SSOAEs within the early portions of the analysis window was a potential concern as the tone-burst repetition rate was 25/s, thereby allowing only 40 ms between adjacent tone-bursts; SSOAEs can persist beyond 80 ms post-stimulus offset in some cases (Sisto et al. 2001).
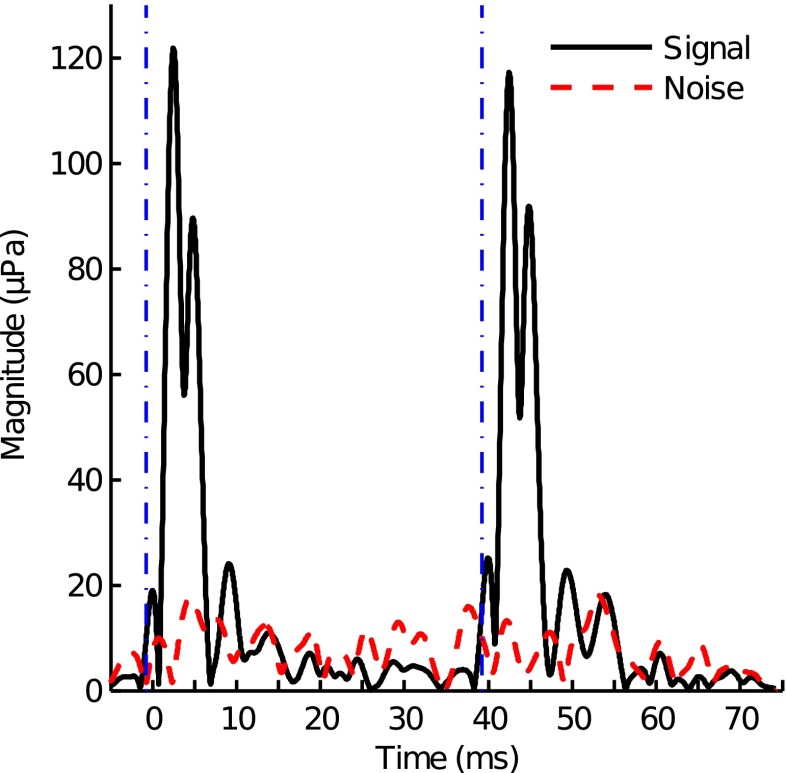
To determine whether the short-latency portions of the TEOAE were due to SSOAE activity, the time windows of the TEOAE waveforms were extended to 35 ms post-stimulus onset and examined for the presence of long-lasting OAE energy. Figure 3 shows the 2 kHz TEOAE envelopes for the highest-level tone burst (86 dB pSPL) from one representative subject. Only the responses for the highest-level tone-burst were examined because this level was most likely to evoke long-lasting SSOAEs. The response shown in the initial 40 ms is the mean TEOAE envelope for odd-numbered stimulus buffers while the response shown in the final 40 ms is the mean envelope for even-numbered stimulus buffers. The two responses have been concatenated to permit visualization of any SSOAE energy that may have spanned the two response cycles. Four magnitude peaks occurred in each 40 ms time frame. The initial peak was at least partially due to non-cancelling stimulus artifact, as it was only measureable for the 86 dB pSPL tone burst and was seen both in the ear canal and an IEC711 ear simulator (Knowles Electronics). The subsequent three peaks corresponded to different-latency TEOAE components. The TEOAE signal did not exceed the physiological noise floor across the final 20 ms of either response. An SSOAE would be expected to appear as either an exponentially decaying signal or a signal with relatively constant magnitude across the duration of the time window. The observation that SSOAEs were not present in the early time windows of the adjacent response implicated that the SL TEOAE components were indicative of a different cochlear phenomenon. SSOAE activity within the early time windows was not observed in any of the subjects participating in this study.
FIG. 3.
Analysis to examine potential SSOAE activity in the early portion of the TEOAE. Analysis of SSOAE activity included extending the total analysis time window to 35 ms post-stimulus onset. The portion of the time window following the longest-latency magnitude peak that occurred in the initial 10 ms post-stimulus onset was examined for non-decaying OAE energy. Such energy has the potential to contribute to the early part the of subsequent data buffer’s time window and present as a SL component. Results are shown for subject 169L. The vertical dash–dot lines indicate stimulus onset. No SSOAE activity was detected in this subject.
RESULTS
Component Latencies and Growth Rates
Figure 4 shows the TEOAE envelopes measured for the tone-burst suppressor condition in six subjects. Multiple magnitude peaks characterized most of the TEOAE envelopes. Of the 10 subjects tested, 2 different-latency TEOAE components were identified for 1 subject (124R; top-right panel), 3 components were identified for 7 subjects (e.g., 161L; top-left panel), and 4 components were identified for 2 subjects (e.g., 116R; bottom-left panel). Across all subjects, several trends were apparent. First, at the lowest stimulus levels, a LL magnitude peak (or component) generally dominated the TEOAE envelope. Second, as stimulus level increased, several SL magnitude peaks (or components) emerged from the noise floor, growing less compressively than the LL peak. Third, at the highest stimulus levels, the peak magnitudes of the SL components were often larger than that of the LL component. And fourth, the time index associated with each of the different magnitude peaks remained nearly constant as stimulus level increased.
FIG. 4.
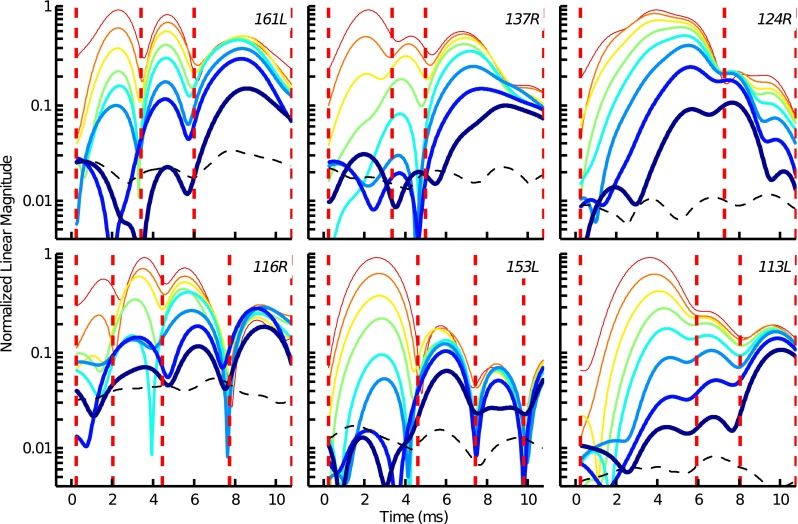
TEOAE envelopes measured for different level tone bursts in the tone-burst suppressor condition. Each panel shows data from an individual subject. Decreasing line thickness indicates increasing stimulus level (44–86 dB pSPL in 6 dB steps). The broken black line in each plot indicates the subject’s noise floor. The time windows for the different-latency components are indicated by the vertical dashed lines.
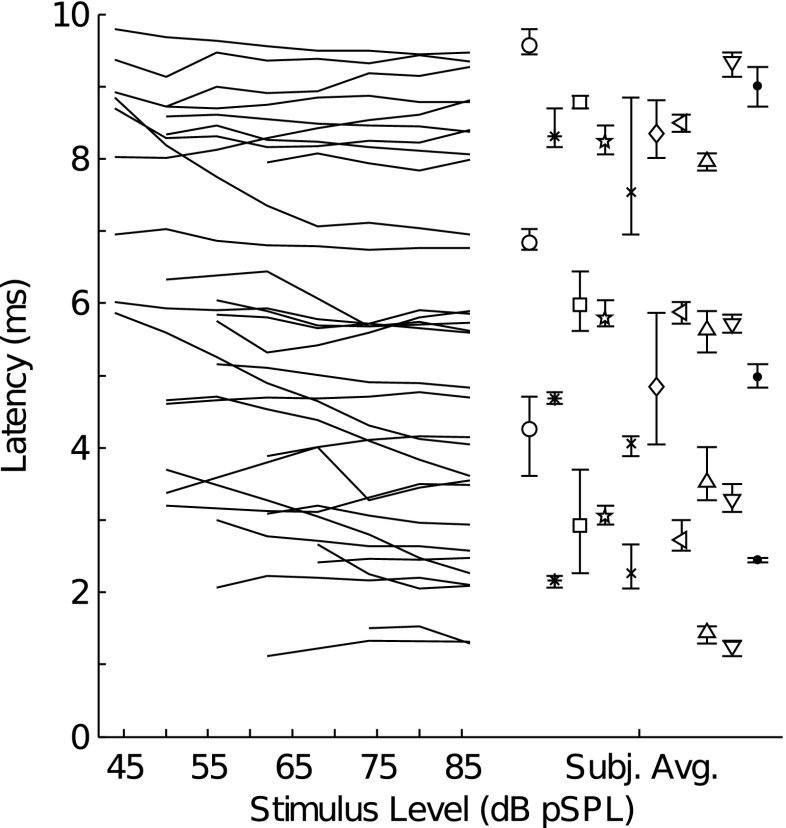
Figure 5 plots the latencies of the different TEOAE components as a function of stimulus level to illustrate the approximate level-invariance of TEOAE-component latency. For this figure, latency was calculated as the power-weighted mean of the time vector for each TEOAE component (see Eq. 5). Each line indicates the latency of a specific component (measured in a single subject) as a function of tone-burst level. TEOAE-component latencies remained nearly constant as tone-burst level increased from 44 dB pSPL to 86 dB pSPL. Also shown in Fig. 5 are the mean latencies (averaged across stimulus level) of the different components and their respective ranges for each subject. With few exceptions, the latency of each component varied by less than ± 0.5 ms across the 42 dB range of stimulus levels. Within subjects, the average difference in latency between adjacent components was 2.77 ms (standard deviation, s.d. = 0.61 ms). When expressed relative to the latency of the later-occurring component, the latency of the earlier-occurring adjacent component was shorter by a factor of 1.81 (s.d. = 0.34) and is similar to previous work that has reported a difference of approximately 1.6 (Goodman et al. 2009; Moleti et al. 2012). The near level-invariance of the different-latency TEOAE components has also been previously reported (Goodman et al. 2009; Goodman et al. 2011; Moleti et al. 2012; Rasetshwane and Neely 2012) and is consistent with the generation of a given component occurring through the same mechanism and at the same cochlear location, regardless of stimulus level.
FIG. 5.
Latency-intensity functions and mean latencies of the different TEOAE components. Data represent measurements for the tone-burst suppressor condition. TEOAE-component latency is plotted as a function of stimulus level. The mean latency (averaged across stimulus level) of each component and its minimum and maximum values are indicated in the right-hand portion of the figure. Data from different subjects are indicated by marker type.
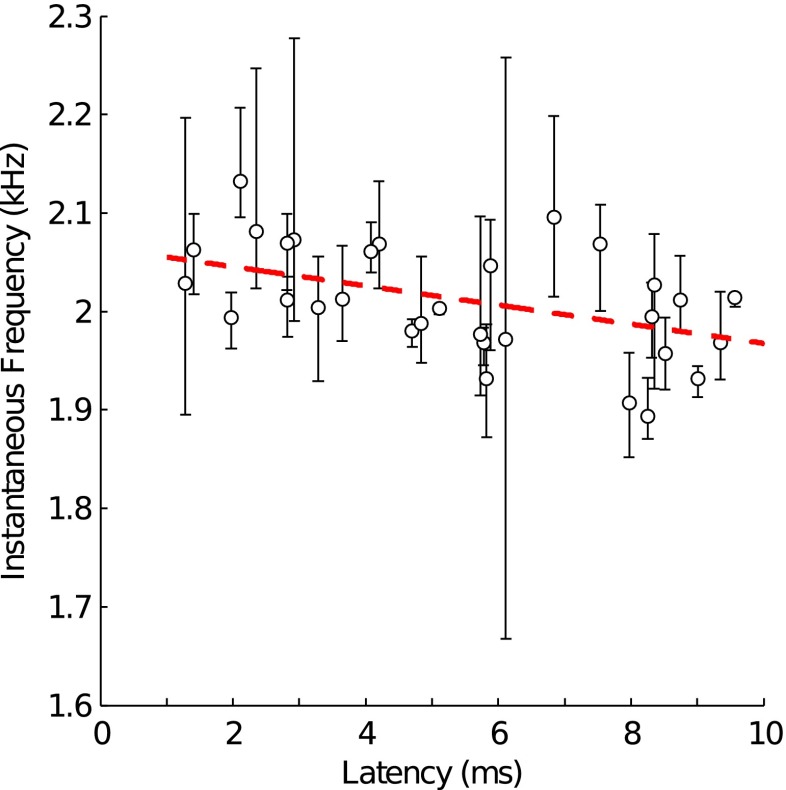
To examine the frequency content of the different-latency components, the instantaneous frequency, , was calculated (see Eq. 4). is sensitive to rapid changes in phase as well as SNR; therefore, was only measured at the time-index in each component’s time window that was associated with the peak in instantaneous magnitude. At this location, phase is relatively constant and the SNR is high, thereby allowing accurate estimation of the dominant frequency of the component. Figure 6 plots the mean and range of , across stimulus levels, of the different-latency components. was inversely related to the latency of the TEOAE component; however, the change in with respect to component latency was small. On average, increased from 1.98 kHz for a component with a 9 ms latency to 2.05 kHz for a component with a 2 ms latency. Thus, despite their different latencies, all components had energy at similar frequencies.
FIG. 6.
Instantaneous frequency as a function of 2 kHz TEOAE-component latency. The mean instantaneous frequency and range of each different-latency component, collapsed across subjects, are indicated by the marker and error bars, respectively. The broken red line is a 1st-order polynomial fit to the data demonstrating the trend of increasing instantaneous frequency as component latency decreases.
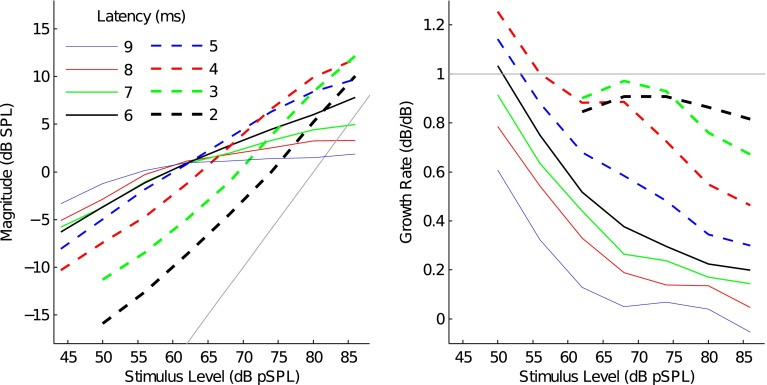
The magnitudes of the different-latency components were collapsed across subjects and LOWESS smoothing was used to formulate I/O functions describing component magnitude as functions of latency and stimulus level. The left panel of Fig. 7 shows the resulting I/O functions of the different-latency TEOAE components. Note that while components with latencies from 2 to 9 ms (1 ms intervals) are plotted in Fig. 7, each subject’s response included only a subset of these (typically 3 components separated by 2.77 ms—Fig. 5). As stimulus level increased, the magnitudes of the different-latency components all increased. At lower stimulus levels, magnitudes were larger for longer-latency components. However, as stimulus level increased, the magnitudes of shorter-latency components grew less-compressively than those of longer-latency components, with the effect that shorter-latency magnitudes often exceeded the magnitudes of the longer-latency components at high stimulus levels.
FIG. 7.
Input/output (left panel) and growth rate (right panel) functions for different-latency TEOAE components. Component latency is indicated by line style. The thin gray line indicates linear growth (1 dB/dB).
The right panel of Fig. 7 shows growth-rate functions for the different-latency components. Note that these data were calculated by smoothing (LOWESS) the derivatives of the raw I/O functions as opposed to the mean I/O functions in the left panel of Fig. 7. All components exhibited compressive growth across most of the stimulus-level range, suggesting that generation occurred within the region over which the cochlear amplifier was active. In general, compression increased with stimulus level and decreased with component latency. For instance, the growth rate of the 9 ms component decreased from 0.61 dB/dB at the lowest stimulus levels to approximately 0 dB/dB (full saturation) at the highest stimulus levels. In contrast, the growth rate of the 4 ms component decreased from 1.14 to 0.3 dB/dB as stimulus level increased to 86 dB pSPL. It is important to note that the nonlinear paradigm used to extract the components attenuates the OAE, the degree of which depends on the emission’s growth rate (attenuation increases as compression decreases; Schairer et al. 2003; Moleti et al. 2012; Lewis and Goodman 2014). Thus, the magnitudes of the shorter-latency components were likely underestimated, especially at the lowest stimulus levels where linear growth presumably occurs.
Component Sensitivity to Suppressor Frequency
Figure 8 shows contour plots describing the change in TEOAE magnitude, as a function of time, caused by the different-frequency pure-tone suppressors for subject 169L (see Fig. 2 for this subject’s TEOAE envelopes). Data are shown for each suppressor-level condition (i.e., dB, dB, and dB where is suppressor level and is probe level) and only for suppressor frequencies through 3.86 kHz, to facilitate comparison of the effect of changing suppressor level. The white region corresponds to the noise level, averaged across all suppressor frequencies. The amount of magnitude change induced by the suppressor is proportional to contour darkness (the same magnitude-shading scale is used in all panels). Each contour line denotes a 3 dB change in SNR. Overlaid on each plot are the time windows corresponding to the locations of the different TEOAE components (determined from the tone-burst suppressor condition). At the highest suppressor level (; left panel), the magnitudes of the different-latency components were sensitive to suppressors across similar frequency regions. These regions were broad and extended from at least 1–2.5 kHz. Some differential sensitivity to suppressor frequency was apparent across the different components, however. For example, the upper frequency limit that induced a magnitude change of the longest-latency component (7.01–10.77 ms) was approximately 2.5 kHz compared to 3 kHz for the earlier adjacent component (3.56–7.01 ms) and at least 4 kHz for the earliest component (0.72–3.56 ms).
FIG. 8.
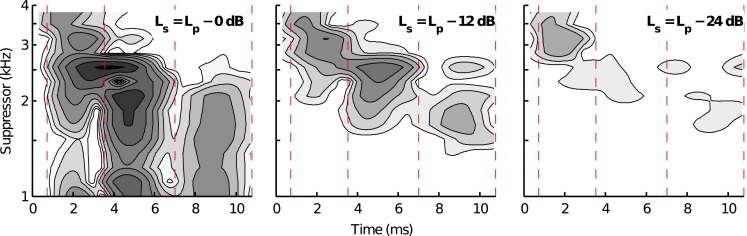
Effect of suppressor level on 2 kHz TEOAE components. Data are shown for the subject whose TEOAE envelopes were plotted in Fig. 2. The darkness of each contour is proportional to the amount of change in TEOAE magnitude caused by the suppressor frequency. Each panel shows a different suppressor-level condition, as indicated in the upper right corner. Vertical dashed lines delineate the time windows for the different-latency components.
Decreasing the suppressor level by 12 dB (; Fig. 8, middle panel) resulted in more pronounced frequency-selective changes to the magnitudes of the different-latency components. In this case, the magnitude of the longest-latency component was most sensitive to frequencies between 1.5 and 2 kHz, compared to 2 and 2.75 kHz for the adjacent shorter-latency component and 2.75 and 3.5 kHz for the shortest-latency component. The improved resolution of the sensitive regions for each component was primarily due to a reduction in the amount of magnitude change caused by lower-frequency suppressors (i.e., suppressor frequencies < 1.5, 2, and 2.75 kHz for the longest-latency, middle-latency, and shortest-latency components, respectively). Reducing the suppressor level by an additional 12 dB (; third panel) resulted in a more narrowly defined suppressor-frequency region to which the shortest-latency component was sensitive; however, the SNRs of the later components were typically poor.
The data for the dB and dB conditions were often insufficient to determine whether the different latency, 2 kHz TEOAE components were differentially sensitive to suppressor frequency. Therefore, only data for the dB condition were further analyzed. Figure 9 shows contour plots for the six subjects whose TEOAE envelopes were shown in Fig. 4. Included in each plot is data for the suppressor frequencies between 1 and 6 kHz, and the band-limited noise (BLN) suppressor. For all subjects, there is a trend of earlier-occurring components being increasingly sensitive to higher-frequency suppressors. The data for subject 161L (Fig. 9, top-left panel) provide an especially clear example of this trend: Suppressor frequencies between 1.37 and 2.2 kHz had the greatest effect on the magnitude of the longest-latency component (6.01–10.77 ms) compared to suppressors between 1.9 kHz and 2.6 kHz for adjacent shorter-latency component (3.4–6.01 ms) and suppressors between 2.5 and 5 kHz for the shortest-latency component (0.25–3.4 ms).
FIG. 9.
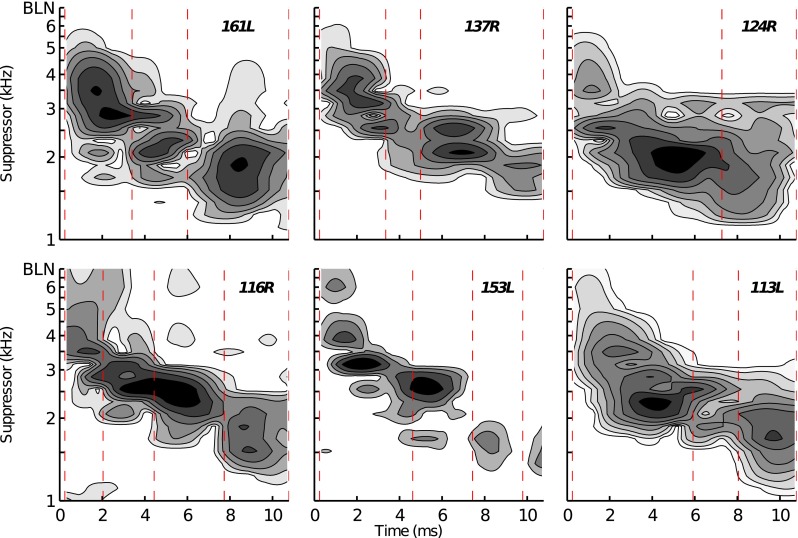
Contour plots showing the effect of different frequency suppressors on the TEOAE. Data is shown for the pure-tone suppressor condition ( dB) and the band-limited noise (BLN) suppressor condition. Each panel shows the data for an individual subject (panels correspond with those of Fig. 4). The darkness of each contour is proportional to the amount of suppression caused by the suppressor on the TEOAE. Time windows for the different-latency components are indicated by the dashed lines.
While the data for subject 161L show sensitivity of each component generally constrained to a single “group” of frequencies, this was not always the case. In some instances, a given component was sensitive to several groups of suppressor frequencies. An example of this is found in the data for subject 153L within the time-window of the shortest-latency component (0.25–4.62 ms; Fig. 9, bottom row, middle panel). This component exhibits sensitivity to four distinct frequency groups centered around 2.6, 3.1, 3.9, and 6 kHz. Each of these different groups caused change to the TEOAE component’s magnitude across slightly different time indices within the analysis window. The 6 kHz suppressor affected an earlier portion of the component compared to the 3.9 kHz suppressor which, in-turn, affected an earlier portion of the TEOAE than the 3.1 kHz suppressor, and so forth.
In certain cases, multiple components were sensitive to similar suppressor frequencies. For instance, the magnitudes of the components between 2.04–4.44 and 4.44–7.73 ms for subject 116R were both sensitive to suppressor frequencies around 2.6 kHz (Fig. 9, bottom row, left column). This overlap was most apparent near the time boundary that separated the adjacent components (4.44 ms), suggesting that it may be an indication of a suppressor frequency enhancing one component while suppressing the other. For instance, if the two components partially overlapped in time and their phases were different, cancellation would occur across the time-indices where they overlapped. When one component is suppressed by a particular frequency, the other component that was previously partially cancelled in the absence of the suppressor would be released from cancellation, or, enhanced. Release from cancellation may also be indicated in the data for subject 161L between the two shortest-latency components (∼3.4 ms) for a 2.9 kHz suppressor. It is also likely that at least some of the overlap between components was due to the distributed nature of the tonal suppressors. Namely, any suppression induced by the suppression occurs not only at the suppressor’s tonotopic place, but also at more basal cochlear places.
Suppressor frequencies above 4 – 5 kHz caused minimal change to TEOAE-component magnitudes. This was especially true for the components whose latencies were longer than 2–3 ms. For shorter-latency components, there were several instances where the 6 kHz suppressor and the BLN changed the magnitude of the component. Consistent with the overall trend of higher-frequency suppressors affecting earlier temporal portions of the TEOAE, the 6 kHz and BLN suppressors had effects very early in time. For example, subject 153L (Fig. 9, bottom row, middle column) shows a region of suppressor-sensitivity beginning around 5 kHz and extending to at least 8 kHz (the lower frequency limit of the noise burst) across the initial 2 ms of the 2 kHz TEOAE.
For each subject, the most effective suppressor frequency of the TEOAE (suppressor frequency causing greatest change in TEOAE magnitude) at each moment in time, , was calculated as,
| 6 |
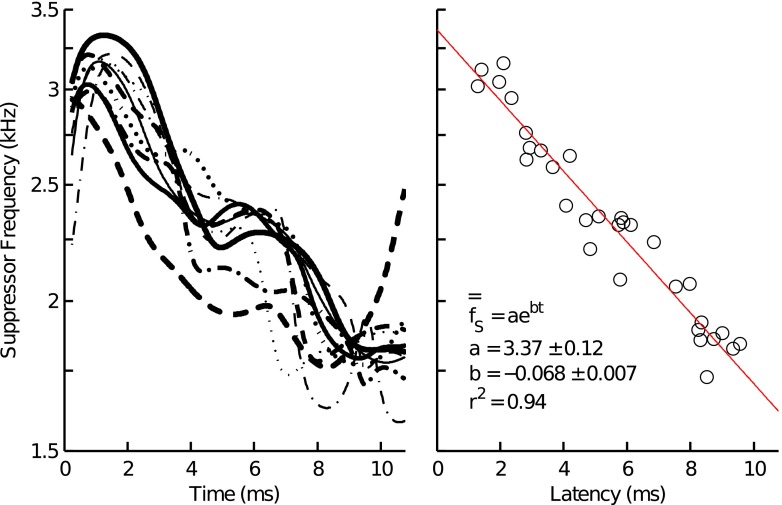
where was the suppressor-frequency vector (1–3.86 kHz, 1/7-octave steps), was the frequency index, and was the instantaneous power of the TEOAE envelope at a moment in time () for a given suppressor frequency (). Equation 6 calculates the power-weighted mean of at each moment in time. Calculation was performed on the log2-transformed vector and only across the 1–3.86 kHz range since these suppressor frequencies had equal octave spacing. Exclusion of the 5 and 6 kHz and BLN suppressor data was not expected to significantly affect the estimation as these suppressors generally caused little change to TEOAE magnitude. The left panel of Fig. 10 plots (transformed to kHz) for all subjects. Consistent with the data reported in Fig. 9, decreased as TEOAE-component latency increased. The time-dependence of was similar across subjects, with values decreasing from around 3 kHz between 2 and 3 ms to 1.8 kHz between 8 and 10 ms. For many subjects, remained relatively constant across time before exhibiting a sudden decrease, such that resembled a staircase function. Rapid decreases in were typically associated with the time boundaries between different-latency components.
FIG. 10.
Most effective suppressor frequency of the different-latency 2 kHz TEOAE components as a function of time (left panel) and for each component (right panel). The left panel plots results from Eq. 6 for each subject (indicated by line type). The right panel plots the results from Eq. 7 for each subject (open circles) and the model fit using a 1st-order exponential function (solid line). Model parameters with 95 % confidence intervals are provided in the lower left corner of the plot.
To estimate the suppressor frequency that caused the greatest change to each component’s magnitude, , was averaged across the component’s time window. was calculated as:
| 7 |
where was the time index bounded within the time window of a given TEOAE component. Equation 7 calculates the power-weighted mean of across the time window of the component. The right panel of Fig. 10 plots for each of the different-latency components. Consistent with the data shown in the contour plots, the magnitudes of the different-latency components were sensitive to different suppressor frequencies. Overlaid on the individual data is a 1st-order exponential fit (; frequency in kHz and time in ms). This model was chosen as it provided the best fit to the data using the fewest number of parameters. Per this model, the most effective suppressor frequency increases from 1.75 kHz for a 9.64 ms component (i.e., the longest-latency component measured) to 3.07 kHz for a 1.36 ms component (i.e., the shortest-latency component measured).
DISCUSSION
Basal Contributions to SL TEOAE Components
The current study extended previous work that has reported on the growth rates and latencies of different-latency TEOAE components (e.g., Goodman et al. 2009; Sisto et al. 2013) by examining the relationship between each component’s latency and the suppressor frequency that caused the greatest change in the component’s magnitude. This relationship was of interest as it provides an empirical test of the hypothesis that shorter-latency components are generated basal to longer-latency components of similar frequency (Withnell et al. 2008; Goodman et al. 2011; Moleti et al. 2013). In light of recent work demonstrating that SL components depend on the active cochlear elements at locations basal to those of the LL component (Moleti et al. 2014), a two-tone suppression paradigm was used to examine the extent of those contributions. Per two-tone suppression theory (e.g., Geisler et al. 1990), suppression of the active elements’ response (at a particular frequency location) to the TEOAE probe will affect (presumably reduce) the magnitude of the associated TEOAE component. Shorter-latency components with a basal origin should, therefore, be sensitive to higher-frequency suppressors than longer-latency components that are generated closer to the tonopic place.
The findings from the current work support the hypothesis that SL TEOAE components are generated basal to the LL components. As TEOAE-component latency decreased, the suppressor frequency that induced greatest change to the component’s magnitude increased. The most effective suppressor frequency of the shortest-latency components (∼3 kHz and ∼1.5 ms, respectively) was, on average, 3/4-octave higher than that of the longest-latency components (∼1.8 kHz and ∼10 ms, respectively). As suppressor frequencies above 3 – 4 kHz generally had only a small effect on SL magnitudes, the primary contributions to the 2 kHz TEOAE appear to be constrained within a region extending 3/5-octave basally from the tonotopic place.
Overall, findings are consistent with the idea that the basilar membrane response to a particular frequency depends on the action of active elements basal to the characteristic frequency (CF) place (Geisler et al. 1990; Patuzzi 1996). Other physiological measures have also implicated distribution of the active elements responsible for frequency-specific amplification being basal to the CF place. For instance, auditory nerve fibers (ANF) exhibit greatest sensitivity to suppressor frequencies slightly higher than the fibers’ CF (10 % to 30 % or 1/7- to 1/3-octaves, e.g., Arthur et al. 1971; Delgutte 1990; Zhang et al. 2001). SFOAE suppression studies using low-level suppressor and probes show a similar phenomenon in that the SFOAE is most sensitive to suppression by frequencies 10 % to 20 % higher (1/7- to 1/4-octaves) than the OAE frequency (Brass and Kemp 1993; Keefe et al. 2008; Lineton and Wildgoose 2009; Charaziak et al. 2013). For higher-level probes, SFOAE sensitivity to suppression shifts to even higher frequencies (∼50 % or 3/5-octave higher than the OAE frequency; see Fig. 3 in Keefe et al. 2008).
In light of the presumed basal distribution of the active elements contributing to the BM response at the CF place, it is curious that the longest-latency components (latencies between 8 and 10 ms) were typically most sensitive to 1.8 – 1.9 kHz suppressors, despite having instantaneous frequencies closer to 2 kHz. This observation may be due, in part, to the use of tonal suppressors. A tonal suppressor induces suppression not only at its tonotopic place, but also at places more basal (i.e., low-side suppression; for review see Robles and Ruggero 2001; in OAEs see Zettner and Folsom 2003 and Keefe et al. 2008). A given suppressor may therefore suppress TEOAE components generated basal to the suppressor’s tonotopic place (as illustrated in Fig. 8 for ), with the effect of biasing the component’s estimated generation region to lower frequencies. The longest-latency components may be especially susceptible to lower-frequency suppressors assuming their highly compressive growth reflects that of the underlying BM response (Pang and Guinan 1997). In this regard, the use of a high-pass noise suppressor with cutoff frequency that is progressively shifted to higher frequencies may be advantageous. Compared to the basal extent of suppression, the suppressor’s effect is significantly reduced apical to the suppressor’s tonotopic place (e.g., Cooper 1996) and any change in the TEOAE between different noise-suppressor conditions could be more definitively associated with contributions from a specific frequency region.
It is difficult to compare the current study’s findings to others that have also empirically estimated the generation region of TEOAEs using suppressor tones (e.g., Tavartkiladze et al. 1994 and Zettner and Folsom 2003), as these earlier studies did not un-mix the TEOAE into its different-latency components. Tavartkiladze et al. concluded that TEOAEs are generated at the tonotopic place, after finding that the tips of the suppression-tuning curves for a 1.5 kHz and 2.5 kHz tone-burst-evoked OAE were roughly 1.5 and 2.5 kHz, respectively. Zettner and Folsom reported the tip of the suppression tuning curve to be within 1/4-octave above the tonotopic place for a 4-kHz tone-burst-evoked OAE. Both investigators used versions of the ILO system (Otodynamics Ltd.), which attenuates the initial 5 ms of the TEOAE to reduce stimulus artifact contamination (Kemp et al. 1986) thereby eliminating and/or reducing the magnitudes of shorter-latency components. Consequently, these studies’ estimates were likely biased to generation of the longer-latency components of the TEOAE and regions closer to the tonotopic place.
Recently, Moleti et al. (2014) estimated the generation region of SL TEOAE components to be within ∼1/5 to 1/10-octave basal to the tonotopic place by calculating the shift in frequency between LL and SL TEOAE spectra measured in ears with noise-induced, high-frequency hearing loss. This region of generation is constrained closer to the tonotopic place than that of the current study; however, the TEOAE extraction technique from Moleti et al. precluded measurement of components within the earliest portion of the TEOAE. For instance, the SL analysis window used by Moleti et al. at 2 kHz was bounded between approximately 4 and 7 ms. In contrast, the current work analyzed 2 kHz components with latencies as short as 1.4 ms. The inclusion of these components is a likely contributor to the difference in generation regions between the current work and that of Moleti et al. In a previous study, Moleti and colleagues (2013) used a cochlear model to simulate TEOAE generation and estimated a generation region of SL components extending to 1/3-octave basal to the tonotopic place, which is closer to the estimate from the current study. Compared to their empirical work, the modeled SL TEOAE component analysis window from Moleti et al. (2013) extended to shorter latencies (∼2 vs. 4 ms) and may account for the model’s more basally distributed estimate of SL generation as well as the better agreement with the current study’s empirical estimate. Regardless of these differences, contributions basal to the tonotopic place appear to explain findings that show basal cochlear trauma can affect the magnitudes and latencies of lower frequency TEOAEs (e.g., Avan et al. 1997; Jedrzejczak et al. 2005; Withnell et al. 2000; Lucertini et al. 2002; Murnane and Kelly 2003; Moleti et al. 2014).
The technique used in this study to examine the effect of different-frequency suppressors on TEOAE magnitude did not permit differentiation between TEOAE suppression and enhancement. The effect of reducing suppressor level on the magnitude of the residual TEOAE (Fig. 8) is generally consistent with suppression in that TEOAE magnitude decreased with suppressor level more rapidly across lower-frequency suppressors. A similar effect is evident in BM two-tone suppression using low-side suppressors (e.g., Ruggero et al. 1997). Distinguishing between suppression and enhancement is not necessarily important as both are expected if the TEOAE at a particular frequency includes contributions across a distributed region of the BM (Withnell and Yates 1998). However, enhancement may also occur if the suppressor tone induces a new region of generation that would not otherwise contribute to the TEOAE (Shera et al. 2004). The observed data are generally not consistent with this form of enhancement as the latencies of the TEOAE components measured with and without the suppressor tones were similar. In other words, the presence of the suppressor did not appear to recruit locations that were not already contributing to the TEOAE.
Generation Mechanisms of TEOAE Components
At low stimulus levels, the TEOAE envelope was dominated by a single, highly compressive-growing, long-latency component (latency between 7 and 10 ms) that was most sensitive to suppressor frequencies between 1.8 and 2 kHz. These characteristics are consistent with generation near the tonotopic place and subsequent propagation to the ear canal through a slow, reverse-traveling cochlear wave. As such, generation of the longer-latency part of the TEOAE through LCR, i.e., the mechanism likely responsible for low-level SFOAE generation (Zweig and Shera 1995; Shera and Guinan 1999), is plausible (Kalluri and Shera 2007a). However, the measured latencies of the longer-latency components in the current study are generally prolonged compared to that of low-level SFOAEs. Per Table I in Shera and Guinan (2003), the predicted latency of a 2-kHz SFOAE is 7.11 ms (95 % confidence interval: 6.03–8.28 ms). The range of latencies for the longest-latency 2-kHz TEOAE components in the current study, 7.54–9.57 ms, was longer by approximately 1.5 ms. One possible explanation for this difference is that the SFOAEs (evoked by 40 dB SPL tones) from which the Shera and Guinan’s latencies were calculated included not only a robust LL component but also a basally generated SL component. Although the contribution of any SL component at a probe level of 40 dB SPL to the total SFOAE would likely be less than the contribution from the LL component, it may be sufficient to bias the latency calculation to shorter values (Siegel et al. 2005; Shera et al. 2010). In support of this hypothesis, SL SFOAE components have recently been measured at probe levels as low as 20 dB SPL (Sisto et al. 2013).
Basal generation of SL TEOAE components is broadly consistent with the hypothesis that the components are generated through intermodulation distortion induced by cochlear interactions between different-frequency components in the evoking-stimulus’ bandwidth (Withnell and Yates 1998; Withnell and McKinley 2005; Withnell et al. 2008; Goodman et al. 2009; Moleti et al. 2012). However, if generated through intermodulation distortion, SL contributions to the OAE would be expected to decrease as the spectral bandwidth of the evoking stimulus decreases—recent work has failed to show such an effect (Sisto et al. 2013; Lewis and Goodman 2014). Instead, the contribution from SL components to both the SFOAE and the OAE evoked by long duration tone bursts with narrow spectral bandwidths is similar to that for the OAE evoked by transient stimuli with broad spectral bandwidths (clicks and short duration tone bursts).
Basal reflection is an alternative mechanism that has been proposed as the origin of SL TEOAE components (Goodman et al. 2011; Moleti et al. 2013). Per this mode of generation, impedance irregularities distributed basal to the tonotopic place reflect a portion of the apically propagating traveling-wave energy. The general agreement between the current study’s empirically based estimate of the SL TEOAE-component generation region and the basal-reflection model-based estimation from Moleti et al. (2013) supports the basal reflection hypothesis. The physical basis for SL generation may lie in the recruitment of basal cochlear regions of coherent reflection as the BM response to the OAE probe extends basally with increasing probe level.
TEOAE-Component Growth and Cochlear Compression
The growth rates of the different-latency TEOAE components are hypothesized to provide a non-invasive assay of cochlear compression across different portions of the traveling wave. The I/O functions for the different-latency TEOAE components plotted in Fig. 7 are qualitatively (if not quantitatively) similar to basilar membrane I/O functions measured in non-human mammals at a fixed place to different-frequency tones (Ruggero et al. 1997; Ren and Nuttall 2001; Ren 2002; Rhode 2007). By re-casting each TEOAE component’s latency in terms of its approximate generation place (using the relationship defined in Fig. 10), the TEOAE-component I/O functions are consistent with (1) the BM response to a fixed-frequency tone becoming increasingly less compressive as the distance basal to the tone’s CF place increases and (2) the peak BM response for a fixed-frequency tone shifting basally as stimulus level increases.
The use of the equal-level double-evoked paradigm in the current study limits more detailed quantitative comparisons between TEOAE and BM growth rates, especially at lower stimulus levels. Specifically, the growth rates measured using a non-equal-level double-evoked paradigm (suppressor 12 dB higher than probe) tend to be less compressive than those measured using a linear paradigm (Goodman et al. 2011). This effect is more pronounced when the suppressor and probe are equal level (as was the case in the current study; Lewis and Goodman 2014).
Generalization to Other TEOAE Frequencies
Data collection and analysis was limited to the different-latency components within the 2 kHz-band of the TEOAE. As such, the generalization of the findings to other frequencies is unclear. Similar temporal spacing between different-latency components and growth rates to those reported in the current study have been observed at frequencies through 8 kHz (e.g., Goodman et al. 2009 and Sisto et al. 2013) and demonstrate that the phenomenon of different-latency components is not unique to the 2 kHz TEOAE. SL components have also been measured for TEOAE frequencies between 1 and 1.5 kHz (e.g., Goodman et al. 2009; Moleti et al. 2012), which is closer to the transition frequency between basal and apical mechanics (Shera et al. 2010; Dhar et al. 2011). Whether a similar phenomenon might be observed at even lower frequencies is unclear. Concerning the generalizability of the estimated cochlear region contributing to SL generation, basal contributions have previously been implicated at TEOAE frequencies between approximately 1 and 5 kHz (Moleti et al. 2013, 2014). However, across this range, there is a trend of the SL generation region becoming increasingly distributed basal to the tonotopic place as frequency decreases, perhaps indicative of a reduction in cochlear tuning (see Fig. 4 in Moleti et al. 2014).
Acknowledgments
Subject compensation was provided by a grant from the Executive Council for Graduate and Professional Students at the University of Iowa. The authors thank Rachel Stanziola and Brittany James who performed the data collection for this study. Portions of this work were presented at the 2013 Annual Meeting of the American Auditory Society and the 2014 Mid-winter Meeting of the Association for Research in Otolaryngology. This research served as part of the first author’s dissertation work at the University of Iowa.
COI Disclosure Statement
Neither of the authors have a commercial interest or other conflict of interest concerning the research detailed in the submitted manuscript. Funds for data collection (subject compensation) were provided by a grant from the Executive Council for Graduate and Professional Students at the University of Iowa.
Contributor Information
James D. Lewis, Phone: 1-402-498-6361, Email: james.lewis@boystown.org
Shawn S. Goodman, Email: Shawn-goodman@uiowa.edu
References
- Arthur RM, Pfeiffer RR, Suga N. Properties of two-tone inhibition in primary auditory neurones. J Physiol. 1971;212:593–609. doi: 10.1113/jphysiol.1971.sp009344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avan P, Elbez M, Bonfils P. Click-evoked otoacoustic emissions and the influence of high-frequency hearing losses in humans. J Acoust Soc Am. 1997;101:2771–2777. doi: 10.1121/1.418564. [DOI] [PubMed] [Google Scholar]
- Brass D, Kemp DT. Suppression of stimulus frequency otoacoustic emissions. J Acoust Soc Am. 1993;93:920–939. doi: 10.1121/1.405453. [DOI] [PubMed] [Google Scholar]
- Carvalho S, Büki B, Bonfils P, Avan P. Effect of click intensity on click-evoked otoacoustic emission waveforms: implications for the origin of emissions. Hear Res. 2003;175:215–225. doi: 10.1016/S0378-5955(02)00745-1. [DOI] [PubMed] [Google Scholar]
- Charaziak KK, Souza P, Siegel JH. Stimulus-frequency otoacoustic emission suppression tuning in humans: comparison to behavioral tuning. J Assoc Res Otolaryngol. 2013;14:843–862. doi: 10.1007/s10162-013-0412-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi YS, Lee SY, Parham K, Neely ST, Kim DO. Stimulus-frequency otoacoustic emission: measurements in humans and simulations with an active cochlear model. J Acoust Soc Am. 2008;123:2651–2669. doi: 10.1121/1.2902184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper NP. Two-tone suppression in cochlear mechanics. J Acoust Soc Am. 1996;99:3087–3098. doi: 10.1121/1.414795. [DOI] [PubMed] [Google Scholar]
- Delgutte B. Two-tone rate suppression n auditory-nerve fibers: dependence on suppressor frequency and level. Hear Res. 1990;49:225–246. doi: 10.1016/0378-5955(90)90106-Y. [DOI] [PubMed] [Google Scholar]
- Dhar S, Rogers A, Abdala C. Breaking away: violation of distortion emission phase-frequency invariance at low frequencies. J Acoust Soc Am. 2011;129:3115–3122. doi: 10.1121/1.3569732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geisler CD, Yates GK, Patuzzi RB, Johnston BM. Saturation of outer hair cell receptor currents causes two-tone suppression. Hear Res. 1990;44:241–256. doi: 10.1016/0378-5955(90)90084-3. [DOI] [PubMed] [Google Scholar]
- Gilman S, Dirks DD. Acoustics of ear canal measurement of eardrum SPL in simulators. J Acoust Soc Am. 1986;80:783–793. doi: 10.1121/1.393953. [DOI] [PubMed] [Google Scholar]
- Goodman SS, Fitzpatrick DF, Ellison JC, Jesteadt W, Keefe DH. High-frequency click-evoked otoacoustic emissions and behavioral thresholds in humans. J Acoust Soc Am. 2009;125:1014–1032. doi: 10.1121/1.3056566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman SS, Mertes IB, Scheperle RA (2011) Delays and growth rates of multiple TEOAE components. In: Shera CA, Olson ES (eds) What fire is in mine ears: progress in auditory biomechanics: Proceedings of the 11th International Mechanics of Hearing Workshop, American Institute of Physics, pp 279-285
- Hoaglin D, Mosteller F, Tukey JW. Understanding robust and exploratory data analysis. New York: Wiley; 1983. [Google Scholar]
- Jedrzejczak WW, Blinowska KJ, Konopka W. Time-frequency analysis of transiently evoked otoacoustic emissions of subjects exposed to noise. Hear Res. 2005;205:249–255. doi: 10.1016/j.heares.2005.03.024. [DOI] [PubMed] [Google Scholar]
- Kalluri R, Shera CA. Near equivalence of human click-evoked and stimulus-frequency otoacoustic emissions. J Acoust Soc Am. 2007;121:2097–2110. doi: 10.1121/1.2435981. [DOI] [PubMed] [Google Scholar]
- Kalluri R, Shera CA. Comparing stimulus-frequency otoacoustic emissions measured by compression, suppression, and spectral smoothing. J Acoust Soc Am. 2007;122:3562–3575. doi: 10.1121/1.2793604. [DOI] [PubMed] [Google Scholar]
- Keefe DH. Double-evoked otoacoustic emissions. I. Measurement theory and nonlinear coherence. J Acoust Soc Am. 1998;103:3489–3498. doi: 10.1121/1.423057. [DOI] [PubMed] [Google Scholar]
- Keefe DH. Moments of click-evoked otoacoustic emissions in human ears: group delay and spread, instantaneous frequency and bandwidth. J Acoust Soc Am. 2012;132:3319–3350. doi: 10.1121/1.4757734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keefe DH, Ling R. Double-evoked otoacoustic emissions. II. Intermittent noise rejection, calibration and ear-canal measurements. J Acoust Soc Am. 1998;103:3499–3508. doi: 10.1121/1.423058. [DOI] [PubMed] [Google Scholar]
- Keefe DH, Ellison JC, Fitzpatrick DF, Gorga MP. Two-tone suppression of stimulus frequency otoacoustic emissions. J Acoust Soc Am. 2008;123:479–1494. doi: 10.1121/1.2828209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keefe DH, Goodman SS, Ellison JC, Fitzpatrick DF, Gorga MP. Detecting high-frequency hearing loss with click-evoked otoacoustic emissions. J Acoust Soc Am. 2011;129:245–261. doi: 10.1121/1.3514527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kemp DT, Bray P, Alexander L, Brown AM. Acoustic emission cochleography—practical aspects. Scand Audiol Suppl. 1986;25:71–95. [PubMed] [Google Scholar]
- Kemp DT, Ryan S, Bray P. A guide to the effective use of otoacoustic emissions. Ear Hear. 1990;11:93–105. doi: 10.1097/00003446-199004000-00004. [DOI] [PubMed] [Google Scholar]
- Lewis JD, Goodman SG (2014) The effect of stimulus bandwidth on the nonlinear-derived tone-burst-evoked otoacoustic emission. J Assoc Res Otolaryngol. doi:10.1007/s10162-014-0484-6 [DOI] [PMC free article] [PubMed]
- Lineton B, Wildgoose CMB. Comparing two proposed measures of cochlear mechanical filter bandwidth based on stimulus frequency otoacoustic emissions. J Acoust Soc Am. 2009;125:1558–1566. doi: 10.1121/1.3068452. [DOI] [PubMed] [Google Scholar]
- Lucertini M, Moleti A, Sisto R. On the detection of early cochlear damage by otoacoustic emission analysis. J Acoust Soc Am. 2002;111:972–978. doi: 10.1121/1.1432979. [DOI] [PubMed] [Google Scholar]
- Mertes IB, Goodman SS. Short-latency transient-evoked otoacoustic emissions as predictors of hearing status and thresholds. J Acoust Soc Am. 2013;134:2127–2135. doi: 10.1121/1.4817831. [DOI] [PubMed] [Google Scholar]
- Moleti A, Botti T, Sisto R. Transient-evoked otoacoustic emission generators in a nonlinear cochlea. J Acoust Soc Am. 2012;131:2891–2903. doi: 10.1121/1.3688474. [DOI] [PubMed] [Google Scholar]
- Moleti A, Al-Maamury AM, Bertaccini D, Bott T, Sisto R. Generation place of the long- and short-latency components of transient-evoked otoacoustic emissions in a nonlinear cochlear model. J Acoust Soc Am. 2013;133:4098–4108. doi: 10.1121/1.4802940. [DOI] [PubMed] [Google Scholar]
- Moleti A, Sisto R, Lucertini M. Experimental evidence for basal place-fixed generation of short-latency TEOAE components. Assoc Res Otolaryngol Midwinter Meet Abstr. 2014;PS-122(37):69–70. [Google Scholar]
- Murnane OD, Kelly JK. The effects of high-frequency hearing loss on low-frequency components of the click-evoked otoacoustic emission. J Am Acad Audiol. 2003;14:525–533. doi: 10.3766/jaaa.14.9.8. [DOI] [PubMed] [Google Scholar]
- Neely ST, Norton SJ, Gorga MP, Jestaedt W. Latency of auditory brain-stem responses and otoacoustic emissions using tone-burst stimuli. J Acoust Soc Am. 1988;83:652–656. doi: 10.1121/1.396542. [DOI] [PubMed] [Google Scholar]
- Pang XD, Guinan JJ., Jr Growth rate of simultaneous masking in cat auditory-nerve fibers: relationship to the growth of basilar-membrane motion and the origin of two-tone suppression. J Acoust Soc Am. 1997;102:3564–3575. doi: 10.1121/1.420147. [DOI] [PubMed] [Google Scholar]
- Patuzzi R. Cochlear micromechanics and macromechanics. In: Dallos P, Popper AN, Fay RR, editors. The cochlea. New York: Springer; 1996. pp. 186–257. [Google Scholar]
- Rasetshwane DM, Neely ST. Measurements of wide-band cochlear reflectance in humans. J Assoc Res Otolaryngol. 2012;13:591–607. doi: 10.1007/s10162-012-0336-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasetshwane DM, Argenyi M, Neely ST, Kopun JG, Gorga MP. Latency of tone-burst-evoked auditory brain stem responses and otoacoustic emissions: level, frequency, and rise-time effects. J Acoust Soc Am. 2013;133:2803–2817. doi: 10.1121/1.4798666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren T. Longitudinal pattern of basilar membrane vibration in the sensitive cochlea. J Neurosci. 2002;99:17101–17106. doi: 10.1073/pnas.262663699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren T, Nuttall AL. Basilar membrane vibration in the basal turn of the sensitive gerbil cochlea. Hear Res. 2001;151:48–60. doi: 10.1016/S0378-5955(00)00211-2. [DOI] [PubMed] [Google Scholar]
- Rhode WS. Basilar membrane mechanics in the 6-9 kHz region of sensitive chinchilla cochleae. J Acoust Soc Am. 2007;121:2792–2804. doi: 10.1121/1.2718397. [DOI] [PubMed] [Google Scholar]
- Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC, Recio A, Narayan SS, Robles L. Basilar-membrane responses to tones at the base of the chinchilla cochlea. J Acoust Soc Am. 1997;101:2151–2163. doi: 10.1121/1.418265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachs RM, Burkhard MD. Insert earphone pressure response in real ears and couplers. J Acoust Soc Am. 1972;52:183. doi: 10.1121/1.1982149. [DOI] [Google Scholar]
- Schairer KS, Fitzpatrick D, Keefe DH. Input-output functions for stimulus-frequency otoacoustic emissions in normal-hearing adult ears. J Acoust Soc Am. 2003;114:944–966. doi: 10.1121/1.1592799. [DOI] [PubMed] [Google Scholar]
- Schairer KS, Ellison JC, Fitzpatrick D, Keefe DH. Use of stimulus-frequency otoacoustic emission latency and level to investigate cochlear mechanics in human ears. J Acoust Soc Am. 2006;120:901–914. doi: 10.1121/1.2214147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera CA, Guinan JJ., Jr Evoked otoacoustic emissions arise by two fundamentally different mechanisms: a taxonomy for mammalian OAEs. J Acoust Soc Am. 1999;105:782–798. doi: 10.1121/1.426948. [DOI] [PubMed] [Google Scholar]
- Shera CA, Guinan JJ., Jr Stimulus-frequency-emission group delay: a test of coherent reflection filtering and a window on cochlear tuning. J Acoust Soc Am. 2003;113:2762–2772. doi: 10.1121/1.1557211. [DOI] [PubMed] [Google Scholar]
- Shera CA, Tubis A, Talmadge CL, Guinan JJ Jr (2004) The dual effect of “suppressor” tones on stimulus-frequency otoacoustic emissions. Assoc Res Otolaryngol Midwinter Meeting Abstract 538 27:181
- Shera CA, Guinan JJ, Jr, Oxenham AJ. Otoacoustic estimation of cochlear tuning: validation in the chinchilla. J Assoc Res Otolaryngol. 2010;11:343–365. doi: 10.1007/s10162-010-0217-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel JH, Cerka AJ, Recio-Spinoso A, Temchin AN, van Dijk P, Ruggero MA. Delays of stimulus-frequency otoacoustic emissions and cochlear vibrations contradict the theory of coherent reflection filtering. J Acoust Soc Am. 2005;118:2434–2443. doi: 10.1121/1.2005867. [DOI] [PubMed] [Google Scholar]
- Sisto R, Moleti A. Transient evoked otoacoustic emission latency and cochlear tuning at different stimulus levels. J Acoust Soc Am. 2007;122:2183–2190. doi: 10.1121/1.2769981. [DOI] [PubMed] [Google Scholar]
- Sisto R, Moleti A, Lucertini M. Spontaneous otoacoustic emissions and relaxation dynamics of long decay time OAEs in audiometrically normal and impaired subjects. J Acoust Soc Am. 2001;109:638–647. doi: 10.1121/1.1336502. [DOI] [PubMed] [Google Scholar]
- Sisto R, Sanjust F, Moleti A. Input/output functions of different-latency components of transient-evoked and stimulus-frequency otoacoustic emissions. J Acoust Soc Am. 2013;133:2240–2253. doi: 10.1121/1.4794382. [DOI] [PubMed] [Google Scholar]
- Stinson MR, Lawton BW. Specification of the geometry of the human ear canal for the prediction of sound-pressure level distribution. J Acoust Soc Am. 1989;85:2492–2503. doi: 10.1121/1.397744. [DOI] [PubMed] [Google Scholar]
- Stinson MR, Shaw EAG, Lawton BW. Estimation of acoustical energy reflectance at the eardrum from measurements of pressure distribution in the human ear canal. J Acoust Soc Am. 1982;72:766–773. doi: 10.1121/1.388257. [DOI] [PubMed] [Google Scholar]
- Tavartkiladze GA, Frolenkov GI, Kruglov AV, Artamasov SV. Ipsilateral suppression effects on transient evoked otoacoustic emission. Brit J Audiol. 1994;28:93–204. doi: 10.3109/03005369409086568. [DOI] [PubMed] [Google Scholar]
- Tognola G, Grandori F, Ravazzani P. Time-frequency distributions of click-evoked otoacoustic emissions. Hear Res. 1997;106:112–122. doi: 10.1016/S0378-5955(97)00007-5. [DOI] [PubMed] [Google Scholar]
- Withnell RH, McKinley S. Delay dependence for the origin of the nonlinear derived transient evoked otoacoustic emission. J Acoust Soc Am. 2005;117:281–291. doi: 10.1121/1.1798352. [DOI] [PubMed] [Google Scholar]
- Withnell RH, Yates GK. Enhancement of the transient-evoked otoacoustic emission produced by the addition of a pure tone in the guinea pig. J Acoust Soc Am. 1998;104:344–349. doi: 10.1121/1.423243. [DOI] [PubMed] [Google Scholar]
- Withnell RH, Yates GK, Kirk DL. Changes to low-frequency components of the TEOAE following acoustic trauma to the base of the cochlea. Hear Res. 2000;139:1–12. doi: 10.1016/S0378-5955(99)00132-X. [DOI] [PubMed] [Google Scholar]
- Withnell RH, Hazlewood C, Knowlton A. Reconciling the origin of the transient evoked otoacoustic emission in humans. J Acoust Soc Am. 2008;123:212–221. doi: 10.1121/1.2804635. [DOI] [PubMed] [Google Scholar]
- Zettner EM, Folsom RC. Transient emission suppression tuning curve attributes in relation to psychoacoustic threshold. J Acoust Soc Am. 2003;113:2031–2041. doi: 10.1121/1.1560191. [DOI] [PubMed] [Google Scholar]
- Zhang X, Heinz MG, Bruce IC, Carney LH. A phenomenological model for the responses of auditory-nerve fibers: I. Nonlinear tuning with compression and suppression. J Acoust Soc Am. 2001;109:648–670. doi: 10.1121/1.1336503. [DOI] [PubMed] [Google Scholar]
- Zweig G, Shera CA. The origin of periodicity in the spectrum of evoked otoacoustic emissions. J Acoust Soc Am. 1995;98:2018–2047. doi: 10.1121/1.413320. [DOI] [PubMed] [Google Scholar]