Skip to main content
NCBI home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2014 Dec 1;18(1):66–73. doi: 10.1111/ele.12385

Measures of precision for dissimilarity-based multivariate analysis of ecological communities

Marti J Anderson 1,*, Julia Santana-Garcon 2
PMCID: PMC4311441  PMID: 25438826

Abstract

Ecological studies require key decisions regarding the appropriate size and number of sampling units. No methods currently exist to measure precision for multivariate assemblage data when dissimilarity-based analyses are intended to follow. Here, we propose a pseudo multivariate dissimilarity-based standard error (MultSE) as a useful quantity for assessing sample-size adequacy in studies of ecological communities. Based on sums of squared dissimilarities, MultSE measures variability in the position of the centroid in the space of a chosen dissimilarity measure under repeated sampling for a given sample size. We describe a novel double resampling method to quantify uncertainty in MultSE values with increasing sample size. For more complex designs, values of MultSE can be calculated from the pseudo residual mean square of a permanova model, with the double resampling done within appropriate cells in the design. R code functions for implementing these techniques, along with ecological examples, are provided.

Keywords: Assemblage data, community ecology, dissimilarities, multivariate analysis, permanova, precision, replicates, sampling design, standard error, variability

Introduction

Studies of ecological communities require key logistic decisions regarding the size and number of individual sampling units that should be used in order to characterise (and analyse) communities of interest. Researchers designing manipulative experiments or embarking on mensurative sampling designs (sensu Hurlbert 1984) may well ask the essential question: How many replicate sampling units are needed to get reasonably precise measures of multivariate variability for purposes of testing relevant null hypotheses regarding community structure?

To measure the density or relative abundance of a single species (univariate), methods exist to allow researchers to assess (e.g. from a series of replicates obtained in preliminary pilot investigations) the adequacy of any given choice of sampling-unit size and/or number (e.g. Andrew & Mapstone 1987; Downing & Downing 1992). In particular, for univariate data one may calculate a value of precision for the mean of a given sample of n units of a given size. Precision measures the degree of concordance among multiple estimates of a given parameter (such as the mean) for the same population (Cochran & Cox 1957). This is reflected by the variability of an estimate; precision improves as variability decreases. Precision is measurable from the sampling programme and improves with increases in the number and size of sampling units.

An appropriate measure of univariate precision of the mean for quantitative abundance data can be calculated from a given sample as the standard error of the mean; namely, Inline graphic, where s is the sample standard deviation and n is the number of sampling units. As values of SE decrease, precision improves. Measures of precision can be calculated from pilot data, a plot of SE vs. n can be drawn, and we expect a gradual decrease and apparent levelling-off in the value of SE with increasing n in such a plot. One may then consider that a value of n around this apparent asymptote in SE (i.e. where the slope of the curve becomes very small) would be reasonable to use for future investigations of the population mean, as further increases in n would not result in substantially greater increases in precision. A standardised measure of precision of the mean is given by Inline graphic, where Inline graphic is the sample mean. This measure is unitless and allows comparisons among different studies. 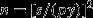Also, given a set of pilot data, one may calculate a value of n required to achieve a desired level of standardised precision set a priori (such as p = 0.2, etc.) as Inline graphic, rounded up to the nearest integer (e.g. Andrew & Mapstone 1987).

For multivariate data, especially multi-species count data that are gathered with the intention of characterising ecological communities, there is no obvious measure of multivariate precision that can be used to assist researchers in decision-making processes regarding adequate sampling. First, what do we mean by ‘the community’? We presume here that the researcher has already defined the community conceptually initially by reference to a particular spatial and temporal inferential domain (e.g. trees on Great Barrier Island, invertebrates within a given depth-range on the Norwegian continental shelf within a particular pre-defined area specified by latitude and longitude, etc.). This domain is also likely to include specificity caused by logistic constraints in sampling organisms which further limits inference (e.g. only macroinvertebrates large enough to be retained on a 0.5 mm sieve, only trees greater than a certain diameter at breast height (dbh), etc.). Although these decisions might be somewhat arbitrary, often based on convenience or historical legacies (hence, the word ‘assemblage’ is preferable to the word ‘community’ for multispecies data sets, see in particular Underwood 1986), we presume the researcher is sampling from the same ‘universe’ with respect to these definitions within a given study (as in Colwell et al. 2004), and that what is required to characterise the community, so defined, from a sampling perspective, will follow directly from this. We acknowledge the complexity of this assumption, however, and recognise that there may be a trade-off when choosing the size of the sampling unit between having enough information about the community and considering the sampling unit to be homogeneous with respect to community structure (Carlile et al. 1989; Dray et al. 2012).

Multivariate analyses of ecological communities are very often based on measures of dissimilarity, such as Bray–Curtis, Hellinger or Jaccard, that appropriately emphasise changes in the composition of the identities or relative abundances of individual species (Legendre & Gallagher 2001; Clarke et al. 2006; De Cáceres et al. 2013). Thus, although a more classical Euclidean-based multivariate analogue of the above univariate precision indices might be considered (e.g. such as the determinant of a variance-covariance matrix on normalised data, see also Kotz & Lovelace 1998; Pearn & Kotz 2006), these implicitly or explicitly rely on assumptions of multivariate normality, and are unlikely to shed any light on ecologically relevant compositional information.

Non-parametric measures of precision for multivariate data have been developed recently by Šiman (2014). These are based on the calculation of multivariate quantiles using half-space depth regions (Rousseeuw & Ruts 1999; Serfling 2002). For a description of half-space depth (Tukey 1975) and its associated properties, see Dutta et al. (2011). Although these ideas might well be applied fruitfully to sample points in a principal coordinate (PCO) space that preserves a chosen dissimilarity measure (e.g. Gower 1966; Legendre & Anderson 1999; McArdle & Anderson 2001), there remain important problems. The regions must be convex, the calculations require a large number of data points, and the computations are so demanding as to make them unfeasible for any more than four or five variables (Šiman 2014). However, data sets in community ecology typically are high-dimensional with many species.

One important aspect of community structure is richness – the number of species – which is known simply to increase with sample size (or sample area). A plot of the cumulative number of species with increases in the number of sampling units (a species-accumulation curve, Gotelli & Colwell 2001; Magurran 2003) can be drawn from a set of samples taken from a given area. The point at which this curve begins to level-off can indicate the number of samples beyond which not many new species will be encountered. The usual purpose of such plots, however, is generally to estimate the total number of species in a given (usually large) area (e.g. Ugland et al. 2003; Colwell et al. 2004; Gray et al. 2004), rather than to infer the number of sampling units required to characterise variation in community structure within that area. Furthermore, the size of individual sampling units is usually driven heavily by logistic constraints (e.g. only 1 m2 plots can be examined within a reasonable length of time in the field while diving under SCUBA, etc.).

Our purpose here is to describe some simple approaches to aid in the assessment of appropriate sampling of ecological communities for subsequent analysis using dissimilarity-based multivariate methods, such as permanova (Anderson 2001a; Anderson et al. 2008), permdisp (Anderson 2006; Anderson et al. 2006) or distance-based redundancy analysis (dbRDA, Legendre & Anderson 1999; McArdle & Anderson 2001).

In some cases, lack of information within individual sampling units requires a group of sampling units to be pooled together prior to analysis. If the sizes of individual sampling units are too small, then many units may contain no species at all (leading to undefined dissimilarity values) and there also may be many pairs of units that have no (or very few) species in common, yielding dissimilarity values that are uninformative (Clarke et al. 2006). Some simple methods designed to assist in the choice of the number of replicates to pool in such cases are provided in an Appendix (see Supporting Information)

Presuming an appropriate replicate sampling unit (potentially comprised of a number of pooled sub-samples) has been defined, we ask: ‘How many replicates are needed to sufficiently characterise the community being sampled with reasonable precision for subsequent dissimilarity-based multivariate analysis?’ We propose the use of a pseudo multivariate dissimilarity-based standard error (MultSE) – a direct analogue to the univariate standard error – as a useful quantity for assessing sample-size adequacy for ecological studies. Specifically, MultSE provides a measure of variability in the position of the sample centroid in the space of the chosen dissimilarity measure under repeated sampling for a given sample size. This can be calculated easily from a single set of pilot data or on residuals after fitting some more complex sampling design or model. We further propose a double resampling technique (permutation followed by bootstrapping) in order to quantify uncertainty in MultSE values with increasing numbers (or sizes) of sampling units.

Methods

A multivariate measure of pseudo standard error

As a direct analogue to the univariate measure of SE of the mean, we consider a multivariate measure of pseudo standard error (MultSE, first described by Anderson et al. 2001), as follows. Let Y be a (n × p) matrix of n sampling units within which the values of each of k = 1,…, p variables have been measured. For example, consider counts of each of p species in each of n quadrats that have been placed at random positions within a particular pre-defined study area. Let D be a (n × n) matrix of dissimilarities {dij} among all pairs of sampling units, i = 1,…, n and j = 1,…, n. The sum of squared interpoint dissimilarities divided by the number of sampling points (n) is directly interpretable as a multivariate measure of pseudo sums of squares in the space of the chosen dissimilarity measure:

graphic file with name ele0018-0066-m5.jpg 1

This is because the quantity in eqn 1 is also equivalent to the sum of squared distances from individual sampling points to their centroid in the space of the chosen dissimilarity measure, a theorem stated in Legendre & Anderson (1999, see Appendix B therein) and Anderson (2001a), proven by Legendre & Fortin (2010, see Appendix 1 therein). Furthermore, dividing this by (n − 1) yields a quantity that is directly interpretable as a multivariate measure of pseudo variance in the space of the chosen dissimilarity measure:

graphic file with name ele0018-0066-m6.jpg 2

Indeed, in the case of a single variable and Euclidean distance, SS is equal to the usual classical univariate sum of squares and V is equal to the usual classical unbiased measure of the sample variance (Anderson 2001a; Legendre & De Cáceres 2013). Unbiasedness is only ensured when sampling is representative of the statistical population under study, as is generally achieved by some appropriate form of random sampling.

Note that the word ‘pseudo’ has been used throughout here to distinguish SS in (1) above from the classical multivariate sums-of-squares-and-cross-products (SSCP) matrix and V in (2) above from the classical multivariate sample variance-covariance matrix. The classical matrices will clearly include measures of relationships among all pairs of variables in the multivariate Euclidean space of the original variables (namely, in the off-diagonal positions of these matrices), whereas these pseudo measures do not. Note also that, in the case of multivariate data and Euclidean distance, SS in (1) is equal to the trace of the classical SSCP matrix and V in (2) is equal to the trace of the classical sample variance-covariance matrix.

Finally, based on the above, a multivariate pseudo standard error therefore can be calculated as:

graphic file with name ele0018-0066-m7.jpg 3

We consider that MultSE in (3) is perfectly suitable as a measure of the variability in the position of the sample centroid for a given group in the space of the chosen dissimilarity measure and within a given study. It provides a novel approach to assess adequacy in sample sizes, as it can be based on a dissimilarity measure of choice (see also Pillar 1998). Note, however, that it produces a value which is not standardised in any way – it will be in the units of the resemblance measure chosen – hence can only be used within the context of a given study, and cannot be compared among studies. Although standardised univariate precision divides the standard error by the sample mean, this is not possible in the present case because the sample mean is clearly a vector here (being multivariate). Thus, although some chosen value of standardised precision for univariate analysis might be suggested as a rule of thumb to be applied to studies across a given field (e.g. p = 0.2 or p = 0.5, etc.), the value of MultSE in (3) is dependent on the scale of the dissimilarity measure chosen and (potentially) also on the number of variables, so no such generalisation for its value across multiple studies is apparent. However, as illustrated by the examples below (see Results), MultSE will still nevertheless be quite useful for examining relative precision for different sample sizes within a given study.

The double resampling method and plots of MultSE vs. sample size

For simplicity of notation in what follows, let s = MultSE. (The use of s is justified here, as s is commonly used to denote a standard deviation, and here we use it to denote the standard deviation of sample centroids for a given sample size in the space of the dissimilarity measure under repeated sampling.) We propose that, given a set of pilot multivariate data having a total of N sampling units, one may draw a random subset (without replacement) of size n = 2, 3, 4,…, N and for each of these random subsets, a value of s can be calculated, which may be denoted in each case by Inline graphic. The superscript π here indicates that the value has arisen from a random subset, whereas the subscript indicates the sample size drawn. Repeat this process for a very large number of random draws (say 10 000), then calculate the mean values obtained across all such random subsets of a given sample size as Inline graphic. A plot of Inline graphic vs. ℓ for ℓ = 2, 3,…, N will then provide the graphic we require to assess variability (and hence, the degree of precision) with increasing sample size. We propose that these means be calculated using sampling without replacement (i.e. using a permutation method) specifically to ensure that the values obtained will be unbiased.

Next, we propose that a bootstrapping method be used to draw error bars on the plot. It is clear that the number of possible permutations for n = N is 1 (i.e. this is simply the full set of data) and further that the number of random subsets without replacement that would yield unique values for Inline graphic (equivalent to simply leaving out one observation at a time) is also limited to just N possible values. Hence, we propose obtaining a further random subset as a random draw with replacement (i.e. a bootstrap sample), of size n = 2, 3, 4,…, N and for each of these to calculate a value of s, denoted in each case by Inline graphic. The superscript β here indicates, in each case, that the value has arisen from a bootstrap sample. Consider the 0.025 and 0.975 quantiles of the bootstrap distribution for each sample size n = ℓ for ℓ = 2, 3,…, N as Inline graphic and Inline graphic respectively. Unlike the permutation approach, the bootstrap distribution is known to be biased (e.g. Davison & Hinkley 1997). An empirical estimate of the bias, for each sample size ℓ, is given by:

graphic file with name ele0018-0066-m15.jpg 4

Hence, estimates of the 0.025 and 0.975 quantiles that attempt to adjust for the bias are provided by

graphic file with name ele0018-0066-m16.jpg 5

respectively. As our proposed method uses permutations to obtain mean values for the plot, and a separate bias-adjusted bootstrapping approach to obtain appropriate error bars, we shall refer to this overall process generally as a ‘double resampling’ method. We note also that clearly other choices of quantiles may easily be calculated here in a similar fashion (e.g. 0.25, 0.75, etc.), if desired.

We provide R code (R Core Team 2014) in the form of a function (‘MSEgroup.d’) which calculates MultSE separately for each group in a one-way design, with double resampling to obtain means and error bars, in each case, for increasing numbers of replicates (see Supporting Information). The routine calculates the means using the permutation approach, whereas the lower and upper quantiles are obtained using the bootstrapping approach, including an adjustment for the bias in the bootstrap, as described above.

Calculating MultSE for more complex designs

The idea of using MultSE as a measure of precision can be readily extended for use with more complex sampling designs by noting that the residual mean square provided from a permanova analysis (Anderson 2001a) is itself a measure of multivariate pseudo error variance in the space of the chosen dissimilarity measure. Suppose some number of multivariate sampling units (and not necessarily the same number) is obtained from each of g groups in a one-way anova design, yielding a total of N sampling units. Then, as described in McArdle & Anderson (2001), let D = {dij} be an (N × N) dissimilarity matrix, let A = {aij} = Inline graphic, and let Inline graphic be Gower's (1966) centred matrix, where 1 is a column of 1's of length N and I is a (N × N) identity matrix. Next, let matrix X be a (N × g) design matrix of full rank that codes for the full permanova model, including intercept (e.g. in a one-way anova design, g would be equal to the number of groups). Finally, let matrix H be the usual projection matrix for the design, namely H = X[X′X]−1X′. Now, the total sum of squares in the space of the dissimilarity measure is given by tr[G], where ‘tr’ denotes the trace of a matrix. This is equivalent to the sum of the total sum of squares for each individual variable (i.e. added up across all variables) if the original dissimilarity measure chosen was the Euclidean distance. A partitioning according to the one-way permanova model is then given by

graphic file with name ele0018-0066-m19.jpg 6

where tr[HG] is the sum of squares explained by the model and tr[(I − H)G] is the residual sum of squares. McArdle & Anderson (2001) go on to describe the pseudo F-statistic:

graphic file with name ele0018-0066-m20.jpg 7

A test of significance (P-value) is then obtained via an appropriate permutation method (Anderson 2001b; Anderson & ter Braak 2003). The only component of this procedure that is of interest here, however, is purely the residual mean square from the permanova model, i.e. the denominator of eqn 7. This estimates error (within-group) variability in the space of the dissimilarity measure and is calculated, in the one-way case, as:

graphic file with name ele0018-0066-m21.jpg 8

After obtaining V from eqn 8, one can then apply eqn 2 to calculate precision and perform the double resampling method for increasing numbers of replicates, as described above. Note, however, that the replicates here occur within the structure of a model framework – a specific anova design. This means the double resampling method must be applied separately for increasing numbers of samples within each individual cell in the design. For example, in the case of a one-way anova model, the double resampling is done separately within each group.

We provide R code (function ‘MSE.d’) which calculates MultSE from the residual mean square of a one-way permanova model, including double resampling, for increasing numbers of replicates, as described above, in Supporting Information.

Results

Choosing an appropriate size or number of replicates using MultSE

The precision of univariate data has been assessed in order to optimise the sampling effort of baited remote underwater video (BRUV) techniques in estuarine (Gladstone et al. 2012) and pelagic environments (Santana-Garcon et al. 2014a,b). The parameters potentially affecting the sampling ability of pelagic stereo-BRUVs include immersion time (the time that cameras are left recording underwater) and the number of replicate deployments.

Data were collected in March 2012 near Tantabiddi Passage in Ningaloo Marine Park (21°53′ S, 113°56′ E), Western Australia. The pelagic stereo-BRUVs used in this study are described in detail elsewhere (Santana-Garcon et al. 2014a,b). The systems were designed to remain in the mid-water at ca. 5 m depth (7.17 ± 0.54 m, Mean ± SE), 30 m above the bottom and were deployed for an immersion time of up to 3 h. There were 12 replicate deployments (six at each of two sites) obtained during daylight hours. Video images were analysed using the software ‘EventMeasure (Stereo)’ (SeaGIS Pty Ltd, Bacchus Marsh, Victoria, Australia). All fish recorded were quantified and identified to the lowest taxonomic level possible. To avoid repeating counts of individual fish re-entering the field of view, a conservative measure of relative abundance (MaxN) was recorded as the maximum number of individuals of the same species appearing at the same time (Priede et al. 1994). MaxN was recorded for each of three different immersion times: 60, 120 and 180 min.

No previous assessment has been done to optimise multivariate precision for dissimilarity-based community analysis of these fish assemblages. We wished to identify: (1) an appropriate length of time that cameras should be deployed; and (2) an appropriate number of replicate deployments beyond which no substantial decreases in MultSE would accrue.

First, we examined the means and quantiles of MultSE with increasing sample size using either the permutation or the bootstrap method alone for the 60-min immersion time, with analyses based on square-root transformed abundances and Bray–Curtis dissimilarities. The permutation method alone yields obvious constraints on the error bars for larger sample sizes, whereas the bootstrap method alone yields means that are biased downwards (Fig.1a). This motivates the use of our double resampling approach, which shows that no appreciable precision is gained by deploying the cameras longer than 120 min, and that a levelling-off in MultSE occurs for sample sizes around n = 7 or 8 (Fig.1b). The R code used for this example (‘R code_Ningaloo.txt’) and the original data (‘Ningaloo.csv’) are provided in Supporting Information.

Figure 1.

Figure 1

Open in a new tab

Multivariate pseudo standard error (MultSE) as a function of sample size on the basis of Bray–Curtis dissimilarities calculated on square-root transformed fish abundance data from Ningaloo (a) for an immersion time of 60 min only, showing results (means with 2.5 and 97.5 percentiles as error bars) from 10 000 resamples obtained using either the permutation or bootstrap approach and (b) for all three immersion times, using the double resampling method, with permutation-based means and bias-adjusted bootstrap-based error bars (with 10 000 resamples for each).

We readily concede that the idea of ‘levelling-off’ must rest in the eyes of the beholder; the approach we suggest is intended to be a heuristic diagnostic tool only, and not a prescription. Nevertheless, the analyses of MultSE in this case coincide well with the results obtained for the precision of either of the univariate measures of richness or total abundance (Santana-Garcon et al. 2014a). This coincidence might not always occur, however, and will depend on the nature of the data and the characteristics that are emphasised by the chosen dissimilarity measure.

A further example of the proposed method yields additional insight. We consider next an analysis of soft-sediment macrofauna described by Ellingsen & Gray (2002), who studied beta diversity and its relationship with environmental heterogeneity in benthic marine systems over large spatial scales in the North Sea. Samples of soft-sediment macrobenthic organisms were obtained from 101 sites occurring in five large areas along a transect of 15 degrees of latitude. A total of 809 taxa were recorded overall, and replicate sampling units here consisted of abundances pooled across five benthic grabs (sub-samples) obtained at each site. For more details, see Ellingsen & Gray (2002), Ugland et al. (2003) and Anderson et al. (2006). Of interest here is to identify the number of replicate sampling units required to adequately sample the benthic communities for comparative analysis on the basis of the Jaccard resemblance measure. MultSE was calculated with the double resampling method for increasing numbers of replicates separately for each of the five areas. Results show clear heterogeneity in the MultSE values across the five different areas, with the greatest variability occurring in area 3, followed by areas 4 and 5, then area 2 and finally area 1 (Fig.2a). This agrees naturally with the differences in multivariate dispersions found previously (using permdisp; Anderson 2006) using the full set of data (Anderson et al. 2006, 2008). What is added to our understanding here by considering values of MultSE with increasing sample size (including the double resampling method) is that these differences in dispersion are already apparent once sample sizes within each area reach about n = 10 to 12 sampling units. Knowledge of what level of sampling may be required to identify significant heterogeneity can be quite useful. When dealing with large areas, for example, better estimates of overall richness can be obtained by generating species accumulation curves for each of several smaller sub-sampled areas, due to heterogeneity in community structure (turnover) across the larger sampling extent (Ugland et al. 2003, 2005). The R code used for this example (‘R code_Norway.txt’) and the original data (‘Norway.csv’ and ‘Areas.csv’) are provided in Supporting Information.

Figure 2.

Figure 2

Open in a new tab

Multivariate pseudo standard error (MultSE) as a function of sample size (a) for each of 5 different areas on the basis of Jaccard dissimilarities for macrofaunal communities from the Norwegian continental shelf and (b) for each of three different times on the basis of Bray–Curtis dissimilarities calculated on log(x + 1)-transformed counts of fishes from the Poor Knights Islands, New Zealand. A double resampling scheme was used to generate means for each sample size using 10 000 permutations and error bars as bias-adjusted 2.5 and 97.5 percentiles from 10 000 bootstrap resamples.

Calculating MultSE from a dissimilarity-based residual mean square

Consider data on fish assemblages from the Poor Knights Islands in New Zealand, described by Willis & Denny (2000) and Anderson & Willis (2003). Divers counted temperate reef fishes belonging to each of 62 species in each of nine 25 m × 5 m transects at each site. Data from the transects were pooled at the site level and a number of sites around the Poor Knights Islands were sampled at each of three different times: September 1998 (15 sites), March 1999 (21 sites) and September 1999 (20 sites). These span the point in time when the Poor Knights Islands were classified as a no-take marine reserve (October 1998).

Analyses of MultSE with the double resampling method vs. increasing sample sizes for each of the three times of sampling (based on log(x + 1)-transformed data and Bray–Curtis dissimilarities), was initially done separately for each time and showed no sign of heterogeneity of dispersions, unlike the Norwegian macrofauna (cf. Fig.2b and Fig.2a). A pooled estimate of MultSE can therefore legitimately be used as a single measure of precision, calculated from the residual mean square of a permanova model (quantity V from eqn 8 above) for the three groups corresponding to the three times of sampling (Fig.3). Precision in this case is seen to level off and does not improve substantially for these assemblages once the number of sites sampled within each time reaches around 7 or 8 (Fig.3). The R code used for this example (‘R code_PoorKnights.txt’) and the original data (‘PoorKnights.csv’) are provided in Supporting Information.

Figure 3.

Figure 3

Open in a new tab

Multivariate pseudo standard error (MultSE) calculated from the residual mean square of a one-way permanova model as a function of sample size on the basis of Bray–Curtis dissimilarities calculated on log(x + 1)-transformed counts of fishes from the Poor Knights Islands, New Zealand. A double resampling scheme was used to generate means for each sample size using 10 000 permutations and error bars as bias-adjusted 2.5 and 97.5 percentiles from 10 000 bootstrap resamples. Resampling was done separately within each of the three sampling times (i.e. within each of the three groups in the one-way permanova model design).

Discussion

We have provided some quantitative tools for assessing an appropriate number and scale of sampling units for dissimilarity-based multivariate analysis of ecological data. We propose here a measure of precision for multivariate data (MultSE) based on inter-point dissimilarities that is a direct analogue of the well-known univariate standard error. More specifically, MultSE measures the amount of variation in the position of the centroid in the space of the chosen dissimilarity measure under repeated sampling for a given sample size. As such, it is clearly highly relevant for assessing sampling adequacy when the goal is to embark on dissimilarity-based multivariate analyses with specific null hypotheses regarding differences among group centroids in such a space (Anderson & Walsh 2013). A double resampling method allows unbiased measures of variation in MultSE to be obtained.

We recognise the clear limitations of this approach. The measure takes no account of the shape of the multivariate data cloud, only its overall dispersion (size). Future developments should include better characterisation of the actual shape of the data cloud in the dissimilarity space of interest. This might be achieved, for example, through the use of multivariate kernel density estimation (KDE) in the PCO space of the resemblance measure. This would require, however, enhanced computer power and programming to cope with analyses of high-dimensional data sets like those typically found in ecology. Furthermore, the use of KDE would also concomitantly require large sample sizes to be effective, which could ultimately limit its utility in the present context. Future work should focus also on how such approaches might compare with, say, a more classical approach to measure multivariate precision, such as the determinant of a normalised variance-covariance matrix in the PCO space.

A further limitation of the approach outlined here is its scale dependency. Values of MultSE will necessarily depend on the dissimilarity measure used, so cannot be easily compared across studies. More work is needed to assess what levels of precision (as measured by MultSE) might be acceptable for different resemblance measures that are bounded and have a common scale, such as Jaccard or Bray–Curtis. Furthermore, we consider it is wise, before embarking on dissimilarity-based modelling, to examine the distributions of dissimilarities directly to check if large numbers of values approach the limits of what the chosen dissimilarity measure is able to measure. If so, then perhaps the choice of dissimilarity measure should be revisited. Another possibility is that large numbers of sparse sampling units are present which should be pooled together to provide enough information regarding the community of interest prior to subsequent analysis. We have provided a general tool for assessing the numbers of sub-samples that might be pooled together to define a reasonable ‘replicate’ in this context (see the Data S1).

Finally, although we have described the analysis of precision using the residual mean square from a permanova model only for a one-way case, extensions to higher-way models are clearly very easy to implement using the formulation in eqn 8 for any model specified fully within matrix X and with appropriate associated residual degrees of freedom. In addition, estimates of pseudo components of variation in the space of a dissimilarity measure can be calculated not just for the residual, but also for other individual terms in more complex permanova models, such as those that arise from hierarchical sampling designs or mixed models (e.g. Anderson et al. 2005; Terlizzi et al. 2007). Empirical measures of variability in the sizes of such components can be estimated using bootstrapping approaches (as in Terlizzi et al. 2007), thus opening the door to quantifying and assessing the adequacy of sampling at each of a number of spatial and/or temporal scales for multivariate community data – clearly a topic for future study. Some care may be needed in such cases, however, to ensure that the double resampling is performed within appropriate combinations of factor levels, given the particular higher-way design and the particular component(s) of interest.

Acknowledgments

MJA was supported by a Royal Society of New Zealand Marsden Grant MAU1005. Logistic support for acquiring the data analysed here from Western Australia was provided by the University of Western Australia and the Department of Fisheries, Government of Western Australia. We thank K. R. Clarke, P. Legendre and two additional anonymous reviewers for providing constructive critical comments to improve the manuscript.

Authorship

The ideas and methods presented in this manuscript were conceived by MJA who also wrote the text, JSG provided the motivating data sets from the Abrolhos Islands and Ningaloo Reef and also contributed to early drafts and final revisions.

Supporting Information

 

ele0018-0066-sd1.zip (111.2KB, zip)

References

  1. Anderson MJ. A new method for non-parametric multivariate analysis of variance. Austral Ecol. 2001a;26:32–46. [Google Scholar]
  2. Anderson MJ. Permutation tests for univariate or multivariate analysis of variance and regression. Can. J. Fish. Aquat. Sci. 2001b;58:626–639. [Google Scholar]
  3. Anderson MJ. Distance-based tests for homogeneity of multivariate dispersions. Biometrics. 2006;62:245–253. doi: 10.1111/j.1541-0420.2005.00440.x. [DOI] [PubMed] [Google Scholar]
  4. Anderson MJ. ter Braak CJF. Permutation tests for multi-factorial analysis of variance. J. Stat. Comput. Simul. 2003;73:85–113. [Google Scholar]
  5. Anderson MJ. Walsh DCI. What null hypothesis are you testing? PERMANOVA, ANOSIM and the Mantel test in the face of heterogeneous dispersions. Ecol. Monogr. 2013;83:557–574. [Google Scholar]
  6. Anderson MJ. Willis TJ. Canonical analysis of principal coordinates: a useful method of constrained ordination for ecology. Ecology. 2003;84:511–525. [Google Scholar]
  7. Anderson MJ, Saunders JE. Creese RG. University of Auckland, New Zealand: 2001. p. 29. Ecological monitoring of the Okura Estuary. Report 1: Results of a pilot study. Technical report prepared by Auckland UniServices for Auckland Regional Council. [Google Scholar]
  8. Anderson MJ, Diebel CE, Blom WM. Landers TJ. Consistency and variation in kelp holdfast assemblages: spatial patterns of biodiversity for the major phyla at different taxonomic resolutions. J. Exp. Mar. Biol. Ecol. 2005;320:35–56. [Google Scholar]
  9. Anderson MJ, Ellingsen KE. McArdle BH. Multivariate dispersion as a measure of beta diversity. Ecol. Lett. 2006;9:683–693. doi: 10.1111/j.1461-0248.2006.00926.x. [DOI] [PubMed] [Google Scholar]
  10. Anderson MJ, Gorley RN. Clarke KR. PERMANOVA+ for PRIMER: Guide to Software and Statistical Methods. Plymouth, UK: PRIMER-E; 2008. [Google Scholar]
  11. Andrew NL. Mapstone BD. Sampling and the description of spatial pattern in marine ecology. Oceanogr. Mar. Biol. Annu. Rev. 1987;25:39–90. [Google Scholar]
  12. Carlile DW, Skalski JR, Batker JE, Thomas JM. Cullinan VI. Determination of ecological scale. Landscape Ecol. 1989;2:203–213. [Google Scholar]
  13. Clarke KR, Somerfield PJ. Chapman MG. On resemblance measures for ecological studies, including taxonomic dissimilarities and a zero-adjusted Bray-Curtis coefficient for denuded assemblages. J. Exp. Mar. Biol. Ecol. 2006;330:55–80. [Google Scholar]
  14. Cochran WG. Cox GM. Experimental designs. 2nd edn. New York: John Wiley & Sons; 1957. [Google Scholar]
  15. Colwell RK, Mao CX. Chang J. Interpolating, extrapolating, and comparing incidence-based species accumulation curves. Ecology. 2004;85:2717–2727. [Google Scholar]
  16. Davison AC. Hinkley DV. Bootstrap Methods and Their Application. Cambridge: Cambridge University Press; 1997. [Google Scholar]
  17. De Cáceres M, Legendre P. He F. Dissimilarity measurements and the size structure of ecological communities. Methods Ecol. Evol. 2013;4:1167–1177. [Google Scholar]
  18. Downing JA. Downing WL. Spatial aggregation, precision, and power in surveys of freshwater mussel populations. Can. J. Fish. Aquat. Sci. 1992;49:985–991. [Google Scholar]
  19. Dray S, Pelissier R, Couteron P, Fortin M-J, Legendre P, Peres-Neto PR, et al. Community ecology in the age of multivariate multiscale spatial analysis. Ecol. Monogr. 2012;82:257–275. [Google Scholar]
  20. Dutta S, Ghosh AK. Chauduri P. Some intriguing properties of Tukey's half-space depth. Bernoulli. 2011;17(4):1420–1434. [Google Scholar]
  21. Ellingsen KE. Gray JS. Spatial patterns of benthic diversity: is there a latitudinal gradient along the Norwegian continental shelf? J. Anim. Ecol. 2002;71:373–389. [Google Scholar]
  22. Gladstone W, Lindfield S, Coleman M. Kelaher B. Optimisation of baited remote underwater video sampling designs for estuarine fish assemblages. J. Exp. Mar. Biol. Ecol. 2012;429:28–35. [Google Scholar]
  23. Gotelli NJ. Colwell RK. Quantifying biodiversity: procedures and pitfalls in the measurement and comparison of species richness. Ecol. Lett. 2001;4:379–391. [Google Scholar]
  24. Gower JS. Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika. 1966;53:325–338. [Google Scholar]
  25. Gray JS, Ugland KI. Lambshead J. Species accumulation and species area curves – a comment on Scheiner (2003) Global Ecol. Biogeogr. 2004;13:473–476. [Google Scholar]
  26. Hurlbert SH. Pseudoreplication and the design of ecological field experiments. Ecol. Monogr. 1984;54:187–211. [Google Scholar]
  27. Kotz S. Lovelace CR. Process Capability Indices in Theory and Practice. New York: Oxford University Press; 1998. [Google Scholar]
  28. Legendre P. Anderson MJ. Distance-based redundancy analysis: testing multispecies responses in multifactorial ecological experiments. Ecol. Monogr. 1999;69:1–24. [Google Scholar]
  29. Legendre P. De Cáceres M. Beta diversity as the variance of community data: dissimilarity coefficients and partitioning. Ecol. Lett. 2013;16:951–996. doi: 10.1111/ele.12141. [DOI] [PubMed] [Google Scholar]
  30. Legendre P. Fortin M-J. Comparison of the Mantel test and alternative approaches for detecting complex multivariate relationships in the spatial analysis of genetic data. Mol. Ecol. Resour. 2010;10:831–844. doi: 10.1111/j.1755-0998.2010.02866.x. [DOI] [PubMed] [Google Scholar]
  31. Legendre P. Gallagher ED. Ecologically meaningful transformations for ordination of species data. Oecologia. 2001;129:271–280. doi: 10.1007/s004420100716. [DOI] [PubMed] [Google Scholar]
  32. Magurran AE. Measuring Biological Diversity. Oxford: Blackwell Publishing; 2003. [Google Scholar]
  33. McArdle BH. Anderson MJ. Fitting multivariate models to community data: a comment on distance-based redundancy analysis. Ecology. 2001;82:290–297. [Google Scholar]
  34. Pearn WL. Kotz S. Encyclopedia and Handbook of Process Capability Indices. Singapore: World Scientific Publishing; 2006. [Google Scholar]
  35. Pillar VDP. Sampling sufficiency in ecological surveys. Abstr. Bot. 1998;22:37–48. [Google Scholar]
  36. Priede IG, Bagley PM, Smith A, Creasey S. Merrett NR. Scavenging deep demersal fishes of the Porcupine Seabight, Northeast Atlantic - Observations by baited camera, trap and trawl. J. Mar. Biol. Assoc. U. K. 1994;74:481–498. [Google Scholar]
  37. R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2014. ISBN 3-900051-07-0, URL http://www.R-project.org/ [Google Scholar]
  38. Rousseeuw PJ. Ruts I. The depth function of a population distribution. Metrika. 1999;49:213–244. [Google Scholar]
  39. Santana-Garcon J, Newman SJ. Harvey ES. Development and validation of a mid-water baited stereo-video technique for investigating pelagic fish assemblages. J. Exp. Mar. Biol. Ecol. 2014a;452:82–90. [Google Scholar]
  40. Santana-Garcon J, Newman SJ, Langlois TJ. Harvey ES. Effects of a spatial closure on highly mobile fish species: an assessment using pelagic stereo-BRUVs. J. Exp. Mar. Biol. Ecol. 2014b;460:153–161. [Google Scholar]
  41. Serfling R. Quantile functions for multivariate analysis: approaches and applications. Stat. Neerl. 2002;56:214–232. [Google Scholar]
  42. Šiman M. Precision index in the multivariate context. Commun. Stat. Theor. Methods. 2014;43:377–387. [Google Scholar]
  43. Terlizzi A, Anderson MJ, Fraschetti S. Benedetti-Cecchi L. Scales of spatial variation in Mediterranean subtidal sessile assemblages at different depths. Mar. Ecol. Prog. Ser. 2007;332:25–39. [Google Scholar]
  44. Tukey JW. Mathematics and the picturing of data. In: Vancouver BC, editor. Proceedings of the International Congress of Mathematicians. Montreal, Quebec: Canad. Math. Congress; 1975. pp. 523–531. Vol. 2. [Google Scholar]
  45. Ugland KI, Gray JS. Ellingsen KE. The species-accumulation curve and estimation of species richness. J. Anim. Ecol. 2003;72:888–897. [Google Scholar]
  46. Ugland KI, Gray JS. Lambshead PJD. Species accumulation curves analysed by a class of null models discovered by Arrhenius. Oikos. 2005;108:263–274. [Google Scholar]
  47. Underwood AJ. What is a community? In: Raup DM, Jablonski D, editors. Patterns and Processes in the History of Life. Berlin: Springer-Verlag; 1986. pp. 351–367. [Google Scholar]
  48. Willis TJ. Denny CM. 2000. Auckland, New Zealand Leigh Marine Laboratory, University of Auckland Effects of Poor Knights Islands Marine Reserve on demersal fish populations. Report to the Department of Conservation, Research Grant No. 2519.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

 

ele0018-0066-sd1.zip (111.2KB, zip)

Articles from Ecology Letters are provided here courtesy of Wiley

RESOURCES