Significance
Quantitative understanding of how individual interactions contribute to the kinetics and thermodynamics of protein folding is critical for deciphering the underlying molecular mechanisms that define the energy folding landscape. We applied a structure-based model that explicitly accounts for the interactions between charges, to folding–unfolding of four different protein pairs: rationally stabilized, via optimization of surface charge–charge interactions, variants, and respective wild types. First, we established that the models predict both thermodynamic and kinetic differences observed experimentally for all four studied protein pairs. Second, we used the results of the computational modeling to provide a molecular level explanation of how optimization of charge–charge interactions leads to an increase in the folding rates of designed variants, without changes in the unfolding rates.
Keywords: protein folding, protein stability, charge–charge interaction, energy landscape, computational design
Abstract
The kinetics of folding–unfolding of a structurally diverse set of four proteins optimized for thermodynamic stability by rational redesign of surface charge–charge interactions is characterized experimentally. The folding rates are faster for designed variants compared with their wild-type proteins, whereas the unfolding rates are largely unaffected. A simple structure-based computational model, which incorporates the Debye–Hückel formalism for the electrostatics, was used and found to qualitatively recapitulate the experimental results. Analysis of the energy landscapes of the designed versus wild-type proteins indicates the differences in refolding rates may be correlated with the degree of frustration of their respective energy landscapes. Our simulations indicate that naturally occurring wild-type proteins have frustrated folding landscapes due to the surface electrostatics. Optimization of the surface electrostatics seems to remove some of that frustration, leading to enhanced formation of native-like contacts in the transition-state ensembles (TSE) and providing a less frustrated energy landscape between the unfolded and TS ensembles. Macroscopically, this results in faster folding rates. Furthermore, analyses of pairwise distances and radii of gyration suggest that the less frustrated energy landscapes for optimized variants are a result of more compact unfolded and TS ensembles. These findings from our modeling demonstrates that this simple model may be used to: (i) gain a detailed understanding of charge–charge interactions and their effects on modulating the energy landscape of protein folding and (ii) qualitatively predict the kinetic behavior of protein surface electrostatic interactions.
The energy landscape theory provides a conceptual framework to describe the ensemble nature of the protein folding process (1–3). However, a more detailed understanding of contributions from specific types of interactions remains an active area of research (4, 5). Particularly, the question of how interactions between charged residues modulate the funneled energy landscape is not well explored. These interactions are long-range and thus can alter the conformational ensemble at every step of the folding process. The interactions between charged residues are also nonspecific and either attractive or repulsive and therefore their potential effects on the folding energy landscape can be highly complex (6, 7). Traditionally, the modulation of electrostatic interactions in proteins was done by changing the pH or to a lesser degree changing the ionic strength of the solution (8, 9). Such approaches are complicated by the difficulties of predicting the titration properties of individual amino acid residues in the context of ensembles of protein conformations that are sampled during the folding reaction (10). A more attractive approach is to modulate electrostatic interactions via substitutions that perturb the thermodynamic and kinetic properties of proteins using simple and computationally tractable model systems. Previously, we have shown that the stability of a diverse set of globular proteins can be modulated by rationally redesigning surface charge–charge interactions (11–26). These redesigned proteins are ideally suited to probe the role of electrostatic interactions in modulating the folding energy landscape. The redesigned variants have higher thermodynamic stability than their wild-type proteins. However, because the redesigned proteins contain very few substitutions (less than 5% of total), and because all of the substitutions are on the protein surface, they do not disrupt the native contacts that are important for defining funneled energy landscape (13, 27). Finally, the properties of these proteins can be compared at the same pH, largely eliminating the need to compute titration profiles. In this work, we used four of these redesigned proteins to experimentally probe their folding kinetics and compared them to their corresponding wild-type proteins. The experimental thermodynamic and kinetic data were further rationalized by molecular dynamics simulations using a structure-based model that incorporates the Debye–Hückel formalism to describe interactions between charges. We found that this model qualitatively predicts experimental thermodynamics and kinetics for all four studied proteins and provides insights of how charge–charge interactions modulate the protein folding energy landscape.
Results and Discussion
Experimental Studies of Stability and Folding Kinetics of Charge-Optimized Variants.
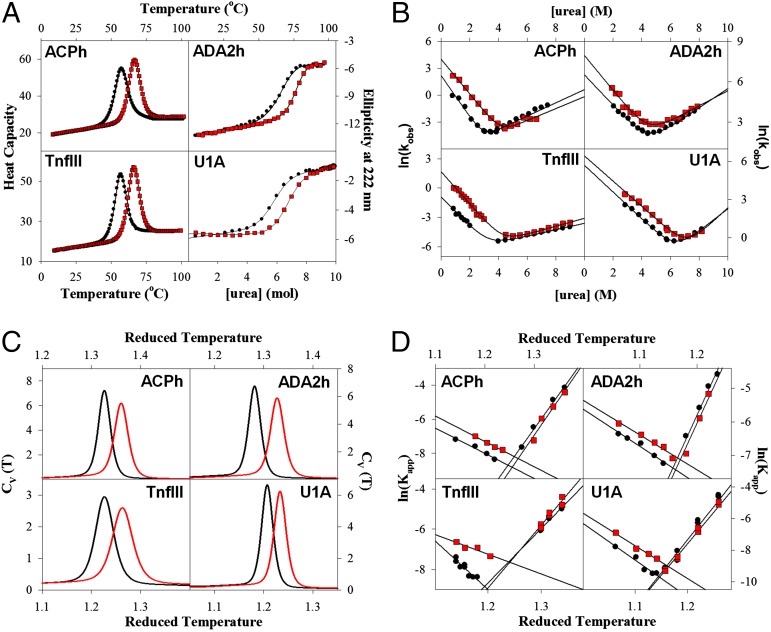
For this work we used four different proteins: human acylphosphatase (ACPh), activation domain of human procarboxypeptidase A2 (ADA2h), the fibronectin type III domain of human tenascin (TnfIII), and the N-terminal RNA-binding domain of human U1A protein (U1A). These proteins differ in size (there are 98, 72, 92, and 100 amino acid residues in the sequences of ACPh, ADA2h, TnfIII, and U1A, respectively), secondary structure, and in tertiary fold topology (Fig. S1). Surface charge–charge interactions in ACPh, ADA2h, TnfIII, and U1A were optimized using a computational design approach described by us previously and the stability of the variants was experimentally compared with the corresponding wild-type (WT) proteins (17, 21). Briefly, the goal of computational design was to optimize the overall energy of charge–charge interactions on the protein surface (22). The optimization does not explicitly include salt bridges, which appear to be of a lesser importance (14, 18, 23, 28) than the long-range charge–charge interactions (Figs. S2–S4). In all cases, experiments showed that the designed variants (des) were thermodynamically more stable than the corresponding WT proteins (Fig. 1A). Because the equilibrium constant is defined by a ratio between the kinetic rate constants for folding and unfolding, the question is, how do these rate constants change to cause an increase in thermodynamic stability? The increase in stability can be achieved by a decrease in the unfolding rate, increase in the folding rate, or a combination of these two. To address this question we experimentally measured and compared the folding and unfolding rate constants for the WT and des pair of variants of these four proteins. Fig. 1B shows typical chevron plots and reveals interesting common properties for all four studied protein pairs. In all cases, the unfolding rates are similar for the WT and des. In contrast, the folding rates are very different, and in all four cases the designed variants fold faster than the corresponding WT proteins. Importantly, how does such stabilization affect the folding energy landscape? Because charge–charge interactions are long-range they can influence the stability of the native state but also other states, including unfolded-state and transition-state (TSE) ensembles. Although experimental approaches do exist to analyze interactions in the TSE [e.g., phi-value (29) or psi-value (30) analyses], the interactions in the unfolded state are more difficult to assess. Alternatively, another promising approach is computational modeling based on statistical mechanics, which provides molecular details of the interactions and direct description of the folding energy landscape (31, 32). Such an approach was used in the present work.
Fig. 1.
Comparison between experimental and modeling results of the thermodynamics and kinetics for the four protein pairs shows good qualitative agreement. (A) Experimentally determined difference in stabilities between WT and des proteins (data and experimental details from refs. 17, 21). (B) chevron plots comparison of the refolding and unfolding kinetics. (C) Comparison of computed heat capacity (Cv) profiles. (D) Comparison of computed folding and unfolding kinetics. Data for the WT proteins and des variants are shown as black circles–lines and red squares–lines, respectively. See Materials and Methods for experimental and computational details. Protein identity is indicated in each plot.
Structure-Based Model with Debye–Hückel Electrostatics Can Qualitatively Describe Experimental Data.
The proteins discussed above are too large to computationally study folding–unfolding equilibrium using all-atom physics-based molecular dynamic simulations. To circumvent this, we used a structure-based model (SBM). The SBMs, also known as Gō-models, are based on the energy landscape theory that relies on the principle of minimal frustration (3, 33–41). There are several computational approaches based on this theory that allow exhaustive sampling of the funneled energy landscape. The simplest model, the so-called Cα-SBM model, represents the protein sequence as a chain of beads, in which each bead represents one amino acid residue (31, 32, 42). The interaction potential between the beads is defined in such a way that only short-range interactions in the native state are favorable, whereas all other interactions are governed by excluded volume and chain connectivity. Here we used such a Cα-SBM model (42), but in addition, to model the changes in the charge–charge interactions between the WT and des variants, we included the Debye–Hückel (DH) electrostatic potential (see Eq. 5) to describe the interactions between charged residues (6, 7). These interactions, which can be attractive in the case of oppositely charged residues, or repulsive in the case of same-charged residues, are long-range. In essence, the electrostatic potential introduces additional long-range native and nonnative interactions on top of the funneled energy landscape. Can such a simple model (referred to here as Cα-SBM/DH) describe the experimental data for the four proteins studied here?
Fig. 1C compares temperature dependencies of the heat capacity functions calculated from the analysis of the simulations using the Cα-SBM/DH model for each pair of proteins. It is very clear that in all four cases the des proteins are more stable than the corresponding WT proteins. This is in striking agreement with the experimental data (Fig. 1A). Furthermore, the Cα-SBM/DH model appears to capture the essence of the folding–unfolding kinetics. Fig. 1D shows chevron plots comparing the calculated rate constants for the folding and unfolding kinetics for the same four protein pairs. The rate constants were calculated from a large number of independent simulations (>1,000) in which randomly selected structures generated at high–low temperatures were allowed to fold–unfold at low–high temperatures. For each simulation, the minimal passage time, as measured by the number of simulation steps required to reach the folded–unfolded state (as measured by the global reaction coordinate the relative fraction of native contacts, Q), was counted and converted into an apparent rate constant. Comparison of the calculated chevron plots shown in Fig. 1D with the experimental plots (Fig. 1B) again reveals striking similarities. Both in the experiments and simulations the unfolding arms of the chevron plots are very similar for the des and WT proteins for all four protein pairs. Also, for all four protein pairs, in both experiments and simulations, the folding rates for the des proteins are faster. Taken together, the data shown in Fig. 1 suggest that the Cα-SBM/DH model captures the essential features of both the thermodynamic and kinetic behavior of des and WT proteins for all four proteins. Such a good qualitative agreement with the experiments has been shown to hold for other systems as well (6, 7, 25). This in turn allows us to analyze the results of the simulations in more detail to obtain insights into possible molecular mechanisms that govern the difference in the folding of charge-optimized des variants.
Charge-Optimized Variants Have Higher Extent of Native-Like Interactions in the TSE.
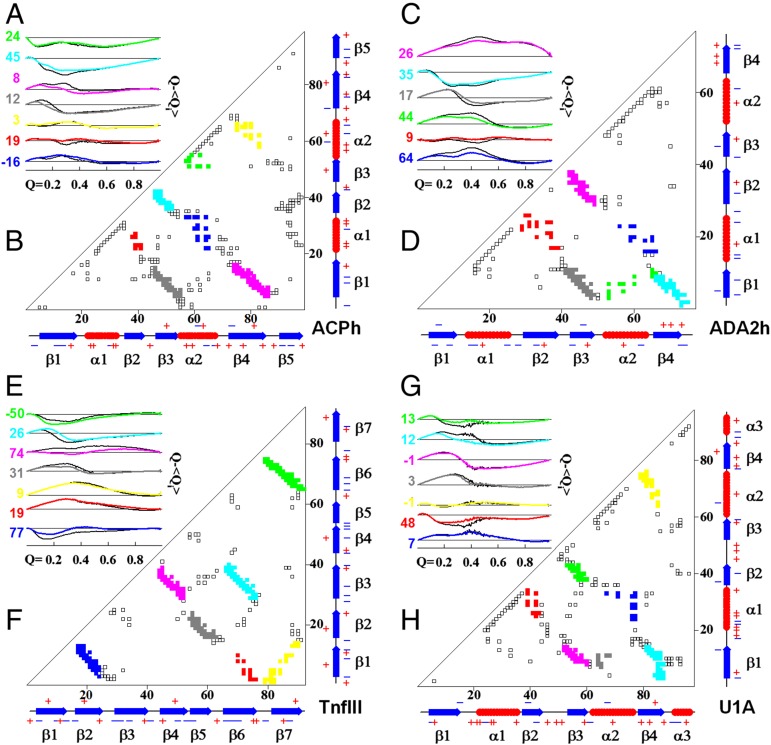
We analyzed our simulation data using the relative fraction of native contacts Q as the global reaction coordinate (31, 33, 43). Analysis of the potential of mean force as a function of Q, PMF(Q), suggests that in all four cases there are only two states, native and unfolded, which are separated by a single energy barrier corresponding to the TSE (Fig. 2 A, C, E, and G). The folding–unfolding kinetics also appeared to be monoexponential, again ruling out the presence of stable intermediate state(s). The PMF(Q) corresponding to TSE for the des variants is always lower than for the WT proteins, suggesting that the folding rates of the des variants are faster (see refs. 25, 44). This is also consistent with the results of direct experimental estimates of the folding rate constants (Fig. 1B). It is important to note that the difference in the absolute values of the apparent folding–unfolding rate constants obtained from direct kinetic simulations is not identical to the difference obtained from PMF(Q) vs. Q analysis. This is probably related to the fact that preexponential factors (proportional to internal friction of the chain) are different in the des and WT proteins as was previously pointed out by Wang et al. (45).
Fig. 2.
Characterization of native contacts in the TSE shows that des proteins have higher fraction of native contacts than the corresponding WT proteins. (A, C, E, and G) The PMF versus global reaction coordinate Q. These plots were used to identify the TSE. Solid black and red lines are for the WT and des, respectively, at their corresponding Tm values, whereas dashed red line is for the des protein at the Tm of the corresponding WT protein. See Materials and Methods for computational details. (B, D, F, and H) Difference in the fraction of native contacts formed in the transition state for the four studied proteins. Open symbols show all native contacts, whereas colored represents contacts in the TSE that differ between WT and des variants. Color scheme changes from blue (more contacts in the WT) to red (more contacts in the des). Protein identity is indicated in each plot.
From a structural point of view, the TSE for des variants contains a larger fraction of native contacts (Fig. 2 B, D, F, and H). This suggests that the optimization of surface charge–charge interactions in the des variants likely results in an enhanced probability to form native contacts. Additionally, some native-like contacts found in the WT proteins become less populated in the TSE of des variants. This suggests that optimization of charge–charge interactions result in certain modulations in the shape of the folding energy funnel.
Optimization of Charge–Charge Interactions Leads to a Less Frustrated Folding Landscape.
To get a better idea on how the folding energy landscape is modulated in des variants versus corresponding WT proteins, as a result of optimization of charge–charge interactions, we analyzed the formation of subsets of native contacts as a function of the global reaction coordinate, Q. For this we first calculated a local order parameter <Qi> that represents a fraction of native interactions formed for a particular pair of structural segments (Fig. 3 B, D, F, and H; see also Materials and Methods and Fig. S5 for details). Fig. 3 A, C, E, and G plots the difference of Q − <Qi> versus Q for the four studied proteins. If Q − <Qi> for an individual subset is close to zero, this means that this particular set of native contacts is following a perfectly funneled energy landscape. Deviations from the zero value suggest some frustration in the folding funnel. Furthermore, changes in the sign of Q − <Qi> suggest that there is a certain degree of “backtracking” in which native-like structural elements need to unfold in order for the overall folding reaction to proceed (Fig. 3 A, C, E, and G). Close inspection of the Q − <Qi> versus Q plots reveals two important features. First, there are indeed instances when Q − <Qi> values change sign, suggesting that a certain degree of topological frustration or even backtracking can occur (see also Fig. S5). Backtracking was first observed for IL-1β protein and has been shown to be a result of topological frustration (46). Further studies have shown that such topological frustration is a consequence of the chain connectivity, and distribution of native contacts along the sequence that dictates which structural element must be formed first (47, 48). Backtracking in the four proteins studied here is not as significant as that in IL-1β and yet it is also primarily related to the topological frustration. This conclusion follows from the analysis of simulations performed using only interactions corresponding to a pure funnel, i.e., Cα-SBM model without DH term for charge–charge interactions, where all four proteins show similar dependence of <Qi> on Q (Fig. S5). Second, on average the Q − <Qi> values for des variants are much closer to zero than those for WT proteins (Fig. 3 A, C, E, and G), indicating a funnel-like landscape in which all contacts form with equal probability along the reaction coordinate. To put a quantitative value on this behavior we introduce the quantity Θi, defined as
| [1] |
Positive Θi means the des variant has a less frustrated folding landscape for a given pair of structural segments, whereas negative Θi corresponds to a less frustrated folding landscape for the WT protein for that same structural segment. It appears that in the case of ADA2h and U1A, all Θi values are positive (Fig. 3 A, C, E, and G). A similar distribution of Θi, although to a lesser degree, is observed for ACPh and TnfIII, where 10 out of 14 Θi values are also positive. Importantly, the major differences in Q − <Qi> are observed at Q values below ∼0.6, i.e., between unfolded and TS ensembles. This suggests that optimization of the charge–charge interactions leads to an overall less frustrated energy landscape between U and TS, which on the macroscopic level manifests itself in the form of faster folding rates. The differences in Q − <Qi> between N and TS are negligible, which will manifest itself in the unchanged unfolding rates for WT and des proteins. Next we explore the underlying principles that charge–charge interactions have on the energy landscape between U and TS.
Fig. 3.
des proteins have less frustrated energy landscape than the corresponding WT proteins. (A, C, E, and G) Changes in the local order parameter <Qi> relative to the global reaction coordinate Q, Q − <Qi>, as a function of Q for the four studied proteins. Colors of the lines correspond to the colors on the contact plot. Colored lines are for the des proteins, black lines are for the corresponding WT. Numbers represent parameter Θi (Eq. 1). Positive values indicate that particular local order parameter for des proteins tracks closer to the global reaction coordinate Q. The absolute values of Θi qualitatively describe the differences between des and WT and cannot be directly compared. (B, D, F, and H) Contact maps with color coding matching the colors in A, C, E, and G. See Materials and Methods for computational details.
Unfolded State and TSE of des Variants Are More Compact.
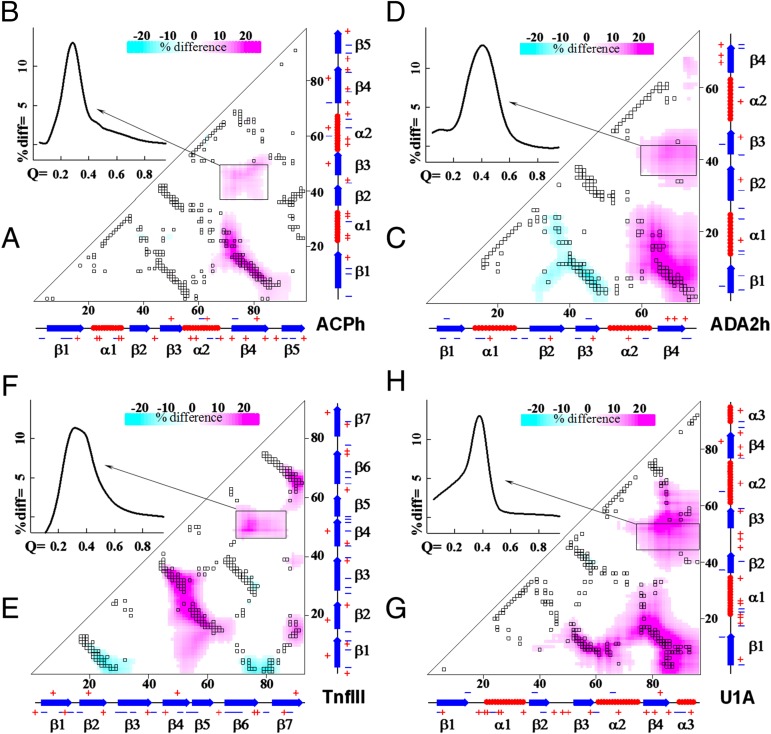
Charge–charge interactions, as modeled by the DH potential, are present throughout the folding–unfolding trajectories. We thus asked a question: what is the effect of these long-range interactions of the folding energy landscape? A useful reaction coordinate to analyze in this case is a matrix, Δi,j (6), of relative changes in all pairwise distances Rij:
| [2] |
Fig. 4 A, C, E, and G shows the heat map representation of Δij for the four studied proteins in the TSE (Q ∼ 0.35–0.45). Cyan color corresponds to the pairs that are closer in the des variant, whereas the magenta-colored area corresponds to the pairs that are closer in the WT proteins. As expected, there is significant overlap of Δij with areas that map onto native contacts in TSE (compare with Fig. 2). Interestingly, there are significant changes in the Δij that show up between residues that are not involved in the native contacts. Does this exist only in the TSE or are they also present throughout the main reaction coordinate, Q, including the unfolded state? To assess this we analyzed parameter corresponding to the regions that show no overlap with native contacts (shown as black rectangles in Fig. 4 A, C, E, and G). Fig. 4 B, D, F, and H shows the dependence of changes in nonnative distances as a function of Q. The dependence is clearly bell-shaped and remarkably the average <Δrel> corresponding to nonnative pairs reaches a maximum at Q values corresponding to the TSE and not to the unfolded or folded states.
Fig. 4.
Comparison of all pairwise distances in the TSE identifies significant changes for residues that are not involved in the native contacts. (A, C, E, and G) Difference in all pairwise distances formed in the TSE for the four studied proteins. Gray symbols show all native contacts, whereas colored shows values Δij that represent the difference in distances in the TSE between WT and des variants (Eq. 2). Color scheme changes from cyan (shorter distances in the WT) to magenta (shorter distances in the des). Black rectangles show areas that have significant changes but lack native contacts. (B, D, F, and H) The <Δrel> for the regions outlined by rectangles in A, C, E, and G as a function of global reaction coordinate Q.
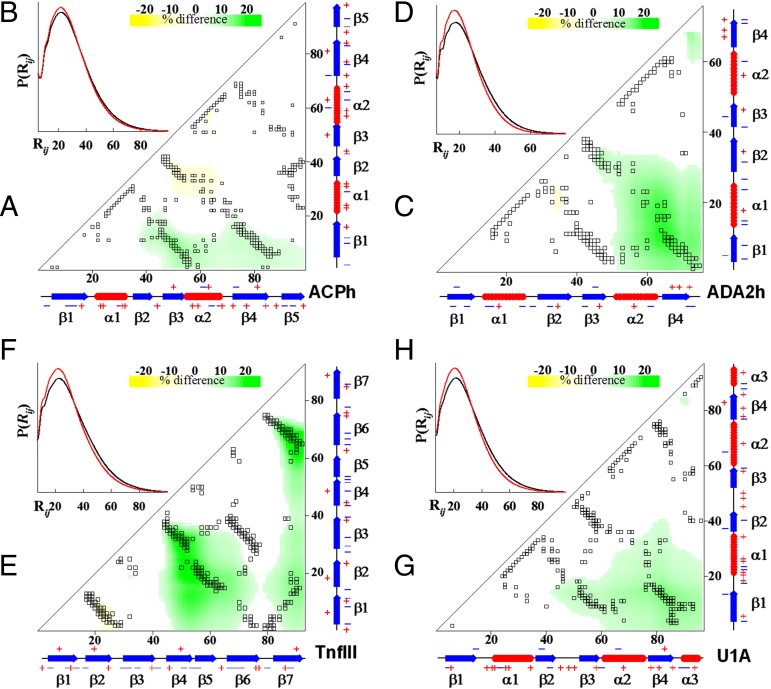
The unfolded state ensemble (Q ∼ 0–0.25) also shows changes in Δij (Fig. 5 A, C, E, and G). These changes partially overlap with the changes in Δij for the TSE. Importantly, the majority of Δij in the unfolded state ensemble exhibit negative values indicating the decrease in pairwise distances in the des protein relative to the corresponding WT. Moreover, for the residue pairs that are not involved in forming native contacts, the majority of the Rij that show a difference between WT and des proteins are on average ∼25–30 Å. This excludes involvement of any specific interactions and suggests that changes in charge–charge interactions modulate overall compactness of unfolded state ensemble and of the TSE. Comparison of the radii of gyration as a function of the global folding coordinate Q shows that indeed des proteins have lower Rg for Q values ranging from 0 to ∼0.4 (Fig. S6). This overall change of compactness can be even better visualized by comparing the distribution of distances of WT and des protein pairs at Q values corresponding to the unfolded (Q < ∼0.25) ensemble (Fig. 5 B, D, F, and H). Thus, one can conclude that the increase in the folding rate of the des variants is also facilitated by a small but statistically significant increase in net compactness of the des proteins in the unfolded state due to long-range nonspecific charge–charge interactions.
Fig. 5.
Comparison of all pairwise distances in the unfolded state shows a decrease in net compactness of the des proteins relative to the corresponding WT proteins. (A, C, E, and G) Difference in all pairwise distances formed in the unfolded state for the four studied proteins. Gray symbols show all native contacts, whereas colored shows values Δij that represent the difference in distances in the TSE between WT and des variants (Eq. 2). Color scheme changes from yellow (shorter distances in the WT) to green (shorter distances in the des). (B, D, F, and H) Probability distribution of pairwise distances P(Rij) as a function of Rij. Data for the WT proteins and des variants are shown as black and red lines, respectively.
Concluding Remarks
We used a combination of experimental and computational approaches to characterize the effects of optimization of charge–charge interactions on the stability and folding energy landscape of four different proteins. Experimentally we observed that designed proteins are more stable and this increase in stability is mainly due to the increase in the folding rate. We showed that the coarse-grain structure-based simulation model that incorporates charge–charge interactions via the DH potential is able to capture the important details observed experimentally, namely increase in thermodynamic stability, increase in the folding rates, and unchanged unfolding rates for the designed variant relative to their corresponding WT proteins. The simulations reveal three important molecular details that rationalize the increase in the folding rates. First, the TSE of the des proteins is more native-like than that of the WT proteins. To use an analogy with experimental data using ϕ-value analysis, this suggests that surface charge–charge interactions have a high ϕ-value. This conclusion resonates well with the results of ionic strength effects on the folding kinetics from other laboratories. Detailed studies of model proteins, fyn SH3 domain (8) and NTL9 (9), have shown that an increase in salt concentration leads to a large increase in the folding rate and only moderate changes in the unfolding rates. Second, optimization of charge–charge interactions leads to a less frustrated energy landscape from the unfolded state to the TSE. This in turn leads to an increase in the folding rate. The energy landscape between the native state and TSE remains largely unperturbed, which results in similar unfolding rates for the WT and des proteins. Third, optimization of charge–charge interactions leads to a more balanced net charge of the proteins that in turn leads to an increase in overall compactness of the unfolded state ensembles (see also ref. 49). Such effects in the unfolded state were previously observed by Azia and Levy (6) for single amino acid substitutions in NTL9. The increase in compactness in the unfolded state would lead to a decrease in the search time for relevant native-like interactions and thus increase probability of TSE formation. This in turn will lead to an increase in the folding rate and will not significantly affect the unfolding rate. Overall, this work shows the utility of the SBMs for understanding general principles of protein folding and, in particular, the role of charge–charge interactions in modulating energy landscape. Finally, the Cα-SBM/DH model may be used as a predictive tool for the kinetic behavior of electrostatics-based mutations in proteins.
Materials and Methods
Protein Expression, Purification, and Characterization.
All proteins used in this work were overexpressed in Escherichia coli BL21 (DE3) or BL21 (DE3)pLys strains at 37 °C, and purified to homogeneity under denaturing conditions (8 M urea) using column chromatography according to previously published protocols (17, 20, 21). ACPh was additionally run across an HPLC C-18 reverse phase column using a shallow linear gradient from 20% ACN:80%H2O:0.05%TFA to 60% ACN:40%H2O:0.05%TFA over a 30-min period to remove a slightly higher molecular weight contaminant as judged from SDS/PAGE gels and MALDI-TOF (Voyager DE-PRO, PerSeptive Biosystems) characterization.
Purities and identities of the recombinant proteins were confirmed by SDS gels and MALDI-TOF mass spectroscopy. In all cases, a single major peak was observed with a mass within 2–5 Da of that expected on the basis of the amino acid sequence of the parental and designed proteins. Protein concentrations were determined spectrophotometrically using the following molar extinction coefficients at 280 nm: 6,971 for ADA2h variants, 9,530 for TnfIII variants, 5,120 for U1A variants, and 13,980 for ACPh variants (17, 21).
Kinetic Stopped-Flow Experiments.
Buffers used for the various proteins in this study were 5 mM sodium acetate pH 5.5 (U1A), 50 mM sodium phosphate pH 7.0 (TnfIII and ADA2h), or 50 mM sodium cacodylate pH 5.5 (ACPh––known to bind orthophosphate). Folding and unfolding reactions were initiated by diluting protein buffered stock solutions (22 µM), to varying concentrations of urea in a 1:11 mixing ratio. The ACPh variants required overnight equilibration in urea before refolding experiments could be successfully initiated.
Data for chevron plots for ACPh, ADA2h, and TnfIII proteins were collected by standard stopped-flow methods on a JASCO J-815 spectropolarimeter operating in fluorescence mode equipped with an SFM 300 mixing module (BioLogic Science Instruments) containing an HDS mixer and a 30-µL FC-15 observation cuvette. The reagent syringes, mixing chamber, and observation cuvette were thermostated using a circulating water bath. Fluorescence emission intensity from an N-WG 320-nm cutoff filter (BioLogic Science Instruments) was collected after excitation at 295 nm through a 10-nm slit from a mercury lamp source. Voltages applied to the photomultiplier tube were set constant based on the fluorescence signal intensity at maximum amplitude. The U1A protein pair relaxation data were collected on a model 400 circular dichroism spectrometer (AVIV Biomedical, Inc.). Excitation was done at 290 nm using a Xenon lamp source and fluorescence emission was collected from an N-WG 305-nm sharp cutoff filter (Oriel Instruments). Due to issues with insufficient signal the final protein concentration was increased from 2 to 4 µM. To maximize efficiency of data collection, kinetic traces were collected at different temperatures for different protein pairs in accordance with their observed kinetic rates. Optimal temperatures were 20 °C (U1A), 25 °C (ADA2h), 30 °C (ACPh), or 37 °C (TnfIII), controlled by a circulating water bath. TnfIII had very slow unfolding kinetics; therefore, kinetic traces via manual mixing were collected on an SPEX FluoroMax4 spectrofluorometer (Horiba Scientific) in 1-cm cuvettes by following the change in fluorescence emission at 350 nm after excitation at 295 nm.
Rate constants, kobs for each data point on the chevron plot were obtained by fitting the raw average of five kinetic traces to exponentials with a correction for sloping baselines commonly associated with the photobleaching effect:
| [3] |
where I(t) is fluorescence intensity as a function of time, yo is the initial fluorescence intensity, A is the amplitude of the change between initial and final fluorescence intensity, kobs is the observed kinetic rate constant associated with the fluorescence intensity relaxation, and pb is the sloping baseline correction for the photobleaching effect used in the Bio-Kine32 software. Curve fitting was done using either the Bio-Kine32 curve-fitting software that came with the SFM 300 mixing module or SigmaPlot v6 graphing software package. Traces fit appropriately to single exponentials as judged by residuals of the fits to Eq. 3. Errors are taken as the SEs of the fits. The natural logarithms of the fluorescence relaxation times associated with these exponential phases were plotted as a function of urea concentration in the form of chevron plots. Instrumental dead-time measurement was assessed using N-acetyltryptophanamide and N-bromosuccinimide according to the procedure of Peterman (50). All buffers were extensively degassed and dead-time assessment was done immediately and within an hour of degassing. Under our current instrumental and experimental conditions a dead time of 6.3 ms was estimated, which is in very good agreement with BioLogic’s Bio-Kine32 software reported value of 6.0 ms. All data collected under these conditions were adjusted accordingly before fitting procedures were used, although in most cases the rates were sufficiently slow that correction was not needed. Extrapolated kf(H2O) and ku(H2O) values were obtained by fitting each chevron to Eq. 4 below (51) using either the Nonlinear Regression Analysis (NLREG) v6.3 software fitting program or the SigmaPlot v6 software fitting package.
| [4] |
where kf(H2O) and ku(H2O) are the folding and unfolding rates in the absence of denaturant, respectively, and mf and mu are the kinetic folding and unfolding m values (measured in kJ/mol per M), respectively (51). This equation appropriately reduces errors in kf(H2O) and ku(H2O) estimation due to heavy influence of the more rapid and less accurately measured kobs rates (51).
Molecular Dynamics Simulations Using SBM.
Cα structure-based potentials were generated using the SMOG web server (42) and default parameters. The following Protein Data Bank (PDB) entries were used: ACPh––common-type human acylphosphatase [PDB ID code: 2ACY (52)], ADA2h––the active domain of human procarboxypeptidase A2 [PDB ID code: 1AYE (53)], TnfIII––the fibronectin type III domain of human tenascin [PDB ID code: 1TEN (54)], and U1A––the N-terminal RNA-binding domain of human U1A protein [PDB ID code: 1URN (55)]. The SBM potentials were supplemented with interactions between charges via the DH potential, Velectro:
| [5] |
where λD is the Debye length, taken to be 0.941, ε is the dielectric constant, taken to be 80, rij is the distance between charges, B(λD) is the Debye coefficient of the solution, taken to be ∼1 for dilute solutions (6), and kelec is the Debye constant. Charges qi and qj were placed on Cα atoms corresponding to the Asp, Glu, Arg, and Lys residues.
Molecular dynamics simulations were performed under GROMACS 4.0.7 environment without modifications (56). For each protein, 50–100 independent molecular dynamics simulations were performed at 20 different temperatures. Each independent simulation ran for 108 steps with each time step having τ = 0.0005 ps. The weighted histogram analysis method (WHAM) was used to combine simulation data from different temperatures into single free-energy profiles (57). This also allowed calculations of the enthalpy and entropy for individual states (Fig. S7) using the approach described by Azia and Levy (6). In the present study, we use the fraction of native contacts Q as the global reaction coordinate. Q is defined as the fraction of natively interacting residues that are in contact, i.e., Q = 0 for the fully unfolded state and Q = 1 for the folded state. To account for structural dynamics for calculation of Q, the native distance was scaled by a factor of 1.2. The local contact order parameter <Qi> was defined based on the Cα-SBM contact maps generated by the SMOG web server (42). <Qi> represents the number of native contacts between nonlocal sequences, i.e., between two β-strands, two α-helices, or an α-helix and a β-strand.
Supplementary Material
Acknowledgments
We thank Angel Garcia for countless discussions and numerous recommendations on implementation of SBM. We also thank Osman Bilsel and Sagar Kathuria from Dr. C. R. Matthews’ lab for assistance with stopped-flow experiments of U1A protein variants, and Dr. Koby Levy for discussions of salt bridges in Cα-SBMs. Core Facilities at the Center for Biotechnology and Computational Center for Nanotechnology Innovations at Rensselaer Polytechnic Institute have been used for some of the described experiments. This work was supported by Grants MCB-0818419 and MCB-1330249 from the National Science Foundation.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1410424112/-/DCSupplemental.
References
- 1.Leopold PE, Montal M, Onuchic JN. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc Natl Acad Sci USA. 1992;89(18):8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84(21):7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 4.Wolynes PG, Eaton WA, Fersht AR. Chemical physics of protein folding. Proc Natl Acad Sci USA. 2012;109(44):17770–17771. doi: 10.1073/pnas.1215733109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dill KA, MacCallum JL. The protein-folding problem, 50 years on. Science. 2012;338(6110):1042–1046. doi: 10.1126/science.1219021. [DOI] [PubMed] [Google Scholar]
- 6.Azia A, Levy Y. Nonnative electrostatic interactions can modulate protein folding: molecular dynamics with a grain of salt. J Mol Biol. 2009;393(2):527–542. doi: 10.1016/j.jmb.2009.08.010. [DOI] [PubMed] [Google Scholar]
- 7.Weinkam P, Pletneva EV, Gray HB, Winkler JR, Wolynes PG. Electrostatic effects on funneled landscapes and structural diversity in denatured protein ensembles. Proc Natl Acad Sci USA. 2009;106(6):1796–1801. doi: 10.1073/pnas.0813120106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.de Los Rios MA, Plaxco KW. Apparent Debye-Huckel electrostatic effects in the folding of a simple, single domain protein. Biochemistry. 2005;44(4):1243–1250. doi: 10.1021/bi048444l. [DOI] [PubMed] [Google Scholar]
- 9.Song B, Cho JH, Raleigh DP. Ionic-strength-dependent effects in protein folding: Analysis of rate equilibrium free-energy relationships and their interpretation. Biochemistry. 2007;46(49):14206–14214. doi: 10.1021/bi701645g. [DOI] [PubMed] [Google Scholar]
- 10.Jimenez-Cruz CA, Makhatadze GI, Garcia AE. Protonation/deprotonation effects on the stability of the Trp-cage miniprotein. Phys Chem Chem Phys. 2011;13(38):17056–17063. doi: 10.1039/c1cp21193e. [DOI] [PubMed] [Google Scholar]
- 11.Loladze VV, Ibarra-Molero B, Sanchez-Ruiz JM, Makhatadze GI. Engineering a thermostable protein via optimization of charge-charge interactions on the protein surface. Biochemistry. 1999;38(50):16419–16423. doi: 10.1021/bi992271w. [DOI] [PubMed] [Google Scholar]
- 12.Sanchez-Ruiz JM, Makhatadze GI. To charge or not to charge? Trends Biotechnol. 2001;19(4):132–135. doi: 10.1016/s0167-7799(00)01548-1. [DOI] [PubMed] [Google Scholar]
- 13.Loladze VV, Makhatadze GI. Removal of surface charge-charge interactions from ubiquitin leaves the protein folded and very stable. Protein Sci. 2002;11(1):174–177. doi: 10.1110/ps.29902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Makhatadze GI, Loladze VV, Gribenko AV, Lopez MM. Mechanism of thermostabilization in a designed cold shock protein with optimized surface electrostatic interactions. J Mol Biol. 2004;336(4):929–942. doi: 10.1016/j.jmb.2003.12.058. [DOI] [PubMed] [Google Scholar]
- 15.Lee CF, Makhatadze GI, Wong KB. Effects of charge-to-alanine substitutions on the stability of ribosomal protein L30e from Thermococcus celer. Biochemistry. 2005;44(51):16817–16825. doi: 10.1021/bi0519654. [DOI] [PubMed] [Google Scholar]
- 16.Permyakov SE, et al. How to improve nature: Study of the electrostatic properties of the surface of alpha-lactalbumin. Protein Eng Des Sel. 2005;18(9):425–433. doi: 10.1093/protein/gzi051. [DOI] [PubMed] [Google Scholar]
- 17.Strickler SS, et al. Protein stability and surface electrostatics: A charged relationship. Biochemistry. 2006;45(9):2761–2766. doi: 10.1021/bi0600143. [DOI] [PubMed] [Google Scholar]
- 18.Gribenko AV, Makhatadze GI. Role of the charge-charge interactions in defining stability and halophilicity of the CspB proteins. J Mol Biol. 2007;366(3):842–856. doi: 10.1016/j.jmb.2006.11.061. [DOI] [PubMed] [Google Scholar]
- 19.Schweiker KL, Zarrine-Afsar A, Davidson AR, Makhatadze GI. Computational design of the Fyn SH3 domain with increased stability through optimization of surface charge charge interactions. Protein Sci. 2007;16(12):2694–2702. doi: 10.1110/ps.073091607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gvritishvili AG, Gribenko AV, Makhatadze GI. Cooperativity of complex salt bridges. Protein Sci. 2008;17(7):1285–1290. doi: 10.1110/ps.034975.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gribenko AV, et al. Rational stabilization of enzymes by computational redesign of surface charge-charge interactions. Proc Natl Acad Sci USA. 2009;106(8):2601–2606. doi: 10.1073/pnas.0808220106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schweiker KL, Makhatadze GI. A computational approach for the rational design of stable proteins and enzymes: Optimization of surface charge-charge interactions. Methods Enzymol. 2009;454:175–211. doi: 10.1016/S0076-6879(08)03807-X. [DOI] [PubMed] [Google Scholar]
- 23.Loladze VV, Makhatadze GI. Energetics of charge-charge interactions between residues adjacent in sequence. Proteins. 2011;79(12):3494–3499. doi: 10.1002/prot.23132. [DOI] [PubMed] [Google Scholar]
- 24.Chan CH, Wilbanks CC, Makhatadze GI, Wong KB. Electrostatic contribution of surface charge residues to the stability of a thermophilic protein: Benchmarking experimental and predicted pKa values. PLoS ONE. 2012;7(1):e30296. doi: 10.1371/journal.pone.0030296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zarrine-Afsar A, et al. Kinetic consequences of native state optimization of surface-exposed electrostatic interactions in the Fyn SH3 domain. Proteins. 2012;80(3):858–870. doi: 10.1002/prot.23243. [DOI] [PubMed] [Google Scholar]
- 26.Keshwani N, Banerjee S, Brodsky B, Makhatadze GI. The role of cross-chain ionic interactions for the stability of collagen model peptides. Biophys J. 2013;105(7):1681–1688. doi: 10.1016/j.bpj.2013.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kurnik M, Hedberg L, Danielsson J, Oliveberg M. Folding without charges. Proc Natl Acad Sci USA. 2012;109(15):5705–5710. doi: 10.1073/pnas.1118640109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Makhatadze GI, Loladze VV, Ermolenko DN, Chen X, Thomas ST. Contribution of surface salt bridges to protein stability: Guidelines for protein engineering. J Mol Biol. 2003;327(5):1135–1148. doi: 10.1016/s0022-2836(03)00233-x. [DOI] [PubMed] [Google Scholar]
- 29.Fersht AR, Sato S. Phi-value analysis and the nature of protein-folding transition states. Proc Natl Acad Sci USA. 2004;101(21):7976–7981. doi: 10.1073/pnas.0402684101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sosnick TR, Krantz BA, Dothager RS, Baxa M. Characterizing the protein folding transition state using psi analysis. Chem Rev. 2006;106(5):1862–1876. doi: 10.1021/cr040431q. [DOI] [PubMed] [Google Scholar]
- 31.Nymeyer H, García AE, Onuchic JN. Folding funnels and frustration in off-lattice minimalist protein landscapes. Proc Natl Acad Sci USA. 1998;95(11):5921–5928. doi: 10.1073/pnas.95.11.5921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Clementi C, García AE, Onuchic JN. Interplay among tertiary contacts, secondary structure formation and side-chain packing in the protein folding mechanism: All-atom representation study of protein L. J Mol Biol. 2003;326(3):933–954. doi: 10.1016/s0022-2836(02)01379-7. [DOI] [PubMed] [Google Scholar]
- 33.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins. 1995;21(3):167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 34.Dill KA, Chan HS. From Levinthal to pathways to funnels. Nat Struct Biol. 1997;4(1):10–19. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 35.Veitshans T, Klimov D, Thirumalai D. Protein folding kinetics: Timescales, pathways and energy landscapes in terms of sequence-dependent properties. Fold Des. 1997;2(1):1–22. doi: 10.1016/S1359-0278(97)00002-3. [DOI] [PubMed] [Google Scholar]
- 36.Shimada J, Kussell EL, Shakhnovich EI. The folding thermodynamics and kinetics of crambin using an all-atom Monte Carlo simulation. J Mol Biol. 2001;308(1):79–95. doi: 10.1006/jmbi.2001.4586. [DOI] [PubMed] [Google Scholar]
- 37.Shimada J, Shakhnovich EI. The ensemble folding kinetics of protein G from an all-atom Monte Carlo simulation. Proc Natl Acad Sci USA. 2002;99(17):11175–11180. doi: 10.1073/pnas.162268099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Clementi C, Plotkin SS. The effects of nonnative interactions on protein folding rates: Theory and simulation. Protein Sci. 2004;13(7):1750–1766. doi: 10.1110/ps.03580104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Shea JE, Onuchic JN, Brooks CL., 3rd Exploring the origins of topological frustration: Design of a minimally frustrated model of fragment B of protein A. Proc Natl Acad Sci USA. 1999;96(22):12512–12517. doi: 10.1073/pnas.96.22.12512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Boczko EM, Brooks CL., 3rd First-principles calculation of the folding free energy of a three-helix bundle protein. Science. 1995;269(5222):393–396. doi: 10.1126/science.7618103. [DOI] [PubMed] [Google Scholar]
- 41.Tripathi S, Makhatadze GI, Garcia AE. Backtracking due to residual structure in the unfolded state changes the folding of the third fibronectin type III domain from tenascin-C. J Phys Chem B. 2013;117(3):800–810. doi: 10.1021/jp310046k. [DOI] [PubMed] [Google Scholar]
- 42.Noel JK, Whitford PC, Sanbonmatsu KY, Onuchic JN. SMOG@ctbp: Simplified deployment of structure-based models in GROMACS. Nucleic Acids Res. 2010;38(suppl 2):W657–W661. doi: 10.1093/nar/gkq498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Guo ZY, Thirumalai D. Kinetics of protein-folding - nucleation mechanism, time scales, and pathways. Biopolymers. 1995;36(1):83–102. [Google Scholar]
- 44.Chan HS, Zhang Z, Wallin S, Liu Z. Cooperativity, local-nonlocal coupling, and nonnative interactions: Principles of protein folding from coarse-grained models. Annu Rev Phys Chem. 2011;62:301–326. doi: 10.1146/annurev-physchem-032210-103405. [DOI] [PubMed] [Google Scholar]
- 45.Wang J, Onuchic J, Wolynes P. Statistics of kinetic pathways on biased rough energy landscapes with applications to protein folding. Phys Rev Lett. 1996;76(25):4861–4864. doi: 10.1103/PhysRevLett.76.4861. [DOI] [PubMed] [Google Scholar]
- 46.Gosavi S, Chavez LL, Jennings PA, Onuchic JN. Topological frustration and the folding of interleukin-1 beta. J Mol Biol. 2006;357(3):986–996. doi: 10.1016/j.jmb.2005.11.074. [DOI] [PubMed] [Google Scholar]
- 47.Capraro DT, Roy M, Onuchic JN, Jennings PA. Backtracking on the folding landscape of the beta-trefoil protein interleukin-1beta? Proc Natl Acad Sci USA. 2008;105(39):14844–14848. doi: 10.1073/pnas.0807812105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gosavi S, Whitford PC, Jennings PA, Onuchic JN. Extracting function from a beta-trefoil folding motif. Proc Natl Acad Sci USA. 2008;105(30):10384–10389. doi: 10.1073/pnas.0801343105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Dominy BN, Minoux H, Brooks CL., 3rd An electrostatic basis for the stability of thermophilic proteins. Proteins. 2004;57(1):128–141. doi: 10.1002/prot.20190. [DOI] [PubMed] [Google Scholar]
- 50.Peterman BF. Measurement of the dead time of a fluorescence stopped-flow instrument. Anal Biochem. 1979;93(2):442–444. doi: 10.1016/s0003-2697(79)80176-1. [DOI] [PubMed] [Google Scholar]
- 51.Maxwell KL, et al. Protein folding: Defining a “standard” set of experimental conditions and a preliminary kinetic data set of two-state proteins. Protein Sci. 2005;14(3):602–616. doi: 10.1110/ps.041205405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Thunnissen MMGM, Taddei N, Liguri G, Ramponi G, Nordlund P. Crystal structure of common type acylphosphatase from bovine testis. Structure. 1997;5(1):69–79. doi: 10.1016/s0969-2126(97)00167-6. [DOI] [PubMed] [Google Scholar]
- 53.García-Sáez I, Reverter D, Vendrell J, Avilés FX, Coll M. The three-dimensional structure of human procarboxypeptidase A2. Deciphering the basis of the inhibition, activation and intrinsic activity of the zymogen. EMBO J. 1997;16(23):6906–6913. doi: 10.1093/emboj/16.23.6906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Leahy DJ, Hendrickson WA, Aukhil I, Erickson HP. Structure of a fibronectin type III domain from tenascin phased by MAD analysis of the selenomethionyl protein. Science. 1992;258(5084):987–991. doi: 10.1126/science.1279805. [DOI] [PubMed] [Google Scholar]
- 55.Oubridge C, Ito N, Evans PR, Teo CH, Nagai K. Crystal structure at 1.92 A resolution of the RNA-binding domain of the U1A spliceosomal protein complexed with an RNA hairpin. Nature. 1994;372(6505):432–438. doi: 10.1038/372432a0. [DOI] [PubMed] [Google Scholar]
- 56.Hess B, Kutzner C, van der Spoel D, Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J Chem Theory Comput. 2008;4(3):435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 57.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculations on biomolecules. 1. The method. J Comput Chem. 1992;13(8):1011–1021. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.