Significance
Biologists have long understood that differences between species in traits such as bill shape or rooting depth can maintain diversity in communities by promoting specialization and reducing competition. Here we test the assumption that phenotypic differences drive the stabilizing niche differences that promote coexistence. Using advances in ecological theory and detailed experiments we quantify average fitness and stabilizing niche differences between 102 plant species pairs and relate these differences to 11 functional traits. Individual traits were correlated with fitness differences that drive competitive exclusion but not stabilizing niche differences that promote coexistence. Stabilizing niche differences could only be described by combinations of traits, representing differentiation in multiple dimensions. This challenges the simplistic use of trait patterns to infer community assembly.
Keywords: coexistence, functional traits, community assembly, competition
Abstract
Understanding the processes maintaining species diversity is a central problem in ecology, with implications for the conservation and management of ecosystems. Although biologists often assume that trait differences between competitors promote diversity, empirical evidence connecting functional traits to the niche differences that stabilize species coexistence is rare. Obtaining such evidence is critical because traits also underlie the average fitness differences driving competitive exclusion, and this complicates efforts to infer community dynamics from phenotypic patterns. We coupled field-parameterized mathematical models of competition between 102 pairs of annual plants with detailed sampling of leaf, seed, root, and whole-plant functional traits to relate phenotypic differences to stabilizing niche and average fitness differences. Single functional traits were often well correlated with average fitness differences between species, indicating that competitive dominance was associated with late phenology, deep rooting, and several other traits. In contrast, single functional traits were poorly correlated with the stabilizing niche differences that promote coexistence. Niche differences could only be described by combinations of traits, corresponding to differentiation between species in multiple ecological dimensions. In addition, several traits were associated with both fitness differences and stabilizing niche differences. These complex relationships between phenotypic differences and the dynamics of competing species argue against the simple use of single functional traits to infer community assembly processes but lay the groundwork for a theoretically justified trait-based community ecology.
Ecologists have long understood that phenotypic differences between species play an important role in maintaining species diversity within communities (1, 2). Differences in bill shape, body size, or rooting depth are often hypothesized to reduce interspecific relative to intraspecific competition and thereby contribute to the stabilizing niche differences that promote coexistence (3–5). Although the niche describes all aspects of species interactions with their environment (6), in ecological theory developed by Chesson (2) “stabilizing niche differences” between species are those differences that cause intraspecific interactions to be more limiting than interspecific interactions. This gives species a demographic advantage when at low relative abundance (2), which stabilizes coexistence. The expected relationship between trait differences and stabilizing niche differences is the basis for a large body of observational studies that use traits to predict patterns of species co-occurrence and compositional change (3, 7–13). Rigorously testing this relationship is critical because it forms the key pathway by which phenotypic traits influence community assembly, the outcome of biological invasions, species diversity effects on ecosystem function, and the impacts of climate change on community dynamics (5, 8, 12, 13).
Although the literature connecting phenotypic differences to competitive outcomes historically emphasizes stabilizing niche differences, not all phenotypic differences favor coexistence, and this complicates efforts to predict community assembly from trait patterns. For example, species may differ in traits that influence their ability to draw down shared limiting resources or produce offspring, and the resulting “average fitness differences” [sensu Chesson (2)] favor competitive exclusion (14–16). Note that Chesson’s use of the term “fitness” differs from its meaning in evolutionary biology. Average fitness differences in this ecological context are those species differences that favor one competitor over the other regardless of their relative abundance (2) and, like stabilizing niche differences, may be precisely defined for a given mathematical model of species interactions (as we do below). In principle, many possible relationships between trait differences and coexistence are possible, with differing implications for competitive outcomes. For example, fitness and stabilizing niche differences could be correlated with distinct sets of traits (17). Moreover, it may be that niche and fitness differences are best described by multivariate suites of traits, supporting a hypothesis of high-dimensional coexistence between species in communities (18–21).
Although competitive outcomes are determined by the opposing effects of stabilizing niche differences favoring coexistence and fitness differences driving exclusion (2), the extent to which phenotypic differences are related to these drivers of coexistence is largely unknown. Prior work has examined the association between species traits and metrics that either aggregate stabilizing niche and average fitness differences (e.g., community membership, competitive dominance, and species abundance) (22–24) or form components of these quantities (e.g., interaction coefficients, relative yield, and competitive suppression) (25, 26). Only now, with recent developments in coexistence theory (15, 27–30), can we begin to directly evaluate the relationship between species traits and stabilizing niche differences and average fitness differences. Doing so is critical because these quantities provide the connection between functional trait differences and competitive outcomes, and thereby offer insight into the functional and phenotypic dimensions that shape species coexistence.
We conducted a field experiment with 18 annual plant species (Table 1) in a California grassland to field-parameterize mathematical models of competition, with which we quantified the stabilizing niche differences, average fitness differences, and predicted competitive outcomes for 102 species pairs (31). As detailed in Materials and Methods and in prior work (31), with our annual plant competition model the stabilizing niche difference proves to be the following (28, 31, 32):
| [1] |
where describes the per capita effect of species j on species i. The stabilizing niche difference therefore reflects the degree to which intraspecific competition (in the denominator) exceeds interspecific competition (in the numerator).
Table 1.
Species used in the experiment
| Species | Code | Family |
| Agoseris heterophylla | AGHE | Asteraceae |
| Agoseris retrorsa | AGRE | Asteraceae |
| Amsinckia menziesii | AMME | Boraginaceae |
| Anagallis arvensis | ANAR | Myrsinaceae |
| Centaurea melitensis | CEME | Asteraceae |
| Clarkia purpurea | CLPU | Onagraceae |
| Erodium botrys | ERBO | Geraniaceae |
| Erodium cicutarium | ERCI | Geraniaceae |
| Euphorbia peplus | EUPE | Euphorbiaceae |
| Geranium carolinianum | GECA | Geraniaceae |
| Hemizonia congesta ssp. luzulifolia | HECO | Asteraceae |
| Lasthenia californica | LACA | Asteraceae |
| Lotus purshianus | LOPU | Fabaceae |
| Lotus wrangelianus | LOWR | Fabaceae |
| Medicago polymorpha | MEPO | Fabaceae |
| Navarretia atractyloides | NAAT | Polemoniaceae |
| Plantago erecta | PLER | Plantaginaceae |
| Salvia columbariae | SACA | Lamiaceae |
The average fitness difference between the competitors is and is expressed (31) as
| [2] |
where describes the seeds produced per seed lost from the seed bank for plant species i (explained in Materials and Methods). The greater the ratio, , the greater the fitness advantage of species j over i, and the faster species j excludes i in the absence of stabilizing niche differences. We refer to the two components of average fitness differences as the “demographic ratio” and “competitive response ratio” . This latter term describes the degree to which species i is more sensitive to intra- and interspecific competition than species j. See Materials and Methods for more details on the model.
To parameterize these expressions, species’ vital rates and pairwise competitive interactions were quantified after sowing each of the 18 species across a density gradient of itself and each of its 17 competitors (Fig. S1) and quantifying how fecundity declined as a function of increasing neighbor density (32). In addition, we sampled 11 key functional traits (Table 2 and Table S1) for each species, corresponding to variation in leaves, roots, seeds, and whole-plant characteristics that are known to describe strategy variation across plant species globally (33–35). We then tested the extent to which these trait differences, representing multiple ecological dimensions, were correlated with stabilizing niche differences (1 − and average fitness differences between species pairs in our study. Finally, we tested how trait differences related to the predicted outcome of competition.
Table 2.
Functional traits sampled in this study
| Organ | Trait | Units |
| Leaf | Leaf area | cm2 |
| SLA | g/cm2 | |
| Leaf nitrogen concentration | mg/g | |
| Leaf dry matter content (LDMC) | mg/g | |
| Seed | Seed mass | g |
| Root | Rooting depth | cm |
| SRL | m/g | |
| Whole plant | Maximum height | cm |
| Canopy shape index | Dimensionless | |
| Phenology (peak fruiting) | Day of year | |
| Carbon isotope composition | δ13C |
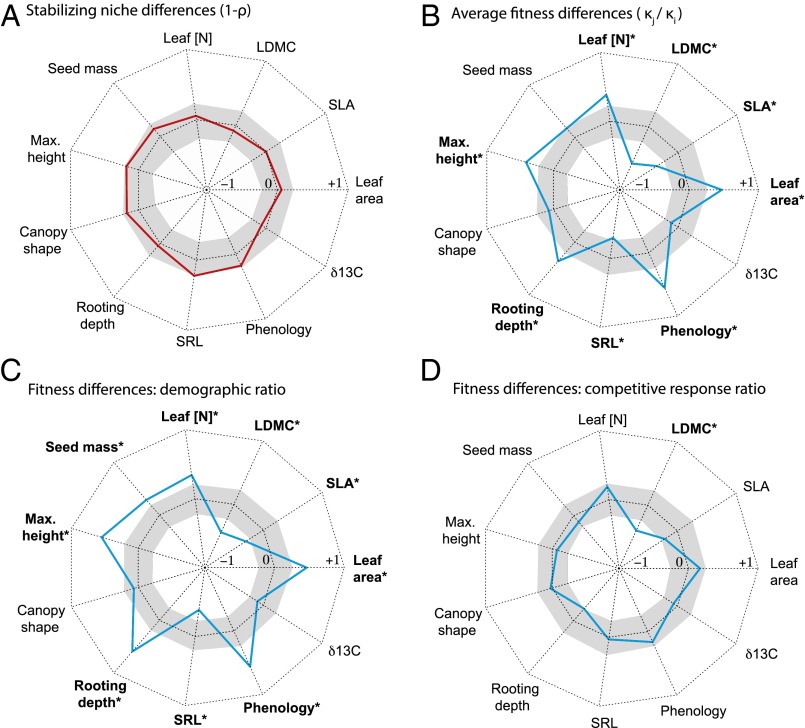
For most of the functional traits we sampled, species differences in individual traits were well correlated with the average fitness differences that determine competitive superiority (Fig. 1 and Fig. S2). Competitive superiority (that is, having higher average fitness than a competitor) was positively correlated with later phenology, larger potential size (larger maximum height and leaf area and deeper rooting depth), and a more resource-conservative foraging strategy (lower specific leaf area and specific root length).
Fig. 1.
Functional trait correlates of stabilizing niche (A) and average fitness (B) differences among 18 annual plants. Because average fitness and stabilizing niche differences are pairwise measures, correlations are calculated with Mantel tests. (C and D) Trait correlations with the two components of fitness differences, the demographic ratio and the competitive response ratio. Colored lines show correlations calculated from the Mantel test, ranging from −1 at the center of the plot to 1 at the margin. Central band of gray denotes the central 95% of null correlation values from the mantel permutations. See Table 2 for trait abbreviations. Results that are significant following Benjamini–Hochberg correction for multiple comparisons (Table S2) are marked in bold with an asterisk.
Counter to the common use of trait differences as proxies for stabilizing niche differences (4, 8, 13), no single functional trait difference was correlated with the substantial variation in stabilizing niche differences that we measured in the experiment (Fig. 1A and Table S2). Despite this finding, these niche differences were well described by a model containing multiple traits (Table 3) including specific root length, seed size, canopy shape, maximum height, and phenology. A model selection routine (36, 37) selected this five-trait model as the best descriptor of niche differences (BEST analysis, rho = 0.408, P = 0.03) out of all possible combinations of the traits sampled.
Table 3.
Results from BEST model selection procedure for testing for correlations with multiple traits
| Model rank | rho | N traits | Traits |
| A. Stabilizing niche differences | |||
| 1 | 0.408 (P = 0.031) | 5 | SRL, canopy shape, maximum height, phenology, seed size |
| 2 | 0.403 | 6 | SRL, canopy shape, maximum height, phenology, seed size, leaf [N] |
| 3 | 0.389 | 5 | SRL, canopy shape, maximum height, phenology, leaf [N] |
| B. Average fitness differences | |||
| 1 | 0.443 (P = 0.035) | 3 | Leaf area, canopy shape, phenology |
| 2 | 0.441 | 4 | Leaf area, canopy shape, phenology, SLA |
| 3 | 0.430 | 5 | Leaf area, canopy shape, phenology, SLA, seed size |
| C. Average fitness differences: demographic component | |||
| 1 | 0.224 (P > 0.4) | 4 | Leaf area, SLA, seed mass, phenology |
| 2 | 0.213 | 5 | Leaf area, SLA, seed mass, phenology, canopy shape |
| 3 | 0.206 | 6 | Leaf area, SLA, seed mass, phenology, canopy shape, SRL |
| D. Average fitness differences: competitive response component | |||
| 1 | 0.359 (P = 0.136) | 4 | SLA, canopy shape, rooting depth, phenology |
| 2 | 0.359 | 5 | SLA, canopy shape, rooting depth, phenology, leaf area |
| 3 | 0.359 | 3 | SLA, rooting depth, phenology |
The significance of the best model is assessed using a permutation test. Traits in bold are selected in the best-fit model.
A multitrait model was also fit for fitness differences , and the best-fit model included two traits (phenology and leaf area) that were strong correlates of fitness differences in univariate analyses (Fig. 1) as well as canopy shape (a measure of investment in vertical vs. lateral growth; Table 3, BEST analysis, rho = 0.443, P = 0.03). The inclusion of this last trait indicated that species with greater investment in lateral spread tended to have higher average fitness. Univariate correlations between each functional trait and the two components of the average fitness difference, the demographic ratio (Fig. 1C) and competitive response ratio (Fig. 1D), suggested that functional traits were a better predictor of the demographic ratio. However, the individual traits are not independent (Fig. S3 and Table S1), and when we conducted multivariate BEST analyses we failed to find a significant combination of traits that was well correlated with either of the two fitness difference components (Table 3, BEST analysis, P > 0.1). Given that the product of these two components, the average fitness difference , was well described by a multitrait model, our results indicate that weak relationships between plant traits and species’ demography and response to competition can nevertheless combine to render a significant relationship with average fitness differences.
Because stabilizing niche differences were only correlated with functional traits in models containing multiple traits (not in univariate analyses), these results reveal that neighborhood-scale stabilizing niche differences in the system result from species differences in multiple ecological dimensions. Two nonmutually exclusive effects may underlie these results. First, different sets of species may be niche-differentiated along distinct axes of functional trait variation. For instance, coexistence between some pairs of species may be stabilized by niche differences resulting from contrasting prostrate and erect growth forms (our canopy shape trait), whereas for others coexistence is stabilized by niche differences related to contrasting fine root foraging strategies (acquisitive vs. resource-conservative, as reflected in specific root length). Second, stabilizing niche differences between these species may require simultaneous differentiation in multiple plant traits (e.g., canopy shape and specific root length), only detectable with the multitrait model. More detailed studies are needed to distinguish between these two alternatives.
Critically, our results also show that species differences in a single phenotypic trait can have opposing effects on coexistence, contributing to both stabilizing niche and average fitness differences. This might be expected because the ecophysiological processes the traits relate to, such as resource uptake or photosynthetic rates, should be key components of both competitive dominance (via average fitness differences) and stabilizing niche differences in many cases. Indeed, both the stabilizing niche difference and average fitness difference expressions estimated here (Eqs. 1 and 2) share the interaction coefficients (albeit arranged in different ways). In our system, we found that whereas higher fitness was associated with later phenology (e.g., Fig. S2), phenology differences also contributed to niche differences (Table 3). Thus, the greater the phenology difference, the greater the competitive superiority of the later phenology competitor (the fitness difference), but also the greater the growth rate advantage for either species when it drops to low relative abundance (the stabilizing niche difference).
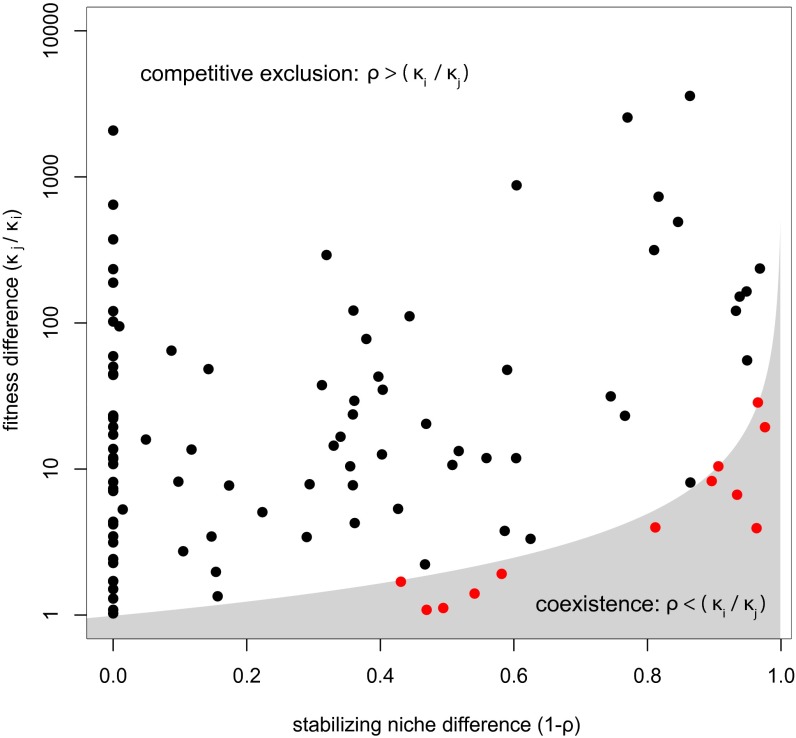
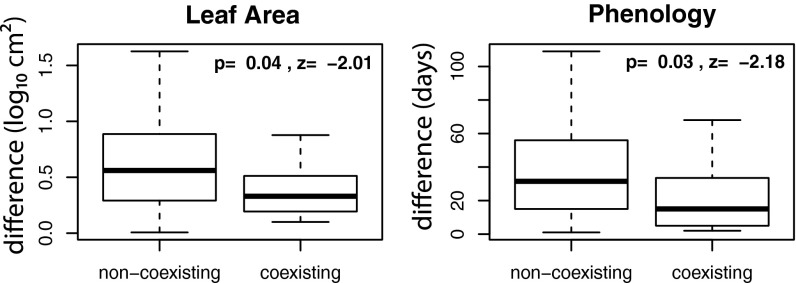
Whether phenology differences (or differences in any trait that is related to both fitness and stabilizing niche differences) ultimately favor or impede coexistence depends on the relative strength of the correlations between phenology differences and stabilizing niche differences vs. phenology differences and average fitness differences. Whether coexisting pairs have greater or lesser trait differences than noncoexisting pairs can be used to infer the relative strengths of these correlations. To accomplish this, we first compared the field-parameterized stabilizing niche differences (1 − to the average fitness differences for each species pair in our experiment, which predicts the outcome of competition at the local neighborhood scale. The condition for coexistence (, where species j is the fitness superior; see Materials and Methods) was met for 12 species pairs (Fig. 2). For all other pairs, average fitness differences overwhelmed the niche differences, predicting competitive exclusion. The 12 pairs of species predicted to coexist under our study conditions (red points in Fig. 2) had significantly smaller phenology differences than other species pairs (Wilcoxon signed-rank test P < 0.05, Fig. 3). This suggests that phenology differences disfavored coexistence, a result that is consistent with phenology being a stronger correlate of average fitness differences than stabilizing niche differences, but runs counter to the notion that all trait differences are necessarily stabilizing. A similar result was found for leaf area (Fig. 3 and Fig. S4).
Fig. 2.
Average fitness and stabilizing niche differences for each pair of species (denoted by a single point) in the experiment. The shaded gray area represents the region where the condition for coexistence is met (, where species j is the fitness superior). Twelve species pairs fall in this region; in all other cases fitness differences exceed niche differences and one species is predicted to eventually exclude the other. Note that our experiment focused on interactions at a neighborhood spatial scale over a single generation and therefore does not capture the spatial and temporal heterogeneity that allows these pairs to coexist at the landscape scale.
Fig. 3.
Trait differences between coexisting and noncoexisting species pairs (as identified in Fig. 2). Pairs predicted to coexist are significantly more similar in leaf area and phenology (Wilcoxon signed-rank test P < 0.05) than species pairs in which one is predicted to exclude the other; all other trait differences are not significant (see Fig. S4).
It may seem surprising that only a small fraction of species pairs that coexist at the landscape scale of the study site are predicted to locally coexist by the parameterized models (Fig. 2). There are two possible reasons for this discrepancy. First, the mathematical models may inadequately describe the interactions between our focal species. Second, it may be that metacommunity processes and spatial and temporal heterogeneity outside the bounds of the model (and the scale of inference for this study) explain coexistence at larger spatial and longer temporal scales. Although both factors must contribute, our past work with annual plant species in the same field plot supports the second interpretation. Godoy and Levine (31) conducted field-based replacement series experiments to empirically validate model predictions of competitive outcomes involving a number of the annual plant species that happen to be in our study. For nine of nine competitive pairs, the outcome of competition predicted by the model matched the results of the replacement series experiment. Moreover, as in the current study, most species that did not coexist at the scale of the experimental plots did coexist at the larger scale of the study site (31). This result, along with the pronounced soil heterogeneity present on the landscape, and the associated turnover in species composition (38), are consistent with an important role for larger-scale heterogeneity contributing to coexistence at greater scales than the plant neighborhood. Given this, our results should not be interpreted as connecting traits to competitive mechanisms arising in heterogeneous landscapes.
This study explores trait correlations with the drivers of the competitive interactions between species pairs. This approach can be scaled to include multispecies communities by considering the difference in traits between a focal species and the trait average of all its competitors. Nonetheless, our pairwise focus does have limitations. Pairs of species might coexist when embedded in diverse model communities that could not coexist in isolation, as they were studied here. Intransitive competitive dominance (“rock–paper–scissor” dynamics) is one driver of such outcomes. Therefore, an important challenge for future research is addressing how trait differences relate to diffuse, multispecies competition, including intransitive competitive networks. Previous theoretical work shows that intransitive competition most easily arises when competitive dominance in different species pairs is mediated by different limiting factors, such as light vs. nutrients (39). Our finding that different traits can be individually correlated with competitive dominance (Fig. 1) and that the correlations between these traits were often weak (Table S1) provides a basis for such competitive intransitivity in the system.
Our experiment was designed to measure the processes influencing species coexistence in an annual plant community at a neighborhood spatial scale and to relate these processes to species average phenotypic traits. Additional processes including soil heterogeneity and interannual variation in climate may also enhance coexistence in this system (2, 13). However, despite the focus of the experiment on pairwise interactions at the neighborhood spatial scale where stabilizing niche and average fitness differences can be reasonably quantified, our results reveal a surprisingly complex link between phenotypic diversity and competitive outcomes. Whereas multiple phenotypic differences may promote coexistence in some circumstances or for some species pairs, phenotypic differences in widely measured plant traits just as easily promote competitive exclusion, yielding a complex mapping between stabilizing niche differences, phenotypic differences, and the processes determining competitive outcomes in ecological communities. These complex relationships argue against the simple use of single traits to infer community assembly processes but lay the foundation for a theoretically robust trait-based community ecology.
Materials and Methods
Study Location and Species Selection.
Our experiment was conducted at the University of California Sedgwick Reserve in Santa Barbara County, USA (34° 40′ N, 120° 00′ W), 730 m above sea level. The climate is Mediterranean with cool, wet winters and hot, dry summers. Precipitation totaled 298 mm over the experimental year (October 2011–July 2012), 21% less than the 50-y average. We selected 18 common annual plant species from within the reserve for use in the experiment (Table 1). The species are drawn from 10 different families within the eudicots and capture a wide range of functional trait variation within the constraints of the Mediterranean climate annual plant lifestyle. Four additional species were selected at the start of the experiment but failed to establish at sufficient density in the experimental treatments and are not discussed further. Seeds for the experiment were collected from 200 to 1,000 mother plants in the spring and summer of 2011, mixed across mother plants, and subsampled to determine species average seed mass, a functional trait in our study (Table 2). We competed all possible heterospecific and conspecific pairs of the 18 species against each other within a 500-m2 area that had been previously cleared of all vegetation (the design is presented in the next section). Soils within the plot are finely textured serpentine soils, and the area was fenced to exclude gophers and deer.
Theoretical Background for Quantifying Niche and Fitness Differences and Field Parameterization of Population Models.
To quantify the stabilizing niche differences (Eq. 1), average fitness differences (Eq. 2), and predicted competitive outcomes between species pairs we specified a mathematical model that captures the dynamics of competing annual plant populations with a seed bank (27, 40). This approach has been used elsewhere (31, 32) and is summarized below. Population growth is described as
| [3] |
where is the per capita population growth rate and is the number of seeds of species i in the soil before germination in the winter of year t. The germination rate of species i, , weights an average of two different growth rates: , the annual survival of ungerminated seed in the soil, and , the viable seeds produced per germinated individual. can be expanded to describe the relationship between per germinant fecundity and the density of competing germinated individuals in the system:
| [4] |
The per germinant fecundity of species i in the absence of competition, , is reduced by the germinated density of conspecifics, , and heterospecifics, . These neighbor densities are modified by interaction coefficients that describe the per capita effect of species j on species i ). With this model, the number of seeds produced per seed lost from the seed bank due to death or germination (in the absence of neighbors), a critical term in the average fitness difference in Eq. 2, is (31)
| [5] |
Critically, empirical work in this system supports the functional form of the model in Eqs. 3 and 4 (27) and shows that it accurately predicts competitive outcomes between species in the study area (31).
Using this model of population dynamics between competing species, we then define stabilizing niche differences (Eq. 1) and average fitness differences (Eq. 2) between species pairs following earlier studies (28, 31, 32). For the model described by Eqs. 3 and 4, the niche overlap, , is , and 1 − becomes the stabilizing niche difference. The average fitness difference between the competitors is , as explained in ref. 31 and as presented in Eq. 2. Following earlier work (31, 32), the condition for coexistence (mutual invasibility) can be expressed as , where species j is the fitness superior.
These models were parameterized with estimates of species’ germination fractions, per germinant fecundities in the absence of neighbors, seed survival in the soil, and all pairwise interaction coefficients using experimentally assembled plant communities (Fig. S1). In October 2011 we established 154 rectangular plots separated by landscape fabric to control weeds. The design involved sowing each species as focal individuals into a density gradient of each potential competitor (including conspecifics). We randomly assigned each plot to be sown with one of the 18 species at a density of 2, 4, 8, or 16 g/m2 of viable seed, with two replicates per density per species. The 2-g/m2 plots were 1.5 × 1.7 m and all other densities were sown into 0.9- × 1.1-m plots. Each plot was divided into 42 subplots (a six row by seven column array) with a buffer of 2.5 cm at the edge of the plot. The equivalent of five viable seeds of one species were then sown into a subplot to establish a focal individual at the center, with two subplots sown per species per plot. After germination these were thinned to one focal individual per subplot. The experimental plots were used to assess germination rates as well as species' per germinant fecundity as a function of neighbor density. In addition, 10 plots were established with no background species to assess focal plant performance in the absence of neighbors. Additional description and discussion of the experimental design can be found elsewhere (32).
Sampling of Functional Traits.
We selected 11 plant functional traits to measure on each species in the experiment (Table 2). These traits are known to capture ecologically important variation in leaves, roots, seeds, and whole-plant function across plant species worldwide (35, 41) and are widely sampled within plant communities. At the time of planting, 20 1-m2 plots were established interspersed with the competition plots for the sole purpose of destructive trait sampling. Each plot was sown with a mixture of species from the experiment at a total density of 8 g/m2. At peak biomass, 40–50 mature individuals from across the trait plots and the experiment were selected for height measurements, used to estimate maximum height within the conditions found in our experiment as the 95th quantile of the distribution of measured heights. Using the trait plots, 8–15 individuals were selected for harvest of aboveground tissues, and from those 8 individuals were selected to have a sample of the root system harvested in a 10- × 10-cm soil core for measurement of fine roots. Low germination for two species (ANAR and ERBO; see Table 1 for species codes) limited harvesting to five individuals per species.
At harvest we first measured the height and canopy shape of each species. The lateral spread of the canopy from the main axis, as viewed from above, was measured at the farthest point from the main axis and at 90° clockwise from this point. The two measurements of lateral extent were averaged, and canopy shape was quantified as the ratio of lateral extent to height. This yields an index that ranges from close to 0 for a plant with primarily erect, vertical growth (such as CLPU) to >> 1 for low, prostrate growth forms (such as LOWR and MEPO). Next, the entire aboveground portion of each plant was placed into a moistened paper towel within a sealed plastic bag and stored in a cooler for transport to the laboratory, where it was kept in dark, refrigerated conditions. Three leaves were selected from each plant, blotted dry, weighed, and then imaged on a flatbed scanner at 600 dpi to determine fresh leaf area. All fresh leaves were processed within 5 h of harvest. Leaves were then dried to constant mass at 60 °C, weighed to determine dry mass, and subsequently bulked by species and ground to a fine powder for nitrogen and carbon isotope analysis by the Center for Stable Isotope Biogeochemistry at the University of California, Berkeley.
Fine root samples in soil cores were placed into sealed bags in a cooler at harvest and kept in refrigeration until they could be processed within 12–36 h. Root samples were gently washed over a 0.5-mm sieve to remove soils, and a sample of the washed root system of each focal plant was transferred to ethanol for later analysis, taking care to remove roots from other individuals. For analysis, a small subsample of fine roots (≤2 mm in diameter) was floated in water, arranged to minimize overlap and scanned at 600 dpi using WinRhizo software (Regent Instruments) to determine total fine root length of the subsample. The root samples were then dried to a constant mass at 60 °C and weighed.
In addition to the harvesting described above, we selected a second set of three to eight individuals per species for root system excavation to estimate rooting depth. Sample size was again limited by poor germination for some species. Soil was carefully removed alongside the main root system a few centimeters at a time until no further roots from the focal plant were apparent, and this depth recorded. More precise measurements from techniques using soil corers or root augers were not possible at the site because of the very shallow rooting depth of many of the species in the experiment and the abundance of rocks and clay aggregates in the soil. Because this method may miss fine roots extending below the point of excavation it likely offers a conservative underestimate of the rooting depth of each species.
Finally, we monitored the fruiting and flowering phenology of the species in the experiment biweekly. Because differences in fruiting and flowering phenology seemed to be well correlated across species in the study we used date of peak fruiting as a measure of gross phenological differences between species. We defined peak fruiting as the date when developing fruits outnumbered flowers on >50% of the reproductive individuals in a species in the experiment.
Following the sampling described above, the functional trait measures in Table 2 were calculated following standard protocols (35, 41). Traits were log-transformed as needed to improve normality before analysis. Trait measurements were averaged across individuals to arrive at species-level trait averages used in analyses.
Analyses.
We tested for correlations between functional trait differences and the stabilizing niche and average fitness differences quantified with parameters from the experiment (e.g., Fig. S2). Because niche and fitness differences are inherently pairwise measures, we focused on analyses that could account for the nonindependence present in pairwise comparison data (e.g., 18 species in all pairwise combinations result in 153 possible heterospecific interactions). At the end of the experiment we had sufficient data to fit models for 102 of 153 potential species pairs. For univariate comparisons we used Mantel tests, with the Benjamini and Hochberg correction for multiple comparisons. For multitrait comparisons we conducted a model selection exercise in a Mantel framework by using the BEST routine in the PRIMER software package (36, 37) to identify the combination of trait differences that best described fitness and niche differences. The BEST routine calculates Spearman’s rho for all combinations of 1–11 functional trait differences and assesses the significance of the best-performing model using a permutation test. Because the test statistic (Spearman’s rho) does not automatically improve with additional variables, no correction (e.g., Akaike information criterion) is needed to compare models with differing numbers of variables. Our analyses focused on testing linear relationships between trait differences and both fitness and niche differences, because an examination of the data did not indicate that nonlinear relationships would be well supported (e.g., Fig. S2). However, more complex relationships may exist in other datasets.
We then evaluated the predicted outcome of competitive interaction between pairs of species in the experiment by comparing the magnitude of the estimated fitness and stabilizing niche difference between them. Stable coexistence based on interactions at the scale of our experiment is predicted when , where species j is the fitness superior (Fig. 2). Using this criterion, we tested whether coexisting pairs differed from noncoexisting pairs with respect to functional traits using a series of Wilcoxon signed-rank tests (Fig. 3 and Fig. S4).
Functional Trait Variation.
Principal components analysis revealed that the primary axis of trait differentiation among our species reflects covariation in traits related to plant size and leaf chemistry (Fig. S3). Specifically, the first principal components axis (26% of variation) reflects maximum height, rooting depth, and leaf area (which varies in part due to allometric size constraints) in addition to leaf nitrogen and dry matter content. Specific leaf area (SLA) and specific root length (SRL) were tightly associated, suggesting a coordination between above- and belowground foraging strategies. In contrast to many global studies (33), SLA and leaf nitrogen concentration were not strongly correlated in our data, perhaps owing to the relatively narrow range of SLA values (123–256 cm2/g) among the annuals in our study. Additional pairwise correlations are summarized in Table S1. Species differences in principal component axis 1 and 2 scores were well correlated with fitness differences between species (Mantel P < 0.001) but not with niche differences (Mantel P > 0.3).
Supplementary Material
Acknowledgments
Lindsey Rice provided field assistance in all stages of the project. We thank Janneke HilleRisLambers and Marti Anderson for discussion and statistical advice and Peter Adler, Mark Vellend, and members of the J.M.L. and N.J.B.K. laboratories for comments. Peter Chesson helped us derive the stabilizing niche difference and average fitness difference in our annual plant model. The D’Antonio laboratory at University of California, Santa Barbara and the Dawson laboratory at University of California, Berkeley made the nutrient and isotope analyses possible.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1413650112/-/DCSupplemental.
References
- 1.MacArthur RH, Levins R. Limiting similarity, convergence and divergence of coexisting species. Am Nat. 1967;101(921):377–385. [Google Scholar]
- 2.Chesson P. Mechanisms of maintenance of species diversity. Annu Rev Ecol Syst. 2000;31:343–366. [Google Scholar]
- 3.Ricklefs RE, Travis J. A morphological approach to the study of avian community organization. Auk. 1980;97(2):321–338. [Google Scholar]
- 4.Silvertown J. Plant coexistence and the niche. Trends Ecol Evol. 2004;19(11):605–611. [Google Scholar]
- 5.HilleRisLambers J, Adler PB, Harpole WS, Levine JM, Mayfield MM. Rethinking community assembly through the lens of coexistence theory. Annu Rev Ecol Evol Syst. 2012;43:227–248. [Google Scholar]
- 6.Chase JM, Leibold MA. Ecological Niches: Linking Classical and Contemporary Approaches. Univ of Chicago Press; Chicago: 2003. p. ix. [Google Scholar]
- 7.Stubbs WJ, Wilson JB. Evidence for limiting similarity in a sand dune community. J Ecol. 2004;92(4):557–567. [Google Scholar]
- 8.McGill BJ, Enquist BJ, Weiher E, Westoby M. Rebuilding community ecology from functional traits. Trends Ecol Evol. 2006;21(4):178–185. doi: 10.1016/j.tree.2006.02.002. [DOI] [PubMed] [Google Scholar]
- 9.Kraft NJB, Valencia R, Ackerly DD. Functional traits and niche-based tree community assembly in an Amazonian forest. Science. 2008;322(5901):580–582. doi: 10.1126/science.1160662. [DOI] [PubMed] [Google Scholar]
- 10.Ingram T, Shurin JB. Trait-based assembly and phylogenetic structure in northeast Pacific rockfish assemblages. Ecology. 2009;90(9):2444–2453. doi: 10.1890/08-1841.1. [DOI] [PubMed] [Google Scholar]
- 11.Swenson NG, Enquist BJ. Opposing assembly mechanisms in a neotropical dry forest: Implications for phylogenetic and functional community ecology. Ecology. 2009;90(8):2161–2170. doi: 10.1890/08-1025.1. [DOI] [PubMed] [Google Scholar]
- 12.Angert AL, Huxman TE, Chesson P, Venable DL. Functional tradeoffs determine species coexistence via the storage effect. Proc Natl Acad Sci USA. 2009;106(28):11641–11645. doi: 10.1073/pnas.0904512106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Adler PB, Fajardo A, Kleinhesselink AR, Kraft NJB. Trait-based tests of coexistence mechanisms. Ecol Lett. 2013;16(10):1294–1306. doi: 10.1111/ele.12157. [DOI] [PubMed] [Google Scholar]
- 14.Tilman D. Resource Competition and Community Structure. Princeton Univ Press; Princeton: 1982. [PubMed] [Google Scholar]
- 15.Adler PB, Hillerislambers J, Levine JM. A niche for neutrality. Ecol Lett. 2007;10(2):95–104. doi: 10.1111/j.1461-0248.2006.00996.x. [DOI] [PubMed] [Google Scholar]
- 16.van Kleunen M, Weber E, Fischer M. A meta-analysis of trait differences between invasive and non-invasive plant species. Ecol Lett. 2010;13(2):235–245. doi: 10.1111/j.1461-0248.2009.01418.x. [DOI] [PubMed] [Google Scholar]
- 17.Mayfield MM, Levine JM. Opposing effects of competitive exclusion on the phylogenetic structure of communities. Ecol Lett. 2010;13(9):1085–1093. doi: 10.1111/j.1461-0248.2010.01509.x. [DOI] [PubMed] [Google Scholar]
- 18.Grime JP. Evidence for the existence of three primary strategies in plants and its relevance to ecological and evolutionary theory. Am Nat. 1977;111:1169–1194. [Google Scholar]
- 19.Westoby M. A leaf-height-seed (LHS) plant ecology strategy scheme. Plant Soil. 1998;199(2):213–227. [Google Scholar]
- 20.Cavender-Bares J, Kitajima K, Bazzaz FA. Multiple trait associations in relation to habitat differentiation among 17 Floridian oak species. Ecol Monogr. 2004;74(4):635–662. [Google Scholar]
- 21.Clark JS, et al. Resolving the biodiversity paradox. Ecol Lett. 2007;10(8):647–659, discussion 659–662. doi: 10.1111/j.1461-0248.2007.01041.x. [DOI] [PubMed] [Google Scholar]
- 22.Violle C, Nemergut DR, Pu Z, Jiang L. Phylogenetic limiting similarity and competitive exclusion. Ecol Lett. 2011;14(8):782–787. doi: 10.1111/j.1461-0248.2011.01644.x. [DOI] [PubMed] [Google Scholar]
- 23.Sterck F, Markesteijn L, Schieving F, Poorter L. Functional traits determine trade-offs and niches in a tropical forest community. Proc Natl Acad Sci USA. 2011;108(51):20627–20632. doi: 10.1073/pnas.1106950108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Maherali H, Klironomos JN. Influence of phylogeny on fungal community assembly and ecosystem functioning. Science. 2007;316(5832):1746–1748. doi: 10.1126/science.1143082. [DOI] [PubMed] [Google Scholar]
- 25.Fritschie KJ, Cardinale BJ, Alexandrou MA, Oakley TH. Evolutionary history and the strength of species interactions: Testing the phylogenetic limiting similarity hypothesis. Ecology. 2014;95(5):1407–1417. doi: 10.1890/13-0986.1. [DOI] [PubMed] [Google Scholar]
- 26.Poorter L, et al. Are functional traits good predictors of demographic rates? Evidence from five neotropical forests. Ecology. 2008;89(7):1908–1920. doi: 10.1890/07-0207.1. [DOI] [PubMed] [Google Scholar]
- 27.Levine JM, HilleRisLambers J. The importance of niches for the maintenance of species diversity. Nature. 2009;461(7261):254–257. doi: 10.1038/nature08251. [DOI] [PubMed] [Google Scholar]
- 28.Chesson P. Species Competition and Predation. In: Meyers R, editor. Encyclopedia of Sustainability Science and Technology. Springer; Berlin: 2012. [Google Scholar]
- 29.Carroll IT, Cardinale BJ, Nisbet RM. Niche and fitness differences relate the maintenance of diversity to ecosystem function. Ecology. 2011;92(5):1157–1165. doi: 10.1890/10-0302.1. [DOI] [PubMed] [Google Scholar]
- 30.Narwani A, Alexandrou MA, Oakley TH, Carroll IT, Cardinale BJ. Experimental evidence that evolutionary relatedness does not affect the ecological mechanisms of coexistence in freshwater green algae. Ecol Lett. 2013;16(11):1373–1381. doi: 10.1111/ele.12182. [DOI] [PubMed] [Google Scholar]
- 31.Godoy O, Levine JM. Phenology effects on invasion success: Insights from coupling field experiments to coexistence theory. Ecology. 2014;95(3):726–736. doi: 10.1890/13-1157.1. [DOI] [PubMed] [Google Scholar]
- 32.Godoy O, Kraft NJB, Levine JM. Phylogenetic relatedness and the determinants of competitive outcomes. Ecol Lett. 2014;17(7):836–844. doi: 10.1111/ele.12289. [DOI] [PubMed] [Google Scholar]
- 33.Westoby M, Falster DS, Moles AT, Vesk PA, Wright IJ. Plant ecological strategies: Some leading dimensions of variation between species. Annu Rev Ecol Syst. 2002;33:125–159. [Google Scholar]
- 34.Westoby M, Wright IJ. Land-plant ecology on the basis of functional traits. Trends Ecol Evol. 2006;21(5):261–268. doi: 10.1016/j.tree.2006.02.004. [DOI] [PubMed] [Google Scholar]
- 35.Pérez-Harguindeguy N, et al. New handbook for standardised measurement of plant functional traits worldwide. Aust J Bot. 2013;61(3):167–234. [Google Scholar]
- 36.Clarke KR, Ainsworth M. A method linking multivariate community structure to environmental variables. Mar Ecol Prog Ser. 1993;92:205–219. [Google Scholar]
- 37.Clarke K, Gorley R. 2006. PRIMER ver. 6.1 (PRIMER-E, Plymouth, UK)
- 38.Gram W, et al. Distribution of plants in a California serpentine grassland: Are rocky hummocks spatial refuges for native species? Plant Ecol. 2004;172:159–171. [Google Scholar]
- 39.Allesina S, Levine JM. A competitive network theory of species diversity. Proc Natl Acad Sci USA. 2011;108(14):5638–5642. doi: 10.1073/pnas.1014428108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chesson PL. Geometry, heterogeneity and competition in variable environments. Philos T Roy Soc B. 1990;330(1257):165–173. [Google Scholar]
- 41.Cornelissen JHC, et al. A handbook of protocols for standardised and easy measurement of plant functional traits worldwide. Aust J Bot. 2003;51(4):335–380. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.