Characterization of plasmonic hole arrays as transparent electrical contacts for organic photovoltaics using high-brightness Fourier transform methods

Abstract

We present a methodology for probing light-matter interactions in prototype photovoltaic devices consisting of an organic semiconductor active layer with a semitransparent metal electrical contact exhibiting surface plasmon-based enhanced optical transmission. We achieve high-spectral irradiance in a spot size of less than 100 μm using a high-brightness laser-driven light source and appropriate coupling optics. Spatially resolved Fourier transform photocurrent spectroscopy in the visible and near-infrared spectral regions allows us to measure external quantum efficiency with high sensitivity in small-area devices (<1 mm²). This allows for rapid fabrication of variable-pitch sub-wavelength hole arrays in metal films for use as transparent electrical contacts, and evaluation of the evanescent and propagating mode coupling to resonances in the active layer.

1. Introduction

It has been proposed that solar devices based on thin film technologies and third-generation materials can greatly benefit from plasmonic and photonic structures that can assist with light trapping and absorption [1]. One promising strategy is to replace the traditional transparent conducting oxide layer with a semitransparent metallic contact that exhibits a surface plasmon at visible wavelengths [2]. Structured appropriately, for example, by perforating with an array of sub-wavelength holes, the metal film can provide the high transparency and conductivity needed in a transparent electrical contact while also actively assisting with photon management. A recent study demonstrated a high-performing organic photovoltaic cell with a metal contact patterned with an array of sub-wavelength holes, providing the contact with broad featureless transmission throughout the visible spectrum and robust coupling to the semiconductor as a function of incident light angle [3]. Despite this progress, a key challenge is to probe and understand the details of the light-matter interactions between the incident photon, the surface plasmon modes of the structured contact, and the absorption properties of the active area.

We have developed a set of small area, high-brightness spectroscopies that are appropriate for characterizing prototypes of light-harvesting devices utilizing plasmonic contact materials, for understanding the details of light-matter interactions in these systems. Our primary interest in developing a set of rapid, high-sensitivity characterization tools capable of probing the influence of the perforated metal nanostructure, including pore size and pitch, as well as film thickness on the optical transmission modes [4], and ultimately the effect on solar cell performance. The aim is both to enable rapid screening of test device structures and to design structures capable of providing specific physical insight into coupling between the device active area and the modes of the patterned metal film.

Our strategy utilizes Fourier transform (FT)-based measurements in the solar portion of the optical spectrum, for optimally combining spatial resolution, spectral resolution, speed, and dynamic range. FT-based measurements are highly advantageous for characterizing nanoscale photovoltaic materials in the visible and near infrared (NIR) portions of the electromagnetic spectrum, although they are more typically applied in the infrared [5]. As compared to scanned techniques, FT photocurrent measurements benefit from the multiplex (Fellgett) advantage because the detectors are not shot-noise-limited [6], unlike in optical measurements employing low-noise photodetectors (e.g. Raman scattering with a high sensitivity CCD or PMT). This is particularly important since, unlike dispersive optical measurements (e.g. transmission, PL, and Raman), photocurrent multi-channel detection with scanned sources is not typically possible. For measurements of photovoltaic phenomena, the throughput advantage (Jacquinot) is much less relevant due to the lower required resolution, when compared to vibrational or high-resolution absorption measurements. This is particularly true when using a high-brightness light source and a small sample size such that the throughput becomes comparable to a scanned source. However, FT-based measurements still typically have more bandwidth capabilities, as there is no need to switch gratings between the visible and the NIR. This leads to overall experimental advantages in speed and simplicity.

2. Experimental methods and setup

The key to the experiment is achieving solar (or higher) spectral irradiance levels in a spot size of <100 μm in order to achieve high signal/noise external quantum efficiency (EQE) measurements on prototype devices. We have recently demonstrated the power of these types of measurements on individual single-walled carbon nanotube field effect transistors [7], but the benefit is equally applicable to other structures with active areas of the order of (100 μm)², such as photonic structures that are difficult and/or time-consuming to fabricate over large areas. Achieving a high irradiance in a small area requires the use of high radiance sources. The alternative – increasing the power without increasing the size of the source or solid angle of radiation – becomes impractical at these size scales, because most of the photon flux would be wasted. In the mid- to far-IR, similar advantages are gained using synchrotron-based sources for microspectroscopy [8].

Here, we achieve these advantages in the solar spectral region with an inexpensive benchtop source – a true-CW high-brightness laser-driven light source (Energetiq EQ-99). This differs significantly from a laser, in that the output radiates incoherently into 4π rather than being highly directional and coherent. We have also examined laser supercontiuum sources for the same purpose (e.g. Fianium SC-450) [9], which are able to achieve even higher brightness levels due to the highly collimated output. However, for photocurrent and photovoltaic applications, we have found the laser-driven light source to be a much better choice for several reasons. Primarily, the pulsed nature of the laser supercontinuum was found to generate small but detectable electrical transients that added significant noise to low-EQE regions of the spectrum. Since a 200 μm core multi-mode fiber is utilized to simplify alignment to the translating microscope optics, this negates the advantage a smaller emitter has in focusing capabilities. Additionally, we have found it difficult to stay in a low-fluence (solar-like) regime with the pulsed laser; focusing ps pulses with the full bandwidth of the laser has resulted in either saturation (resulting in signal non-linearity) or damage to samples and optical detectors, even with significant attenuation of the beam. We did not encounter the same issue for similar power levels in a true CW source. Lastly, the laser-driven light source unit is significantly cheaper than the laser supercontinuum (~5 × difference). Similarly, other groups have found that despite the higher spectral power density of a supercontinuum source, the sensitivity of absorption-based measurements are higher with the LDLS due to superior long-term stability [10].

The laser-driven light source output is collimated by an off-axis parabolic mirror (1.5′′ diameter, 2′′ EFL, NA = 0.375) and coupled into a commercial FT spectrometer (Bruker v80) using the backward input. The light is modulated using a broadband CaF₂ UV–vis-NIR beam splitter and the slowest “rapid-scan” setting available on our instrument (2.5 kHz referenced to the HeNe line). The modulated light is sent to an output port of the spectrometer, where the remaining UV portion of the beam (<420 nm) is filtered out. The broadband light is focused into a 200 μm core multimode fiber used to couple the light into an upright optical microscope (Nikon FN-1) using a reflective collimating optic and a set of steering mirrors attached to an epi-illuminator. This microscope is designed for a stationary stage, such that electrical probes can be contacted with a sample via micromanipulators. As such, the microscope itself sits on a translating stage for sample visualization and beam alignment. The use of an optical fiber for coupling ensures that the beam stays aligned to the microscope even during translation. A 50–50 beam splitter is used to simultaneously image and excite the device under test.

For photoconductivity measurements, the photocurrent interferogram is sent through a trans-impedance amplifier (DL Instruments, 1210) and an electronic band-pass filter (Stanford Research, SR650) before being digitized by the spectrometer bench electronics. To correct for the lamp spectrum and the transmission function of the bench and microscope optics, a set of photodiodes with known responsivity curves are used to generate reference spectra. The resulting single-beam spectra from test devices are corrected by these reference spectra, which are collected at the same time as the unknown devices. The spot sizes at the output of the microscope are measured using a calibrated beam profiler (Ophir-Spiricon). For transmission spectra, the sample compartment of the spectrometer is used, resulting in a spot size of 0.75 mm at the focus. Samples are aligned to the beam using a XYZ translating mount and the transmitted light is detected with a pyrolelectric detector (La-DTGS).

We define arrays of sub-wavelength holes across areas of (300 μm)² by focused ion beam (FIB) milling completely through 50 nm thick Ag films sputter deposited on glass. Holes with average diameter of 200 nm are milled using a beam of Ga ions (0.26 nA), with dwell times ranging from 2 to 8 ms for hole separations (pitch) ranging from 240 to 560 nm, respectively. The total patterned area is 300 × 300 μm². After defining the perforated Ag electrode, the subsequent organic photovolatic device fabrication steps include: thermal evaporation of 9 nm thick of MoO₃ electron-blocking layer; spin coating (700 RPM for 60 s) the 170 nm thick semiconductor active layer, a 1:1 wt. blend of poly(3-hexlythiophene): phenyl-C₆₁-butyric acid methyl ester (P3HT:PCBM) (3 wt. % in chlorobenzene); and thermal evaporation of a 200 nm Al film, which serves as an electron-collecting (and hole-blocking) electrode.

3. High-brightness broadband measurements for solar applications

3.1. Optimizing étendue

We match the source, coupling, and focusing optics in order to optimize the throughput and achieve a high-brightness white-light spot. The critical quantity is the optical extent or étendue (G) of the system that will maximize the light throughput to the sample. It is this quantity that needs to be appropriately matched throughout the system to maximize the spectral irradiance, rather than the numerical aperture of the individual optical components. Because G is proportional to both the area of the source and the solid angle into which it propagates, we aim to match the collimating and focusing optics without introducing a bottleneck (e.g. the multimode optical fiber). The combination of the laser-driven light source and a parabolic mirror results in G ~ 3 × 10⁻³ mm² sr, a value well matched to a 0.22 numerical aperture fiber with a 0.2 mm core size (~4.5 × 10⁻³ mm² sr maximum G).

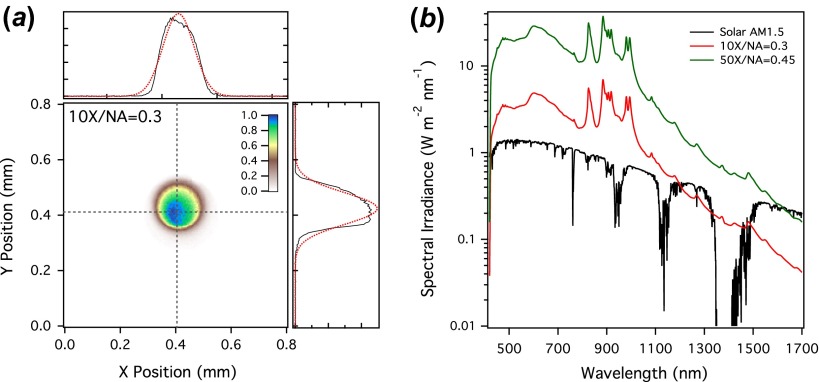
The effective étendue of the sample is determined by the spot size of the light and the microscope objective used to image and focus the light. The numerical aperture of the objective determines the solid angle, but the spot size is not determined by the nominal magnification, which is referenced to a 200 mm tube lens. We assume that the reference specifying the magnification value is a 200 mm tube lens. Here, the value of the objective magnification is now defined by the numerical aperture of the fiber itself and the collimating optic. As a result, the magnification of the objective is considerably smaller than the 10×/50× values specified. For the 10× objective, we obtain nearly 1:1 imaging, with the core diameter of the multimode fiber limiting the ultimate spot size. For example, focusing the broadband FT-modulated light source with a 10 × (0.3 numerical aperture) long-working distance objective yields a measured spot size of ~215 μm (beam profile shown in Figure 1(a)). We can achieve a smaller spot size using the 50× objective, for two reasons. First, the higher numerical aperture results in additional magnification, and second, the smaller entrance aperture of the higher NA objective slightly reduces the collimated beam size (thereby reducing the effective source size and the étendue out of the fiber). The net result is a reduction in spot size to ~40 μm using the nominal 50 × (0.45 numerical aperture) objective. As we discuss below, this small reduction in throughput still results in an overall higher spectral irradiance. These larger-than-diffraction-limit spots are due to the necessity of using of a multimode optical fiber to accommodate a large spectral bandwidth. Using a single-mode fiber and a monochromatic solid-state laser, we can achieve near diffraction-limited spots using these same optics. From the measured spot sizes and the focal length of the objectives, we can determine the éntendu of the sample in order to find the overall limiting factor in the optical system. In all cases, the éntendue of the 10× objective is higher than that of the source and fiber, meaning that the limiting factor is not the small area of the detector (i.e. sample).

Figure 1.

(a) Beam profile of the image formed using the EQ-99 laser-driven light source and a low magnification 10× objective. The spot size is approximately 215 μm with the 10× and 40 μm with the 50× . (b) Spectral irradiance in the visible and near infrared with the 10× and 50× objectives compared to the solar air mass 1.5 standard (ASTM G-173). (The colour version of this figure is included in the online version of the journal.)

3.2. Solar irradiance and photon flux

With the combination of a high-radiance light source and microscope focusing optics, we can achieve high-spectral irradiances for highly sensitive quantum efficiency measurements on small area devices. The spectral irradiance is shown in Figure 1(b) for the output of the LDLS microscopy system with the 10× and 50× objectives, along with the solar air mass 1.5 (ASTM G173-03) spectrum for comparison. The key metric is that the solar spectral irradiance can be matched or exceeded across the visible and NIR, particularly in the visible region of the spectrum, where we achieve in excess of 10 times higher irradiances. These numbers can be further improved since a 50:50 beam splitter (optimized for the visible) is used to direct light into the microscope objective. Replacing the dielectric optic with a metallic one would double the output in the visible, but result in even more significant gains in the NIR. However, for the purposes of this study, the irradiances achieved are more than sufficient for our measurements. The overall photon flux achieved is also quite high due to strong focusing of the light beam, exceeding 4.5 × 10²² m⁻²s⁻¹ with high spatial resolution.

4. Application to organic photovoltaic devices with a transparent, plasmonic-metal electrical contact

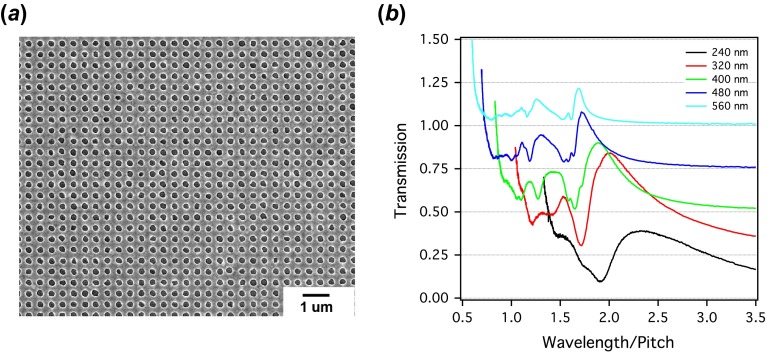
In order to demonstrate the utility of a technique having simultaneously high spatial resolution, spectral resolution, and high sensitivity, we examined a set of prototype organic photovoltaic devices that employed a nanostructured plasmonic Ag thin film as a transparent electrical contact. First, we discuss the photophysical properties of the perforated metal films with sub-wavelength apertures, in order to best match the contact’s optical properties to the light absorption bands in the organic active area. We fabricated the nanostructured electrical contacts by depositing a thin Ag film on glass and using a FIB tool (FEI Helios DualBeam) to mill square arrays of uniformly sized holes across typical areas of (0.3 mm)² (scanning electron micrograph, Figure 2(a)). We can fully characterize even these small-area samples because of the high-brightness light source, therefore minimizing the associated fabrication time. The advantage of using the FIB for fabrication is that the design can be varied (e.g. adjusting hole size and/or diameter) without the need for any process re-optimization. The variation in an average hole size introduced by our fabrication approach does not significantly affect the optical properties of the array. The absolute optical transmission spectra of Ag films fully perforated with hole arrays having pitches ranging from 240 to 560 nm on glass show a series of peaks and troughs resulting from the plasmon and diffraction modes in the array (Figure 2(b). Spectra are offset for clarity). As predicted from momentum conservation arguments, these mode positions are nearly constant on a wavelength-to-pitch ratio scale [11].

Figure 2.

(a) Scanning electron micrograph of a silver thin film perforated with a hole array having a pitch of 400 nm. (b) Absolute optical transmission spectra of 100 nm thick Ag films with a total area of (300 μm)² on glass vs. the wavelength/pitch ratio, for different pitch values. Each transmission spectrum is offset by 0.25 for clarity. (The colour version of this figure is included in the online version of the journal.)

The optical transmission properties of these perforated metal films are sensitive to the dielectric interfaces on either side, such that the modes of the film when assembled into solar cell will shift compared to those of the same metal film on glass. In order to understand the metal film transmission properties of our target device structure, we coat the perforated Ag film (100 nm thick, 200 nm average hole diameter, and 400 nm average pitch) with a 220 nm thick polymer layer (Microposit S1811) that mimics the dielectric constant of the organic semiconductor in the non-resonant regime of the spectrum, but does not exhibit significant absorption at visible wavelengths. To best imitate the device structure, we insert a 17 nm thick TiO₂ layer between the Ag and polymer films, because such selective electronic transport layers are essential for organic device operation [12]. We use finite difference time domain (FDTD) calculations (Lumerical Solutions, Inc.) to understand the origin of the primary transmission resonances and their effect on the target photovoltaic device. We find reasonably good agreement between the measured (Figure 3(a), black) and calculated (Figure 3(a), red) transmission curves, with a primary maximum in the transmission spectrum at ~1020 nm and a minimum near ~930 nm. We believe the peak broadening in the NIR results from hole size inhomogeneities. However, the hole pitch uniformity generates a resonance peak that is well matched to the calculation.

Figure 3.

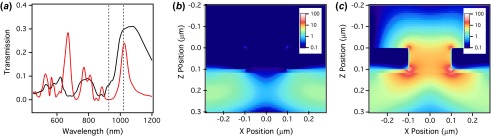
(a) Experimental (black line) and FDTD transmission spectrum (red) of a glass/perforated Ag electrode (height = 100 nm, diameter = 200 nm, pitch = 400 nm)/TiO₂ (h = 17 nm)/polymer (220 nm)/air dielectric stack. Normalized field intensity distributions, |E|²/|E ₀|² for light with (b) λ = 927 nm and (c) λ = 1020 nm. In (b) and (c), the glass spans from z = −0.2 μm to z = 0 μm, the Ag MHA spans from z = 0 μm to z = 0.1 μm (and the hole in the Ag layer spans from x = −0.1 μm to x = 0.1 μm), the TiO₂ layer spans from z = 0.1 μm to z = 0.117 μm, and the polymer layer spans from z = 0.117 μm to z = 0.337 μm. (The colour version of this figure is included in the online version of the journal.)

Our calculations allow us to examine the light intensities of corresponding spatial modes in order to identify the mechanism for light dissipation or transport. In Figure 3(b) and (c), we plot the normalized field intensity |E|²/|E ₀|² in the xz plane (where incident light propagates in the +z direction, downwards in the figure). This calculation shows that at 927 nm (Figure 3(b)), near the transmission minimum, the field intensity is delocalized throughout the polymer active area, with a minimum under the hole open area. This calculated spatial distribution is consistent with that of a Wood’s anomaly (evanescent mode), which redirects the light propagation due to diffraction [11]. In contrast, the normalized field intensity profile |E|²/|E ₀|² for a wavelength near the transmission maximum (1020 nm) shows feature characteristics of the near-field enhancement due to surface plasmon modes in the perforated metal film, resulting in “hot spots” of electric field intensity near the edges of the contacts along the metal-polymer layer. Though one benefit of these plasmon modes is enhanced light transmission through sub-wavelength apertures, there is also an opportunity for modification of the absorption and radiative properties of the active layer via the Purcell effect [13,14]. Though this subject is beyond the scope of the current manuscript, it does imply that the benefits of perforated metal films as electrical contacts potentially extend beyond their role as passive, light-transmitting elements [15].

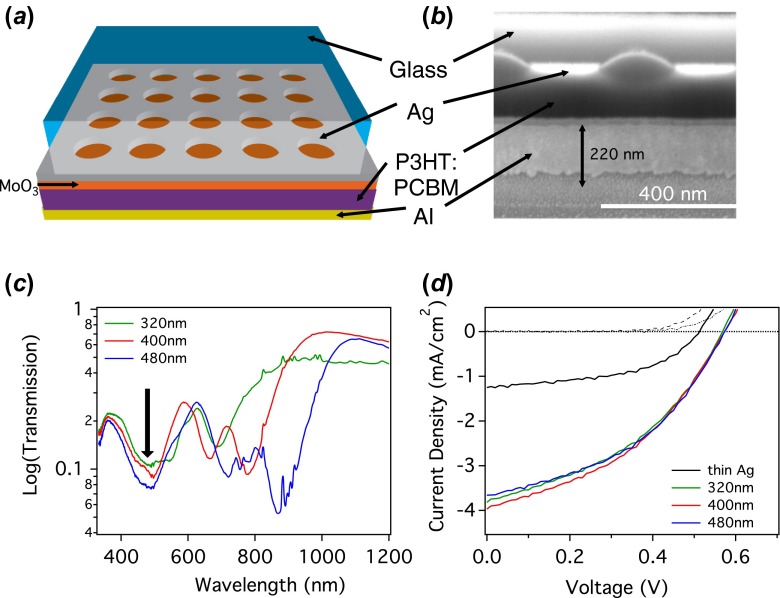
Because the primary features in the transmission spectrum of the perforated metal film result from light-matter interactions at the metal/polymer interface, we can leverage this structure for design of a solar cell transparent electrical contact. In this demonstration, we employ a 35 nm thick Ag film (perforated with a square array of 200 nm diameter holes on a 410 nm pitch) to couple light into a 160 nm thick active layer of blended organic P3HT:PCBM. The device also includes both hole transporting (10 nm thick MoO₃) and electron transporting (220 nm thick Al) on either side of the organic active layer (schematic in Figure 4(a) and cross-sectional SEM image in Figure 4(b).

Figure 4.

(a) Device schematic and (b) SEM cross-section of an organic photovoltaic device with a perforated Ag film as transparent contact. The device area is (300 μm)². (c) Device optical transmission spectra prior to Al contact formation. The high extinction due to absorption by the active layer occurs around 500 nm and is indicated by the arrow. (d) Dark (dot-dash) and illuminated (lines) J − V curves for fully fabricated devices using the Ag/polymer materials shown in (c). Device hole array pitches are: 320 nm (green), 400 nm (red), and 480 nm (blue). Also shown is the performance of a similar device having an unpatterned 50 nm thick Ag electrical contact (dark: dashed, illuminated: black). (The colour version of this figure is included in the online version of the journal.)

The optical transmission spectra of organic devices having metal contacts with a hole array of pitches 320, 400, and 480 nm (Figure 4(c), measured prior to forming the Al electrical contact) contain features in the NIR region that are similar to that of the non-resonant model system (Figure 3(a)), but show dramatic differences in the spectral regions where the P3HT:PCBM blend absorbs. The primary polymer absorption manifests as dramatic dip around 500 nm (indicated with an arrow in Figure 4(c)). The magnitude of the transmission (<10%) is similar to that of the electrode evanescent mode near 900 nm, and is consistent with an active area thickness of ~170 nm [16].

Although the primary propagating mode of the perforated Ag film (>700 nm) is far from the organic material absorption peak (at 500 nm), higher order surface plasmon modes (visible at shorter wavelengths in Figure 3(a)) can nevertheless couple light efficiently into the device structure in order to generate photocurrent. For example, the current-voltage (J − V) characteristics of fully assembled devices under illumination by 1 SUN simulated AM 1.5G radiation display average photocurrent (J _sc) in the range of J _sc~ 4 mA/cm² (nearly independent of hole array pitch), open circuit voltage, V _oc  = 0.58 V, and power conversion efficiencies around ~1% (Figure 4(d)). Although conventional transparent contact materials (e.g. indium tin oxide) have achieved power conversion efficiencies around ~4% in P3HT:PCBM devices, there are opportunities for considerable improvement by better matching the electrode’s propagating mode to the absorption resonance in the organic layer. Potential approaches to achieving performance improvements include scaling the hole arrays to smaller pitches, or leveraging recent breakthroughs in utilizing NIR absorbing polymers [17] which are better matched to the size of the perforated metal contacts described in this work.

The high-brightness photocurrent measurement is ideal for acquiring high-sensitivity EQE spectra of these small-area devices (300 μm)² (Figure 5). Although in these measurements we are not required to match the lamp spectrum to the solar spectrum, we nevertheless target an overall spectral irradiance comparable to that of solar illumination in order to avoid high-fluence recombination processes [18]. The achievable spot size under low magnification is 215 μm, well matched to our device area of (300 μm)² and to the solar irradiance in the active region of the device. This measurement has not only high spatial resolution, but also extremely high speed. These measured EQE spectra result from averaging for approximately one minute in total, because the entire spectrum (from 420 to 2500 nm) is collected in a single shot.

Figure 5.

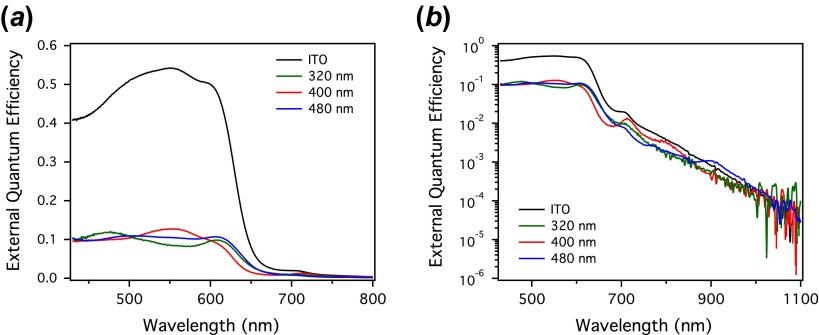
FT photocurrent spectra of (300 μm)² area devices on a (a) linear and (b) log scale for organic photovoltaic devices with perforated metal film transparent contacts (hole array pitches of 320 nm (green), 400 nm (red), and 480 nm (blue), along with a reference device (black) utilizing an ITO transparent contact. On a log scale, weak absorption by CT states can be visualized with over six orders of magnitude dynamic range. (The colour version of this figure is included in the online version of the journal.)

The integrated EQE of the organic devices using perforated metal films as transparent electrical contact (Figure 5(a), green, red, and blue colors) is approximately five times lower than a similar organic device having a traditional ITO transparent contact (Figure 5(a), black), due primarily to low-light transmission through the contact in the wavelength range where the organic material absorbs strongly. Unlike the J − V measurement (Figure 4(d)), the EQE spectrum more clearly demonstrates the effect of changing hole array pitch on the device performance. The primary absorption changes shape as a function of pitch and relative to the ITO contact (Figure 5(a)), with the most apparent difference being a flattening of the absorption spectra moving towards the UV region, compared to the conventional ITO device. Small fluctuations in the main absorption edge are also visible.

The high sensitivity of our high-brightness FTPC measurement facilitates detailed investigations of the NIR spectral regions, where although the polymer shows weak absorption, the effect of coupling to surface plasmon modes is expected to be the strongest. Previous high-sensitivity measurements on organic photovoltaic devices have shown that weak absorption characteristics of charge transfer (CT) states contribute to the overall photocurrent signal [19,20]. The response of these CT states are readily seen on a log scale of the EQE spectra (Figure 5(b)) in both the ITO and hole array contact devices. Although the primary absorption features of the polymer are considerably weaker than the control devices, the CT absorption is not. In fact, structure in the CT absorption can be seen, leading to fluctuations (particularly in the 480 nm pitch device) that exceed those of the control. Work is still on-going to separate the relative contributions of the propagating (plasmonic) and evanescent (wave-guiding) modes to the change in the overall EQE spectrum, and this will be the subject of future work. Here, we stress that these types of studies are enabled by our ability to look at photocurrent spectra with more than six orders of magnitude of sensitivity with high spatial resolution. This allows us to quickly prototype and characterize photovoltaic devices employing plasmonic and photonic structures.

5. Conclusion

We demonstrate that high-sensitivity photocurrent spectroscopy can be achieved on small-area organic photovoltaic devices with greater than six orders of magnitude dynamic range in the EQE spectra. These methods can be used to understand the interactions between the plasmonic modes of sub-wavelength metal hole arrays and an organic absorber. There are several factors that must be considered when evaluating performance of these devices, including scattering of light perpendicular to the direction of incidence, enhancement of absorption and radiative rates in near fields via the Purcell effect, and photonic confinement of the propagating modes in the fully assembled device stack.