DFT Study of the Role of Al³⁺ in the Fast Ion-Conductor Li_7–3xAl³⁺_xLa₃Zr₂O₁₂ Garnet

Abstract

We investigate theoretically the site occupancy of Al³⁺ in the fast-ion-conducting cubic-garnet Li_7–3xAl³⁺_xLa₃Zr₂O₁₂ (Ia-3d) using density functional theory. By comparing calculated and measured ²⁷Al NMR chemical shifts an analysis shows that Al³⁺ prefers the tetrahedrally coordinated 24d site and a distorted 4-fold coordinated 96h site. The site energies for Al³⁺ ions, which are slightly displaced from the exact crystallographic sites (i.e., 24d and 96h), are similar leading to a distribution of slightly different local oxygen coordination environments. Thus, broad ²⁷Al NMR resonances result reflecting the distribution of different isotropic chemical shifts and quadrupole coupling constants. From an energetic point of view, there is evidence that Al³⁺ could also occupy the 48g site with its almost regular octahedral coordination sphere. Although this has been reported by neutron powder diffraction, the NMR chemical shift calculated for such an Al³⁺ site has not been observed experimentally.

Introduction

The fast Li-ion conductor with the nominal composition Li₇La₃Zr₂O₁₂ (LLZO) is receiving much scientific attention since its discovery in 2007.¹ It has a garnet-based structure, and it occurs in at least two structural modifications.^2,3 At room temperature, LLZO is tetragonal (I4₁/acd) while the cubic modification (Ia-3d) is stable above approximately 150 °C.⁴ Geiger et al. argued that the better conducting cubic phase can be stabilized at room temperature (RT) through the incorporation of small amounts of Al³⁺.⁴ The stabilizing effect of Al³⁺ has now been confirmed by a number of subsequent investigations.⁵⁻¹⁹ The exact role Al³⁺ plays in cubic Al-bearing LLZO is important because LLZO shows a high ionic conductivity of about 10^–4 S/cm at RT. This is approximately 2 orders of magnitude higher than that for the lower symmetry Al-free tetragonal LLZO phase. LLZO also has good chemical and thermal stability, as well as a wide energy potential window making it an excellent candidate for use as an electrolyte in an all-solid-state lithium-ion battery.^1,20

As has been shown recently, ionic conductivity also seems to depend on the amount of Al³⁺ incorporated during synthesis.^6,8 Further work, however, is needed to quantify this effect. For this purpose, the chemical and physical properties governing Li⁺ diffusion have to be understood in detail; in particular this includes the important question as to which crystallographic sites the Al³⁺ ions preferably occupy in the cubic phase of LLZO.

Considerable experimental research has been undertaken to obtain information about Al³⁺ in LLZO, including its local coordination and site partitioning behavior. In this context, ²⁷Al magic angle spinning (MAS) nuclear magnetic resonance (NMR) spectroscopy is a key method. Several NMR studies have proposed that the resonance observed at a chemical shift ranging from 64 to 68 ppm corresponds to Al³⁺ located at the “standard garnet” tetrahedral site.⁴⁻⁷ There is uncertainty, however, about the interpretation and assignment of the other measured NMR lines that have chemical shifts ranging from approximately 78 to 82 ppm. The interpretations given so far include Al³⁺ residing at nontetrahedral Li⁺ sites (4-fold to possibly 6-fold coordinated) and tetrahedrally coordinated sites in the neighborhood of La³⁺ or Zr⁴⁺ vacancies in Al-rich LLZO.^4,5 In particular, mechanochemically prepared LLZO samples with a high amount of Al³⁺, but reduced in La³⁺ and Zr⁴⁺ content, even indicate two magnetically inequivalent tetrahedral sites.⁶ Neutron powder diffraction (NPD) measurements were interpreted as indicating that Al³⁺ is located at an octahedrally coordinated site in the garnet framework.¹¹

Summarizing the various published experimental results, there is no clear understanding as to which sites are occupied by Al³⁺ in cubic LLZO. This also concerns the detailed interpretation of ²⁷Al NMR MAS spectra and diffraction results. To address the important role of Al³⁺ in LLZO and to obtain a better understanding of the various experimental results, we undertook a density functional theory (DFT) investigation of Al-bearing cubic LLZO with the aim to calculate (relative) ²⁷Al NMR parameters such as chemical shifts and electric quadrupole coupling constants.

Computational Methods

In order to understand the computational models used in this investigation, we provide a short description of the crystal structure of cubic LLZO garnet (Figure 1).

Figure 1.

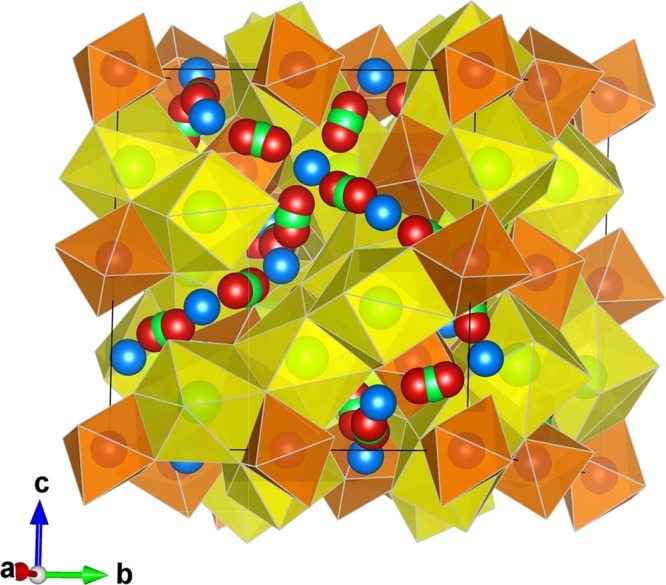
Crystal structure of cubic LLZO. The yellow dodecahedrally coordinate La³⁺ (at the Wyckoff position 24c) and orange octahedrally coordinate Zr⁴⁺ (16a). The blue spheres correspond to tetrahedrally coordinated (24d) Li⁺, green spheres to octahedrally coordinated (48g) Li⁺, and red ones to distorted 4-fold coordinated (96h) Li⁺.

“Garnet” is the common name for a large number of natural and synthetic metal oxide and fluoride phases.²² Conventional oxide garnets have the general formula A₃B₂C₃O₁₂ and crystallize with cubic symmetry Ia-3d. In the case of LLZO, the O^2– ions, located at general crystallographic positions, 96h, form an oxygen-ion framework with interstices occupied by the A cations (La³⁺) at an 8-fold coordinated position 24c (point symmetry 222), by B cations (Zr⁴⁺) at a 6-fold coordinated position 16a (point symmetry −3), and by C cations (Li⁺) at a 4-fold coordinated 24d position (point symmetry −4). In addition to these cation sites, there are other interstices within the oxygen framework that are empty in the conventional garnet structure,²³ such as the 6-fold coordinated 48g positions (point symmetry 2) and a general 96h position, sometimes described as 4-fold coordinated with two additional longer bonds greater than 2.8 Å in length,²⁴ 5-fold⁴ coordinated or 6-fold¹¹ coordinated (point symmetry 1). These interstices can be filled by “extra” cations (such as Li⁺), giving rise to compositions with nonstandard garnet stoichiometry. An important property is the partial occupancy of the structural sites (24d, 48g, and 96h) where Li⁺ is located and also delocalization of Li⁺ ions throughout.

Several theoretical DFT studies on LLZO have been published before.²⁵⁻³⁰ They concentrate on the basic structural properties and on the Li⁺ diffusion, but none of them considers Al³⁺ ions explicitly.

For our first-principle calculations, the ions in LLZO were arranged on the basis of crystal structure descriptions in the literature.²⁵ Three different structural models were used with all having a body centered (I-type) Bravais lattice with a = b = c = 12.972 Å and α = β = γ = 90°. Three garnet compositions were chosen, namely Li₄₄Al₄La₂₄Zr₁₆O₉₆ with Al³⁺ at 24d, 48g and 96h, Li₅₆Al₄La₂₀Zr₁₆O₉₆ with Al³⁺ solely at 24c, and Li₆₀Al₄La₂₄Zr₁₂O₉₆ with Al³⁺ solely at 16a. The Li⁺ ions were distributed over the 24d and the 96h sites following Xu et al.²⁶ No significant effect on the results was observed by choosing a different Li⁺ arrangement. The highest symmetry possible was maintained to save computational costs. The first model was used to understand the behavior of Al³⁺ at various possible sites occupied by Li⁺. The calculations were made with 17 different local Al³⁺ positions located among the 24d, 96h, and 48g sites. To avoid cation repulsion, all Li⁺ ions close to Al³⁺ were removed. The various Al³⁺ positions were fixed during relaxation and all Al³⁺ ions are equivalent in the unit cell.

All calculations are based on DFT methods using the all-electron full potential linearized augmented plane wave (LAPW) method as implemented in the Wien2k code.^31,32 The Perdew Burke Ernzerhof (PBE) generalized gradient approximation (GGA) was employed.³³ The atomic positions were optimized by minimization of the forces (below 2 mRy/au) acting on the atoms simultaneously with the self-consistent-field cycle as implemented by Marks.³⁴ The eigenvalue problem was solved by an “iterative diagonalization” using an efficient preconditioning (inverse of H - λS) and the block-Davidson method.³⁵ The radii of the atomic spheres (R_MT) for the Li⁺, La³⁺, Zr⁴⁺, O^2-, and Al³⁺ ions were chosen to be 1.46, 2.27, 1.93, 1.71, and 1.40 au, respectively. The cutoff for the plane wave R_MTK_max = 6.0 and the maximum Fourier expansion of charge density cutoff G_max = 12 (au)⁻¹ were applied. The separation parameter between the valence and core states was chosen to be −6.0 Ry. We used 1 k-points in the irreducible Brillouin zone. The computational considerations were checked by increasing R_MTK_max and the number of k-points, but no significant changes with respect to the energy, geometry, and the electric field gradient (EFG) around Al³⁺ were observed.

The behavior of Al³⁺ at different crystallographic sites was analyzed qualitatively by weighing the various Al³⁺ positions, x_i, with their corresponding energy, E(x_i). The various local energies for Al³⁺ at and around the crystallographic positions where Li can also be located, were described by fitting a polynomial, describing a possible diffusion pathway. The ocuppation probabilities for an Al³⁺ ion along this path are described using a normalized Boltzmann factor given by

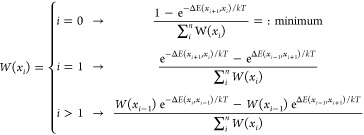where k is Boltzmann’s constant, and where x_i+1 indicates the states next to x_i, x_i–1 indicates the states before x_i with an interval of 0.01 Å, and T is 298.15 K. The site preference energy, ΔE, is defined as ΔE = E(x_i) – E^global, where E^global is the global energy minimum and corresponds to Al³⁺ located at 24d. It has the lowest total energy for all the calculated arrangements of Al in LLZO.

In NMR spectroscopy, the chemical shift, δ, of a nucleus, i, describes the nuclear shielding effect of an applied (external) static magnetic field and the locally induced magnetic field arising from the surrounding electrons with a certain probability of presence near the corresponding nuclear site i. The magnitude of the resulting effective field, B_eff, is given by B_eff = B₀(1 – σ_i), where σ_i is a second-rank nuclear shielding tensor, 1 is the unit matrix and B₀ is a uniform external field along the z-axis. The resonance NMR frequency, ν_i, is then given by v_i = (γ_i/2π) B_eff, where γ_i is the magnetogyric ratio of the nucleus under observation. The isotropic chemical shift, δ_iso (henceforth δ), describes the relation between the NMR resonance frequency for the nucleus of interest, ν_i, and the corresponding resonance frequency for a reference compound, ν_ref, giving δ = 10⁶ × (v_i – v_ref)/v_ref. Because of the orientation in systems with periodic boundary conditions, all anisotropic interactions causing line broadening are projected onto the axis of rotation where they collapse at the magic angle.³⁶ To compute δ, we used the relaxed geometry and applied the NMR module³⁷⁻³⁹ of the Wien2k code.³² These chemical shift calculations are based on an all-electron linear response method where one obtains the induced current density considering the perturbation of the ground state wave functions due to the external magnetic field. The resulting magnetic shielding is then obtained by integration of the all-electron current according to Biot–Savart’s law without further approximations. Because there is agreement in the literature⁴⁻⁷ that the ²⁷Al NMR resonance at 66 ± 2 ppm represents tetrahedrally coordinated Al³⁺ at 24d in LLZO (δ_24d = 68 ppm), we calculate the difference of the chemical shifts (Δδ) for Al³⁺ at other positions x_i with a δ_xi as follows

Besides the chemical shift, the interaction of the quadrupole moment, Q, of the ²⁷Al nucleus (spin-quantum number I = 5/2) with a sufficiently large electric field gradient (EFG), which is produced by a nonspherical charge distribution around the nuclear site, also affects the central NMR transition. Second order quadrupolar effects, influencing the shape of the NMR central line, cannot be (completely) eliminated by magic angle spinning. From the simulation of spectra recorded under MAS conditions, the quadrupole coupling constant

and the corresponding asymmetry parameter

can be estimated. Here, e is the positive elementary charge, h denotes Planck’s constant, and V_xx , V_yy and V_zz are the elements of the traceless EFG tensor V with |V_zz| ≥ |V_xx| ≥ |V_yy|. V_zz = eq denotes its principal component. The shape of the NMR central line depends sensitively on the asymmetry of the electronic charge density close to the nucleus. The parameter η describes the deviation of the EFG from axial symmetry and it can take values between 0 and 1. Second order quadrupole interactions also affect the position of the NMR line in terms of a quadrupolar shift. A larger external magnetic field, however, lowers the effect. Here, we compute the EFG from the all-electron charge distribution without further approximation and C_Q is obtained using the nuclear quadrupole moment Q(²⁷Al) = 1.616 × 10^–29 m² determined from the slope of the linear regression proposed by Body et al.⁴⁰ The data visualization were performed using the program VESTA.⁴¹

Results

Crystal Chemistry of Al-bearing LLZO and Al³⁺ Partitioning Behavior

The most energetically favorable position of Al³⁺ in LLZO is at the tetrahedrally coordinated crystallographic special 24d position. Al³⁺ can be displaced toward a neighboring vacant general 96h site, which leads to a distortion of its oxygen coordination polyhedron. Calculated Al–O bond lengths for this coordination at 0 K are between 1.76 Å and 1.79 Å and the tetrahedral volume is 2.86 ų (see Table 1).

Table 1. Various Calculated Interatomic Al–O Distances (d) [Å] and Coordination Polyhedra Volumes (V) [ų] in Cubic Li₇La₃Zr₂O₁₂.

	24d	96h	48g	16a	24c
	Al–O	Al–O	Al–O	Al–O	Al–O
d	1.76	1.76	2.12	1.90	1.95
d	1.78	1.92	1.93	2.11	1.95
d	1.78	1.84	1.93	2.03	1.94
d	1.79	1.82	2.00	1.90	1.94
d		2.90	2.00	2.03	2.82
d		3.15	2.12	2.11	2.82
d					2.92
d					2.92
⟨d⟩	1.78	1.83a	2.02	2.01	1.94a
V	2.86	2.69a	10.67	10.69	22.86b

^aBased on 4-fold coordination.

^bBased on 8-fold coordination.

Our calculations show that Al³⁺ at 96h is 4-fold coordinated, and distorted from tetrahedral coordination, with Al–O bond lengths varying from 1.76 to 1.92 Å, because of the displacement of Al³⁺ towards a vacant 24d site. Additionally, there are two O^2– ions further away that have on average approximately 1 Å longer bond distances. If they would be included in the local coordination sphere around Al³⁺, a distorted octahedral coordination polyhedron with a volume of 16.33 ų would result. The volume for the 4-fold coordinated polyhedron is 2.69 ų. Al³⁺ could also possibly be located at the special 48g site with three different pairs of Al–O bonds and calculated bond lengths of 1.93 Å, 2.00 Å and 2.12 Å, respectively, yielding a coordination volume of 10.67 ų. Any possible Al³⁺ at the 16a site would also be 6-fold coordinated with again three pairs of Al–O bonds with lengths of 1.90 Å, 2.03 Å, and 2.11 Å and a coordination volume of 10.69 ų. Al³⁺ at the 24c site would have four shorter Al–O bond lengths equal to 1.94 Å and four longer bonds of 2.84 Å length. This would give rise to a quasi-4-fold planar coordination for Al³⁺. Assuming, on the other hand, 8-fold coordination around the 24c site, the resulting polyhedron would have a volume of 22.86 ų. The various hypothetical Al³⁺ coordination polyhedra at 0 K, along with their associated site preference energy, are shown in Figure 2.

Figure 2.

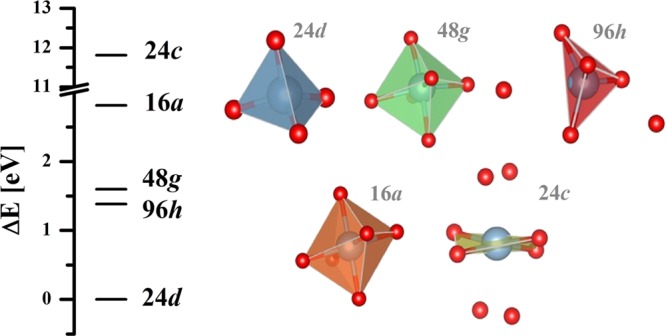
Various coordination polyhedral around Al³⁺ located at the 24d, 48g, 96h, 16a, and 24c sites. (Nonbonded red spheres indicate additional O^2– ions not considered as next nearest neighbors in the first coordination sphere. Their distances are given in Table 1.) Their associated site preference energies in cubic LLZO.

The calculated site preference energies, ΔE, for Al³⁺ in LLZO are as follows: 24d > 96h > 48g > 16a ≫ 24c. Al³⁺ at the 24d site has the global energy minimum and is 1.38 eV more stable than Al³⁺ at 96h and 1.60 eV more stable than Al³⁺ at 48g. The latter two sites are energetically similar with an energy difference of just 0.22 eV. The site preference energy for Al³⁺ at 16a and 24c is 0.41 and 1.74 eV higher, respectively, when referenced to the global energy minimum. The site preference energies for Al³⁺ at various structural positions between 48g and 24d are shown in Figure 3.

Figure 3.

Site preference energies, ΔE, for Al³⁺ at various structural positions (gray crosses) at and near the 48g, 96h and 24d sites in LLZO garnet. The solid lines represent polynomial fits to the various ΔE values. The fits were used to calculate the Boltzmann distribution, W(x_i) (see text), discussed below. The different distributions of Al³⁺ at the various crystallographic sites are normalized to 1 and indicate the room temperature probability of finding Al³⁺ at a distinct position.

Calculated ²⁷Al NMR Parameters

Calculated ²⁷Al NMR parameters for Al³⁺ at the different structural sites in LLZO are shown in Table 2. The corresponding polyhedra (Figure 4) around Al³⁺, slightly displaced from 24d and 96h (Figure 3), were used to analyze the experimental NMR spectra. The calculations show that Al³⁺ coordinations given by 1 to 5 (Figure 4) have Δδ values between −3.7 and 0.2 ppm, C_Q values between −1.38 and 5.01 MHz and η values between 0.20 and 0.70. Al³⁺ for coordinations given by 9 to 13 have Δδ values between 10.0 and 14.4 ppm, C_Q values between 2.4 and 3.3 MHz and η values between 0.24 and 0.70. On the other hand, Al³⁺ located at 48g has an extremely large calculated Δδ value of 133.5 ppm, 118.5 ppm at 24c, and 108.5 ppm at 16a. The latter three sites have δ values that are much larger than any experimentally observed NMR resonances.

Table 2. Calculated ²⁷Al NMR Parameters for Al³⁺ at Various Sites in Cubic Li₇La₃Zr₂O₁₂ Compared to Experimental Values from the Literature.

	positiona	δb [ppm]	Δδc [ppm]	VZZd [1021 V/m2]	CQe [MHz]	ηf	assignment
Geiger et al.4		68.0	13.0		5.0–5.2	0.0–0.1	24d
		81.0			3.3	0.7	96h
Buschmann et al.5 and Düvel et al.6		64.0	14.0				24d
		78.0	18.0
		82.0
Hubaud et al.7		68.4			4.8	0.40	24d
		73.5	5.1		6.9	0.13	24d
Our calculations	1	68.0		–1.38	–0.8	0.10	24d
	2	68.2	0.2	2.14	1.3	0.94
	3	64.3	–3.7	3.03	1.8	0.79
	4	64.5	–3.5	3.97	2.3	0.71
	5	64.8	–3.2	5.01	2.9	0.66
	13	79.9	11.9	4.03	2.4	0.28
	12	78.0	10.0	4.08	2.4	0.24	96h
	11	79.4	11.4	4.63	2.7	0.45
	10	82.4	14.4	5.03	3.0	0.54
	9	82.2	14.2	5.63	3.3	0.70

^aThe position corresponds to Al³⁺ with the coordination polyhedra in Figure 4 and the site preference energies in Figure 3.

^bCalculated values are referenced to the global minimum given by δ = 68 ppm at position 1.

^cLiterature: Δδ = δ – δ_24d; Calculation: Δδ = δ – 68 ppm.

^dPrincipal component of the EFG.

^eQuadrupole coupling constant.

^fAsymmetry parameter.

Figure 4.

Oxygen coordination polyhedra around Al³⁺ for Al–O distances less than 2.6 Å at 17 local positions starting with 24d (1) and going to 96h (12) and beyond and ending at 48g (20) in cubic LLZO.

Discussion

In this DFT study, we investigated the crystal-chemical role of Al³⁺ in LLZO. Specifically, we address the question of the coordination and the site distribution behavior of Al³⁺. The results of the calculations can be used, together with published experimental results, to achieve a better understanding of the nature of Al³⁺ incorporation in LLZO. We find that Al³⁺ at the 24d site is energetically the most stable state, followed by Al³⁺ at 96h and 48g, whereby the site preference energies for the latter two are similar. Al³⁺ at both the 16a and 24c sites is energetically unfavorable. Based on our DFT calculations, Al³⁺ should be exclusively located at 24d at 0 K, which would give rise to a single NMR resonance. Thus, the question arises why additional resonances are observed in the ²⁷Al MAS NMR spectra (Figure 5).⁴⁻⁷

Figure 5.

Experimental ²⁷Al NMR MAS spectra⁴⁻⁷ compared to calculated δ values. The gray areas represent the variation in chemical shift values, Δδ, (13 to 18 ppm) in literature. The reference point refers to Δδ = 0 given by the calculations.

Before discussing our results, we briefly outline the NMR results from the various studies with respect to the Al³⁺ site occupation in LLZO. In all recent studies the resonance at approximately 66 ± 2 ppm is assigned to Al³⁺ at the 24d site.⁴⁻⁷ Other NMR lines also indicate 4-fold coordinated Al³⁺ ions,⁴⁻⁷ because their chemical shift values of 78 to 82 ppm are usually indicative of tetrahedral coordination. Geiger et al. assigned the resonance at 81 ppm to Al³⁺ residing at the 96h sites.⁴ In particular, the spectra presented in ref (6) indicate that several NMR lines contribute to a signal occurring between 75 to 85 ppm. It should be noted that the latter has been reported for LLZO samples with a high amount of Al³⁺ and lower than stoichiometric La³⁺ and Zr⁴⁺ contents.⁶ Such samples were prepared by mechanochemical activation combined with subsequent annealing at moderate temperatures.

Düvel et al. observed a stronger NMR signal at 64 ppm and a less intense line at 78 ppm for garnets with Al³⁺ contents up to 0.30 per formula unit (pfu). However, at concentrations above 0.60 Al³⁺ pfu the resonance at 78 ppm becomes the most intense. At even higher Al³⁺ contents a new NMR line at 81 ppm emerges, which notably appears in La- and Zr-deficient LLZO samples.

Geiger et al. made, in addition to ²⁷Al MAS NMR experiments, also ²⁷Al MQMAS NMR measurements.⁴ The latter spectra show a resonance at δ = 81 ppm, a coupling constant, C_Q, of 3.3 MHz and an asymmetry parameter, η, of 0.7. These parameters indicate a strongly distorted local coordination geometry. The second resonance observed at δ = 68 ppm shows a stronger quadrupolar interaction with C_Q = 5.0 to 5.2 MHz and a lower η value between 0.0 and 0.1 that suggests axial symmetry at the site. It should be noted that the ²⁷Al MAS NMR spectrum was recorded at 156.26 MHz, thus providing a sufficiently high resolution to simulate its line shape. Such a simulation yields a resonance with δ = 81 ppm, C_Q = 3.3 MHz and η = 0.7, and for the second signal values of δ = 70 ppm, C_Q = 5.5 MHz and η = 0.5.

The calculated NMR parameters (Table 2) are in good agreement with an assignment of Al³⁺ to 96h for the resonance at 81 ppm. The calculated NMR parameters for the NMR line at 68 ppm that is assigned to Al³⁺ at 24d, however, disagree with those determined from the MQMAS NMR experiments. For the latter, it has been proposed that possibly more than one Al³⁺ site is reflected by this broad resonance. This possibility was underlined by Hubaud et al.⁷ They made ²⁷Al MQMAS NMR spectroscopic measurements to investigate this resonance at 68 ppm for an Al-doped LLZO garnet synthesized at 850 °C. Their line shape analysis yielded two NMR lines with the first having δ = 68.4 ppm and C_Q = 4.8 MHz and the second δ = 73.5 ppm and C_Q = 6.9 MHz. Both resonances were assigned to tetrahedrally coordinated Al³⁺ at 24d in two different garnet phases. The two tetrahedral sites have slightly different distortions and thus different δ and C_Q values. Hubaud et al. report that this interpretation is consistent with their high-resolution XRPD results, and they proposed that slow Al³⁺ diffusion within the lattice is responsible for the disordering over the two sites.

Our DFT calculations permit a somewhat different interpretation of the experimental results. For the first step, we calculated the NMR parameters for Al³⁺ at all crystallographic sites, via 24d, 48g, 96h, 16a, and 24c. According to our results, the resonance at 80 ± 2 ppm should be assigned to Al³⁺ residing at the 96h sites and the resonance at 66 ± 2 ppm to Al³⁺ occupying 24d. These results agree with interpretations of experimental NMR spectra.⁴⁻⁶ There is good agreement between the calculated C_Q value for Al³⁺ at 96h, but disagreement between C_Q values for Al at 24d. Hubaud et al. proposed a large C_Q value for Al³⁺ at 24d, but it cannot be easily explained why the symmetric 24d site should yield a C_Q value approximately two times larger than Al³⁺ at the more distorted 96h site.⁷

To understand this issue better, we calculated the NMR parameters for Al³⁺ at all positions at and around 24d and 96h that are occupied by a certain probability. Shifting Al³⁺ away from 24d and 96h leads to a distribution of slightly different local oxygen coordination environments. Thereby, broad ²⁷Al MAS NMR resonances could result, which would reflect a distribution of slightly different δ and C_Q values. We note that our calculations for η for Al³⁺ at 24d do not agree with experiment, but η was obtained from the experimental spectra by using only one⁴ or two⁷ Al³⁺ resonances to simulate this broad feature at 66 ± 2 ppm.

The NMR signal located at 78 to 82 ppm is also asymmetric in shape. This is possibly due to the slightly different geometries of local Al³⁺ coordinations, as given by their calculated probabilities, toward the 48g minimum versus those in the direction of 24d. This situation could produce two overlapping resonances having similar values of δ and C_Q (see also the agreement with experimental results and the discussion in ref (6)).

Although experiment and calculations are in broad agreement in terms of the crystal chemical role of Al³⁺ in LLZO, it is not clear based on the DFT calculations alone, why Al³⁺ is not located exclusively at 24d⁶ as suggested by the site energies. Al³⁺ at 96h and 48g must also be considered, which, however, would lead to an additional NMR line which is usually not observed experimentally. (For the sake of completeness, let us note that an additional NMR line has been observed at 93 ppm for Al-doped Li_6.5La_2.5Ba_0.5ZrTaO₁₂ [42] and for some of the Al-doped LLZO samples prepared via mechanosynthesis [6]; the prominent NMR line at 65 ppm, however, is absent in these cases.) Here, it must be stated that the exact thermodynamic state of LLZO, as obtained in the various sintering experiments, is not known. It is possible that metastable structural states are obtained that can depend on a number of experimental factors (dopant concentration, sintering temperature and time, heating rate, grain sizes, starting materials, etc.). Thus, Al³⁺ could potentially be incorporated metastably at 96h and 48g as well in cubic LLZO, because both sites have similar site energies.

The different site energies for Al³⁺ at 24d and 96h could provide an explanation for differences in published NMR spectra of LLZO. The relationship between Al³⁺ concentration and variations in the intensities of the different resonances (and thus Al³⁺ site occupancies), as observed by Düvel et al., can be interpreted crystal chemically. When an Al³⁺ ion is located at 24d, because of its large effective charge radius, it could create a larger inaccessible region around 24d compared to the situation for Al³⁺ at 96h. This region cannot be occupied by other ions. This leads to a reduction of entropy and a loss of energy possibly making the 96h site energetically more accessible for Al³⁺ with increased Al³⁺ contents in contrast to the 24d site. Similar considerations were made by Bernstein et al.³⁷ They showed by using molecular dynamics simulations that the introduction of vacancies in LLZO does indeed reduce the free energy. This indirectly supports our suggestion.

Lastly, we consider the coordination geometry around the 96h site in LLZO, which has been described differently.^4,11,24 It is, of course, a matter of definition as to what constitutes a bond in a first coordination sphere. According to Li et al. in their description of Al at 96h, the average Al–O bond distance is d^[4] = 2.08 Å, with a difference of 0.38 Å between the length of the shortest and the longest bonds. There are two further O^2– ions that give Al–O = 2.69 Å and 2.80 Å, thus being 0.46 Å and 0.57 Å longer compared to the longest bond in strict 4-fold coordination. Based on our calculations, Al³⁺ at 96h has a locally 4-fold distorted coordination (Figure 4). It is worth mentioning that long-range structural properties, as determined by the diffraction experiment, such as neutron powder diffraction, can differ from those measured via spectroscopy, for example, NMR, which probes structure at shorter length scales.

Conclusion

Based on our DFT results, we propose that Al³⁺ could have a number of slightly different local 4-fold coordinations around the crystallographic 24d and 96h sites in cubic LLZO garnet. The calculations are in general agreement with published experimental ²⁷Al NMR spectra. It should be noted further that Li et al.,¹¹ in a neutron diffraction study of cubic LLZO garnet, proposed that Al³⁺ is located at the 48g site in octahedral coordination. In terms of calculated site energies, this site could be partially occupied. However, the calculated Al NMR chemical shift value for such coordination has not been observed in experimental NMR spectra.

The authors declare no competing financial interest.