Crystal Phase Transitions in the Shell of PbS/CdS Core/Shell Nanocrystals Influences Photoluminescence Intensity

Abstract

We reveal the existence of two different crystalline phases, i.e., the metastable rock salt and the equilibrium zinc blende phase within the CdS-shell of PbS/CdS core/shell nanocrystals formed by cationic exchange. The chemical composition profile of the core/shell nanocrystals with different dimensions is determined by means of anomalous small-angle X-ray scattering with subnanometer resolution and is compared to X-ray diffraction analysis. We demonstrate that the photoluminescence emission of PbS nanocrystals can be drastically enhanced by the formation of a CdS shell. Especially, the ratio of the two crystalline phases in the shell significantly influences the photoluminescence enhancement. The highest emission was achieved for chemically pure CdS shells below 1 nm thickness with a dominant metastable rock salt phase fraction matching the crystal structure of the PbS core. The metastable phase fraction decreases with increasing shell thickness and increasing exchange times. The photoluminescence intensity depicts a constant decrease with decreasing metastable rock salt phase fraction but shows an abrupt drop for shells above 1.3 nm thickness. We relate this effect to two different transition mechanisms for changing from the metastable rock salt phase to the equilibrium zinc blende phase depending on the shell thickness.

Introduction

The wet-chemical synthesis of colloidal nanocrystals (NCs) is a well established method providing highly monodisperse quantum dots^1,2 for applications such as bright and stable fluorophores.³⁻⁶ Among these, the IV–VI lead chalcogenides (PbX, X = S, Se, or Te) NCs provide efficient emission over a large spectral range in the infrared. They are promising for applications, e.g., where PbS NCs act as optical active materials in organic photodiodes for the near-infrared.⁷ The applications for pure lead salt NCs are limited, however, because of their instability in the emission quantum yield over time caused by surface oxidation processes. This problem can be overcome by growing a protective shell around the NCs⁸ for chemical passivation with the advantage of an additional electronic passivation preventing the transfer of excitonic energy to surface trap states.⁹⁻¹¹ The core/shell architecture for nanostructures also allows semiconductor–metal hybrid nanoparticles with enhanced functionalities to be realized that are otherwise not accessible.¹² In contrast to other postsynthetic shell growth techniques like epitaxial shell growth on top of the core^13,14 or galvanic replacement applied to nobel metal NCs,^2,15 we investigate in this study the core/shell growth driven by cationic exchange.^16,17 The replacement of Pb by Cd is achieved by adding an excess of Cd oleate to the PbX NC suspension resulting in a well-defined CdX shell around the PbX core as it was shown for PbSe,¹⁸PbTe,¹⁹ and PbS.^18,20,21

Recently it has been shown that especially PbS/CdS core–shell NCs show strongly enhanced photoluminescence (PL) quantum yield as compared to pure PbS NCs, whereas the passivating hard protective CdS shell allows additionally the PbS/CdS NCs to be stabilized in water²² or to be encapsulated in an amorphous glass matrix.²³ The PbS/CdS NCs also show a higher efficiency and stability within photodetectors²⁴ and within solar cells.²⁵ The maximum quantum yield was found for a thin layer of around 0.7 nm and is reduced again for shell thicknesses exceeding 2 nm.²² This was explained by defect formation caused by the 2% lattice mismatch between the rock salt (RS) crystal structure of the core and zinc blende (ZB) structure of the shell.^18,22

In this study, we investigate the cationic exchange process for three different initial PbS NC diameters of 4.7 nm (small), 6.3 nm (medium), and 8.7 nm (large), resulting in three different final CdS shell thicknesses t_shell of 0.9, 1.5, and 2 nm after maximum exchange time. The chemical composition profiles of the individual core/shell NC ensembles as a function of reaction time are derived from anomalous small-angle X-ray scattering (ASAXS) using synchrotron radiation. The crystalline structure of the NCs is retrieved from X-ray diffraction (XRD) experiments combined with transmission electron microscopy (TEM) analysis. We relate this received chemical and structural information to the measured PL intensities of the core/shell NCs to probe if the crystal structure of CdS-shell affects the optical properties.

Experimental Section

Pristine PbS nanocrystals (NCs) were prepared according to the method proposed by Hines and Scholes.²⁶ Briefly, in a typical synthesis of 9 nm PbS nanocrystals, PbO (0.45 g), oleic acid (OA, 10 mL), and 1-octadecene (ODE, 10 mL) were loaded in a three-neck flask and heated up to 110 °C under vacuum. During this time, Pb oleate is formed, indicated by the discoloration of the reaction mixture. Then, the reaction flask was backfilled with Ar, and the temperature was increased to 150 °C. At 150 °C, the injection mixture, containing 0.21 mL of hexamethyldisil-thiane and 10 mL of anhydrous ODE, was injected, after which the temperature dropped to about 130 °C. The reaction flask was allowed to cool down to 100 °C within 3 min. The temperature of 100 °C was kept for another 5 min before quenching the reaction by means of a water bath. Samples were washed by a 1:1 hexane/ethanol mixture three times and redispersed in hexane. Smaller sizes of PbS nanocrystals were prepared by decreasing the amount of oleic acid, while keeping a constant total volume of the solution.

The PbS/CdS core/shell NCs were synthesized following the method of Pietryga et al.¹⁸ A PbS NC solution, containing 90 mg PbS NCs, was dried, and NCs were redispersed in 5 mL of anhydrous OA. After the PbS/OA solution was heated to 80 °C, 20 mL of 0.4 M Cd oleate solution in anhydrous diphenylether was added. The reaction temperature was kept constant and after several time step aliquots were taken, which were cooled rapidly to room temperature. These samples were washed and dissolved again in toluene or hexane with a concentration of 1–2 wt %. Alternatively, the Cd oleate solution (0.4M, 20 mL) was added every hour, which provided thicker CdS shells at shorter reaction times. This method was applied to the growth of the large core/shell NCs, whereas for the growth of the medium and small NCs only in the beginning of the cationic exchange process was a sufficiently large amount of Cd oleatic solution added. The Cd solution was prepared as described in ref (18).

A JEOL 2011 FasTEM transmission electron microscope (TEM) operated at an acceleration voltage of 200 kV was used to obtain high resolution TEM images. The direct electron beam intensity used for the imaging mode was detected by a CCD camera. The TEM images were created and analyzed by a supplementary Digital Micrograph software package. TEM image contrast differences can be created by many types of amplitude and phase contrasts.²⁷ In this work, the darkfield images were created by using the diffraction contrast method, where either the rock salt Bragg peaks or the zinc blende peaks alone were used to create the TEM image.

The excitation source for the photoluminescence (PL) measurements was a Spectra Physics continuous wave argon-ion laser, model 163A 5216, emitting at a wavelength of 514 nm. The maximum emission power of 50 mW was utilized for the experiments. The exciting beam was chopped by a chopper wheel and focused on the cuvettes containing the NCs in solution. The photoluminescence (PL) was collected by two CaF₂ lenses and spectrally resolved by an Acton Research Corporation Spectra Pro 150 monochromator. The monochromatic light was detected by a nitrogen cooled Judson J10-M204-R10 M InSb photodiode. This signal was amplified with a Judson PA-7 preamplifier and a Stanford Research System SR510 lock-in amplifier, which used the excitation source chopper frequency as a reference. A self-written program running on a personal computer operated the monochromator over the desired spectral range and evaluated the amplified signals at the different wavelengths to obtain the photoluminescence spectra. To quantify the luminescence enhancement, the optical density of all samples was adjusted to have the same value at a wavelength of 500 nm.

The contrast variation in anomalous small-angle X-ray scattering (ASAXS) is due to the energy dependency of the atomic scattering factor f(Z,E) in the vicinity of X-ray absorption edges, where E is the X-ray energy and Z the atomic number. It can be shown²⁸⁻³⁰ that the total measured intensity is composed of a nonresonant and a resonant scattering contribution. The nonresonant scattering term depends only on the total electron density within a material and is related to the overall elementary composition and the bulk density, whereas the resonant scattering term depends on E. Thus, the total amplitude deviates significantly from the atomic number Z by varying the energy around an elemental absorption edge. By tuning the X-ray energy just below the Pb-L_III-edge at E = 13.035 keV, the contribution of Pb as the strongest scatterer with Z = 82e^– to the total scattering amplitude f(Z,E) and hence to the total scattering intensity I(q,E) can be varied significantly. Hence, for ASAXS experiments synchrotron X-ray sources have to be used where the X-ray energy can be continuously varied. The ASAXS spectra for the large and small sample series have been measured at the 7T-MPW-SAXS beamline at the BESSY II synchrotron (HZB Berlin, Germany), whereas the medium sized NCs have been recorded at the beamline ID01 at the European Synchrotron Radiation Facility ESRF (Grenoble, France).

In ASAXS the scattered intensity is a function of the scattering vector q and the X-ray energy E, with q = 4π sin θ/λ and λ the X-ray wavelength. For a minimum set of three scattering curves measured at different energies the Pb-electron density and the total electron density within the core and the shell can be derived independently. This is achieved by applying a unique spherical core/shell model to fit up to five different scattering curves. All scattering curves have been calibrated into absolute units (i.e., macroscopic scattering cross sections in units of cross-section per unit volume cm²/cm³ = cm^–1). For all energies the scattering of the solvents toluene and hexane was measured with the same statistical accuracy and was removed from the scattering curves of the sample before applying the fitting procedure. By varying randomly the scattering data within the experimental error band and repeating the fitting procedures up to 20 times, the stability of our results is tested and the errorbars for the density profiles are obtained.

The Rutherford Backscattering Spectrometry (RBS) method is based on elastic collisions between light, energetic ions (H, He with a few hundred keV up to 2 MeV) and the atomic nuclei in a stationary sample. Thus, the method is free from any matrix effects. Scattering kinematics permits the elements present in a thin layer to be identified from the yield of particles backscattered from the sample in a large angle. RBS measurements were performed, employing the Van de Graaff accelerator AN700 (30–700 keV).³¹ The low beam currents employed guarantee a nondestructive analysis of the samples. Scattered ions were detected by two semiconductor surface barrier detectors. The Monte Carlo program SIMNRA³² was used to evaluate the sample compositions by fitting the peaks corresponding to the individual elements in the measured spectra.

X-ray diffraction (XRD) experiments in transmission geometry were performed with the Nanostar instrument from Bruker AXS, in the wide-angle X-ray scattering (WAXS) configuration with a sample to detector distance of 6 cm. This allows diffraction peaks up to a 2Θ angle of around 44° to be recorded with the Cu–Kα X-ray wavelength of 1.5418 Å. Twelve of the 14 individual NC ensembles used for the ASAXS experiments were measured sealed in quartz-glass capillaries of 1.5 mm diameter. The 2D detector (Bruker HiStar) images showed X-ray diffraction powder rings, and thus for the data analysis line scans were extracted from the 2D images by azimuthal integration. For further analysis of the peak width Δq the detector resolution of this setup was determined using the peak widths of a diffraction standard (Al2O3-powder). From the Δq-value we derive directly D as a measure for the crystalline diameter using the Scherrer formula D = K·2π/Δq with a K-value close to one for the NCs without a shell.³³ These values are only 10% to 20% smaller as compared to ASAXS, which can be related to an additional peak broadening due to imperfections in the crystal structure.

Results and Discussion

Cation Exchange to Realize PbS/CdS Core/Shell Nanocrystals

We modified the previously reported method for the synthesis of PbS/CdS NCs.¹⁸ In particular, we applied multiple injections of the cadmium precursor, which leads to a faster CdS shell growth and consequently to shorter growth times. After heating the PbS NC solution in toluene up to 80 °C, Cd–oleatic acid was injected. Aliquots were taken after defined time steps as shown in the reaction scheme in Figure 1a. The shell formation for the large core/shell NCs was proven by high resolution TEM (HR-TEM) studies. In Figure 1b the structure of one single PbS/CdS NC is shown after 3 h of exchange time, where the core (indicated by a red dashed line) depicts different lattice spacings as compared to the shell region. For the core with about 7 nm diameter we derive the rock salt (RS) crystal structure (Fm3m), whereas within the ∼1 nm shell the lattice plane configuration indicates the zinc blende (ZB) structure (F43m). These two crystalline phases are also visible in dark field HRTEM images, where either the RS or the ZB electron diffraction peaks were used for highlighting the corresponding crystalline phase within HR-TEM images (see Figure S1, Supporting Information). From the aliquot samples PL spectra were recorded and compared to that of the pure PbS NCs (see Figure 1c). The peak maximum at around 1800 nm is increased by a factor of 4 for the samples after 1 and 2 h reaction time, but after 3 h this enhancement in the peak maximum is again slightly decreased. The resolution of our TEM analysis, however, did not allow differences to be revealed in the thickness or the composition of the CdS shells between 1 and 3 h exchange time. Furthermore, TEM analysis alone is restricted to a small sample set of NCs (typically around 100 individual NCs) deposited on a flat substrate, but the PL spectra are produced by a large ensemble of individual NCs in solution. As complementary methods we have chosen X-ray scattering techniques that allow mean structural parameters of a large ensemble of NCs with subnanometer resolution to be determined. The scattering experiments were directly performed on the NC solutions sealed in glass capillaries of 1.5 mm diameter resulting in NC ensembles of ∼10¹² individual particles probed during one single X-ray measurement. Therefore, we can probe in detail the influence of the mean structural and compositional core/shell parameters of the NCs on their optical output. This analysis was done for the three samples series (large, medium, and small) with initial particle diameters from 9 to 5 nm at various reaction time steps, resulting in 14 different NC ensembles.

Figure 1.

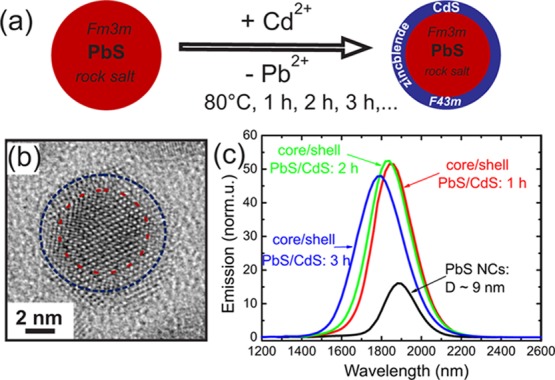
(a) Scheme of the synthesis of PbS/CdS core/shell nanocrystals driven by cationic Cd for Pb exchange starting with pure PbS NCs (red sphere) in the rock salt crystal phase and resulting in core/shell particle with the same diameter, but surrounded by a CdS shell (blue). (b) High resolution TEM image of a single 9 nm sized core/shell NC after 3 h of exchange time, where the dashed circles indicate the PbS core (red) and the CdS shell region (blue). (c) PL spectra of large sized PbS and PbS/CdS NCs with diameters D of around 9 nm, measured after different reaction time steps.

Mean Chemical Core/Shell Profiles Derived by ASAXS

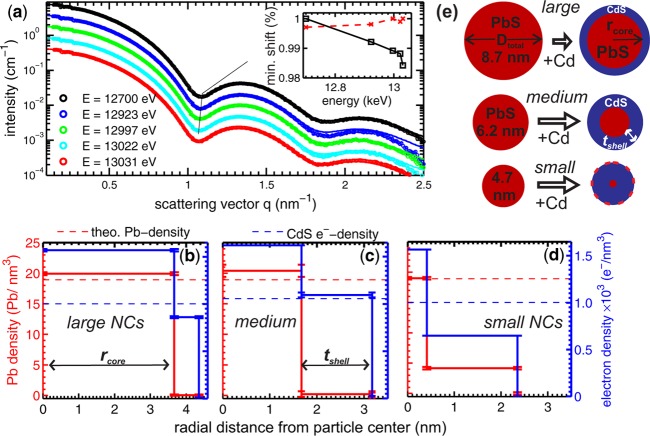
Small angle X-ray scattering (SAXS) is a method widely used in the analysis of nanoscale structures.³⁴ An extension of SAXS, ASAXS²⁸⁻³⁰ allows element specific contrast variation³⁵ and hence the possibility to determine the chemical compositions of the core and the shell of a macroscopic ensemble of NCs. The contrast variation in ASAXS is due to the energy dependency of the atomic scattering factor f(Z,E) in the vicinity of X-ray absorption edges. From a minimum set of three ASAXS patterns measured at different energies we can separate independently the total electron density from the Pb-electron density inside the core/shell NCs. This was achieved by applying a step-like spherical core/shell model to fit all scattering curves (see the section Methods and the Supporting Information for a detailed description of the ASAXS method). In Figure 2a the experimental scattering curves are shown together with the model fits for the large core/shell NCs measured after 1 h of exchange time. All five curves were fitted with the same unique spherical core/shell model with the following fitting parameter: The inner radius r_core, the shell thickness t_shell, the Pb density, and the total electron density in the core and the shell, as well as the total size distribution σ of the spherical core/shell NCs (σ is assumed to be equal for the core and the shell). The accordance between data and fit is generally excellent; small deviations are only visible at large q-values, where the error band of the scattering data is getting larger due to statistics. To illustrate the energy dependent effect, the position in q of the first minimum in the ASAXS curves (see Figure 2a) is plotted over E in the inset. The resonant shift is in the range of ∼2%, whereas the reference minimum-position of Pb NCs without CdS-shell (dashed red line) is constant within 0.3%. This shift can be directly related to a difference in the Pb electron densities between core and shell.

Figure 2.

(a) Experimental ASAXS curves (symbols) fitted with a unique spherical core/shell model (lines) for the large core/shell PbS/CdS NC-sample after 1 h of reaction time. The absolute intensity I(q,E) plotted over the scattering vector q was recorded at five different X-ray energies below the Pb-L_III-edge. The curves, except the black one, are shifted vertically by a factor of 2 for clarity. Inset: The squares show the shift in q of the first minimum in the ASAXS curve as a function of E, whereas the red dashed line shows the position of the pure PbS NC as reference. In (b), (c), and (d) the resulting density profiles for the large, medium, and small sized PbS/CdS samples are depicted. The Pb-density (red line) is plotted on the left axis and the total electron density (blue line) on the right axis as a function of the distance from the particle center. (e) Scheme of the final shell formation for all three initial particle sizes, i.e., large, medium, and small, after maximum exchange time.

The received structural parameters from Figure 2a result in the density profile shown in Figure 2b. The red line depicting the Pb-density (left axis) gives a value of 19.9 ± 0.25 Pb-atoms/nm³ within the core with a diameter of 7.34 ± 0.03 nm (r_core = 3.67 nm). This is close to the theoretical value of 18.9 Pb/nm³ for PbS. Also the total electron density shown on the right axis in Figure 2b with 1568 ± 13 e^–/nm³ matches the expected value of 1566 e^–/nm³ for PbS. No Pb can be traced in the 0.69 nm shell, whereas the e^–-density reaches 86% of that expected for bulk CdS in the ZB crystal phase. This slight discrepancy can be related to a small deviation of the NC from the spherical shape due to surface roughness or facetting, which is not included in our model. From the composition profile we can conclude, however, on an atomically sharp interface between PbS-core and a pure CdS-shell as was already reported for the PbX/CdX core/shell systems.^18,19,21

A similarly well-defined but much thicker CdS-shell is formed around the medium sized PbS-NCs as shown in Figure 2c. This density profile is derived from measurements and fits shown in Figure S2a in the Supporting Information. We start from pure PbS NCs with an initial diameter of around 6 nm applying a similar synthesis procedure as for the large core/shell NCs. Here we took more samples at times even below 1 h reaction time and we monitored the shell growth up to 18 h. Within a total diameter D_total of 6.2 nm a 3.4 nm diameter PbS-core is formed surrounded by a 1.5 nm thick CdS-shell. The Pb-density (red line) and the total e^–-density (blue line) of the core meet quite closely the expected values for PbS, and the electron density of the shell that for CdS, respectively. Again no Pb can be detected in the shell.

A different profile results from the ASAXS data of the small PbS NCs (see Figure S2b, Supporting Information) with initial 5 nm size as shown in Figure 2d. In the core/shell NCs with a D_total of 4.7 nm only a 0.8 ± 0.05 nm PbS-core remains, whereas a 1.9 ± 0.02 nm thick shell is formed containing 4.5 ± 0.25 Pb/nm³ within the CdS shell. This would correspond to ∼24% of Pb within a ternary alloy of Cd_1–xPb_xS. The e^–-density of the shell, however, reaches only 65% of the value for pure CdS (blue line in Figure 2d). The low total shell electron density is a strong indication that no Cd_1–xPb_xS alloy is formed, because such a ternary compound should have a significantly larger density value with respect to pure CdS and not a lower one. A similar amount of Pb is detectable for all small NC samples taken at different time steps during the Pb²⁺ ⇒ Cd²⁺ exchange up to 29 h reaction time. In our simple core/shell model we can not unambiguously determine where exactly the detected Pb is located within the shell to give the observed result. Two extreme Pb positions within the shell are possible: (i) The Pb can be located close to the remaining PbS-core, or (ii) the Pb-atoms can be bound on top of the CdS shell surface forming an additional Pb-surface shell. The last scenario (ii) may be related to the proposed growth mechanism for a cationic shell growth thicker than one monolayer:³⁶ The Pb²⁺ ions have to diffuse toward the particle surface, where they are subsequently exchanged by the Cd²⁺ ions of the Cd–oleatic compound within the solution (see more details in the Supporting Information and in ref (36)). If this last reaction step is not fully completed, e.g., due to a too low Cd–oleate concentration, a submonolayer (ML) of Pb-atoms should remain on the surface. The 4.5 Pb/nm³ found within the CdS shell would correspond to an ∼75% ML-coverage of Pb on top of the CdS shell. Thus, an additional second surface shell with a reduced electron density should be detectable with a thickness in the range of two times the ionic radius of Pb with 0.133 nm³⁷ and the [111]-ML thickness of PbS of around 0.34 nm. Analyzing the data with an extended model consisting of three density steps, i.e., a core plus two shells, the fit at a fixed X-ray energy gives indeed a surface shell with 0.38 nm thickness and a reduced electron density of around 800 e^–/nm³. Moreover, the derived e^–-density value of the thick intermediate CdS-shell of 1.5 nm thickness matches now to 96% of the CdS value (see Figure S3, Supporting Information).

The alternative model (i), where the total Pb amount in the small core/shell NCs is concentrated close to the particle center, would require a PbS-core with nearly 3 nm diameter. The simulated data using this large PbS core compared to the experimental SAXS data shows, however, that the model (i) for the Pb-distribution can be ruled out (see Figure S3a, Supporting Information). Thus, our detailed SAXS analysis suggests that the small core/shell NCs are surrounded by a second surface shell consisting of a sub-ML of Pb atoms remaining after a not fully completed Cd for Pb exchange (see Figure S3d, Supporting Information).

To test the reliability of the retrieved Pb-density distributions, we calculate from these core/shell profiles the total Pb-concentrations within the NCs. We compare these values with the Pb concentrations that are derived from an independent method, which is not sensitive to the internal Pb-distribution. For this purpose, the elementary ratio of Pb:Cd:S was probed by Rutherford backscattering spectroscopy (RBS)³⁸ for all investigated large and small PbS/CdS NCs (summarized in Table S1, see Supporting Information). The amounts of Pb derived from both methods, RBS and ASAXS, are in very good agreement as can be seen in Figure 3d, where the Pb-concentration is plotted as a function of the exchange time. The small core/shell NCs contain a large amount of Cd and only a small amount of Pb in the range of 13 atom % to 18 atom %, which is in good accordance with a profile with a thick CdS shell, a small PbS core, and some remaining surface Pb atoms. It can bee seen for all three sample series that the total Pb amount decreases while the CdS-shell increases and remains constant when the maximum shell thickness is reached, corresponding to a decreasing PbS core during the Cd for Pb exchange. In Figure 2e we summarize schematically the final core/shell parameters as obtained from ASAXS for all three sample series. A clear trend is visible: The CdS shell increases and hence the PbS cores decrease with decreasing initial PbS-NC diameter. The shrinkage of the PbS core is also reflected in a shift of the peak wavelength in the PL spectra to shorter wavelengths³⁹ (see Figure 1c and Figure S5, Supporting Information). A detailed investigation of the peak shift as a function of the core diameter and of the CdS shell thickness is presented in the Supporting Information and shown in Figure S6.

Figure 3.

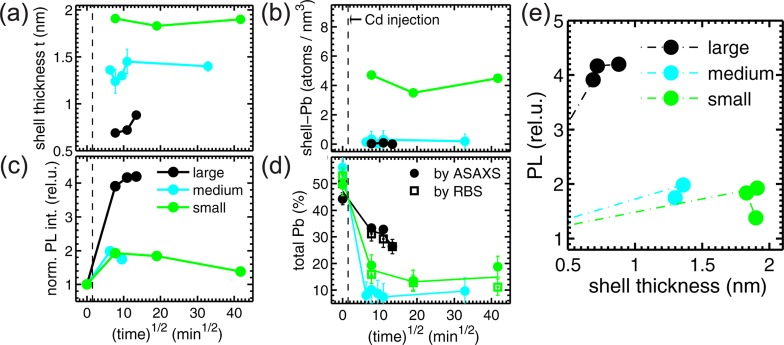
(a) CdS-shell thickness t_shell vs exchange time^1/2 for the large (black), medium (cyan), and small (green) core/shell NCs. (The time^1/2 representation has been chosen primarily for practical reasons). In (b) the time dependence of the Pb amount within the shell is shown, whereas in (c) the normalized integrated PL emission of the NCs vs time is depicted. (d) The total Pb-amount within all NCs derived from the ASAXS profiles (full circles) together with the RBS values (open squares) are shown over the exchange time. The full lines are only guides to the eyes. (e) The integrated PL emission normalized to the values of the pure PbS NCs is plotted over the CdS-shell thickness.

Exchange Time Dependence of the Core/Shell Profiles and the Photoluminescence

Additional important conclusions can be drawn from the time dependence of the core/shell structural parameters, when relating them to the optical performance of the large, medium, and small NCs. In Figure 3a the time evolution of the CdS-shell thickness t_shell is plotted over the square root of the exchange time in minutes to cover the whole range of the investigated time steps, starting from 20 min up to 29 h. The values at growth time zero originate from the pure starting PbS-NCs. The initial diameter and the total core/shell diameter D_total remains constant within the error bars during the cationic exchange process that means the CdS-shell increases with the same rate as the PbS-core shrinks.^18,23 The large CdS-shell of the small NCs (green symbols) is already fully formed after 60 min exchange time and remains quite constant up to the maximum growth time of 29 h. For the medium sized NCs (cyan symbols) we can observe between 40 and 120 min after Cd-injection small variations in the t_shell-value, whereas after 2 h the final shell thickness of ∼1.5 nm is reached. For the large NCs (black symbols) the CdS-shell increases from 0.7 nm up to 0.9 nm after 3 h. Whether this is already the final shell thickness cannot be answered here, since no data above 3 h are available.

No significant increase in the total size distribution as reported for PbTe/CdTe core/shell NCs¹⁹ is found during the whole exchange time. The initial size distributions of 12%, 14%, and 15% for the large, medium, and small NCs is found to be constant within 1%.

Over the whole time series no Pb can be traced within the CdS-shells of the large and medium sized core/shell NCs (black and cyan symbols in Figure 3b), whereas the amount of Pb on top of the thick CdS shell of the small NCs (green symbols) varies between 3.5 ± 0.2 and 4.7 ± 0.3 Pb-atoms/nm³. The Pb-amount within the PbS-core is found to be also constant within 0.7 Pb/nm³ around the theoretical value for rock salt PbS of 18.9 Pb/nm³ for all three sample series.

In Figure 3c we depict the PL emission of all three sample series also as a function of the exchange time and can thus relate the optical performance of the core/chell NCs to their different structural and chemical compositions. The integral PL emission is derived from the total area under the PL emission spectra with peak wavelengths between 1200 and 1900 nm increasing from the small to the large NC samples (see Figure 1c and Figure S5, Supporting Information). The integral intensity values are all normalized to one at the corresponding value of the initial pure PbS NCs. The strongest relative increase in the normalized PL, and hence the relative increase in the quantum yield, is observed for the thin shell growth around the large PbS/CdS NCs. The intensity is enhanced by a factor of over 4 with respect to the pure PbS NCs sample. After the strong enhancement after 1 h growth time the further increase after 2 h is moderate and constant after 3 h, although the CdS-shell increases in the last growth step from 0.7 to 0.9 nm (black symbols).

The medium and small core/shell NCs reveal a smaller enhancement of the PL by a factor of ∼2, but only after short growth times (cyan and green symbols). For both series in the further reaction time steps a decrease in the PL and hence in the quantum yield can be observed. This decrease cannot be directly related to a pronounced change in the chemical composition profile of the core/shell NCs as shown in Figure 3a,b,d, where only small variations in the shell thickness are visible. This effect is better visualized in Figure 3e, where the integrated PL intensity is plotted as a function of the shell thickness t_shell, where initially an increase of the PL-enhancement with growing shell thickness can be observed. After this initial increase, however, the relative PL intensity levels off and even decreases from a maximum PL value with longer exchange times.

Metastable Crystal Phase in the CdS Shell Revealed by X-ray Diffraction

Since there is no evidence for a compositional origin of this unexpected optical behavior, we have additionally investigated the crystal structure of the core/shell NCs by recording powder X-ray diffraction patterns. In Figure 4a the diffraction patterns of the large, medium, and small initial PbS NCs are shown together with their fits using Gaussian peak shapes on top of a linear background. The vertical dashed lines mark the positions of the Bragg peaks for rock salt (RS) PbS (a_PbS = 5.936 Å) and zinc blende (ZB) CdS (a_CdS = 5.818 Å) bulk structures. The peak positions for the pure PbS NCs matches very well the theoretical values indicating that the NCs are fully relaxed. From the fits we derive the peak maximum value, the center position, the full width half-maximum, and the area under the peaks giving the integrated crystal peak intensity I_int.

Figure 4.

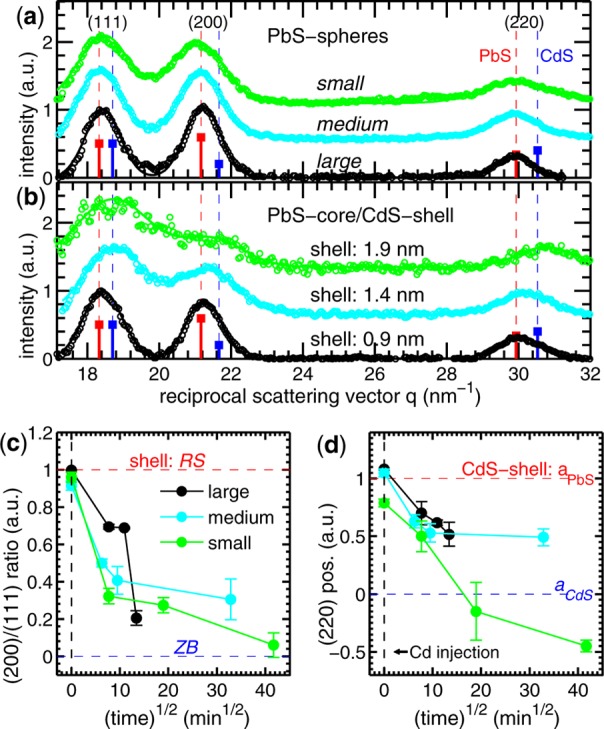
(a) Experimental diffraction pattern of the large, medium, and small initial PbS NCs are shown (open circles) together with their fits (lines). The vertical dashed lines mark the positions of the Bragg peaks for rock salt (RS) PbS and zinc blende (ZB) CdS bulk structures. (b) The XRD pattern for PbS/CdS core/shell NCs after maximum exchange time. In (c) the ratio between the integrated peak intensity of the (200) and (111) diffraction peaks is shown over the exchange time, in (d) the position in q of the (220) peak maximum.

An interpretation of the core/shell diffraction patterns shown in Figure 4b cannot be done in a straightforward manner due to the strong overlapping of two broad peaks related to the small lattice constant difference of ∼2% between PbS and CdS. One can observe, however, directly a change in the peak intensity ratio between the (111) and the (200) peak, as well as a shift in the peak position toward the CdS bulk position. These effects are most pronounced for the medium and small core/shell samples, where the diffracted intensity mainly originates from the thick CdS shells (see Figure 4b). The intensity ratio change can be interpreted in terms of a change in the crystals structure from rocksalt to zinc blende, because the ZB structure of bulk CdS depicts a strongly reduced (200) Bragg peak with respect to the RS structure of PbS (blue and red squares in Figure 4a,b). The shift of the peak positions, especially that of the (220) Bragg peak, where we are most sensitive to changes in the lattice spacings, can be caused by both a different crystal phase and strain effects.

The assumption of a metastable RS phase fraction in the CdS shell is motivated by the fact that due to cationic exchange in NCs the chemically new compound can preserve the crystal structure of the starting NC.⁴⁰ In our case the CdS shell should keep to a certain extent the RS structure of the PbS core. We aim in this study to retrieve the quantitative amount of the RS–ZB phase ratio within the shell as a function of the exchange time and the shell thickness. For this we calculate the individual diffraction patterns for all pure PbS NCs and the PbS/CdS NCs by means of the Debeye formula^33,41 using the individual chemical composition data for 12 different sample sets as retrieved from ASAXS (see the Supporting Information for a detailed description). We assume for the PbS core always a pure RS structure, but for the CdS-shell either the RS or the ZB structure. Fitting the simulated diffraction data with the same procedure as the experimental data (see Figures S8–S10, Supporting Information) we retrieve for each single chemical composition the theoretical intensity ratio and peak shift for the CdS shell being either 100% in the RS (red dashed lines in Figure 4c,d) or 100% in the ZB phase (blue dashed lines). This allows the relative amount of the two crystalline phases within the CdS shell to be determined, where a value of one means pure RS-phase and a value of zero a pure ZB-phase, respectively. In Figure 4c the (200)/(100) intensity ratio of all samples and hence a measure for the RS–ZB phase fractions is shown over the exchange time. The reliability of our model is reflected by the values for the pure RS PbS NCs (black dashed line) in the range between 0.95 and 1. For the large core/shell NCs (black symbols) the peak intensity ratio for the two slightly thinner CdS shells formed after 1 and 2 h gives values of around 0.70. After 3 h the signal drops, however, significantly to a lower value corresponding to ∼20% of a remaining RS phase.

A similar behavior, decreasing amount of the RS phase with exchange time, is visible for the medium (cyan symbols) and small (green symbols) sized core/shell samples, but here already the first formed shells depict a significantly lower amount of CdS in the RS phase. The shell of the medium sized NCs with 1.4 nm thickness exhibits 50% of RS phase fraction, whereas the nearly 2 nm shell of the small NCs contains only 30% of this metastable phase. Furthermore, only the 2 nm thick CdS shell reaches the ZB phase finally after 29 h of exchange time, whereas the medium sized NCs keep within their shell 30% of the metastable RS crystal phase.

The same trend is also reflected in the shift of the (220) Bragg peak depicted in Figure 4d. The CdS shells of the large NCs show a quite linear shift from the PbS lattice constant to the CdS value, whereas the shell lattice constant in the medium sized core/shell NCs finally seems to remain constant in the middle between PbS and CdS. Both sample series are chemically stable during the growth time as derived from the ASAXS profiles, so the peak shift can be related to different crystalline phases within the shell. To conclude from the lattice constant values alone on the amount of crystalline phases within the shell is not unambiguous, due to the fact that the lattice spacing can be altered by strain. This is reflected in the lattice constant values of the small sample series, where after maximum exchange time the lattice constant of the shell is even smaller than that of the bulk CdS value. This can be explained by a compressive strain caused by a surface relaxation due to the high surface/volume ratio for the small sized NCs. This can be already seen for the small pure PbS NCs depicting a 0.4% smaller lattice constant with respect to the bulk PbS value. The lattice spacing for the 2 nm thick CdS shell after the longest growth time is even 0.9% smaller. This effect was already reported for ZnS nanocrystals,⁴² where the magnitude of the compressive strain for 5 nm nanocrystals is in the same order of magnitude.

The different crystal structures, the RS and ZB-phase, can be realized by keeping the anionic S position in both lattice types constant, whereas only the positions of the cations differ. The Pb-ions in the RS structure have six nearest neighbors and occupy a face-centered-cubic (fcc) sublattice displaced by (1/2, 1/2, 1/2) of the cubic lattice constant a_PbS. The more covalent bound Cd ions are fourfold coordinated, which occupy fcc positions that are displaced by (1/4, 1/4, 1,4)a_CdS (see Figure 5a). Hence, we explain the appearance of the metastable RS structure within the shell by a fast Cd for Pb exchange process, where the Cd cations occupy in the beginning the same lattice positions as the expelled RS core Pb-ions. The change from this metastable RS phase to the ZB-phase is caused by a subsequent Cd-ion transition to their equilibrium positions within the ZB lattice, whereas the anionic S-sublattice in both crystal structures is unchanged. Such a stable anionic sublattice was recently found for the homogeneous cationic exchange in CdSe NCs.⁴⁰ A continuous anionic sublattice between the RS and the ZB structure is also identified by HR-TEM and verified by ab initio simulations for PbTe quantum dots embedded in a CdTe matrix.⁴³

Figure 5.

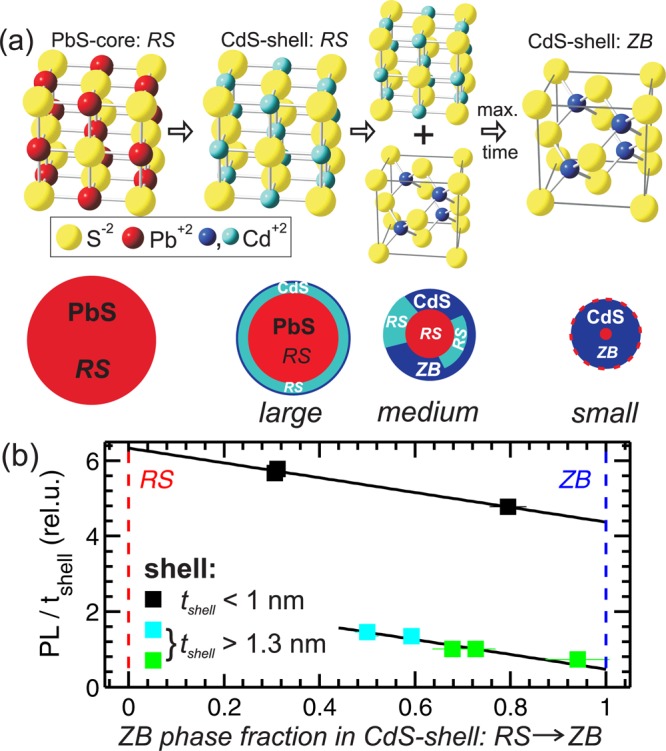
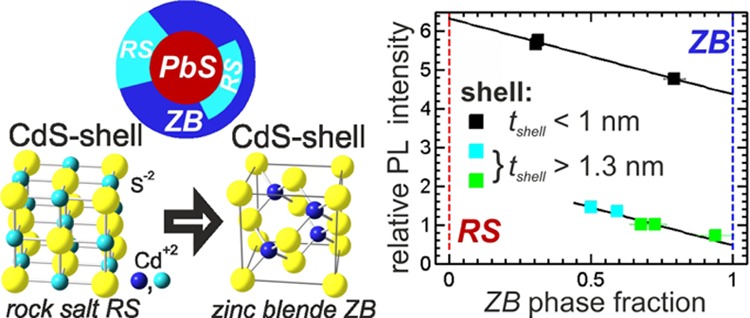
(a) Scheme of the crystals phases of CdS occurring during the cationic Cd for Pb exchange. First the CdS-shell mimics nearly fully the core rock salt (RS) structure of PbS, and later both the RS (cyan) and the equilibrium zinc blende (ZB) phase (blue) of CdS can be found within the shell. These transitions are figuratively shown in the sketch below. The indicated distribution of the metastable RS phases within the shell is only a suggestion. (b) Integrated PL intensity normalized to the CdS layer thickness plotted over the ZB phase fraction within the shell.

The Cd structural transition starts to a certain extent directly after the Cd for Pb exchange; the full rearrangement of the Cd-ions in the ZB structure, however, takes up to 30 h at a temperature of 80 °C as can be deduced from Figure 4c,d. We could not observe any change of the phase fractions with time after cooling the samples to room temperature. The proposed scheme is sketched in Figure 5a, where it is also indicated that the highest amount of RS-phase is found for the thinnest CdS shell, i.e., for the largest initial sphere diameter. The influence of the shell thickness on the RS phase fraction is shown by comparing RS phase fraction values at 1 h exchange time. We found values of 70%, 50%, and 30% for the RS phase for the large, medium, and small NCs, respectively (see Figure 4c). We expect that these amounts of metastable crystal phases are not homogeneously distributed along all crystallographic directions, but our current XRD data do not allow preferred crystallographic directions to be identified, in which this metastable phase is enriched. An additional indication for the coexistence of the ZB and RS phases within one single shell is found in the dark field HRTEM images of a large core/shell NC after 3 h of exchange time. In Figure S1d,e (Supporting Information) either the RS or the ZB electron diffraction peaks are used for highlighting the corresponding crystal phase. The bright RS core phase in Figure S1d extends in the shell region, whereas in Figure S1e the bright ZB phase depicts an inhomogeneous distribution within the shell. This suggests that both phases coexist within a single CdS-shell. This kind of polytypism of crystal phases within one shell was also found for shells grown epitaxial on top of the core.^44,45

The driving force for the thickness dependence of the amount of the RS phase fraction can be related to the strain energy built up within the CdS-shell due to the lattice mismatch of around 2% between PbS and CdS. This lattice misfit creates a tensile strain in the CdS shell.

The piled up tensile strain with increasing number of MLs of the thicker shells can be fast relaxed by creating stacking faults^46,47 that can trigger the transition from the RS to the ZB crystal structure. The relation between phase fraction and shell strain is summarized in Figure S11 (Supporting Information). These defects in the shell should be reflected in a reduced PL emission due to a partial extension of the exciton wave function into the shell material.¹³ Indeed, the core/shell NCs with medium and thick shells depict only half of the PL increase with respect to the thin-shell samples.

Influence of the Metastable Phase on the Photoluminescence

To investigate only the influence of the RS-ZB phase fraction on the PL we relate in Figure 5b the ratio of the RS to the ZB phase to the normalized PL emission values. Here, the PL intensity values of the samples are additionally normalized to the individual shell thickness values.

Two distinct features are visible: A decrease of the PL with decreasing RS phase fraction is visible for all three samples series. Additionally, a pronounced jump in the relative PL increase between the large samples with shells below 1 nm and the medium and small NCs with shells above 1.3 nm is visible. These thick-shell samples depict more than three times lower relative PL values as the thin-shell samples compared at the same phase fraction value of around 0.5. The slope of the decrease, however, is constant for all three sample series. This is demonstrated by the two black lines in Figure 5b having the same slope as derived from a linear fit to the data of the thin-shell samples only. Within the three thin-shell samples the metastable RS phase fraction changes from 70% to 20% while the relative PL is decreased by around 16%. The thick-shell samples start already with 75% decreased relative PL value at 50% RS phase fraction and reach only 10% of the initially relative PL increase.

These experimental findings suggest that two different mechanisms are involved to mediate the transition from the metastable RS phase to the equilibrium ZB structure of the CdS shell. One mechanism for transitions between fourfold and sixfold coordinated crystal structures was reported for NCs^46,47 that implies a collective sliding of crystal planes accompanied by the creation of stacking folds. This martensitic-like phase transition from a fourfold to a sixfold phase is induced by high external applied pressures.

In contrast, in our PbS/CdS core/shell NCs the sliding of the Cd-sublattice planes from the sixfold RS phase to the fourfold ZB structure, i.e., in the reverse direction, is driven by the tensile stress within the CdS shell. During this phase transition the strain within the CdS shell is relaxed. An alternative transition-path mechanism can avoid the creation of stacking faults but is based on the uniaxial compression of crystal planes and results in an increase of the surface energy.^48,49 In theoretical studies by Grünwald et al.^49,50 it was shown that the fourfold to a sixfold phase transition starts via the compression path mechanism nucleating on the crystal surface and is continued by the sliding plane mechanism, but depending on the size and surface structure also a mixture of both is possible.⁴⁹ Moreover, very recently it was shown by the same group that the transformation mechanisms for metastable phases within core/shell NCs depends strongly on the shell thickness.⁵¹ For shells below 3 MLs thickness only the surface nucleation mechanism was observed.

Taking these studies into account we interpret our observations summarized in Figure 5b as follows: For the thin-shell samples the transformation between the metastable RS phase and the ZB phase, and hence the relaxation of the shell-strain, is realized by the surface nucleation mechanism, which results in an only moderate decrease of the PL due to surface defects. For the thick-shell samples the initial transformation proceeds via the sliding plane mechanism resulting in stacking faults that considerably decrease the PL intensity. Due to the stacking fault formation, thin shell layers below 3 MLs are created, in which the compression mechanism mediates a further RS to ZB phase transition with reduced influence on the PL. The physical origin of this pronounced influence of the shell on the PL intensity is related to the delocalization of charge carriers over the whole core/shell volume.^13,22

Conclusions

In conclusion, we have demonstrated that, during the CdS shell growth around PbS nanocrystals due to a Cd for Pb cationic exchange, the shell initially maintains the metastable rock salt crystal structure of the core within a chemically pure CdS shell. Such a metastable phase within a core/shell system, which does not occur in the bulk material under ambient pressure, was quite recently theoretically predicted.⁵¹ For the first time we have determined the quantitative amount of the metastable phase in the shell as a function of the exchange time and the shell thickness. Moreover, the core/shell NCs show a pronounced PL enhancement after the CdS shell formation with the PL showing a clear dependence on the RS/ZB phase fraction: It decreases with decreasing RS phase and increasing ZB structure. This revealed correlation is related to the formation of lattice distortions during the phase transitions. The control of this metastable phase within the shell to optimize the core/shell interface will have significant impact on tailoring the optical properties of core/shell NCs also in related material systems.

Supporting Information Available

Bright- and dark-field HR-TEM images. Detailed description of the ASAXS and extended SAXS analysis. RBS spectrum and summarized composition data of the NCs derived by RBS and ASAXS. PL spectra and detailed analysis of the PL peak shift. Description of the XRD data analysis. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^⊥ (M.Y.) Laboratory for Nanoelectronics, Dept. of Electrical Engineering and Information Technology, ETH Zurich, 8092 Zurich, Switzerland.

Author Present Address

^# (D.P.) Ion Physics, Department of Physics and Astronomy, Uppsala University, 751 20, Uppsala, Sweden.

The authors declare no competing financial interest.