Nanooptics of Molecular-Shunted Plasmonic Nanojunctions

Abstract

Gold nanoparticles are separated above a planar gold film by 1.1 nm thick self-assembled molecular monolayers of different conductivities. Incremental replacement of the nonconductive molecules with a chemically equivalent conductive version differing by only one atom produces a strong 50 nm blue-shift of the coupled plasmon. With modeling this gives a conductance of 0.17G₀ per biphenyl-4,4′-dithiol molecule and a total conductance across the plasmonic junction of 30G₀. Our approach provides a reliable tool quantifying the number of molecules in each plasmonic hotspot, here <200.

Organic electronics is developing into one of the key technologies of the 21st century, with the potential to be cheap, flexible, and transparent.^1,2 While emerging devices include organic light-emitting diodes,^3,4 organic solar cells,^5,6 and organic transistors,⁷ one major goal is to reduce active operation to a few molecules only. This would enable low switching energies, ultrahigh information densities, fast operation speeds, and cheap manufacturing. However, the realization of reliable molecular electronic devices has been challenging. With only a few molecules in each switch, their conformation,⁸ alignment, and connection to electrodes plays a crucial role.⁹ Despite progress in the past few years, reliably probing the properties of such a small number of molecules within a nanometer sized gap is nontrivial.

A possible solution explored recently is to combine molecular layers with metal nanostructures that support light-driven coherent collective electron oscillations, whose quanta are known as plasmons.^10,11 Plasmonic structures can confine light below the diffraction limit¹² and as a result can be used for ultrasensitive sensing down to the single molecule level.^13,14 Recent advances in nanometer-scale confinement of light make structures with optical characteristics astonishingly sensitive to the molecular state. Hybrid “organo-plasmonic” devices could thus function as an interface between low-cost, flexible electronics and ultrasensitive, fast nanophotonics.

A key outstanding question is how molecular conductivity influences a surrounding plasmonic junction. Theoretical simulations have shown that partially conducting linkers shift the resonance energy of the coupled plasmon and create a screened coupled plasmon mode.¹⁵ At the same time a new “charge-transfer” plasmon (CTP) mode emerges for conductances of a few 100 G₀ (where G₀ = 2e/h is the conductance quantum).¹⁵⁻¹⁸ Recently, the presence of CTP modes for molecular linkers has been observed by analyzing the electron energy loss spectrum of nanocubes linked by conducting and insulating molecules.¹⁹

To demonstrate the predicted blue-shift of the coupled plasmon mode experimentally in a chemically relevant environment, here we study pure and mixed self-assembled monolayers (SAMs) of biphenyl-4-thiol (BPT) and biphenyl-4,4′-dithiol (BPDT) molecules. BPDT has two thiol groups that form covalent bonds to gold, with the thiol bond ensuring a conductive link through the π-orbitals of the two phenyl rings from its strong overlap to the Au electrons.²⁰ BPT lacks the second thiol group and is therefore not able to create a conductive link (Figure 1). The rotation of the phenyl rings relative to each other strongly influences the conductivity, decreasing in proportion to the relative angle.^21,22 By fixing this relative angle using homologues and measuring the relative intensities of vibrational Raman lines, Cui et al. demonstrated that it is possible to monitor this rotation angle by surface enhanced Raman spectroscopy (SERS).²³ Thus, molecular orientation and electronic transport are coupled in this system and potentially optically accessible.

Figure 1.

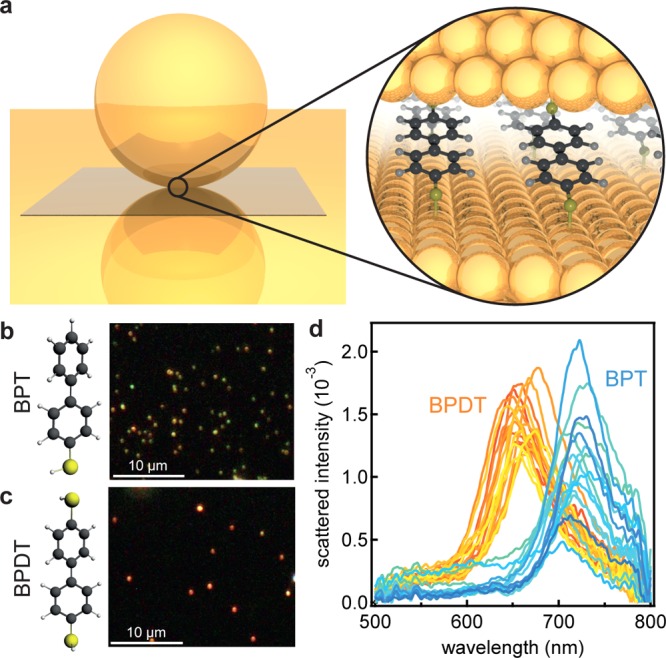
Conductive and nonconductive self-assembled monolayers in plasmonic junctions. (a) Schematic of nanoparticle on mirror geometry: a gold nanoparticle is placed on a gold film, separated by a thin molecular spacer layer. (b, c) Dark field images of 60 nm gold nanoparticles on BPT and BPDT, respectively. (d) Normalized scattered intensity from individual 60 nm gold nanoparticles on BPT and BPDT.

We assemble these SAMs in the so-called nanoparticle on mirror (NPoM) geometry (Figure 1a) in which a gold nanoparticle placed on a gold film is separated only by the thin molecular spacer layer. The surface plasmons of each nanoparticle couple to their image charges in the gold film forming a spatially tightly confined plasmonic hotspot, similar to a nanoparticle dimer.^24,25 Not only does this allow for probing a small number of molecules, but both the electric field and molecular dipole orientations are well-fixed. For spacer thicknesses of order 1 nm as here, the intensity in the plasmonic hotspots is locally over 1000 times larger than the impinging light, enabling precise spectroscopy of few to single molecules^26,27 as well as monolayer materials such as MoS₂, CdSe,²⁸ and graphene.²⁹ The greatest advantage of this geometry over others such as dimers or aggregated nanoparticles³⁰ is the high reproducibility and relative ease of assembly. For every sample SAM, thousands of identical plasmonic junctions with the same orientation can be investigated.³¹

When changing the spacer layer from the insulating BPT to the conductive BPDT, a strong blue-shift of the plasmon resonance can be observed. This blue-shift manifests itself both in the observed color of the nanoparticles (NPoMs) in the dark field images (Figure 1b and c) and in the scattering spectra of each individual nanoparticle (Figure 1d). For BPT the average scattering resonance is at 714 ± 1.6 nm, with corresponding dark field images showing green nanoparticles. This green color arises from the transverse plasmon mode situated near 540 nm,²⁹ as the coupled mode is too far into the infrared to be detected by the camera. In contrast for BPDT an average resonance at 664 ± 1.3 nm is observed, so correspondingly these nanoparticles appear red in dark field images. This blue-shift corresponds to that predicted¹⁶⁻¹⁸ and has also been observed for direct quantum tunnelling between plasmonic structures.^32,33 To exclude the possibility that the observed blue-shift originates from variations in the gap size and/or refractive index, phase modulated ellipsometry measurements of both BPT and BPDT layers are performed. For BPT a thickness of 1.3 ± 0.1 nm and for BPDT of 1.1 ± 0.1 nm are found with a refractive index of 1.45. While this 15% thickness change might account for up to a 20 nm spectral shift (Supporting Information), it would actually move in the opposite direction to that seen experimentally (as for thinner spacers a red shift of the plasmon is expected). Changes in refractive index also cannot account for the spectral shift as an unfeasible change from n = 1.45 to n = 1.15 would be needed (see Supporting Information). A simple estimate shows that charging each linker with electrons from the gold, thus slightly reducing the electron density and hence plasma frequency, would provide spectral shifts of order 1 nm only and is thus not the cause of the observed blue-shift. The modification of the plasmon spectrum for each NPoM is thus due to changes in molecular conductivity, as we discuss below.

Samples with different conductivities were prepared by assembling mixed SAMs of BPT and BPDT with varying BPDT mole fraction x. The average plasmon resonance was determined by investigating 100 nanoparticles per sample and analyzing the observed resonance spectra. The distribution of the central resonance peak position (shown for the pure BPT and BPDT samples in Figure 2a) shows an evident continuous blue shift of the plasmon resonance with increasing conductivity (Figure 2b) (statistical analysis of all samples in Supporting Information). Full electrodynamical simulations confirm this result (Figure 2b and c). This continuous wavelength shift confirms that homogeneous mixed SAMs exist in the gap between nanoparticle and planar mirror. A simple analytical description considers a capacitor shorted by molecules with individual conductance G_M. The charge conducted through these resistors relative to the charge stored when the capacitor is isolated is proportional to the relative frequency shift of the coupled plasmon mode (see derivation in Supporting Information). This gives for the wavelength λ_NPoM of the coupled plasmon mode at conductance G,

1

with dimensionless proportionality factor b, RC time constant τ_RC = RC (R: total resistance, C: capacitance), and plasmon frequency ω. As in refs (15 and 16), we use a plate capacitor model to describe the capacitance C = ε₀n_gap²(A/d), using the refractive index in the gap n_gap, the area A, and the gap separation d. Describing the molecules in the plasmonic gap as a number of parallel resistors yields for the junction conductance, G = R^–1 = NxG_M, for a total of Nx connected molecules each of conductance G_M. Expressing the number of molecules by the total area of the junction divided by the area per molecule A_M yields:

2

Using eqs 1 and 2 allows this analytical model to be fit to the experimental data (Figure 2b) faithfully capturing the nonlinear slope with conductivity. From this fit and based on the typical area per molecule in the SAM³⁴ of A_M = 0.22 nm², the conductance per BPDT molecule is found to be G_M = (0.17 ± 0.01)G₀.

Figure 2.

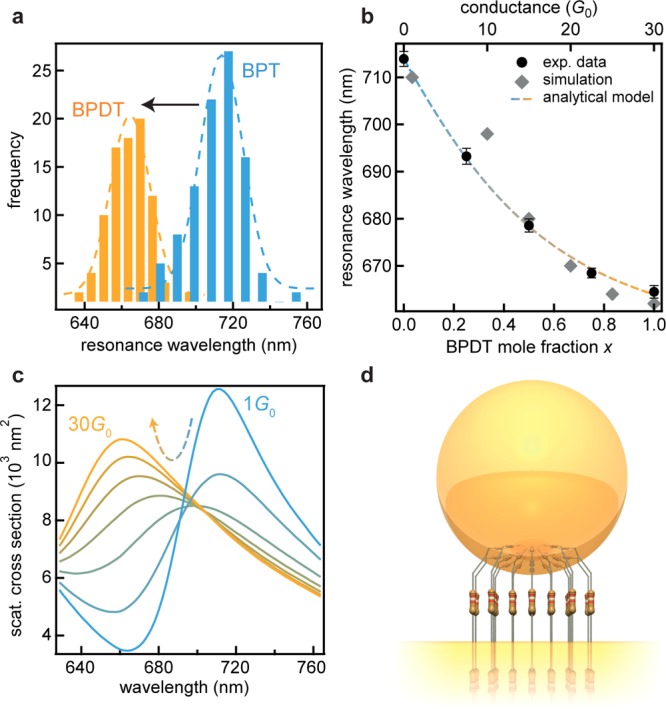
Conductance dependent shift of the plasmon resonance. (a) Distributions of the plasmon resonance wavelength for BPT and BPDT in 100 plasmonic gaps. (b) Blue-shift of the coupled plasmon resonance with increasing BPDT mole fraction x in mixed SAMs together with fitted analytical model (bottom axis) and full electrodynamical simulations (top axis). (c) Simulated scattering spectra for increasing total junction conductance between 1 and 30G₀. The simulation assumes a facet with a diameter of 4 nm, forming a conductive link with refractive index of 1.5 (dielectric function as in ref (15)). (d) Illustration of the modeled system.

While DC conductivity of individual BPDT molecules has indeed been calculated to be >0.1G₀, single-molecule transport experiments give somewhat lower values (with suggestions that this is due to modifications in topology of both molecule and Au junction atoms as well as their precise atomic-scale connection)^20,21 and are highly variable. Here the regular close-packed SAM helps to stabilize the molecular junctions, allowing minimal flexing as confirmed below. According to our full electrodynamical simulations a total conductance of around 30G₀ is necessary to produce the observed blue-shift (Figure 2b and c). From this total optical conductance and the optical conductance per molecule, the number of molecules in each gap can be estimated to be around 176. The patch in which the molecules form conducting bridges is thus 35 nm² corresponding to a circle with a radius of 3.3 nm, which is reasonable for facet sizes on 60 nm gold nanoparticles. The narrow spectral distributions (Δλ_NPoM < 30 nm) together with the narrow spectral resonances (<50 nm) confirms the robustness of this system to coopt an almost fixed number of molecules.

In parallel to dark-field microscopy, a local spectroscopic study of the molecular-linked plasmonic junctions by surface enhanced Raman spectroscopy (SERS) allows access to information about the molecular conformation. Correlating observed conductance changes with SERS can reveal if the local morphology of the self-assembled monolayer alters. Furthermore, comparing SERS intensities in the conductive and nonconductive cases allows the influence of charge conduction on the optical near-field to be quantified.

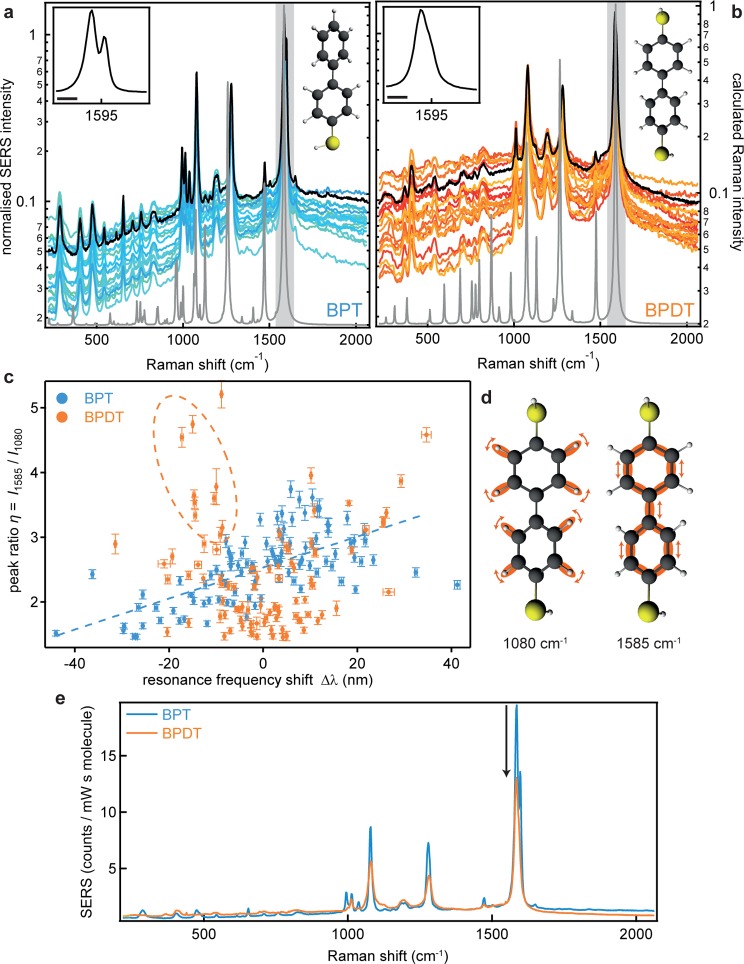
The spectral features in both the SERS and the simultaneous dark-field spectroscopy are found to be extremely reproducible between the individual nanoparticles (Figure 3a,b and Supporting Information). The Raman spectra of BPT and BPDT are in excellent agreement with theoretical spectra (gray lines). In contrast to typical tip enhanced Raman spectroscopy (TERS) measurements³⁵ which show dramatic temporal fluctuations and both broad and peaked spectra, we find stable sharp line spectra with signal-to-noise >100 (note log scale in Figure 3a and b) emphasizing how molecules are unable to randomly flex within a SAM in stark contrast to other layers such as lipids.²⁰

Figure 3.

Surface enhanced Raman spectra of individual nanoparticle on mirror constructs. (a,b) SERS spectra of 20 nanoparticles, with average (black line) and modeled spectra (gray line) for BPT and BPDT, respectively. Laser wavelength 633 nm, 0.33 mW power, 10 s integration time, spectra normalized to 1585 cm^–1 peak. Insets shows magnified coupled ring mode peak, the length of the scale bar is 20 cm^–1. (c) Ratio of coupled ring mode (1585 cm^–1) to C–H rocking mode (1080 cm^–1) vs the resonance wavelength shift (100 nanoparticles each). (d) Schematic of C–H rocking and coupled ring modes. (e) Average SERS spectra normalized by the number of molecules, comparing SERS intensities from BPDT and BPT.

Minor systematic differences between BPT and BPDT are mainly caused by the lower symmetry of BPT: because the second thiol group is absent (breaking molecular symmetry), some peaks are split. This is readily visible in the main peak of BPT (a coupled vibration of both phenyl rings) which is split into two peaks at 1585 and 1597 cm^–1, whereas for BPDT the same mode consists of only a single peak at 1584 cm^–1 (insets Figure 3a,b). A similar splitting is seen around 1000 cm^–1. As previously reported, a change of the rotation angle between the phenyl rings changes the molecular conductivity and is correlated to the Raman intensity ratio η between the coupled vibration of phenyl rings at 1584 cm^–1 and the C–H rocking mode at 1080 cm^–1 (Figure 3d).²¹⁻²³ When this ratio η is plotted against the plasmon spectral shift Δλ, different dependencies are seen for BPT and BPDT (Figure 3c). For BPT the slow increase of peak ratio with longer plasmon wavelength (dashed blue line) is due to changing Raman enhancements of the vibrational lines as they move spectrally compared to the plasmon. While BPDT also shows this trend, an additional steep increase is seen for shorter resonance wavelengths (dashed orange ellipse in Figure 3c). We suggest this arises from nanoparticles sitting on BPDT molecules with a different conformation, for example at defects in the SAM, and with a higher conductivity that leads to a blue-shift of the plasmon resonance.

By using the number of molecules determined from the conductance-induced blue-shifts, we obtain quantitative SERS spectra with intensities normalized by the number of molecules (Figure 3e). This shows that for each vibrational line on each molecule, 1 photon is obtained from 4.5 × 10¹⁴ photons incident on this NPoM antennae. We also find systematically that the SERS intensity for the conductive molecules is lower than from the nonconductive ones, mainly since the current across the gap screens the local field. More quantitatively, the actual difference in Raman intensities is even higher because different Raman enhancements are produced by the shifted spectral positions of the plasmons. Appropriately correcting the observed Raman intensities of the coupled ring mode (Supporting Information) shows that the conducting molecules have SERS vibrational peaks which are 2.4 times weaker (for the other modes similar values between 2 and 2.4 are found). Although a previous empirical relation between near-field intensity and spectral position (solely based on capacitive coupling) predicts a 5-fold reduction in SERS amplitude,³⁶ we find our electromagnetic simulations predict a 140-fold decrease (Supporting Information). This suggests that there is a 100-fold increase in global Raman cross-section in the conducting case (for all vibrational lines). This surprising result indicates a correlation between carrier transport and vibration coupling, possibly as electrons passing through the molecules are inelastically scattered and excite further molecular vibrations.

In conclusion, we experimentally show the influence of a molecular conductive link between neighboring plasmonic structures on their optical spectrum. A clear blue-shift of the coupled plasmon mode is observed for increasing conductivity, which is used to optically measure the resistivity of nanometer sized organic films. A great advantage of plasmonic detection over conventional techniques is that its sensitivity increases with decreasing gap size, opening up single molecule capabilities.³² The high level of robust and reproducible response of thousands of such nanoparticles emphasizes the potential for real time chemistry on few molecules. At the same time, designing switchable molecules appropriate to this architecture will allow real time control of the plasmonic resonance, through electrochemical or optical gating, opening up the field of organo-plasmonic devices.

Methods

Sample Preparation

A 100 nm thick gold film was evaporated on a silicon (100) wafer on top of a 10 nm Ti adhesion layer (Kurt J. Lesker Company, PVD 200). Using an evaporation rate of 0.1 Å/s for both layers with a base pressure of ≈1 × 10^–7 mbar ensures the formation of a smooth gold film. Biphenyl-4,4′-dithiol (Sigma-Aldrich, 95%) was dissolved in a small amount of dichloromethane (Sigma-Aldrich, >99.8%) and diluted in absolute water-free ethanol (Sigma-Aldrich, >99.5%). Biphenyl-4-thiol was directly dissolved in ethanol. The solutions were mixed to obtain 1 mM solutions with the desired mixing ratio. The gold substrates were cleaned in air plasma for 30 min and subsequently immersed in the growth solution for 22 h. Afterward, the samples were thoroughly rinsed with ethanol and briefly cleaned in an ultrasonic bath to remove excess unbound thiols. After blowing the samples dry with nitrogen, the samples were stored under a constant nitrogen flow until they were used. As a reference for the ellipsometry measurements an octadecane-1-thiol (Sigma-Aldrich, 98%) SAM was deposited with the same parameters. 60 nm gold nanoparticles were used as received from BBI Solutions (2.60 × 10¹⁰ particles/mL). To deposit the nanoparticles on the SAM, the previously prepared samples were immersed in a 1:10 diluted nanoparticle solution. The time was adjusted in order to reach a uniform but sparse coverage that allows spectroscopic investigations of individual nanoparticles. Excess nanoparticles were rinsed off with distilled water, and the samples were dried with nitrogen.

Experimental Section

Combined SERS and scattering experiments were performed using a modified Renishaw inVia Raman microscope. The samples were illumined with a focused white light source (40 W halogen lamp, angle of incidence of 60°). The scattered light was collected with a ×100 objective (NA 0.8) and analyzed with a fiber-coupled Ocean Optics QE65000 cooled spectrometer. The scattering spectra of nanoparticles on mixed SAMs were recorded on an Olympus BX51 microscope in a reflective dark field geometry. The scattered light was collected with a ×100 long working distance objective (NA 0.75) and analyzed with the same Ocean Optics QE65000 spectrometer. For each sample type in total 100 nanoparticles from different, separately deposited samples were investigated.

Ellipsometry

The thickness of BPT, BPDT, and C₁₈ (octadecane-1-thiol) SAMs was measured with a Jobin-Yvon UVISEL spectroscopic ellipsometer. The angle of incidence was set to 70°, and the wavelength was varied between 300 and 800 nm in 5 nm steps. Data were modeled and fitted with a simple three-layer system using DeltaPsi2 software. Values for the base layer were obtained from a clean gold substrate, while the SAM layers were modeled using a Cauchy approximation with an assumed refractive index of n_inf = 1.45. The measured thickness of 2.4 ± 0.2 nm the C₁₈ SAM is consistent with literature³⁷ and was obtained for comparison only.

Simulations

Raman simulations: The geometry of both molecules was preoptimized with the semiempirical MOPAC2012³⁸ package, and subsequently the main optimization was carried out with the ADF³⁹ package. The triple Z + 1 polarization function basis set and a small frozen core was used in the DFT simulations, which was checked to provide optimal converged solutions. Raman active modes were selected by numerical differentiation of the polarization tensor.⁴⁰

Electrodynamic simulations: Throughout the paper, far-field extinction spectra and near-field amplitude maps were calculated by numerical simulations using the full electrodynamic boundary-element method (BEM).^41,42 The BEM method solves Maxwell’s equations for inhomogeneous media characterized by local dielectric functions in terms of surface-integral equations of the induced charges and currents, which are obtained through discretization of the surface integrals and solution of the resulting matrix equations. The EM field is then calculated in terms of these induced charges and currents. A sufficient number of discretization points were used to ensure full convergence of all results.

Supporting Information Available

Statistical analysis, derivation of the analytical model, simulated near field distributions, Raman control measurements, and comparison of experimental and theoretical plasmon line widths. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

Experiments were planned and executed by F.B., B.d.N., D.O.S., A.S., S.D.E., and J.J.B., with support for ellipsometry measurements from L.P. Full electromagnetic simulations were performed by C.T., L.O.H., and J.A. DFT simulations were performed by F.B. The data were analyzed by F.B. and J.J.B., and all authors contributed to the manuscript.

The authors declare no competing financial interest.