Abstract
Purpose:
Descriptions of the structure of brain tissue as a porous cellular matrix support application of a poroelastic (PE) mechanical model which includes both solid and fluid phases. However, the majority of brain magnetic resonance elastography (MRE) studies use a single phase viscoelastic (VE) model to describe brain tissue behavior, in part due to availability of relatively simple direct inversion strategies for mechanical property estimation. A notable exception is low frequency intrinsic actuation MRE, where PE mechanical properties are imaged with a nonlinear inversion algorithm.
Methods:
This paper investigates the effect of model choice at each end of the spectrum of in vivo human brain actuation frequencies. Repeat MRE examinations of the brains of healthy volunteers were used to compare image quality and repeatability for each inversion model for both 50 Hz externally produced motion and ≈1 Hz intrinsic motions. Additionally, realistic simulated MRE data were generated with both VE and PE finite element solvers to investigate the effect of inappropriate model choice for ideal VE and PE materials.
Results:
In vivo, MRE data revealed that VE inversions appear more representative of anatomical structure and quantitatively repeatable for 50 Hz induced motions, whereas PE inversion produces better results at 1 Hz. Reasonable VE approximations of PE materials can be derived by equating the equivalent wave velocities for the two models, provided that the timescale of fluid equilibration is not similar to the period of actuation. An approximation of the equilibration time for human brain reveals that this condition is violated at 1 Hz but not at 50 Hz. Additionally, simulation experiments when using the “wrong” model for the inversion demonstrated reasonable shear modulus reconstructions at 50 Hz, whereas cross-model inversions at 1 Hz were poor quality. Attenuation parameters were sensitive to changes in the forward model at both frequencies, however, no spatial information was recovered because the mechanisms of VE and PE attenuation are different.
Conclusions:
VE inversions are simpler with fewer unknown properties and may be sufficient to capture the mechanical behavior of PE brain tissue at higher actuation frequencies. However, accurate modeling of the fluid phase is required to produce useful mechanical property images at the lower frequencies of intrinsic brain motions.
Keywords: elastography, poroelastic, viscoelastic, MRE
1. INTRODUCTION
Magnetic resonance elastography (MRE) is a technique to produce images of tissue mechanical properties, where changes in shear modulus have been linked to diseases in organs including the brain,1–3 liver,4 breast,5 and heart.6,7 In MRE, motion sensitive MRI sequences are employed to measure the displacement of tissue resulting from some mechanical stimulus.8 Mechanical properties are then estimated using an inversion algorithm that assumes a mechanical model to describe the tissue behavior. Continuum mechanical models only approximate the bulk response of tissue, which is influenced by numerous microscale interactions of cellular and extracellular components in both solid and fluid phases.
The wide range of mechanical actuation frequencies possible in MRE adds additional complexity to the choice of model. The tissue stimulus is often provided by external actuation (EA); a frequency around 50 Hz is usually applied in human imaging to balance the wavelength and attenuation attributes of the induced shear waves.9,10 More recently, an intrinsic actuation (IA) technique has bypassed the need for specialized actuators by measuring the low frequency (≈1 Hz) motion resulting from blood pressure variation across the cardiac cycle.11
To minimize bias in the estimated mechanical properties from model-data mismatch, it is desirable to select an appropriate continuum model which reflects the tissue behavior at the relevant frequency without unnecessary complexity. Two mechanical models commonly applied to elastography data are considered in this work: viscoelasticity (VE), which models a material as a single phase network of elastic springs and viscous dashpots, and poroelasticity, which models tissue as a porous elastic solid with an interstitial viscous fluid that allows flow relative to the solid matrix.
1.A. Viscoelastic tissue modeling
The assumption of VE results in a model that includes both elastic energy storage and viscous energy dissipation, and the harmonic case at frequency ω is described by the inhomogeneous Navier’s equation12
| (1) |
Here, the VE material properties are the complex-valued shear modulus, μ = μs + iμL, and the first Lamè constant, λ. λ is related to the bulk modulus, K, through K = λ + 2μ/3. We assume K to be real-valued in this work (negligible viscous behavior for dilatational motion). It is useful to define a viscoelastic Poisson’s ratio, νv = λ/2(λ + μ). As νv → 0.5 + 0i, the material becomes incompressible13 (note that true incompressibility in the case of real-valued K can only occur when μ is also real-valued). ρ is the material density and is usually assumed to be 1000 kg m−3 for soft tissues. The displacement, , is a complex-valued motion amplitude, so that the time dependent spatial displacement of coordinate is . The real and imaginary components of the complex-valued viscoelastic shear modulus are known as the storage modulus, μs, and the loss modulus, μL, respectively. μs captures the elastic behavior of the extracellular matrix and solid cellular components, and μL lumps viscous losses in the extracellular and intracellular fluid compartments together with energy loss in the solid tissue components to produce a single effective attenuation parameter, which is an attractive simplification from a parameter estimation perspective. However, viscoelasticity may not be an appropriate assumption for biphasic tissues because fluid flow due to pressure gradients is not modeled explicitly. Viscoelasticity of tissue has been investigated extensively in vivo using EA-MRE at higher frequencies (>25 Hz); however, the low frequencies of IA-MRE have not been studied. In simple viscoelastic elements, the loss modulus is determined by the viscous dashpot constants multiplied by the frequency.9 Therefore, if the springs and dashpots of the viscoelastic elements are assumed to be intrinsic tissue properties, one should expect μL(1 Hz) ≈ μL(50 Hz)/50. Although assuming constant viscoelastic elements across frequencies is an oversimplification,14 it may be sufficient to gauge the expected values of low frequency loss moduli.
1.B. Poroelastic tissue modeling
The poroelastic (PE) constitutive model was introduced by Biot in 1956,15,16 and was later extended to accommodate oscillatory behavior.17,18 A PE material is modeled as a biphasic continuum, comprising a porous elastic matrix with an infiltrating pore fluid. Volumetric deformation of the solid matrix leads to fluid flow in the material. Conversely, fluid forced into the material causes deformation of the matrix. Brain tissue is a good candidate for poroelastic modeling because it consists of a matrix of neurons and glial cells saturated by both intracellular and extracellular fluid.19 Approximately 20% of tissue volume consists of extracellular fluid,20 which can move within the interstitium through the network of capillaries and the glymphatic system21 and acts as the infiltrating pore fluid. The network of neural and glial cells provides structural support for the tissue, therefore, can act as the porous elastic matrix. Mechanical testing under controlled drainage conditions indicates that the behavior of brain tissue is well described by a poroviscoelastic model,22,23 and poroelastic modeling using finite elements has been successful in previous studies of brain deformation.24–30 Equation (2) shows the time-harmonic form of the poroelastic constitutive equations, with simplifications relevant to biological tissue (full saturation, incompressible constituents).17
| (2a) |
| (2b) |
| (2c) |
These equations govern the response of a PE continuum at a given frequency, ω, and are solved for the solid phase displacement, , and the pore pressure field, p, with the finite element (FE) method. μp are the shear modulus and Lame constant of the porous matrix; a fully saturated material and incompressible constituents have been assumed in deriving Eq. (2) so the material is incompressible as a whole; however, the pore spaces allow volumetric strain of the solid matrix if redistribution of the infiltrating fluid occurs. Volume change of the solid matrix is required for poroelastic fluid flow; therefore, the Poisson’s ratio of the porous solid matrix,
| (3) |
needs to be less than 0.5 to achieve differential motion of the solid and fluid phases. The hydraulic conductivity, κ, is an important property governing how easily fluid can flow through the porous matrix (a function of geometry and fluid viscosity),31 and has a strong effect on the level of motion attenuation and apparent compressibility of a PE material. Additional PE properties include solid, fluid, and apparent densities, ρ, ρf, and ρa, respectively, and the porosity, ϕp. Typical values in tissue are given by Perriñez.17
1.C. Choice of model for brain tissue
VE and PE modeling of brain tissue has been investigated previously through mechanical testing.22,23,32 Additionally, Bardet demonstrated that an equivalent viscoelastic model can be derived by equating expressions for VE energy storage and attenuation with the analogous PE expressions.33 The VE equivalent model closely matched PE behavior except in certain conditions, including when the actuation period is on the same order as the fluid equilibration time,34 approximated by
| (4) |
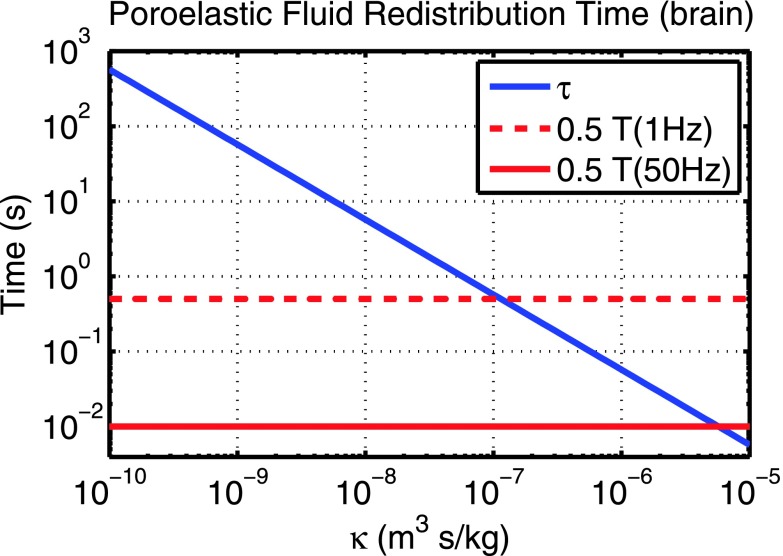
τ is the time constant for reaching equilibrium compressive strain over a characteristic distance, L, which is usually approximated based on the geometry—for example, half of the thickness of a cylindrical sample when fluid flows through the top and bottom surfaces, and half of the diameter when fluid flows through the cylinder walls.34–36 For the brain, the shortest bounded distance fluid can flow occurs between the ventricle and the brain surface (≈40 mm); therefore, L was approximated as 20 mm. The Young’s modulus, Ep = 2μp(1 + νp), has an upper bound of 3μp for incompressible cases, and a value of 8 kPa was estimated from the literature values to evaluate τ in this paper. Figure 1 plots τ over a range of hydraulic conductivity, κ. Experimentally, estimating κ for brain tissue is technically difficult—values reported in the literature are derived from a limited set of experiments and range from 4 × 10−12 to 10−9 m3s/kg.23,28,37,38 In our experience with MRE higher values up to 10−7 m3s/kg reproduced experimentally measured motion data more closely.11 Thus, τ approaches the actuation period at 1 Hz, but not at 50 Hz, suggesting that lower frequencies are likely to lead to a greater degree of VE and PE model mismatch in brain MRE experiments. An extension of this approach has been presented for heterogeneous materials, where the equivalent VE model matched PE behavior far from material interfaces; however, significant errors were observed close to the interface.39 This finding is an important consideration in MRE: using an incorrect mechanical model may affect the detectability of tissue interfaces, which is critical if MRE is to achieve its full potential as a spatially resolved imaging modality,40,41 rather than simply a method to estimate bulk average tissue properties.
FIG. 1.
PE fluid equilibration time of brain tissue, τ [Eq. (4)] as a function of hydraulic conductivity. When τ approaches half of the actuation period, T, VE equivalent models of PE materials are inaccurate. T/2 at frequencies corresponding to IA (1 Hz) and EA (50 Hz) are indicated on the plot.
Simulation can also gauge the effect of frequency on poroelastic fluid flow. The viscoelastic model involves a single phase, so the poroelastic response differs substantially when the relative size of the fluid flow component, , is large,
| (5) |
where and are the absolute displacements of the solid and fluid components of the poroelastic material, respectively. The fluid flow can be calculated from the poroelastic displacement fields using42
| (6) |
Simulation experiments reveal that the relative size of the fluid flow for constrained compression is largest at low frequencies, with other smaller local maxima corresponding to resonant frequencies, and lends further support to the observation that PE effects are enhanced at lower motion frequencies.
External and intrinsic actuation operate in very different frequency ranges: 50 Hz EA usually generates a shear wavelength which is smaller than the brain dimensions; therefore, wave patterns emerge and the tissue is essentially in free vibration where the elastic and inertial forces are balanced. Conversely, the shear wavelength for 1 Hz IA is on the order of meters for most tissue, inertial forces are small and the deformation is due to constrained compression; the elastic forces in the tissue are produced by boundary constraints and internal pressure sources.
In the literature for nonlinear inversion MRE of the brain to date, VE models for 50 Hz EA data10,40,43,44 and PE models for 1 Hz IA (Ref. 11) have been employed due to the empirical observation that these combinations of frequencies and models produce more spatially accurate and repeatable results. This paper presents VE and PE mechanical property reconstructions of both 50 and 1 Hz brain MRE data collected from healthy volunteers to compare the response of each model in vivo, and investigates the effect of model choice under ideal conditions through simulation experiments. The fluid equilibration time estimated by Eq. (1) supports the in vivo and simulation results.
2. METHODS
2.A. Viscoelastic and poroelastic inversions of EA and IA brain tissue data
Independent validation of MRE measurements of brain tissue is difficult because reliable independent techniques are not available; however, images from repeated examinations of the same subject are expected to have low variation when an appropriate model is used. Data from five repeated examinations of a healthy volunteer are available for both 50 Hz external actuation40,43 and 1 Hz intrinsic actuation.11 The IA subject was a 51 yr old male and the five MRE datasets were acquired over a 22 month period, whereas the EA subject was a 24 yr old male and the MRE data were acquired over a two month period. The OSS-SNR of the EA data exceeded the threshold of 3 required for accurate MRE inversion.45 Poroelastic46 and viscoelastic43 mechanical property reconstruction algorithms were applied to each data source, and the variation of the shear modulus (μs for VE and μp for PE) images of the rigidly registered image volumes was analyzed over the repeated scans in terms of the coefficient of image variation (COIV),
| (7) |
where σμj and are the standard deviation and mean of the jth image voxel across the five registered image volumes, and the mean is taken over the common voxels present in all five datasets.
2.B. Inversion of simulated data
A series of experiments were performed using VE and PE FE models to generate simulated MRE data with ideal VE and PE behavior under realistic EA and IA MRE conditions. Here, we opted not to add Gaussian noise to the synthetic measurement data in order to isolate the impact of data-model mismatch when applying the VE and PE inversions to the PE and VE simulated data (the algorithms themselves and the impact of measurement noise have been studied in previous publications31,47). A realistic 3D simulation was generated from a high resolution FE mesh of one quadrant of a brain MRI, with two material classes representing gray matter (GM) and white matter (WM), where material properties were assigned based on the literature values (presented in Table I).10 Fixed displacement boundary conditions were assigned from experimental 50 Hz EA or 1 Hz IA data, with one face remaining stress free to avoid unrealistic dilatational stresses from fully constraining the boundaries with noisy experimental data. Both poroelastic and viscoelastic FE solvers were used to generate high resolution displacement fields at 50 and 1 Hz, which were then sampled at isotropic 2 mm resolution to simulate MRE measurements. Table I gives material property values.
TABLE I.
Values of mechanical properties assigned to GM and WM tissue regions in the simulations. A range of some properties was investigated, indicated by asterisks.
| Property | GM | WM |
|---|---|---|
| μs, μp (kPa) | 2.2 | 2.8 |
| μL (50 Hz) (kPa) | μstan(δ)∗ | 1.69 × μstan(δ)∗ |
| μL (1 Hz) (kPa) | 0.05 | 1.69 × 0.05 |
| K (50 Hz) (kPa) | 1650 | 1650 |
| K (1 Hz) (kPa) | K∗ | K∗ |
| νp | 0.3 | 0.3 |
| κ | κ∗ | κ∗ |
| ρ, ρf (kg/m−3) | 1000 | 1000 |
| ρa (kg/m−3) | 150 | 150 |
| ϕp | 0.2 | 0.2 |
The simulated datasets were then processed with both VE and PE nonlinear inversion (NLI) algorithms using the same parameters as the in vivo data. VE inversions recovered μs and μL in all cases,43 and also Re{K}47 for cross-model inversions when an appropriate value was not known. PE inversions recovered μp and λp in all cases,46 and also κ (Ref. 31) for cross model inversions where an appropriate value was not known. Recovered properties from the cross-model inversions will be strongly influenced by properties with a similar effect in the forward model. Some VE and PE mechanical properties are heterogeneous and imprecisely known; therefore, a range of values were investigated in the simulations. Inversions of VE simulated data were analyzed as a function of the damping ratio, tanδ = μL/μs at 50 Hz (with νv = 0.499), and as a function of the Poisson’s ratio, νv at 1 Hz (assuming incompressibility for VE inversions of in vivo IA brain MRE data produces unstable results, indicating some compressibility is required for the model to adequately reproduce the measured data). Inversions of PE simulated data were investigated as a function of hydraulic conductivity, κ for both frequencies.
3. RESULTS
3.A. In vivo data results
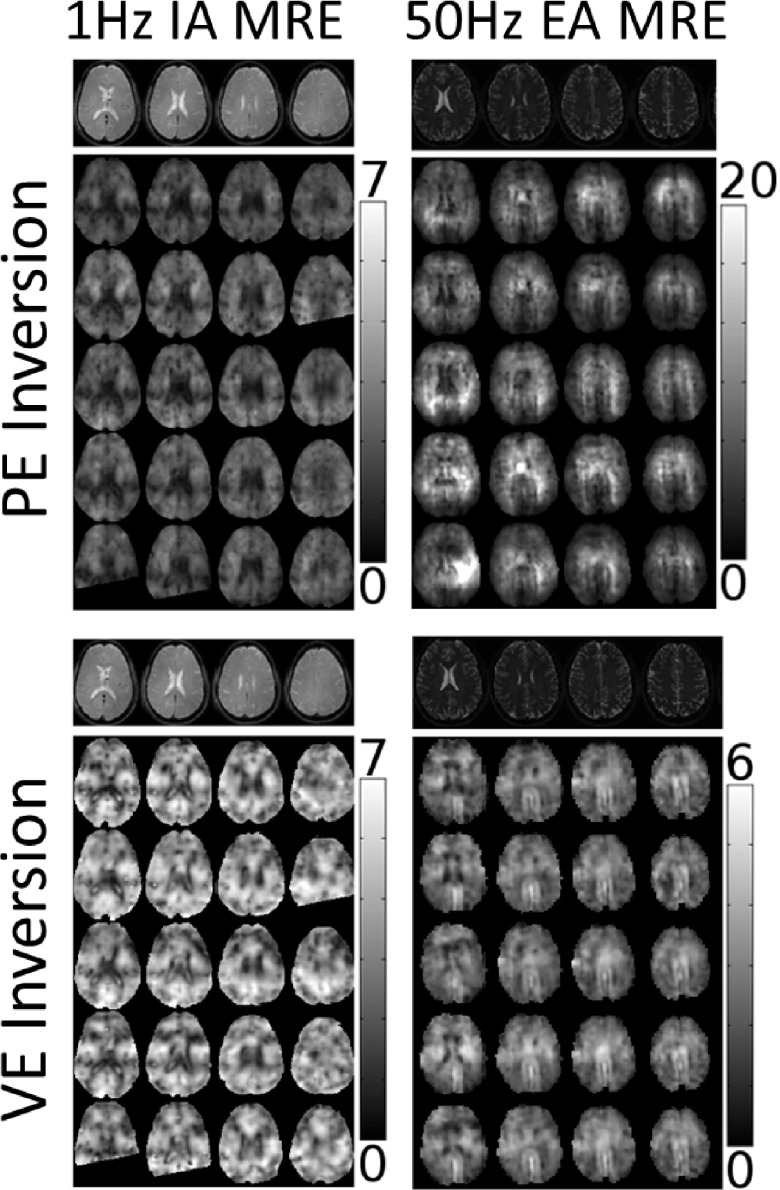
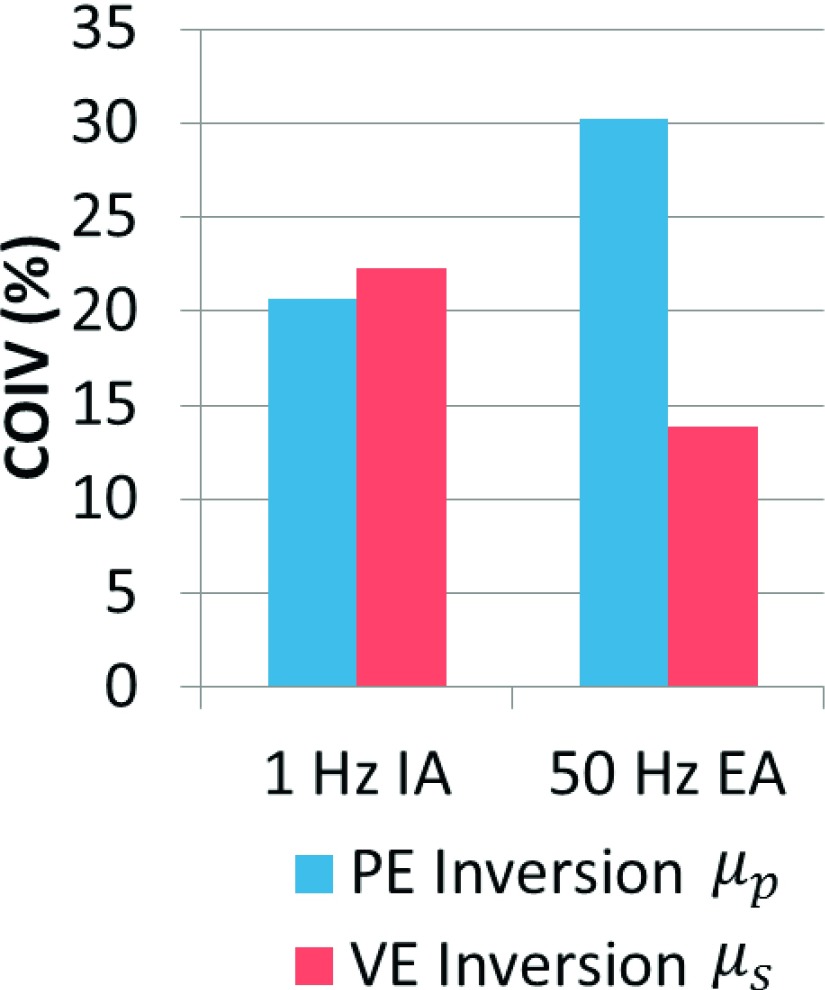
Figure 2 provides examples of poroelastic and viscoelastic mechanical property images for 50 Hz EA and 1 Hz IA. The repeatability (COIV) of the stiffness parameter images (μs and μp) is also presented in Fig. 3. At 50 Hz, VE inversion images correspond to anatomical structure and have much lower variation across repeated scans (COIV) compared to PE inversions. For IA data, the PE inversion COIV is lower than VE; although, the difference is not as great as for the 50 Hz EA results. Qualitative evaluation of the IA property images in Fig. 2 reveals that VE–IA inversions have spatial artifacts appearing in different locations across scans, and other than the ventricle boundaries, anatomical structures are not evident. PE–IA inversions on the other hand, contain fewer artifacts, and structural features correspond to the underlying anatomy and appear consistently across the repeated scans. Therefore, we conclude PE inversion performed better than VE at 1 Hz.
FIG. 2.
Repeated brain MRE shear modulus inversions using viscoelastic (μs) and poroelastic (μp) models. The left column corresponds to 1 Hz IA data and the right column results from 50 Hz EA data. Both PE (top row) and VE (bottom row) images are given for each data source. The columns within each image panel show four representative MRE slices whose positions are indicated by the anatomical images in the top row. The bottom five rows show the coregistered repeated MRE shear modulus images for each model.
FIG. 3.
Coefficient of image variation [Eq. (7)] for PE and VE inversion of multiple scans of the same healthy volunteer, for both 50 Hz external actuation and 1 Hz intrinsic actuation.
3.B. Inversion of simulated data
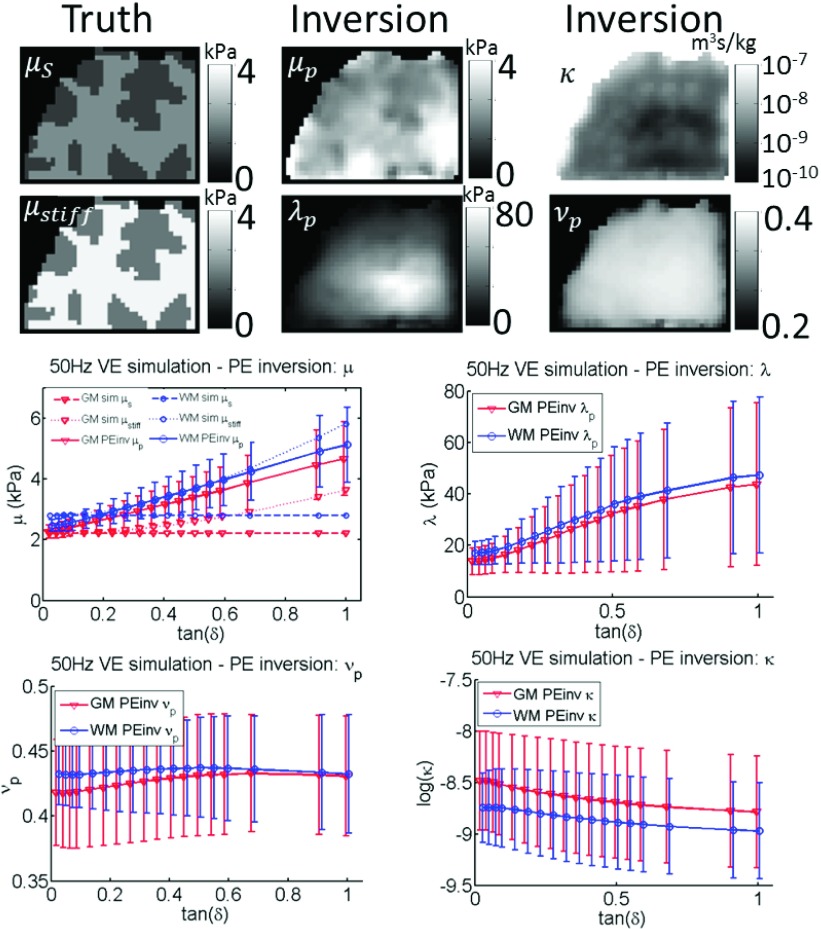
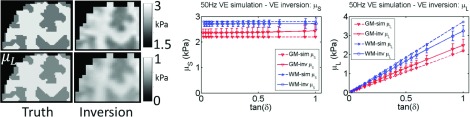
Inversion of simulated data using the correct model works well for both VE and PE cases. Figure 4 shows very good agreement between estimated and true values from the simulation for 50 Hz VE, for both μs and μL, although contrast is reduced due to blurring at interfaces. The 1 Hz VE results are presented in Fig. 5—the storage modulus reconstruction recovered the expected contrast; however, μL images were only accurate with unrealistically large simulated μL values. As the VE material became more incompressible (νv → 0.5), a downward bias of storage moduli values occurred. The poroelastic simulations with the correct inversion are shown in Figs. 6 and 7, and are reasonably accurate for μp, whereas, the λp images have some errors.
FIG. 4.
Correct model: VE inversion of 50 Hz simulated VE data. Values prescribed in the simulation are shown as dotted lines, and recovered values from the inversion are represented by solid lines. Simulated gray matter (GM) and white matter (WM) tissue classes are plotted, and a range of VE damping ratios, tanδ, was investigated.
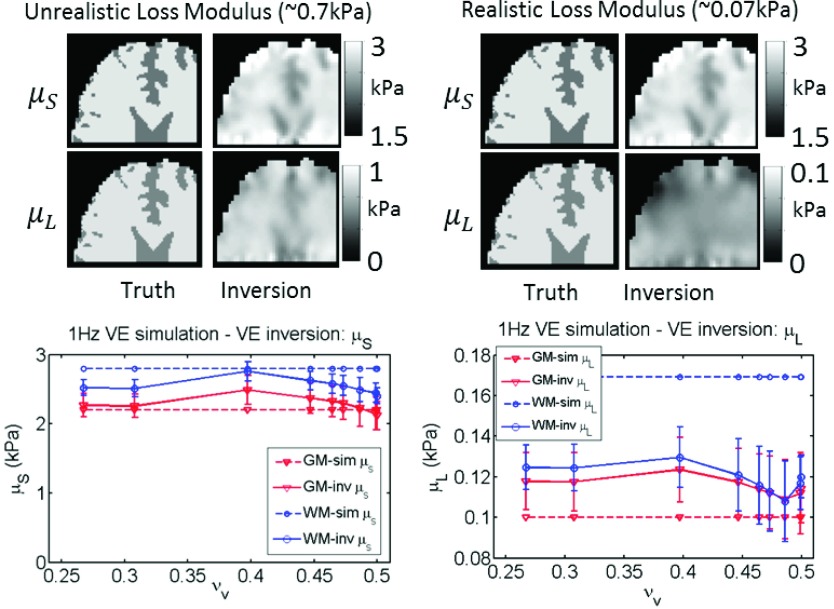
FIG. 5.
Correct model: VE inversion of 1 Hz simulated VE data. Low μL values are expected in this frequency range, the property maps demonstrate that spatially accurate μL images are not attainable unless unrealistically high μL values are prescribed. A range of VE Poisson’s ratios (νv) was investigated. Property values prescribed in the simulation are shown as dotted lines, and recovered values from the inversion are represented by solid lines. Simulated gray matter (GM) and white matter (WM) tissue classes are plotted.
FIG. 6.
Correct model: PE inversion of 50 Hz simulated PE data. Values prescribed in the simulation are shown as dotted lines, and recovered estimates from the inversion are represented by solid lines. Simulated gray matter (GM) and white matter (WM) tissue classes are plotted, and a range of PE hydraulic conductivity (κ) was investigated.
FIG. 7.
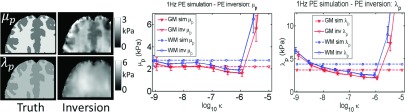
Correct model: PE inversion of 1 Hz simulated PE data. Values prescribed in the simulation are shown as dotted lines, and recovered values from the inversion are represented by solid lines. Simulated gray matter (GM) and white matter (WM) tissue classes are plotted, and a range of PE hydraulic conductivity (κ) was investigated.
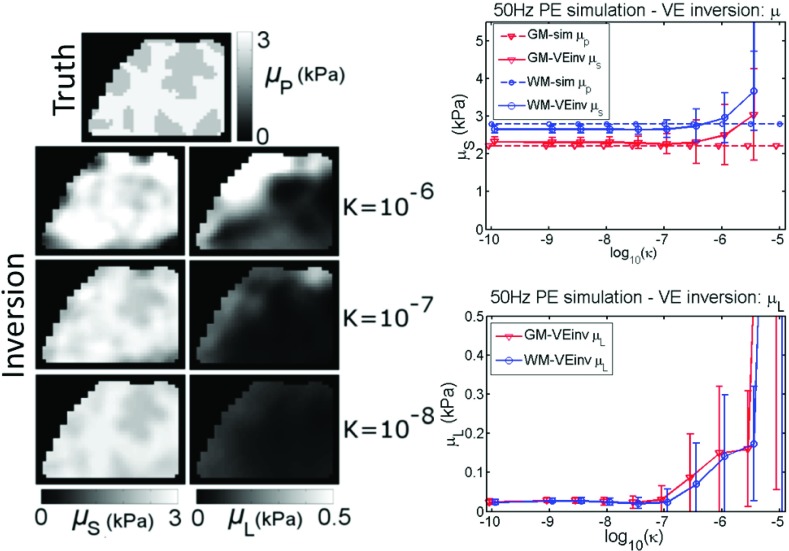
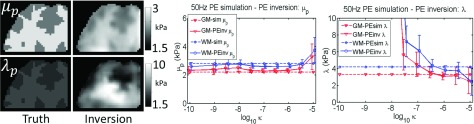
Results from experiments where the simulated data were inverted using an incorrect model are presented in Figs. 8–11. At 50 Hz, the choice of models is not critical to recovering contrast in stiffness; the VE μs is close to the simulated PE μp (Fig. 8) until κ > 10−6, and Fig. 9 indicates that the PE μp recovered from the inversion is a surrogate for the VE “shear stiffness,” μstiff, which reflects the shear wavespeed in a damped medium,48
| (8) |
The parameters in the PE inversion which govern attenuation (κ,λp, νp) in Fig. 9 do not reflect the distribution of the VE attenuation parameter (μL) from the simulation (although averaged values of PE parameters are sensitive to changes in μL). Similarly, in Fig. 8, the images of μL for the VE inversion do not show any contrast between the two tissue classes defined in the PE simulation (although the distribution of κ and νp were homogeneous for the simulation so the degree to which contrast should be expected is not clear). Nevertheless, VE μL values remained low until κ exceeded 10−7. When the frequency decreases to 1 Hz, the consequences of using an incorrect model are more severe. Images of the stiffness parameters (μs and μp) are spatially and quantitatively inaccurate for VE inversion of PE data (Fig. 10) and PE inversion of VE data (Fig. 11). Attenuation parameters also convey little spatial information, although, some interesting trends are present. μL in Fig. 10 peaks at an intermediate value of κ, which is expected because PE energy loss is a balance between the level of fluid flow (increases with κ) and the resistance to the fluid flow (decreases with κ). Additionally, Fig. 11 shows that the PE Poisson’s ratio, νp, is slightly below the value of νv for the viscoelastic simulation. This effect is expected because the apparent compressibility of a PE material results from a combination of the solid matrix compressibility and the resistance to fluid flow. If no resistance to flow occurs, the compressibility would be equivalent to the solid matrix, and if no fluid flow occurs, the material would appear completely incompressible.
FIG. 8.
Incorrect model: VE inversion of 50 Hz simulated PE data. A range of PE hydraulic conductivity (κ) was investigated, representative VE property images are shown for three selected κ values. The plots show values prescribed in the simulation as dotted lines, and recovered estimates from the inversion are represented by solid lines. Simulated gray matter (GM) and white matter (WM) tissue classes are plotted.
FIG. 11.
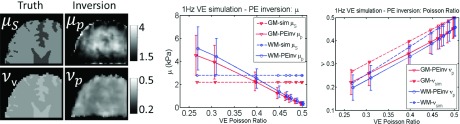
Incorrect model: PE inversion of 1 Hz simulated VE data. A range of VE Poisson’s ratios (νv) was investigated. Property values prescribed in the simulation are shown as dotted lines, and recovered values from the inversion are solid lines. Simulated gray matter (GM) and white matter (WM) tissue classes are plotted.
FIG. 9.
Incorrect model: PE inversion of 50 Hz simulated VE data. Simulated and reconstructed properties from Eqs. (1) and (2) are shown, as well as the effective VE shear stiffness defined in Eq. (8) and the PE Poisson ratio calculated using Eq. (3). Simulated gray matter (GM) and white matter (WM) tissue classes are plotted. Values prescribed in the simulation are shown as dotted lines, and recovered values from the inversion are represented by solid lines. A range of VE damping ratios, tanδ, was investigated.
FIG. 10.
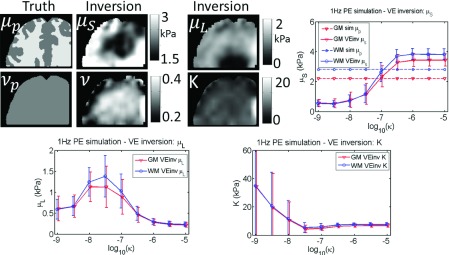
Incorrect model: VE inversion of 1 Hz simulated PE data. Values prescribed in the simulation are shown as dotted lines, and recovered estimates from the inversion are solid lines. Simulated gray matter (GM) and white matter (WM) tissue classes are plotted, and a range of PE hydraulic conductivity values (κ) was investigated.
3.B.1. Discussion
Descriptions of brain tissue as a cellular matrix saturated in mobile extracellular fluid and blood supports use of a poroelastic material model to describe the mechanical behavior of tissue. There have been previous applications of poroelastic tissue modeling, primarily in low frequency situations such as model based image deformation26 and in ultrasound elastography.49,50 The most prominent example of high frequency mechanical modeling of brain tissue occurs in traumatic brain injury simulations, where viscoelastic models have been more commonly applied.51–54 Initial experience in brain MRE also follows this trend—higher actuation frequencies use VE, whereas low frequency IA employs PE models. Figures 2 and 3 show the first examples of both PE and VE inversions of in vivo 50 Hz EA and 1 Hz IA MRE data, and VE is clearly preferable at higher frequencies, whereas PE works better at lower frequencies. With recent improvements in EA-MRE acquisition sequences, full brain 3D motions can be measured in 6 min,55 which would allow both EA and IA MRE data to be collected in a single imaging session. Mechanical property images obtained at these two frequencies could provide complementary diagnostic information; therefore, understanding how competing models perform in each frequency range is likely to be important.
PE is a more complicated model than VE. Assuming the solid and fluid densities are known, PE [Eq. (2)] has five properties (μp, λp, κ, ϕp, and ρa) which need to be estimated a priori or added to the set of parameters which are estimated during the NLI process, whereas VE [Eq. (1)] has three (μs, μL, and λ), which can be reduced to two if incompressibility is assumed. Inaccurate a priori estimates of PE parameters can lead to modeling errors, and each additional imaging unknown complicates the inversion process and places greater demands on data SNR and measurement resolution, as well as model accuracy. Continuum models are only approximations; the best model for NLI imaging will capture the most important tissue mechanical behaviors while minimizing model complexity. PE fluid flow is largest at very low frequencies, and the theory of fluid equilibration time suggests that a VE approximation of PE behavior is more appropriate at higher actuation frequencies, suggesting that PE modeling may be more important at lower motion frequencies and less critical for higher frequency actuation.
The simulation framework applied in this paper minimizes the “inverse crime” by computing high resolution simulated data which is subsequently interpolated to the imaging resolution and processed with the same NLI inversion protocol as in vivo MRE data.56 The coarse inverse FE model is not able to exactly support the high resolution property and displacement fields from the forward model, which better simulates a real MRE experiment where continuous displacement fields are sampled at a finite number of MR voxels. The data were not corrupted by synthetic noise to approximate the “ideal” measurements for each model, while still including interpolation and discretization errors which are unavoidable in a practical NLI imaging algorithm.
Inversions of simulated data using the correct model give an indication of the property estimation performance under ideal conditions. The VE inversions of VE data shown in Figs. 4 and 5 demonstrate that the storage modulus recovery is quantitatively accurate and able to recapitulate the fine details in gray/white matter boundaries, with some loss of contrast due to the regularization required to stabilize the NLI (causing smoothing at the boundaries). The quality of the loss modulus (μL) images at 50 Hz is comparable to that of the storage modulus; however, realistic μL values were not accurately imaged at 1 Hz because of low relative sensitivity compared to μs. The slight loss of accuracy at 1 Hz as the material became incompressible was not due to numerical instabilities in the finite element solution commonly encountered in solid mechanics, since the VE model has been stabilized to the incompressible limit.57 These errors are likely due to the large imbalance of resistances to volumetric and shear deformation—the displacements in the simulation were dominated by incompressibility, resulting in a lower sensitivity to changes in shear modulus. The PE shear modulus inversions of PE data in Figs. 6 and 7 were acceptable, although an instability occurs at very high κ values (which should not be problematic in tissue as κ is expected to be less than 10−6 in brain). The λp reconstructions suffer from greater inaccuracies, possibly due to the linear tetrahedral elements in the PE inversion which incur larger discretization errors at 2 mm resolution. To date, λ reconstructions have not been useful in MRE, possibly because of the inability to compute accurate values even without model data mismatch and measurement noise. Currently, we can only expect approximate values for λp; however, moving the PE model into the more stable multimesh framework with the quadratic elements employed in the VE model43 may improve λp images to the point where they could be diagnostically valuable.
The more interesting experiments involve inversions assuming incorrect models. At 50 Hz, Eq. (4) indicates that the fluid equilibration time is much shorter than the actuation period for κ < 10−6; therefore, a reasonable VE approximation to PE behavior exists. Figure 8 supports this assertion—the VE μs images resemble the PE μp from the simulation until κ → 10−6. Additionally, the PE inversion of VE data in Fig. 9 recovers a μp distribution which produces a shear wavelength approximating the shear wavelength of the VE simulation. Motion attenuation is another important factor for high frequency MRE, spatially averaged values of μL have been found to be diagnostically relevant for pathologies including breast cancer14 and multiple sclerosis.1 The mechanism of energy loss is different between VE and PE models—VE attenuation occurs in response to shear strain, whereas PE fluid flow occurs in regions of volumetric strain. Hence, not surprisingly, images of attenuation parameters do not convey any spatial information under incorrect inversion model assumptions. Even if an inappropriate model is assumed, both the elastic and attenuation parameters of the inversion model are still a function of the forward model parameters. Averaged property values will be sensitive to tissue structural changes which affect the parameters of the “true” tissue model. If brain tissue behavior is really PE, modeling errors may be a contributing factor to the difficulties encountered to date in producing μL images which accurately reflect anatomy with EA MRE.
At 1 Hz, the detrimental effects of incorrect inversion model choice are more severe. Spatial and quantitative accuracy of all parameters were poor for PE inversion of VE data (Fig. 11), and VE inversions of PE data (Fig. 10) for all of the PE and VE parameter combinations investigated. Although the fluid equilibration time theory at 1 Hz predicts reasonable VE equivalents of PE materials exist at very low κ values, the PE finite element model begins to encounter numerical problems in this range because the PE equations begin to resemble an incompressible single phase material. The VE model uses quadratic elements stabilized to the incompressible limit; however, the linear tetrahedral finite elements used in the PE model are susceptible to volume locking which causes inaccurate solutions. Hence, we did not observe evidence of model equivalence at very low κ values.
4. CONCLUSIONS
Empirically, VE models have been observed to produce better reconstructions at 50 Hz whereas PE is superior at 1 Hz. The poroelastic fluid equilibration timescale theory supports this observation—at 50 Hz, the equilibration time is much longer than the motion period; therefore, VE can be an adequate approximation of PE behavior and constitutes a simpler model for parameter estimation. However, VE is a poor approximation at 1 Hz because the equilibration time is on the same order as the actuation period, so correct modeling of PE materials is essential. This theory is supported by evidence from a comprehensive set of simulated MRE experiments investigating the effect of inappropriate model choice. Future work is focused on extending the 1 Hz poroelastic inversion and IA MRE acquisition protocol to enable estimates of parameters related to tissue structure and function, such as hydraulic conductivity, porosity, and internal pressure sources which are likely to be relevant to a wide range of neurological conditions.
ACKNOWLEDGMENT
We gratefully acknowledge support from the NIH Grant No. R01-EB018230-01.
REFERENCES
- 1.Wuerfel J., Paul F., Beierbach B., Hamhaber U., Klatt D., Papazoglou S., Zipp F., Martus P., Braun J., and Sack I., “MR-elastography reveals degradation of tissue integrity in multiple sclerosis,” NeuroImage 49(3), 2520–2525 (2010). 10.1016/j.neuroimage.2009.06.018 [DOI] [PubMed] [Google Scholar]
- 2.Murphy M. C., Huston J., Jack C. R., Glaser K. J., Manduca A., Felmlee J. P., and Ehman R. L., “Decreased brain stiffness in alzheimer’s disease determined by magnetic resonance elastography,” J. Magn. Reson. Imaging 34(3), 494–498 (2011). 10.1002/jmri.22707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Streitberger K.-J.et al. , “In vivo viscoelastic properties of the brain in normal pressure hydrocephalus,” NMR Biomed. 24(4), 385–392 (2011). 10.1002/nbm.1602 [DOI] [PubMed] [Google Scholar]
- 4.Chen J., Talwalkar J. A., Yin M., Glaser K. J., Sanderson S. O., and Ehman R. L., “Early detection of nonalcoholic steatohepatitis in patients with nonalcoholic fatty liver disease by using MR elastography,” Radiology 259(3), 749–756 (2011). 10.1148/radiol.11101942 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Siegmann K. C., Xydeas T., Sinkus R., Kraemer B., Vogel U., and Claussen C. D., “Diagnostic value of MR elastography in addition to contrast-enhanced MR imaging of the breast: Initial clinical results,” Eur. Radiol. 20(2), 318–325 (2010). 10.1007/s00330-009-1566-4 [DOI] [PubMed] [Google Scholar]
- 6.Sack I., Rump J., Elgeti T., Samani A., and Braun J., “MR elastography of the human heart: Noninvasive assessment of myocardial elasticity changes by shear wave amplitude variations,” Magn. Reson. Med. 61(3), 668–677 (2009). 10.1002/mrm.21878 [DOI] [PubMed] [Google Scholar]
- 7.Kolipaka A., McGee K. P., Araoz P. A., Glaser K. J., Manduca A., Romano A. J., and Ehman R. L., “MR elastography as a method for the assessment of myocardial stiffness: Comparison with an established pressure–volume model in a left ventricular model of the heart,” Magn. Reson. Med. 62(1), 135–140 (2009). 10.1002/mrm.21991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Weaver J. B., Van Houten E. E. W., Miga M. I., Kennedy F. E., and Paulsen K. D., “Magnetic resonance elastography using 3D gradient echo measurements of steady-state motion,” Med. Phys. 28, 1620–1628 (2001). 10.1118/1.1386776 [DOI] [PubMed] [Google Scholar]
- 9.Klatt D., Hamhaber U., Asbach P., Braun J., and Sack I., “Noninvasive assessment of the rheological behavior of human organs using multifrequency MR elastography: A study of brain and liver viscoelasticity,” Phys. Med. Biol. 52(24), 7281–7294 (2007). 10.1088/0031-9155/52/24/006 [DOI] [PubMed] [Google Scholar]
- 10.Johnson C. L., McGarry M. D. J., Houten E. E. W., Weaver J. B., Paulsen K. D., Sutton B. P., and Georgiadis J. G., “Magnetic resonance elastography of the brain using multishot spiral readouts with self-navigated motion correction,” Magn. Reson. Med. 70(2), 404–412 (2013). 10.1002/mrm.24473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Weaver J. B., Pattison A. J., McGarry M. D., Perreard I. M., Swienckowski J. G., Eskey C. J., Lollis S. S., and Paulsen K. D., “Brain mechanical property measurement using MRE with intrinsic activation,” Phys. Med. Biol. 57(22), 7275–7287 (2012). 10.1088/0031-9155/57/22/7275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sadd M. H., Elasticity: Theory, Applications, and Numerics (Elsevier, Waltham, MA, 2009). [Google Scholar]
- 13.Tschoegl N. W., Knauss W. G., and Emri I., “Poisson’s ratio in linear viscoelasticity—A critical review,” Mech. Time-Depend. Mater. 6(1), 3–51 (2002). 10.1023/A:1014411503170 [DOI] [Google Scholar]
- 14.Sinkus R., Siegmann K., Xydeas T., Tanter M., Claussen C., and Fink M., “MR elastography of breast lesions: Understanding the solid/liquid duality can improve the specificity of contrast-enhanced MR mammography,” Magn. Reson. Med. 58(6), 1135–1144 (2007). 10.1002/mrm.21404 [DOI] [PubMed] [Google Scholar]
- 15.Biot M. A., “Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range,” J. Acoust. Soc. Am. 28, 168–178 (1956). 10.1121/1.1908239 [DOI] [Google Scholar]
- 16.Biot M. A., “Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range,” J. Acoust. Soc. Am. 28(2), 179–191 (1956). 10.1121/1.1908241 [DOI] [Google Scholar]
- 17.Perriñez P. R., Kennedy F. E., Van Houten E. E. W., Weaver J. B., and Paulsen K. D., “Modeling of soft poroelastic tissue in time-harmonic MR elastography,” IEEE Trans. Biomed. Eng. 56(3), 598–608 (2009). 10.1109/TBME.2008.2009928 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cheng A. H. D., Badmus T., and Beskos D. E., “Integral equation for dynamic poroelasticity in frequency domain with bem solution,” J. Eng. Mech. 117(5), 1136–1157 (1991). 10.1061/(ASCE)0733-9399(1991)117:5(1136) [DOI] [Google Scholar]
- 19.Guyton A. C. and Hall J. E., Textbook of Medical Physiology (Elsevier Saunders, Philadelphia, PA, 2006). [Google Scholar]
- 20.Syková E. and Nicholson C., “Diffusion in brain extracellular space,” Physiol. Rev. 88(4), 1277–1340 (2008). 10.1152/physrev.00027.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nedergaard M., “Garbage truck of the brain,” Science 340(6140), 1529–1530 (2013). 10.1126/science.1240514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Franceschini G., Bigoni D., Regitnig P., and Holzapfel G. A., “Brain tissue deforms similarly to filled elastomers and follows consolidation theory,” J. Mech. Phys. Solids 54(12), 2592–2620 (2006). 10.1016/j.jmps.2006.05.004 [DOI] [Google Scholar]
- 23.Cheng S. and Bilston L. E., “Unconfined compression of white matter,” J. Biomech. 40(1), 117–124 (2007). 10.1016/j.jbiomech.2005.11.004 [DOI] [PubMed] [Google Scholar]
- 24.Nagashima T.et al. , “The finite element analysis of brain oedema associated with intracranial meningiomas,” Acta Neurochir. Supplementum 51, 155–157 (1990). 10.1007/978-3-7091-9115-6_52 [DOI] [PubMed] [Google Scholar]
- 25.Nagashima T., Tamaki N., Takada M., and Tada Y., “Formation and resolution of brain edema associated with brain tumors. A comprehensive theoretical model and clinical analysis,” Acta Neurochir. Supplementum 60, 165–167 (1994). 10.1007/978-3-7091-9334-1_44 [DOI] [PubMed] [Google Scholar]
- 26.Paulsen K. D., Miga M. I., Kennedy F. E., Hoopens P. J., Hartov A., and Roberts D. W., “A computational model for tracking subsurface tissue deformation during stereotactic neurosurgery,” IEEE Trans. Biomed. Eng. 46(2), 213–225 (1999). 10.1109/10.740884 [DOI] [PubMed] [Google Scholar]
- 27.Roberts D. W., Hartov A., Kennedy F. E., Miga M. I., and Paulsen K. D., “Intraoperative brain shift and deformation: A quantitative analysis of cortical displacement in 28 cases,” Neurosurgery 43(4), 749–758 (1998). 10.1097/00006123-199810000-00010 [DOI] [PubMed] [Google Scholar]
- 28.Miga M. I., Paulsen K. D., Hoopes P. J., F. E. Kennedy, Jr., Hartov A., and Roberts D. W., “In vivo quantification of a homogeneous brain deformation model for updating preoperative images during surgery,” IEEE Trans. Biomed. Eng. 47(2), 266–273 (2000). 10.1109/10.821778 [DOI] [PubMed] [Google Scholar]
- 29.Miga M. I.et al. , “In vivo modeling of interstitial pressure in the brain under surgical load using finite elements,” J. Biomech. Eng. 122(4), 354–363 (2000). 10.1115/1.1288207 [DOI] [PubMed] [Google Scholar]
- 30.Platenik L. A., Miga M. I., Roberts D. W., Lunn K. E., Kennedy F. E., Hartov A., and Paulsen K. D., “In vivo quantification of retraction deformation modeling for updated image-guidance during neurosurgery,” IEEE Trans. Biomed. Eng. 49(8), 823–835 (2002). 10.1109/TBME.2002.800760 [DOI] [PubMed] [Google Scholar]
- 31.Pattison A., McGarry M., Weaver J., and Paulsen K., “Spatially-resolved hydraulic conductivity estimation via poroelastic magnetic resonance elastography,” IEEE Trans. Med. Imaging 33(6), 1373–1380 (2014). 10.1109/TMI.2014.2311456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kyriacou S. K., Mohamed A., Miller K., and Neff S., “Brain mechanics for neurosurgery: Modeling issues,” Biomech. Model. Mechanobiol. 1(2), 151–164 (2002). 10.1007/s10237-002-0013-0 [DOI] [PubMed] [Google Scholar]
- 33.Bardet J. P., “A viscoelastic model for the dynamic behavior of saturated poroelastic soils,” J. Appl. Mech. 59(1), 128–135 (1992). 10.1115/1.2899417 [DOI] [Google Scholar]
- 34.McCutchen C. W., “Cartilage is poroelastic, not viscoelastic (including and exact theorem about strain energy and viscous loss, and an order of magnitude relation for equilibration time),” J. Biomech. 15(4), 325–327 (1982). 10.1016/0021-9290(82)90178-6 [DOI] [PubMed] [Google Scholar]
- 35.Galli M., Comley K. S. C., Shean T. A. V., and Oyen M. L., “Viscoelastic and poroelastic mechanical characterization of hydrated gels,” J. Mater. Res. 24(3), 973–979 (2009). 10.1557/jmr.2009.0129 [DOI] [Google Scholar]
- 36.Grodzinsky A. J., Roth V., Grossman W. D., Mow V. C., and Myers E., “The significance of electromechanical and osmotic forces in the nonequilibrium swelling behavior of articular cartilage in tension,” J. Biomech. Eng. 103(4), 221–231 (1981). 10.1115/1.3138284 [DOI] [PubMed] [Google Scholar]
- 37.Basser P. J., “Interstitial pressure, volume, and flow during infusion into brain tissue,” Microvasc. Res. 44(2), 143–165 (1992). 10.1016/0026-2862(92)90077-3 [DOI] [PubMed] [Google Scholar]
- 38.Morrison P. F., Chen M. Y., Chadwick R. S., Lonser R. R., and Oldfield E. H., “Focal delivery during direct infusion to brain: Role of flow rate, catheter diameter, and tissue mechanics,” Am. J. Physiol.: Regul., Integr. Comp. Physiol. 277(4), R1218–R1229 (1999). [DOI] [PubMed] [Google Scholar]
- 39.Morochnik V. and Bardet J. P., “Viscoelastic approximation of poroelastic media for wave scattering problems,” Soil Dyn. Earthquake Eng. 15(5), 337–346 (1996). 10.1016/0267-7261(96)00002-4 [DOI] [Google Scholar]
- 40.Johnson C. L., McGarry M. D. J., Gharibans A. A., Weaver J. B., Paulsen K. D., Wang H., Olivero W. C., Sutton B. P., and Georgiadis J. G., “Local mechanical properties of white matter structures in the human brain,” NeuroImage 79, 145–152 (2013). 10.1016/j.neuroimage.2013.04.089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Guo J., Hirsch S., Fehlner A., Papazoglou S., Scheel M., Braun J., and Sack I., “Towards an elastographic atlas of brain anatomy,” PLoS One 8(8), e71807 (2013). 10.1371/journal.pone.0071807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Perriñez P. R., “Magnetic resonance poroelastography,” Ph.D. thesis, Thayer School of Engineering at Dartmouth College, 2008. [Google Scholar]
- 43.McGarry M. D. J., Van Houten E. E. W., Johnson C. L., Georgiadis J. G., Sutton B. P., Weaver J. B., and Paulsen K. D., “Multiresolution MR elastography using nonlinear inversion,” Med. Phys. 39(10), 6388–6396 (2012). 10.1118/1.4754649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.McGarry M., Johnson C., Sutton B., Georgiadis J., Van Houten E., Weaver J., and Paulsen K., “Including spatial information in nonlinear inversion MR elastography using soft prior regularization,” IEEE Trans. Med. Imaging 13(10), 1901–1909 (2013). 10.1109/TMI.2013.2268978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.McGarry M. D. J., Van Houten E. E. W., Perriñez P. R., Pattison A. J., Weaver J. B., and Paulsen K. D., “An octahedral shear strain-based measure of SNR for 3D MR elastography,” Phys. Med. Biol. 56, N153–N164 (2011). 10.1088/0031-9155/56/13/N02 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Perriñez P. R., Pattison A. J., Kennedy F. E., Weaver J. B., and Paulsen K. D., “Contrast detection in fluid-saturated media with magnetic resonance poroelastography,” Med. Phys. 37(7), 3518–3526 (2010). 10.1118/1.3443563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Van Houten E. E. W., Doyley M. M., Kennedy F. E., Paulsen K. D., and Weaver J. B., “A three-parameter mechanical property reconstruction method for MR-based elastic property imaging,” IEEE Trans. Med. Imaging 24(3), 311–324 (2005). 10.1109/TMI.2004.842451 [DOI] [PubMed] [Google Scholar]
- 48.Manduca A., Oliphant T. E., Dresner M. A., Mahowald J. L., Kruse S. A., Amromin E., Felmlee J. P., Greenleaf J. F., and Ehman R. L., “Magnetic resonance elastography: Non-invasive mapping of tissue elasticity,” Med. Image Anal. 5(4), 237–254 (2001). 10.1016/S1361-8415(00)00039-6 [DOI] [PubMed] [Google Scholar]
- 49.Konofagou E. E., Harrigan T. P., Ophir J., and Krouskop T. A., “Poroelastography: Imaging the poroelastic properties of tissues,” Ultrasound Med. Biol. 27(10), 1387–1397 (2001). 10.1016/S0301-5629(01)00433-1 [DOI] [PubMed] [Google Scholar]
- 50.Righetti R., Righetti M., Ophir J., and Krouskop T. A., “The feasibility of estimating and imaging the mechanical behavior of poroelastic materials using axial strain elastography,” Phys. Med. Biol. 52(11), 3241–3259 (2007). 10.1088/0031-9155/52/11/020 [DOI] [PubMed] [Google Scholar]
- 51.Raul J.-S., Deck C., Willinger R., and Ludes B., “Finite-element models of the human head and their applications in forensic practice,” Int. J. Leg. Med. 122(5), 359–366 (2008). 10.1007/s00414-008-0248-0 [DOI] [PubMed] [Google Scholar]
- 52.Takhounts E. G., Ridella S. A., Hasija V., Tannous R. E., Campbell J. Quinn, Malone D., Danelson K., Stitzel J., Rowson S., and Duma S., “Investigation of traumatic brain injuries using the next generation of simulated injury monitor (SIMon) finite element head model,” Stapp Car Crash J. 52, 1–31 (2008). [DOI] [PubMed] [Google Scholar]
- 53.Brands D. W. A., Peters G. W. M., and Bovendeerd P. H. M., “Design and numerical implementation of a 3-D non-linear viscoelastic constitutive model for brain tissue during impact,” J. Biomech. 37(1), 127–134 (2004). 10.1016/S0021-9290(03)00243-4 [DOI] [PubMed] [Google Scholar]
- 54.Sabet A. A., Christoforou E., Zatlin B., Genin G. M., and Bayly P. V., “Deformation of the human brain induced by mild angular head acceleration,” J. Biomech. 41(2), 307–315 (2008). 10.1016/j.jbiomech.2007.09.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Johnson C. L., Holtrop J. L., McGarry M. D. J., Weaver J. B., Paulsen K. D., Georgiadis J. G., and Sutton B. P., “3D multislab, multishot acquisition for fast, whole-brain MR elastography with high signal-to-noise efficiency,” Magn. Reson. Med. 71(2), 477–485 (2014). 10.1002/mrm.25065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kaipio J. and Somersalo E., “Statistical inverse problems: Discretization, model reduction and inverse crimes,” J. Comput. Appl. Math. 198(2), 493–504 (2007). 10.1016/j.cam.2005.09.027 [DOI] [Google Scholar]
- 57.Cervera M., Chiumenti M., and Codina R., “Mixed stabilized finite element methods in nonlinear solid mechanics: Part I: Formulation,” Comput. Methods Appl. Mech. Eng. 199(37), 2559–2570 (2010). 10.1016/j.cma.2010.04.006 [DOI] [Google Scholar]