Independent calculation of monitor units for VMAT and SPORT

Abstract

Purpose:

Dose and monitor units (MUs) represent two important facets of a radiation therapy treatment. In current practice, verification of a treatment plan is commonly done in dose domain, in which a phantom measurement or forward dose calculation is performed to examine the dosimetric accuracy and the MU settings of a given treatment plan. While it is desirable to verify directly the MU settings, a computational framework for obtaining the MU values from a known dose distribution has yet to be developed. This work presents a strategy to calculate independently the MUs from a given dose distribution of volumetric modulated arc therapy (VMAT) and station parameter optimized radiation therapy (SPORT).

Methods:

The dose at a point can be expressed as a sum of contributions from all the station points (or control points). This relationship forms the basis of the proposed MU verification technique. To proceed, the authors first obtain the matrix elements which characterize the dosimetric contribution of the involved station points by computing the doses at a series of voxels, typically on the prescription surface of the VMAT/SPORT treatment plan, with unit MU setting for all the station points. An in-house Monte Carlo (MC) software is used for the dose matrix calculation. The MUs of the station points are then derived by minimizing the least-squares difference between doses computed by the treatment planning system (TPS) and that of the MC for the selected set of voxels on the prescription surface. The technique is applied to 16 clinical cases with a variety of energies, disease sites, and TPS dose calculation algorithms.

Results:

For all plans except the lung cases with large tissue density inhomogeneity, the independently computed MUs agree with that of TPS to within 2.7% for all the station points. In the dose domain, no significant difference between the MC and Eclipse Anisotropic Analytical Algorithm (AAA) dose distribution is found in terms of isodose contours, dose profiles, gamma index, and dose volume histogram (DVH) for these cases. For the lung cases, the MC-calculated MUs differ significantly from that of the treatment plan computed using AAA. However, the discrepancies are reduced to within 3% when the TPS dose calculation algorithm is switched to a transport equation-based technique (Acuros™). Comparison in the dose domain between the MC and Eclipse AAA/Acuros calculation yields conclusion consistent with the MU calculation.

Conclusions:

A computational framework relating the MU and dose domains has been established. The framework does not only enable them to verify the MU values of the involved station points of a VMAT plan directly in the MU domain but also provide a much needed mechanism to adaptively modify the MU values of the station points in accordance to a specific change in the dose domain.

1. INTRODUCTION

External beam radiation therapy is generally comprised of delivery of a series of station points (or control points) in either a discretized station-by-station or a continuous fashion via interpolation between consecutive station points.^1,2 Briefly, a station point is characterized by a set of parameters, such as the MLC aperture, gantry/collimator angle, and couch position. Along this line, the concept of a general station parameter optimized radiation therapy (SPORT) has been introduced to unite various therapeutic delivery schemes, such as three-dimensional conformal radiotherapy (3DCRT), intensity-modulated radiation therapy (IMRT), and volumetric modulated arc therapy (VMAT), and, more importantly, to provide a conceptual basis for optimizing the distribution of the station points. The premise of SPORT is that it allows us to realize the enormous potential of digital Linacs through optimal weighting and spatial distribution of the station points (including noncoplanar and even nonisocentric station points).³ VMAT (Refs. 4–6) represents a special case of SPORT with stationary couch and angularly uniformly distributed station points.

A significant question in the implementation of VMAT, or more generally, SPORT, is how to calculate the monitor units (MUs), which are the machine parameters directly related to dose delivery, independent of the treatment planning system (TPS). The need of an independent MU verification was discussed in a number of publications^7–11 and also mentioned in AAPM TG-114 and 120.^12,13 In 3DCRT, it is a standard practice to verify the MUs through an independent hand calculation, in which the beam data and radiological depth of a reference point are used to ensure the correctness of the MU of each treatment beam. The verification for IMRT and VMAT treatment plan is rather intractable and usually done in the dose domain,^7,14,15 in which an independently measured dose or dose distribution in phantom is compared with the treatment plan, and a pass or failure decision is made based on the preset criterion of an evaluation metric (e.g., gamma index).^16–22 However, it is important to note that, in this commonly used plan verification approach, the only thing common to the original treatment plan and the phantom plan is the beam arc sequence. As thus, any dosimetric inaccuracy specific to the patient is not reflected in the homogenous phantom measurement. Additionally, phantom measurement generally does not provide 3D dose distribution because of the limited number of detectors. Phantom measurement validates, at best, the output of the machine and deliverability of the dose delivery file from the TPS, which can be realized with much simplified design. Finally, the passing or failure criterion using gamma index may be somewhat arbitrary as the resultant passing rate may depend heavily on the selected region of interest (ROI).²³

The purpose of this work is to develop a general strategy for independent MU calculation of VMAT/SPORT with an independent dose calculation algorithm. The proposed approach allows us to verify a treatment plan on a patient anatomy model, eliminating the potential inaccuracy associated with the use of an unrealistic surrogate phantom. Since the MU is a fundamental machine delivery parameter associated with the treatment beam, the approach allows us to pin-down the individual station point(s) that may be problematic in a treatment plan. In Secs. 2–5, we first present the principle and procedure of the independent MU calculation method. The technique is then applied to a series of clinical cases, including different disease sites, beam modalities, and TPS dose calculation algorithms, to illustrate the accuracy and robustness of the proposed strategy.

2. METHOD AND MATERIAL

2.A. Formulation for MU verification

For a given VMAT plan with a known set of station points {s}, the dose d_i at a point i in the patient or phantom can be obtained by summing the contributions delivered from all the station points, given by

$${\displaystyle d_i=\sum _{s=1}^S\left(A_{i,s}\times {\text{MU}}_s\right),}$$ (1)

where A_i,s is a dose matrix element characterizing the dosimetric contribution of the sth station point to the ith voxel with unit MU, MU_s is the monitor units of the sth station point. The equation can be written in a matrix form as D = A ⋅ MU. For a given dose calculation algorithm, the MU values of the involved station points of a VMAT treatment plan can be obtained by inverting the above equation, that is

$${\displaystyle \mathrm{MU}=A^{-1}D.}$$ (2)

The above equations form the basis for our VMAT/SPORT plan verification. The verification can proceed in either dose domain or MU domain. The former is to use the MUs from the treatment plan to compute the dose distribution in the patient or deliver the same plan to a phantom and measure the dose distribution, and then compare the result with the treatment plan. The latter is to use the dose distribution of treatment plan to derive the MUs using an independently computed dose matrix A, and then compare the results with the MUs of the treatment plan. A key issue in this approach is how to obtain reliably the dose matrix, A, using an independent dose algorithm. The role of the matrix is similar to the beam data in the MU check of conventional 3DCRT plan. In this work, an in-house Monte Carlo (MC) dose calculation engine is employed to derive the plan specific A-matrix. The problem expressed by Eq. (2) may be ill-posted depending on the number and positions of sampling points and the accuracy of TPS dose calculation. In an ideal situation, where the TPS dose algorithm is as accurate as the MC calculation and sufficient sampling points are chosen, the problem is well-defined and a unique solution exists. Otherwise, the “optimal” set of MU values that best reproduces the prescribed dose distribution will be generated.

2.B. Monte Carlo calculation of A-matrix and dose

An in-house implemented voxel-based Monte Carlo (VMC) system^24–26 is employed to compute the A matrix in Eq. (1) or (2). The patient’s DICOM-RT file exported from our clinical Eclipse treatment planning system is used as the input of the MC dose calculation engine, which includes the CT images, segmented structures, and station point settings. The MU values of the involved station points are set to unity before the calculation. Two phase–space datasets are used in the MC dose calculation engine. The primary phase space PS_A, located above the upper jaws, is precalculated using BEAMnrc.²⁷ PS_A does not change with the treatment plans as all parts above the upper jaws are assumed fixed. The secondary phase space PS_B, located in the plane below the MLC, represents the output of the Linac, acting as a source of particle transporting into the patient or phantom. The PS_B is calculated for all station points by weighting PS_A with fluence maps that are fabricated based on the apertures of secondary collimator (jaws) and the tertiary collimator (MLC). For each station point of a VMAT plan, the absolute dose per MU (cGy/MU) at the prescription point(s) or user-selected points are computed. At least ten millions of particles passing through the target, primary collimator, flattening filter, monitor chamber, and mirror are used for each simulation.^18,22 A statistical uncertainty less than 1%–2% within a voxel (0.25 × 0.25 × 0.25 cm³) is set to ensure the accuracy of resultant calculation. The in-house dose calculation system has been commissioned for the Varian Linacs used in our clinic.

2.C. MU verification

Our independent MU calculation technique proceeds in two steps: (1) assigning a unit MU to each station point in the VMAT arc sequence file and calculating the dose matrix elements {A_i,s} for a set of points using an independent dose calculation algorithm and (2) obtaining the MUs by optimally reproducing the TPS dose distribution on the prescription surface with the MC-derived influence matrix. Note that, for MU verification, a full 3D dose distribution is not necessary and only the doses at a number of spatial points, e.g., the points located on the surface of dose prescription (for many clinical cases at Stanford, this is the isodose surface covering 95% of PTV volume) are needed. In general, the number of points should be greater than that of the station points involved. In our implementation, a line passing through the center of each beam is drawn, and the intersection points of the rays and the prescription surface are selected as the calculation points.

Because of the inherent difference between the dose calculation algorithms used in TPS and MU verification, an exact inversion of Eq. (1) of the TPS dose distribution with MC-derived A-matrix may not exist. This is similar to that, in the dose domain, the TPS and MC doses may differ for the same set of {MU_s}. The MU values in our approach are determined in such a way that the dose distribution computed by MC is closest to the planned one in the least-squares sense. An iterative algorithm is thus developed to minimize the least-squares difference between the two dose distributions

$${\displaystyle \mathrm{\Phi }\left(\overrightarrow{m}\right)=\sum _{i=1}^I{\left(\underset{i}{\overset{\mathrm{TPS}}{d}}-\underset{i}{\overset{\mathrm{MC}}{d}}\right)}^2=\sum _{i=1}^I{\left(\underset{i}{\overset{\mathrm{TPS}}{d}}-\sum _{s=1}^S\underset{i,s}{\overset{\mathrm{MC}}{A}}\cdot {\mathrm{MU}}_S\right)}^2,}$$ (3)

where $d_i^{\text{TPS}}$ and $d_i^{\text{MC}}$ are the planned and MC doses, respectively for a given set of MUs, $A_{i,s}^{\text{MC}}$ is the MC dose matrix element representing the dose delivered per MU from the sth station point, S is the number of station points, and I is the number of the voxel points of interest. An iterative algorithm was applied to obtain the optimal MUs.

2.D. Evaluation of the proposed MU verification method

The proposed independent MU calculation technique is evaluated by using 16 VMAT treatment plans (Table I), including treatments of different diseases, prescriptions, treatment modalities, energies, and machines. These VMAT plans are generated using Eclipse treatment planning system (Varian Medical Systems, Palo Alto, CA). Anisotropic analytical algorithm (AAA) is used in planning for all sites but lung where two plans, one with AAA and the other with Acuros XB algorithm, are made. For each case, the MC-MUs obtained using the proposed approach are compared with that of the original Eclipse treatment plan. In addition, the MC and Eclipse-computed dose distributions are compared quantitatively in the dose domain using a few dosimetric metrics, including isodose curves, characteristic dose profile, gamma index, and dose volume histogram (DVH).

TABLE I.

Summary of 16 representative cases used for the evaluation of the proposed MU verification method and the final results.

Case no.	Site	Prescribed dose (cGy)	No. of fraction	Linac	Energy (MV)	No. of arcs	Algorithm	Mean difference (<Δ%) in MU	Max difference (<Δ%) in MU
1	HN	7000	33	Trilogy™	6	2	AAA	1.7	1.8
2			7000	33	Clinac 21 ex™	6	4	AAA	1.8	1.9
3			6300	28	Clinac 21 ex™	6	2	AAA	2.2	2.4
4	Pros	500	25	Clinac 21 ex™	15	4	AAA	2.5	2.6
5			7800	39	TrueBeam™	15	2	AAA	2.4	2.6
6			7800	38	TrueBeam™	15	2	AAA	2.5	2.6
7			4500	23	TrueBeam™	15	2	AAA	2.2	2.4
8		Brain	7000	33	Clinac 21 ex™	6	3	AAA	2.4	2.4
9			4500	25	TrueBeam™	6	1	AAA	2.6	2.7
10	Liver	3170	1	TrueBeam™	10 FFF	1	AAA	1.8	2.0
11	GI	4500	25	Clinac 21 ex™	15	2	AAA	2.3	2.4
12	Esophagus	4500	25	Clinac 21 ex™	15	3	AAA	2.5	2.5
13	Lung	6500	1	TrueBeam™	10 FFF	Partial	AAA	6.5	6.8
														AXB	1.9	2.1
14			6800	1	TrueBeam™	10 FFF	1	AAA	7.2	7.4
														AXB	2.0	2.3
15			6000	20	Clinac 21ex™	6	2	AAA	9.3	9.5
														AXB	2.1	2.3
16			6600	30	Trilogy™	6	2	AAA	5.1	5.4
														AXB	1.7	1.9

3. RESULTS

3.A. Monte Carlo-based MU verification

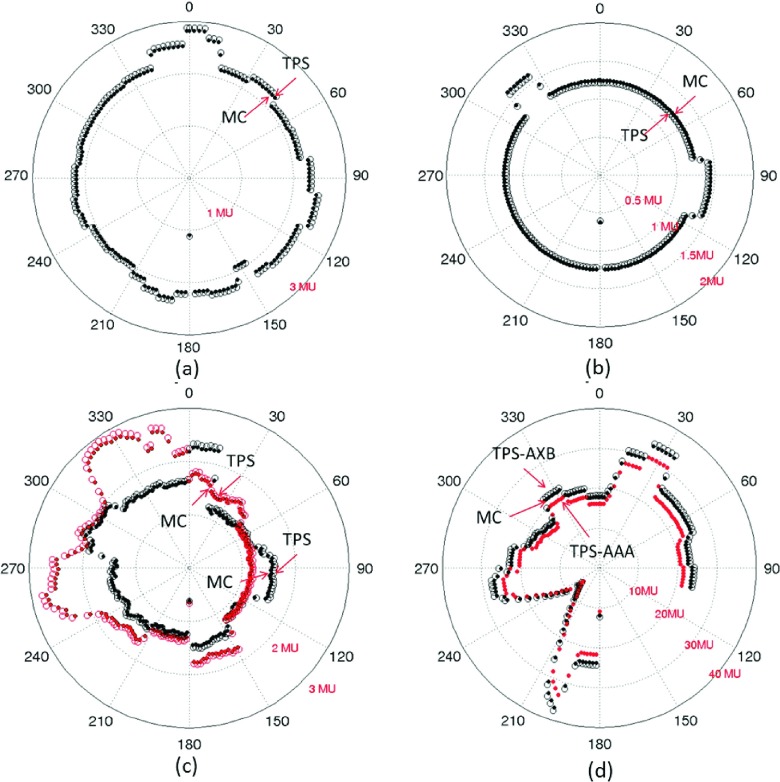
MC and Eclipse-calculated MUs for all the station points of four representative cases (case 1, 5, 9, and 14 in Table I) are shown in Fig. 1. From the first three polar plots of the MU difference vs the station point (or the gantry angle), it is seen that the MC-MUs agree with TPS-MU very well. The relative difference of MUs calculated by TPS and MC is listed in Table I. The mean difference between MC-MUs and TPS-MUs is 2.6% for the one-arc brain treatment with 177 station points [Fig. 1(a), case #9], 1.7% for the two-arc head-and-neck case with 354 station points [Fig. 1(b), case #1], and 2.4% for the two-arc prostate case with 354 station points [Fig. 1(c), case #5]. The maximum discrepancies for all the station points are found to be 1.8%, 2.6%, 2.7%, respectively, for the three cases. Similarly, excellent agreement is found for all other cases listed in Table I, except the lung cases #13–16.

FIG. 1.

Comparison of MC-MUs and TPS-MUs computed using Anisotropic Analytical Algorithm (AAA) and Acuros algorithm (AXB) for (a) an one-arc brain plan (case #9), (b) a two-arc head-and-neck plan (case #1), (c) a two-arc prostate plan (case #5), and (d) a partial-arc lung plan (case #14).

In Figs. 1(d) and 1(a), partial arc lung SBRT treatment (case #14) with 138 station points is shown. Both Eclipse Acuros and AAA algorithms are applied to this case and the results are compared with the MC calculation. It is found that the MC-MU differs about 2% from the Acuros-planned MU. However, both MC- and Acuros-MUs differ significantly from the AAA MUs (>7%), which reveals the importance of an accurate algorithm in the presence of tissue inhomogeneity. In another lung case (#15), the discrepancy between MC and AAA-MU values is even larger (9.3%). The Acuros yields much improved results.

3.B. Comparison of dose distributions

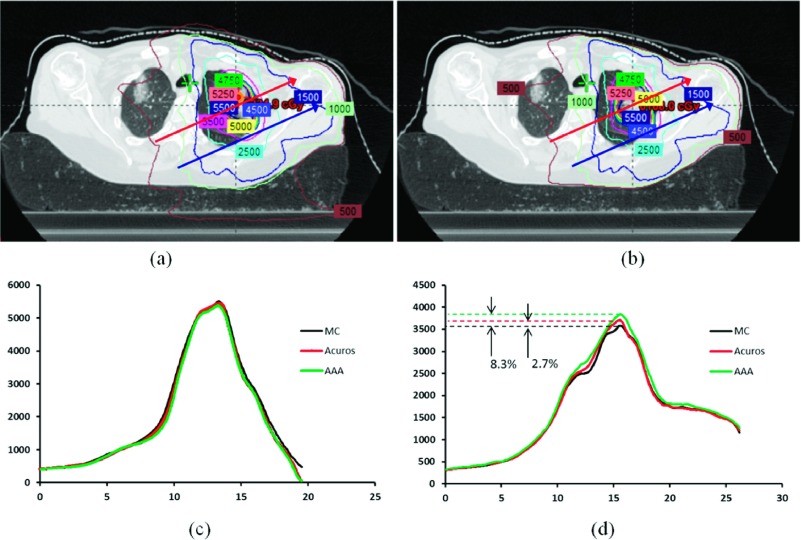
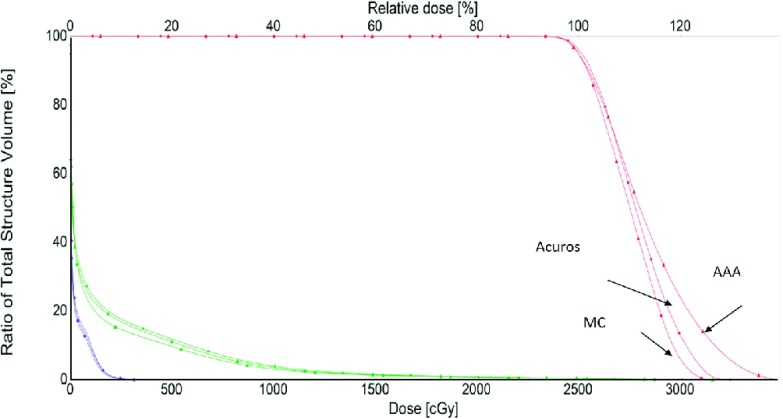
The accuracy of the proposed plan validation approach is also tested in the dose domain. Logically, if the calculated MUs match well with the TPS plan, the resulting MC dose distribution should be in a good agreement with that from the Eclipse dose calculation engine. In Figs. 2(a) and 2(b), MC and Acuros-computed isodose distributions are displayed for the lung case studied above [#14 in Table I, Fig. 1(d)]. In Fig. 2(c), the MC, Acuros, and AAA dose profiles along the blue line are plotted. It is seen that the differences between three algorithms are negligible in the absence of tissue density heterogeneity. On the other hand, the results along the red line passing through the lung tissue show significant differences (up to 8.3%) between MC, AAA, and Acuros calculations. The maximum difference between MC and Acuros is, however, found to be less than 2.7% for points along this line. In Fig. 3, the DVHs of MC, AAA, and Acuros plans are compared for the lung case #14. It is demonstrated that there is no significant difference between the MC and Acuros doses. However, a significant difference between the MC and Eclipse AAA is observed. These results are consistent with that observed in the MU domain.

FIG. 2.

Dose distributions calculated using MC (a) and Eclipse Acuros (b) for case #14. The dose profiles of MC, Acuros, and AAA calculations along the upper and lower lines in (a) are shown in (c) and (d).

FIG. 3.

DVHs of PTV, right lung, and left lung obtained using different dose calculation algorithms for a lung SBRT case.

4. DISCUSSION

Up to this point, patient specific VMAT QA has been done in the dose domain either experimentally using a phantom or computationally using a software tool. These techniques use the MUs and dose delivery leaf sequence file of a patient treatment plan to obtain the doses at selected points in the phantom or patient model. While the MUs and dose distribution are closely related, it is important to point out the difference between plan validations in dose and MU domains as well as potential utility of independent MU calculation. A forward MC calculation followed with a comparison with the TPS dose distribution provides a useful tool for validating a VMAT/SPORT plan. In reality, while the dosimetric discrepancy between TPS and MC calculations is inevitable, the acceptable dosimetric uncertainty should be evaluated differentially, depending on the position(s) in the patient. A QA criterion that can differentially deal with one or more specific subsets of dose points is highly desirable. The MUs in our work are derived from a subset of dose points along the prescription isodose. As thus, the MU verification here is, to a large extent, equivalent to verifying the dose on the prescription isodose surface (this is similar to the MU verification in 3DCRT where the dose at a reference point is validated through an independent MU calculation). In other words, a special attention is paid to the dose points of prescription. Validating the MUs (or the dose at the prescription points) confirms the accuracy of dose calculation. Of course, to ensure the delivery of prescribed dose to the right location also needs positive verification of the delivery system and RT information system as well as the accurate execution of the treatment.

It is important to realize that, because the MUs are related to the machine delivery directly, the MU calculation represents an “upstream” verification as compared with a dose domain comparison. In general, dose and MUs represent two important facets of a radiation therapy treatment. Passing of a QA in a “downstream” dose comparison does not automatically guarantee the accuracy of the “upstream” MU values, as the QA criterion (e.g., the gamma index) does not always “overlap” with the MU domain criterion. In a sense, the proposed MU calculation provides a self-consistency check of the plan validation system, with the emphasis on the correctness of dose points on the prescription isodose (this type of inverse test or consistency check is often done for a complicated computational algorithm, e.g., deformable image registration²⁸). In practice, it may be beneficial to combine the forward MC dose comparison and the “backward” MU calculations for optimal QA decision-making. The chief merit of this work is that it provides a computational framework for relating formally the “upstream” MU values to the “downstream” doses at a set of prespecified points to enable the prioritized QA decision-making.

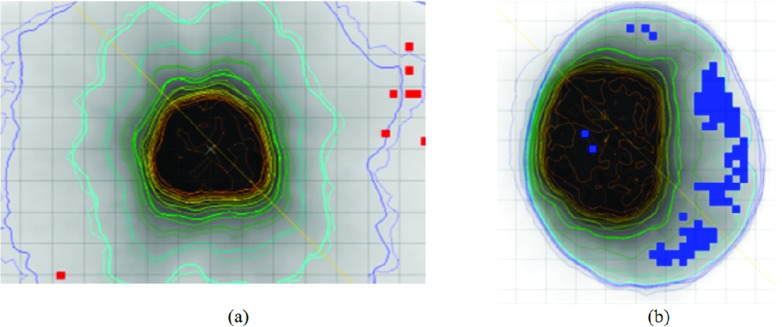
MU verification is equivalent to examining the dosimetric agreement for the points on the prescription surface, instead of an arbitrary ROI in the 3D patient volume, and thus, passing the MU QA does not automatically guarantee the accuracy of the dose at every voxel inside the patient. The same is the case for most dose domain QAs. Figure 4 shows two examples (#5 and #9 in Table I) that have passed the MU domain tests. In dose domain, however, a few failed points are present in low dose regions when the (3 mm, 3%) gamma index criterion is employed. The results here are, of course, not surprising and reiterate the need for a QA strategy of combining dose domain and MU calculation.²⁹ Just like the MU test is aimed to ensure adequate PTV coverage, more specific test(s) than the gamma index in the dose domain could be designed with prioritized goals to meet different clinical needs in the future.

FIG. 4.

The points that failed (3%/3 mm) gamma index criteria in the low dose regions in a prostate plan (a) (case #5) and a brain plan (b) (case #1).

In addition to plan validation, the technique may have additional clinical applications in the future, which include (1) interchange of treatment machines: clinically, a patient treatment sometimes needs to be realized in a similar but different machine during a course of treatment. In this case, instead of reoptimizing the treatment plan using the new machine data on TPS, it is straightforward to derive a set of MUs (and thus the VMAT arc sequence) based on the already optimized dose distribution. In reality, this can be implemented as a function in TPS; and (2) adaptive (minor) modification of the MUs for treatment delivery. Broadly, it is envisioned that the MUs may need to be modified either on-line or off-line during the course of a treatment (e.g., the MUs need to be scaled slightly in accordance with the results of dosimetric QA measurement/calculation). The proposed MU calculation scheme provides a mechanism to modify the MUs on a station-point specific basis and it, thus, is valuable for the future realization of adaptive radiation therapy. Of course, the two possible applications here may be subject to the constraints of delivery system (such as gantry speed, MLC speed, collimator speed, and dose rate) and this issue should be considered to ensure that the deliverability of the revised plan.

While the realization of the above functions may eventually require the commitment from commercial companies providing the TPSs, this work lays foundation for these applications. The proposed method requires the calculation of the A-matrix elements at a series of points of interest and optimization of Eq. (3). While different techniques can be employed to compute the A-matrix, we chose the MC method which is known to be the most accurate dose calculation algorithm. In the absence of tissue density inhomogeneity, other types of algorithm, such as a superposition/convolution method, should be also acceptable. The superposition/convolution algorithm is computationally more efficient than a stochastic MC method. However, with the use of a cloud-based computing environment or other high performance computing technique,^30,31 a fully fledged MC calculation can be done efficiently, making it feasible for routine clinical applications.

5. CONCLUSION

A novel independent MU calculation technique has been proposed. By verifying the machine delivery settings of VMAT/SPORT treatment plans, the technique provides a higher level of confidence about the accurate delivery of the prescribed dose. Compared to the phantom-measurement based approach, the technique allows us to validate the plan in the realistic CT-derived patient models. With the use of a cloud-based MC platform for dose matrix generation, the system can be computationally efficient and applicable for routine clinical use. When implemented clinically, the proposed approach may provide a new paradigm for future VMAT/SPORT QA.

The proposed technique has been applied to 16 representative clinical cases. Our results indicated that the independently computed MUs agree with that of Eclipse values to within 2.7% for all VMAT plans except for the lung cases, in which the discrepancy greater than >3% between MC- and AAA-MUs has been found. It should be noted that the proposed method is not limited to VMAT and should be applicable to any form of SPORT, including IMRT and 3DCRT.