Abstract
Clustered data commonly arise in epidemiology. We assume each cluster member has an outcome Y and covariates 
. When there are missing data in Y, the distribution of Y given 
in all cluster members (“complete clusters”) may be different from the distribution just in members with observed Y (“observed clusters”). Often the former is of interest, but when data are missing because in a fundamental sense Y does not exist (e.g., quality of life for a person who has died), the latter may be more meaningful (quality of life conditional on being alive). Weighted and doubly weighted generalized estimating equations and shared random-effects models have been proposed for observed-cluster inference when cluster size is informative, that is, the distribution of Y given 
in observed clusters depends on observed cluster size. We show these methods can be seen as actually giving inference for complete clusters and may not also give observed-cluster inference. This is true even if observed clusters are complete in themselves rather than being the observed part of larger complete clusters: here methods may describe imaginary complete clusters rather than the observed clusters. We show under which conditions shared random-effects models proposed for observed-cluster inference do actually describe members with observed Y. A psoriatic arthritis dataset is used to illustrate the danger of misinterpreting estimates from shared random-effects models.
Keywords: Bridge distribution, Immortal cohort inference, Informative missingness, Missing not at random, Mortal cohort inference, Semi-continuous data
1. Introduction
Clustered data are common in epidemiology. Repeated measures are clustered in individuals; teeth in patients; pups in litters. Suppose interest is in the association between outcome Y and covariates 
measured on members of the clusters. Often Y and 
are missing for some members of sampled clusters. For simplicity, we assume that a member's 
is observed whenever Y is observed. We call members with observed Y “observed members,” those with missing Y “missing members,” the original clusters “complete clusters,” and the subclusters that remain after discarding missing members “observed clusters.”
Missing data may arise because although a variable could, in principle, be measured, circumstances meant it was not, for example, because an individual missed a visit. We call such missing data “potentially observable.” When missing data are potentially observable, a model can be proposed for the distribution of Y given 
in all cluster members, and methods used that, under specified assumptions about the missingness (e.g., missing at random, MAR), give consistent estimates for this model. We call this “complete-cluster inference.”
Alternatively, missing data may arise because in a fundamental sense a variable does not exist. We call such missing data “unobservable.” Three examples of unobservable Y are measures of: (1) cognitive function of an individual after death; (2) degree of disablement of an individual who is not disabled; (3) health of a tooth that has been lost. Although missing Y could be set to zero when a patient is dead/not disabled/tooth is lost, in practice often a model is instead proposed for Y given 
in observed members only (so conditional on alive/disabled/tooth not lost). We call this “observed-cluster inference.” Sometimes observed-cluster inference may be of interest even when missing data are potentially observable. When missing data are unobservable “complete-cluster” inference is philosophically problematic: what does it mean to model cognitive function in dead people?
When the size M of complete clusters varies, it is usually assumed that Y is independent of M given 
. In observed clusters, however, Y and N may be conditionally dependent given 
, where N is size of observed cluster. For example, in a dental study, the fewer teeth a patient has, the worst their condition tends to be. This is called “informative cluster size” (ICS).
So far we have assumed observed clusters are generated from complete clusters by excluding missing members, but ICS can also arise where observed clusters are complete in themselves. For example, in toxicology, exposed dams who are more sensitive to a toxin may tend to have smaller litters and offspring with greater probability of deformation than less sensitive dams, so that Y (pup being deformed) and N (litter size) are dependent given X (exposure of dam).
We shall show that three of the methods proposed for observed-cluster inference under ICS, viz. weighted and doubly weighted generalized estimating equations (GEE) and shared random effects models, can be seen as actually giving inference for complete clusters. When the Y’
associations in complete and observed clusters are the same, the distinction is unimportant. However, ICS causes them to differ in general. So, it is important to understand when methods proposed for observed-cluster inference really do describe observed clusters. In the literature on modeling repeated measures in cohorts with high death rates (Dufouil et al., 2004; Kurland et al., 2009) a distinction has been made between complete-cluster (termed “immortal-cohort”) inference and observed-cluster (“mortal-cohort”) inference. However, conditions under which the two inferences are equivalent have not been set out, and in the wider literature the distinction seems to be less well recognized.
In Section 2011 we define notation and discuss methods for complete-cluster inference from observed data. Section 2004 defines ICS and discusses how ICS relates to missing-data mechanisms. Section 2011 relates two weighted GEE methods, one proposed for complete-cluster inference in the missing-data literature, and one for observed-cluster inference in the ICS literature. We also show that doubly weighted GEE, proposed for observed-cluster inference, actually give complete- rather than observed-cluster inference, and that, moreover, there is no single complete-cluster inference. Shared random-effects models give complete-cluster inference, but have also been used for observed-cluster inference. In Section 2011 we discuss when this is valid, and in Section 2011 we use a psoriatic arthritis dataset to illustrate that some parameters of such a model may be relevant to observed clusters but others not. In brief, we replicate an analysis of association between disability and covariates, with measurements clustered by patient. Our interest is in how sex affects degree of disability in the “observed clusters” of measurements where degree is greater than zero, that is, given disability. The analysis uses models for probability of disability and for degree of disability given disability which share a random intercept. Because probability of disability is higher in women than in men with the same intercept and other covariates, intercept and sex are not independent given disability and other covariates. Consequently, the effect of sex on degree of disability given disability is less than is suggested by the estimated parameter.
2. Notation and Complete-Cluster Inference
Let K be the number of complete clusters in the sample. When needed we use subscript i to index cluster, but usually omit this. Let M (known) be size of complete cluster. Let 
and 
(
) be outcome and covariate vector, respectively, for member j of the complete cluster, and 
and 
. Let 
if 
is observed, 
if 
is missing, and 
. 
is always observed. Members with 
are “observed members”; those with 
are “missing members.” Let 
be size of observed cluster. Assume 
are i.i.d. For any value 
of 
, partition 
, where 
belongs to 
if 
and to 
if 
. For example, 
and 
. Partition 
likewise, except that if some elements of 
are observed even on missing members, these elements belong to 
.
Data are missing at random (MAR) if 
for some function 
(informally, 
) and missing completely at random (MCAR) if 
(Seaman et al., 2013) (note M is a function of 
, as 
has M columns). Otherwise they are missing not at random (MNAR). We say data are missing with equal probability (MWEP) if 
. MCAR means that which members are observed does not depend on 
or Y values in the cluster. This would be so if, for example, missing data had been lost by the researchers. MAR allows missingness to depend on data on observed members plus any observed data on missing members. For example in a longitudinal study individuals’ probability of dropout may depend on past health measurements but not on current health. If it also depends on current health, the data are MNAR. MWEP means the number N of observed members may depend on 
and Y but given this number all sets of N observed members are equally likely. This could be so if missingness depends only on cluster-level summaries of 
and Y.
The missingness process is monotone if 
. 
then defines 
and vice versa. If 
are exchangeable given M, we say “members of complete clusters are exchangeable.” Indices 
can then be assigned to observed members and 
to missing members. Missingness is then monotone.
To make “complete-cluster” inference, a model is specified for 
given 
. To fit this using observed data (
), an assumption (e.g., MAR) is made about the missingness process and a method used that is valid under this assumption, for example, inverse probability weighting (IPW) or random-effect models (Albert and Follmann, 2009). We consider two approaches to complete-cluster inference that relate to methods proposed for observed-cluster inference. The first specifies a (marginal) model for 
and assumes
 |
(1) |
so that we can define 
. This model is fitted to observed clusters using GEE with IPW. The second approach uses a shared random-effects model. This gives cluster-specific inference, but random effects can be integrated out to get 
.
3. Informative Cluster Size
3.1. Semi-Parametric Marginal Models
For each cluster with 
, let H be the index of a randomly selected member of the observed cluster. So, 
. Marginal inference for the population of typical observed members and marginal inference for the population of all observed members mean estimating the parameters of a model for 
and for 
, respectively. Whereas 
is the expectation of Y given 
giving equal weight to each observed cluster, 
gives equal weight to each observed member. Clusters with 
play no role in 
or 
.
Hoffman et al. (2001), Williamson et al. (2003) and Benhin et al. (2005) define non-informative cluster size (NICS) as 
. Otherwise cluster size is informative (ICS). Under NICS, 
. Under ICS, 
in general. They advocate using 
. Use of 
has been proposed for mortal cohorts when missing data are due to death, and for modeling degree of disability or health of teeth when missing data are due to non-disabled patients or absent teeth (Dufouil et al., 2004; Kurland et al., 2009; Su et al., 2011; Li et al., 2011). Hoffman et al. (2001) gave an estimator for 
. Williamson et al. (2003) and Benhin et al. (2005) gave an asymptotically equivalent and computationally less intensive method: weighted independence estimating equations (WIEE) (see also Wang et al. (2011) for three-level data). The same equations without weighting (IEE) estimate 
. We describe WIEE and IEE in Section 2007.
3.2. Random-Effects Models
Dunson et al. (2003), Gueorguieva (2005), Chen et al. (2011), and Neuhaus and McCulloch (2011) consider cluster-specific inference using a linear or generalized linear mixed model (LMM/GLMM). They interpret NICS to mean the random effects 
in the mixed model are independent of N, and ICS to mean they are not. NICS in this sense implies NICS in the sense of Hoffman et al., but the converse is not true. To deal with ICS when fitting the LMM/GLMM, several authors have combined it with a model for N or 
, with the same or correlated random effect (Dunson et al., 2003; Gueorguieva, 2005; Chen et al., 2011; Su et al., 2009; Su et al., 2011; Li et al., 2011). We discuss this model in Section 2011.
3.3. Relating ICS to Missingness Mechanisms
Hoffman et al. (2001) wrote that ICS is “closely related” to violation of the MCAR condition. In fact, MCAR is not a sufficient condition for NICS. For example, suppose all complete clusters have size 
and have 
, there are no covariates, and 
. It is easy to show that 
but 
.
Proposition 1
Cluster size will be non-informative if data are MCAR and, moreover, either i) equation 2009 holds, or ii) 
and the data are MWEP.
Note 2009 is often assumed with GEEs, but 
is unlikely, as 
. Proofs of Propositions are in Web Appendices A and E. Just as both ICS and NICS can arise from MCAR mechanisms, so they can from MAR and MNAR (examples in Web Appendix B).
When 2009 holds, so 
is defined, a sufficient condition for 
is MWEP and 
, because the Y-X relation in a randomly chosen member of an observed cluster is then the same as in a random member of the corresponding complete cluster.
4. Weighted and Doubly Weighted GEE
4.1. Weighted GEE (WGEE)
Assume 2009 holds and 
, where g is a link function. If 
and 
were observed, 
could be estimated with GEE. With missing data, WGEE can be used. These weight member j by 
. Robins et al. (1995) proposed use of WGEE when M does not vary, missingness is monotone and MAR, and 
.
When data are MWEP and 
, weights 
can be used instead (proof in Web Appendix C). In this case, 
(Section 2001), so WGEE with weights 
also give observed-cluster inference. In fact, with independence working correlation they are the WIEE proposed by Williamson et al. (2003) for estimating 
in 
. So, WIEE have a dual interpretation: they estimate 
under any missingness mechanism; and 
when data are MWEP and 
.
WIEE without weights (IEE) estimate 
in a model 
(Dufouil et al., 2004).
4.2. Doubly Weighted GEE (DWGEE)
If there is ICS and the distribution of 
depends on N, interpretation of 
may be awkward, because the Y’
association is confounded by N (Williamson et al., 2003). For example, let X be binary and 
and 
be increasing functions of N. Then typical members with 
tend to come from larger clusters than typical members with 
, so 
even though X has no effect on Y within clusters.
Huang and Leroux (2011) proposed DWGEE1 and DWGEE2. DWGEE1 can be used when 
is categorical and every observed cluster contains at least one member with each of the possible values of 
. DWGEE1 are the same as WIEE except that member j is inversely weighted not by 
but by the total number of observed members in the same cluster who have 
. Thus the total weight of members with 
is the same for all possible 
. Rather than estimating 
, DWGEE1 estimate 
in the population formed by each cluster in the population contributing one member with each possible value of 
.
DWGEE2 was proposed for when not all observed clusters contain a member with each possible value of 
. In DWGEE2 observed member j is inversely weighted by the expected (rather than actual, as in DWGEE1) number of observed members with 
. In Web Appendix D we show that DWGEE2 estimates 
in a population of larger “complete” clusters in which each cluster contains at least one member with each possible value of 
. Each cluster in the dataset is considered to be the observed component of one of these larger clusters, with the rest being missing. The problem with this is that, unless observed clusters really do arise from larger clusters in which all values of 
are represented (which is not so in Huang and Leroux's example), the larger clusters are purely hypothetical and it is unclear why they should be of scientific interest. Further, as shown in Web Appendix D, the distribution of Y given 
in the hypothetical population of complete clusters depends on which predictors are included in the model for the expected number with 
, and there is no obvious reason to prefer one set of predictors to any other.
5. Random-Effect Models
5.1. LMM, GLMM, and Shared Random Effect Model
The general form of the LMM is (continuing to omit the subscript i for cluster)
 |
(2) |
 |
(3) |
 |
(4) |
where 
is a subvector of 
, and 
a cluster-specific latent variable. This is a model for Y’
association in complete clusters. Assumption 
means that 
and hence that size of complete clusters is non-informative. Elements of 
not in 
are said to have fixed effects; those in 
have random effects. It follows from 2005 and 2011 that 
. So, 
also has a marginal interpretation in complete clusters. LMMs are a special case of GLMMs. In GLMMs, 
is assumed to belong to the exponential family, 2005 is replaced by
 |
(5) |
where 
is the link function, and 2011 and 2004 are assumed to hold.
If Y is binary, 
and 
has a bridge distribution with rescaling parameter 
(
), then 
and so 
(in combination with 
) has a marginal interpretation in complete clusters (Wang and Louis, 2003). More generally, 
does not have a marginal interpretation, though 
can be calculated as 
.
The MLE of 
from fitting the mixed model to observed clusters is consistent when data are MAR, but not, in general, when MNAR. However, Neuhaus and McCulloch (2011) showed that for LMMs, if (i) 
includes an intercept term, (ii) 
are i.i.d., (iii) 
, and (iv) the only random effect is an intercept (i.e., 
), then 
is consistently estimated except for the intercept. They found the same was approximately true of GLMMs. More generally, they say that if 
and 
are subvectors of 
and 
with 
and 
, then their results suggest that the MLE of elements of 
corresponding to 
will be approximately unbiased.
For MNAR data, a model for 
can be added to the LMM/GLMM. The result is a shared random-effects model (Albert and Follmann, 2009). When
 |
(6) |
for some function 
, the MLEs of 
and 
from this model are consistent. An indirect way (Su et al., 2009; Li et al., 2011; Su et al., 2011) to model 
is to introduce another random effect 
, assume 
, and specify models 
for the distribution of 
and 
for 
. We call the resulting model for 
“a correlated random-effects model.” It is a special case of the shared random-effects model, with 
and 
.
5.2. Interpretation of 
and 
in Complete Clusters
Partition 
and 
as 
and 
, where 
and 
are the lth elements of 
and 
, respectively. If 
has a random effect, partition 
as 
, where 
corresponds to 
, and partition 
similarly. If 
has a fixed effect, 
, 
and 
. Let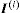 
denote a vector of the same length as 
, with lth element equal to one and all other elements equal to zero.
within-cluster effects
If 
is cluster varying with fixed effect, 
is its within-complete-cluster effect in clusters of size 
. That is, if two members of the same complete cluster have 
values that differ only by 
for some 
, then their expected Y values differ by 
for an LMM. In a GLMM, the expected value is transformed by link function g; for example, for logit link, 
is their log odds ratio. If 
is cluster varying with random effect, 
and 
are the mean and variance of the within-cluster effect.
between-cluster effects
and 
can be interpreted in terms of differences between expected Y in members of different complete clusters. That is, if for some 
, two complete clusters are randomly sampled conditional on one containing a member with 
and the other a member with 
, then the difference between the expected Y values of these two members is
 |
(7) |
This reduces to 
for the LMM and to 
for the GLMM with bridge distribution.
causal effects
If 
is manipulable, for example, treatment, 
may be interpretable as a causal effect in complete clusters. Let 
be the potential outcome of member j when 
is manipulated to equal x. We make the following “causal assumptions” (Vansteelandt, 2007). First, 
, that is, observed outcome equals outcome that would be seen if 
were set to its observed value. Second, manipulating 
does not affect 
or 
or Y values of other members. Third, 
, where 
is set of possible values of 
. With these assumptions, the conditional expected causal effect 
of 
given 
and 
is 
. For LMMs, 
reduces to 
. The conditional expected causal effect 
of 
given 
is 
, which reduces to 
for LMMs and to 
for GLMMs with bridge distribution.
5.3. Interpretation of 
and 
in Observed Clusters
Section 1995 discussed how 
and 
in the model defined by 2005–2004 or 2011–2003 describe the Y’
association in complete clusters. Now we discuss how the same
and 
relate to associations in observed clusters.
within-cluster fixed effects
When 2005 holds and 
is cluster varying with fixed effect, 
is not only the within-complete-cluster effect of 
, it is also the within-observed-cluster effect, which is the same in all observed clusters of size 
. That is, if two members of the same observed cluster of size 
have 
values that differ only by 
for some 
, then their expected values (transformed by link function g in the case of the GLMM) of Y differ by 
.
When considering within-observed-cluster effects of covariates with random effects, between-observed-cluster effects and causal effects, we find it convenient to introduce the concept of the LMM/GLMM given by equations 2005–2004 or 2011–2003 “describing observed random subclusters.” For a cluster with 
, let 
denote the set of indices of a simple random sample of size n from the N observed members, and let 
. Note that 
is the same as what we denoted in Section 2004 by H. We say “the LMM given by 2005–2004 describes observed random subclusters of size n from observed clusters of size 
” (or, more concisely, “the LMM describes observed random subclusters of size n”) if
 |
(8) |
 |
(9) |
 |
(10) |
 |
(11) |
where 
and 
in 2011–2011 are the same parameters (i.e., have the same values) as in equations 2005–2004. Similarly, “the GLMM (given by 2011–2003) describes observed random subclusters of size n” if
 |
(12) |
and 2007–2011 hold. If 2011–2011 or 2007–2011 hold for one or more values of n, we have a basis for interpreting the estimates of 
and 
obtained by fitting the LMM/GLMM given by 2005–2003 (which describes complete clusters) in terms of effects in observed clusters. We give these interpretations below. Later (Proposition 2) we give sufficient conditions for the LMM/GLMM to describe observed random subclusters of size n and (Section 2008) show what can happen when these conditions are not satisfied. Note that the statement that LMM/GLMM describes random subclusters of size n is a statement about the Y’
relation only in observed members of clusters with 
; the association in missing members or in clusters with 
is not relevant. We shall focus on 
when discussing between-cluster effects, but for within-cluster effects we need 
, because within-cluster comparisons only make sense in clusters with at least two members. In most realistic settings, if the sufficient conditions (Proposition 2) are satisfied for n, they are also satisfied for 
.
within-cluster random effects
If the LMM/GLMM describes observed random subclusters of size n (with 
) and 
is a cluster-varying covariate with random effect, then 
and 
are the mean and variance of the within-observed-cluster effect of 
. That is, if an observed cluster is randomly sampled conditional on 
and on n members randomly chosen from it having 
values that differ only in 
, then the expected values (transformed by link function g) of Y of any pair of these n members differ by 
, where 
is the difference between their 
values, and the distribution of 
is given by 
.
between-cluster effects
If the LMM/GLMM describes observed random subclusters of size 
, 
are the between-observed-cluster effects of 
. That is, if two clusters each with 
are randomly sampled conditional on 
in one cluster and 
in the other, then the difference between the expectations of 
in the two clusters is
 |
(13) |
Since 1995 has the same form as 2001, between-cluster effects in observed and complete clusters are equal and 
and 
describe them both. As with 2001, 1995 reduces to 
for the LMM. When 
has fixed effect, this is true even if 
is not independent of N, so 2009 is not necessary for 
to be interpreted as a between-observed-cluster fixed effect in a LMM.
causal effects
Let 
be manipulable and the “causal assumptions” of Section 1995 hold. Let 
and 
. If the LMM/GLMM describes observed random subclusters of size n (
) and 
, then 
and 
describe a causal effect of 
in observed random subclusters of size n. That is, the expected causal effect given 
and 
in the members whose indices belong to 
is equal to 
with 
, and the expected causal effect given 
is equal to 
. For the LMM when 
has fixed effect, 
reduces to 
even if 2009 does not hold. Note that if 
depends on 
, this causal interpretation is problematic because membership of observed clusters may change as 
is manipulated, that is, some observed members would not have been observed if their 
values had been otherwise, while some missing members would have been observed.
Proposition 2
The LMM/GLMM describes observed random subclusters of size n if (i) 
, where 
is a cluster-constant subvector of 
; either (iia) 
are exchangeable given M or (iib) 
whenever 
is a permutation of 
; and (iii) 
.
Note that (iii) holds if the minimum possible observed cluster size is 
, but is unlikely to hold otherwise; and if (iii) is replaced by the weaker condition 
, then 2011, 2007 and 2011 still hold, but 2009 may not.
5.4. Situations Where Complete- and Observed-Cluster Effects Differ
With the exceptions mentioned above (i.e., within-cluster fixed effects, and between-cluster and causal fixed effects in LMMs when 2007 holds), 
and 
may not be so interpretable in terms of effects in observed clusters if 2007 or 2009 do not hold.
Suppose that 2009 with 
does not hold and 
has a random effect. The between-observed-cluster effect of 
is given by 1995 with 
replaced by 
. In particular, it does not reduce to 
for the LMM unless 
. Similarly, the observed-cluster causal effect 
is, in general, not the same as the complete-cluster causal effect 
; and the within-observed-cluster effect will not, in general, have mean 
and variance implied by 
.
In the following example, 2007 does not hold for 
. Suppose clusters are old people in a cohort study of cognitive function Y. A LMM is used, with a random effect for time because rate of cognitive decline varies between people. Assume a fixed effect for the intercept. The only missing data are due to death: 
if person i is alive at time j; 
if dead. So, 
, 
, 
and missingness is monotone. Suppose people with more rapid decline (more negative 
) tend to die earlier. The within-complete-cluster effect of 
has mean 
and variance 
. The mean and variance of the within-observed-cluster effect are functions of 
: they both diminish as 
increases. This is because the subsample still alive at later times is enriched for high 
. In this setting “complete-cluster” inference has been called inference for a hypothetical immortal cohort, and it has been suggested that “observed-cluster” inference (describing the population still alive at each timepoint) is of more interest (Dufouil et al., 2004). See Section 2011 and Web Appendix F for examples of between-cluster or causal effects differing in complete and observed clusters.
5.5. Observed Clusters Without Complete Clusters
Dunson et al. (2003), Chen et al. (2011) and Gueorguieva (2005) wanted observed-cluster inference when “complete clusters” do not exist, for example, toxicology experiments where clusters are litters. Dunson et al. and Gueorguieva assumed cluster-constant 
, 
and 
. Chen et al. assumed 
was cluster constant or a function of j (e.g., 
), 
and 
. It can be seen that these methods give complete-cluster inference for a hypothetical population of complete clusters in which 
and from which the population of observed clusters would be generated by applying monotone missingness mechanism 
. However, they do not only provide complete-cluster inference. When, as in Dunson et al. and Gueorguieva, 
is cluster constant and 
, conditions (i), (iia) and (iii) of Proposition 2 hold with 
, so 
and 
are also between-cluster or causal effects in observed clusters. When, as in Chen et al., 
is cluster varying, 
and 
, non-intercept elements of 
are within-observed-cluster effects.
6. Example: Psoriatic Arthritis
This example shows a model that ostensibly describes observed clusters but some of whose parameters relate only to a population of complete clusters with no obvious meaning. Husted et al. (2007) analyzed a cohort of 382 psoriatic arthritis (PsA) patients. Physical function was measured by the health assessment questionnaire score (HAQ). HAQ is semi-continuous: it is zero (no disability) with positive probability and otherwise varies continuously up to 3 (severe disability). 31% of the 2107 HAQ scores were zero. They separately modeled 
(the “binary-part”) and HAQ given 
(the “continuous-part”), using, respectively, logistic regression with random intercept 
and linear regression with random intercept 
. Both parts had the same covariates (sex, time since onset, etc.), and all covariates had fixed effects. Among the conclusions was that being female predicted higher HAQ when 
, adjusting for other covariates.
Here, clusters are patients and “observed cluster” means a patient's set of non-zero scores. Su et al. (2009) noted that estimates for the continuous part might be biased because separate modeling of binary and continuous parts did not account for ICS caused by the model for the binary part determining the observed cluster size in the continuous part. So, they modified Husted et al.’s model by replacing 
by 
, where 
is unknown. They called this shared random-effect model the “latent-process model” (SAS code provided in Web Appendix G). They also used a correlated random effects model, but results were similar.
In the original (misspecified) model of Husted et al., the estimated sex effect in the continuous part was 0.181 (SE 0.051). In the latent-process model, it was 0.246 (SE 0.052) ( Table 1). We focus on the meaning of this latter estimate. We emphasize there is nothing intrinsically wrong with the latent-process model. It can validly be used to predict HAQ. What is important is not to misinterpret the parameters in the continuous part. As this is an LMM and sex is cluster-constant with fixed effect, the estimated sex effect, 0.246, describes the between-cluster effect in “complete clusters,” that is, in a hypothetical world in which all scores are somehow non-zero. The meaning and scientific interest of this hypothetical world, analogous to the world of “immortal cohorts,” is unclear.
Table 1.
Estimates for latent process model and marginal model fitted to psoriatic arthritis data
| latent process model |
marginal model |
|||||
|---|---|---|---|---|---|---|
| binary part |
continuous part |
|||||
| Parameter | estim | SE | estim | SE | estim | SE |
| Intercept | −0.9909 | 0.3556 | 0.1748 | 0.0555 | 0.263 | 0.0669 |
| Age at onset | 0.6392 | 0.1538 | 0.0984 | 0.0250 | 0.115 | 0.0267 |
| Female | 2.0037 | 0.3149 | 0.2461 | 0.0523 | 0.100 | 0.0580 |
| PsA disease duration | 0.0166 | 0.0220 | 0.0044 | 0.0032 | 0.004 | 0.0041 |
| Actively inflamed joints | 0.1380 | 0.0465 | 0.0243 | 0.0027 | 0.023 | 0.0045 |
| Clinically deformed joints | 0.0179 | 0.0238 | 0.0051 | 0.0031 | 0.007 | 0.0037 |
| PASI score | 0.1543 | 0.1017 | 0.0257 | 0.0134 | −0.005 | 0.0237 |
| Morning stiffness | 1.5691 | 0.2018 | 0.1620 | 0.0262 | 0.273 | 0.0444 |
| ESR | 0.2971 | 0.1103 | 0.0374 | 0.0126 | 0.065 | 0.0232 |
| Medication: | ||||||
| NSAIDs | 0.2960 | 0.2439 | −0.0181 | 0.0280 | −0.235 | 0.0467 |
| DMARDs | 0.3138 | 0.2197 | 0.0226 | 0.0272 | 0.003 | 0.0442 |
| steroids | 0.9927 | 0.4355 | 0.0481 | 0.0441 | 0.049 | 0.0553 |
Actively inflamed joints disease duration |
0.0003 | 0.0031 | −0.0005 | 0.0002 | 0.0000 | 0.0002 |
Clinically deformed joints disease duration |
0.0018 | 0.0011 | 0.0003 | 0.0001 | 0.0000 | 0.0001 |
| Var(u) | 4.2641 | 0.9001 | ||||
 |
0.2074 | 0.0210 | ||||
 |
0.0779 | 0.0039 | ||||
Su et al. (2009) do not comment on the meaning of their estimated sex effect, but suppose one wished to interpret it as an effect in observed clusters, as done in Husted et al. (2007). As all the covariates have fixed effects, estimates for cluster-varying covariates can be interpreted unproblematically as within-cluster effects in complete or observed clusters. However, sex is cluster-constant. To illustrate the problem with interpreting the estimated sex effect, 0.246, as a between-cluster effect in observed clusters, we obtained the empirical Bayes estimate of each patient's random intercept 
. While the means of 
were 0.005 and 0.016 for men and women, respectively, means of 
for observations on men and women when 
were 0.165 and 0.043. This difference arises because in the binary part of the model the estimated sex effect is 2.00 (SE 0.31), meaning that a woman was more likely to have 
than a man with the same values of other covariates. So, if we compare a man and woman who both have 
and have the same time since onset and other covariate values, we expect the woman's HAQ to be not 0.246 greater but only 
greater. Note that in Su et al.’s model, none of the conditions of Proposition 2 hold for any n.
We also used IEE to fit a model for 
, the conditional mean of HAQ given sex, time since onset, etc. and 
( Table 1). The estimated sex effect is 0.100 (SE 0.031), which is close to the effect, 0.124, worked out above using empirical Bayes estimates.
In conclusion, the estimated sex effect in the continuous part of the latent-process model (and correlated random-effects model) describes the association between sex and HAQ in a hypothetical population of little scientific interest; for this dataset it overstates the size of the effect in the population of scientific interest. In further work, Su et al. (2011) found an association of genotype HLA-B27 with HAQ when 
. The same interpretation problem applies here: this association refers to the hypothetical “complete” clusters.
7. Discussion
We have shown that shared random-effect models do not always describe observed clusters, except for cluster-varying covariates with fixed effects or under the conditions of Proposition 2. The models of Dunson et al. (2003), Gueorguieva (2005) and Chen et al. (2011) are unnecessarily restrictive. They assume either cluster-constant 
or that N does not depend on 
. Proposition 2 shows 
can be cluster varying if N depends only on cluster-constant elements. The assumptions required do, however, remain restrictive. WIEE relate to IPW for missing data. DWGEE2 give inference for a hypothetical population of complete clusters that is, in general, neither unique nor of scientific interest.
For binary Y, Li et al. (2011) used a correlated random-intercepts model with bridge distributions, so that 
. For a single binary X, they compared the log odds ratios in complete and observed clusters. They found the difference was small when the variance of the random intercepts or the correlation between them was small. However, when random-intercept variances and/or correlation are small, cluster size is only weakly informative; when size is strongly informative, inferences for complete and observed clusters will differ more. We replicated Li et al's study and found the two log odds ratios could differ by as much as 25% when 
, and 56% when 
(see Web Appendix H).
We have assumed Y and 
are observed in all members for which we wish to make inference. Dufouil et al. (2004) and Shardell and Miller (2008) give methods for when this is not so.
Having illustrated the danger of misinterpreting estimates, we recommend careful thought about which inference is of scientific interest and which analysis method will give it.
8. Supplementary Materials
Web Appendices referenced in Sections 3–7 are available with this paper at the Biometrics website on Wiley Online Library.
Acknowledgments
SRS is funded by MRC grants U1052 60558 and MC_US_A030_0015, AJC and MP by MRC grant G0600657. We thank Brian Tom for helpful comments on a draft of this article, and Li Su for providing the PsA data and advising on the use of SAS.
Supporting Information
Additional Supporting Information may be found in the online version of this article.
Supporting Information.
References
- Albert P, Follmann D, Fitzmaurice G, Davidian M, Verbeke G, Molenberghs G. Shared-parameter models. Longitudinal Data Analysis. 2009. pp. 433–452. Chapman & Hall/CRC, Boca Raton, Florida.
- Benhin E, Rao J, Scott A. Mean estimating equation approach to analysing cluster-correlateddata with nonignorable cluster sizes. Biometrika. 2005;92:435–450. [Google Scholar]
- Chen Z, Zhang B, Albert P. A joint modeling approach to data with informative cluster size:Robustness to the cluster size model. Statistics in Medicine. 2011;30:1825–1836. doi: 10.1002/sim.4239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dufouil C, Brayne C, Clayton D. Analysis of longitudinal studies with death and drop-out: A casestudy. Statistics in Medicine. 2004;23:2215–26. doi: 10.1002/sim.1821. [DOI] [PubMed] [Google Scholar]
- Dunson D, Chen Z, Harry J. A Bayesian approach for joint modeling of cluster size andsubunit-specific outcomes. Biometrics. 2003;59:521–530. doi: 10.1111/1541-0420.00062. [DOI] [PubMed] [Google Scholar]
- Gueorguieva R. Comments about joint modelling of cluster size and binary andcontinuous subunit-specific outcomes. Biometrics. 2005;61:862–867. doi: 10.1111/j.1541-020X.2005.00409_1.x. [DOI] [PubMed] [Google Scholar]
- Hoffman E, Sen P, Weinberg C. Within-cluster resampling. Biometrika. 2001;88:1121–1134. [Google Scholar]
- Huang Y, Leroux B. Informative cluster size for subcluster-level covariates and weightedgeneralized estimating equations. Biometrics. 2011;67:843–851. doi: 10.1111/j.1541-0420.2010.01542.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Husted J, Tom B, Farewell V, Schentag C, Gladman D. A longitudinal study of the effect of disease activity and clinicaldamage on physical function over the course of psoriatic arthritis: Does theeffect change over time. Arthritis and Rheumatism. 2007;56:840–849. doi: 10.1002/art.22443. [DOI] [PubMed] [Google Scholar]
- Kurland B, Johnson L, Egleston B, Diehr P. Longitudinal data with follow-up truncated by death: Match theanalysis method to research aims. Statistical Science. 2009;24:211–222. doi: 10.1214/09-STS293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Bandyopadhyay D, Lipsitz S, Sinha D. Likelihood methods for binary responses of present components in acluster. Biometrics. 2011;67:629–635. doi: 10.1111/j.1541-0420.2010.01483.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuhaus J, McCulloch C. Estimation of covariate effects in generalized linear mixed modelswith informative cluster sizes. Biometrika. 2011;98:147–162. doi: 10.1093/biomet/asq066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins J-M, Rotnitzky A, Zhao L-P. Analysis of semiparametric regression models for repeated outcomes inthe presence of missing data. Journal of the American Statistical Association. 1995;90:106–121. [Google Scholar]
- Seaman S, Galati J, Jackson D, Carlin J. What is meant by ‘missing at random’? Statistical Science. 2013;28:257–268. [Google Scholar]
- Shardell M, Miller R. Weighted estimated equations for longitudinal studies with death andnon-monotone missing time-dependent covariates and outcomes. Statistics in Medicine. 2008;27:1008–25. doi: 10.1002/sim.2964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su L, Tom B, Farewell V. Bias in 2-part mixed models for longitudinal semicontinuous data. Biostatistics. 2009;10:374–389. doi: 10.1093/biostatistics/kxn044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su L, Tom B, Farewell V. A likelihood-based two-part marginal model for longitudinalsemi-continuous data. Statistical Methods in Medical Research. 2011 doi: 10.1177/0962280211414620. DOI: 10.1177/0962280211414620. Available at: http://smm.sagepub.com/content/early/2011/08/25/0962280211414620.abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt S. On confounding, prediction and efficiency in the analysis oflongitudinal and cross-sectional clustered data. Scandinavian Journal of Statistics. 2007;34:478–498. [Google Scholar]
- Wang M, Kong M, Datta S. Inference for marginal linear models for clustered longitudinal datawith potentially informative cluster sizes. Statistical Methods in Medical Research. 2011;20:347–367. doi: 10.1177/0962280209347043. [DOI] [PubMed] [Google Scholar]
- Wang Z, Louis T. Matching conditional and marginal shapes in binary random interceptmodels with a bridge distribution function. Biometrika. 2003;90:765–775. [Google Scholar]
- Williamson J, Datta S, Satten G. Marginal analyses of clustered data when cluster size is informative. Biometrics. 2003;59:36–42. doi: 10.1111/1541-0420.00005. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information.