Dynamic Connectivity at Rest Predicts Attention Task Performance

Abstract

Consistent spatial patterns of coherent activity, representing large-scale networks, have been reliably identified in multiple populations. Most often, these studies have examined “stationary” connectivity. However, there is a growing recognition that there is a wealth of information in the time-varying dynamics of networks which has neural underpinnings, which changes with age and disease and that supports behavior. Using factor analysis of overlapping sliding windows across 25 participants with Parkinson disease (PD) and 21 controls (ages 41–86), we identify factors describing the covarying correlations of regions (dynamic connectivity) within attention networks and the default mode network, during two baseline resting-state and task runs. Cortical regions that support attention networks are affected early in PD, motivating the potential utility of dynamic connectivity as a sensitive way to characterize physiological disruption to these networks. We show that measures of dynamic connectivity are more reliable than comparable measures of stationary connectivity. Factors in the dorsal attention network (DAN) and fronto-parietal task control network, obtained at rest, are consistently related to the alerting and orienting reaction time effects in the subsequent Attention Network Task. In addition, the same relationship between the same DAN factor and the alerting effect was present during tasks. Although reliable, dynamic connectivity was not invariant, and changes between factor scores across sessions were related to changes in accuracy. In summary, patterns of time-varying correlations among nodes in an intrinsic network have a stability that has functional relevance.

Introduction

Studies of spontaneous fluctuations in the blood oxygenation level-dependent signal measured at rest with functional magnetic resonance imaging (fMRI) have greatly advanced our understanding of how cortical regions interact in large-scale systems. Consistent spatial patterns of coherent activity, representing large-scale networks, have been reliably identified in multiple populations (Beckmann et al., 2005; Damoiseaux et al., 2006). Most often, these studies have examined “stationary” connectivity, which is blind to time-varying changes in connectivity that may occur over the duration of a several-minute scan. However, there is a growing recognition that there is a wealth of information in the time-varying dynamics of networks which has neural underpinnings, which changes with age and disease and that supports behavior (Chang and Glover, 2010; Hutchison et al., 2012, 2013; Jones et al., 2012; Smith et al., 2012).

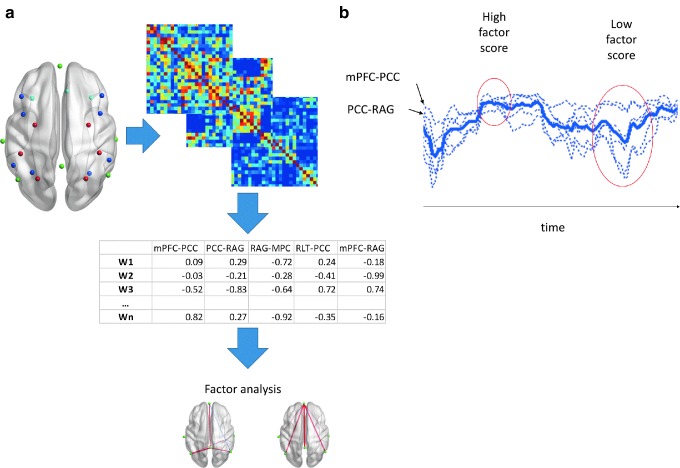
There are many ways to measure dynamic connectivity (for a recent review, see Hutchison et al., 2013). We describe our approach briefly here. We have observed in an earlier work (Madhyastha and Grabowski, 2013) that not only do correlations among network nodes (computed from sliding windows) change throughout a scan, but they also do so in a structured way (i.e., certain groups of nodes increase or decrease their intercorrelations together). Using factor analysis, we can identify covarying correlations and describe how closely they are coupled. This is illustrated in Figure 1. Although a mean factor score, which summarizes the time-varying coupling of a subset of nodes across the scan, is clearly related to the stationary functional connectivity of the nodes in that subset, factor analysis more accurately quantifies the coupling of correlations, information lost in ordinary stationary analyses.

FIG. 1.

Overview of dynamic correlation factor analysis. (a) Dynamic correlation analysis uses the z-transformed correlations of the time courses among all regions of interest within sliding windows (W1…Wn) as an input to a factor analysis, yielding factors that describe sets of edges with covarying connectivity. (b) The dotted blue lines show sliding window correlations among nodes with covarying connectivity within a factor as shown in (a), and the heavy blue line is the mean of these values. One can observe that there is a relationship between the mean correlation and the factor score, but the latter is a more direct measurement of the coupling. During a scan, these correlations may be more tightly coupled, yielding a high factor score (first red circle) or more loosely coupled, yielding a lower factor score (second red circle).

We previously observed (Madhyastha and Grabowski, 2013) that specific factors describing dynamic connectivity were negatively correlated with age. We hypothesized that this age-related decoupling of covarying correlations could be caused by numerous age-related processes (e.g., alterations in dopaminergic tone, age-related sensory decline, vascular insufficiency, and damaged white matter microstructure). Due to the heterogeneity in a normally aging sample, we expect that several of these processes contribute to age-related breakdown of dynamic connectivity.

In this study, we examine data from healthy controls and participants with Parkinson disease (PD). Idiopathic PD is diagnosed on the basis of motor impairments caused by progressive loss of striatal dopamine, but cognitive impairment and dementia are key symptoms of the disease. Although similar to aging, PD also involves multiple pathophysiologic processes; subjects share a common phenotypic presentation with known deficits in lateral frontoparietal networks that support attention and task control. These networks have been conceptualized as the fronto-parietal task control network (FPTC), comprising anterior prefrontal, dorsolateral prefrontal, dorsomedial superior frontal/anterior cingulate, anterior inferior parietal lobule, and anterior insular cortex (Dosenbach et al., 2007); and the dorsal attention network (DAN), comprising frontal eye fields (FEF) and intraparietal sulci (Corbetta and Shulman, 2002). These “task-positive” networks are also identifiable at rest (Fox et al., 2005). Cortical regions that support these networks are affected early in PD, as evidenced by cortical thinning (Jubault et al., 2011; Pereira et al., 2012) and metabolic covariance analysis (Eckert et al., 2007). A metabolic covariance network characterized by reductions in the posterior parietal cortex, left prefrontal cortex, precuneus, and supplementary motor area has been shown in PD to be specifically related to cognitive (vs. motor) symptoms (Huang et al., 2007). In addition to cortical pathology, impairment of multiple interacting ascending control systems, including the dopaminergic, noradrenergic, cholinergic, and serotonergic systems, contributes to deficits and is difficult to disentangle (Barone, 2010; Mattila et al., 2001). We, therefore, expect that PD participants should display a wide range of abnormalities in both ascending modulation of attention networks and cortical function of areas that support these networks. This population enables us to evaluate whether differences in dynamic connectivity in attention networks are specifically related to attention network function.

To assess attention function, we administered the Attention Network Test (ANT), adapted for the MRI environment by Fan et al. (2005), which is a combination of a cued reaction time task and a Flanker task. The task is designed to measure the efficiency of the alerting, orienting, and executive control networks, each of which is posited to be primarily modulated by a different neurotransmitter system known to be affected in PD. The alerting attention network involves the ability to maintain the alert state and respond to a cue, and is considered to be modulated by the noradrenergic system. The orienting network directs attention to a target stimulus and is considered to be related to the cholinergic system (Posner, 2008). The executive network manages the ability to resolve conflict, as measured here by the difference in reaction time between the Incongruent and Congruent Flanker tasks. It involves activation of the anterior cingulate cortex, and is considered to be related to dopaminergic function (Fan et al., 2003). There is likely to be a substantial interaction in neurotransmitter modulation of these attentional networks; for example, through changes in reactive pupil dilation, Geva et al. (2013) show a role for the noradrenergic system in modulating all three networks. Conventional task analysis (see Results section) shows that the regions activated by this task include areas in the FPTC and DAN.

Our hypothesis is that measurements of dynamic connectivity obtained at rest and during tasks in attention networks should be related to behavioral markers of attention network function, and that dynamic connectivity is a more reliable and sensitive measurement than stationary functional connectivity to assess within-network dynamic coupling.

Materials and Methods

Participants

This analysis includes 25 subjects with PD (M_age=66, 45–86) and 21 controls (M_age=62, 41–76), selected from a larger study. Potential participants were excluded if they had a history of any primary neurodegenerative disease other than idiopathic PD, brain surgery (including placement of a deep brain stimulator), moderate to severe dyskinesia, significant head trauma, stroke history, severe or unstable cardiovascular disease, contraindications to MRI, or a Montreal Cognitive Assessment score (MoCA) (Nasreddine et al., 2005) lower than 23. Four subjects from the larger study were excluded from fMRI analysis; one became claustrophobic in the scanner, one could not adequately perform the task, one fell asleep during both the resting and task scans, and another dropped out after the first session.

See Table 1 for sample characteristics. Participants were predominantly right handed. PD patients did not differ significantly from controls with regard to age, education, or scores on the MoCA. Although the PD participants are within the range of normative values for controls (Nasreddine et al., 2005) and do not differ from study controls on the MoCA, they have declined from their premorbid abilities, such that 14 PD participants are classified via consensus rating as having mild cognitive impairment (see Cholerton et al., 2013 for details on consensus rating procedure). PD participants had significantly higher scores on the UPDRS motor subscale, indicating greater motor impairment (Goetz et al., 2007) [t(44)=−11.82, p<0.001].

Table 1.

Demographics of Sample

	PD	Control	Total
n	25	21	46
Age at scan	66.04 (10.05)	61.90 (10.00)	64.15 (10.13)
Sex (number males)	18 (72%)	9 (43%)	27 (59%)
Education (years)	16.17 (2.08)	15.90 (2.39)	16.04 (2.20)
Hoen and Yahr	2.04 (1–2.5)	NA
Handedness (right)	21	19	40
Dominant side of motor symptoms	7 Left/18 right
UPDRS Part I	9.96 (5.74)	NA	9.96 (5.74)
UPDRS Part II	8.76 (5.33)	NA	8.76 (5.33)
UPDRS Part III	23.56 (8.71)	0.81	13.17 (13.14)
UPDRS Part IV	2.00 (3.70)	NA	2.00 (3.70)
Levodopa (current)	16	0	16
Dopamine agonist (current)	11	0	11
Time since symptom onset	8.47 (4.79)	NA
MoCA	26.40 (2.12)	27.29 (1.95)	26.80 (2.07)
Hopkins Verbal Learning Test	24.72 (5.64)
Golden Stroop (total correct)	189.24 (25.90)
Trails B (sec)	74.42 (32.31)

Groups differ significantly on the UPDRS Part III (motor subscale), t(44)=−11.82, p<0.001, and in proportion male t(44)=−2.05, p=0.047. They do not differ significantly in education, age, or MoCA score.

MoCA, Montreal Cognitive Assessment score; PD, Parkinson disease.

Men were over-represented in the PD group, consistent with higher incidence rates of PD in men (Wooten et al., 2004). PD patients ranged from Hoehn and Yahr (1967) stage 1 to 2.5 with most at stage 2 (n=20; bilateral involvement without impairment of balance) and had been experiencing symptoms for an average of 8.47 years. At diagnosis, the motor symptoms for most patients were predominantly on the right. At the time of the scan and corresponding neuropsychological evaluations, most PD patients were taking dopaminergic medications (28% were taking both levodopa and a dopamine agonist, 36% were taking only levodopa, 16% were taking only a dopamine agonist, and 20% were taking no dopaminergic medications). This study was approved by the University of Washington Institutional Review Board. All participants provided written informed consent.

Materials and procedures

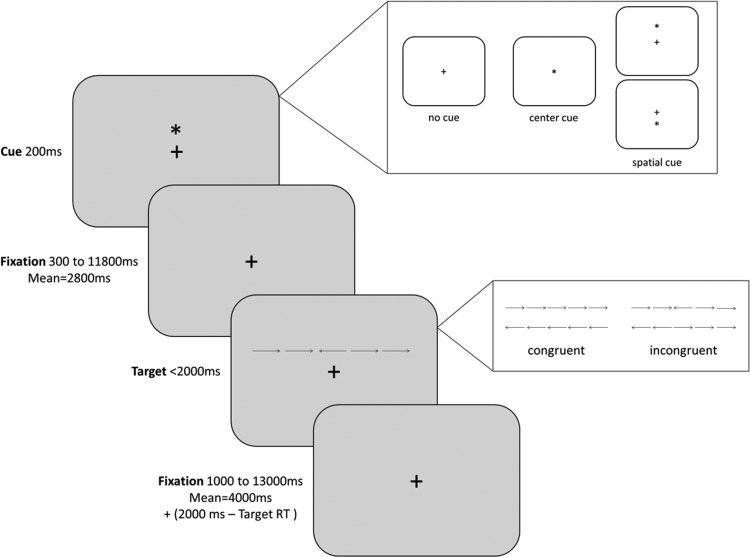
Participants completed two scanning sessions (Session 1 and Session 2), without intervention, 1–3 weeks apart. Scans were performed after morning doses of dopaminergic medication (if applicable). During each session, participants were scanned while viewing a fixation cross at rest and during performance of the ANT (Fan et al., 2005) (Fig. 2). The ANT was chosen as an index of function in cortical networks differentially affected by ascending neuromodulatory systems. Participants performed six runs of the ANT. Each run contained 2 buffer trials followed by 36 analyzed trials. During each trial, a cue appeared on the screen for 200 msec, providing varying degrees of information about when and where to expect the target to appear. The cue was an asterisk in the center of the screen (Center Cue), an asterisk above or below the fixation cross indicating where the target would appear (Spatial Cue), or nothing at all (No Cue). The cue was followed by a jittered delay before a target set of five arrows (each subtending 0.56° of visual angle, separated by 0.05°) that appeared 1.06° above or below the fixation cross. The target arrows remained on the screen until the participant responded, or 2000 msec elapsed. Participants used a button box in each hand to indicate which direction (left or right) the center arrow was pointing to while ignoring the direction of the flanking arrows on each side.

FIG. 2.

Schematic of Attention Network Test (Fan, 2005). During each trial, a cue (No Cue, Center Cue, or Spatial Cue) appeared on the screen for 200 msec. This was followed by a fixation delay before a target set of five Congruent or Incongruent arrows appeared above or below fixation. The target arrows remained on the screen until the participant responded, or 2000 msec elapsed, and was followed by fixation of jittered duration.

Half of the trials were Congruent, meaning that the flanking arrows pointed in the same direction as the center arrow and half were Incongruent, meaning that the flanking arrows and the center arrow pointed in opposite directions. Each of these target trial types was also equally divided among the three cue conditions. In the No Cue condition, participants viewed an unchanging fixation cross. In the Center Cue condition, an asterisk appeared briefly at the center of the screen, providing temporal information about an upcoming target. In the Spatial Cue condition, an asterisk appeared above or below the fixation, providing spatiotemporal information about an upcoming target. Trials in each run were presented in a predetermined counterbalanced order in which each condition followed the other condition equally as often as it followed itself. The six conditions (3 cue conditions×2 target conditions) were rotated within the counterbalance across the six runs. Both the cue-target interval (mean 2800 msec) and the time between the end of onset of the target in one trial and the onset of the cue in the next (mean 6000 msec) were independently jittered across 12 predetermined values to approximate an exponential distribution. The cue-target interval was one of a set of 12 discrete time points from 300 to 11,800 msec, including three 300-msec intervals, as well as 550, 800, 1050, 1550, 2300, 3300, 4800, 6550, and 11,800 msec, approximating an exponential distribution with a mean interval of 2800 msec (Fan et al., 2005). The time between the end of onset of target and the onset of cue was one of a set of 12 discrete time points from 3000 to 15,000 msec, including 3000, 3250, 3500, 3750, 4000, 4500, 5000, 5500, 6500, 8000, 10,000, and 15,000 msec, approximating an exponential distribution with a mean of 6000 msec (Fan et al., 2005).

MRI acquisition

Data were acquired using a Philips 3T Achieva MR System (software version 3.2.2; Philips Medical Systems, Best, The Netherlands) with a 32-channel SENSE head coil. During each session, whole-brain axial echo-planar images (43 sequential ascending slices, 3 mL isotropic voxels, field of view=240×240×129, repetition time=2400 msec, echo time=25 msec, flip angle=79°, and SENSE acceleration factor=2) were collected parallel to the anterior-commissure–posterior commissure (AC-PC) line for all functional runs. The first five dummy volumes in our fMRI acquisition are automatically discarded to achieve steady-state imaging. Run duration was 300 volumes (12 min) for the resting-state run and 149 volumes (5.96 min) for each task run. A sagittal T1-weighted 3D MPRAGE (176 slices, matrix size=256×256, inversion time=1100 msec, turbo-field echo factor=225, repetition time=7.46 msec, echo time=3.49 msec, flip angle=7°, and shot interval=2530 msec) with 1 mm isotropic voxels was also acquired for registration.

MRI processing

Functional images from rest or tasks were processed identically using a pipeline developed using software from FSL (Jenkinson et al., 2011), FreeSurfer (Fischl and Dale, 2000), and AFNI (Cox, 1996). Processing steps for each analysis [dynamic connectivity, independent components analysis (ICA), and univariate general linear model (GLM)] were kept as similar as possible, with a few exceptions (noted below) where necessary to improve the quality of the analysis following FSL recommendations.

Data were corrected for motion using FSL MCFLIRT (Jenkinson et al., 2002). The pipeline removed spikes using AFNI, performed slice timing correction using FSL, and regressed out time series motion parameters and the mean signal for eroded (1 mm in 3D) masks of the lateral ventricles and white matter (derived from running FreeSurfer on the T1-weighted image). We did not regress out the global signal. We did not perform bandpass filtering to avoid artificially inflating correlations or inducing structure that was not actually present in the data, and because resting-state networks exhibit different levels of phase synchrony at different frequencies (Handwerker et al., 2012; Niazy et al., 2011). Factor analysis explicitly models error that might be introduced into correlations by higher frequencies. Three-dimensional spatial smoothing was performed using a Gaussian kernel with a full width at half maximum (FWHM) of sigma=3 mm. Co-registration to the T1 image was performed using boundary-based registration based on a white matter segmentation of the T1 image (epi_reg in FSL).

We performed a conventional group ICA of the resting-state data. Data were preprocessed as described earlier except that motion, cerebrospinal fluid (CSF), and white matter regressors were not removed from the data (because motion and physiological signals are accurately separated from signal using ICA) (Salimi-Khorshidi et al., 2014). A Temporally Concatenated Probabilistic Group Independent Components Analysis (TC-GICA) was implemented using Multivariate Exploratory Linear Decomposition into Independent Components (MELODIC) Version 3.12 (Beckmann and Smith, 2004) to generate large-scale components across all resting-state scans for all participants. In this data set, a probabilistic Principal Component Analysis using the Laplace approximation to the Bayesian evidence of the model order estimated a 22-dimensional subspace into which data were projected (Beckmann and Smith, 2004). The whitened observations were decomposed into sets of vectors that described the signal variation across the concatenated time courses and across the spatial maps by optimizing for non-Gaussian spatial source distributions using a fixed-point iteration technique (Hyvarinen, 1999). A dual-regression approach implemented in FSL (Filippini, 2009) was used to identify session-specific time courses for each subject corresponding to the spatial maps identified in the ICA, then to identify session-specific spatial maps for each subject corresponding to these time courses. An average spatial map for each subject was created for each component of interest by averaging the Session 1 and Session 2 maps. A group-level analysis comparing PD patients with controls was performed by nonparametric testing (5000 permutations) on the single-subject spatial maps for the group-level components of interest. Maps were thresholded at a Bonferroni-corrected probability of 0.05 with threshold-free cluster enhancement.

We also performed a univariate GLM analysis on the task data. For inclusion in this analysis, functional task data were processed as previously described except that data were submitted to a high-pass filter at sigma=16.5 after motion correction; data were spatially smoothed with a Gaussian kernel with an FWHM of sigma=4 mm, and regression of nuisance covariates (e.g., motion, white mater, and CSF) were included later as a part of the first-level GLM. The high-pass filter is necessary in the GLM to remove low-frequency signals that obscure signals of interest. Spatial smoothing for the GLM is larger than used for the dynamic factor analysis to improve between-subject anatomical alignment, a step that does not occur with dynamic analysis. The GLM was implemented using FSL's fMRI expert analysis tool (FEAT) version 6.0. Time series statistical analysis was carried out using FILM with local autocorrelation correction (Woolrich et al., 2001). Onsets of each cue (No Cue, Center Cue, and Spatial Cue) and target (Congruent, Incongruent) condition were entered as explanatory variables and convolved with a double-gamma hemodynamic response function. Error trials were modeled separately but not analyzed. Temporal derivatives were included in the model. The first derivative of the time series motion parameters as well as the original motion parameters, and CSF and white mater signals were regressed out as nuisance covariates. Contrasts for the alerting (Center Cue–No Cue), orienting (Spatial Cue–Center Cue), and executive (Incongruent–Congruent) effects were generated for each run for each participant. Contrast images were registered to standard space using FLIRT to apply parameters determined by boundary-based registration of each functional run to the subject's own T1 image and 12-dof linear registration of the subject's T1 to standard Montreal Neurological Institute (MNI) space. Registered contrast images were then carried forward into higher-level models to generate a single contrast image for each participant across all runs in both sessions. These contrast images were fed into a group comparison model using FMRIB's Local Analysis of Mixed Effects (FLAME) stage 1 (Beckmann et al., 2003; Woolrich, 2008; Woolrich et al., 2004). Z-statistic images were thresholded using clusters determined by Z>2.3 and a corrected cluster significance threshold of p=0.05 (Worsley, 2001).

Dynamic connectivity analysis

We selected MNI coordinates that have been identified as nodes in the default mode network (DMN), DAN, and FPTC, republished by Power et al. (2011) and derived from Raichle et al. (2001) and Dosenbach et al. (2007) (Supplementary Table S1; Supplementary Data are available online at www.liebertpub.com/brain). For each coordinate, we created a 10 mm diameter mask in standard space and transformed that to subjects' native space to calculate mean subject-specific time courses for each region of interest.

To analyze changes in connectivity, we calculate pairwise correlations between nodes in each network in overlapping windows, using a method of dynamic connectivity analysis previously described (Madhyastha and Grabowski, 2013). The choice of window length is pragmatic and motivated by the need to obtain reliable correlations while quantifying the individual variability throughout the scan; as in an earlier work, we use a window length of ∼40 sec (17 frames at TR=2.4 or 40.8 sec). These correlations were transformed by Fisher's z-transform to convert them to a normally distributed variable for subsequent factor analysis. In contrast to our previous work, we used overlapping windows, moving forward 1TR each window from the beginning of the scan. For each resting-state scan, this yielded 283 data points per subject. For each task run, this yielded 132 data points per subject. A schematic of this analysis is shown in Figure 1.

We conducted an exploratory factor analysis using chained P-technique factor analysis on the pairwise correlations between nodes (dynamic patterns of connectivity) within each network to obtain a factor structure (Madhyastha and Grabowski, 2013). P-technique factor analysis (Cattell, 1963) applies the common factor model to multivariate repeated measures of one individual obtained over many occasions. This type of factor model is appropriate to obtain information about both covariation patterns and level of correlations (Molenaar and Nesselroade, 2009; Nesselroade and Ford, 1985). Here, we concatenate subject data, a method called chained P-technique (Cattell, 1966), and apply varimax rotation to the factor loading matrix. We concatenated data from both sessions to enable factor scores to be compared between sessions. The approach of concatenating data is analogous to a group ICA, and makes the analogous underlying assumption that the structure of fluctuating correlations is the same across individuals, reflecting a common functional architecture, but that individual scores for each latent factor may be different. This assumption may also be tested explicitly (see Discussion section), making factor analysis a powerful technique for separating measurement error from change. Conceptually, varimax rotation is an orthogonal rotation that tries to create a loading matrix with a simple structure (a pattern of loadings where items load most strongly on one factor, and more weakly on the other factors) (Kaiser, 1958). The resulting factors represent subgroups of correlations that covary in time across all individuals.

We extract four factors for each network at rest to be consistent with a previous work (Madhyastha and Grabowski, 2013), where we determined a stable number of factors via congruence in a split-half analysis of a large sample of elderly adults. Four factors per network are also suggested by a Cattell scree test of these data. A factor score is obtained for each sliding window for each factor using Bartlett's method, which produces unbiased estimates of the true factor scores (Hershberger, 2005); we average these scores for each factor for each individual at each session. Therefore, for each network, we obtain four factor scores per individual at each session. Scores represent the expression of each factor (e.g., how tightly coupled the links with high loadings on the factor are). The intuitive meaning of this analysis is illustrated in Figure 1b.

Since the rotation of the factor solution is determined by the varimax criterion, it is not unique, and, therefore, might be different at tasks and rest solely because of the rotation. To compare factor analyses obtained during tasks with those at rest, we rotate four factor solutions obtained during task runs to maximal congruence with the analogous network solutions obtained during rest using orthogonal Procrustes rotation (as used in McCrae et al., 1996). This procedure maximizes the size of the total congruence coefficient by optimally aligning real factors. To evaluate the similarity of the solutions, we computed the congruence of the factors and the significance of the Procrustes statistic.

Statistical analyses

All analyses were conducted using Revolutions R Enterprise Version 6.2.0 (www.revolutionanalytics.com). Mean differences in response latencies obtained from the ANT task across different experimental conditions were analyzed to obtain a measurement of the alerting effect (No Cue–Center Cue), orienting effect (Center Cue–Spatial Cue), and executive effect (Incongruent–Congruent) for each subject for Session 1 and Session 2. Independent sample t-tests were used to compare response latencies and alerting, orienting, and executive effects across PD and control groups. Nonparametric Mann–Whitney U tests were used to compare accuracies across PD and control groups, which were non-normally distributed due to ceiling effects.

Reliability of stationary connectivity between nodes is computed as the Pearson correlation of the Fisher z-transformed correlations of their time courses. Reliability of factors obtained from dynamic connectivity analysis is computed as the Pearson correlation of the normally distributed mean factor scores. To compare reliability of stationary connectivity with dynamic connectivity, we use a Mann–Whitney U test, a nonparametric test of the null hypothesis that the distribution of the reliability coefficients obtained from pairwise stationary connectivity analysis is identical to the distribution of the reliability coefficients obtained from dynamic connectivity analysis.

Since resting-state scans occurred before task scans in each of the two baseline sessions, we computed aggregate mean individual factor scores for resting-state dynamic factors and examined whether these scores could be used to predict reaction time effects, using linear regression, in each session independently. The dependent variable is the reaction time effect and the predictors are the factor score, group, and group×factor interaction. Similarly, we computed mean individual factor scores from all task runs in the two task sessions and repeated this analysis. We attempted to replicate results for both rest and tasks in both sessions to identify reliable effects.

Results

PD participants are slower to respond, showing a significant alerting response latency effect

PD participants had slowed response latencies across all conditions (Table 2) and a significant group difference in the alerting effect (No Cue–Center Cue) (Table 3). Accuracy was extremely high with only 2.3% of trials missed, on average, but even so, PD participants had a significantly lower accuracy in the Center Cue condition (Table 2) and a marginal reduction in accuracy in the Incongruent condition. Behaviorally, PD participants showed a generalized slowing of response latencies, but only the alerting effect was significantly different between PD and controls. This is because while PD participants are slower than controls, they are even slower when there is No Cue (i.e., note in Table 2 that the difference between PD and controls is 115 msec in the No Cue condition).

Table 2.

Attention Network Test Task Behavioral Summary Statistics, Computed Over Two Sessions

	Flanker type		Cue type
Group	Congruent	Incongruent	Center	Spatial	No cue
Mean response latencies (msec) and standard deviations
PD	869 (167)	1003 (205)	942 (177)	876 (188)	989 (193)
Controls	771 (116)	887 (136)	846 (125)	766 (122)	874 (130)
Difference (PD–controls)	97	115	95	109	115
p	0.024	0.027	0.038	0.022	0.021
Mean accuracy
PD	97.7	96.4	96.6	97.7	96.9
Controls	98.8	98.0	98.3	98.3	98.5
Difference (PD–controls)	−1.03	−1.53	−1.63	−0.66	−1.54
p	0.268	0.090	0.024	0.463	0.110

Accuracy values are highly skewed toward ceiling, so p-values for accuracy comparisons were computed using a Mann–Whitney U test.

Table 3.

Summary Statistics for Mean Alerting, Orienting, and Executive Response Latency Effects Computed Over Two Sessions

	PD		Controls
Effect (msec)	M	SD	M	SD	t	p
Alerting	47	33	28	22	2.32	0.025
Orienting	66	33	80	27	−1.59	0.120
Executive	134	59	116	43	1.20	0.240

M, mean; SD, standard deviation.

We evaluated the possibility that the PD participants were slower to respond solely because of motor impairment by comparing mean response latency for correct Flanker responses on subjects' dominant side of motor impairment with the mean response latency for correct Flanker responses on their nondominant side. By design, half of the Flanker tasks required pushing the left button box and half required pushing the right button box. If motor impairment were a primary reason for slow responses, it should be slower on the predominantly affected side. The mean response latency for all subjects on their side of dominant motor impairment was 935.5 msec (standard deviation [SD]=193 msec) and for the nondominant side, it was 945.3 msec (SD=183 msec). A paired t-test indicated that these latencies were not significantly different [t(24)=1.37, p=0.184].

The complete results of the corresponding GLM task analysis will be discussed in a forthcoming paper; however, importantly, we observe that the regions activated by the cue as a group (Any Cue–No Cue) include frontoparietal and DAN regions (Fig. 3), confirming the salience of our focus on attention networks.

FIG. 3.

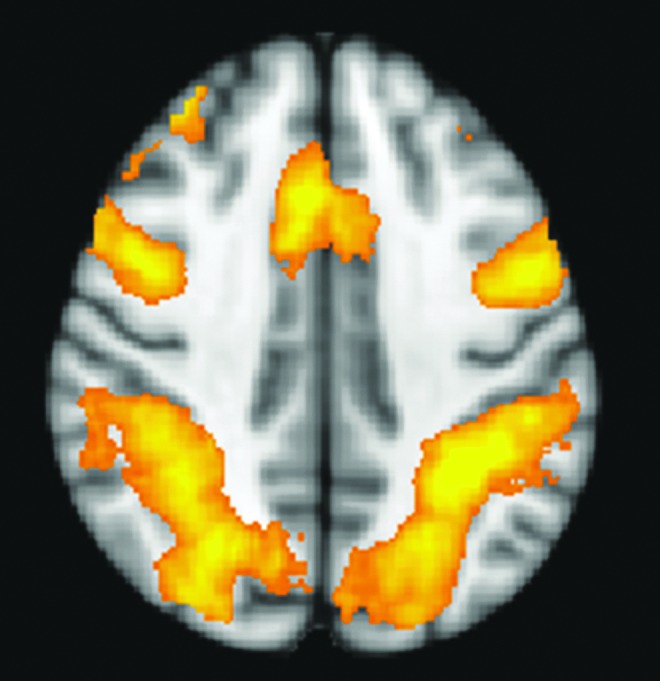
Attention network activated by cueing in the Attention Network Task. Contrast shown is all subjects (Any Cue–No Cue), overlaid on a Montreal Neurological Institute axial slice at z=40 mm.

ICA analysis reveals no significant resting network differences between PD and control groups

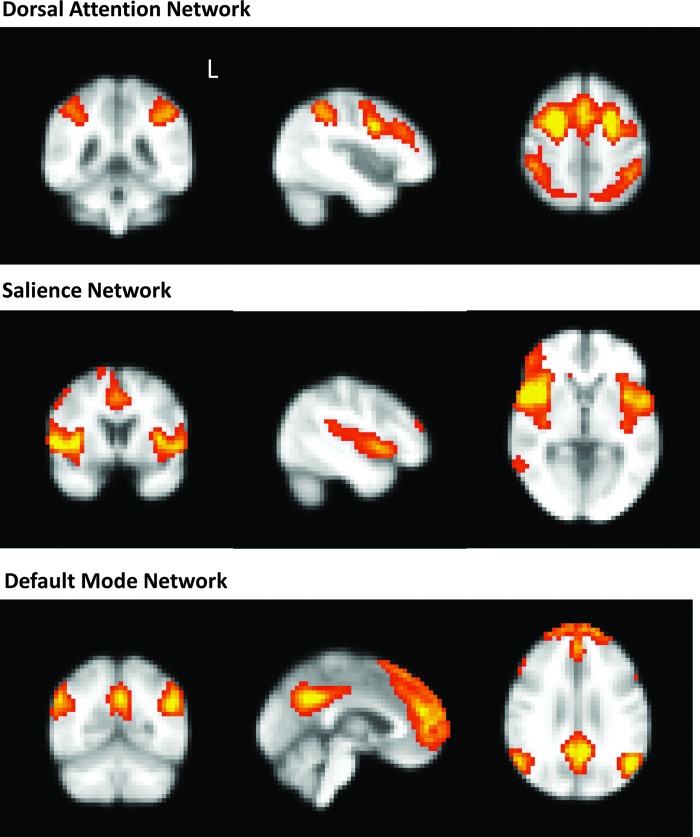
Group-level components from TC-GICA analysis were examined to identify three resting-state networks of interest (Fig. 4). The DAN was identified as the spatial map composed of bilateral intraparietal sulcus (IPS), bilateral FEF, and dorsal anterior cingulate cortex. The salience network was identified as the spatial map containing anterior cingulate cortex and bilateral insular cortex. The DMN was identified as the spatial map containing precuneus/posterior cingulate cortex (PCC), medial frontal/frontopolar/superior frontal cortex, bilateral angular gyrus, and bilateral superior/middle temporal gyrus. Dual regression analysis revealed no significant group differences in these networks between PD participants and controls.

FIG. 4.

Group-level components from Temporally Concatenated Probabilistic Group Independent Components Analysis (TC-GICA) analysis identify a dorsal attention network (DAN), salience network, and default mode network (DMN).

Reliability of dynamic factors is higher than reliability of individual correlations

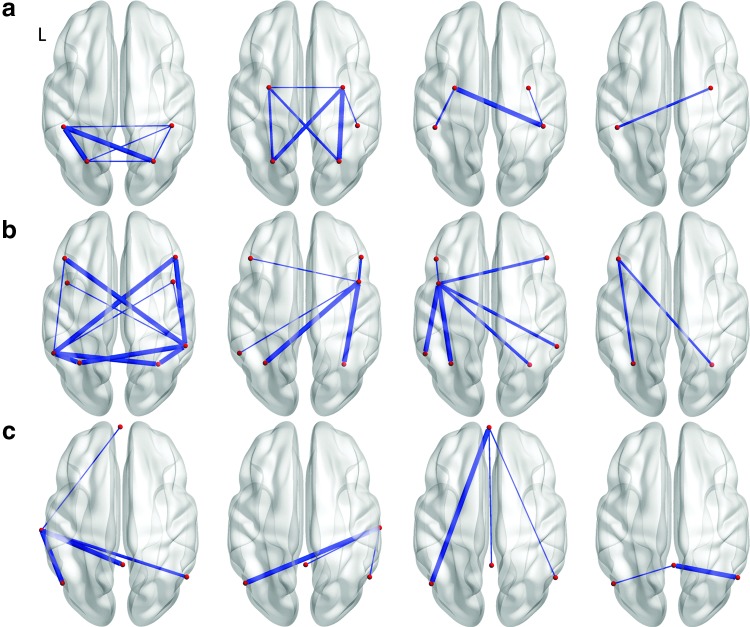
We extracted four factors for each network (DAN, FPTC, and DMN) from the correlations between nodes in the network. Loading tables are provided in Supplementary Tables S2–S4, and loadings >0.4 are illustrated in Figure 5. The DAN is split into (1) a posterior factor that interconnects the left and right anterior and posterior IPS, (2) an anterior/posterior factor which interconnects the left and right FEF and posterior IPS, (3) an anterior factor interconnecting the left FEF with the right anterior IPS, and (4) a symmetric and weaker anterior factor interconnecting the right FEF with the left anterior IPS. The FPTC is split into (1) a symmetric anterior/posterior factor, (2) a factor connecting the right frontal to other nodes, (3) a factor connecting the left frontal to other nodes, and (4) a factor connecting the left dorsal lateral prefrontal cortex (dlPFC) to the IPS. The DMN is subdivided into (1) a factor connecting the left lateral temporal lobe to the PCC, medial prefrontal cortex (mPFC), and left and right angular gyrus; (2) a symmetric right opposite with weaker connectivity to the mPFC; (3) an anterior factor connecting the mPFC with the PCC and left and right angular gyrus; and (4) a posterior factor connecting the PCC and left and right angular gyrus.

FIG. 5.

Dynamic factor structures obtained from all subjects, two sessions of resting-state data. (a) DAN four-factor solution, (b) fronto-parietal task control network four-factor solution, and (c) DMN four-factor solution.

Despite methodological differences between this and our earlier work (i.e., this was a smaller sample including participants with PD, individual acquisition time was longer, we used overlapping sliding windows, and the rotation was specific to this solution), factors were qualitatively similar to those obtained from an aging sample (Madhyastha and Grabowski, 2013). Consistent with heterogeneity that might be introduced by PD, factors in this sample described a smaller total variance than in our earlier work (DMN factor solution explained 45.8% of the variance vs. 52%, DAN factor solution explained 46.2% of the variance vs. 57%, and FPTC explained 34% of total variance vs. 44%).

The reliability of the factor scores obtained at rest is high across the two occasions, compared with the reliability of the correlations of the links themselves. We measure reliability as the Pearson correlation of the measures for each individual on both occasions (either the mean factor scores or the Fisher z-transformed pairwise correlations within each network). For the DAN, the reliability of the factor scores is 0.56, 0.55, 0.64, and 0.61 for Factors 1–4, respectively. For the FPTC, reliability is 0.52, 0.52, 0.69, and 0.35 for Factors 1–4, respectively. For the DMN, the reliability of the factor scores is 0.62, 0.57, 0.64, and 0.78 for Factors 1–4, respectively. All values are significant at p<0.001 except for FPTC Factor 4 (p=0.01). The median reliability of factor scores on each occasion is higher than the median reliability of the pairwise correlations among the network nodes. A Mann–Whitney U test indicates that the median reliability of factor scores for the DAN (0.58) is higher than the median internode correlation reliability (0.45), p=0.020. Similarly, reliability of factor scores for the DMN (0.63) is higher than the median DMN internode correlation reliability (0.53), p=0.036. The median reliability of factor scores for the FPTC (0.52) is higher than the median internode correlation reliability (0.38), but this difference is only marginally significant (p=0.082). Supplementary Tables S5–S7 show the mean inter-node correlations for each link and reliability of these links.

Motion is an important potential confound in resting-state analyses (Power et al., 2012). We compared groups and sessions on total relative and absolute motion (parameters estimated from motion correction); there were no significant differences either between PD and controls or between Session 1 and Session 2. However, there were three PD participants who had moved more than 3 mm from the reference volume during Session 2. Motion affects the computation of mean correlations more than it does the dynamic factor analysis, given that the purpose of factor analysis is to identify the shared variance among several changing correlations across individuals, explicitly modeling error (as might be introduced by motion). To verify that motion was not responsible for decreased reliability, we repeated the reliability analysis using correlations and factors obtained by excluding those three subjects; our pattern of results was unchanged.

Dynamic factors provide different information than stationary connectivity

The dynamic connectivity score for an individual during a scan is a mean measure of how closely correlations that covary in a population are coupled in an individual (e.g., referring to Fig. 1b, on average does the time-varying structure of correlations have a higher or lower factor score?). This is different from measurements of stationary connectivity—the mean correlations between nodes calculated from the duration of the scan—because it characterizes the structure and dynamics of a system of nodes. To illustrate the difference between these two types of measurements, we conducted a post hoc analysis to examine the correlations between the connectivity of each pair of nodes (transformed by Fisher's z) and the alerting effect in the DAN. Table 4 shows these results. Only the stationary connectivity between the left frontal eye field and the right aIPS is significantly related to the alerting effect at both time points. This is the connection with the highest loading in the DAN Factor 3. The correlation at each timepoint (0.35 and 0.38) is comparable within a 95% confidence interval to the correlation of the DAN Factor 3 at each timepoint (0.46 and 0.31). However, the other links with high loadings in this factor are not significantly correlated to the alerting effect at both timepoints. The system of coupled time-varying correlations that is related to the alerting effect is not visible from a stationary connectivity analysis.

Table 4.

Correlation Between Stationary Connectivity Within the DAN and Alerting Reaction Time Effect at Each Session

	Session 1		Session 2
	r	p	r	p
LpIPS.RpIPS	0.06	0.75	−0.09	0.56
LpIPS.RaIPS	0.07	0.62	−0.03	0.86
LpIPS.LaIPS	−0.05	0.73	−0.14	0.34
RpIPS.RaIPS	−0.20	0.17	−0.13	0.37
RpIPS.LaIPS	−0.14	0.35	−0.13	0.39
RaIPS.LaIPS	0.21	0.16	0.10	0.49
LFEF.RaIPS	0.35	0.02	0.38	0.01
LFEF.LaIPS	0.13	0.37	0.18	0.24
RFEF.RaIPS	0.12	0.42	0.36	0.02
RFEF.LaIPS	−0.05	0.73	0.33	0.03
LpIPS.RFEF	−0.25	0.09	0.15	0.34
RpIPS.RFEF	−0.14	0.36	0.25	0.09
LFEF.RpIPS	−0.09	0.55	0.10	0.49
LpIPS.LFEF	−0.06	0.68	0.02	0.89
LFEF.RFEF	0.15	0.32	0.24	0.10

Gray highlighting denotes links significantly related to alerting effect at p<0.05, at both sessions, uncorrected for multiple comparisons.

DAN, dorsal attention network; FEF, frontal eye fields; IPS, intraparietal sulcus.

Dynamics of resting-state connectivity predict alerting and orienting response latency effects

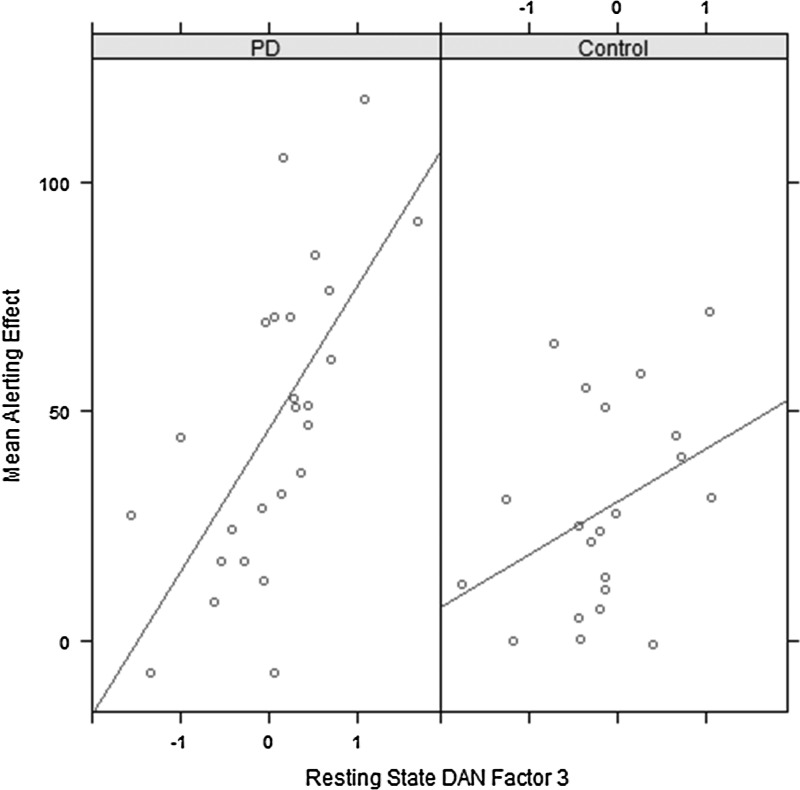
We calculate the predictive value of the dynamic factor scores, computed during rest in each network, for the alerting, orienting, and executive effect calculated in that session. For the DAN, Factor 3 (anterior DAN) predicted the magnitude of the alerting effect on both occasions [Session 1: t(44)=3.46, p=0.001, R²=0.21, Session 2: t(44)=2.15, p=0.037, R²=0.09]. The anterior DAN factor remained significant in all comparisons after controlling for age.

Figure 6 shows the relationship between the average alerting effect across both time points and the DAN Factor 3 computed at the second session. The different slopes for PD and control suggest a group-by-factor interaction, which we investigated. We added the group and group×Factor 3 terms to the model and found that at Session 1, there was a main effect of Factor 3 [t(42)=5.27, p<0.001], group [t(42)=−2.65, p=0.011], and a group×Factor 3 interaction [t(42)=−3.2, p=0.002]. However, at Session 2, Factor 3 remained only marginally significant in predicting the alerting effect on the first occasion [t(42)=1.72, p=0.094], with no significant main effect of group or group×Factor 3 interaction. Thus, the effect of the factor appears individually in both sessions but the interaction does not.

FIG. 6.

Relationship between mean alerting effect (average of both task sessions) and DAN Factor 3 computed from resting-state scan at Session 2.

FPTC Factor 3 predicted the magnitude of the orienting effect at Session 1 but did not reach significance at Session 2 [Session 1: t(44)=2.70, p=0.010, Session 2: t(44)=1.6, p=0.116]. These relationships are unchanged controlling for age. There is no significant effect of group or group×factor interaction.

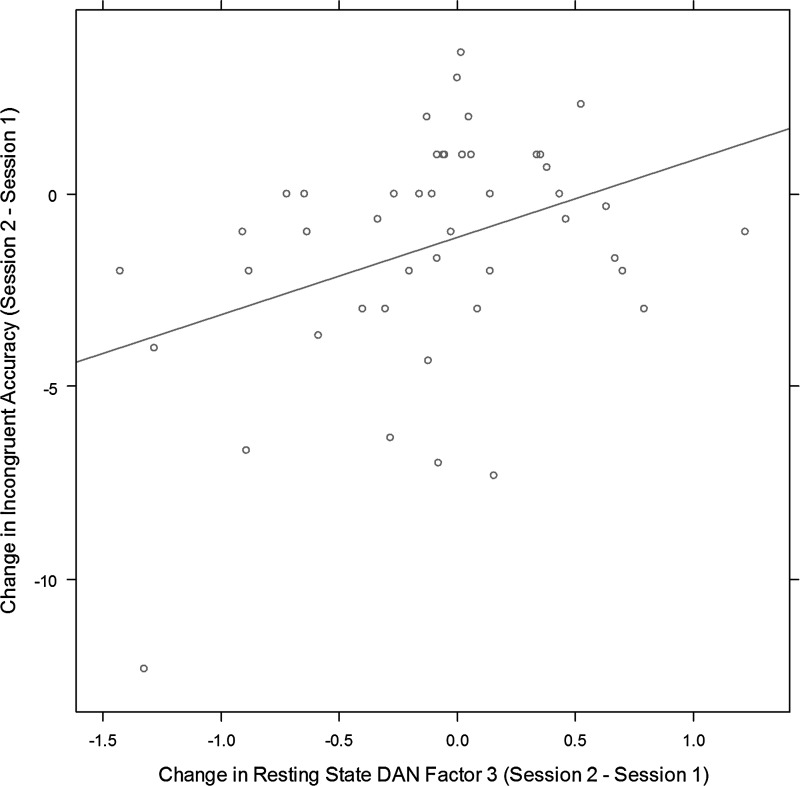
Given the change in predictive ability of DAN and FPTC Factor 3 computed during the resting state on the alerting and orienting effect at the two sessions, we hypothesized that these changes in dynamic connectivity might reflect a learning effect to trade off speed for accuracy. We investigated this possibility further by correlating change in factor scores across sessions with change in accuracy (though see Gardner and Neufeld, 1987 and Discussion section for difficulties in interpreting related change scores). The PD group had a significantly lower accuracy than controls in the Incongruent Flanker condition and the Center Cue and No Cue conditions. We found a significant correlation of increase in DAN Factor 3 with improvement in accuracy in the Incongruent Flanker condition [r(44)=0.37, p=0.011, see Fig. 7], but this relationship was not significant in the Center Cue condition [r(44)=0.121, p=0.23] or in the No Cue condition [r(44)=−0.05, p=0.714]. Similarly, we found a significant correlation of increase in FPTC Factor 3 with improvement in accuracy in the Incongruent Flanker condition [r(44)=0.39, p=0.007] and in the Center Cue condition [r(44)=0.32, p=0.027] but not in the No Cue condition [r(44)=−0.05, p=0.731].

FIG. 7.

Change in resting-state DAN Factor 3 is positively correlated with change in accuracy between sessions.

No factors in the DAN and FPTC were related to the executive effect. There was also no relationship between factors in the DMN and any reaction time effects.

Dynamics of task connectivity predict alerting, but not orienting, response latency effects

We examined whether the relationships between dynamic factors and performance at rest would be replicated in tasks. Since the rotation of a factor solution is not unique, we used the solution identified at rest as a target and used an orthogonal Procrustes rotation to rotate the factor solution derived from the task run to maximum congruence with the target. The rotated matrix was then used to compute new factor scores, which were then averaged for each individual over the six task runs as for each resting-state run.

The factor structure identified for the DAN during task was highly congruent with the factor structure identified during rest (Procrustes correlation was 0.93 at Session 1 and 0.89 at Session 2, p=0.001). Reliability of the DAN factors computed during tasks was slightly lower than that obtained from resting-state data (0.49, 0.62, 0.62, and 0.34 for Factors 1–4, respectively).

DAN Factor 3 computed during tasks predicted the magnitude of the alerting affect at Session 1 and was marginally significant at Session 2 [Session 1: t(44)=2.36, p=0.023, R²=0.11, Session 2: t(44)=1.644, p=0.107, R²=0.06]. The change in DAN Factor 3 that occurred between Session 1 and Session 2 was positively correlated with the change in accuracy in the Incongruent Flanker condition [r(44)=0.299, p=0.043] and was marginally significantly correlated with the change in accuracy in the Center Cue condition [r(44)=0.26, p=0.074], but not in the No Cue condition [r(44)=0.169, p=0.25]. Interestingly, during tasks, the DAN Factor 3 had a significant or marginally significant negative relationship with the orienting effect at both sessions [Session 1: t(44)=−1.67, p=0.097, R²=0.06, Session 2: t(44)=−2.581, p=0.013, R²=0.13]. For reference, during rest, the DAN Factor 3 had a negative relationship with the orienting effect that was not significant [Session 1: t(44)=−1.344, p=0.186, R²=0.03, Session 2: t(44)=−0.37, p=0.713, R²=0.003].

We added the group and group×Factor 3 terms to the model to predict the Alerting effect and found that at Session 1, there was a main effect of Factor 3 [t(42)=3.69, p<0.001], group [t(42)=−2.15, p=0.037], and a group×Factor 3 interaction [t(42)=−2.80, p=0.008]. However, at Session 2, no predictors were significant in the extended model. In a similarly extended model to predict the orienting effect from Factor 3, group, and group×Factor 3, no predictors were significant at either session.

The factor structure identified from the FPTC during tasks was less similar to that obtained at rest than the DAN (Procrustes correlation was 0.78 at Session 1 and 0.83 at Session 2). Analogously, the reliability of the factor scores obtained during tasks was lower than that at rest (0.30, 0.39, 0.27, and 0.32 for Factors 1–4, respectively). FPTC Factor 3 did not predict the orienting effect during tasks [Session 1: t(44)=0.427, p=0.671, Session 2: t(44)=0.064, p=0.949].

The factor structure of the DMN during tasks was very similar to that obtained during rest (Procrustes correlation was 0.87 at Session 1 and 0.97 at Session 2). Reliability of factor scores across the two runs is similar to that obtained at rest (0.66, 0.39, 0.67, and 0.76). No DMN factors computed during tasks predict any response time effects.

Discussion

The primary contribution of this work is to demonstrate that measurements of dynamic functional connectivity obtained at rest have behavioral correlates in a subsequent attention task. This is significant, because it indicates that there is stability of patterns of time-varying correlations among nodes in an intrinsic network, and this stability is functionally relevant. We are able to replicate our findings within our sample in two baseline resting-state runs and for the alerting effect in two task runs. We also show that dynamic connectivity is reliable; factor scores for all networks obtained at the two baseline sessions are more highly correlated than the mean correlations among nodes in these networks, and this difference is statistically significant for the DMN and DAN.

Increasing the reliability of measurement decreases the magnitude of the effect size necessary to observe a group difference or longitudinal change at a given sample size and power. We observe that the reliability of the structure of time-varying correlations is higher for the DAN than for the FPTC both during tasks and at rest, suggesting that the DAN may be a reasonable testbed for further studies of the nature of network dynamics and their behavioral correlates.

The method of dynamic connectivity analysis we describe identifies groups of correlations that covary in time. Clearly, as shown by Figure 1b, a lower factor score is related to lower correlations in the links with high factor loadings. However, we believe that this structure of covarying correlations, and changes to this structure or to the expression of the factors, is a more informative and precise abstraction than mean correlations. Here, we showed that a post hoc inspection of the mean correlations within the network does not provide the same information. Individual correlations do not reflect the functioning of a system of nodes. Moreover, a factor analysis identifies structure among the covarying links, indicating where to look in the first place.

One reason that the reliability of factor scores is higher than that of the individual correlations is that the purpose of factor analysis is to uncover a latent structure which may not be visible from individual, potentially error-contaminated, measurements. A fairer comparison would be to obtain a latent measurement of stationary connectivity. This is challenging; measurement issues are confounded with the stability of the construct that we are measuring. Our comparison tells us that we can only obtain a measurement of the dynamics of connectivity which is reliable across timepoints.

Using dual regression ICA analysis, we found no significant group differences in attention and DMNs (Fig. 4). The most likely explanation for this, consistent with behavioral information, is that in our sample of early stage PD participants and controls, any differences in these networks are subtle. Although MCI is prevalent in our PD participants, they do not differ from controls in most neuropsychological measurements. Heterogeneity in PD progression and dopaminergic medication might also contribute to between-subject variability, and we may simply lack statistical power to detect differences.

Factors in the DAN and FPTC are consistently related to the alerting and orienting effects derived from the ANT task. In the DAN, larger coupling of connections between the FEF and anterior IPS was related to a larger alerting effect, and in the FPTC, larger coupling of the left frontal gyrus to other regions in the FPTC was related to a larger orienting effect. In both of these networks, higher coupling was associated with a larger effect, or worse performance without the advantage of a cue (alerting) or a Spatial Cue (orienting). Although higher connectivity is usually considered positive, in the context of a dynamic analysis of an attention network whose components support many specific functions, it may reflect more effortful information processing, or an underlying rigidity in the ability to reallocate resources. Further work will be necessary to determine whether this higher dynamic connectivity is compensatory or pathological, and whether it is generalizable to other attention tasks.

Factors in the DMN obtained from rest and task data were consistently unrelated to reaction time effects. We interpret this as evidence of specificity of dynamic factors. However, a failure to suppress the DMN has been related to reaction time (Kelly et al., 2008). Such a phenomenon might be visible by examining higher-order dynamic factor structures of task-positive and DMNs, which we have not yet explored.

In both rest and tasks during the first session, PD participants had a larger alerting effect for a given score of the related DAN factor. One of the symptoms of even early PD is reduced cerebral metabolism in frontal and parietal association areas, along with cortical thinning (Huang et al., 2007; Jubault et al., 2011), indicating that early cortical involvement is a part of the disease. However, the locus coeruleus (LC), which sends noradrenergic projections to most brain regions, is highly involved in alerting and attention through interactions with the dopaminergic system (Sara, 2009). Loss of noradrenergic neurons in the LC is an important factor in PD (Delaville et al., 2011), and may occur even earlier than destruction of dopaminergic neurons (Braak et al., 2004). Since alerting and orienting effects are related to DAN and FPTC dynamic factors in both the PD participants and healthy controls, neuromodulatory influences may play a role in dynamic connectivity and reconfiguration.

The expression of dynamic connectivity was reliable across baseline sessions, though not invariant, and changes in individual expression of dynamic connectivity had a behavioral correlate. We observed in rest and tasks that an increase in dynamic connectivity of the DAN Factor 3 between the baseline sessions was correlated with an increase in accuracy of the Incongruent trials across the sessions, and that the effect of group and group×factor interaction was not significant in the second session. This effect may be due simply to learning or might be a marker of compensation among PD participants. Mechanisms of neural plasticity and compensation may initially mask disruption to cognitive systems. It is possible that deviations from the normal pattern of variability are an early physiological indicator of impending cognitive impairment, analogous to intra-individual variability of behavior (MacDonald et al., 2003, 2006; Wojtowicz et al., 2013).

An important caveat is that our sample is small and we did not correct for multiple comparisons. However, we acquired two baseline resting-state and task scans, and were able to replicate our findings in multiple runs. This reduces the probability that the results are caused by spurious aspects of the analysis or data acquisition. They could still be sample dependent, and, thus, require replication in a different population.

We used correlations of simple change scores to examine the significance of changes in dynamic connectivity between the two baseline sessions. Although intuitive, correlations of change should be interpreted with caution (Gardner and Neufeld, 1987). In this case, an alternative interpretation may be that the factor structure of the network dynamic connectivity changed between sessions or for certain individuals, making the exact meaning of the scores suspect.

In an earlier work, we have demonstrated the replicability of dynamic factor structure in a data-driven split-half analysis (Madhyastha and Grabowski, 2013) and using exploratory factor analysis in a structural equation modeling framework with two independent samples (Madhyastha et al., 2013). In light of this reproducibility among aging adults, it is reasonable to simplify interpretation by treating patterns (factor structure) of connectivity in a sample as fixed, and examining how the expression (scores) of these patterns changes. This is the approach that we took in this study, and despite important differences in sample, acquisition, and methodology, we identified qualitatively similar factor structures to our earlier work, with the most similarity in the DMN solution. However, the factor structures we identified reflect the common dynamic structure of PD participants (half of whom have mild cognitive impairment) and controls across two sessions. The variance described by a four-factor solution among PD participants and controls is uniformly slightly lower than that described by a four-factor solution among a sample of cognitively normal elderly, suggesting that there may be a breakdown of dynamic structure in this sample. If dynamic connectivity reflects normal variability of correlations, dysfunction in one or more of the cortical regions in the system, or the system itself, would cause factor scores to be elevated or depressed during tasks or rest. This suggests an analytic approach where factors defined in a normal population could be used as a template against which to compare a patient population. Alternatively, invariance of the factor structure of groups or individuals at different timepoints can be formally established using techniques such as exploratory factor analysis in a structural equation modeling framework (Asparouhov and Muthén, 2009). Much research remains to be done on modeling approaches to best quantify how altered functional connectivity dynamics reflect early neurophysiological changes that occur with disease.

In summary, we observe that the time-varying patterns of correlations across nodes in an intrinsic network are stable across rest and tasks and this stability is functionally meaningful. However, even though factors describing the coupling of these correlations are reliable across scanner sessions, they are not invariant, and individual changes in factor scores between sessions reflect behavioral changes across sessions. There is selectivity to our findings, in that factors describing time-varying correlations within attention networks predict measurements obtained from an attention task, and factors describing the DMN do not. More generally, the finding can be interpreted as higher coupling reflecting a greater benefit from a relevant cue, suggesting that network dynamics may index mechanisms relevant to neural compensation and/or incipient dysfunction.

Acknowledgment

This research was supported by grants from the National Institutes of Health (1RC4NS073008-01 and P50NS062684).

Author Disclosure Statement

No competing financial interests exist.