The topology of fullerenes

Abstract

Fullerenes are carbon molecules that form polyhedral cages. Their bond structures are exactly the planar cubic graphs that have only pentagon and hexagon faces. Strikingly, a number of chemical properties of a fullerene can be derived from its graph structure. A rich mathematics of cubic planar graphs and fullerene graphs has grown since they were studied by Goldberg, Coxeter, and others in the early 20th century, and many mathematical properties of fullerenes have found simple and beautiful solutions. Yet many interesting chemical and mathematical problems in the field remain open. In this paper, we present a general overview of recent topological and graph theoretical developments in fullerene research over the past two decades, describing both solved and open problems. WIREs Comput Mol Sci 2015, 5:96–145. doi: 10.1002/wcms.1207

Conflict of interest: The authors have declared no conflicts of interest for this article.

For further resources related to this article, please visit the WIREs website.

INTRODUCTION

Buckminsterfullerene C₆₀ - I_h is a convex and ‘spherical’ molecule (in the sense that the atoms lie on the surface of a sphere) with a highly symmetric icosahedral structure. It was originally conjectured independently by Ōsawa in 1970^1,2 and Stankevich, Bochvar, and Galpern in 1973,^3,4 discovered by mass spectrometry in 1985 by Kroto et al. through laser evaporation of graphite,^5–8 and synthesized in larger amounts by Krätschmer et al.⁹ in 1990 (the first mass-spectroscopic studies on small carbon cluster were performed by Mattauch et al.¹⁰ in 1943). Fullerenes are the polyhedral analogs to the two-dimensional graphene sheets.^a They occur in nature and have been detected in interstellar space, albeit in minute amounts.^11–14 In general, (classical) fullerenes are cage-like, hollow molecules of pseudo-spherical symmetry consisting of pentagons and hexagons only, resulting in a trivalent (and in the most ideal case) convex polyhedron with exactly three edges (bonds) joining every vertex occupied by carbon, idealized as sp² hybridized atoms.¹⁵ In graph theoretical terms, fullerenes belong to the class of cubic, planar, three-connected, and simple graphs, consisting of 12 pentagons only (the 12 Pentagon Theorem) and F₆ hexagons. This gives the general formula of (F₆ ≥ 0 and F₆ ≠ 1) for carbon fullerenes, with the number of hexagonal faces F₆ = 20 for C₆₀. The smallest possible fullerene is C₂₀ (F₆ = 0), a dodecahedron consisting of 12 connected pentagons, and the only Platonic solid in the family of fullerene polyhedra.¹⁶ The truncated icosahedron C₆₀ belongs to the class of Archimedean solids.¹⁷ C₆₀ - I_h is the minimal arrangement such that no two pentagons share an edge (isolated pentagons): The edges of each pentagon join only hexagons, and the edges of each hexagon alternately join pentagons and hexagons. Thus, it is the smallest member in the class of fullerenes fulfilling the so-called isolated pentagon rule (IPR), which brings thermodynamic stability to a fullerene cage.¹⁸

There are infinitely many fullerenes, the number of isomers growing as for N carbon atoms as shown in Figure 1.¹⁹ The reason for the N⁹ growth comes from algebraic geometry, and is discussed below. These isomers come in many different shapes depending on the distribution of the pentagons as shown in Figure 2.^b As experimental techniques advance to synthesize new fullerene isomers²¹ with many interesting chemical and physical applications,^22–25 see for example the recent bottom-up synthesis of C₆₀ by Scott et al.²⁶ and Kabdulov et al.,²⁷ one naturally wants to know more about their thermodynamic stability and electronic properties.²⁸ As the isomer space rapidly grows into the millions and beyond, this becomes a daunting task for larger fullerenes. Even when the search is restricted to fullerenes that have isolated pentagons, known to yield the best stability, the number of candidates for most thermodynamically stable isomers is huge, many orders of magnitude too large for quantum chemical methods to be a viable means of analyzing stability. But, remarkably, the fullerene graphs contain all the information we need, and we are able to sort through the millions of isomers, finding a few candidates for the most stable, by way of simple, easily computed topological indicators,^29,30 such as the neighbor indices for pentagons or hexagons,³¹ or the incremental assignment of heat of formations to certain face patches.^32,33

Figure 1.

Number of distinct (non-isomorphic) fullerene isomers C_N (with and without fulfilling the IPR) with increasing number of carbon atoms N up to N = 400 (double logarithmic scale). (Data taken from the House of Graphs Ref 34)

Figure 2.

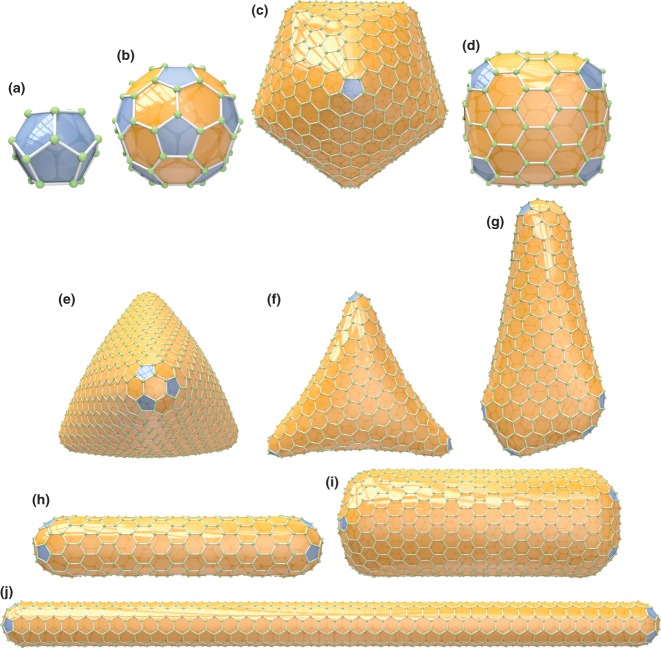
A selection of different 3D shapes for regular fullerenes (distribution of the pentagons D_P are set in parentheses). ‘Spherically’ shaped (icosahedral), for example, (a) C₂₀-I_h, (b) C₆₀-I_h, and (c) C₉₆₀-I_h (D_P = 12 × 1); barrel shaped, for example, (d) C₁₄₀-D_3h (D_P = 6 × 2); trigonal pyramidally shaped (tetrahedral structures), for example, (e) C₁₁₄₀-T_d (D_P = 4 × 3); (f) trihedrally shaped C₄₄₀-D₃ (D_P = 3 × 4); (g) nano-cone or menhir C₅₂₄-C₁ (D_P = 5 + 7 × 1); cylindrically shaped (nanotubes), for example, (h) C₃₆₀-D_5h, (i) C₁₁₅₂-D_6d, (j) C₈₄₀-D_5d (D_P = 2 × 6). The fullerenes shown in this figure and throughout the paper have been generated automatically using the Fullerene program.³⁵

There has been an intense activity in the field of topological and graph theoretical descriptions of molecules such as fullerenes^{29,31,36–40} over the past 20 years, to the extent that it has become a major sub-discipline within mathematical chemistry. It comes perhaps as a surprise that graph theory applied to molecular structures has not yet made it into main-stream university teaching. Furthermore, since the publication of the standard reference work in this area, An Atlas of Fullerenes by Fowler and Manolopoulos,³¹ there has not been a comprehensive review on this subject highlighting the many activities in recent times. In contrast, there are excellent reviews and books available on the chemistry and physics of fullerenes^{22,23,41–47} or on their electronic structure calculations.²⁸ In this overview we aim to close this gap and report on the many new and exciting developments in the topological and graph theoretical treatment of fullerenes, which have taken place over the past decade or so.^c

TOPOLOGICAL PROPERTIES OF FULLERENES

A Short Introduction to Graph Theory and Embeddings

A graph is a pair , where defines a set of vertices, and is a set of edges, each an unordered pair connecting two vertices. If a graph can be drawn in the two-dimensional plane without edge crossings, then it is called planar, and in this case it can also be drawn using only straight lines. A planar embedding is a map assigning a 2D-coordinate to each vertex such that straight-line drawings of the edges do not cross. For planar graphs in general, planar embeddings are not unique. But whenever at least three vertices must be removed before the graph separates into two disconnected components, the graph is called three-connected, and there is essentially only one way^d to embed it in the plane.⁴⁸ Because of this, a three-connected planar graph has a well-defined set of faces, . We can therefore represent a three-connected planar graph as without ambiguity, and will do so where convenient.

Whenever a graph is planar, it can also be embedded onto a surface of a sphere without edge crossings, and vice versa. Once again, this embedding is unique (in the same sense as for a planar embedding) if and only if the graph is three-connected, and we obtain the same faces. In fact, the graphs describing three-dimensional polyhedra are exactly the three-connected planar graphs,⁴⁹ and are therefore called polyhedral graphs.

The number of neighbors to a vertex v, that is, the number of edges incident to v, is called its degree, abbreviated as deg(v). If every vertex of a graph G has the same degree k, then G is called k-valent or k-regular. The special case of three-valent graphs is called cubic, and has a host of attractive mathematical properties, not least of which is their deep connections to algebraic geometry.¹⁹

Fullerenes have the neat property that the graphs formed by their bond structure are both cubic, planar, and three-connected, for which all faces are either pentagons or hexagons. Because of this, the mathematics describing them is in many cases both rich, simple, and elegant. We are able to derive many properties about their topologies, spatial shapes, surface, as well as indicators of their chemical behaviors, directly from their graphs.

Planar connected graphs fulfil Euler's polyhedron formula,

1

with being the number of vertices (called the order of the graph), E = | | the number of edges, and F = | | the number of faces (for fullerenes these are hexagons and pentagons). The hand-shaking lemma in graph theory tells us that

2

Since for fullerenes deg(v_i) = 3 for all vertices, we obtain⁵⁰

3

Hence, for fullerenes and fulleroids^e one has an even number of vertices. The total number of faces is F = F₅ + F₆, where F₅ and F₆ are the number of pentagons and hexagons respectively. From this we derive from Eq 3 E = 3F₅ + 3F₆ − 6 and N = 2F₅ + 2F₆ − 4. On the other hand, each pentagon (hexagon) has five (six) edges, which gives E = (5/2)F₅ + 3F₆. From these equations together with Eq 1 we obtain F₅ = 12 for regular fullerenes (the ‘12 Pentagon Theorem’ for fullerenes), which gives the number of hexagons as F₆ = (N − 20)/2 with N ≥ 20, and the general formula for fullerenes. Hence, from the fact that we only allow for cubic planar graphs consisting of pentagons and hexagons, we restrict the number of pentagons to exactly 12 (no more and no less!), and every addition of a hexagon adds two new vertices. Moreover, N = 22 with just 1 hexagon and 12 pentagons is not valid, but every number of hexagons two or greater yields at least one fullerene.⁵¹ The most stable C₂₂ molecule is, however, a cage-like fulleroid with a four-membered ring.⁵²

In this article, we will often work with the dual graph. The dual graph G* of a planar connected graph G has a vertex corresponding to each face of G, and an edge joining two neighboring faces in G. By this process, the old vertices become the new faces. The dual of a planar graph is itself a planar graph, and for fullerenes it is a triangulation with 12 vertices of degree 5 and the remaining of degree 6. For planar graphs in general, the dual is not unique, but as discussed above, it is unique for three-connected graphs such as fullerenes, and hence the dual operation is well defined.⁴⁸ The dual operation is an involution, that is, (G*)* = G, so we can think of the dual as just another representation of the same graph. Figure 3 shows the duals of two representative fullerenes with their corresponding 2D graph representation discussed in the next section.

Figure 3.

Planar embeddings of fullerene graph and dual (blue color and dotted lines for the dual representation), and 3D embeddings of the duals: (a) C₂₀-I_h, for which the dual is the icosahedron; (b) C₆₀-I_h, for which the dual is the pentakis-dodecahedron.

A useful representation of a graph is the adjacency matrix A_ij well known to chemists, as it is widely used in Hückel theory of conjugated organic molecules. The adjacency matrix is a symmetric matrix defined by A_ij = 1 if the graph G contains an edge v_i − v_j, and A_ij = 0 otherwise. It is equivalent to the edge-set representation, and is much easier to work with in many settings. As the number of edges for fullerenes is E = 3N/2, the adjacency matrix is very sparse. If two graphs G₁ and G₂ are isomorphic, the corresponding adjacency matrices A₁ and A₂ are related by vertex permutation, and thus share the same set of eigenvalues and eigenvectors. Matrices play a special role in chemical graph theory, and the reader is referred to Ref 53 for more details.

Drawing Fullerene Graphs: Methods for Planar Embedding

Planar embeddings can be drawn on paper and give us a way to visualize the structures of planar graphs. However, not all choices of embeddings are equally informative. We want the drawings to be simple, not too cluttered, and to expose as much as we can of the graph's structure and symmetry. In general the full symmetry group can not be realized in two dimensions, but we can find embeddings that show as much of it as possible. Figure 4 shows planar drawings of three icosahedral fullerenes, C₂₀ - I_h, C₆₀ - I_h, and C₅₄₀ - I_h, exposing 10-fold D₅-symmetry out of the full I_h group. In this section, we will discuss methods for constructing good planar embeddings.

Figure 4.

Planar embeddings (no crossing edges) for three different fullerenes obtained from a perspective projection. (a) icosahedron C₂₀-I_h; (b) truncated icosahedron C₆₀-I_h; (c) C₅₄₀-I_h.

While a small graph can easily be drawn by hand, larger graphs such as C₅₄₀ shown in Figure 4(c) require a computer algorithm and a drawing program. The first method we will discuss is called the Schlegel projection, and requires first an embedding of the graph as a three-dimensional polyhedron. In 1886, Victor Schlegel showed that a planar graph can be obtained from a three-dimensional polyhedron by projection in the following way: A point is placed slightly above one of the faces, and a plane P is chosen to lie below the polyhedron. Lines are then drawn from through each of the polyhedron's vertices. The intersection of each line with P defines the 2D coordinate of the vertex v. If is chosen sufficiently close to the face, and if the points of the polyhedron lie on a sphere, the resulting 2D embedding will be planar. While Schlegel only proved that the projection produces a planar layout when the vertices lie on a sphere, it still works in many cases where this is not the case, and the method is widely used to the extent that planar graph embeddings sometimes (incorrectly) are called Schlegel diagrams. However, Schlegel diagrams are specifically the embeddings that result from the Schlegel projection. The Schlegel projection is illustrated in Figure 5(a).

Figure 5.

(a) Schlegel projection of C₆₀-I_h. (b) Cone projection of disk-shaped C₇₂-D_6d.

A problem with the Schlegel projection is that it often fails, and produces crossing edges, when used with many non-spherical polyhedra or when the parameters are not well chosen. The cone-projection method, shown in Figure 5(b), which projects the vertices out on an enveloping cone of the fullerene polyhedron and then down onto a plane, seems to be more robust.³⁵

Both the cone-projection and the Schlegel projection require first a polyhedral embedding of the graph, and on top of that often necessitate bit of hand-tuning to produce a planar embedding. The third method we mention is called the Tutte embedding,⁵⁴ and is guaranteed to always yield a planar embedding for three-connected planar graphs. In the Tutte embedding, one fixes the coordinates of a single, outer face, and solves a sparse linear system

4

such that in the result, every vertex is placed in the barycenter of its neighbors. For fullerenes, T_ij = δ_ij − A_ij/3 and for every i where v_i is not a fixed vertex, and for the vertices v_i on the outer face, T_ij = δ_ij and is the fixed coordinate. While the Tutte embedding is guaranteed to be planar, the solution to the linear system results in exponential crowding of the vertices when embedding large graphs, making the result difficult to interpret. Hence, it is useful to follow the Tutte embedding by an optimization to make the face sizes more even.³⁵ We note that there are many different graph drawing algorithms available, each with advantages and disadvantages, but none that are guaranteed to always yield good results.^54–57

The Large Isomer Space

How does the number of C_N-isomers grow as we increase the number of vertices N? Naively one might assume a hypothetical sphere of ‘connected’ hexagons (which is of course impossible because of Euler's theorem) and substitute 12 hexagons by pentagons to obtain a set containing all possible fullerene isomers fulfilling Euler's theorem (just like playing Lotto), we obtain an upper bound for the number of isomers of the order . This is, however, three orders of magnitude too large, but the proof is nontrivial. In 1998, William Thurston showed that all the triangulations of the sphere with vertex degree at most 6 form a lattice of integer points in a complex hyperbolic space C(1, 9) through a parameterization as described in Ref 19. The triangulations with N vertices or less correspond to the lattice points inside the intersection between a certain cone and a ball of radius in this space. Hence their number is roughly proportional to N¹⁰, and the number of triangulations with exactly N vertices is roughly proportional to

5

or, in short, . Because they are the largest class of the finitely many triangulation classes with vertex degree six or less, the fullerenes have the same asymptotic count. Hence, the number of C_N isomers grows as . We note in passing that the connection of fullerenes to combinatorial manifolds is a deep one and gives rise to many of the beautiful mathematical properties exhibited by fullerenes.

The high order polynomial growth of fullerene isomer counts makes it difficult to establish a complete database for fullerene graphs up to high vertex numbers.³⁴ Moreover, the proportion of IPR isomers to the total number of isomers grows with increasing N, gradually approaching 1 with increasing N, as is shown on Figure 4.

Face Spiral Representations of Fullerene Graphs

One of the first methods for encoding fullerene graphs was the face spiral algorithm by Manolopoulos et al.,⁵⁸ which unwinds all faces of a fullerene ‘like an orange peel’ (the Manolopoulos face spiral algorithm). More specifically, starting with a sequence of three mutually adjacent faces, new faces are added to the string such that the next face is adjacent to the previous one and the one that was added to the string earliest, and that has neighboring faces left which are not part of the spiral string (yet). As the result, one obtains a string of length F of 12 fives and F − 12 sixes, corresponding to the sizes of faces.

There are 6N possible spiral starts resulting in up to 6N spirals per fullerene graph. In most fullerenes, some spirals cannot be completed because the two rules for choosing the next face cannot be both fulfilled. Since a fullerene spiral always consists of 12 fives and N/2 − 10 sixes, this spiral string can be abbreviated as a list of the 12 pentagon positions, called the face spiral pentagon indices (FSPI) {S_n|n = 1, …, 12}. The lexicographically smallest of all successful spirals is the canonical spiral representation of the graph. For example, for C₆₀ we have the canonical FSPI of {1, 7, 9, 11, 13, 15, 18, 20, 22, 24, 26, 32} as shown in Figure 6.³¹

Figure 6.

(a) Canonical face spiral for C₆₀-I_h. (b) The first fullerene (C₂₈-D₂) with a failing face spiral.

While it was initially conjectured that every fullerene can be unwound into a face spiral⁵⁸ (for good reason: the first counterexample comes after over 10¹² isomers) there is an exceedingly small proportion of fullerene graphs⁵⁹ (but infinitely many in total) that do not admit a face spiral,⁶⁰ that is, where all 6N spiral starts fail. See Figure 6 for a case where a face spiral fails. The smallest of these unspiralable fullerenes is C₃₈₀ - T.⁶¹ Manolopoulos et al.,⁶⁰ Fowler et al.,⁶² Yoshida et al.,⁶³ and Brinkmann et al.⁶⁴ compiled lists of non-spiral fullerenes with up to 1000 atoms and selected point groups (all T₊, all isolated pentagon triple (IPT) fullerenes with D₂ and T symmetry, all D_3 +, and all truncated IPT fullerenes respectively). Two of those are shown in Figure 7.

Figure 7.

B3LYP optimized structures for the two smallest non-spiralable fullerenes (a) C₃₈₀-T and (b) C₃₈₄-D₃ (see Ref 59 for details).

In order to encode any fullerene graph, it is necessary to extend the face spiral algorithm to a general version in which the spiral may ‘jump’ from one face to a non-adjacent face. Both Brinkmann⁶⁵ and Fowler et al.⁶⁶ published general face spiral algorithms for cubic polyhedral graphs, including fullerene graphs. Fowler's algorithm extends the two above mentioned rules such that the subgraph that has not been added to the spiral yet never gets disconnected, and as a result the spiral never gets stuck. Brinkmann's algorithm, in contrast, adds faces as defined by the non-general version, but defines how to proceed if all neighbors of the current face have been added to the spiral already. Both algorithms yield the same spiral string as the non-general algorithm if no jump is required.

For the non-general as well as both general algorithms for finding the canonical face spiral of a graph, there is an inverse algorithm that efficiently regenerates the graph from the (general) spiral string representation. With the extension to general spirals, all fullerene isomers with any vertex number can be generated. In addition, all the information of the fullerene graph is contained in a general face spiral consisting of 12+ numbers (12 for most fullerenes). This makes it rather convenient for database storage as the face spiral uniquely defines the fullerene.

In a similar way to face-spirals we can introduce vertex spirals (or Hamilton spirals) useful for identifying locations of substituents (such as hydrogen) or reaction centers⁶⁷ (for details see Ref 68). For fullerenes with no vertex spirals the scheme can be extended to general spirals with jumps similar to general face spirals.

Generation of Fullerene Graphs

In order to explore chemical, physical, or graph theoretical properties for a wide range of fullerenes, it is important to have access to a list of (stored) fullerene graphs. For this, one requires an exhaustive and efficient generator for all fullerene isomers of a given vertex number N. The general face spiral algorithm is well suited for compactly storing and recreating specific fullerene graphs. It also allows for sorting all isomers of C_N for a given vertex number N according to their FSPIs including information about jumps if required. It is, however, extremely inefficient to generate all isomers C_N directly through a face spiral algorithm. In the non-general case one attempts to create graphs from spiral strings while the number of non-isomorphic graphs only grows ∼ N⁹. A large and quickly growing portion of all potential spiral strings are either non-canonical spirals, duplicates or are not successful for coding a fullerene. Including general spirals increases the overhead by two orders of magnitude, as jumps could be inserted at any step and with arbitrary lengths l < N.

A different approach to generating fullerene graphs is by adding faces to an existing graph, while considering different sites for addition at each step. Liu et al.⁶⁹ introduced a method which grows a graph starting with a single face and thus only reaches a fullerene graph in the last step. Brinkmann et al.⁷⁰ use patches, rather than single faces, as building blocks. These patches can be obtained by subdividing existing fullerene graphs.

Further development in efficient graph generation came from transforming an existing fullerene graph into a new, larger one by adding faces. Using C₂₄ as a ‘seed’, Brinkmann et al.⁷¹ were able to generate almost all fullerene graphs up to C₂₀₀. However, three graphs were not accessible by the applied set of transformations. To cure this shortcoming, Hasheminezhad et al.⁷² defined a set of patch replacements (or growth operations) which, starting from either C₂₀ or C₂₈ - T_d, yield every fullerene in a systematic way. The set consists of one single operation that elongates a nanotube with minimal caps, one class of linear generalized Stone-Wales transformations^73,74 that depend on one parameter, and one class of bent generalized Stone-Wales transformations that depend on two parameters. Brinkmann et al.⁷⁵ used this set of growth operations to define a fast and complete algorithm that recursively generates all fullerene isomers up to a given maximal N. The algorithm prunes the recursion tree in such a way that the only one representative of each isomorphism class is ever considered. Without such a scheme, exhaustively generating all fullerene graphs would succumb to combinatorial explosion.⁷⁶ The result is an incredibly efficient algorithm which has been used to generate an exhaustive database up to C₄₀₀, which is available at the House-of-Graphs website.³⁴ Sometimes one is not interested in generating exhaustive isomer lists (which are huge for large N), but rather to generate in a directed fashion fullerenes that have specific properties. For this, one may start with one specific isomer C_N and derive others by certain transformations. This will be discussed in the following section.

Transformation of Fullerene Graphs

Transformations of fullerene graphs can be divided into local transformations that leave all but a certain region of the graph unchanged, and global transformations such as the Goldberg-Coxeter transformation.^77,78 A planar graph can be transformed locally by replacing one fullerene patch^74,79–84 by either a different patch or the same patch in a different orientation. A patch is a set of faces that is bounded by a simple cycle,^82,85 that is, a cycle that traverses no vertex or edge twice. Some authors relax this condition and allow cycles that are non-selfintersecting, but are permitted to traverse any edge at most twice. This definition includes patches that have bridges, and is used in the complete characterization of fullerenes by Hasheminezhad et al.⁷²

Two patches can be exchanged if they share the same boundary code. The boundary code of a patch is the sequence of free valencies of the vertices that lie on the boundary (in case of cubic graphs, a sequence of zeros and ones). A few patch replacements are shown in Figure 8.

Figure 8.

(a) Endo-Kroto (EK) 2-vertex insertion. (b) Stone-Wales (SW) transformation. (c) Example of an extended Stone-Wales transformation. (d) A patch replacement which introduces one heptagon.

Replacing patches of equal size can be understood as a formal isomerization, while replacement by larger or smaller patches, referred to as vertex insertion or deletion, or growth operations, formally derives a molecular graph of a different size. Two fullerene graph patches with the same boundary code contain the same number of pentagons, as can be seen from Euler's polyhedron formula. The most prominent example for formal isomerizations is the Stone-Wales (or pyracylene) transformation (SW),⁸⁶ which can be generalized^73,87 by allowing a variable distance between the two pentagons. Astakhova et al.⁸⁸ extended this rearrangement mechanism even further to higher numbers of pentagons. Brinkmann et al.⁸³ generated a catalog of isomerization pairs with up to five pentagons.

Isomerization operations can be reformulated as sequences of vertex-pair switches, called 2-switches.⁸⁹ According to Berge's switching theorem,⁹⁰ the whole isomer space of a given C_N is accessible by repeated application of 2-switches. However, intermediate structures of this procedure might have faces different from pentagons and hexagons, or result even in non-planar graphs.

Growth operations can be classified according to the number of pentagons and the number of vertices that are added. There are no growth operations for fullerene graphs that involve no or only one pentagon.⁸¹ The smallest example is the Endo-Kroto transformation (EK),⁹¹ which involves two pentagons and adds two vertices. Additional noteworthy examples are the addition of four and six vertices at a patch that contains three pentagons and has C₃ symmetry.⁹² Brinkmann et al.⁸⁴ compiled an extensive list of growth pairs. The three classes of patch replacements defined by Hasheminezhad et al.⁷² form the basis of the currently fastest fullerene graph generator, as discussed in a previous section.⁷⁵

With respect to the polyhedral representation of a fullerene graph, growth operations can be understood as the capping of a domain by additional vertices. As a result the pentagons in that domain move toward each other. Patches in which all pentagons are fused cannot be capped. Conversely, the inverse of a growth operation corresponds to the truncation of a domain of high curvature: The distances between the affected pentagons increase.

While patch replacements are useful from a graph theoretical point of view to obtain new fullerene isomers, the EK C₂ insertion and the SW transformation have also been suggested to resemble viable reaction pathways.^{86,91,93–95} As Stone and Wales pointed out in their initial article, a concerted mechanism for the SW transformation ([2+2]) is Woodward-Hoffmann forbidden in the electronic ground state.⁸⁶ Other mechanisms that involve the breaking of one bond^93,96,97 or the catalysis by additional carbon atoms⁹⁸ are therefore more likely. For a discussion of different mechanisms see Ref 93. For every suggested pathway, however, the activation barrier is so high that SW transformations are only feasible at very high temperatures.^93,94 The SW transformation is believed to be one of the main mechanisms by which fullerene cages equilibrate during formation to form the most stable isomer.^99,100 Starting at C₆₀ - I_h, 1709 out of the 1811 other isomers are accessible by consecutive SW transformations.¹⁰¹

Endo and Kroto proposed a concerted mechanism for what has since been known as the EK C₂ addition.⁹¹ However, more recent experimental and theoretical investigations show, that the concerted reaction leads to an unstable adduct and is followed by C₂ ejection.¹⁰² For a summary of alternative mechanisms of the C₂ addition to fullerene cages see Ref 95.

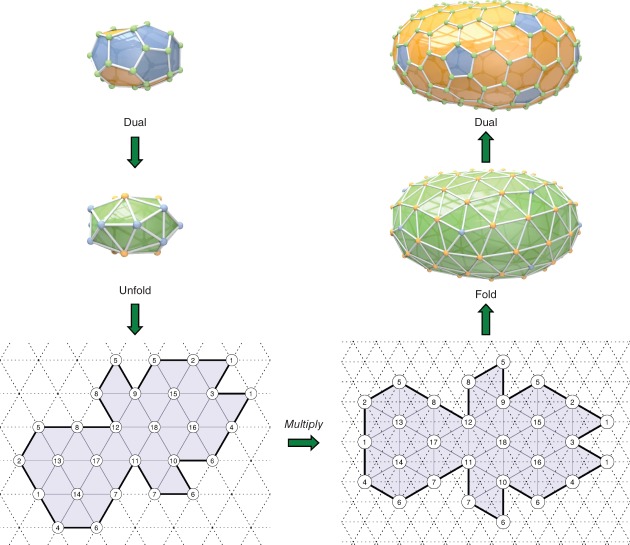
Given any fullerene, it is possible to construct an infinite series of larger ones with (essentially) the same three-dimensional shape. This is possible through the Goldberg-Coxeter transformation, named after an infinite series of icosahedral-symmetry polyhedra described by Goldberg in 1937.⁷⁷ By superimposing a hexagonal mesh on the surface of the dodecahedron, as shown in Figure 9(a), a new polyhedron is obtained with the same number of pentagons and an increased number of hexagons. The number of vertices in the new polyhedron is k² + kl + l², where k and l are integers describing the scale and orientation of the mesh, as shown for the dual in Figure 9(b). The construction used by Goldberg was discovered independently, and applied to the shapes of vira, by Caspar and Klug in the 1960s, and later popularized by Coxeter.⁷⁸

Figure 9.

Illustration of GC-transform. (a) Original figure of a hexagonal sheet from Goldberg's paper.⁷⁷ (b) The GC-transform acting on a face in the fullerene dual for various values of k and l.

While originally only defined for C₂₀, yielding exactly all the fullerenes of icosahedral symmetry, Dutour and Deza have shown that it is well defined for all cubic planar graphs.¹⁰³ However, it is not trivial to determine how to automatically perform the general transform, the main difficulty lying in how to ‘glue’ the graph back together when the new edges cross the transformed triangles in complex ways. The general construction by Dutour and Deza is quite algebraically heavy handed, and is not easily understood, nor lends itself easily to implementation. In the case of fullerenes, however, it is quite easy to give a procedural description of the transformation in terms of the fullerene dual: Because a fullerene dual is a triangulation of the sphere with no vertices of degree more than 6, it can be unfolded onto the plane of equilateral triangles, called the Eisenstein plane. The unfolded surface forms a polygon in the Eisenstein plane with every degree 5 vertex on the polygon periphery, and with each edge on the periphery appearing twice, once in each direction.

The vertices in the Eisenstein triangulation is a sub-ring of the complex plane, and we can write

6

Because it is a sub-ring, multiplication by Eisenstein integers (a, b) are exactly the operations that bring (1, 0) into every other vertex point. Because ω² = ω − 1, we get the multiplication rule

7

and the magnitude of (a, b) is (a + bω)(a + bω^− 1) = a² + ab + b². Hence, if T is an equilateral triangle with unit area, the area of (k, l)T is k² + kl + l². This is no coincidence: multiplication in the Eisenstein ring exactly corresponds to the Goldberg-Coxeter transformation in the dual formulation. This yields a simple and practical formulation of the Goldberg-Coxeter transform of any triangulation of the sphere with deg(v) ≤ 6:

8

The procedure is illustrated in Figure 10. Details for how to efficiently perform the fold and unfold operations are given in Avery (unpublished manuscript). Note that two successive GC-transformations on a graph G* can be expressed as a single GC-transformation by multiplying the two Eisenstein numbers together. Similarly, a GC-transformation can be inverted by dividing instead of multiplying. For any particular fullerene, we can even use Euclid's algorithm to find out whether it is a GC-transform of a smaller fullerene, and to find the smallest such ‘parent’ fullerene.⁵⁹

Figure 10.

The steps in the GC_2,1 Goldberg-Coxeter transformation from C₃₂-D_3h(5) to C₂₂₄-D_3h. The transform and the diagrams of the unfolded fullerenes were automatically generated using the program Fullerene.³⁵

Notice, that if one were to cut out the two diagrams in Figure 10, gluing together the edges so that the numbers on the vertices match, one obtains the three dimensional structure of the given C₃₂ and C₂₂₄ fullerenes. The reader is invited to do so.

There are two special cases of the Goldberg-Coxeter transformation that warrant closer study: the case l = 0, named the halma transform (or k-inflation) for the construction's similarity to the game board of halma, or ‘Chinese Checkers’; and the case k = l = 1, called the leapfrog transform. Both of these types of Goldberg-Coxeter transformations are simple to understand: every triangle is subdivided and reconnected the same way, as illustrated on Figure 11. While the GC-transform in general can introduce, reverse, or remove chirality (but otherwise preserves symmetry), both the halma and leapfrog transformation always preserve symmetry.

Figure 11.

Subdivision of a triangle in the dual graph; (a) for the leapfrog transformation (k = l = 1), and (b) for the lowest few halmas (l = 0).

Geometry of Fullerenes

Many of the beautiful properties of fullerenes derive from their relation to algebraic and differential geometry. This relation is mostly out of scope for this review, but in this section we will touch on the subject informally. The subject is treated in great depth by Thurston¹⁹ and others.

An important quantity for understanding the geometry and shapes of fullerenes is the Gaussian curvature. The Gaussian curvature is the product of the two principal curvatures, which for each point on the surface are the maximal and minimal curvatures in any direction through that point. By the Bertrand-Diquet-Puiseux theorem, the Gaussian curvature in a point is the same as the difference between 2π and the angle required to make a circle in a neighborhood around this point. Figure 12 illustrates three categories of surfaces with zero, positive, and negative Gaussian curvature respectively. If the Gaussian curvature is zero in a point, the surface only bends in one direction around that point. A surface that has zero Gaussian curvature everywhere is characterized by being ‘flat’ in the sense that it can be unwrapped onto a plane without tearing. Positive Gaussian curvature bends the same way in all directions. A positive curvature surface can be cut open and unwrapped onto a plane. Finally, negative curvature around a point constitutes a saddle point, yielding a wobbly pringle-like surface. Negative curvature surfaces cannot be unwrapped onto a plane, because there is no room: around a negative curvature point, the angle of a circle is greater than 2π. If one were to make a cut in a negative curvature surface, it could only be flattened out by allowing parts of it to overlap itself.

Figure 12.

Examples of surfaces with zero (a), positive (b), and negative (c) Gaussian curvature around a point.

The Gaussian curvature only depends on the topology of the surface, and is independent of how it is isometrically embedded in space. In the same way, the surface metric (or Riemann metric), which determines the geodesics and distances between points along the surface, can be derived directly from the graph (Avery et al., unpublished manuscript), and is also independent of the spatial embedding. However, while we do not require a 3D embedding to analyze these surface properties, they themselves do determine the possible ways that the surface can embed isometrically into space, and what is its ‘natural’ three-dimensional shape.

Fullerenes are all closed surfaces with non-negative Gaussian curvature everywhere. Surprisingly, this is simply due to them having faces no larger than hexagons! In fact, the slightly larger class of three-connected cubic planar graphs with largest face size 6, and their dual triangulations, are in a sense all the positive curvature genus 0 surfaces.^f

It is most easy to understand the geometry of fullerenes when considering their duals. These are equilateral triangulations of a closed surface. The equilateral triangle plane, also called the Eisenstein plane, is the dual of a hexagonal mesh. Hexagon planes (like graphene) and their dual degree-six triangulations are flat in the sense that they have Gaussian curvature 0 everywhere: any surface of equilateral triangles with vertex degree only six can be unwrapped into the plane without stretching or tearing. What happens now if we set the degree to 5 of a single vertex in the plane? To do this, we must cut out an infinite triangular wedge of angle 2π/6. Gluing together the edges forms an infinite cone with Gaussian curvature zero everywhere except the degree 5 vertex at the cone's apex, which introduces the positive curvature 2π/6. Every time we introduce a vertex of degree 5 (or a pentagon in the hexagonal plane), it introduces a surface cut that is glued together to locally introduce the positive Gaussian curvature 2π/6 at the vertex. After 12 pentagons we reach 4π, the Gaussian curvature of the sphere, closing the surface.^g Unfolding again along the 12 cuts would result in a polygon similar to the diagrams shown in Figure 10. Had we instead introduced, for example, degree 4 vertices, each would contribute with curvature 2π/3, requiring only 6 to close the surface. The positions at which we placed the 12 pentagons determine where and how strongly the surface bends, and through that the natural shape of the fullerene, giving rise to the many interesting polyhedral shapes shown in Figure 12.

Because fullerenes always have exactly 12 curvature-2π/6 bends, with the remaining surface of Gaussian curvature zero, they adopt polyhedral shapes rather than being spherical in nature (the latter defined as atoms lying on a sphere), and the most symmetric shapes that they can achieve have icosahedral symmetry. The non-spherical nature of fullerenes was pointed out already by Bakowies and Thiel in 1995.^104,105

The curvature of cubic graph surfaces also provides an intuitive understanding of why fullerenes, having only hexagon and pentagon faces, would be more prevalent in nature than other polyhedral carbon structures: smaller face sizes introduce much sharper bends, reducing stability. Heptagons by themselves introduce no sharper bends than pentagons, but each heptagon necessitates an extra pentagon to balance out the negative Gaussian curvature and reach a closed surface, increasing the total number of bends by two. However, with the right distribution of heptagons and pentagons, it is possible to construct quite smoothly curving near-spherical fulleroid surfaces that could potentially be stable in nature. We discuss fulleroids, a generalization of fullerenes that allow arbitrary face sizes, in the final section.

Generating Accurate 3D Geometries

The Cartesian coordinates for the ideal molecular geometry of small highly symmetric fullerenes such as C₂₀ - I_h or C₆₀ - I_h can be calculated directly using basic geometry.¹⁰⁶ This is not the case for fullerenes in general: They come in many different shapes, most of which do not have a simple mathematical formula. However, we do know that the ideal geometry (in which the faces of the dual polyhedron are equilateral triangles) can be derived directly from the fullerene graph. This is because of their special properties discussed above. However, while we know that a fullerene graph determines the ideal 3D structure as a conformal, isometric embedding of the surface into space, it is not yet known how to compute it directly. However, we can use numerical optimization methods to obtain good 3D structures—both efficiently and with results that are very close to the physical molecular geometry.

Generating Initial Structures

Before optimizing a fullerene structure by for example a force-field method, we need a reasonable initial structure. Specifically, we need an embedding of the graph as a polyhedron (i.e., no crossing edges) such that its faces are the same ones as in the final polyhedron, and such that the magnitude of the force experienced by the vertices does not vary too greatly, causing slow convergence or numerical instability. We here outline two methods for obtaining initial geometries that are suitable for input to the fullerene force-field optimization.

The Fowler-Manolopoulos 3D embedding algorithm (also called Adjacency Matrix Eigenvector or AME algorithm) diagonalizes the N × N adjacency matrix A_ij of the fullerene graph to obtain eigenvectors , of which three ‘P-type eigenvectors’ with one nodal plane are chosen to construct the Cartesian coordinates (termed topological coordinates by Manolopoulus and Fowler) for the initial structure.^31,107 This often yields suitable coordinates because fullerenes can be modeled as spherical aromatic systems fulfilling approximately the Laplace differential equation with real spherical harmonics Y_lm(θ, ϕ) as eigenfunctions, of which the three Y_lm (l = 1) are associated with the coordinates (x_i, y_i, z_i).^31,108 Cartesian coordinates constructed in this way already reflect the space symmetry of the fullerene. The P-type eigenvectors can easily be found for near-spherical fullerenes like C₂₀ or C₆₀ - I_h, because the sequence of eigenvalues mimics the spherical harmonics. However, for distorted fullerenes, or for very large fullerenes where the spectrum of the adjacency matrix becomes very dense with quasi-degeneracies, it becomes difficult to find the appropriate eigenvectors, and the assumption that the eigenvectors resemble spherical harmonics becomes decreasingly valid. For example, for large fullerene nano-tubes aligned around the z-axis, such as the one shown in Figure 12, the eigenvalues belonging to the P_x- and P_y-type eigenvectors do not lie close to the P_z eigenvalue. Hence, one must search for the appropriate set of eigenvectors, and identifying them is not always easy.^109–111 Second, the bond lengths tend to vary substantially in the constructed fullerene, leading to unreasonable large bond distances once the minimum bond distance is set to ≈1.4 Å, and a scaling procedure for the eigenvectors may only solve part of this problem.³¹ Finally, because it is often necessary to search for the right eigenvectors and hence calculate a large number of them, the algorithm scales up to , which quickly becomes a heavy operation as N grows.

We have found it useful to sacrifice some accuracy in the initial geometry for a method that is more stable, and which scales approximately as . The fullerene force-field optimization is insensitive enough to the starting geometry that the difference is not noticeable. The method starts with any planar embedding of the fullerene graph. We choose the Tutte-embedding, which is guaranteed to be planar, and can be computed in near-linear time by solving two sparse linear systems of equations.⁵⁴ The planar embedding is then mapped onto the surface of a sphere (or e.g., ellipsoid, if the fullerene is a priori known to be elongated) in the following way: For every vertex v, let the topological distance from the outer face (the ‘depth’ of the vertex) be d_v, and its coordinate in the Tutte-embedding be . Let D be the maximum depth, and be the barycenter in the embedding. We assign one angle ϕ(v) = (d_v + 1/2)π/D + 1, placing vertex layers equidistantly along the ϕ-angle according to their depth. The second angle θ(v) is the angle of around . Then assigning the angles v ↦ (θ(v), ϕ(v)) yields an embedding on the sphere with no crossings, since the Tutte-layout is guaranteed to be planar, but which avoids the exponential crowding of the planar Tutte-embedding, such that the vertices are distributed in a reasonable manner across the surface of the sphere.^h It remains, however, a challenge to embed the fullerene graph on a more realistic surface.

Fullerene Force-Field

This section describes how to obtain good results for the molecular geometry numerically by way of specially tailored force-field optimization methods. This yields geometries that are very close to the ones obtained by long and computationally heavy quantum chemical calculations, as we shall see.

It is common for molecular force-field optimizations to distinguish between single and double bonds, even introducing different types of single and double bonds depending on atoms and groups in close proximity. For each bond, that is, edge in the graph, one sums over all the Kekulé structures and assigns fractional double bond character to each edge. This strategy is not practical for fullerenes, even for small cages like C₆₀,^112,113 due to exponential growth in perfect matchings and hence Kekulé structures, as discussed below. Force fields for fullerenes should therefore be designed in a way that avoids explicit treatment of double bonds. As a good approximation it is assumed that the properties of bonds, angles, and dihedral angles in a fullerene are determined by the size of their neighboring faces alone. The force fields discussed below are specifically designed for fullerenes based on this assumption.

The first force field tailored to fullerenes by Wu et al.¹¹⁴ was designed for C₆₀ - I_h and uses harmonic force field terms. It distinguishes between two bond types: bonds adjacent to two hexagons, and bonds adjacent to a pentagon and a hexagon, which are optimized for bond lengths r₀ with values of 1.54 Å and 1.41 Å, respectively. Angles are either part of a pentagon (θ₀ = 3/5 π) or a hexagon (θ₀ = 2/3 π). The force constants k₁ through k₄ are given (in 10⁵ dyn/cm) as 11.0, 10.0, 1.0, and 1.0. No further parameters are taken into account.

In the following years a number of extensions and modifications to the Wu force field were published, taking into account an increased number of parameters. These extensions include improved force constants,¹¹⁵ torsions,¹¹⁶ angles and distances to second and third neighbors,¹¹⁷ mixed terms between distances and angles,^118,119 the volume of the tetrahedron defined by an atom and its three neighbors,¹¹⁸ a complete force field for C₆₀ - I_h,¹²⁰ and a strategy for defining complete force fields for any deltahedron or trivalent polyhedron using mixed terms of distances and angles.¹²¹ Except for the force field by Ceulemans et al.,¹²¹ all above mentioned force fields have been exclusively designed for and applied to C₆₀ - I_h.

The program Fullerene³⁵ includes a 22-parameter force field with explicit dihedral angles. It takes into account three types of distances (bonds that are part of 0, 1, or 2 pentagons), two angles (part of a pentagon or a hexagon) and four types of improper dihedral angles, defined between a vertex and its three neighbors (where the starting vertex is part of 0, 1, 2, or 3 pentagons). It is applicable to all fullerenes and yields structures that are in very good agreement with DFT optimized structures. For example, for C₃₈₀ - T, the rms error between the B3LYP/SVP and the force field optimized structure is only 0.038 Å. For many purposes, the force-field optimized molecular geometry, which is computed in milliseconds, is good enough to be used instead of a more computer time intensive quantum chemical optimization (although semiempirical methods including density functional based tight-binding are also very computer time efficient and have yielded good results¹²²).

Fullerene Symmetry

There are two symmetry groups associated with a fullerene: the ideal or topological symmetry group of the fullerene graph, and the real or physical symmetry group of the molecule in 3D space. The physical symmetry group is a subgroup of the ideal one, due to (first or second order) Jahn-Teller distortions, variation of bond-lengths, or other effects from external perturbations. But because the shape is often only mildly altered from the ideal shape, the ideal symmetry group carries useful information about the physical system.

A surprising theorem by Mani¹²³ shows that any three-connected cubic planar graph can be embedded in space as a convex polyhedron, the point group of which realizes the full symmetry group of the graph. That is: every graph automorphism of a fullerene is also a rotation or reflection of its ideal polyhedral shape. In addition, it can be shown¹²⁴ that the point group for a fullerene must be one of the 28 point groups listed in Table1. The largest group is the icosahedral group I_h of order 120, and each of the 27 remaining attainable point groups are subgroups of I_h.

Table 1.

The 28 Possible Point Groups for Fullerenes Sorted According to Their Order of the Group ³¹

Order	Point Groups	Order	Point Groups	Order	Point Groups
120	Ih	60	I	24	Td, Th, D6h, D6d
20	D5h, D5d	12	T, D6, D3h, D3d	10	D5
8	D2h, D2d	6	D3, S6, C3h, C3v	4	D2, S4, C2h, C2v
3	C3	2	C2, Cs, Ci	1	C1

Can we automatically determine the symmetry group for the fullerene directly from the graph, without referring to spatial coordinates? (The latter requires first finding a maximally symmetric 3D embedding) For general graphs, this is a difficult problem. However, in the case of cubic polyhedral graphs, for which general face spirals determine isomorphism, it is both simple and efficient to do so.

Before moving on, we take note of an ambiguity in terminology. The terms symmetry group and automorphism group often refer simply to the group formed by operations that leave the system invariant. In the group theoretical sense, a group is fully defined by its multiplication table. Point groups, however, are not just groups, but are isometries of space and carry additional information about how they transform space. For example, the point groups D₆, C_6v, D_3d, and D_3h are all the exact same group, but differ as point groups. It is unfortunate for this reason that ‘point groups’ are called ‘groups’. To make the distinction explicit, we will use the term abstract group for the symmetry group in the group theoretical sense, and either point group or symmetry group for the isometries.

Assume that we are given the fullerene graph dual G*, constructed from a generalized spiral S = (d₁, d₂, …, d_F), and wish to compute the automorphism group of G*. Since G* is constructed from S, the entries in S are the degrees of vertex number 1, 2, …, F in G*. For every vertex v of degree d₁, we have 2d₁ different spiral starts: d₁ for clockwise and d₁ for counter-clockwise traversal. If a spiral start (f₁, f₂, f₃) unwinds G* to the input spiral S, there is an automorphism of G* that maps (1, 2, 3) ↦ (f₁, f₂, f₃). These are all the automorphisms, and the number of starts that unwind to S is the order of the automorphism group. This construction lets us easily obtain the actual group: The spiral start determines the entire spiral, and by simply writing down the vertex names in G* while unwinding the spiral, we obtain a permutation representation of the group element

9

This is a faithful (but not irreducible) representation of the group, and if we wish, we can easily build the multiplication table by composing all pairs of the permutations. Similarly, we can calculate characters, irreducible representations, and all other properties, and we can identify the group. There are a number of ways to make this efficient. In Wirz et al. (unpublished manuscript), we present a general, but efficient, -algorithm that works for all cubic polyhedral graphs, including all fullerenes and fulleroids.

The permutation representation π_F allows us to not only find the abstract symmetry group, but contains enough information to identify the point group, that is, the isometries of the three-dimensional fullerene polyhedron. Fowler and Manolopoulos published a program for identifying the point group of any spiralable fullerene in Ref 31, based on site symmetries and counting group orbits. The symmetry points of interest in a fullerene are the vertices, midpoints of edges, the barycenter of the polygons and the whole cage, the latter having the full symmetry of the point group. They have certain site symmetries according to the rotational axes or mirror planes going through these symmetry points,³¹ which are collected in Table2. The full isometry group , which correspond to the rotations, reflections, roto-inversions, and inversions that leave the ideal polyhedron invariant, also act as permutations of the symmetry points,^107,125,126 the action always being a subgroup of . The permutations of the symmetry points in fact completely determine the point group symmetry, and we can find the full point group of the graph G (or, equivalently, its dual G*) as follows:

Table 2.

The Site Symmetries of the Local Symmetry Points in a Fullerene³¹

Symmetry Points	Site Symmetries (Order)
Vertices	C3v(6), C3(3), Cs(2), C1(1)
Edge centers	C2v(4), C2(2), Cs(2), C1(1)
Pentagon centers	C5v(10), C5(5), Cs(2), C1(1)
Hexagon centers	C6v(12), C6(6), C3v(6), C3(3), C2v(4), C2(2), Cs(2), C1(1)
Cage center	Full point group

The order of the site-symmetry group is given in parentheses (the maximum value of any site symmetry group order is 12).

In step 1, one computes the face permutation representation π_F of the abstract group, as described above. From this one derives vertex and edge permutation representations π_V and π_E by acting with every group operation on the dual graph.

In step 2 one computes the vertex, edge, and face group orbits by acting with the permutation representations on every vertex, edge, and face.¹²⁷ Each orbit belongs to a certain site-symmetry group as shown in Table2. The site-symmetry groups are determined by the orbit sizes. For example, the site-symmetry group of the face f_i has order . By counting the number of sites belonging to each site-symmetry group, we obtain a signature that uniquely identifies the point group:

10

The information can be condensed to a site-symmetry count for each site-group order:

11

In the final step, the point group is determined by the site-symmetry counts by the decision tree structure shown in Figure 13. The method can be extended to any fullerene and fulleroid by using general spirals. However, for every possible point group, the site-symmetry signature must be worked out and added to the decision tree.

Figure 13.

The decision tree for determining the symmetry point group for any fullerene from the group order and orbit counts.

Once the point group has been determined, the number of infra-red and Raman active lines, as well as the ¹³C NMR pattern can be derived.^31,107 Moreover, point groups lacking an inversion center are further divided into polar and chiral point groups. A chiral point group is one without any roto-inversion symmetry elements, and a polar point group allows for the fullerene to have a dipole moment. A point group with an inversion center or a mirror plane perpendicular to the axis of rotation cannot be polar. The nine chiral point groups for fullerenes are I, T, D₆, D₅, D₃, D₂, C₃, C₂, and C₁.³¹ The polar fullerenes belong to either of the point groups C_3v, C₃, C_2v, C₂, C_s or C₁.³¹ For larger fullerenes, the fraction of low-symmetry to high-symmetry isomers grows rapidly, and the C₁ point group increasingly dominates. This can be intuitively understood combinatorially from distributing pentagons on a sphere. Already at C₁₀₀, more than 99% of the isomers are C₁.

The separation of spiral starts into equivalence classes by their spirals yields an interesting relation:

12

where is the number of symmetry distinct (general) spirals. For I_h symmetry we have |I_h| = 120, which gives . Hence, I_h-fullerenes can only occur when N is a multiple of 20. In a similar way, for I symmetry we have , and for T_d, T_h, D_6h, or D_6d we obtain . This explains why some of these high symmetry groups are not found in certain isomer lists.

In the case of icosahedral symmetry, we have a full characterization of when they occur: As described by Dutour and Deza,¹⁰³ every fullerene of I_h or I symmetry is a Goldberg-Coxeter transform of C₂₀.⁷⁷ This means that they occur exactly when N = 20(k² + kl + l²) for integers k and l. It is also possible to determine when these are of I_h and when they are of I symmetry. Halma and leapfrog transformations, which correspond to Goldberg-Coxeter transforms of l = 0 and k = l, respectively, both preserve symmetry.¹²⁸ Hence, there is a fullerene with I_h symmetry at N = 20j² and N = 20(3j²) for every j ∈ ℕ, corresponding to a single Halma or leapfrog transformation on C₂₀. Consecutive application of the two shows that isomers with I_h symmetry are found for every N = 20(3ⁱj²) (j ∈ ℕ and i = 0, 1). Moreover, general Goldberg-Coxeter (k, l) transforms with k ≠ l and l ≠ 0 (k > 0) break horizontal mirror plane symmetry.

Shapes: Volume and Surface Area, Sphericity, and Convexity

For ideal C₆₀ - I_h, where all edges are of equal length, the geometric volume V, and surface area A can be obtained through simple algebraic and geometric considerations. The volume and surface are of a regular 20-sided polyhedron (icosahedron, see Figure 3) made out of equilateral triangles with edge length a is,

13

Cutting out 12 pentagonal pyramids at length a/3 gives the ideal truncated icosahedron C₆₀ - I_h with

14

where r_e = a/3 is the length of the edge (C–C bond length). This gives the ratios and between the two volumes and surface areas. C₆₀ has, however, two different bond lengths as the crystal structure shows,¹²⁹ r₅ = 1.455 Å (edge at pentagon-hexagon fusion) and r₆ = 1.391 Å (edge at hexagon-hexagon fusion). A smaller bond distance in the hexagon implies that more of the original icosahedron is cut off,

15

For r₅ = r₆ we obtain Eq 14. If r₆ = 0 (r₅ = a/2) the hexagons become equilateral triangles and for r₅ = 0 we just get a hollow icosahedral C₁₂ cluster. For C₂₀ (equal edge lengths) the vertices lie in the center of each face of an icosahedron, and the volume and surface area are easily obtained,

16

How can we get the volume V and surface area A for any fullerene isomer? As fullerene cages are not guaranteed to have planar faces, their volume or surface area are only approximately defined. There are, however, a number of definitions according to which we can express both quantities. We could triangulate all faces by adding a barycenter to each face with lines to each vertex of that face. We call the polyhedron obtained in this way a triangulated face polyhedron, TFP. For a fullerene, the graph representing the TFP is identical to the dual structure of its leap-frog transform. The total surface area A is obtained by summing over all areas A_i of the triangles obtained, which works even for faces where the vertices do not lie on a plane. Using Gauss' theorem (divergence theorem), the volume V is found by summing over the face normals,

17

where is any point on face i, and A_i is the area of the face.

The different volumes and surfaces areas can be used for calculating some important measures for fullerenes, such as the sphericity S (how spherical a fullerene is) and convexity C (how convex a fullerene is). The surface of a triangulated fullerene may not be convex. We can measure the non-convexity by comparing to the convex hull of the fullerene cage, which is the smallest convex polyhedron that contains all the points. The convex hull (CH) is uniquely defined, and there are several algorithms available, such as the incremental 3D convex hull algorithm.¹³⁰ A measure for convexity C is obtained from the proportion of ‘empty space’ between the non-convex polyhedron and the convex hull by comparing the volumes or surface areas, that is, C_A = A/A_CH and C_V = V/V_CH.

The simplest measure of sphericity is the isoperimetric quotient q_IPQ,¹³¹ defined for a polyhedron as

18

where q_IPQ = 1 for an ideal sphere and D_IPQ is a measure of the deviation from an ideal spherical shape. D_IPQ is shown for several fullerenes in Figure 14.

Figure 14.

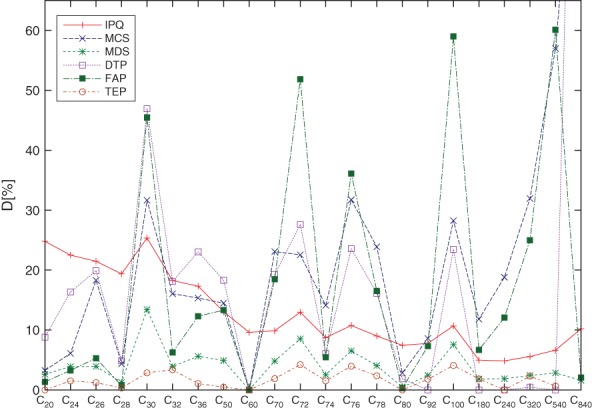
Various deformation parameters D (in percent) for a series of fullerenes selected according to stability. For larger fullerenes, Goldberg-Coxeter transformed structures of C₂₀ were chosen. Geometries were obtained from DFT (up to C₅₄₀) or force field optimizations. IPQ: isoperimetric quotient; MCS: Minimum covering sphere; MDS: Minimum distance sphere; DTP: Diaz-Tendero parameter; FAP: Fowler asymmetry parameter; TEP: (1 − ρ) from the topological efficiency parameter ρ.

We usually regard C₂₀ - I_h and C₆₀ - I_h as almost spherical because all vertices lie on a (covering) sphere. We may therefore analyze whether or not the vertices of a given fullerene lie on a sphere. For this, we define the minimum covering sphere as a sphere of minimum radius that encloses all vertices in the polyhedral embedding (J. J. Sylvester, 1857).^132,133 Mathematically, this translates into finding the solution to the problem^134,135

19

where ‖ · ‖ denotes the Euclidian norm, is the location of the vertex v_i in 3D space, and is the center of the MCS with radius R and is usually close to the barycenter of the fullerene. The MCS is uniquely defined^134,135 and can be obtained using an efficient algorithm, such as the one proposed by Yıldırım.¹³⁶ The convex hull of a 3D embedding of a graph G is contained entirely within the MCS. For fullerenes with an ellipsoidal shape like C₇₂ - D_6d, or with a cylindrical shape such as a nanotube¹³⁷ (see Figure 2), it is more appropriate to use a minimum covering ellipsoid or cylinder instead of a sphere. The ellipsoidal problem has been addressed recently, and is known as the minimum volume axis-aligned ellipsoid problem (MVAE).^138–141

We can now define a number of useful measures for sphericity. The MCS distortion (normalized to the smallest C–C distance in the fullerene) is given by,

20

The MCS definition for the distortion is biased to the case of few atoms sticking out on a sphere and another measure may therefore be more appropriate. We define the minimum distance sphere as

21

with

22

A similar definition that uses the mean deviation from the average distance taken from the barycentric point has been introduced by Nasu et al.¹⁴²

Some other useful sphericity parameters are the Diaz-Tendero (DTP) parameter,^143,144

23

where a ≥ b ≥ c are the rotational constants, and the Fowler asymmetry parameter (FAP),

24

where R_i is the radial distance of atom i from the barycenter, and R_av is the average distance.¹⁴⁵ If all atoms lie on a sphere, we have λ_FAP = 0.

Figure 4 shows a comparison of sphericity parameters for a number of stable fullerenes. As C₂₀ is slightly deformed due to Jahn-Teller distortion, the vertices do not lie exactly on a sphere anymore, and D_MDS ≠ 0. In contrast, the purely topological efficiency parameter (1 − ρ) (see discussion in the topological indicator section) is exactly zero for C₂₀ (and for C₆₀, C₈₀, and C₂₄₀). For C₆₀, all vertices lie on a sphere and all deformation parameters are zero, except for the IPQ, which except for its simple definition is perhaps not the best measure for sphericity. All deformation parameters reveal the highly deformed fullerenes (spikes in Figure 4).

Toward the Solid State: Hilbert's Problem and Space Fillings

Solid C₆₀ - I_h packs in a rotationally disordered face centered cubic (fcc) structure with a lattice constant of a_fcc = 14.17 ± 0.01 Å,^129,146 which according to Fischer et al. implies a close packing of spheres of a diameter of 10.02 Å.¹⁴⁶ C₆₀ undergoes a phase transition below 255 K to a simple cubic (sc) structure, from which one can infer a lattice parameter of a_sc = 14.04 ± 0.01 Å.^147,148 The only other solid state fullerene obtained by experiment is that of C₇₀ - D_5h, which adopts a closed packed structure of either hcp or fcc symmetry^138,149 with a fcc lattice constant of a_fcc = 14.96 Å. In the solid state, the interactions between the fullerenes are of Van der Waals type. Note that the polarizability and therefore the Van der Waals coefficients grow linearly with increasing number of carbon atoms in the fullerene cage,¹⁵⁰ which should converge toward the graphene limit for the per-atom value. Experimentally, the solid state behavior of C₆₀ has been studied in great detail. One interesting fact is that the bulk moduli of C₆₀ (B = 6.8 GPa for the simple cubic phase and 8.8 GPa for the fcc phase) and C₇₀ (11 GPa for the rhombohedral phase) are quite small as applied pressure will just squeeze out the compressible Van der Waals space.^151–153 These bulk moduli are only twice as large compared to the rare gas solids,¹⁵⁴ and much smaller than that of diamond (442 GPa¹⁵⁵). However, once the Van der Waals space is squeezed out and the fullerene cages touch, the bulk modulus increases substantially, as the fullerene cage is not easily compressible, similar to the high in-plane stiffness of graphite or graphene.¹⁵⁶ We mention that it requires high pressures above 20 GPa to turn C₇₀ into graphite (using step-like shock-wave compression).¹⁵⁷ For overviews on solid-state properties of fullerenes, see Zettl and Cumings¹⁵³ or Fischer et al.¹⁴⁶

From the experimental data of C₆₀ - I_h, we can adjust the Van der Waals radius of the C₆₀ cage such that the experimental lattice constant is obtained, that is, we use a hard sphere model for periodic packing (fcc is the closest packing available for hard spheres as proven by computer by Hales in 2000^158,159). We can do this by using the MCS introduced in Eq 19, but we have to add the carbon Van der Waals radius (r_VdW(C) = 1.415 Å) to the MCS radius,

25

Figure 15 shows lattice constants for a number of fullerenes using this hard sphere model, which can be taken as an upper bound to experimental lattice constants. For the other experimentally known fullerene crystal structure, C₇₀, the fcc lattice constant a_fcc of 14.96 Å is in reasonable agreement with the hard-sphere value of 15.78 Å, considering the fact that the IPR C₇₀ isomer is slightly prolate and distorted. The dependence of the a_fcc lattice constant on the vertex number can be expressed as , where the shift follows from the geometry of the fcc cell and the -term represents the dependence of the fullerene radius on N. In the hard sphere model we have a_fcc ∼ R, and the cage radius of the fullerene is R ∼ A^1/2 ∼ N^1/2 (A being the surface area of the MCS).

Figure 15.

fcc lattice constant a_fcc for a hard sphere model as a function of the number of carbon atoms N.

For distorted fullerenes, the packing problem becomes far more complicated. For example, we could add the Van der Waals radius to every carbon atom and take the convex hull around this Van der Waals layer. We are then faced with close packing of complicated polyhedral structures, which is a difficult, unsolved problem. However, there exist algorithms for packing arbitrary polyhedra in finite spaces,^160,161 and it is possible that one could approximate properties of the (periodic) close packing solution by making the finite cell large enough. For some fullerenes, ellipsoidal, or cylindrical covers are more appropriate as already mentioned.^141,162 The close packing of ellipsoids was recently investigated by Donev et al, who showed that the maximum packing density can exceed that of a close sphere packing.¹⁶³ Nevertheless, the question still remains how fullerenes of a certain topology pack in 3D space. This is related to one of Hilbert's fundamental problems: How can one arrange most densely in space an infinite number of equal solids of given form, e.g., spheres, with given radii, that is, how can one so fit them together that the ratio of the filled to the unfilled space may be as great a possible? A more rigorous mathematical proof (beside Hales' complete computer algorithm^158,159) for fcc packing of hard spheres as the most dense packing is still missing, and packing any other deformed spheres remains an open area of research. One possible approximation is to expand the shape of a fullerene in terms of multipole deformations and study the 3D packing of such smooth topologies.

Topological and Chemical Indicators

Chemists can deduct many useful properties of a chemical system just by looking at its structure. For fullerenes, the distribution of the 12 pentagons on a surface, for example, a sphere, can tell us qualitatively how stable the fullerene is or how it would pack in the solid state. Moreover, the symmetry of the underlying structure determines many useful spectroscopic properties. It is perhaps a realistic goal to connect the graph theoretical properties of a fullerene directly with its physical properties by mapping the fullerene graph G into a number describing that property. In more general terms, we define a topological indicator as a map τ_I from the graph G into a finite series of numbers,

26

where the numbers x_i are called topological indices and can be chosen to be integers, rationals, or reals. A topological index is called a chemical index if it is related to a chemical (or physical) property. Topological indicators may be placed in the same category as crude chemical bonding models, except that they can be strictly defined in graph theoretical terms and sometimes have interesting mathematical properties. There is no restriction that the mapping between fullerene graphs and any topological indicator be one-to-one, and indeed, most of the commonly used topological indicators are the same for many different isomers. Of course, any chemical or physical property is ruled by its underlying electronic structure governed by the Schrödinger equation. However, solving the electronic structure problem for any large fullerene is a daunting task and therefore, topological indices that are easily obtained can be very useful as we shall see.

To give some (trivial) examples, we can list all the possible point groups for fullerenes and define x_i = 0 for the ideal point group not matched by the fullerene graph, and x_i = 1 if the point group is. The order of the ideal point group as shown in Table1 is also a topological index. Another example for a topological index is the 12 face spiral pentagon indices as described above.

The first topological index of chemical relevance was introduced by Wiener in 1947.¹⁶⁴ He defined a so-called path number (Wiener index) as the sum of the entries in the topological distance matrix d_ij, consisting of the length of the shortest path between every pair of vertices in the chemical graph representing the non-hydrogen atoms in the molecule,

27

where d_ii = 0. The Wiener index provided a good measure of compactness for acyclic alkanes and gave a reasonable correlation to boiling points.¹⁶⁴ The first application of the Wiener index to fullerenes came from Ori and co-workers, who obtained W = 8340 for C₆₀ - I_h.¹⁶⁵ For fullerenes, low Wiener indices provide a measure of high compactness of the cage. This can be seen from the scaling law, which has been found to behave like for ‘spherical’ fullerenes¹⁶⁶ and for fullerene nanotubes. For carbon nanotubes, analytical formulae in terms of polynomials in the vertex number are available, for example, for the smallest D_5h/D_5d nanotubes we have W(k) = 1/3(100k³ + 1175k − 2010) with N = 10k and k ≥ 5,¹⁶⁷ and for the smallest D_6h/D_6d nanotubes we have W(k) = 12(4k³ + 69k − 136) with N = 12k and k ≥ 7.¹⁶⁸ It is conjectured that the Wiener index grows like (N^2 + 1/d), where d describes the dimensionality of the system (the Wiener dimensionality).¹⁶⁶ The almost cubic growth with increasing number of vertices can make the Wiener index unwieldy for larger fullerenes. Therefore, Ori and coworkers defined a topological efficiency index ρ, derived from the Wiener index^169,170

28

which has the advantage that, unlike the Wiener index, it does not grow to large numbers. Small values of ρ ≥ 1 indicate topologically efficient structures, for example, both C₂₀ - I_h and C₆₀ - I_h have ρ = 1.¹⁶⁸ It can be seen as a measure of sphericity that does not involve 3D Cartesian coordinates, as shown nicely in Figure 4. Vukičević et al. showed that among the 4478 isomers of C₆₆, the joint information of the Wiener index and the topological efficiency index correctly identifies the C₆₆ - C_2v(11) as the most stable molecule¹⁶⁹ (as detected experimentally in endohedral Sc₂@C₆₆¹⁷¹).

Many different topological indices have been introduced and studied since, mainly for the structural and statistical analysis of molecules, polyhedra, and graphs in general, often yielding interesting mathematical properties (for a list of topological indices see for example Ref 172). The distance matrix d_ij gives rise to a number of very useful topological indices including the topological radius R and diameter D,¹⁷³ Hosoya polynomials¹⁷⁴ and related Wiener indices, the Szeged index S_z,¹⁷⁵ and the Balaban index J,^29,176 to name but a few (for fullerenes one has W ∼ S_z and W ∼ − J).^29,177 There are also a number of topological indices connected to the adjacency matrix (or Hückel matrix), for example Hückel orbital energies and related properties (occupation numbers, band gap,³¹ spectral moments¹⁷⁸ etc.),³¹ and the Estrada index.^179,180 For a more detailed discussion of topological indices see Refs ^29,89,173, and ¹⁸¹.

Some of these topological indices can directly be related to the stability of the fullerene cage. For example, the Fowler-Manolopoulos pentagon indices {p_n|n = 0, …, 5} define the number of pentagons attached to n other pentagons (n is called the neighbor index),³¹ that is, for IPR fullerenes we have p₀ = 12 and p_n = 0 for n ≥ 1. For any fullerene, we of course must have p₁ + … + p₅ = 12. Fowler-Manolopoulos hexagon indices are similarly defined and useful for IPR fullerenes, that is, {h_i|i = 0, …, 6}, where h_n defines the number of hexagons with neighbor index n. In an IPR fullerene every hexagon is adjacent to a minimum of three others and we can restrict the list of hexagon neighbor indices for example to (h₃, h₄, h₅, h₆).³¹

We may contract the neighbor indices to one useful topological index describing the stability of fullerenes.³¹ The single pentagon signature P₁ is defined as

29

max(P₁) = 30 (for C₂₀ only), and for IPR fullerenes such as C₆₀ we have P₁ = 0. For IPR fullerenes a more useful single topological index is defined through the hexagon signatures. The standard deviation σ_h of the hexagon neighbor index distribution is defined as

30

where

31

We call the topological index H_n the n-th moment hexagon signature. For general fullerene isomers, low P₁ values and high H_i values correlate with high thermodynamic stability.³¹ It turns out, however, that H₁ stays constant for a given vertex count in IPR fullerenes, as this index is related to certain face patterns as we shall see. Fowler et al. advocated the use of the index σ_h instead, as low values of σ_h are better predictors for stability, and the strain is minimized when all hexagon neighbor indices are as similar as possible.³¹ For example, for C₆₀ we have {h_i} = {0, 0, 0, 20, 0, 0, 0} giving H₁ = 60, H₂ = 180, and σ_h = 0. Fowler et al. devised the following scheme for estimating the internal order among fullerenes sorted by stability:¹⁷³ First order the isomers according to lowest P₁-value (each pentagon-pentagon fusion carries a penalty of about 20–25 kcal/mol). If multiple IPR fullerenes are present, that is, P₁ = 0, we order these first by largest H₂-value, and finally by lowest Wiener index W (which indicates high compactness of the fullerene cage). The result is an efficient but effective screening method to find the most stable fullerene isomers.

Ju et al. presented a relationship between the Fowler-Manolopoulos hexagon indices and a particular hexagon structure count to provide a graphical interpretation.¹⁸² The complete list of different pentagon and hexagon combinations up to three connected faces are shown in Figure 16. Note that for connecting two or three faces we have

32

where the notation is described in Figure 6. For example n₅₅₆ is the sum of all occurring ring patterns containing the combination of two pentagons and one hexagon. Ju et al. showed that for the second moment hexagon signature one gets¹⁸²

33

and

34

Figure 16.

The 15 basic shapes for the two- and three-ring (face) adjacencies on the surface of a fullerene; (l) denotes linear, (b) bent, (o) open, and (c) closed ring patterns (see Ref 183).

Hence for IPR fullerenes, σ_h and H₂ are related through the simple equation

35

and one requires only H₂ to discuss the stability of IPR fullerenes. Stevanović extended these relations to general fullerenes (IPR or not),¹⁸⁴

36

and

37

This not only illustrates nicely the current development in the area of topological indices, it also suggests that the stability of fullerenes can be approximated by counting different face patterns.¹⁸³

Indeed, Cioslowski et al.'s incremental scheme for the heat of formation for IPR fullerenes³³ uses 25 linearly independent face patterns (structural motifs) of up to 13 connected hexagons and pentagons to calculate the energy E_FP, including an additional curvature term E_C,

38

where m_i stands for the total count of a specific face pattern (FP) that appears in the fullerene, ε_i is the FP energy contribution, and the second term in Eq 38 is the curvature term (C), which is repulsive for C₂₀ and approaches zero for N → ∞. For example, for C₆₀ - I_h we just have one pattern in Cioslowski et al.'s scheme consisting of a hexagon surrounded by 3 pentagons and 3 hexagons. There are 20 of these in C₆₀, and with ε = 44.281 kcal/mol, we obtain ΔH_f = 616.814 kcal/mol for C₆₀.³³ This compares rather well with the estimated NIST listed heat of formation for C₆₀ (612 ± 25 kcal/mol), although this value should probably be corrected downwards to a value of 602.7 kcal/mol as recently pointed out by Karton et al. using high-level theoretical procedures.¹⁸⁵ The rms error for the standard enthalpies of formation for the 115 IPR isomers chosen was 4.0 kcal/mol compared to B3LYP/6-31G* calculations.

Alcami et al. devised a similar scheme for general fullerenes.³² By analyzing the most stable structures from B3LYP-DFT calculations of C₂₀ to C₇₂, and using only connections between four faces with varying number of pentagons with a total of 9 different motifs, an expression similar to Cioslowski et al. was used for E_FP, but without the curvature term E_C. This scheme gives ΔH_f = 654.0 kcal/mol for C₆₀ - I_h. For all fullerenes studied the rms error is 15.4 kcal/mol for the enthalpy of formation compared to DFT calculations, or 0.31 kcal/mol per carbon atom.

The question is: How well are topological indices suited to describe fullerene stability? Table3 shows a comparison of stabilities for all C₃₄ isomers obtained from DFT geometry optimizations (using the PBE functional¹⁸⁶ and a def2-SVP basis set for carbon¹⁸⁷) in comparison with several topological indicators.³⁵ According to the pentagon signature, isomer C₃₄ - C₂(5) has the lowest P₁ value, but with a very small HOMO-LUMO gap obtained from Hückel theory. This is indeed the case as the DFT results show. Alcami et al.'s stability indicator correctly predicts the most stable (P₁ = 14) and the least stable isomer (P₁ = 17). For the four isomers with pentagon signature P₁ = 15, the two results (ΔE^DFT and ΔE^A) do not agree in their sequence (note that Alcami et al.'s scheme was not designed to distinguish between different isomers of a fixed vertex count). The different fullerene isomers are all very similar in surface area and volume. Concerning the HOMO-LUMO gap, the most stable isomer does not correspond to the one with the largest HOMO/LUMO gap. Moreover, these values are very sensitive to the method applied, and a better measure for the gap given by the singlet-triplet separation. The fullerenes with the smallest HOMO-LUMO gaps (isomers 2 and 6) prefer in fact the triplet ground state. The Hückel HOMO/LUMO gap on the other hand is only good for a qualitative discussion. We note that the two different fullerene isomers 3 and 5 have identical Wiener indices, and the isomer 6 with the smallest Wiener index is not the most stable isomer.

Table 3.

Stability and Topological Indicators for the Six Isomers of C₃₄

LI	PG	P1	ΔEDFT	ΔEA				A	V	W	NHC	NPM
1	C2	17	74.93	13.5	0.069	0.424	0.0267	81.41	60.30	1978	28	212
2	Cs	15	28.10	4.2	0.120	0.150	−0.153	81.27	61.70	1975	58	219
2(T)	Cs	15	24.55	4.2	—	—	—	81.32	61.69	1975	58	219
3	Cs	15	31.48	4.0	0.368	0.406	0.0945	81.42	61.80	1973	52	196
4	C2	15	15.19	5.5	0.343	0.619	0.2229	81.32	62.06	1976	33	229
5	C2	14	0	0	0.006	0.480	0.1333	81.28	62.27	1973	42	204
6	C3v	15	33.70	7.8	0	0.225	−0.094	81.42	61.79	1971	66	195
6(T)	C3v	15	31.54	7.8	—	—	—	81.40	61.75	1971	66	195

L_I is the numbering scheme according to the lexicographically ordered face spiral pentagon indices, PG the ideal point group, P₁ the pentagon signature, energy differences (in kcal/mol) ΔE^DFT the DFT(PBE) energy difference to the most stable isomer (kcal/mol), ΔE^A the Alcami energy difference to the most stable isomer (kcal/mol), energy gaps (in eV) the Hückel HOMO-LUMO gap, the PBE HOMO-LUMO gap, the singlet-triplet gap (in eV), A the surface area (Ų), V the volume (ų), W the Wiener index (see Ref 188), N_HC the number of Hamiltonian cycles, and N_PM the number of perfect matchings. The symbol (T) for isomers 2 and 6 in the first column indicates that the triplet electronic state is taken instead of the singlet state.

The first halma transform of C₂₀ is C₈₀ and therefore of I_h symmetry. There are seven IPR isomers out of a total of 31,924 isomers as possible candidates for the energetically most stable one. Table4 shows the properties of all IPR isomers of C₈₀. With larger fullerenes the band gap becomes very small (graphene is a semi-metal or zero-gap semiconductor¹⁸⁹), and one has to check for states of higher spin multiplicity. For C₈₀, Hückel theory indicates an open-shell case for the isomers 6 and 7. In fact, the results show that four of the isomers have a triplet ground state, with the singlet and triplet states for C₈₀ - I_h being quasi-degenerate. The DFT calculations further show that the most stable fullerene is not the high symmetry C₈₀ - I_h isomer, but the first one in the IPR isomer list, which is of D_5d symmetry and has the largest H₂ value (previously, isomer 2 has been predicted to be the most stable isomer¹⁹⁰). The results show that the first three isomers are very close in energy and it requires perhaps a more sophisticated electron correlation treatment to sort out the sequence in stability. Isomer 1 also has the highest count in perfect matchings among all IPR isomers (although the non-IPR C₆₀ - D_3d(4) nanotube has a much higher perfect matching count of N_PM = 524, 250). The volumes and surface areas are all very similar with the highest symmetry isomer C₈₀ - I_h being largest.

Table 4.

Stability and Topological Indicators for the Seven IPR Isomers of C₈₀

LI	PG	H2	ΔEDFT	ΔEA	ΔEC	ΔEHRE				A	V	W	NHC	NPM
1	D5d	500	0	0	4.34	2.12	0.220	0.355	0.168	203.70	255.16	17340	10450	270153
2	D2	496	2.63	3.0	0.75	0.0	0.528	0.460	0.293	203.85	257.72	17352	10642	237585
3	C2v	488	1.81	10.5	0.04	14.7	0.102	0.009	0.091	203.92	260.80	17412	9918	201623
4	D3	492	7.03	7.5	7.17	6.70	0.408	0.098	−0.036	203.87	258.71	17368	9906	222588
4(T)	D3	492	6.21	7.5	7.17	—	—	—	—	203.85	258.40	17368	9906	222588
5	C2v	484	6.33	16.5	2.92	24.7	0.298	0.038	−0.090	203.99	262.48	17454	9004	182555
5(T)	C2v	484	4.25	16.5	2.92	—	—	—	—	203.98	262.41	17454	9004	182555
6	D5h	480	6.81	22.5	0	37.7	0	0.081	−0.002	204.01	263.50	17500	10970	169375
6(T)	D5h	480	6.38	22.5	0	—	—	—	—	204.00	263.49	17500	10970	169375
7	Ih	480	17.49	30.0	14.2	63.4	0	0.115	−0.003	204.02	263.61	17600	10500	140625
7(T)	Ih	480	17.43	30.0	14.2	—	—	—	—	204.02	263.63	17600	10500	140625

L_I is the numbering scheme according to the lexicographically ordered IPR face spiral pentagon indices, PG the ideal point group, H₂ the second moment hexagon signature, energy differences (in kcal/mol) ΔE^DFT the DFT(PBE) energy difference to the most stable isomer, ΔE^A the Alcami energy difference to the most stable isomer, ΔE^C the Cioslowski energy difference to the most stable isomer, ΔE^HRE the Hückel resonance energy (taking the resonance value as β = –60 kcal/mol), energy gaps (in eV) the Hückel HOMO-LUMO gap, the PBE HOMO-LUMO gap, the singlet-triplet gap (in eV), A the surface area (Ų), V the volume (ų), W the Wiener index, N_HC the number of Hamiltonian cycles, and N_PM the number of perfect matchings. The symbol (T) indicates that the triplet electronic state is taken instead of the singlet state.

The results shown here clearly demonstrate that the topological indicators help enormously to sort out the most stable isomers. The situation is often quite complicated as seen from the DFT calculations here, or for example from the work of other authors who compared stabilities within a list of isomers.^191–193 In the next section we introduce topological indicators that are connected to π-electron resonance structures (Kekulé structures) in fullerenes.

Kekulé Structures and Perfect Matchings, Clar and Fries Structures, and the Pauling Bond Order

Every chemist learns how to draw double bonds into an aromatic system called a Kekulé (or resonance) structure, sometimes also called a benzenoid graph.¹⁹⁴ For benzene there are only two possible Kekulé structures with three double bonds as we all know, but for C₆₀ there are as many as 12,500 Kekulé structures with 30 double bonds (a fullerene has exactly n_DB = N/2 double bonds), of which only 158 are symmetry distinct, that is, non-isomorphic.^195–197 A Kekulé structure is the same as a perfect matching in the chemical graph , where the edges of the matching correspond to double bonds. We write for the set of all perfect matchings of the graph, and the number of different Kekulé structures is called the Kekulé number. In graph theory, a perfect matching is a selection of edges such that every vertex of the graph G is part of exactly one edge in the matching. The edges of the matching correspond to the double bonds.

Chemists know from basic Hückel theory that for two different benzenoid graphs B₁ and B₂, K(B₁) > K(B₂) implies that B₁ is more stable than B₂ because of resonance stabilization. Schmalz et al. calculated the Kekulé number for several small fullerenes up to C₈₄.⁵⁰ Their work showed that for C₆₀, the least stable isomer C₆₀-D_5h(1) has K = 16,501, while for the most stable isomer C₆₀-I_h(1812) we have K = 12,500.⁵⁰ In fact, Austin et al. showed that 20 isomers of C₆₀ have a higher Kekulé numbers than C₆₀-I_h.¹⁹⁸ The Kekulé number is therefore not a good indicator for fullerene stability,¹⁹⁸ but useful for rationalizing the different bond lengths in fullerenes as we shall see.

All cubic graphs have exponentially many perfect matchings and hence exponentially many Kekulé structures.¹⁹⁹ While the theoretical lower bounds proved in Refs ^113,199 have small exponents, the actual exponential behavior kicks in rapidly, as seen in Figure 17: The mean number of perfect matchings for a C_N isomer is approximately 20 · 2^{(N − 20)/4}. In general, calculating the number of perfect matchings for graphs is intractable,ⁱ but for planar graphs (such as fullerenes) the Kekulé number can be computed in time using the Pfaffian matrix (the Fisher-Kasteleyn-Temperley algorithm).²⁰⁰

Figure 17.

Minimum, median, and maximum perfect matching count for all isomers of C_N up to C₁₂₀. (a) When looking at the plot for all N, we notice three distinct series depending on the value of N mod 6. (b) For each of the three series, both the maximum and minimum counts follow a simple exponential function (shown as dashed lines). Here, the ‘peak series’ at N mod 6 = 2 is shown. (c) The bounds for the IPR isomers (solid curves) are shown together with the bound for all isomers (dashed curves) for the series N mod 6 = 0. The other two series behave similarly.

Pauling, Brockway, and Beach introduced bond orders derived from Kekulé structures in order to rationalize the differences in the C–C bond lengths encountered for polycyclic aromatic compounds.²⁰¹ The Pauling bond order (PBO) P_ij of an edge v_i − v_j is defined as the sum over all appearances of double bonds in perfects matchings

39

where β_ij = 1 if the edge v_i − v_j has a double bond in the perfect matching M, otherwise β_ij = 0. This gives 0 ≤ P_ij ≤ 1, with 0 being a pure C–C single bond and 1 a pure C=C double bond. In C₆₀-I_h there are two different type of bonds and therefore two different PBOs, depending if the edge shares two hexagons (P_hh = 11/25 = 0.44) or a hexagon and a pentagon (P_hp = 7/25 = 0.28).²⁰² Note that the Hückel bond orders derived from the eigenvectors of the adjacency matrix are generally larger with P_hh = 0.6010 and P_hp = 0.4758 for C₆₀-I_h.²⁰³

Narita et al. derived a linear relationship between the PBO and the bond distance in a fullerene obtained from X-ray diffraction,²⁰²

40

Figure 18 shows an AFM picture of one of the symmetry equivalent hexagons in C₆₀ clearly showing the two different types of bonds. The measured bond lengths are r_hh = 1.38(2) Å and r_hp = 1.454(12) Å,²⁰⁴ in excellent agreement with the values obtained from Eq 40 (r_hh = 1.378 Å and r_hp = 1.442 Å).

Figure 18.

Atomic force microscopy (AFM) image for C₆₀ by Gross and co-workers²⁰⁴ at a tip height of z = 3.3 Å showing the different bond orders of individual carbon-carbon bonds in a hexagon. (Copyright © 2012, American Association for the Advancement of Science)

Kekulé structures containing benzenoid moieties are of special interest. These are the Fries and Clar structures. Fries structures are Kekulé structures with maximum number of benzenoid hexagons. The Fries number Fries(G) of a benzenoid graph is the maximum number of benzenoid hexagons over all of its Kekulé structures, and a Fries structure is a perfect matching that realizes this maximum (there could be many). Similarly, the Clar number Clar(G) is the largest number of independent sets of benzenoid faces (separated from each other) over all Kekulé structures, and a Clar structure is a perfect matching that realizes this (there could be many). It is clear that a Clar structure localizes benzenoid structures in fullerenes. For C₆₀-I_h we have Fries(G) = 20 and Clar(G) = 8, and an example for a Fries and Clar structure of C₆₀-I_h is shown in Figure 19. One might naively assume that a set of Clar structures form a subset of Fries structures, but this is generally not the case for fullerenes.²⁰⁵

Figure 19.

One of the Fries structures of C₆₀, and superimposed the structure with highest Clar number (Clar(C₆₀) = 8). Double bonds are shown in red and isolated aromatic hexagons are shaded in.

We expect maximum stability for fullerenes with the highest Clar number. For example, C₆₀-I_h is unique among all other isomers in that it has a Fries structure where all hexagons contain three double bonds and all pentagons none. This is also seen as a reason for the unique stability of C₆₀. However, finding the Clar number is not a trivial problem as it is computationally NP-hard.²⁰⁶ Ye and Zhang recently showed that for C₆₀ there are exactly 18 fullerenes with maximal Clar number of 8.²⁰⁷ Some of them contain as many as 6 fused pentagons. Hence the Clar number alone is not a good measure for stability. However, out of the 18 fullerenes with Clar number 8, C₆₀ has the largest Kekulé count.²⁰⁸ Fowler showed that leapfrog transforms of fullerenes not only are closed shell, but also have the maximum proportion of benzenoid hexagons.²⁰⁹

Figure 17(c) shows that the expected number of perfect matchings is no different for IPR fullerenes than it is for all fullerenes, except for small fullerenes for which it is larger than average. However, the maximum number is always significantly lower for IPR fullerenes. One could assume that the larger the Kekulé number is the more Clar sextets can be found and the more stable the fullerene is. While this has not been explored in detail, Table4 shows that for C₈₀ the most stable D_5h isomer has the lowest perfect matching count. There are, however, some good lower and upper bounds of these topological indices known. Došlić showed that the number of Kekulé structures grows exponentially with a lower bound of 2^N/8.²¹⁰ This is not a very tight bound, however, as for C₆₀ it predicts at least 181 Kekulé structures, and there are as many as 12,500. The upper bound for Fries numbers is well known, Fries(G) ≤ N/3, which is seen to be the graphenic limit. Fries structures with a maximum N/3 Fries number are called complete Fries structures²¹¹ or perfect Clar structures. This happens exactly for Clar structures that use every vertex. In that case, the Clar and the Fries structure is the same, and corresponds to a ‘soccer ball coloring’ of the faces. An interesting result comes from Pisanski who proved in a paper with Fowler that the fullerenes with maximum Fries number N/3 are exactly the class of leapfrog fullerenes.²¹² Given a leapfrog, we can find a perfect Clar structure, and given a perfect Clar structure, we can derive an inverse leapfrog transformation. This gives an easy way to test whether a particular isomer admits a perfect Clar structure: simply test whether the inverse leapfrog operation is successful. An upper bound for Clar numbers has been obtained by Zhang and Ye, Clar(G) ≤ (N/6 − 2).²¹³ Both IPR fullerenes, C₆₀-I_h, and C₇₀-D_5h with Clar(C₇₀) = 9 achieve this upper bound. Such fullerenes are called extremal fullerenes.²¹³

Finally we mention that the Kekulé structures can be used to determine the resonance stability of fullerenes. To start with a very simple model, Randić et al. took the Kekulé structures of fullerenes ranging from C₂₀ to C₇₂, and calculated the π-content P_π of hexagons and pentagons, which is obtained by summing all the Pauling bond orders in a specific ring.¹⁹⁷ For C₆₀-I_h this gives for a hexagon, and . High hexagon π-count together with low pentagon π-count gives stability to a fullerene. High hexagon π-count increases the aromaticity in the system (for more details see Ref 197). Klein et al. applied Herndon's resonance theory^214,215 using counts of 2m-resonance cycles to obtain the resonance energy.¹⁹⁵ They correctly pointed out that the reduced p_π-orbital overlap in strongly curved fullerenes will reduce the resonance energy and has to be taken into account.¹⁹⁵ Here we should mention again that obtaining all Kekulé structures for a fullerene is an exponential problem, and it is more advantageous to apply methods that scale polynomially in time, such as Hückel or more sophisticated (semi-empirical) theories.

Hamiltonian Cycles, IUPAC Rules, and Naming Fullerene

For naming an alkene, the IUPAC rules state that one has to find the longest continuing carbon chain containing as many double bonds as possible. For a cyclic system one chooses the longest cyclic chain, and if there are multiple longest cycles, one must choose the one that maximizes the number of double bonds along the chain. This is related to finding a Hamilton cycle, which is a closed path in a graph that visits every vertex exactly once. If at least one such cycle exists, we say that the graph is Hamiltonian. In this case, the Hamilton cycles are the longest carbon chains, and the optimal one must be chosen among these.

It is an open problem whether every fullerene has a Hamilton cycle.^j In practice, however, we find that fullerenes are not only Hamiltonian, but admit exponentially many Hamilton cycles. The mean number of Hamilton cycles taken over all C_N-isomers grows approximately as 8 · 2^{(N − 20)/5.8} for N mod 4 = 0 and as 12 · 2^{(N − 20)/6} for N mod 4 = 2 (Schwerdtfeger et al., unpublished manuscript). Because of this, naming fullerenes according to the IUPAC alkene rules is a computationally heavy task: we must search through all the exponentially many Hamiltonian cycles (main rings) to find the one in which the secondary bridges are labeled in the lexicographically smallest way. This is computationally feasible only for small fullerenes such as the ones shown in Figure20.

Figure 20.

One of the Hamiltonian cycles out of the many for (a) C₆₀-I_h (N_HC = 1090), and (b) the C₆₀-D_5h carbon nanotube (N_HC = 3040).

In addition to being infeasible to calculate, as N grows, the name resulting for a fullerene from the IUPAC alkene rules rapidly becomes long and unmanageable. Even for a relatively small fullerene such as C₆₀-I_h, the name^k is already unreadable, and the name length keeps growing with the fullerene size.²¹⁶ The IUPAC alkene name for fullerenes is now seen mostly as a curiosity—and a good example of how a well meant rule has is limits.

IUPAC employs an alternative naming scheme for fullerenes: C_N-PG[5, 6]fullerene, where PG stands for the (ideal) point group, and [5, 6] denotes a polyhedral cage with only pentagon and hexagon faces. For example, the IPR C₆₀ fullerene has the official IUPAC name C₆₀-I_h[5, 6]fullerene. While computing the name of a fullerene according to this scheme is easy and efficient, and contrary to the alkene naming scheme is short and easy to understand, we find that this scheme is not much better than the IUPAC alkene nomenclature. On the one hand it is unnecessarily long: ‘fullerene’ implies ‘[5, 6]’, and vice versa. On the other hand, it does not uniquely specify a fullerene, since many isomers share the same vertex count and symmetry. For example, while C₁₂₀-T_d[5, 6]fullerene happens to be unique, C₁₂₀-C₂[5, 6]fullerene refers to 10,787 different fullerene isomers, and C₁₂₀-C₁[5, 6]fullerene refers to no less than 1,660,007 different molecules. We therefore advocate the use of one of the following two names to uniquely specify fullerenes, based on the (generalized) canonical face spiral pentagon indices (FSPI), see the chapter on face spirals above. Both schemes uniquely and compactly identify a specific fullerene molecule.

1. For moderate values of N, we can specify the fullerene by its canonical index, which is the lexicographic number of its FSPI among the isomers. For example, the IPR C₆₀ molecule can be written as C₆₀-I_h(1812) or C₆₀-I_h(IPR−1), as it is the last fullerene of the 1812 C₆₀ isomers in the lexicographically ordered FSPI list.

2. For large C_N, for which it is not feasible to compile databases for all isomers, we annotate instead with the FSPI. For the vast majority of fullerenes, this is a list of 12 small integers. For the extremely rare cases where jumps are necessary (there are only two non-spiral fullerenes out of the 2.6 × 10¹² fullerenes up to C₄₀₀), two extra integers are required per jump. No currently known case requires more than one jump. With this scheme, C₆₀-I_h(IPR−1) is written C₆₀-I_h{1, 7, 9, 11, 13, 15, 18, 20, 22, 24, 26, 32}, and the unspiralable C₃₈₀ is written C₃₈₀-T{110, 2; 45, 70, 71, 82, 83, 110, 119, 120, 144, 184, 185, 192}. In the latter example, the two numbers before the semicolon denote a cyclic shift of length 2 before adding face number 110.⁵⁹

The canonical FSPI notation is especially advantageous for more reasons than being compact and complete without needing to refer to a precomputed database. The procedure to construct a fullerene graph from the FSPI (the ‘windup’ operation) is geometrically intuitive—visualized like peeling an orange—and the algorithm is so simple that it can be performed with pen and paper. Thus, one can even reconstruct fullerenes of moderate sizes from the FSPI by hand, without the help of a computer.

The algorithm for the windup operation is , and the inverse operation, unwind, takes expected time to find a single generalized spiral, and to find the canonical one.⁵⁹ The canonical FSPI constitutes a canonical labeling of fullerene graphs up to isomorphism. Hence one can check whether two fullerene graphs are isomorphic simply by testing whether they have the same canonical FSPI, and the canonical FSPI gives us a unique graph representative of each isomorphism class via the windup procedure. As discussed later, the FSPI representation makes it easy to directly compute the ideal symmetry group of the fullerene. Because the generalized face spiral algorithm is complete for all connected planar cubic graphs, a compressed form of the face spiral similar to the FSPI can be used in general for fulleroids, to be introduced in the last chapter.

Thermodynamic Stability and the Graphene Limit

The spherical shape of C₆₀-I_h with no adjacent pentagons is seen as the main reason for its unusual stability,²¹⁷ which underlines the importance of Kroto's isolated pentagon rule (IPR).¹⁸ For example, Nagase and co-workers investigated the stability of potential candidates for the lowest energy structure of C₇₄, with the sole IPR D_3h isomer being 16 kcal/mol lower in energy than the C₂ isomer containing two fused pentagons.²¹⁸ It is therefore convenient to compare the stability of a fullerene to C₆₀-I_h (relative fullerene stability, RFS) by using the isodesmic reaction C₆₀/60 → C_N/N,

41

where E[C_N] is the total energy for a C_N fullerene. For N → ∞ we obtain the graphene limit, which can be estimated to be approximately ΔE^RFS(∞) = − 9 kcal/mol.

As E ∼ N, E/N approaches a constant value for infinite systems, for example, the graphene limit if the pentagons are as separated as possible from each other, so that the polyhedral surface is mainly constituted of flat graphene sheets. Alternatively, for nanotube fullerenes with pentagon caps, the infinite particle limit is just the corresponding infinite nanotube. For the graphene limit, the next dominant term in a 1/N expansion will be the surface tension or curvature term, which is ∼ N^− 1 as for example used by Cioslowski et al.,³³ see Eq 38 (although a N^− 1/2 law has been also suggested before⁵⁹). Indeed, as Figure 21 shows, the stability follows approximately a linear behavior in our 1/N fit (we set ΔE_RFS = 0 for N = 60),

42

that is fullerenes become more energetically stable with increasing vertex number N. It was already shown experimentally that C₇₀ is more electronically stable than C₆₀.²¹⁹ Alcami et al.'s scheme predicts the correct graphene limit (N → ∞), and Cioslowski's scheme performs well for medium sized IPR fullerenes, but has an incorrect convergence behavior toward the graphene limit.^32,33 C₂₀ is the smallest member of the fullerene family, and as seen from Figure 21 also the least electronically stable one. It has been detected in 2000 by Prinzbach¹⁶ (see also Ref 220), and a current review on the state of affair concerning C₂₀ is given by Fei et al.²²¹

Figure 21.

The stability of fullerenes C_N in comparison to C₆₀ obtained from density functional calculations up to the graphene limit (N → ∞). Topological stability indices from resonance energies²²² (TRE using β = − 216 kcal/mol) or ring patterns by Alcami³² and Cioslowski³³ are also shown. The graphene limit is estimated from the heat of formation of C₆₀.¹⁸⁵

It becomes more and more difficult to extract the most stable isomers from the huge isomer space as the size of the fullerene increases. Besides using topological indicators, Hückel theory can be used to determine the resonance stability of a fullerene. It requires diagonalization of the adjacency matrix A_ij (the Hückel matrix is defined as H_ij = αδ_ij + βA_ij, where α is the Coulomb and β the resonance integral, and δ_ij is the unit matrix), and the occupied Hückel orbitals determine the Hückel resonance stability (HRS) of a fullerene (in units of β),

43

where n_i = 0, 1, 2 are the occupation numbers, ε_i the orbital energy for Hückel orbital i, and the last term comes from subtracting the non-resonant ethene value (single double bond). This gives E_HRS = 33.161β for C₆₀. Per π-electron this gives a resonance energy of 0.5527β much higher compared to benzene with exactly β/3. This should indicate that C₆₀ is more aromatic than benzene, which has been a matter of some debate in the past (see the review by Bühl and Hirsch²²³). The problem is that the π-overlap in non-planar systems is not ideal and there is substantial mixing (hybridization) with the p_σ orbitals of carbon, thus questioning the σ-π-separability in Hückel theory. Hence there should be a correction accounting for the curvature at each carbon atom. Such curvature corrections, for example through using the π-orbital axis vector method (POAV), have been considered before with some success,^224,225 and the different approaches are discussed in detail by Bakowies and Thiel.²²⁶ For example, Haddon et al. showed that C₂₄₀ is significantly more stable than C₆₀,²²⁵ which is indeed the case as Figure 1 shows. Clearly, as the fullerene system becomes larger, the curvature term becomes smaller. Moreover, for similar shaped fullerenes the Hückel resonance energy might still be a good approximation. Indeed, as Table4 for C₈₀ shows, the first two isomers are the most stable ones predicted by the simple Hückel resonance energy term in agreement with DFT calculations, and isomer 7 is the least stable one. The Hückel method only requires a diagonalization of the adjacency matrix, and for obtaining bond orders and resonance energies it is computationally more efficient than sorting out Kekulé structures.

We mention that the Hückel spectrum {ε_i} for fullerenes shows some interesting mathematical properties.^227,228 The largest eigenvalue (which translates into the lowest occupied level as the resonance integral β is negative) in a fullerene is always ε_max = + 3. The smallest eigenvalue (highest unoccupied level) is largest for C₂₀ with , and for the IPR isomers C₆₀ we have . As a geometric consequence, the famous golden ratio appears here as it does in the volume and surface area calculations discussed above. We also mention that in general, different graphs can have the same Hückel spectrum,²²⁹ and this is the case also for fullerenes: the eigenvalues do not uniquely determine the fullerene graph.¹⁰⁸

It is well known that the Hückel scheme for canonical resonance structures is of rather limited use, and Aihara²³⁰ and Gutman et al.²³¹ therefore introduced a different reference system by defining the topological resonance energy (TRE) for a graph G as

44

where the reference energy E^MP(G) is the sum of all roots given by the matching polynomial, which for a fullerene is

45

Here the polynomial coefficients c(G, k) define the number of ways of choosing k non-adjacent edges from the graph G. Balasubramanian gave polynomial coefficients c(G, k) for a number of fullerenes up to C₅₀,²³² Babić determined the coefficients for C₇₀,²¹⁶ and Salvador for C₆₀ and C₇₀ to C₁₀₀.²³³ The first few polynomial coefficients are known as they are independent of the isomers for a specific vertex count, that is, c(G, 0) = 1, c(G, 1) = − 3N/2, c(G, 2) = 3N(3N − 10)/8, c(G, 3) = − (9N³ − 90N² + 232N)/16.²³² The last coefficient c(G, N/2) is just the number of perfect matchings in the graph. The computation of these coefficients soon becomes computationally intractable.²³³ Babić et al. found, however, a good correlation between E^MP and E^π values for fullerenes, and the E^π value suffices to calculate the topological resonance energy approximately as (in units of β),²²²

46

In order to give reasonable results for the isodesmic reaction energy (Eq 41), a rather low value of β = − 216 kcal/mol has to be applied. This scaled TRE plot is shown in Figure 21, which is in reasonable agreement with the results obtained from DFT calculations.

The five or six Pauling bond orders in a pentagon or hexagon respectively can be added to give the Pauling ring bond order.²³⁴ For C₆₀-I_h this gives 1.40 (5 × 11/25) for a pentagon and 2.16 (3 × 11/25 + 3 × 7/25) for a hexagon compared to 3.00 for benzene. According to Randić this suggests only moderate aromaticity for C₆₀-I_h.²³⁴ We are not going into the controversy of aromaticity of fullerenes,²³⁵ but refer to a recent paper by Schleyer and co-workers,²³⁶ who find that both C₂₀-I_h and C₆₀-I_h are not spherically π aromatic²³⁷ but spherically π anti-aromatic, which for C₆₀ explains the large heat of formation. In this respect it is interesting that Schleyer and co-workers conclude that fullerenes are not highly stable molecules,²³⁶ which perhaps is in line with the data shown in Figure 1 showing no ‘magic’ stability for C₆₀ compared to the other fullerenes. We finally mention that fullerene cage abundance is not only guided by thermodynamics, but mostly by kinetic stability. For example, the relative isomer abundance of fullerenes and carbon nanotubes correlates well with kinetic stability.²³⁸

Electronic Aspects to Structure and Stability

So far we have discussed topological aspects to determine the structure and stability of fullerenes and basic Hückel theory gives us a first insight into the electronic structure.²³⁹ For example, Fowler and co-workers have shown that leapfrog fullerenes adopt a closed-shell structure,^212,240,241 and have equal numbers of positive and negative eigenvalues.²⁴² For a more detailed discussion on this subject see Ref 243. However, as we have already seen, more detailed quantum chemical calculations are required to describe the bonding in fullerenes accurately (see also the work by Thiel and co-workers^244–246). For example, the IPR isomer C₈₀-C_2v(5) shown in Table4 prefers a triplet ground state (at the DFT-PBE level of theory) contrary to Hückel theory, which predicts a singlet state. This is perhaps not surprising as already Hückel theory predicts a small HOMO/LUMO gap. As the band gap closes further with an increasing number of vertices (see for example the recent paper by Noël et al.²⁴⁷), we cannot expect anymore to predict the correct spin ground state from simple topological arguments. Moreover, the system becomes more multi-reference in nature, making even a quantum theoretical treatment difficult. As an example, C₅₀-D_5h(271) was investigated by Lu et al. who showed that two singlet states with different HOMO symmetries are quasi-degenerate.²⁴⁸

In addition, some fullerenes may undergo first- or second-order Jahn-Teller (JT) distortions (which could, however, be very small and almost undetectable for larger fullerenes), that is, they can distort to subgroups of the ideal point group symmetry given by the fullerene topology.^249,250 For example, C₂₀ is well known to distort away from the ideal I_h symmetry, which has led to much discussion and debate over the correct electronic ground state.²⁵¹ The JT distortion in C₂₀ is a consequence of two electrons being distributed over four energetically degenerate g_u-orbitals, resulting in a rather complicated topology of the JT energy hypersurface.^{248,250,252–254} JT distortions for highly symmetric open- or closed-shell fullerenes may require a multi-reference treatment. It is therefore often difficult to predict the correct electronic ground state and corresponding physical point group symmetry of a fullerene.

The Gas Phase Formation of Fullerenes

Since the discovery of fullerenes almost 30 years ago, there has been considerable activity, both from the experimental and theoretical side, to gain a detailed understanding of fullerene formation in the gas phase. However, the formation mechanism and especially the high yield of C₆₀-I_h and C₇₀-D_5h remains elusive and somewhat controversial.

Fullerenes can be produced by (a) evaporating a carbon target (graphite, amorphous carbon, fullerenes), optionally with addition of metal oxides with a laser,⁵ (b) an electric arc between carbon electrodes,⁹ or (c) by partial combustion of carbon rich organic compounds.²⁵⁵ Each of these methods can be adjusted by several experimental parameters (gas pressure, carrier gas, rod feeding rate, amount of oxygen, etc., and therefore indirectly the carbon vapor concentration, expansion rate, annealing time, etc.). Furthermore, fullerenes are found in space,¹⁴ at meteor impact sites, after lightnings and bush-fires, and soot from household candles.⁹⁹ These conditions are similar in that carbon vapor is formed at very high temperatures with a deficit of possible reactants like oxygen or hydrogen. The distribution of yielded fullerene cage sizes depends on the production method and the above-mentioned experimental parameters; however, C₆₀-I_h and C₇₀-D_5h are always among the most abundant species.

A large number of formation mechanisms have been proposed.⁹⁹ First, inspired by their resemblance to graphene sheets or nanotubes, it was suggested that graphene curls or nanotubes break apart to form fullerene cages, followed by various bottom-up strategies that suggest the successive addition of faces (party line^256,257, pentagon road²⁵⁷) or polyyne rings (ring stacking^258,259) before the cage is closed, the folding of chains to form a cage (ring fusion zipper²⁶⁰), or the growth of already existing cages (fullerene road²⁶¹, closed network growth⁹⁸), and many others. The currently most widely accepted mechanism comes from Irle, Zheng, Wang, and Morokuma, and is called the ‘shrinking hot giant road’.⁹⁹ It is based on the concept of self organizing structures under non-equilibrium conditions, backed by extensive QM/MD simulations.

This mechanism can be divided into five phases: First, linear polyyne chains and cycles form. In the second stage (nucleation), entangled carbon chains rehybridize and form faces. It is to be noted, that pentagons and hexagons are close in energy at the given temperatures,⁹⁹ however, smaller and larger faces are formed as well. Third, more carbon dimers attach to the side chains of an existing nucleus (growth), allowing for the formation of additional faces. Fourth, after the formation of sufficiently many faces of sizes <6, the cage may close spontaneously (cage closure), leaving a carbon cage with face sizes not restricted to 5 and 6 and with polyyne side chains attached to it. The final step is the ejection of carbon dimers off side chains and the cage in combination with rapid isomerization of the cage structure resulting in a fullerene without side chains and faces of sizes 5 and 6 only. Fullerenes can not only shrink but also grow in steps of C₂,^95,98,262 and the existence of C₂ and C₃ fragments is backed by spectroscopy.²⁶³ The addition and ejection of small carbon fragments (especially C₂) to and from forming fullerene cages is a fast equilibrium. While the non-cage carbon concentration is high addition prevails; as the carbon vapor expands ejection begins to dominate.⁹⁵ The first four steps are exothermic, while the last step is endothermic but increases the overall entropy.

As shown in Figure 1, large fullerenes are more electronically stable than small ones, with graphene having a lower energy than any fullerene. In an equilibrium one would therefore anticipate the formation of graphene—the formation of strained cages and especially the high yield of C₆₀-I_h and C₇₀-D_5h require further explanation. The experimental conditions of the cooling and expanding carbon vapor are, however, far from an equilibrium, and the whole formation must be understood as a process of self-organization that is governed by kinetics more so than thermodynamics. Once fullerenes have formed they are subject to restricted equilibration only. Curl et al. have shown numerically that exchange of carbon dimers between existing cages is sufficient to explain the high yield of C₆₀-I_h and C₇₀-D_5h as well as a broad distribution of larger cages.²⁶⁴ They show, that the driving forces for the C₂ exchange are the energy difference between C_N and C_N ± 2 and the high stability of C₆₀-I_h and C₇₀-D_5h relative to their isomers rather than entropy; even at 4000 K entropic effects are not strong enough to explain the existence of small cages.²⁶⁴

The experimental observation of endohedral metallofullerenes supports a top-down formation mechanism in two ways: As any enclosed fragments need to enter the cage before it is closed, fullerenes containing fragments that use up most of the space available in the carbon cage must either be formed top down or their existence implies the breaking and reformation of carbon bonds to open and close the cage after it was formed. Secondly, enclosed metal fragments may stabilize otherwise unstable fullerenes: Zhang et al.²⁶⁵ report the finding of non-IPR M₂C₂@C₈₄(51383), which they interpret to be a missing link in the top-down road, and which would have ejected further C₂ fragments without the stabilizing metal carbide.

How Much Space Is Inside a Fullerene? Endohedral Fullerenes and Buckyonions

We consider only topological aspects here as there are several reviews on the chemistry of endohedral fullerenes available.^22,266,267 We only note that endohedral enclosure can change the stability between different isomers.²⁶⁸ For example, Tb₃N@C₈₄ has been isolated and shows one fused pentagon pair.²⁶⁹ Rodríguez-Fortea et al. argued that if the enclosed metal atom or cluster donates electrons to the fullerene cage, the negative charge resides mostly at the pentagons.²⁷⁰ As this creates a Coulomb repulsion between the pentagons, one can introduce the inverse pentagon separation index (IPSI),

47

with R_ij being the Euclidian distance between the pentagons (although the topological distance might be used instead). Small IPSI-values are preferred²⁷⁰ as these correspond to a small Coulomb repulsion.

It is clear that the cavity in the fullerene cage should be large enough to encapsulate atoms, molecules, or even smaller fullerenes.^22,271–282 The size of the cavity can be estimated from fitting shapes such as spheres or ellipsoids inside a fullerene cage as discussed above.

Conversely to the minimum covering sphere problem (MCS), we wish to find the largest sphere that is fully contained within the polyhedron. This is called the maximal inscribed sphere (MIS), or simply inscribed sphere, and its radius for a given polyhedron P is

48

where is constrained to the points interior to P. In the case of convex polyhedra, the MIS is unique, and can be computed directly by finding the Chebyshev centre of the polyhedron.²⁸³ The inscribed radius is then determined by a linear programming problem. However, in the non-convex case, the MIS is no longer unique: Consider two overlapping circles in 2D space with the points lying on these circles. We now have two equivalent possibilities for placing our inner circle. The same argument holds for peanut-shaped fulleroids, which are introduced in the last chapter. Hence, in the non-convex case, we only search for one of the possibly many largest spheres contained entirely inside the polyhedron, giving us a numerical optimization problem.

Once the MIS has been obtained, we can estimate whether an atom or molecule fits inside the fullerene without coming close to the repulsive wall of the fullerene cage. For example, the space available inside C₆₀-I_h is roughly R_MIS(C₆₀) − R_VdW(C) ≈ 3.550 − 1.415Å = 2.135Å. If we compare this to the Van der Waals radii for the rare gas atoms, which are 1.40 Å for He, 1.54 Å for Ne, 1.88 Å for Ar, 2.02 Å for Kr, and 2.16 Å for Xe,²⁸⁴ we see that they all fit into C₆₀-I_h as experimentally already verified^285–291 (even for the borderline case of Xe as theoretical investigations show^292–294). Even molecules like water fit into C₆₀.^295,296 If we take C₂₀ as a endohedral host molecule we arrive at a different picture as R_MIS(C₂₀) − R_VdW(C) = 2.040 − 1.415Å = 0.635Å, and even He does not fit anymore into the C₂₀ cage.^297,298 We note the important role of dispersion interactions in endohedral fullerenes.²⁹⁹ Further, C₆₀ is a very stiff molecule,³⁰⁰ and the cage cannot so easily be expanded by endohedral atoms or molecules. In other words, the endohedral system can become repulsive very soon if the size of the endohedral atom or molecule becomes too large.³⁰¹

As a further example we consider hyperfullerenes (also called buckyonions),^{271,272,274,302} that is, fullerenes which contain smaller fullerenes inside their cage. They have already been detected and studied by theoretical methods.^{271,272,274,277–280} In a similar way to the rare gas estimates, we can derive approximately the following (conservative) condition for a non-repulsive enclosing hyperfullerene,

49

This only holds for ideal spherical systems, but can be seen as a lower limit for the guest C_M fullerene. For C₂₀@C₆₀ we get ΔR_60,20 = (3.553 − 2.084 − 2 × 1.415) Å = − 1.361 Å and it is therefore predicted to be thermodynamically very unstable. Indeed, DFT(B3LYP) calculations predict C₂₀ @ C₆₀ → C₂₀ + C₆₀ − 1230 kcal/mol (−15 kcal/mol per carbon atom), the high energy required to expand the C₆₀ cage. In fact, analyzing C₂₀@C₆₀ we find that the carbon atoms of C₂₀ close bonds with the carbon of the C₆₀ cage, that is, the structure should be considered as a carbon cluster rather than a hyperfullerene. Moreover, the volume of C₂₀@C₆₀ increases by 22% compared to C₆₀. In contrast, C₆₀ fits nicely into C₂₄₀, and C₂₄₀ just into C₅₄₀ in agreement with the analysis of Bates and Scuseria (see Figure 22).³⁰³ Here we get ΔR_240,60 = 0.583Å and ΔR_540,240 = 0.066Å.

Figure 22.

The buckyonion structure C₆₀@C₂₄₀@C₅₄₀.

The buckyonions, which have been considered in the past, are all Goldberg-Coxeter transforms of C₂₀ and have the most spherical appearance as they are of icosahedral symmetry. It has been suggested that the rather high sphericity observed for buckyonions in experiments in contrast to the faceted polyhedral structure predicted (see Figure 22) is due to C₂ removal in a [c5666] fragment consisting of 1 pentagon and 3 hexagons (notation of Figure 16 is used here) introducing one heptagon and an additional pentagon, that is, [l575].³⁰³ As heptagons introduce local negative Gaussian curvature (see discussion below), the fragment flattens out and the buckyonion becomes more spherical in shape.³⁰³

For the buckonions one can establish a simple relationship between the number of vertices N > M of the buckyonions C_M@C_N. As (R being the radius of the cage), an analysis of GC_k,l-transforms of fullerenes up to k = 6 shows that . This gives a very simple estimate from Eq 49 for such fullerenes,

50

and we see that this is fulfilled for the cases already discussed, and for the largest buckyonion C₆₀@C₂₄₀@C₅₄₀@C₉₆₀@C₁₅₀₀ considered by Bates and Scuseria.³⁰³ In fact, Casella et al. recently showed by using dispersion corrected DFT that the formation of C₆₀@C₁₈₀ from the two fullerenes is endothermic while C₆₀@C₂₄₀ is exothermic, and in the latter case only because dispersion interactions have been accounted for.³⁰⁴ We finally note that (possibly damaged) buckyonions are the main product in most gas phase fullerene generation procedures.²⁶²

Weird Fulleroidal Shapes: Generalizing Fullerene Structures

Finally, what happens if we relax the rules a little bit, and allow for other types of three-valent (sp²) carbon frameworks? There are many generalizations that lead to structures of beautiful shapes that have both elegant mathematical theory and physical realizations: allowing for polygons with faces different from pentagons and hexagons; for surfaces other than a sphere (genus 0), such as a torus (genus 1), a Klein bottle or a double torus (genus 2); negatively curved Mackay-Terrones or Vanderbilt-Tersoff surfaces; etc.^{121,242,305–309}

We will discuss mainly two types of carbon frameworks: fulleroids, which are fullerene-like structures, and Schwarzites, which are periodic negative-curvature surfaces. Different authors employ a wide range of working definitions for fulleroids. We advocate the following definition, generalizing fullerenes: A fulleroid graph is a three-connected trivalent polyhedral graph. The definition is identical to that of fullerenes, except that there is no restriction on face sizes. Hence, a fullerene is a fulleroid with only pentagon and hexagon faces. We further generalize to genus-n fulleroids, abbreviated G_n-fulleroids, defined as the three-connected trivalent genus-n graphs.

What kind of fulleroids are allowed? Can we tile a sphere or a torus with heptagons only (the answer is no), or with only pentagons and heptagons? (the answer is yes, with the right number.) And how can we construct such fulleroids?³¹⁰ In order to answer these questions, we need to generalize Euler's equation to the Euler-Poincaré polyhedral formula for orientable^l surfaces,

51

where g is the genus of the graph,^m and the corresponding value χ is called the Euler characteristic.³⁹ The Klein bottle is a non-orientable surface (like the Möbius strip), and the corresponding (non-orientable) genus is g′ = 2 with an Euler characteristic of χ = 0 (here we take χ = 2 − g′ instead).

What happens when we allow vertex degrees r > 3? Consider a possibly irregular genus-n graph with N vertices. Let N_r be the number of vertices with degree r, and F_n be the number of n-gonal faces. Then we trivially have

52

Combining this with the Euler-Poincaré polyhedral formula, we obtain

53

If we only allow for three-valent graphs (fulleroids), the first term on the left hand side of Eq 53 conveniently vanishes (hence their special place in graph theory). This gives,³¹¹

54

From this equation we make a number of observations. a) We can play with as many hexagons as we want to build fullerenes or fulleroids, but the number of n-gons with n ≠ 6 is limited by Eq 54 or 53. b) While both equations allow for a large variety of face combinations, certain combinations are not allowed. The hand-shaking lemma (last formula in Eq 52) allows only for an even number of vertices. We already know that there exist no polyhedral structures of the type C₂₂[5,6]. To give another example, for C_N[5,7] polyhedra with pentagons and heptagons only (no hexagons) one requires at least two heptagons since, analogous to C₂₂, the combination of 13 pentagons and one heptagon is not valid despite being allowed by Euler's formula. Because of this, the smallest [5,7]-fulleroid is C₂₈-D_7d with 14 pentagons and 2 heptagons, as shown in Figure 23.ⁿ Structures containing only one heptagon are not forbidden, however, but requires introducing hexagons to form C_N[5,6,7]-structures. These can be obtained by replacing a [c5666] fragment by [l575],³⁰³ and can even be energetically favorable. For example, Fowler and co-workers showed that C₆₂ consisting of one heptagon, 13 pentagon, and 19 hexagon faces is of lower energy than all the 2385 regular fullerene isomers of C₆₂.³¹² c) For cubic planar graphs with only one type of face we get F₃ = 4 (tetrahedron), F₄ = 6 (cube), and F₅ = 12 (dodecahedron), which are the three three-valent polyhedra of the five Platonic Solids, the other two, the octahedron and icosahedron, require r = 4 and r = 5, respectively, in Eq 53; d) If we allow for two different n-gons, we arrive at the 13 Archimedean solids including our famous buckyball C₆₀-I_h. e) Of course, we can tile a surface with triangles and the duals of fulleroids are prime examples, but in order to do this beside the tetrahedron, we must allow for different valencies of the vertices. f) We can tile a toroid (g = 1) with hexagons only, consistent with Eq 54, see Figure 24. The torus is the only closed, orientable surface that can be tiled exclusively with hexagons. However, the plane, which is not closed, can be tiled with hexagons as well (graphene), as can the Klein-bottle (which is not orientable). Introducing pentagons into a toroid requires higher n-gons such as heptagons, since its total Gaussian curvature must be 2π(2 − 2 · 1) = 0. The Euler-Poincaré's formula allows to introduce pentagons into toroids if we introduce an equal number of heptagons, for example, we can tile a torus exclusively with pentagons and heptagons. Such ‘defects’ are well known in carbon nanotubes,³¹³ which can be realized as infinite toroids with g = 1 and χ = 0. Tiling in a pattern with alternating pentagons and heptagons yields a toroidal arrangement of azulenes, called azuloids.³¹⁴

Figure 23.

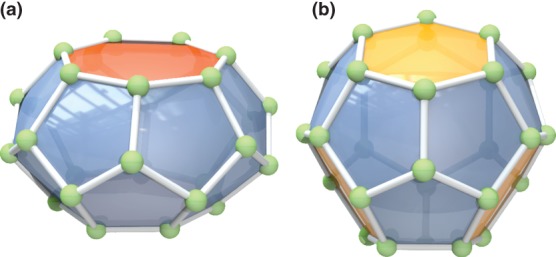
C₂₈[5,7]-D_7d, the smallest fulleroid with heptagon extension, compared to the most stable (by ΔE= −102 kcal/mol) C₂₈-T_d[5,6] fullerene isomer.

Figure 24.

Torus consisting of hexagons only with 1/3 of the edges tangential (a) and perpendicular (b) to the toroidal direction.

A few examples should be mentioned here. The smaller fullerenes (N < 60) are not very stable compared to C₆₀ because of the energy penalty one has to pay for fusing pentagons. As a result, structures deviating from the classical fullerenes can be more stable energetically or lie close by. For example, for C₂₆, An et al. found six low lying isomers with the lowest structure being the fullerene C₂₆-D_3h[5,6], but only 3 kcal/mol lower in energy than the C₂₆-C_s[4,5,6], a fulleroid that contains one square.³¹⁵ Some combinations with heptagons are, however, disfavored energetically. For example, a Stone-Wales transformation^o of four connected hexagons to two pentagons and two heptagons in C₅₄₀-D_2h costs 260 kcal/mol.³¹⁷

Turning to toroidal fulleroids (also called toroids) with g = 1 and χ = 0, there are different techniques to construct such structures using either combinatorial or geometric approaches.^318–320 Like in the nano-tubes, the hexagons can be oriented in different ways around the torus ring. For example, Figure 24(a) shows hexagons with 1/3 of the edges aligned tangential to the toroidal direction. We could also chose the hexagons to be aligned with 1/3 of the edges perpendicular to the toroidal direction (Figure 24(b)), and similar to nanotubes there are also chiral alignments depending on the chirality vector. Kirby and Pisanski showed how 2D graph drawings of toroids can be obtained.³¹⁴ Borštnik and Lukman³²¹ as well as Diudea and Kirby³²² considered the structure and stability of such toroids using simple molecular mechanics. Faghani analyzed the symmetry of toroidal fulleroids.¹²⁶ Kang analyzed the band gap in such toroids by graph theoretical means.³²³ Deza et al. pointed out that leapfrog toroids and Klein-bottles have equal numbers of positive and negative eigenvalues, but with 4 and 2 eigenvalues being zero respectively.²⁴² Interestingly, the leapfrog transformation performed on toroids (such as the one shown in Figure 24) results in an open shell toroid.³²⁴

As discussed earlier, the positive curvature in fullerenes originate from the pentagons, because sheets of hexagons like to be planar. Introducing heptagons or even octagons into a fullerene requires additional faces of size less than 6 to outweigh them, and results in a highly non-convex structure with often strong negative local Gaussian curvature,³²⁵ introducing a saddle-type topology to the structure. Two examples of such fulleroids are shown in Figure 25. In this figure, every patch consisting of a pentagon surrounded by hexagons is replaced by six pentagons surrounded by five heptagons, for three different fullerenes, yielding characteristic ‘spiky’ fulleroids. In Figure 26, heptagons are introduced in a fashion that leads to peanut shaped fulleroids,³²⁶ and in fact, many types of interesting shapes can be constructed.

Figure 25.

Spiky fulleroids with negative curvature containing heptagons derived from fullerenes through patch replacement. (a) C₂₆₀-I[5, 7] fulleroid derived from C₁₄₀-I. (b) C₃₀₀-D_6h[5, 6, 7] derived from C₁₈₀-D_6h. (c) C₃₁₀-D_5h[5, 6, 7] derived from C₁₉₀-D_5h.

Figure 26.

Peanut shaped fulleroids. (a) C₁₂₀-D_5d[5, 6, 7] with 10 heptagons and 22 pentagons. (b) C₁₆₈-D_3d[5, 6, 7] with 18 heptagons and 30 pentagons.

More interesting fulleroid shapes can be found in a recent paper by Diudea et al.³²⁷ Negatively curved fulleroids of higher genus (so-called perforated fullerenes) have been explored by Terrones and Terrones,³²⁸ who studied their electronic structures.³²⁹ Under specific conditions fullerenes can be combined by coalescence, forming larger carbon structures such as deformed nano-tubes or nano-peapods.³³⁰ For an overview of such carbon nano-peapods see Ref 331.

Structures of negatively curved graphitic carbon, which can be periodically extended to a lattice, have been proposed in 1991 by Mckay and Terrones,³⁰⁵ and subsequently explored by experiment.^332–335 These so-called ‘spongy’ carbon frameworks or Schwarzites are named in honor of the mathematician Hermann Schwarz (1843–1921), who investigated minimal surfaces with zero mean Gaussian curvature.³³⁶ Schwarzites are structures containing (beside hexagons) heptagons and/or octagons and are of genus g ≥ 3. These Schwarzites can be periodically continued through so-called junctions as shown in Figure 27 for the case g = 3 (Figure 27(a)). The two structures in Figure 27 are termed P-type and D-type, and can be approximately represented by the simple formulae derived from the Weierstrass-Enneper parameterization for minimal surfaces,³³⁷

55

56

Figure 27.

Periodic P-type (a) and D-type (b) Schwarzite surfaces.

Relevant reviews on such minimal surface carbon networks have been given by Terrones and Mackay³¹¹ and by Terrones and Terrones.³³⁸

Lenosky et al. have performed local density functional calculations for two different g = 3 periodic Schwarzite structures with 216 atoms and a tessellation of hexagons and 24 heptagons within the unit cell.³³⁹ The vertices on such surfaces can be obtained through the Weierstrass representation.^340,341 These calculations reveal a higher thermodynamic stability compared to C₆₀, but not surprisingly lower compared to the graphene sheet (or graphite). D-type Schwarzites have the structure of a ‘diamond shaped’ lattice so that the unit cell can be split into two identical elements having 12 heptagons each, whereas P-type Schwarzites have the structure of a simple cubic lattice (see Figure 7). In principle, Schwarzites can be associated to any kind of lattice, either periodic or amorphous, the latter are realized in so-called random Schwarzites observed experimentally.^332–335 Such random Schwarzites show rather nice transmission electron microscope (TEM) images (Figure 28) rather different to periodic Schwarzites. A recent comprehensive review over experimental and theoretical studies on Schwarzites has been given by Benedek et al.³³⁵

Figure 28.

Comparison between a small portion of a TEM image of a P-type Schwarzite and the surface described by Eq 55 projected onto a plane normal to the z-direction (see Ref 333 for details). (Copyright © 2013 AIP Publishing LLC)

Finally, we consider non-cubic (n-valent) polyhedral structures. In chemistry this is realized by using elements from the periodic table which can share more (or less) than three bonds with its neighbors. Prime examples are all-boron ‘fullerenes’,³⁴² gaudiene C₇₂-O_h (with two- and three-valent carbon as analogs to graphyne),^343,344 and golden ‘fullerenes’^345–348 (we shall call these structures polyhedral molecules rather than fullerenes). For example, Au₃₂ and Au₇₂ are a triangulated surfaces of icosahedral symmetry.^346–348 It is well known that small gold clusters adopt 2D structures with the most coordinated gold atom having a valency of six.³⁴⁹ Extended to infinity, this gives the dual structure of a graphene sheet, that is a triangulation of the plane with vertices of degree six (see Figure 29). In complete analogy to the fullerenes, golden ‘fullerenes’ are the duals of fullerene structures, for example, Au₃₂-I_h is the dual of C₆₀-I_h, Au₄₂-I is the dual of C₈₀-I, and Au₇₂-I is the dual of C₁₄₀-I (the Goldberg-Coxeter transform of C₂₀ with k = 2 and l = 1). We may ask how many possible isomers are there for Au₇₂? Since the mapping from the fullerene isomer space into the dual space is bijective, there are as many isomers for Au₇₂ as there are for C₁₄₀, and there are 7,341,204 of these. The stability of these structures have not been explored yet! A smaller dual-type golden fullerene structure, Au , has been observed spectroscopically by Bulusu et al.³⁴⁵ Here the fullerene analog is C₂₈, where we have only two isomers, of T_d and D₂ symmetry. Only the Au -T_d structure has been investigated presently.

Figure 29.

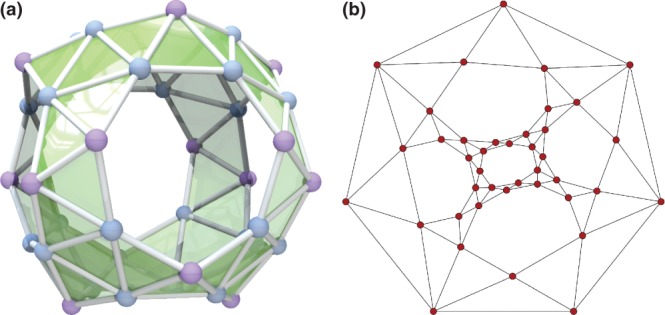
All boron fullerene B₄₀ (adapted from Ref 350). (a) 3D structure; (b) 2D graph.

As a second example, the all-boron B₄₀ fullerene has been identified by photoelectron spectroscopy only very recently by Wang and co-workers (as the anionic species B ),³⁵⁰ consisting of 4 heptagons, 2 hexagons, and 48 triangles (see Figure 29). In this intriguing new polyhedral structure the vertices are of degrees 4 and 5. To be more precise, we have F₃ = 48, F₆ = 2, F₇ = 4, N₄ = 16, N₅ = 24 for B₄₀, which gives according to Eq 52 E = 92 for the number of edges.

CONCLUSIONS

To review the many developments in the topology and graph theory of fullerenes or fulleroids would be a monumental task. We have only outlined a few important concepts in order to give the reader a good introduction into this exciting field. There is certainly the need of a more comprehensive review or book. Nevertheless, we hope to have shown that the interplay between mathematics and structural chemistry is both interesting, rich and well alive. As more sophisticated method in the synthesis of carbon and other materials become available, we hope that some of the exotic, but very beautiful, structures become accessible with many useful applications in chemistry and materials science.