Plasmonic photonic crystals realized through DNA-programmable assembly

Significance

DNA-programmable methods provide unprecedented control over the assembly of nanoparticles into complex structures, including superlattices with deliberately tailorable compositions, crystal symmetries, lattice constants, and crystal habits. In principle, such bottom-up approaches can be used to assemble interesting photonic structures, including ones containing quantum dots and metal nanoparticles. Herein we show that we can tune the interaction between light and the collective electronic modes of gold nanoparticles by independently adjusting lattice constants and gold nanoparticle diameters. This opens up exciting possibilities for tuning the interaction between light and highly organized collections of particles at the nanoscale for applications ranging from lasers to quantum electrodynamics to biosensing. The structures reported herein are the first devices to our knowledge prepared by DNA guided colloidal crystallization.

Abstract

Three-dimensional dielectric photonic crystals have well-established enhanced light–matter interactions via high Q factors. Their plasmonic counterparts based on arrays of nanoparticles, however, have not been experimentally well explored owing to a lack of available synthetic routes for preparing them. However, such structures should facilitate these interactions based on the small mode volumes associated with plasmonic polarization. Herein we report strong light-plasmon interactions within 3D plasmonic photonic crystals that have lattice constants and nanoparticle diameters that can be independently controlled in the deep subwavelength size regime by using a DNA-programmable assembly technique. The strong coupling within such crystals is probed with backscattering spectra, and the mode splitting (0.10 and 0.24 eV) is defined based on dispersion diagrams. Numerical simulations predict that the crystal photonic modes (Fabry–Perot modes) can be enhanced by coating the crystals with a silver layer, achieving moderate Q factors (∼10²) over the visible and near-infrared spectrum.

Enhancing light–matter interactions is essential in photonics, including areas such as nonlinear optics (1), quantum optics (2, 3), and high-Q lasing (4). In general, there are two ways of achieving this in optical cavities: (i) with long cavity lifetimes (high Q factors) and (ii) with strong photonic confinement (small mode volume, V) (2, 3). In particular, 3D dielectric photonic crystals, with symmetry-induced photonic band gaps (Bragg gaps), enhance light–matter interactions via high Q factors (4–6). However, the coupling strength between photons and electronic transitions within such systems is intrinsically weak owing to diffraction-limited photonic confinement (3, 7). Recently, it was suggested that a plasmonic counterpart of photonic crystals can prohibit light propagation and open a photonic band gap by strong coupling between surface plasmons and photonic modes (a polariton gap) if the crystal is in deep subwavelength size regime (8); these crystals have been referred to as polaritonic photonic crystals (PPCs) (9–12). This opens up the exciting possibility of combining plasmonics with 3D photonics in the strong coupling regime and optimizing the photonic crystals as small-mode-volume devices owing to the strong plasmonic mode confinement (13). However, such systems require control over the positioning of the plasmonic elements in the crystal on the nano- or deep subwavelength scale (8), and owing to this synthetic challenge such 3D PPCs have largely remained unexplored in the visible wavelength range.

The recent discovery that DNA can be used to program the assembly of high-quality single crystals with well-defined crystal habits consisting of nanoparticles occupying sites in a preconceived lattice (14) opens up possibilities for fine tuning the interaction between light and highly organized collections of particles as a function of lattice constant and particle size. Here, we report that 3D plasmonic photonic crystals made by DNA-programmable assembly can be used to establish strong light–plasmon coupling with tunability based upon the DNA interconnects and the corresponding volume fraction of the plasmonic elements. The strong coupling is manifested in crystal backscattering spectra and mode splitting (0.10 and 0.24 eV) in dispersion diagrams. Simulation results that we also include show that, by coating the crystals with a silver layer, Fabry–Perot photonic modes of crystals can be enhanced, with moderate cavity Q factors (∼10²) over the visible and near-infrared (NIR) spectrum. In addition to being the first devices made by DNA-programmable colloidal crystallization, they illustrate the potential of the technique for making novel 3D crystals for photonic studies and applications.

The plasmonic PPCs are synthesized from two batches of gold nanoparticles, each functionalized with oligonucleotide sequences that are hybridized to complementary linker sequences that induce the assembly of the particles into rhombic dodecahedra single crystals with a body-centered-cubic (BCC) arrangement of the particles (14) (Supporting Information, sections S1 and S2, Fig. S1, and Tables S1 and S2). The lattice constants and gold nanoparticle diameters of the three PPCs that we present (denoted PPC1, PPC2, and PPC3) are 27.2 and 5.6 nm, 32.2 and 9.0 nm, and 44.0 and 20.0 nm, respectively, resulting in substantially different gold volume fractions (PPC1 ∼0.91, PPC2 ∼2.3, and PPC3 ∼9.8%).

PPCs can exhibit Fabry–Perot cavity modes (FPMs) owing to light interference induced by two parallel facets (15) in the microcavity geometry (Fig. 1 A and B) as long as the size of the PPCs is much larger than the wavelength of light (Supporting Information, section S3 and Fig. S2). FPMs can be detected via backscattering spectra (16) (Fig. 1 A and B) and allow one to probe the optical response of the PPCs. Importantly, within the PPCs the propagating photonic modes are expected to strongly couple to the gold nanoparticle surface plasmons (Fig. 1 B and C), forming a polariton band gap (8, 17). This is probed by optical experiments and theoretical calculations (Fig. 2, Supporting Information, sections S4–S6, and Figs. S3–S6). The backscattering spectra from the PPC center spots (Fig. 2 A, C, and E, Bottom) show Fabry–Perot interference patterns in the visible region (Fig. 2 B, D, and F, red lines). The agreement between a finite-difference time-domain (FDTD) simulation with a rhombic dodecahedron shape and an infinite slab model (Supporting Information, section S5 and Fig. S5) reveals the Fabry–Perot nature of these backscattering spectra, because FPMs are the only existing modes in the infinite slab geometry. Significantly, the Fabry–Perot oscillations are suppressed only around the surface plasmon resonance energy (∼530 nm; ∼2.3 eV) for PPC1 and PPC2, indicating the suppression of light propagation owing to coupling to surface plasmons. This behavior provides direct evidence for polariton band gap formation that is consistent with the theoretical predictions (8, 9, 18). These experimental results are in remarkably good agreement with two different infinite slab models, one with BCC crystal geometry and the other an effective medium theory (EMT) approximation that is based simply on the gold volume fraction without the effect of interparticle coupling (Fig. 2 B, D, and F; blue solid and dashed lines). For PPC3, FPMs are not observed below 500 nm (Fig. 2F) because of the strong absorption caused by the gold interband transition at relatively higher gold volume fraction. The discrepancy between the two models in FPM cutoff location (Fig. 2F, denoted by the two vertical lines) indicates that a considerable amount of interparticle coupling exists close to the surface plasmon resonance because EMT does not include interparticle coupling.

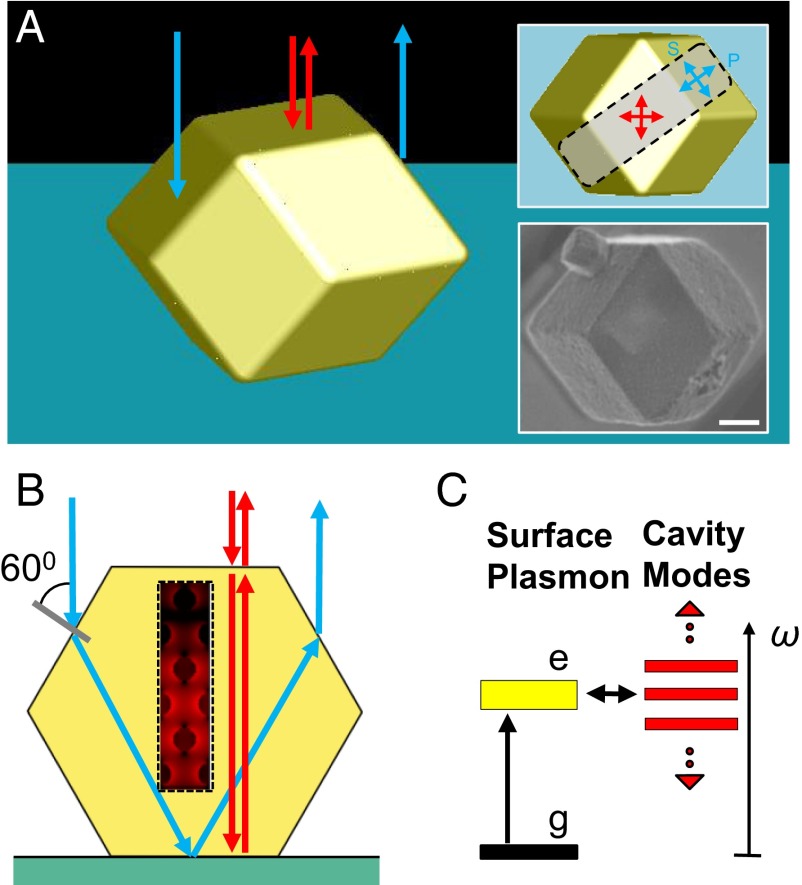
Fig. 1.

A polaritonic photonic crystal made by DNA-programmable assembly. (A) Three-dimensional illustration of a plasmonic PPC, in the shape of a rhombic dodecahedron, assembled from DNA-modified gold nanoparticles. Red arrows indicate light rays normal to the underlying substrate, impinging on and backscattering through a top facet of the crystal (FPMs). The blue ones represent light rays entering through the slanted side facets and leaving the PPC through the opposite side, not contributing to the FPMs (Fig. S2). The top right inset shows the top view of the crystal with two sets of arrows defining two polarization bases at the top and side facets. The bottom right inset shows an SEM image of a representative single crystal corresponding to the orientation of the top right inset. (Scale bar, 1 µm.) (B) A 2D scheme showing the geometric optics approximation of backscattering consistent with the explanation in A. The hexagon outline is a vertical cross-section through the gray area in the top right inset of A parallel to its long edge. The box enclosed by a dashed line depicts the interaction between localized surface plasmons and photonic modes (red arrows; FPMs) with a typical near-field profile around gold nanoparticles. The contribution of backscattering through the side facets (blue arrows) to FPMs is negligible. (C) Scheme of plasmon polariton formation. The localized surface plasmons (yellow bar) strongly couple to the photonic modes (red bars; FPMs).

Fig. 2.

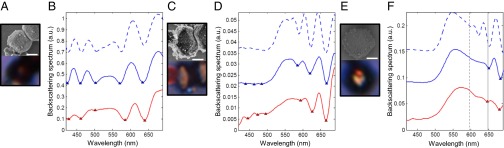
Experimental and theoretical backscattering spectra of PPC1–3. (A) SEM image (Top) and optical bright field reflection mode image (Bottom) of PPC1 on a silicon substrate. (Scale bar, 1 µm.) (B) Measured backscattering spectrum (red solid line) of PPC1 from the center red spot in A, Bottom. Calculated backscattering spectra based on two infinite slab models with BCC crystal geometry (blue solid line) and EMT approximation (blue dashed line). FPMs are indicated by markers. (C–F) The same datasets for PPC2 and PPC3 as in A and B. PPC2 and PPC3 are on indium tin oxide (ITO)-coated glass slides. The optical images show bright spots at the center owing to backscattering from the top and bottom facets. Two vertical lines in F indicate spectral positions where FPMs are suppressed. (Scale bars, 1 µm.)

Based on the spectral results, we examine the strong coupling behavior between the surface plasmons and FPMs in the PPCs with dispersion diagrams generated by FDTD photonic crystal analyses, including changes in the light–matter interactions by tailoring the lattice constant and gold nanoparticle size (Fig. 3 and Supporting Information, section S5). When the mode energies of PPC1 and PPC2 grow close to that of the localized surface plasmon resonance (LSPR), $\hslash {\omega }_0$ (∼2.3 eV), the dispersion curves of the propagating modes form band gaps (Fig. 3 A and B). This is clearer in the absence of interband transition (insets of Fig. 3 A–C and Fig. S7 A–F). The origin of these band gaps is not the BCC translational symmetry of the crystals (Bragg gap) as in conventional dielectric photonic crystals (6). For Bragg gap formation in the visible, photonic crystals require a lattice constant an order of magnitude larger than those in this work (∼λ/2). Instead, the origin of the gaps is strong coupling between the surface plasmons and photonic modes owing to deep subwavelength lattice constants that define the separation of the polarizable particle components (high-density localized surface plasmons) (8, 9). In each crystal type (Fig. 3 A and B), coupling of this kind creates plasmon polaritons with anticrossing upper and lower branches in the dispersion diagrams forming a polariton band gap between the two branches, where propagating photonic modes are prohibited (8, 9, 17). The strength of the coupling is quantified by the mode splitting, $\hslash {\mathrm{\Omega }}_R$, (Supporting Information, section S7 and Fig. S7), which is the energy gap between the two branches at the resonant coupling point (17) ($\hslash {\mathrm{\Omega }}_R$∼0.10 and 0.24 eV for PPC1 and PPC2, which are about ∼5 and ∼10% of $\hslash {\omega }_0$; Fig. 3D). These mode splittings are comparable to a recently reported value based on 1D nanowire arrays on waveguide substrates (17). The EMT-generated curve without the effect of the interband transition (9) predicts a monotonically increasing mode splitting with the increase in gold volume fraction (1–10%; Fig. 3D), which agrees well with the FDTD photonic crystal analyses (Supporting Information, sections S6 and S7 and Fig. S7). This suggests the possibility of using metal volume fraction as a parameter to control coupling strength based on fine geometric tuning afforded by the DNA-programmable assembly technique (19). For PPC3, owing to the strong gold interband transition the upper branch in the dispersion diagram (Fig. 3C; <500 nm in Fig. 2F) is not clearly observable in the experiment, and therefore the mode splitting is not measurable. Based on a photonic crystal analysis without the presence of interband transitions, the upper branch of PPC3 is observed (Fig. 3C, Inset), and the mode splitting is ∼30% of $\hslash {\omega }_0$ (Supporting Information, section S7 and Fig. S7). This large value arises due to the capability of the PPCs to coherently couple a large number of oscillators within a single microcavity.

Fig. 3.

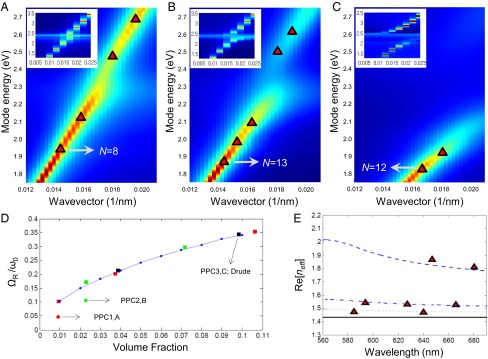
Calculated photonic mode dispersion, mode splitting, and effective mode index of PPC1–3. (A) The spectral density in the ΓN direction is presented for PPC1 (red is high, blue is low). Log10 scale is used. Red triangular markers are the FPMs in Fig. 2B (red markers). They are assigned to peak positions of the spectral densities and the mode number (N) is assigned on one FPM. (Inset) The same spectral density calculated based on the Drude model for gold (where there is no interband transition). (B and C) The same information as in A for PPC2 and PPC3. (D) The mode splitting to plasmonic mode energy ratio, $\hslash {\mathrm{\Omega }}_R/\hslash {\omega }_0$, is shown in terms of gold volume fraction. Blue dots are calculated based on EMT with the Drude model for gold. Squares are generated by a FDTD photonic crystal analysis with the Drude model for gold (red, green, and black: nanoparticle diameters 5.6, 9.0, and 20 nm; volume fraction of PPC3 indicated for 20 nm), and circles with experimentally measured gold permittivity (red and green: nanoparticle diameters 5.6 and 9.0 nm; PPC1 and PPC2). (E) EMT-based effective indices, Re[n_eff], for PPC1 (dotted line), PPC2 (dash-dot line), and PPC3 (dashed line). The index of the silica host medium (black solid line) is added as a reference. Red markers are Re[n_eff] based on the FPMs in A–C.

Significantly, the strong coupling that we observe is further evidenced by quantifying the effective mode indices, Re[n_eff] (Fig. 3E). As the gold volume fraction increases to that of PPC3, the effective mode index drastically increases (Re[n_eff] ∼2) close to the LSPR frequency, indicating strong light coupling to surface plasmons and a large mode momentum gain (18, 20, 21). This is also apparent in the spectral profile, which shows an abrupt suppression of FPMs (two vertical lines in Fig. 2F) and a sharp increase in reflectance from 650 to 550 nm. This transition from Fabry–Perot to mirror-like behavior is due to an increase in both Re[n_eff] and Im[n_eff] close to the LSPR frequency (Fig. S6) that causes strong facet reflection and damping of the FPMs (18).

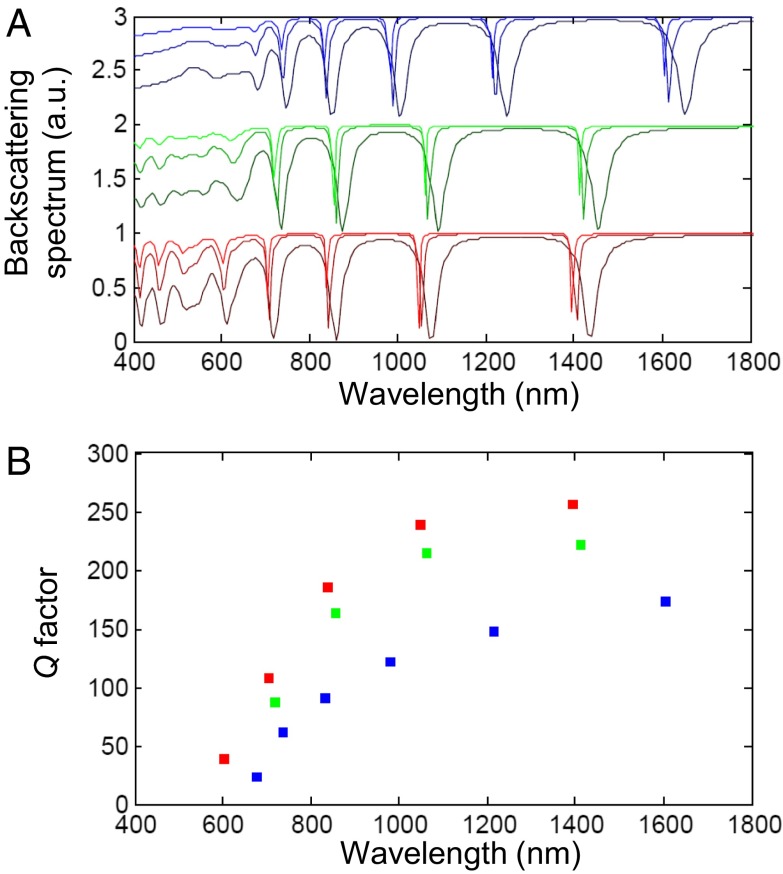
The PPCs with lattice constants in the deep subwavelength regime can also behave as plasmonic cavity devices for studies such as cavity quantum electrodynamics (QED) (3, 22, 23). The plasmonic PPCs have, within a single structure, optical elements working on two different length scales: the plasmonic nanoparticles and the Fabry–Perot microcavity. Owing to localized surface plasmons, the gold nanoparticles exhibit extremely tight light confinement [a small mode volume, V <10⁻⁴(λ/n) (3), in the visible and NIR] around their metallic surfaces that augments light–matter interactions such as exciton–photon coupling (13, 24). These highly confined modes can be further enhanced (23, 25) if Q factors of Fabry–Perot modes are increased by coating the crystals with a silver layer (10–30 nm) (see Fig. S8 for the calculation approach and Figs. S9 and S10 for the experimental process). By simplifying the 3D shape of PPCs to a slab we can use the infinite slab model with a BCC crystal geometry to predict moderate Q factors (∼10²) of FPMs with varying silver layer thickness in the visible and NIR for PPC1–3 (Fig. 4). At ∼30-nm silver layer thickness, the Q factor saturates, and PPC1 exhibits the highest Q values owing to the lowest gold volume fraction. These numbers (∼10²; Fig. 4) are comparable to those of other plasmonic cavities in the literature (20, 23). This shows the possibility of tuning not just plasmonic modes by controlling BCC crystals but also enhancing the properties of photonic modes (FPMs) for further applications with excitonic materials such as dyes and quantum dots (26).

Fig. 4.

Prediction of backscattering spectra and Q factor of silver-coated PPC1–3. (A) Backscattering spectra of PPC1–3 (from bottom to top: PPC1, PPC2, and PPC3) based on the infinite slab model with BCC crystal geometry. The thickness of the slabs is ∼1.3 µm, and that of silver coating layer is varied from 10 to 30 nm. As the coating thickness increases the line shape becomes sharper. The spectra of PPC1 and 2 are translated for comparison. (B) Q factors of each silver-coated slab are shown at FPMs (PPC1, red; PPC2, green; and PPC3, blue). The coating thickness is 30 nm.

This work has shown how bioprogrammable colloidal crystallization can be used to access a new class of PPCs and related optical devices. Although the ability to create well-formed crystals via this technique is essential, it is the ability to tune light–plasmon coupling and plasmonic particle volume fraction that makes this approach so powerful from both fundamental science and potential device application standpoints. We anticipate that the studies herein and the single crystals realizable through the methodology will open the door to studying exciton–photon coupling in novel PPC plasmonic cavities and lead to new directions in cavity QED (22, 27), quantum optics (28–30), and quantum many-body dynamics (31, 32).

Methods

FDTD Calculation.

The FDTD simulations were performed with a commercial package (Lumerical FDTD solutions v.8.7.0). See Supporting Information for the details of various FDTD models used in this work.

EMT Approximation.

EMT is used to approximate the refractive indices of PCCs based on the Maxwell–Garnett equation, ${\epsilon }_{eff}-{\epsilon }_{host}/{\epsilon }_{eff}+2{\epsilon }_{host}=FF\left({\epsilon }_{inc}-{\epsilon }_{host}/{\epsilon }_{inc}+2{\epsilon }_{host}\right)$, where ε_eff, ε_inc, and ε_host are dielectric constants of the PPCs, gold, and silica host medium, and FF is the gold volume fraction.

Optical Experiments.

Microspectrophotometry was performed by detecting the backscattered light from the PPCs. The signal was extracted from the bright spots at the center of the PPCs in reflection mode, and then it was normalized by the lamp spectral profile, which was separately collected by transmission mode. The measurements were made using a 50× objective (N.A. 0.8) and a CCD (Princeton Instruments) coupled to a spectrometer (Princeton Instruments).

More detailed methods can be found in Supporting Information.