Integrative analysis of sequencing and array genotype data for discovering disease associations with rare mutations

Significance

High-throughput DNA sequencing provides an unprecedented opportunity to discover rare genetic variants associated with complex diseases and traits. However, sequencing a large number of subjects is prohibitively expensive. It is common to select subjects for sequencing from the cohorts that have collected genotyping array data. We impute the sequencing data from the array data for the cohort members who are not selected for sequencing and perform gene-level association tests for rare variants by properly combining the observed genotypes for sequenced subjects and the imputed genotypes for nonsequenced subjects. This integrative analysis is substantially more powerful than the use of sequencing data alone and can accelerate the search for disease-causing mutations.

Abstract

In the large cohorts that have been used for genome-wide association studies (GWAS), it is prohibitively expensive to sequence all cohort members. A cost-effective strategy is to sequence subjects with extreme values of quantitative traits or those with specific diseases. By imputing the sequencing data from the GWAS data for the cohort members who are not selected for sequencing, one can dramatically increase the number of subjects with information on rare variants. However, ignoring the uncertainties of imputed rare variants in downstream association analysis will inflate the type I error when sequenced subjects are not a random subset of the GWAS subjects. In this article, we provide a valid and efficient approach to combining observed and imputed data on rare variants. We consider commonly used gene-level association tests, all of which are constructed from the score statistic for assessing the effects of individual variants on the trait of interest. We show that the score statistic based on the observed genotypes for sequenced subjects and the imputed genotypes for nonsequenced subjects is unbiased. We derive a robust variance estimator that reflects the true variability of the score statistic regardless of the sampling scheme and imputation quality, such that the corresponding association tests always have correct type I error. We demonstrate through extensive simulation studies that the proposed tests are substantially more powerful than the use of accurately imputed variants only and the use of sequencing data alone. We provide an application to the Women’s Health Initiative. The relevant software is freely available.

Recent technological advances have made it possible to conduct high-throughput DNA sequencing studies on rare variants, which have a stronger impact on complex diseases and traits than common variants (1). However, it is still economically infeasible to sequence all subjects in a large cohort, and, therefore, only a subset of cohort members can be selected for sequencing. A cost-effective sampling strategy is to preferentially select subjects in the extremes of a quantitative trait distribution or those with a specific disease (2, 3). For case−control studies, an equal number of cases and controls provides more power than other case−control ratios. For quantitative traits, the power increases as more extreme values are sampled (2).

Trait-dependent sampling has been adopted in many sequencing studies, including the National Heart, Lung, and Blood Institute (NHLBI) Exome Sequencing Project (ESP) and the Cohorts for Heart and Aging Research in Genomic Epidemiology (CHARGE) resequencing project. The NHLBI ESP consists of three studies that sequenced subjects with the largest and smallest values of body mass index (BMI), low-density lipoprotein, and blood pressure, one case−control study on myocardial infarction, and one case-only study on stroke (2). The CHARGE resequencing project selected subjects with the highest values of 14 quantitative traits, as well as a random sample (4).

The cohorts from which subjects are drawn for sequencing often have collected genotyping array data on all or most cohort members through genome-wide association studies (GWAS). This is certainly the case with the cohorts used in the NHLBI ESP and CHARGE projects. If we impute the sequencing data from the GWAS data for the cohort members who are not selected for sequencing, we will dramatically increase the number of subjects with information on rare variants. Indeed, such imputation is being carried out in the Women’s Health Initiative (WHI) (5), which is a major component of the NHLBI ESP, and other cohorts (6). The algorithms for rare variant imputation include MaCH (Markov chain based haplotyper) (7), IMPUTE2 (8), BEAGLE (9), and minimac (10), all of which impute rare variants by leveraging the linkage disequilibrium (LD) between sequenced and GWAS variants.

The aforementioned imputation algorithms have been routinely used to impute untyped common single nucleotide polymorphisms (SNPs) (i.e., variants not present on the genotyping array) in GWAS (11, 12). Common SNPs can be imputed with high degrees of accuracy, and single-SNP association tests treating imputed genotype values as observed quantities have reasonable control of the type I error (13, 14).

There are major differences between imputing common SNPs in GWAS and imputing rare variants in sequencing studies. First, the former uses an external reference panel, such as the HapMap (15) or the 1,000 Genomes (16), whereas the latter relies primarily on an internal reference panel, i.e., the subset of GWAS subjects who are sequenced. Second, rare variants cannot be imputed very accurately because of the low minor allele count and weak LD. Third, untyped common SNPs are unobserved and imputed for all subjects in GWAS whereas rare variants are observed in a subset of the study subjects (i.e., sequenced subjects) and imputed for the rest (i.e., nonsequenced subjects) in sequencing studies, creating within-study differential quality in genotype data. If the selection of subjects for sequencing depends on the trait values, then the variance of the trait for sequenced subjects is generally different from that of nonsequenced subjects. The combination of differential genotype quality and differential trait variability between the sequenced and nonsequenced samples will cause inflation of the type I error in association testing, as will be explained in Methods section.

To reduce within-study differential quality in genotype data, one may use a postimputation quality control (QC) procedure (6) to filter out variants that have been imputed with high degrees of uncertainty. As stated, the imputation accuracy for rare variants is typically low; therefore, the use of any reasonable QC filter will remove a large number of rare variants. The removal of variants results in loss of important information because the observed genotype data for sequenced subjects cannot be used if a variant is excluded due to low imputation quality for nonsequenced subjects and because the imputed genotypes, even for a variant that cannot be imputed accurately, may still contain valuable information about the association.

In this article, we show how to perform valid and efficient association tests when rare variants are imputed for nonsequenced subjects. Because single-variant tests and commonly used gene-level tests, such as burden (17, 18), variable threshold (VT) (19, 20), and sequence kernel association test (SKAT) (21), are all based on the score statistic for testing the associations between the genotypes of individual variants and the trait of interest, we investigate the properties of the score statistic based on the observed genotypes for sequenced subjects and the imputed genotypes for nonsequenced subjects. We find that the score statistic is unbiased (provided that there is no strong population stratification). We show that the standard variance estimator for the score statistic is valid if a random subset of the GWAS subjects is selected for sequencing but is invalid if the selection depends on the trait values and the imputation is inaccurate. In addition, we derive a robust variance estimator that reflects the true variability of the score statistic regardless of the sampling scheme and imputation quality, such that the corresponding association tests are guaranteed to have correct type I error. We show, in realistic simulation studies, that the proposed approach is substantially more powerful than the use of accurately imputed variants only and the use of sequencing data alone. We further demonstrate the advantages of the new methodology in an application to empirical data from the WHI.

Methods

We first consider single-variant analysis without covariates. Let G denote the genotype (i.e., number of minor alleles) at the variant site, and let Y denote the trait of interest. Suppose that a total of N unrelated cohort members are measured on Y and GWAS SNPs and that a subset of n subjects is selected for sequencing and thus measured on G. The selection may be completely random or trait dependent. For example, when Y is quantitative, one may select subjects with the largest and smallest values of Y, and when Y is binary, one may draw a case−control sample with an equal number of cases (i.e., $Y=1$) and controls (i.e., $Y=0$) (regardless of the proportion of cases in the entire cohort) or a case-only sample.

We infer the unknown values of G for the $\left(N-n\right)$ nonsequenced subjects from their GWAS data by using the LD between the variant of interest and the GWAS SNPs among the sequenced subjects. We impute G by the expected count of the minor allele (i.e., dosage). The imputation is performed by any of the commonly used algorithms (7–10) without considering the trait information (e.g., by combining cases and controls in a case-control study). Let $\tilde{G}$ denote the imputed value of G for the nonsequenced subject and the observed value of G for the sequenced subject.

We relate quantitative Y to G through the linear regression model

$$Y={\gamma }_0+\beta G+\mathit{ϵ},$$

and binary Y to G through the logistic regression model

$$\text{Pr}\left(Y=1\right)=\frac{e^{{\gamma }_0+\beta G}}{1+e^{{\gamma }_0+\beta G}},$$

where ${\gamma }_0$ is the intercept, β is the association parameter, and ϵ is normal with mean zero and variance ${\sigma }^2$. The score statistic for testing the null hypothesis $H_0:\beta =0$ based on the data $\left(Y_i,{\tilde{G}}_i\right)$ $\left(i=1,\dots ,N\right)$ is

$$U={\displaystyle \sum _{i=1}^N\left(Y_i-\overline{Y}\right){\tilde{G}}_i},$$

where $\overline{Y}=N^{-1}{\displaystyle {\sum }_{i=1}^N{Y}_i}$. The standard variance estimator for U based on the Fisher information is

$$V_{\text{std}}=N^{-1}{\displaystyle \sum _{i=1}^N{\left(Y_i-\overline{Y}\right)}^2}{\displaystyle \sum _{i=1}^N{\left({\tilde{G}}_i-\overline{G}\right)}^2},$$

where $\overline{G}=N^{-1}{\displaystyle {\sum }_{i=1}^N{\tilde{G}}_i}$.

Let us order the data such that the first n subjects are the sequenced ones. By some simple algebra, $U={\displaystyle {\sum }_{i=1}^n{Y}_i\left({\tilde{G}}_i-\overline{G}\right)}+{\displaystyle {\sum }_{i=n+1}^N{Y}_i\left({\tilde{G}}_i-\overline{G}\right)}$. Under the null hypothesis $H_0$, Y is independent of $\tilde{G}$ in both the sequenced and nonsequenced samples. By Eq. S2 of SI Appendix, SI Method A, the means of $\tilde{G}$ are the same as the mean of $\overline{G}$ in both samples. Thus, the mean of U is zero regardless of the imputation quality. However, the standard variance estimator $V_{\text{std}}$ may not fully capture the variability of U with imputed rare variants, as explained below. First, the imputed values are less variable than the observed values when the imputation accuracy is not sufficiently high. Second, the variance of Y may be different between sequenced and nonsequenced subjects when the selection for sequencing depends on Y. Thus, the variance of Y may be related to the variance of $\tilde{G}$. Consequently, the standard variance estimator $V_{\text{std}}$, which treats the variance of Y and the variance of $\tilde{G}$ as unrelated, tends to underestimate the true variance of U; a formal proof is provided in SI Appendix, SI Method B.

The following robust variance estimator fully captures the variability of U under any sampling scheme by properly adjusting for the imputation accuracy:

$$V_{\text{rob}}={\displaystyle \sum _{i=1}^n{\left\{Y_i-\overline{Y}-\left(1-r^2\right)\left({\overline{Y}}_{\text{seq}}-\overline{Y}\right)\right\}}^2{\left({\tilde{G}}_i-\overline{G}\right)}^2}+{\displaystyle \sum _{i=n+1}^N{\left(Y_i-\overline{Y}\right)}^2{\left({\tilde{G}}_i-\overline{G}\right)}^2},$$ [1]

where ${\overline{Y}}_{\text{seq}}=n^{-1}{\displaystyle {\sum }_{i=1}^n{Y}_i}$, $r^2=\rho \sqrt{\text{Rsq}}$, ρ is the Pearson correlation coefficient between the true and imputed genotypes, and Rsq (7) is the ratio of the variance of the imputed genotype to the variance of the true genotype. Eq. 1 is a special case of Eq. S13 derived in SI Appendix, SI Method C. Note that $r^2$ pertains to the imputation accuracy. In Eq. 1, the residuals of sequenced subjects are adjusted by $\left(1-r^2\right)\left({\overline{Y}}_{\text{seq}}-\overline{Y}\right)$, which results from the dependence of the imputed genotypes of nonsequenced subjects on the observed genotypes of sequenced subjects. (The more correlated the imputed genotypes are with their true values, the less dependent they are on the genotypes of other subjects.) We show in SI Appendix, SI Method A that Rsq is equivalent to ${\rho }^2$ when the imputed posterior genotype probabilities are accurately calibrated. Thus, in calculating $V_{\text{rob}}$, we replace $r^2$ by the sample Rsq (7), which does not involve the true genotypes. Specifically, the sample Rsq is the ratio of the sample variance of the imputed genotype to $2\widehat{p}\left(1-\widehat{p}\right)$, where $\widehat{p}$ is the estimated minor allele frequency (MAF) under Hardy−Weinberg equilibrium.

If the imputation is so accurate that $r^2=1$ or the sampling is balanced between the two extremes of a quantitative trait such that ${\overline{Y}}_{\text{seq}}=\overline{Y}$, then $V_{\text{rob}}$ reduces to

$${\displaystyle \sum _{i=1}^N{\left(Y_i-\overline{Y}\right)}^2{\left({\tilde{G}}_i-\overline{G}\right)}^2},$$ [2]

which is the empirical variance estimator based on efficient score functions (22). Moreover, if ${\left(Y-\overline{Y}\right)}^2$ and ${\left(\tilde{G}-\overline{G}\right)}^2$ are uncorrelated, which can be achieved by perfectly imputing the missing genotypes or by selecting subjects for sequencing in a totally random manner, then expression 2 is equivalent to $V_{\text{std}}$. In other words, $V_{\text{std}}$ will be valid if the imputation is perfectly accurate or the selection for sequencing is totally random. When the selection is totally random, $\tilde{G}$ is completely independent of Y, so the standard analysis is valid.

In SI Appendix, SI Method C, we extend our methodology in several directions. First, we consider multiple variants in a gene and derive a robust estimator for the variance−covariance matrix of the (vector-valued) score statistic, from which all commonly used gene-level tests (e.g., burden, VT, and SKAT) can be constructed (23). Second, we incorporate covariates (e.g., demographic variables and principal components for ancestry) into the regression model and show that the score statistic continues to be unbiased as long as covariates are independent of genotypes. (This implies that the score statistic is approximately unbiased when there is no strong population stratification.) We also provide the corresponding robust variance estimator in Eq. S13 in SI Appendix. Third, we accommodate other types of traits such as ordinal and count data by adopting the class of generalized linear models. Fourth, we modify the robust variance estimator for binary traits to improve numerical stability; see Eq. S14 in SI Appendix. Finally, we show how to perform meta-analysis of multiple studies.

Results

Simulation Studies.

We conducted extensive simulation studies to evaluate the performance of the proposed methods in realistic settings. We chose one gene, NPHS2 (nephrosis 2, idiopathic, steroid-resistant) (accession NM_014625), on chromosome 1 and restricted our analysis to variants with MAFs $\le 5\text{\%}$ that are nonsense, missense, or splice site. For the 360 African Americans in the WHI who were sequenced by the NHLBI ESP, there are five variants in NPHS2, with MAFs of 0.002, 0.004, 0.001, 0.022, and 0.005 for snp.98398, snp.98400, snp.98401, snp.98418, and snp.98419, respectively. The number of variants and the total MAF (i.e., sum of MAFs over variant sites) for NPHS2 equal the median number of variants and the median total MAF for all genes, respectively, making this gene a good representation. We used GWAsimulator (24) to generate genotype data for the variants identified by sequencing and for the flanking GWAS SNPs by mimicking the MAFs and LD patterns observed in the WHI genotype data.

We considered a cohort of 5,000 subjects. We generated quantitative traits from the linear regression model $Y=\beta S+{\gamma }_{1}X+\mathit{ϵ}$ and binary traits from the logistic regression model $\text{logit}\left\{\text{Pr}\left(Y=1\right)\right\}=\beta S+{\gamma }_{1}X+{\gamma }_0$, where S is the total number of mutations the subject carries in the gene, X is a normal random variable with mean $\xi S$ and variance one, ϵ is an independent standard normal variable, and ${\gamma }_0$ is the intercept which controls the disease rate. Note that X is a potential confounder that may represent population stratification. We selected a subset of cohort members for sequencing. For quantitative traits, we considered five sampling schemes: (Q1) a random sample of 500 subjects; (Q2) 250 subjects with the largest values of Y and 250 with the smallest values; (Q3) 500 subjects with the largest values of Y and 250 with the smallest values; (Q4) 250 subjects with the largest values of Y plus a random sample of 250 from the remaining cohort; and (Q5) 250 subjects with the largest values of Y plus a random sample of 1,000 from the remaining cohort. For binary traits, we considered five disease rates: 50%, 30%, 20%, 10%, and 5%, to be referred to as B1, B2, B3, B4, and B5, respectively, and we selected 250 cases and 250 controls regardless of the disease rate. (Note that B1 is equivalent to the situation in which a random subset of subjects from the parent case−control GWAS with the same case−control proportion is sequenced.) For subjects that were not selected, we masked the genotypes for the variants identified by sequencing and used minimac (10) (a low-memory, computationally efficient variant of the MaCH algorithm for haplotype-to-haplotype imputation) to impute them. Due to the computational burden of phasing all replicates, we avoided phasing the reference panel and the target sample but retained the haplotype information generated from the simulation. The average Rsq is 0.22 for snp.98418, which is relatively common; it is less than 0.1 for the other variants.

We constructed the burden, VT, and SKAT tests based on $V_{\text{rob}}$ and $V_{\text{std}}$. For the burden test, we adopted the MAF threshold of 5%, which corresponds to T5. For SKAT, we used the default weighted linear kernel function. We refer to these methods as T5-rob, T5-std, VT-rob, VT-std, SKAT-rob, and SKAT-std. As a benchmark, we included the tests based on sequenced subjects only, which are referred to as T5-seq, VT-seq, and SKAT-seq. We set the nominal significance level at 0.001.

We first considered the situation of no confounding (i.e., $\xi =0$) and set ${\gamma }_1=0.2$. The simulation results for the T5 tests under the null hypothesis are summarized in Table 1. As expected, the score statistic is virtually unbiased in every scenario, and $V_{\text{rob}}$ accurately reflects the true variability of U. Consequently, T5-rob always has correct control of the type I error. Under random sampling (i.e., Q1 and B1), $V_{\text{std}}$ is accurate and yields proper type I error. Under other sampling schemes, $V_{\text{std}}$ underestimates the true variability of U, and the type I error rate can be 50 times the nominal level. The results for VT and SKAT exhibit the same patterns as those of T5.

Table 1.

Simulation results for the T5 tests under the null hypothesis

			$V_{\text{rob}}$		$V_{\text{std}}$
Sampling scheme	Bias	SE	SEE	Size	SEE	Size
Q1: random sample of 500 subjects	0.000	0.120	0.118	0.87	0.118	1.02
Q2: 250 largest and 250 smallest values	−0.001	0.181	0.180	0.68	0.118	36.22
Q3: 500 largest and 250 smallest values	−0.006	0.192	0.191	0.96	0.131	27.95
Q4: 250 largest and random sample of 250	−0.006	0.134	0.130	0.89	0.118	3.61
Q5: 250 largest and random sample of 1,000	−0.005	0.171	0.169	0.97	0.152	3.39
B1: 50% disease rate	0.000	0.060	0.059	0.78	0.059	0.93
B2: 30% disease rate	−0.001	0.057	0.056	0.94	0.054	1.63
B3: 20% disease rate	−0.002	0.053	0.052	0.91	0.047	3.16
B4: 10% disease rate	−0.003	0.047	0.046	1.00	0.036	13.47
B5: 5% disease rate	−0.003	0.043	0.041	1.09	0.026	50.95

Q1, Q2, Q3, Q4, and Q5 are five different sampling schemes for quantitative traits; B1, B2, B3, B4, and B5 are five different sampling schemes for binary traits; $V_{\text{rob}}$ and $V_{\text{std}}$ are the robust and standard variance estimators, respectively. Bias and SE are, respectively, the bias and SE of the score statistic of T5. SEE is the mean of the SE estimator, and size is the type I error rate divided by the nominal significance level of 0.001. Each entry is based on 100,000 replicates.

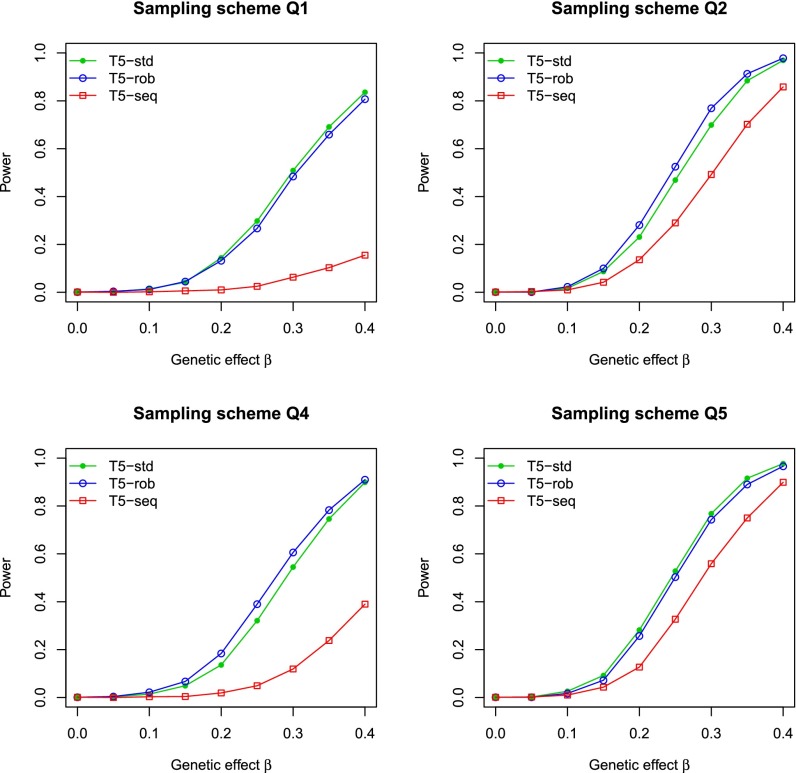
Fig. 1 and SI Appendix, Fig. S1 compare the power of various T5 tests for quantitative and binary traits, respectively. The results for sampling scheme Q3 are not included in Fig. 1 because they are similar to those of Q5. The results for B3 are intermediate between those of B2 and B4 and thus omitted from SI Appendix, Fig. S1. It is clear that T5-rob is uniformly more powerful than T5-seq, demonstrating the benefit of integrating sequencing and GWAS data. Under sampling scheme Q1, T5-std is slightly more powerful than T5-rob. Under B1, the two tests have the same power. Under other schemes, T5-std has inflated type I error (Table 1), so the power comparisons would not be meaningful. To make fair comparisons, we calculated the power of T5-std by resetting the critical values to attain correct type I error. The power of T5-std so calculated is similar to or much lower than the power of T5-rob.

Fig. 1.

Power of the T5 tests at the nominal significance level of 0.001 for the integrative analysis of sequencing and GWAS data based on the robust (T5-rob) and standard variance estimators (T5-std) and for the analysis of sequenced data only (T5-seq). The trait of interest is quantitative. The β values of 0.2, 0.3, and 0.4 correspond to 0.26%, 0.58%, and 1.0% of the trait variance explained by the causal variants. In Q2, Q4, and Q5, the critical values for T5-std were reset to achieve correct type I error. Each power estimate is based on 1,000 replicates.

We examined the robustness of the proposed methods to confounding (i.e., $\xi \ne 0$). We set $\xi =0.1$ and 0.2, which correspond to Pearson correlation coefficients of ∼0.03 and ∼0.057, respectively. (The correlation coefficient of 0.03 is the third quartile of the correlation coefficients between the T5 burden scores and the percentage of African ancestry in the WHI.) In this case, the mean of the score statistic may not be zero. As shown in SI Appendix, Fig. S2, however, the type I error of T5-rob is still reasonable, especially for binary traits.

As mentioned previously, a common practice is to use a postimputation QC procedure to filter out inaccurately imputed variants before association analysis. For example, Auer et al. (6) excluded variants if their Rsq values were less than the thresholds chosen such that within each MAF category, variants passing the threshold had an average Rsq of 0.8 or higher. In particular, they chose Rsq thresholds of 0.3, 0.6, 0.8, and 0.9 for variants with MAFs 3–5%, 1–3%, 0.5–1%, and 0.1–0.5%, respectively, and excluded all variants with MAFs $<0.1\text{\%}$. If we had adopted such a QC procedure in our simulation studies, we would have excluded the gene NPHS2 entirely since the largest Rsq of the variants was merely 0.22. By contrast, our integrative analysis not only allowed association tests for this poorly imputed gene but also gained substantial power over the analysis of sequenced subjects only.

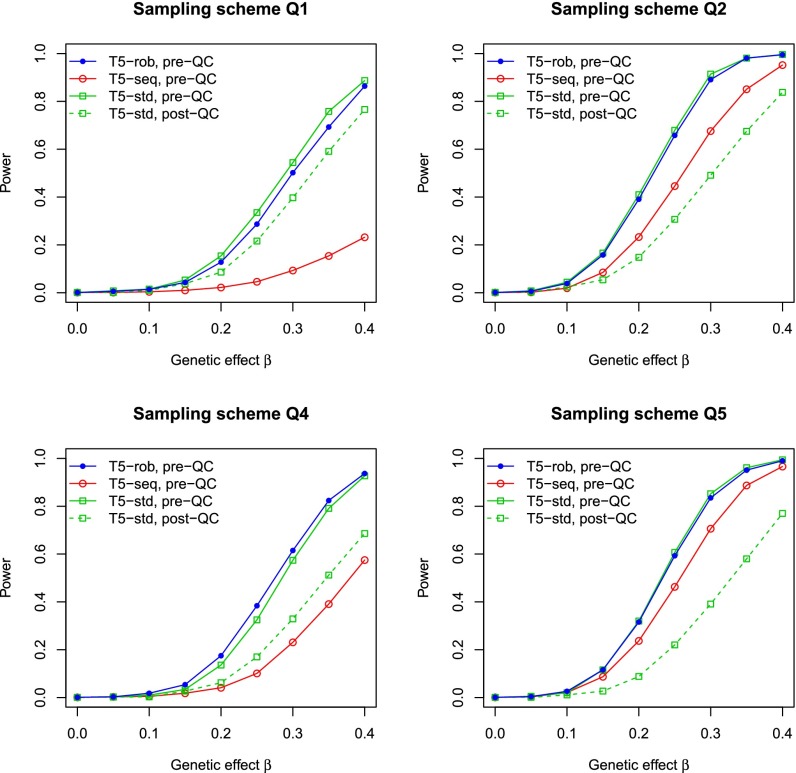
To further demonstrate the benefits of using inaccurately imputed variants, we considered a second gene, OR10J3 (olfactory receptor, family 10, subfamily J, member 3) (accession NM_001004467), on chromosome 1 that has seven variants, snp.88226, snp.88228, snp.88232, snp.88236, snp.88240, snp.88241, and snp.88244, with MAFs of 0.016, 0.01, 0.008, 0.002, 0.001, 0.008, and 0.002, respectively. The Rsq is 0.67 for snp.88226 and almost zero for the other variants. With the use of a QC procedure (6), only snp.88226 would be retained. As shown in Fig. 2 and SI Appendix, Fig. S3, the T5-rob test based on pre-QC variants is substantially more powerful than the T5-std test based on post-QC variants.

Fig. 2.

Power at the nominal significance level of 0.001 for the T5 test based on the robust variance estimator and pre-QC variants (T5-rob, pre-QC), the T5 test based on the standard variance estimator and pre-QC variants (T5-std, pre-QC), and the T5 test based on the standard variance estimator and post-QC variants (T5-std, post-QC) in the integrative analysis of sequencing and GWAS data on the gene OR10J3. The power of T5 for the analysis of pre-QC variants based on sequenced subjects only (T5-seq, pre-QC) is also included. The trait of interest is quantitative. In Q2, Q4, and Q5, the critical values for T5-std (pre-QC) were reset to achieve correct type I error. Each power estimate is based on 1,000 replicates.

The aforementioned simulation studies were based on two specific genes. We also considered all genes on chromosome 1 and generated a binary trait from the logistic regression model $\text{logit}\left\{\text{Pr}\left(Y=1\right)\right\}=\beta S+{\gamma }_{1}X+{\gamma }_0$, where S is the total number of mutations the subject carries in five genes, and $\beta =0$ and 1.2 under the null and alternative hypotheses, respectively, ${\gamma }_1=0.2$, and ${\gamma }_0$ was chosen to yield 10% disease rate. We simulated a cohort of 5,000 subjects, selected 250 cases and 250 controls for sequencing, and imputed the genotypes of the variants identified by sequencing for subjects that were not selected. As shown in SI Appendix, Fig. S4, the test based on $V_{\text{rob}}$ correctly controls the type I error and identifies three out of five causal genes after Bonferroni correction. The test based on $V_{\text{std}}$ and pre-QC variants has inflated type I error, while the one based on $V_{\text{std}}$ and post-QC variants identifies only one causal gene.

WHI Data.

The WHI was established by the National Institutes of Health in 1991 to address major health issues causing morbidity and mortality among postmenopausal women (5). We focused on the BMI values for the African American participants of the WHI cohort. Among the 8,142 African American participants who were genotyped by the Affymetrix 6.0 arrays, 360 with BMI values > 40 or < 25 were selected for whole-exome sequencing in the NHLBI ESP (2). The distribution of the BMI values is displayed in SI Appendix, Fig. S5.

We used the 360 sequenced subjects as an internal reference panel to impute sequencing data from the GWAS data for the nonsequenced subjects. Specifically, we used MaCH (7) to construct a reference panel of 720 phased haplotypes consisting of both the variants discovered by exome sequencing and the SNPs on the GWAS arrays. We also prephased haplotypes at the GWAS SNPs for the remaining cohort members. We then used minimac (10) to impute genotypes at the variants discovered by exome sequencing for the nonsequenced subjects. We restricted our attention to nonsense, missense, and splice site variants with MAFs $\le 5\text{\%}$. We ended up with a total of 19,135 genes containing at least one polymorphic site and a total of 143,273 variants in those genes. SI Appendix, Fig. S6 shows the Rsq values for the variants whose MAFs are lower than the 5% and 1% thresholds. The variants with MAFs ≤ 1% account for a majority (83.3%) of all variants with MAFs $\le 5\text{\%}$ and are associated with lower Rsq values than those with MAFs $>1\text{\%}$.

We used the log-transformed BMI value as the quantitative trait and included age and the proportion of African ancestry estimated by FRAPPE (frequentist approach for estimating individual ancestry proportion) (25) as covariates. The Pearson correlation coefficients between the ancestry variable and the burden scores of the variants with MAFs $\le 5\text{\%}$ have the first quartile, median, and third quartile of $-0.013$, 0.013, and 0.030, respectively. We refer to the burden tests with MAF thresholds of $1\text{\%}$ and $5\text{\%}$ as T1 and T5, respectively. We constructed the T1, T5, VT, and SKAT tests based on $V_{\text{rob}}$ and $V_{\text{std}}$. We also included the tests using only sequenced subjects.

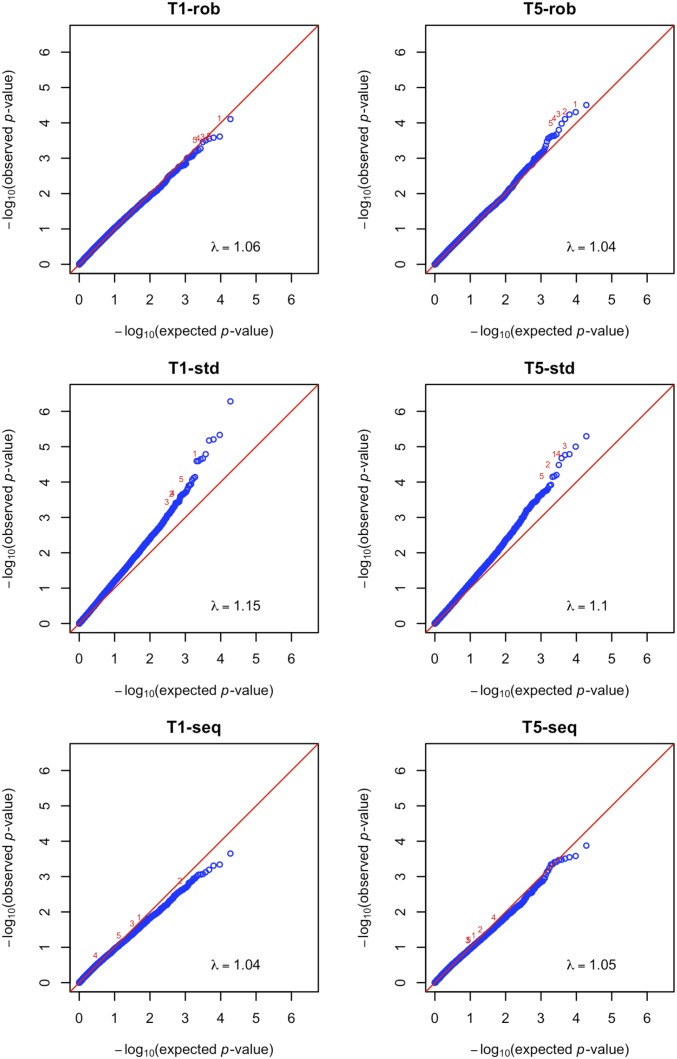
The quantile−quantile plots are displayed in Fig. 3 and SI Appendix, Fig. S7. For all tests based on $V_{\text{rob}}$, the observed P values agree very well with the global null hypothesis of no association, except at the extreme right tails. By contrast, the observed P values for all tests associated with $V_{\text{std}}$ show early departures from the global null distribution, reflecting inflation of the type I error. All tests using only sequenced subjects yield less extreme P values than their counterparts in the integrative analysis based on $V_{\text{rob}}$.

Fig. 3.

Quantile−quantile plots of $-{\log }_{10}$(P values) for the T1 and T5 tests in the analysis of the BMI data in the WHI. (Left) The top five genes identified by T1-rob are marked as 1–5. (Right) The top five genes identified by T5-rob are marked as 1–5.

The top 10 genes identified by T5-rob are listed in Table 2. The top gene ODF2L (accession NM_020729) is ranked the second by VT-rob and the fourth by SKAT-rob, and its imputation accuracy is quite high, with an average Rsq of 0.685. The common SNPs in the seventh gene BDNF were previously found to be associated with BMI in several GWAS (26, 27). This gene is not in the top 10 list by any test with $V_{\text{std}}$.

Table 2.

Top 10 genes for BMI identified by T5-rob in the analysis of the WHI data

					P value
Gene	Accession	Chr	m	Rsq	T5-rob	T5-std	T5-seq
ODF2L	NM_020729	1	11	0.685	$3.1\times {10}^{-5}$	$1.7\times {10}^{-5}$	$4.9\times {10}^{-2}$
ITSN1	NM_003024	21	7	0.609	$5.0\times {10}^{-5}$	$3.3\times {10}^{-5}$	$3.3\times {10}^{-2}$
KDM6B	NM_001080424	17	30	0.266	$5.8\times {10}^{-5}$	$1.0\times {10}^{-5}$	$6.7\times {10}^{-2}$
SOCS1	NM_003745	16	2	0.348	$7.8\times {10}^{-5}$	$1.6\times {10}^{-5}$	$1.5\times {10}^{-2}$
ODF2L	NM_001007022	1	9	0.689	$1.1\times {10}^{-4}$	$7.1\times {10}^{-5}$	$6.4\times {10}^{-2}$
ACADVL	NM_000018	17	15	0.189	$1.6\times {10}^{-4}$	$6.8\times {10}^{-5}$	$1.1\times {10}^{-1}$
BDNF	NM_170734	11	2	0.628	$2.1\times {10}^{-4}$	$2.5\times {10}^{-4}$	$1.0\times {10}^{-1}$
TRDMT1	NM_004412	10	3	0.718	$2.3\times {10}^{-4}$	$1.8\times {10}^{-4}$	$8.1\times {10}^{-2}$
FAM60A	NM_001135811	12	1	0.768	$2.3\times {10}^{-4}$	$4.0\times {10}^{-4}$	$6.5\times {10}^{-1}$
PDGFRA	NM_006206	4	12	0.563	$2.4\times {10}^{-4}$	$2.2\times {10}^{-4}$	$1.4\times {10}^{-3}$

Chr is the chromosome number, m is the number of variants in the gene, and Rsq is the Rsq value averaged over the variant sites in the gene. T5-rob and T5-std are the T5 tests in the integrative analysis of sequencing and GWAS data with the robust and standard variance estimators, respectively, and T5-seq is the T5 test using only sequenced subjects.

For any type of test, the version based on $V_{\text{std}}$ prioritized the top genes differently from the one based on $V_{\text{rob}}$, as shown by the numerical marks in Fig. 3 and SI Appendix, Fig. S7. A gene identified by a test based on $V_{\text{std}}$ but not by its counterpart based on $V_{\text{rob}}$ typically has very low average Rsq (i.e., $<0.1$). For example, the top gene TPSG1 (accession NM_012467) identified by T5-std is not among the top 10 genes by T5-rob and has an average Rsq of only 0.028. Because the tests based on $V_{\text{std}}$ tend to generate significant results when there are substantial differences in the genotype quality between the sequenced and nonsequenced subjects, the top genes identified by these tests are not reliable.

Applying the postimputation QC procedure of Auer et al. (6) to the WHI data, we found that only 17.1% of variants and 47.9% of genes passed the QC criteria. To be specific, 92.8% of variants with MAFs 3–5% passed QC, 69.6% with MAFs 1–3%, 29.5% with MAFs 0.5–1%, and only 3.5% with MAFs 0.1–0.5%. We repeated our association analysis for the post-QC variants and genes. As shown in SI Appendix, Figs. S8 and S9, the tests with $V_{\text{std}}$ no longer exhibit inflation of the type I error. However, their top P values are less extreme than those of $V_{\text{rob}}$ without QC. We list the top 10 genes identified by T5-std in SI Appendix, Table S1, which can be compared with Table 2. We see that the association signal for BDNF is weaker after QC. None of the other genes in SI Appendix, Table S1 has previously been found to be associated with BMI.

Discussion

This article provides a valid and efficient approach to integrative analysis of sequencing and GWAS data. The approach is very general in several aspects: (i) It can handle any type of trait and any sampling scheme; (ii) it encompasses all commonly used gene-level tests for rare variants; (iii) it includes single-variant tests as a special case; and (iv) it allows for covariates. The computation is the same as the usual gene-level tests except for the replacement of the standard variance estimator with the robust one. The proposed methods have been implemented in the software program SEQGWAS (integrative analysis of SEQuencing and GWAS data), which is freely available at web1.sph.emory.edu/users/yhu30/software.html. It took ∼2 h on an IBM HS22 machine to analyze the WHI data.

For binary traits, the GWAS subjects may come from a cohort or case-control study. The standard variance estimator is valid if the case−control ratios are the same between the sequencing study and the parent study. This condition typically holds when the parent study is a case−control study but likely fails when the parent study is a cohort study.

It is also desirable to integrate other types of genetic data. For example, a subset of the WHI African Americans was genotyped on Metabochip (28) and used as the reference panel to impute Metabochip variants for the remaining African Americans with GWAS data (29). In addition, the GWAS genotyping arrays can be replaced by the Metabochip (28) or the Exomechip (30), which can then be imputed against sequencing data (28). Our approach can be readily used to analyze such mixtures of observed and imputed data.

Our approach is built upon existing imputation algorithms and focused on properly analyzing a mixture of observed and imputed genotype data. Thus, we can take full advantage of newly developed imputation programs to improve imputation accuracy and computational efficiency. Although imputed data may pertain to the genotype dosage, the most likely genotype, or the genotype probabilities, our approach is tailored to the dosage data. In practice, the dosage is the most commonly used because, unlike the most likely genotype, it partially accounts for the uncertainty in the imputed value and because the dosage is computationally more tractable than the genotype probabilities while still retaining most information.

The postimputation QC process can alleviate the inflation of the type I error caused by the use of $V_{\text{std}}$. However, this strategy tends to remove many rare variants. The removal of variants results in loss of important information because the observed genotype data for sequenced subjects cannot be used if a variant is excluded due to low imputation quality and because the imputed genotypes, even for a variant with low Rsq, may still contain valuable information about the association. Our approach does not exclude any variants with low Rsq. The imputed values for those variants have small variances and do not add much noise. When Rsq is close to zero, the integrative analysis reduces to the analysis of sequenced subjects only and thus can at least use the information in sequenced subjects. Our approach can certainly be applied to data after QC, but the QC criteria can be much less stringent.