Strength and duration of perisomatic GABAergic inhibition depend on distance between synaptically connected cells

Significance

The activity dynamics of cortical circuits are directly determined by the composing cells and their connections. Inhibitory interneurons are important regulators of neuronal network function. However, how the functional properties of their output synapses relate to the spatial dimension of the network is unknown. Here, we show that perisoma-inhibiting fast-spiking interneurons differentially inhibit close and distant principal cells: inhibitory strength declines and signal duration increases with distance between the presynaptic interneurons and the postsynaptic principal cell. This feature of cortical GABAergic inhibitory signaling supports the interneuron’s potential to synchronize large principal cell populations at gamma (>30 Hz) frequencies, a prerequisite for the encoding and storing of information in neuronal networks.

Abstract

GABAergic perisoma-inhibiting fast-spiking interneurons (PIIs) effectively control the activity of large neuron populations by their wide axonal arborizations. It is generally assumed that the output of one PII to its target cells is strong and rapid. Here, we show that, unexpectedly, both strength and time course of PII-mediated perisomatic inhibition change with distance between synaptically connected partners in the rodent hippocampus. Synaptic signals become weaker due to lower contact numbers and decay more slowly with distance, very likely resulting from changes in GABA_A receptor subunit composition. When distance-dependent synaptic inhibition is introduced to a rhythmically active neuronal network model, randomly driven principal cell assemblies are strongly synchronized by the PIIs, leading to higher precision in principal cell spike times than in a network with uniform synaptic inhibition.

GABAergic parvalbumin (PV)-expressing fast-spiking perisoma-inhibiting interneurons (PIIs) provide powerful synaptic inhibition to large numbers of target cells distributed over several hundred micrometers of cortical space (1–5). Extent and density of their axonal projection together with the perisomatic location of their output synapses close to the site of postsynaptic action potential generation are thought to provide tight control over the activity of target cells. Moreover, PIIs usually interact with other PIIs by reciprocal chemical and electrical synapses, thereby forming interneuron (IN) networks (4, 6, 7), which have been proposed to orchestrate the activity of cortical circuits. PIIs have been shown to receive rapid synaptic excitation (8) and to provide fast, strong, and faithful inhibitory signals to their postsynaptic partners (3, 5, 6). This fast and reliable signaling phenotype has been hypothesized to support the synchronization of neuronal networks leading to rhythmic activity patterns predominantly in the gamma frequency ranges [30–50 Hz, low gamma; 50–90 Hz, midfrequency gamma; 90–150 Hz, high gamma (7, 9)]. Several lines of evidence indeed indicate that PIIs are critical for the emergence of gamma activity. PIIs discharge at high frequencies tightly phase-locked to gamma cycles in vivo (10–13), they can entrain the activity of large principal cell assemblies (2, 14, 15), and silencing them impairs cortical gamma oscillations (14, 16). Thus, fast-spiking PIIs are generally regarded as a reliably active IN type that paces activity of large principal cell populations by strong and fast uniform inhibition.

However, uniformity of PII output signaling has only been assumed and never been tested experimentally. In fact, quantitative analysis of the PII axon morphology shows a gradual decline in axon collateral density with distance from the soma (17–19) frequently interpreted as a reduction in connection probability at larger distances (20, 21), comparable to observations from excitatory glutamatergic neurons in the neocortex (22, 23). However, conclusive physiological data on the functional properties of output synapses from one PII to several postsynaptic partners are lacking. In the face of the central role of fast-spiking PIIs in cortical network computation, a description of their spatiotemporal output is of major importance to our understanding of neuronal information processing.

Here, we addressed this issue using the well-studied synapse between hippocampal PV-positive PIIs and granule cells (GCs) (3, 6) as a model of GABAergic perisomatic inhibition.

Results

Distance-Dependent Changes in Amplitude and Time Course of PII-Mediated Unitary Inhibitory Postsynaptic Currents.

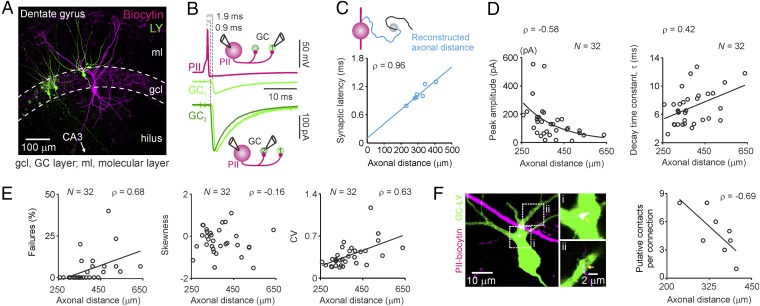
To test whether inhibition provided by single PIIs is uniform over space and time (21, 24, 25), we performed sequential paired whole-cell patch-clamp recordings between a single PII and multiple consecutively recorded target GCs in the dentate gyrus of postnatal day 17 (P17) to P23 rats (Fig. 1). Unexpectedly, we found a marked heterogeneity in synaptic latency, peak amplitude, and decay time constant (τ) of unitary inhibitory postsynaptic currents (uIPSCs) (Fig. 1 A and B). Synaptic latency is largely determined by action potential propagation. Its heterogeneity could therefore indicate different axonal PII–GC distances. Indeed, axon reconstructions from subsets of pairs showed that synaptic latency correlated strongly with axonal (Fig. 1C; seven reconstructed PII–GC pairs, P = 0.003; spike conduction velocity, 0.29 m⋅s⁻¹) and less with intersomatic distance (Fig. S1F; P = 0.023). We therefore used the linear relationship between synaptic latency and axonal distance to estimate in nonreconstructed PII–GC pairs their axonal distances. uIPSC peak amplitudes declined, whereas decay time constants increased over axonal distances of 0.1–0.6 mm and intersomatic distances of 20–200 μm for sequential pairs (Fig. S2 A and B; P < 0.005 and P < 0.05 for amplitude and τ, respectively) and pooled paired recordings (Fig. 1D; P < 0.001 and P = 0.016, respectively). In contrast, the uIPSC 20–80% rise time was distance independent (P = 0.383; Fig. S2C).

Fig. 1.

PIIs provide distance-dependent inhibition to dentate gyrus GCs. (A) Maximum-intensity projection of intracellularly biocytin-filled PII and Lucifer Yellow (LY)-labeled GCs. (B) Representative sequential paired recording of one PII and two GCs. Upper trace, PII action potential; lower traces, average uIPSCs; GC₁ uIPSC was peak-normalized and superimposed to GC₂ uIPSC. (C) Synaptic latency vs. reconstructed axonal distance (mean of all contacts). Circles represent individual reconstructed PIIs (seven cells). (D) uIPSC peak amplitudes decline exponentially, and decay time constants (τ) increase linearly with axonal distance. (E, Left to Right) Transmission failures, skewness, and CV of uIPSC peak amplitude distributions, vs. distance. (F, Left) Maximum-intensity projection of LY-filled GC and biocytin-filled PII axon. Arrows point to putative PII–GC contacts. (Right) Number of putative contacts per connection vs. distance. Lines represent linear, and curves represent exponential fits to data.

To determine whether distance-dependent GABAergic signaling is a particular property of PIIs of the dentate gyrus, we analyzed previous PII–pyramidal cell paired recordings from CA1 (6) and found a similar relationship (Fig. S3). The amplitude declined exponentially, whereas the decay time constant increased linearly with synaptic latency (P = 0.017 and P = 0.017, respectively; five pairs), indicating that distance-dependent perisomatic inhibition is a general principle of hippocampal circuits. Moreover, in a separate set of PII–GC paired recordings, we found that distance-dependent changes in amplitude and decay time course of inhibition are also evident in adult P30–P45 animals (Fig. S4; P = 0.017 and P = 0.001; amplitude and τ, respectively; eight pairs). Thus, distance-dependent perisomatic inhibition does not reflect a developmental phenomenon but rather appears to be a general principle of hippocampal network function.

PIIs Establish Less Release Sites on Remote GCs.

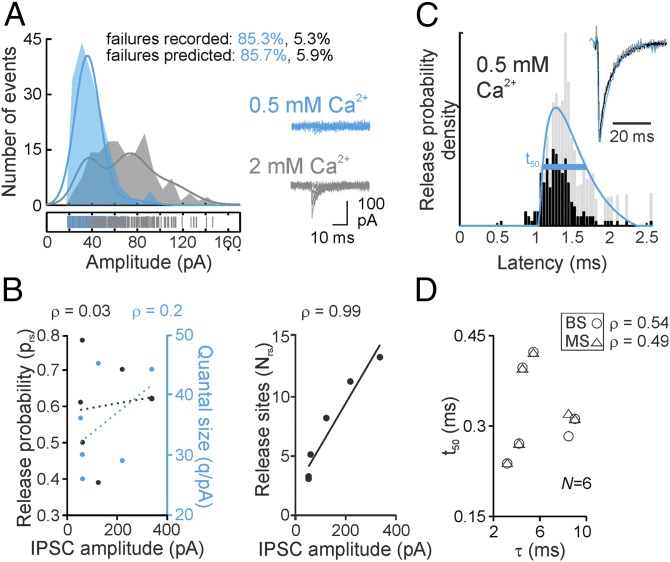
Our results indicate that strength and time course of uIPSCs are not uniform but depend on the distance between presynaptic and postsynaptic neurons. Which mechanisms may underlie these distance-dependent changes? A decrease in strength could be explained by a reduced number of release sites (N_rs). Indeed, the percentage of transmission failures significantly increased (Fig. 1E; P < 0.001), and the number of morphologically identified putative synaptic contacts per connection in labeled pairs declined with axonal distance (Fig. 1F; P = 0.033, left-tailed). Consistent with a decline in the number of release sites, the coefficient of variation (CV) of peak amplitudes increased with distance, whereas the skewness was unchanged (Fig. 1E; P < 0.001 and P = 0.377, respectively). To corroborate our results, we performed multiple probability-compound binomial analysis (MP-CBA) (3) of PII–GC uIPSCs recorded in 0.5 and 2 mM extracellular Ca²⁺ (Fig. 2A). This analysis revealed that N_rs correlated significantly with uIPSC amplitude (P = 0.003), whereas release probability (p_rs) and quantal size (q) did not (P = 1, P = 0.714, respectively; Fig. 2B). Thus, distance-dependence of synaptic strength could be explained by a decline in the number of morphological contacts and functional release sites.

Fig. 2.

Quantal release characteristics at PII–GC synapses. (A) Representative peak amplitude distribution of a PII–GC pair recorded in 2 (gray) and 0.5 mM (cyan) extracellular Ca²⁺. (Left) Curves represent MP-CBA functions. (Right) Representative uIPSCs including failures. (B) MP-CBA–based estimates of p_rs, q (Left), and N_rs (Right) for six pairs with different uIPSC peak amplitudes. Note that q tends to increase with uIPSC peak amplitude. (C) First-latency distribution (black) corrected according to Barrett and Stevens (BS) (26) (gray). Curve represents γ-function fit (8) to BS-corrected data. (Inset) Amplitude-normalized and superimposed uIPSC (black), quantal IPSC (gray), and reconvolved uIPSC (cyan). (D) t₅₀ of the BS- or Minneci et al. (MS) (27)-corrected first-latency distributions do not correlate with τ of uIPSCs.

Composition of GABA_A Receptor Subunits at PII–GC Connections Changes with Distance.

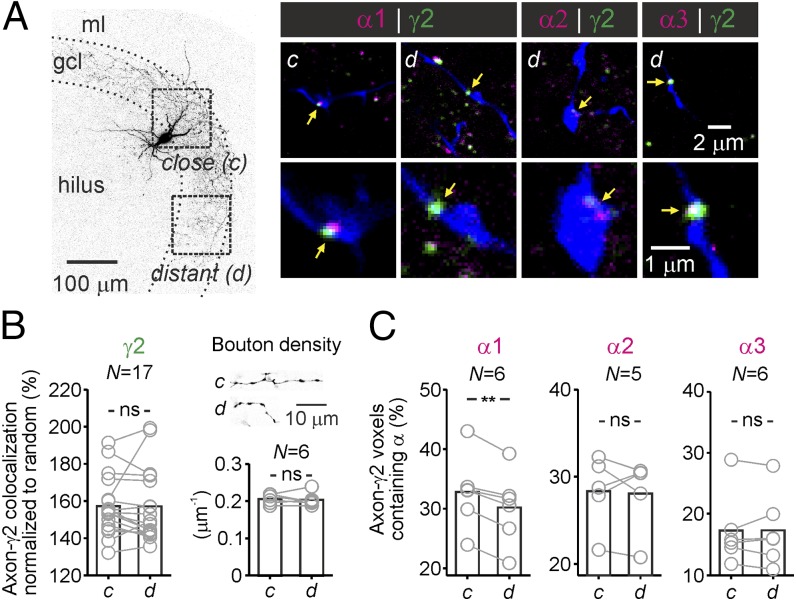
What might cause distance-dependence in the kinetics of PII-mediated uIPSCs? The uIPSC time course is critically determined by the transmitter release time course (RTC). We therefore quantified RTC using a first-latency approach (8, 26, 27). The full width at half-maximum (t₅₀) of the first-latency distribution did not correlate with τ (Fig. 2D; P = 0.3), indicating a uniform RTC. To further confirm spatial uniformity of transmitter release, we loaded PIIs with the Ca²⁺ indicator OGB-1 and recorded by two-photon microscopy at different positions along the PII axon spike-induced fluorescence transients in individual putative synaptic boutons (Fig. S5). Although not reflecting the true Ca²⁺ concentration in an unperturbed presynaptic terminal, OGB-1 signals may provide information about possible distance-dependence of presynaptic Ca²⁺ transients, which strongly influence the probability and time course of transmitter release (28) and consequently the amplitude and time course of the postsynaptic response (29). Neither the amplitude nor the decay time constant of OGB-1 fluorescence changes in presynaptic terminals varied with the distance from the PII soma, suggesting homogeneity of presynaptic release mechanisms (Fig. S5). Furthermore, electrotonic filtering of inhibitory signals did not contribute to distance-dependent uIPSC slowdown (30). PIIs formed putative synapses at equal electrotonic distances between synapse location and GC soma (Fig. S1 A–D). Alternatively, variations in the subunit composition of postsynaptic GABA_A receptors (GABA_ARs) could cause deceleration of uIPSCs. Deactivation kinetics of GABA_ARs are determined by α-subunits (31, 32). At postsynaptic sites, GCs predominantly express α1, α2, and α3, which confer fast, intermediate, and slow deactivation, respectively (31–33). We therefore probed α-immunoreactivity in γ2-subunit–immunopositive puncta, a marker for GABAergic synapses, in close vicinity of intracellularly labeled PII axons (Fig. 3). The density of γ2-positive puncta as well as morphological boutons was similar at close and distant axonal collaterals (P = 0.983 and P = 0.785, respectively; Fig. 3 A and B). However, we observed that over distance, α1 expression decayed (P = 0.001), whereas α2 and α3 labeling remained constant (P = 0.81 and P = 0.951, respectively; Fig. 3C and Fig. S6). Thus, a distance-dependent decline of α1-containing PII–GC synapses may underlie the observed changes in the decaying phase of uIPSCs, thereby resulting in a prolongation of PII-mediated synaptic inhibition. To further support this hypothesis, we recorded IPSCs in GCs evoked subsequently by two extracellular stimulation pipettes located in the GC layer with one positioned close to and the other distant from the recording site (Fig. 4). We assessed the sensitivity of IPSCs to 0.1–1 µM zolpidem, an α1-subunit–selective GABA_AR agonist (34). Zolpidem significantly prolonged IPSCs evoked at short but not long distances from the recorded GC, indicating reduced α1 content at long-distance synaptic contact sites (Fig. 4B).

Fig. 3.

PII output synapses show a close-to-distant gradient in α1-subunit expression. (A, Left) PII maximum-intensity projection with close and distant analysis regions (c/d). (Right) Confocal images of PII axons (blue) and immunostainings against GABA_AR subunits α1–3 and γ2 are magnified below. Arrows highlight putative synapses. (B, Left) Random-normalized percentage of γ2-colocalization with close and distant PII axons. (Right) Density of morphologically identified boutons. (C) α1- but neither α2- nor α3-content of γ2⁺-contacts declines with distance. Circles connected by lines represent average data from one PII. **P = 0.001.

Fig. 4.

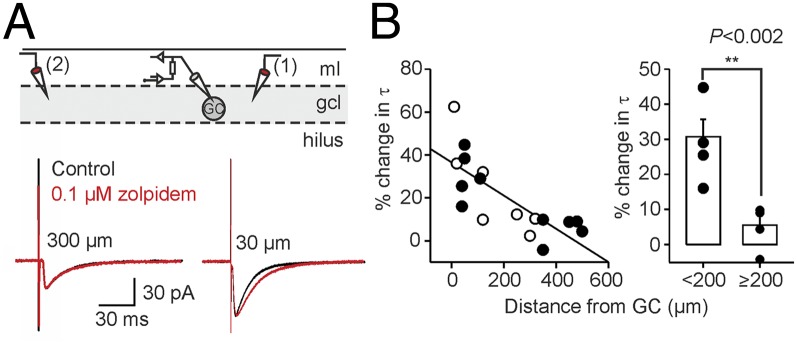
Effect of zolpidem on closely and distantly evoked somatic IPSCs. (A, Top) Schematic illustration of the experimental design. IPSCs were recorded in GCs during extracellular stimulation in the GC layer (gcl) in an alternating fashion (0.2 Hz) by a close (1) and a distant (2) electrode. (Bottom) Average IPSCs (50 traces) evoked at 30-µm (Right) and 300-µm (Left) distances from the recorded GC soma in control conditions (black) and after application of 0.1 μM zolpidem (red) are shown superimposed. (B, Left) Percent changes in the decay time constant (τ) of evoked IPSCs are plotted against distance. Filled circles represent dual stimulation experiments (five cells), and open circles show data from single-site stimulations (seven cells). (Right) Summary of zolpidem effects on IPSCs evoked at distances above or below 200 µm shows modulatory effects specifically at close synaptic inputs; ml, molecular layer.

Distance-Dependent Inhibition Improves Entrainment of Principal Cell Populations.

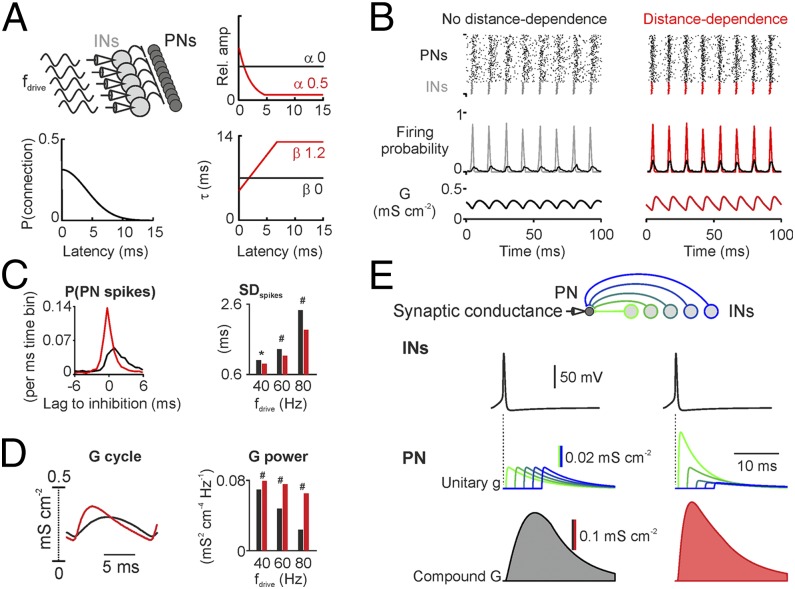
Does distance-dependent PII-mediated inhibition influence GC population activity? To address this question, we developed a computational network model containing rhythmically active fast-spiking INs connected to GCs with either uniform (nodd model) or distance-dependent (dd model) inhibitory synapses (Fig. 5). Amplitudes and decay time constants in the nodd model were set to the mean values of all paired recordings (Fig. 1D) over all connection distances. Synaptic properties in the dd model changed with the connection distance, reproducing the experimentally defined distance-dependence. The total inhibitory conductance per GC in both models was equal to ensure that any difference between both network models was an effect of the distance-dependent distribution of the synaptic properties and not of changes in the excitation-to-inhibition balance (Fig. 5A; SI Materials and Methods). To examine the impact of PII-mediated distance-dependent inhibition on principal cell pacing, we randomly excited GCs by Poisson trains of excitatory synaptic inputs and synchronously discharged the IN population at gamma frequencies (40–80 Hz; Fig. 5 A and B). This generated an oscillatory inhibitory output onto the GC population (total inhibitory conductance G; Fig. 5B). Synchronized activity of PIIs and GCs was evident from the raster plots (Fig. 5B) and the corresponding spike-probability distributions (Fig. 5 B and C). Spike-time precision in GCs was much higher in the dd than the nodd model, as indicated by the sharper spike-probability distribution over a broad range of gamma frequencies (40–80 Hz; Fig. 5C, Right). This effect was caused by a more phasic compound inhibitory conductance (G) with higher peak amplitude and shorter half-duration in the dd model (Fig. 5D). These findings were robust against variations of the model parameters such as the unitary inhibitory conductance (g) or the excitatory drive to principal cells, supporting the validity of our conclusions over a large range of network parameters (Fig. S7).

Fig. 5.

Distance-dependent inhibition improves spike timing in principal neuron (PN)–interneuron (IN) networks. (A, Top Left) The 400 PNs receive random and 100 INs oscillatory excitation at gamma frequency (f_drive). (Bottom Left) Connection probability (P) distribution. (Right) Uniform (black) vs. distance-dependent (red) distribution of uIPSC amplitude and τ. (B) Raster plots (Top) and mean probability (Middle) of PN (black) and IN firing; average inhibitory conductance (G) in PNs (Bottom). (C, Left) PN spike histograms relative to maximal IN activity (f_drive = 80 Hz). (Right) SD of PN spike times during gamma-frequency oscillations. (D) Shape (Left; f_drive = 80 Hz) and power (Right) of average G received by PNs. (E) G is the sum of converging unitary inhibitory conductances (g) generated by close (green) and distant (blue) INs (Top) during synchronous presynaptic activity (Middle). Convergence of distance-dependent inputs results in a stronger, sharper G.

Finally, we dissected the two distance-dependent synaptic parameters and included them separately into the network models. This approach revealed that distance-dependent amplitudes but not τ improved the precision in spike timing of the GC population (Fig. S8). This finding fits to our hypothesis that a reduced impact of long-distance inhibitory inputs limits the duration of the compound inhibition received by GCs in the oscillating network and thereby supports their entrainment particularly at higher gamma frequencies. To test this hypothesis, we clipped the axonal projection of PIIs in the nodd model at different connection distances and analyzed GC entrainment (nodd_clipped models; Fig. S9). As expected, shortening the axonal length in the nodd_clipped model boosted the entrainment of GCs particularly at upper gamma frequencies (80 Hz; Fig. S9C). This was paralleled by the emergence of compound inhibitory signals in target cells with a shorter half-duration in the nodd_clipped model (Fig. S9C). Such a short-duration inhibition is an ideal synchronizing signal in networks oscillating at fast gamma but is too short to precisely pace GC firing at slow-gamma (40 Hz) frequency. This is reflected in higher spike time precision in fast compared with slow-gamma oscillations (Fig. S9). In contrast to a mere clipping of PII axons, distance-dependent distribution of uIPSC amplitudes seems to offer the optimal compromise between entrainment at high- and low-gamma frequencies.

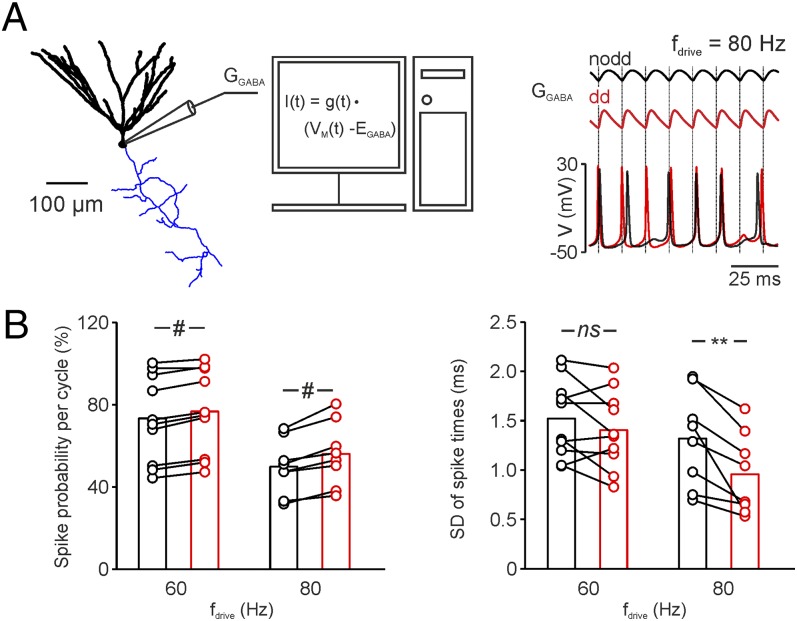
To test whether the proposed improvement in spike timing by distance-dependent inhibition also holds in real cells, we applied artificial compound inhibitory conductances to dentate gyrus GCs by a dynamic clamp (35) (Fig. 6). We generated distance-dependent and non–distance-dependent compound inhibitory conductances resembling the inhibition in the nodd or dd oscillating PII network model (Fig. 6A). Action potential time points in GCs were controlled by the repetitively injected inhibitory conductance. Distance-dependent inhibition significantly improved GC spike timing at upper gamma frequency (80 Hz; P = 0.002) and increased its discharge probability per oscillatory cycle (P < 0.001, at 60- to 80-Hz gamma frequencies; Fig. 6B). These effects were accompanied by an earlier time point of action potential generation relative to the onset of inhibition in the dd condition, as it is expected for a shorter duration of the compound inhibitory conductance (nodd vs. dd: 0.1 vs. −1.3 ms at 60 Hz; 1.8 vs. 0.6 ms at 80 Hz; P < 0.001 for both frequencies). Thus, distance-dependent inhibition provided by dynamic clamp improved spike timing in GCs and thereby closely reproduced the effect of the dd-network model.

Fig. 6.

Distance-dependent inhibitory conductances effectively entrain GC action potentials at upper gamma frequencies. (A, Left) Schematic illustration of the dynamic-clamp configuration applied to a GC (soma and dendrites in black; axon in blue). (Right) Action potentials were generated in a GC by depolarizing current injections. An artificial compound inhibitory conductance (G_GABA) was injected in the GC at different gamma frequencies (f_drive) to reproduce synchronous inhibitory signals of a nodd (black trace) or dd (red trace) PII network. The dynamic-clamp current was calculated in real time from the conductance (G_GABA), the voltage (V; lower traces), and the reversal potential of synaptic inhibition (E_GABA) and injected in the GC. Note that spike timing is tightly locked to G_GABA in the dd condition. (B) Bar graphs summarize the probability of action potential generation in GCs per oscillatory cycle (Left) and spike timing quantified as the SD of the action potential time points relative to the onset of inhibition for f_drive = 60 and 80 Hz. Dots connected by lines represent average values for individual GC recordings. **P < 0.01; ^#P < 0.001; ns, not significant.

In conclusion, the precise temporal and spatial structure of the inhibitory synaptic output in the network defined by distance-dependent cellular and molecular mechanisms sharpens the synchrony of GC activity. This may facilitate encoding of information in the dentate gyrus circuitry.

Discussion

Several studies have shown that functional synaptic properties depend markedly on the nature of the presynaptic and postsynaptic neurons (6, 36–38). However, here we identified a profound functional heterogeneity in the output from individual INs to multiple target cells of the same type. This variability is not randomly distributed over the postsynaptic population but follows a spatial rule (Fig. 5E). With increasing connection distance, the amplitudes of postsynaptic signals become smaller and their duration longer. The communication distance between two connected neurons is defined by the presynaptic axonal length until the synaptic contacts to the postsynaptic cell. However, due to action potential propagation times, distance between communication partners in neuronal networks has not only a spatial but also a temporal dimension. This temporal dimension is reflected by the synaptic latency, which influences the relative timing of converging neuronal signals on a millisecond timescale (37), a critical parameter of neuronal coding (39, 40), some forms of long-term plasticity (41), and the synchronization of neuronal networks (Fig. 5).

Our data suggest two distinct cellular mechanisms underlying the observed changes in amplitude and time course of uIPSCs at PII–GC synapses. First, the amplitude of uIPSCs at PII–GC synapses correlated with the number of mathematically defined transmitter release sites (Fig. 2). Second, a distance-dependent prolongation of inhibitory signals was paralleled by a reduction in the ratio of fast (α1) and slowly (α2, α3) deactivating GABA_AR subunits [Fig. 3 (32)]. How can both distance-dependent signaling mechanisms emerge in the dentate gyrus network? The density of PII axonal collaterals declines with tangential distance from the PII soma in the granule cell layer (18, 19). Here, we demonstrate that this drop in axon density with distance directly translates into a smaller connection probability (Fig. S1G) and a reduced number of release sites per PII–GC connection. Thus, a distance-dependent decline in inhibitory strength at PII–GC synapses can be explained by presynaptic axon morphology. In contrast, a distance-dependent change in the expression profile of soma-near postsynaptic GABA_AR subunits seems to require the interaction between the presynaptic and the postsynaptic cell. Indeed, Neurexins expressed in the axon (42) and their interacting partners, the Neuroligins, located at somatodendritic compartments (43), are important regulators in the functional maturation of GABAergic synapses. Among the different Neuroligin isoforms (43), Neuroligin 2 recruits postsynaptic GABA_AR α1-subunits, accelerating the decay of GABA_AR-mediated IPSCs (44). Thus, distance-dependent τ of PII-mediated uIPSCs could be mediated by a spatially differential expression of molecular regulators such as Neurexins/Neuroligins in the PII axon and the postsynaptic target cell, thereby defining the functional characteristics of inhibitory synapses. Our data show that the distance-dependent gradient of synaptic properties established during development persists into adulthood (Fig. S4). However, we cannot exclude that late development during aging or even experience-dependent plasticity will further modify the spatial scale or the slope of distance-dependent signaling in hippocampal circuits.

Our findings fit to functional mapping studies in the neocortex demonstrating a decline in connection probability for glutamatergic as well as GABAergic cells with intersomatic distance within and among cortical layers (21–25, 45, 46). However, our data contrast the canonical model established by these studies, that PIIs show a high local intracolumnar connectivity with uniform functional properties of their output synapses including strength, duration, and reliability of GABAergic transmission in the entire target cell population (21, 24, 45). However, most neocortical studies disregarded the functional synaptic properties in their analysis. Thus, functional mapping studies are needed to investigate whether similar distance-dependent signaling characteristics exist for principal cells and other IN types in different cortical circuits. Intriguingly, our CA1 data (Fig. S3) indicate that distance-dependent perisomatic inhibition of principal cells is a general phenomenon of hippocampal circuits (5). It will be of interest to characterize other IN types providing widespread inhibition, such as bistratified cells with a strong contribution to hippocampal network oscillations (47, 48).

How does distance-dependent inhibition boost the synchronization of neuronal networks at gamma frequencies? In a synchronously oscillating network, GCs receive a compound inhibitory signal, which is composed of all converging unitary inhibitory inputs (Fig. 5E). Although PIIs discharge coincidentally, the synaptic inputs arrive at GCs in a temporally staggered fashion at time points defined by the axonal distances between presynaptic and postsynaptic neurons. Thus, the shape of the compound inhibitory signal (G) is the consequence of uIPSC properties (amplitude and time course) and the distribution of synaptic latencies (Fig. 5E). Our computational analysis revealed that, during synchronous gamma oscillations, networks with distance-dependent inhibition generate compound inhibitory conductances with larger amplitudes and a more phasic shape than models including uniform inhibition (Fig. 5). Consequently, GCs were efficiently silenced for a shorter period and could recover from inhibition earlier before the next gamma cycle started (Figs. 5 and 6). This effect was strongest at high-gamma frequencies (80 Hz) where the time between recovery from inhibition and onset of the following cycle is particularly short. Thus, for optimal spike time precision, the temporal shape of the compound inhibitory conductance should correspond to the period of the ongoing oscillation. With uniform synaptic properties, PII networks are well equipped to pace GC networks at low-gamma frequencies of ≤40 Hz because the duration of their compound inhibitory output fits the period of slower gamma oscillations. To efficiently pace GCs at high-gamma frequencies of ≥80 Hz, PII networks with uniform synaptic properties should have shorter axon projections, which drastically impair low-gamma oscillations (Fig. S9). Thus, distance-dependent synaptic inhibition offers an ideal compromise as it allows tight control of principal cell spike timing at low- and high-gamma frequencies (Figs. 5 and 6).

In conclusion, the inhibitory synaptic output from PIIs in the dentate gyrus is distance-dependent. Inhibition is strong and fast at short distance, but becomes weaker and slower at longer distances between presynaptic and postsynaptic neurons. In a synchronously active network, convergence of distance-dependent inputs results in a stronger, sharper compound inhibitory conductance in GCs. Thus, distance-dependent inhibition improves spike timing in GCs and may thereby support information processing in the dentate gyrus.

Materials and Methods

Paired Recordings.

Transverse hippocampal slices (300-µm thickness) were cut from brains of 17- to 23-d-old (adolescent) or 30- to 45-d-old (adult) Wistar rats of either sex with a VT 1200 S (Leica Microsystems) vibratome. Animals were decapitated in accordance to European and national legislation (European Directive 2010/63/EU; German “Tierschutzgesetz”) and institutional guidelines (reviewed and approved by Regierungspräsidium Freiburg, Germany). To assess PII-mediated uIPSCs, paired whole-cell patch-clamp PII–GC recordings were established as previously described (6). To obtain information on perisomatic inhibition in CA1, we accessed our database and analyzed paired recordings published in ref. 6. For solutions, electrophysiological details, and the analysis of paired recording data, see SI Materials and Methods.

Morphological Analysis.

During recordings, cells were filled with biocytin (1 mg⋅mL⁻¹). After withdrawal of the pipettes, slices were fixed, and cells were visualized using either streptavidin conjugated to Alexa Fluor 488 or Alexa Fluor 647 (1:500; Invitrogen), or avidin–biotinylated horseradish peroxidase complex and 3,3′-diaminobenzidine as chromogen. To relate synaptic latency to axonal distances, PII axons from paired recordings were reconstructed using Fiji based on ImageJ 1.47g. Using linear fitting of the synaptic latency–axonal distance relation (Fig. 1C), we obtained an action potential propagation velocity of 0.29 m⋅s⁻¹. This velocity was similar to that determined from direct axon recordings in dentate gyrus PIIs at 22–25 °C in a recent study by Hu and Jonas (49), but markedly slower than the corresponding estimate at 30–33 °C. Several factors may account for this apparent difference. These include the following: (i) shrinkage of slice material upon fixation in the present paper, but not in ref. 49; (ii) bias toward thicker axons in direct axonal recordings (49), leading to faster propagation velocity (ref. 49, their figure S8); (iii) bias toward axons with smaller number of en passant boutons and branch points in direct axonal recordings (49), leading to faster propagation velocity (ref. 49, their figure S1); (iv) statistical errors due to a limited number of data points at 30–33 °C in ref. 49, because of the high degree of difficulty of the experiments; and (v) uncertainty about the exact value of the synaptic delay and a possible distance-dependence in this uncertainty. For further details, see SI Materials and Methods.

Statistics.

Experimental values are given as mean ± SEM. Statistical analysis was performed using either SigmaPlot 11 (Systat Software) or MATLAB 7 (The Mathworks). All further data analysis was done in MATLAB. For correlation analysis, Spearman’s rank correlation coefficient ρ was used. If not indicated otherwise, the difference in the mean of two samples of normally distributed data was tested by a two-tailed unpaired t test. To compare close and distant colocalizations (Fig. 3 B and C and Fig. S6), a paired t test was used. Normality of data was tested using Lilliefors test.

Network Simulations.

Networks of 100 INs and 400 principal neurons (PNs) arranged on a ring were modeled in the NEURON 7.2 environment. Neurons were represented as single compartments with Hodgkin-Huxley–type conductances endowing INs with a fast-spiking and PNs with a regular-spiking phenotype. INs randomly formed conductance-based synapses with on average 80 PNs. Connection probabilities dropped with distance in a Gaussian profile. For further details regarding the network model, the implementation of distance-dependent inhibition, and the evaluation of network activity, please see SI Materials and Methods.