The contribution of de novo coding mutations to autism spectrum disorder

Abstract

We sequenced exomes from more than 2,500 simplex families each having a child with an autistic spectrum disorder (ASD). By comparing affected to unaffected siblings, we estimate that 13% of de novo (DN) missense mutations and 42% of DN likely gene-disrupting (LGD) mutations contribute to 12% and 9% of diagnoses, respectively. Including copy number variants, coding DN mutations contribute to about 30% of all simplex and 45% of female diagnoses. Virtually all LGD mutations occur opposite wild-type alleles. LGD targets in affected females significantly overlap the targets in males of lower IQ, but neither overlaps significantly with targets in males of higher IQ. We estimate that LGD mutation in about 400 genes can contribute to the joint class of affected females and males of lower IQ, with an overlapping and similar number of genes vulnerable to causative missense mutation. LGD targets in the joint class overlap with published targets for intellectual disability and schizophrenia, and are enriched for chromatin modifiers, FMRP-associated genes and embryonically expressed genes. Virtually all significance for the latter comes from affected females.

Introduction

ASD is characterized by impaired social interaction and communication, repetitive behavior and restricted interests. It has a strong male bias, especially in high-functioning affecteds. The contribution from transmission has long been suspected from increased sibling risk¹, but more recently the role of germline de novo (DN) mutation has been established, first from large scale copy number variation (CNV) in simplex families^2–5, and subsequently from exome sequencing. The smaller DN variants observed by DNA sequencing pinpoint candidate gene targets^6–8. These developments have promoted a new model for causation, and re-evaluation of sibling risk^9,10.

We report here whole exome sequencing of the Simons Simplex Collection (SSC)¹¹ and an extensive list of DN mutated targets, including 27 recurrent LGD (nonsense, frameshift and splice site) targets. The size and uniformity of this study allow an unprecedented evaluation of genetic vulnerability to ASD. We subdivide target sets by mutation type (missense and LGD) and affected child status (gender and nonverbal IQ, to which we refer throughout as simply “IQ”), and explore the overlap between target sets and their enrichment for certain gene categories. We make estimates of the number of genes vulnerable to a given mutation type and the proportion of simplex autism resulting from DN mutation for each affected subpopulation.

Results

SSC sequencing and validation

We report on 2,517 of ~2,800 SSC families including ~800 previously published^6–8. We sequenced 2,508 affected children, 1,911 unaffected siblings and the parents of each family. Within the SSC, the overall gender bias in affecteds, 7 males to 1 female, is nearly twice that typically reported. Exomes were analyzed at Cold Spring Harbor Laboratory (CSHL), Yale School of Medicine, and University of Washington (Extended Data Figs. 1 and 2, Supplementary Table 1). Pipelines were blind with respect to affected status. For uniformity, all data were reanalyzed with the CSHL pipeline, allowing comparison of analysis tools. All calls were validated or strongly supported, as listed (Supplementary Table 2) and described (Methods).

DN mutation rates, contribution and targets of de novo mutation

For greatest precision we measured DN rates in quad familes (one affected and one unaffected child) over genomic positions at which all family members had ≥40× sequence coverage (Methods, Supplementary Table 3). This ‘joint 40× region’ in the SSC was 32 Gbp in total, or 48% of the targeted exome, from 1,867 quads. DN events were shared by siblings 1% of the time (Supplementary Table 2); and 1% of mutations had nearby nucleotide positions altered, presumably by single mutagenic events (Supplementary Table 4)^12–14. The overall rate of base substitution is 1.8*10⁻⁸ (±10⁻⁹) per base pair (Supplementary Table 5).

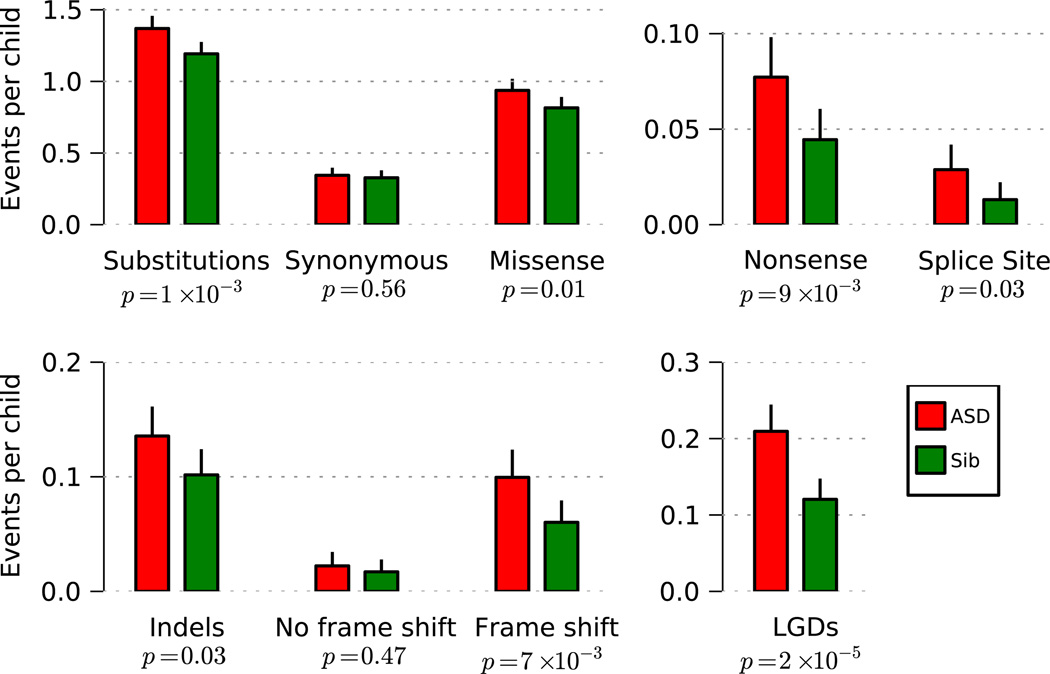
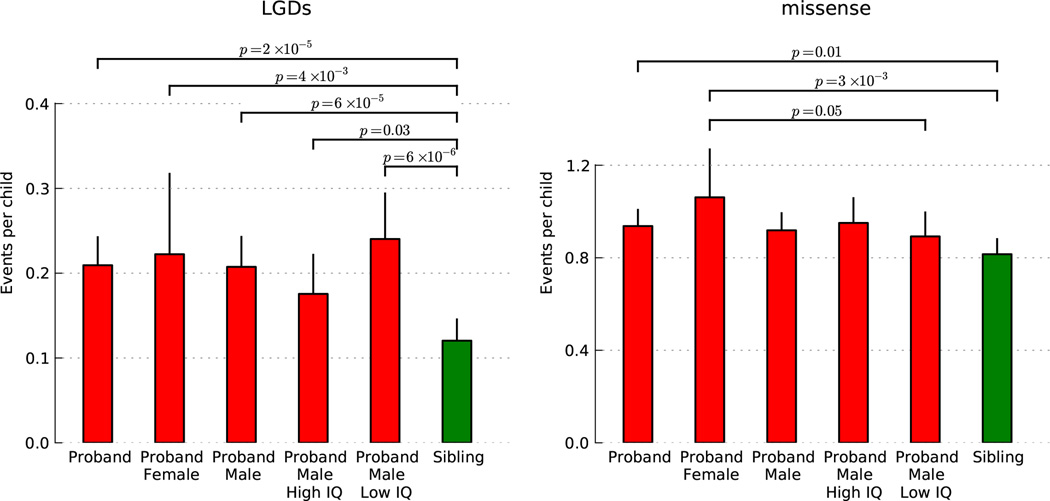
Rates of DN synonymous mutation in affected (0.34 per child) and unaffected siblings (0.33 per child) do not differ significantly (Fig. 1). By contrast, LGD mutations occur at significantly higher rates in affected vs. unaffected siblings (Fig. 1, Extended Data Fig. 3). The rate of LGDs is 0.12 in unaffected siblings and 0.21 in affected probands, an ‘ascertainment differential’ of 0.21–0.12 = 0.09 (p-value 2*10⁻⁵). Thus, we estimate ~42% (0.09/0.21) of LGD events in probands contribute to ASD diagnoses. For DN missense, the rate is 0.82 for unaffected siblings and 0.94 for affected probands, an ascertainment differential of 0.12 (p-value 0.01). We estimate only ~13% (0.12/0.94) of DN missense events in probands contribute to ASD diagnoses. There is a wide confidence interval for the missense ascertainment differential (Supplementary Table 6); for this reason, we consider primarily the LGD events for our analysis and look upon missense data as supporting.

Fig. 1. Rates of de novo events by mutational type in the SSC.

Rates per child are estimated from the 40× joint coverage target region, then extrapolated for the entire exome. Mutation types are displayed by class, and the combined rate for all LGDs is shown at the bottom right. For each event type, the significance between probands and unaffected is given.

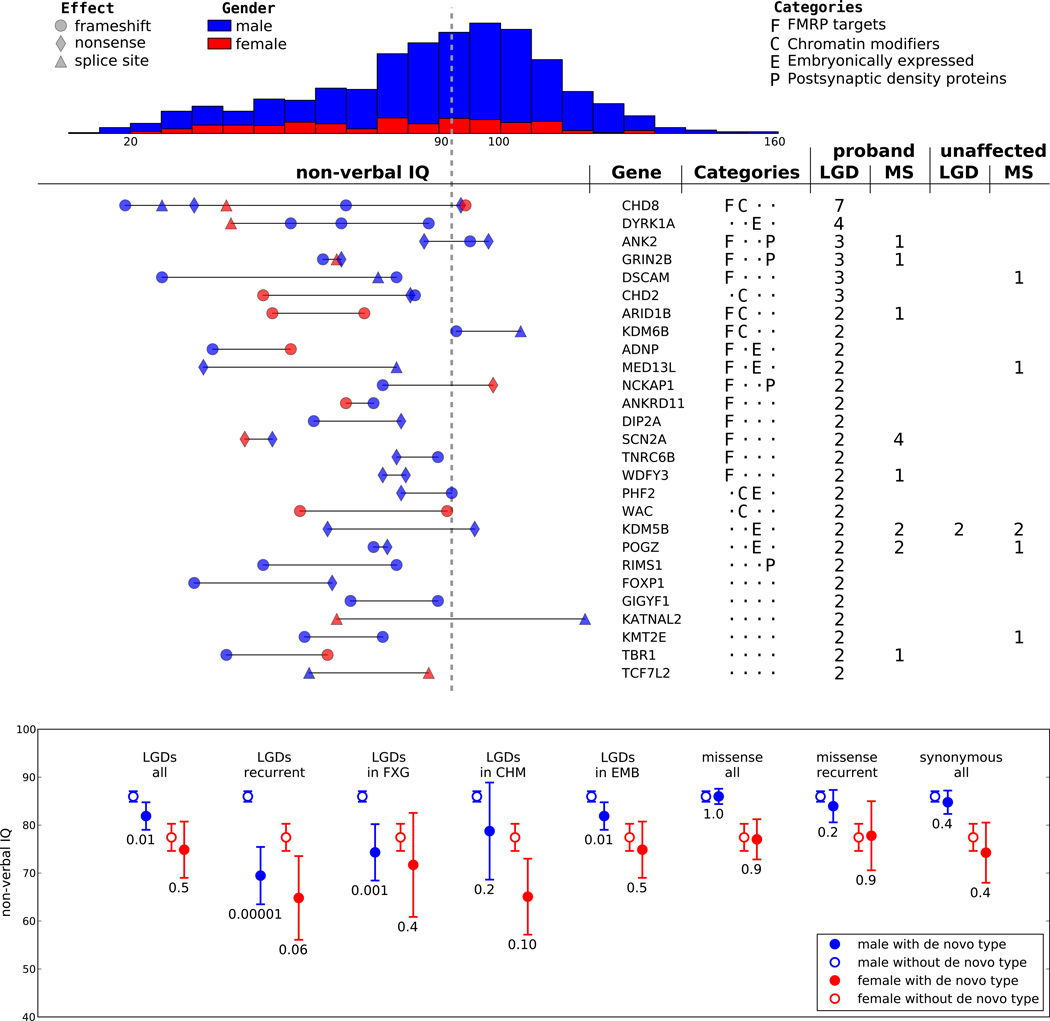
To identify gene targets for DN mutation, we examined all family data including trios. We provide a complete list of all mutations (Supplementary Table 2) along with the number of mutations of each type in each gene (Supplementary Table 7). 391 DN LGD mutations in 353 target genes were identified and validated in autism probands. 27 target genes were recurrent (Fig. 2). Among 1,500 missense targets in probands, 145 were recurrent.

Fig. 2. Recurrently hit genes and non-verbal intelligence quotient (IQ).

Affected females account for 13.5% of the SSC with mean IQ of 78, whereas affected males have mean IQ of 86 (upper panel, p-value 10⁻⁷ by Student's t-test). The vertical dashed line indicates an IQ of 90. The middle panel (left) shows IQ for affected children with LGD mutations in genes hit recurrently (right). Recurrently mutated genes are clustered into four categories as shown. The last four columns give overall numbers of DN LGD and missense (MS) mutations. In the bottom panel, we consider eight classes of DN mutations: all LGDs, recurrent LGDs, LGDs in FMRP targets (FXG), LGDs in chromatin modifiers (CHM), LGDs in embryonically expressed genes (EMB), all missense mutations, recurrent missense mutations and synonymous mutations. Probands are divided by the presence of DN mutations and gender. Means, 95% confidence intervals and p values (Student's t-test) are shown.

We examined all alleles transmitted opposite a DN LGD target. We saw no instance in 391 observations in which the allele opposite an LGD target carried a rare transmitted LGD variant (in <1% of parental exomes), and only four in which such an allele carried a rare missense variant. Thus, the DN mutations do not generally cause homozygous loss-of-function of their target (Supplementary Table 8).

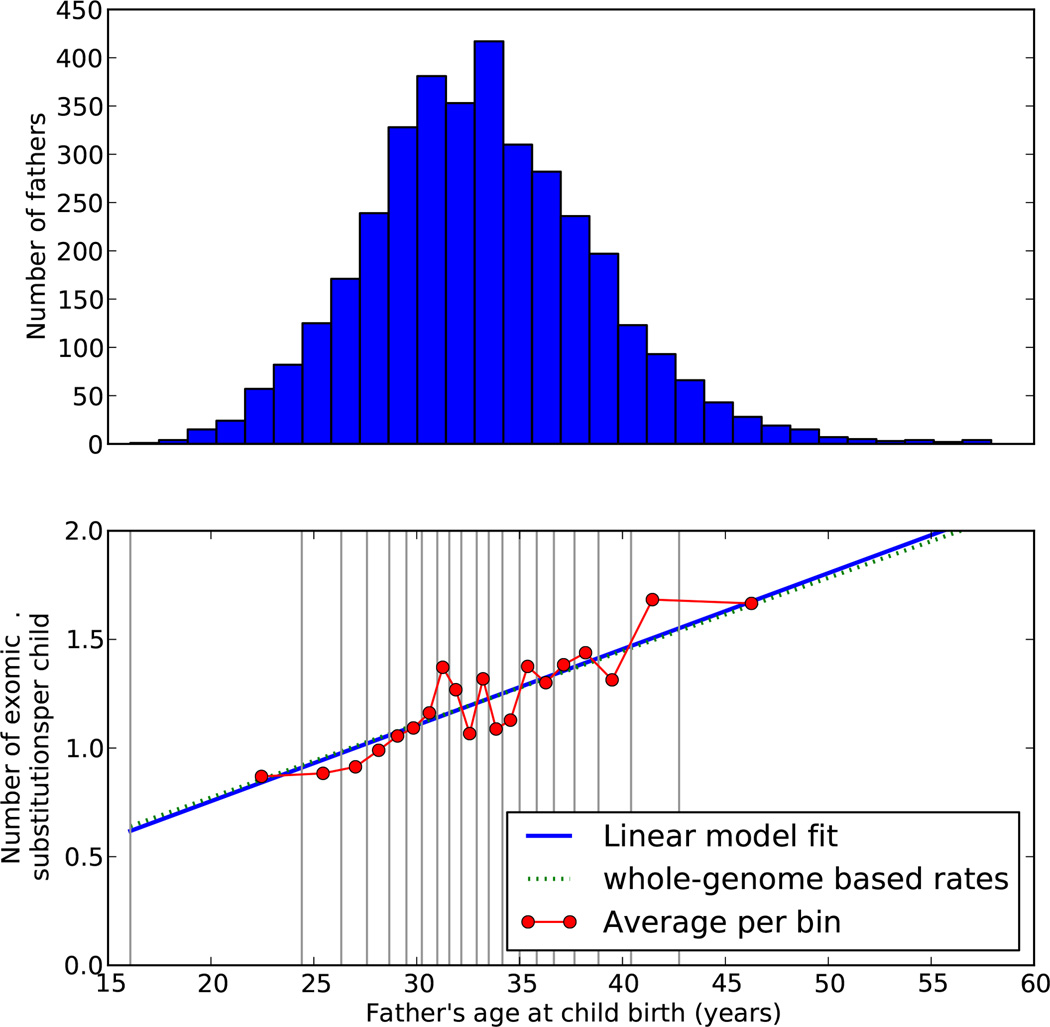
Confirming previous results^7,8,15, a DN mutation occurs three times as often on the paternal background as the maternal, and mutation rates rise with age of either parent (Extended Data Fig. 4, Methods). The latter may provide a partial explanation for increased autism rates in children born of older parents.

Functional clustering in target genes

Previous studies presented evidence of functional clustering in targets of DN LGD mutation in affected individuals^6–8,16. Our larger dataset was examined with an improved null ‘length model’ for mutation in which the probability of DN mutation in a gene is proportional to its length (Methods, Extended Data Fig. 5). We tested for enrichment within DN LGD and missense targets in probands and siblings for six gene classes, those: 1) that are FMRP targets, with transcripts bound by the fragile X mental retardation protein^8,17; 2) encoding chromatin modifiers; 3) expressed preferentially in embryos^18,19; 4) that encode postsynaptic density proteins²⁰; 5) that are essential²¹; and 6) identified as Mendelian disease genes²² (Table 1, Supplementary Table 6, Methods). These data provide the strongest evidence yet for overlap of DN LGD targets in affected probands with FMRP targets (55 observed vs. 34.1 expected; p-value 4*10⁻⁴) and chromatin modifiers (26 observed vs. 11.8 expected; p-value 3*10⁻⁴). We also observed signal from mutation in genes expressed in embryonic development²³ (65 observed vs. 45.0 expected; p-value 2*10⁻³). The latter signal comes mainly from the small number of female affecteds (23 observed vs. 8.5 expected from 67 LGD targets; p-value 5*10⁻⁶). The 27 genes with recurrent LGDs show strong enrichment for FMRP targets (14 observed vs. 2.6 expected; p-value 4*10⁻⁸) and chromatin modifiers (6 observed vs. 0.9 expected; p-value 2*10⁻⁴). In contrast, no significant enrichment for these gene sets is seen for the DN LGD targets in unaffected siblings.

Table 1. Enrichment of de novo mutations in six gene classes.

We tested eight classes (Methods) for enrichment against five lists of targets of DN mutations. These ncludegenes with 1) recurrent DN LGD mutations in probands (rec. DN LGDs in ASD), 2) DN LGD mutations in probands (DN LGDs in ASD), 3) DN missense mutations in probands (DN missense in ASD), 4) DN LGDs in siblings, and 5) DN missense mutations in siblings. Observed (Obs) and expected (Exp) numbers are shown with p values (pVal) obtained from two-sided binomial tests. Expected numbers and p values are based on a length model in which DN mutations occur randomly in all genes, proportional to length.

Gene class	No. of genes	rDN LGDs (aut)			DN LGD (aut)			DN miss (aut)			DN LGD (sib)			DN miss (sib)
		overlap (27)			overlap (353)			overlap (1,513)			overlap (176)			overlap (1,066)
		Obs	Exp	pVal	Obs	Exp	pVal	Obs	Exp	pVal	Obs	Exp	pVal	Obs	Exp	pVal
FMRP	842	14	2.6	4×10−8	55	34.1	4×10−4	171	144.8	0.03	14	17.0	0.52	117	102.9	0.15
Chromatin	428	6	0.9	2×10−4	26	11.8	3×10−4	57	50.0	0.31	5	5.9	1.00	37	35.6	0.80
Embryonic	1,912	6	3.4	0.15	65	45.0	2×10−3	220	191.4	0.03	20	22.5	0.65	142	136.0	0.58
PSD	1,445	4	2.5	0.31	34	32.5	0.78	159	138.1	0.07	22	16.2	0.15	113	98.1	0.12
Essential	1,750	7	3.2	0.04	50	42.4	0.22	201	180.3	0.10	20	21.2	0.91	127	128.1	0.96
Mendelian	256	0	0.6	1.00	3	8.0	0.07	31	34.0	0.66	5	4.0	0.61	20	24.1	0.47
dn LGD (Scz)	93	2	0.3	0.03	9	3.7	0.01	16	15.7	0.90	2	1.8	0.71	8	11.2	0.45
dn LGD (ID)	30	3	0.1	1×10−4	8	1.2	3×10−5	10	4.9	0.04	0	0.6	1.00	5	3.5	0.41

The 1,500 DN missense targets in probands are also enriched for FMRP targets and embryonically expressed genes. We observe 171 FMRP targets (144.8 expected; p-value 0.03), and 220 embryonically expressed genes (191.4 expected; p-value 0.03). As before, the signal for embryonically expressed genes comes almost entirely from the small number of female affecteds (48 observed, 31.1 expected from 244 targets; p-value 0.002). With the exception of chromatin modifiers, contributory DN missense and LGD mutations tend to strike similar functional classes of genes.

De novo mutation and IQ

Higher IQ probands are heavily skewed towards males²⁴. For further analyses, we chose to divide the affected male population roughly in half into higher and lower IQ sets. We investigated whether higher IQ (>90) males comprise a population with a distinguishable genetic signature. There is a decreased ascertainment differential for DN LGD mutations in male children with higher IQ relative to other affecteds (Extended Data Fig. 3, Supplementary Table 6). This is not statistically significant over the joint 40× region. However, over the entire data set, the drop in IQ is 5 points for males with DN LGD mutation compared to those without mutation (p-value 0.01; Fig. 2). Mean IQ of affected males with recurrent DN LGDs drops 20 points (p-value 0.00001, Fig. 2). Significance is also evident as we examine targets by functional class. Males with LGD mutations in FMRP targets have an average 14-point drop (p-value 0.001). This trend continues with LGD targets in the other functional classes—chromatin modifiers and embryonically expressed genes—but with reduced significance. We observe little signal from DN missense mutation, even in recurrent targets, either because these events are less likely to contribute or they are less severe. Female probands show the same trends as males, but as they comprise a smaller population, the significance is weak (Fig. 2).

Further evidence for a distinguishable signature among the higher IQ comes from the functional enrichment within DN target gene sets. LGD targets in females are enriched for all three functional gene classes. LGD targets in lower IQ affected males are significantly enriched for the FMRP-associated and chromatin modifier gene classes (Supplementary Table 6). However, for LGD targets in higher IQ males we see no statistically significant enrichment for any of the gene categories.

Overlaps between targets in groups of children and types of mutation

We partitioned children into four primary groups, unaffected siblings, affected females, affected males with higher IQ, and affected males with lower IQ. We analyzed these and various combinations for three types of DN mutations: LGDs, missense and synonymous (Supplementary Table 6). Targets of synonymous mutations in all children and targets of LGD and missense mutations in unaffected siblings have no significant overlap with targets from any other group. We see no significant overlap between targets in higher IQ males with targets from other groups. In strong contrast, the 67 LGD targets from affected females overlap significantly with the 166 LGD targets from lower IQ affected males (10 observed, 1.3 expected, p-value 7*10⁻⁷). We therefore refer to the group of lower IQ males and affected females as a ‘joint’ class. In this class, the 874 missense and 223 LGD targets also overlap significantly (39 observed, 22.1 expected, p-value 0.0008). Thus, not only do missense and LGD mutation target genes with shared functionality, the same genes are sometimes targeted.

Number of vulnerable genes

Our analysis of functional clustering and overlaps within target classes suggests that the mutations ascertained in probands target restricted sets of vulnerable genes. We next sought evidence for excess recurrence of targets. We first examined synonymous mutations and mutations in unaffected children. Among the 647 synonymous events in probands, there are 25 gene targets found in more than one child, close to the null expectation of 19.9 (p-value 0.13). Recurrent LGD (n=3/179 events) or missense targets (70/1,143 events) in unaffected siblings are also close to null expectations (p-value 0.2 and p-value 0.04, respectively). In affected males with higher IQ there are no excess recurrent targets among 137 LGDs mutations (2 observed, 1.0 expected, p-value 0.3) or among 728 missense mutations (26 observed, 24.7 expected, p-value 0.4). In contrast, among probands the number of recurrent LGD (n=27/391 events) and missense targets (145/1,675 events) are not compatible with the null expectation of 7.6 (p<0.0001) and 115.0 (p-value 0.001), respectively. Given these findings, as well as the lack of overlap between targets of higher and lower IQ males, we focused on the joint class of female probands and affected males of lower IQ. For the joint class, there were 22 recurrent LGD targets among 254 events with 3.3 expected (p-value <0.0001). For the 944 missense events, 60 recurrent targets are observed with 40.2 expected (p-value 0.0005).

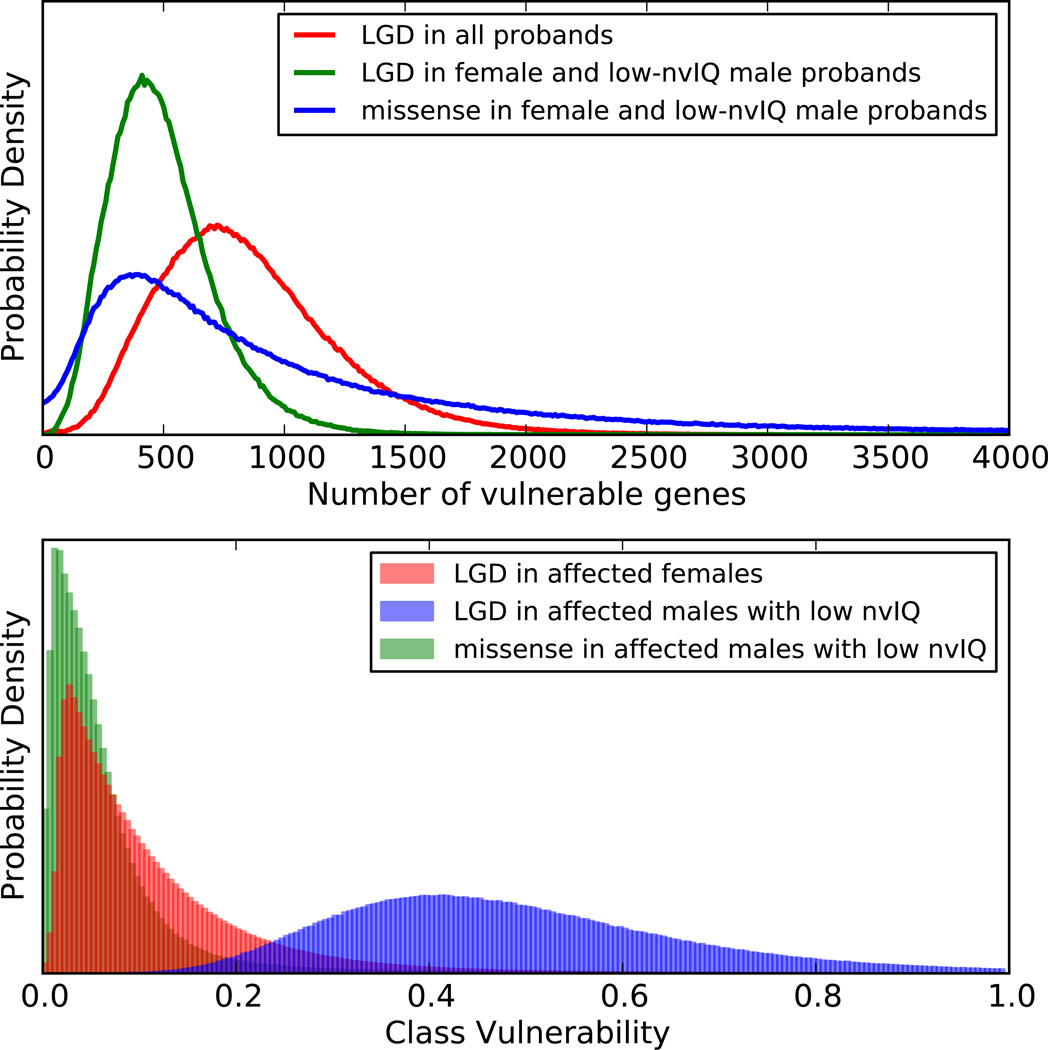
We next used recurrence analysis and the length model to estimate the number of vulnerable genes (Fig. 3) and the probability that a recurrent mutation of a given type is contributory (Methods). The most likely number of genes vulnerable to DN mutations in the joint class is estimated to be 387 for LGD targets with a 95% credibility interval (CI) of (149, 915), and 404 for DN missense targets (CI: (71, 3050)). From the length model and our estimate that only 42% of LGD mutations are contributory, we have 90% confidence that a given LGD mutation contributes to autism in a gene recurrently hit by an LGD mutation (Methods). By the same methods, we compute 35% confidence in contribution from missense mutations in recurrent targets. Using existing models for prioritizing targets⁷, we list all targets of recurrent DN coding mutation according to their rank (Supplementary Table 9).

Fig. 3. Number of vulnerable genes and class vulnerability.

We assume the property of being vulnerable gene is independent of gene length, but the probability of being hit by mutation is proportional to gene length. We use the observed rates of mutation of a given type in specified populations and number of recurrent mutations to estimate the number of genes vulnerable to those mutations (top). The degrees of vulnerability in those classes are the distributions shown in the lower panel (Methods).

Discussion

The SSC was assembled with the explicit hypothesis that finding targets of DN mutation would be a path to gene discovery. We now have 353 candidate LGD gene targets, 27 genes recurrently hit by LGD events, and 145 recurrent missense targets, each with about 40%, 90% and 35% chance of being contributory, respectively.

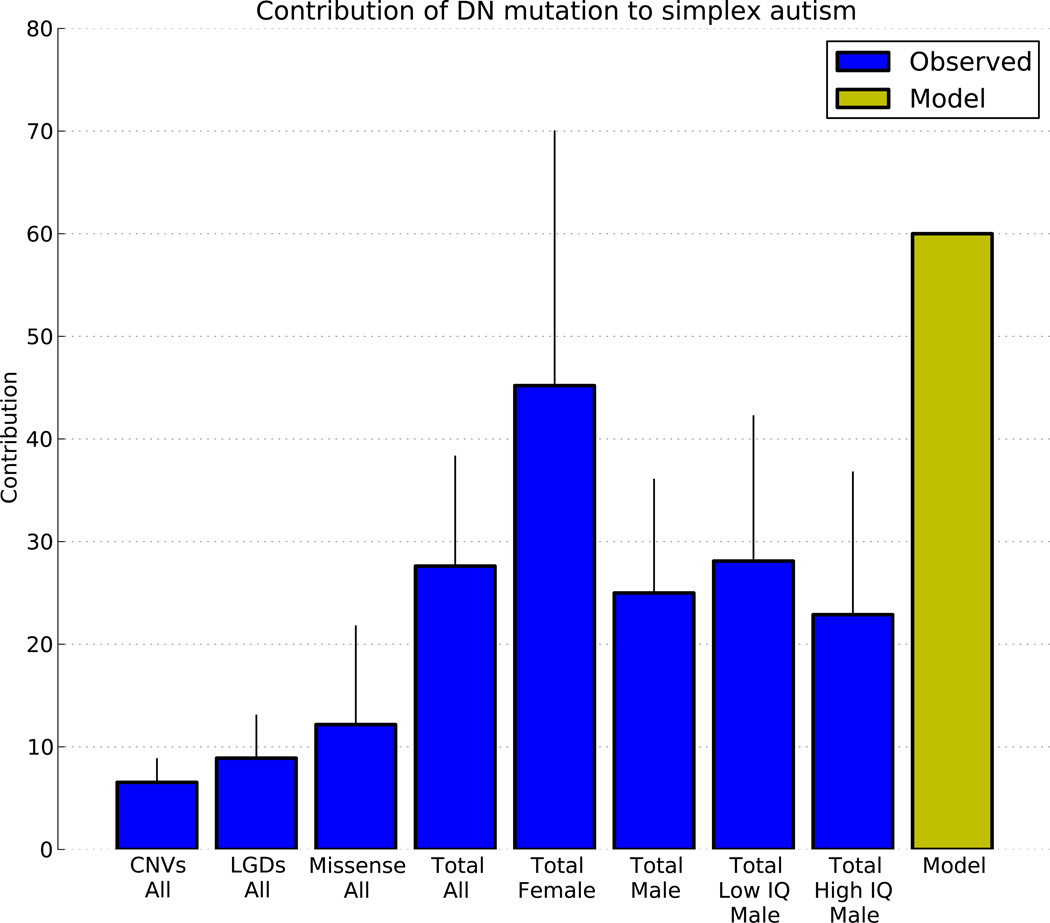
We use the ascertainment differential as an estimate of contribution. The sum of the ascertainment differentials for missense, nonsense, consensus splice site disruption and frameshift DN mutations is 0.21 per affected child. Adding 0.06, the ascertainment differential from large DN CNVs^2,3, brings the total to 0.27 (Fig. 4). Excluding higher IQ males, the value is 0.33. In affected females it is 0.45. This is a conservative estimate for the role of DN mutation in the SSC families because we have not yet ascertained intermediate-size DN CNVs, copy-neutral rearrangements, regulatory mutations or mutations of noncoding genes.

Fig. 4. Estimated contributions of CNVs, LGDs and missense DN mutations to simplex ASD.

Ascertainment differentials for three types of DN mutation (CNVs, LGDs and Missense) are interpreted as a measure of ‘Contribution,’ the percent of probands in whom the mutation contributed to diagnosis. We combine the three mutation types in ‘Total’ on the assumption of additivity. We present this measure for ‘All’ probands and selected subpopulations as indicated. We also show the expected contribution of all DN mutation in a simplex collection computed from a simple genetic model⁹ (‘Model’). Error bars represent 95% credibility intervals.

Although the SSC is a simplex collection, it is likely only marginally depleted for high-risk families because small brood size prevents the birth of multiple affected children, especially if the unaffected sibling is female. We estimate¹⁰ and confirm⁹ by gender bias in unaffected siblings (1400 females and 1264 males, p-value 0.0089) that ~40% of the SSC families are high-risk. In a simple genetic model, DN mutation plays no role in high-risk families but is obligatory for low risk families¹⁰, so DN mutation would contribute to ~60% of the SSC. The sum of the ascertainment differential for all observable DN types in all the probands is about 30%, about half of that. If the number of unobserved and consequential DN mutations is similar to the number of observed and consequential DN exome mutations, the actual contribution is not far from that predicted by this simple model.

Targets and cognitive defects

We examined the incidence and targets of DN LGD mutations for children with lower and higher IQs. Affected children with higher IQs have a greater incidence of LGD mutations than unaffected siblings, but a lower incidence than affected females or males with lower IQ. Moreover, there are few recurrently hit genes among the DN LGD targets of affected males with higher IQ, and little overlap with the DN LGD targets of affected males with lower IQ or females. LGD targets in higher IQ males are not enriched for the FMRP-associated genes. These observations suggest a different distribution of genetic mechanisms causing ASD in higher IQ males.

We can examine overlap between LGD targets for autism, with published targets for intellectual disability (ID) and schizophrenia (Scz)^25–29. We applied our length model for mutation incidence and found significant overlap of ID and Scz targets with ASD targets (Table 1), but only in the joint class of affected males with lower IQ and females (Supplementary Table 6). The overlap can have many explanations: diagnostic conflation; pleiotropy for the same mutation; different consequences for different mutations in the same gene; and varying genetic or environmental background. The DN targets of affected males with higher IQ do not overlap these sets, again suggesting distinct mechanisms.

Properties of target classes

This study is sufficiently large and uniform to enable inferences about targets, distinguished by mutation types, properties of affected children and target functions. We observe a significant contribution from missense mutations, with an overall magnitude comparable to that from LGD mutations. Both LGD and missense mutation targets are enriched in the same functional gene sets, especially among lower IQ males (Supplementary Table 6). Excluding higher IQ males, we estimate the most likely number of genes vulnerable to LGDs is ~400, with a similar number genes vulnerable to missense. The two sets overlap substantially.

Targets in autism are enriched in certain functional categories, providing deeper support for previously published observations^6–8. FMRP-associated genes and chromatin modifiers are prominent targets in all groups except higher IQ males. The former are thought to function in neuroplasticity. Embryonically expressed genes are significantly enriched as LGD or missense targets, but only in females. Enrichment in these genes may reflect that these contributory mutations cause alterations before a female protective effect takes place.

Recurrent LGD targets encode receptors, ion channels and synaptic proteins likely to function directly in neuro-circuitry (e.g. SCN2A, GRIN2B and RIMS1), but also proteins functioning in cytoskeletal remodeling (e.g. ANK2 and MED13L) and transcriptional regulation. Chromodomain helicase gene family members carry many recurrent LGDs. The most frequently hit gene is CHD8 (ref. 30), followed by CHD2 (3 LGDs) and four other members (1 LGD each) of that family. CHD8 is a transcriptional regulator thought to be important for suppression of the Wnt-beta-catenin signaling pathway through histone H1 recruitment³¹. Another intriguing target is the protein kinase DYRK1A, hit four times and located in the Down syndrome critical region⁷.

Gene vulnerability and molecular mechanisms

We cannot determine the penetrance of specific mutations observed here, as we do not see them often enough in an unselected population. Nevertheless, we introduce the term ‘gene vulnerability’ as the probability that a given type of mutation in a given gene contributes to a given condition. Genes with non-zero vulnerability define the vulnerable class. We can extend this concept to ‘class vulnerability’, defined as the mean gene vulnerability over a class of genes. Mathematically, class vulnerability V is computed by solving the following equation for V:

$$\mathrm{F}*\mathrm{A}=\mathrm{P}*\mathrm{H}*\mathrm{V}$$ (EQ 1)

where F is the prevalence of the condition, A is the ascertainment differential for DN mutations of a given type in the gene class, P is the expected proportion of the population with DN mutations of that given type, and H is the probability that such mutations hit the gene class.

We can compute a distribution of class vulnerability for all vulnerable genes targeted by a given mutational type (Methods) because F, A, and P have empirically sampled distributions and H has a distribution inferred from the total length of the gene class. The distribution of class vulnerability for DN LGDs in males with lower IQ has a mode around 0.4 (Fig. 3). In other words, ~40% of DN LGDs in vulnerable genes in a male contribute to diagnoses of lower IQ ASD. Similarly, ~10% of missense mutations in vulnerable genes contribute to diagnoses of lower IQ autism (Fig. 3). The mode for LGD vulnerability in females is four-fold lower than for lower IQ males, mainly because the prevalence is four-fold lower. Reduced penetrance in females is not well understood, but may be consequent to sexually dimorphic development. Support for this is seen in the relative enrichment of embryonically expressed genes as targets in females.

Partial gene vulnerability can be explained in several ways: some LGD mutations result in autism, some have little effect, and some produce other diagnoses or even lethality. Regardless, many LGD mutations will strongly predispose to ASD. We expect this to be reflected in decreased functional variation in the human gene pool, as we have previously shown for FMRP-associated genes⁸.

Given our analysis of gene vulnerability and the lack of evidence for compound heterozygosity, damage to a single allele will often have severe consequences for development. What underlies vulnerability to haploinsufficiency? Half the normal gene dosage can result in half the level of gene products, and there are many examples where physiology requires proper dosage^32–37. Also, having two copies of a gene will reduce variability of expression³⁸. With only one functional allele, there could be increased variation in levels of expression, including dangerously low levels at critical moments in lineage development, altering the composition of tissues. Monoallelic expression also needs to be considered³⁹. Finally, some truncation events might lead to dominant negative alleles.

Present and future implications

From the clinical perspective, early diagnosis and family counseling are complicated if there are hundreds of genetic targets, especially if few are known with certainty. Sequencing of more cohorts is thus clearly warranted. From the therapeutic perspective, the good news is that in almost all cases DN mutations occur in probands in whom a normal allele is also present. It is theoretically possible that enhancing activity of the remaining alleles might alleviate symptoms. So in our view, the long-term prognosis for treating ASD is positive. Moreover, ASD targets overlap with targets for intellectual disability and schizophrenia, so mechanism-based treatments might work for different diagnostic categories. In the intermediate term, functional clustering suggests that treatments might be tailored to a smaller number of convergent pathways.

Methods

Sample collection

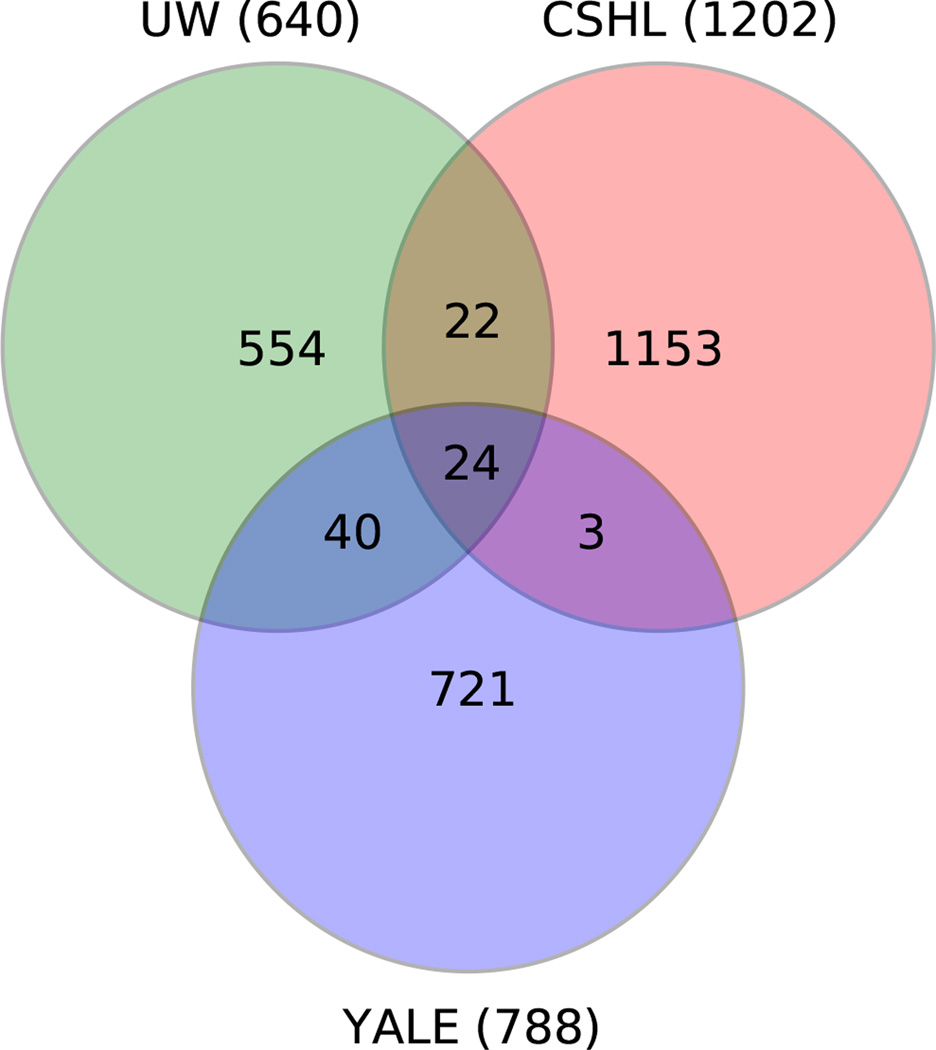
The majority of the families (2,517) came from current or former members of the Simons Simplex Collection (SSC). The SSC was assembled at 13 clinical centers, accompanied by detailed and standardized phenotypic analysis as reported previously¹¹. Multiple IQ measures (verbal, nonverbal and full spectrum) were recorded; in this work, we stratified probands by nonverbal IQ, which we refer to as simply “IQ” throughout the text. Families with single probands and unaffected siblings were preferentially recruited, whereas families with two probands were specifically excluded¹¹. Families from two associated collections were also sequenced: the Simons Ancillary Collection (SAC, n=123), and the Simons Twin Collection (STC, n=13). The SAC includes families that failed inclusion criteria for the SSC, typically because a parent, sibling or second- or third-degree relative of the affected participant has been diagnosed with ASD, or for cases in which the proband’s ASD diagnosis was questionable. The STC consists of families of monozygotic twins in which at least one co-twin is affected by ASD. The institutional review boards of Cold Spring Harbor Laboratory, Yale Medical Center and University of Washington, Seattle approved this study. Written informed consent from all subjects was obtained by SFARI. Blood samples were drawn from parents and children (affected and unaffected) and sent to the Rutgers University Cell and DNA Repository (RUCDR) for DNA preparation. DNAs from 2,517 families (of ~2,800 total in the SSC) were used in this study. Results from 774 of the SSC families included here were published in earlier work^6–8. The samples were split across the three centers: Cold Spring Harbor Laboratory (CSHL), the Department of Genetics at the Yale School of Medicine (YALE), and Department of Genome Sciences at the University of Washington (UW). The split was not uniform with respect to number of families or the proportions of 1) female probands and 2) probands with lower IQ (Extended Data Fig. 2, Supplementary Table 1). A number of families were sequenced at multiple centers, with 24 families sequenced in all three centers (Extended Data Fig. 1, Supplementary Table 1).

Exome capture, sequencing and validation

The three centers differed in the precise exome capture platform, read length and validation protocols.

CSHL

The protocols described in Iossifov et al.⁸ were applied to the families newly sequenced at CSHL. Briefly, SeqCap EZ Human Exome Library v2.0 (Roche NimbleGen) reagents were used with a custom barcoding protocol that enabled simultaneous exome enrichment of ≤4 genomes and the sequencing of ≤8 individuals per Illumina HiSeq 2000 lane. All exome sequencing was performed using paired-end 100-bp reads. All strong and weak LGD candidate variants as well as additional variants from families sequenced at CSHL were subjected to experimental validation. Gene-specific primers were designed for PCR amplification of candidate SNVs and indels, and amplicons were pooled and sequenced on an Illumina MiSeq. Approximately 100 variants were validated per lane with paired-end 150-bp reads. Where possible, the parental origin was determined by phasing of linked transmitted SNVs.

UW

Samples were captured and sequenced by one of three methods. In the pilot set (19 quads), samples were captured using SeqCap EZ Human Exome Library v1.0 (Roche NimbleGen) reagents (UW-M1)^7,40. The remaining samples were captured using SeqCap EZ Human Exome Library v2.0 (Roche NimbleGen) reagents⁷. Newly sequenced samples were either processed as in O’Roak et al.⁷ (UW-M2) or with a modified (UW-M3) protocol (Supplementary Table 10). For UW-M2, single-plex captures and single-plex sequencing runs (non-pooled) were performed as described previously⁷. For UW-M3, single-plex capture was performed as in UW-M2; however, in the post-capture PCR, an 8-bp index barcode was added. Post-PCR libraries were quantified and pooled in sets of ~96. These pools were then sequenced on the Illumina MiSeq platform to evaluated library complexity and sample distribution. Pools were rebalanced based on performance, then sequenced across multiple HiSeq 2000 lanes using paired-end 50-bp reads. Additional lanes were added until samples reached target coverage (20×: ~80%; 8×: ~90%). If additional coverage was required for some samples, subpools were also generated. For samples processed with UW-M1 and UW-M2, predicted de novo calls were validated using standard PCR and Sanger sequencing⁷. For UW-M3 processed samples, custom MIP (Molecular Inversion Probe) capture probes were designed with targeting arms flanking regions of interest. Probes were designed without or with degenerate tags, and pools of ~50–100 probes were generated^30,41. As described earlier⁴¹, sets of families (~96 samples) were captured using these pools with 50–100 ng of genomic DNA as template. Capture products were then pooled and sequenced on an Illumina MiSeq. Candidate sites failing MIP QC or capture, or showing evidence of significant shifts in allele balance, were validated using the standard PCR/Sanger method. If sites repeatedly failed the assay, they were discarded. Novel sites called by the CSHL pipeline were validated using the same methods as UW-M3.

YALE

Whole blood-derived genomic DNA was enriched for exonic sequences using SeqCap EZ Human Exome Library v2.0 (Roche NimbleGen) reagents. All family members were barcoded and each pool of four samples was sequenced using 75-bp paired-end reads on single lanes of the Illumina HiSeq 2000 instrument. Where possible, all four family members were sequenced on the same lane to minimize batch effects. All strong and weak LGD candidate variants from the CSHL pipeline, along with an additional set of LGD candidates from the Yale pipeline, were subjected to experimental validation as follows: variant-specific primers were designed for PCR amplification of candidate SNVs and indels from all family members, and amplicons were sent for Sanger sequencing.

Sequence Analysis Pipelines

Sequence data were interpreted as family genotypes using pipeline tools at each respective data center. Almost all of the data were reanalyzed with the CSHL pipeline. We show the coverage (Extended Data Fig. 6) and yields (Extended Data Fig. 7) for de novo calls from each center. The 24 families sequenced at all three centers demonstrated good agreement between pipelines and platforms (Supplementary Tables 11 and 12).

The analysis pipelines generated candidate de novo events, defined as variants present in the child and absent in both parents. We filtered out variants seen frequently in the parents of the collection (allele frequency >0.3%), reasoning that most of these would be false positives due to uneven coverage in a parent. Candidates generated by local pipelines or by the common CSHL pipeline were validated at the respective centers with re-sequencing and 2,504 were verified. In our final call set, we include all verified calls from each center, and omit any call that was rejected. In addition, because almost all (1,640 of 1,644) strong point mutations generated by the common CSHL pipeline were verified when successfully tested (Supplementary Table 11), such strong candidates are included in our call set even if the validation test failed or if the candidate event was not tested. All frameshift mutations were validated, and we exclude all that were rejected. All de novo calls used in the subsequent analysis, along with their validation status, are listed in the Events Table (Supplementary Table 2). Pipelines for analysis and validation were blind with respect to affected and unaffected status.

CSHL (uniform) pipeline

Sequence data from the three centers were analyzed with the computational pipeline described in Iossifov et al.⁸ In brief, the Illumina analysis pipeline (CASAVA 1.8) was used for base calls, and custom software was used to de-multiplex reads and trim barcodes from CSHL derived data. Data from Yale and UW were de-multiplexed at the respective centers prior to analysis through the CSHL pipeline. BWA⁴² was used to align sequence reads to the hg19 reference genome, and both Picard (http://picard.sourceforge.net/) and GATK⁴³ were used for marking PCR duplicates, family-based sequence realignment and quality score recalibration. As described previously, a multinomial model-based family genotyper was used to generate candidate SNV and indel ‘Mendel violators,’ each annotated with: 1) a confidence score (denovoScr) that reflects the posterior probability of Mendel violation at the locus; 2) a goodness-of-fit-score (chi2Score) showing the degree to which the assumptions of the multinomial model are applicable to the observed data; 3) counts of reads per allele and per family member; and 4) allele frequency and noise rates for the candidate position based on the whole collection. Candidates SNVs with denovoScr ≥60 and chi2Score >0.0001 were labeled ‘strong’ provided that the position was not polymorphic or noisy in the population, and that the parents were homozygous for the reference allele.

For SNVs, a cutoff denovoScr value of 60 was dictated by the desire to keep false positives to a minimum, and was chosen after computing the proportion of de novo candidates that appear at polymorphic loci (a surrogate for false positives) as a function of the score (see the Supplement of Iossifov et al.⁸). The low false positive rate (<5%) was also confirmed through experimental validation (Supplementary Table 11). In addition, we observe that only 1% of DN mutations are shared between two siblings (Supplementary Table 2), putting a 3% cap on false positives due to failure to correctly observe parents. At stringent thresholds the false negative rate is generally high, but through simulations we determined that, even with stringent thresholds, regions with deep coverage (40× or higher joint coverage) had low false negative rates (<5%).

Indels were treated differently than SNVs. The multinomial model assumes a small allele bias, appropriate when calling SNVs, but not for de novo indels—particularly for long events (>10 bp). To address this, cutoffs for ‘strong’ indels were lowered (denovoScr >30 and chi2Score >10⁻⁹). To reduce noise, we added requirements for ‘clean’ read counts: parents were not allowed to have any reads containing the candidate indel, and were required to have at least 15 reads supporting the reference allele. At least one of the children had to have ≥6 reads with the candidate variant, and those reads had to comprise ≥5% of reads. Experimental validation demonstrated that the false positive rate in the strong indels is <10%, and simulations for indels without extreme allele bias (the majority of those <10 bp) reveal that the false negative rate in well-covered regions (40×) is <5%.

All ‘strong’ SNVs and indels are reported here unless rejected by validation. To address the high false negative rates, we defined a class of ‘weak’ SNV and indels drawn from thresholds lower than strong candidates. All weak LGD candidates were subjected to validation, and only those successfully validated are reported. In addition, during method development (e.g. Scalpel⁴⁴ or through manual inspection), we validated a large number of candidates that did not meet even the weak definition. Candidate variants found as valid under these circumstances are reported here and labeled as “not called.” This label is also used when the CSHL uniform pipeline missed a call from the UW and YALE data that was successfully validated.

UW pipeline

All samples using UW-M1 and UW-M2 protocols were processed as described earlier⁷. For UW-M3, updated versions of BWA (0.5.9-r16), Picard-tools (1.48) and GATK (1.0-6125) were used. GATK’s Unified Genotyper was used in single sample mode with filter flags (AB >0.75, low quality, QD <5.0, QUAL ≤50.0) and in parallel with the SAMtools pipeline as described previously⁴⁰. Only positions with ≥8-fold coverage were considered. Child genotype calls were compared to the parental genotypes to identify possible de novo events. Predicted DN SNVs were analyzed against a set of 946 exomes to remove recurrent artifacts and likely undercalled sites. Indels were also called with the GATK Unified Genotyper and SAMtools⁴⁵, and included only those with ≥25% of reads showing a variant at a minimum depth of 8×. These were then filtered against a larger set of 1,779 exomes (as with SNVs). Those sites passing (i.e. not present) in the exome screen and also not present in multiple UW-M3 processed families were manually evaluated by inspecting alignments in the Integrative Genomics Viewer (http://www.broadinstitute.org/igv/home). Sites with obvious misalignments (e.g. non-gapped indels or soft-clipped only reads) were removed. Moreover, if reads supporting the predicted DN mutation were present in ≥5% of 20 (or more) reads in one of the parents, the site was excluded. For sites with lower coverage, a variant was excluded if present in ≥10% (e.g. 1/10 or 2/20) of parent reads or (for quads) if at least one variant read was present in one parent and the other child.

Yale pipeline

The Yale data were analyzed as described in Sanders et al.⁶ Briefly, CASAVA 1.8 was used for demultiplexing and base calling, reads were aligned to hg19 with BWA⁴², and SAMtools⁴⁵ was used for marking PCR duplicates and genotyping. In-house scripts were used for family-based assessment of de novo mutations and annotation against genes and the exome variant server (varianttools.sourceforge.net/Annotation/EVS).

Recurrence and overlaps

Null models for target overlaps and recurrence

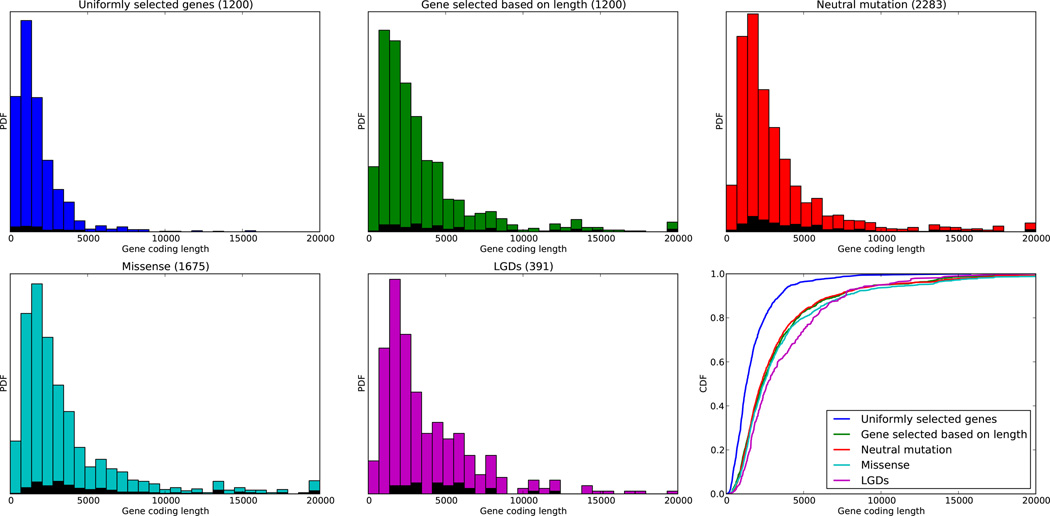
We introduce the term mutation-child-type to refer to a set of events of a certain mutational type (e.g. missense or LGD) in children of a certain type (e.g. male affecteds with higher IQ or unaffected siblings). We observe target enrichment in gene classes, and document overlaps and recurrence between and within mutation-child-types. To measure significance, we use a null model in which the probability that a gene is hit by mutation is proportional to its length, a model supported by observation (Extended Data Fig. 5). We examine the distributions of lengths of gene targets of de novo synonymous, missense and LGD mutation in affected children and siblings. These distributions are compared to simulations of genes picked at random or in proportion to their length. The data fit well with the model that mutation frequency is linearly dependent on gene length. The group with the largest deviation from this rule is the set of DN targets in affected children, both for missense (p-value 0.001) and for LGDs (p-value 0.001, Supplementary Table 13). These p-values are defined as the probability that the median length of the target class can arise under the null model, and are computed by simulations of equal number of genes weighted by length. While the deviation is statistically significant, it is of such a minor amount that we ignore it for the null model.

Measuring overlaps

We test for overlaps between targets of a given mutation-child-type and other sets of genes (e.g. overlap of DN LGD targets in affected girls with FMRP-associated genes) as well as overlaps between targets of two different mutation-child-types (e.g. overlap between the targets of DN missense in all probands and the targets of DN LGDs in all probands). In both cases, observed overlaps are compared to those expected under the length-based null model discussed above.

Let T be the targets of mutation of a given type in a child of a given type, S a predefined gene set, and O the intersection of T and S. We ask for any gene G that carries a single mutation, what the probability p(S) is that the mutation (and hence G) falls in S. We estimate p(S) by collapsing all recurrent hits to one, and applying the length-based null model to S. Thus p(S) is the ratio of (1), the sum of exome-captured lengths of the genes of S, divided by (2), the sum of the exome-captured lengths of all genes. Supplementary Table 7 shows the length of the captured portion of all genes in the exome we analyze. Using “‖” to designate the number of members in a set, we then perform a two-sided binomial test of |O| outcomes in |T| opportunities given the probability of success p(S).

When we test overlaps between targets of two different mutation-child-types, we take one of the targets as T and compare the other targets as S. However, before constructing T and S, we cleanup targets shared by T and S that result from mutations shared between siblings in the same family, or from multiple mutations of different types affecting a single gene in one child. We then apply the method of the paragraph above. Finally, we reverse the procedure for creating of S and T, and report both results (Supplementary Table 6).

Test for excessive recurrence

If we have R recurrent genes in K events in a mutation-child-type class, we test for excess recurrence by comparing R to the number of recurrent genes expected under the gene length-based null model. We build the expectation by performing 10,000 simulations. In each simulation, we sample K genes with replacement where the probability of sampling a gene is proportional to its length. We then count the number of recurrences.

Estimation of the number of vulnerable genes

To estimate the number of vulnerable genes for a given mutation-child-type, we start with the observed number of events (K), the observed number of recurrent events (R), the estimated posterior distributions for the rates of mutations of the given type in the ascertained (Mdist) and for the unaffected (Pdist) population. We then explore possible number of vulnerable genes (T) from 1 to 4000. For each T, we estimate (through a simulation described in the next paragraph) the likelihood L(T) = P(R|T, Mdist, Pdist, K). Assuming all numbers of vulnerable genes from 1 to 4000 are equally likely, we compute a posterior distribution of the number of genes p(T) proportional to L(T) and determine the maximum value and 95% confidence intervals.

To estimate the likelihood, L(T) = P(R|T, Mdist, Pdist, K), we perform 10,000 simulations for every T. In each simulation:

1. We randomly select T distinct vulnerable genes from all genes, without respect to length. Unlike mutation, which strikes a gene according to its length, we assume that the chance a gene can cause autism if mutated is independent of its length.

2. We select the number N of contributory events by sampling from a binomial distribution Binom(K, A/M), where P a randomly selected rate from Pdist, M is a randomly selected from Mdist, A=M-P is a sampled ascertainment differential, and A/M is an estimate of the proportion of contributory events.

3. We simulate N contributory mutation events by selecting N events with replacement from the T vulnerable genes proportional to their length.

4. To simulate random events, we select K-N genes from all well-covered genes with replacement proportional to their length.

5. We record the number of recurrent events in the K selected events from above.

We set L(T)= P(R|T, Mdist, Pdist, K) to be the proportion of simulations in which the number of recurrent events is exactly R. P(T) is obtained by normalizing L(T). For every simulation in which the number of recurrent events is exactly R, we also record 1) the proportion of contributory events among the recurrent events and 2) the vulnerability point estimate as discussed in the next section.

Vulnerability

We use the equation described in the text:

$$\mathrm{F}*\mathrm{A}=\mathrm{P}*\mathrm{H}*\mathrm{V}$$ (Eq 1)

where F is the prevalence of the given condition in the population, A is the ascertainment differential for DN mutations of a given type in persons ascertained for that condition, P is the expected proportion of the population with such DN mutations, H is the probability that such a mutation hits the target, and V is the mean class vulnerability. These variables are in fact random variables with empirically derived distributions.

We first demonstrate the method for computing the class vulnerability point estimate for genes vulnerable to LGD mutations for the ASD males of lower IQ, assuming that the variables are fixed. One in 75 males is diagnosed with autism, and we estimate (from empirically derived gender biases) that 3/4 of these males are of lower IQ, yielding a prevalence F = 1/100. From our study, 0.23 of these have an LGD. Because the expected proportion of people with a DN LGD mutation is P = 0.11, only A = 0.12 of this subpopulation have an LGD in a vulnerable gene that contributes to ascertainment. Thus F*A = 1.2*10⁻³ is the proportion of males that have lower IQ and autism resulting at least partially from a DN LGD. This proportion is also given by P*H*V where H is the probability that the LGD hits within the genes vulnerable to LGD mutations, and V is the mean class vulnerability for these genes. P, as already stated, is 0.11. We have computed the number of genes vulnerable to LGD mutations, N, for the affected males with lower IQ to be about 400 genes (Supplementary Table 6). Assuming membership in the target class is independent of gene length, and about 20,000 genes, we calculate H = 400/20,000 = 0.02, and solve V to be 0.55.

We assume the following prevalence: F=1/75 for ASD in males, F=1/100 for ASD with lower IQ in males, F=1/300 for ASD with higher IQ in males, and F=1/300 for ASD in girls. A and P are empirically derived gamma distributions from the sampled Poisson rates of DN LGD mutations in affected and unaffected siblings. By keeping the observed number of LGD events and the observed proportion of LGD events constant, we sample from the distribution of target number N and the distributions on A and P as described in the previous section. We set H to be the ratio of the total length of uniformly sampled vulnerable genes to the total length of the analyzed captured exome, and compute a vulnerability point estimate as described just above. These sampled values are displayed in Fig. 3 lower panel. The mode for V is 0.4 for males of lower IQ.

Parental age and phasing of DN mutations

We used two different strategies for modeling the relationship between rates of DN substitutions and the ages of the parents.

The first strategy does not depend on knowledge of the parent of origin for DN substitutions, which we do not know for the vast majority of DN substitutions. Because the ages of the mother and the father are strongly correlated, we can effectively use this strategy only to explore the relationship between the father’s age and the rates of DN substitutions. Over probands and siblings in the 40×-joint family target, we model the number of mutations per child as sampled from a Poisson distribution with rate R_c=T_c*(A*F_c+B), where R_c is the rate of DN substitutions per child, F_c is the age of the father at the birth of the child, T_c is the ratio of the length of the 40×-target in that child to the total exome length, and A and B are whole population parameters, estimated by maximizing the likelihood over all children.

The second strategy is applicable only to DN mutations for which we have successfully ‘phased’ the parent of origin by proximity to a linked polymorphism. For each parental gender, we separately perform a two-sided one-sample t-test to compare the parental ages of each phased DN mutation to the mean of parental ages in our population.

DN substitutions increase ~0.4 per paternal decade (Extended Data Fig. 4), consistent with previous studies¹⁵ and the increase in autism as a function of paternal age^46,47. Where we could determine parental phase, DN substitutions arose more frequently in the paternal (287) than in the maternal (80) background. Among phased DN events, the mean age at birth was 34.6 for the father and 32.0 years for the mother, whereas the respective mean ages were 33.2 and 31.1 years for fathers and mothers in the whole population (p-values of 0.0001 and 0.047, respectively, that these differences arise by chance).

Gene class definition

For determining overlap with de novo mutations, functional gene classes were defined as follows. “FMRP” are genes encoding transcripts that bind to FMRP¹⁷. “Chromatin” indicates chromatin modifiers as defined by GO (http://www.geneontology.org/). “PSD” is a set of genes encoding proteins that have been identified in postsynaptic densities²⁰. “Mendelian” represent positionally identified human disease genes²², and “Essential” genes are human orthologues of mouse genes associated with lethality in the Mouse Genome Database²¹. “dn LGD (Scz)” are de novo LGDs in schizophrenia^26,48,49 and “dn LGD (ID)” are de novo LGDs in intellectual disability^25,29.

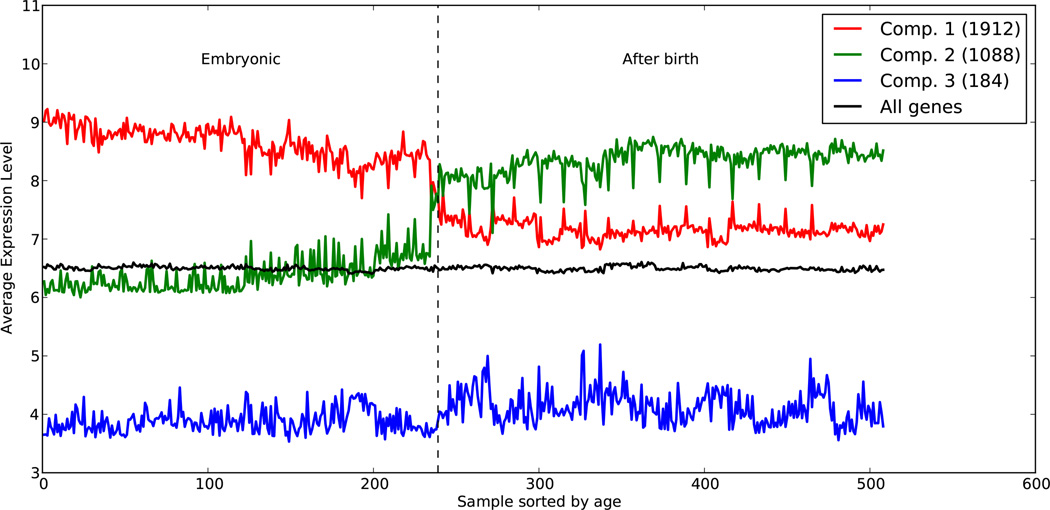
“Embryonic” genes are those expressed in post-mortem human embryonic brains¹⁹, derived from downloaded expression data¹⁸ (http://www.brainspan.org/static/download.html). This data set provides normalized expression levels for ~17,000 genes across brain regions from 36 individuals, 18 of which were from embryos. Each brain was further subdivided into 14 anatomical regions for a total of 508 regions. We computed correlation values for the 17,000 genes, and generated a graph by connecting genes that had correlations >0.85, then identified connected components and averaged the expression of genes within these components as a function of the annotated age of the brain and by region. Each region is sorted first by age, then by type (Extended Data Fig. 8). The averaged normalized expression of the 1,912 genes in the first component decreases after birth, and hence we call this set embryonic.

Supplementary Table 7 shows the genes in the eight functional classes that are within the captured exome regions and were used in all analyses.

Extended Data

Extended Data Figure 1. Number of families sequenced by center.

The numbers of families sequenced at the three centers are plotted as a Venn diagram. Families sequenced at more than one center are indicated by the overlapping regions between circles. CSHL: Cold Spring Harbor Laboratory; UW: University of Washington, Seattle; YALE: Yale Medical Center.

Extended Data Figure 2. SSC sequencing by pedigree type and nonverbal IQ.

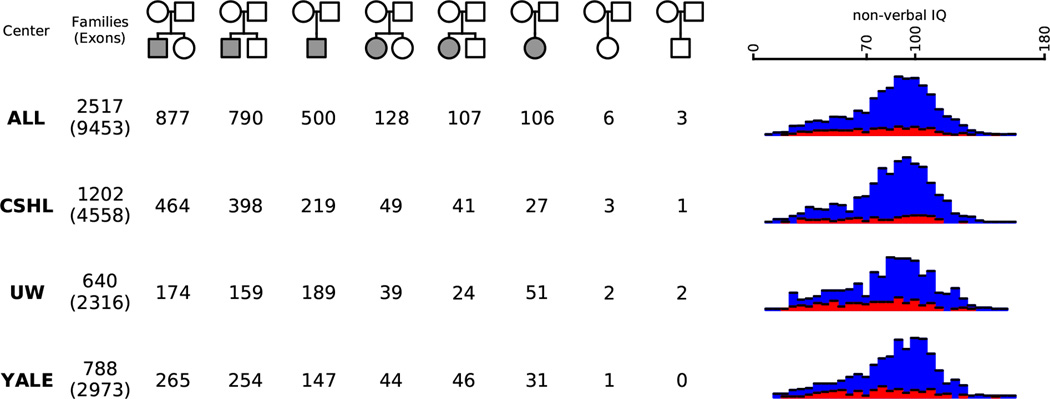
A summary of all SSC families sequenced is indicated across the “ALL” row. Numbers of SSC families with complete exome sequencing data are displayed by center in the following rows (see Extended Data Figure 1 legend for center designations). The top number in entries under the “Families” column indicates the total number of families sequenced, and the number in parentheses below indicates the total number of individuals. Family pedigree structures are shown across the top row with gender indicated by shape (square for male, circle for female) and affected status indicated by color (white for unaffected, gray for affected). Distributions of non-verbal IQ within each cohort are shown for male probands (blue) and female probands (red).

Extended Data Figure 3. Rates of de novo LGD and missense mutations in the SSC by child status.

On the left we show the LGD rate per child in six types of children, labeled on the X-axis, defined by their affected status, gender, and non-verbal IQ. We test for equal rates for every pair of child types and we show the ones with p-value >0.05 with thin lines on the top of the figure. Although not significant, the rates in affected females and in affected males of lower nvIQ are larger than the rate in males of higher nvIQ. On the right, we show the missense rates per child for the same six groups of children.

Extended Data Figure 4. Paternal age and de novo mutation rate at child birth.

Distribution of paternal age at birth of children (top) and rates of de novo mutation in offspring as a function of paternal age are shown (bottom). Children were ordered by paternal age at birth and split into 20 groups of similar size, as shown in the lower panel. The red curve shows the mean observed rates of de novo exomic substitutions in each of the 20 groups, with the×coordinate equal to the mean each of the fathers’ ages within each group. The blue line shows a linear fit to the observed rates. The dotted green line represents de novo mutation rates from whole genome sequencing data (Kong et al., Nature 488, 471–475, 2012) scaled to rates per exome based on representation in the SeqCap EZ Human Exome Library v2.0 (Roche NimbleGen).

Extended Data Figure 5. Coding region size distribution for query sets of genes.

PDFs and CDFs (right bottom panel) of the distributions of the coding region length in base pairs of five sets of genes: a set of 1200 genes picked uniformly from the set of exome-targeted genes (blue); a separate set of 1200 genes picked with probabilities proportional to length of the coding region (green); the set of gene targets of neutral mutations, including 1) synonymous mutations in probands and siblings and 2) missense mutation in siblings (red); genes with de novo missense mutations in probands (cyan); and genes with de novo LGDs in probands (magenta). Black within the histograms shows the distribution of lengths of the recurrently hit genes from each class. Coding region length distribution under a uniform model does not fit the lengths of the genes with observed mutations, and genes with LGD mutations are longer than predicted by a simple length-based model (bottom right).

Extended Data Figure 6. Distributions of sequencing depth.

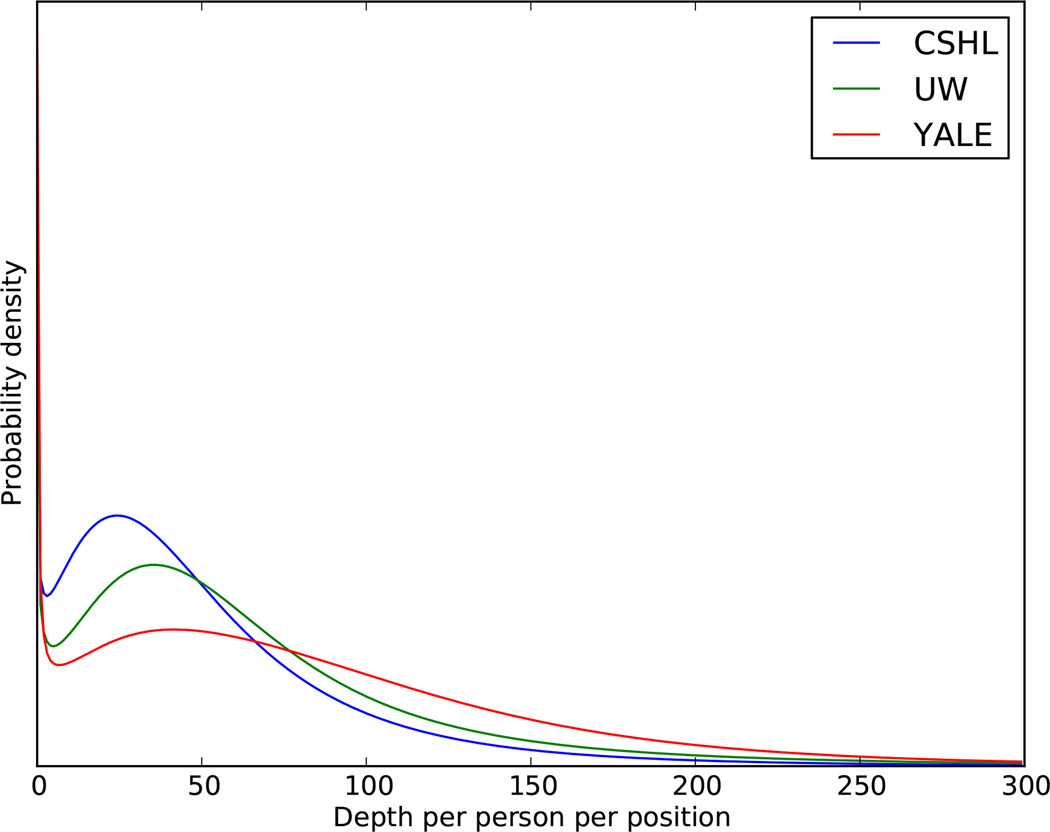
Distributions of sequencing depth (number of sequence reads covering a given genomic position) per person per position for the three sequencing centers are plotted. Center designations are as in Extended Data Figure 1.

Extended Data Figure 7. Yield of de novo LGD and missense mutations.

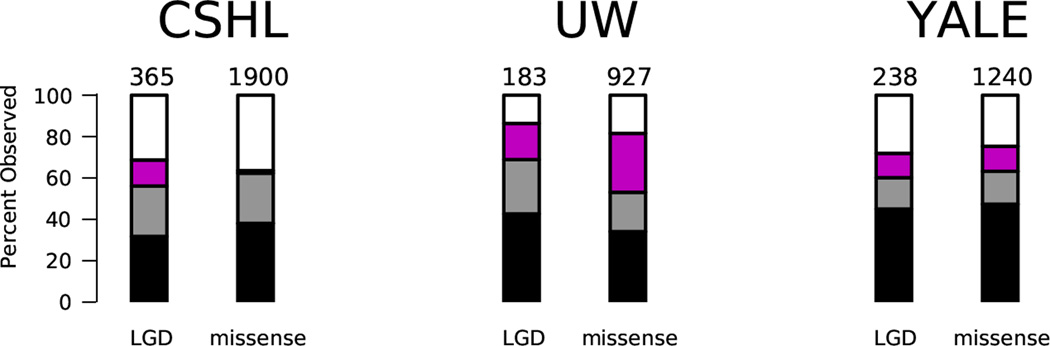
We plot the yield of de novo LGD and missense mutations per sequencing center (designations as in Extended Data Figure 1). In each case we show the number of mutations we expect to see based on the estimated rates per child, indicated by the numbers above the bars. We also show what percentage of the expected number we have observed. Black refers to strong calls in the 40× target, gray refers to strong calls outside of 40× target, and magenta refers to weak (but valid) calls. The white region represents the difference between the expected and observed numbers of variants.

Extended Data Figure 8. Categorization of embryonically expressed genes.

We downloaded expression data (Kang, H. J. et al. Nature 478, 483–489, 2011) from http://www.brainspan.org/static/download.html. The data set provides normalized expression levels for ~17,000 genes across brain regions from 36 individuals, 18 of which were from embryos. Each brain was further subdivided into 14 anatomical regions for a total of 508 regions. We computed correlation values for the 17,000 genes, and generated a graph by connecting genes that had correlations >0.85. We then identified connected components and averaged the expression of genes within these components as a function of the annotated age of the brain and by region. Each region is sorted first by age, then by type. The averaged normalized expression of the 1,912 genes in the first component decreases after birth, and hence we call this set “embryonic.” See Supplementary Table 7 for the list of embryonic genes.