Comparing two correlated C indices with right-censored survival outcome: a one-shot nonparametric approach

Abstract

The area under the receiver operating characteristic (ROC) curve (AUC) is often used as a summary index of the diagnostic ability in evaluating biomarkers when the clinical outcome (truth) is binary. When the clinical outcome is right-censored survival time, the C index, motivated as an extension of AUC, has been proposed by Harrell as a measure of concordance between a predictive biomarker and the right-censored survival outcome. In this work, we investigate methods for statistical comparison of two diagnostic or predictive systems, of which they could either be two biomarkers or two fixed algorithms, in terms of their C indices. We adopt a U-statistics based C estimator that is asymptotically normal and develop a nonparametric analytical approach to estimate the variance of the C estimator and the covariance of two C estimators. A z-score test is then constructed to compare the two C indices. We validate our one-shot nonparametric method via simulation studies in terms of the type I error rate and power. We also compare our one-shot method with resampling methods including the jackknife and the bootstrap. Simulation results show that the proposed one-shot method provides almost unbiased variance estimations and has satisfactory type I error control and power. Finally, we illustrate the use of the proposed method with an example from the Framingham Heart Study.

1. Introduction

Methods for assessing and comparing diagnostic performance are of increasing importance as new biomarkers and high-throughput molecular diagnostics are in rapid development. When a diagnostic test for a binary outcome, e.g., non-diseased and diseased, is based on an observed variable that lies on the ordinal scale, the receiver operating characteristic (ROC) curves and the area under the ROC curves (AUC) are commonly used diagnostic accuracy measures [1, 2, 3, 4, 5].

A number of methods have been proposed to estimate the AUC and its variance [2, 6, 7, 8]. There have also been parametric and nonparametric methods developed to compare correlated AUCs. Metz et al. [9] proposed a bivariate binormal model. Hanley and McNeil [10] provided a table that converts the observed correlations in diagnostic scores between two modalities into a correlation between two AUCs. DeLong et al. [11] presented a nonparametric method for comparing correlated AUCs based on a structural components variance estimate following the work of Sen [12] and the asymptotic normality of the U-statistic AUC estimator.

Despite the prevailing use of AUC as a summary index of the ROC curve in the context of dichotomous outcomes [13, 14, 15], it has limitations in evaluating and comparing biomarkers with censored survival outcomes. Essentially, ROC analysis requires a reference standard that categorizes subjects into diseased and non-diseased populations. However, the survival outcome, i.e., time to event, is typically continuous rather than binary. Additionally, the conventional ROC analysis cannot handle censored outcome data.

There have been generalizations of ROC analysis that can overcome these constraints. The time-dependent ROC curves [16, 17, 18] have been proposed in thinking ROC curves as a varying function of time t. Intuitively, the censored outcome can be dichotomized given time point t, e.g., being 1 if a subject has died prior to time t and 0 otherwise. Correspondingly, the area under the time-dependent ROC curves has been considered [19].

Smith et al. [20] generalized the area under the empirical ROC curve to a concordance measure that allows for polytomous ordinal patient outcomes. Obuchowski [21] proposed a concordance-type measure of diagnostic accuracy that differs from Smith et al. in how it deals with ties in the reference standard. While these methods accommodate polytomous and continuous data, neither handles censoring of clinical outcomes such as those in survival analysis.

The overall C index, motivated as an extension of AUC to survival analysis, has been proposed by Harrell et al. [22, 23]. It is a conditional concordance probability measure between a survival outcome that is possibly right censored and a predictive score variable, which can represent a measured biomarker or a composite-score output from an algorithm that combines multiple biomarkers. Various popular extensions of the C index have been proposed in the literature since then [19, 24, 25]. Pencina et al. [26] studied these different C statistics systematically and concluded that the C index proposed by Harrell et al. [22, 23] is the most appropriate in capturing the discriminating ability of a predictive variable to separate those with longer event-free survival from those with shorter event-free survival within some time horizon of interest.

Here we consider a dataset collected on a cohort of n subjects. The actual right-censored survival time of each subject is denoted as X_i with censoring indicator δ_i (i = 1, 2, …, n), where δ_i = 1 if an event of interest occurred (e.g., death) and 0 if censored. Together with two predictive variables denoted as Y and Z, the collected data can be arranged in a matrix form with each row representing observations for a subject

$$\left(\begin{array}{cccc}X& \delta & Y& Z\\ X_1& {\delta }_1& Y_1& Z_1\\ X_2& {\delta }_2& Y_2& Z_2\\ ⋮& ⋮& ⋮& ⋮\\ X_n& {\delta }_n& Y_n& Z_n\end{array}\right).$$ (1)

Upon randomly drawing a pair of subjects, Harrell et al. [22] defined the overall C index between the right-censored survival time X and the predictive score Y (or Z) as the probability that the subject with the higher values of Y (or Z) had the longer survival time X, given that the order of two survival times can be validly inferred. Values of C near 0.5 indicate that the predictive score is no better than tossing a coin in determining which subject will live longer while values of C near 0 or 1 indicate the score, lower or higher, virtually always determines which subject has a better prognosis [22].

For two predictive tests performed on the same cohort of patients, it is essential to account for the correlated nature of the data to make a formal statistical comparison in terms of the C index. Pencina and D’Agostino [27] and Nam [28] investigated asymptotic variance estimations as well as confidence interval constructions for a single C. Antolini et al. [29] developed methods for comparing two correlated C indices, in which a consistent estimator for the variance of the difference of two C indices was derived via the jackknife approach. In this article, we develop a one-shot estimator that does not require resampling for the variance of the difference of two C indices. A z-score test is then constructed to statistically compare the two C indices. For comparison purposes, we also consider a bootstrap resampling approach [30, 31].

The rest of our article is organized as follows. In Section 2, we discuss the C index in detail and present the relationship between the C index and the generalized Kendall’s tau. In Section 3, we present the proposed variance estimator and the test statistic for the difference between two correlated C indices. Moreover, the procedures for carrying out the jackknife approach [29] and the bootstrap resampling approach are also described. We present extensive simulation studies in Section 4 for validating the performance of the proposed test statistic and compare that with the jackknife and the bootstrap approach in terms of type I error rate and statistical power. In Section 5, we apply the proposed method to an example from the Framingham Heart Study data [32] to compare the ability of biomarkers in predicting heart-disease-free survival. Finally, a broader discussion on assessing and comparing diagnostic/prognostic accuracy is presented in Section 6.

2. The C Index

In this section, we provide a review of the historical development of Smith et al.’s prediction probability P_K [20], the C index [22, 27], and their relationships with various versions of Kendall’s tau. We show under a unified framework that the C index is a linear function of our generalized Kendall’s tau. Because of this relation, the generalized Kendall’s tau will serve as a vehicle for making inference about the C index.

2.1. Outcomes with no censoring

First, assume that the survival time X is actually observed without any censoring, i.e., δ_i = 1 (i = 1, 2, …, n). Following Smith et al. [20], upon randomly drawing a pair of subjects, say (i, j), i ≠ j, we may have five types of pairs between the survival time X and the predictive score Y,

1. a concordance with probability Π_c = P(X_i < X_j and Y_i < Y_j or X_i > X_j and Y_i > Y_j);

2. a discordance with probability Π_d = P(X_i < X_j and Y_i > Y_j or X_i > X_j and Y_i < Y_j);

3. an X-only tie with probability Π_tX = P(X_i = X_j and Y_i > Y_j or X_i = X_j and Y_i < Y_j);

4. a Y-only tie with probability Π_tY = P(X_i < X_j and Y_i = Y_j or X_i > X_j and Y_i = Y_j);

5. a joint tie in both X and Y with probability Π_tXY = P(X_i = X_j and Y_i = Y_j).

These five possibilities for a random pair are comprehensive and mutually exclusive, and therefore

$${\mathrm{\Pi }}_c+{\mathrm{\Pi }}_d+{\mathrm{\Pi }}_{tX}+{\mathrm{\Pi }}_{tY}+{\mathrm{\Pi }}_{\mathit{tXY}}=1.$$

Recall that our interest is to assess the ability of the predictive scores in predicting survival. Smith et al. [20] considered Kim’s measure [33] d_X·Y,

$$d_{X·Y}=\frac{{\mathrm{\Pi }}_c-{\mathrm{\Pi }}_d}{{\mathrm{\Pi }}_c+{\mathrm{\Pi }}_d+{\mathrm{\Pi }}_{tY}}=\frac{{\mathrm{\Pi }}_c-{\mathrm{\Pi }}_d}{1-{\mathrm{\Pi }}_{tX}-{\mathrm{\Pi }}_{\mathit{tXY}}},$$ (2)

which is the probability of a concordance minus the probability of a discordance, both conditioned on the occurrence of distinct values of outcome X, for quantifying the degree of relationship between X and Y. The subscript for Kim’s measure d_X·Y indicates the intent to predict X from Y. Smith et al. [20] showed that a prediction probability P_K (related to Kim’s measure),

$$P_K=\frac{1}{2}(d_{X·Y}+1)=\frac{{\mathrm{\Pi }}_c+\frac{1}{2}{\mathrm{\Pi }}_{tY}}{{\mathrm{\Pi }}_c+{\mathrm{\Pi }}_d+{\mathrm{\Pi }}_{tY}},$$ (3)

which is the probability of a concordance plus one-half the probability of a predictive-score-only (Y-only) tie, both conditioned on distinct values of state or outcome X, is a direct generalization of the trapezoidal AUC to polytomous ordinal patient outcomes. When the outcome X is dichotomous, P_K reduces to the trapezoidal AUC.

2.2. Survival outcomes with Type I censoring assuming continuous predictive score

Pencina and D’Agostino [27] assumed a continuous distribution of the predictive score Y, i.e., P(Y_i = Y_j) = 0. This eliminates Π_tY and Π_tXY, and in this case, Kim’s measure d_X·Y in Equation (2) is simplified to

$$d_{X·Y}^{\prime }=\frac{{\mathrm{\Pi }}_c-{\mathrm{\Pi }}_d}{{\mathrm{\Pi }}_c+{\mathrm{\Pi }}_d}=\frac{{\mathrm{\Pi }}_c-{\mathrm{\Pi }}_d}{1-{\mathrm{\Pi }}_{tX}},$$ (4)

which is the modified Kendall’s tau presented by Pencina and D’Agostino [27].

They only considered the ties caused by equal survival times X of subjects who remained in the study to the end T_final without developing the event of interest. This type of censoring has been defined as Type I censoring [34]. Under this assumption, they showed that Harrell’s definition of the C index [22] can be expressed in terms of functions of the probability of a concordance and the probability of a discordance,

$$C_{XY}=P(X_i<X_j\text{and}{Y}_i<Y_j\text{or}{X}_i>X_j\text{and}{Y}_i>Y_j\mid X_i\ne X_j)=\frac{{\mathrm{\Pi }}_c}{{\mathrm{\Pi }}_c+{\mathrm{\Pi }}_d}.$$

Comparing the above equation to Equation (3), we can connect the dots and relate C_XY back to AUC via P_K [20].

Pencina and D’Agostino also showed that a linear relationship exists between the overall C and Kim’s measure $d_{X·Y}^{\prime }$ (their modified Kendall’s tau) in Equation (4) as

$$C_{XY}=\frac{1}{2}(d_{X·Y}^{\prime }+1).$$

2.3. Survival outcomes with random right-censoring without assuming continuous predictive score

The censoring type that Pencina and D’Agostino [27] considered is Type I censoring. In addition, they assumed no ties in predictive scores. To overcome these limitations, we develop a general C index estimator that allows for various right-censoring (e.g., random drop-outs) in survival time and ties in predictive scores.

Define sign and csign (sign with censoring) functions as below,

$$\mathit{sign}(Y_i,Y_j)=I(Y_i\ge Y_j)-I(Y_i\le Y_j),$$ (5)

$$c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)=I(X_i\ge X_j){\delta }_j-I(X_i\le X_j){\delta }_i,$$ (6)

where I(·) is the indicator function. It can be verified that sign and csign functions take values in {−1, 0, 1}. The order of two survival times X_i and X_j can be unambiguously determined if and only if csign (X_i, δ_i, X_j, δ_j) ≠ 0. Notice that here we may determine the order even when X_i = X_j if only one of the two is censored. The observation that the higher value of Y corresponds to the longer survival time X is mathematically equivalent to csign (X_i, δ_i, X_j, δ_j) sign (Y_i, Y_j) = 1. Under such setting, we formulate the general C index as a conditional probability between the survival time X and the predictive score Y as

$$C_{XY}^g=P(c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)\mathit{sign}(Y_i,Y_j)=1\mid c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)\ne 0)+\frac{1}{2}P(\mathit{sign}(Y_i,Y_j)=0\mid c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)\ne 0).$$ (7)

If we categorize randomly drawn pairs into the following mutually exclusive types using our sign and csign functions,

1. a generalized concordance with probability ${\mathrm{\Pi }}_c^g=P(c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)\mathit{sign}(Y_i,Y_j)=1)$;

2. a generalized discordance with probability ${\mathrm{\Pi }}_d^g=P(c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)\mathit{sign}(Y_i,Y_j)=-1)$;

3. a generalized X-only tie with probability ${\mathrm{\Pi }}_{tX}^g=P(c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)=0,\mathit{sign}(Y_i,Y_j)\ne 0)$;

4. a generalized Y-only tie with probability ${\mathrm{\Pi }}_{tY}^g=P(c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)\ne 0,\mathit{sign}(Y_i,Y_j)=0)$;

5. a generalized joint tie in both X and Y with probability ${\mathrm{\Pi }}_{\mathit{tXY}}^g=P(c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)=0,\mathit{sign}(Y_i,Y_j)=0)$,

we can then express $C_{XY}^g$, analogous to P_K in Equation (3), in terms of the probabilities defined above,

$$C_{XY}^g=\frac{{\mathrm{\Pi }}_c^g+\frac{1}{2}{\mathrm{\Pi }}_{tY}^g}{{\mathrm{\Pi }}_c^g+{\mathrm{\Pi }}_d^g+{\mathrm{\Pi }}_{tY}^g}=\frac{{\mathrm{\Pi }}_c^g+\frac{1}{2}{\mathrm{\Pi }}_{tY}^g}{1-{\mathrm{\Pi }}_{tX}^g-{\mathrm{\Pi }}_{\mathit{tXY}}^g}.$$

Define our generalized Kendall’s tau ${\tau }_{XY}^g=\frac{{\mathrm{\Pi }}_c^g-{\mathrm{\Pi }}_d^g}{{\mathrm{\Pi }}_c^g+{\mathrm{\Pi }}_d^g+{\mathrm{\Pi }}_{tY}^g}=\frac{{\mathrm{\Pi }}_c^g-{\mathrm{\Pi }}_d^g}{1-{\mathrm{\Pi }}_{tX}^g-{\mathrm{\Pi }}_{\mathit{tXY}}^g}$, which is analogous to d_X·Y in Equation (2), the linear relationship holds immediately between $C_{XY}^g$ and ${\tau }_{XY}^g$,

$$C_{XY}^g=\frac{1}{2}({\tau }_{XY}^g+1).$$ (8)

Notice that $C_{XY}^g$ and ${\tau }_{XY}^g$ deal with censoring while P_K and d_X·Y do not. At the same time, realizing that,

$${\tau }_{XY}^g=\frac{{\mathrm{\Pi }}_c^g-{\mathrm{\Pi }}_d^g}{1-{\mathrm{\Pi }}_{tX}^g-{\mathrm{\Pi }}_{\mathit{tXY}}^g}=\frac{E[c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)\mathit{sign}(Y_i,Y_j)]}{E\left[c\mathit{sign}{(X_i,{\delta }_i,X_j,{\delta }_j)}^2\right]},$$

we can construct an estimator for our generalized Kendall’s tau, based on which we obtain a point estimator of the C index and make statistical comparison between two C indices.

2.4. A point estimate of the C index based on a random sample

Define t_ijXY = csign (X_i, δ_i, X_j, δ_j) sign (Y_i, Y_j), $t_{\mathit{ijXX}}^{\ast }=c\mathit{sign}{(X_i,{\delta }_i,X_j,{\delta }_j)}^2$, the sample estimate

$$t_{XY}=\frac{1}{n(n-1)}\sum _i\sum _{j\ne i}{t}_{\mathit{ijXY}}$$

is a U statistic based estimator for E[csign (X_i, δ_i, X_j, δ_j) sign (Y_i, Y_j)], i.e., the numerator of ${\tau }_{XY}^g$. Similarly,

$$t_{XX}^{\ast }=\frac{1}{n(n-1)}\sum _i\sum _{j\ne i}{t}_{\mathit{ijXX}}^{\ast }$$

is a U statistic for the denominator of ${\tau }_{XY}^g$. Thus, a plug-in estimator for the general $C_{XY}^g$ based on the sample is

$${\widehat{C}}_{XY}^g=\frac{1}{2}\left(\frac{t_{XY}}{t_{XX}^{\ast }}+1\right).$$

3. The Proposed Method for Comparing Two Correlated C Indices

Because the sample ${\widehat{C}}_{XY}^g$ is a continuous function of U statistics [35], it can be shown that ${\widehat{C}}_{XY}^g$ is asymptotically normal [36]. Consequently, the difference between two correlated sample C indices is also asymptotically normal, provided that the asymptotically bivariate normal distribution of two C indices does not degenerate. Given another predictive score Z, we can obtain

$$\begin{array}{l}\mathit{var}({\widehat{C}}_{XY}^g-{\widehat{C}}_{XZ}^g)=\mathit{var}({\widehat{C}}_{XY}^g)+\mathit{var}({\widehat{C}}_{XZ}^g)-2\mathit{cov}({\widehat{C}}_{XY}^g,{\widehat{C}}_{XZ}^g)\\ =\frac{1}{4}\left[\mathit{var}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)+\mathit{var}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)-2\mathit{cov}\left(\frac{t_{XY}}{t_{XX}^{\ast }},\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right].\end{array}$$ (9)

3.1. The Delta method for variance estimators

Based on the multivariate Delta method [37], the variance and covariance terms in Equation (9) can be approximated as

$$\mathit{var}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\approx \left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XY}}{t_{XX}^{\ast 2}}\end{array}\right)\left[\begin{array}{cc}\mathit{var}(t_{XY})& \mathit{cov}(t_{XX}^{\ast },t_{XY})\\ \mathit{cov}(t_{XX}^{\ast },t_{XY})& \mathit{var}(t_{XX}^{\ast })\end{array}\right]{\left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XY}}{t_{XX}^{\ast 2}}\end{array}\right)}^T,$$ (10)

$$\mathit{var}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\approx \left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XZ}}{t_{XX}^{\ast 2}}\end{array}\right)\left[\begin{array}{cc}\mathit{var}(t_{XZ})& \mathit{cov}(t_{XX}^{\ast },t_{XZ})\\ \mathit{cov}(t_{XX}^{\ast },t_{XZ})& \mathit{var}(t_{XX}^{\ast })\end{array}\right]{\left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XZ}}{t_{XX}^{\ast 2}}\end{array}\right)}^T,$$ (11)

$$\mathit{cov}\left(\frac{t_{XY}}{t_{XX}^{\ast }},\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\approx \left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XY}}{t_{XX}^{\ast 2}}\end{array}\right)\left[\begin{array}{cc}\mathit{cov}(t_{XY},t_{XZ})& \mathit{cov}(t_{XX}^{\ast },t_{XY})\\ \mathit{cov}(t_{XX}^{\ast },t_{XZ})& \mathit{var}(t_{XX}^{\ast })\end{array}\right]{\left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XZ}}{t_{XX}^{\ast 2}}\end{array}\right)}^T.$$ (12)

The details are provided in the Appendix. Now the problem boils down to obtaining estimates for the variance and covariance matrix terms in Equations (10–12). In general, in addition to the random variables X (with censoring) and Y (without censoring), given another pair of random variables U (reference variable with censoring) and Z (predictive score without censoring), we present the following lemma providing an unbiased estimator for cov(t_XY, t_UZ), which will be used for obtaining variance and covariance estimates in Equations (10–12) and thus the variance estimate of ${\widehat{C}}_{XY}^g-{\widehat{C}}_{XZ}^g$ in Equation (9).

Lemma 3.1

An unbiased estimator for cov(t_XY, t_UZ) is

$$\widehat{\mathit{cov}}(t_{XY},t_{UZ})=\frac{4{\displaystyle \sum _i}\left({\displaystyle \sum _j}{t}_{\mathit{ijXY}}{\displaystyle \sum _{j^{\prime }}}{t}_{i{j}^{\prime }UZ}\right)-2{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXY}}{t}_{\mathit{ijUZ}}-\frac{2(2n-3)}{n(n-1)}{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXY}}{\displaystyle \sum _{i^{\prime }}}{\displaystyle \sum _{j^{\prime }}}{t}_{i^{\prime }{j}^{\prime }UZ}}{n(n-1)(n-2)(n-3)}.$$

The proof is given in the Appendix.

From Lemma 3.1, we may obtain unbiased estimators for terms $\mathit{var}(t_{XX}^{\ast })$, var(t_XY), var(t_XZ), $\mathit{cov}(t_{XX}^{\ast },t_{XY}),\mathit{cov}(t_{XX}^{\ast },t_{XZ})$ and cov(t_XY, t_XZ) in Equations (10–12) by replacing subscripts. For example,

$$\widehat{\mathit{var}}(t_{XX}^{\ast })=\frac{4{\displaystyle \sum _i}{\left({\displaystyle \sum _j}{t}_{\mathit{ijXX}}^{\ast }\right)}^2-2{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXX}}^{\ast 2}-\frac{2(2n-3)}{n(n-1)}{\left({\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXX}}^{\ast }\right)}^2}{n(n-1)(n-2)(n-3)}.$$

See the Appendix for more details. Putting all the variance and covariance estimates together, $\widehat{\mathit{var}}({\widehat{C}}_{XY}^g-{\widehat{C}}_{XZ}^g)$ is acquired.

In view of the above results, we form a z score based on the large sample approach [38] for testing the null hypothesis $H_0:C_{XY}^g=C_{XZ}^g$. The test statistic is

$$z=\frac{{\widehat{C}}_{XY}^g-{\widehat{C}}_{XZ}^g}{\sqrt{\widehat{\mathit{var}}({\widehat{C}}_{XY}^g-{\widehat{C}}_{XZ}^g)}},$$

and we would reject the null hypothesis if we observe |z| > z_1−α/2, where z_1−α/2 is the upper α/2 quantile from a standard normal distribution.

Antolini et al. [29] considered the jackknife approach to estimate $\mathit{var}({\widehat{C}}_{XY}^g-{\widehat{C}}_{XZ}^g)$. The procedure lies in leaving out one observation, say, individual i, at a time from the sample set and recomputing the difference between two C indices based on remaining n − 1 observations, i.e., ${\widehat{C}}_{XY}^{g(-i)}-{\widehat{C}}_{XZ}^{g(-i)}$. An estimate for the variance of the two C’s difference can be calculated from this new set of replicates { ${\widehat{C}}_{XY}^{g(-i)}-{\widehat{C}}_{XZ}^{g(-i)}$}, i = 1, 2, …, n. Antolini et al. [29] showed that the jackknife estimate of variance converges to the true value asymptotically.

Alternatively, we can utilize the bootstrap resampling approach [30, 31] for variance estimations when testing difference between two correlated C indices. The procedure is as follows. We resample the original data matrix shown in Equation (1) by row (individuals) with replacement and compute the estimated ${\widehat{C}}_{XY}^g-{\widehat{C}}_{XZ}^g$ based on the resampled data. Repeat this step B = 500 times and each time we get an estimate of the difference between ${\widehat{C}}_{XY}^g$ and ${\widehat{C}}_{XZ}^g$. The sample variance of the bootstrap replicates of ${\widehat{C}}_{XY}^g-{\widehat{C}}_{XZ}^g$ is considered a bootstrap variance estimate for $\mathit{var}({\widehat{C}}_{XY}^g-{\widehat{C}}_{XZ}^g)$. A z score can be similarly formed for testing the same hypothesis.

4. Simulation Studies

We conducted extensive simulations in validating the performance of our proposed method in terms of type I error rate and power. We also compared our method with the jackknife and the bootstrap methods.

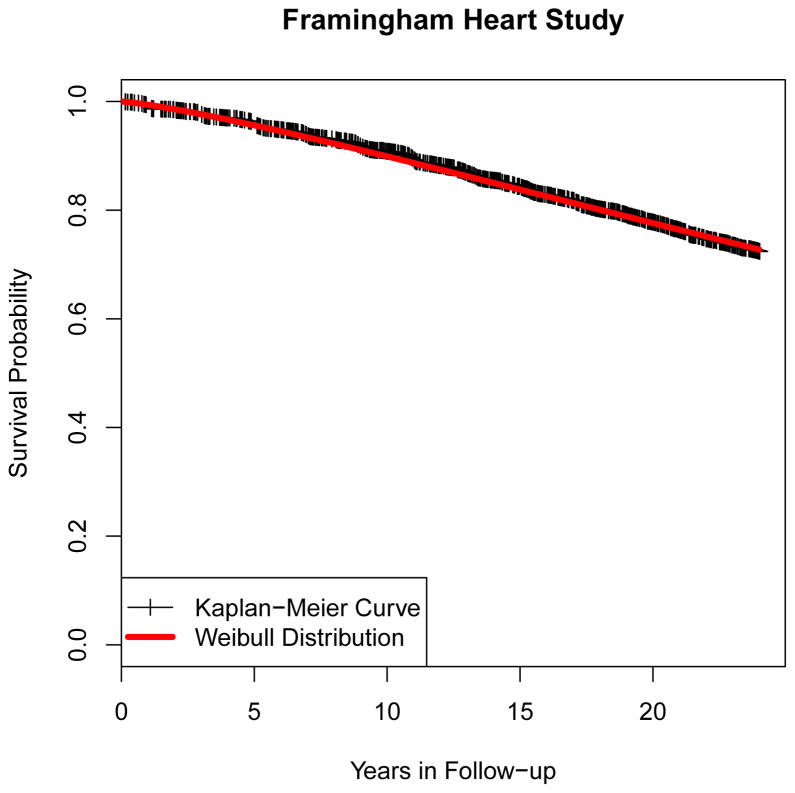
The survival time data is generated from either an exponential or a Weibull distribution. The exponential distribution assumes a fixed failure rate and has been widely used in continuous survival time modeling [39, 34]. The Weibull distribution [34], which is a generalization to the exponential distribution by allowing the failure rate to vary over the time, was also selected because it was found to fit the Kaplan-Meier survival curve in the Framingham Heart Study example as shown in Figure 1. We used both distributions in our simulations. Of course, it should be expected that our proposed method is nonparametric and thus should work for any distribution.

Figure 1.

Empirical survival function based on Framingham Heart Study. Vertical tick represents loss of a patient (censoring). The Weibull distribution with λ = 60, k = 1.25 was found to fit this survival data quite well.

We consider non-informative random censoring for each subject. The observed right-censored survival time X is recorded as the minimum of censoring time and survival time. The event indicator δ is 1 if the right-censored survival time is indeed the true survival time or 0 if the right-censored survival time is censoring time. In our simulation, the censoring time is generated using exponential distributions with various failure rates such that the censoring percentage is controlled at certain levels, ranging from 0% to 50%. Determining the failure rate parameters given the censoring percentage is achieved by iterative approximations based on sufficiently large sample sizes.

Conditioned on true survival times, two predictive scores Y and Z for each subject are simulated from bivariate normal distributions with different means and varying correlations. For simplicity, the standard deviations of two scores are fixed at 1. The means are set such that the true Δc = C_XY − C_XZ is 0.00, 0.05 or 0.10, respectively. The individual values of C_XY and C_XZ are given in Tables 1–3 and online supplementary Tables S1–S3. Again, determining mean parameters given the target C index value is achieved by iterative approximations based on sufficiently large sample sizes. It is important to keep in mind that the individual C index does depend on the censoring distribution [40], and the individual C indices reported in the tables are calculated approximately based on sufficiently large sample sizes, conditional on true survival times (without censoring). However, as we will show later in this section, the Δc = C_XY − C_XZ does not change with varying correlations and censoring percentages.

Table 1.

Bias and RMSE given as a percent of the true variance for all three variance estimators of Δc. This case study used an exponential model for survival data with 20% data censored and the correlation between two scores set to 0.50

			Delta+Ub		Bootstrap		Jackknife
Effect Size	Sample Size n	True Variancea (×104)	Relative Biasc (%)	Relative RMSEd (%)	Relative Biasc (%)	Relative RMSEd (%)	Relative Biasc (%)	Relative RMSEd (%)
Δc = 0.00	50	27.9	−0.29%	33%	14%	36%	11%	36%
CXY = 0.6	65	21.2	−0.38%	28%	10%	31%	8%	30%
CXZ = 0.6	80	16.8	−0.19%	25%	9%	28%	7%	27%
	95	14.1	−0.26%	23%	7%	25%	5%	24%
Δc = 0.05	50	29.8	−0.26%	32%	13%	35%	11%	35%
CXY = 0.6	65	22.8	−0.34%	27%	9%	30%	7%	29%
CXZ = 0.55	80	18.0	−0.13%	25%	8%	27%	6%	26%
	95	15.1	−0.24%	22%	7%	24%	5%	24%
Δc = 0.10	50	32.2	−0.35%	31%	12%	33%	10%	33%
CXY = 0.6	65	24.6	−0.45%	26%	8%	28%	7%	28%
CXZ = 0.5	80	19.5	−0.26%	24%	7%	26%	6%	25%
	95	16.4	−0.39%	21%	6%	23%	5%	22%

^aTrue variance is estimated from 100,000 MC samples.

^bDelta+U refers to the proposed variance estimator, which is a U-statistic applied to a multivariate Delta method.

^cRelative Bias (%) = Bias/TrueVariance ×100%

^dRelative RMSE (%) = RMSE/TrueVariance ×100%

Table 3.

Bias (×10⁴) for the difference estimator of two C indices. This case study used an exponential model for survival data.

Effect Size	Sample Size n	Correlation = 0.50				Correlation = 0.95
		Censoring Percentage				Censoring Percentage
		0%	10%	20%	50%	0%	10%	20%	50%
Δc = 0.00	50	−0.8653	−0.8514	−0.8428	−0.8757	−0.8505	−0.8622	−0.8430	−0.8682
CXY = 0.6	65	−0.7375	−0.7564	−0.7354	−0.7397	−0.7504	−0.7619	−0.7567	−0.7412
CXZ = 0.6	80	−0.6400	−0.6457	−0.6575	−0.6552	−0.6486	−0.6537	−0.6584	−0.6395
	95	−0.5833	−0.5658	−0.5743	−0.5557	−0.5673	−0.5740	−0.5802	−0.5691
Δc = 0.05	50	−0.7888	−0.7996	−0.7951	−0.8097	−0.7918	−0.8009	−0.7890	−0.7959
CXY = 0.6	65	−0.6594	−0.6469	−0.6412	−0.6508	−0.6446	−0.6477	−0.6396	−0.6419
CXZ = 0.55	80	−0.5485	−0.5507	−0.5452	−0.5443	−0.5373	−0.5419	−0.5334	−0.5392
	95	−0.4288	−0.4319	−0.4379	−0.4187	−0.4229	−0.4307	−0.4199	−0.4263
Δc = 0.10	50	−0.7185	−0.7296	−0.7177	−0.7163	−0.7179	−0.7223	−0.7162	−0.7135
CXY = 0.6	65	−0.5719	−0.5888	−0.5627	−0.5767	−0.5680	−0.5757	−0.5673	−0.5692
CXZ = 0.5	80	−0.4404	−0.4427	−0.4536	−0.4397	−0.4468	−0.4529	−0.4441	−0.4437
	95	−0.3603	−0.3693	−0.3734	−0.3561	−0.3683	−0.3718	−0.3668	−0.3655

Above observed with exponential survival data based on 100,000 samples; values in the table equal original bias ×10⁴

The first scenario with Δc = 0.00 corresponds to the null hypothesis whereas the latter two correspond to the alternative. The null hypothesis that there is no difference between two correlated C is rejected if |z| > z_1−α/2, where α = 0.05 for all simulations. For each configuration with different sample size n, censoring percentage, bivariate normal correlation and true Δc, we sample data from the designated distributions and apply our method, the jackknife method, and the bootstrap to perform hypothesis testing. We repeat the Monte Carlo (MC) simulation nsim = 100, 000 times to calculate the proportion of rejection being observed in these simulation experiments. This fraction is the empirical type I error rate under the null hypothesis and the empirical statistical power under the alternative.

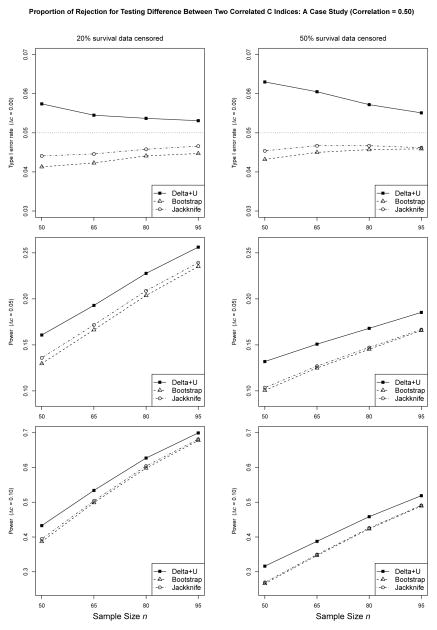
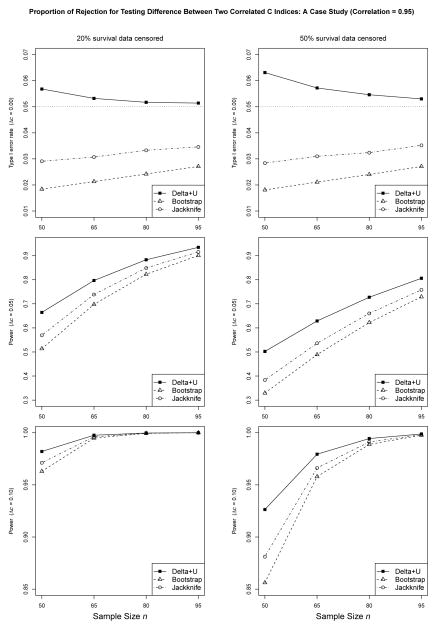
Figures 2 and 3 show the proportion of rejection under various settings with exponential survival data and the correlation between two predictive scores set to 0.50 and 0.95, respectively. From Figures 2 and 3, we see the observed error rate of our method is nominally higher than the expected rate at small sample sizes, e.g., n = 50 (detailed numbers can be found in the online supplementary Table S1). The inflation of the type I error rate is more obvious with more data censored, which can be explained by the fact that censoring reduces the effective amount of data for calculating the statistics. Nevertheless, the results indicate that the observed error rate of our method converges steadily to the expected rate as n increases. Furthermore, with increased correlations between two predictive scores Y and Z, the type I error rate is more close to the nominal level.

Figure 2.

Proportion of rejection for testing difference between two correlated C indices. This case study used an exponential model for survival data and the correlation between two scores set to 0.50. Detailed numbers can be found in the online supplementary Table S1.

Figure 3.

Proportion of rejection for testing difference between two correlated C indices. This case study used an exponential model for survival data and the correlation between two scores set to 0.95. Detailed numbers can be found in the online supplementary Table S1.

In contrast, the observed error rates of the jackknife and the bootstrap methods are further from the nominal level in the conservative direction. With 20% survival data censored and a correlation of 0.95 between two predictive variables, the observed error rates of the jackknife and the bootstrap could go as low as 0.0291 and 0.0184 at n = 50, respectively. Even with sample size n = 95, the observed error rates of the jackknife and the bootstrap are 0.0346 and 0.0271, respectively. As n increases, the error rates of the jackknife and the bootstrap methods would converge to the expected rate. Yet, it is evident that with increased correlations between two predictive scores Y and Z, the type I error rate is further away from the nominal level.

Under the alternative hypothesis, the proposed method has larger power than either the jackknife or the bootstrap method, which is consistent with the conservativeness we have just observed. For instance, when the effect size Δc = 0.05, with 20% exponential survival data censored and the correlation of 0.95 between two predictive variables, the observed power of our method is 0.7969 at n = 65, compared to 0.7388 and 0.6979, for the jackknife and the bootstrap method, respectively. Table S2 in the online supplement showing the proportion of rejection under various settings with Weibull survival data tells similar trends in the type I error rate and power.

To further understand the differences of observed type I error rate and power among different methods, we empirically assess the bias and the root mean square error (RMSE) for all three variance estimators. The true variance for the difference between two correlated C indices is estimated by the sample variance of 100,000 MC sample estimates of the difference. For every MC sample, each of our proposed method, the jackknife, and the bootstrap method, would give an estimate of the variance for the difference. The mean and the variance, as well as the bias and the RMSE, for each variance estimator can be obtained across 100,000 MC samples.

Tables 1 and 2 show the bias and the RMSE given as a percent of the true variance associated with each variance estimator with the correlation between two predictive scores set to 0.50 and 0.95, respectively. It demonstrates that our proposed variance estimator is almost unbiased across a large range of correlations even with a small to moderate sample size (downward bias < 1% for all the simulations). By contrast, the variance estimator based on the bootstrap or the jackknife is substantially biased upwards and the relative bias and RMSE increase while the correlation is higher. With sufficiently large sample sizes, all three methods converge in theory. These results explain conservative type I error rate and underpower with the jackknife and the bootstrap methods. To gain more insights on the variance estimators, we present the sampling distributions of all the variance estimates in the 100,000 MC experiments for the three variance estimators corresponding to Tables 1 and 2 in online supplementary Figures S1–S6. Again, under both the null and the alternative, our proposed variance estimator is almost unbiased while the bootstrap and the jackknife are substantially biased upwards.

Table 2.

Bias and RMSE given as a percent of the true variance for all three variance estimators of Δc. This case study used an exponential model for survival data with 20% data censored and the correlation between two scores set to 0.95

			Delta+Ub		Bootstrap		Jackknife
Effect Size	Sample Size n	True Variancea (×104)	Relative Biasc (%)	Relative RMSEd (%)	Relative Biasc (%)	Relative RMSEd (%)	Relative Biasc (%)	Relative RMSEd (%)
Δc = 0.00	50	3.6	−0.34%	44%	44%	67%	27%	55%
CXY = 0.6	65	2.6	−0.41%	38%	35%	55%	21%	46%
CXZ = 0.6	80	2.1	−0.44%	34%	31%	48%	18%	40%
	95	1.7	−0.18%	31%	27%	43%	16%	36%
Δc = 0.05	50	4.8	−0.31%	44%	38%	61%	24%	53%
CXY = 0.6	65	3.5	−0.36%	38%	30%	50%	18%	44%
CXZ = 0.55	80	2.7	−0.37%	34%	26%	45%	15%	39%
	95	2.3	−0.16%	31%	22%	40%	13%	35%
Δc = 0.10	50	7.7	−0.52%	44%	27%	53%	18%	49%
CXY = 0.6	65	5.7	−0.44%	38%	21%	45%	13%	42%
CXZ = 0.5	80	4.5	−0.51%	34%	17%	40%	11%	37%
	95	3.7	−0.35%	32%	15%	36%	9%	34%

^aTrue variance is estimated from 100,000 MC samples.

^bDelta+U refers to the proposed variance estimator, which is a U-statistic applied to a multivariate Delta method.

^cRelative Bias (%) = Bias/TrueVariance ×100%

^dRelative RMSE (%) = RMSE/TrueVariance ×100%

We mention in Section 2.3 that our formulation of the general C index can accommodate ties in predictive scores. To evaluate the robustness of our method to ties in predictive scores, we carried out simulations similar to those above except using discrete predictive scores that have ties. We use numerical rounding as a way to generate data with ties. Specifically, the simulated bivariate normal continuous scores are rounded to one decimal place as well as to the nearest integers, which results in approximately 40% and 90% of the subjects having tied score value with another subject, respectively. Then, similar to the MC simulations with the continuous data presented above, we apply our proposed method, the jackknife, and the bootstrap method to perform hypothesis testing. The results with the discrete predictive scores are generally the same as those with the continuous scores, indicating robustness of our method to data with ties. See Table S3 in the online supplement for details.

Last but not least, as we point out in the beginning of this section, it is known that the estimate of a single C index is affected by the percentage of censored observations [40], but to what extent the difference between two C indices is affected by censoring remains a concern. To this end, we evaluate the effect of censoring and the correlation between two predictive scores on the estimation of the difference between two correlated C indices via a simulation study. The result summarizing the empirical bias estimate is in Table 3. From Table 3, although there are fluctuations in empirical bias estimates, there is no evidence that the differences, all less than 0.0001, between two C indices are affected by censoring. By contrast, the bias associated with a single C index estimate may vary from 0.012 to 0.084, when the censoring percentage is increased from 10% to 50% within one of our simulation studies. The results indicate that when comparing two correlated C indices conditional on the same censored survival outcome, the biases for each C index caused by censoring are cancelled out. It is also observed that, the correlation does not have an effect on the estimation of the difference between two correlated C indices. This is within our expectation, as the correlation usually does not affect the marginal difference but does impact the variance/covariance terms.

5. Analysis of Framingham Heart Study Data Example

The Framingham Heart Study is a long term prospective study of the etiology of cardiovascular disease in a population of free living subjects in the community of Framingham, Massachusetts [32]. It was a landmark study in epidemiology in that it was the first prospective study of cardiovascular disease and identified risk factors and their joint effects. Much of the now-common knowledge concerning heart disease, such as the effects of diet, exercise, and medications, is based on this study [41, 42, 43].

The study began in 1948 and 5209 subjects were initially enrolled in the study. Participants have been examined since the inception of the study and all subjects are continuously followed through regular surveillance for cardiovascular outcomes. Clinic examination data has included cardiovascular disease risk factors and markers of disease such as blood pressure, blood chemistry, lung function, smoking history, health behaviors, ECG tracings, echocardiography, medication use and etc. Through regular surveillance of area hospitals, participant contact, and death certificates, the Framingham Heart Study reviews and adjudicates events for the occurrence of angina pectoris, myocardial infarction, heart failure, cerebrovascular disease and death [32]. Part of the dataset in this study is publicly available [44] and we use this subset of the data (4434 participants) to demonstrate the application of our proposed method.

In this application, the event time of interest is the first time that a subject had a cardiovascular disease event (angina pectoris, myocardial infarction, coronary insufficiency, or fatal coronary heart disease) during the interval of baseline to end of follow-up. The Kaplan-Meier estimates for the survival distributions of the event time and the censoring are given in Figure 1.

We consider baseline measurements (PERIOD = 1) serum total cholesterol (TOTCHOL, mg/dL), body mass index (BMI, weight in kilograms/height meters squared), systolic blood pressure (SYSBP, mmHg) and diastolic blood pressure (DIABP, mmHg) as predictive variables for the event-free survival time. These are common risk factors for cardiovascular diseases [45, 46, 47]. We conducted testing to determine if a certain biomarker has better prognosis than others in terms of the C index.

The estimated sample values of C are 0.4018, 0.4021, 0.3651 and 0.3938 for TOTCHOL, BMI, SYSBP and DIABP, respectively. Note that the C values are less than 0.5, which suggests that lower values, not higher values, of the biomarkers correlate with longer event-free survival time. The difference between two values of C from SYSBP and DIABP is 0.0287 with a p-value < 0.0001 using our proposed method. Although the difference of 0.0003 between two C indices from TOTCHOL and BMI is quite small, it reports a p-value of 0.0388. That is to say, SYSBP is better than DIABP, and TOTCHOL might be slightly better than BMI, in predicting event-free survival time. Our finding is consistent with Stamler et al.’s result that systolic blood pressure relates more strongly to all cardiovascular risk than diastolic blood pressure [48].

6. Discussion

In this article, we investigated the problem of assessing the performance of biomarkers or classifiers in predicting right-censored survival outcomes in terms of the C index. We developed a nonparametric approach for comparing two correlated C indices for two tests (biomarkers or classifiers) performed on a common cohort of subjects. Specifically, we derived analytical one-shot estimators for the variance of the C index estimator and the covariance between two C indices. The one-shot estimators require no resampling procedure and thus are computationally efficient. These provided the necessary recipes for using the z score test to statistically compare two tests in regard to their C indices. Our extensive simulations showed that our proposed approach had satisfactory performance in terms of type I error control and statistical power with moderate to large sample sizes. We also showed that our approach compares favorably to resampling methods such as the jackknife method [29] and the bootstrap method as it provides an almost unbiased variance estimator for the difference estimate between two correlated C indices. Finally, we applied our method to the Framingham Heart Study data for an application in the problem of biomarker comparison for survival prognosis.

Given the negligible bias of our proposed variance estimator across a large range of correlations and sample sizes shown in the simulation studies, it is clear that the proposed variance estimator is not impacted by the correlations or the sample sizes. On the contrary, the bias and the RMSE associated with the bootstrap or the jackknife variance estimator increase significantly when the correlations are higher, indicating that the accuracy of the bootstrap or the jackknife variance estimator heavily depends on the correlations. Meanwhile, our simulation results indicate that the type I error rate of our proposed test is not impacted much by the correlations either, as compared to the increasing conservativeness for the test based on the bootstrap or the jackknife variance estimator when the correlations are increasingly higher. In short, the relative gain of our proposed method as compared to the resampling methods when the correlations are higher is not because our method depends on the correlations, but because of the dependence of the resampling methods on the correlations, i.e., they perform a lot worse when the correlations increase. By theory, our proposed method appropriately accounts for the correlations in estimating the variance of the difference between two correlated C indices and thus we do not expect the performance to depend on varying correlations.

Linking up with the fact that our proposed variance estimator works quite well across a large range of correlations and sample sizes, the inflated type I error rate at small sample sizes observed in our results indicates that the only limitation of our proposed method is the use of the standard normal distribution for the test statistic at very small sample sizes. The test statistic for the comparison of two general C indices is not quite normal at small sample sizes, because we are estimating the variance; we do not know the population variance parameter exactly. Consequently the distribution of the test statistic is wider. It may be possible to account for this by using the t distribution with an appropriate estimate of the degree of freedom. This will be addressed in our future work.

In the meantime, the seemingly fine controlled type I error rate for the z score test based on the bootstrap or the jackknife variance estimator when the correlations are moderate is in fact caused by the compromise of two types of errors, 1) an overestimate of the true variance of Δc = C_XY − C_XZ, and 2) an underestimate of the critical value based on standard normal distribution. These two types of errors sometimes happen to cancel out so the type I error rate looks just fine. However, when the correlations are much higher, the error caused by the overestimation of the true variance of Δc would outweigh the error caused by using an underestimated critical value based on the standard normal distribution, and thus we observe extreme conservativeness. We suggest that caution be taken before using the z score test based on the bootstrap or the jackknife variance estimator as people may not realize that errors are being mixed in producing p-values.

Besides the C index we have considered in this article, various accuracy measures have been suggested to assess the ability of a predictive score Y in predicting the censored survival time X. Some examples of these include proportion of explained variation [49, 50, 51], integrated Brier score [52], time-dependent ROC measure [16, 17, 18, 19], to name a few. Specifically, by choosing appropriate weight functions w(t), it can be shown that a weighted average of the area under an incident time-dependent ROC curve at time t, AUC_t = ∫ROC_t(u)du, where ${\text{ROC}}_t(u)={\text{TPR}}_t\{{\text{FPR}}_t^{-1}(u)\}$, TPR_t(y) = P(Y ≥ y|X = t), FPR_t(y) = P(Y ≥ y|X > t), is equivalent to the C index [17].

Our method for comparing two correlated C indices is analogous to the role of DeLong et al.’s method [11] for comparing two correlated AUCs with binary disease outcomes. We reiterate that predictive scores in this article can be measured values of biomarkers, composite patient scores output from algorithms combining multiple biomarkers, predicted survival times or predicted probabilities of survival until any fixed time point based on mathematical models. We account for ties in the predictive scores. This is more robust than existing methods that assume continuous scores because ties in predictive scores can occur in many practical applications. For instance, ties occur naturally in categorical predictive variables and they may even occur in theoretically continuous variables due to categorization or discretization.

We note that our method cannot deal with the problem of limit of detection (LoD) that may occur in biomarker measurements. Vexler et al. [53] considered comparing the correlated AUCs of diagnostic biomarkers whose measurements are subject to a limit of detection. Their approach may be extended to the C index metric for dealing with both censored outcome and LoD in predictive scores. It is also possible to extend our method by properly modifying the csign function in Equations (5–6) to deal with LoD. It remains interesting future work for such extensions and comparisons.

In recent years, many investigators, e.g., [54, 55], have noticed empirically that the DeLong et al.’s method based on U-statistics [11] for testing two correlated AUCs resulting from nested models (reduced versus full model), often produces a non-significant result in assessing the incremental value when a corresponding Wald test or likelihood ratio test from the underlying regression model is significant. We have investigated this interesting problem in a recent paper [56]. The reported “problems” of the DeLong et al.’s method is essentially because the method is misused (i.e., used in a fashion that the method is not designed for) by training and testing the models using the same dataset. The DeLong et al.’s test is designed for comparing two fixed models that are tested on a common dataset that is independent of the training set. The DeLong et al.’s variance estimator does not incorporate the variance caused by the model training process, and therefore, fitting the full model and the reduced model based on the training dataset and then testing two correlated AUCs based on the same dataset would violate the assumption of the DeLong et al.’s method, and thus lead to an incorrect variance estimate. Similarly, for our proposed method, when the predictive scores are outputs from an algorithm that combines multiple biomarkers, our method assumes that the algorithm is trained and fixed and ready to be tested on an independent test dataset. In other words, our method cannot be used to compare two resubstitution C indices that are obtained by training and testing the algorithm using the same dataset.

A supplementary R package to implement the methods described in this article is available for download and ready to use at http://code.google.com/p/assessment-of-classifiers/. An example demo on how to use the software can be found in the package.

A. The Multivariate Delta Method for Variance Estimators

Following the formula of Casella and Berger [37], we have

$$\begin{array}{l}\mathit{var}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\approx {\left[\frac{\partial }{t_{XY}}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]}^2\mathit{var}(t_{XY})+{\left[\frac{\partial }{t_{XX}^{\ast }}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]}^2\mathit{var}(t_{XX}^{\ast })+2\left[\frac{\partial }{t_{XY}}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XX}^{\ast }}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\mathit{cov}(t_{XY},t_{XX}^{\ast })\\ =\left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XY}}{t_{XX}^{\ast 2}}\end{array}\right)\left[\begin{array}{cc}\mathit{var}(t_{XY})& \mathit{cov}(t_{XX}^{\ast },t_{XY})\\ \mathit{cov}(t_{XX}^{\ast },t_{XY})& \mathit{var}(t_{XX}^{\ast })\end{array}\right]{\left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XY}}{t_{XX}^{\ast 2}}\end{array}\right)}^T,\\ \mathit{var}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\approx {\left[\frac{\partial }{t_{XZ}}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]}^2\mathit{var}(t_{XZ})+{\left[\frac{\partial }{t_{XX}^{\ast }}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]}^2\mathit{var}(t_{XX}^{\ast })+2\left[\frac{\partial }{t_{XZ}}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XX}^{\ast }}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\mathit{cov}(t_{XZ},t_{XX}^{\ast })\\ =\left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XZ}}{t_{XX}^{\ast 2}}\end{array}\right)\left[\begin{array}{cc}\mathit{var}(t_{XZ})& \mathit{cov}(t_{XX}^{\ast },t_{XZ})\\ \mathit{cov}(t_{XX}^{\ast },t_{XZ})& \mathit{var}(t_{XX}^{\ast })\end{array}\right]{\left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XZ}}{t_{XX}^{\ast 2}}\end{array}\right)}^T,\\ \mathit{cov}\left(\frac{t_{XY}}{t_{XX}^{\ast }},\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\approx \underset{=0}{\underbrace{\left[\frac{\partial }{t_{XY}}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XY}}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\mathit{var}(t_{XY})}}+\underset{=0}{\underbrace{\left[\frac{\partial }{t_{XZ}}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XZ}}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\mathit{var}(t_{XZ})}}\\ +\left[\frac{\partial }{t_{XX}^{\ast }}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XX}^{\ast }}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\mathit{var}(t_{XX}^{\ast })\\ +\left[\frac{\partial }{t_{XY}}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XZ}}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\mathit{cov}(t_{XY},t_{XZ})+\underset{=0}{\underbrace{\left[\frac{\partial }{t_{XZ}}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XY}}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\mathit{cov}(t_{XY},t_{XZ})}}\\ +\left[\frac{\partial }{t_{XY}}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XX}^{\ast }}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\mathit{cov}(t_{XY},t_{XX}^{\ast })+\underset{=0}{\underbrace{\left[\frac{\partial }{t_{XX}^{\ast }}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XY}}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\mathit{cov}(t_{XY},t_{XX}^{\ast })}}\\ +\underset{=0}{\underbrace{\left[\frac{\partial }{t_{XZ}}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XX}^{\ast }}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\mathit{cov}(t_{XZ},t_{XX}^{\ast })}}+\left[\frac{\partial }{t_{XX}^{\ast }}\left(\frac{t_{XY}}{t_{XX}^{\ast }}\right)\right]\left[\frac{\partial }{t_{XZ}}\left(\frac{t_{XZ}}{t_{XX}^{\ast }}\right)\right]\mathit{cov}(t_{XZ},t_{XX}^{\ast })\\ =\left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XY}}{t_{XX}^{\ast 2}}\end{array}\right)\left[\begin{array}{cc}\mathit{cov}(t_{XY},t_{XZ})& \mathit{cov}(t_{XX}^{\ast },t_{XY})\\ \mathit{cov}(t_{XX}^{\ast },t_{XZ})& \mathit{var}(t_{XX}^{\ast })\end{array}\right]{\left(\begin{array}{cc}\frac{1}{t_{XX}^{\ast }}& -\frac{t_{XZ}}{t_{XX}^{\ast 2}}\end{array}\right)}^T.\end{array}$$

B. Covariance Estimation of Kendall’s τ

Given random variables X (with censoring) and Y (without censoring), Kendall’s τ_XY quantifies the concordance between ordinal relations on two variables,

$${\tau }_{XY}=E[c\mathit{sign}(X_i,{\delta }_i,X_j,{\delta }_j)\mathit{sign}(Y_i,Y_j)]$$

for a pair of subjects (i, j), i ≠ j. Define t_ijXY = csign (X_i, δ_i, X_j, δ_j) sign (Y_i, Y_j), the sample estimate for τ_XY is

$$t_{XY}=\frac{1}{n(n-1)}\sum _i\sum _{j\ne i}{t}_{\mathit{ijXY}},$$

and it is easy to verify that t_XY is an unbiased estimator for τ_XY.

In general, given another pair of random variables U (with censoring) and Z (without censoring),

$$\mathit{cov}(t_{XY},t_{UZ})=E[t_{XY}{t}_{UZ}]-{\tau }_{XY}{\tau }_{UZ}.$$

Note that $t_{XY}{t}_{UZ}=\frac{1}{n^2{(n-1)}^2}{\displaystyle \sum _i}{\displaystyle \sum _j}{\displaystyle \sum _{i^{\prime }}}{\displaystyle \sum _{j^{\prime }}}{t}_{\mathit{ijXY}}{t}_{i^{\prime }{j}^{\prime }UZ}$, where i, j, i′ and j′ represent sampled individuals,

$$\begin{array}{l}E(t_{XY}{t}_{UZ})=\frac{1}{n^2{(n-1)}^2}\sum _i\sum _{j\ne i}\sum _{i^{\prime }}\sum _{j^{\prime }\ne i^{\prime }}E[t_{\mathit{ijXY}}{t}_{i^{\prime }{j}^{\prime }UZ}]\\ =\frac{1}{n^2{(n-1)}^2}\sum _i\sum _{j\ne i}\{E[t_{\mathit{ijXY}}{t}_{\mathit{ijUZ}}]+\sum _{\begin{array}{l}{j}^{\prime }\ne j\\ j^{\prime }\ne i\end{array}}E[t_{\mathit{ijXY}}{t}_{i{j}^{\prime }UZ}]+\sum _{\begin{array}{l}{i}^{\prime }\ne i\\ i^{\prime }\ne j\end{array}}E[t_{\mathit{ijXY}}{t}_{i^{\prime }\mathit{jUZ}}]+\sum _{i^{\prime }\ne i}\sum _{\begin{array}{l}{j}^{\prime }\ne j\\ j^{\prime }\ne i^{\prime }\end{array}}E[t_{\mathit{ijXY}}{t}_{i^{\prime }\mathit{jUZ}}]\}\\ =\frac{1}{n(n-1)}E[t_{\mathit{ijXY}}{t}_{\mathit{ijUZ}}]+\frac{n-2}{n(n-1)}E[t_{\mathit{ijXY}}{t}_{i{j}^{\prime }UZ}]+\frac{n-2}{n(n-1)}E[t_{\mathit{ijXY}}{t}_{i^{\prime }\mathit{jUZ}}]+\frac{(n-1)(n-2)+1}{n(n-1)}E[t_{\mathit{ijXY}}{t}_{i^{\prime }\mathit{jUZ}}].\end{array}$$

For each term, the coefficient is simply obtained by counting. Realizing that t_ijXY = t_jiXY and t_ijXY t_i′jUZ = t_jiXY t_ji′UZ = t_ijXY t_ij′UZ,

$$E(t_{XY}{t}_{UZ})=\frac{2}{n(n-1)}E[t_{\mathit{ijXY}}{t}_{\mathit{ijUZ}}]+\frac{4(n-2)}{n(n-1)}E[t_{\mathit{ijXY}}{t}_{i{j}^{\prime }UZ}]+\frac{(n-2)(n-3)}{n(n-1)}E[t_{\mathit{ijXY}}{t}_{i^{\prime }{j}^{\prime }UZ}],$$

with each term corresponding to two subscripts, one subscript and no subscript in common, respectively, regardless of order. Therefore,

$$\begin{array}{l}\mathit{cov}(t_{XY},t_{UZ})=\frac{2}{n(n-1)}[\mathit{cov}(t_{\mathit{ijXY}},t_{\mathit{ijUZ}})+{\tau }_{XY}{\tau }_{UZ}]+\frac{4(n-2)}{n(n-1)}[\mathit{cov}(t_{\mathit{ijXY}},t_{i{j}^{\prime }UZ})+{\tau }_{XY}{\tau }_{UZ}]+\frac{(n-2)(n-3)}{n(n-1)}{\tau }_{XY}{\tau }_{UZ}-{\tau }_{XY}{\tau }_{UZ}\\ =\frac{2}{n(n-1)}\mathit{cov}(t_{\mathit{ijXY}},t_{\mathit{ijUZ}})+\frac{4(n-2)}{n(n-1)}\mathit{cov}(t_{\mathit{ijXY}},t_{i{j}^{\prime }UZ}).\end{array}$$

It is of interest to obtain an unbiased estimate for cov(t_XY, t_UZ). We could directly apply U-statistics to the two terms above, but the forms would be awkward to program (sums would not run over all samples). Here, we present similar results with Cliff and Charlin [57] but correct their estimators and then show the unbiasedness. The estimators presented in the following are easier to implement.

Lemma B.1

An unbiased estimator for cov(t_XY, t_UZ) is

$$\widehat{\mathit{cov}}(t_{XY},t_{UZ})=\frac{4{\displaystyle \sum _i}\left({\displaystyle \sum _j}{t}_{\mathit{ijXY}}{\displaystyle \sum _{j^{\prime }}}{t}_{i{j}^{\prime }UZ}\right)-2{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXY}}{t}_{\mathit{ijUZ}}-\frac{2(2n-3)}{n(n-1)}{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXY}}{\displaystyle \sum _{i^{\prime }}}{\displaystyle \sum _{j^{\prime }}}{t}_{i^{\prime }{j}^{\prime }UZ}}{n(n-1)(n-2)(n-3)}.$$

Proof B.1

Taking expectation of each term in the numerator, we have

$$\begin{array}{l}E\left[4\sum _i\left(\sum _j{t}_{\mathit{ijXY}}\sum _{j^{\prime }}{t}_{i{j}^{\prime }UZ}\right)\right]=4n(n-1)E(t_{\mathit{ijXY}}{t}_{\mathit{ijUZ}})+4n(n-1)(n-2)E(t_{\mathit{ijXY}}{t}_{i{j}^{\prime }UZ})\\ E\left[2\sum _i\sum _j{t}_{\mathit{ijXY}}{t}_{\mathit{ijUZ}}\right]=2n(n-1)E(t_{\mathit{ijXY}}{t}_{\mathit{ijUZ}})\\ E\left[\frac{2(2n-3)}{n(n-1)}\sum _i\sum _j{t}_{\mathit{ijXY}}\sum _{i^{\prime }}\sum _{j^{\prime }}{t}_{i^{\prime }{j}^{\prime }UZ}\right]=2(2n-3)E\left[t_{\mathit{ijXY}}\sum _i\sum _j{t}_{\mathit{ijUZ}}\right]\\ =2(2n-3)[2E(t_{\mathit{ijXY}}{t}_{\mathit{ijUZ}})+4(n-2)E(t_{\mathit{ijXY}}{t}_{i{j}^{\prime }UZ})+(n-2)(n-3)E(t_{\mathit{ijXY}}{t}_{i^{\prime }{j}^{\prime }UZ})]\end{array}$$

Combine all terms above,

$$\begin{array}{l}E[\widehat{\mathit{cov}}(t_{XY},t_{UZ})]=\frac{2(n-2)(n-3)E(t_{\mathit{ijXY}}{t}_{\mathit{ijUZ}})}{n(n-1)(n-2)(n-3)}+\frac{4{(n-2)}^2(n-3)E(t_{\mathit{ijXY}}{t}_{i{j}^{\prime }UZ})}{n(n-1)(n-2)(n-3)}-\frac{2(2n-3)(n-2)(n-3)E(t_{\mathit{ijXY}}{t}_{i^{\prime }{j}^{\prime }UZ})}{n(n-1)(n-2)(n-3)}\\ =\frac{2(n-2)(n-3)[\mathit{cov}(t_{\mathit{ijXY}},t_{\mathit{ijUZ}})+{\tau }_{XY}{\tau }_{UZ}]}{n(n-1)(n-2)(n-3)}+\frac{4{(n-2)}^2(n-3)[\mathit{cov}(t_{\mathit{ijXY}},t_{i{j}^{\prime }UZ})+{\tau }_{XY}{\tau }_{UZ}]}{n(n-1)(n-2)(n-3)}-\frac{2(2n-3)(n-2)(n-3){\tau }_{XY}{\tau }_{UZ}}{n(n-1)(n-2)(n-3)}\\ =\frac{2}{n(n-1)}\mathit{cov}(t_{\mathit{ijXY}},t_{\mathit{ijUZ}})+\frac{4(n-2)}{n(n-1)}\mathit{cov}(t_{\mathit{ijXY}},t_{i{j}^{\prime }UZ})\\ =\mathit{cov}(t_{XY},t_{UZ})\end{array}$$

In the case of the variances and covariances involving a shared variable,

$$\begin{array}{l}\widehat{\mathit{var}}(t_{XX}^{\ast })=\frac{4{\displaystyle \sum _i}{\left({\displaystyle \sum _j}{t}_{\mathit{ijXX}}^{\ast }\right)}^2-2{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXX}}^{\ast 2}-\frac{2(2n-3)}{n(n-1)}{\left({\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXX}}^{\ast }\right)}^2}{n(n-1)(n-2)(n-3)},\\ \widehat{\mathit{var}}(t_{XY})=\frac{4{\displaystyle \sum _i}{\left({\displaystyle \sum _j}{t}_{\mathit{ijXY}}\right)}^2-2{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXY}}^2-\frac{2(2n-3)}{n(n-1)}{\left({\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXY}}\right)}^2}{n(n-1)(n-2)(n-3)},\\ \widehat{\mathit{cov}}(t_{XY}^{\ast },t_{XY})=\frac{4{\displaystyle \sum _i}\left({\displaystyle \sum _j}{t}_{\mathit{ijXX}}^{\ast }{\displaystyle \sum _{j^{\prime }}}{t}_{i{j}^{\prime }XY}\right)-2{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXX}}^{\ast }{t}_{\mathit{ijXY}}-\frac{2(2n-3)}{n(n-1)}{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXX}}^{\ast }{\displaystyle \sum _{i^{\prime }}}{\displaystyle \sum _{j^{\prime }}}{t}_{i^{\prime }\mathit{jXY}}}{n(n-1)(n-2)(n-3)},\\ \widehat{\mathit{cov}}(t_{XY},t_{XZ})=\frac{4{\displaystyle \sum _i}\left({\displaystyle \sum _j}{t}_{\mathit{ijXY}}{\displaystyle \sum _{j^{\prime }}}{t}_{i{j}^{\prime }XZ}\right)-2{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXY}}{t}_{\mathit{ijXZ}}-\frac{2(2n-3)}{n(n-1)}{\displaystyle \sum _i}{\displaystyle \sum _j}{t}_{\mathit{ijXY}}{\displaystyle \sum _{i^{\prime }}}{\displaystyle \sum _{j^{\prime }}}{t}_{i^{\prime }{j}^{\prime }XZ}}{n(n-1)(n-2)(n-3)}.\end{array}$$