In Situ Ca²⁺ Titration in the Fluorometric Study of Intracellular Ca²⁺ Binding

Abstract

Imaging with Ca²⁺-sensitive fluorescent dye has provided a wealth of insight into the dynamics of cellular Ca²⁺ signaling. The spatiotemporal evolution of intracellular free Ca²⁺ observed in imaging experiments is shaped by binding and unbinding to cytoplasmic Ca²⁺ buffers, as well as the fluorescent indicator used for imaging. These factors must be taken into account in the interpretation of Ca²⁺ imaging data, and can be exploited to investigate endogenous Ca²⁺ buffer properties. Here we extended the use of Ca²⁺ fluorometry in the characterization of Ca²⁺ binding molecules within cells, building on a method of titration of intracellular Ca²⁺ binding sites in situ with measured amounts of Ca²⁺ entering through voltage-gated Ca²⁺ channels. We developed a systematic procedure for fitting fluorescence data acquired during a series of voltage steps to models with multiple Ca²⁺ binding sites. The method was tested on simulated data, and then applied to 2-photon fluorescence imaging data from rat posterior pituitary nerve terminals patch clamp-loaded with the Ca²⁺ indicator fluo-8. Focusing on data sets well described by a single endogenous Ca²⁺ buffer and dye, this method yielded estimates of the endogenous buffer concentration and K_d, the dye K_d, and the fraction of Ca²⁺ inaccessible cellular volume. The in situ K_d of fluo-8 thus obtained was indistinguishable from that measured in vitro. This method of calibrating Ca²⁺-sensitive fluorescent dyes in situ has significant advantages over previous methods. Our analysis of Ca²⁺ titration fluorometric data makes more effective use of the experimental data, and provides a rigorous treatment of multivariate errors and multiple Ca²⁺ binding species. This method offers a versatile approach to the study of endogenous Ca²⁺ binding molecules in their physiological milieu.

1. Introduction

Fluorometric Ca²⁺ indicators have served as powerful tools in the study of Ca²⁺ in living cells [1–5]. Photometric experiments with these probes provide measurements of cytoplasmic free Ca²⁺ concentration ([Ca²⁺]_Free), and imaging experiments in real time have provided insight into the spatiotemporal dynamics of [Ca²⁺]_Free as it rises and falls during physiological processes. Changes in [Ca²⁺]_Free are modified in amplitude, time course, and spatial spread by molecules that bind Ca²⁺, including both fluorescent indicators and endogenous Ca²⁺ buffers. Quantitative Ca²⁺ fluorometry can provide useful information about endogenous Ca²⁺ buffers, provided that care is taken to resolve the contributions to Ca²⁺ binding by the various relevant species. By evaluating the effects of different dye concentrations on Ca²⁺ signals one can estimate the endogenous buffering capacity [4,6–9].

Most studies of cytoplasmic Ca²⁺ buffering simply measure buffering capacity without determining the K_d and concentration of endogenous Ca²⁺ binding molecules. Furthermore, relatively few studies have used measurements of amount of added Ca²⁺ and cellular volume to estimate the change in total Ca²⁺ concentration ([Ca²⁺]_Total). Measurements of radiolabeled Ca²⁺ [10], photoreleased Ca²⁺ [11,12], and Ca²⁺ current (I_Ca) [13] have all been used to estimate the added Ca²⁺ in conjunction with fluorometric [Ca²⁺]_Free in various cell types. Loss of cellular Ca²⁺ can also be determined from the current of the Ca²⁺/Na⁺ exchanger [14] or from changes in extracellular Ca²⁺ [15], and used to estimate buffer capacity. By titrating Ca²⁺ with multiple steps using I_Ca [16] or added Ca²⁺ [17], one can follow the saturation of cytoplasmic binding sites as a function of [Ca²⁺]_Free. The buffering capacity decreases as [Ca²⁺]_Free rises and this saturation provides a determination of the K_d and concentration of endogenous Ca²⁺ buffer [16]. A variation of this approach treated the Ca²⁺ entry per pulse as a parameter and analyzed the rise in [Ca²⁺]_Free with a two-binding site model to determine the endogenous buffer properties [18].

Previous studies of in situ Ca²⁺ titration used the average [Ca²⁺]_Free for each step rather than the initial and final [Ca²⁺]_Free [16,18], and relied on a morphological estimate of the available cellular volume [16]. In the case of cardiac myocytes, optical signals were quite large and the buffering contribution of the Ca²⁺ indicator was relatively small [16]. In an effort to improve the utility of Ca²⁺ titration and apply it more broadly to different preparations, we developed a more robust method of analyzing the titration of cellular Ca²⁺ binding sites. Starting with the mass balance relation between initial and final [Ca²⁺]_Free for each pulse together with I_Ca, we developed a procedure for fitting to a model with multiple binding sites that accounts for the errors in all three relevant measurements. We applied this method to patch clamp/imaging experiments in peptidergic nerve terminals of the rat posterior pituitary [19], estimated the concentration and K_d of an endogenous buffer, the K_d of the Ca²⁺-sensitive dye fluo-8, and the fraction of Ca²⁺ inaccessible volume.

2. Materials and Methods

2.1 Posterior Pituitary Slice preparation

Sprague-Dawley rats (aged 6–9 weeks) were anesthetized with isoflurane and decapitated according to procedures approved by the Animal Care and Use Committee at the University of Wisconsin. The posterior pituitary gland was removed and sliced at 70 μm with a VT1200S vibratome (Leica Biosystems) in ice cold artificial cerebrospinal fluid (aCSF) consisting of 125 mM NaCl, 4 mM KCl, 1.25 mM NaH₂PO₄, 26 mM NaHCO₃, 2 mM CaCl₂, and 1 mM MgCl₂ saturated with 95% O₂/5% CO₂. Slices were used immediately or stored in aCSF at room temperature for up to four hours. The posterior pituitary consists primarily of peptidergic nerve terminals, many of which are over 10 μm in diameter [20], and patch clamp recordings provide estimates of capacitance consistent with this size [21,22]. Morphological studies of patch clamped structures in posterior pituitary slices revealed fine appended axons [23]. These axons have ~20-fold smaller diameters than the swellings and should have minimal effects on Ca²⁺, but as an added precaution we discarded recordings when axons were visible in order to minimize the effects of Ca²⁺ diffusion into axons on fluorescence measurements. We also discarded recordings in which I_Ca recordings showed notches or humps that indicate poor space clamp.

2.2 Electrophysiology

Large nerve terminals with diameters of ~10 μm were located at the surface of a slice under visual guidance using laser scanning gradient contrast microscopy [24,25]. An Axopatch 200B patch clamp amplifier (Molecular Devices) was used to record from nerve terminals in the whole-terminal configuration. Signals were digitized by a digidata 1322A interface connected to a computer running pClamp 8. Slices were perfused with a solution consisting of 121 mM NaCl, 4 mM CsCl, 10 mM CaCl₂, 1 mM MgCl₂, 20 mM tetraethylammonium chloride, 2 mM 4-aminopyridine, 10 mM glucose, 3 μM tetrodotoxin, and 10 mM HEPES, pH 7.3. Patch pipettes fabricated from borosilicate glass capillaries (King Precision Glass) had resistances of 2–5 MΩ when filled with a solution consisting of 130 mM CsCl, 10 mM Na phosphocreatine, 15 mM tetraethylammonium chloride, 4 mM Mg-ATP, 0.3 mM GTP, and 10 mM HEPES, pH 7.3. These solutions blocked voltage-gated Na⁺ and K⁺ channels to isolate I_Ca [26]. In addition, the pipette solution contained 50 or 100 μM of the Ca²⁺ indicator dye Fluo-8 (Teflabs). Leak current was subtracted by a P/4 protocol.

2.3 Calcium imaging and two-photon microscopy

Fluorescence was imaged with a Prairie Ultima two-photon microscope using galvanometer based scanning (Bruker Corporation). A chameleon Ti-sapphire laser (Coherent) tuned to λ = 920 nm delivered sub-100 fs pulses to the sample. Epifluorescence and transfluorescence were collected by a 60x, NA 0.9 water immersion objective and an oil immersion, NA 1.4 condenser (Olympus), respectively.

We used the dynamic range Ca²⁺ indicator fluo-8. At equilibrium the fluorescence of such a dye can be used to calculate [Ca²⁺]_Free as:

$${[{Ca}^{2+}]}_{\text{Free}}=K_d\frac{F-1/R_F}{1-F}$$ (1)

F is the ratio of fluorescence to the maximal fluorescence when the dye is saturated with Ca²⁺ (f/f_max). R_F is the dynamic range, the ratio of bound/free dye fluorescence (f_max/f_min). According to the manufacturer (Teflabs), R_F ~150 in vitro. We determined a somewhat lower dynamic range of ~100, but this difference may be due to limitations in the dynamic range of our system. In general, for very large values, errors in R_F introduce only small errors in calculated [Ca²⁺]_Free [27]. This uncertainty between R_F = 100 versus 150 contributed an error to our determination of [Ca²⁺]_Free of only ~0.7% for [Ca²⁺]_Free near K_d, which is well below the other sources of error.

Dye loading after break-in was monitored by observing the rise in resting fluorescence. Fluorescence stabilized within about one minute of break-in. Experiments began only after this stable state had been reached. Nerve terminals retained their fluorescence for up to an hour after the termination of a recording, making it unlikely that dye efflux pathways could create a steady state with lower dye concentration in a nerve terminal than in the pipette. We therefore took the intracellular dye concentration as equal to that in the pipette.

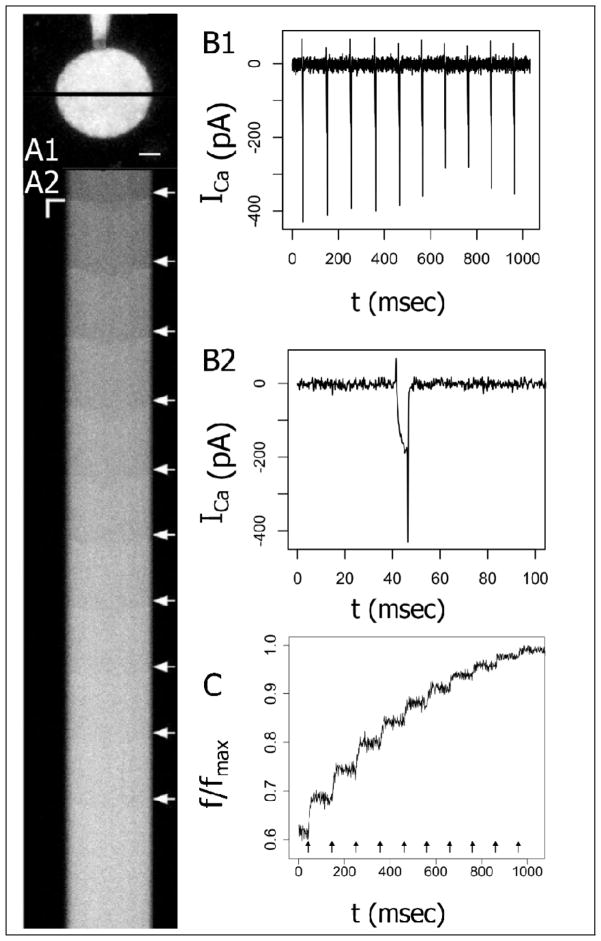
Fluorescence was acquired in line-scan mode with a temporal resolution of ~1 msec per line and diffraction limited spatial resolution (Fig. 1A). Immediately after the application of a voltage step, a spatial fluorescence gradient appeared across the nerve terminal and collapsed over the course of several milliseconds. This is indicated by the delayed rise in the center of the scanned lines (Fig. 1A2). Subsequent to the collapse of the gradient, [Ca²⁺]_Free was taken as spatially uniform. Fluorescence averaged over the scanned line through the nerve terminal (Fig. 1A1) increased (Fig. 1C) as voltage pulses evoked I_Ca (Figs. 1B1 and 1B2). For each 5 msec pulse, the fluorescence trace was averaged off-line over the inter-stimulus time interval (during which it is nearly constant) to produce measurements of initial fluorescence f_I before the pulse, and final fluorescence f_F after the pulse.

Fig 1.

A1. Two-photon fluorescence micrograph of a posterior pituitary nerve terminal loaded with 100 μM fluo-8. The dye-filled patch electrode is visible above. The black line indicates the segment selected for line-scanning. Scale bar = 2 μm. A2. Line scans show fluorescence versus time. Fluorescence increases were evoked by a train of 5 msec voltage steps from −80 mV to 10 mV at 100 msec intervals delivered at the white arrows. The horizontal axis corresponds to the spatial dimension along the black line shown in A1 (scale bar = 2 μm). The vertical axis corresponds to time (scale bar = 25 msec). B1. Ca²⁺ current (I_Ca) was recorded during the train of 10 pulses. B2. I_Ca from the first pulse is shown on an expanded time scale. C. Fluorescence was averaged over the scanned line through the nerve terminal (indicated in 1A1) and plotted versus time.

2.4 Ca²⁺ binding Model

We treat a volume, V, determined from a z-series of optical sections. Nerve terminals with visible axons [23] were not used, in order to avoid their contributions to volume, although as noted above the small diameters of axons should minimize their effects on our measurements. A fraction of the volume that excludes Ca²⁺ (V_E) will reduce the effective volume. V_E will be estimated in the course of our analysis.

Our model cell has a concentration B_T,D of Ca²⁺-sensitive fluorescent dye (with dissociation constant, K_d,D) as well as endogenous Ca²⁺ buffers. Each species has a buffering capacity, κ_j:

$${\kappa }_j=\frac{\partial [B_j]}{\partial {[{Ca}^{2+}]}_{\mathit{Free}}}$$ (2)

where B_J denotes the Ca²⁺ bound form of the J^th Ca²⁺-binding species. The total buffering capacity of the cytoplasm then becomes a sum of the contributions from each species:

$$\begin{array}{l}{\kappa }_{\mathit{Total}}=\frac{\partial {[{Ca}^{2+}]}_{\mathit{Total}}}{\partial {[{Ca}^{2+}]}_{\mathit{Free}}}\\ =\frac{\partial }{\partial {[{Ca}^{2+}]}_{\mathit{Free}}}({[{Ca}^{2+}]}_{\mathit{Free}}+{\sum }_j[B_J])\\ =1+{\sum }_j{\kappa }_j\end{array}$$ (3)

This sum includes contributions from both the dye and endogenous Ca²⁺ buffers (K_d,E1, K_d,E2, etc.). Each species saturates as Ca²⁺ concentration rises, leading to the following concentration dependence for κ_j[6,16,18]:

$${\kappa }_j=\frac{K_{d,j}{B}_{T,j}}{{(K_{d,j}+{[{Ca}^{2+}]}_{\mathit{Free}})}^2}$$ (4)

Each voltage pulse gives us a pair of fluorescence measurements, the initial value before the pulse, F_I (=f_I/f_max) and the final value immediately after, F_F (=f_F/f_max). We can calculate the corresponding [Ca²⁺]_Free,I and [Ca²⁺]_Free,F, from Eq. 1. For a single buffer (with B_T and K_d), the change in [Ca²⁺]_Total is the sum of the change in [Ca²⁺]_Free and the change in the concentration of Ca²⁺-buffer complex:

$$\mathrm{\Delta }{[{Ca}^{2+}]}_{\mathit{Total}}={[{Ca}^{2+}]}_{\mathit{Free},F}-{[{Ca}^{2+}]}_{\mathit{Free},I}+B_T[\frac{{[{Ca}^{2+}]}_{\mathit{Free},F}}{(K_d+{[{Ca}^{2+}]}_{\mathit{Free},F})}]-\frac{{[{Ca}^{2+}]}_{\mathit{Free},I}}{(K_d+{[{Ca}^{2+}]}_{\mathit{Free},I})}$$ (5)

Assuming that I_Ca is the sole source of Ca²⁺ during a voltage step, we can determine Δ[Ca²⁺]_Total in Eq. 5 from the integral of I_Ca over one voltage pulse extended to include the I_Ca tail current. This leads to the following expression:

$$\frac{1}{2\mathrm{V}(1-{\mathrm{V}}_{\mathrm{E}})\mathrm{Q}}{\int }_{\text{pulse}}{\mathrm{I}}_{\text{Ca}}dt=\mathrm{\Delta }{[{Ca}^{2+}]}_{\mathit{Total}}=K_d(x_2-x_1)+B_T\left(\frac{1}{(1+1/x_2)}-\frac{1}{(1+1/x_1)}\right)$$ (6)

In dividing the integrated I_Ca by volume, we must correct the total volume, V, measured from microscopy by the fraction of volume that excludes Ca²⁺, V_E. Q is Faraday’s constant. We used Eq. 1 to replace [Ca²⁺]_Free in Eq. 5 with F and then substituted $x_2=\frac{F_F-1/R_F}{1-F_F},x_1=\frac{F_I-1/R_F}{1-F_I}$ to simplify the notation.

Eq. 6 does not have a unique solution. Changes in the factor 1-V_E can be compensated by proportional changes in K_d and B_T. Thus, Eq. 6 defines a family of solutions of the form $\left(\frac{1-V_E}{\alpha },\alpha K_d,\alpha B_T\right)$ for any positive value of α. This will be discussed further below.

Eq. 6 can be extended to an arbitrary number of Ca²⁺ binding species. For a fluorescent dye and one endogenous buffer (dissociation constant K_d,E1 and concentration B_T,E1) we have:

$$\frac{1}{2\mathrm{V}(1-{\mathrm{V}}_{\mathrm{E}})\mathrm{Q}}{\int }_{\text{pulse}}{\mathrm{I}}_{\text{Ca}}dt=K_{d,D}(x_2-x_1)+B_{T,D}\left(\frac{1}{(1-x_1)}-\frac{1}{(1+x_2)}\right)+K_{d,E1}{B}_{T,E1}\left(\frac{1}{(K_{d,E1}+K_{d,D}{x}_1)}-\frac{1}{(K_{d,E1}+K_{d,D}{x}_2)}\right)$$ (7)

The terms containing x₁ and x₂ have been rearranged to make the expression simpler.

Eqs. 6 and 7 represent models that relate three measured quantities, Δ[Ca²⁺]_Total (as determined from I_Ca), F_I, and F_F. Each voltage step provides one triplet data point and each train of pulses provides 10–20 such triplets. The strategy of the present work is to vary the parameters in the model to fit these triplets of data. This work extends previous applications of Ca²⁺ titration [16,18] by using the initial and final fluorescence rather than a time average, by incorporating multiple binding sites, and by incorporating V_E as a free parameter. Furthermore, our use of line scans provides data in which uncertainty due to spatial variations can be avoided.

As noted following Eq. 6, Eq. 7 also defines a family of solutions $\left(\frac{1-V_E}{\alpha },\alpha K_{d,D},\alpha B_{T,D},\alpha K_{d,E1},\alpha B_{T,E1}\right)$, and a scaling factor, α, must be determined. We can take α = 1 in the present scenario by equating the cytoplasmic dye concentration with the concentration in the pipette (2.3 Methods). Scenarios with α not equal to one include cases where the dye fails to equilibrate between the pipette and cell, or with dye loading as an AM ester such that its concentration is unknown. If the dye concentration in the cell cannot be equated with that in the pipette then independent knowledge of another parameter is needed. This extends the sphere of problems to which this method can be applied, as will be expanded upon in the discussion. Simulations indicated that with realistic noise levels, the estimation of the parameters K_d,D and K_d,E1 remained robust, even under the condition of strong Ca²⁺ buffering (Supplemental Material). Examination of Eq. 7 makes the important point that parameter determination requires measurements over a wide range of [Ca²⁺]_Free. κ must change in order for the different terms in parentheses to make their presence felt.

2.5 Simulations and data analysis

Simulated and experimental data were fitted to Eq. 7 by varying some or all of the parameters V_E, K_d,D, B_T,D, K_d,E1, and B_T,E1 and using the method of total least squares (TLS) to evaluate the quality of the fit. (Supplemental Material develops this method in detail). Briefly, the standard method of minimizing the sum of the squared residuals, or ordinary least squares (OLS), relies on the assumption that errors in the independent variables are negligibly small and errors in the dependent variable are independent, identically distributed random normal variables. Our data set consists of triplet measurements: F_I, F_F, and integrated I_Ca. Although the error in I_Ca is very small compared to the errors in F_I and F_F, we cannot choose two independent variables that satisfy the condition of negligibly small errors. The OLS estimator yielded unreliable estimates of the parameters with simulated data. TLS accounted for the errors in the independent variables and its application to simulated data yielded unbiased parameter estimates with small variance. Supplemental Material presents simulations with data generated by taking an experimental F_I value and integrated I_Ca from a single nerve terminal to calculate F_F from Eq. 7. We fitted models to data with a stochastic gradient descent algorithm that converged with high probability to the same set of parameters from any starting estimates. Goodness of fit was assessed with the F-test using a cutoff of P = 0.05. Data analysis was performed in the statistical computing environment R [28]. The code and a sample data set are available as Supplemental Material. Model fits for single data sets are reported as the TLS estimator with standard errors determined by bootstrap resampling with 10000 resampled data sets [29]. Parameter errors were also estimated with the block jackknife method [29], and the differences between the results of the two procedures were not statistically significant. Parameter estimates from the population of nerve terminals in this study are presented as mean ± s.e.m. The standard deviations calculated by averaging over nerve terminals were found to be similar to the uncertainty estimated by the bootstrap and jackknife estimates for errors in the individual fits.

3. Results

3.1 Saturation of dye and determination of f_max

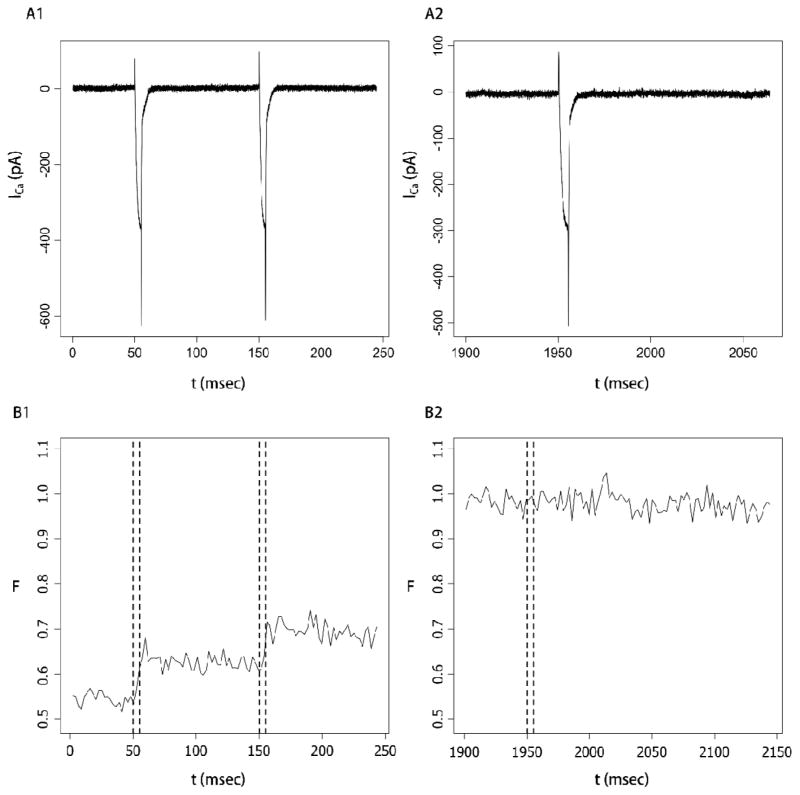
Nerve terminals were held at −80 mV and depolarized in trains of 10 or 20 steps of 5 msec to +10 mV at 100 msec intervals. I_Ca and fluorescence were recorded simultaneously. This stimulus protocol has been shown to be effective in elevating [Ca²⁺]_Free in this preparation [19,26]. Initial fluorescence before the start of a train was generally slightly above 0.5, consistent with a resting [Ca²⁺]_Free of pituitary nerve terminals that is close to the K_d of fluo-8 [7,26]. Voltage pulses opened Ca²⁺ channels, and early in a train these pulses produced clear increases in fluorescence in register with I_Ca (Figs. 2A1 and 2B1). These increments became smaller as the train continued, and the last pulse produced little or no fluorescence increase (Figs. 1C and Fig. 2B2). Because I_Ca varied by less than 30% throughout the train of voltage steps we can conclude that pulses continued to allow substantial amounts of Ca²⁺ to enter as the fluorescence leveled off. Fluorescence remained high following the final pulse with no visible decay for at least 100 msec (Fig. 2B2). By contrast, after early pulses the fluorescence showed a modest but clear decay starting immediately (Fig. 2B1). This decay reflects the activity of Ca²⁺ extrusion and sequestration processes. These processes presumably extruded Ca²⁺ at the end of the last pulse as well, but when [Ca²⁺]_Free was high the fraction of dye bound to Ca²⁺ did not fall. Thus, the plateau in fluorescence at the end of a train reflected saturation of the dye rather than a balance between Ca²⁺ entry and removal.

Fig. 2.

A. Ca²⁺ current for the first two pulses (A1) and final pulse (A2) of a train of 20 steps from −80 to +10 mV. B. Simultaneous fluorescence recordings during the first two (B1) and last (B2) pulse. The dashed vertical lines in B1 and B2 indicated the times of the voltage pulses in A1 and A2. Fluorescence increased during the first two pulses but not during the final pulse. Fluorescence remained constant for at least 200 msec after the final pulse. Note that different scales and offsets were used for I_Ca and F in A2 and B2 in order to display a longer time in fluorescence with no decay. The nerve terminal contained 100 μM fluo-8.

The saturation of dye during trains thus provided an estimate of f_max, the fluorescence when all of the fluo-8 is bound to Ca²⁺. We evaluated the fluorescence before and after the final pulse and considered saturation to have occurred when there was no statistically significant difference. When p < 0.1 we concluded that dye saturation had not been reached and these data sets were not analyzed. Because of the uncertainty of [Ca²⁺]_Free inherent in Eq. 1 when f approaches f_max, we only used f measurements more than 2 standard deviations below f_max. Our analysis of Ca²⁺ binding depends on this measurement, but more generally, the calculation of [Ca²⁺]_Free using Eq. 1 also depends on knowledge of f_max [27].

3.2 Saturation of endogenous buffers

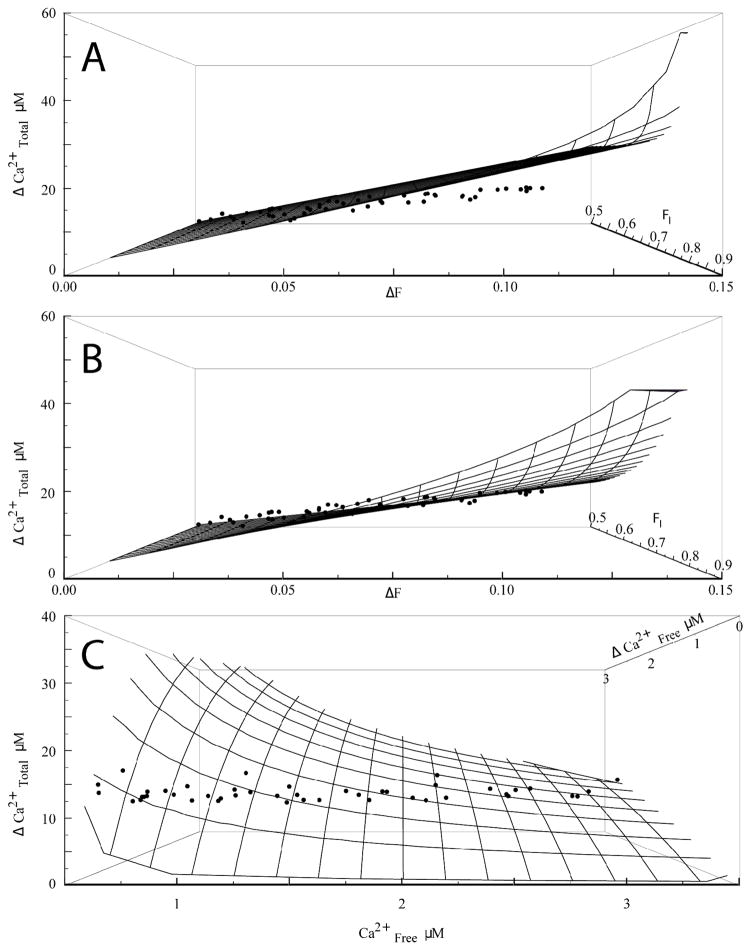
With f_max determined as described above from the fluorescence at the end of a train, we converted initial and final fluorescence readings to normalized values F_I and F_F that appear in Eq. 6 or 7. Initial tests modeling the relationship between F_I, F_F, and I_Ca showed that a model with only one Ca²⁺ binding species (dye) failed to fit our data. This is illustrated in a 3-dimensional surface plot with Δ[Ca²⁺]_Total, F_I, and ΔF=F_F−F_I (Fig. 3A). The model defines a surface in this coordinate system, represented as a wire mesh in the figure. With only one species at 100 μM (the concentration of fluo-8) the points fell well below the wire mesh computed from Eq. 6 for the best fitting parameter values. Furthermore, the fit returned an unrealistic value for V_E of −0.52. The failure is most pronounced for small values of F_I (low initial [Ca²⁺]_Free), where ΔF (and Δ[Ca²⁺]_Free) was high. Adding a second buffer improved the fit (Fig. 3B) and yielded highly significant p-values for the parameters. We were thus able to estimate K_d,D = 424 nM, B_T,E1 = 110 μM, K_d,E1 = 2.79 μM, and V_E = 0.33, from the experiment used to create Fig. 3.

Fig. 3.

A. and B. Δ[Ca²⁺]_Total was plotted as a function of initial fluorescence (F_I) and change in fluorescence ΔF. Points represent data from a single nerve terminal stimulated with a train of 20 pulses, and the train was repeated 10 times. The wire mesh shows the surface calculated from Eq. 7 with parameters determined by fitting to a model with one buffer (A, K_d=278±11 nM, V_E = −0.52±0.08) or two (B, K_d,D =424±5 nM, K_d,E1 = 2.79±46 μM, B_T,E1 =110±1.6 μM, V_E =0.33±0.01). Adding a second buffer improved the fit significantly over the simpler model (p < 10⁻¹⁵⁰ by the F-test). C. Δ[Ca²⁺]_Total is plotted as a function of [Ca²⁺]_Free,I and Δ[Ca²⁺]_Free, calculated from the fluorescence in A–B, and the wire mesh is the model prediction as in B for two buffers.

We performed the analysis described for Fig. 3 on data from 21 nerve terminals that were significantly better fitted by one endogenous buffer plus dye (Eq. 7) than by dye alone (Eq. 6), but for which the addition of a second endogenous buffer did not significantly improve the fit. The parameter values obtained are presented in Table 1. In much of our data, a second endogenous buffer significantly improved the fit when we fixed K_d,D, and these results will be published separately. We also displayed the 3-dimensional surface plot for computed [Ca²⁺]_Free (Fig. 3C). Although the fitting was performed based on fluorescence, this plot illustrates the larger increments Δ[Ca²⁺]_Free for lower [Ca²⁺]_Free, and again shows how the data points fell on a path within the surface defined by Eq. 7.

Table 1.

Parameters obtained from fits of Eq. 7 to data from 21 nerve terminals are presented as mean ± s.e.m.

Kd,D	VE	Kd,endo	BT,endo
0.38±.045 μM	0.38±.04	2.2±.27 μM	100±18μM

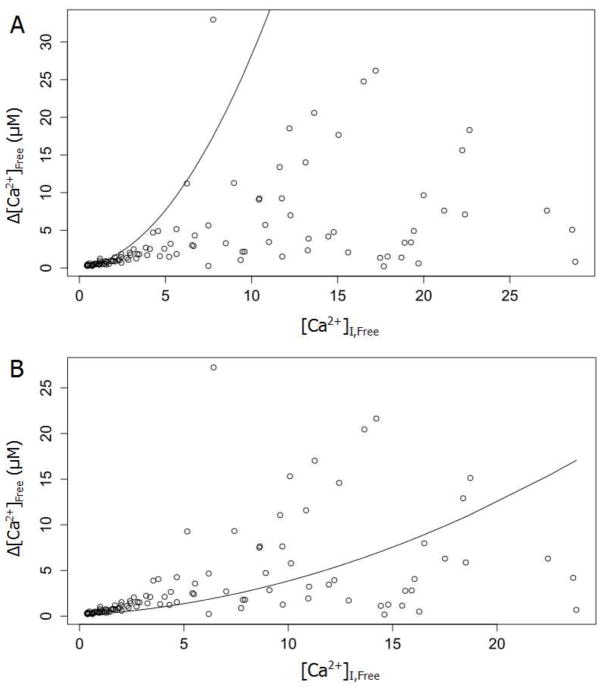
We can evaluate the model with respect to [Ca²⁺]_Free in more accessible 2-dimensional plots by noting that variations in I_Ca (and Δ[Ca²⁺]_Total) were generally less than 30% (~15% in the example in Fig. 3). This variation was much less than that of [Ca²⁺]_Free and Δ[Ca²⁺]_Free. Thus, a simple plot of [Ca²⁺]_Free,I versus Δ[Ca²⁺]_Free illustrated the important features of the 3-dimensional plots in Fig. 3. With one buffer the model clearly failed to fit the data and the points deviated from the model over the entire range (Fig. 4A). The deviation at high [Ca²⁺]_Free reflected the large uncertainty resulting from the nonlinearity of Eq. 1. However, the deviation at low [Ca²⁺]_Free was also clear and systematic. This 2-dimensional plot illustrated once again that incorporating the endogenous buffer yielded a model that predicted the relation between [Ca²⁺]_Free,I and Δ[Ca²⁺]_Free more accurately (Fig. 4B).

Fig. 4.

Data from Fig. 3 were projected into the Δ[Ca²⁺]_Free,I, [Ca²⁺]_Free plane. A. The solid curve is Eq. 7 with parameters from in Fig. 3A. B. The solid curve is Eq. 7 with parameters from Fig. 3B. As in Fig. 3, the addition of a second buffer improved the fit. Note that the data in the two panels are scaled differently according to the respective K_d,D values from Fig. 3A versus Fig. 3B.

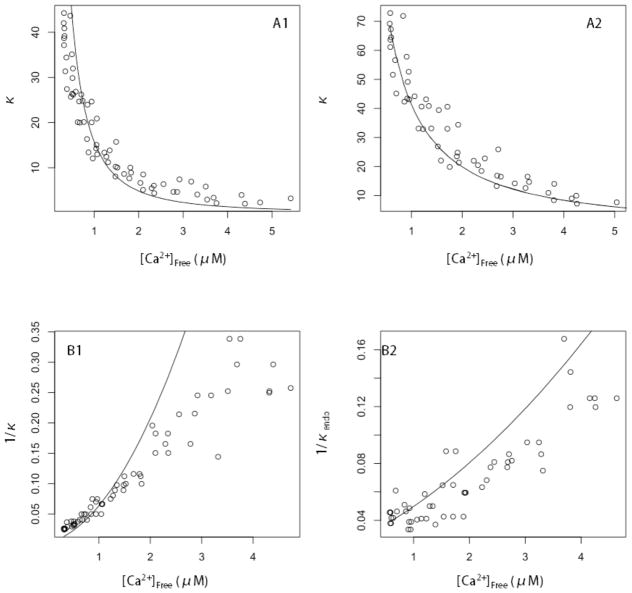
To illustrate the properties of the endogenous buffer, and its saturation as [Ca²⁺]_Free rises, we plotted the total Ca²⁺ buffering capacity versus [Ca²⁺]_Free (Fig. 5A1 and 5A2). Previous studies have used these plots to illustrate the saturation of Ca²⁺ binding sites in situ [16,18]. Eqs. 3 and 4 provide the predicted behavior. With one buffer the curve fell below the data points (Fig. 5A1) at high [Ca²⁺]_free and above them at low [Ca²⁺]_Free, and with both dye and endogenous buffer the fitted curve was very close to the data (Fig. 5A2). We also plotted 1/κ versus [Ca²⁺]_Free as these plots have a simple parabolic shape for one Ca²⁺ binding species (Figs. 5B1 and 5B2). Fig. 5B1 was simply a transform of Fig. 5A1 and shows the disagreement between the model and data more clearly. Fig. 5B2 shows the results with both dye and endogenous buffer included in the fit, and with κ_endo of the endogenous buffer plotted rather than total κ. Fig. 5 clearly demonstrated the saturation of Ca²⁺ binding sites in pituitary nerve terminals, and this saturation reflected Ca²⁺ binding to both the fluorescent dye and an endogenous buffer.

Fig. 5.

A. The total Ca²⁺ buffering capacity, κ, calculated from data as Δ[Ca²⁺]_Total/Δ[Ca²⁺]_Free plotted versus Δ[Ca²⁺]_Free. A1. For exogenous dye alone, the solid curve is κ calculated from Eq. 3. Without endogenous buffer, the fit yielded V_E=−0.52 (as already noted) and the resulting curve fell below the data points. Including dye plus one endogenous buffer (A2) yielded V_E=0.33 and a better fit to the data. B1. 1/κ was plotted versus Δ[Ca²⁺]_Free for the same fit in A1. The solid curve was obtained by inverting Eq. 4. B2. κ_endo was calculated as Δ[Ca²⁺]_Total/Δ[Ca²⁺]_Free−κ_dye, with κ_dye from Eq 4. 1/κ_endo was plotted as a function of Δ[Ca²⁺]_Free. The solid curve is 1/κ_endo from Eq. 4 with K_d,E1 and B_T,E1 from Fig. 3B. Note that in A1 and B1 different values for the dye K_d (278 nM vs. 424 nM) altered the concentration scales from those in A2 and B2.

3.3 K_d of fluo-8

Quantitative interpretation of Ca²⁺ fluorometry experiments depends on accurate measurements of the K_d of the Ca²⁺ indicator, but this quantity can vary between in vitro solutions where it is typically determined versus cellular environments where it is used [4–6,26,30–35]. The difference presumably reflects the influence of the local chemical environment on the Ca²⁺ binding equilibrium; the K_d is sensitive to pH, ionic strength, temperature, and physiological concentrations of protein [35] (see the Table 19.2 of Molecular Probes Handbook for a number of examples; http://www.lifetechnologies.com). The K_d of Ca²⁺ indicators in different cellular environments nearly always exceeds in vitro values, sometimes by as much as 8-fold [31,32,36], and in the few cases where the in vitro K_d exceeds the in situ K_d, the difference is very small. K_d values also vary between cell type, subcellular compartment, and laboratory.

Calibrating a dye K_d in situ is difficult and the methods have significant limitations [30,33,37–39]. One approach entails loading cells through a patch pipette with calibration solutions in which Ca²⁺ concentration has been fixed by a chelator such as EGTA or BAPTA [40]. However, Ca²⁺ binding to these chelators should have a similar dependence on environment, as they are structurally closely related to the Ca²⁺ indicators. Environment effects on the K_d of BAPTA have been reported [17]. This will give rise to errors in the calculated [Ca²⁺]_Free of the calibration solutions that are comparable to those based on the in vitro K_d of a fluorescent dye. A second calibration method employs solutions with chelators to control [Ca²⁺]_Free outside a cell. Dye is then loaded into the cell, and a Ca²⁺ ionophore (such as ionomycin) is used to allow extracellular Ca²⁺ to enter and equilibrate [30,41]. This approach places the chelator in an environment where its K_d is known precisely, but it requires complete blockade of cellular Ca²⁺ extrusion and sequestration mechanisms. Cells have different Ca²⁺ handling machinery and sensitivities to drugs, so that intracellular [Ca²⁺]_Free may not equal extracellular [Ca²⁺]_Free.

When we allowed K_d,D in Eq. 7 to vary, the fit yielded a value for the K_d,D for fluo-8 in situ of 380 ± 45 nM, which is not significantly different from the in vitro value of 390 nM provided by the manufacturer. Our simulations indicated that this estimate is robust and insensitive to errors in the estimate of f_max on the order of typical noise levels (Supplemental Material).

4. Discussion

We have investigated intracellular Ca²⁺ binding molecules by in situ titration with Ca²⁺ supplied through voltage-gated Ca²⁺ channels [16,18]. This method entailed fitting a model with multiple binding sites to sets of 3-tuple data consisting of F_I, F_F, and I_Ca, measured over a train of voltage steps. We have systematically explored the information contained in this form of data, provided a framework for fitting models, and explored the efficiency of parameter determination under different conditions. This method builds on earlier work in which Ca²⁺ entry could not be measured directly [18]. That study estimated values of ~500 nM and ~130 μM for the K_d and concentration, respectively, of the endogenous Ca²⁺ buffer in dentate gyrus granule cell nerve terminals. The major endogenous buffer of these neurons, calbindin D_28K was subsequently shown by patch clamp loading and immunohistochemistry to be present in the cell bodies of these neurons at a concentration of 33 μM, which with four binding sites per molecule gives a binding site concentration of 152 μM [42]. This agreement may seem surprising considering the washout of cytoplasmic proteins during patch clamp recording, but diffusion out of nerve terminals hundreds of microns down an axon presumably takes more time than diffusion out of a nerve cell body. Washout might be expected to have a greater impact in the present study because here the nerve terminals were patch clamped directly. However, a previous patch clamp study of posterior pituitary nerve terminals showed little if any buffer washout for up to 5 minutes [7].

Although we developed our method for dynamic range indicators, simple modifications to the equations would render the method applicable to ratiometric Ca²⁺ indicators [43,44], which would obviate the need for saturation of the dye with Ca²⁺ for measurement of f_max. This method depends on Ca²⁺ channels as the only source of cytoplasmic Ca²⁺, and cannot be applied to cells with Ca²⁺-induced Ca²⁺ release. The posterior pituitary nerve terminals studied here are insensitive to IP₃ receptor and ryanodine receptor antagonists, and appear to lack Ca²⁺-operated stores [7] in the absence of μ-opioid receptor activation [45]. Use of this method in cells with mobile Ca²⁺ stores would require eliminating this source of Ca²⁺.

Fitting Eq. 7 to data such as ours defines a family of solutions $\left(\frac{1-V_E}{\alpha },\alpha K_{d,D},\alpha B_{T,D},\alpha K_{d,E1},\alpha B_{T,E1}\right)$ related by a factor α. Here we took α=1 by setting the cellular dye concentration equal to that in the patch pipette. Other experimental designs may dictate alternative approaches. For example, one could determine α from the K_d of the indicator, if one had a reliable in situ measurement, or from an independent measurement of V_E. With a ratiometric dye for which an in situ calibration is available it is possible to show that the fluorescence intensity is proportional to the product (1−V_E)B_T, and with a calibrated photometric system this measurement can also be used to determine α. Knowledge of any one of the parameters of Eq. 7 enables fitting to extract the remaining parameters. In experiments with dye loaded as an AM-ester or with a genetically-encoded sensor, a Ca²⁺ ionophore could be used to control Ca²⁺ and estimate K_d,D [30]. In experiments with caged Ca²⁺ the amount of Ca²⁺ liberated by a pulse of light may be specified and serve as a unit of measure, with other parameters determined in these units. Experimental designs along these lines could also be applied to diffusionally isolated subcellular compartments which are difficult to access directly, such as dendritic spines.

In situ Ca²⁺ titration depends on knowledge of V_E in order to convert the integral of I_Ca into Δ[Ca²⁺]_Total. We estimated a value for V_E of 0.38. Ultrastructural studies of posterior pituitary provide measurements of vesicle numbers and average diameter [20] from which we estimated V_E=0.6. Given the difference between these two experimental methods, these values should be viewed as qualitatively similar. We can be confident that both Ca²⁺ and dye are excluded from the same compartments, as both are charged and should not readily cross intracellular membranes. As already noted, intracellular Ca²⁺ stores would present a problem for this method. Rapid movement of Ca²⁺ into dye-inaccessible compartments would reduce V_E for Ca²⁺ below that for dye. [Ca²⁺]_Free calculated from Eq. 1 would apply only to the dye-accessible compartment, but [Ca²⁺]_Total would apply to a larger volume, so Eq. 7 would no longer be valid. A dye with access to compartments that exclude Ca²⁺ would be a problem not only for titration, but more fundamentally for calculating [Ca²⁺]_Free with Eq. 1. Dye in a Ca²⁺-inaccessible compartment would increase the background and reduce the effective dynamic range of the dye. For a large dynamic range this effect has little impact, as noted in 2.3 Methods.

In this study, we made a preliminary estimate of the K_d and concentration of the endogenous buffer in pituitary nerve terminals. With our values for B_T.E1 and K_d,E1 from Table 1 Eq. 4 gives k~35, which is clearly much lower than the value of 175 measured by the classical analysis of the relation between Ca²⁺ rise and dye buffering capacity [7]. This may reflect differences between dissociated nerve terminals and intact slices, or it may reflect errors in the classical method arising from the failure to address endogenous buffer saturation [18]. In fact, it is likely that nerve terminals contain more than one Ca²⁺ buffer and their concentrations may vary from terminal to terminal. Here, to illustrate the method we focused on nerve terminals that were adequately described by a single endogenous buffer. Although in these data sets adding a second endogenous buffer did not significantly improve the fit, additional species would be missed if the fluorescence noise was high. Although Muller et al [42] raised the concern that low affinity species could increase the Ca²⁺ buffering capacity above that estimated in Ca²⁺ imaging experiments, Eq. 4 indicated that low affinity molecules would need to have implausibly high concentrations to make a significant contribution. For example, ATP binds Ca²⁺ but despite its high concentration contributes very little to Ca²⁺ buffering due to its low affinity. Our simulations suggested that for the worst case of noise near the maximum we encountered, a nerve terminal with two buffers (K_d,E1~0.1 μM, K_d,E2~1 μM, B_T,E1=B_T,E2~100 μM) could be adequately fitted by a model with a single buffer, and a second species did not improve the fit. Significantly, in these simulations, estimations of K_d,D remained robust. In view of the fact that two endogenous buffers were required to fit many of our data sets, the K_d and concentration obtained from the single endogenous buffer fits likely reflect aggregate behavior of multiple buffers. Our primary goal here was to illustrate the method and a more thorough analysis of endogenous buffers will be reported separately.

We used our method to estimate the K_d of the fluorescent dye fluo-8 in situ. As a dye calibration method this approach is a significant improvement over previous methods as it avoids relying on in vitro properties of other Ca²⁺ chelators. While the assumptions underlying the previous calibration methods are difficult to assess and violations difficult to correct, our method was sufficiently robust that we were able to test many of our assumptions. Our estimate for the K_d of fluo-8 was remarkably close to the in vitro estimate. This example suggests that the environment of these nerve terminals does not perturb the binding of this particular dye. However, the large variations reported in the literature [31,32,36] suggest that more dyes should be subjected to this form of analysis.

Titration of Ca²⁺ binding in situ provided estimates of the K_d and concentration of endogenous Ca²⁺ buffers. Such molecules shape the spatial and temporal dynamics of Ca²⁺ signals and play a critical role in determining the physiological consequences of Ca²⁺ entry [4,46–53]. The saturation of endogenous buffers has been shown to contribute to synaptic facilitation [49,54,55], and dysregulation of cellular Ca²⁺ buffering has serious pathological consequences [56–58]. More detailed studies of Ca²⁺ signaling in situ will be necessary to understand the molecular basis of these diseases. Thus, the quantitative characterization of Ca²⁺ binding processes in situ should have a number of useful applications.

Highlights.

1. Endogenous Ca²⁺ buffers can be probed in situ by titrating Ca²⁺ binding sites.

2. Our extension exploits information available in Ca²⁺ fluorometry more effectively.

3. We analyzed fluo-8 Ca²⁺ 2-photon imaging data from pituitary nerve terminals.

4. We estimated the excluded volume and endogenous Ca²⁺ buffer K_d and concentration.

5. An estimate of the in situ K_d of fluo-8 was very close to the in vitro value.