The Utility and Accuracy of Oral Reading Fluency Score Types in Predicting Reading Comprehension

Abstract

This study used data from the Dynamic Indicators of Basic Early Literacy Skills (DIBELS; Good & Kaminski, 2002) oral reading fluency (ORF) probes to examine variation among different ORF score types (i.e., the median of three passages, the mean of all three passages, the mean of passages 2 and 3, and the score from passage 3) in predicting reading comprehension as a function of student reading fluency level and to compare the screening accuracy of these score types in predicting student reading comprehension. The results revealed that the relation between oral reading fluency and reading comprehension varied as a function of students' oral reading fluency and that different score types had varying predictive validity for year-end reading comprehension. The mean of all three passages demonstrated a marginally better balance in screening efficiency from September to December of grade one (especially for low-performing students), whereas in grades two and three, the median score was the best predictor. Furthermore, across all grades, increasing reading rates were observed for the three administered passages within an assessment period. The observed patterns mimicked previous experimental studies (Francis et al., 2008; Jenkins, Graff, & Miglioretti, 2009), suggesting that practice effects are an important consideration in the administration of multiple passages assessing oral reading fluency.

Accurate and rapid reading of connected text, known as oral reading fluency¹, has recently received much attention as producing an efficient measure of overall reading skills, particularly for students in primary grades (Roehrig, Petscher, Nettles, Hudson, & Torgesen, 2008). Theoretically, efficient and automatic word reading allows students to use cognitive resources for understanding meaning in text rather than identifying and decoding words (Perfetti, 1985). Prior research has demonstrated strong correlations between oral reading fluency and reading comprehension, ranging from .67 (Good, Simmons, & Kame'enui, 2001) to .76 (Roberts, Good, & Corcoran, 2005) for students in grades one to three.

Given the theoretical importance (Fuchs, Fuchs, Hosp, & Jenkins, 2001; Hudson, Pullen, Lane, & Torgesen, 2009; LaBerge & Samuels, 1974; Perfetti, 1985) and empirical evidence for the relation between oral reading fluency and reading comprehension (Buck & Torgesen, 2003; Ridel, 2007; Roberts et al., 2005; Roehrig et al., 2008), oral reading fluency has been widely used as a measure to identify students at risk of future reading challenges (i.e., screening purposes) or as a measure to monitor student progress in overall reading skills (i.e., as a proxy for reading comprehension). One of the most widely used oral reading fluency measures in the United States is from the Dynamic Indicators of Basic Early Literacy Skills (DIBELS; Good & Kaminski, 2002). In grades one through six, DIBELS uses Reading-Curriculum-Based Measurement (R-CBM) for oral reading fluency by asking students to read passages and calculating the number of words correctly read per minute.

Variation in text difficulty

One of the challenges for any oral reading fluency measure is developing texts or passages that are appropriate for student reading level and equivalent in difficulty. Text difficulty is usually gauged by various readability formulae. The DIBELS developers used numerous readability formulae to ensure passage equivalency but relied heavily on the Spache readability formula (Spache, 1953) because the Spache index was found to be most predictive of student reading skills in grade two (Good & Kaminski, 2002). However, as shown by recent research (Ardoin, Suldo, Witt, Aldrich, & McDonald, 2005; Francis et al., 2008), utilizing a series of readability formulae does not guarantee equivalence in passage difficulty. Various readability indices may produce significantly different difficulty levels for the same passage. Even when considering a readability index with a narrow range of scoring (e.g., Spache), a wider range of difficulty was observed on the same passage when using other readability indices (Francis et al., 2008; Good & Kaminski, 2002). Furthermore, readability indices have limited utility for predicting differences in oral reading rate across passages. Although DIBELS development research showed the Spache index to be most predictive of student reading skills, Ardoin et al. (2005) found that the Forecast (Sticht, 1973) and Fog (Gunning, 1968) indices were the best predictors of WCPM, with the Spache and Dale–Chall (Dale & Chall, 1948) being the worst. Moreover, even the best predictors were only moderately related to oral reading rate (rs=.41 and .46 for Fog and Forecast, respectively).

Another attempt to alleviate form (i.e., passage) effects by the DIBELS developers, in addition to using readability formulae, is the administration of multiple passages (i.e., three passages) and use of the median score for decision making (Good & Kaminski, 2002). However, the scientific basis for the use of the median score compared to other options has not been established, and thus, it is not clear whether the median score is superior to alternative scores in representing reading fluency. Alternative score types include the mean of all three passages, the mean of the second and third passages, and the score from the third passage. From a measurement perspective, the mean of all three passages could provide the most accurate representation of reading fluency because it uses more observed score information to increase the precision of assessing student reading rate. The mean of the second and third passages may be another promising alternative because recent studies have shown that student performance is consistently lower on the first passage, even when passage order is systematically randomized (Francis et al., 2008; Jenkins, Graff, & Miglioretti, 2009). Consequently, the mean of the second and third passages might provide more accurate information about oral reading fluency, as the first passage might act as a practice (i.e., warm-up) passage. Finally, the score of the third passage alone might be useful because previous research suggested that the third passage score was the most predictive score type of reading comprehension compared with the score from either passage one or two (Petscher, Schatschneider & Kim, 2008).

Measurement and fluency

From a measurement perspective, observed differences in students' reading fluency scores across individual passages largely reflect the relation between observed scores and latent fluency ability. As Francis et al. (2008) noted, measurement invariance is a necessary condition for observed reading rates to be unbiased when informing about true reading rates. In other words, unless the latent means, variances, and error variances are similar for all forms within a time point, the means and variances for observed reading rates across the passages will vary. Although Francis and his colleagues stated that the effect of differences across forms on estimation of change in true reading rates is unknown, their effect on the estimation of their relation to a criterion measure is also unknown. As such, our first goal in the present study was to understand how much of the variance in fluency scores is due to observed reading rate differences across passages, as opposed to differences across students. Substantive fluency rate differences between forms have typically been used as evidence to suggest that forms should be equated. For example, in a study of five forms of a teacher certification test, scores were equated to correct for average differences across forms that ranged from near 0 to .40 standard deviations (Parshall, Houghton & Kromney, 1995). Meaningful differences in fluency scores due to passage effects would suggest that equating should take place for two potentially important reasons: (a) scores from individual passages could differentially predict outcome scores and risk status and (b) the prediction could vary by student skill levels.

One critical, implicit assumption in the use of using ORF as a screening and progress monitoring tool is that it is a strong predictor of future reading outcomes (e.g., reading comprehension) for students of all reading levels. If this assumption is correct, the relation between oral reading fluency and reading comprehension should be similarly strong for all students. However, Catts, Petscher, Schatschneider, Bridges, and Mendoza (2009) examined how students' oral reading fluency performance in grades one and two was related to reading comprehension in grade three, and results showed that prediction was stronger for students with higher DIBELS oral reading fluency scores than those with lower scores, particularly in grade one. One of the reasons for the differential relations might be floor effects for students in the lower end of the distribution, because floor effects obscure individual differences and limit predictive validity. Given that students acquire literacy through the acquisition of multiple, overlapping skills, floor effects in some measures may be inevitable at a particular point of development. However, it is important to have a precise understanding about the predictive validity of oral reading fluency for reading comprehension for students, including those with low reading fluency, because small differences in reading fluency scores at the beginning of grade one effect reading fluency growth throughout grade one (Kim, Petscher, Schatschneider, & Foorman, 2010). Thus, the second goal of the present study was to examine the variability of predictive validity of oral reading fluency for reading comprehension at the end of each year (in grades one to three, respectively) for children with varying reading skills. In particular, we compared the predictive validity of oral reading fluency using four different score types (i.e., the median across the three passages, the mean of the three passages, the mean of passages 2 and 3, and the scores on passage 3) to investigate the extent of heteroscedastic relations when using different scores (i.e., whether particular score types mitigate differential prediction).

The third goal of the present study was to compare these alternative score types in terms of screening accuracy for students' later reading comprehension performance from grades one to three. Previous studies have demonstrated the concurrent and predictive screening accuracy of DIBELS oral reading fluency for reading comprehension (e.g., Good & Kaminski, 2002; Roehrig et al., 2008). However, these studies have used the median score in the analyses, and thus, little is known about screening accuracy when using alternative score types. The choice of scores has important practical implications, because screening accuracy is critical for effective decision making, and alternative score types may enhance accuracy.

In summary, we investigated the following research questions: (a) How much of the variation in reading fluency scores can be attributed to differences among individuals and differences among passages? (b) What is the relation between various score types from the DIBELS passages (i.e., the median across the three passages, the mean of the three passages, the mean of passages 2 and 3, and the scores on passage 3) and reading comprehension at different levels of reading fluency? and (c) What is the relation between different score types and the identification of students as at-risk for future reading comprehension challenges?

METHOD

Data source

The sample included students who were enrolled in Florida Reading First schools in which assessors used handheld wireless devices (i.e., mCLASS: DIBELS) for entering and monitoring student records, and it constituted approximately 25% of all Reading First schools in the state. During Reading First, school principals had the opportunity to use the pencil and paper version of DIBELS or pay a fee to use the handheld wireless devices. Many schools freely elected to use handheld wireless devices, and some districts mandated that all of their schools use it. Despite the two methods for administering the DIBELS and recording scores, the average median fluency scores for each method did not practically differ in grades 1 to 3 for any DIBELS assessment (Cohen's d range=.007 to .09). Data from schools using the handheld wireless devices were used because all individual DIBELS oral reading fluency passage scores (as opposed to only median scores) were recorded in the database.

Participants

Participants were 34,855 students in the first (n=9,003), second (n=12,597), and third (n=13,255) grades. According to school records, these students reflected the diversity found in the population of students in Florida. A summary of the student demographics and the demographics for all students in the state are provided in Table 1. Students were fairly similar across grades in their demographic characteristics, with a slightly increased representation of boys. Fairly equal proportions of White and African American students were observed, but Latino students had slightly less representation. Across all grades, a large proportion of students were eligible for free or reduced price lunch, and approximately 20% of students were identified as English language learners. Lastly, nearly 15% of students in each grade were served on an individual education plan for a disability. The sample characteristics resembled the overall Florida population very well, with the largest discrepancies noted between the sample and the population in the proportion of White students and those eligible for free or reduced price lunch (6% each).

Table 1.

Sample (and population) demographic characteristics.

Demographics	Grade 1	Grade 2	Grade 3
Boy	52% (52%)	52% (52%)	52% (52%)
White	36% (30%)	37% (29%)	37% (29%)
Black	35% (38%)	37% (38%)	37% (40%)
Latino	25% (28%)	21% (26%)	20% (27%)
Asian	1% (1%)	2% (1%)	2% (1%)
Multiracial	2% (3%)	3% (4%)	3% (3%)
Native American	<1% (<1%)	<1% (<1%)	<1% (<1%)
FRL	83% (77%)	82% (76%)	71% (75%)
ELL	25% (20%)	14% (17%)	20% (15%)
Speech impaired	5% (6%)	3% (5%)	3% (4%)
Language impaired	2% (3%)	2% (3%)	3% (3%)
Specific learning disability	4% (3%)	5% (5%)	5% (6%)
Other	4% (4%)	4% (4%)	4% (4%)

Note. FRL=Free and/or reduced price lunch, ELL=English language learners. Florida state demographics reported in parentheses.

Measures

Oral reading fluency

DIBELS ORF (Good, Kaminski, Smith, Laimon, & Dill, 2001) is a measure that assesses oral reading rate in grade-level connected text. This standardized, individually administered test of accuracy and reading rate in connected text was designed to identify students who may need additional instructional support and monitor progress toward instructional goals (Good & Kaminski, 2002). The specific DIBELS measures administered vary by grade level. In kindergarten, measures focus primarily on phonological awareness, letter knowledge, and decoding. As students progress into first through third grades, the focus is placed on oral reading fluency, and only the oral reading fluency scores were used in this study. During a given administration of ORF, students are asked to read three previously unseen passages out loud consecutively, for 1 min per passage. Students are given the prompt to “be sure to do your best reading” (Good, Kaminski, Smith, Laimon & Dill, 2001; Good, Simmons & Kame'enui, 2001, p. 30). Between the administration of each passage, students are given a break, in which the assessor simply reads the directions again before the task resumes. Words omitted, substituted, and hesitations of more than 3 s are scored as errors, although errors that are self-corrected within 3 s are scored as correct. Errors are noted by the assessor, and the score produced is the number of words correctly read per minute (WCPM). From the three passages, the median score of the three passages is the score type used for decision making about the level of risk and the level of intervention needed. Information about how the risk levels for ORF benchmarks were developed and what ranges of scores correspond to various levels of risk are available from several technical reports by the DIBELS authors (e.g., Good et al., 2002). Speece and Case (2001) reported a parallel form reliability of .94, and a strong interrater reliability (.96) has been observed in Florida (Progress Monitoring and Reporting Network, 2005). Research has demonstrated adequate to strong predictive validity of DIBELS ORF for reading comprehension outcomes (.65 to .80; Barger, 2003; Good, Kaminski, et al., 2001; Good, Simmons & Kame'enui, 2001; Roehrig et al., 2008; Shaw & Shaw, 2002; Wilson, 2005).

For the sample used in the present study, DIBELS was administered four times during the year, in September (fall), December (winter 1), February/March (winter 2), and April/May (spring). This administration schedule differs from the typical administration of three times per year (i.e., fall, winter, and spring). In addition, in Florida, DIBELS ORF was administered in fall of grade one, which is different from the DIBELS protocol (Good & Kaminski, 2002), but it is part of common assessment practices in several states (e.g., Maryland; Greenberg, S., personal communication, 2010). Regarding the passages for the four assessment administrations, the fall and spring benchmarks used the same passages as the three assessment administration (with the exception of grade one, when different benchmarks were used in fall), and the winter 1 benchmark in the four assessment administration corresponded to the fall benchmark of the three assessment administration.

When benchmark passages varied from the original benchmarks, they were selected based on directions from the DIBELS developers. From the bank of available passages, Good and Kaminski (2002) noted that benchmark passages were selected by a process whereby (a) an estimate of relative readability was assigned to each passage; (b) all passages were sorted in an increasing manner according to relative readability and categorized into three (easier, moderate, and difficult); and (c) a randomly selected passage from each set of passages was chosen such that relatively easy, moderate, and difficult passages were represented. According to the authors, the first passage should be the most readable, the second passage should be less readable than the first, and the last passage should be the most difficult. The ORF criteria from the four assessment window were then estimated based on linear, curvilinear, or rational analysis of progress over the year using the information from the three assessment administration criteria as an anchor (DIBELS Data System, 2010).

According to Good and Kaminski (2002), the passages within each grade level are considered to be approximately equivalent with regard to difficulty of the passage based on Spache readability. Table 2 reports the story name, the order in which the passages were read by students, and the Spache readability index (Spache, 1953) for each passage that was administered to students across assessment periods and grades. Consistent with the intentions of Spache readability, the DIBELS authors reported that the grade one passages had an average Spache index of 2.2 (ranging from 2.0 to 2.3), which is identical to the reported mean of all DIBELS ORF passages within grade one (Good & Kaminski, 2002). Second grade passages had a mean Spache value of 2.6 (range of 2.4 to 2.7), compared to the overall DIBELS ORF mean of 2.6, and third grade passages also displayed average readability of 3.0, compared with the overall DIBELS ORF mean of 2.9.

Table 2.

DIBELS ORF passage name and reported difficulty.

Grade	Passage number	Fall		Winter 1		Winter 2		Spring
		Passage	Spache	Passage	Spache	Passage	Spache	Passage	Spache
Grade 1	1	Party	2.0	Nest	2.0	Aunt Rose	2.3	Spring	2.0
	2	Ice Cream	2.2	Camping	2.1	Big Sister	2.1	Sand Castle	2.2
	3	Kitty	2.2	Lemonade	2.2	Rocks	2.3	Check-up	2.3
Grade 2	1	Story	2.5	Job	2.4	Robot	2.5	Rollercoaster	2.6
	2	Babysitter	2.7	Handprints	2.6	Grandpa	2.6	Moving Day	2.7
	3	Shuffleboard	2.6	Meals	2.7	Bottle	2.7	Stars	2.6
Grade 3	1	Dreams	3.0	Field Trip	2.9	Pots	3.0	Friend	2.8
	2	Clouds	3.0	Whale	3.1	Tracks	2.9	Camping	3.1
	3	Firefighters	2.9	Email	3.0	Parents	2.9	Garden	3.0

Note. Party=The Block Party, Ice Cream=Ice Cream, Kitty=Our Sick Kitty, Story=Writing My Life Story, Babysitter=I'm a Good Babysitter, Shuffleboard=Playing Shuffleboard, Dreams=Dream Catchers, Clouds=Clouds and Weather, Firefighters=Firefighters, Nest=The Robin's Nest, Camping=Camping at Home, Lemonade=My Lemonade Stand, Job=Mom's New Job, Handprints=My Handprints, Meals=Means on Wheels, Field Trip=The Field Trip, Whale=Keiko the Killer Whale, Email=Getting Email, Aunt Rose=Visiting Aunt Rose, Big Sister=My Big Sister, Rocks=The Rock Collection, Robot=If I had a Robot, Grandpa=My Grandpa Snores, Bottle=My Drift Bottle, Pots=Pots, Tracks=Animal Tracks, Parents=My Parents, Spring=Spring is Coming, Sand Castle=Sand Castle, Check-up=Having a Check-up, Rollercoaster=Riding the Rollercoaster, Moving Day=Moving Day, Stars=Stars of the Sea, Friend=My Friend, Camping=Going to Family Camp, Garden=Planting a Garden.

Reading comprehension

The Stanford Achievement Test-10th Edition (SAT-10; Harcourt Brace, 2003a) is a group-administered, untimed, standardized measure of reading comprehension. Students answer a total of 54 multiple-choice items that assess their initial understanding, interpretation, critical analysis, and awareness and usage of various reading strategies. The internal consistency for the SAT-10 on a nationally representative sample of students was .88.Validity was established with other standardized assessments of reading comprehension, providing strong evidence of content, criterion, and construct validity (coefficients > .70; Harcourt Brace, 2003b). Students in the first and second grades were administered the SAT-10 in February or March, and third graders were administered the SAT-10 in April or May.

Data analytic approach

Multiple analytic methods were employed to address the research questions. Our first research question concerned the quantification of variance across the three oral reading fluency scores. The fluency scores from each of the passages were used in a series of cross-classified random effects models (CCREM; Raudenbush & Bryk, 2002) for individual assessments and grades. The cross-classified approach is a method that partitions the variance in the dependent variable (i.e., ORF rate) to that which is attributable to differences across passages and students. CCREM allows for reliable interpretations at the passage and student classification levels, as well as for the interaction between the two. Similar to other models with multilevel structures, a CCREM begins with the specification of the unconditional model, generally defined as

$$Y_{\text{ijk}}={\theta }_0+b_{00\mathrm{j}}+c_{00\mathrm{k}}+e_{\text{ijk}}$$ (1)

where Y_ijk is the predicted score for a student with student characteristics j and passage k and student by passage specifics i. θ₀ is the mean ORF WCPM for all students across all passages, b_00j is the random main effect of students averaged over all passages, c_00k is the random main effect of passages averaged over all students, and e_ijk is the students' deviation from the cell mean. b_00j, c_00k, and e_ijk are all assumed to be normally distributed with variances τ_b00, τ_c00, and σ², respectively.

Partitioning the amount of variance between the levels of cross-classification is then a function of the variance component between-students (τ_b00), between-passages (τ_c00), and within-cell sizes (σ²). Estimation of the intraclass correlation (ICC) between students and passages were calculated with the following:

$$\text{Student Variance}=\frac{{\tau }_{\mathrm{b}00}}{{\tau }_{\mathrm{b}00}+{\tau }_{\mathrm{c}00}+{\sigma }^2}$$ (2)

$$\text{Passage Variance}=\frac{{\tau }_{\mathrm{b}00}}{{\tau }_{\mathrm{b}00}+{\tau }_{\mathrm{c}00}+{\sigma }^2}$$

Because only one observation occurred within each cell of the student by passage matrix (i.e., one score for each student for each passage), σ² became a non-informative parameter. As such, Eq. (2) in the current study dropped σ² in the denominator and variance estimation was adjusted accordingly. Although intraclass correlation values of .10 have typically been used to demonstrate practically important findings (Peugh, 2010), we previously noted that even small estimates of variability may have practically important implications (Parshall, Houghton & Kromney, 1995).

Quantile regression was used to answer our second research question, concerning the differential relation between oral reading fluency and reading comprehension by score types. A full description of quantile regression is beyond the scope of the present study; the reader may wish to review Koenker (2005) for further details. Quantile regression may be thought of as an analytic approach that provides a method of dispersion to an ordinary least squares regression. Studies that analyze the prediction of reading comprehension have primarily relied on ordinary least squares estimation, which examines the average relation between predictors and a selected outcome. However, this standard methodology may miss what is crucial to the process of screening, namely, how prediction of achievement varies for students at different levels of the predictor variable. For example, although prediction of reading comprehension scores may not be as important to study for students with above average ORF, it would be useful to know how well ORF scores are related to reading comprehension scores for students with low ORF scores. Thus, quantile regression addresses not only the question of “How well does oral reading fluency predict reading comprehension?” but also, “How well does oral reading fluency predict reading comprehension for students with low ORF, average ORF, or high ORF?”

Similar to an ordinary least squares regression, a quantile regression will produce raw or standardized coefficients that will describe the relation between a dependent variable and predictors at the specified quantile level. In the present study, we chose to report standardized estimates, which are interpreted as correlation coefficients between ORF and SAT-10 at each quantile level. Moreover, by entering a dummy-code covariate into the regression model representing score type, we were able to test the interaction between the dummy-code and the students' scores at a given quantile, which would indicate the extent to which score types differed in the regression coefficient (i.e., correlation) at a specific quantile. For each of the statistical tests, it was also important to estimate the level of practical importance for a difference in correlations across score types. A useful heuristic for evaluating the practical importance between the two correlations is to estimate the difference between two score types at each quantile. A difference of .14 or greater would correspond to an ΔR²≥2%, which is considered to be a small but practically important estimate (Cohen, 1988). Effects accounting for 2% to 13% of the variance are considered to be small, 14 to 26% medium, and greater than 26% large.

The last research question, pertaining to the differential identification of students as at-risk using different scores, was addressed with a series of receiver operating characteristic (ROC) curves to examine the following statistics: the proportion of students correctly identified as at risk on the SAT-10 and ORF (i.e., sensitivity), the proportion of students correctly classified as not at-risk on both measures (i.e., specificity), the proportion of students who were identified by ORF scores as being at risk who ultimately were identified as at-risk on the SAT-10 (i.e., positive predictive value), the proportion of students who were identified by ORF scores as being not at-risk who were not at-risk according to SAT-10 scores (i.e., negative predictive value), and overall classification accuracy (i.e., area under the curve [AUC]). The AUC has been identified as sufficient as an estimate of effect size (Streiner, 2003) with values from .50 to .59 indicating low diagnostic accuracy, .60 to .65 as moderate diagnostic accuracy, and .66 to 1.00 as high diagnostic accuracy (Rice & Harris, 1995). Hanley and McNeil's test (1983) for comparing AUCs was run as a post-hoc analysis to evaluate the extent to which score types significantly differed in their screening accuracy.

Using the benchmark scores provided by DIBELS (Good & Kaminski, 2002), it was possible to examine the extent to which various scores differed in their correct classification of students as at risk or not at risk. ORF scores that were identified as placing a student at “moderate risk” or “high risk” were recoded as “0” to indicate that they did not meet the expected benchmark. Conversely, student scores which indicated “low risk” were recoded as “1” to indicate they met the grade level expected benchmark. Based on previous practices, the 40th percentile was selected as the benchmark to evaluate grade-level performance on the SAT-10. This cut-point has been utilized as the bench mark for grade-level proficiency on state outcome tests by 28 of the 50 states (American Institute for Research, 2007).

RESULTS

Preliminary data analyses

An examination of the proportion of missing data revealed that across all passages, the percent of missing data was 1.6% in grade one, 1.8% in grade two, and 1.5% in grade three. Although the prevalence of missingness was low, Little's test of data missing completely at random (Little, 1988) indicated that the data were not missing completely at random in either grade one, χ²(334) = 1792.18, pb.001, grade two, χ² (297) = 2285.71, pb.001, or grade three, χ² (200) = 1997.78, pb.001. Missingness was higher for students eligible for free or reduced price lunch and minority students (Schafer & Olsen, 1998); thus, multiple imputation was used to correct for an unbalanced design and potential biases in parameter estimation. Multiple imputation was conducted at the student level in SAS PROC MI analysis, with the free or reduced price lunch, minority status, and item scores variables using a Markov Chain Monte Carlo estimation with 10 imputations. Because the scores were cross-classified by students and passages, rather than nested (e.g., students with classrooms), an imputation at the student level does not compromise the integrity of the data as a single level analysis is used. Analyses for subsequent research questions were combined with PROC MIANALYZE.

Means and standard deviations for ORF (i.e., WCPM) by assessment period and passage are reported in Table 3. Within grade one, the large standard deviations indicated that there was a large degree of variability across students. Conversely, the standard deviations across most passages in the second and third grades were fairly homogeneous in magnitude (approximately 37). This phenomenon has been reported previously (Catts et al., 2009) and indicates the possibility of floor effects in grade one. Empirically testing for floor effects can be a difficult task, as skewness and kurtosis may not provide correct identification (Catts et al., 2009). Alternatively, these effects were identified by examining the percentage of the sample that performed at the floor of the distribution. We converted the raw scores to a standardized metric (i.e., z-score) and constrained the range of scores to those that fell between −3 and +3. In a normal distribution of scores, 7% of the data would be expected to fall within the lowest quarter of the −3 to +3 range (Catts et al., 2009). When considering the mean of the three passages in fall of grade one, 72.1% of the data fell in the lowest quarter. Similarly, 71.3%, 69.4%, and 66.7% of the data were within the lowest quarter at the winter 1, winter 2, and spring administrations, respectively.

Table 3.

Descriptive statistics for fluency score types for each assessment by grade.

Grade	Score type	Fall		Winter 1		Winter 2		Spring
		M	SD	M	SD	M	SD	M	SD
Grade 1	Passage 1	14.9	15.5	20.9	21.2	31.8	28.5	39.9	32.7
	Passage 2	17.4	17.6	23.8	23.7	39.3	31.7	46.4	35.9
	Passage 3	19.9	19.9	26.9	27.1	45.9	34.7	52.8	38.9
	Median	17.4	17.5	24.0	23.4	39.6	31.0	46.4	35.8
	Mean P123	17.4	17.2	23.9	23.1	38.8	30.3	48.4	36.2
	Mean P23	18.6	18.5	25.4	24.8	42.3	32.3	50.1	36.7
Grade 2	Passage 1	42.5	30.0	56.9	34.0	66.6	34.8	78.4	35.5
	Passage 2	51.5	33.9	65.1	36.6	77.6	38.2	85.0	38.9
	Passage 3	60.2	37.8	76.3	39.6	88.1	39.2	98.3	41.5
	Median	51.3	33.4	64.6	35.0	77.7	37.8	85.0	38.3
	Mean P123	51.1	32.5	65.4	35.4	77.2	36.8	85.2	37.4
	Mean P23	55.6	34.5	69.9	36.9	82.6	38.4	93.7	40.1
Grade 3	Passage 1	66.1	36.3	74.7	38.6	86.9	35.0	92.9	34.5
	Passage 2	73.6	36.7	88.3	36.4	97.0	35.5	101.9	36.4
	Passage 3	81.6	38.1	102.3	37.2	108.6	35.8	114.9	38.2
	Median	73.5	35.5	87.7	35.9	97.0	35.4	101.9	36.2
	Mean P123	72.5	35.3	87.8	36.4	97.4	34.9	101.4	36.9
	Mean P23	76.5	35.9	94.7	36.2	102.7	35.4	108.7	35.5

Note. Mean P23=Mean of Passages 2 and 3, Mean P123=Mean of Passages 1, 2, and 3.

Despite the large variability within passages for particular assessment periods, the correlations among the passages were strong within each grade, with average correlations within each time point and grade estimated at r=.97. Distal associations within grade between fall and spring passages had an average correlation of .85, which indicates that students consistently performed at similar levels across the passages throughout the year.

The descriptive statistics from Table 3 show an interesting trend that is observed across passages 1, 2, and 3 for each assessment period and grade level. For example, in fall of grade 1, the average fluency rate increased from 14.9 on passage 1 to 17.4 on passage 2, and then to 19.9 on passage 3. Not only did the oral reading rates increase by passage, but the gap in rates between the first and third passages grew from fall of grade one to spring of grade three. In fall, there was a maximum of 5 WCPM difference in mean scores, which widened to 13 WCPM in the spring of the same grade. The largest observed discrepancies were during the winter 2 and spring administrations of ORF in grade three, where a maximum mean difference of nearly 22 WCPM occurred. These results indicate the potential presence of order effects in oral reading fluency assessment (Jenkins et al., 2009).

Table 3 also presents descriptive information for the three created score types (i.e., median passage score, the means of all three passages [Mean P123], and the mean of passages 2 and 3 [Mean P23]. Across assessment periods and grades, a close correspondence in means was observed between the passage 2 scores and median scores. Passage 2 scores were the median score in 94% of first grade cases, 98% of second grade cases, and 97% of third grade cases. The Mean P123 score type also had a close correspondence to the passage 2 score, and the Mean P23 score type had the highest values of the three created score types; however, students' performance on Passage 3 consistently represented the largest fluency score for all grades and assessment periods.

Research question 1: estimation of passage variance

Given the variability in observed oral reading rates across passages, we estimated what percent of variance in scores was due to differences across passages and differences across students. First-grade intraclass correlations (see Table 4) indicated that 2% to 4% of the variance in fluency rates was due to the presence of a potential passage effect, an order effect, or both across the four administration periods. Conversely, most of the variability was estimated at the student level ranging from 81% at winter 1 to 89% in spring. Much higher rates of variance were observed in grade two, with 5% to 6% attributed to passage differences across the year, and 85% to 91% due to student differences. Similarly, higher rates were estimated in grade three, with 3% to 9% passage and 85% to 91% student variances observed.

Table 4.

Cross-classified model results.

Grade	Assessment	Intraclass correlation
		Student	Passage
Grade 1	Fall	.85	.02
	Winter 1	.81	.02
	Winter 2	.83	.04
	Spring	.89	.02
Grade 2	Fall	.85	.05
	Winter 1	.88	.05
	Winter 2	.89	.06
	Spring	.91	.05
Grade 3	Fall	.91	.03
	Winter 1	.85	.09
	Winter 2	.89	.07
	Spring	.90	.06

Research question 2: differential prediction of reading comprehension by ORF

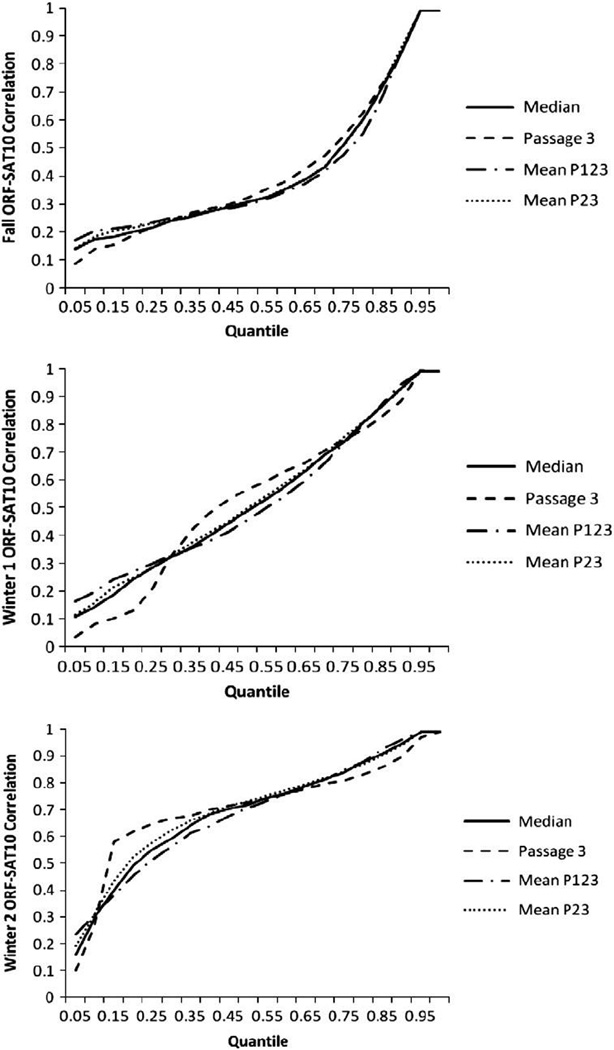
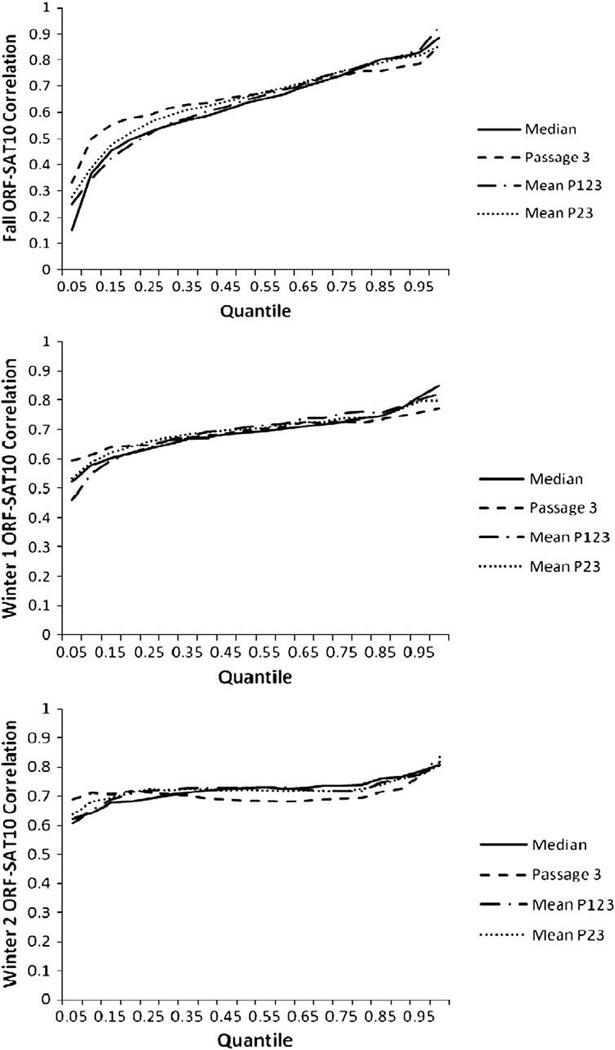
It was of interest to test whether the relation between ORF and SAT-10 scores significantly differed at the quantile level. Because the spring assessment of ORF occurred after SAT-10 testing, quantile plots for spring were not generated. Figs. 1 through 3 display the relation between ORF performance (x-axis) and the relation between ORF and SAT-10 (y-axis) using the median score, passage 3, the mean of all three passages (P123), and the mean of passages 2 and 3 (P23). The plots reflect the expected relation between ORF and SAT-10 by ORF performance. A horizontal line across all levels of the x-axis (i.e., ORF quantiles) would indicate that despite different performance levels on ORF, the predictive validity of ORF would be the same across all skill levels. Given the hypothesized equivalence in difficulty of ORF passages, it might be expected that the individual lines for an individual grade within an assessment should overlap. Non-overlapping plots for the score types would suggest a differential prediction of SAT-10. Across the score types and assessment periods, practically important differences were estimated at 3 of the 99 quantiles (3%) in grade one, compared with 4 of the 99 quantiles in grade two (4%). No practically important differences were observed in grade 3.

Fig. 1.

Quantile plots for Fall, Winter 1, and Winter 2 — Grade 1.

Fig. 3.

Quantile plots for Fall, Winter 1, and Winter 2 — Grade 3.

The three plots in Fig. 1 show the relation between ORF and the SAT-10 across the four score types within each of three assessments in grade one (fall, winter 1, and winter 2). In fall of grade one, the relation between ORF and SAT-10 scores became progressively stronger as the student's ORF skills increased, and was likely due, in part, to floor effects in ORF. However, the four score types were fairly homogenous in the magnitude of the correlation. In general, the trend in fall suggested that the correlations between ORF and SAT-10 were similar for all score types across the quantiles. At the lowest end of the distribution (i.e., .05 to .25 quantiles), the mean of all three passages demonstrated the strongest relation between ORF and SAT-10 (.20 to .22) compared with the other scores, whereas the passage 3 score had the weakest relation (.10 to .18). At the winter 1 assessment, the mean of all three passages demonstrated the strongest correlation for the students with the lowest fluency rate (5th to 25th quantile), and passage 3 was the weakest. The maximum difference in correlations between the mean and passage 3 was .14 at the 5th quantile, which was statistically significant (p<.001, ΔR² = 2%) and corresponded to a small amount of variance explained. Conversely, for students whose fluency was between the 30th and 60th quantiles, passage 3 retained the strongest correlation between fluency and comprehension compared to the other three score types, with a maximum correlation difference of .11 for the mean of all three passages (p<.01, ΔR² = 1%), a non-meaningful difference.

A differential trend was observed at the winter 2 assessment, whereby the mean of all three passages was significantly differentiated from passage 3 scores (p<.001, ΔR² = 2%), but only at the 5th quantile. Moreover, passage 3 was the best score for students with fluency rates between the 15th and 40th quantiles, with a maximum difference of r=.20 with the mean of all three passages observed at the 15th quantile (p<.001, ΔR² = 4%), a small difference.

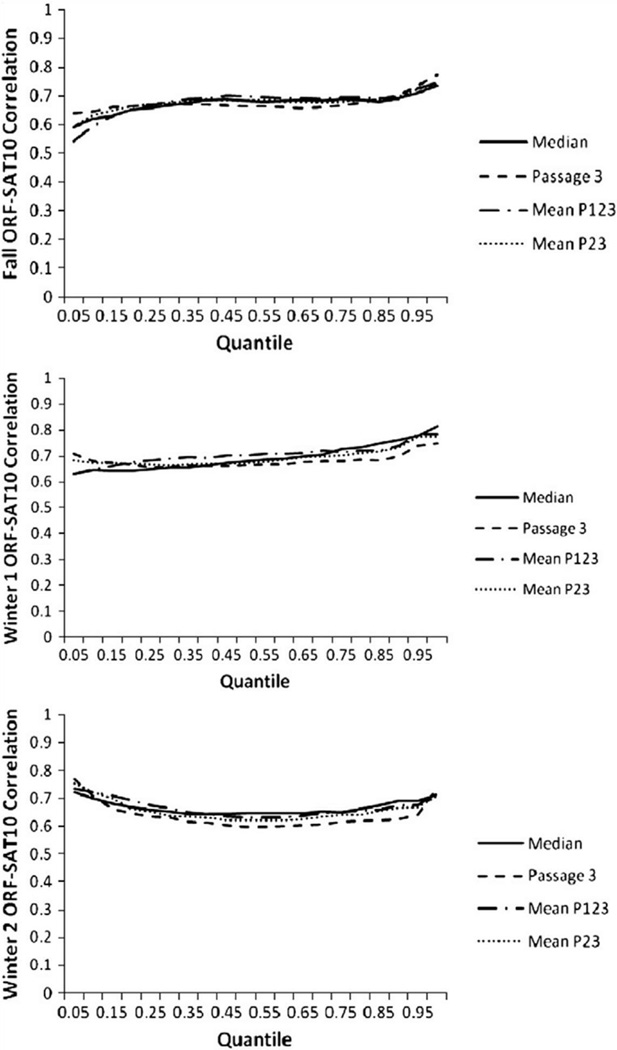
Second grade quantile plots (Fig. 2) for the fall assessment followed a similar, although less steep, slope as grade one. Although fluency scores at the lower end of the distribution generated weaker correlations with the SAT-10 compared with performance at the median or upper end of the distribution, some distinct observations were noted. The most stable correlation was produced by using the score from passage 3, with a range of r=.33 at the 5th quantile to r=.85 at the 95th quantile. The largest discrepancies with the other score types were r=.18 at the 5th quantile with the median score (p<.001, ΔR² = 3%), r=.15 at the 10th quantile with the mean of all three passages (p<.001, ΔR² = 2%), and r=.14 at the 15th quantile with the mean of all three passages (p<.001, ΔR² = 2%). The winter 1 quantile plot showed homogeneous, moderate to strong relations between ORF and SAT10 across both quantile and score types, with the largest discrepancy of r=.14 between the passage 3 and the mean of all three passages at the 5th quantile (p<.001, ΔR² = 2%). For the winter 2 assessment of grade two and all three assessments of grade three (Fig. 3), no practically important differences between score types were observed across the quantile levels.

Fig. 2.

Quantile plots for Fall, Winter 1, and Winter 2 — Grade 2.

Research question 3: differential screening accuracy of ORF

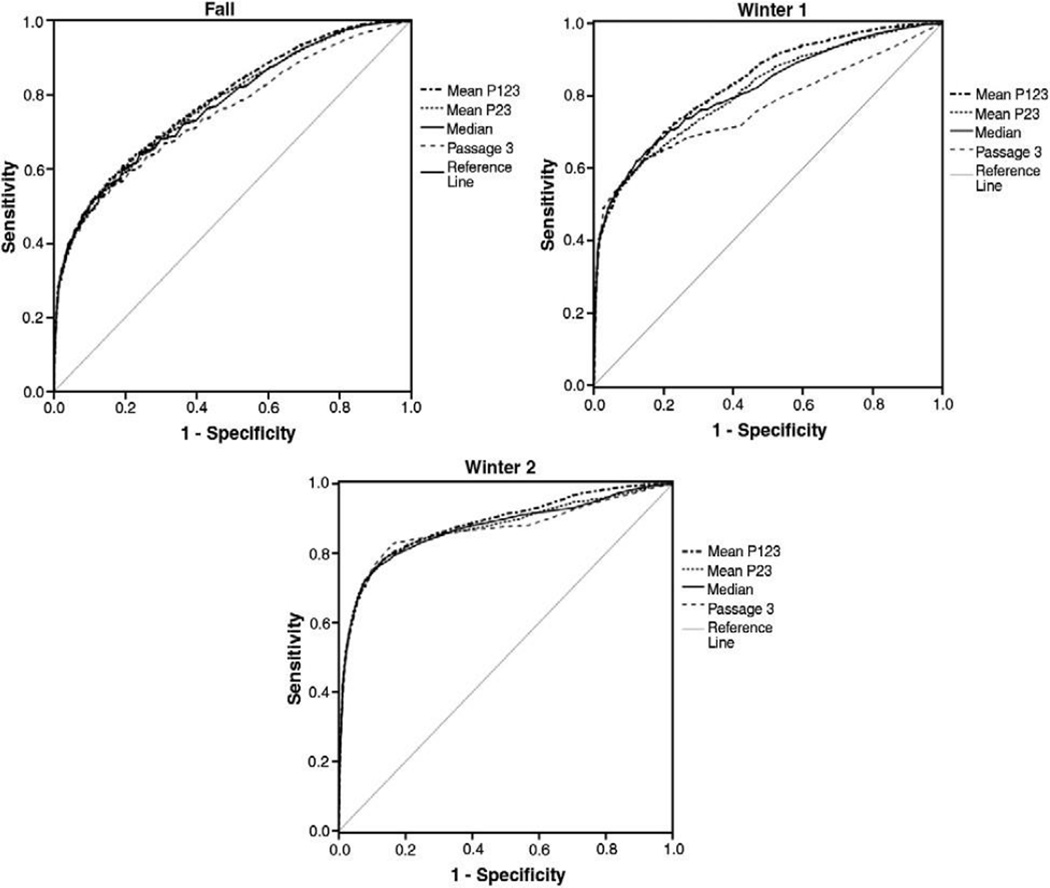
The final question was the accuracy of different ORF score types in identification of students as at risk for reading comprehension problems on the SAT-10. The ROC analyses in Fig. 4 and Table 5 highlight the relation between various ORF score types and prediction of risk on the SAT-10 (performing below the 40th percentile). In grade one, the ROC curves for the fall assessment demonstrated that the mean of all passages, the mean of passages 2 and 3, the median score, and student performance on passage 3 were fairly homogenous in the trace line. The AUC index (Table 5) was largest for the mean of all three passages (.78), compared with the mean of passages 2 and 3 (.77), the median passage score (.77), and passage 3 (.75). In fall of grade one, the sensitivity was consistently weak, regardless of score type, with a maximum value of .32 for the median score. Similarly, the specificity was strong across all score types, indicating that students identified as not at risk on ORF were likely to perform at or above the 40th percentile on the SAT-10. Both positive and negative predictive value estimates were the strongest for the mean of all three passages at .79 and .63, respectively. A post-hoc analysis at each time point was conducted to test if the mean of all three passages was more predictive of SAT-10 risk than the median score. Results indicated that the score types did not significantly differ at fall (z = 1.56), but the mean score provided a significantly better classification in winter 1 (z = 2.56) and winter 2 (z = 2.13) time points.

Fig. 4.

ROC curves for the Fall, Winter 1, and Winter 2 assessments for Grade 1.

Table 5.

Screening accuracy of DIBELS ORF score.

	Test Scores	Sensitivity	Specificity	PPV	NPV	AUC
Grade 1	Fall Median Passage	.32	.92	.75	.63	.77
	Fall Mean P123	.30	.94	.79	.63	.78
	Fall Mean P23	.30	.93	.76	.63	.77
	Fall Passage 3	.30	.89	.69	.62	.75
	Winter 1 Median Passage	.63	.78	.69	.73	.82
	Winter 1 Mean P123	.59	.84	.74	.72	.83
	Winter 1 Mean P23	.58	.81	.70	.71	.81
	Winter 1 Passage	.62	.71	.63	.71	.77
	Winter 2 Median Passage	.85	.78	.75	.87	.87
	Winter 2 Mean P123	.85	.79	.76	.87	.88
	Winter 2 Mean P23	.80	.82	.77	.84	.87
	Winter 2 Passage	.70	.85	.79	.78	.87
Grade 2	Fall Median Passage	.73	.79	.74	.78	.82
	Fall Mean P123	.75	.77	.72	.79	.83
	Fall Mean P23	.67	.84	.77	.76	.83
	Fall Passage 3	.61	.88	.81	.73	.83
	Winter 1 Median Passage	.75	.77	.73	.79	.84
	Winter 1 Mean P123	.74	.78	.73	.78	.85
	Winter 1 Mean P23	.69	.83	.77	.77	.85
	Winter 1 Passage	.65	.87	.80	.75	.85
	Winter 2 Median Passage	.77	.76	.73	.80	.86
	Winter 2 Mean P123	.75	.78	.74	.80	.86
	Winter 2 Mean P23	.70	.84	.78	.77	.86
	Winter 2 Passage	.63	.89	.82	.75	.85
Grade 3	Fall Median Passage	.83	.64	.54	.88	.83
	Fall Mean P123	.84	.63	.54	.88	.83
	Fall Mean P23	.80	.69	.57	.87	.83
	Fall Passage 3	.76	.74	.60	.86	.83
	Winter 1 Median Passage	.84	.65	.55	.89	.84
	Winter 1 Mean P123	.82	.68	.57	.88	.85
	Winter 1 Mean P23	.75	.77	.63	.86	.85
	Winter 1 Passage	.63	.86	.71	.82	.84
	Winter 2 Median Passage	.81	.68	.57	.87	.84
	Winter 2 Mean P123	.80	.70	.57	.87	.84
	Winter 2 Mean P23	.74	.76	.61	.85	.84
	Winter 2 Passage	.65	.83	.66	.82	.83

Note. Mean P23=Mean of Passages 2 and 3; Mean P123=Mean of Passages 1, 2, and 3; SE=Sensitivity; SP=Specificity; PPV=Positive Predictive Value; NPV=Negative Predictive Value; AUC=Area Under the Curve.

ROC results for both second and third grades suggested that the discriminating power of ORF score types were nearly identical within grade and time points, with the actual curves overlapping (not shown but available from the first author upon request). At fall of grade two, the AUC was .83 for all four score types. Although the mean of all the three passages had the strongest estimate for sensitivity in fall, the median passage score provided the best fit across sensitivity, specificity, and positive and negative predictive values. This fit was observed for all assessment periods of second and third grades.

DISCUSSION

Oral reading fluency is a critical developmental skill to assess in elementary students due to its important role in reading comprehension (see Fuchs, Fuchs, & Compton, 2001; Jenkins, Fuchs, van den Broek, Espin, & Deno, 2003; Schwanenflugel et al., 2006). In particular, DIBELS oral reading fluency has been widely used in many schools across North America for both screening and progress monitoring students who may be at risk for difficulties in future reading comprehension. Efforts to ensure equivalence of passage difficulty in DIBELS included the use of readability formulae and the median score for screening and progress monitoring purposes. The former has been reported to be problematic (Ardoin et al., 2005; Francis et al., 2008), and the latter had not been examined empirically. Thus, in the present study, we investigated predictive and screening accuracy of DIBELS ORF for students' reading comprehension achievement at the end of the year in the first, second, and third grades using four different score types (i.e., the median of three passages, the mean of all three passages, the mean of passages 2 and 3, and the score from passage 3) using data from Reading First schools in Florida.

Results revealed that passages that appeared to be equivalent based on readability formulae varied substantially in terms of the numbers of words students read per minute. Scores on passages differed by as much as 28 WCPM. The vast majority of variability in students' performance on oral reading fluency was attributable to differences among students, but variability due to passages was also fairly sizeable (i.e., up to 9%). In the present study, the reading rate increased steadily from passages 1 to 3. Based on the mean WCPM scores from Table 3, it can be seen that, on average, ORF scores from students in grade one increased by 16% as they read subsequent passages within an assessment. Similarly, second grade student performance increased by an average of 15%, and grade three performance improved by an average of 13%. Such progression is counter to what the DIBELS readability estimates would suggest because the third passages at each assessment period have higher readability scores (Good & Kaminski, 2002) and thus should be more difficult to read. This pattern of increasing fluency rates across the three passages suggests a potential practice effect. Although the order of passages was not randomized in the present study, given that this increasing rate was observed across assessment periods and grades, along with evidence from experimental studies (Francis et al., 2008; Jenkins et al., 2009) showing an identical pattern, practice effects seem to play an important role in ORF assessments using multiple passages.

For practical purposes, if the practice effect truly exists such that students' oral reading fluency scores improve from the first to third passages, then it might be advisable to use score types other than the median score, such as the mean of all three passages or mean of passages 2 and 3, for decision making. Despite the relatively weak overall screening accuracy for scores at fall of grade one, the evidence suggested that both the median score and the mean score across all passages provided the most appropriate balance to the magnitude of efficiency estimates across score types for this assessment, though differences were marginal at both winter assessments in grade one. However the data suggested that the mean score is a better classifier of risk status on the SAT-10 than the median score, although in both second and third grades, the median score was the best predictor.

The implicit assumption that oral reading fluency may be uniformly predictive of later reading comprehension skills for student of all ability levels was partially supported in the present study, based on the small number of quantiles in which practically important differences were observed. The predictive validity of oral reading fluency varied as a function of students' reading fluency level; quantile analysis showed that oral reading fluency had a weaker relation with reading comprehension for students with lower reading fluency than for those with higher reading fluency in grade one and fall of grade two. This heteroscedastic relation between oral reading fluency and reading comprehension in fall of grade one may be partly due to floor effects (see also Catts et al., 2009), particularly for students at the lower end of the distribution. During these periods, scores other than the median score may need to be considered to enhance predictive validity. The mean of all three passages tended to have a stronger relation with students' reading comprehension at the end of grade one for students at the lowest end of the distribution. In contrast, the third passage was more strongly related to reading comprehension for students in the middle range. A similar trend was found for fall of grade two.

It should be noted that in Florida, oral reading fluency probes was administered in fall of grade one, which is not part of the DIBELS protocol. Thus, although students' mean WCPM in fall of grade one does not appear to be absolutely at the floor (i.e., near zero), and there is sizable variability about the mean (WCPM ranging from 14 to 19, see Table 3), the weak relation between oral reading fluency and reading comprehension in the beginning of grade one may be attributed to the floor effect (e.g., Harn, Stoolmiller, & Chard, 2008; Stoolmiller, M., personal communication, April, 2010). If school personnel choose to assess oral reading fluency in fall of grade one, they should do so knowing that these effects will adversely influence prediction, especially for students with low reading skills.

Given that DIBELS ORF is typically used for screening purposes, we examined its screening accuracy using different scores from the three passages. The results of the present study suggest that students' mean performance on all three passages might be considered as an alternative score to use, in grade one in particular, for identifying children at risk and not at risk for future reading difficulties. Although the difference in screening accuracy may not appear large, given the current practice of using the median score and the critical importance of early identification of children and the difficulty in remediating students in later grades (Torgesen, 1998, 2002; Vellutino, Scanlon, Small, & Fanuele, 2006), this finding may have critical implications for decision making in schools. Additionally, this result indicates that, although there might be a practice effect when assessing oral reading fluency with multiple passages, including students' performance information in the first passage is important because the mean of all the passage provided more predictive information than the mean of passages 2 and 3 in the two periods in grade one.

In addition to using alternative scores, the results of the present study contribute to the extant literature recommending against using students' oral reading fluency as the sole measure for making important identification and instructional decisions regarding children's reading. As is true for using assessment information in general, it is advisable for educators to utilize multiple sources of information when drawing inferences and making decisions about students' needs (Shapiro, Solari, & Petscher, 2008). Therefore, it is critical to use oral reading fluency tests with other assessment instruments to enhance screening precision in identifying students who are in need of more intense instruction. For instance, for students with low reading fluency scores from reading words out of context (i.e., in a list format) were shown to uniquely contribute to reading comprehension (Jenkins et al., 2003). When using DIBELS, additional measures, such as Nonsense Word Fluency, Letter-Naming Fluency, or Phonemic Segmentation Fluency are administered from kindergarten to fall of grade two (Good, Simmons, Kame'enui, Kaminski, & Wallin, 2002).

These additional measures are used in conjunction with oral reading fluency to assess reading skills. For instance, the proportion of explained variance of year-end reading comprehension increased by 4% when students' performance on the DIBELS Letter-Naming Fluency and Nonsense Word Fluency in the beginning of grade one was included in addition to Oral Reading Fluency (Kim et al., 2010). Furthermore, although according to the DIBELS protocol, Letter-Naming Fluency is administered only until fall of grade one, it might be useful to use it afterward, along with other assessment instruments, with students with weak oral reading fluency skills. Similarly, research has demonstrated that assessing phonological awareness is important because it becomes an increasingly important predictor of reading comprehension over time (Pennington & Lefly, 2001; Torgesen, Wagner, Rashotte, Burgess, & Hecht, 1997). Inclusion of information on students' oral language skills (e.g., vocabulary) in addition to oral reading fluency might also be considered because students' vocabulary size increases for the prediction of year-end reading comprehension performance for students in first through third grades (Kim et al., 2010).

A few limitations of the present study are worth noting. The study included a large number of students from Reading First schools, and thus, generalizability of the findings is limited to similar populations. For example, the sample included a large proportion of students receiving free or reduced priced lunches and students who were English language learners. Furthermore, the SAT-10 was used as the criterion reading comprehension measure in the present study. Although the SAT-10 is widely used across many states, the results of the present study may be limited to the particular reading comprehension measure from this test. As noted earlier, the order of passages was not randomized, and thus, a future study with an experimental design should replicate the findings of the present study. Lastly, because these data were derived from an archival data source, there is not complete knowledge as to what procedures were used in collecting and scoring data; however, because these data were collected as part of the Reading First initiative, standardized procedures were mandated by the state for data collection.

Despite these limitations, the results of the present study, in conjunction with a previous experimental study (Francis et al., 2008), suggest that empirically equating passages (i.e., using reading rate information) to adjust for passage difficulty, in addition to other means (e.g., readability formulae and lexile scores), may enhance the technical adequacy of oral reading fluency measures. The present study, along with a few previous studies (e.g., Ardoin et al., 2005; Francis et al., 2008), took steps into this direction, but further work is warranted. For example, the impact of passage effects on growth in reading is not clear yet, and future studies using large samples are needed to investigate the effects of the level of passage difficulty used for equating (i.e., easiest, median, and most difficult). Overall, based on our findings, we encourage researchers and practitioners to be cognizant of practice effects that may occur when administering multiple passages assessing oral reading fluency and to carefully consider using alternative score types at appropriate grade levels when reporting students' reading rate.