Abstract
This study examines the effects of cartilage endplate (CEP) calcification and the injection of intervertebral disc (IVD) cells on the nutrition distributions inside the human IVD under physiological loading conditions using multiphasic finite element modeling. The human disc was modeled as an inhomogeneous mixture consisting of a charged elastic solid, water, ions (Na+ and Cl−), and nutrient solute (oxygen, glucose and lactate) phases. The effect of the endplate calcification was simulated by a reduction of the tissue porosity (i.e., water volume faction) from 0.60 to 0.48. The effect of cell injection was simulated by increasing the cell density in the NP region by 50%, 100%, and 150%. Strain-dependent transport properties (e.g., hydraulic permeability and solute diffusivities) were considered to couple the solute transport and the mechanical loading. The simulation results showed that nutrient solute distribution inside the disc is maintained at a stable state during the day and night. The physiological diurnal cyclic loading does not change the nutrient environment in the human IVD. The cartilage endplate plays a significant role in the nutrient supply to human IVD. Calcification of the cartilage endplate significantly reduces the nutrient levels in human IVD. Therefore, in cell based therapy for IVD regeneration, the increased nutrient demand as a result of cell injection needs to be addressed. Excessive numbers of injected cells may cause further deterioration of the nutrient environment in the degenerated disc. This study is important for understanding the pathology of IVD degeneration and providing new insights into cell based therapies for low back pain.
Keywords: Intervertebral disc (IVD), Mixture theory, Finite element method, Cartilage endplate, Nutrient supply, Tissue regeneration, Disc degeneration, Low back pain
INTRODUCTION
Low back pain is a major public health problem which causes significant social and economic burdens in the United States [1–3]. Although the exact cause for low back pain is unclear, the degenerative changes of the intervertebral disc (IVD) have been implicated as a possible primary etiologic factor [4, 5]. One of the factors which may lead to disc degeneration is the nutrient supply deficiency in the IVD [6, 7]. The nutrient environment inside the IVD has a significant effect on cell viability, proliferation rate, and cell energy metabolism [8–14]. A fall in nutrient supply leads to a lowering of oxygen tension, glucose concentration, or pH (due to increased lactate concentrations). As a result, the ability of the disc cells to synthesize matrix proteins (e.g., collagen and proteoglycan) [15–17], and maintain its extracellular matrix (ECM) homeostasis (synthesize/breakdown) may be impaired, thus, leading to the onset of disc degeneration.
The IVD is the largest avascular cartilaginous structure in human body which lies between the bony vertebral bodies. It contributes to the flexibility and load support in the spine. To accomplish these functions, the disc has a unique architecture consisting of a centrally located nucleus pulposus (NP) surrounded superiorly and inferiorly by cartilage endplates (CEP) and peripherally by the annulus fibrosus (AF) [18]. The NP is composed of rich hydrophilic proteoglycans with negative charge, which helps to sustain axial compression. The AF is formed by a series of lamellae (concentric rings) within which the rich collagen fibers lie parallel. This highly organized collagen fiber bundle helps to resist tension and shearing forces. The CEP is a thin layer of hyaline cartilage surrounding the cranial and caudal surfaces of the disc, playing an important role in fluid and solute transport in/out of the disc.
The nutrients in the disc are mainly supplied by the capillaries and canals in the vertebral body [19–21]. The nutrients have to penetrate through the cartilage endplate layer to reach the disc extracellular matrix. It is believed that the endplate route is the main pathway for nutrition supply to the disc cell [7, 17]. Due to aging and other pathological conditions, the CEP may calcify, which reduces proteoglycan and water content, thus changing the transport properties (e.g., hydraulic permeability and solute diffusivities) of the endplate [22, 23]. Convection and diffusion through the calcified endplate is likely to be stinted thus affecting the nutrition supply to the disc [17, 24]. Therefore, under physiological loading conditions, the calcification of the CEP may significantly affect the nutrient concentrations within the disc.
Since the in vivo biomechanical response, transport of solutes, and cellular activities in the human IVD are difficult to measure, numerical simulation using finite element models (FEM) became an essential tool to help understand the biomechanical and nutrient environment in the IVD. Earlier studies have been limited to analyzing diffusion of the nutrient solutes inside the disc without considering the mechanical loading [25, 26]. Based on the mixture theory, we developed a multiphasic mechano-electrochemical finite element model to study the effects of static and dynamic loading on fluid and solute transport inside the human IVD [27–30]. Most recently, cellular energy metabolic rates were considered in finite element models to predict the nutrient environment within the IVD [30–32]. In these studies, the consumption rates of oxygen and glucose, as well as the production rate of lactate, were coupled with local oxygen concentrations and pH values. In addition, the relationship between cell viability and glucose concentration was also incorporated into the finite element models of the human IVD [14, 33, 34]. However, to our knowledge, the effect of cartilage endplate calcification on nutrient transport (diffusion and convection) inside the human IVD has not been fully elucidated under physiological loading conditions (i.e., day-night cyclic loading). Recently, the injection of IVD cells/stem cells in the NP region has been proposed for IVD regeneration in cell based therapies for low back pain treatment [35–37]. The success of this therapeutic approach first depends on the cell viability after the injection. Usually, the nutrient transport in degenerated discs is hindered by the calcified endplate. The increased nutrient demand due to the increase of cell density may further deteriorate the nutrient environment in the degenerate disc. Without restoring the nutrient environment, this procedure may accelerate the process of degeneration [36]. However, the impact of a cell injection coupled with already present degeneration on the nutrient environment of the disc has not been determined.
Therefore, the objective of this study was to further develop a multiphasic mechano-electrochemical 3D finite element model of human IVD by considering the disc cell energy metabolism. This model was then applied to examine the effects of endplate calcification and the injection of IVD cells on the nutrition environment inside the human IVD under physiological loading conditions. The effect of endplate calcification was simulated by a reduction of the tissue porosity (i.e., water volume faction). The effect of a cell injection was simulated by increasing the cell density in the NP region. The role of physiological mechanical loading in regulating the disc nutrient environment was also clarified by considering strain-dependent transport properties (e.g., hydraulic permeability and solute diffusivities). This study is important for understanding the pathology of IVD degeneration and provided new insights into cell based therapies for low back pain.
MATERIALS AND METHODS
Theoretical formulation
A theoretical model [27–29], based on the triphasic theory [38, 39], was used in this study. The human disc was modeled as an isotropic inhomogeneous mixture consisting of an intrinsically incompressible elastic solid (with fixed charge), water, ions (Na+ and Cl−), and nutrient solute (oxygen, glucose and lactate) phases. The balance of linear momentum for the mixture and the conservation of mass for each of phases or species led to the following governing equations [28, 29, 33]:
| (1) |
| (2) |
| (3) |
| (4) |
where σ is the total stress of the mixture (IVD tissue); vs is the velocity of the solid phase; Jw, Ji, and Jn are the flux of water, ions, and nutrient solutes relative to the solid phase respectively; Øw is the fraction of water volume in the tissue (tissue porosity); ci (i: Na+ and Cl−) is the cation and anion concentrations in interstitial water; cn (n: oxygen, glucose, and lactate) is the nutrient/metabolite solutes concentrations in interstitial water; and Qn is the cellular metabolism rate (consumption/production rate) of nutrient/metabolite solutes.
Together with the constitutive relation for each phase, all the variables in the governing equations were related to the displacement of solid phase u and modified electrochemical/chemical potential of water εw, ions εi, and nutrient/metabolite solutes εn [28]:
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where p is the fluid pressure; I is the identity tensor; λ and µ are Lame coefficients of the solid matrix; E is the infinitesimal stain tensor; ϕ is the osmotic coefficient; Bw is the interphase coupling coefficient; R is gas constant; T is absolute temperature; the transport parameters; k, Hi, Hn, Di, and Dn represent, respectively, the hydraulic permeability of the water, the hindrance factor of the ions and nutrient solutes for the convection, and the intra-tissue diffusivity of the ions and nutrient solutes. In this study, notice that the hindrance factor Hα (α = i, n) has not been determined for IVD tissue. The values of these parameters were assumed to be unity [29]. Also, the interphase coupling coefficient Bw was assumed to be zero [40].
The modified electrochemical/chemical potentials (εw, εi, εn) in equations 5–8 were related to fluid pressure (p), electrical potential (ψ), and solute concentrations (ci, cn) by [28, 41]:
| (10) |
| (11) |
| (12) |
where e is the dilatation; Fc is the Faraday constant, γi and γn are the mean activity coefficients for ion and nutrient solutes, ψ is the electrical potential. Notice that the mean activity coefficients γi and γn in this study were assumed to be unity.
Based on the electroneutrality condition, the concentrations of cation (Na+) and anion (Cl−) are related to the value of negatively fixed charge density (cf) in the disc tissues [38] by:
| (13) |
In this study, strain-dependent tissue compositions were taken into consideration. The tissue fixed charge density and porosity related to the tissue dilatation and the tissue porosity at reference configuration by [38]:
| (14) |
| (15) |
where and are the initial porosity and negative fixed charge density of the tissue before deformation (i.e. e = 0), while e is the tissue dilatation.
In this study, the following constitutive relationships were used for strain-dependent hydraulic permeability (k) and solute diffusivities (Di, Dn):
| (16) |
| (17) |
where and rα (α = ions and nutrient solutes) are the diffusivity in aqueous solution and hydrodynamic radius of ions and nutrient solutes. a and b are material constants related to tissue composition and structure (Table 1). Since the tissue porosity was related to the tissue dilatation and the porosity at the reference configuration, the hydraulic permeability, ion diffusivity, and nutrient solute diffusivity were all strain-dependent.
Table 1.
Disc tissue properties used in the numerical model.
| NP | AF | CEP | |
|---|---|---|---|
| Initial water content (Water content: ) |
0.86 a | 0.75 a | Normal:0.6 b, Calcified:0.45 |
| Elastic constant λ (MPa) |
0.02 c | 0.2 c | 0.1 d |
| Elastic constant µ (MPa) |
0.015 c | 0.15 c | 0.2 d |
| Cell density (cells/mm3) |
Normal:4000 e, Cell based therapy: 6000, 8000, 10000 |
9000 e | 15000 e |
| Parameter for hydraulic permeability k = α1(Øw/Øs)b1 |
a1=0.00339 nm2
f, b1=3.24 f |
a1=0.00044 nm2
g, b1=7.193 g |
a1=0.0248 nm2
h, b1=2.154 h |
| Parameter for diffusivity α: ions and nutrient solutes |
a2=1.25 nm i, b2=0.681 i |
a2=1.29 nm i, b2=0.372 i |
a2=1.29 nm i, b2=0.372 i |
Where is hydrodynamic radius of ions and nutrient solutes , is diffusivity of ions and nutrient solutes in aqueous solution .
Yao and Gu, 2007.
Roberts et al., 1989; Setton et al., 1993.
Yao and Gu, 2006.
Mow et al., 2002; Yao and Gu, 2004.
Maroudas et al., 1975.
Gu et al., 2003, from agarose gels.
Gu and Yao, 2003, from porcine AF tissue.
Maroudas et al., 1975; Yao and Gu, 2004.
Gu et al., 2004, from porcine AF tissue and agarose gels.
The energy metabolic rates of the disc cells were taken into consideration based on the experimental results in the literature. The consumption rate of oxygen depended on oxygen concentration, as well as pH value [12]. The rate of production of lactate was based on that of NP cells in the literature [11]. A linear relationship between the pH value and lactate concentration was used to calculate the pH values in the disc [11, 31]. The glucose is primarily consumed through the process of glycolysis, in which one molecule of glucose is broken down into two lactate molecules [15, 42]. Thus, the consumption rate of glucose was set as half of the lactate production rate in this study. The following constitutive relations for the disc cell metabolic rates were used in this study:
| (18) |
| (19) |
| (20) |
| (21) |
where the unit of oxygen consumption rate Qn (n = oxygen, glucose, and lactate) is nmol/l/h, the unit of oxygen concentration coxy is µM, is 5.27 nmol/million cells/hr in the NP region and 3.64 nmol/million cells/hr in the AF region. is 3.4 µM in the NP region and 12.3 µM in the AF region, the unit of oxygen tension [O2] is kPa which could be converted into to µM using oxygen solubility in water (1.0268 µmol/kPa-100ml), the unit of lactate concentration clac is mM, the units of lactate production rate Qlac and glucose consumption rate Qglu are nmol/l/h. Note that the single cell metabolic rates in the CEP were assumed to be equal to the values in the NP due to the lack of experimental data in the CEP.
Initial and boundary conditions
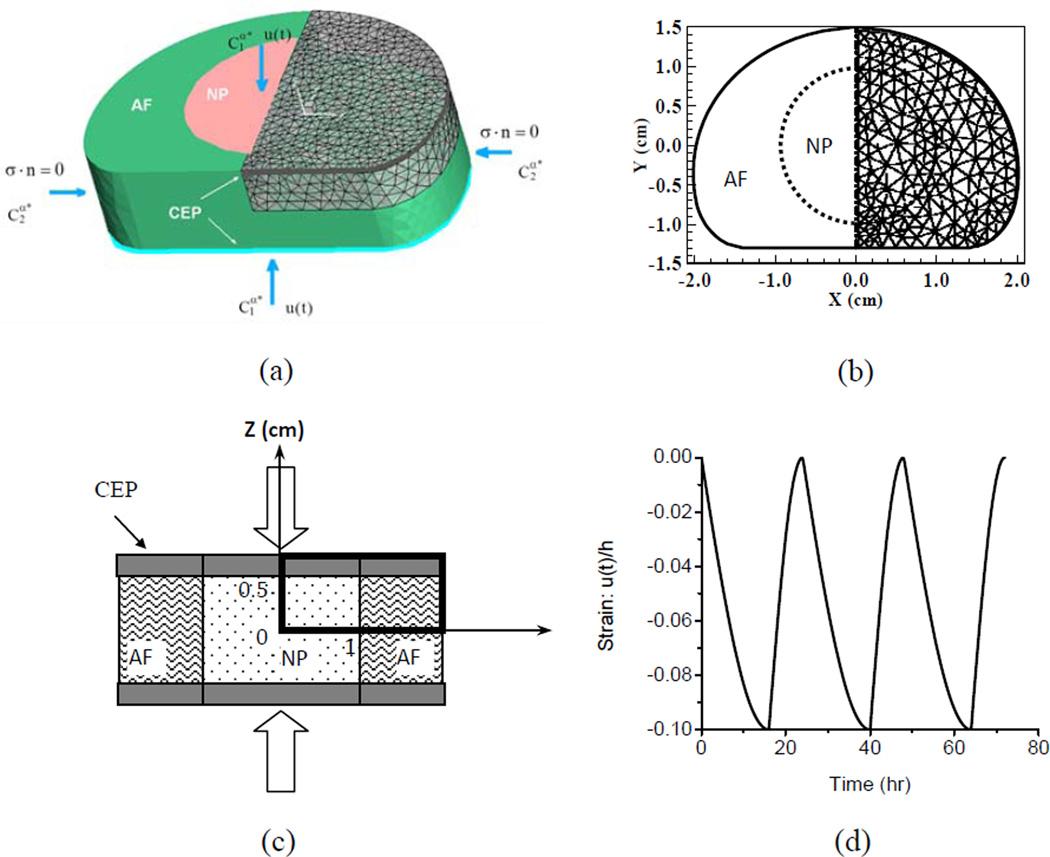
The human IVD was modeled as an inhomogeneous material with three different regions (NP, AF and CEP, Figure 1a). Responses of nutrient solute transport in the human lumbar disc to unconfined compression (cyclical loading) were analyzed. For this 3D problem of interest, only the upper quadrant of the sample was modeled due to the symmetry with respect to plane X=0 and plane Z=0. Initial conditions:
| (22) |
Boundary conditions:
| (23) |
| (24) |
| (25) |
| (26) |
(α: ions and nutrient solutes) Here ux and uz are the components of the solid displacement u in X and Z directions, respectively. −u(t) is the pre-described displacement history (Figure 1d) to simulate physiological loading during the day and night.
Figure 1.
Geometry of the human lumbar IVD model and loading protocol in the simulation. (a) 3D view of the disc model, (b) disc geometry, (c) test configuration, and (d) cyclic loading on the top and bottom of the disc (Strain = cyclic displacement u(t) / initial height of the disc h).
Finite Element analysis
A human lumbar IVD was modeled as an inhomogeneous material with three distinct regions: NP, AF and CEP (Figure 1a). The size and geometry of the human IVD in the simulation are based on previous experimental results [29, 43]. The thickness of the IVD sample was 10 mm. The thickness of the CEP was 0.6 mm [6, 44]. To investigate the effect of the CEP thickness on the nutrient environment, a thin calcified CEP with the thickness of 0.3mm was also defined and simulated. The IVD sample was initially equilibrated under pre-loaded conditions to maintain the original disc thickness. The solute concentrations at the boundaries were: cNaCl is 0.15 M, cglu is 4 mM at the CEP boundary and 5 mM at the lateral AF surface, clac is 0.8 mM at the CEP boundary and 0.9 mM at the lateral AF surface, coxy is 5.1 kPa at the CEP boundary and 5.8 kPa at the lateral AF surface. The IVD sample was then subjected to a cyclical loading between the two endplates (Figure 1d). The amplitude of the compressive strain on the whole disc for the cyclical loading was 10%. The cyclic loading included 16-hour compression and 8-hour recovery to mimic the physiological diurnal disc height changes [26]. The boundary of CEP was permeable to both water and solutes.
The 3D weak form of the finite element formulation was based on the previous work [24, 29, 41]. COMSOL software (Version 3.4, COSMOL Inc., Burlington, MA) was used to solve this 3D initial- and boundary-value problem. The program was set to the weak form mode. The upper right quadrant of the disc was modeled with 7016 second-order, tetrahedral Lagrange elements (Fig. 1a). As for the cyclic loading, the maximum time step for beginning each ramp compression was 10 seconds. The time step used in cyclic loading ranged from 5 seconds to 100 seconds. The convergence of the numerical model was examined by refining the mesh and tightening the tolerance. The numerical accuracy of this study was validated with the results of the 3D stress relaxation cases published in the literature [28, 29].
In this study, the effect of endplate calcification on nutrient solute transport was simulated by a reduction of the tissue porosity (i.e., water volume faction), since the hydraulic permeability and solute diffusivity are related to the tissue water content, see equations (16–17). The tissue porosity of normal CEP was 0.6, while this value in calcified endplate was 0.48 (i.e., a 20% reduction) [6, 22]. In addition, the cell density in the NP region was increased by 50%, 100%, and 150% in order to analyze the effect of cell injections in cell based therapies for low back pain treatment. The material properties for the AF, NP, and CEP were summarized in Table 1.
RESULTS
The biomechanical response (strain, stress, water flux, and water pressure), electrical signals (ion concentrations and ion current/potential), and nutrient solutes transport (oxygen, glucose, and lactate concentration) in the human IVD under the physiological loading were simultaneously obtained from this multiphasic finite element model of the IVD. Only the results for the oxygen, glucose, and lactate concentration profiles were reported here.
Effect of diurnal cycle loading
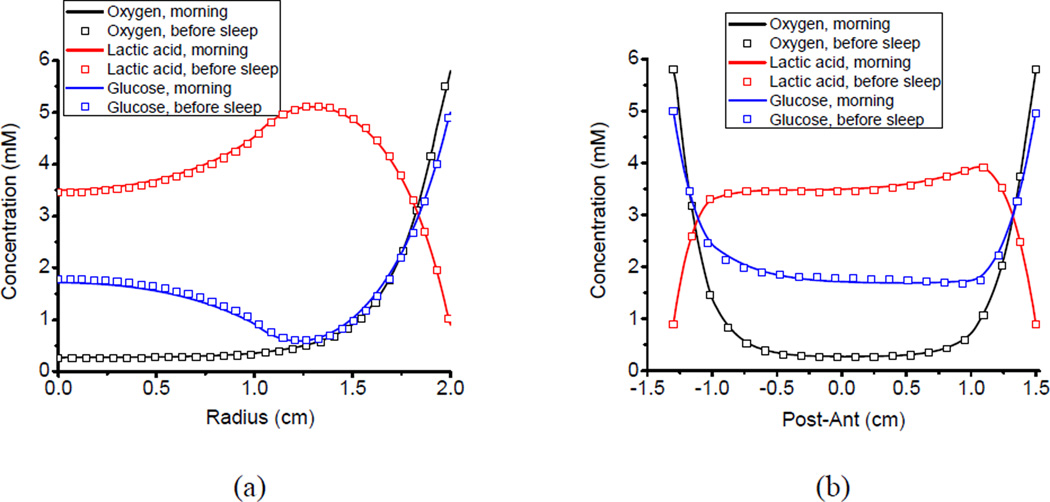
The human IVD was subjected to a diurnal cyclic loading, including a 16-hour compression and 8-hour recovery. The oxygen, glucose, and lactate concentration distributions in the normal IVD at the end of the day (i.e., the end of compression), as well as at the beginning of the day (i.e., the end of recovery), were shown in Figure 2. It was apparent that the nutrient concentration profiles remained almost identical during the day and night. The changes of the concentration profiles were less than 1% under the diurnal cyclic loading. Although the nutrient concentration levels were different compared to the IVD with a normal CEP, the concentration profiles also remained almost identical during the day and night in the IVD with a calcified CEP (results not shown).
Figure 2.
Nutrient solute (oxygen, glucose and lactate) concentration distributions inside the human IVD in the morning (end of the recovery) and at night (end of the compression): (a) in the x-direction from the center to the lateral and (b) in the y-direction from the posterior to the anterior.
The nutrition concentration distributions were not uniform in the human IVD (Figure 3). Generally, the oxygen and glucose concentrations decreased moving away from the blood supply at the margin of the disc. In contrast, the lactate concentration increased toward the center of the disc. Significant nutrient concentration gradients existed inside the disc with a normal CEP. The posterolateral region of the disc within the AF possessed the lowest glucose concentration of 0.540 mM, compared to the concentration of 5mM at the lateral boundary of the AF. This region also had the highest lactate concentration of 5.207 mM, compared to the concentration of 0.9mM at the at the lateral boundary of the AF. The center region of the disc within the NP possessed the lowest oxygen concentration of 0.3 kPa, compared to the concentration of 5.1 kPa at the boundary of the CEP.
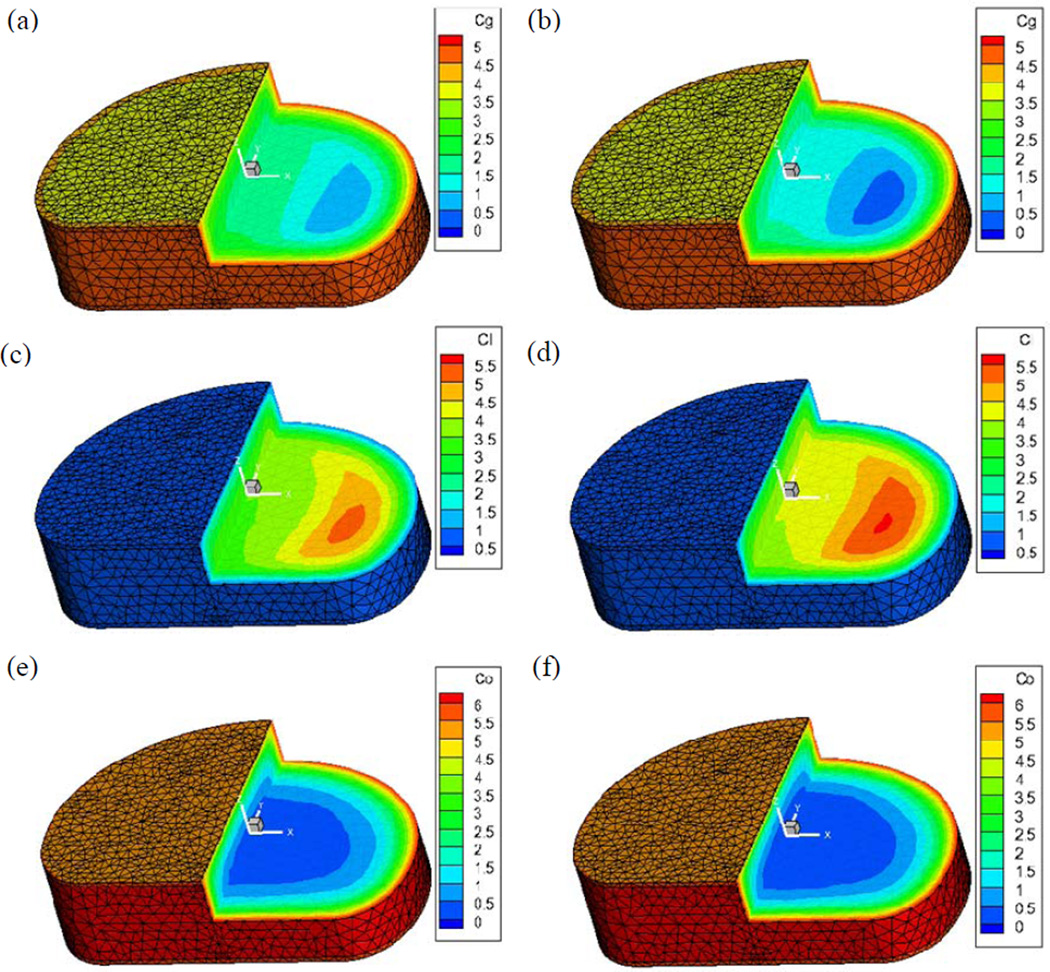
Figure 3.
Effect of CEP calcification on 3D nutrient solute (oxygen co, glucose cgand lactate cl) concentration distributions inside the human IVD: (a) (c) (e) with a normal CEP and (b) (d) (f) with a calcified CEP. (Concentration unit: mM)
Effect of CEP calcification
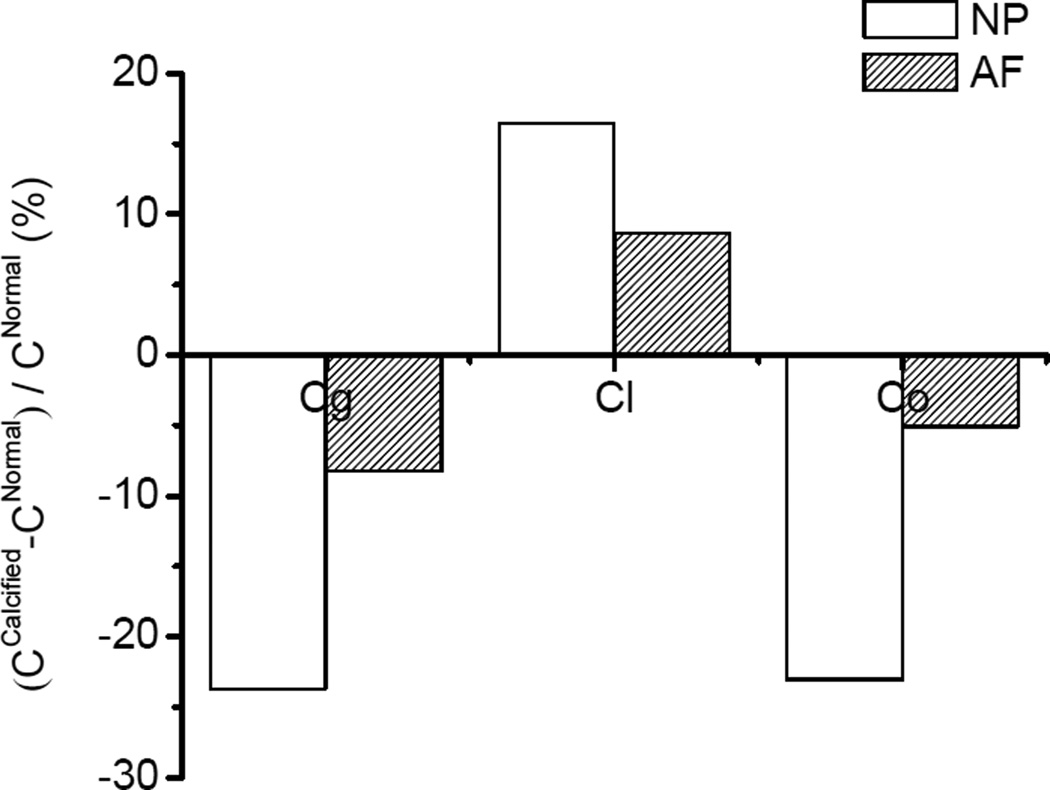
The calcification of the CEP dramatically decreased the glucose and oxygen concentrations and increased the lactate concentration inside the IVD (Figure 3). There were 69.3% and 33.9% decreases in minimum glucose and oxygen concentrations in the disc with a calcified endplate, respectively. In contrast, there was a 7.3% increase in maximum lactate concentration in the disc with the calcified endplate. Moreover, the nutrient concentration levels in the NP region, compared to the AF region, were more significantly affected by the calcified CEP (Figure 4). There were 23.0% and 23.7% decreases in the mean concentrations of oxygen and glucose in the NP region, while 5.1% and 8.2% decreases were found in the AF region. Meanwhile, a 16.5% percent increase of mean lactate concentration was found in the NP region while an 8.7% increase was found in the AF region. The mean concentration was calculated by: , α = oxygen, glucose, and lactate.
Figure 4.
Effect of CEP calcification on mean concentrations in the NP and AF regions. The change of the concentration was normalized by the concentration with a normal CEP.
Effect of NP cell injection
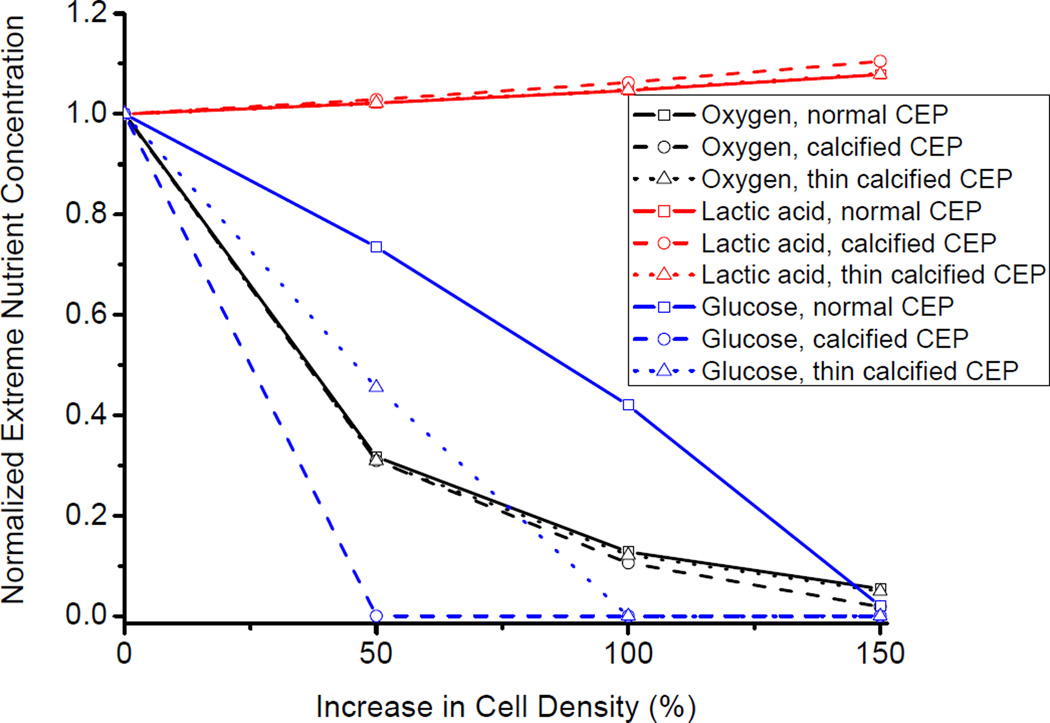
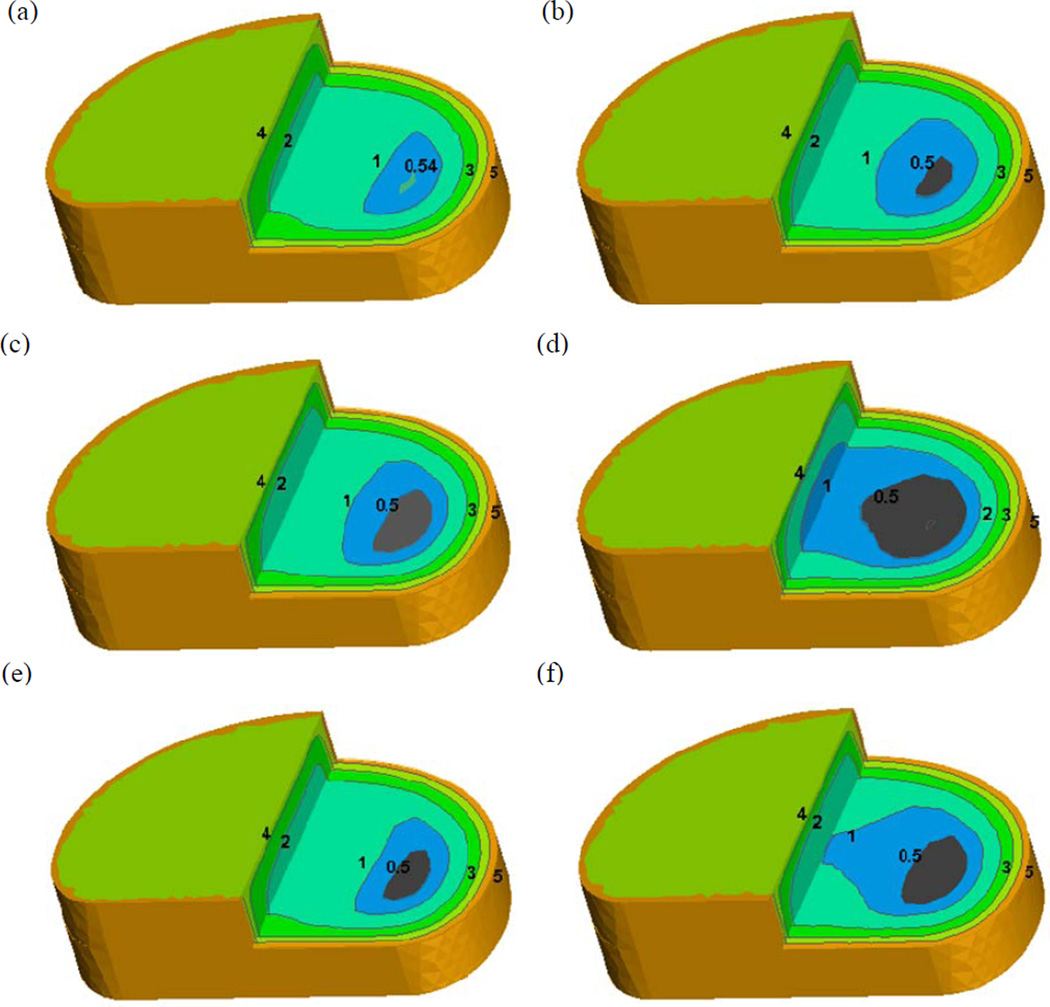
The increase in cell density within the NP region due to the NP cell injection significantly decreased the extreme oxygen and glucose concentrations (lowest concentration inside the disc), while increasing the extreme lactate concentration (highest concentration inside the disc), as shown in Figure 5. The magnitude of the change of the extreme concentrations due to the cell injection also depended on the conditions of the CEP (i.e., normal, calcified, and thin calcified). Moreover, the condition of the CEP had a more significant impact on the extreme glucose concentration, than on the extreme lactate and oxygen concentrations. Specifically, the extreme glucose concentration sharply reached zero (Figure 5) when the NP cell density increased only 50% with the calcified CEP. Glucose concentration is a limiting factor for disc cell viability [8–10]. A Critical Zone was defined as a disc region in which the glucose concentration is lower than 0.5mM [10]. With the normal CEP, a small volume Critical Zone (0.016 cm3) appeared in the AF region when the NP cell density increased 50% (Figure 6a–b). With the calcified CEP, a 50% increase of the NP cell density caused a 105. 6% increase in the volume of the Critical Zone (Figure 6c–d). With the thin calcified CEP, the increase in the volume of the Critical zone was reduced to 75.8% (Figure 6e–f).
Figure 5.
Effect of increase in cell density on the extreme nutrient concentrations inside human IVD. Cell density in the NP region is increased by 50%, 100%, and 150%. The simulated cases include disc with a normal CEP, calcified CEP, and thin calcified CEP (50% of the full thickness).
Figure 6.
Effect of increase in cell density on 3D glucose concentration distribution in the disc with a normal CEP (a) (b), calcified CEP (c) (d), and thin calcified CEP (e) (f). The grey color regions indicate the Critical Zones in which the glucose concentration is lower than 0.5 mM [10].
DISCUSSION
The object of this study was to develop a multiphasic mechano-electrochemical 3D finite element model of human IVD to investigate the effects of endplate calcification and the injection of IVD cells on the nutrition environment inside the human IVD under physiological loading conditions. In comparison with earlier models [25–33], the present study is the first to compute the 3D concentration profiles of oxygen, glucose, and lactate in a human lumbar disc under physiological diurnal cyclic loading. For the baseline case (i.e., no CEP calcification and no cell injection), the computed minimum oxygen concentration of 0.3 kPa at the center region of the disc falls within measured range of 0.3–1.1 kPa [42]. The computed minimum glucose concentrations of 0.54 mM in the inner AF is in agreement with the measured range of 0.5–2.5 mM in the AF of scoliotic discs [9]. The computed maximum lactate concentration of 5.21 mM also falls within measured range of 2–6 mM [45]. These agreements between the model predictions and experimental measurements validated the present finite element model of human IVD to a certain extent. In addition, the values of the extreme oxygen, glucose, and lactate concentrations in the disc with a normal CEP are also consistent with the previous simulation studies [14, 46, 47].
The advantage of our model was that it was capable of simulating the nutrient solute transport inside the disc coupled with mechanical loading. The strain dependent hydraulic permeability and nutrient solute diffusivities, as shown in Equations (16) and (17), were determined in previous experimental studies (Table 1). A decrease in water content due to the tissue consolidation could thus reduce the hydraulic permeability and solute diffusivities. Consequently, the convection and diffusion could be hindered. The human IVD experiences a diurnal cyclic loading in vivo [26]. In this study, a cyclical loading (compression during the day then recovery during the night) was considered to mimic the physiological loading on the IVD. Our results showed that there were no significant differences in nutrient solute concentration distributions inside the disc between the day and night (Figure 2). It indicates that the loading induced fluid flow doesn’t alter the nutrient transport and the nutrient environment maintains stable inside the IVD under the physical diurnal loading condition. Previous studies [48–50] have proposed that fluid flow induced by the mechanical loading may enhance or hinder the solute transport in the disc. However, for small solutes such as oxygen, glucose, and lactate, diffusion is a dominate transport mechanism inside the disc since the convective contribution by ‘pumping’ of small solutes is relatively small [23, 26, 42, 51]. Although several studies have shown that the long-term sustained static compression may change the nutrient concentration distribution inside the IVD [27, 28, 30, 33, 34], the present study further confirmed that the nutrient environment maintains a stable state under the physiological diurnal loading condition. With a stable nutrient environment, the disc cell energy metabolism also keeps a constant rate during the day and night under the physiological condition. This may be beneficial to disc cell homeostasis.
Along with the aging process, calcification of the CEP may appear and cause perturbation in its transport properties [22, 23]. The reduction of the fluid and solute permeability due to the CEP calcification may impede nutrition supply to the disc [14, 46, 47]. As shown in our results, calcification of the CEP significantly changes the nutrient solute distribution inside the human IVD, including a significant fall of the minimum oxygen and glucose concentrations and a significant increase of maximum lactate concentration (Figure 3). Moreover, the effect of CEP calcification is more significant in the NP region (Figure 4) as the main source of nutrition supply for the NP is from capillaries and canals in the vertebral body adjacent to the endplate [19–21]. Our results also showed that the CEP calcification significantly increased the size of the Critical Zone (Figure 6). Note that the Critical Zone is defined as a disc region in which the glucose concentration is lower than 0.5mM. The glucose concentration is a limiting factor for the disc cell viability. A previous cell culture study has shown that disc cell death occurs if the glucose concentration is lower than 0.5 mM for more than 3 days [8]. Therefore the CEP calcification results in a decrease of nutrient supply to the disc. This may lead to changes in the disc cell viability and cellular metabolism, which in turn alters the extracellular matrix homeostasis (breakdown/synthesize). The imbalance of the matrix synthesis and degradation implies the onset of the process of disc degeneration.
In order to develop new treatments for the IVD degeneration associated low back pain, injection of autologous NP/chondrocyte cells or mesenchymal stem cells (MSCs) to the degenerated disc has been proposed for disc regeneration [35–37]. Our results have shown that increasing the cell density in the NP region may increase cellular metabolism, which in turn causes further deterioration of the nutrient environment in the degenerated disc. Even in a disc with a normal CEP, a critical zone appeared immediately once the cell density in the NP region increased by 50% (Figure 5(b)). The critical zone was doubled with the presence of a calcified CEP. Interestingly, after cutting down the calcified CEP to a half of its thickness, the volume of the Critical Zone was decreased to a half of its volume with the full thickness CEP. Our results suggested that nutrient supply is an essential factor which needs to be considered in cell based therapies for human IVD regeneration. Unless it can be assured that a degenerate disc has a nutrient supply which can support the implanted cells, treatment using a cell therapy approach is both pointless and unethical [52]. Our results also suggested that reducing the thickness of the calcified CEP could be an option to restore the nutrient environment in degenerative discs for cell based therapies. In addition, in order to address the nutrition supply concern, large animal species will be a more appropriate model for testing this approach.
There are a few limitations in our finite element model. In order to improve the accuracy of the simulation, more information about the geometry of the CEP and the region of calcification are needed. The simplified geometry in this study may overestimate the size of the CEP. The mechanical and transport properties (Table 1) used in this study are mainly from the animal data. These properties for human IVD, especially for the CEP, are largely unavailable. The anisotropy of the mechanical and transport properties need to be considered, especially in the AF region, in our future work [53, 54]. As for energy metabolism properties in the NP and AF, there is barely any data available for the human IVD. Consequently, bovine and porcine cell data were used in this study. Moreover, the glucose consumption rate (GCR) was assumed to be the half of the lactic production rate based on the glycolysis assumption. The GCR may also depend on the oxygen level [8]. Meanwhile, the cell viability needs to be considered in future studies by correlating it with the pH value and glucose concentration. The development of a new constitutive relation for IVD cell viability, based on experiment data, is needed to further improve our model.
The effect of mechanical strain on fix charge density was incorporated in this model, see equations (14) and (15). Mechanical loading could alter extracellular osmotic environment by changing the fixed charge density in the ECM. Moreover, disc degeneration will induce loss of PG content from the matrix, resulting in change of fix charge density and the extracellular osmotic environment. Previous studies have found that cellular responses such as gene expression and collagen synthesis were significantly affected by the osmotic environment [55,56]. Therefore, the energy metabolic activities of IVD cells may also be changed due to the change in the extracellular osmotic environment. A more accurate prediction of the nutrient distribution in the human IVD could be expected once the effects of osmolarity on energy metabolic activities of IVD cells are quantitatively characterized in the future.
In summary, we found that the nutrient solute distribution inside the disc is maintained at a stable state during the day and night. The physiological diurnal cyclic loading does not change the nutrient environment in the human IVD. The cartilage endplate plays a significant role in the nutrient supply to the human IVD. Calcification of the cartilage endplate significantly reduces the nutrient levels in the human IVD. Therefore, in cell based therapies for IVD regeneration, the increased nutrient demand by cell injection needs to be seriously considered. Excessive amounts of injected cells may cause further deterioration of the nutrient environment in the degenerated disc. This study is important for understanding the pathology of IVD degeneration and providing new insights into cell based therapies for low back pain.
ACKNOWLEDGEMENTS
This study was supported by NIH grants AR055775, DE018741 and DE021134, a grant (SCIRF0307) from the South Carolina Spinal Cord Injury Research Fund, a NSF RII grant fellowship (EPS-00903795) to YW, and a NIH T32 predoctoral fellowship DE017551 to SEC.
Footnotes
CONFLICT OF INTEREST:
None of the authors of this paper have a conflict of interest that might be construed as affecting the conduct or reporting of the work presented.
REFERENCES
- 1.van Tulder MW, Koes BW, Bouter LM. A cost-of-illness study of back pain in The Netherlands. Pain. 1995;62(2):233–240. doi: 10.1016/0304-3959(94)00272-G. [DOI] [PubMed] [Google Scholar]
- 2.Maniadakis N, Gray A. The economic burden of back pain in the UK. Pain. 2000;84(1):95–103. doi: 10.1016/S0304-3959(99)00187-6. [DOI] [PubMed] [Google Scholar]
- 3.Deyo RA, Weinstein JN. Low back pain. N Engl J Med. 2001;344(5):363–370. doi: 10.1056/NEJM200102013440508. [DOI] [PubMed] [Google Scholar]
- 4.Buckwalter JA. Aging and degeneration of the human intervertebral disc. Spine (Phila Pa 1976) 1995;20(11):1307–1314. doi: 10.1097/00007632-199506000-00022. [DOI] [PubMed] [Google Scholar]
- 5.Battie MC, Videman T. Lumbar disc degeneration: epidemiology and genetics. J Bone Joint Surg Am. 2006;88(Suppl 2):3–9. doi: 10.2106/JBJS.E.01313. [DOI] [PubMed] [Google Scholar]
- 6.Roberts S, Menage J, Urban JP. Biochemical and structural properties of the cartilage end-plate and its relation to the intervertebral disc. Spine. 1989;14(2):166–174. doi: 10.1097/00007632-198902000-00005. [DOI] [PubMed] [Google Scholar]
- 7.Urban JP, Winlove CP. Pathophysiology of the intervertebral disc and the challenges for MRI. J Magn Reson Imaging. 2007;25(2):419–432. doi: 10.1002/jmri.20874. [DOI] [PubMed] [Google Scholar]
- 8.Horner HA, Urban JP. 2001 Volvo Award Winner in Basic Science Studies: Effect of nutrient supply on the viability of cells from the nucleus pulposus of the intervertebral disc. Spine (Phila Pa 1976) 2001;26(23):2543–2549. doi: 10.1097/00007632-200112010-00006. [DOI] [PubMed] [Google Scholar]
- 9.Bibby SR, Fairbank JC, Urban MR, Urban JP. Cell viability in scoliotic discs in relation to disc deformity and nutrient levels. Spine. 2002;27(20):2220–2228. doi: 10.1097/00007632-200210150-00007. [DOI] [PubMed] [Google Scholar]
- 10.Bibby SR, Urban JP. Effect of nutrient deprivation on the viability of intervertebral disc cells. Eur Spine J. 2004;13(8):695–701. doi: 10.1007/s00586-003-0616-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bibby SR, Jones DA, Ripley RM, Urban JP. Metabolism of the intervertebral disc: effects of low levels of oxygen, glucose, and pH on rates of energy metabolism of bovine nucleus pulposus cells. Spine. 2005;30(5):487–496. doi: 10.1097/01.brs.0000154619.38122.47. [DOI] [PubMed] [Google Scholar]
- 12.Huang CY, Yuan TY, Jackson AR, Hazbun L, Fraker C, Gu WY. Effects of low glucose concentrations on oxygen consumption rates of intervertebral disc cells. Spine. 2007;32(19):2063–2069. doi: 10.1097/BRS.0b013e318145a521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Guehring T, Wilde G, Sumner M, Grunhagen T, Karney GB, Tirlapur UK, Urban JP. Notochordal intervertebral disc cells: sensitivity to nutrient deprivation. Arthritis Rheum. 2009;60(4):1026–1034. doi: 10.1002/art.24407. [DOI] [PubMed] [Google Scholar]
- 14.Shirazi-Adl A, Taheri M, Urban JP. Analysis of cell viability in intervertebral disc: Effect of endplate permeability on cell population. J Biomech. 2010;43(7):1330–1336. doi: 10.1016/j.jbiomech.2010.01.023. [DOI] [PubMed] [Google Scholar]
- 15.Ishihara H, Urban JP. Effects of low oxygen concentrations and metabolic inhibitors on proteoglycan and protein synthesis rates in the intervertebral disc. J Orthop Res. 1999;17(6):829–835. doi: 10.1002/jor.1100170607. [DOI] [PubMed] [Google Scholar]
- 16.Horner HA, Roberts S, Bielby RC, Menage J, Evans H, Urban JP. Cells from different regions of the intervertebral disc: effect of culture system on matrix expression and cell phenotype. Spine. 2002;27(10):1018–1028. doi: 10.1097/00007632-200205150-00004. [DOI] [PubMed] [Google Scholar]
- 17.Urban JP, Smith S, Fairbank JC. Nutrition of the intervertebral disc. Spine. 2004;29(23):2700–2709. doi: 10.1097/01.brs.0000146499.97948.52. [DOI] [PubMed] [Google Scholar]
- 18.Lundon K, Bolton K. Structure and function of the lumbar intervertebral disk in health, aging, and pathologic conditions. J Orthop Sports Phys Ther. 2001;31(6):291–303. doi: 10.2519/jospt.2001.31.6.291. discussion 04-6. [DOI] [PubMed] [Google Scholar]
- 19.Ayotte DC, Ito K, Tepic S. Direction-dependent resistance to flow in the endplate of the intervertebral disc: an ex vivo study. J Orthop Res. 2001;19(6):1073–1077. doi: 10.1016/S0736-0266(01)00038-9. [DOI] [PubMed] [Google Scholar]
- 20.Ayotte DC, Ito K, Perren SM, Tepic S. Direction-dependent constriction flow in a poroelastic solid: the intervertebral disc valve. J Biomech Eng. 2000;122(6):587–593. doi: 10.1115/1.1319658. [DOI] [PubMed] [Google Scholar]
- 21.Accadbled F, Laffosse JM, Ambard D, Gomez-Brouchet A, de Gauzy JS, Swider P. Influence of location, fluid flow direction, and tissue maturity on the macroscopic permeability of vertebral end plates. Spine. 2008;33(6):612–619. doi: 10.1097/BRS.0b013e318166e0d7. [DOI] [PubMed] [Google Scholar]
- 22.Roberts S, Menage J, Eisenstein SM. The cartilage end-plate and intervertebral disc in scoliosis: calcification and other sequelae. J Orthop Res. 1993;11(5):747–757. doi: 10.1002/jor.1100110517. [DOI] [PubMed] [Google Scholar]
- 23.Roberts S, Urban JP, Evans H, Eisenstein SM. Transport properties of the human cartilage endplate in relation to its composition and calcification. Spine. 1996;21(4):415–420. doi: 10.1097/00007632-199602150-00003. [DOI] [PubMed] [Google Scholar]
- 24.Urban MR, Fairbank JC, Etherington PJ, Loh FL, Winlove CP, Urban JP. Electrochemical measurement of transport into scoliotic intervertebral discs in vivo using nitrous oxide as a tracer. Spine. 2001;26(8):984–990. doi: 10.1097/00007632-200104150-00028. [DOI] [PubMed] [Google Scholar]
- 25.Selard E, Shirazi-Adl A, Urban JP. Finite element study of nutrient diffusion in the human intervertebral disc. Spine. 2003;28(17):1945–1953. doi: 10.1097/01.BRS.0000087210.93541.23. [DOI] [PubMed] [Google Scholar]
- 26.Ferguson SJ, Ito K, Nolte LP. Fluid flow and convective transport of solutes within the intervertebral disc. J Biomech. 2004;37(2):213–221. doi: 10.1016/s0021-9290(03)00250-1. [DOI] [PubMed] [Google Scholar]
- 27.Yao H, Gu WY. Physical signals and solute transport in cartilage under dynamic unconfined compression: finite element analysis. Ann Biomed Eng. 2004;32(3):380–390. doi: 10.1023/b:abme.0000017540.84764.6f. [DOI] [PubMed] [Google Scholar]
- 28.Yao H, Gu WY. Physical signals and solute transport in human intervertebral disc during compressive stress relaxation: 3D finite element analysis. Biorheology. 2006;43(3–4):323–335. [PubMed] [Google Scholar]
- 29.Yao H, Gu WY. Three-dimensional inhomogeneous triphasic finite-element analysis of physical signals and solute transport in human intervertebral disc under axial compression. J Biomech. 2007;40(9):2071–2077. doi: 10.1016/j.jbiomech.2006.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Huang CY, Gu WY. Effects of mechanical compression on metabolism and distribution of oxygen and lactate in intervertebral disc. J Biomech. 2008;41(6):1184–1196. doi: 10.1016/j.jbiomech.2008.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Soukane DM, Shirazi-Adl A, Urban JP. Analysis of nonlinear coupled diffusion of oxygen and lactic acid in intervertebral discs. J Biomech Eng. 2005;127(7):1121–1126. doi: 10.1115/1.2073674. [DOI] [PubMed] [Google Scholar]
- 32.Soukane DM, Shirazi-Adl A, Urban JP. Computation of coupled diffusion of oxygen, glucose and lactic acid in an intervertebral disc. J Biomech. 2007;40(12):2645–2654. doi: 10.1016/j.jbiomech.2007.01.003. [DOI] [PubMed] [Google Scholar]
- 33.Jackson AR, Huang CY, Brown MD, Gu WY. 3D finite element analysis of nutrient distributions and cell viability in the intervertebral disc: effects of deformation and degeneration. J Biomech Eng. 2011;133(9) doi: 10.1115/1.4004944. 091006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhu Q, Jackson AR, Gu WY. Cell viability in intervertebral disc under various nutritional and dynamic loading conditions: 3d Finite element analysis. J Biomech. 2012 doi: 10.1016/j.jbiomech.2012.08.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sakai D, Mochida J, Iwashina T, Watanabe T, Nakai T, Ando K, Hotta T. Differentiation of mesenchymal stem cells transplanted to a rabbit degenerative disc model: potential and limitations for stem cell therapy in disc regeneration. Spine (Phila Pa 1976) 2005;30(21):2379–2387. doi: 10.1097/01.brs.0000184365.28481.e3. [DOI] [PubMed] [Google Scholar]
- 36.Watanabe K, Mochida J, Nomura T, Okuma M, Sakabe K, Seiki K. Effect of reinsertion of activated nucleus pulposus on disc degeneration: an experimental study on various types of collagen in degenerative discs. Connect Tissue Res. 2003;44(2):104–108. [PubMed] [Google Scholar]
- 37.Ganey T, Libera J, Moos V, Alasevic O, Fritsch KG, Meisel HJ, Hutton WC. Disc chondrocyte transplantation in a canine model: a treatment for degenerated or damaged intervertebral disc. Spine (Phila Pa 1976) 2003;28(23):2609–2620. doi: 10.1097/01.BRS.0000097891.63063.78. [DOI] [PubMed] [Google Scholar]
- 38.Lai WM, Hou JS, Mow VC. A triphasic theory for the swelling and deformation behaviors of articular cartilage. J Biomech Eng. 1991;113(3):245–258. doi: 10.1115/1.2894880. [DOI] [PubMed] [Google Scholar]
- 39.Gu WY, Lai WM, Mow VC. A mixture theory for charged-hydrated soft tissues containing multi-electrolytes: passive transport and swelling behaviors. J Biomech Eng. 1998;120(2):169–180. doi: 10.1115/1.2798299. [DOI] [PubMed] [Google Scholar]
- 40.Mow VC, Sun DN, Guo XE, Likhitpanichkul M, Lai WM. Fixed negative charges modulate mechanical behavior and electrical signals in articular cartilage under unconfined compression—A triphasic paradigm. In: Ehlers W, Bluhm J, editors. Porous Media: Theory, Experiments and Numerical Application. Berlin: Springer; 2002. pp. 227–247. [Google Scholar]
- 41.Sun DN, Gu WY, Guo XE, Lai WM, Mow VC. A mixed finite element formulation of triphasic mechano-electrochemical theory for charged, hydrated biological soft tissues. Int J Numer Meth Engng. 1999;45:1375–1402. [Google Scholar]
- 42.Holm S, Maroudas A, Urban JP, Selstam G, Nachemson A. Nutrition of the intervertebral disc: solute transport and metabolism. Connect Tissue Res. 1981;8(2):101–119. doi: 10.3109/03008208109152130. [DOI] [PubMed] [Google Scholar]
- 43.Iatridis JC, Laible JP, Krag MH. Influence of fixed charge density magnitude and distribution on the intervertebral disc: applications of a poroelastic and chemical electric (PEACE) model. J Biomech Eng. 2003;125(1):12–24. doi: 10.1115/1.1537190. [DOI] [PubMed] [Google Scholar]
- 44.Accadbled F, Laffosse JM, Ambard D, Gomez-Brouchet A, de Gauzy JS, Swider P. Influence of location, fluid flow direction, and tissue maturity on the macroscopic permeability of vertebral end plates. Spine (Phila Pa 1976) 2008;33(6):612–619. doi: 10.1097/BRS.0b013e318166e0d7. [DOI] [PubMed] [Google Scholar]
- 45.Bartels EM, Fairbank JC, Winlove CP, Urban JP. Oxygen and lactate concentrations measured in vivo in the intervertebral discs of patients with scoliosis and back pain. Spine (Phila Pa 1976) 1998;23(1):1–7. doi: 10.1097/00007632-199801010-00001. discussion 8. [DOI] [PubMed] [Google Scholar]
- 46.Jackson AR, Huang CY, Gu WY. Effect of endplate calcification and mechanical deformation on the distribution of glucose in intervertebral disc: a 3D finite element study. Comput Methods Biomech Biomed Engin. 2011;14(2):195–204. doi: 10.1080/10255842.2010.535815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mokhbi Soukane D, Shirazi-Adl A, Urban JP. Investigation of solute concentrations in a 3D model of intervertebral disc. Eur Spine J. 2009;18(2):254–262. doi: 10.1007/s00586-008-0822-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Urban JP, Holm S, Maroudas A, Nachemson A. Nutrition of the intervertebral disc: effect of fluid flow on solute transport. Clin Orthop Relat Res. 1982;(170):296–302. [PubMed] [Google Scholar]
- 49.O'Hara BP, Urban JP, Maroudas A. Influence of cyclic loading on the nutrition of articular cartilage. Ann Rheum Dis. 1990;49(7):536–539. doi: 10.1136/ard.49.7.536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.McMillan DW, Garbutt G, Adams MA. Effect of sustained loading on the water content of intervertebral discs: implications for disc metabolism. Ann Rheum Dis. 1996;55(12):880–887. doi: 10.1136/ard.55.12.880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Yao H, Gu WY. Convection and diffusion in charged hydrated soft tissues: a mixture theory approach. Biomech Model Mechanobiol. 2007;6(1–2):63–72. doi: 10.1007/s10237-006-0040-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kandel R, Roberts S, Urban JP. Tissue engineering and the intervertebral disc: the challenges. Eur Spine J. 2008;17(Suppl 4):480–491. doi: 10.1007/s00586-008-0746-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Travascio F, Gu WY. Anisotropic diffusive transport in annulus fibrosus: experimental determination of the diffusion tensor by FRAP technique. Ann Biomed Eng. 2007;35(10):1739–1748. doi: 10.1007/s10439-007-9346-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jackson AR, Yuan TY, Huang CY, Travascio F, Yong Gu W. Effect of compression and anisotropy on the diffusion of glucose in annulus fibrosus. Spine (Phila Pa 1976) 2008;33(1):1–7. doi: 10.1097/BRS.0b013e31815e4136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wuertz K, Urban JP, Klasen J, Ignatius A, Wilke HJ, Claes L, Neidlinger-Wilke C. Influence of extracellular osmolarity and mechanical stimulation on gene expression of intervertebral disc cells. J Orthop Res. 2007;25(11):1513–1522. doi: 10.1002/jor.20436. [DOI] [PubMed] [Google Scholar]
- 56.Oswald ES, Ahmed HS, Kramer SP, Bulinski JC, Ateshian GA, Hung CT. Effects of hypertonic (NaCl) two-dimensional and three-dimensional culture conditions on the properties of cartilage tissue engineered from an expanded mature bovine chondrocyte source. Tissue engineering Part C, Methods. 2011;17(11):1041–1049. doi: 10.1089/ten.tec.2011.0212. [DOI] [PMC free article] [PubMed] [Google Scholar]