Proportional Hazards Model with Covariate Measurement Error and Instrumental Variables

Abstract

In biomedical studies, covariates with measurement error may occur in survival data. Existing approaches mostly require certain replications on the error-contaminated covariates, which may not be available in the data. In this paper, we develop a simple nonparametric correction approach for estimation of the regression parameters in the proportional hazards model using a subset of the sample where instrumental variables are observed. The instrumental variables are related to the covariates through a general nonparametric model, and no distributional assumptions are placed on the error and the underlying true covariates. We further propose a novel generalized methods of moments nonparametric correction estimator to improve the efficiency over the simple correction approach. The efficiency gain can be substantial when the calibration subsample is small compared to the whole sample. The estimators are shown to be consistent and asymptotically normal. Performance of the estimators is evaluated via simulation studies and by an application to data from an HIV clinical trial. Estimation of the baseline hazard function is not addressed.

1. INTRODUCTION

Survival data often arise in biomedical studies where the outcome of interest is time to an event of interest (failure). The proportional hazards model is the most widely used survival model to characterize the relationship between survival time and covariates. However, some covariates, say X, could be measured with error in practice. For example, important covariates such as CD4 counts in HIV studies are subjected to substantial measurement error due to both imperfect instruments and biological fluctuation.

It is well-known that the naive approach that ignores measurement error can lead to biased estimation and erroneous inference (e.g. Prentice, 1982). Various approaches have been proposed to deal with measurement error. The regression calibration (Prentice, 1982; Wang et al. 1997; Dafni and Tsiatis, 1998; Liao et al., 2011) approximates the hazard function conditional on the observed covariates. It can reduce estimation bias but is still inconsistent. Likelihood based approaches are usually computationally intensive (e.g. Wulfson and Tsiatis, 1997; Hu, Tsiatis and Davidian, 1998, Song et al., 2002a; Wang, 2008). Consistent estimation based on corrected scores (parametric correction) was first proposed by Nakamura (1992) which required no distributional assumption on the underlying true covariates, but the standard deviation was assumed known. Huang and Wang (2000) developed a nonparametric correction approach that further relaxed the distributional assumption on the measurement error, but required repeated measurements. The correction approaches were extended to more general measurement error models (Hu and Lin, 2002; Wang, 2006; Tapsoba et al., 2011) and more general error assessment sets (Huang and Wang, 2006). A related approach is the conditional score (Tsiatis and Davidian, 2001; Song et al., 2002b), which is asymptotic equivalent to the corrected score. The conditional score approach has better finite sample performance (Song and Huang, 2005), but still depends on the normality assumption of the error. Motivated by the difference in the corrected score and conditional score estimating functions, Song and Huang (2005) proposed refined parametric correction and nonparametric correction approaches. The refined parametric correction estimator has comparable finite sample performance as the conditional score estimator. While the literature of proportional hazards regression with covariate measurement error is rich, to our knowledge, existing approaches require either knowledge of the measurement error standard deviation, repeated error-prone measurements, longitudinal error-prone measurements, or a validation set. Such information may not be available in practice.

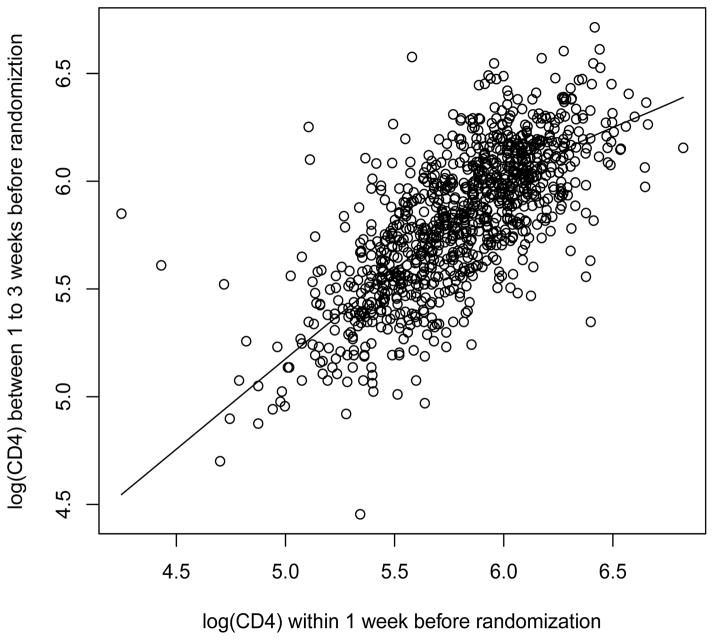
Instead, instrumental variables may be observed in a subset of the sample. Instrumental variables are variables correlated with X, independent of the measurement error, and independent of the outcome given the covariates (Carroll et al., 2006, chapter 6; Stock and Watson, 2010, chapter 12). They are widely used in econometrics when the covariates are correlated with disturbance due to omitted variables, errors-in-variables, or simultaneous causality (Stock and Watson, 2010, chapter 12). Standard approaches that ignore the correlation between the covariates and disturbance usually lead to inconsistent estimators. Instrumental variables are used to obtain consistent estimators of the regression coefficients under this situation. Here we consider the case when the instrumental variables are observed in a subset of the sample. An example is AIDS clinical Trials Group (ACTG) 175, a randomized trial to compare zidovudine alone, ziduvudine plus didanosine, zidovudine plus zalcitabine, or didanosine alone in HIV-infected subjects on the basis of time to progression to AIDS or death (Hammer et al., 1996). It is of interested to assess the effect of treatments on survival time adjusted for baseline CD4 counts X. The closest CD4 measurement within one week before randomization was taken as the baseline CD4 measurements. It is well known that observed CD4 counts are contaminated by substantial measurement error. Among the 2174 randomized patients with at least one baseline CD4 measurements, there were no replicated baseline CD4 measurements on the same day. However, 989 patients had at least one CD4 measurement between one to three weeks prior to randomization. Since the underlying true CD4 counts might change over time, these CD4 measurements were not simple replication of baseline CD4 counts. But they may be used as instrumental variables. Figure 1 shows the scatter plot and a Loess smooth of log CD4 counts within one to three weeks versus one week before randomization. The logarithmic transformation was applied to CD4 counts to achieve approximate constant variance. The Loess curve indicates a possible nonlinear relationship between log CD4 counts during these two time periods.

Figure 1.

Scatter plot of log(CD4) within one to three weeks versus one week before randomization. The curve was obtained by Loess smooth.

Instrumental variables have been used in literature to deal with measurement error when there are no replicates or validation datasets (Carroll et al., 2006, chapter 6), mostly based on a parametric model between the instrumental variables and the covariates. But it may not be easy to identify the relationship between the instrumental variables and the covariates when the covariates are measured with error. Carroll et al. (2004) relaxed the parametric model assumption and adopted a varying coefficient model that is linear in X. The linearity assumption may still be too restricted as indicated in Figure 1. In this paper, we adopt a more general nonparametric model for the instrumental variables. The instrumental variables may be observed only in a subsample as in the ACTG 175 study. As in Huang and Wang (2001, 2006), we assume a functional measurement error model with no specification on the error distribution. We develop novel nonparametric correction methods under this general framework. The methods will have broader applications than those described by Huang and Wang (2006) due to the flexibility of the instrumental variable model.

The paper is organized as follows. In Section 2, we give the model definition. We develop a simple nonparametric correction estimator in Section 3 and propose an improved generalized methods of moments nonparametric correction estimator in Section 4. The asymptotic properties are derived with the proofs given in the Appendix. The performance of the estimators is assessed by simulations in Section 5 and illustrated by an application in Section 6. The paper concludes with a discussion in Section 7.

2. MODEL DEFINITION

Let T denote the survival time and C the censoring time. The observed survival data are V = min(T, C) and Δ = I(T ≤ C), where I(·) is the indicator function. Let X denote a vector of p covariates that can be measured with error and Z denote a vector of q accurately measured covariates. The hazard of failure depends on covariates X and Z through the proportional hazard model

$$\lambda (t)={\lambda }_0(t)exp({\beta }_0^{T}X+{\gamma }_0^{T}Z),$$

where λ₀(t) is an unspecified baseline hazard function, and (β₀, γ₀) are the regression parameters. We assume that the survival time T is independent of the censoring time C given (X, Z).

Suppose that the true value of X is not observable. Only an error contaminated measurement W is available, which satisfies the classical measurement error model

$$W=X+e,$$

where e denotes the additive measurement error with E(e) = 0, and X and e are independent. In addition, measurements are available on an instrumental variable R in a subset of subjects such that

$$R=g(X,Z,\epsilon ),$$ (1)

where g(·) is an unknown function, and ε is a set of unspecified random variables that are independent of (T, C) given (X, Z) and independent of e. This includes as special cases the replicates R = X + ε, linear instrument R = a₀ + a₁X + ε, varying coefficient instrument R = a₀(Z)+a₁(Z)+ ε (Carroll et al., 2004), and nonparametric instrument R = g_*(X, Z) + ε, where g_*(X, Z) is an unspecified function of (X, Z). The instrumental variable R may depend on both X and Z. It may also depend on other variables as included in ε, but R and (T, C) are independent given (X, Z). The dimension s of R should satisfy s ≥ p to ensure identifiability. For simplicity, we assume s = p. An extension to s > p is discussed in Section 7. Assume that the errors e and ε are independent of (T, C, X, Z) and each other. Note that no other assumptions are placed on X, e, ε and the function g(·). Let η = I(R is observed) be the indicator of whether the instrument variable is observed. Assume η is independent of {T, C, X, Z, e, ε}.

Suppose {T_i, C_i, V_i, Δ_i, X_i, W_i, Z_i, e_i, ε_i, η_i} are independent and identically distributed samples of {T, C, V, Δ, X, W, Z, e, ε, η} and the observed data set is {(V_i, Δ_i, η_i, W_i, η_iR_i, Z_i) : i = 1, …, n}. For brevity of notations, we may drop the subscript i throughout the paper when there is no confusion. We focus on estimating the regression parameters ${\theta }_0={({\beta }_0^T,{\gamma }_0^T)}^T$.

3. SIMPLE NONPARAMETRIC CORRECTION

Huang and Wang (2000, 2006) proposed nonparametric correction estimation based on (V, Δ, W). The essential idea is to correct the naive estimating function such that the bias is removed. However, their approach requires replicated measurements on W or a linear instrument variable, and thus cannot be used directly in our case. Alternatively, using the instrumental variable R, we may develop a nonparametric correction estimator in the same spirit.

Let θ = (β^T, γ^T)^T, N_i(t) = I(V_i ≤ t, Δ_i = 1) be the counting process of failures, and Y_i(t) = I(V_i ≥ t) the at risk process. For any scalar, vector or matrix H_i, let F_i(t, θ; H, X) = Y_i(t)H_i exp(β^TX_i + γ^TZ_i). Here H_i can be either fixed or random. Note that F_i also depends on (Z_i, V_i, Δ_i), which are dropped in the notation for simplicity. Let $\widehat{G}(t,\theta ;H,X)=n^{-1}{\sum }_{i=1}^n{F}_i(t,\theta ;H,X)$ and G(t, θ; H, X) = E{F_i(t, θ; H, X)}. Note that G(t, θ; H, X) is a fixed function of t and θ.

The naive estimating function replaces the true covariates X by W in the partial likelihood function and can be written as

$${\widehat{U}}_{NR}(\theta ;{(W^T,Z^T)}^T,W)=n^{-1}\sum _{i=1}^n{\int }_0^L\left\{{(W_i^T,Z_i^T)}^T-\frac{\widehat{G}(t,\theta ;{(W^T,Z^T)}^T,W)}{\widehat{G}(t,\theta ;1,W)}\right\}{dN}_i(t)$$

at a given time L. This estimating function is biased (Prentice, 1982), which is essentially due to the “bias” of the ratio term Ĝ(t, θ; (W^T, Z^T)^T, W)/Ĝ(t, θ; 1, W) from Ĝ(t, θ; (X^T, Z^T)^T, X)/Ĝ(t, θ; 1, X) when replacing X by W. When the measurement error is normal with known variance, Nakamura (1992) proposed a corrected score approach which added a correction term to compensate the bias. In the same spirit, Huang and Wang (2000) took an nonparametric correction when replications of W_i were available. The key idea of Huang and Wang (2000) was to substitute different replicates for W in the ratio term. Due to the independence of the errors in the replicates, the bias of the ratio term is corrected. The estimating function can be represented by Û_NR(θ; ( ${\widehat{U}}_{NR}(\theta ;{(W_{\ast }^T,Z^T)}^T,W)$, Z^T)^T, W) with W_* being another replicate of W and averaging over all possible combinations of replicates. We do not have a replicated W_*, but we may consider replacing W_* by R in Û_NR(θ; ( ${\widehat{U}}_{NR}(\theta ;{(W_{\ast }^T,Z^T)}^T,W)$, Z^T)^T, W).

As R is only observed on a subset of the subjects, we consider

$${\widehat{U}}_C(\theta )=n^{-1}\sum _{i=1}^n{\int }_0^L{\eta }_i\left\{{(R_i^T,Z_i^T)}^T-\frac{\widehat{G}(t,\theta ;\eta {(R^T,Z^T)}^T,W)}{\widehat{G}(t,\theta ;\eta ,W)}\right\}{dN}_i(t)=0.$$ (2)

Note that Û_C(θ) converges to

$$U_0(\theta )=E\left[{\int }_0^L\left\{\eta {(R^T,Z^T)}^T-\frac{G(t,\theta ;\eta {(R^T,Z^T)}^T,W)}{G(t,\theta ;\eta ,W)}\right\}dN(t)\right].$$ (3)

When R = X, U₀(θ) is the limit of the standard partial likelihood estimating function. Let 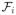(t) = {N_i(u), Y_i(u), X_i, W_i, R_i, Z_i : u ≤ t}. By lemma 1 and the independence of η from (V, Δ, W, R, Z), with iterated expectations,

$$\begin{array}{l}E\left\{{\int }_0^L\eta {(R^T,Z^T)}^{T}dN(t)\right\}=E(\eta )E\left[E\left\{{\int }_0^L{(R^T,Z^T)}^{T}dN(t)\mid {\mathcal{F}}_i(t)\right\}\right]\\ =E(\eta )E\left\{{\int }_0^{L}G(t,\theta ;{(R^T,Z^T)}^T,X)dt\right\}.\end{array}$$

In addition, we have $E\left\{{\int }_0^L\eta dN(t)\right\}=E(\eta )E\left\{{\int }_0^{L}G(t,\theta ;1,X)dt\right\}$, G(t, θ; η, W) = E(η)E{exp(β^Te)}G(t, θ; 1, X),and

$$G(t,\theta ;\eta {(R^T,Z^T)}^T,W)=E(\eta )E\{exp{\beta }^{T}e)\}G(t,\theta ;{(R^T,Z^T)}^T,X).$$

Hence it can be easily seen that U₀(θ) = 0. Therefore Û_C(θ; (R^T, Z^T)^T, W) is asymptotically unbiased and (2) is a simple nonparametric correction equation.

Let

$$\mathrm{\Gamma }({\theta }_0)={\int }_0^L\left[\frac{G(t,{\theta }_0;{(R^T,Z^T)}^T(W^T,Z^T),W)}{G(t,{\theta }_0;1,W)}-\frac{G(t,{\theta }_0;{(R^T,Z^T)}^T,W)G(t,{\theta }_0;(W^T,Z^T),W)}{G^2(t,{\theta }_0;1,W)}\right]dE\{N(t)\}.$$ (4)

We derive the asymptotic properties of the simple nonparametric correction estimator using empirical process theory.

Theorem 1

Under conditions A–E given in the Appendix, a solution θ̃ = (β̃^T, γ̃^T)^T of (2) exists and converges to θ₀ almost surely. Further, n^1/2(θ̃ − θ₀) is asymptotically normal with mean zero and variance $V_C={\{{\mathrm{\Gamma }}_{\eta }^{-1}({\theta }_0)\}}^T\mathit{var}\{{\omega }_{\eta i}({\theta }_0)\}{\mathrm{\Gamma }}_{\eta }^{-1}({\theta }_0)$, where

$$\begin{array}{l}{\mathrm{\Gamma }}_{\eta }({\theta }_0)={\int }_0^L[\frac{G(t,{\theta }_0;\eta {(R^T,Z^T)}^T(W^T,Z^T),W)}{G(t,{\theta }_0;\eta ,W)}-\frac{G(t,{\theta }_0;\eta {(R^T,Z^T)}^T,W)G(t,{\theta }_0;\eta (W^T,Z^T),W)}{G^2(t,{\theta }_0;\eta ,W)}]dE\{\eta N(t)\}\\ =E(\eta )\mathrm{\Gamma }({\theta }_0),\end{array}$$

and

$${\omega }_{\eta i}({\theta }_0)={\eta }_i{\int }_0^L\left({(R_i^T,Z^T)}^T-\frac{G(t,{\theta }_0;\eta {(R^T,Z^T)}^T,W)}{G(t,{\theta }_0;\eta ,W)}\right)\times \{{dN}_i(t)-\frac{F_i(\theta ;1,W)dE\{\eta N(t)\}}{G(t,{\theta }_0;\eta ,W)}\}.$$

A consistent estimator of the variance can be obtained by substituting θ̃ for θ₀ and the empirical means for the population means in the variance formula.

Remark

Condition E requires Γ(θ₀) to be nonsingular. It can be easily shown that Γ(θ₀) = 0 when R is independent of X. Thus R and X should be dependent. But R and X may have a nonlinear association, for example, R = X² + ε with X having a distribution symmetric around zero and ε independent of X, although the linear correlation is zero. This is due to the nonlinearity of the model, which is different from the linear instrumental model in econometrics (Stock and Watson, 2010, chapter 12).

To better understand what factors affect the variance of θ̃, we expand V_C in Theorem 1 although it is not needed for estimation of V_C. With some algebra, it can be shown that Γ(θ₀) = Γ_*(θ₀), where Γ_*(θ₀) is Γ(θ₀) with W replaced by X, that is,

$${\mathrm{\Gamma }}_{\ast }({\theta }_0)={\int }_0^L[\frac{G(t,{\theta }_0;{(R^T,Z^T,X)}^T(X^T,Z^T))}{G(t,{\theta }_0;1,X)}-\frac{G(t,{\theta }_0;{(R^T,Z^T)}^T,X)G(t,{\theta }_0;(X^T,Z^T),X)}{G^2({\theta }_0;1,X)}]dE\{N(t)\}.$$

Further,

$$V_C=E^{-1}(\eta )(V_I+V_A),$$ (5)

where

$$\begin{array}{l}{V}_I={\{{\mathrm{\Gamma }}_{\ast }^{-1}({\theta }_0)\}}^T{S}_1({\theta }_0;{(R^T,Z^T)}^T,X){\mathrm{\Gamma }}_{\ast }^{-1}({\theta }_0),\\ V_A={\{{\mathrm{\Gamma }}_{\ast }^{-1}({\theta }_0)\}}^T{S}_2({\theta }_0;{(R^T,Z^T)}^T,X){\mathrm{\Gamma }}_{\ast }^{-1}({\theta }_0),\end{array}$$

with

$$\begin{array}{l}{S}_1({\theta }_0;{(R^T,Z^T)}^T,X)=E\{{\int }_0^L\left({(R^T,Z^T)}^T-\frac{G(t,{\theta }_0;{(R^T,Z^T)}^T,X)}{G(T,{\theta }_0;1,X)}\right)\times {\left[{dN}_i(t)-\frac{F_i(t,\theta ;1,X)dE\{N(t)\}}{G(t,{\theta }_0;1,X)}\right]\}}^{\otimes 2},\\ S_2({\theta }_0;{(R^T,Z^T)}^T,X)=\left\{\frac{E\{exp(2{\beta }^{T}e)\}}{E^2\{exp({\beta }^{T}e)\}}-1\right\}\times E{\left[{\int }_0^L\left({(R^T,Z^T)}^T-\frac{G\{t,{\theta }_0;{(R^T,Z^T)}^T,X\}}{G(t,{\theta }_0;1,X)}\right)\frac{F_i(t,\theta ;1,X)dE\{N(t)\}}{G(t,{\theta }_0;1,X)}\right]}^{\otimes 2}.\end{array}$$

It can be easily seen that V_I is the variance of θ̃ when var(e) = 0, and V_A is a nonnegative definite matrix. Expression (5) indicates that the efficiency of θ̃ improves with the increase of Pr(η = 1) = E(η) or the decrease of E{exp(2βe)}/E²{exp(β^Te)}. When the error e is normal, E{exp(2β^Te)}/E²{exp(β^Te)} = exp{3β^Tvar(e)β/2} is an increasing function of var(e). In the special case that R = g_*(X, Z) + ε with ε independent with (V, Δ, X, Z, e), it can be shown that V_c increases with the increase of var(ε). Although the variance V_C may depend on the variance of e and other unknown quantities, estimation of V_C does not require estimating these quantities.

A drawback of the simple nonparametric approach is that it only uses the calibration subsample Ω_C = {(V_i, Δ_i, Z_i, W_i, R_i) : η_i = 1} where both the error contaminated variable W_i and the instrumental variable R_i are observed. The information in the non-calibration subsample Ω_C̄ = {(V_i, Δ_i, Z_i, W_i) : η_i = 0} with missing R_i is not used. When the calibration subsample is small compared to the sample size, it can be very inefficient. It is expected that the efficiency can be improved if we could use the whole sample Ω = Ω_C ∩Ω_C̄. This motivates us to develop an improved estimator.

4. GMM NONPARAMETRIC CORRECTION

Note that the nonparametric correction based on W_i only uses the whole sample (Song and Huang, 2005; Huang and Wang, 2006). The corresponding estimating equation can be written as

$${\widehat{U}}_F(\theta )=n^{-1}\sum _{i=1}^n{\int }_0^L\left({(W_i^T,Z_i^T)}^T+{(c^T(\theta ),0_q^T)}^T-\frac{\widehat{G}(t,\theta ;{(W^T,Z^T)}^T,W)}{\widehat{G}(t,\theta ;1,W)}\right){dN}_i(t)=0,$$ (6)

where

$$c(\theta )=\frac{E\{eexp({\beta }^{T}e)\}}{E\{exp({\beta }^{T}e)\}}.$$

However, to estimate θ based on (6), the correction term c(θ) needs to be estimated by replicated measurements on W_i, which is not available in our case. Note that, if θ is known, we may estimate c₀ = c(θ₀) based on the first p-equations of (6). As we have already obtained an estimate θ̃ based on (2), we may plug it in (6) and obtain an estimator of c₀ based on the calibration subsample Ω_C,

$$\widehat{c}=\widehat{c}(\stackrel{\sim }{\theta })=-{\left[{\int }_0^{L}d\widehat{E}\{\eta N(t)\}\right]}^{-1}{\int }_0^L\left[d\widehat{E}\{\eta W^{T}N(t)\}-\frac{\widehat{G}(t,\stackrel{\sim }{\theta };\eta W,W)}{\widehat{G}(t,\stackrel{\sim }{\theta };\eta ,W)}d\widehat{E}\{\eta N(t)\}\right],$$

where Ê is the operator for empirical mean such that $\widehat{E}(a)=n^{-1}{\sum }_{i=1}^n{a}_i$.

To utilize the information on the whole sample, we propose an improved nonparametric correction estimator θ̂(A) by minimizing the quadratic form

$$Q(\theta ;\widehat{c},A)={\widehat{U}}^T(\theta ;\widehat{c})A\widehat{U}(\theta ;\widehat{c}),$$

where A is a (2p + q) × (2p + q) nonzero semi-positive definite matrix and

$$\widehat{U}(\theta ;\widehat{c})=n^{-1}\sum _{i=1}^n\left(\begin{array}{l}{\int }_0^L{\eta }_i\left\{R_i-\widehat{G}(t,\theta ;\eta R,W)/\widehat{G}(t,\theta ;\eta ,W)\right\}{dN}_i(t)\hfill \\ {\int }_0^L\left\{W_i+\widehat{c}-\widehat{G}(t,\theta ;W,W)/\widehat{G}(t,\theta ;1,W)\right\}{dN}_i(t)\hfill \\ {\int }_0^L\left\{Z_i-\widehat{G}(t,\theta ;Z,W)/\widehat{G}(t,\theta ;1,W)\right\}{dN}_i(t)\hfill \end{array}\right).$$

The (2p + q) dimensional vector Û(θ; ĉ) contains the estimating functions in (2) and (6), which include the information on the whole sample Ω. Since the number of estimating functions in Û(θ; ĉ) is larger than the number of parameters (p + q), there is generally no estimate for Û(θ; ĉ) = 0. To derive an estimator, the quadratic form Q(θ; ĉ, A) is minimized instead. The derivation of the improved estimator has adopted similar techniques for the generalized methods of moments (GMM) (Hansen, 1982), and thus we call it the GMM nonparametric correction estimator. The GMM is a general methodology in econometrics literature (e.g. Cragg, 1983; Newey 1988; Newey and McFadden, 1994; Stock and Wright, 2000). It combines economic data with population moment conditions to produce estimators of parameters in statistical models. It is an extension of the method of moments to allow more moment conditions than the parameters to estimate. The GMM estimator is obtained by minimizing a quadratic form in the sample moments conditions.

The matrix A plays a role similar to weights for the estimating functions. The estimator will be different with a different choice of the matrix A. Our goal is to find an optimal matrix A_opt such that the estimator θ̂(A_opt) is most efficient among such estimators.

For this purpose, we first derive the asymptotic properties of θ̂(A). Let I_s denote an s-dimensional identity matrix.

Theorem 2

Under conditions A–H, θ̂(A) is a consistent estimator of θ₀. Further, n^1/2(θ̂(A) − θ₀) is asymptotically normal with mean zero and variance

$$V(A)={\{D^T({\theta }_0)AD({\theta }_0)\}}^{-1}{D}^T({\theta }_0)AB({\theta }_0)AD({\theta }_0){\{D^T({\theta }_0)AD({\theta }_0)\}}^{-1},$$

where

$$\begin{array}{l}D({\theta }_0)=\mathit{diag}(E(\eta )I_p,I_p{I}_q){\int }_0^L\{G(t,{\theta }_0;{(R^T,W^T,Z^T)}^T(W^T,Z^T),W)\\ -\frac{G(t,{\theta }_0;{(R^T,W^T,Z^T)}^T,W)G(t,{\theta }_0;(W^T,Z^T),W)}{G(t,{\theta }_0;1,W)}\}\frac{dE\{N(t)\}}{G(t,{\theta }_0;1,W)},\\ B({\theta }_0)=\mathit{var}\{{\phi }_i({\theta }_0)\}\text{with}{\phi }_i({\theta }_0)={\rho }_i({\theta }_0)+(0_p^T,{\tau }_i^T({\theta }_0),0_q^T),{\rho }_i({\theta }_0)={({\rho }_{iR}^T({\theta }_0),{\rho }_{iW}^T({\theta }_0),{\rho }_{iZ}^T({\theta }_0))}^T,\\ {\rho }_{iR}({\theta }_0)={\eta }_i{\int }_0^L\left(R_i-\frac{G(t,{\theta }_0;\eta R,W)}{G(t,{\theta }_0;\eta ,W)}\right)\times \left[{dN}_i(t)-\frac{F_i(t,{\theta }_0;\eta ,W)}{G(t,{\theta }_0;\eta ,W)}dE\{\eta N(t)\}\right],\\ {\rho }_{iW}({\theta }_0)={\int }_0^L\left\{W_i-\frac{G(t,{\theta }_0;W,W)}{G(t,{\theta }_0;1,W)}\right\}\times \left[{dN}_i(t)-\frac{F_i(t,{\theta }_0;1,W)dE\{N(t)\}}{G(t,{\theta }_0;1,W)}\right]+c_0\int {dN}_i(t),\\ {\rho }_{iZ}({\theta }_0)={\int }_0^L\left(Z_i-\frac{G(t,{\theta }_0;Z,W)}{G(t,{\theta }_0;1,W)}\right)\times \left[{dN}_i(t)-\frac{F_i(t,{\theta }_0;1,W)}{G(t,{\theta }_0;1,W)}dE\{\eta N(t)\}\right],\\ {\tau }_i^T({\theta }_0)=E\left\{{\int }_0^{L}dE\{N_i(t)\}\right\}\{{\xi }_i({\theta }_0)+{\zeta }_i({\theta }_0)\},\\ {\xi }_i({\theta }_0)=-{\left[{\int }_0^{L}dE\{\eta N(t)\}\right]}^{-1}{\int }_0^L{\eta }_i\left\{W_i-\frac{G(t,{\theta }_0;\eta W,W)}{G(t,{\theta }_0;\eta ,W)}\right\}\times \left[{dN}_i(t)-\frac{F_i(t,{\theta }_0;\eta ,W)}{G(t,{\theta }_0;\eta ,W)}dE\{\eta N(t)\}\right]-{\left[{\int }_0^{L}dE\{\eta N(t)\}\right]}^{-1}{c}_0\left\{{\int }_0^L{\eta }_i{dN}_i(t)\right\},\\ {\zeta }_i({\theta }_0)=-{\left[{\int }_0^{L}dE\{\eta N(t)\}\right]}^{-1}{\int }_0^L[G\frac{(t,{\theta }_0;\eta W(1,W^T),W)}{G(t,{\theta }_0,\eta ,W)}-\frac{G(t,{\theta }_0,\eta W,W)G(t,{\theta }_0,\eta W^T,W)}{G^2(t,{\theta }_0,\eta ,W)}]dE\{\eta N(t)\}\times {\{E(\eta )\mathrm{\Gamma }({\theta }_0)\}}^{-1}{\omega }_i({\theta }_0).\end{array}$$

A consistent estimator of the variance can be obtained by substituting θ̂(A) for θ₀ and the empirical means for the population means in the variance formula.

To find the optimal matrix A_opt, we minimize the variance V(A) of the estimator θ̂(A). This can be achieved by simple matrix algebra by analogy to the generalized methods of moments (Newey and McFadden, 1994) and the result is given in the following theorem.

Theorem 3

Under conditions A–H, the most efficient estimator of θ̂(A) is achieved at A_opt = B⁻¹(θ₀) with the variance V(A_opt) = {D^T(θ₀)B⁻¹D(θ₀)}⁻¹.

The GMM estimator θ̂(A_opt) is generally more efficient than the simple estimator θ̃ This can be easily seen when there is no Z is the model. Specifically, without Z, noting that $\widehat{U}(\theta ;\widehat{c})={({\widehat{U}}_c^T(\theta ;{(R^T,Z^T)}^T),{\widehat{U}}_F(\theta ;\widehat{c}))}^T$, the simple nonparametric correction estimator minimizes Q(θ, ĉ, A_c) with A_c = diag(I_p, 0_q×q), where 0_q×q is a q × q zero matrix. In practice, A_opt can be approximated by Â_opt = B̃⁻¹ with B̃ = n⁻¹ Σ{φ̂_i(θ̃) − Êφ̂(θ̃)}^⊗2, where φ̂_i(θ̃) is obtained by substituting the unknown quantities in φ_i(θ̃) by their empirical estimates. The variance of θ̂(Â_opt) can be estimated by {D̂^TÂ_opt D̂}⁻¹ D̂^T Â_opt B̂ Â_optD̂{D̂^T Â_opt D̂}⁻¹, where D̂ = −∂Û(θ̂(Â_opt))/∂θ^T, and B̂ = Σ{φ̂_i(θ̂(A_opt)) − Êφ̂(θ̂(A_opt))}^⊗2.

Remark

There could be a few variations of the above estimator by varying the data set used in estimating the correction term c₀ and the data set in the objective function Q(·) corresponding to the covariates W. Let Θ_c denote the former and Θ_Q the latter. Both data sets could be elements of {Ω, Ω_C, Ω_C̄} as long as Θ_c ≠ Θ_Q. Our numerical studies indicate that the performance of the GMM estimator seems similar for various choices of Θ_c and Θ_Q except in some extreme cases, such as a very small sample calibration subsample or non-calibration subsample. We use Θ_c = Θ_C and Θ_Q = Ω in our illustration.

5. SIMULATION STUDIES

Simulation studies were conducted to evaluate the performance of the estimators. First, we considered the case of a single covariate X, which was generated from a standard normal distribution. The instrumental variable was set as R = 0.5X² + 2X +1+0.5ε₁ +Xε₁ +ε₂, where ε₁ was generated from a standard normal distribution correlated with X with correlation −0.3 which may denote a variable that was not in the proportional hazard model, and ε₂ from a normal distribution independent of X with mean 0 and variance 0.4 which may denote independent noise. The error e was generated from a normal or a skewed bimodal mixture of two normals as described in Davidian and Gallant (1993, mixing proportion p = 0.3 and distance between the means equal to sep = 2 times standard deviation) with mean 0 and variance σ² = 0.1 or 0.2. The true Cox model coefficient was taken to be β₀ = −1. The baseline hazard λ₀(t) = exp{−2}t^−0.5. The censoring time was generated from a uniform distribution on [0,40], leading to a censoring rate of about 37%. The proportion of calibration subsample Pr(η = 1) was set to 0.3, 0.5 or 0.7.

We carried out simulations for n = 500 and 2000. In each scenario, 1000 Monte Carlo data sets were simulated. For each data set, we fitted the model using (i) the “ideal” approach, in which the true values of X were used; (ii) the naive approach, in which W substituted for X in the partial likelihood estimating equation; (iii) the simple nonparametric correction estimator θ̃; (iv) the GMM nonparametric correction estimator θ̂ (Â_opt). For each estimator, the 95% Wald confidence interval was constructed.

The results are shown in tables 1 and 2 respectively for the normal and the mixture normal error models. The naive estimator is biased with a coverage probability well below the nominal level. The performance gets worse with the sample size growing or the error variance increasing. The nonparametric correction estimators have negligible bias close to the unachievable “ideal” estimator and the coverage probabilities are close to the nominal level. Their performance improves when the sample size increases or the error variance decreases. The GMM estimator is more efficient than the simple estimator, especially when Pr(η = 1) is small. For either correction approach, the standard deviations are close to the standard errors, and the efficiency improves with the increase of the proportion of calibration subsample or the decrease of the magnitude of measurement error.

Table 1.

Simulation Results in the case of a single covariate contaminated with normal error.

			n = 500				n = 2000
	Pr(η = 1)		Est	SD	SE	CP	Est	SD	SE	CP
		Ideal	−1.001	0.070	0.069	0.947	−0.999	0.035	0.035	0.948
σ2 = 0.1		Naive	−0.874	0.065	0.064	0.476	−0.871	0.033	0.032	0.034
	0.3	SNC	−1.014	0.178	0.165	0.930	−1.005	0.084	0.080	0.936
		INC	−1.005	0.142	0.127	0.931	−1.003	0.068	0.063	0.947
	0.5	SNC	−1.012	0.136	0.126	0.935	−1.004	0.065	0.062	0.947
		INC	−1.007	0.118	0.107	0.930	−1.002	0.057	0.053	0.932
	0.7	SNC	−1.008	0.111	0.107	0.939	−1.001	0.056	0.053	0.935
		INC	−1.004	0.104	0.096	0.928	−0.999	0.051	0.048	0.943
σ2 = 0.2		Naive	−0.777	0.062	0.060	0.054	−0.773	0.031	0.030	0.000
	0.3	SNC	−1.021	0.193	0.171	0.931	−1.007	0.090	0.081	0.923
		INC	−1.004	0.160	0.137	0.927	−1.002	0.074	0.066	0.931
	0.5	SNC	−1.016	0.146	0.129	0.928	−1.005	0.069	0.063	0.928
		INC	−1.008	0.130	0.111	0.921	−1.001	0.062	0.054	0.923
	0.7	SNC	−1.011	0.116	0.108	0.922	−1.002	0.059	0.053	0.919
		INC	−1.004	0.110	0.098	0.915	−0.999	0.054	0.049	0.925

SNC, simple nonparametric correction; INC, GMM nonparametric correction. SD, empirical standard deviation across simulated data sets; SE, average of estimated standard errors; CP, coverage probability of the 95% Wald confidence interval.

Table 2.

Simulation Results in the case of a single covariate contaminated with a mixture of normal error.

			n = 500				n = 2000
	Pr(η= 1)		Est	SD	SE	CP	Est	SD	SE	CP
		Ideal	−1.000	0.070	0.069	0.958	−1.001	0.034	0.035	0.951
σ2 = 0.1		Naive	−0.877	0.066	0.064	0.515	0.877	0.032	0.032	0.026
	0.3	SNC	−1.021	0.184	0.167	0.932	−1.003	0.085	0.080	0.940
		INC	−1.006	0.143	0.127	0.934	−1.001	0.064	0.063	0.944
	0.5	SNC	−1.007	0.138	0.126	0.931	−1.003	0.063	0.062	0.943
		INC	−1.006	0.117	0.106	0.933	−1.002	0.054	0.053	0.942
	0.7	SNC	−1.006	0.112	0.106	0.935	−1.004	0.055	0.052	0.944
		INC	−1.006	0.103	0.096	0.936	−1.003	0.051	0.048	0.938
σ2 = 0.2		Naive	−0.784	0.062	0.061	0.074	−0.783	0.030	0.030	0.000
	0.3	SNC	−1.027	0.195	0.170	0.929	−1.005	0.088	0.081	0.927
		INC	−1.006	0.153	0.133	0.930	−1.000	0.069	0.066	0.935
	0.5	SNC	−1.010	0.146	0.127	0.922	−1.004	0.066	0.062	0.935
		INC	−1.006	0.126	0.110	0.913	−1.002	0.058	0.054	0.938
	0.7	SNC	−1.009	0.118	0.107	0.925	−1.004	0.058	0.052	0.932
		INC	−1.005	0.110	0.098	0.923	−1.003	0.053	0.049	0.927

SNC, simple nonparametric correction; INC, GMM nonparametric correction. SD, empirical standard deviation across simulated data sets; SE, average of estimated standard errors; CP, coverage probability of the 95% Wald confidence interval.

Next we added a covariate Z = ε₁ to the proportional hazards model with γ₀ = −1. The censoring rate was 38%. The results for the normal error model with σ² = 0.1 and var(ε₂) = 0.4 are shown in Table 3. We observe similar results for estimation of β₀ as above. The estimation of γ₀ shows similar pattern. Note that the naive estimator of γ₀ also shows some bias and the coverage probability is only 83% for n = 500 and 52% for n = 2000. This indicates that estimation of the coefficient of the error free covariate Z can be affected by the measurement error on X as well.

Table 3.

Simulation Results in the case of two covariates.

			n = 500				n = 2000
	Pr(η = 1)		Est	SD	SE	CP	Est	SD	SE	CP
β		Ideal	−1.002	0.071	0.072	0.951	−1.000	0.036	0.036	0.948
		Naive	−0.868	0.068	0.067	0.466	−0.864	0.034	0.033	0.026
	0.3	SNC	−1.019	0.194	0.180	0.939	−1.005	0.092	0.088	0.943
		INC	−1.007	0.155	0.139	0.944	−1.002	0.076	0.070	0.934
	0.5	SNC	−1.014	0.148	0.137	0.942	−1.003	0.071	0.068	0.935
		INC	−1.008	0.130	0.117	0.930	−1.001	0.062	0.059	0.935
	0.7	SNC	−1.012	0.118	0.115	0.955	−1.003	0.060	0.057	0.934
		INC	−1.008	0.108	0.105	0.949	−1.001	0.054	0.053	0.940
γ		Ideal	−1.002	0.073	0.072	0.941	−1.002	0.037	0.036	0.939
		Naive	−0.935	0.072	0.070	0.829	−0.933	0.037	0.035	0.518
	0.3	SNC	−1.013	0.161	0.148	0.923	−1.009	0.075	0.072	0.943
		INC	−1.007	0.107	0.095	0.926	1.003	0.050	0.048	0.943
	0.5	SNC	−1.011	0.121	0.114	0.935	−1.005	0.058	0.056	0.952
		INC	−1.007	0.097	0.087	0.920	−1.003	0.046	0.043	0.941
	0.7	SNC	−1.009	0.100	0.095	0.940	−1.002	0.051	0.047	0.935
		INC	−1.007	0.087	0.082	0.931	−1.003	0.044	0.041	0.921

SNC, simple nonparametric correction; INC, GMM nonparametric correction. SD, empirical standard deviation across simulated data sets; SE, average of estimated standard errors; CP, coverage probability of the 95% Wald confidence interval.

The relationship between R and X may impact the performance of the estimators as well. We conducted simulations in the case of one covariate with normal error as described above with different instrumental variables. We considered two cases when R and X were non-linearly associated with zero linear correlation, R = X² + ε and R = X⁴ + ε, and compared them to the case when R = X + ε, where ε was normal and independent of X with mean 0 and variance 0.2. The results for σ² = 0.1, Pr(η = 1) = 0.5 and n = 2000 are shown in Table 4. The nonparametric corrections estimators still work when R = X² + ε or X⁴ + ε, but the standard errors are larger than when W = X + ε. The performance is better when R = X² + ε than when R = X⁴ + ε.

Table 4.

Simulation Results when R = X + ε, X² + ε, and X⁴ + ε.

		Est	SD	SE	CP
	Ideal	−0.999	0.035	0.035	0.948
	Naive	−0.871	0.033	0.032	0.034
R = X + ε	SNC	−1.003	0.058	0.056	0.939
	INC	−1.001	0.048	0.046	0.940
R = X2 + ε	SNC	−1.006	0.123	0.115	0.943
	INC	−0.979	0.116	0.103	0.913
R = X4 + ε	SNC	−1.020	0.141	0.134	0.940
	INC	−0.989	0.131	0.119	0.916

SNC, simple nonparametric correction; INC, GMM nonparametric correction. SD, empirical standard deviation across simulated data sets; SE, average of estimated standard errors; CP, coverage probability of the 95% Wald confidence interval.

We also conducted simulations to assess the sensitivity of nonparametric correction approaches to the assumption that R is independent of (T, C) given X and Z. In the single covariate model described above, the proportional hazards model can be rewritten as log(T) = a + 2X + 2ε_*, where a is a constant and ε_* is an extreme-value-distributed random variable with variance π²/6 and independent of X. We replaced v the instrumental variable by $R=X+b\sqrt{6}{\epsilon }_{\ast }/(10\pi )$ so that R and T are correlated given X if b ≠ 0. We show the results for b = 0, 0.5, 1, 2 with normal error, σ² = 0.1, Pr(η = 1) = 0.5 and n = 500 and 1000 in Table 5. The nonparametric correction estimators are not consistent in this case. Their performance tends to get worse with increasing b, which represents an increasing association between R and T given X. The bias may be large if violation of conditional independence is not small.

Table 5.

Simulation Results when $R=X+b\sqrt{6}{\epsilon }_{\ast }/(10\pi )$.

		n = 500				n = 1000
		Est	SD	SE	CP	Est	SD	SE	CP
	Ideal	−1.009	0.073	0.070	0.940	−1.003	0.049	0.049	0.940
	Naive	−0.878	0.068	0.064	0.514	−0.873	0.046	0.045	0.210
b = 0.0	SNC	−1.016	0.137	0.125	0.934	−1.008	0.091	0.088	0.932
	INC	−1.007	0.118	0.105	0.925	−1.003	0.079	0.074	0.928
b = 0.5	SNC	−1.095	0.145	0.127	0.882	−1.085	0.096	0.088	0.843
	INC	−1.084	0.125	0.107	0.868	−1.078	0.083	0.075	0.821
b = 1.0	SNC	−1.179	0.155	0.129	0.722	−1.166	0.101	0.089	0.565
	INC	−1.164	0.134	0.109	0.699	−1.158	0.088	0.077	0.468
b = 2.0	SNC	−1.362	0.185	0.136	0.246	−1.342	0.117	0.092	0.052
	INC	−1.339	0.159	0.117	0.179	−1.329	0.102	0.081	0.024

SNC, simple nonparametric correction; INC, GMM nonparametric correction. SD, empirical standard deviation across simulated data sets; SE, average of estimated standard errors; CP, coverage probability of the 95% Wald confidence interval.

6. APPLICATION

We applied the approaches to the AIDS Clinical Trial Group (ACTG) 175 study. Our aim was to evaluate the effect of treatments for the time to AIDS or death adjusted for baseline CD4 counts. The primary analysis found ziduvudine alone to be inferior to the other three therapies; thus, further investigations focused on two treatment groups, zidovudine alone and the combination of the other three.

This dataset has been analyzed previously. By definition, baseline CD4 counts should be true CD4 counts at randomization. However, CD4 counts were only measured for less than 50% of the patients on randomization day. Huang and Wang (2000) assumed the CD4 measurements within three weeks of randomization were replicates of the underlying baseline CD4 counts. As the underlying CD4 counts may change over time during the three weeks period, these CD4 measurements may not be simple replicates of the baseline CD4 counts. We took an alternative strategy here. Assuming the CD4 counts is relatively stable within a short period, say one week, the closest measurement W within one week before randomization was taken as the baseline CD4 measurement. The closest measurement R between one to three weeks before randomization was used as an instrumental variable. Among the 2174 subjects with baseline CD4 measurement, the instrumental variable was observed among 989 patients. The median follow up time was 33 months. A total of 275 events was observed.

A proportional hazards model was adopted with two covariates, the true baseline X = log(CD4) and the treatment indicator Z = I(treatment ≠ ziduvudine). The logarithm transformation was applied to the CD4 counts to achieve approximate constant variance. The same transformation was applied on the observed CD4 counts W and R. We first examine whether R is an appropriate instrumental variable. It is reasonable to assume that R is independent of the measurement error at baseline. Under this assumption, Figure 1 indicates that R is correlated with X. To be an instrumental variable, R needs to be independent of the time to AIDS or death given X and Z. This assumption seems to be appropriate based on our understanding of CD4 counts and AIDS risk, but cannot be tested from the data (Stock and Watson, 2010, chapter 12). Note that the assumption that R is a instrumental variable is weaker than R and W are replicates.

We estimated the regression coefficients using the naive, simple and GMM non-parametric correction approaches. The results are shown in Table 4. Both baseline CD4 and treatment are significant. The nonparametric correction estimates show stronger effects than the naive estimates, and the GMM estimates have smaller estimated standard errors than the simple estimates.

7. DISCUSSION

We have proposed nonparametric correction estimators for the proportional hazards model with error-contaminated covariates. The estimators are useful when no replicated observations are available on the error-prong covariates while observations available on instrumental variables.

For simplicity, we only consider the case when the dimension of the instrumental variables s equals the dimension p of the error-prone covariates. In the case of s > p, θ̃ may be obtained by minimizing the quadratic form ${\widehat{U}}_C^T{A}_C{U}_C$ and the optimal AC can be obtained by analogy to A_opt. The GMM estimator θ̂; can then be derived similarly as in section 4.

The function g(·) and the variables ε are unspecified in (1), this allows great flexibility in adopting instrumental variables. However, the format of g(·) may affect the efficiency of the simple and the GMM nonparametric correction estimators. The instrumental variables need not be linearly correlated with X, but cannot be independent of X. The proposed methods may break down if the instrumental variables are only weakly related with the underlying true covariates.

Our simulation studies reveal that the performance of the approaches depends on the magnitude of the measurement error, the sample size and the relationship between the error contaminated variables and the instrumental variables. When the measurement error is large, the methods might not work properly for small sample sizes with the possibility of nonconvergence and outlier estimates. This is a common issue for parametric/nonparametric correction approaches (Song and Huang, 2005). A possible improvement for the finite sample performance is to use the refined non-parametric correction technique (Song and Huang, 2005). The bootstrap confidence interval may work better when the measurement error is large (Huang and Wang, 2001).

Table 6.

Results for ACTG 175 data.

	logCD4 (β)		Treatment (γ)
	Est	SE	Est	SE
Naive	−1.465	0.162	−0.474	0.129
SNC	−2.359	0.398	−0.618	0.193
INC	−2.562	0.358	−0.581	0.133

SNC, simple nonparametric correction; INC, GMM nonparametric correction.

APPENDIX A: PROOFS

Regularity Conditions

We assume the following mild regularity conditions.

1. λ₀(u) is continuous in [0, L].

2. Pr(V ≥ L) > 0.

3. E(X^TX) < ∞, E{R^TR < ∞, E(Z^TZ) < ∞, E(e^Te) < ∞.

   For a compact neighborhood 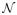(θ₀) of θ₀,

   E [ 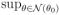X^TX exp {2(β^TX + γ^TZ)}]< ∞,

   E [ 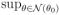Z^TZ exp {2(β^TX + γ^TZ)}]< ∞,

   E [ 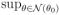R^TR exp {2(β^TX + γ^TZ)}]< ∞,

   E [ 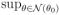exp {2(β^T e)}]< ∞.

4. E(η) > 0.

5. The matrix Γ(θ₀) defined in (4) is nonsingular.

6. Pr(T < C, T < L) > 0.

7. The matrix A is positive definite.

Lemma 1

Suppose H_i is a predictable random vector with respect to the filtration (t) = {N_i(u), Y_i(u), X_i, W_i, R_i, Z_i: u ≤ t}. If $E[H_i^T{H}_i]<\infty$, then

$$E^{\prime }[H_i{N}_i(t)]={\lambda }_0(t)G(t,{\theta }_0;H,X).$$

Proof

Note that $M_i(t)=N_i(t)-{\int }_0^t{\lambda }_0(u)Y_i(u)exp({\beta }_0^{T}X+{\gamma }_0^{T}Z)dt$ is a martingale with respect to the filtration (t) as N_i(u) is independent of (W_i, R_i) given (X_i, Z_i). By iterated expectations and the predictability of H_i,

$$E\{H_i{M}_i(t)\}=E[E\{H_i{M}_i(t)\mid {\mathcal{F}}_i(t-)\}]=E[H_{i}E\{M_i(t)\mid {\mathcal{F}}_i(t-)\}]=0.$$

Substituting M_i by $N_i(t)-{\int }_0^t{\lambda }_0(u)Y_i(u)exp({\beta }_0^{T}X+{\gamma }_0^{T}Z)\text{dt}$ in the left side of the above equation, we have

$$E\{H_i{N}_i(t)\}-E\left\{H_i{\int }_0^t{\lambda }_0(u)Y_i(u)exp({\beta }_0^T{X}_i+{\gamma }_0^T{Z}_i)du\right\}=0.$$

Taking derivative with respect to t, under conditions A and C together with $E[H_i^T{H}_i]<\infty$, we obtain

$$E^{\prime }\{H_i{N}_i(t)\}-E\{H_i{\lambda }_0(t)Y_i(t)exp({\beta }_0^T{X}_i+{\gamma }_0^T{Z}_i)\}=0.$$

This completes the proof.

Proof for Theorem 1

First consider the consistency. Conditions B–D ensure G(t, θ; η) and G(t, θ; 1) are bounded away from zero in (θ₀). Note that Û_C(θ) can be rewritten as

$${\widehat{U}}_C=(\theta )={\int }_0^L\left\{d\widehat{E}\{{(R^T,Z^T)}^T{\eta }_i{N}_i(t)\}-\frac{\widehat{G}(t,\theta ;\eta {(R^T{Z}^T)}^T,W)}{\widehat{G}(t,\theta ;\eta ,W)}\right\}d\widehat{E}\{\eta N(t)\}.$$ (7)

Follow the extended strong law of large numbers as given in Appendix III of Andersen and Gill (1982), under condition C, the four empirical processes in (7) converge almost surely (a.s.) to their limits uniformly for t ∈ (0, L) and θ ∈ (θ₀). By the chain law, Û_C(θ) converges uniformly a.s. for θ ∈ (θ₀) to

$$\begin{array}{l}{U}_C(\theta )={\int }_0^L\left\{dE\{{(R_i^T,Z_i^T)}^T{\eta }_i{N}_i(t)\}-\frac{G(t,\theta ;\eta {(R^T,Z^T)}^T,W)}{G(t,\theta ;\eta ,W)}\right\}dE\{\eta N(t)\}\\ ={\int }_0^L\left\{dE\{{(R^T,Z^T)}^T\eta N(t)\}-\frac{G(t,\theta ;{(R^T,Z^T)}^T,X)}{G(t,\theta ;1,X)}\right\}dE\{\eta N(t)\}.\end{array}$$

By Lemma 1 and the independence of η from (V, Δ, X, Z), we have

$$\begin{array}{c}dE\{\eta N(t)\}={\lambda }_0(t)E(\eta )G(t,{\theta }_0;1,X)dt,\\ dE\{{(R^T,Z^T)}^T\eta N(t)\}={\lambda }_0(t)E(\eta )G(t,{\theta }_0;{(R^T,Z^T)}^T,X)dt.\end{array}$$

It follows that U_C(θ₀) = 0. Similarly it can be shown that ∂Û_C(θ)/∂θ converges uniformly a.s. to Γ_η(θ) = E(η)Γ(θ) for θ ∈ (θ₀). Under Condition E, θ₀ is the unique zero crossing for U_C(θ) in a neighborhood of θ₀. The consistency of θ̃ then follows.

Next, we show the asymptotic normality. By a Taylor expansion of Û_C(θ̃) at θ₀,

$$0={\widehat{U}}_C(\stackrel{\sim }{\theta })={\widehat{U}}_C({\theta }_0)+\frac{\partial }{\partial {\theta }^T}{\widehat{U}}_C({\stackrel{\sim }{\theta }}^{\ast })(\stackrel{\sim }{\theta }-{\theta }_0),$$

where θ̃^* lies between θ₀ and θ̃ Thus

$$n^{1/2}(\stackrel{\sim }{\theta }-{\theta }_0)={\left\{\frac{\partial }{\partial {\theta }^T}{\widehat{U}}_C({\stackrel{\sim }{\theta }}^{\ast })\right\}}^{-1}{n}^{1/2}{\widehat{U}}_C({\theta }_0).$$

With a functional Taylor expansion and straight algebra,

$$\begin{array}{l}{n}^{1/2}{\widehat{U}}_C(0)=n^{-1/2}\sum _{i=1}^n{\eta }_i{\int }_0^L\left({(R_i^T,Z_i)}^T-\frac{G(t,{\theta }_0;\eta {(R^T,Z^T)}^T,W)}{G(t,{\theta }_0;\eta ,W)}\right){dN}_i(t)\\ -{\int }_0^L\left(\frac{F_i(t,{\theta }_0;\eta {(R^T,Z^T)}^T,W)}{G(t,{\theta }_0;\eta ,W)}-\frac{F_i\{{\theta }_0;\eta ,W\}G(t,{\theta }_0;\eta {(R^T,Z^T)}^T,W)}{G^2(t,{\theta }_0;\eta ,W)}\right)\times dE\eta N(t)+o_p(1)=n^{-1/2}\sum _{i=1}^n{\omega }_i({\theta }_0)+o_p(1).\end{array}$$ (8)

This, together with the uniform convergence of ∂Û_C(θ; (R^T, Z^T)^T)/∂θ^T, establishes the asymptotic normality. One can then show the consistency of the variance estimator with similar arguments.

Proof of Theorem 2

First, we consider the asymptotic properties of the estimator ĉ. Under condition F, ${\int }_0^{L}dE\{N_i(t)\}>0$. By similar arguments as for the consistency in Theorem 1, we have

$$\widehat{c}\stackrel{a.s.}{\to }-{\left[{\int }_0^{L}dE\{\eta N(t)\}\right]}^{-1}{\int }_0^L\left[dE\{\eta W^{T}N(t)\}-\frac{G(t,{\theta }_0;\eta W,W)}{G(t,{\theta }_0;\eta ,W)}dE\{\eta N(t)\}\right].$$ (9)

With some simple algebra, it can be shown that

$$\frac{G(t,{\theta }_0;\eta W,W)}{G(t,{\theta }_0;\eta ,W)}=\frac{G(t,{\theta }_0;X,X)}{G(t,{\theta }_0;1,X)}+c_0.$$

By Lemma 1, we have dE {ηN(t)} = λ₀(t)E(η)G(t, θ₀; 1,X) and dE {ηWN(t)} = dE [ηXN(t)] = λ₀(t)E(η)G(t, θ₀;X,X). Thus the right side of (9) equals c₀. With a functional Taylor expansion and some algebra, it can be shown that

$$n^{1/2}\{\widehat{c}({\theta }_0)-c_0\})=n^{-1/2}\sum _{i=1}^n{\xi }_i({\theta }_0)+o_p(1).$$ (10)

Applying a Taylor expansion at θ₀, together with (8), we have

$$n^{1/2}\left\{\widehat{c}(\stackrel{\sim }{\theta })-\widehat{c}({\theta }_0)\right\}=n^{-1/2}\sum _{i=1}^n{\zeta }_i({\theta }_0)+o_p(1).$$ (11)

A combination of (10) and (11) gives

$$n^{1/2}\{\widehat{c}-c_0\}=n^{-1/2}\sum _{i=1}^n\{{\xi }_i({\theta }_0)+{\zeta }_i({\theta }_0)\}+o_p(1).$$ (12)

Now we consider the asymptotic properties of θ̂ (A). By the consistency of ĉ and empirical process theory, Û (θ; ĉ) converges uniformly a.s. to

$$U(\theta )={\int }_0^L\left\{\left(\begin{array}{c}dE\{{\eta }_i{R}_i{N}_{i}t)\}\\ dE\{W_i{N}_i(t)\}+c_{0}dE\{N_i(t)\}\\ Z_i\end{array}\right)+\left(\begin{array}{c}{G}^T(t,\theta ;R,W)\\ G^T(t,\theta ;W,W)\\ G^T(t,\theta ;W,W)\end{array}\right){\{G(t,\theta ;1,W)\}}^{-1}\right\}\times dE\{\eta N(t)\}.$$

Note that U(θ₀) = 0. Under condition C, θ₀ is the unique solution to U_(p+1;p+2q)(θ) = 0, where U_(p+1;p+2q)(θ) denote the p+1 to p+2q elements of U(θ) (Huang and Wang, 2000). Thus θ₀ is the unique solution to U(θ) = 0 and hence the unique minimum of U^TAU. The consistency of θ̂(A) then follows.

Next we consider the asymptotic normality. Note that Û (θ; c) is linear in c, and

$$\sqrt{n}\widehat{U}(\theta ;\widehat{c})=\sqrt{n}\widehat{U}(\theta ;c_0)+\frac{\partial \widehat{U}(\theta ;c)}{\partial c^T}\sqrt{n}(\widehat{c}-c_0),$$ (13)

where $\partial {\widehat{U}}^T(\theta ;c)/\partial c=(0_{p\times p},\partial {\widehat{U}}_{(p+1,2p)}^T(\theta ;c)/\partial c,0_{p\times p})$,

$$\partial {\widehat{U}}_{(p+1,2p)}^T(\theta ;c)/\partial c=n^{-1}\sum {\int }_0^L{dN}_i(t)I_p\stackrel{a.s.}{\to }\left[{\int }_0^{L}dE\{N(t)\}\right]I_p,$$

and 0_p×p is a p × p zero matrix. It can be shown by a functional Taylor expansion that

$$\sqrt{n}\widehat{U}(\theta ;c_0)=n^{-1/2}\sum _{i=1}^n{\rho }_i(\theta )+o_p(1).$$

Substituting this and (12) into (13), we have

$$\sqrt{n}\widehat{U}(\theta ;\widehat{c})=n^{-1/2}\sum _{i=1}^n{\phi }_i(\theta )+o_p(1).$$

Since θ̂ (A) is the minimum of Q(θ; ĉ, A),

$$0=\frac{\partial Q(\widehat{\theta }(A);\widehat{c},A)}{\partial \theta }=2\frac{\partial {\widehat{U}}^T(\widehat{\theta }(A);\widehat{c})}{\partial \theta }A{\widehat{U}}^T(\widehat{\theta }(A);\widehat{c}).$$

By a Taylor expansion on Û^T(θ̂(A); ĉ) at θ₀, we have

$$0=2\frac{\partial {\widehat{U}}^T(\widehat{\theta }(A);\widehat{c})}{\partial \theta }A\widehat{U}({\theta }_0,\widehat{c})+2\frac{\partial {\widehat{U}}^T(\widehat{\theta }(A);\widehat{c})}{\partial \theta }A\frac{\partial \widehat{U}({\widehat{\theta }}^{\ast }(A);\widehat{c})}{\partial {\theta }^T}(\widehat{\theta }(A)-{\theta }_0),$$

where θ̂^*(A) lies between θ̂(A) and θ₀. Thus

$$\sqrt{n}(\widehat{\theta }(A)-{\theta }_0)=-{\left(\frac{\partial {\widehat{U}}^T(\widehat{\theta }(A);\widehat{c})}{\partial \theta }A\frac{\partial \widehat{U}({\widehat{\theta }}^{\ast }(A);\widehat{c})}{\partial {\theta }^T}\right)}^{-1}\frac{\partial {\widehat{U}}^T(\widehat{\theta }(A);\widehat{c})}{\partial \theta }A\widehat{U}({\theta }_0,\widehat{c}).$$

It can be shown that −∂Û (θ; ĉ)/∂α^T converges uniformly a.s. to D(θ). Therefore,

$$\sqrt{n}(\widehat{\theta }(A)-{\theta }_0)={\{D^T({\theta }_0)AD({\theta }_0)\}}^{-1}{D}^T({\theta }_0){An}^{-1/2}\sum _{i=1}^n{\phi }_i({\theta }_0)+o_p(1).$$

where D^T(θ₀)AD(θ₀) is positive definite under conditions D, E and G. The asymptotic normality follows from the central limit theorem and the Slutsky Theorem.