Doubly robust estimation of the local average treatment effect curve

Summary

We consider estimation of the causal effect of a binary treatment on an outcome, conditionally on covariates, from observational studies or natural experiments in which there is a binary instrument for treatment. We describe a doubly robust, locally efficient estimator of the parameters indexing a model for the local average treatment effect conditionally on covariates V when randomization of the instrument is only true conditionally on a high dimensional vector of covariates X, possibly bigger than V. We discuss the surprising result that inference is identical to inference for the parameters of a model for an additive treatment effect on the treated conditionally on V that assumes no treatment–instrument interaction. We illustrate our methods with the estimation of the local average effect of participating in 401(k) retirement programs on savings by using data from the US Census Bureau's 1991 Survey of Income and Program Participation.

1. Introduction

Economists and biostatisticians have long been concerned with the problem of how to estimate the causal effect of a treatment on an outcome of interest, and how this effect is modified by baseline covariates. Estimation of average treatment effects is often facilitated by the unconfoundedness assumption that a vector of measured covariates suffices to control for all confounding of the treatment–outcome relationship. When this assumption is thought implausible, but instrumental variables (IVs) satisfying the monotonicity assumption given in Section 2.1 are available, it is possible to estimate the so-called local average treatment effect contrasts. These are treatment effect contrasts for the subpopulation of compliers, i.e. subjects for whom treatment and instrument agree. Beginning with the seminal paper of Imbens and Angrist (1994), non-parametric and semiparametric IV methods for estimation of local average treatment effects have received considerable attention in the literature (Angrist and Imbens, 1995; Angrist et al., 1996, 2000; Abadie, 2002, 2003; Abadie et al., 2002; Froelich, 2007; Tan, 2006a, 2010; Kasy, 2009, Cheng et al., 2009a, b).

In this paper we consider estimation of models for the dependence of local average treatment effects on baseline covariates V. We assume that the treatment and instrument are binary and that the outcome support is either the real line, the non-negative real line or the non-negative integers. Like Abadie (2003), Tan (2006a), Froelich (2007), and Uysal (2011), we consider settings in which conditioning on a set of covariates X is necessary for the identifying IV assumptions to be valid. These settings are important because in practice the instrument may itself be confounded, and conditioning on covariates X may be required to make the key condition of instrument randomization plausible (Abadie, 2003). We extend this previous work to allow X to be larger than V. This is an important contribution of our methodology, providing desirable flexibility in the definition of the target estimand as often investigators wish to report the treatment effect at low aggregation levels. Specifically, the covariate vector X is the set of variables that must be conditioned on for the instrument–outcome and instrument–treatment relationships to be unconfounded within levels of covariates; however, local average treatment effects conditional on V, a subset of X, may be the relevant contrasts to help guide decision makers who, because of limited resources, will have access only to information about the subset V of X. For example, consider a study conducted in a sophisticated health maintenance organization. Suppose that the instrument is the therapy prescribed by the physician, the treatment is the therapy actually followed by the patient and X is a vector of measured risk factors for the outcome that were used by the health maintenance organization physician to decide on the therapy prescription. The covariates X could include the results of expensive tests administered to patients at high risk for disease, such as magnetic resonance angiograms, that would not be available to community physicians. Thus, community physicians would need to decide what therapy to prescribe on the basis of just the subset V of X that encodes the data that are available to them. Estimation of effect modification of the local average treatment effects by V is then critical to enable community physicians to make informed treatment decisions.

The literature on local average treatment effects has primarily focused on the estimation of the local average treatment effect on the additive scale, LATE, defined as the difference in means of the two potential outcomes (under treatment and under no treatment) in the subpopulation of compliers. Identification of the multiplicative local average treatment effect contrast, MLATE, i.e. the ratio of the potential outcome means among compliers, follows trivially from results of Abadie (2003) but, to our knowledge, estimators of parametric specifications for the dependence of MLATE on covariates has not been discussed in the literature. In this paper we consider estimation of models for LATE and MLATE as functions of V.

When the dimension of the covariate vector X is large, as will often be required in practice for the assumption of a conditionally unconfounded instrument to hold, non-parametric estimation of LATE (Froelich, 2007), of MLATE and of parametric specifications for the dependence of these contrasts on covariates V is not feasible, owing to the curse of dimensionality. When V is null, Tan (2006a) and Uysal (2011) derived estimators of LATE that are consistent provided that either two models for two specific conditional means given the instrument and X or a model for the instrument propensity score (the probability that the instrument is equal to 1 conditionally on the covariates X) are correctly specified. In this paper we derive a new class of doubly robust estimators of parametric specifications for the dependence of LATE or MLATE on covariates V which remain consistent and asymptotically normal provided that either the propensity score model or a model for another conditional mean given the instrument and X is correctly specified. When V is non-null, the conditional mean models that are required by our doubly robust estimator are guaranteed to cohere with a parametric specification for the dependence of the local average treatment effect on V. Extensions of the doubly robust methods that were proposed by Tan (2006a) and Uysal (2011) to the case V non-null do not have this property.

In Section 2 we introduce the notation, models and assumptions. We also review existing non-parametric and semiparametric methods for estimating local average treatment effects with instruments confounded by X. In Section 3 we describe the doubly robust estimating procedures proposed and discuss efficiency properties and estimation under incorrect specifications for the dependence of LATE or MLATE on V. In Section 4 we explain a surprising result that was earlier noted in the absence of covariates X by Clarke and Windmeijer (2010): inference under our models for the local average treatment effects is identical to inference under models proposed by Robins (1994) and Tan (2010) for a very different causal effect measure, namely the treatment effect on the treated. In Section 5 we reanalyse the data used in Póterba et al. (1995) and Abadie (2003) with the goal of estimating the causal effect of participating in 401(k) retirement programmes on savings by using eligibility for a 401(k) programme as a binary instrument. Section 6 concludes the paper.

2. Background and notation

Suppose that we observe a random sample of size n of the vector O = (Z, D, X, Y), where D is a binary variable denoting the presence (D = 1) or the absence (D = 0) of a treatment whose effect on the outcome Y we wish to investigate, X is a vector of baseline covariates and Z is a binary IV. Define D_z to be the potential treatment status that would be observed if Z were externally set to z, and define Y_dz to be the potential outcome that would be observed if D were externally set to d and Z to z, with d, z = 0, 1. Following Angrist et al. (1996), we say a subject is a complier if D₁ > D₀, an always-taker if D₁ = D₀ = 1, a never-taker if D₁ = D₀ = 0, and a defier if D₁ < D₀.

2.1. Assumptions and identification

Following Abadie (2003), Tan (2006a), Froelich (2007), and Uysal (2011), we make the following assumptions:

1. conditional unconfoundedness of the instrument, i.e. (Y₀₀, Y₀₁, Y₁₀, Y₁₁, D₀, D₁) is conditionally independent of Z given X;

2. exclusion of the instrument, i.e. P(Y_1d = Y_0d) = 1 for d ∈ {0, 1};

3. common support of the instrument, i.e. 0 < P(Z = 1|X) < 1 with probability 1;

4. instrumentation, i.e. P(D₁ = 1|V) ≠ P(D₀ = 1|V) with probability 1;

5. monotonicity, i.e. P(D₁ ⩾ D₀) = 1;

6. consistency, i.e. Y = DY₁ + (1 − D)Y₀ and D = ZD₁ + (1 − Z)D₀, where Y_d ≡ Y_1d = Y_0d by assumption (b).

When assumptions (a)–(d) and (f) hold, Z is said to be an IV for the effect of D on Y. Assumption (a) says that, within levels of X, Z is as good as randomly assigned. Assumption (b) postulates that the effect of Z on the outcome is entirely mediated by D. It implies that Y_dz is independent of z, and therefore we write Y_d throughout. Assumption (c) requires that there is a positive probability of receiving each instrument value within each level of X or, equivalently, that the support of X is the same among those with Z = 1 and Z = 0. Assumption (e) excludes the existence of defiers. Assumption (f) states that the observed outcome is equal to the potential outcome evaluated at the observed treatment value, and that the observed treatment is equal to the potential treatment evaluated at the observed instrument value. Finally, under assumption (e), assumption (d) is the same as P(D₁ = 1|V) > P(D₀ = 1|V) which, in turn, under (a) and (f) it is the same as P(D = 1|Z = 1, V) > P(D = 1|Z = 0, V). So it is tantamount to the assumption of positive correlation between Z and D. Abadie (2003) noted that assumptions (a)–(f) are conditional versions of the assumptions that were made by Angrist et al. (1996), and Vytlacil (2002) noted that they are equivalent to the assumptions imposed by a non-parametric selection model (Heckman, 1976) in which treatment is seen as an indicator of whether a latent index, e.g. expected treatment utility, has crossed a particular threshold.

Abadie (2003) showed that under assumptions (a)–(f) E(Y₁|D₁ > D₀, V) and E(Y₀|D₁ > D₀, V) are identified, and consequently so is

$$\text{LATE}(\mathbf{v})\equiv E(Y_1|D_1>D_0,\mathbf{V}=\mathbf{v})-E(Y_0|D_1>D_0,\mathbf{V}=\mathbf{v}).$$

Under the additional assumption

• (g)non-null complier mean under control, i.e. E (Y₀ | D₁ > D₀, V) ≠ 0 with probability 1, the contrast
  $$\text{MLATE}(\mathbf{v})\equiv E(Y_1|D_1>D_0,\mathbf{V}=\mathbf{v})/E(Y_0|D_1>D_0,\mathbf{V}=\mathbf{v})$$

  is well defined with probability 1 and is identified.

For conciseness, we shall refer to assumptions (a)–(f) if referring to inference about LATE(·) or (a)–(g) if referring to inference about MLATE(·) as the IV assumptions.

The curves LATE(v) and MLATE(v) describe how treatment effects in the complier subpopulation vary with values v of V, the first quantifying the effects on an additive scale and the second on a multiplicative scale. Theorem 1 of Tan (2006a) implies that under the IV assumptions LATE(v) is equal to the conditional version of the IV estimand,

$$\text{IV}(\mathbf{v})\equiv \frac{E\{E(Y|Z=1,\mathbf{X})-E(Y|Z=0,\mathbf{X})|\mathbf{V}=\mathbf{v}\}}{E\{E(D|Z=1,\mathbf{X})-E(D|Z=0,\mathbf{X})|\mathbf{V}=\mathbf{v}\}},$$ (1)

and MLATE(v) is

$$\text{MIV}(\mathbf{v})\equiv -\frac{E\{E(\mathit{\text{YD}}|Z=1,\mathbf{X})-E(\mathit{\text{YD}}|Z=0,\mathbf{X})|\mathbf{V}=\mathbf{v}\}}{E[E\{Y(1-D)|Z=1,\mathbf{X}\}-E\{Y(1-D)|Z=0,\mathbf{X}\left\}\right|\mathbf{V}=\mathbf{v}]}$$ (2)

(see also theorem 3.1 of Abadie, (2003)). The M in front of the functional MIV is a reminder that this functional identifies a multiplicative treatment effect. The functionals IV(·) and MIV(·) are the target of inference when, as we shall assume throughout, the IV assumptions are valid and interest is in estimation of LATE(·) and MLATE(·).

2.2. Review of existing estimators

The estimators that we shall propose in Section 3 can accommodate any setting in which V is a subset of X. Previous proposals for estimators of LATE have generally cosidered only the special cases in which V is null or V is equal to X; to our knowledge the case in which V is a strict, non-empty subset of X has not been addressed in the literature.

For the special case in which V is null, Froelich (2007) studied the asymptotic distribution theory of estimators of the IV functional that rely on two distinct non-parametric estimation methods for the four curves E(Y|Z = z, X = ·) and E(D|Z = z, X = ·), z = 0, 1, namely local polynomial regression and non-parametric series regression. His estimators, however, suffer from the curse of dimensionality. If the dimension of X is large, as will be so in many applications to render the unconfoundedness assumption plausible, the IV functional will not in general be estimable in moderately sized samples, essentially because no two units will have values of X that are sufficiently close to each other to allow for the borrowing of information that is needed for the smoothing implicit in these methods. Again, for the special case in which V is null, Tan (2006a) considered estimating the IV functional under parametric models for each of the conditional means E(Y|D = d, Z = z, X = ·) and E(D|Z = z, X = ·), d, z = 0, 1. The consistency of the estimator of the IV functional then hinges on the correct specification of both of these models. See Section 3 for a contrast between these models and the models that must be specified to carry out the doubly robust estimation approach that is proposed in this paper.

Neither Froelich (2007) nor Tan (2006a) addressed the case when V is a non-empty, strict subset of X, but further difficulties arise for each of their strategies in this case. Extending Froelich's approach to estimate the functionals IV(V) and MIV(V) non-parametrically not only requires smooth estimators of the aforementioned conditional means, but also of the conditional means given V of the differences that are involved in the numerators and denominators of these functionals. One possible extension of Tan's (2006a) fully parametric approach along the lines proposed there for the case X = V, would also require specifying parametric models for the conditional means given V in the numerator and denominator of the IV(V) functional. As noted by Abadie (2003), this approach will generally produce parametric specifications for the LATE(·) and MLATE(·) curves that are difficult to interpret. For example, linear specifications for each of the four conditional-on-V mean functions involved in the IV(V) functional do not imply a linear model for LATE(V). An alternative strategy that avoids this particular difficulty would be to use the approach of Tan (2010); however that approach involves specifying working models that may not cohere with the assumed model for LATE(·).

For the special case in which V is null, and with the goal of reducing sensitivity to model misspecification, Tan (2006a) and Uysal (2011) described doubly robust estimators of the IV functional whose consistency depends on correct parametric specification either of the instrument propensity score or, in the case of Uysal, of E(Y|Z = z, X = ·) and E(D|Z = z, X = ·), z = 0, 1, and, in the case of Tan, of E(Y|D = d, Z = z, X = ·) and E(D|Z = z, X = ·), d, z = 0, 1.

The special case of V = X was considered by Abadie (2003), Tan (2006a), Hirano et al. (2000), and Little and Yau (1998). Tan's (2006a) estimator of LATE(X) again requires parametric specifications of the four conditional expectations that are involved in the IV(X) functional, which results in a specification of LATE(X) that may be difficult to interpret. Hirano et al. (2000) and Little and Yau (1998) specified fully parametric likelihood functions for the observed data and unobserved compliance types (complier, defier, always-taker, never-taker) and used Bayesian methods to estimate the posterior distribution of Y conditionally on compliance type, treatment and instrument. Abadie (2003) proposed an estimating procedure in which models for E(Y_d|D₁ > D₀, X = ·), d = 0, 1 ensure that the resulting model for LATE(X) is easily interpretable. His method hinges on consistent estimation of the instrument propensity score P(Z = 1|X = ·). Abadie considered estimation of the propensity score under a parametric model as well as by nonparametric power series methods. When X is high dimensional and the sample size is moderate, non-parametric propensity score estimation yields poorly behaved estimators of parametric specifications of E(Y_d|D₁ > D₀, X = ·), d = 0, 1 owing to the curse of dimensionality.

3. New methods

In this section we describe estimation of the parameters indexing the following parsimonious models for LATE(V) and MLATE(V):

$$\text{LATE}(\mathbf{v})\in {ℱ}_1=\{m_1(\mathbf{v};\beta ):\beta \in B\subset R^p\}$$ (3)

and

$$\text{MLATE}(\mathbf{v})\in {ℱ}_2=\{m_2(\mathbf{v};\beta ):\beta \in B\subset R^p\}$$ (4)

for specified functions m_j (·, ·) smooth in β, j = 1, 2. For inference under model (ℱ₁ we assume that Y has unbounded support and for inference under model (ℱ₂ we assume that Y has support equal to the non-negative real line or the non-negative integers.

For the special case in which V = X, Abadie (2003) also considered estimation of LATE(X) under a parametric specification for the curve. However, his approach estimates LATE(X) as the difference of the estimators of the means E(Y_d|D₁ > D₀, X), d = 0, 1, under separate parametric models for each of them. We prefer to estimate LATE(X) under a model that parameterizes just this contrast rather than under separate models for each of the counterfactual means to reduce the opportunities of model misspecification.

For estimation of LATE and MLATE, i.e. when V is null, the doubly robust estimators that we describe in this section, like the doubly robust estimators that were proposed by Tan (2006a) and Uysal (2011), are consistent under a correct parametric specification of the propensity score curve P(Z = 1|X = ·). Like the estimators of Tan and Uysal, our estimators remain consistent even under incorrect specification of the propensity score curve provided another set of curves is correctly parameterized. Tan's approach requires modeling E(Y|Z = ·, D = ·, X = ·,) and E(D|Z = ·, X = ·), and Uysal's approach requires modeling E(Y|Z = ·, X = ·) and E(D|Z = ·, X = ·). Our approach, by contrast, requires modeling the conditional mean E{φ(X)|V = ·} of a user-specified function φ (X) (if V ≠ X) and the conditional expectation E(H_j|Z = ·, X= ·) (j = 1 if inference is about LATE and j = 2 if is about MLATE), where

$$H_1\equiv Y-D\text{IV}(\mathbf{V})$$

and

$$H_2\equiv Y\text{MIV}{(\mathbf{V})}^{-D}.$$

The issue of which curves must be modeled in the doubly robust procedure, i.e. those in Tan (2007), Uysal (2011) or our proposal, is inconsequential when V is null. However, it is an important issue if V is non-empty. As shown in the supplementary Web appendix, when Y has unbounded support, E{φ(X)|V = ·}, E(H₁|Z = ·, X = ·) and P(Z = 1|X = ·) are variation independent with IV(·) and, when Y has support equal to [0, ∞) or the non-negative integers, E{φ(X)|V = ·}, E(H₂|Z = ·, X = ·) and P(Z = 1|X = ·) are variation independent with MIV(·). Therefore, our doubly robust procedure offers two genuine independent opportunities to produce consistent estimators of parametric specifications for LATE(·) or MLATE(·), as neither the models for E{φ(X)|V = ·} and E(H₁|Z = ·, X = ·) nor the model for P(Z = 1|X = ·) can conflict with parametric specifications of IV(V = ·) and neither the models for E{φ(X)|V = ·} and E(H₂|Z = ·, X = ·) nor the model for P(Z = 1|X = ·) can conflict with parametric specifications of MIV(V = ·). Essentially, the variation independence of H₁ and H₂ respectively with IV(·) and MIV(·) is a consequence of the fact that the restrictions imposed on the law of H₁ and H₂ by the IV assumptions do not depend on the functional form of IV(·) and MIV(·)respectively. In contrast, restrictions on E(Y|Z = ·, X = ·) and E(D|Z = ·, X = ·) or on E(Y|Z = ·, D = ·, X = ·) and E(D|Z = ·, X = ·) impose restrictions on IV(·) and therefore may conflict with parametric specifications for it. One could reasonably argue that this conflict is of no great importance for practice because all models are almost certainly misspecified to a larger or smaller extent. Furthermore, it may be easier to build and check models for E(Y|Z = ·, D = ·, X = ·) and E(D|Z = ·, X = ·) than models for E(H_j|Z = ·, X = ·). Although we do not disagree with these points, we nevertheless find it conceptually important to demonstrate that there is methodology that, under the assumptions stated, is internally consistent.

3.1. Estimation of LATE(·) and MLATE(·) under models for the propensity score or outcome regression

The following theorem gives two key expressions for the moment restrictions that are satisfied by the functionals IV(V) and MIV(V) on which our proposed estimators rely.

Theorem 1. For j ∈ {1, 2}, if the denominators of IV(V) and MIV(V) are non-zero with probability 1, then

$$E\{E(H_j|Z=1,\mathbf{X})-E(H_j|Z=0,\mathbf{X})|\mathbf{V}\}=0\text{with probability}1$$ (5)

and

$$E\{{(-1)}^{1-Z}p{(Z|\mathbf{X})}^{-1}{H}_j|\mathbf{V}\}=0\text{with probability}1,$$ (6)

where p(Z|X) ≡ P(Z = 1|X)^Z {1 − P(Z = 1|X) }^{1 −Z}.

Proof. Equation (5) with j = 1 follows by algebra from the definition (1) and with j = 2 it follows from the definition (2). Specifically, to arrive at result (5) from definition (1) when j = 1 note that the difference between the numerator on the right-hand side of definition (1) and the product of IV(v) with the denominator on the right-hand side of definition (1) is the same as the left-hand side of result (5). Likewise, to arrive at result (5) from (2) when j = 2 note that the sum of the denominator on the right-hand side of definition (2) with the product of the numerator on the right-hand side of definition (2) times MIV(v)⁻¹ is the same as the left-hand side of equation (5). Equation (6) is equivalent to equation (5) because

$$E\{{(-1)}^{1-Z}p{(Z|\mathbf{X})}^{-1}{H}_j|\mathbf{V}\}=E[\{\mathit{\text{Z p}}{(Z|\mathbf{X})}^{-1}-(1-Z)p{(Z|\mathbf{X})}^{-1}\}{H}_j|\mathbf{V}],E\{\mathit{\text{Z p}}{(Z|\mathbf{X})}^{-1}{H}_j|\mathbf{V}\}=E\{E(H_j|Z=1,\mathbf{X})|\mathbf{V}\}$$

and

$$E\{(1-Z)p{(Z|\mathbf{X})}^{-1}{H}_j|\mathbf{V}\}=E\{E(H_j|Z=0,\mathbf{X})|\mathbf{V}\}.$$

Theorem 1 suggests that well-behaved estimators of β can be obtained under parametric specifications of either P(Z = 1 |X) or E (H_j|Z, X) where throughout we assume j = 1 if β indexes the parametric specification (3) for LATE(V) and j = 2 if β indexes the specification (4) for MLATE(V). We now describe such estimators.

Define

$$H_1(\beta )\equiv Y-D{m}_1(\mathbf{V};\beta )$$

and

$$H_2(\beta )\equiv Y{m}_2{(\mathbf{V};\beta )}^{-D}$$

where m₁ (V; β) and m₂ (V; β) are the parametric specifications for LATE(v) defined in equation (3) and for MLATE(v) defined in equation (4) respectively. Throughout we let β₀ denote the true the value of β under the given specification (3) or (4).

A consistent and asymptotically normal estimator β̂_ipw of β₀ under a parametric class for the instrument probabilities

$$P(Z=1|\mathbf{X}=\mathbf{x})\equiv \pi (\mathbf{x})\in P=\{\pi (\mathbf{x};\alpha ):\alpha \in \mathbb{A}\subset R^d\}$$ (7)

where π(·; ·) is a specified function that is smooth in α and 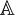is a specified subset of R^d, is computed as the solution of

$$E_n\{q(\mathbf{V};\beta ){(-1)}^{1-Z}p{(Z|\mathbf{X};\widehat{\alpha })}^{-1}{H}_j(\beta )\}=0$$ (8)

where p(Z|X; α) ≡ π(X; α)^Z {1 − π(X; α)}^{1 − Z},q(V; β) is a user specified p × 1 vector-valued function (e.g. q(V; β) = ∂m_j (V; β) /∂β), and

$$\widehat{\alpha }=arg\underset{\alpha }{max}{E}_n(log[\pi {(\mathbf{X};\alpha )}^Z{\{1-\pi (\mathbf{X};\alpha )\}}^{1-Z}])$$ (9)

is the maximum likelihood estimator of α. Throughout E_n(·) stands for the empirical mean operator. Identity (6) implies that under the IV assumptions, under the parametric specification (3), and with j = 1 in display (5), √n(β̂_ipw − β₀) converges in law to a mean 0 normal distribution when condition (7) and regularity conditions hold and, in addition, for some σ and z = 0, 1, P(Z = z|X; α) > σ > 0. The same holds under the parametric specification (4) and with j = 2 in display (5).

Alternatively, one can compute a consistent and asymptotically normal estimator β₀ under a parametric class for E(H_j | Z, X) that respects the constraint (5). To aid the specification of such a parametric class, we re-express the constraint (5) as the condition that, for some r(X),

$$E(H_j|Z=1,\mathbf{X})-E(H_j|Z=0,\mathbf{X})=r(\mathbf{X})-E\{r(\mathbf{X})|\mathbf{V}\}.$$

When V ≠ X we derive a flexible parametric specification for E(H_j | Z, X) that respects constraint (5) from the following three specifications:

1. a linear parametric specification for r(X),

   $$r(\mathbf{X})\in \mathcal{R}=\{{\rho }^T\phi (\mathbf{X}):\rho \in R^K\}$$ (10)

   where φ (X) ≡ (φ₁ (X), …, φ_K (X))^T and φ_s, s ∈ {1, …, K}, are user-specified real-valued functions,

2. a linear model for the mean of φ(X) given V,

   $$E\{\phi (\mathbf{X})|\mathbf{V}\}\in \mathcal{M}=\{\varphi (\mathbf{V};\mathrm{\gamma }):\mathrm{\gamma }\in \mathrm{\Gamma }\}$$ (11)

   where ϕ (V; γ) ≡ (ϕ₁ (V; γ), …, ϕ_K(V; γ))^T, Γ is a subset of a Euclidean space and φ_k, k ∈ {1, …, K}, are user-specified real-valued functions (when V is null we set ϕ(V; γ) = γ, thus leaving ℳ unrestricted) and

3. a parametric specification for E(H_j| Z = 0, X), i.e.

   $$E(H_j|Z=0,\mathbf{X})\in \mathcal{K}=\{k(\mathbf{X};\nu ):\nu \in \Upsilon \}$$ (12)

   where k (·; ·) is a specified function smooth in ν and ϒ is a subset of a Euclidean space.

Specifications (10)–(12) imply the following model respects the constraint (5):

$$E(H_j|Z=z,\mathbf{X}=\mathbf{x})\in \mathcal{H}=\{h(z,\mathbf{x};\eta ,\mathrm{\gamma }):\eta \in R^K\times \Upsilon ,\mathrm{\gamma }\in \mathrm{\Gamma }\}$$ (13)

where η ≡ (ρ, ν) and h (z, x; η, γ) = k (x; ν) + ρ^T {φ(x) − ϕ(v; γ)} z.

When V = X, we ignore specification (11) and replace specification (13) with

$$E(H_j|Z=z,\mathbf{X}=\mathbf{x})\in \mathcal{H}=\{h(\mathbf{X};\eta ):\eta \in \Upsilon \}$$ (14)

where h(·; ·) is a specified function that is smooth in η and ϒ is a subset of a Euclidean space. This specification also respects the constraint (5) because when V = X this constraint is the same as the condition that E(H_j |Z, X = x) does not depend on Z.

An estimator β̂_reg that is consistent and asymptotically normal for β₀ under specifications (11) and (13) when V ≠ X or specification (14) when V = X can be computed as the first component of the vector (β̂_reg, η̂) solving

$$E_n\{l(Z,\mathbf{X};\beta ,\eta ,\widehat{\mathrm{\gamma }}){\varepsilon }_j(\beta ,\eta ,\widehat{\mathrm{\gamma }})\}=0$$ (15)

where l(·, ·; ·, ·, ·) is a user-specified vector-valued function of the same dimension as (β, η),

$${\varepsilon }_j(\beta ,\eta ,\mathrm{\gamma })\equiv H_j(\beta )-h(Z,\mathbf{X};\eta ,\mathrm{\gamma })$$

and γ̂ solves E_n[{ ∂ϕ(V; γ)^T/∂γ} {φ(X) − ϕ(V; γ)}] = 0 if V ≠ X, ε_j(β, η, γ) ≡ H_j(β) − h(X; η) if V = X. One practical choice of l(Z, X; β, η, γ̂) is

$$l(Z,\mathbf{X};\beta ,\eta ,\mathrm{\gamma })=\left(\begin{array}{c}{l}_{\eta }(Z,\mathbf{X};\eta ,\mathrm{\gamma })\\ l_{\beta }(Z,\mathbf{X};\beta )\end{array}\right)=\left(\begin{array}{c}\partial h(Z,\mathbf{X};\eta ,\mathrm{\gamma })/\partial \eta \\ Z\partial m(\mathbf{V};\beta )/\partial \beta \end{array}\right).$$ (16)

Under specifications (11) and (13) when V ≠ X or specification (14) when V = X, the IV assumptions and the parametric specification (3) if j = 1 or specification (4) if j = 2, E{ε_j (β₀, η₀, γ₀)|Z, X} = 0 where (η₀, γ₀) are the true values of (η, γ), so √n(β̂_reg − β₀) converges in law to a mean 0 normal distribution provided standard regularity conditions for convergence of M-estimators hold.

Selection of the parametric class for E(H_j|Z, X) can be aided with the following α-level score type test of the null hypothesis ℍ₀ : η₂ = 0 where $\eta ={({\eta }_1^{\mathrm{T}},{\eta }_2^{\mathrm{T}})}^{\mathrm{T}}$ and η₂ is of dimension, say, d₂. Let

$$R_n=E_n[\{\partial h({\stackrel{\sim }{\beta }}_{\text{reg}},{\stackrel{\sim }{\eta }}_1,{\eta }_2,\widehat{\mathrm{\gamma }})/\partial {\eta }_2{|}_{{\eta }_2=0}\}{\varepsilon }_j({\stackrel{\sim }{\beta }}_{\text{reg}},{\stackrel{\sim }{\eta }}_1,0,\widehat{\mathrm{\gamma }})]$$

where (β̃_reg, η̃₁) solves

$$E_n\{{[\partial h(Z,\mathbf{X};{\eta }_1,0,\widehat{\mathrm{\gamma }})/\partial {\eta }_1^{\mathrm{T}},l_{\beta }{(Z,\mathbf{X};\beta )}^{\mathrm{T}}]}^{\mathrm{T}}{\varepsilon }_j(\beta ,{\eta }_1,0,\widehat{\mathrm{\gamma }})\}=0.$$

Under ℍ₀, √nR_n converges in law to a mean 0 d₂-variate normal distribution with variance–covariance matrix, say, J. Thus, if Ĵ is a consistent estimator of J, a test that rejects ℍ₀ when $R_n^{\mathrm{T}}$ Ĵ R_n > χ_{1 −α,d2} where χ_{1 −α,d2} is the (1 − α)-quantile of a χ²-distribution with d₂ degrees of freedom is an asymptotic α-level test of ℍ₀. A consistent variance estimator Ĵ can be derived from standard Taylor expansion arguments for M-estimators (Stefanski and Boos, 2002).

3.2. Doubly robust estimation of LATE (·) and MLATE (·)

In this section we derive a doubly robust estimator β̂_dr of β which satisfies that √n(β̂_dr − β₀) converges to a mean 0 normal distribution under the IV assumptions and regularity conditions provided that one of the following two conditions (a) or (b) holds, even if both do not hold simultaneously:

1. specifications (11) and (13) are correct when V ≠ X, or specification (14) is correct when V = X,

2. specification (7) is correct.

The estimator β̂_dr solves the estimating equations

$$E_n(q(\mathbf{V};\beta ){(-1)}^{1-Z}p{(Z|\mathbf{X};\widehat{\alpha })}^{-1}[H_j(\beta )-a\{\mathbf{X};\widehat{\alpha },\widehat{\eta }(\beta ),\widehat{\gamma }\}])=0$$ (17)

where, for each fixed β, η̂(β) solves E_n{l_η (Z, X; β, η, γ̂) ε_j (β, η, γ̂)} = 0 with l_η defined as in equation (16) and

$$a(\mathbf{X};\alpha ,\eta ,\gamma )\equiv \{1-\pi (\mathbf{X};\alpha )\}h(1,\mathbf{X};\eta ,\gamma )+\pi (\mathbf{X};\alpha )h(0,\mathbf{X};\eta ,\gamma )$$

if V ≠ X or a(X; α, η, γ) ≡ h(X; η) if V = X.

The estimator β̂_dr is consistent for β₀ when (b) holds because

$$E\{q(\mathbf{V};\beta ){(-1)}^{1-Z}p{(Z|\mathbf{X};{\alpha }_0)}^{-1}a(\mathbf{X};\alpha ,\eta ,\gamma )\}=0$$

for all β since E{(−1)^1−Z p(Z|X; α₀)|X} = 0.

In contrast, consistency when condition (a) holds can be seen after re-expressing equation (17) as

$$E_n\left[q(\mathbf{V};\beta )\frac{{(-1)}^{1-Z}}{p(Z|\mathbf{X};\widehat{\alpha })}{\varepsilon }_j\{\beta ,\widehat{\eta }(\beta ),\widehat{\gamma }\}\right]+E_n(q(\mathbf{V};\beta )[h\{1,\mathbf{X};\widehat{\eta }(\beta ),\widehat{\gamma }\}-h\{0,\mathbf{X};\widehat{\eta }(\beta ),\widehat{\gamma }\}])=0$$

and noting that, by virtue of equality (5) of theorem 1, E[q(V; β){h(1, X; η₀, γ₀) − h(0, X; η₀, γ₀)}] = 0 and, by E{ε_j(β, η₀, γ₀)|Z, X} = 0, E{b(Z, X) ε_j(β, η₀, γ₀)} = 0 for all b(Z, X) and, in particular, for b(Z, X) = q(V; β)(−1)^1−Z p(Z|X; α)⁻¹ with arbitrary α.

The convergence of √n(β̂_dr − β₀) to a normal distribution follows after noticing that (β̂_dr, η̂, γ̂, α̂) where η̂ ≡ η̂(β̂_dr) is an M-estimator, i.e. it solves a joint system of estimating equations. The accuracy of this asymptotic result in finite samples hinges on the strength of the instrument Z, i.e. on how close Δ(V) = E{E(D|Z = 1, X) − E(D|Z = 0, X)|V} is to 0. Theoretical results exploring the asymptotic distribution of β̂_dr as Δ(V) shrinks to 0 at different rates with sample size, similarly to those in the conventional IV literature, should be explored but are beyond the scope of this paper.

The asymptotic variance of β̂_dr can be consistently estimated with the standard empirical sandwich variance estimator (Stefanski and Boos, 2002) or with the non-parametric bootstrap (Gill, 1989).

In the special case of estimation of β₀ ≡ LATE, i.e. when V is null, we have that H₁(β) = Y − βD and our doubly robust estimator is similar to that in Tan (2006a) and that in Uysal (2011), except that they replaced h{Z, X; η̂(β), γ̂} with Ê(Y|Z, X) − βÊ(D|Z, X). Tan computed estimators Ê(Y|Z, X) and Ê(D|Z, X) under parametric models for E(Y|D = d, Z = z, X = ·) and E(D|Z = z, X = ·), d, z = 0, 1 whereas Uysal (2011) computed them under parametric models for E(Y|Z = z, X = ·) and E(D|Z = z, X = ·), z = 0, 1.

3.3. Local efficiency under correct parametric specification of the propensity score model

In addition to β̂_ipw and β̂_dr, there are other consistent and asymptotically normal estimators of β₀ under the propensity score specification (7) and the IV assumptions. Specifically, given a user-specified p × 1 function s(x; β), consider the estimator β̂_S solving

$$E_n[q(\mathbf{V};\beta ){(-1)}^{1-Z}p{(Z|\mathbf{X};\widehat{\alpha })}^{-1}\{H_j(\beta )-s(\mathbf{X})\}]=0.$$

Because E{q(V; β)(−1)^1−Z p(Z|X)⁻¹ s(X)} = 0 it follows that under regularity conditions, when condition (7) holds, √n(β̂_s − β₀) converges to a mean 0 normal distribution with variance Σ_q,s, where Σ_q,s depends on q(·) and on s(·). Invoking the theory of inverse-probability-weighted (IPW) estimation in Robins and Rotnitzky (1992), in the supplementary Web appendix we show that for each fixed q(·) the optimal choice s_opt,j(X), in the sense that Σ_q,s − Σ_q,sopt,j ⩾ 0 (i.e. semipositive definite), is given by

$$s_{\text{opt},j}(\mathbf{X})=\{1-\pi (\mathbf{X})\}E(H_j|Z=1,\mathbf{X})+\pi (\mathbf{X})E(H_j|Z=0,\mathbf{X}).$$

In the supplementary Web appendix we also show that, when the specifications (11), (13) and (7) hold if V is not equal to X or when the specifications (14) and (7) hold if V = X, the limiting distribution of √n(β̂_dr − β₀) has variance precisely equal to the bound Σ_q,sopt,j. The estimator β̂_dr, however, may have asymptotic variance even larger than that of β̂_ipw if specification (11) and/or (13) is incorrect when V ≠ X or if specification (14) is incorrect when V = X. Using ideas similar to those in Tan (2006b, 2010) we can construct another doubly robust estimator β̃_dr that remedies this flaw. The estimator β̃_dr is computed by solving

$$E_n({(-1)}^{1-Z}p{(Z|\mathbf{X};\widehat{\alpha })}^{-1}[H_j(\beta )\mathit{\text{Id}}-a\{\mathbf{X};\widehat{\alpha },\widehat{\eta }(\beta ),\widehat{\gamma }\}\widehat{C}{(\beta )}^{\mathrm{T}}]q(\mathbf{V};\beta ))=0,$$ (18)

where Id is the p × p identity matrix and Ĉ(β) is the p × p matrix formed by the first p columns of the p × (p + d) matrix

$$E_n\{{(-1)}^{1-Z}p{(Z|\mathbf{X};\widehat{\alpha })}^{-1}{H}_j(\beta )q(\mathbf{V};\beta )K(\beta )\}\times E_n{\left\{\right(\begin{array}{c}q(\mathbf{V};\beta ){(-1)}^{1-Z}p{(Z|\mathbf{X};\widehat{\alpha })}^{-1}h\{Z,\mathbf{X};\widehat{\eta }(\beta ),\widehat{\gamma }\}\\ \partial log\{p(Z|\mathbf{X};\alpha )\}/\partial \alpha {|}_{\alpha =\widehat{\alpha }}\end{array})K(\beta )\}}^{-1}$$

with

$$K(\beta )=\{q{(\mathbf{V};\beta )}^{\mathrm{T}}{(-1)}^{1-Z}p{(Z|\mathbf{X};\widehat{\alpha })}^{-1}a\{\mathbf{X};\widehat{\alpha },\widehat{\eta }(\beta ),\widehat{\gamma }\},\partial log\{p(Z|\mathbf{X};\alpha )\}/\partial {\alpha }^{\mathrm{T}}{|}_{\alpha =\widehat{\alpha }}\}.$$

Like β̂_dr, the estimator β̃_dr is doubly robust and has asymptotic variance equal to Σ_q,sopt,j when specifications (11), (13) and (7) are correct (specifications (14) and (7) are correct if V = X), but unlike β̂_dr, it is guaranteed to be the most efficient estimator, asymptotically, among the class of estimators solving equations of the form (18) with Ĉ(β) replaced by an arbitrary p × p constant matrix C. In particular, letting C = 0 we conclude that under model (7), β̃_dr is never less efficient asymptotically than β̂_ipw. See the supplementary Web appendix for a sketch of the proof of the asymptotic properties of β̃_dr.

A further result, which is derived in the supplementary Web appendix, establishes that for j ∈ {1, 2} the optimal function q_opt,j(·), in the sense that Σ_q,sopt,j − Σ_{qopt,j,sopt,j} ⩾ 0 for any q (·), is

$$q_{\text{opt},j}(\mathbf{V};\beta )=\{\partial m_j(\mathbf{V};\beta )/\partial \beta \}{c}_j(\mathbf{V};\beta )$$

where

$$c_j(\mathbf{V};\beta )=-m_j{(\mathbf{V};\beta )}^{2(1-j)}E\{{(-1)}^{1-Z}p{(Z|\mathbf{X})}^{-1}{\mathit{\text{DY}}}^{j-1}|\mathbf{V}\}\times E{[p{(Z|\mathbf{X})}^{-2}{\{H_j-s_{\text{opt},j}(\mathbf{X})\}}^2|\mathbf{V}]}^{-1}.$$

The optimal function q_opt,j(·) depends on the unknown observed data distribution and hence it is not available for data analysis. However, we can estimate it under working parametric specifications for its unknown constituents,

$$E\{{(-1)}^{1-Z}p{(Z|\mathbf{X})}^{-1}{\mathit{\text{DY}}}^{j-1}|\mathbf{V}\}\in {\varepsilon }_j=\{e_j(\mathbf{V};\delta ):\delta \in \Delta \}$$ (19)

and

$$E[p{(Z|\mathbf{X})}^{-2}{\{H_j-s_{\text{opt},j}(\mathbf{X})\}}^2|\mathbf{V}]\in {\mathcal{T}}_j=\{t_j(\mathbf{V};\omega ):\omega \in \mathrm{\Omega }\}$$ (20)

where e_j (·; ·) and t_j (·) are smooth functions and Δ and Ω are included in Euclidean spaces. To do so we estimate δ and ω with the weighted least squares estimators δ̂ and ω̂ by regressing (−1)^1−Z p(Z|X; α̂)⁻¹ DY^j−1 and p(Z|X; α̂)⁻²[H_j(β̂_dr) − a{X;α̂, η̂(β̂_dr), γ̂}]² on V under models (19) and (20) respectively, where β̂_dr is a preliminary doubly robust estimator of β computed using an arbitrary q(V; β). We then estimate q_opt,j(V; β) with

$${\widehat{q}}_{\text{opt},j}(\mathbf{V};\beta )\equiv -\{\partial m(\mathbf{V};\beta )/\partial \beta \}{m}_j{(\mathbf{V};\beta )}^{2(1-j)}{e}_j(\mathbf{V};\widehat{\delta })t_j{(\mathbf{V};\widehat{\omega })}^{-1}.$$

When specification (7) is correct and P(Z = z|X) > σ > 0 for z = 0 or z = 1, the estimators β̂_dr and β̃_dr that use q̂_opt,j(V; β) for q(V; β) and the estimator β̃_C that solves equation (18) with Ĉ(β) replaced by an arbitrary p × p constant matrix C and with q̂_opt,j(V; β) instead of q(V; β) satisfy under regularity conditions

1. √n(β̂_dr − β₀), √n(β̃_dr − β₀) and √n(β̃_C − β₀) converge to mean 0 normal distributions with variances Σ_dr, Σ_better.dr and Σ_C respectively. Furthermore, Σ_better.dr − Σ_C ≤ 0 and Σ_better.dr − Σ_dr ≤ 0.

2. If, additionally, the specifications (11) and (13) are correct when V ≠ X, or specification (14) is correct when V = X, then Σ_dr = Σ_better.dr = Σ_{qopt,j,sopt,j} .

3.4. Estimation of least squares approximations under incorrect specifications of local average treatment effect curves

A slight modification of the procedure for computing β̂_dr and β̃_dr yields estimators that are doubly robust for least squares approximations of the true local average treatment effect curves when the parametric specifications for these curves are incorrect.

Given a real-valued function w(v), the w-weighted least squares approximation of the LATE(·) curve is

$${\beta }_{w,0}\equiv arg\underset{\beta }{min}E[w(\mathbf{V}){\{\text{LATE}(\mathbf{V})-m_1(\mathbf{V};\beta )\}}^2|D_1>D_0].$$ (21)

In the supplementary Web appendix we show that, under the IV conditions, β_w,0 satisfies

$$E\{q_w(\mathbf{V}){(-1)}^{1-Z}p{(Z|\mathbf{X})}^{-1}{H}_1({\beta }_{w,0})\}=0$$ (22)

where q_w(V) ≡ w(V) ∂m₁(V;β)/∂β|_β=βw,0. Arguing as in section 3.2, we conclude that, when condition (b) of Section 3.2 holds (i.e. when the propensity score specification (7) is correct), the estimators β̂_dr and β̃_dr that use q(V; β) = q_w(V; β) ≡ w(V)∂m₁(V; β)/∂β converge in probability to β_w,0 even if the specification (3) is incorrect.

However, unfortunately, β̂_dr and β̃_dr need not converge to β_w,0 for any w when the propensity score model is incorrect even if condition (a) of Section 3.2 holds. This happens essentially because equation (22) is equivalent to

$$E(q_w(\mathbf{V})[E\{H_1({\beta }_{w,0})|Z=1,\mathbf{X}\}-E\{H_1({\beta }_{w,0})|Z=0,\mathbf{X}\}])=0,$$ (23)

which involves E{H₁(β_w,0)|Z, X} but not E(H₁|Z, X). Nevertheless, the equality (23) suggests that consistent and asymptotically normal estimators of β_w,0 under parametric models for E{H₁(β_w,0)|Z, X} should exist. However, some care must be taken in formulating such models. For instance, one cannot postulate that E{H₁(β_w,0)|Z, X} ∈ ℋ where ℋ is defined in specification (13) with j = 1 since this specification is necessarily wrong if the model (11) is correct. This happens because ℋ respects the constraint (5) but E {H₁(β_w,0)|Z, X} does not, since of all random variables of the form H₁(m) = Y − m(V)D for any m(V), only H₁ = Y − IV(V)D satisfies the constraint (5) as this constraint identifies the IV(·) curve.

A slight modification to the class ℋ yields a new class that respects the constraint (23) but not necessarily the stronger constraint

$$E([E\{H_1({\beta }_{w,0})|Z=1,\mathbf{X}\}-E\{H_1({\beta }_w,0)|Z=0,\mathbf{X}\}]|\mathbf{V})=0$$

and thus gives the opportunity of formulate a correctly specified model for E{H₁(β_w,0)|Z, X}. Specifically, the parametric specification

$$E\{H_1({\beta }_{w,0})|Z=z,\mathbf{X}=\mathbf{x}\}\in {\mathcal{H}}_w=\{k(\mathbf{x};\nu )+{\lambda }^{\mathrm{T}}\{\phi (\mathbf{x})-\theta q_w(\mathbf{v})\}z:\lambda \in R^K,\nu \in \Upsilon ]$$ (24)

where φ(·) and k(·; ·) are user-chosen functions as defined in Section 3.1 and

$$\theta =E\{\phi (\mathbf{X})q_w{(\mathbf{V})}^{\mathrm{T}}\}E{\{q_w(\mathbf{V})q_w{(\mathbf{V})}^{\mathrm{T}}\}}^{-1}$$ (25)

necessarily respects constraint (23) but not the aforementioned stronger constraint.

A modification in the computation of β̂_dr yields a new estimator β̂̂_dr, which is described below, that satisfies for a given, user-specified, weight function w(·) the following two conditions:

1. √n(β̂̂_dr − β₀) converges to a normal distribution if the parametric specification (3) for LATE(·) is correct and either condition (a) or condition (b) of Section 3.2 holds, and

2. √n(β̂̂_dr − β_w,0) converges to a normal distribution if the parametric specification (3) for LATE(·) is incorrect but either condition (b) of Section 3.2 or the parametric specification (24) holds.

Consider first the case V ≠ X. The estimator β̂̂_dr solves equation (17) with q_w(V; β) instead of q(V; β), and with a{X; α̂, η̂(β), γ̂} replaced by

$$b(\mathbf{X};\alpha ,\eta ,\gamma ,\theta )\equiv \{1-\pi (\mathbf{X};\alpha )\}{h}_w(1,\mathbf{X};\beta ,\eta ,\gamma ,\theta )+\pi (\mathbf{X};\alpha )h_w(0,\mathbf{X};\beta ,\eta ,\gamma ,\theta ),$$

where η = (ν, ρ, λ),

$$h_w(z,\mathbf{x};\beta ,\eta ,\gamma ,\theta )\equiv k(\mathbf{x};\nu )+{\rho }^{\mathrm{T}}\{\phi (\mathbf{x})-\phi (\mathbf{v};\gamma )\}z+{\lambda }^{\mathrm{T}}\{\phi (\mathbf{x})-\theta q_w(\mathbf{v};\beta )\}z,$$ (26)

η̂(β) solves

$$E_n([\partial h_w\{Z,\mathbf{X};\beta ,\eta ,\widehat{\gamma },\widehat{\theta }(\beta )\}/\partial \eta ]){\varepsilon }_w\{\beta ,\eta ,\widehat{\gamma },\widehat{\theta }(\beta \})=0$$

with

$${\varepsilon }_w(\beta ,\eta ,\mathrm{\gamma },\theta )\equiv H_1(\beta )-h_w(z,\mathbf{x};\beta ,\eta ,\gamma ,\theta ),$$

γ̂ solves

$$E_n[\{\partial \varphi {(\mathbf{V};\gamma )}^{\mathrm{T}}/\partial \gamma \}\{\varphi (\mathbf{X})-\varphi (\mathbf{V};\gamma )\}]=0$$

and

$$\widehat{\theta }(\beta )\equiv E_n\{\phi (\mathbf{X})q_w{(\mathbf{V})}^{\mathrm{T}}\}{E}_n{\{q_w(\mathbf{V})q_w{(\mathbf{V})}^{\mathrm{T}}\}}^{-1}.$$

When V = X, β̂̂_dr is computed analogously except that ρ is set to 0 and γ is absent.

The desired properties (a) and (b) of the estimator β̂̂_dr are deduced from the following considerations. When condition (b) holds, the estimator β̂̂_dr is consistent and asymptotically normal for β_w,0 regardless of whether or not specification (3) holds because E_n[q_w(V; β)(−1)^1−Z × p(Z|X; α̂)⁻¹ b{X; β, α̂, η̂(β), γ̂, θ̂(β)}] converges to 0 in probability for all β. In contrast, the convergence of β̂̂_dr to β₀ when specification (3) and condition (a) hold, and the convergence of β̂̂_dr to β_w,0 when specification (3) is incorrect but condition (24) holds follows arguing as in Section 3.2 for the convergence of β̂_dr to β₀ when condition (a) holds, after noting that the class

$${\mathcal{H}}^{e\mathbf{x}t}\equiv \{h_w(z,\mathbf{x};\beta ,\eta ,\gamma ,\theta ):\rho \in R^K,\lambda \in R^K,\beta \in R^p,\gamma \in \Gamma \}$$

with θ defined as in equation (25) includes both the class ℋ (corresponding to λ = 0) and the class ℋ_w (corresponding to ρ = 0).

An estimator β̃̃_dr satisfying properties (a) and (b) and additionally guaranteed to be at least as efficient asymptotically as β̂_ipw is constructed just like β̃_dr in Section 3.2 but replacing a{X; α̂, η̂(β), γ̂} with b{X; β, α̂, η̂(β), γ̂, θ̂(β)}, q(V; β) with q_w(V; β) and h{Z, X; η̂(β), γ̂} with h_w{Z, X; β, η, γ̂, θ̂(β)}. In the supplementary Web appendix we also describe an estimator β̂̂_opt,dr which satisfies property (a) and has limiting normal distribution with variance equal to Σ_{qopt,1,sopt,1} when conditions (a) and (b) of Section 3.2 hold and yet converges to a weighted least squares approximation when the specification (3) for LATE(V) is wrong.

For estimation of the MLATE(·) curve in the supplementary Web appendix we show that the estimator β̂̂_dr that is computed by using H₂(β) instead of H₁(β) and with q_w(V; β) redefined as m₂(V; β) {∂m₂(V; β) /∂β}w(V) satisfies properties (a) and (b) where in the statements of these properties, specifications (3) and (24) are replaced with specification (4) and the specification that E{H₂(β_w,0)|Z = z, X = x} ∈ ℋ_w respectively, and β_w,0 is redefined as

$${\beta }_{w,0}\equiv arg\underset{\beta }{min}E[e_0(\mathbf{V})w(\mathbf{V}){\{\text{MLATE}(\mathbf{V})-m_2(\mathbf{V};\beta )\}}^2|D_1>D_0],$$

with e₀(v) ≡ E(Y₀|D₁ > D₀, V = v). Note that, unlike definition (21), β_w,0 is now a weighted least squares approximation with weights that are unknown to the data analyst since they depend on the unknown function e₀(V). It does not appear to be possible to construct doubly robust estimators of weighted least squares approximations to the MLATE(·) curve for known, i.e. user-specified, weights.

4. Connections to models for the treatment effect on the treated

Robins (1994) and Tan (2010) considered estimation of the so-called additive treatment effect on the treated contrast

$$\text{ATT}(z,\mathbf{v})\equiv E(Y_1|D_z=1,\mathbf{V}=\mathbf{v})-E(Y_0|D_z=1,\mathbf{V}=\mathbf{v}).$$

This contrast quantifies the effect of treatment D on the subset of the subpopulation with baseline covariates V = v comprised of subjects who would be treated with D = 1 if Z were set to z. Robins (1994) showed for V = X and Tan (2010) showed for V a strict subset of X, that ATT(z, v) is identified under the IV assumptions (a)–(d) and (f) in Section 2.1 and specific restrictions on ATT(·, ·). In particular, Robins (1994) showed that, when V = X, ATT(z, v) is identified under assumptions (a)–(d) and (f), and the no additive treatment–instrument interaction on the treated: ATT(z, v) = ATT(v) does not depend on z (assumption v-ATT).

Remarkably, Robins showed that under these assumptions ATT(v) = IV(v).

In fact, it is easy to show that the preceding assertions remain true when V is a strict subset of X. We thus see that, under assumptions (a)–(d) and (f) in Section 2.1, the structural interpretation of the observed data functional IV(v) depends on which of the assumptions (e) or (v-ATT) is adopted. The only exception is when P(D₀ = 1) = 0, or equivalently when P(D = 1|Z = 0) = 0, since in such a case the complier subpopulation is the same as the subpopulation defined by condition D₁ = 1, and consequently LATE(v) = ATT(v).

A further deep connection exists between the works of Robins (1994) and Tan (2010) and the problem that is addressed in this paper. For short, refer to the model defined by assumptions (a)–(f) in Section 2.1 as ‘our additive model’ and to the model defined by assumptions (a)–(d), (f) and v-ATT as the ‘Robins–Tan additive model’. Remarkably, the problem of estimating the parameter β indexing a parametric specification m₁ (v; β) for LATE(v) under our additive model is formally identical to the problem of estimating the parameters β indexing a parametric specification m₁ (v; β) for ATT(v) under the Robins–Tan additive model. This surprising fact is explained by the following three results whose proofs will be sketched below:

1. under the intersection model that assumes (a)–(f) in Section 2.1 and v-ATT, i.e. the model that makes simultaneously the assumptions of our additive model and of the Robins–Tan additive model, LATE(v) and ATT(v) are indeed identical causal effect contrasts;

2. our model is statistically indistinguishable from the intersection model, i.e., given our model, the intersection model imposes restrictions that always fit the observed data perfectly and hence cannot be rejected by any statistical test;

3. the restrictions that are imposed on the observed data law by the intersection model and not imposed by the Robins–Tan additive model are only inequality constraints.

Results (a) and (b) imply that a functional of the observed data law is equal to LATE(v) = ATT(v) under the intersection model if and only if it is equal to LATE(v) under our additive model. If this were not so, there would be some observed data law functional equal to LATE(v) under the intersection model but not under our additive model (the opposite is not possible because our additive model is bigger than the intersection model). But in such a case, there would be a restriction, specifically the restriction that sets the new functional equal to LATE(v), that would be satisfied under the intersection model but not under our additive model, thus contradicting result (b).

Result (c) implies that a functional of the observed data law is equal to ATT(v) under the intersection model if and only if it is equal to ATT(v) under the Robins–Tan additive model. If this were not so, the intersection model would satisfy an equality constraint that is not satisfied by the Robins–Tan additive model, namely the constraint that sets a new functional of the observed data law equal to ATT(v), thus contradicting result (c).

Results (a)–(c) then imply that any functional of the observed data law that is equal to ATT(v) under the Robins–Tan model must be equal to LATE(v) under our additive model and vice versa. This, in turn, proves that the problem of conducting inference about the parameters β of models m₁(v; β) for ATT(v) under the Robins–Tan assumptions is formally the same as the problem of conducting inference about the parameters β indexing a parametric specification m₁(v; β) for LATE(v) under our additive model.

A further result (result (d) stated below) implies that IV(v) is indeed the only functional of the observed data law that is equal to LATE(v) under our additive model and, consequently, the only observed data functional equal to ATT(v) under the Robins–Tan additive model:

• (d)the only restrictions imposed on the observed data law by our additive model are inequality constraints on certain conditional distributions.

As indicated, result (d) implies that no functional of the observed data law other than IV(v) can be equal to LATE(v) under our additive model. If this were not so, then the observed data law would satisfy an equality constraint under our model, namely the equality that sets IV(v) equal to the other functional that agrees with LATE(v), thus contradicting result (d).

We now demonstrate results (a)–(d). Results (a) and (b) are a consequence of the fact that the intersection model can be equivalently defined as the model that imposes restrictions (a)–(f) in Section 2.1 and the additional restriction

$$E(Y_1-Y_0|T=\text{co},\mathbf{V})=E(Y_1-Y_0|T=\text{at},\mathbf{V})$$ (27)

where T denotes compliance type, i.e. T = at if and only if D₁ = D₀ = 1 (always-taker), T = nt if and only if D₁ = D₀ = 0 (never-taker), T = co if and only if D₁ > D₀ (complier) and T = de if and only if D₁ < D₀ (defier). This equivalence holds because assumption v-ATT is the same as the assumption that

$$E(Y_1-Y_0|T\in \{\text{at},\text{co}\},\mathbf{V})=E(Y_1-Y_0|T\in \{\text{at},\text{de}\},\mathbf{V}).$$ (28)

Thus, when no defiers exist, i.e. when assumption (e) holds, equation (28) is equivalent to equation (27).

Result (a) follows because restriction (27) implies that ATT(v) ≡ E(Y₁ − Y₀|T ∈ {co, at}, V = v) = E(Y₁ − Y₀|T = co, V = v) ≡ LATE(v), so under the intersection model, LATE(v) is indeed equal to ATT(v). Result (b) follows because, under assumptions (a)–(f), a test of the intersection model is a test that restriction (27) holds. No test can be constructed with power to detect departures from equation (27) because E(Y₀|T = at, V) is not identified and the law of the observed data does not bound its range, when, as we have assumed throughout, Y has unbounded support.

Results (c) and (d) are a consequence of the following lemmas whose proofs are given in the supplementary Web appendix.

Lemma 1. The only restrictions on the observed data law encoded by our additive model are 0 < P(Z = 1|X) < 1 and the following inequality constraints. For any y < y′,

$$Pr(y<Y\le y\prime ,D=1|Z=1,\mathbf{X})-Pr(y<Y\le y\prime ,D=1|Z=0,\mathbf{X})⩾0,$$ (29)

$$Pr(y<Y\le y\prime ,D=0|Z=0,\mathbf{X})-Pr(y<Y\le y\prime ,D=0|Z=1,\mathbf{X})⩾0,$$ (30)

$$E\{E(D|Z=1,\mathbf{X})|\mathbf{V}\}-E\{E(D|Z=0,\mathbf{X})|\mathbf{V}\}>0.$$ (31)

Lemma 2. The only restrictions on the observed data law that are imposed by the Robins–Tan additive model are 0 < P(Z = 1|X) < 1 and E {E (D|Z = 1, X) |V} − E{E(D|Z = 0, X) |V} ≠ 0.

It is interesting to contrast the structural interpretation of the functional E(H₁|Z, X) under our additive model and the Robins–Tan additive models. In the supplementary Web appendix we show that, under the Robins–Tan additive model,

$$E(H_1|Z=z,\mathbf{X})=E(Y_0|\mathbf{X})-\{\text{ATT}(\mathbf{V})-\text{ATT}(z,\mathbf{X})\}P(D_z=1|\mathbf{X})$$

and under our additive model,

$$E(H_1|Z=z,\mathbf{X})=E(Y_0|\mathbf{X})+\{E(Y_1-Y_0|\mathbf{X},T=\text{at})-\text{LATE}(\mathbf{X})\}P(T=\text{at}|\mathbf{X})+\{\text{LATE}(\mathbf{X})-\text{LATE}(\mathbf{V})\}\{zP(T\in \{\text{at},\text{co}\}|\mathbf{X})+(1-z)P(T=\text{ne}|\mathbf{X})\}.$$ (32)

Abadie (2003) has previously derived result (32) in the special case V = X under our additive model. Observe that only under the Robins–Tan additive model and only for the special case V = X, E(H₁|Z, X) has a simple structural interpretation, namely as E(Y₀|X = x) (since by v-ATT implies ATT(z, X) = ATT(X) when V = X). No simple structural meaning can be given to E(H₁|Z, X) in all other cases. It is this counterintuitive aspect of the functional E(H₁|Z, X) that we believe may have delayed the discovery of the doubly robust estimators of β proposed in this paper.

Robins (1994) and Tan (2010) also discussed inference about models for the multiplicative treatment effect on the treated curve MTT(z, v) ≡ E(Y₁|D_z = 1, V = v) /E(Y₀|D_z = 1, V = v). Deep connections along the lines made in this section also exist between the work of Robins (1994) and Tan (2010) for inference about MTT(z, v) and the proposal for estimation about MLATE(v) in this paper.

5. Data Analysis

We apply the procedures that are discussed in this paper to estimate the local average treatment effect of participation in 401(k) programs on household saving. 401(k) tax-deferred retirement plans were introduced in the 1980s with the goal of encouraging household saving; they have since grown to be the most popular retirement plans in the USA. But economists have hypothesized that 401(k) plans may not represent increased saving; rather they may replace other modes of saving for those who participate. Among people who are eligible to participate in 401(k) plans, those who choose to participate are likely to be more inclined to save than those who choose not to participate. Therefore, standard methods for examining the effect of 401(k) participation on savings based on covariate adjustment are inappropriate as underlying saving preference is an unmeasured confounder of the treatment–outcome relationship. Using 401(k) eligibility as an instrument for 401(k) participation, estimation of the local average treatment effect of 401(k) participation on savings is feasible.

Poterba et al. (1994, 1995) and Abadie (2003) analysed data from the US Census Bureau's 1991 Survey of Income and Program Participation to test whether participation in 401(k) plans increases household savings. Here we reanalyze the data that were analyzed by Abadie (2003), consisting of a sample of 9725 household reference subjects aged 25–64 years and their spouses, with annual income between $10000 and $200000. In our analysis as in Abadie's, the outcome Y is net financial assets, the instrument Z is an indicator of 401(k) eligibility, the treatment D is an indicator of 401(k) participation and the vector of covariates is X = (X₁, X₂, X₃, X₄) where X₁ is age (approximated to the closest integer year after subtracting the minimum age in the sample), X₂ is an indicator of marital status (married or not), X₃ is family size and X₄ is annual household income (in thousands of dollars).

In this example, the instrumentation assumption (d) and monotonicity assumption (e) hold trivially because it is not possible to choose to participate in 401(k) plans if not eligible to do so (D₀ = 0 with probability 1). The exclusion restriction (b) is very plausible because 401(k) plans are run through employers with only some employers granting eligibility to their employees; evidence suggests that the effect of an employer's offer of 401(k) eligibility on an employee's saving behaviour operates only through the employee's choice to participate or not in the programme (Poterba et al., 1995). Finally, the randomization assumption is also likely to hold when we include in X the measured predictors income, age, marital status and family size of eligibility and savings. Because D₀ = 0 there can be no defiers or always takers and the complier subpopulation is comprised of all eligible subjects who chose to participate; consequently LATE(·) = ATT(·) is estimable with these survey data.

To illustrate our methodology we considered estimation of the parameters indexing models for LATE(V) for two choices of V, namely V =X₄ (income) and V = null. We shall see that the analysis when V = X₄ showed that income was a significant determinant of LATE. This gave us the opportunity to explore the behaviour of the proposed estimators under misspecification of the model for the LATE(·) curve. Specifically, we applied the procedures in this paper to estimate a scalar parameter β under the specification m(X;β) = β, i.e. under a, probably misspecified, model that assumes that LATE(X) does not depend on income or any of the other covariates in X. This specification was also used to analyze these data in Abadie (2003).

Table 1 reports the estimators of β with their bootstrap standard errors in parentheses in the case V = X₄ under the specification m(X₄;β) = β₀ + β₁X₄. Table 1 reports results for eight estimators: five doubly robust estimators β̂_dr, two IPW estimators β̂_ipw and one outcome regression estimator β̂_reg. The estimator β̂_reg was computed by using the function l(Z, X; β, η, γ) given in expression (16). Three of the doubly robust estimators, denoted by ${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$, ${\widehat{\beta }}_{\text{dr},\pi -\text{fixed}}^{\text{opt}}$, ${\widehat{\beta }}_{\text{dr},h-\text{fixed}}^{\text{opt}}$, used q(V) equal to q̂_opt,1 (V) as defined in Section 3.3. In the calculation of q̂_opt,1 (V), log [e₁(V; δ)/{1 − e₁(V; δ)}] and log{t₁(V; ω)} were linear functions of income and income². (When, as in this data set, Z = 0 implies D = 0, e₁(V; δ) is a model for E{E(D|X, Z = 1) |V}.) The fourth doubly robust estimator, which is denoted with ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$, used q(V) = ∂m(V;β) /∂β = (1, X₄)^T and the last doubly robust estimator, which is denoted by ${\widehat{\beta }}_{\text{dr}}^{\text{ineff},\text{stable}}$ used q(V) = (1, X₄)^T {expit(ζ̂₀ + ζ̂₁X₄) − expit(ζ̂₀ + ζ̂₁X₄)²} where expit(ζ̂₀ + ζ̂₁X₄)^dr was the fitted value from a logistic regression of Z on X₄. These last two choices of q(V) were also used to construct the two IPW estimators, which are denoted by ${\widehat{\beta }}_{\text{ipw}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{ipw}}^{\text{ineff},\text{stable}}$ respectively.

Table 1. Estimators of (β₀,β₁) and their bootstrap standard errors under model LATE(income) =β₀ + β₁ income.

Parameter	Results for the following powers k of income in the outcome regression and propensity score models:
	1	2	3	4	5	8
Intercept
${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$	−4640 (2940)	−1845 (3220)	−1888 (2940)	−1490 (2900)	−1623 (2907)	−1566 (2896)
${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$	1774 (5720)	−12860 (10720)	−3846 (5797)	−14201 (11244)	−3877 (7061)	−1578 (7009)
${\widehat{\beta }}_{\text{dr}}^{\text{ineff},\text{stable}}$	−418 (4827)	−4958 (5547)	−2049 (4385)	−1814 (4527)	−2448 (4465)	−1590 (4543)
${\widehat{\beta }}_{\text{dr},h-\text{fixed}}^{\text{opt}}$	−1572 (3292)	−1411 (3146)	−1285 (2873)	−1490 (2900)	−1592 (2989)	−1674 (2914)
${\widehat{\beta }}_{\text{dr},\pi -\text{fixed}}^{\text{opt}}$	−2093 (2961)	−1421 (2947)	−1911 (2816)	−1490 (2900)	−1650 (2826)	−1517 (2920)
${\widehat{\beta }}_{\text{ipw}}^{\text{ineff}}$	17075 (7870)	−18515 (11587)	−4905 (6487)	−858 (6841)	−1980 (6732)	−593 (7655)
${\widehat{\beta }}_{\text{ipw}}^{\text{ineff},\text{stable}}$	12331 (6076)	−3489 (5632)	−2775 (4101)	−1478 (4019)	−1537 (4202)	−1179 (4409)
β̂reg	−6992 (7019)	1929 (7665)	−2652 (6886)	−1266 (6796)	−1721 (6702)	−1494 (7004)
Income
${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$	382 (88)	337 (92)	338 (83)	328 (82)	330 (83)	328 (83)
${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$	205 (171)	634 (290)	390 (165)	351 (197)	392 (197)	329 (196)
${\widehat{\beta }}_{\text{dr}}^{\text{ineff},\text{stable}}$	272 (128)	425 (149)	345 (115)	340 (123)	354 (122)	331 (120)
${\widehat{\beta }}_{\text{dr},h-\text{fixed}}^{\text{opt}}$	319 (96)	323 (90)	326 (80)	328 (82)	329 (82)	332 (84)
${\widehat{\beta }}_{\text{dr},\pi -\text{fixed}}^{\text{opt}}$	342 (84)	328 (82)	340 (84)	328 (82)	332 (82)	328 (79)
${\widehat{\beta }}_{\text{ipw}}^{\text{ineff}}$	−139 (218)	785 (306)	425 (178)	320 (181)	347 (181)	311 (201)
${\widehat{\beta }}_{\text{ipw}}^{\text{ineff},\text{stable}}$	14 (161)	385 (154)	368 (119)	339 (117)	336 (114)	329 (123)
β̂reg	510 (187)	272 (210)	361 (181)	345 (183)	357 (180)	353 (194)

In the calculation of the doubly robust and IPW estimators we used the propensity score model 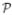^k_π which assumed that log[π (x; α) / {1 − π (x; α)}] was linear in indicator variables of the combined levels of marital status and age as well as in all powers of income up to the power k_π. As in Abadie (2003), we did not include family size because it did not significantly predict Z. Also, the outcome regression model in the calculation of the doubly robust estimators and of β̂_reg, which is denoted in what follows by ${\mathcal{H}}_{\upsilon }^{k_h}$, assumed that E{H₁(β₀)|Z, X} = k(X; ν) + ρ^T{φ(X) − φ(V; γ)}Z. The function k(x; ν) was linear in powers of income up to power k_h and in indicators of the combined levels of age, marital status and family size (dichotomized at its mean). The function φ(x) was a vector of indicators of combined levels of age, marital status and family size; each entry of φ(v; γ) was a linear logistic regression model for the corresponding entry of φ(x) with covariates being income, income², …, income^k_h. The estimators ${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$, ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{dr}}^{\text{ineff},\text{stable}}$ were computed by using models ( 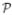^k_π and ${\mathcal{H}}_{\upsilon }^{k_h}$ with k_π = k_h ≡ k. In Table 1 the first three rows report these estimators by using k as indicated by the column labels. The estimator ${\widehat{\beta }}_{\text{dr},\pi -\text{fixed}}^{\text{opt}}$ had k_π fixed at 4 and k_h as indicated by the column labels. Likewise the estimator ${\widehat{\beta }}_{\text{dr},h-\text{fixed}}^{\text{opt}}$ had k_h fixed at 4 and k_π as indicated by the column labels. The estimators ${\widehat{\beta }}_{\text{ipw}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{ipw}}^{\text{ineff},\text{stable}}$ had k_π as indicated by the column labels. Finally, the estimator β̂_reg had k_h as indicated by the column labels. In the data set as well as in each bootstrap replication we first estimated the propensity scores, then threw out the data from subjects in the bottom and top 1% of the estimated values of π(X; α̂), and finally carried through the entire procedure for arriving at the estimators of β using the remaining data. In the data set, this pruning did not noticeably change the values of our estimators, suggesting that the data pruning did not result in substantial bias, but it had a dramatic effect on stabilizing the bootstrap standard error estimators.

According to the theory that is presented in this paper, ${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$ with k_π = k_h sufficiently large should result in optimal inference about β. We therefore first examine the rows corresponding to ${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$ and the columns with k_π = k_h equal 4, 5 and 8 in Table 1. We note that the coefficient of income is roughly 330 with a standard error around 80, suggesting that 401(k) plans have more effect on the savings of families of higher income. For example, for k_π = k_h = 4, the estimated effect of 401(k) participation for an eligible person with annual income $50000 who chooses to participate in the programme is to increase her family's net financial assets by $14910 whereas the increase for a person with an income of $100000 is $31310.

Unlike the slope coefficient, the intercept does not appear to be significantly different from 0; a 95% confidence interval for the intercept would include 0 as the point estimate is roughly half its standard error. For this reason, we henceforth focus attention on the behaviour of the remaining estimators of the income coefficient. Since the three doubly robust estimators ${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$, ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{dr}}^{\text{ineff},\text{stable}}$ with k_π = k_h ⩾ 4 are all approximately equal to 330, we conclude that it is likely that the linear model for LATE(X₄) is approximately correct. If it were not, the estimators ${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$, ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{dr}}^{\text{ineff},\text{stable}}$ would not be expected to exhibit similar values as they would have different probability limits because they use different functions q(V). Therefore, in what follows, we shall refer to an estimator of the slope coefficient as ‘unbiased’ if it is roughly equal to 330. Observe that, as predicted by theory, the doubly robust estimators that use q̂_opt,1(V) are more efficient than the IPW or any of the other doubly robust estimators. (In fact, these doubly robust estimators are even more efficient than the estimator β̂_reg; presumably this reflects the fact that the choice (16) that we recommended for ease of calculation is not optimal). A comparison of the IPW estimators with the estimator ${\widehat{\beta }}_{\text{dr},h-\text{fixed}}^{\text{opt}}$ and of the outcome regression estimator with ${\widehat{\beta }}_{\text{dr},\pi -\text{fixed}}^{\text{opt}}$ illustrates the advantage of doubly robust estimation over IPW and outcome regression estimation. These comparisons reveal that doubly robust estimators require only one of the two models to be nearly correct and the analyst does not need to know which one is correct. Note that whereas the IPW estimators are severely ‘biased’ if k_π is 1 or 2, the doubly robust estimator ${\widehat{\beta }}_{\text{dr},h-\text{fixed}}^{\text{opt}}$ that uses the same model for the propensity score but a model ${\mathcal{H}}_{\upsilon }^{k_h}$ with k_h = 4 is roughly ‘unbiased’. Likewise, the outcome regression estimator that has k_h equal to 1 or 2 is biased but the ‘bias’ is corrected by the estimator ${\widehat{\beta }}_{\text{dr},\pi -\text{fixed}}^{\text{opt}}$.

Turn now to estimation of β under a model m(X; β) for LATE(X) that assumes that m(X; β) = β. This model is presumably wrong because, as we have already seen from the previous analysis, income modifies the effect of treatment D among the compliers. Additional evidence for misspecification is presented in Fig. 1, which displays the values of three different doubly robust estimators β̂_dr, denoted with ${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$, ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{dr}}^{\text{ineff},\text{stable}}$ which used respectively q(X) = e₁(X; δ̂)t₁(X; ω̂), q(X) = ∂m(X; β)/∂β = 1 and q(X) = π(X, α̂) − π(X, α̂)², where log [e₁(X; δ)/{1 − e₁(X; δ)}] and log{t₁(X; ω)} were linear functions of family size, income, income² and indicators of age and marital status. The estimators assumed model 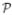^k_π for the propensity score and an outcome regression model ${\mathcal{H}}_x^{k_h}$ that specifies that E{H₁(β₀)|Z, X} = k(x; ν) where k(x; ν) is the same function as defined earlier. (Recall that under the assumption that the model m(X; β) is correct, E{H₁(β₀)|Z, X} does not depend on Z). The plot displays the values of ${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$, ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{dr}}^{\text{ineff},\text{stable}}$ as k_h = k_π ≡ k varies from 1 to 8. Each estimator stabilizes for k ⩾ 3; however each stabilizes to a different value. This is as predicted by the theory of Section 3.4 according to which, when model m(X; β) is incorrect and model 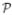^k_π is correct, each estimator converges in probability to a distinct weighted least squares approximation β_0,w with a weight that depends on the choice of function q(X). Specifically, when 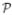^k_π is correct and the model m(X; β) for LATE(X) is misspecified, ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$, ${\widehat{\beta }}_{\text{dr}}^{\text{ineff},\text{stable}}$ and ${\widehat{\beta }}_{\text{dr}}^{\text{opt}}$ converge in probability to distinct values β_0,wineff, β_{0,wineff,stable} and β_0,wopt where w_ineff(X) = 1, w_ineff,stable(X) = π(X, α₀) − π(X,α₀)² and w_opt(X) = e₁(X; δ*)t₁(X; ω*) with δ* and ω* the probability limits of δ̂ and ω̂.

Fig. 1.

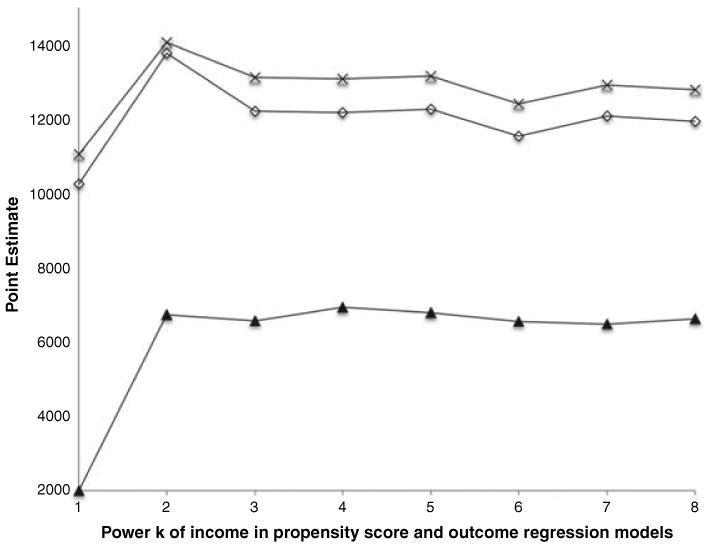
Estimation of the marginal LATE based on incorrectly assuming that $\text{LATE}(\mathbf{X})=\text{LATE}:▲,{\widehat{\beta }}_{\text{dr}}^{\text{opt}};\diamond ,{\widehat{\beta }}_{\text{dr}}^{\text{ineff}};\times ,{\widehat{\beta }}_{\text{dr}}^{\text{ineff},\text{stable}}$

The parameter β_0,wineff is of particular interest as an easy calculation shows that β_0,wineff is equal to the marginal LATE, i.e. to β_null ≡ LATE(V) when V = null. Thus, the estimator ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ converges to β_null when the model 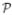^k_π is correct. In fact, the IPW estimator ${\widehat{\beta }}_{\text{ipw}}^{\text{ineff}}$ that uses the same q(X) as ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ and the same model ^k_π also converges to β_null when model ^k_π is correct. This is so because β̂_dr and β̂_ipw have the same probability limits when they use the same correctly specified propensity score model regardless of whether or not the parametric specification for LATE(·) is correct. These theoretical results are confirmed in Fig. 2, which displays the estimators ${\widehat{\beta }}_{\text{ipw}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ computed under model ^k_π and model ${\mathcal{H}}_x^{k_h}$ with k_h = k_π = k. In addition, Fig. 2 displays the doubly robust estimator β̂_null,dr of β_null, i.e. of the marginal LATE. This estimator is computed under model ^k_π and a model ${\mathcal{H}}_{\text{null}}^{k_h}$ that assumes that E{H₁(β_null)|Z, X} = k(X; ν) + ρ^T[φ(X) − E{φ(X)}]Z with k(x; ν) as defined earlier and φ(x) a vector function of indicators of the combined levels of age, marital status, family size (dichotomized at its mean) and powers of income up to power k_h. Note that in Fig. 2 ${\widehat{\beta }}_{\text{ipw}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ are both close to β̂_null,dr for k_π ⩾ 4.

Fig. 2.

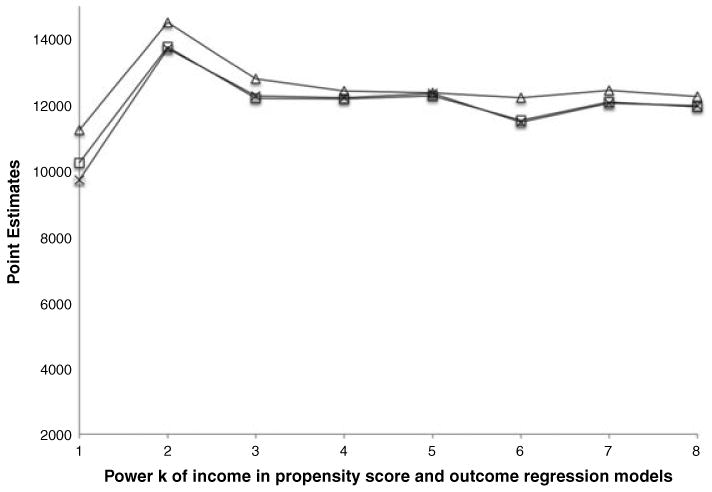
Doubly robust estimation of the marginal LATE versus estimation based on incorrectly assuming that $\text{LATE}(\mathbf{X})=\text{LATE}:\Delta ,{\widehat{\beta }}_{\text{ipw}}^{\text{ineff}};\square ,{\widehat{\beta }}_{\text{dr}}^{\text{ineff}};\times ,{\widehat{\beta }}_{\text{null},\text{dr}}$

If model ^k_π is wrong and m(X; β) = β is an incorrect specification for LATE(X) both ${\widehat{\beta }}_{\text{ipw}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ are inconsistent for β_0,wineff = β_null. This occurs because, as discussed in Section 3.4, ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ is not doubly robust for β_0,wineff under incorrect specification of the model for the LATE(·) curve. In contrast, β̂_null,dr is double robust for β_null, i.e. it is consistent either if model ^k_π is correct or if model ${\mathcal{H}}_{\text{null}}^{k_h}$ is correct. In fact, β̂_null,dr is a member of the class of estimators β̂̂_dr that were described in Section 3.4; it is algebraically equal to the estimator β̂̂_dr that uses q_w(V) = 1 with V = X. Recall that, unlike β̂_dr, the estimator β̂̂_dr that uses a given q_w(V) is doubly robust for β_0,w. Table 2 illustrates these points. The row that is labelled ‘Model ^k_π’ lists estimators that were computed under model ^k_π with k_π = 4. The row that is labelled ‘Model ^wrong’ lists estimators that were computed under the model ^wrong that incorrectly sets P(Z = 1|X) to be equal to the constant $\frac{1}{2}$. For estimators β̂_null,dr and ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$, k_h was chosen to be 4. All the estimators in the first row are approximately equal. However, a column-by-column comparison of the two rows reveals that of the three estimators only β̂_null,dr remains approximately unchanged when it is computed under ^wrong. This is as predicted by theory (provided that the model ${\mathcal{H}}_{\text{null}}^{k_h}$ with k_h = 4 is approximately correct). To confirm that these findings were unlikely to be due to chance, we computed for each column the ratio $\widehat{T}=\widehat{\Delta }/\widehat{\text{SE}}$ where Δ̂ is the difference between the first and second row, and $\widehat{\text{SE}}$ is the bootstrap standard error of Δ̂. Under the null hypothesis that the probability limits of the estimators in the two rows are the same, T should approximately have a standard normal distribution. For β̂_null,dr, T̂ was 0.51 whereas, for ${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$ and ${\widehat{\beta }}_{\text{ipw}}^{\text{ineff}}$, T̂ was −1.91 and −3.14 respectively.

Table 2. Estimation of the marginal LATE effect.

Model	Point estimators†
	β̂null,dr=β̂̂dr	${\widehat{\beta }}_{\text{dr}}^{\text{ineff}}$	${\widehat{\beta }}_{\text{ipw}}^{\text{ineff}}$
kπ=4	12213	12179	12434
wrong	11859	13140	17651
	Test statistic‡
	0.51	−1.91	−3.14

^†β̂_dr is the estimator of Section 3.4 that uses q_w(V) =1.

^‡Test statistic is the difference of the estimators in the first and second rows divided by the bootstrap standard error of the difference.

6. Conclusion

In this paper we introduced a new class of estimators for parametric forms for additive and multiplicative local average treatment effect curves as functions of covariates V, where V may be a subset of the covariates X required for the candidate instrument to be a valid IV Our estimators are doubly robust, i.e. they are consistent and asymptotically normal if either one of two dimension reducing models is correctly specified. Unlike other proposals, these dimension reducing models are always compatible with the assumed parametric functional form for the local average treatment effect on the additive scale if Y has unbounded support, and with the assumed parametric functional form for the effect on the multiplicative scale if Y has support in the positive real line and is unbounded. We discussed the connection between our model for the local average treatment effects and the Robins–Tan model for the effect of treatment on the treated, and we argued that the correspondence between the two models is unsurprising because the restrictions on the observed data law that is imposed by the two models differ only in inequality constraints, and because under an untestable assumption about the distribution of the counterfactual outcomes the two estimands are identified by the same functional of the observed data.

Future work is needed to explore the performance of our estimators for weak instruments in finite samples. Another potential topic for future work arises from the fact that, when Y is binary, the outcome regression model and the model for MLATE(·) are not variation independent. Thus, the model m₂(·; β) could conflict with a proposed model for E(H₂|Z, X). If the propensity score model is correctly specified the resulting estimator of β₀ will still be consistent; however, this variation dependence implies that we may not have two independent opportunities for valid inference about β₀. In forthcoming work, we reparameterize the model for MLATE when Y is binary to recover doubly robustness.