Internal Coordinate Molecular Dynamics: A Foundation for Multiscale Dynamics

Abstract

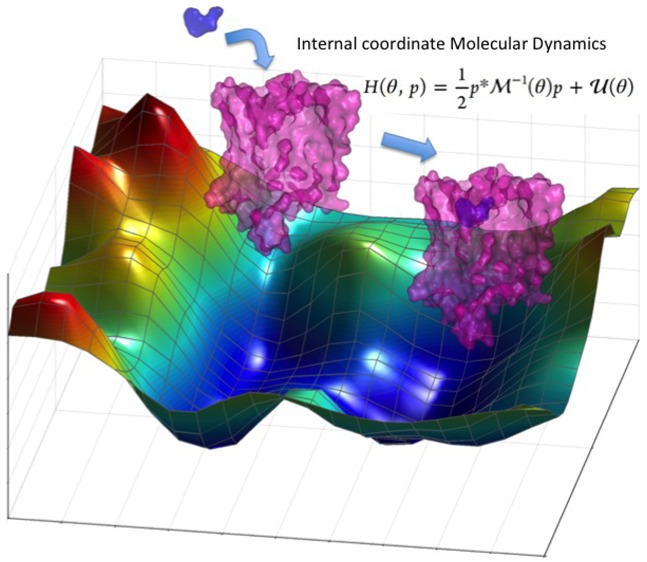
Internal coordinates such as bond lengths, bond angles, and torsion angles (BAT) are natural coordinates for describing a bonded molecular system. However, the molecular dynamics (MD) simulation methods that are widely used for proteins, DNA, and polymers are based on Cartesian coordinates owing to the mathematical simplicity of the equations of motion. However, constraints are often needed with Cartesian MD simulations to enhance the conformational sampling. This makes the equations of motion in the Cartesian coordinates differential-algebraic, which adversely impacts the complexity and the robustness of the simulations. On the other hand, constraints can be easily placed in BAT coordinates by removing the degrees of freedom that need to be constrained. Thus, the internal coordinate MD (ICMD) offers an attractive alternative to Cartesian coordinate MD for developing multiscale MD method. The torsional MD method is a special adaptation of the ICMD method, where all the bond lengths and bond angles are kept rigid. The advantages of ICMD simulation methods are the longer time step size afforded by freezing high frequency degrees of freedom and performing a conformational search in the more important low frequency torsional degrees of freedom. However, the advancements in the ICMD simulations have been slow and stifled by long-standing mathematical bottlenecks. In this review, we summarize the recent mathematical advancements we have made based on spatial operator algebra, in developing a robust long time scale ICMD simulation toolkit useful for various applications. We also present the applications of ICMD simulations to study conformational changes in proteins and protein structure refinement. We review the advantages of the ICMD simulations over the Cartesian simulations when used with enhanced sampling methods and project the future use of ICMD simulations in protein dynamics.

1. Introduction

Molecular dynamics (MD) simulations are commonly used for (a) studying dynamics of protein structures, (b) protein structure prediction, and (c) calculating thermodynamic properties such as free energies, enthalpy, and entropy of conformational states of proteins.^1,2 All-atom Cartesian MD simulations is a classical mechanics based toolkit using Cartesian coordinates as degrees of freedom. The Cartesian MD method is used widely for calculating statistical and thermodynamic properties of materials and biomaterials. One of the attractive features of the Cartesian all-atom dynamics model which uses absolute coordinates is its mathematical simplicity. There has been extensive development of all-atom Cartesian dynamics algorithms for thermostats and simulation ensembles such as constant temperature (NVT), constant pressure (NPT), and constant stress (grand canonical ensemble).² The thermodynamic properties calculated from these ensemble simulations can be directly compared with experimental measurements. Additionally, constraints and/or bias potentials are often used in Cartesian MD to increase the time step size, enhance conformational sampling, and simulate large-scale conformational changes. The addition of these constraints into the Cartesian dynamics makes the equations of motion differential algebraic, requiring differential-algebraic equation solvers that can adversely impact simulation robustness and complexity.

Importance of Internal Coordinate Molecular Dynamics Simulation Methods

Bond length, bond angle, and torsion angle (BAT) relative coordinates are more natural than Cartesian absolute coordinates for describing the bonded structure of proteins. MD simulations in BAT coordinates are referred to as internal coordinate MD (ICMD) methods. In ICMD models of proteins, degrees of freedom that are nonessential for effecting large scale conformational changes in proteins, such as high frequency bond length degrees of freedom, can be constrained by simply excluding them from the model.³⁻⁶ Not only do the resulting ICMD models have fewer number of degrees of freedom, but they also retain the simpler structure of ordinary differential equations instead of the more complex differential-algebraic structure required for constrained Cartesian models. Other advantages of ICMD are the following:

• 1.The low-frequency torsional coordinates allow larger time steps for integration of the equations of motion.
• 2.Conformational search is more effective in the low frequency torsional degrees of freedom⁷⁻¹³ and leads to significant conformational changes.^{3,7,8,10,13,14}
• 3.Enhanced sampling methods are more effective when performed in torsional space.^4,13,15
• 4.The six translation and orientation degrees of freedom for a molecule are explicit coordinates rather than implicit as in Cartesian models. This is useful when calculating the conformational entropy using quasi-harmonic analysis.
• 5.They provide a large range of options for selecting and controlling the granularity of the dynamics model.^6,10,14
• 6.Fixman¹⁶ potential corrections for constraint-induced biases in the partition function are easier to apply.^17,18

The ability of the ICMD simulation methods to control the granularity of the dynamics model makes them highly suitable for the development of multiscale methods and strategies for the simulation of protein macromolecular complexes and polymeric materials. Our vision is to develop a robust and advanced ICMD method that capitalizes on the inherent advantages of ICMD, and to use these methods to develop a comprehensive ICMD simulation toolkit for tackling important problems in structural biology. The coupled nature of the ICMD coordinates and the higher complexity of ICMD models however demands far more sophisticated mathematical techniques and algorithms.¹⁹

Challenges in the ICMD Methods and Solutions to the Bottlenecks

Torsional MD is a well-known example of an ICMD method that constrains all bond lengths and bond angles. Many research groups have used the torsional MD method for simulating the dynamics of peptides and proteins^3,20−22 in addition to clarifying the stubborn challenges associated with the torsional MD methods.^20,22−24 The wider usage of torsional MD methods has been hampered by serious bottlenecks that slowed their progress and viability of ICMD methods as a structural biology tool. Two long-standing concerns have been (a) the mathematical and computational complexity of the equations of motion associated with the ICMD models and (b) the increased rigidity in the torsional MD dynamics resulting from keeping the bond lengths and angles constrained, affecting the transition barriers and probability density functions of states in a protein.

When all the bond lengths and bond angles are constrained in torsional MD, the equations of motion in the dihedral angle space become computationally expensive with the solution scaling as the cubic power of the number of torsion degrees of freedom. This has been a major bottleneck that stunted the use and growth of ICMD methods. We developed the generalized Newton–Euler inverse mass operator (GNEIMO) method that is based on the wealth of mathematical theory and analysis using spatial operator algebra techniques originally developed for spacecraft and robot dynamics domains.¹⁹ There has been a considerable amount of research over the years on the development of the spatial operator algebra methods¹⁹ for the analysis of robot multibody system dynamics. The key insights that have been developed included analytical techniques for the factorization and inversion of the mass matrix for tree-topology systems. These techniques have opened up the opportunities to revisit and advance torsional MD simulations and make it computationally accessible to the wider community. Our spatial operator algebra based ICMD algorithm for solving the equations of motion was the first to overcome the ICMD computational cost bottleneck by reducing costs to being just linearly, instead of cubically, proportional to the number of degrees of freedom.^5,25 This low cost algorithm has been adopted by other groups to implement torsional MD capability.^9,26−29 The GNEIMO method has been applied to study a wide variety of structural biology problems such as protein folding, protein structure refinement, and domain motion in proteins.^7,8,10−14 This algorithm is now being used routinely in refining NMR structures (in the software called CYANA) and X-ray crystal structures (in the software called NIH-XPLOR). However, these two applications require only short time scale dynamics and do not require calculation of accurate thermodynamic properties from simulations.

Although the first challenge was eliminated making torsional MD simulations computationally feasible with the spatial operator algebra based solution, the second bottleneck arising from the rigidity of the model still persisted. The increased rigidity of the dynamic model stemming from freezing degrees of freedom led to fewer dihedral transitions and to systematic errors in the probability density functions for proteins and peptides. Researchers have observed that the use of rigid constraints in both bond lengths and bond angles in the torsional MD simulations alters the potential energy surface and the free energy surface of the system compared with unconstrained MD simulations.^{9,20,23,24,30−34} Addressing the rigidity of the dynamics model imposed in the torsional MD simulations, Fixman in the 1970s proposed a compensating potential that rigorously corrects for treating stiff and uncoupled bond angles as rigid in the ICMD model, and generates a partition function that gives probability density functions closer to that of all-atom Cartesian simulations.^23,24,30 While the Fixman potential removes such biases for those bond angles that are stiff, it remained intractable and hence not tested for larger branched molecules. By developing a spatial operator algebra based general purpose and low-cost computational method to calculate the Fixman potential for all linear and branched molecules,^17,18 we have solved the longstanding problem of using the Fixman potential in ICMD simulations to remove constraint-induced biases in thermodynamic properties and the probability density function. Our studies verify that, as predicted, the inclusion of the Fixman potential recovers the equilibrium probability density function of the conformational states, the transition barrier crossing rates, and the free energy surface for serial and branched molecules.¹⁸ To the best of our knowledge, this is the first time that the Fixman potential has been used for ICMD of large and realistic branched polymers.

Overcoming the two long-standing bottlenecks along with several theoretical and algorithmic advances in the GNEIMO ICMD method made in the past five years has led to a robust long time scale ICMD simulation method and an associated software package for use to study protein structural dynamics.^14,35 The highlights of these methods are described in section 2, and the highlights of the results for several protein simulation applications and their comparison to experimental findings are given in section 3. The current state of the ICMD methods and the areas that need further development are discussed in section 4.

2. Methods

The ICMD method is a molecular dynamics simulation method performed in BAT coordinates also known as internal coordinates. The GNEIMO method is a generalized ICMD method based on spatial operator algebra, for performing multibody dynamics of macromolecules. Constraints on the high frequency bond lengths can be placed in the GNEIMO method to perform ICMD simulations with the bond angles and torsion angles as degrees of freedom. If both the bond lengths and bond angles are kept rigid, the resulting torsional MD method is also supported by GNEIMO. In the GNEIMO torsional MD method, the bond length and bond angle degrees of freedom are treated as rigid and the macromolecule of tree topology is modeled as a collection of rigid bodies (of varied sizes) connected by flexible hinges. The rigid bodies also known as clusters can vary in size and shape ranging from a single atom to a methyl group, or a helix or an entire domain of a protein. The hinges connecting the rigid clusters are the torsional degrees of freedom. However, these hinges have one to six degrees of freedom, with the one degree of freedom being just the torsion angle. When the hinge has six degrees of freedom, it allows the bond stretch, bond angle bending, and torsion about the bond connecting the clusters. The default cluster model of proteins in the GNEIMO method is shown in Figure 1.

Figure 1.

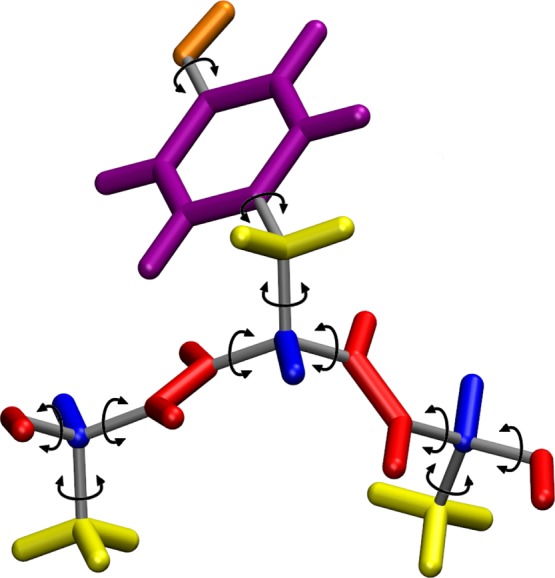
Standard clustering scheme used for torsional MD in GNEIMO shown for the tripeptide Ala-Tyr-Ala. The rigid clusters are shown in a single color, and these clustered atoms move together as a single unit. The gray rods and arrows represent hinges connecting two clusters. Material: Reprinted with permission from ref (35). Copyright 2014 Wiley Periodicals Inc.

When the bond lengths and bond angles are treated as rigid, the equations of motion in ICMD become coupled and are shown in eq 1

1

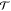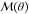where θ is the vector of the generalized coordinates (e.g., torsional angles), denotes the vector of generalized forces (e.g., torques), denotes the mass matrix (moment of inertia tensor), and 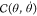includes the velocity dependent Coriolis forces. The dynamics of motion is obtained by solving eq 1 for the θ̈ acceleration and integrating them to obtain new velocities and coordinates. With conventional algorithms, the equations of motion involve calculating the inverse of the dense mass matrix that scales as the cubic power of the number of degrees of freedom.⁴ The GNEIMO method uses a spatial operator algebra based method to derive an analytical expression for the inverse of the mass matrix followed by the following expression for θ̈

2

The 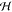, ψ, 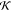, etc., terms in the above expression are associated with mass matrix related factorizations and are described in detail in refs (5 and 19).

The expression on the right can be evaluated using recursive algorithms whose cost scales just linearly with the number of degrees of freedom and thus provides a computationally tractable method for solving the equations.^5,10,14,25 This recursive algorithm described in detail in ref (5) avoids the computationally intensive inversion of the dense mass matrix shown in the matrix equation in eq 1. We further extended this method to simulate the canonical N, V, T ensemble with constant temperature dynamics using the Nosé–Hoover^36,37 thermostat method. The torsional MD equations of motion for the Nosé–Hoover ICMD method are given below.

3

4

Here 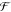is the additional frictional force term due to the canonical ensemble²⁵ which is dependent on η, the dynamic variable representing the thermostat, τ is the mass parameter of the thermostat, T is the instantaneous temperature, and T_B is the thermostat temperature. Since the GNEIMO Nosé–Hoover equations of motion shown above are similar to the equations of motion in eq 1, all the spatial operator equations and factorization discussed in ref (5) hold good for these equations as well. The Nosé–Hoover thermostat mass parameter τ was optimized to be 10 times the time step size for torsional MD simulations.²⁵ The accuracy and stability of the GNEIMO torsional MD simulations were measured by the conservation of the total Hamiltonian and the extent of fluctuations in the temperature. We had applied this form of the GNEIMO method to studying protein dynamics.^7,8 Other research groups such as Brooks and co-workers and Schweiters and co-workers adapted the GNEIMO algorithm into CHARMM and NIH-XPLOR programs for ICMD simulations.^9,27

However, the systematic biases in the probability density functions calculated from ICMD simulations arising from the rigidity of the model remain to be solved. To rigorously correct for the systematic biases in the probability density function caused by treating stiff bond angles as rigid, Fixman proposed a compensating potential of the form¹⁶

5

where 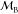denotes the mass matrix in the full BAT coordinates, q₀ the coordinates for the frozen degrees of freedom, k the Boltzmann constant, and T the temperature. While the Fixman potential¹⁶ removes such biases, it was computationally intractable for generalized branched molecules and hence remained untested and unused for several decades for ICMD simulations, except for small model systems such as C4 or C5.^24,31,32 We derived a spatial operator algebra based algorithm that calculates the Fixman potential with just 24% additional cost in the computation time.^17,18 This method which we call GNEIMO-Fixman is rigorous, general purpose, low-cost, and applicable to general linear and branched systems with little additional cost. More significantly, the GNEIMO-Fixman method is also able to compute the partial derivatives of the Fixman potential. These partial derivatives define the additional forces, i.e., the Fixman torque, to be applied within constrained MD simulations. This makes it feasible to use the Fixman potential during the torsional MD simulations and test the effect of the Fixman potential on recovering the accuracy of the probability density functions and the dihedral transition rates.

Testing of the Effectiveness of the Fixman Potential and Torques in Torsional MD Simulations

To study the effectiveness of the Fixman potential in recovering the thermodynamic probability density function of torsion angles, we performed torsional MD simulations with Langevin force for various linear and branched molecular systems without force fields. The effect of the Fixman potential can be most clearly seen by comparing the probability density functions calculated from torsional MD simulations with the Fixman potential to the probability density functions calculated from unconstrained Cartesian MD simulations. The results for the alanine dipeptide are shown in Figure 2. Figure 2 has been adapted from ref (18). Figure 2 shows the joint probability distribution function of the two main chain torsion angles in alanine dipeptide. It is seen from the plots that the torsional MD introduces biases in the joint probability density function that are removed when the torsional MD simulations are performed with the Fixman potential and the torques. The magnitude of the Fixman potential is much smaller in comparison to the potential energy from the all-atom force field. There are some bond angles in the protein that are weakly coupled to the dihedrals and the nonbond forces while other bond angles such as backbone bond angles that show strong coupling to the dihedrals and the nonbond forces. Although the Fixman potential corrects for the errors in the probability density function stemming from treating stiff and uncoupled bond angles as rigid, it does not do so for soft bond angles that couple to the torsion angles or the nonbond interactions.

Figure 2.

Joint probability distribution function of the two backbone torsion angles in alanine dipeptide: (a) Cartesian simulations; (b) ICMD simulations; (c) ICMD + Fixman simulations. The bin size for each axis is dθ = 18°. Material: Reprinted with permission from ref (18). Copyright 2013 AIP Publishing LLC.

There are two approaches for eliminating the bias in the potential energy surface imposed by treating the bond angles that are coupled to torsions and nonbond interactions, as rigid. The first approach is to open up some of the bond angles and treat them as movable degrees of freedom in the ICMD simulations. We refer to this as “hybrid internal coordinate molecular dynamics”. This approach reduces rigidity and the error in probability density function and transition rates, with little impact on time step size. The second approach is to use correction torsional potentials that compensate for the rigidity in the coupled bond angles to recover the probability density function. Examples of this approach are the ECEPP family of force fields^38,39 or ICMFF^9,34 that correct the torsional angle potential for all of the bond angles. The ICMFF corrects the force constants used for the torsional angle potentials by refitting the torsional energy curve obtained from the rigid model to the torsional energy curve calculated using the flexible model. The force constants thus obtained will reproduce the torsion energy barriers of the flexible Cartesian model. Chen et al. showed that this method enhances the number of dihedral transitions during the torsional MD simulations. The possible caveat with this method is that it is not rigorous and is system specific. The ICMFF has been tested for alanine dipeptide and remains to be tested for larger systems. In summary, it is necessary to treat the bond angles that show strong coupling to torsion angles as flexible degrees of freedom in order to achieve thermodynamic accuracy in the probability density function. However, this is not required if the torsional MD simulations are used for structure prediction applications. This is because the goal in structure prediction applications, such as refining the loop structures in proteins, is to enrich the native ensemble by widening the conformational sampling and generally not in recovering the accuracy of the partition function of the Cartesian MD simulations.

Theoretical Methods and Algorithm Development for a Robust Long Time Scale GNEIMO ICMD Simulation Method

Besides the two major challenges (described above) that have hampered ICMD method development, there were other developments that were required to make the ICMD method robust and suitable for long time scale simulations. Several research groups have shown that constrained ICMD models are not the limiting case of stiff Cartesian models.^22,40 To address the differences between constrained ICMD models and Cartesian models of the molecule, we showed that the application of the conventional equipartition theorem that is based on the Cartesian model to the ICMD model in internal coordinates does not yield an equipartition principle analogous to that for Cartesian models. Instead, the ensemble averages involve configuration dependent coupled coordinates, that are not easy to interpret or use. Therefore, we introduced a coordinate transformation to modal coordinates that transforms the system’s kinetic energy into a decoupled form similar to that for Cartesian models. Additionally, we showed that using the “modal velocity” coordinates one can derive an equipartition principle for the ICMD model that is analogous to the one for Cartesian models. This principle holds even though the modal coordinates are not canonical coordinates in the Hamiltonian sense. The equipartition principle based on modal coordinates provides a method for the thermodynamically correct initialization of velocities in ICMD simulations.^14,41

Software and Scalability of the GNEIMO Method

We have developed a modular software package called GneimoSim for efficient implementation of ICMD simulations.³⁵ GneimoSim is quite possibly the first software package to include advanced features such as the ICMD equipartition principle and methods for including the Fixman potential to eliminate systematic statistical biases introduced by the use of hard constraints. Moreover, GneimoSim’s architecture allows it to be extended and easily interfaced with third party force field packages for ICMD simulations. GneimoSim includes interfaces to LAMMPS,⁴² OpenMM,⁴³ and Rosetta force field⁴⁴ packages. The availability of a comprehensive Python interface to the underlying C++ classes and their methods provides a powerful and versatile mechanism for users to develop simulation scripts to configure the simulation as well as to control the simulation flow. GneimoSim has been used for the application studies highlighted in this paper. The alpha version of the GneimoSim software is available for use for the research community at http://dartslab.jpl.nasa.gov/GNEIMO/index.php.

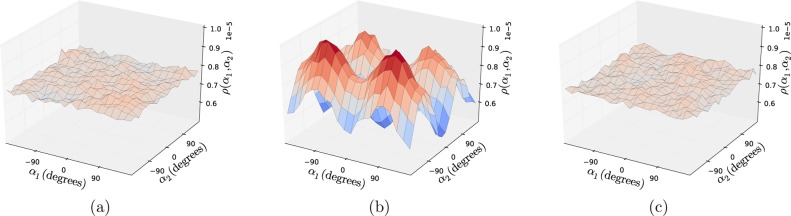
In Figure 3, the blue line shows the average run time for a simulation for the start-up and solution of the equations of motion in the GNEIMO algorithm without using a force field. It shows the effective linear scaling of the dynamics equations solver cost for the GNEIMO method in GneimoSim. The average run time for calculating the forces using OpenMM with GBSA (on a GPU) and using LAMMPS and Rosetta force fields on a CPU are shown in yellow, red, and green lines, respectively. The cost of running the equations of motion solver in GNEIMO is equivalent to the force field cost of using the AMBER force field with the generalized Born solvation module on GPU using the openMM force field engine. However, for larger systems, the cost of the GNEIMO equations of motion solver will have a linear dependence while the cost of the calculation of forces will show a higher order increase in computational time. Additionally, the increase in computational time for ICMD is compensated to an extent by the ability to take larger time steps than are possible in a Cartesian simulation.

Figure 3.

Average run times per step for the GneimoSim simulation using different force fields. Systems tested correspond to different proteins with increasing residue number. Standard clustering was used. 7165 cluster = human alpha-2-macroglobulin with 20 426 atoms. Material: Reprinted with permission from ref (35). Copyright 2014 Wiley Periodicals Inc.

Capabilities in the GneimoSim Software

We have implemented in GneimoSim several methods that are routinely used in MD simulations such as

• 1.Advanced integrators including Runge–Kutta, Lobatto, adaptive CVODE, and Verlet integrators for stable long time scale (microseconds) torsional MD simulations.¹⁴
• 2.An adaptation of the generalized Born solvation method (GBSA) for implicit solvation.
• 3.Support for multiple molecules of any type, including explicit solvent.
• 4.A temperature-based replica-exchange (REMD) method⁴⁵ in which temperatures may be switched randomly or probabilistically using the Metropolis algorithm.
• 5.Periodic boundary conditions for simulations with explicit water.
• 6.Support for standard Cartesian simulations for comparison.
• 7.User defined harmonic distance restraints between pairs of atoms.
• 8.More recently, we have added Langevin dynamics⁴⁶ and accelerated MD (aMD)⁴⁷ methods to GneimoSim.

3. Results and Discussion

Building a Multiscale Simulation Method with ICMD

The BAT coordinates are natural coordinates to describe a bonded system like proteins and polymers. They also lend themselves readily to freezing and thawing any internal coordinate degree of freedom. For example, many torsional degrees of freedom can be kept constrained during dynamics such as freezing a whole helixin a protein structure, if needed. This freeze and thaw can be done at the start of the simulation or during the course of the MD simulations in the GNEIMO ICMD method. We refer to the freeze and thaw technique on the fly during the dynamics simulations as “dynamic clustering”.¹⁴ The dynamic clustering scheme can be applied automatically on the basis of user specified criteria to freeze and thaw internal coordinate degrees of freedom. The default clustering scheme for the GNEIMO torsional MD treats all the torsions of the backbone and main chain as degrees of freedom. All-torsion MD simulations may not be adequate for simulating long time scale events such as large conformational changes in proteins. Adaptable clustering strategies that allow change in the cluster model of the protein during the simulations are more suitable for simulating large conformational changes. Poursina et al. demonstrated the use of an adaptive clustering strategy for RNA simulations.⁴⁸ Wagner et al. used criteria to freeze secondary structure elements when performing folding simulations at high temperature replicas and allow them to thaw at lower temperature replicas. This approach was taken from methods described in a previous work.²¹ However, it should be noted that, since the freeze and thaw mechanism can alter the pathway of the process being simulated, it is advisable to use this method for conformational search purposes only. Other criterion to freeze or thaw a degree of freedom is by using an upper threshold for the velocity, a hinge can be treated as flexible if its velocity stays closer to the threshold velocity. This ensures that torsions that undergo significant motion are not treated as rigid. Additionally, monitoring the accumulation of stress forces at a hinge that is treated rigid can be used to make it flexible. This strategy has not yet been implemented in the GneimoSim code.

Freeze and Thaw Scheme for Folding Proteins

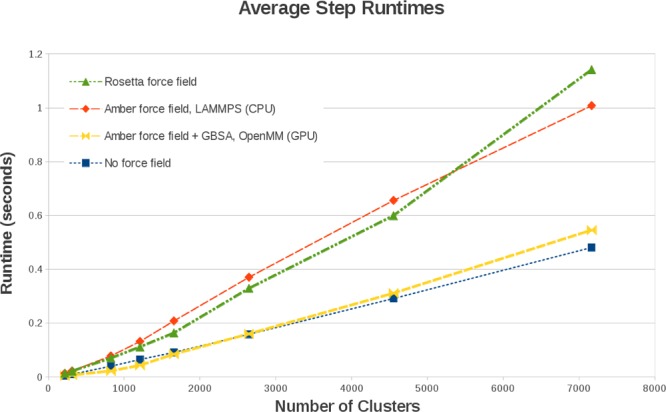
We have used the freeze and thaw strategy to fold four proteins starting from their respective extended structure. The secondary structure elements were predicted using sequence information and built into the extended structure. GNEIMO torsional MD with the replica exchange method was used to run the folding simulations. The adaptive time step CVODE⁴⁹ integrator using the Adams–Moulton method was used in simulations for dynamic clustering. The CVODE adaptive integrator ensures stable simulations while allowing rapid conformational sampling of clustered rigid bodies, by adjusting the time step size to avoid clashes that destabilize the MD simulations. Using the MD trajectory of the B domain of staphylococcal protein A, we calculated the population density histogram shown in Figure 4. This figure also shows the corresponding representative structures from each of the conformational clusters. The x-axis is the root-mean-square deviation (RMSD) of the backbone atom coordinates from the crystal structure. Most of the conformations of 1BDD fall between 5 and 7 Å. We used 12 temperature replicas ranging from 300 to 1050 K. The folding process begins with the extended structure with just the predicted helices using secondary structure prediction methods. Initially, a small number of interhelical contacts are made that collapses the structure to a RMSD range of 12–16 Å. At 8–11 Å, slightly incorrect protein topologies are explored that finally fold to the correct topology below 7 Å. This example demonstrates the rapid conformational sampling realized using the dynamic clustering strategy.

Figure 4.

Backbone CRMSD histogram of a “dynamic clustering” replica-exchange simulation of 1BDD, beginning from an extended conformation containing predicted secondary structure elements with representative structures. Helices treated as rigid bodies are shown in broad ribbons. Material: Reprinted with permission from ref (14). Copyright 2013 Wiley Periodicals Inc.

Studying Domain Motion with GNEIMO

Large scale domain motion caused by the low frequency modes in a protein are often difficult to capture with Cartesian MD simulations. The conformational transitions between the substates are often affected by long time scale and rare events difficult to capture within the relatively short (hundreds of nanoseconds) time scale MD simulations. Enhanced sampling methods are therefore often used to simulate the conformational transitions in proteins.^47,50−53 Some of the enhanced sampling methods require explicit knowledge of the conformations for which the transitions are being simulated, and therefore not readily applicable to unknown systems. The temperature based REMD method when used with Cartesian MD simulations often leads to unraveling and reforming of secondary structure motifs. Thus, the transitions are wasted in high frequency modes and the extra thermal energy is not focused on searching in the low frequency modes. We studied the use of REMD with GNEIMO torsional MD simulations to see how effective they are in conformational search in two highly flexible proteins, namely, fasciculin and calmodulin.¹³ Calmodulin is a calcium signaling protein that belongs to the EF-hand family of proteins. The three-dimensional structure of calmodulin consists of two domains, namely, the amino terminus (N-terminus) domain and the carboxy-terminus (C-terminus) domain, that are connected by a long helical stretch. Calmodulin is a dynamic protein that exhibits major conformational changes in response to calcium binding as revealed by NMR studies.⁵⁴⁻⁵⁶ Upon binding to calcium, calmodulin samples a large ensemble of structures that allows it to bind to a wide range of proteins. There are several experimental studies on the dynamics and conformational changes in calmodulin. These studies show that there are two major steps involved in the conformational changes: (1) upon removal of the bound calcium, the central helix that connects the carboxy terminal domain and the amino terminal domain collapses followed by (2) the dynamics of the N-terminus domain relative to the static C-terminus domain.^54,55 Cartesian MD simulations in explicit solvent showed the collapse of the central helix connecting the two domains but could not map the entire dynamics ensemble obtained from the NMR study.^57,58 The GNEIMO-REMD simulations with no bias potential were performed on the entire calmodulin protein. The trajectory showed conformational sampling of the collapse of the central helix, and the sampling of various conformations resulting from the relative reorientation of the two domains. Although the collapse was observed in the Cartesian MD, the flexibility of the N-terminus domain was observed only in the GNEIMO-REMD simulations. Comparison of the ensemble of conformations of the carboxy terminus domain to the ensemble of conformations from NMR experiments is shown in Figure 5. It is seen that the GNEIMO conformations (shown in blue in Figure 5) cover most of the NMR conformations.

Figure 5.

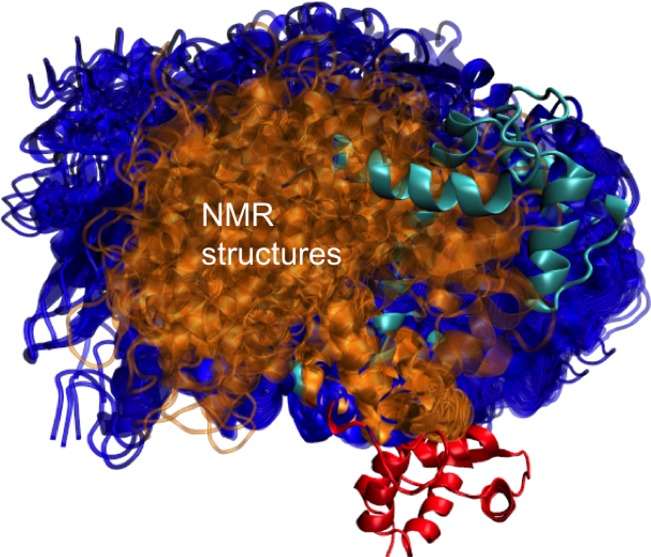
Overlay of the conformations sampled in the GNEIMO-REMD torsional MD simulations (shown in blue) of calmodulin without calcium, to the NMR structures pdb ID: 1DMO (shown in gold).

Quantitative comparison of the average hydrogen bond distances between residues showing hydrogen bonds in the NMR structures⁵⁶ (PDB ID: 1DMO) to those in the GNEIMO-generated trajectories shows that about half of the average distances calculated fall within one standard deviation of the corresponding distances in the NMR structures. GNEIMO torsional MD simulations on proteins such as crambin and BPTI at 310 K have shown that the correlations in the torsional motions of residues that are farther apart in space can be captured in a shorter simulation time scale than with Cartesian MD simulations. For example, in the case of BPTI, analysis of correlation in the backbone torsion angles⁵⁹ of residues in two loops connected by a disulfide bond was shown to be strong in the millisecond level simulations of Shaw and co-workers.⁶⁰ We have shown that we could capture the torsional angle correlations between residues 9 to 18 and residues 35 to 40 in 100 ns of NVT GNEIMO torsional MD simulations at 310 K.¹³

Application of GNEIMO to Protein Structure Refinement

The GNEIMO algorithm has been implemented in the software package CYANA for NMR structure refinement²⁹ and in NIH-XPLOR for X-ray crystal structure refinement.²⁷ Brooks and co-workers have tested torsional MD simulations based on the GNEIMO algorithm for few proteins.⁹ However, this method has not been tested for refining protein homology models of lower accuracy compared to their respective crystal structures. Due to the large number of protein structures of similar proteins available in the protein data bank, homology or template based modeling of related protein sequences has been shown to be the most feasible and accurate method of predicting protein structures. However, the target sequence has to have a > 60% sequence similarity to the template crystal structure. The accuracy of the model derived using homology modeling methods depends on the sequence similarity between the template and the target. There is an increasing need for high throughput computational methods that refine low accuracy homology models.⁶¹ Using Cartesian MD simulation methods leads to refined structures only when used with restraints—with the choice of restraints remaining arbitrary and system dependent and hence difficult to automate.^9,62−67 Starting from the homology based models, robust structure refinement methods are important to derive high useful accuracy models.

An efficient conformational sampling method and an accurate energy function to identify the native structure are the two important components of a structure refinement algorithm. We have evaluated the usefulness of the conformational sampling afforded by GNEIMO-REMD with the generalized Born solvation method in enriching the refined structures compared to the starting decoy. This has been studied for 30 CASP target proteins and other small proteins.^11,12 The GNEIMO-REMD method leads to a refinement of up to 1.3 Å for 28 out of 30 CASP target proteins. These torsional MD simulations using GNEIMO were done without any experimental information as restraints. Figure 6 shows the contact map for one target (T0453) as an example of the refinement using the GNEIMO method. Figure 6 shows the contact map for refinement of the target protein T0453. The contact map shows far is a given residue in the GNEIMO refined model from its crystal structure. The white color regions indicate the residue positions that are closer to the native structure than the residues in the deep red regions. It is evident from Figure 6 that the GNEIMO refined structure shows significant refinement in the packing of the loop structure against the core of the protein. The long-range contacts between the loop residues 30 to 40 to those residues between 40 and 60 improve remarkably from 14 to 16 Å to 2 to 4 Å, as seen in Figure 6.

Figure 6.

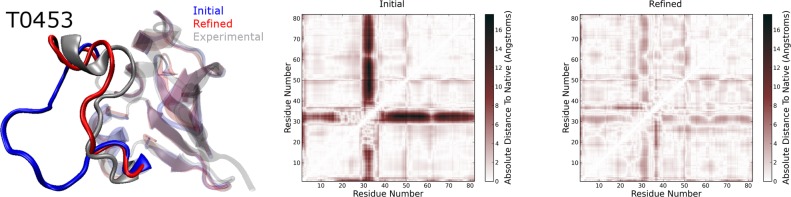
Refinement of the loop structure of the CASP target T0453. The contact map shows the distance to the decoy structure, and the contact map in the third column shows how far each residue is refined corresponding to the native structure. Material: Reprinted with permission from ref (12). Copyright 2014 American Chemical Society.

While the GNEIMO method leads to substantial refinement in the loop packing, the unconstrained Cartesian REMD method shows unraveling and reformation of secondary structure elements and hence is less effective in conformational search. Thus, starting from homology models of varying accuracy, the GNEIMO method shows improvement in structure refinement without unraveling the structures. The overall extent of refinement across many targets was modest and needs further improvement. Additionally, the challenging problem of picking the best refined structure still remains.

4. Conclusions

Future Advancements in the GNEIMO ICMD Simulation Method

The ICMD simulation method is not a replacement for the Cartesian MD method. We envision developing an ICMD simulation method to perform MD simulations in bond, angle, and torsion (BAT) coordinate systems. Such a MD simulation method is highly suitable for selecting and controlling the granularity of the dynamics model of proteins and polymers, and is a foundation for the development of multiscale simulation methods for the simulation of protein macromolecular complexes. The multiscale ICMD simulation method can also be used for real space refinement of structural model fitting to low resolution crystallography or electron microscopy data of large protein complexes.⁶⁸ Such a multiscale MD method is not available to date.

Currently, studies of the large scale dynamics that govern protein function commonly use all-atom Cartesian MD simulations, often with geometric constraints. Such geometric constraints can adversely impact the integration time-step size and the stability of the dynamics. On the other hand, such constraints to ICMD models are straightforward. ICMD simulations thus yield larger integration time steps. Our recent theoretical developments based on spatial operator algebra have led to a robust long time scale ICMD simulation method GNEIMO and associated toolkit known as GneimoSim. We have demonstrated the power of the GNEIMO ICMD technique with applications to protein domain motion studies and homology model refinement studies. The results of these applications have shown great promise in the wider use of this ICMD technique. However, there remain extensions of the methods that need to be addressed to harness the advantages of ICMD methods to their fullest. Some of the possible extensions are the following:

• 1.To calculate accurate conformational entropy using the GNEIMO torsional MD simulation trajectories with the quasi-harmonic analysis (QHA) method to improve the accuracy while correctly including traditionally difficult metric tensor correction terms.⁶⁹
• 2.The second advancement in ICMD simulations will be to extend the ICMD simulation method to allow movement of certain bond angles that show strong coupling to the dihedral angles. For example, it has been shown that the bond angle hinged on the Cα atoms of a protein have strong coupling to the backbone dihedral angles.⁷⁰⁻⁷³ We will extend the GNEIMO ICMD method to free up desired bond angle degrees of freedom. This will lead to a comprehensive suite of hybrid ICMD models that bridge the wide gap between coarse grain torsional MD and fine grain all-atom MD models. These hybrid ICMD models, with all bond angles open, can also be used for accurately calculating conformational entropy as discussed here.
• 3.GneimoSim software has enhanced sampling methods such as Langevin dynamics, replica exchange method implemented. GNEIMO can be readily combined with other enhanced sampling techniques such as steered MD, umbrella sampling, or accelerated MD (aMD)⁴⁷ to name a few.

With these improvements, the GNEIMO method will be useful for applications to large protein dynamics simulations with explicit solvent. The GNEIMO method can be used with any type of force field such as an all-atom force field or a coarse grain force field. We also envision using the GNEIMO torsional MD method combined with the torsional Monte Carlo method for protein structure prediction applications. In summary, the GNEIMO method offers a comprehensive ICMD simulation method that allows easy coarse graining of the dynamics model ranging from all-atom to large domains of proteins being treated as clusters.

Biographies

Nagarajan Vaidehi is a Professor in the Department of Immunology at the Beckman Research Institute of the City of Hope Cancer Center in Duarte, CA. She received her M.S. and Ph.D. in Theoretical Chemistry from the Indian Institute of Technology, India. Her research interests are in the area of developing molecular dynamics methods to study the long time scale structural dynamics of proteins. Her research focus is also in applying these methods to understand the mechanism of activation and design drugs for the superfamily of membrane proteins called the G-protein-coupled receptors.

Abhinandan Jain is a Senior Research Scientist at the NASA Jet Propulsion Laboratory (JPL) in Pasadena, CA. He received a Ph.D. from the Rensselaer Polytechnic University in 1986. His research interests are in the area of computational dynamics and control for robotics, aerospace, and biomolecular application domains. He leads the JPL DARTS Laboratory, which is responsible for the development of advanced physics-based modeling, theoretical techniques, and software tools for NASA space missions.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States