Computational Study of the “DFG-Flip” Conformational Transition in c-Abl and c-Src Tyrosine Kinases

Abstract

Protein tyrosine kinases are crucial to cellular signaling pathways regulating cell growth, proliferation, metabolism, differentiation, and migration. To maintain normal regulation of cellular signal transductions, the activities of tyrosine kinases are also highly regulated. The conformation of a three-residue motif Asp-Phe-Gly (DFG) near the N-terminus of the long “activation” loop covering the catalytic site is known to have a critical impact on the activity of c-Abl and c-Src tyrosine kinases. A conformational transition of the DFG motif can switch the enzyme from an active (DFG-in) to an inactive (DFG-out) state. In the present study, the string method with swarms-of-trajectories was used to computationally determine the reaction pathway connecting the two end-states, and umbrella sampling calculations were carried out to characterize the thermodynamic factors affecting the conformations of the DFG motif in c-Abl and c-Src kinases. According to the calculated free energy landscapes, the DFG-out conformation is clearly more favorable in the case of c-Abl than that of c-Src. The calculations also show that the protonation state of the aspartate residue in the DFG motif strongly affects the in/out conformational transition in c-Abl, although it has a much smaller impact in the case of c-Src due to local structural differences.

Introduction

Protein tyrosine kinases are crucial functional elements of cellular signaling pathways regulating cell growth, proliferation, metabolism, differentiation and migration. In their active state, tyrosine kinases catalyze the transfer of γ-phosphate of an adenosine triphosphate (ATP) molecule covalently onto a tyrosine residue in substrate proteins and peptides. To maintain normal regulation of cellular signal transductions, the activity of tyrosine kinases is tightly regulated.¹⁻⁶ Mutations of certain residues can disrupt normal inhibitory mechanisms and make tyrosine kinases constitutively active, leading to a number of diseases, particularly cancers.⁷⁻⁹ For this reason, kinases represent attractive drug targets for certain types of cancers.^3,10−12 Designing inhibitors that are targeting specific tyrosine kinases in the active state is, however, difficult because they all present structurally similar catalytic pockets¹³ owing to the common enzymatic function requiring ATP binding. Inhibitors that are targeting inactive conformations of the kinases appear to be more selective.¹¹ One notable example of inhibitors targeting an inactive state of tyrosine kinases is Gleevec (Novartis). Gleevec is used to treat chronic myeloid leukemia (CML), which is caused by Bcr-Abl kinase.¹⁴⁻¹⁶ It is also a potent inhibitor of receptor tyrosine kinase PDGFR and c-Kit.^11,17

As is observed in the X-ray crystallographic structures of c-Abl in complex with Gleevec, the conformation of a three-residue motif comprising Asp381-Phe382-Gly383 (DFG, c-Abl 1a numbering) near the N-terminus of the activation (A-) loop covering the catalytic side is critical for Gleevec binding.^16,18,19 Gleevec only binds a particular conformation called DFG-out in which the DFG motif is flipped by almost 180° relative to the standard active conformation (DFG-in). The conformation change alters the local shape of the binding pocket, creating more space to accommodate Gleevec. The conformation of the DFG motif is also an important component of the overall regulatory mechanisms for c-Abl kinase.^6,20,21 In the active state, the DFG motif is involved in catalysis by coordinating the binding of magnesium ions through its aspartate residue.⁵ In the DFG-out conformation, the aspartate residue points away from the active site, resulting in a loss of coordination with magnesium ions. Furthermore, the DFG-out conformation also correlates with a disruption of the structural integrity of the hydrophobic spines, which are critical element of an active catalytically competent kinase.^12,22,23 In the DFG-out conformation, the side chain of Phe382 occupies the active site, which disrupts ATP binding. Hence, DFG-flip not only disassembles the regulatory (R-) spine but also breaks the catalytic (C-) spine. The X-ray crystallographic structure of the down-regulated state of c-Abl kinase displays a DFG motif in the out conformation.^20,21 Besides being observed in protein tyrosine kinases, the conformational change has also been noted in serine/threonine kinases as well (e.g., in B-Raf²⁴), which highlights its importance in the protein kinase domain activation/deactivation.

The remarkable effectiveness of Gleevec raised the hope that one might be able to develop novel cancer treatments by designing a variety of specific kinases inhibitors. However, the situation is complicated by the fact that Gleevec displays a much lower inhibitory effect on c-Src, even though these two kinases display a high level of sequence identity (47%) and similar structural scaffolds (active conformation of the kinase domains shown in Figure S1).²⁵ A simple conformational selectivity mechanism was proposed to account for the difference in Gleevec binding based on the assumption that c-Src cannot adopt the DFG-out conformation. Indeed, unlike c-Abl kinase, the X-ray crystallographic structure of the down-regulated (autoinhibited) state demonstrates that c-Src still adopts the DFG-in conformation.²⁶ The autoinhibition in c-Src kinase domain comes from the outward rotation of the αC-helix, which breaks the R-spine and a catalytically important salt-bridge, and from the partially folded (“closed”) conformation of the A-loop which occludes both binding of substrates and exposing tyrosine 416 (chicken c-Src numbering). However, a subsequent discovery of c-Src kinase structures in complex with Gleevec and several other inhibitors in which the DFG motif is in the “out” conformation clearly demonstrates that this state is accessible.^25,27,28 Therefore, it seems likely that the inactive DFG-out conformation is a genuine aspect of the regulatory mechanism for these kinases. Then, interesting questions such as what is (are) the difference(s) between DFG-flips in c-Abl and c-Src, whether DFG-flip is a competing mechanism that controls the activation of c-Src, and whether there are multiple pathways for DFG-flip that would naturally arise. A better understanding of DFG-flips in c-Abl and c-Src kinases may improve our understanding of kinase regulations and may guide the design of novel kinase inhibitors.

The DFG-flip conformational transition has been the subject of several computational studies.²⁹⁻³⁶ Shan et al. investigated the DFG-flip in c-Abl kinase using long unbiased molecular dynamics (MD) simulations.³² A notable result from these simulations was the suggestion that the protonation state of Asp381 in the DFG motif could serve to promote the in/out conformational transition. Experiments designed to test this idea showed that the binding kinetics of Gleevec to Abl was indeed pH dependent, in apparent accord with the proposed mechanism. However, the equilibrium binding free energy of Gleevec measured experimentally appeared to remain unaffected by pH, in contradiction with the computational results. It was concluded that the protonation state of Asp381 serves as a switch that controls the transition rate without affecting the thermodynamics of Gleevec binding. In another study, Simonson and Aleksandrov calculated the relative binding free energies of Gleevec to DFG-out conformations of c-Abl, c-Src, and other kinases using alchemical free energy perturbation molecular dynamics (FEP/MD) simulations and the molecular mechanics Poisson–Boltzmann with surface area (MM/PBSA) method.²⁹ By observing similar relative binding free energies for c-Abl and c-Src, they inferred that the relative stability of the DFG-out conformation in c-Abl and c-Src should be responsible for the difference in Gleevec binding specificity. Subsequently, Lovera et al. calculated a free energy landscape of the DFG-flip transition in c-Abl and c-Src using meta-dynamics MD simulations with explicit solvent.³¹ The free energies for the DFG-flip from these simulations based on the AMBER force field were 4.0 and 6.0 kcal/mol in Abl and c-Src, respectively. Combining computational investigation with isothermal titration calorimetry, they concluded that the better inhibitory effect of Gleevec on c-Abl was mainly caused by an easier accessibility of the DFG-out conformation in c-Abl compared to c-Src. In addition, their free energy landscape of c-Abl demonstrated large conformational flexibility and hence supported a conformational selection mechanism for Gleevec binding. They also estimated the pK_a values for c-Abl and c-Src for both the DFG-in and DFG-out by extracting protein snapshots taken from the meta-dynamics trajectories and feeding the latter into the program PROPKA (solvent molecules were discarded).³¹ This mixed MD/PROPKA approach yielded pK_a values of 3.4, for c-Abl DFG-in, 4.4 for c-Abl DFG-out, 4.0 for c-Src DFG-in, and 2.6 for c-Src DFG-out. More recently, Lin et al. reported a complete calculation of the binding affinity of Gleevec for Abl and c-Src based on methodology combining alchemical free energy perturbation (FEP) and potential of mean force (PMF) umbrella sampling simulations with explicit solvent molecules.³⁶ The free energies for the DFG-flip from these simulations based on the CHARMM force field were 1.4 and 5.4 kcal/mol in Abl and c-Src, respectively. Although considerable efforts have been devoted to understand the conformational transition of the DFG motif, the impact of the protonation state of the aspartic residue on the free energy surface associated with the conformational transition has not been elucidated.

In the present study, we try to address these questions by determining the conformational transition pathways of the DFG motif in c-Abl and c-Src kinase domain and characterizing the effect of protonation of Asp381 (Asp404) on DFG-flips. A special attention is given to the existence of multiple transition pathways. In order to evaluate the role of DFG-flip in the activation/deactivation of c-Src kinase domain, we put these results within the broader context of the conformational changes involving the αC-helix and the A-loop in c-Src. Free energy landscapes for c-Abl (with Asp381 unporotonated and protonated) and c-Src (with Asp404 unprotonated and protonated) were calculated using two-dimensional (2D) umbrella sampling (US) simulations. As a comparison, we also calculated the free energy landscape associated with the movement of the αC-helix and the A-loop. To facilitate the convergence of US simulations and to reduce the computational cost, the string method with swarms-of-trajectories calculations, was carried out prior to US calculations. With the help of the minimum free energy pathways (MFEPs) determined by the string method, US windows can be initiated in well-relaxed starting configurations for optimal computational efficiency.

Theory and Methods

Simulation Systems

DFG-in and DFG-out conformations of c-Abl kinase domain were prepared based on PDB entry 2F4J(37) and 1OPK,²¹ respectively. For the sake of simplicity, only the kinase domain was considered and the regulatory domains were not included in any of the simulation conducted in this paper. Both crystal structures contain one mutation to the wild-type protein. The mutated residue in each structure was mutated back to the corresponding wild-type sequence. Hydrogen atoms were built to the crystallographic structures using the HBUILD module of CHARMM.^38,41 The all-atom structures were then solvated in a truncated octahedral solvent box constructed from an 86 × 86 × 86 ų cube with 13 688 TIP3P water molecules.³⁹ 45 K⁺ ions and 34 Cl^– ions were added to the system to make it charge neutral, corresponding to a salt concentration of approximately 150 mM. Any ligand or inhibitor was removed from those crystal structures. No ATP or magnesium ions were added to the active site because the DFG motif clashes with ATP in the DFG-out conformation. The entire solvated c-Abl system comprised about 45 000 atoms. DFG-in and DFG-out conformations of c-Src kinase domain were prepared based on PDB entries 1Y57(40) and 2OIQ,²⁵ respectively. The missing part of the A-loop in 2OIQ was built based on 1Y57. Hydrogen atoms were added to the initial structures using the HBUILD module of CHARMM.⁴¹ The all-atom structures were then solvated in a truncated octahedral solvent box constructed from a 80 × 80 × 80 ų cube with 11 216 TIP3P water molecules.³⁹ 22 Na⁺ ions and 19 Cl^– ions were added to the system to neutralize the total charge of the system and to simulate a salt concentration of approximately 150 mM. As in the preparation of c-Abl structures, any ligand or inhibitor was removed from crystal structures. The final c-Src system contained approximately 40 000 atoms. Figure 1 illustrates representatives of the DFG-in active conformation and the DFG-out inactive conformation of c-Abl. The DFG-in and DFG-out conformations of c-Src are similar to those of c-Abl and are not shown. In the above atomic systems, the aspartate residue in the DFG motif is deprotonated. In order to understand how the protonation state of this specific residue affects DFG-flip, we also protonated the aspartate residue for each existing atomic system. One positive ion was removed from each system in order to maintain the charge neutrality.

Figure 1.

Crystal structures of c-Abl kinase domain. (A) DFG-in conformation (PDB code 2F4J). The side chain of Asp381 is pointing toward the active site. (B) DFG-out conformation (PDB code 1OPK). In this conformation, the side chain of Asp381 is pointing away from the active site. In both conformations, the phosphate-binding (P-) loop (residues 248–257, c-Abl 1a numbering), αC-helix (residues 280–294), and activation (A-) loop (residues 381–402) are colored in green, yellow, and orange, respectively.

An alternative conformational change based on the autoinhibitory conformation of c-Src was also considered and compared with the DFG-flip. To accomplish that, the inactive and active conformations of c-Src kinase domain were prepared based on PDB entries 2SRC(26) and 1Y57,⁴⁰ respectively. Since the DFG motif did not flip in this case, an ATP molecule and two magnesium ions were added to the active site. The solvated systems contain the same number of water molecules and ions and have the same shape and size as described in the deprotonated c-Src system. c-Src kinase domain in its active and inactive conformations is presented in Figure 2.

Figure 2.

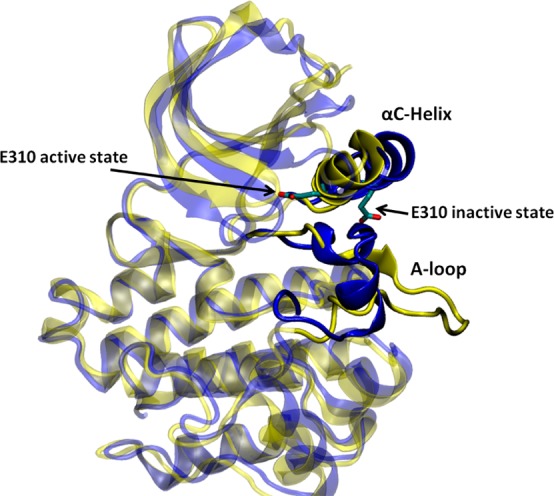
Kinase domain of c-Src in the down-regulated (colored in blue, PDB code 2SRC) and active (color in yellow, PDB code 1Y57) conformation. The E310 (chicken c-Src numbering) in the αC helix is shown to demonstrate the movement of the αC helix. E310 is pointing outward in the inactive conformation, whereas it is pointing inward in the active-like conformation. The A-loop is partially folded in the inactive kinase, but it becomes fully extended in the active-like conformation.

All energy minimization and MD propagations (including string method and umbrella sampling calculations) were performed using version 2.7 of the molecular simulation package NAMD⁴² and the CHARMM27 force field.⁴³ The isobaric–isothermal ensemble was employed for all MD calculations. The pressure and temperature were controlled by the Langevin piston method⁴⁴ and Langevin dynamics and kept at 1 atm pressure and 300 K, respectively. Periodic boundary conditions were applied and particle mesh Ewald (PME)⁴⁵ was used to treat long-range nonbonded interactions. The short-range nonbonded interactions were truncated at 12 Å, with a switching function turned on from 10 to 12 Å. The nonbonded list was updated at every MD step with a cutoff distance of 16 Å. Covalent bonds involving hydrogen atoms were constrained at their equilibrium distances.⁴⁶

The solvated DFG-in and DFG-out systems were initially subjected to energy minimization of 200 steps using steepest descent algorithm. Next, they were equilibrated using the following procedures: each system was first equilibrated with harmonic restraint (force constant is 1 kcal/(mol·Å²)) on all the non-hydrogen atoms for 200 ps, then only on Cα atoms for 300 ps, and further equilibrated for another 2 ns without any restraint. The stability of each solvated protein system was monitored by the fluctuation of the root-mean-square deviation (rmsd) of Cα atoms relative to the corresponding crystal structure during the 2 ns of MD equilibration process (see Figure S2). Each system had shown a plateau around 1.5 Å. Thus, our simulation protocol of equilibration was able to maintain the overall structures. The resulting structures (final snapshots) were used as the end-points in string method calculations.

String Method with Swarms-of-Trajectories Calculations

Even though a direct measurement of the time-scale of DFG-flip in either c-Abl or c-Src is lacking, nuclear magnetic resonance spectroscopy of DFG-flip in mitogen-activated protein kinases (MAPK) p38α suggested a time-scale of millisecond.⁴⁷ This time-scale suggests that studying DFG-flip with brute force MD appears impractical. To overcome this time-scale gap, the string method with swarms-of-trajectories⁴⁸ was employed in our study. The string method with swarms-of-trajectories aims to discover the MFEP connecting two stable conformations in a space defined by a set of “collective variables” (CVs).^48,49 In this method, a pathway (string) is represented by a parametrized curve z(i), where i = 0 is the starting state and i = 1 is the ending state. In practice, the curve is discretized into a “chain of images”, representing configurations along the transition pathway. The average drift for an ensemble (swarm) of unbiased short trajectories is calculated. Each image is refined until the “dynamical propagation” is such that each image evolves only along the pathway on average. The propagation–refinement process is iterated until the MFEP is found. A more detailed description of the methodology, realization, and how to compute a free energy profile along a string with mean force calculation is given in Supporting Information. The CVs that were utilized to characterize DFG-flip are given in Table S1. For both c-Abl and c-Src, two end-points obtained from the structural relaxation stage were used to generate an initial string, via targeted MD (TMD). In both cases, the DFG-out conformation was chosen to be the “target”. Instead of application of a harmonic restraint on the rmsd with reference to the DFG-out structure, a weak harmonic restraint on the non-hydrogen atoms was used so that the TMD would converge faster. TMD simulations were carried out for 10 ps with a force constant of 1 kcal/(mol·Å²). Twenty-nine snapshots were extracted from each TMD simulation such that those configurations in a string were approximately equally distant in the CV space. Therefore, each string consists of a total of 31 images, where image 0 represents the DFG-in conformation and image 30 is the DFG-out conformation.

Using string method in practice still requires caution because it requires an initial pathway obtained from targeted MD or steered MD calculation. The effect of the unphysical biasing force is always a concern for the transition pathways generated by those methods.⁵⁰ Applying to complicated free energy landscape, string method calculations may not yield the global MFEP or may miss one or more important pathways. The problem regarding multiple pathways might be especially severe when there are competing pathways. In fact, all methods based on pathways are susceptible to the issue of multiple pathways. To address the issue of multiple possible pathways in string method, four pathways were considered when studying DFG-flip in c-Abl. There were two possible directions (clockwise or counterclockwise) to “flip” either the aspartate or the phenylalanine residue in the dihedral angle space. Thus, a total of four different combinations could be found to achieve “in” to “out” transition. Each one of the four combinations corresponds to one possible pathway. The labels of those four possible pathways and their corresponding rotations can be found in Table S2. Pathway 1 was obtained from the TMD calculation mentioned above. Another nine TMD simulations were launched with different initial velocities. Those TMD simulations could only generate one new pathway: pathway 4. Therefore, pulling simulations in dihedral angles were required to produce initial strings of pathways 2 and 3. In a pulling simulation, a harmonic biasing potential with its center changing as θ(t) = θ(α=0) + [θ(α=1) – θ(α=0)]·t/t_s, where t was the actual time in simulation, t_s was the total pulling time, and α was the parameter described in the string method algorithm, was applied on each dihedral angle. The pulling in dihedral angles were performed for 10 ps with a force constant of 500 kcal/(mol·rad²).

All strings were iterated following the five-step procedure that is described by Pan et al.⁴⁸ For each of the 31 images, a swarm of 20 unbiased MD trajectories was launched with different seed to randomize initial velocity; each lasted 5 ps in length. Then the trajectories in a swarm were averaged to provide an updated image. Once this averaging was completed for all the images, the string was smoothed, reparametrized, and relaxed for 200 ps. The resulting structures were then averaged, followed by smoothing, reparametrization, and equilibration. Except for pathway 2 (reason explained later) of c-Abl, each string was iterated 50 times. The convergence of string iterations (displayed in Figure S3) was monitored by examining the Euclidean distance in CV space of an image relative to the corresponding image in the initial string, as a function of iteration index. In both systems, strings gradually evolved away from the initial one and stabilized. To further confirm convergence, the same measure relative to the string at iteration 50 (final iteration) was also applied. As expected, plateaus were also found near iteration 50 for each pathway. This behavior suggests that the last a few iterations were close to convergence. The converged strings were then used to initiate the US simulations for optimal computational efficiency.

Umbrella Sampling Calculations

The PMF along one or more order parameters (ξ) is a central quantity when exploring conformational transitions such as the DFG-flip. It illustrates the free energy landscape that governs the conformational transition. US⁵¹ simulations are often employed to generate PMFs. All-atom umbrella sampling simulations have been performed previously to elucidate activation mechanisms of Src-family kinases in the view of free energy landscapes. Results from those calculations indicate that utilizing umbrella sampling method to explore kinase conformational equilibrium is feasible. In this study, we performed 2D US calculations to study the DFG-flip conformational transition in c-Abl and c-Src kinases. Two dihedral angles were utilized as order parameters in order to characterize the flip of aspartate and phenylalanine residues. A harmonic biasing potential with a force constant of 0.02 kcal/(mol·deg²) and a uniform spacing of 5° was applied on each order parameter.

In the case of c-Abl, dihedral angles C_β(Ala380)–C_α(Ala380)–C_α(Asp381)–Cγ(Asp381) and C_β(Ala380)–C_α(Ala380)–C_α(Phe382)–Cγ(Phe382) served as order parameters in the US calculations. A graphical representation of the two order parameters is given in Figure 3A. In order to probe the effect of multiple pathways, the entire range (from −180° to 180°) of each dimension should be covered. Hence, a total of 5184 (72 for each dimension) umbrella windows were employed. Strings from the last iterations were utilized to provide a starting structure for each umbrella window in such a way that the chosen image was closest to that window.

Figure 3.

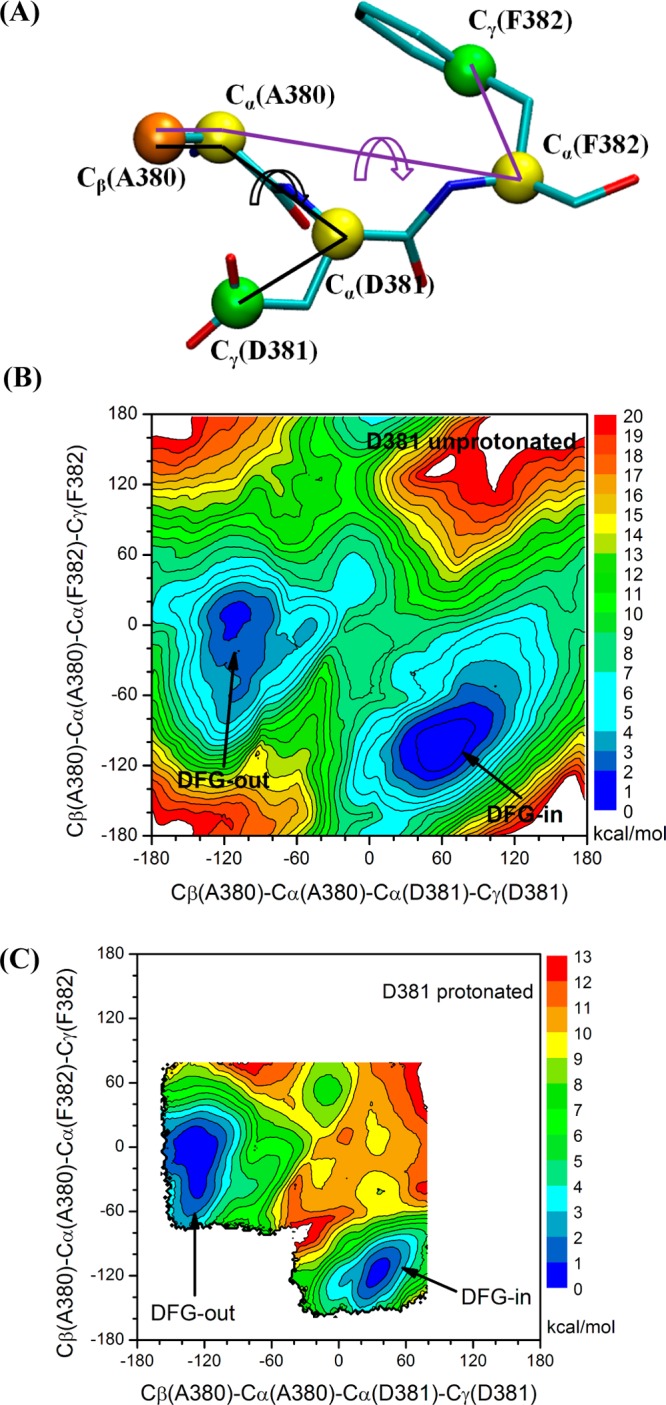
2D PMF of the DFG-flip conformational transition in c-Abl. All units of the 2D PMFs are in kcal/mol. (A) Graphical representation of the order parameters used in 2D PMF. (B) Asp381 deprotonated. (C) Asp381 protonated; US windows are focused on pathway 1 in order to reduce the computational cost because only the thermodynamic properties are considered when investigating the impact of Asp381 protonation. The free energy basin to the left corresponds to the DFG-out conformation.

Dihedral angles C_β(Ala403)–C_α(Ala403)–C_α(Asp404)–C_γ(Asp404) and C_β(Leu407)–C_α(Leu407)–C_α(Phe405)–C_γ(Phe405) were the order parameters in the US simulations of c-Src. Figure 4A illustrates both order parameters in this set of umbrella sampling calculations. In order to save the computational cost, US windows only populated the vicinity of the converged strings. By integration with string method calculations, computational resource can be focused on sampling the low free energy valley along the transition pathway rather than on exploring the high free energy region. The same strategy can be extended to studying conformational transitions with other enhanced sampling method, such as metadynamics. Therefore, 401 umbrella windows were employed to patch the “in” and “out” conformations in the case of c-Src. The starting structure of an umbrella sampling window was taken from the final string, based on the same manner as used in c-Abl. To directly address the effect of protonation of Asp381(Asp404) on the free energy difference between DFG “in” and “out” conformations, we carried out another set of US calculations in which Asp381(Asp404) became protonated. 1481 umbrella windows were used in the case of c-Abl, while the same 401 windows were employed for c-Src.

Figure 4.

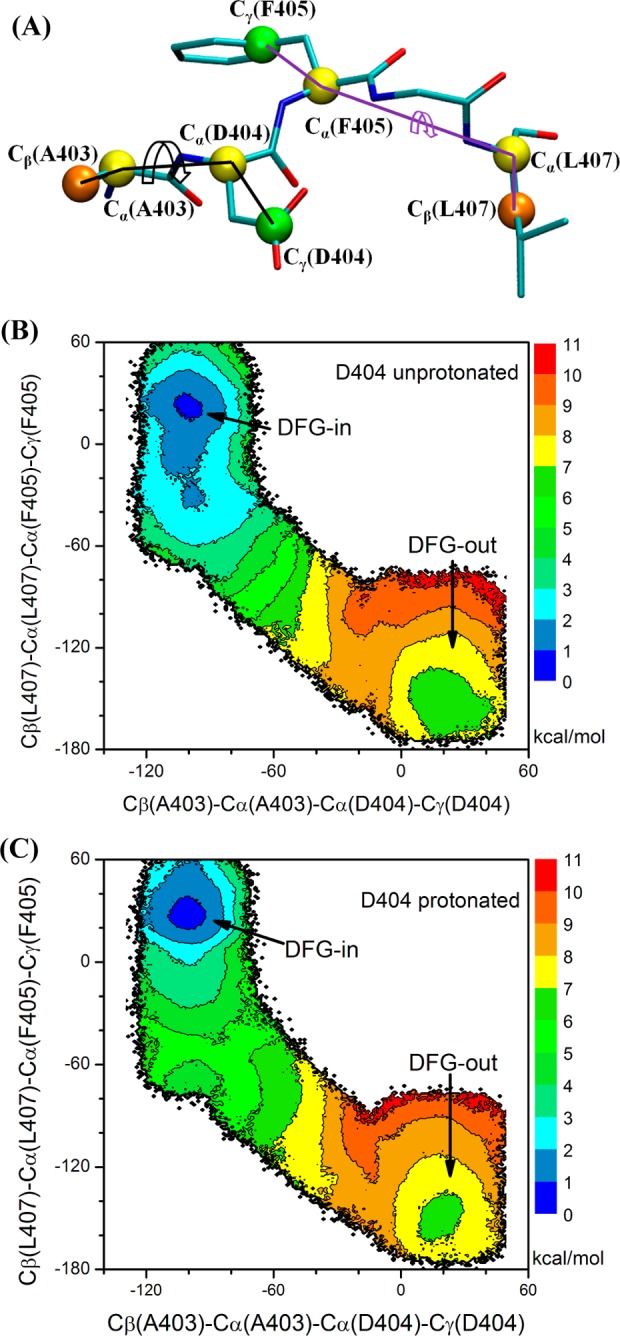
2D PMF of the DFG-flip conformational transition in c-Src. All units of the 2D PMFs are in kcal/mol. (A) Graphical representation of the order parameters used in 2D PMF. (B) Asp404 deprotonated. (C) Asp404 protonated. The free energy basin on the lower right corner corresponds to the DFG-out conformation.

We also launched 2D self-learning adaptive US calculations⁵² to explore the free energy landscape of conformational transition involving the αC helix and the A-loop in the case of c-Src. The difference between Glu310–Arg409 salt-bridge distance (d₁) and Glu310–Lys295 salt-bridge distance (d₂) was used to characterize the rotation of αC helix during the activation process, while the average of three distances (d₃) was used to reflect the opening of A-loop in the process. Those three distances are between O(Asp413) and N(Thr417), O(Asn414) and N(Ala418), and O(Glu415) and N(Arg419). A self-learning adaptive US approach was employed to concentrate sampling to a region where the free energy is less than 7.2 kcal/mol and is within 1 Å distance to the projection of the converged string. A harmonic biasing potential with a force constant of 20 kcal/(mol·Å²) and a uniform spacing of 0.25 Å were applied on each order parameter. A total of 1101 umbrella windows were used in this set of umbrella sampling calculations. A total of 4.5 ns of MD propagation was carried out per US window for all US calculations. Thus, approximately 30.0 and 8.6 μs of aggregate sampling time was spent on the c-Abl and c-Src US calculations, respectively. The time series generated during the last 4 ns of simulations were used by the weighted histogram analysis method (WHAM)^53,54 to generate 2D PMFs. To evaluate the convergence of the free energy landscape, 2D PMFs generated using the last 3 and 4 ns of simulation data (as shown in Figure S4) are compared. The root-mean-squared error (rmse) between the 2D PMFs is 0.16 and 0.59 kcal/mol for c-Abl and c-Src, respectively. Such small rmse values suggest that adding one more nanosecond of sampling time for each window yielded almost identical PMFs, indicating that converged 2D PMFs have been obtained.

Results and Discussion

Free Energy Landscape of DFG-Flip in c-Abl

The 2D-PMF of DFG-flip in c-Abl with Asp381 deprotonated is shown in Figure 3B. The PMF is representative of a two-state equilibrium between DFG-in and DFG-out conformations. The free energy basin around (60°, −100°) corresponds to the DFG-in conformation, while the basin around (−100°, 10°) corresponds to the DFG-out conformation. The lowest free energy barrier separating the “in” and “out” conformations is ∼7 kcal/mol, which reflects that DFG-flip in c-Abl is unlikely to be a fast transition. To the best of our knowledge, no direct measurement of the time-scale of DFG-flip is available for c-Abl from experiments. Vogtherr et al.⁴⁷ have shown that the DFG-flip in MAPK p38α takes place on a millisecond time scale using NMR. Although a direct simulation of such a slow process by brute-force MD is almost becoming feasible, the combination of string method and umbrella sampling offers an effective computational strategy to explore the microscopic mechanism underlying the DFG-flip process. Thermodynamically, the conformational change can be characterized through the free energy difference ΔG_in→out ≡ G_out – G_in. This free energy difference can be computed by integrating the Boltzmann-weighted probabilities built from the 2D PMF. We chose C_β(Ala380)–C_α(Ala380)–C_α(Asp381)–Cγ(Asp381) = −30° to define a separator between the two conformations. Regions to the left belong to the DFG-in conformation, while those to the right are categorized as the DFG-out conformation. After integration, ΔG_in→out(c-Abl) is 1.4 kcal/mol. This free energy difference is consistent with the view that the DFG-in and DFG-out in c-Abl are in near balance when Asp381 is deprotonated.³² According to the calculations, the DFG-out conformation accounts for approximately 9% of the total population. This non-negligible population implies that the DFG-out conformation is accessible even in the absence of type II inhibitors, as pictured by a conformational selection mechanism. However, the positive ΔG_in→out indicates that the active conformation of c-Abl kinase domain is dominant. Other conformational changes as well as myristoylated N-terminal cap binding are necessary to properly control the catalytic activity of c-Abl.^{6,20,21,55,56} One should also note that the positive ΔG_in→out was calculated from a protein construct comprising only the kinase domain. Whether the ΔG_in→out is still positive in the c-Abl when the SH2 and SH3 regulatory modules are present, especially in the down-regulated state, is an interesting question that is not addressed by the present computations.

The minimum free energy pathway (MFEP) obtained from the string method provides an advantageous set of starting configurations for the biased US window simulation. The configurations from the string method ought to nicely lie along the “reaction tube” in the space of the collective variables, and US simulations would be expected to converge rapidly. To illustrate this point, we projected the initial transition path generated from TMD, as well as the string 1 at iterations 39 and 49 onto the 2D-PMF of c-Abl (Figure S5). The transition path from TMD clearly moves through high free energy regions, while the MFEPs from the string method move through low free energy regions. Mapping the MFEP onto free energy landscape confirms the idea that the string method with swarms-of-trajectories relaxes the initial transition path from high to low free energy regions. It also supports the idea that the converged paths provide optimal starting configurations for US calculations.

In recent years, methodologies aimed at extracting kinetic information (e.g., the mean first passage time) of conformational changes from MD simulations have reached a high level of maturity.^50,57−59 One example is provided by a recent study based on Markov state models (MSM) of the activating/deactivating conformational changes in the c-Src kinase domain.⁶⁰ In studies of conformational changes, the issue of multiple pathways is almost always a concern. Not accounting for some pathways can lead to an incomplete picture of the mechanism as well as an underestimation of the transition rate. In the case of the DFG-flip in c-Abl, the 2D-PMF from umbrella sampling can help to address such issues. According to the 2D-PMF, there are three MFEPs and they correspond to calculated strings 1, 3, and 4. As illustrated in Figure 3B, the energy barrier of pathway 1 is approximately the same as that of pathway 4, while the barrier of pathway 3 is slightly higher than that (2.4 kcal/mol higher). Pathways 1 and 4 have almost the same barrier height, suggesting that those two pathways are competing with each other. Using a single pathway (such as pathway 1 only) would lead to an incorrect estimation of the transition rate for the DFG-flip in c-Abl, even though a converged pathway and an accurate model to calculate the rate are employed. It is also interesting to note that TMD, used to initiate the string method iteration, was able to generate the two pathways that have the lowest barriers (pathways 1 and 4) but failed to discover pathway 3. To avoid such problems, it would be desirable to have a robust method to generate multiple pathways to initiate the string method.

Protonation of Asp381 Inverts the Population of DFG-In/Out Conformation in c-Abl

Shan et al. proposed that protonation of aspartic acid 381 in the DFG motif of c-Abl serves as an energetic switch that controls the DFG conformation.³² A ΔG_in→out of −1.1 kcal/mol when Asp381 is protonated was estimated on the conformational populations extracted from unbiased MD simulations. In this model, the DFG-motif flipped conformation spontaneously only when Asp381 is protonated.³² Lovera et al.³¹ also addressed the issue in their meta-dynamics investigations of the DFG-flip by feeding protein snapshots (solvent molecules discarded) extracted from the MD trajectories into the empirical PROPKA program. This mixed MD/PROPKA approach suggested that protonation of Asp381 in c-Abl stabilizes the DFG-out conformation by 1.4 ± 0.9 kcal/mol (though the DFG-in conformation remains dominant). Although both studies shed light on the impact of the protonation state of the aspartate residue could affect the conformational equilibrium of the DFG motif, quantitative results obtained directly from explicit solvent free energy simulations are still lacking.

To address this issue, we repeated the US calculations on the DFG flip in c-Abl with Asp381 protonated. Because of the difficulty in defining a reaction coordinate associated with the DFG-flip transition occurring in a concerted fashion with a protonation event, we did not attempt to estimate the kinetic aspects of the process and only investigated the effect of protonation on equilibrium properties. To reduce the computational cost, US windows in the simulation of c-Abl were concentrated near pathway 1 in the 2D subspace of order parameters. Figure 3C displays the 2D-PMF of DFG-flip when Asp381 is protonated. The location of DFG-out conformation in the free energy landscape is almost unchanged, while the location of the DFG-in energy basin shifts ∼30° to the left along the C_β(Ala380)–C_α(Ala380)–C_α(Asp381)–Cγ(Asp381) coordinate. Another feature of Figure 3C is that the low free energy region (region colored in dark blue) corresponding to the DFG-out conformation broadens and occupies a larger area than that of the DFG-in conformation. This calculation shows that protonation of Asp381 significantly affects the underlying free energy landscape of DFG-flip in c-Abl. By use of the same criterion to distinguish DFG-out conformation from DFG-in conformation, the ΔG_in→out becomes −0.9 kcal/mol after integrating the 2D PMF with Boltzmann weights. Once Asp381 becomes protonated, the DFG-out conformation becomes dominant, ∼82% of the total population. Our results are in excellent agreement with the hypothesis previously inferred by Shan et al.³² that the protonation state of Asp381 acts as an energetic switch on the DFG flip. The two 2D-PMFs shown in Figure 3 indicate a four-state model for c-Abl in which (i) DFG-in, Asp381 deprotonated; (ii) DFG-out, Asp381 deprotonated; (iii) DFG-in, Asp381 protonated; and (iv) DFG-out, Asp381 protonated are at equilibrium and transition from DFG-in to DFG-out can occur at either protonation state of Asp381. In this model, the population of the DFG-out conformation can be expressed as a function of pH. The ΔG_in→out of c-Abl when Asp381 is protonated and deprotonated and the pK_a value of Asp381 in DFG-in conformation are parameters. A more detailed explanation of the four-state model is given in the Supporting Information.

Thermodynamics of Gleevec Binding to c-Abl and pH-Independence

Isothermal titration calorimetry (ITC) indicates that the binding thermodynamics of Gleevec to c-Abl is not pH-dependent.³² At first, this observation may appear inconsistent with the protonation effects of Asp381 presented above. Nevertheless, this must be interpreted with caution because various pH-dependent effects may cancel out in the overall binding process. To address this issue, one could in principle recompute the absolute binding free energy of the ligand using a constant-pH dynamical algorithm⁶¹⁻⁶³ to account for the possible changes in protonation states of the ionization groups during the binding process. However, when only a small number of ionizable groups are involved as in the present situation, pH effects can be assessed by computing the relative free energies between the relevant ionization states using alchemical FEP/MD simulations. Here only two moieties, Asp381 and Gleevec, are likely to be affected by pH. Formally, the binding free energy of Gleevec can be expressed into two contributions: the free energy for the DFG-flip and the binding free energy of Gleevec to the kinase in the DFG-out apo conformation. For the first contribution, our US calculations yield a ΔG_in→out of 1.4 and −0.9 kcal/mol for c-Abl with Asp381 deprotonated and protonated, respectively. The difference in ΔG_in→out, defined as

is −2.3 kcal/mol. To cancel this value and maintain the appearance of an overall pH-independent binding, a positive free energy, defined as,

of 2.3 kcal/mol is thus needed. To evaluate the binding of Gleevec to the DFG-out conformation of c-Abl with Asp381 protonated, we performed alchemical free energy perturbation (FEP) calculations, following the protocol described in Lin et al.³⁶ The force field parameters of Gleevec are given by Aleksandrov and Simonson.⁶⁴ In our alchemical FEP calculations, Gleevec stays positively charged so that the piperazinyl group can form hydrogen bonds with Glu258.⁶⁵ The ΔΔG_binding as a function of alchemical free energy calculation cycles (Figure S6) demonstrates that Gleevec binding to c-Abl with Asp381 protonated is penalized, compared with c-Abl with Asp381 deprotonated by about 1.3 kcal/mol (averaging over the last seven cycles of the alchemical FEP). By combination of the ΔΔG values from DFG-flip and binding, the total change with pH is thus about −1.0 kcal/mol. Taking into consideration the various inaccuracies of the force field and the overall uncertainty of the alchemical FEP calculations (3.3 ns per λ), it is reasonable to infer that the present results for c-Abl are consistent with the observation from ITC experiments. According to our calculations, both the DFG-flip and Gleevec binding to the DFG-out conformation in c-Abl are affected by changing the protonation state of Asp381 but in an opposite manner. The apparent pH-independence of the binding thermodynamics of Gleevec, according to this analysis, results from the cancelation of the two pH-dependent processes. This conclusion is consistent with our result that the binding specificity of Gleevec is governed by both conformational selection and binding affinity. Therefore, both factors need to be considered in the process of designing type II kinase inhibitors. One should note that a different pH range was used in the ITC equilibrium binding affinity and kinetic experiments. The ITC experiments were performed at a pH ranging from 5.5 to 7.5, while the binding kinetics measurements were performed at a pH ranging from 7.0 to 9.0.³² As the pK_a value of the piperazinyl group in Gleevec is 7.7, the change in pH in ITC is expected to affect the protonation state of the Asp381 side chain of c-Abl (rather than that of Gleevec), whereas the change in pH in the kinetic experiments is likely to affect the protonation state of Gleevec (rather than that of Asp381). Thus, the pH-dependence in the kinetic experiments should reflect the impact on the binding process in c-Abl rather than on the DFG-flip. The present simulations are aimed at examining the effect of protonation of Asp381 on the DFG-flip and the equilibrium binding process.

Free Energy Landscapes of DFG-Flip in c-Src

In the 2D-PMF of c-Src (Figure 4B), the DFG-in conformation is around (−100°, 20°), while the DFG-out conformation is around (20°, −160°). A small free energy barrier of about 2 kcal/mol separates the two conformations. The resulting ΔG_in→out is 5.4 kcal/mol after integrating the Boltzmann-weighted probability from the 2D PMF. A large ΔG_in→out and a very small barrier imply that the DFG-out conformation of c-Src is only marginally stable. Even if a DFG-flip transition occurs, the DFG-out conformation would be expected to quickly interconvert back to the more stable DFG-in conformation. This large free energy difference is consistent with the difficulty of designing inhibitors that are targeting the DFG-out conformation (type II inhibitors) in c-Src, as those must overcome a large ΔG_in→out in order to bind with high affinity. Nonetheless, such inhibitors can exist. For example, the G6G molecule designed by Seeliger et al.²⁸ can bind to c-Src with a fairly high affinity (IC₅₀ ≈ 2.8 nM) by forming sufficiently strong interactions to overcome the cost of the DFG-flip.⁶⁶

To quantify the impact of the ionization state of aspartic acid of the DFG motif on the conformational flip transition in c-Src, the US calculations were repeated with Asp404 protonated. The 2D PMF is shown in Figure 4C. Comparison with Figure 4B shows that protonation of Asp404 has little impact on the free energy landscape underlying DFG-flip in c-Src. The ΔG_in→out(c-Src) is 5.5 kcal/mol with Asp404 protonated, which is also very close to 5.4 kcal/mol yielded from simulation with Asp404 deprotonated. Unlike the DFG-out conformation that becomes dominant in c-Abl when Asp381 is protonated, the DFG-out conformation in c-Src is still marginally stable. The large impact of protonation observed in the case of c-Abl is not reflected in c-Src, which suggests that the impact of protonation is not universal. One possible reason for the lack of impact is that Asp404 lies in a different environment from that Asp381 is in. Comparing the DFG-out conformation in c-Abl and c-Src, one could see that Asp381 is buried in a hydrophobic pocket and protonation will stabilize Asp381 in that state. The free energy landscape presented in Figure 3 is consistent with this model. In contrast to the situation in c-Abl, Asp404 in c-Src is solvent accessible. The protein does not clearly provide a favorable environment for the protonated state.

Importance of the CDK/Src-like Inactive State for c-Src Kinase

The X-ray crystallographic structures of the down-regulated (autoinhibited) c-Src reveal a different type of deactivation from DFG-flip.^26,67 The conformational change from the active conformation to the inactive one mainly involves the motion of the αC-helix and the A-loop. Similar inactive configurations are also observed in many other kinases such as the serine/threonine kinase cyclin-dependent kinase 2 (CDK2),⁶⁸ Src-family kinase Hck,⁶⁹ tyrosine kinases ZAP70⁷⁰ and EGFR,⁷¹ highlighting the importance of this type of inactivation mechanism in the general regulation of kinases. Because this inactive configuration was first observed in the CDKs and Src kinases, it is commonly referred to as the “CDK/Src-like inactive state”.⁷² The structural details of both the DFG-out and CDK/Src-like inactivated states are of consequence in the design of potent and selective kinase inhibitors. In order to evaluate the relative importance of these two mechanisms with regard to the overall activation/deactivation of c-Src kinase, 2D US calculations were carried out to characterize the free energy landscape associated with the transition to the CDK/Src-like inactive state. Figure 5 illustrates the free energy landscape underlying the conformational change associated with the αC-helix and the A-loop. In Figure 5, the free energy basin around (2.5, −12.0) is the inactive state in which the A-loop is closed and partially folded, preventing substrate from entering active site. Moreover, the αC helix is rotated outward and Glu310 in the αC helix makes a salt-bridge with Arg409 (in the A-loop). In this inactive state, the DFG motif adopts the “in” conformation. The free energy basin around (11.0, 12.0) corresponds to the same DFG-in active conformation as shown in Figure 4. In contrast to the DFG-flip conformational transition, the conformational transition involves movements of the αC helix and the A-loop favors the inactive state. The free energy difference from the inactive state to the active state is 3.9 kcal/mol. Combining the two pathways, one can see that the DFG-out conformation is very unlikely to be observed in c-Src. The DFG-flip is not a dominant step in the normal regulation of c-Src. The activation/deactivation in c-Src kinase domain is achieved through the conformational changes in the αC helix and the A-loop. But when the normal regulation is hijacked, the DFG-flip pathway can be exploited by potent inhibitors to reduce the kinase activity. Of particular significance regarding the activation of the c-Src kinase domain is the trans-phosphorylation reaction. Although the inactive conformation of c-Src kinase domain is the most populated in Figure 5, the active conformation can still be visited (albeit rarely) and the trans-phosphorylation reaction can proceed. The active conformation will be stabilized by the phosphorylation of the A-loop, and the catalytic activity will increase. Our simulations agree with the experimental observation that the isolated c-Src kinase domain is intrinsically active (i.e., displays high catalytic activity).⁷³ Figure 5 also suggests that compounds that stabilize the inactive and the intermediate conformations of the kinase domain can be used as c-Src inhibitors, as they can prevent c-Src kinase domain visiting the active conformation. Currently, inhibitors that bind to the vicinity of the αC-helix are also under development.⁷⁴ This type of inhibitor (type III) aims to prevent the αC-helix from adopting an active conformation. Both type II and type III inhibitors avoid binding to the structurally highly similar active site and intend to achieve specificity.

Figure 5.

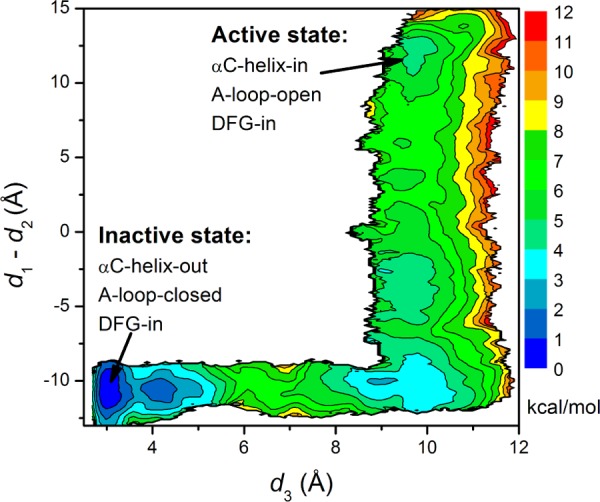
2D PMF underlying the motion of the αC-helix and the A-loop in c-Src. The unit of this PMF is in kcal/mol. d₁ is the distance between E310 Cδ atom and R409 Cζ atom. d₂ is the distance between E310 Cδ atom and K295 Nζ atom. d₃ is the average of the following three distances and is used to reflect the opening of the A-loop in the process. Those three distances are between O(Asp413) and N(Thr417), O(Asn414) and N(Ala418), and O(Glu415) and N(Arg419). The free energy basin that is located at the lower left corner is the inactive conformation, while that at the top right corner corresponds to the active conformation.

Hydrophobic Regulatory Spine (R-Spine) in c-Abl

Protein kinases have evolved to be dynamic molecular machines that are toggling between the catalytically “on” and “off” states.^12,75 The discovery of hydrophobic spines in protein kinases has introduced an important structural marker for the occurrence of a competent catalytic machinery. Two spines,^12,22,23,76 an R-spine and a C-spine, are formed in active kinases. Both spines consist of conserved and noncontiguous amino acids in kinases. They both can be dynamically assembled and broken, switching the kinase activity on and off. The R-spine consists of four residues extending from the N-lobe to the C-lobe: L301, M290, F382, and H361 (see Figure 6A) in c-Abl.^22,77 Among those four residues, M290 comes from the αC helix, F382 from the DFG motif, and H361 from the HRD motif. In the DFG-out conformation, the flip of Phe382 disrupts the integrity of the R-spine. The conformational transition mechanism that is governed by the landscape shown in Figure 5 also correlates with the breaking of the R-spine: the outward rotation of the αC-helix deforms the R-spine. Both conformational changes are consistent with the view that the αC helix and the A-loop can be mobile, and hence, the R-spine can be dynamically assembled and disassembled.^12,23 Figure 6B, showing the 1D PMFs as a function of the rmsd of the R-spine relative to the DFG-in active conformation, demonstrates the free energy profile of the stability of the R-spine before and after Asp381 is protonated. Both 1D PMFs were calculated on the basis of the existing umbrella windows (no additional US calculation were performed to obtain those PMFs). Two stable conformations of the R-spine are present, regardless of the protonation state of Asp381. The conformation that is around 1.2 Å corresponds to the conformation in which the R-spine is formed (“on” conformation). The stable conformation around 3.5 Å associates with the conformation where the R-spine is broken (“off” conformation). However, as illustrated in Figure 6B, the free energy basin corresponding to the “off” conformation of the R-spine is broader and lower in energy when Asp381 is protonated than that in c-Abl with Asp381 is deprotonated. This observation reveals that protonation of Asp381 destabilizes the assembly of the R-spine in c-Abl. However, protonation of Asp381 does not change the barrier height significantly, suggesting that toggling between inactive and active conformations remains a slow process under those conditions. The brute-force MD simulations performed by Shan et al. are also consistent with this view.³² In their simulations, protonation of Asp381 alone did not enable barrier crossing. M290, which is one component of the R-spine, needed to be substituted with an alanine residue to observe DFG-flip in their MD simulations. Mutating a methionine residue to the shorter alanine residue weakens the interaction between that residue and F405 and hence accelerates the flipping of the DFG motif. One interesting question is whether replacing M290 with an alanine alone (i.e., M290A and Asp381 will be kept deprotonated) should alter the free energy landscape underlying DFG-flip.

Figure 6.

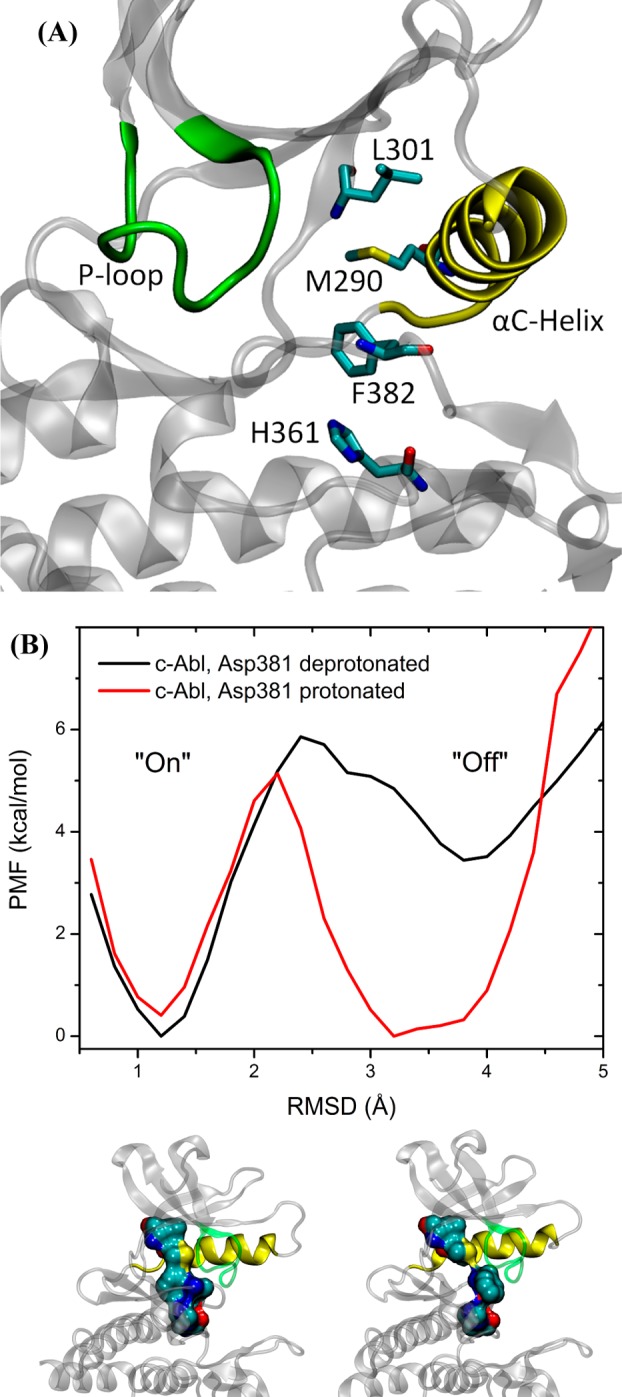
(A) Representative structure of the R-spine. (B) 1D PMFs as a function of the rmsd of the regulatory spine (R-spine) relative to the DFG-in conformation, in which the R-spine is formed. All heavy atoms in the R-spine are used in the calculation of rmsd.

Interactions Affecting DFG-Flip in c-Abl and c-Src When Asp381(Asp404) Is Deprotonated

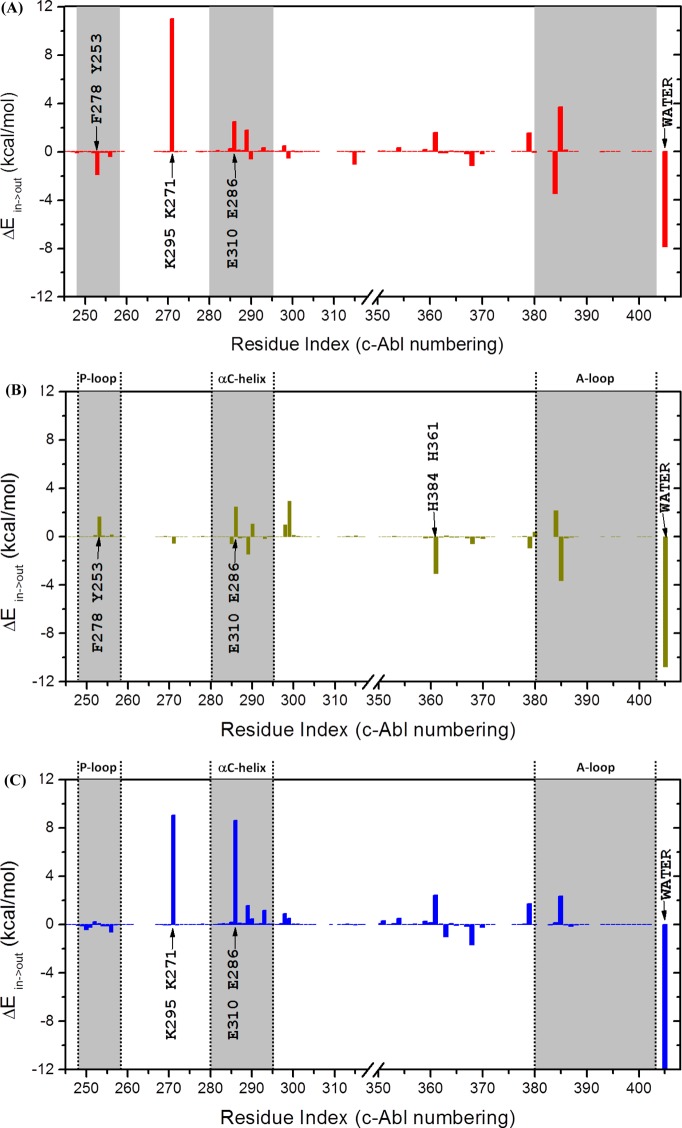
Residues that affect DFG-flip significantly could be identified by analyzing their interaction energies with the DFG motif. Therefore, van der Waals (vdW) and electrostatic energies between DFG motif and the rest of the protein as well as water molecules that are within 5 Å of it were computed for DFG-in and DFG-out conformations of both c-Abl and c-Src kinases. The sum of the electrostatic and vdW terms is utilized to represent the overall interaction between a particular residue and the DFG motif in a given conformation. Once the interaction energy values were obtained, ΔE_in→out was then computed as ΔE_in→out ≡ E(DFG-out) – E(DFG-in). The effect of a residue upon DFG-flip can be evaluated by ΔE_in→out. By its definition, a positive ΔE_in→out means that DFG-flip will raise the interaction energy between a residue and the DFG motif, making that residue less stable. Therefore, that residue prefers DFG-in conformation and destabilizes DFG-flip. A negative ΔE_in→out value means the opposite. ΔE_in→out and its two components, as a function of residue index, are illustrated in Figures 7, S7, and S8. The values of ΔE_in→out are essentially zero for those residues after the A-loop and thus are not shown in the figures. Table 1 displays the ΔE_in→out and its two components of all residues, the phosphate-binding loop (P-loop, residues 248–257, c-Abl 1a numbering), the αC-helix (residues 280–294, c-Abl 1a numbering), and the A-loop (residues 381–402, c-Abl 1a numbering). The overall ΔE_in→out indicates that DFG-flip is unfavored in both c-Abl and c-Src. The overall ΔE_in→out also reveals that DFG-flip is penalized (in energy) more in c-Src than in c-Abl. This qualitatively agrees with our results from umbrella sampling calculations.

Figure 7.

Differences in interaction energies between DFG-in and DFG-out conformations: (A) c-Abl with Asp381 deprotonated; (B) c-Abl with Asp381 protonated; (C) c-Src.

Table 1. Energy Decomposition Results of DFG-Flip^a.

	ΔEin→out
	all residues	P-loop	αC-helix	A-loop
c-Abl	6.4	–2.7	4.7	0.4
c-Src	10.3	–1.5	12.5	2.2

	ΔEin→out,ele
	all residues	P-loop	αC-helix	A-loop
c-Abl	6.8	0.1	–1.5	0.3
c-Src	8.6	0.3	5.7	1.2

	ΔEin→out,vdW
	all residues	P-loop	αC-helix	A-loop
c-Abl	–0.4	–2.8	6.2	0.1
c-Src	1.7	–1.8	6.7	1.0

^aAsp381(Asp404) is deprotonated. All values are in kcal/mol.

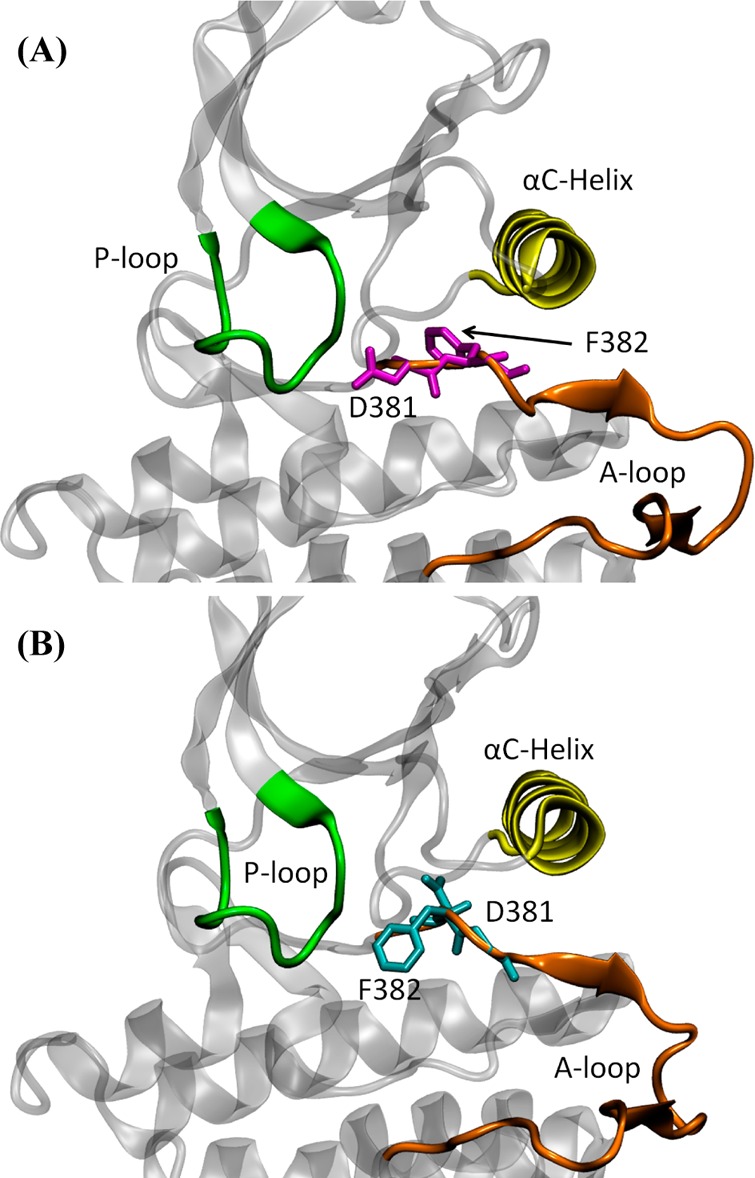
The conformation of the P-loop was proposed to be essential for the high selectivity of Gleevec. A kinked (W-shaped; see Figure S9) conformation of the P-loop in c-Abl was believed to be critical in Gleevec binding. This W-shaped conformation makes the P-loop stabilize Gleevec in the pocket. Our residual decomposition results shows that the P-loop also plays an important role in the conformational transition. The P-loop stabilizes DFG-flip in both c-Abl and c-Src, mainly through vdW interactions. In the DFG-out conformation of c-Abl, Phe382 moves to the vicinity of the W-shaped P-loop and resultes in a stabilizing dispersive interaction. In c-Abl, the stabilizing interaction provided by the P-loop is dominated by the contribution from Tyr253, which forms a contact with Phe382 (as displayed in Figure S9A). In c-Src, the P-loop is in an extended conformation (see Figure S9) and thus is not as close to the phenylalanine in the DFG motif as that in c-Abl. Therefore, this stabilizing effect is much less significant in c-Src. According to Figure 7C, the counterpart of Tyr253-Phe382 interaction is missing in c-Src because of the extended conformation possessed by the P-loop. The αC-helix and the A-loop provide a destabilizing effect on DFG-flip in both kinases. Among those residues in the αC-helix, one could see Glu286 contributed the most to ΔE_in→out. For the A-loop, our calculation reveals that only the residues that are next to DFG motif have nontrival interactions. In c-Abl, the impact of residue 384 and 385 is almost canceled, which makes the overall ΔE_in→out from the A-loop residues only slightly greater than zero. Lys271 is another residue that interacts with the DFG motif strongly. The positively charged side chain of Lys271 forms a salt-bridge with the carboxylic group of Asp381 in the DFG-in conformation. Although the vdW component favored DFG-out conformation, the “flip” is heavily penalized by breaking the salt-bridge.

Key Segments and Residues Affecting DFG-Flip in c-Abl When Asp381 Is Protonated

Table 2 demonstrates the ΔE_in→out and its two components of c-Abl with Asp381 protonated. The overall ΔE_in→out indicates that DFG-flip is favored in c-Abl with Asp381, which qualitatively agrees with our results from umbrella sampling calculations. However, if only considering the nonsolvent interactions, the net ΔE_in→out is 0.4 kcal/mol: DFG-flip is unfavored by the rest of the protein even with Asp381 protonated. This small destabilizing factor is balanced by a possibly overnegative interaction energy with solvent. Therefore, the aqueous environment is vital for DFG-flip after Asp381 is protonated.

Table 2. Energy Decomposition Results of DFG-Flip in c-Abl^a.

	all residues	P-loop	αC-helix	A-loop
ΔEin→out	–10.4	2.0	1.1	–1.7
ΔEin→out,ele	–8.2	–0.1	3.1	–1.5
ΔEin→out,vdW	–2.2	2.1	–2.0	–0.2

^aAsp381 is protonated. All values are in kcal/mol.

Protonation of Asp381 alters the role of the P-loop and the A-loop on DFG-flip. Contrary to the stabilizing/destabilizing effect that is exerted by the P-loop/A-loop in c-Abl with Asp381 deprotonated, Table 2 demonstrates that the P-loop/A-loop acts as a destabilizing/stabilizing factor on DFG-flip in c-Abl with Asp381 protonated. As shown in Figure 7B, many interaction energies from the P-loop and the A-loop change signs after Asp381 is protonated. However, the αC-helix still provides a destabilizing effect on DFG-flip. Out of all residues in the P-loop, Tyr253 still has the largest contribution to ΔE_in→out, even though it is an opposite effect now. Likewise to the Glu286 in c-Abl with Asp381 deprotonated, Glu286 still has the largest positive ΔE_in→out among residues in the αC-helix. To display the counteraction of Asp381 being protonated on DFG-flip in c-Abl, Figure S10 plots the ΔΔE_in→out as a function of residue index, using the ΔE_in→out shown in Figure 7A as a reference. A negative sign in ΔΔE_in→out indicates that the counteraction favors DFG-flip. According to Figure S10, the effect of protonation is disbuted among multiple residues. There are nine residues whose absolute values of ΔΔE_in→out are greater than 2 kcal/mol. Four residues possess ΔΔE_in→out that are larger than 4 kcal/mol in absolute value. Among all the actions on DFG-flip in c-Abl, the one from Lys271 is affected the most by the protonation of Asp381 (see Figure S10). Protonation of Asp381 completely eliminates the large destabilizing interaction between the DFG motif and Lys271 which can be seen in Figure 7A. When Asp381 becomes protonated, the large electrostatic interaction between side chains of Asp381 and Lys271 is greatly reduced in the DFG-in conformation such that it does not have a significant influence on DFG-flip.

Residual decomposition analysis also sheds light on how the R-spine (excluding Phe382) influences DFG-flip after Asp381 is protonated. Among those three residues, ΔE_in→out is 1.1, 0.0, and −3.1 kcal/mol for Met290, Leu301, and His361, respectively. Three residues have three different impacts on DFG-flip. Leu301 has no impact because it is the farthest away from the DFG motif. Met290 unfavors the DFG-flip even with Asp381 is protonated. Our residual decomposition results of Met290 agree with what was observed in the brute-force MD simulations:³² Met290 still needed to be mutated to alanine in order to facilitate DFG-flip to occur even after Asp381 is protonated. Compared with methionine, alanine is a less obstructing residue because of its smaller size. His361 favors the DFG-out conformation when Asp381 is protonated. It stabilizes both Asp381 and Phe382 in the DFG-out conformation. The total ΔE_in→out from the R-spine is −2.0 kcal/mol. The negetive sign suggests that the R-spine is even internally less stable (components of the R-spine prefer the DFG-flip to occur and consequently disassemble the R-spine) when Asp381 becomes protonated.

Conclusions

The string method combined with the umbrella sampling technique was utilized to determine the free energy cost associated with the conformational transition converting the DFG motif of the (apo) c-Abl and c-Src tyrosine kinases from the active “in” to the inactive “out” state. The calculated free energy landscapes describing the DFG-flip conformational change show that the DFG-out conformation can be stable in c-Abl even in the absence of Gleevec, whereas it corresponds to a state of high free energy in c-Src. The impact of protonation of the aspartic residue of the DFG motif (Asp381 in c-Abl and Asp404in c-Src) was also quantified. The calculated free energy landscapes show that protonation of Asp381 has a considerable impact on the DFG-flip in c-Abl but that protonation of Asp404 has very little impact on the DFG-flip in c-Src. The calculated free energy difference between DFG-in and DFG-out conformations reveals that the DFG-out conformation becomes dominant once Asp381 becomes protonated. However, the protonation of Asp381 also reduces the binding affinity of Gleevec to the DFG-out conformation, resulting in a very small change in the overall binding affinity. This result explains why the experimentally measured binding affinity of Gleevec to c-Abl is not sensitive to pH. Protonation of Asp381 also has a considerable effect on the stability of the hydrophobic R-spine. After Asp381 is protonated, the disassembled form of the R-spine is greatly favored as a consequence of the DFG-out conformation becoming more energetically favorable.

It is instructive to use the DFG-flip in c-Abl as an example of a computational exploration of system with multiple transition pathways. The existence of the latter is explicit when considering the 2D PMF of c-Abl (pathways with comparable free energy barriers). This necessarily becomes an important issue for a complete investigation of the kinetics aspects of the DFG-flip transition. The present results suggest that the free energy landscape underlying a conformational transition should be characterized thoroughly before tackling the task of calculating kinetic factors. Moreover, the unphysical biasing potential that is used in targeted MD calculations affects the initial pathway generations. Thus, a systematic way of generating starting conditions for the string method should be employed when multiple pathways need to be considered.

The conformation of P-loop (residues 248–257, c-Abl numbering) was proposed to be essential for the high selectivity of Gleevec.²⁸ This W-shaped conformation makes P-loop stabilize Gleevec in the pocket. Our residual decomposition analysis shows that the P-loop also stabilizes DFG-flip in both c-Abl and c-Src, mainly through vdW interactions, when Asp381(Asp404) is deprotonated. However, the P-loop in c-Abl exerts an opposite action on DFG-flip after Asp381 becomes protonated. Despite a destabilizing effect on DFG-flip from the P-loop, our residual decomposition analysis reveals an overall favorable effect on DFG-flip after Asp381 is protonated. The counteraction of Asp381 being protonated on DFG-flip is distributed among many residues with the largest from Lys271.

Supporting Information Available

Descriptions of the string method with swarms-of-trajectories, mean-force calculations using converged strings, and the four-state equilibrium of c-Abl given in the METHODS section; Table S1 listing the collective variables used in the string method calculations; indices of possible DFG-flip pathways in the study of c-Abl in Table S2; Figure S1 displaying the structural comparison of c-Abl and c-Src kinase domains in their DFG-in (active) conformation; Figure S2 showing the convergence of MD simulations in the structural relaxation stage; convergence of string method calculations plotted in Figure S3; Figure S4 illustrating the convergence of c-Abl and c-Src umbrella sampling calculations, when the aspartate residue in the DFG motif is deprotonated; projection of strings at three iterations onto the free energy landscape of c-Abl (Asp381 is deprotonated) shown in Figure S5; ΔΔG_binding (defined as ΔG_binding(AspH) – ΔG_binding(Asp)) as a function of alchemical free energy calculation cycles plotted in Figure S6; Figure S7 showing the ΔE_in→out obtained from residual energy decomposition analysis as a function of residue index for c-Abl; Figure S8 showing the ΔE_in→out as a function of residue index for c-Src; structural comparison of P-loop conformations and key residue interactions for c-Abl and c-Src displayed in Figure S9; difference in ΔE_in→out between c-Abl (deprotonated Asp381) and c-Abl (protonated Asp381) plotted against residue index in Figure S10. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States