Modeling Response Selection in Task Switching: Testing the Contingent Encoding Assumption

Abstract

The contingent encoding assumption is the idea that response selection in task-switching situations does not begin until the cue and the target have both been encoded. The authors tested the assumption by manipulating response congruency, stimulus order, and stimulus onset asynchrony (SOA) in two experiments. They found evidence of response selection prior to cue encoding for congruent targets with target−cue order at a long SOA, indicating that the contingent encoding assumption is invalid. The authors describe how contingent encoding can be removed from an existing task-switching model by introducing baseline evidence—task-neutral evidence that serves as a baseline for response selection prior to stimulus encoding. Simulations revealed that the modified model could reproduce the full pattern of response time data and generate responses prior to cue encoding. The authors conclude by discussing directions for further model development.

Task switching is a challenge for the human cognitive system, but not an insurmountable one. It is a challenge because it is rife with ambiguity: Stimuli are usually multivalent, affording multiple responses that are appropriate for different tasks. However, the challenge is not insurmountable because people can deal with this ambiguity: Task-appropriate responses can be selected for multivalent stimuli, often with considerable speed and accuracy. How this is accomplished is not entirely clear, but we think much can be gained by developing and testing computational models of response selection in task switching. The purpose of the present study was to test an important assumption about response selection that can be found in various task-switching models.

The Contingent Encoding Assumption

In a typical task-switching experiment, a cue indicates a task to perform on an ambiguous target. For example, for tasks involving the referents of target words (e.g., elephant and pebble), the cue Origin might indicate a living-or-nonliving judgment and the cue Size might indicate a small-or-large judgment (relative to a basketball). The targets are ambiguous because each is associated with two categories (e.g., elephant is living and large) that may or may not be mapped to the same response (e.g., living and small might be mapped to a left response key and nonliving and large might be mapped to a right response key). Under these circumstances, cues can be necessary to accurately select responses for targets (Kantowitz & Sanders, 1972; Schneider & Logan, 2009; Sudevan & Taylor, 1987), leading to the issue of how cues and targets are used together in response selection.

The contingent encoding assumption is the idea that response selection in task-switching situations does not begin until the cue and the target have both been encoded. The assumption is often made in verbal theorizing about task switching, where it is argued that the cue is used to prepare the cognitive system for the task that is subsequently performed on the target (for reviews, see Kiesel et al., 2010; Vandierendonck, Liefooghe, & Verbruggen, 2010). Without the cue, the cognitive system might not be in a suitable state for task performance. Without the target, there would be nothing on which to perform the task. Thus, both stimuli have to be encoded to select a task-appropriate response. The contingency is more clearly evident in certain computational models of task switching that specify how responses are selected, as in the following examples:

In Altmann and Gray’s (2008) model, a target is not categorized and response selection does not begin until a task representation is available in the model’s focus of attention. Task representations are based on task codes retrieved from episodic memory that were created earlier as products of cue encoding. If a target has been encoded perceptually but the model is unable to bring a task representation into its focus of attention because it cannot retrieve a task code, then nothing happens—the processing cycle is wasted (Altmann & Gray, 2008, p. 610). The model attempts to retrieve a task code on the next cycle and continues to do so until it succeeds. On most (but not all) trials, the task representation used by the model is based on the task code created from the current cue. If the cue has not been encoded, then the associated task code and task representation will be unavailable, forcing the model to either wait for cue encoding to finish or retrieve an alternative task code from a previous trial. In any case, response selection does not begin until a task representation is available, even if the target has been available for some time. Thus, the model includes the contingent encoding assumption.

In Sohn and Anderson’s (2001) model, a target is not encoded and response selection does not begin until the relevant task is known. The task is identified by encoding the cue and retrieving its meaning from memory. If a target is available but the task is unknown, then nothing happens—the model must wait for task identification. Once the task is known, the target is encoded and categorized with respect to the relevant task, then a response is selected based on that categorization. Given that response selection does not begin until the cue and the target have been encoded (in that order), the model includes the contingent encoding assumption.

In Schneider and Logan’s (2005, 2009) model, response selection does not begin until the cue and the target have both been encoded. Cue and target encoding involve forming task-relevant categorical representations of the stimuli (Arrington, Logan, & Schneider, 2007; Schneider & Logan, 2010). Each stimulus representation then retrieves evidence for its associated task categories from memory. The evidence is combined multiplicatively and used to drive a random-walk decision process that favors selection of the response to which the category with the most evidence is mapped. Given the multiplicative combination of evidence, the joint evidence from the cue and the target is zero if either the cue or the target (or both) have not been encoded, making response selection inactive. Thus, the model includes the contingent encoding assumption.

The fact that the contingent encoding assumption is present in verbal theorizing and shared by at least three different computational models suggests that it is an important explicit or implicit consideration in theoretical work on task switching. It is also important because a critical aspect of task switching is response selection for ambiguous targets, an understanding of which may provide insight about flexibility in cognitive control more generally. Despite its importance, the assumption has never been tested, raising the question of whether it is valid.

The Present Study

We report data from two experiments designed to test the contingent encoding assumption. A key feature of the experiments was a manipulation of response congruency: whether a target required the same response (congruent) or different responses (incongruent) for the two tasks. For example, for the origin and size tasks described earlier, if living and small are mapped to a left response key and nonliving and large are mapped to a right response key, then congruent targets are either living and small (e.g., spider) or nonliving and large (e.g., tuba), and incongruent targets are either living and large (e.g., elephant) or nonliving and small (e.g., pebble). A robust finding in the task-switching literature is a response congruency effect: performance is slower and more error-prone for incongruent targets compared with congruent targets (e.g., Brown, Reynolds, & Braver, 2007; Kiesel, Wendt, & Peters, 2007; Meiran, 2005; Meiran, Chorev, & Sapir, 2000; Meiran & Kessler, 2008; Monsell, Sumner, & Waters, 2003; Schneider & Logan, 2009; Sudevan & Taylor, 1987).

Response congruency is of interest for testing the contingent encoding assumption because incongruent and congruent targets differ regarding whether response selection is contingent on encoding the cue. For an incongruent target, response selection is not possible without encoding the cue because the target categories for both tasks are mapped to different responses. For a congruent target, response selection is possible without encoding the cue because the target categories for both tasks are mapped to the same response. If the possibility of response selection prior to cue encoding were realized, then the contingent encoding assumption would be proven invalid and task-switching models that include the assumption would have to be revised.

We introduced the opportunity for response selection prior to cue encoding by manipulating response congruency in conjunction with stimulus order, presenting the cue before the target (cue−target order) or the target before the cue (target−cue order). Stimulus order has been manipulated in previous task-switching studies (Bernstein & Segal, 1968; Biederman, 1973; Davis & Taylor, 1967; LeMay & Simon, 1969; Ruge, Braver, & Meiran, 2009; Shaffer, 1965, 1966; Sohn & Carlson, 1998) and yielded evidence of advance target processing with target−cue order. The nature of this processing has been hypothesized to range from perceptual encoding (Shaffer, 1965) to stimulus categorization and response selection (Bernstein & Segal, 1968; Biederman, 1973; Davis & Taylor, 1967). However, previous studies made unambiguous response selection dependent on knowing the cue, which may have limited the extent of advance target processing. In the present study, we removed this dependency by making response selection logically possible for congruent targets and allowing subjects to respond before cue presentation.

Stimulus order was blocked in Experiment 1 but not in Experiment 2. The stimulus-order manipulation consisted of presenting the cue at a stimulus onset asynchrony (SOA) of 0, 400, or 800 ms before the target (cue−target order) or after the target (target−cue order). With cue−target order, target encoding would begin after the SOA and likely finish after cue encoding. Given that response congruency is defined by the target, we predicted a typical response congruency effect at all SOAs. With target−cue order, target encoding might finish before cue encoding at the non-zero SOAs, allowing response selection to begin early. However, such advance response selection is feasible only for congruent targets because they are mapped to the same response regardless of the cue. Response selection for incongruent targets would be postponed until the cue has been encoded.

If response selection begins prior to cue encoding for congruent targets with target−cue order, then two predictions follow for that condition. Our first prediction is that there should be a response congruency effect that increases with SOA because a longer SOA affords more time for response selection to finish for a congruent target, whereas response selection for an incongruent target is contingent on the cue. A task-switching study by Ruge et al. (2009) that involved a manipulation of stimulus order provides some evidence in support of this prediction: They observed a large response congruency effect at a long SOA with target−cue order, although they did not find significant response congruency effects with cue−target order, which is uncommon in the literature. Our second prediction is that if the SOA is long enough (e.g., 800 ms), response selection may finish and the response might be executed for a congruent target before the cue is even presented. To assess this prediction, we allowed early responses (i.e., responses occurring before the second stimulus was presented) in our experiments, which is a novel advance over previous studies involving stimulus-order manipulations. Early responses for congruent targets with target−cue order at a long SOA would indicate unequivocally that response selection occurred before both stimuli had been encoded and represent a fatal blow to the contingent encoding assumption.

Experiments 1 and 2

Method

Subjects

Forty-eight students from Vanderbilt University participated for course credit. There were 24 subjects per experiment.

Apparatus, tasks, and stimuli

The experiments were conducted with E-Prime software (Psychology Software Tools, Pittsburgh, PA) running on computers that displayed stimuli on monitors and registered responses from QWERTY keyboards. The tasks were origin (living or nonliving) and size (small or large, relative to a basketball) judgments of the referents of target words. The origin task was cued by the word ORIGIN or the word LIFE and the size task was cued by the word SIZE or the word MAGNITUDE. We used two cues per task to maintain continuity with our previous task-switching work (e.g., Arrington et al., 2007; Logan & Schneider, 2006; Schneider & Logan, 2005, 2006, 2011). There were 10 targets for each combination of the origin and size categories (see Appendix A). Mean word length was 5.1 letters and mean word frequency was 3.9 occurrences per million; separate 2 (origin) × 2 (size) analyses of variance (ANOVAs) on each variable revealed no significant effects, all Fs < 1. Targets and cues were displayed in white 12-point Courier New font on a black background. Viewing distance was approximately 50 cm.

Procedure

Instructions were presented onscreen and explained by the experimenter. In Experiment 1, half the blocks involved cue−target order and half involved target−cue order. The relevant stimulus order was indicated at the start of each half and the order in which the stimulus orders were experienced was counterbalanced across subjects. In Experiment 2, all blocks involved both stimulus orders, randomly intermixed. Subjects were instructed to use the information provided by the first stimulus on each trial to prepare and improve their performance, regardless of the stimulus order.

Each experiment was divided into 14 blocks of 60 trials, with rest periods between blocks. Each trial began with the presentation of two vertically arranged fixation crosses for 500 ms, then both crosses disappeared and the first stimulus was presented. After an SOA of 0, 400, or 800 ms, the second stimulus was presented. The cue and the target were always presented in place of the top and bottom fixation crosses, respectively, to avoid uncertainty about their locations. The cue, target, and SOA were chosen randomly on each trial, subject to the constraint that the SOAs were used equally often. Each combination of cue and SOA occurred five times per block and each target occurred three times within consecutive pairs of blocks.

Subjects were informed that a response was allowed any time after presentation of the first stimulus and they did not have to wait until both stimuli were displayed if they were able to make a correct response during the SOA. Responses were made with the Z and / keys on the keyboard, with same-task categories assigned to different keys and all possible category−response mappings counterbalanced across subjects. Reminders of the mappings appeared in the bottom corners of the screen during the experiment.

The freedom to respond after presentation of the first stimulus allowed for three possible outcomes for the non-zero SOAs. First, a response could occur before the SOA had elapsed. In this situation, the response was recorded and the trial continued for the remaining duration of the SOA, after which time the second stimulus was displayed for 250 ms, then the screen was cleared. This was done so that both stimuli appeared on every trial and a nominal task transition could be coded for target−cue order. Second, a response could occur after the SOA but before the second stimulus had been displayed for 250 ms. In this situation, to ensure a minimum display time for the second stimulus, the trial continued until the second stimulus had been displayed for 250 ms, then the screen was cleared. Third, a response could occur after the SOA and after the second stimulus had been displayed for at least 250 ms. In this situation, the screen was cleared immediately after the response. After the screen was cleared in all three situations, it remained blank for 500 ms, after which time the fixation display for the next trial was presented.

Results

In Experiment 1, the first block of each half was considered practice. In Experiment 2, the first block of the whole experiment was considered practice. Practice blocks, the first trial of each block, and trials with response times (RTs) exceeding 3,000 ms (2.0% and 1.5% of trials in Experiments 1 and 2, respectively) were excluded from all analyses. Error trials were excluded from the RT analyses. RT was defined with respect to the onset of the second stimulus regardless of stimulus order (following Davis & Taylor, 1967; Shaffer, 1965, 1966). Consequently, any responses occurring prior to the onset of the second stimulus were coded as having negative RTs. Note that whether RT is defined with respect to the onset of the first or the second stimulus affects overall RT, but not differences in RT such as response congruency effects.

Our analyses focused on mean RT, mean error rate (ER), and the mean percentage of early responses (i.e., responses occurring prior to the onset of the second stimulus), which we denote p(early). Repeated-measures ANOVAs were computed for these measures with response congruency, stimulus order, and SOA as factors. Given that stimulus order was blocked in Experiment 1, the 0-ms SOA could be associated with a stimulus order, resulting in three levels of SOA (0, 400, and 800 ms) in the ANOVAs. In Experiment 2, the 0-ms SOA could not be associated with a stimulus order, so there were two levels of SOA (400 and 800 ms) in the ANOVAs. When reporting ANOVA results, we focus on the highest order effects that were significant (α = .05).

The data are presented as a function of response congruency, stimulus order, and SOA in Figure 1, which shows similar patterns across experiments (see Appendix B for information about task-switching effects). The RT data pattern consisted of two parts. First, there was a large response congruency effect with target−cue order that increased substantially with SOA: In Experiment 1, the response congruency effect increased from 236 to 311 to 517 ms across SOA; in Experiment 2, the effect increased from 207 to 322 to 455 ms across SOA. Second, there was a smaller (but still sizable) response congruency effect with cue−target order that decreased with SOA: In Experiment 1, the response congruency effect decreased from 129 to 111 to 92 ms across SOA; in Experiment 2, the effect decreased from 207 to 172 to 152 ms across SOA. A net result of these divergent changes in response congruency effects was that overall RT was shorter with target−cue order than with cue−target order (800 vs. 970 ms in Experiment 1; 715 vs. 919 ms in Experiment 2, excluding the 0-ms SOA). The pattern described above is reflected in a three-way interaction among response congruency, stimulus order, and SOA that was significant in Experiment 1, F(2,46) = 37.50, MSE = 12,804, p < .001, η_p² = .62, and in Experiment 2, F(1,23) = 10.91, MSE = 19,252, p < .01, η_p² = .32.

Figure 1.

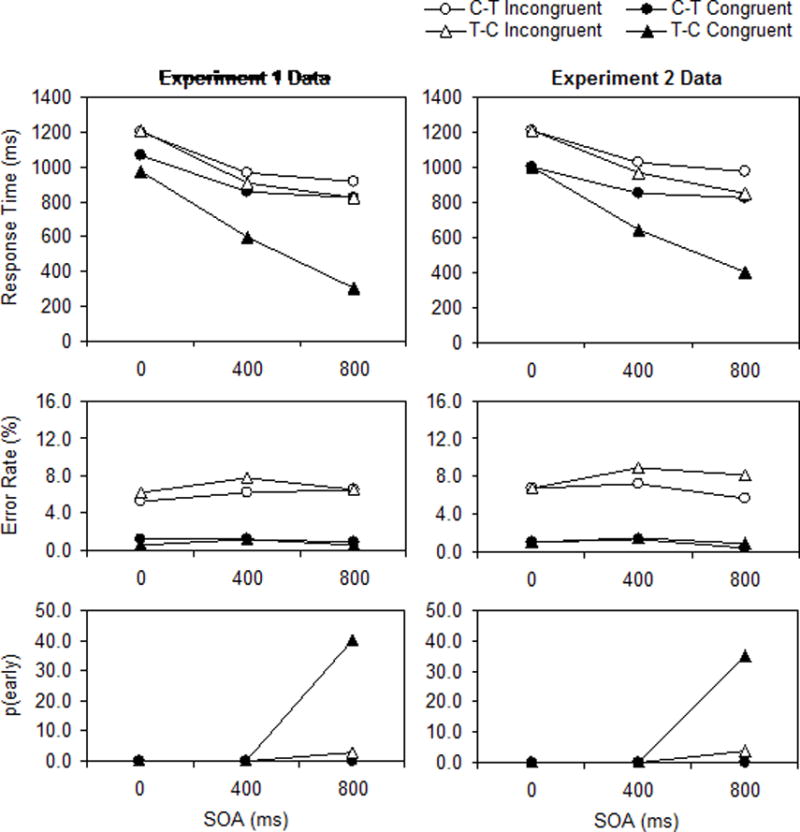
Data (means) from Experiments 1 and 2 (left and right panels, respectively). C−T = cue−target order, T−C = target−cue order, SOA = stimulus onset asynchrony, p(early) = percentage of early responses.

The ER data pattern (see Figure 1) consisted of a large response congruency effect with both stimulus orders across all SOAs, averaging 5.5% and 6.2% in Experiments 1 and 2, respectively. The main effect of response congruency was significant in Experiment 1, F(1,23) = 41.00, MSE = 157, p < .001, η_p² = .64, and in Experiment 2, F(1,23) = 74.18, MSE = 79, p < .001, η_p² = .76. In Experiment 2, excluding the 0-ms SOA, the response congruency effect was reliably larger for target−cue order (7.3%) than for cue−target order (5.5%), F(1,23) = 4.32, MSE = 28, p < .05, η_p² = .16, and overall ER decreased slightly from 4.8% to 3.8% as SOA increased from 400 to 800 ms, F(1,23) = 6.57, MSE = 21, p < .05, η_p² = .22. Similar effects were numerically but not reliably present in Experiment 1.

The p(early) data pattern (see Figure 1) consisted of a large p(early) value for congruent trials with target−cue order at an SOA of 800 ms (40.2% and 35.3% in Experiments 1 and 2, respectively); p(early) was less than 1.0% for all other conditions except for incongruent trials with target−cue order at an SOA of 800 ms (2.8% and 3.6% in Experiments 1 and 2, respectively).¹ This pattern is reflected in a three-way interaction among response congruency, stimulus order, and SOA that was significant in Experiment 1, F(2,46) = 58.03, MSE = 145, p < .001, η_p² = .72, and in Experiment 2, F(1,23) = 51.79, MSE = 173, p < .001, η_p² = .69.

Discussion

The experiments revealed robust and distinct data patterns for RT, ER, and p(early) arising from manipulations of response congruency, stimulus order, and SOA. For RT, there was a response congruency effect that increased substantially across SOA with target−cue order but decreased across SOA with cue−target order, resulting in RT being shorter for target−cue order than for cue−target order. For ER, there was a response congruency effect that varied little across SOA and was slightly larger for target−cue order than for cue−target order. For p(early), there was a large p(early) value for congruent targets with target−cue order at an SOA of 800 ms, but near-zero values for all other conditions.

The p(early) data represent unequivocal evidence of response selection prior to cue encoding. Despite not knowing the relevant task, subjects engaged in advance response selection when presented with target−cue order, which uniquely benefitted performance with congruent targets. This advance response selection accounts for the marked decrease in RT with SOA for congruent targets with target−cue order, which led to the shorter RT and larger response congruency effect for target−cue order than for cue−target order.

A direct implication of these findings is that the contingent encoding assumption in verbal theorizing and computational models of task switching is invalid. Response selection for congruent targets is neither logically nor empirically contingent on cue encoding, indicating that the assumption has to be abandoned and models have to be revised to accommodate this change. These objectives are realized in the next section, where we describe modifications to one model and apply it to our data.

Modeling

Compound Cue Retrieval

Although the contingent encoding assumption applies to multiple models, we focus on its role in a model of response selection in task-switching situations called compound cue retrieval (Schneider & Logan, 2005, 2009). The reason for this decision is practical: We are most familiar with the model and were able to see how it could be modified to accommodate the findings from the present study that invalidate the contingent encoding assumption. Our decision should not be taken to imply that other models might not also be suitably modified to account for our data. Instead, we offer this modeling work as an example of one approach for addressing the contingent encoding assumption.

Compound cue retrieval involves using the cue and the target in tandem to select a response from memory (Schneider & Logan, 2005, 2009). As mentioned earlier, the cue and the target are encoded as task-relevant categorical representations of the stimuli (Arrington et al., 2007; Schneider & Logan, 2010). Each stimulus representation then retrieves evidence (represented by numerical η values) for its associated task categories from memory, which is combined multiplicatively:

$$\eta (\mathit{\text{category}}|\mathit{\text{cue}},\mathit{\text{target}})=\eta (\mathit{\text{category}}|\mathit{\text{cue}})\times \eta (\mathit{\text{category}}|\mathit{\text{target}}).$$ (1)

If a stimulus has not been encoded, then it provides no evidence for any category (i.e., η = 0). The evidence for a category corresponds to the rate at which that category is retrieved from memory (Schneider & Logan, 2005). The probability of retrieving category i is the ratio of its evidence over the summed evidence for all categories j belonging to the set of relevant categories R:

$$P({\mathit{\text{category}}}_i|\mathit{\text{cue}},\mathit{\text{target}})=\frac{\eta ({\mathit{\text{category}}}_i|\mathit{\text{cue}},\mathit{\text{target}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j|\mathit{\text{cue}},\mathit{\text{target}})}.$$ (2)

With two categories (associated with different tasks) mapped to each response key, the probability of retrieving evidence for response key k is the sum of the probabilities of retrieving the categories i that are mapped to it:

$$P({\mathit{\text{key}}}_k|\mathit{\text{cue}},\mathit{\text{target}})={\displaystyle \sum }_{i\in k}P({\mathit{\text{category}}}_i|\mathit{\text{cue}},\mathit{\text{target}}).$$ (3)

The evidence retrieved for the alternative responses drives a random-walk decision process (for an overview, see Ratcliff, 2001), which is simulated by computing Equations 1–3 for a specific cue and target combination (with a modification introduced below), then stochastically accumulating units of evidence for the responses according to the probabilities from Equation 3. Following Schneider and Logan (2005, 2009; see also Logan & Gordon, 2001; Nosofsky & Palmeri, 1997), the time it takes to retrieve and accumulate each unit of evidence (i.e., take a step of the random walk) is:

$$T(\mathit{\text{step}}|\mathit{\text{cue}},\mathit{\text{target}})=\frac{1}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j|\mathit{\text{cue}},\mathit{\text{target}})}.$$ (4)

Evidence accumulation continues at these discrete time steps until the relative difference in evidence between the responses meets or exceeds a criterion C, at which point the response with the most evidence has been selected. The time for response selection is the product of the number of steps to finish the random walk and the time per step computed with Equation 4.

Schneider and Logan (2009) demonstrated that compound cue retrieval not only achieves accurate response selection, but also produces the response congruency effect. The model produces the effect because it assumes the evidence for each response is the sum of the evidence for the categories associated with it (Equation 3). Congruent targets provide evidence for categories associated with the same response, whereas incongruent targets provide evidence for categories associated with different responses. The summed evidence for the correct response is greater for congruent targets than for incongruent targets, leading to faster and more accurate response selection for the former compared with the latter.

Before discussing how we modified the model, a final point worth mentioning is that compound cue retrieval should not be confused with direct, nonmediated retrieval of a response using a configural representation of the cue and the target, without reference to task-related representations. The cue and the target are represented separately in the model and each retrieves evidence for associated task categories, which then determines which response is selected via the random walk. We explained compound cue retrieval in this way in previous articles (Logan & Schneider, 2010; Schneider & Logan, 2005, 2009). Thus, the model is compatible with research showing that typical task-switching performance is mediated by task-relevant categorical knowledge (e.g., Dreisbach, Goschke, & Haider, 2006, 2007).

Introducing Baseline Evidence

The preceding text described the basic model of compound cue retrieval used in previous work (Logan & Schneider, 2010; Schneider & Logan, 2005, 2009). The critical modification to the model in the present study involves abandoning the contingent encoding assumption. More specifically, the assumption is that if a stimulus has not been encoded, it provides no evidence for any category (i.e., η = 0 for that stimulus), meaning that the combined evidence computed with Equation 1 equals zero and response selection is inactive. Here, we allow for the possibility of response selection before both stimuli have been encoded by introducing baseline evidence (similar to background-noise elements; Nosofsky & Alfonso-Reese, 1999). The model is initialized with evidence that is neutral with respect to all task categories (i.e., a common, non-zero η value) and this evidence serves as a baseline for response selection prior to stimulus encoding. In other words, η > 0 instead of η = 0 for an unencoded stimulus. Baseline evidence is used from the start of a trial until a stimulus is encoded, at which point the evidence for a category changes to reflect the strength of association between the encoded stimulus and that category. Once both stimuli are encoded, baseline evidence no longer plays a role in response selection because evidence comes exclusively from the stimuli.

From a theoretical perspective, baseline evidence can be thought of as representing a “resting level” for the response selection process in the absence of stimuli. Due to noise in the cognitive system, response selection might never be completely inactive. Instead, it could proceed in a stochastic manner at a low rate, remaining undetected unless premature responses are made by chance before any stimuli have been presented. Such cognitive activity is consistent with the general knowledge that neural activity in the brain does not cease when a task is not being performed. There continues to be a modest level of activity reflecting either task-unrelated processing or simply background noise, and our conception of baseline evidence is an abstract representation of such activity at a cognitive level. From this point of view, one could argue that baseline evidence makes the model more physiologically plausible.

The introduction of baseline evidence leads to two modes of response selection in the model: a guessing mode and a progress mode. When the model is in guessing mode, it retrieves evidence for the alternative responses with equal probabilities; therefore, the model is effectively “guessing” which response to select. When the model is in progress mode, it retrieves evidence for the alternative responses with unequal probabilities; therefore, the model makes progress toward selecting the response with the higher retrieval probability. As stimuli are encoded during a trial, the model transitions from the guessing mode to the progress mode. Note that this transition reflects a quantitative change in the model’s behavior—its structure remains unchanged—and does not reflect a mixture of separate, independent processes (for other models with similar transitions, see Ratcliff, 1980; White, Ratcliff, & Starns, 2011).

To understand when and why the model is in the guessing and progress modes, we consider how the model operates in each of the six possible stimulus encoding scenarios that could occur during a trial. To facilitate this effort, we provide numerical examples in Appendix C. We also indicate when each scenario occurs during a trial in Figure 2, which illustrates how response selection changes as the cue and the target are encoded for both stimulus orders.

Figure 2.

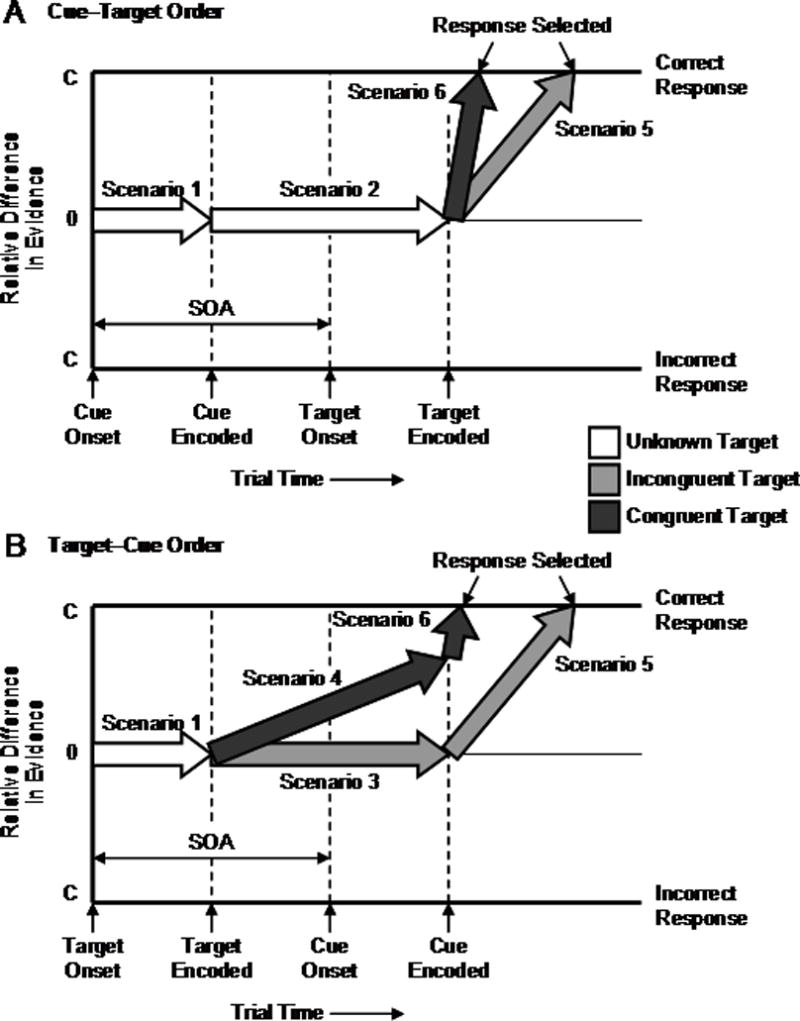
Schematic illustration of response selection in the model with baseline evidence. Block arrows are associated with scenarios that reflect modes of response selection; horizontal block arrows reflect the guessing mode and inclined block arrows reflect the progress mode. See text for further details. SOA = stimulus onset asynchrony, C = criterion for response selection.

Scenario 1: Cue unencoded, target unencoded

This scenario exists at the start of every trial (see Figure 2). Given that both stimuli are unencoded, response selection is driven by baseline evidence. Consequently, evidence is accumulated for the alternative responses with equal probabilities and the model is in guessing mode.

Scenario 2: Cue encoded, target unencoded

Once the cue is encoded, the evidence it provides for a category reflects the strength of association between the cue and that category. However, the categories that are strongly associated with the cue are mapped to different response keys. Consequently, evidence is accumulated for the alternative responses with equal probabilities and the model remains in guessing mode (see Figure 2A).

Scenario 3: Cue unencoded, incongruent target encoded

This scenario is the complement to Scenario 2. Once the target is encoded, the evidence it provides for a category reflects the strength of association between the target and that category. However, the categories that are strongly associated with the target are mapped to different response keys because the target is incongruent. Consequently, evidence is accumulated for the alternative responses with equal probabilities and the model remains in guessing mode (see Figure 2B).

Scenario 4: Cue unencoded, congruent target encoded

This scenario differs from Scenario 3 in that the categories that are strongly associated with the target are mapped to the same response key because the target is congruent. This fact makes advance response selection possible in principle; baseline evidence makes it possible in practice. Evidence is accumulated for the correct response with a higher probability than for the incorrect response, transitioning the model from guessing mode (Scenario 1) to progress mode (see Figure 2B).

Scenario 5: Cue encoded, incongruent target encoded

The cue alone (Scenario 2) or the incongruent target alone (Scenario 3) provides insufficient evidence for discriminating between the alternative responses. However, multiplication of the evidence from both stimuli provides sufficient evidence for response selection—this is the essence of compound cue retrieval. Consequently, evidence is accumulated for the correct response with a higher probability than for the incorrect response, transitioning the model from guessing mode (Scenario 2 or 3) to progress mode (see Figure 2). Baseline evidence is no longer involved in response selection at this point.

Scenario 6: Cue encoded, congruent target encoded

This scenario differs from Scenario 5 in that the congruent target alone (Scenario 4) does provide sufficient evidence for discriminating between the alternative responses. However, the cue provides additional evidence that can facilitate response selection in conjunction with the target evidence. Consequently, evidence is accumulated for the correct response with a higher probability than for the incorrect response, transitioning the model from guessing mode (Scenario 2) to progress mode in the case of cue encoding finishing before target encoding (see Figure 2A), or keeping the model in progress mode in the case of target encoding finishing before cue encoding (see Figure 2B). Baseline evidence is no longer involved in response selection at this point.²

The key to accounting for our data is Scenario 4, where baseline evidence allows progress in response selection for congruent targets prior to cue encoding (see Figure 2B). Such progress would occur with target−cue order, which provides the opportunity for advance response selection, and it would be more pronounced at longer SOAs, which provide the opportunity for response selection to finish and the response to be executed before the cue has been encoded or even presented. In principle, this means that advance response selection should result in a non-zero p(early) value for congruent targets with target−cue order at a long SOA, a decrease in RT with SOA for congruent targets with target−cue order, and the net effects of a shorter RT and a larger response congruency effect for target−cue order than for cue−target order. To determine whether this can be accomplished in practice, we simulated our modified model and fit it to our data.

Simulation Details

Individual trials representing our experimental conditions were simulated as follows. Cue and target encoding times were sampled from exponential distributions with means μ_c and μ_t, respectively. We used exponential distributions based on work showing that cue encoding time tends to be distributed exponentially (Logan & Bundesen, 2003). For simplicity, we assumed target encoding time was also distributed exponentially. Cue encoding and target encoding commenced at times dependent on the stimulus order and SOA. Both encoding processes could occur in parallel with each other and with response selection, which commenced at the start of each trial using baseline evidence, represented by η_b. Once the cue was encoded, the evidence for a category changed to reflect the association between the cue and that category, which was either strong (η_c−a) or weak (η_c−u). Once the target was encoded, the evidence for a category changed to reflect the association between the target and that category, which was either strong (η_t−a) or weak (η_t−u). Weak associations were represented by the same evidence value for the cue and the target, η_ct−u (i.e., η_c−u = η_t−u = η_ct−u).³

Evidence was used in Equations 1–4 (see Appendix C) to simulate the random-walk process for response selection. The time for response selection was added to a constant (RT_base, the time for response execution) to produce the model’s RT relative to the onset of the first stimulus. With response selection commencing at the start of each trial and occurring in parallel with stimulus encoding, any stimulus encoding time that elapsed prior to the completion of response selection was subsumed in response selection time. Given that experimental RT was defined relative to the onset of the second stimulus, we subtracted the SOA from the model’s RT.

We simulated the experimental conditions representing the factorial combination of stimulus order (cue−target order or target−cue order), response congruency (congruent or incongruent), and SOA (0, 400, or 800 ms). However, because the 0-ms SOA could not be associated with a stimulus order in Experiment 2 and the model does not predict a difference between stimulus orders at that SOA, only 10 distinct experimental conditions were simulated. We fit the model simultaneously to the RT, ER, and p(early) group data from both experiments (a total of 66 data points; 36 from Experiment 1 and 30 from Experiment 2) because of their similar data patterns. There were eight free parameters (μ_c, μ_t, RT_base, C, η_c−a, η_t−a, η_ct−u, and η_b) and the same parameter values were used for all conditions and for all dependent measures, which strongly constrains the model. Parameter optimization was done using a simplex algorithm that minimized the following composite root mean squared deviation (RMSD) between data and model predictions:

$$\mathit{RMSD}={\mathit{RMSD}}_{\mathit{RT}-\mathit{Exp}1}+{\mathit{RMSD}}_{\mathit{RT}-\mathit{Exp}2}+3\times {\mathit{RMSD}}_{\mathit{ER}-\mathit{Exp}1}+3\times {\mathit{RMSD}}_{\mathit{ER}-\mathit{Exp}2}+5\times {\mathit{RMSD}}_{\mathit{\text{p(early)}}-\mathit{Exp}1}+5\times {\mathit{RMSD}}_{\mathit{\text{p(early)}}-\mathit{Exp}2},$$ (5)

where Exp1 and Exp2 refer to Experiments 1 and 2, respectively. Model-fitting exercises indicated that Equation 5 gave relatively equal emphasis to the RMSDs for RT, ER, and p(early). Besides RMSD, we also computed the correlation (r) between data and model predictions separately for each dependent measure. After parameter optimization we obtained a final set of model predictions by simulating the model for 1,000,000 trials (1,000 virtual subjects × 10 conditions × 100 trials per condition) and computing means across virtual subjects.

Results and Discussion

Model with baseline evidence

Model RT, ER, and p(early) are presented as a function of response congruency, stimulus order, and SOA in the left panels of Figure 3. The fitted parameter values and fit indices are provided in Table 1. The model reproduced all the critical effects in the RT data (compare the top-left panel of Figure 3 with the top panels of Figure 1). There was a response congruency effect that increased substantially across SOA with target−cue order (from 158 to 326 to 566 ms) but decreased to a lesser degree across SOA with cue−target order (from 158 to 76 to 44 ms), resulting in RT being shorter for target−cue order than for cue−target order (679 vs. 934 ms, excluding the 0-ms SOA). This pattern replicates the three-way interaction among response congruency, stimulus order, and SOA that was significant in both experiments. The model produces this pattern primarily because advance response selection occurs for congruent targets with target−cue order (Scenario 4).

Figure 3.

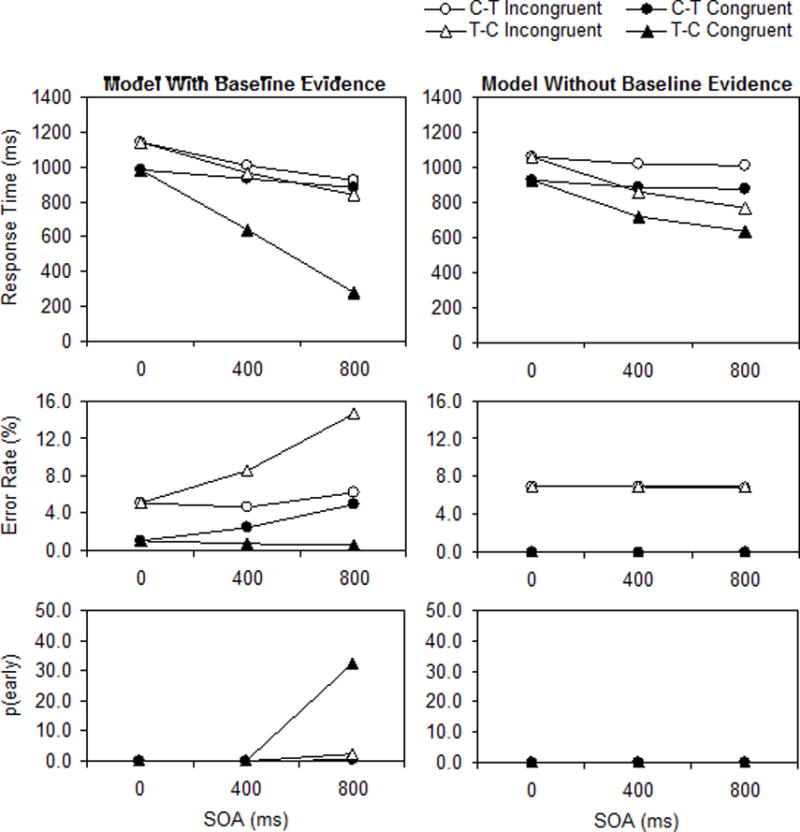
Predictions (means) of the model with and without baseline evidence (left and right panels, respectively). C−T = cue−target order, T−C = target−cue order, SOA = stimulus onset asynchrony, p(early) = percentage of early responses.

Table 1.

Fitted parameter values and fit indices for two model variants

Variable	Model with baseline evidence	Model without baseline evidence
Parameters
μc	563	173
μt	513	515
RTbase	260	265
C	9	6
ηc−a	0.194	0.183
ηt−a	0.439	0.281
ηct−u	0.010	0.081
ηb	0.047	0
Fit indices
Experiment 1
RMSDRT	53	132
rRT	.976	.913
RMSDER	2.7	0.9
rER	.757	.980
RMSDp(early)	2.3	11.6
rp(early)	1.000	undefineda
Experiment 2
RMSDRT	58	107
rRT	.972	.919
RMSDER	2.7	1.1
rER	.770	.968
RMSDp(early)	1.0	11.2
rp(early)	.999	undefineda

Note. RMSD = root-mean-squared deviation between data and model predictions; r = correlation between data and model predictions; RT = response time; ER = error rate; p(early) = percentage of early responses. See text for description of model parameters.

^aFor the model without baseline evidence, the variance of predicted p(early) equals zero; therefore, r is undefined.

The model also reproduced all the critical effects in the p(early) data (compare the bottom-left panel of Figure 3 with the bottom panels of Figure 1). There was a large p(early) value of 32.3% for congruent targets with target−cue order at an SOA of 800 ms that compares favorably with the data (40.2% and 35.3% in Experiments 1 and 2, respectively). The p(early) values were near zero for all other conditions, although the model did reproduce a small p(early) value of 2.3% for incongruent targets with target−cue order at an SOA of 800 ms that was also present in the data (2.8% and 3.6% in Experiments 1 and 2, respectively). This pattern replicates the three-way interaction among response congruency, stimulus order, and SOA that was significant in both experiments. The model produces this pattern because advance response selection occurs for congruent targets with target−cue order at an SOA of 800 ms (Scenario 4), sometimes culminating in response execution prior to cue onset. Advance response selection also occurs for incongruent targets with target−cue order at an SOA of 800 ms, but more rarely because the model is in guessing mode (Scenario 3); hence, p(early) is only slightly above zero.

The main weakness in the model fit is with respect to the ER data (compare the middle-left panel of Figure 3 with the middle panels of Figure 1). Although the model produced a response congruency effect (5.9%) that compares favorably with the data (5.5% and 6.2% in Experiments 1 and 2, respectively), it predicted increases in ER across SOA for congruent targets with cue−target order and incongruent targets with target−cue order. The increase for congruent targets with cue−target order is better understood as a decrease as SOA goes to 0 ms because at a long enough SOA, the prediction for congruent targets would converge with the prediction for incongruent targets. This is a consequence of the model being in guessing mode for a long time—given enough time, guessing can lead to response selection, but at the expense of more errors. However, as SOA goes to 0 ms, target encoding will finish sooner for congruent targets, which will facilitate response selection and reduce errors because the model will transition from guessing mode to progress mode (Scenario 4 or 6). The increase for incongruent targets with target−cue order reflects the model being in guessing mode for a long time. The increase is larger than for incongruent targets with cue−target order because although the model is in guessing mode for approximately the same time, the time per step is shorter in the case of target−cue order because the summed evidence in Equation 4 is greater (a result of η_t−a > η_c−a; see Table 1). It may be possible to limit the errors produced by the model during prolonged guessing by introducing leakage that constrains evidence accumulation (e.g., Usher & McClelland, 2001), although it is unclear how leakage would affect how the model accounts for other aspects of the data.

In summary, the model with baseline evidence fully reproduced the RT and p(early) data patterns, but it only partially reproduced the ER data pattern. There are three important considerations to keep in mind when interpreting the fit to the ER data. First, the predicted interactions were null effects in the data, and it is customary to treat null effects with caution. Second, the overall ER was quite low, which may have limited our ability to observe interactions that span the range predicted by the model. Third, the model was fit simultaneously to all three dependent measures with the same parameter values, raising the possibility that the quality of the fit to the ER data was sacrificed a bit to enable high-quality fits to the RT and p(early) data. These considerations notwithstanding, we think the simulation results are encouraging. They suggest that the introduction of baseline evidence is a useful modification to the model, allowing it to capture the RT and p(early) data patterns in a way that would not have been possible if the contingent encoding assumption had been retained. To confirm this is the case, we also simulated the model without baseline evidence.

Model without baseline evidence

According to the contingent encoding assumption, if a stimulus has not been encoded, it provides no evidence for any category (i.e., η = 0 for that stimulus). The assumption can be implemented in the model by setting η_b = 0, such that response selection is inactive until both stimuli are encoded (Scenarios 5 and 6). Consequently, response selection commences in progress mode and is never in guessing mode. This nested, seven-parameter model was fit to the data and its RT, ER, and p(early) are presented as a function of response congruency, stimulus order, and SOA in the right panels of Figure 3. The fitted parameter values and fit indices are provided in Table 1.

It is evident that the model could not reproduce the critical effects in the RT data (compare the top-right panel of Figure 3 with the top panels of Figure 1). There was a response congruency effect, but it did not vary across SOA with target−cue order (ranging from 135 to 138 to 137 ms) or with cue−target order (ranging from 135 to 130 to 133 ms). RT was shorter for target−cue order than for cue−target order (743 vs. 946 ms, excluding the 0-ms SOA), but this was due to estimation of a much longer target encoding time than cue encoding time (515 vs. 173 ms; see Table 1). Such a difference in stimulus encoding times prolongs RT more for cue−target order than for target−cue order because a longer encoding time for the second stimulus further delays the onset of response selection (recall that response selection is contingent on having both stimuli encoded in this case). This model yielded much larger RMSDs (132 and 107 ms for Experiments 1 and 2, respectively) than the model with baseline evidence (53 and 58 ms for Experiments 1 and 2, respectively). Regarding the correlation between data and model predictions, it fit worse than the model with baseline evidence, significantly for Experiment 1, F(1,4) = 10.04, p < .05, but not for Experiment 2, F(1,2) = 3.63, p = .20.

The model also failed to reproduce the critical effects in the p(early) data (compare the bottom-right panel of Figure 3 with the bottom panels of Figure 1). Not surprisingly, the model predicted a p(early) value of zero in every condition because response selection did not begin until both stimuli were encoded.

The only highlight of the model fit was that it generally reproduced the ER data pattern (compare the middle-right panel of Figure 3 with the middle panels of Figure 1). The model produced a response congruency effect (6.9%) that compares favorably with the data (5.5% and 6.2% in Experiments 1 and 2, respectively), although it is larger because the predicted ER for congruent targets was almost zero (0.1%) instead of slightly above zero (1.0% and 1.1% in Experiments 1 and 2, respectively). The model did not predict any interactions with stimulus order or SOA, allowing it to achieve smaller RMSDs and higher correlations than the model with baseline evidence (see Table 1).

In summary, the model without baseline evidence was unable to reproduce the RT and p(early) data patterns, although this inability resulted in the fitting algorithm finding parameter values that allowed the model to reproduce the ER data pattern. The model’s failures regarding RT and p(early) indicate that the contingent encoding assumption simply does not give the model the necessary flexibility in response selection to accommodate the data from our experiments. It seems clear that baseline evidence, in one form or another, is required for the model to engage in advance response selection when the opportunity arises.

General Discussion

The purpose of the present study was to evaluate the contingent encoding assumption, which is the idea that response selection in task-switching situations does not begin until the cue and the target have both been encoded. We tested the assumption by manipulating response congruency, stimulus order, and SOA in two experiments. Advance response selection is possible in principle for congruent targets with target−cue order at a long SOA, but the contingent encoding assumption does not allow it in practice. Thus, finding evidence of advance response selection would be a fatal blow to the assumption.

Both experiments revealed data patterns consistent with advance response selection. There was a response congruency effect on RT that increased substantially across SOA with target−cue order, resulting in RT being shorter for target−cue order than for cue−target order. There was also a large percentage of early responses for congruent targets with target−cue order at an SOA of 800 ms, indicating that some responses were not only selected but also executed prior to cue onset.

These findings indicate that task-switching models that include the contingent encoding assumption need to be modified. To demonstrate how this can be done, we modified Schneider and Logan’s (2005, 2009) model of compound cue retrieval by introducing baseline evidence. The model is initialized with evidence that is neutral with respect to all task categories and this evidence serves as a baseline for response selection prior to stimulus encoding. As stimuli are encoded, the evidence for a category moves away from baseline to reflect the strength of association between the stimuli and that category. Simulation of the model with baseline evidence revealed that it could reproduce the RT and p(early) data patterns, although it achieved only partial success with the ER data pattern. In contrast, simulation of a model without baseline evidence revealed that it could not reproduce the RT and p(early) data patterns, although it achieved better success with the ER data pattern. Collectively, the simulation results support abandoning the contingent encoding assumption and suggest that introducing baseline evidence is a useful way of extending compound cue retrieval.

As noted earlier, there are other models besides compound cue retrieval that include the contingent encoding assumption (e.g., Altmann & Gray, 2008; Sohn & Anderson, 2001). Whether the introduction of baseline evidence or an alternative change would enable those models to account for our data is unclear, but we think the possibility of successful modification exists. It also remains to be seen whether task-switching models that do not seem to include the contingent encoding assumption can explain our findings. For example, in Gilbert and Shallice’s (2002) model, response selection is not (necessarily) contingent on cue encoding. The model includes processing units associated with target input, response output, and task demand. Task demand units, which bias the activation of the model toward the relevant task, initially have residual, non-zero activation from the previous trial. Their activation is subsequently modulated by top-down control input once the cue has been encoded. Target input and response output units, on the other hand, initially have their activations set to zero. Target input units do not become active until the target has been encoded, at which point activation can spread from the target input units and the task demand units to the response output units. Activation cycles through the model until the response output units have selected a response. In principle, the model could begin response selection once the target has been encoded but before the cue has been encoded because the task demand units (which receive cue-related input) start with residual, non-zero activation levels. The extent to which advance response selection would occur is difficult to ascertain because the residual activation is weak and biased toward the previous task (which is no longer relevant on task-switch trials). Nevertheless, it seems possible for some progress to be made toward selecting the correct response for a congruent target prior to cue encoding.

Even if our model and others can be modified to accommodate the results of the present study, much work remains to be done in developing a more comprehensive model of response selection in task switching. For example, the explanation of the response congruency effect offered by compound cue retrieval and other models is likely incomplete because there is evidence that the effect reflects two distinct routes for mapping targets to responses: the mediated route and the nonmediated route (Kiesel et al., 2007; Meiran & Kessler, 2008; Schneider & Logan, 2009).

The mediated route involves mapping a target to task-relevant categories (e.g., categorizing boulder as nonliving and large), then mapping the categories to responses. Thus, the path from target to response is mediated by a categorical representation of the target (Schneider & Logan, 2010). The mediated route can produce a response congruency effect because the two task-relevant categories will activate the same response for a congruent target, facilitating response selection, and different responses for an incongruent target, interfering with response selection. The nonmediated route involves mapping a target directly to a response via memory retrieval (e.g., retrieving the knowledge that boulder requires a right keypress response) without the intermediate step of categorization. The nonmediated route can produce a response congruency effect because a congruent target will always retrieve the same response, facilitating response selection by bypassing time-consuming categorization, whereas an incongruent target will retrieve different responses, interfering with response selection. For both routes, a correct response can still be selected for an incongruent target (albeit more slowly than for a congruent target) by using a task cue to isolate the task-relevant category (mediated route) or response (nonmediated route).

The task-switching literature provides some support for the existence of each route. Meiran and Kessler (2008) found that the response congruency effect on RT was present for tasks that readily afforded categorization of targets but absent for tasks that did not, implicating the mediated route. As demonstrated in the present study and in previous work (Schneider & Logan, 2009), the response congruency effect can be modeled with compound cue retrieval, which is a formal implementation of the mediated route. Wendt and Kiesel (2008) found that the response congruency effect was reversed when the congruency of targets was reversed by changing the response mapping for one of the tasks, implicating the nonmediated route (see also Kiesel et al., 2007).

The preceding text suggests that both routes may be responsible for the response congruency effect, although the way in which they are related from a modeling perspective is an open question. One possibility is that they are independent and run in parallel, racing against each other to determine a response (Logan, 1988). Alternatively, they could run in parallel, but the evidence that each route provides for a response could be integrated into a common evidence accumulator. Yet another possibility is that the routes do not run in parallel, with subjects either choosing to use one route or the other (Rickard, 1997), or attempting to use one route and switching to the other if the first one fails (Anderson & Lebiere, 1998). These candidate dual-route models could be implemented and fit to appropriate data sets to see whether one approach is superior to the others. A modeling endeavor of this sort is beyond the scope of the present study, but it represents a worthwhile avenue for future research.

An important take-home message from this discussion and the present study is that cognitive modeling is an ongoing enterprise that is never finished. Every model is wrong in some respects and accounts for only certain aspects of human performance. Progress can be achieved in cognitive psychology by continually working to identify and resolve these limitations. In the present study, we identified an assumption about response selection in task switching that was evident in certain computational models but lacked empirical verification. We conducted experiments to test the assumption and found it was invalid. Instead of simply rejecting all models to which the assumption applied, we showed how one particular model could be modified to account for the challenging data, resulting in a version that is arguably better than the original. We think this process of testing and modification is a vital aspect of modeling even though it rarely occurs in the domain of task switching. It is important because it leads to cumulative model development (e.g., Anderson, 2007; Logan, 2002, 2004; Newell, 1990; Schneider & Anderson, 2011), by which new models inherit the successes of their predecessors while extending them to explain more phenomena. Cumulative model development is not an easy venture, but we think the payoff in terms of attaining a better understanding of human cognition makes it worth the effort.

Appendix A Target words used in the experiments

Target categories	Targets
living and small	ant	bacteria	beetle	flea	frog
	mosquito	mouse	rat	spider	wasp
living and large	camel	dolphin	donkey	elephant	elk
	pony	shark	tiger	wolf	zebra
nonliving and small	bead	bracelet	cigar	dime	eraser
	pebble	peg	sock	spoon	wallet
nonliving and large	asteroid	bathtub	boulder	canoe	dorm
	gym	patio	pier	sofa	tuba

Appendix B

Our primary analyses focused on the effects of response congruency, stimulus order, and SOA because they are most relevant for testing the contingent encoding assumption. For completeness, here we report the effects of task switching, but with an important caveat. Given that our data show clear evidence of advance response selection prior to cue encoding with target−cue order (see Figure 1 and main text), one can infer that subjects were sometimes performing both tasks on the target during a trial. This implies that the nominal task transition indicated by the cue did not always reflect the mental task transition of the subjects (if one occurred at all). Consequently, we recommend that any task-switching effects be interpreted with caution.

With two cues per task, there were three possible task transitions across trials (Logan & Bundesen, 2003; Mayr & Kliegl, 2003; Schneider & Logan, 2007, 2011): task switches (task and cue both switch; e.g., ORIGIN followed by SIZE), task repetitions (task repeats but cue switches; e.g., MAGNITUDE followed by SIZE), and cue repetitions (task and cue both repeat; e.g., SIZE followed by SIZE). Task transition was included as a factor in the reported ANOVAs, but it did not participate in any significant four-way interactions with the other factors, so it does not alter the data patterns reported in the main text.

RT became shorter going from task switches to task repetitions to cue repetitions in Experiment 1 (929 to 905 to 821 ms) and in Experiment 2 (835 to 819 to 797 ms). The main effect of task transition was significant in Experiment 1, F(2,46) = 33.63, MSE = 27,610, p < .001, η_p² = .59, and in Experiment 2, F(2,46) = 4.10, MSE = 16,474, p < .05, η_p² = .15. In Experiment 1, the spread among task transitions was greater with cue−target order (means of 1,034; 1,000; and 875 ms for task switches, task repetitions, and cue repetitions, respectively) than with target−cue order (means of 824, 811, and 766 ms for task switches, task repetitions, and cue repetitions, respectively), reflected by a significant interaction between task transition and stimulus order, F(2,46) = 15.16, MSE = 13,465, p < .001, η_p² = .40. However, this interaction was not significant in Experiment 2, F < 1. No other interactions involving task transition were significant for RT.

ER was higher for task switches than for task repetitions and cue repetitions, but this effect was restricted to incongruent trials. In Experiment 1, incongruent ERs were 8.2%, 5.4%, and 5.6% for task switches, task repetitions, and cue repetitions, respectively, whereas the corresponding congruent ERs were 1.1%, 1.0%, and 0.8%, respectively. In Experiment 2, incongruent ERs were 9.3%, 6.3%, and 6.8% for task switches, task repetitions, and cue repetitions, respectively, whereas the corresponding congruent ERs were 1.1%, 0.9%, and 1.3%, respectively. The interaction between task transition and response congruency was significant in Experiment 1, F(2,46) = 6.88, MSE = 23, p < .01, η_p² = .23, and in Experiment 2, F(2,46) = 4.80, MSE = 24, p < .05, η_p² = .17. The only remaining significant effect involving task transition was a three-way interaction between task transition, response congruency, and SOA in Experiment 2, F(2,46) = 4.93, MSE = 15, p < .05, η_p² = .18. However, this interaction did not conform to any interpretable pattern and it was not significant in Experiment 1, F < 1.

There were no significant effects involving task transition in the p(early) data.

Appendix C

To understand when and why the model is in the guessing and progress modes of response selection, we provide numerical examples for the six possible stimulus encoding scenarios that could occur during a trial in our experiments. For each scenario, we calculate Equations 1–3 using the following evidence values: η_b = 3, representing baseline evidence; η_c-a and η_t-a = 20, representing evidence for a category strongly associated with an encoded cue or an encoded target, respectively; and η_c-u and η_t-u = 1, representing evidence for a category weakly associated with an encoded cue or an encoded target, respectively. These evidence values were chosen for illustrative purposes only. These calculations assume that living and small are mapped to the left response key, nonliving and large are mapped to the right response key, the cue is for the living/nonliving task, the incongruent target is living and large, and the congruent target is living and small. The left response key is the correct response for all scenarios. See the main text for discussion.

Scenario 1: Cue Unencoded, Target Unencoded (Guessing Mode)

$$\begin{array}{l}\eta (\mathit{\text{living}})={\eta }_b\times {\eta }_b=3\times 3=9\hfill \\ \eta (\mathit{\text{nonliving}})={\eta }_b\times {\eta }_b=3\times 3=9\hfill \\ \eta (\mathit{\text{small}})={\eta }_b\times {\eta }_b=3\times 3=9\hfill \\ \eta (\mathit{\text{large}})={\eta }_b\times {\eta }_b=3\times 3=9\hfill \end{array}$$ Equation 1

$$\begin{array}{l}P(\mathit{\text{living}})=\frac{\eta (\mathit{\text{living}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{9}{36}=.25\hfill \\ P(\mathit{\text{nonliving}})=\frac{\eta (\mathit{\text{nonliving}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{9}{36}=.25\hfill \\ P(\mathit{\text{small}})=\frac{\eta (\mathit{\text{small}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{9}{36}=.25\hfill \\ P(\mathit{\text{large}})=\frac{\eta (\mathit{\text{large}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{9}{36}=.25\hfill \end{array}$$ Equation 2

$$\begin{array}{l}P(\mathit{\text{left}})={\displaystyle \sum }_{i\in \mathit{\text{left}}}P({\mathit{\text{category}}}_i)=.25+.25=.50\hfill \\ P(\mathit{\text{right}})={\displaystyle \sum }_{i\in \mathit{\text{right}}}P({\mathit{\text{category}}}_i)=.25+.25=.50\hfill \end{array}$$ Equation 3

Scenario 2: Cue Encoded, Target Unencoded (Guessing Mode)

$$\begin{array}{l}\eta (\mathit{\text{living}})={\eta }_{c-a}\times {\eta }_b=20\times 3=60\hfill \\ \eta (\mathit{\text{nonliving}})={\eta }_{c-a}\times {\eta }_b=20\times 3=60\hfill \\ \eta (\mathit{\text{small}})={\eta }_{c-u}\times {\eta }_b=1\times 3=3\hfill \\ \eta (\mathit{\text{large}})={\eta }_{c-u}\times {\eta }_b=1\times 3=3\hfill \end{array}$$ Equation 1

$$\begin{array}{l}P(\mathit{\text{living}})=\frac{\eta (\mathit{\text{living}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{60}{126}=.48\hfill \\ P(\mathit{\text{nonliving}})=\frac{\eta (\mathit{\text{nonliving}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{60}{126}=.48\hfill \\ P(\mathit{\text{small}})=\frac{\eta (\mathit{\text{small}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{3}{126}=.02\hfill \\ P(\mathit{\text{large}})=\frac{\eta (\mathit{\text{large}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{3}{126}=.02\hfill \end{array}$$ Equation 2

$$\begin{array}{l}P(\mathit{\text{left}})={\displaystyle \sum }_{i\in \mathit{\text{left}}}P({\mathit{\text{category}}}_i)=.48+.02=.50\hfill \\ P(\mathit{\text{right}})={\displaystyle \sum }_{i\in \mathit{\text{right}}}P({\mathit{\text{category}}}_i)=.48+.02=.50\hfill \end{array}$$ Equation 3

Scenario 3: Cue Unencoded, Incongruent Target Encoded (Guessing Mode)

$$\begin{array}{l}\eta (\mathit{\text{living}})={\eta }_b\times {\eta }_{t-a}=3\times 20=60\hfill \\ \eta (\mathit{\text{nonliving}})={\eta }_b\times {\eta }_{t-u}=3\times 1=3\hfill \\ \eta (\mathit{\text{small}})={\eta }_b\times {\eta }_{t-u}=3\times 1=3\hfill \\ \eta (\mathit{\text{large}})={\eta }_b\times {\eta }_{t-a}=3\times 20=60\hfill \end{array}$$ Equation 1

$$\begin{array}{l}P(\mathit{\text{living}})=\frac{\eta (\mathit{\text{living}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{60}{126}=.48\hfill \\ P(\mathit{\text{nonliving}})=\frac{\eta (\mathit{\text{nonliving}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{3}{126}=.02\hfill \\ P(\mathit{\text{small}})=\frac{\eta (\mathit{\text{small}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{3}{126}=.02\hfill \\ P(\mathit{\text{large}})=\frac{\eta (\mathit{\text{large}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{60}{126}=.48\hfill \end{array}$$ Equation 2

$$\begin{array}{l}P(\mathit{\text{left}})={\displaystyle \sum }_{i\in \mathit{\text{left}}}P({\mathit{\text{category}}}_i)=.48+.02=.50\hfill \\ P(\mathit{\text{right}})={\displaystyle \sum }_{i\in \mathit{\text{right}}}P({\mathit{\text{category}}}_i)=.02+.48=.50\hfill \end{array}$$ Equation 3

Scenario 4: Cue Unencoded, Congruent Target Encoded (Progress Mode)

$$\begin{array}{l}\eta (\mathit{\text{living}})={\eta }_b\times {\eta }_{t-a}=3\times 20=60\hfill \\ \eta (\mathit{\text{nonliving}})={\eta }_b\times {\eta }_{t-u}=3\times 1=3\hfill \\ \eta (\mathit{\text{small}})={\eta }_b\times {\eta }_{t-a}=3\times 20=60\hfill \\ \eta (\mathit{\text{large}})={\eta }_b\times {\eta }_{t-u}=3\times 1=3\hfill \end{array}$$ Equation 1

$$\begin{array}{l}P(\mathit{\text{living}})=\frac{\eta (\mathit{\text{living}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{60}{126}=.48\hfill \\ P(\mathit{\text{nonliving}})=\frac{\eta (\mathit{\text{nonliving}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{3}{126}=.02\hfill \\ P(\mathit{\text{small}})=\frac{\eta (\mathit{\text{small}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{60}{126}=.48\hfill \\ P(\mathit{\text{large}})=\frac{\eta (\mathit{\text{large}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{3}{126}=.02\hfill \end{array}$$ Equation 2

$$\begin{array}{l}P(\mathit{\text{left}})={\displaystyle \sum }_{i\in \mathit{\text{left}}}P({\mathit{\text{category}}}_i)=.48+.48=.96\hfill \\ P(\mathit{\text{right}})={\displaystyle \sum }_{i\in \mathit{\text{right}}}P({\mathit{\text{category}}}_i)=.02+.02=.04\hfill \end{array}$$ Equation 3

Scenario 5: Cue Encoded, Incongruent Target Encoded (Progress Mode)

$$\begin{array}{l}\eta (\mathit{\text{living}})={\eta }_{c-a}\times {\eta }_{t-a}=20\times 20=400\hfill \\ \eta (\mathit{\text{nonliving}})={\eta }_{c-a}\times {\eta }_{t-u}=20\times 1=20\hfill \\ \eta (\mathit{\text{small}})={\eta }_{c-u}\times {\eta }_{t-u}=1\times 1=1\hfill \\ \eta (\mathit{\text{large}})={\eta }_{c-u}\times {\eta }_{t-a}=1\times 20=20\hfill \end{array}$$ Equation 1

$$\begin{array}{l}P(\mathit{\text{living}})=\frac{\eta (\mathit{\text{living}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{400}{441}=.91\hfill \\ P(\mathit{\text{nonliving}})=\frac{\eta (\mathit{\text{nonliving}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{20}{441}=.045\hfill \\ P(\mathit{\text{small}})=\frac{\eta (\mathit{\text{small}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{1}{441}=.00\hfill \\ P(\mathit{\text{large}})=\frac{\eta (\mathit{\text{large}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{20}{441}=.045\hfill \end{array}$$ Equation 2

$$\begin{array}{l}P(\mathit{\text{left}})={\displaystyle \sum }_{i\in \mathit{\text{left}}}P({\mathit{\text{category}}}_i)=.91+.00=.91\hfill \\ P(\mathit{\text{right}})={\displaystyle \sum }_{i\in \mathit{\text{right}}}P({\mathit{\text{category}}}_i)=.045+.045=.09\hfill \end{array}$$ Equation 3

Scenario 6: Cue Encoded, Congruent Target Encoded (Progress Mode)

$$\begin{array}{l}\eta (\mathit{\text{living}})={\eta }_{c-a}\times {\eta }_{t-a}=20\times 20=400\hfill \\ \eta (\mathit{\text{nonliving}})={\eta }_{c-a}\times {\eta }_{t-u}=20\times 1=20\hfill \\ \eta (\mathit{\text{small}})={\eta }_{c-u}\times {\eta }_{t-a}=1\times 20=20\hfill \\ \eta (\mathit{\text{large}})={\eta }_{c-u}\times {\eta }_{t-u}=1\times 1=1\hfill \end{array}$$ Equation 1

$$\begin{array}{l}P(\mathit{\text{living}})=\frac{\eta (\mathit{\text{living}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{400}{441}=.91\hfill \\ P(\mathit{\text{nonliving}})=\frac{\eta (\mathit{\text{nonliving}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{20}{441}=.045\hfill \\ P(\mathit{\text{small}})=\frac{\eta (\mathit{\text{small}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{20}{441}=.045\hfill \\ P(\mathit{\text{large}})=\frac{\eta (\mathit{\text{large}})}{{\displaystyle \sum }_{j\in R}\eta ({\mathit{\text{category}}}_j)}=\frac{1}{441}=.00\hfill \end{array}$$ Equation 2

$$\begin{array}{l}P(\mathit{\text{left}})={\displaystyle \sum }_{i\in \mathit{\text{left}}}P({\mathit{\text{category}}}_i)=.91+.045=.955\hfill \\ P(\mathit{\text{right}})={\displaystyle \sum }_{i\in \mathit{\text{right}}}P({\mathit{\text{category}}}_i)=.045+.00=.045\hfill \end{array}$$ Equation 3